Ross McKitrick

1999 veröffentlichten Myles Allen und Simon Tett einen Artikel in der in der Zeitschrift Climate Dynamics (im Folgenden als „AT99“ bezeichnet), in dem sie ein Verfahren – den optimalen Fingerabdruck – beschrieben, um beobachtete Klimaveränderungen den zugrunde liegenden Ursachen zuzuordnen, mit besonderem Augenmerk auf den durch Treibhausgase verursachten Antrieb. Sie schlugen auch eine Methode vor, die als Residualkonsistenztest (RC) bezeichnet wird, um festzustellen, ob das statistische Modell gültig ist.

Das Optimal Fingerprinting, das manchmal auch als Optimal Detection bezeichnet wird, wurde sofort angenommen und vom IPCC in seinem Dritten Bewertungsbericht (TAR) von 2012 und wird seitdem in jedem IPCC-Bewertungsbericht erwähnt. TAR Anhang 12.1 trug die Überschrift „Optimale Erkennung ist Regression“ und begann:

Die Nachweismethode, die in den meisten Erkennungsstudien zum „optimalen Nachweis“ verwendet wurde, hat mehrere gleichwertige Darstellungen. Kürzlich wurde erkannt, dass es sich als ein multiples Regressionsproblem in Bezug auf verallgemeinerte kleinste Quadrate dargestellt werden kann (Allen und Tett, 1999; siehe auch Hasselmann, 1993, 1997.

2014 wies eine Gruppe von Autoren unter der Leitung von Jara Imbers, zu der auch Myles Allen als Koautor gehörte, auf die Auswirkungen hin, welche das statistische Verfahren in den vergangenen Jahren gehabt hatte:

Die Aussage des Zwischenstaatlichen Ausschusses für Klimaänderungen (IPCC), dass es ’sehr wahrscheinlich‘ sei, dass anthropogene Emissionen das Klima beeinflussen, basiert auf einer statistischen Nachweis- und Zuordnungsmethode, die stark von der Charakterisierung der internen Klimavariabilität abhängt, wie sie von [Klimamodellen] simuliert wird .³

Die Förderung und das Vertrauen des IPCC in das Optimum Fingerprinting hält bis heute an.4 Sie wurde in Dutzenden und möglicherweise Hunderten von Studien im Laufe der Jahre verwendet. wo auch immer man in der Fachliteratur beginnt, alle Wege führen zurück zu Allen und Tett (oft über das Folgepapier Allen und Stott 2003). Außerdem stützt sich die Literatur fast ausschließlich auf den RC-Test zur Überprüfung der Gültigkeit der Ergebnisse. Also spielen die Fehler und Unzulänglichkeiten des Papiers auch zwei Jahrzehnte später noch eine akute Rolle.

Ich habe einen Artikel in Climate Dynamics veröffentlicht, der zeigt, dass das optimale Fingerprinting-Verfahren, wie es in AT99 und dem Nachfolgepapier angewendet worden war, theoretisch fehlerhaft ist und sinnlose Ergebnisse liefert.6 Es beweist nicht, dass alle Ergebnisse dieser Methode falsch sind, aber es zeigt, dass die Grundlage, auf der sie für richtig gehalten wurden, nicht vorhanden ist.

Über die Logik und die Implikationen meiner Ergebnisse

Eine sorgfältige Erklärung der Auswirkungen meiner Feststellung muss ein elementares Prinzip der Logik beachten. Wir können ohne Angst vor Widersprüchen sagen:

Angenommen, A impliziert B. Wenn A wahr ist, ist auch B wahr.

Ein Beispiel: Alle Hunde haben ein Fell. Ein Beagle ist ein Hund, also hat ein Beagle hat ein Fell. Wir können dies jedoch nicht sagen:

Angenommen, A impliziert B. A ist nicht wahr, also ist B nicht wahr.

Beispiel: Alle Hunde haben ein Fell; eine Katze ist kein Hund, also hat eine Katze kein Fell. Aber natürlich können wir auch sagen:

Angenommen, A impliziert B; A ist nicht wahr, also wissen wir nicht, ob B wahr ist.

Beispiel: Alle Hunde haben ein Fell. Ein Delphin ist kein Hund, also wissen wir wissen wir nicht, ob ein Delfin ein Fell hat.

Betrachtet man die Auswirkungen meiner Ergebnisse, so ist „A“ das mathematische Argument, das Allen und Tett anführten, um ‚B‘ zu beweisen, nämlich die Behauptung, dass ihr Modell unvoreingenommene und genaue Ergebnisse liefert. In meiner Kritik habe ich gezeigt, dass ‚A‘, ihr mathematisches Argument, falsch ist. Wir haben also keine Grundlage, um etwas über „B“ zu sagen, und schon gar nicht, dass ihr Modell unvoreingenommene und genaue Ergebnisse liefert. Die Kritik trifft auch auf den RC-Test zu: Er liefert nichtssagende Antworten. In meinem Artikel führe ich die Bedingungen auf, die nachgewiesen werden müssen, um die Behauptungen über ihre Methode zu bestätigen. Ich glaube nicht, dass dies möglich ist, aus Gründen, die in dem Papier genannt werden, aber ich lasse die Möglichkeit offen. In Ermangelung eines solchen Beweises lassen die Ergebnisse ihres Verfahrens über die letzten 20 Jahren keine Aussagen über den Einfluss von Treibhausgasen auf das Klima machen. Hier werde ich versuchen, die wichtigsten Elemente des statistischen Arguments zu erläutern.

Regression

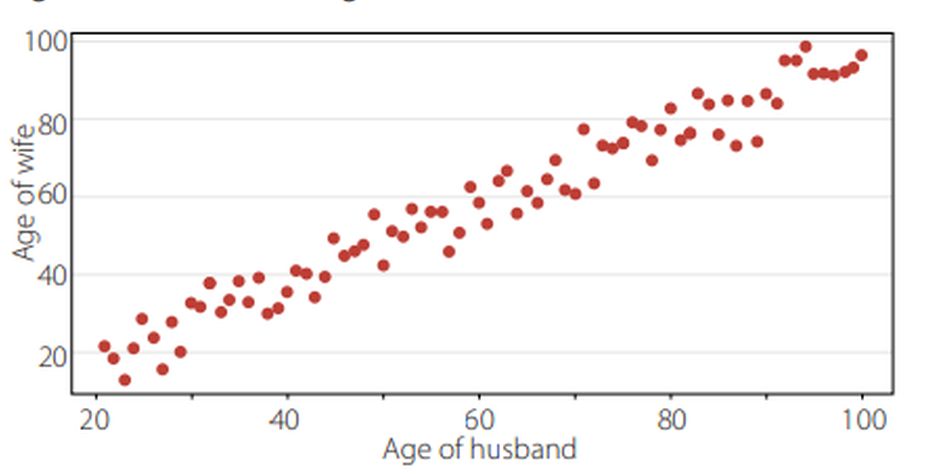
Die meisten Menschen mit einem gewissen Maß an wissenschaftlicher Bildung sind mit dem Gedanken vertraut, eine Linie der besten Anpassung durch eine Daten-Punktwolke zu ziehen. Dies wird als lineare Regression bezeichnet. Betrachten Sie Abbildung 1. Sie zeigt für eine Stichprobe von Ehepaaren das Alter der Ehefrau im Vergleich zum Alter des Ehemannes:

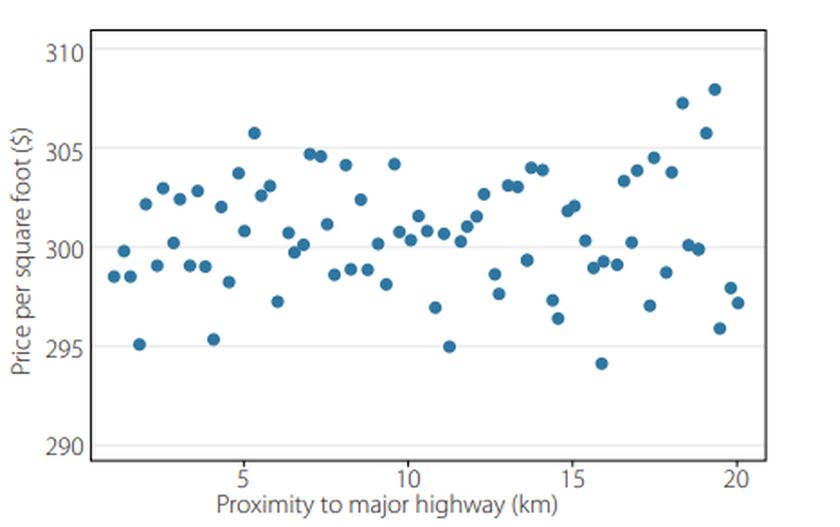
Abbildung 1: Ehepaare: Altersvergleich von Ehefrauen und Ehemännern

Es besteht ein eindeutiger Zusammenhang zwischen beiden: Ältere Männer haben ältere Ehefrauen und umgekehrt. Sie können sich leicht vorstellen, eine gerade Linie der durch die Punkte zeichnen. Es ist üblich, die horizontale Achse als x-Achse und die vertikale Achse als y-Achse zu bezeichnen. Die Linie kann mit zwei Zahlen definiert werden: der Steigung und dem Achsenabschnitt auf der y-Achse. Wenn die Steigung positiv ist, sind höhere Werte auf der Werte auf der x-Achse auch mit höheren Werten auf der y-Achse verbunden. Dies ist im obigen Beispiel eindeutig der Fall; jede vernünftige Linie durch die Stichprobe würde sich nach oben neigen. Aber in anderen Fällen ist es nicht so offensichtlich. Abbildung 2 zeigt zum Beispiel den Wert von Immobilien im Verhältnis zu ihrer Nähe zu einer Hauptverkehrsstraße:

Abbildung 2: Vergleich von Immobilienpreisen relativ zur Nähe einer Autobahn

Hier kann eine Linie der besten Anpassung nahezu horizontal verlaufen, aber auch ansteigend sein. Um zu veranschaulichen, warum die statistische Theorie für die Interpretation der Regressionsanalyse wichtig ist, sollte man sich eher Abbildung 2 als Abbildung 1 vor Augen halten. Wir haben selten Daten, bei denen die Beziehung so offensichtlich ist wie im Beispiel des Ehepaares. Viel häufiger versuchen wir, subtile Muster aus viel mehr streuenden Daten herauszufinden.

Es kann besonders schwierig sein, zu erkennen, ob Steigungslinien positiv sind, wenn wir in mehreren Dimensionen arbeiten. In Abbildung 2 gibt es viele andere Variablen als die Nähe zu einer Autobahn, die die für Schwankungen bei den Immobilienwerten verantwortlich sein könnten. Wenn, sagen wir, es drei mögliche Einflussfaktoren für den Wert von Einzelhandelsimmobilien gibt, müssen wir schätzen.

Beachten Sie, dass Regressionsmodelle eine Korrelation herstellen können, aber Korrelation ist keine Kausalität. Ältere Männer verursachen nicht, dass ihre Frauen älter sind; es ist nur so, dass Menschen, die heiraten, dazu neigen, jemanden aus der gleichen Altersgruppe zu wählen. Wenn wir feststellen, dass weiter von Autobahnen entfernt liegende Grundstücke wertvoller sind, könnte das bedeuten, dass die Entfernung zu einer Autobahn den Immobilienwert beeinflusst, oder es könnte bedeuten, dass Autobahnen tendenziell auf Land gebaut werden, das aus anderen Gründen weniger wertvoll war. Regressionsmodelle können die Interpretation der Kausalität unterstützen, wenn es andere Gründe für einen solchen Zusammenhang gibt, aber man muss hierbei sehr vorsichtig vorgehen und kann erst nach einer strengen Prüfung beurteilen, ob das Modell wichtige erklärende Variablen ausgelassen hat.

Stichproben und Varianz

Unabhängig davon, wie wir den Steigungsparameter (oder die Parameter) schätzen, brauchen wir eine Möglichkeit zu testen, ob er definitiv positiv ist ist oder nicht. Das erfordert ein wenig mehr Theorie. Abbildung 1 war eine Darstellung einer Stichprobe von Daten. Es handelt sich eindeutig nicht um die gesamte Sammlung von Ehemännern und Ehefrauen auf der Welt. Eine Stichprobe ist eine Teilmenge einer Grundgesamtheit. Wenn wir eine statistische Analyse durchführen, müssen wir die Tatsache berücksichtigen, dass wir mit einer Stichprobe arbeiten und nicht mit der gesamten Grundgesamtheit. (Grundsätzlich gilt: Je größer die Stichprobe, desto repräsentativer ist sie für die Gesamtbevölkerung.)

Die Linie der besten Anpassung durch die Stichprobe kann immer nur eine Schätzung des wahren Wertes der Steigung liefern, und da es sich um eine Schätzung handelt, können wir nur von einem Bereich möglicher Werte sprechen. Die Regression ergibt also eine Verteilung möglicher Schätzungen, von denen einige wahrscheinlicher sind als andere. Wenn Sie eine Linie durch die Daten mit einem einfachen Programm wie Excel an die Daten anpasst, gibt es vielleicht nur den zentralen Schätzung, aber die zugrunde liegende Theorie liefert eine Verteilung von möglichen Werten.

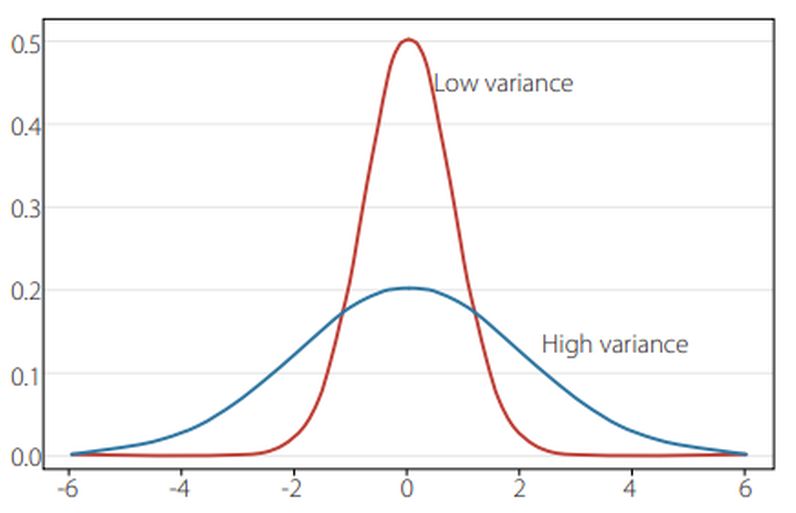
Die meisten Menschen sind mit dem Gedanken einer Daten zusammen fassenden „Glockenkurve“ vertraut. Ein Beispiel wäre die Verteilung der Zensuren in einer Klasse, bei der viele Werte um den Mittelwert gruppiert sind, aber immer weniger werden, je weiter man sich vom Mittelwert entfernt. Die Streuung einer Verteilung wird durch eine Zahl zusammengefasst der sogenannten Varianz. Ist die Varianz niedrig, ist die Verteilung eng, ist sie hoch, ist sie breit (Abbildung 3).

Die Regressionsanalyse liefert also neben der Schätzung der Steigung auch einen Schätzwert für die Varianz. Ein eng verwandtes Konzept ist die Standardabweichung der Steigung – wiederum ein Maß dafür, wie wie eng die Punkte in der Stichprobe um die gerade Linie streuen, die wir an sie angepasst haben.7 Die statistische Theorie sagt uns, dass solange das Regressionsmodell eine Reihe von Bedingungen erfüllt, mit 95-prozentiger Wahrscheinlichkeit den wahre Wert der Steigung (der den man erhalten würde, wenn man eine Stichprobe der gesamten Population nehmen könnte) innerhalb von etwa plus/minus zwei Standardabweichungen der Schätzung der Steigung erhält. Dies wird als 95%-Konfidenzintervall Intervall bezeichnet.

Abbildung 3: Varianz

Wir können also Regressionsverfahren anwenden, um eine Linie durch eine Stichprobe von Daten – z. B. Häufigkeit von Hurrikanen und Temperatur – zu ziehen, und wenn die geschätzte Steigung mehr als zwei Standardabweichungen über Null liegt, können wir sagen, dass wir „zuversichtlich“ sind, dass ein Anstieg der Temperatur zu einer Zunahme der Hurrikane führt. Wenn dies nicht der Fall ist, sagen wir dass die Beziehung positiv, aber statistisch nicht signifikant ist.

Bias, Effizienz und Konsistenz

Die Steigungsschätzung wird mit Hilfe einer Formel ermittelt, in welche die Anzahl der Stichprobendaten eingeht und die eine Zahl erzeugt. Es gibt viele Formeln die verwendet werden können. Die gängigste Formel ist die Ordinary Least Quadrate (OLS).8 OLS liefert auch einen Schätzwert für die Varianzen eines jeden Koeffizienten.

Es ist möglich, die Verteilung der Steigungsschätzungen mit Hilfe eines nach der Wahrscheinlichkeit gewichteten Durchschnitts auf einen einzigen Wert herunterzubrechen. In der Statistik wird dies als Erwartungswert bezeichnet. Mit Hilfe der statistischen Theorie lässt sich zeigen, dass, solange das Regressionsmodell eine Reihe von Bedingungen erfüllt, der Erwartungswert gleich dem Wert für die Grundgesamtheit ist. In diesem Falle sagen wir, dass der Schätzer unvoreingenommen ist. Wenn die oben genannte Gruppe von Bedingungen erfüllt ist, ist auch die Varianzschätzung unverzerrt.

Da es neben der OLS-Schätzung viele weitere mögliche Schätzformeln gibt, müssen wir uns überlegen, warum wir OLS den anderen Formeln vorziehen. Ein Grund ist, dass OLS unter allen Optionen, die zu unverzerrten Schätzungen führen, die geringste Varianz aufweist.9 Sie nutzt also die verfügbaren Daten am besten aus und liefert das kleinste 95%ige Konfidenzintervall. Wir nennen dies Effizienz.

Einige Formeln (oder „Schätzer“) liefern uns geschätzte Steigungs-Koeffizienten oder Varianzen, die bei einem kleinen Stichprobenumfang verzerrt sind, aber mit zunehmendem Stichprobenumfang verschwinden. Die Verzerrung und die Varianz gehen dann gegen Null, so dass die Verteilung auf den wahren Wert kollabiert. Dies wird als Konsistenz bezeichnet. Ein inkonsistenter Schätzer hat die unerwünschte Eigenschaft, dass wenn wir immer mehr Daten erhalten, wir keine Sicherheit haben, dass unsere Koeffizienten der Schätzungen näher an die Wahrheit herankommen. Bei inkonsistenten Schätzern kann die Varianz mit zunehmendem Stichprobenumfang schrumpfen, aber die Verzerrung erreicht nie Null, was bedeutet, dass die Schätzung nicht zum wahren Wert konvergiert.

Wann sind Schätzungen zuverlässig?

Ich habe mehrfach auf „eine Reihe von Bedingungen“ hingewiesen, die ein Regressionsmodell erfüllen muss, damit OLS unvoreingenommene, effiziente und konsistente Schätzungen liefert. Diese Bedingungen sind in jedem einführenden Ökonometrie-Lehrbuch aufgelistet und werden als Gauß-Markov-Bedingungen (GM) bezeichnet. Ein Großteil des Bereichs der Ökonometrie (dem Zweig der Statistik, der versucht, Regressionsanalyse zur Erstellung von Wirtschaftsmodellen zu nutzen) ist auf das Aufspüren von Fehlern in den GM-Bedingungen konzentriert und daruf, wenn diese gefunden werden, Abhilfemaßnahmen vorzuschlagen.

Einige Ausfälle der GM-Bedingungen implizieren nur, dass die Varianz-Schätzungen verzerrt sind; die Steigungsschätzungen bleiben unverzerrt. Mit anderen Worten, wir erhalten eine sinnvolle Schätzung des Steigungsparameters, aber unser Urteil darüber, ob er signifikant ist oder nicht, ist unzuverlässig. Andere Ausfälle der GM-Bedingungen bedeuten, dass die Schätzungen sowohl der Steigung als auch der Varianz verzerrt sind. In diesem Fall kann die Analyse verfälscht und völlig bedeutungslos sein.

Ein Beispiel für ein schlechtes Forschungsdesign: Angenommen, wir haben Daten aus Hunderten von US-Städten über viele Jahre, die sowohl die die jährliche Zahl der Straftaten in der Stadt und die Zahl der Polizeibeamten auf den Straßen zeigen. Wir können eine Linie durch die Daten ziehen, um um zu prüfen, ob die Kriminalität zurückgeht, wenn mehr Polizisten eingesetzt werden. Es gibt jedoch mehrere Probleme, die wahrscheinlich zum Scheitern von mehreren GM-Bedingungen führen würden. Erstens besteht die Stichprobe aus Klein- und Großstädten zusammen, und wir können sehr unterschiedliche Kriminalitätsstatistiken in größeren und kleineren Städten erwarten. Wenn wir das nicht berücksichtigen, erhalten wir verzerrte Schätzungen der Varianzen der Steigungskoeffizienten.

Zweitens gibt es Verzögerungseffekte: Eine Veränderung der Zahl der Polizeibeamten kann erst nach einer gewissen Zeit zu einer Veränderung der Kriminalität führen. Auch dies kann die Steigungskoeffizienten und Varianzschätzungen verzerren. Drittens kann die Kriminalität zwar von der Zahl der Polizeibeamten abhängen, die Zahl der Polizeibeamten kann aber auch von der Höhe der Kriminalität abhängen, so dass beide Variablen durch die jeweils andere Variable bestimmt werden: eine ist nicht eindeutig außerhalb des Modells bestimmt. Dies kann die Koeffizienten stark verzerren und zu falsche Schlussfolgerungen führen (z. B. dass mehr Polizeiarbeit zu einer höheren Kriminalitätsrate führt).

Schließlich hängen sowohl Kriminalität als auch Polizeiarbeit von Faktoren ab, die nicht im Modell enthalten sind, und wenn diese externen Faktoren nicht mit dem Ausmaß der Polizeiarbeit korreliert sind, werden die Steigungs- und Varianzschätzungen verzerrt sein.

Daher ist es von entscheidender Bedeutung, ein Versagen der GM-Bedingungen zu testen. In der Ökonometrie gibt es eine umfangreiche Literatur zu diesem Thema, das Spezifikationstest genannt wird. Studenten, die Regressionsanalyse lernen, lernen Spezifikationstests von Anfang an. Wenn ein Regressionsmodell für die Wirtschaftsforschung verwendet wird, würden die Ergebnisse niemals für bare Münze genommen werden, ohne dass zumindest einige elementare Spezifikationstests angegeben werden.

Bei einigen Verstößen gegen die GM-Bedingungen besteht die Abhilfe in einer Transformation der Daten vor der Anwendung von OLS. Ein Beispiel wäre die Umwandlung aller Daten in Pro-Kopf-Werte. Wenn wir eine Datentransformation anwenden, um einen Verstoß gegen eine oder mehrere GM-Bedingungen zu beheben, sprechen wir von der Anwendung der Generalized Least Squares (GLS). Die Anwendung einer GLS-Transformation bedeutet nicht, dass wir davon ausgehen können, dass die GM-Bedingungen automatisch gelten; sie müssen immer noch getestet werden. In manchen Fällen reicht eine GLS-Transformation nicht aus, und weitere Änderungen am Modell sind erforderlich, um unverzerrte und konsistente Schätzungen zu erhalten.

Das Verfahren von Allen und Tett

Verschiedene Autoren hatten vor AT99 vorgeschlagen, beobachtete Klimamesswerte – z. B. Veränderungen der Temperatur, der Hurrikanhäufigkeit oder des Auftretens von Hitzewellen – mit Klima-Simulationen mit und ohne Treibhausgase zu vergleichen. Wenn die Einbeziehung von Treibhausgasen zu einer deutlich besseren Übereinstimmung mit den Beobachtungen führt, könnten die Wissenschaftler die menschlichen Emissionen als Ursache verantwortlich machen. Diese Verfahren wird als „Fingerprinting“ bezeichnet.

Diese Autoren hatten auch argumentiert, dass die Analyse durch eine Anpassung der Daten an die lokalen Klimaschwankungen gestützt werden muss, indem Gebiete mit einem von Natur aus stabileren Klima stärker gewichtet werden und Gebiete, in denen das Klima „unruhiger“ ist, weniger stark. Die erforderlichen Gewichtungen werden anhand der so genannten „Klima-Rausch-Kovarianz-Matrix“ berechnet, die die Variabilität des Klimas an jedem Ort misst und für jedes Paar von Orten angibt, wie ihre Klimabedingungen miteinander korrelieren. Die damit verbundene Mathematik würde den Rahmen dieser Abhandlung sprengen, aber für das Verständnis der Kernfragen ist es einfach notwendig zu verstehen, dass einer der erforderlichen Schritte darin besteht, die Inverse der Matrix zu berechnen.

Dies erwies sich jedoch in der Praxis als schwierig. Anstatt die Matrix anhand von Beobachtungsdaten zu berechnen, haben Klimatologen lange Zeit lieber Klimamodelle bevorzugt. Es gab zwar Gründe für diese Entscheidung, führte jedoch zu vielen Problemen (die ich in meinem Beitrag erörtere). Eines davon war, dass die Klimamodelle keine ausreichende Auflösung haben, um alle Elemente der Matrix unabhängig voneinander zu identifizieren. Dies bedeutete, dass die Matrix keine Inverse hatte.11 Daher waren die Wissenschaftler gezwungen, eine Annäherung zu verwenden, die als „Pseudo-Inverse“ bezeichnet wird, um die benötigten Gewichte zu berechnen. Dies führte zu weiteren Problemen.

Der Fehler

Die Argumentation von Allen und Tett lautete in etwa so: Sie stellten fest, dass die Anwendung eines Gewichtungsschemas das Fingerprinting Modell mit einer GLS-Regression vergleichbar macht. Und da ein richtig spezifiziertes GLS-Modell die GM-Bedingungen erfüllt, liefert ihre Methode unvoreingenommene und effiziente Ergebnisse. Das ist eine leichte Vereinfachung ihrer Argumentation, aber nicht viel. Und der Hauptfehler ist offensichtlich. Man kann nicht wissen, ob ein Modell die GM-Bedingungen erfüllt – es sei denn, man testet auf spezifische Verstöße. AT99 hat die GM-Bedingungen falsch formuliert, eine wichtige Bedingung ganz weggelassen und es versäumt, irgendwelche Tests für Verletzungen vorzuschlagen.

In der Tat haben sie die ganze Idee der Spezifikationsprüfung entgleisen lassen, indem sie argumentierten, dass sie nur testen müssten, ob die Rauschkovarianzschätzungen des Klimamodells „zuverlässig“ seien (ihr Begriff, den sie nicht definierten), und sie schlugen etwas vor, das sie die Residual Consistency (RC) nannten. Sie boten keinen Beweis dafür, dass der RC-Test das tut, was er angeblich tut.12 Tatsächlich lieferten sie nicht einmal eine mathematische Aussage darüber, was er testet; sie sagten nur, dass wenn die von ihnen vorgeschlagene Formel eine kleine Zahl ergibt, die Regression des Fingerabdrucks gültig ist. In meiner Studie habe ich erklärt, dass es leicht Fälle geben kann, in denen der RC-Test eine kleine Zahl ergeben würde, selbst bei Modellen, die bekanntermaßen als falsch spezifiziert und unzuverlässig gelten.

Zusammenfassend lässt sich also sagen, dass Allen und Tett mit ihrem Verfahren nicht sicherstellen konnten, dass die GM-Bedingungen erfüllt waren, und konnten daher nicht beurteilen, ob ihre Schätzungen zuverlässig waren. Wie ich in meinem Papier dargelegt habe, versagt die Methode von Allen und Tett, wie sie in ihrem Papier dargelegt ist, automatisch bei mindestens einer GM-Bedingung, wahrscheinlich sogar mehreren. Daher müssen die Ergebnisse als unzuverlässig angesehen werden.

In den Jahren seit der Veröffentlichung des Papiers sind jedoch niemandem die Fehler in der AT99-Diskussion über die GM-Bedingungen aufgefallen, niemand bemerkte das Fehlen einer Ableitung des RC-Tests, und keine der nachfolgenden Anwendungen der AT99-Methode wurde einer konventionellen Spezifikationsprüfung unterzogen. Das heißt, wir haben keine Grundlage für die Akzeptanz von Behauptungen, die sich auf das optimale Fingerprinting-Verfahren stützen.

Nebenbei: die leichte Modifikation

Der optimale Fingerabdruck-Ansatz von Allen und Tett wird mit nur einer geringfügigen Änderung seit 20 Jahren von den Klimawissenschaftlern verwendet.

Die leichte Änderung erfolgte 2003, als Myles Allen und ein anderer Koautor, Peter Stott, vorschlugen, von GLS auf einen anderen Schätzer mit der Bezeichnung Total Least Squares (TLS) überzugehen.13 Dabei wird die Klimavariabilität nach wie vor gewichtet, aber die Steigungskoeffizienten werden mit einer anderen Formel geschätzt. Die Begründung dafür war, dass die vom Klimamodell generierten Variablen in der Fingerprinting-Regression selbst ziemlich „verrauscht“ sind, was dazu führen kann, dass GLS Koeffizientenschätzungen liefert, die nach unten verzerrt sind. Das ist richtig, aber Ökonometriker gehen mit diesem Problem mit einer Technik namens Instrumentalvariablen (IV) an. Wir verwenden TLS nicht (in der Tat verwendet es fast niemand außerhalb der Klimatologie), weil TLS unter anderem dann, wenn das Regressionsmodell falsch spezifiziert ist, eine Überkorrektur vornimmt und den Ergebnissen eine Verzerrung nach oben verleiht. Außerdem ist sie im Vergleich zur OLS extrem ineffizient. IV-Modelle können konsistent und unverzerrt sein. TLS-Modelle können das nicht, es sei denn, der Forscher macht einige restriktive Annahmen über die Varianzen im Datensatz, die selbst nicht getestet werden können; mit anderen Worten es sei denn, der Modellierer ’nimmt das Problem weg‘. Ich werde dies in einer nachfolgenden Studie behandeln.

Implikationen und die nächsten Schritte

Optimales Fingerprinting erfüllt nicht die GM-Bedingungen. Allen und Tett behaupteten fälschlicherweise das Gegenteil, und spätere Autoren zitierten und beriefen sich auf diese Behauptung. Das Verfahren (einschließlich der TLS-Variante) liefert Ergebnisse, die zufällig richtig sein könnten, aber im Allgemeinen verzerrt und inkonsistent sind und daher nicht als zuverlässig angesehen werden können. Nichts in der Methode selbst (einschließlich der Verwendung des RC-Tests) erlaubt es den Wissenschaftlern, mehr als das zu behaupten.

Neben der Untersuchung der Verzerrungen, die durch die Verwendung von TLS in Fingerprinting-Regressionen eingeführt werden, untersuche ich die Auswirkungen der Anwendung grundlegender Spezifikationstests auf Fingerprinting-Regressionen und die Behebung der daraus resultierenden Fehler.

Soweit dieser Beitrag. Es folgt noch eine längere Erwiderung auf Kommentare dazu sowie eine Liste von Referenzen.

Das vollständige PDF ist hier:

Übersetzt von Christian Freuer für das EIKE

Zusammenfassung aus dem Vortrag von R.McKittrick auf der 14.Climate Conference des Heartland Institutes

—————————————-

Es folgt noch ein Kommentar hierzu von der EIKE-Redaktion (Michael Limburg):

Was Ross herausgefunden hat, ist für mich und viele andere, die mit den Grenzen der Statistik einigermaßen vertraut sind, wirklich keine Überraschung. Aber es ist sehr gut erklärt für alle, die 1. wirklich gläubig sind und 2. sich für die Grenzen dieser Methoden interessieren, aber nicht in der Lage sind, die Methode so klar zu entwickeln wie Ross es tut. So z.B. für mich.
Aber es gibt noch einen weiteren Aspekt, den Ross (zumindest habe ich ihn noch nicht gesehen) in seiner Kritik völlig ausklammert. Nämlich, dass die „Fingerabdruck“-Methode selbst unecht ist. (in einem Sinne von „unberechtig“). Das liegt daran, dass sie als Grundlage annimmt, dass CO2 einen zurechenbaren Einfluss auf die Lufttemperatur hat. (Diese Temperatur selbst ist ein unwissenschaftlicher Begriff, sobald man sich mit „Mitteltemperatur“ beschäftigt. Eine Temperatur braucht in der Physik immer einen Ort und ein Medium, wo sie gemessen wird, um überhaupt ein gültiger Begriff zu sein). Die Modellierer sind also gezwungen, diese Abhängigkeit in ihre Modelle einzubauen. Sonst kann der Computer nicht rechnen. Also ist alles, was die Modelle zeigen, das was die Programmierer ihnen vorher gesagt haben. Das ist in meinem Verständnis ein Zirkelschluss, aber keineswegs ein Beweis. Noch schlimmer ist, dass sie alle natürlichen Kräfte, insbesondere die der Sonne, außen vor lassen.

image_pdfBeitrag als PDF speichernimage_printBeitrag drucken