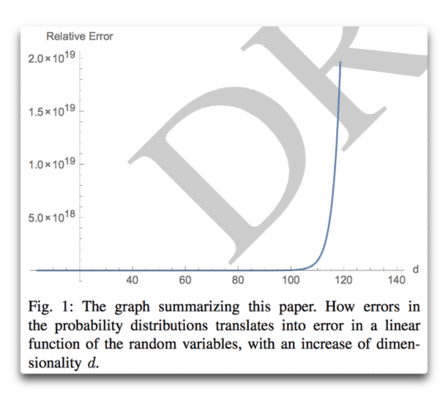
Abstract: Dem allgemeinen Gefühl zufolge hat das Hinzufügen von kleinen Variablen mit begrenzter Varianz eine lineare, sublineare oder asymptotische Auswirkung auf die Gesamtheit, und zwar von der Additivität der Varianz, was zu einer Konvergenz von Mittelwerten führt. Allerdings werden dabei nicht die meisten winzigen Modellfehler oder Ungenauigkeiten bei der Messung der Wahrscheinlichkeit berücksichtigt. Wir zeigen, wie das Hinzufügen von Zufallsvariablen aus irgendeiner Verteilung dazu führt, dass der Gesamtfehler (von der initialen Messung der Wahrscheinlichkeit) divergiert; er wächst auf konvexe Art. Es gibt einen Punkt, an dem das Hinzufügen einer einzigen Variablen den Gesamtfehler verdoppelt. Wir zeigen den Effekt bei der Wahrscheinlichkeit (via copulas [?]) und payoff space (via Sums of r. v.)
Höherdimensionale Systeme werden eventuell total unvorhersagbar beim Auftreten des geringsten Fehlers bei den Messungen, unabhängig von der Wahrscheinlichkeits-Verteilung der individuellen Komponenten.
Die hier gezeigten Ergebnisse sind frei von Verteilung und gelten für jedwede kontinuierliche Wahrscheinlichkeits-Verteilung mit Unterstützung in R.
Und schließlich bieten wir einen Rahmen an, um den Ausgleich zwischen hinzugefügter Dimension und Fehler zu kalibrieren (oder abzuschätzen, welche Reduktion des Fehlers auf dem Niveau der Wahrscheinlichkeit notwendig ist für hinzugefügte Dimensionen).
Mann! All das Gerede über Alarmismus, das ist furchterregendes Zeug. Hier folgt ein Zitat:
Tatsächlich sind Fehler so konvex, dass der Beitrag einer einzigen zusätzlichen Variablen den Gesamtfehler größer machen kann als diejenige zuvor. Die n-te Variable bringt mehr Fehler ein als zuvor die n-1 Variablen!
Dieser Punkt ist von einiger Bedeutung für die „Vorhersage“ in komplexen Gebieten wie Ökologie oder in irgendwelchen höherdimensionalen Problemen (Ökonomie). Aber es konterkariert die Vorhersagbarkeit in Domänen, die als „klassisch“ angesehen werden und nicht als komplex bei einer Vergrößerung des Raumes der Variablen.
Man lese die Studie. Selbst ohne Verständnis der darin enthaltenen Mathematik sind die Schlussfolgerungen verstörend.
Link: http://wattsupwiththat.com/2015/07/11/nassim-taleb-strikes-again/
Anthony Watts führt diesen Beitrag von Willis Eschenbach noch weiter umfassend aus:
,Robuste‘ Analyse ist nicht das, was es sein sollte: die besten 10 Wege, die Wissenschaft vor ihrem statistischen Selbst zu retten
Als Folge der jüngsten Ausführungen von Willis Eschenbach zu Nassim Taleb mit seiner Aussage „Tatsächlich sind Fehler so konvex, dass der Beitrag einer einzigen zusätzlichen Variablen den Gesamtfehler größer machen kann als diejenige zuvor“ habe ich mir gedacht, dass es angebracht ist, diese Zerschlagung der Über-Zuverlässigkeit statistischer Verfahren in der Wissenschaft weiter auszuführen; vor allem, da unsere globale Temperaturaufzeichnung vollständig eine statistische Konstruktion ist.
Auszüge aus dem Artikel von Tom Siegfried in Science News:
Wissenschaft ist heldenhaft. Sie befeuert die Wirtschaft, füttert die Welt und bekämpft Krankheiten. Sicher, sie führt auch zu manchem Unangenehmen – Wissen ist Macht für das Schlechte ebenso wie für das Gute – aber insgesamt gebührt der Wissenschaft Dank für die Schaffung der Grundlage des Komforts und der Bequemlichkeiten der modernen Zivilisation.
Aber trotz all dieser heroischen Errungenschaften weist Wissenschaft ein tragisches Manko auf: Sie richtet sich nicht immer nach dem Image, das sie von sich selbst erschaffen hat. Gemeiniglich steht Wissenschaft für Loyalität gegenüber Ursachen, strikter Logik und der Suche nach Wahrheit frei von den Dogmen der Autoritäten. In der Praxis ist Wissenschaft jedoch großenteils unterwürfig gegenüber der Autorität von Zeitschriften-Herausgebern; durchsetzt mit Dogma und sich nicht bewusst der logischen Fehler bei den primären Verfahren zu Untersuchungen: statistische Analysen experimenteller Daten zum Testen von Hypothesen. Als Folge sind wissenschaftliche Studien nicht so zuverlässig wie sie von sich behaupten. Dogmatische Ergebenheit gegenüber traditionellen statistischen Verfahren ist eine Achillesferse, die anzuerkennen die Wissenschaft sich weigert, womit sie ihren heldenhaften Status in der Gesellschaft aufs Spiel setzt.
…
Noch nachdrücklicher: Eine in psychologischen Journalen veröffentlichte Analyse von 100 Ergebnissen zeigt, dass die meisten dieser Ergebnisse einfach verpuffen, wenn die gleiche Studie erneut durchgeführt worden ist. Dies schrieb kürzlich das Journal Nature. Und dann gibt es da das Fiasko über sich ändernde Haltungen zu gleichgeschlechtlichen Hochzeiten, was in einer (inzwischen zurück gezogenen)Studie zu lesen war, die ganz offensichtlich auf fabrizierten Daten basierte.
Aber Betrug ist nicht das prominenteste Problem. Noch öfter können unschuldige Faktoren konspirieren, um ein wissenschaftliches Ergebnis schwierig zu reproduzieren zu machen, wie meine Kollegin Tina Hesman Saey kürzlich in Science News dokumentiert hat. Und selbst unabhängig von diesen praktischen Problemen garantieren statistische Schwächen, dass sich viele Ergebnisse als unecht herausstellen. Wie ich schon bei vielen Gelegenheiten erwähnt habe, die Standardmethoden in Statistik zur Evaluierung von Beweisen werden gewöhnlich missbraucht, fast immer falsch interpretiert. Außerdem sind sie nicht sehr informativ, selbst dann, wenn sie korrekt verwendet und interpretiert werden.
Niemand in der wissenschaftlichen Welt hat diese Dinge deutlicher beim Namen genannt als der Psychologe Gerd Gigerenzer vom Max-Planck-Institut für Bildungsforschung in Berlin. In einer jüngst erschienenen Studie (hier), die er zusammen mit Julian Marewski von der University of Lausanne durchgeführt hatte, vertiefte sich Gigerenzer in einige der Gründe für diese beklagenswerte Situation.
Trotz allem besteht ihrer Analyse zufolge das Problem, weil das Streben nach „statistischer Signifikanz“ sinnlos ist. „Die Bestimmung der Signifikanz ist zu einem Ersatz für gute Forschung geworden“, schreiben Gigerenzer und Marewski in der Februar-Ausgabe des Journal of Management. In vielen wissenschaftlichen Zirkeln wurde „statistische Signifikanz“ zu einem Idol, zu dem man pilgern musste auf dem Weg zur Wahrheit. „Angesehen als das einzige verfügbare Mittel vor Ort wird dieses Streben praktiziert auf eine gewohnheitsmäßige, mechanische Weise – ohne danach zu fragen, ob das sinnvoll ist oder nicht“.
Normalerweise wird statistische Signifikanz beurteilt durch die Berechnung eines Wertes P, also der Wahrscheinlichkeit, dass die beobachteten Ergebnisse (oder extremere Ergebnisse) erzielt werden würden, falls kein wirklicher Unterschied besteht zwischen den getesteten Faktoren (zum Beispiel wie bei einem Medikament oder einem Placebo zur Behandlung von Krankheiten). Aber es gibt andere Verfahren. Oftmals wollen Forscher Vertrauensintervalle berechnen – Bandbreiten, die sehr der Fehlerbandbreite in öffentlichen Meinungsumfragen ähneln. In einigen Fällen könnten verfeinerte statistische Tests angewendet werden. Eine Lehrmeinung bevorzugt das Bayesianische Verfahren, seit Langem Rivale der Standardmethode.
…
Warum unternehmen Wissenschaftler nichts gegen diese Probleme? Konträre Motivationen! In einem der wenigen populären Bücher, die sich mit diesen statistischen Dingen eingehend befassen, zeigt der Physiker und Statistiker Alex Reinhart, dass es sich kaum für Wissenschaftler auszahlt, dem gegenwärtigen statistischen System Widerstand zu leisten.
„Unglückliche Anreize … zwingen Wissenschaftler, rasch kleine Studien mit schlampigen statistischen Verfahren zu veröffentlichen“, schreibt Reinhard in Statistics Done Wrong. „Promotionen, Beschäftigungsverhältnisse, Finanzierung und Job-Angebote sind allesamt abhängig davon, eine lange Lise mit Veröffentlichungen in prestigeträchtigen Journalen vorweisen zu können. Daher gibt es einen starken Anreiz, vielversprechende Ergebnisse so schnell wie möglich zu veröffentlichen“.
Und die Veröffentlichung von Studien erfordert es, die von den Herausgebern der Journale festgelegten Spielregeln einzuhalten.
„Herausgeber von Journalen versuchen zu beurteilen, welche Studien die größten Auswirkungen haben und das größte Interesse erregen, und wählen konsequenterweise jene mit den überraschendsten, kontroversesten oder neuesten Ergebnissen“, führt Reinhart aus. „Dies ist ein Rezept für Inflation von Wahrheit“.
Wissenschaftliche Veröffentlichungen sind daher durchsetzt mit Falschheiten.
Read all of part 1 here
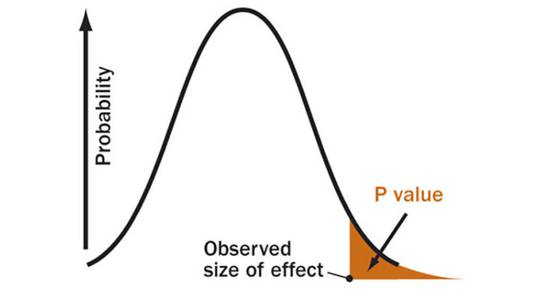
Wertlos: Ein Wert P ist die Wahrscheinlichkeit, dass ein Ergebnis genauso extrem oder noch extremer ist als die beobachteten Daten, falls es de facto gar keine Auswirkung hat. P-Werte sind keine zuverlässige Maßzahlen von Beweisen.
Auszüge als Teil 2:
Statistik ist in der Wissenschaft das, was Steroide für Baseball sind. Suchterzeugendes Gift. Aber zumindest hat Baseball versucht, dem Problem zu begegnen. Die Wissenschaft leugnet dieses Problem zumeist.
Sicher, nicht jeder Gebrauch von Statistik in der Wissenschaft ist des Teufels, genauso wie Steroide manchmal geeignete Medizin ist. Aber ein spezielles statistisches Verfahren, nämlich das Testen von Null-Hypothesen, verdient das gleiche Schicksal wie Pete Rose im Baseball: Verbannung.
[Anmerkung des Übersetzers: Es würde zu weit führen, den nicht mit der US-Sportart Baseball vertrauten Lesern diesen Vergleich zu erläutern. Pete Rose war eine Baseball-Berühmtheit, bevor er aus irgendwelchen Gründen in der Versenkung verschwand.]
Zahlreiche Experten haben das statistische Austesten von Null-Hypothesen – das Grundverfahren wissenschaftlicher Methodik – als den Hauptschuldigen ausgemacht, der viele Forschungsergebnisse unreproduzierbar und vielleicht – eher mehr als weniger – irrig macht. Viele Faktoren tragen zu dieser abgründigen Lage bei. In den Biowissenschaften beispielsweise sind Probleme mit biologischen Mitteln und Referenzmaterialien eine wesentliche Quelle unreproduzierbarer Ergebnisse. Das zeigt ein neuer Bericht in PLOS Biology. Aber Schwierigkeiten mit „Datenanalyse und Berichterstattung“ werden ebenfalls angesprochen. Wie die Statistikerin Victoria Stodden kürzlich dokumentierte, führt eine Reihe statistischer Dinge zu Unreproduzierbarkeit. Und viele dieser Dinge drehen sich um Tests der Null-Hypothese. Anstatt wissenschaftliches Verständnis zu vertiefen, garantiert das Testen von Null-Hypothesen häufig falsche Schlussfolgerungen.
10. Verbanne P-Werte
9. Empfehle Schätzung
8. Überdenke Vertrauensintervalle
7. Verbessere Meta-Analysen
6. Rufe ein Journal of Statistical Shame ins Leben
5. Bessere Leitlinien für Wissenschaftler und Herausgeber von Journalen
4. Verlange Vorab-Registrierung von Studien-Designs
3. Setze dich für bessere Lehrbücher ein
2. Verändere Strukturen für Anreize
1. Überdenke die Berichterstattung über Wissenschaft in den Medien.
Noch mehr Gründe hinter dieser Liste in Teil 2 hier.
Ich würde dieser Top-10-Liste noch einen Punkt hinzufügen:
0.Verbanne den Gebrauch des Wortes ,robust‘ aus wissenschaftlichen Studien.
Angesichts dessen, was wir gerade hier und von Nassim Taleb gelesen haben, und da vor allem die Klimawissenschaft dieses Wort in Studien zu lieben scheint, denke ich, dass es nicht mehr ist als eine Projektion des Egos des/der Autor/en vieler klimawissenschaftlicher Studien ist und nicht ein unterstützenswertes Statement bzgl. statistischen Vertrauens.
Ein weiterer Punkt; ein Absatz aus Teil 1 von Tom Siegfried liest sich so:
Es ist langfristig für die Wissenschaft immer noch die oberste Strategie, umfassendes Wissen über die Natur zu etablieren. Mit der Zeit trennen akkumulierende wissenschaftliche Beweise im Allgemeinen das Gute vom Schlechten. (Mit anderen Worten, Klimawissenschafts-Leugner und Impfverweigerer werden durch heilloses statistisches Durcheinander in individuellen Studien nicht gerechtfertigt). Nichtsdestotrotz sind zu viele individuelle Studien in begutachteten Journalen nicht zuverlässiger als Meinungsumfragen vor Wahlen in UK.
Dieses hässliche Etikett über Klimaskeptiker beschädigt einen sonst exzellenten Artikel über Wissenschaft. Es zeigt auch, dass Mr. Siegfried sich nicht wirklich diesem Thema (d. h. Skeptizismus) genauso sorgfältig angenommen hat wie er es hinsichtlich des Missbrauchs der Wissenschaft getan hat.
Sollte Mr. Siegfried dies lesen, möchte ich ihm klarmachen, dass viele Klimaskeptiker zu Klimaskeptikern geworden sind, seit wir einmal damit angefangen haben, einige der schäbigen statistischen Verfahren zu untersuchen, die in wissenschaftlichen Studien verwendet oder sogar eingeführt worden sind. Die fragwürdige statistische Arbeit von Michael Mann allein (in Kombination mit dem Hype in den nicht nachfragenden Medien) hat Legionen von Klimaskeptikern hervorgebracht. Vielleicht sollte Mr. Siegfried doch etwas Zeit dafür aufbringen, die statistischen Kritiken von Stephen MyIntyre zu lesen und uns dann zu sagen, wie Dinge wie eine einzige Baumring-Stichprobe (hier) oder verkehrt herum präsentierte Daten (hier) oder vorab festgelegte Daten (hier) „robuste“ Klimawissenschaft erzeugen, bevor er das Etikett „Klimaleugner“ noch einmal in den Mund nimmt.
Link: http://wattsupwiththat.com/2015/07/12/robust-analysis-isnt-what-it-is-cracked-up-to-be-top-10-ways-to-save-science-from-its-statistical-self/
Übersetzt von Chris Frey EIKE
















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Als ehemaliger Meßknecht kenne ich die vielen Fehler,die bei elektrischer Temperaturmessung auftreten können.Das beginnt beim Pt 100,Klasse A oder B.Welche Sensorspeisung,konstante Spannung oder konstanter Strom.Sensorverkabelung,2,3,oder 4 Draht Speisung.Linearisierung,das Pt 100 ist unlinear.Datenverarbeitung,oft wird Auflösung mit Genauigkeit verwechselt.Datendarstellung.
Gibt es eine Norm für den elektrischen Aufbau der gesmten Meßkette?Man müßte mal den Aufbau der Temperaturmeßkette sehen,um eine Fehlerbetrachtung machen zu können.
Ich habe auch oft auf die Frage,wie genau messen sie,geantwortet:ganz genau!Das hat oft auch genügt,wenn die Frager nichts von Meßtechnik kannten.
Messfehler gibt es mit Sicherheit bei der großen Anzahl von Messwerten die z.B. bei Klimaberechnungen verarbeitet werden.
Das ist aber nicht weiter tragisch, Messfehler treten ja nach oben genauso wie nach unten auf, in der Summe heben die sich gegenseitig auf, bist auf irgendwelche Kommastellen, wenn überhaupt.
Extreme Abweichungen nach oben genauso wie nach unten werden ja nochmal geprüft.
So geschehen bei Hitzerekord (seit 1881) am 5.7.2015 in Kitzingen mit 40,3 Grad, hat auch der Deutsche Wetterdienst die Messung und die Messgeräte überprüft und als korrekte Messung freigegeben.
Das der Deutsche Wetterdienst da was mauschelt glaube ich dann doch nicht, das ist OK so mit den 40,3° usw.
Gruß