Eine Untersuchung anhand von Gezeitenpegel-Daten – Teil 2: Kurvenanpassung
Dr. Alan Welch FBIS FRAS
Kurvenanpassung
Die einzelnen Gezeitenmessgeräte werden zuerst verarbeitet. Sie decken einen weiten Bereich von Gesamtperioden ab, und bei einigen fehlen Daten, in der Regel kleine Lücken, gelegentlich jedoch auch erhebliche Zeiträume, die sich auf die Berechnungen auswirken und berücksichtigt werden müssen. Die Ergebnisse aus Aberdeen werden vollständig dargestellt, während die underen Gezeitenmessgeräte in einem stundardisierten, gekürzten Layout gezeigt werden.
Aberdeen
Die Daten aus Aberdeen decken den Zeitraum von 1862 bis 2022 ab, also einen Zeitraum von 161 Jahren. Die Spektralanalyse ergab drei Kurven mit einer Periode von mehr als 11 Jahren (P1, P2 und P3), nämlich (84,9, 43,0 und 18,1) Jahre. Damit verbunden sind drei Amplitudenwerte (amp1, amp2 und amp3) von (32,7, 15,1 und 10,3). Jeder dieser Werte hat eine zugehörige Sinuskurve, die durch Gleichung 1 gegeben ist. Die drei Amplitudenwerte der Kurven (AMP1, AMP2 und AMP3) stehen mit den Werten (amp1, amp2 und amp3) in Beziehung zu Gleichung 2, woraus sich die relativen Werte (a1, a2 und a3) im Verhältnis (5,7, 3,9 und 3,2) ergeben, welche die Quadratwurzelwerte von (amp1, amp2 und amp3) sind.
Die letzten drei Werte (a1, a2 und a3) sind relativ und müssen mit einem Faktor F multipliziert werden, um die tatsächlichen Amplituden der Sinuskurven zu erhalten. F kann geschätzt werden, oder wenn eine ausreichende Anzahl von Zyklen vorliegt, würde der Extrembereich nahe am Bereich der einzelnen maximalen und minimalen Amplituden (Amax und Amin) der Daten liegen, was zu einem Wert von F gemäß Gleichung 3 führt.
F = (Amax – Amin) / 2 x (a1 + a2 + a3) Equation 3
Für die Aberdeen-Daten: Amax = 35.7 und Amin = -42.2 also eine Bundbreite von 77.9
Und mit (a1 + a2 + a3) = (5.7 + 3.9 + 3.2) = 12.8
F = 77.9 / 25.6 = 3.04
was zu Amplituden (AMP1, AMP2 und AMP3) von (17,3, 11,9 und 9,7) führt.
Diese Werte sind wahrscheinlich zu niedrig angesetzt, daher werden die etwas höheren Werte 18, 12,5 und 10 ausprobiert.
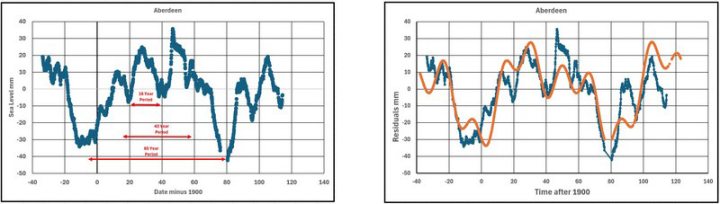
Abbildung 14 zeigt die Daten aus Aberdeen (ein gleitender Durchschnitt über etwa 8 Jahre), auf denen die drei Zeiträume dargestellt sind.
Abbildung 15 zeigt die Daten aus Aberdeen mit den kombinierten Werten der drei Sinuskurven. Sie zeigt eine angemessene Anpassung, wird jedoch nicht weiter verfolgt, da die gemittelten Ist-Daten stellenweise durch Lücken im ursprünglichen vollständigen Datensatz beeinflusst sind. Außerdem wurden die Phasenverschiebungen der Sinuskurven visuell bestimmt und es wurde kein Konstantenterm (CONST) einbezogen, d. h. die Sinuskurven oszillieren um den Nullrestwert . Die verwendeten Verschiebungen (SHIFT1, SHIFT2 und SHIFT3) betragen (-30, -20 und -90).
Abbildung 14 Abbildung 15
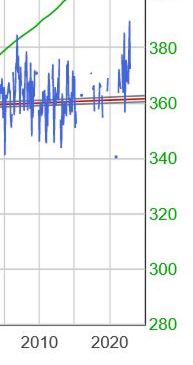
Die größten Abweichungen treten ungefähr zum Zeitpunkt = 110 (2010) auf. Von 2016 bis 2021 fehlen viele Daten, wie aus den NOAA-Daten im Abschnitt über Aberdeen oben ersichtlich ist. Teile der NOAA-Daten sind unten in Abbildung 16 dargestellt:
Abbildung 16
Bergen
Die Daten aus Bergen decken den Zeitraum von 1915 bis 2022 ab, also 108 Jahre, mit zwei mittleren Lücken in den 1940er und 1970er Jahren.
(P1, P2 und P3) = (66.9, 28.9 und 19.2) Jahre
(amp1,amp2 und amp3) = (13.3, 10.2 und 10.1)
(a1, a2 und a3) = (3.6, 3.2 und 3.2)
(Amax und Amin) = (32.3 und -40.9)
Die Anwendung von Gleichung 3 in
F = 73.2 / 20.0= 3.66
ergibt jeweils (AMP1, AMP2 und AMP3) 13.2, 11.7 und 11.7
Es werden die Amplitudenwerte 14, 12 und 12 ausprobiert.
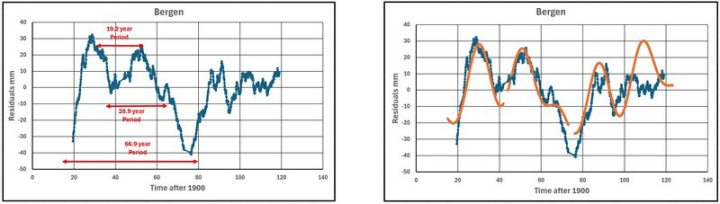
Abbildung 17 zeigt die Daten aus Bergen (ungefährer gleitender 8-Jahres-Durchschnitt), auf denen die drei Perioden dargestellt sind.
Abbildung 18 zeigt die Daten aus Bergen mit den kombinierten Werten der drei Sinuskurven. Die verwendeten Verschiebungen (SHIFT1, SHIFT2 und SHIFT3) betragen (-50, -40 und -90).
Abbildung 17 Abbildung 18
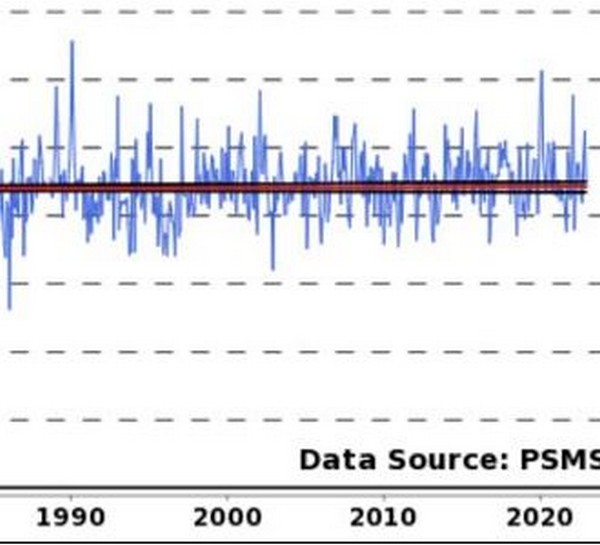
Die einzigen wesentlichen Abweichungen treten ungefähr zum Zeitpunkt = 110 (2010) auf, wenn in den Daten kein Peak zu erkennen ist. Es gibt keine Erklärung dafür, aber Abbildung 19 wurde eingefügt, um die vollständigen NOAA-Daten zu diesem Zeitpunkt zu zeigen:
Pause zum Nachdenken
In dieser Phase haben zwei Beispiele für die Anpassung von Sinuskurven zu einem zufriedenstellenden Ergebnis geführt.
Ist das ein Aha-Erlebnis oder mache ich mir etwas vor?
Der Prozess läuft darauf hinaus, dass mithilfe der Spektralanalyse die Hauptmodi ermittelt werden, die auf Zeiträume von etwa 11 Jahren beschränkt sind. Auf der Grundlage dieser Modi wird eine Reihe von Sinuskurven gebildet, welche die Perioden und berechneten Amplituden zusammen mit den bekannten Spitzen- und Minimalwerten sowie den maximalen Restwerten verwenden, die aus einem gleitenden Durchschnitt der Residualwerte über einen Zeitraum von etwa 8 Jahren ermittelt wurden. Die Phasenverschiebungen für jede Sinuskurve werden visuell bestimmt und eine kombinierte Kurve erstellt. Ist dieser Prozess etwas zyklisch oder verzerrt, sodass er gut aussehende Anpassungen erzeugt?
Der Prozess wird auf die underen 7 Fälle mit kürzerer Periode angewendet und anschließend wird das Verfahren erneut bewertet. Der Grund dafür ist, dass dies dazu beitragen kann, die Eignung der Methode zu beurteilen und ein vollständigeres Bild der 9 Gezeitenpegel-Datensätze zu erhalten.
Narvik
Bei diesem Datensatz umfassen die verbleibenden Datensätze weniger als 100 Jahre, was die Analyse erschweren kann. Narvik weist zu Beginn eine große Lücke in den Daten sowie seltsame Werte für das erste Jahr oder so auf. Die Datendatei wurde daher gekürzt, und die verwendeten Daten beginnen mit dem Jahr 1947.
Die unvollständigen Daten für Narvik decken den Zeitraum von 1947 bis 2022 ab, also einen Zeitraum von 76 Jahren.
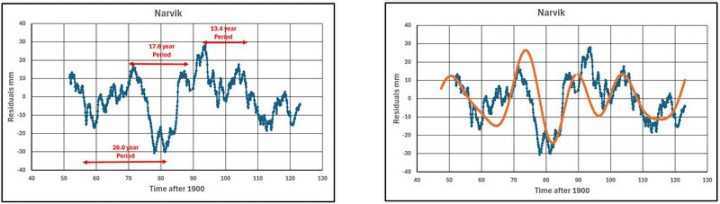
(P1, P2 und P3) = (26.0, 17.6 und 13.4) Jahre
(amp1,amp2 und amp3) = (2.6, 5.0 und 1.9)
(a1, a2 und a3) = (1.6, 2.2 und 1.4)
(Amax und Amin) = (28.9 und -30.4)
Die Anwendung von Gleichung 3 in
F = 59.3 / 10.4= 5.7
ergibt (AMP1, AMP2 und AMP3) = (9.1, 12.6 und 8.0)
Es könnten Werte von Amplitude 9,0, 13,0 und 8,0 ausprobiert werden.
Abbildung 20 zeigt die Narvik-Daten (ungefährer gleitender 8-Jahres-Durchschnitt), auf denen die drei Perioden dargestellt sind.
Abbildung 21 zeigt die Narvik-Daten mit den kombinierten Werten der 3 Sinuskurven. Die verwendeten Verschiebungen (SHIFT1, SHIFT2 und SHIFT3) sind (-30, -30 und -90).
Das Ergebnis ist recht zufriedenstellend.
Reykjavik
Die Daten für Reykjavik umfassen den Zeitraum von 1956 bis 2022, also 67 Jahre.
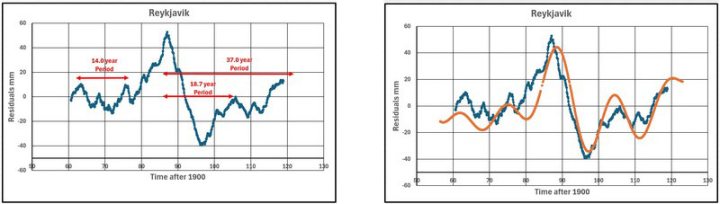
(P1, P2 und P3) = (37.0, 18.7 und 14.0) Jahre
(amp1,amp2 und amp3) = (12.5, 9.2 und 9.0)
(a1, a2 und a3) = (3.5, 3.0 und 3.0)
(Amax und Amin) = (52.8 und -39.4)
Anwendung von Gleichung 3 führt zu
F = 92.2 / 19.0= 4.85
ergibt (AMP1, AMP2 und AMP3) = (17.0, 14.6 und 14.6)
Es könnten die Werte Amplitude 18,0, 15,0 und 15,0 ausprobiert werden.
Abbildung 22 zeigt die Daten aus Reykjavik (ungefährer gleitender 8-Jahres-Durchschnitt), auf denen die drei Perioden dargestellt sind.
Abbildung 23 zeigt die Daten aus Reykjavik mit den kombinierten Werten der drei Sinuskurven. Die verwendeten Verschiebungen (SHIFT1, SHIFT2 und SHIFT3) sind (-80, -16 und -4).
Das passt alles ziemlich gut.
Murmansk
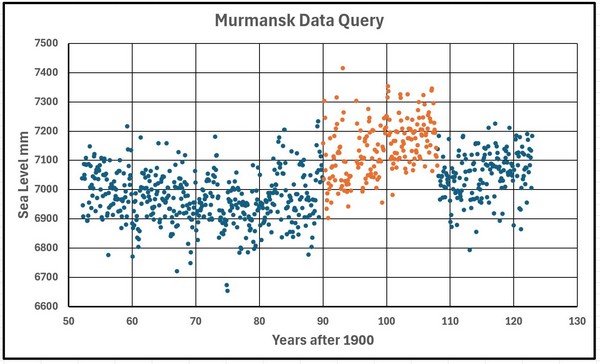
Die Daten umfassen den Zeitraum von 1952 bis 2022, also 71 Jahre, weisen jedoch zwischen 1990 und 2010 eine merkwürdige Abweichung auf, da der Meeresspiegelanstieg hier offenbar um etwa 100 mm über dem allgemeinen Trend liegt (Abbildung 24). Dies wird sich auf die Spektralanalyse auswirken, aber der Prozess wird mit den vollständigen Daten abgeschlossen werden.
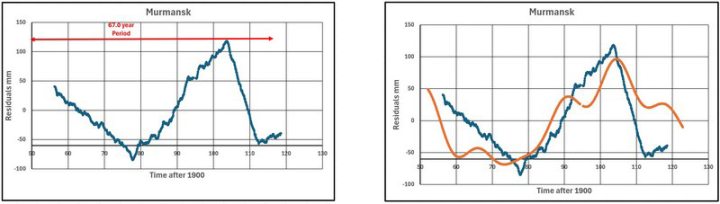
(P1, P2 und P3) = (65.2, 17.6 und 13.1) Jahre
(amp1,amp2 und amp3) = (143.5, 9.8 und 5.0)
(a1, a2 und a3) = (12.0, 3.1 und 2.2)
(Amax und Amin) = (112.5 und -79.7)
Gleichung 3 angewendet
F = 192.2 / 34.6= 5.55
ergibt (AMP1, AMP2 und AMP3) = (66.6, 17.2und 12.2)
Es könnten Werte von Amplitude 18,0, 15,0 und 15,0 ausprobiert werden.
Es könnten Werte von Amplitude 67, 17,5 und 12,5 ausprobiert werden. Diese sind etwas höher, da bei einer kürzeren Gesamtperiode die Wahrscheinlichkeit geringer ist, dass die Spitzen und Tiefpunkte der drei Kurven zusammenfallen.
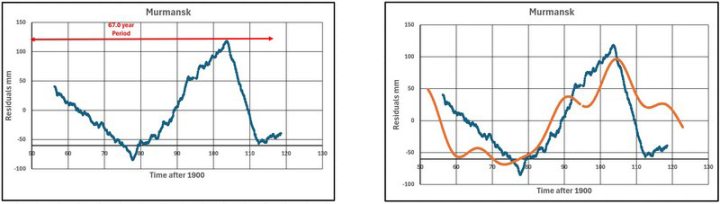
Abbildung 25 zeigt die Murmansk-Daten (ungefähr 8-Jahres-Gleitender Durchschnitt), wobei nur die längste Periode dargestellt ist. Die beiden kurzen Perioden werden nicht gezeigt, da die seltsamen Daten zwischen 1990 und 2010 den Plot stark beeinflussen. Die verwendeten Verschiebungen (SHIFT1, SHIFT2 und SHIFT3) sind (-45, -20 und -100).
Abbildung 26 zeigt die Daten aus Murmansk mit den kombinierten Werten der drei Sinuskurven.
Die Auswirkung der seltsamen Daten zwischen 1990 und 2010 zeigt sich in einem untypischen Diagramm, in dem die kleineren Schwankungen von einer Sägezahnform des Hauptmodus‘ dominiert werden.
Barentsburg
Die Daten für Barentsburg umfassen den Zeitraum von 1948 bis 2022, also 75 Jahre.
(P1, P2 und P3) = (41.6, 17.8 und 13.4) Jahre
(amp1,amp2 und amp3) = (15.2, 16.3 und 14.0)
(a1, a2 und a3) = (3.9, 4.0 und 3.7)
(Amax und Amin) = (26.5 und -56.7)
Gleichung 3 angewendet
F = 83.2 / 23.2= 3.59
ergibt (AMP1, AMP2 und AMP3) = (14.0, 14.3 und 13.3)
Es könnten die Werte Amplitude 15, 15 und 14 ausprobiert werden.
Abbildung 27 zeigt die Barentsburg-Daten (ungefährer gleitender 8-Jahres-Durchschnitt), auf denen die drei Perioden dargestellt sind.
Abbildung 28 zeigt die Barentsburg-Daten mit den kombinierten Werten der 3 Sinuskurven. Die verwendeten Verschiebungen (SHIFT1, SHIFT2 und SHIFT3) sind (-50, -30 und -97).
Die beiden Kurven in Abbildung 27 haben im Allgemeinen die gleiche Form. In diesem Fall gab es drei ähnliche Spitzen, was die Beurteilung der Phasenverschiebungen erschwerte.
Lerwick
Die Daten aus Lerwick decken den Zeitraum von 1957 bis 2022 ab, also 66 Jahre, mit einer mittleren Lücke um das Jahr 2002 und späteren kleineren Lücken.
(P1 und P2) = (21.4 und 12.8) Jahre
(amp1 und amp2) = (5.5 und 3.05)
(a1 und a2)= (2.35 und 1.75)
(Amax und Amin) = (17.1 und -20.0)
Anwendung Gleichung 3
F = 37.1 / 8.20 = 4.52
errgibt (AMP1 und AMP2)= (10.6 und 7.9)
Es könnten die Werte Amplitude 11 und 8 ausprobiert werden.
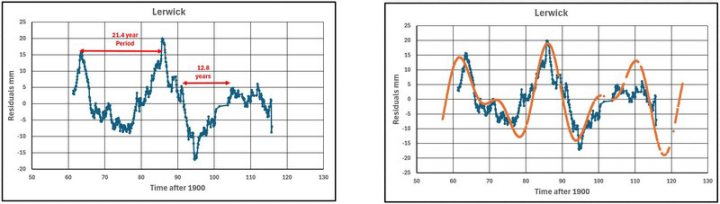
Abbildung 29 zeigt die Lerwick-Daten (ungefähr 8-Jahres-Durchschnitt), auf denen die beiden Perioden dargestellt sind.
Abbildung 30 zeigt die Lerwick-Daten mit den kombinierten Werten der 3 Sinuskurven. Die verwendeten Verschiebungen (SHIFT1 und SHIFT2) betragen (-54 und -25).
Das passt sehr gut.
Tiksi
Die Tiksi-Daten umfassen den Zeitraum von 1949 bis 2010, also 62 Jahre.
(P1 und P2) = (47.4 und 18.1) Jahre
(amp1 und amp2) = (0.835 und 4.28)
(a1 und a2)= (0.91 und 2.07)
(Amax und Amin) = (35.6 und -28.6)
Anwendung Gleichung 3
F = 64.2 / 5.96 = 10.77
ergibt (AMP1 und AMP2)= (9.8 und 22.3)
Es könnten Werte von Amplitude 10 und 24 ausprobiert werden.
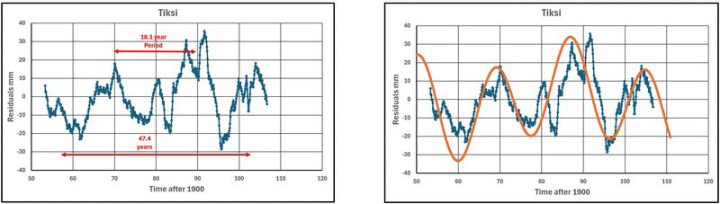
Abbildung 31 zeigt die Tiksi-Daten (ungefähr 8-Jahres-Gleitender Durchschnitt), auf denen die beiden Perioden dargestellt sind.
Abbildung 32 zeigt die Tiksi-Daten mit den kombinierten Werten der 3 Sinuskurven. Die verwendeten Verschiebungen (SHIFT1 und SHIFT2) betragen (-54 und -20).
Torshavn
Die Daten aus Torshavn umfassen den Zeitraum von 1957 bis 2006, also 50 Jahre.
(P1, P2 und P3) = (38.1, 18.7 und 13.1) Jahre
(amp1,amp2 und amp3) = (1.27, 6.72 und 4.19)
(a1, a2 und a3) = (1.13, 2.59 und 2.05)
(Amax und Amin) = (26.5 und -17.7)
Anwendung Gleichung 3
F = 44.2/ 11.54 = 3.83
ergibt (AMP1, AMP2 und AMP3) = (4.33, 9.92 und 7.85)
Es könnten die Werte Amplitude 4,5, 10 und 8 ausprobiert werden.
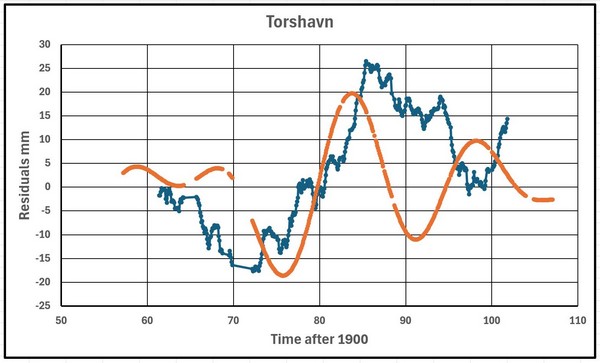
Abbildung 33 zeigt die Torshavn-Daten mit den kombinierten Werten der 3 Sinuskurven.
Die verwendeten Verschiebungen (SHIFT1, SHIFT2 und SHIFT3) sind (-10, -8 und -82).
Die Anpassung ist aufgrund der kurzen Dauer des Datensatzes und mehrerer Unterbrechungen in den Daten nicht sehr gut. Die Grafik, die die Zeiträume zeigt, wird nicht dargestellt.
Vor einer allgemeinen Diskussion ist es angebracht, das entwickelte Verfahren auf die Daten aus Brest anzuwenden.
Brest
Die Daten aus Brest decken den Zeitraum von 1807 bis 2022 ab, also einen Zeitraum von 216 Jahren. Abbildung 10 zeigt die Spitzenwerte der Spektralanalyse für die Residuen.
(P1, P2, P3 und P4) = (92.8, 36.1, 28.2 und 19.0) Jahre
(amp1,amp2, amp3 und amp4) = (16.6, 8.8, 15.6 und 9.0)
(a1, a2, a3 und a4) = (4.1, 3.0, 3.9 und 3.0)
(Amax und Amin) = (50.0 und -38.4)
Anwendung Gleichung 3
F = 88.4 / 28.0= 3.16
ergibt (AMP1, AMP2, AMP3 und AMP4) = (12.9, 9.5, 12.3 und 9.5)
Es könnten die Werte Amplitude 14,0, 10,0, 13,0 und 10,0 ausprobiert werden.
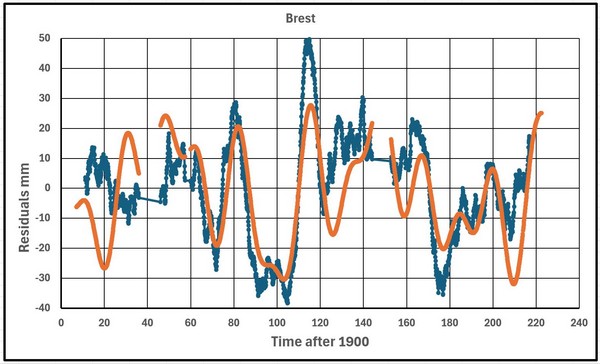
Abbildung 34 zeigt die Brest-Daten (ungefährer gleitender 8-Jahres-Durchschnitt), auf denen die vier Perioden dargestellt sind.
Die verwendeten Verschiebungen (SHIFT1, SHIFT2, SHIFT3 und SHIFT4) sind (-55, -70, 101 und -120).
Alles passt recht gut, außer zu den Zeitpunkten, an denen Daten fehlen, d. h. um 1850 und 1950.
Diskussion
Die wichtigste Erkenntnis ist, dass jeder Gezeitenmesser zusätzlich zu den vielen Oszillationen unterhalb von 11 Jahren, die aufgrund von Strahlungsschwankungen oder El Niño/La Niña-Zyklen auftreten, zwei oder mehr Oszillationen in den Residual-Meeresspiegeln zwischen 11 und 100 Jahren aufweist. Über einen Zeitraum von 20 Jahren variieren diese Schwankungen von Messgerät zu Messgerät in ihren Perioden, und der kombinierte Effekt ist schwer zu bestimmen, aber wenn sie nicht über den nördlichen Meeren gemessen würden, würde dies die „globalen” Messwerte der Satelliten beeinträchtigen.
Die Gültigkeit der verwendeten Verfahren ist nach wie vor umstritten.
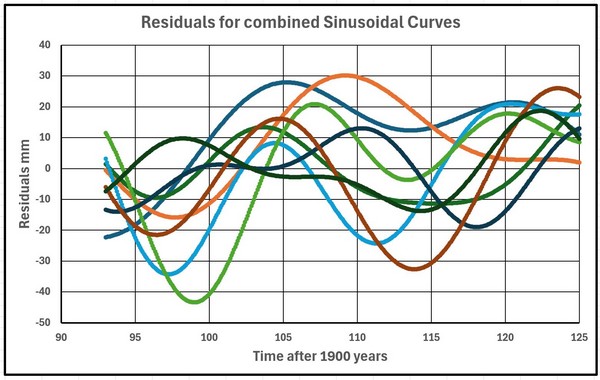
Abbildung 35 zeigt eine Grafik, die alle kombinierten Sinuskurven der Gezeitenpegel von 1993 bis 2025 darstellt, mit Ausnahme von Murmansk aufgrund möglicher fehlerhafter Daten und Brest, da es sich hierbei um eine zusätzliche Studie handelte. Die Kurven weisen eine gewisse Ähnlichkeit auf:
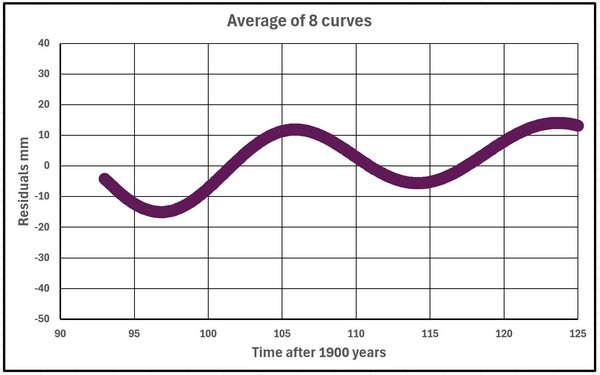
Die 8 Kurven wurden gemittelt und in Abbildung 36 im gleichen Maßstab dargestellt. Sie zeigen einen ungefähren 18-Jahre-Zyklus.
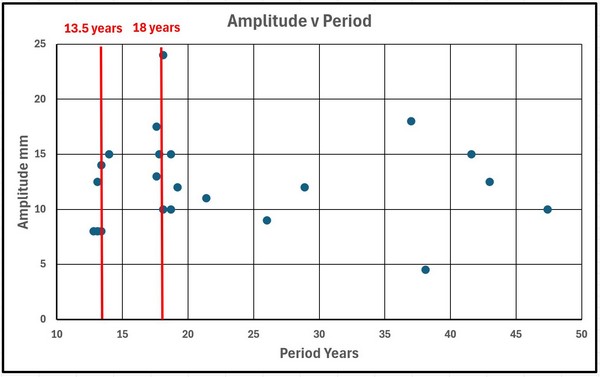
Die Signifikanz des 18-Jahre-Zyklus‘ lässt sich anhand der Amplituden und Perioden jeder Gruppe von Sinuskurven nachvollziehen, wie in Abbildung 23 (plus Murmansk) dargestellt. Es gibt zwei Cluster. Einer mit einer Periode von 13,5 Jahren, an dem 6 der 9 Kurven beteiligt sind, und einer mit einer Periode von 18 Jahren, an dem 8 der 9 Kurven beteiligt sind, wobei der 9. Wert 21,4 Jahre beträgt. Die zweite Gruppe entspricht dem 18-Jahres-Zyklus in Abbildung 36.
Die Gemeinsamkeit der Perioden könnte ein Hinweis auf eine oder mehrere kurze dekadische Schwankungen sein. Auf Grundlage der Satellitenanalysen wurde nach Werten im Bereich von etwa 25 bis 30 Jahren gesucht. Die Periode der Satellitenabdeckung betrug nur 32 Jahre, und das nicht abgedeckte Gebiet umfasste zwar hauptsächlich die oberen Atlantikregionen, aber auch andere Teile des Arktischen Meeres und kleinere Meeresgebiete rund um die Antarktis. Es ist nicht unwahrscheinlich, dass die nicht überwachten Gebiete sinusförmige Schwankungen in den „globalen” Ergebnissen hervorrufen könnten.
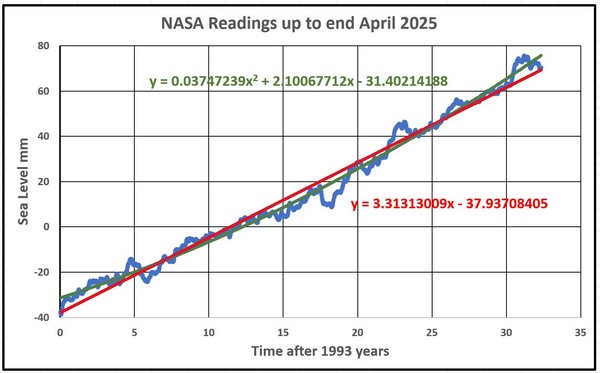
Anlass für diese Arbeit war die sinusförmige Schwankung im Bereich von 26 bis 29 mm/Jahr2, die bei der Untersuchung von NASA-Satellitendaten festgestellt wurde. Diese Schwankung wurde für die Residualwerte bestimmt, die aus der linearen Bestfit-Anpassung der Daten berechnet wurden. Die Ergebnisse der Gezeitenpegel beziehen sich auf die Residuen, die aus einer quadratischen Kurve über den gesamten Datensatz berechnet wurden. Über den kurzen Zeitraum (33 Jahre) der Satellitendaten wurde angenommen, dass die Abweichung der besten Anpassung von einer geraden Linie minimal ist, aber mit zunehmender Dauer der Satellitenbeobachtung könnte es wichtiger werden, dies zu berücksichtigen.
Zunächst wurden die neuesten Daten der NASA geprüft. Leider gab es aus politischen Gründen eine Unterbrechung und zuvor einen Rückgang der Menge der veröffentlichten verarbeiteten Daten. Daher werden die Daten vom April 2025 verwendet, da dies der letzte Datensatz mit einer vollständigeren Form der Daten ist, den ich seit Beginn im Jahr 2018 analysiert und veröffentlicht habe. Abbildung 38 zeigt die Daten vom April 2025, auf die am besten passende lineare und quadratische Kurven angewendet wurden:
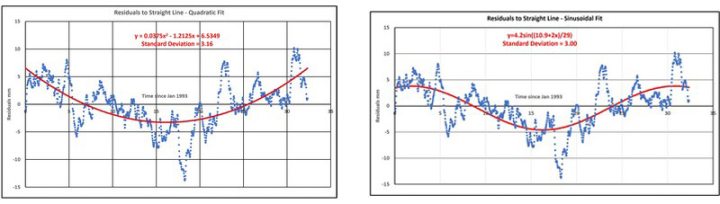
Die Anpassung quadratischer und sinusförmiger Kurven an die Residuen (Istwerte – Werte der Geraden) ergab die Abbildungen 39 und 40. Statistisch gesehen ist die sinusförmige Kurve genauer als die quadratische, wenn man die Fehler betrachtet.
Es wurden vier Spektralanalysen durchgeführt
• Vollständige Daten (wie in Abbildung 38 dargestellt – blaue Linie)
• Residuen (wie in Abbildung 39 oder 40 dargestellt – blaue Punkte)
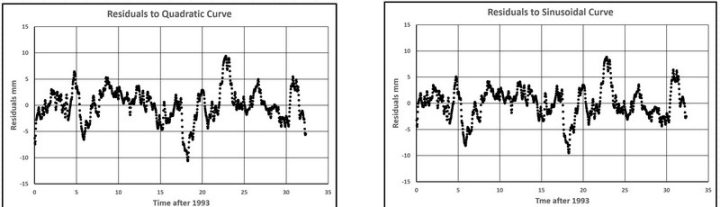
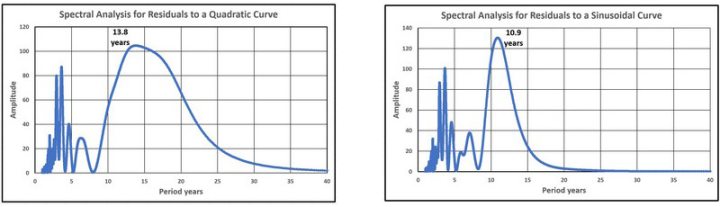
• Unterschiede der Residuen zur quadratischen Kurve (Abbildung 41)
• Unterschiede der Residuen zur Sinuskurve (Abbildung 42)
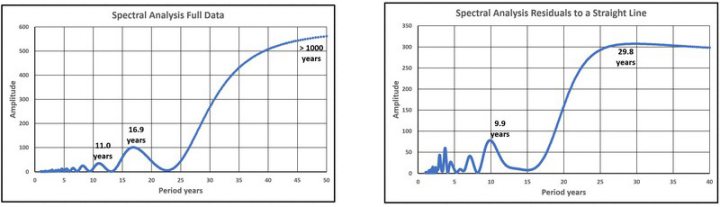
Die Ergebnisse der 4 Spektralanalysen sind in den Abbildungen 43 bis 46 dargestellt.
Was sagen die Abbildungen 43 bis 46 aus? Alle vier Abbildungen weisen mehrere Spitzen unterhalb einer Periode von etwa zehn Jahren auf, aber für diese Studie sind die übrigen Spitzen von Interesse.
In Abbildung 43 sind drei Spitzenwerte dargestellt. Zunächst ein sehr langfristiger Spitzenwert, dessen tatsächliche Periode aufgrund der kurzen Messdauer nicht bestimmt werden kann. Dann eine Periode von 16,9 Jahren, die mit den bei allen Gezeitenmessgeräten festgestellten Perioden übereinstimmt. Und schließlich eine Periode von 11 Jahren, die möglicherweise auf Schwankungen der Sonneneinstrahlung (Sonnenzyklus) zurückzuführen ist.
Abbildung 44 weist auf den untersuchten 29-Jahre-Zyklus und erneut auf einen Peak um 10 Jahre hin. Wie oben erwähnt, wird dieser auf der Grundlage einer geraden Linie erhalten und entstand bei der Beurteilung der Verwendung der quadratischen Kurvenanpassung und der damit verbundenen Extrapolation. Als Alternative wurde die sinusförmige Kurvenanpassung untersucht, worüber in einer Reihe von Artikeln berichtet wurde, zuletzt hier, der den Zeitraum bis Ende 2024 abdeckt.
Abbildung 45 zeigt möglicherweise zwei kombinierte, eng beieinander liegende Spitzen um 14 bis 15 Jahre.
Abbildung 46 weist eine einzelne, sehr scharfe Spitze bei 10,9 Jahren auf, die ebenfalls möglicherweise auf Schwankungen der Sonneneinstrahlung zurückzuführen ist. Die Abbildungen 41 und 42 sehen auf den ersten Blick sehr ähnlich aus, aber die Sinuskurve, die etwas besser passt, erzeugt ein klareres Spektrum.
Die allgemeine Schlussfolgerung lautet, dass die 29-jährige Schwankung mit der linearen Anpassung zusammenhängt, aber es gibt eine allgemeine Schwankung von etwa 18 Jahren in allen Gezeitendiagrammen, die in den vollständigen Satellitendaten zu sehen ist.
Übersetzt von Christian Freuer für das EIKE

















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Häää ! Dort drüben steht der Bahnhof, den ich nur verstehe ! 🤭
Oh Entschuldigung ! 🤭
Bevor man sich hier eigene Gedanken machen kann, müsste einmal dargestellt werden, wie ein Meerespegel mit stochastischer Wellendynamik überhaupt bestimmt wird.
Aus meiner Sicht benötigt man da einen über einen Tiefpass angekoppelten Messbehälter mit einer Zeitkonstanten, die mindestens 10-mal so groß wie die zeitlichen Ebbe/Flut Ereignisse sind, besser mit noch höherem Faktor.
Ob Satellitenmessungen das mit Modellen ähnlich den verkorksten Klimamodellen leisten können?