Die globale durchschnittliche SST (Meeresoberflächentemperatur) ist eine sehr wichtige Komponente der globalen durchschnittlichen Temperatur, und zwar aus dem einfachen Grund, dass der globale Ozean fast 71 % der Erdoberfläche bedeckt. Wir haben also die gerasterten SST-Daten von 1850 bis 2024 vom Hadley Centre (HadSST v4.1), von der NOAA (ERSST v5) und vom SST-Datenspeicher der NOAA (ICOADS v3) heruntergeladen und die Daten in Abbildung 1 dargestellt:
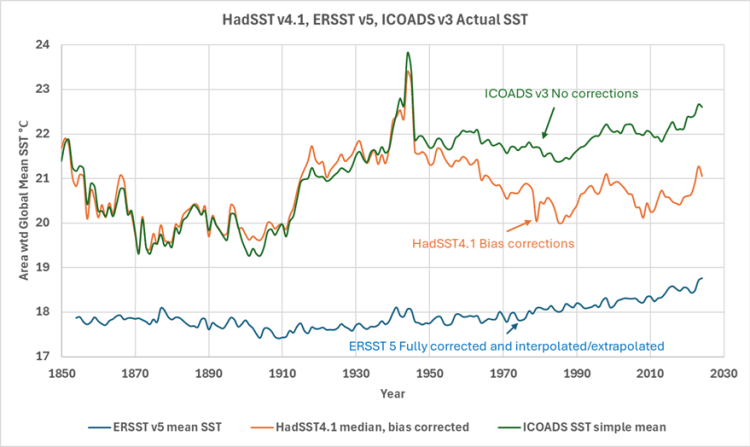
Abbildung 1. Flächengewichtete globale Durchschnittstemperatur aus ICOADS, HadSST und ERSST für 1850-2024. Die Daten wurden von den jeweiligen Agenturen heruntergeladen. Ein Klick auf die Graphik zeigt dieselbe in voller Auflösung; dies gilt auch für die anderen Abbildungen in diesem Beitrag.
Es gibt gute Gründe für die große Streuung der SST-Werte in Abbildung 1, und wir werden in diesem Beitrag auf einige von ihnen eingehen, aber die ursprüngliche Frage bleibt bestehen: „Wie hoch ist die globale durchschnittliche SST?“ Die globale durchschnittliche Temperatur hat sich seit 1850 angeblich um etwa ein Grad erhöht, aber die Unterschiede in den aufgezeichneten Daten sind größer als das.
ICOADS v. 3
ICOADS (International Comprehensive Ocean-Atmospheric Data Set) ist die eigentliche Quelle für fast alle in Abbildung 1 dargestellten Daten. Fast alle ursprünglichen Schiffs-, Bojen- und anderen Rohdaten, die vom Hadley Centre und der NOAA ERSST-Gruppe (Extended Reconstructed SST) verwendet werden, stammen aus ICOADS v. 3. Zusätzlich zur Erfassung der Rohdaten stellen sie auch ein eigenes einfaches Mittelwert-Gitterprodukt zur Verfügung, wie in Abbildung 1 in Grün dargestellt. Alle in diesem Beitrag gezeigten globalen Durchschnittstemperaturdaten sind flächengewichtet. Die von den Agenturen verwendeten Raster sind Breiten- und Längengrade, und während die Breitengrade überall gleich verteilt sind, sind es die Längengrade nicht. Sie liegen am Äquator etwa 111 km auseinander und konvergieren an den Polen gegen Null, so dass sich die Fläche jeder Gitterzelle mit dem Kosinus des Breitengrades ändert, was ich korrigiert habe. Der in Abbildung 1 dargestellte einfache ICOADS-Mittelwert kommt den Rohdaten so nahe wie nur möglich.
HadSST v. 4.1
Das Hadley Centre bietet viele Informationen über die Schritte, die es unternimmt, um zu seinem endgültigen globalen SST-Durchschnitt zu gelangen, und stellt für mehrere Schritte ein Zwischenprodukt zur Verfügung (siehe hier). Dies ist sehr lobenswert und lehrreich. Wir haben die endgültige „Kern“-Temperaturanomalie, die unbereinigte Anomalie und den „Ist“-Datensatz in Grad Celsius heruntergeladen, die in Abbildung 2 dargestellt sind:
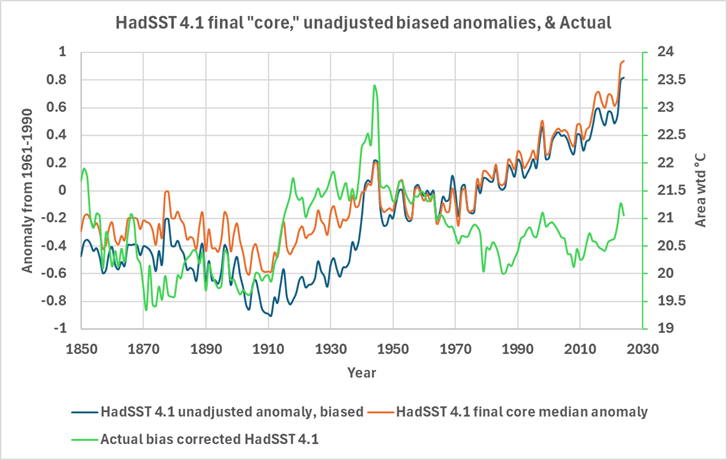
Abbildung 2. Zwei Zwischenprodukte von HadSST 4.1 und das endgültige „Kern“-SST-Produkt im Vergleich. Die tatsächliche bias-korrigierte grüne Kurve ist in Grad angegeben und verwendet die richtige Skala. Daten von der Website des Hadley Centre hier.
Der Prozess, den das Hadley Centre anwendet, um von den in Abbildung 1 dargestellten ICOADS-Rohdaten zu dem in Abbildung 2 gezeigten HadSST-Kernprodukt zu gelangen, wird in mehreren Veröffentlichungen beschrieben (Rayner, et al., 2006), (Kennedy J. J., Rayner, Smith, Parker, & Saunby, 2011), (Kennedy J. J., Rayner, Smith, Parker, & Saunby, 2011b), und (Kennedy J., Rayner, Atkinson, & Killick, 2019).
Ihr Verfahren wird dadurch erschwert, dass ihre Mess-„Stationen“ ständig in Bewegung sind, mit Ausnahme einiger stationärer Bojen. Daher besteht der erste Schritt darin, ein Referenz-Klimatologie-Gitter zu erstellen. Im Falle des Hadley Centre ist dies ein globales Ozeangitter von einem Grad mal einem Grad. Für jede nutzbare Ozean-Gitterzelle müssen monatliche Durchschnittswerte für den Referenzzeitraum von 1961-1990 vorliegen. Die meisten dieser Werte werden von Schiffen aus gemessen. Für einige Jahre oder Monate lagen nicht für alle Gitterzellen tatsächliche Messungen im Bezugszeitraum vor, so dass eine Interpolation und eine gewisse Extrapolation sowohl in zeitlicher als auch in räumlicher Hinsicht erforderlich war, um die Klimatologie 1961-1990 zu vervollständigen (Rayner et al., 2006).
Zur Berechnung der Werte für jede Referenz- und monatliche Messzelle wird eine spezielle Funktion der Mittelwertbildung verwendet, die Extremwerte abschneidet, das so genannte winsorisierte Mittel (Rayner, et al., 2006). Später werden die Ein-Grad-Gitter zu den größeren Fünf-Grad-Gittern kombiniert, die zur Erstellung der in diesem Beitrag gezeigten Mittelwerte und des endgültigen „Kern“-SST-Anomalieprodukts verwendet werden, das in Abbildung 2 in orange dargestellt ist.
Das Hadley Centre beginnt mit den in Abbildung 1 gezeigten Rohdaten von ICOADS v. 3, schließt aber einige Daten aus, um sie später zur Qualitätskontrolle zu verwenden oder weil sie sie für minderwertige Daten halten (Kennedy J., Rayner, Atkinson, & Killick, 2019). Die brauchbaren Daten werden zunächst in ihre Gitterzelle gelegt und in eine Anomalie umgewandelt, indem der Klimatologie-Referenzmittelwert für den Monat vom Monatsmittelwert abgezogen wird (Kennedy J., Rayner, Atkinson, & Killick, 2019). Die Messung stammt offensichtlich nicht aus der gleichen Quelle wie der Klimareferenzwert.
Nach der Berechnung der anfänglichen Anomalien werden die potenziellen Verzerrungen für die einzelnen Werte auf der Grundlage der Datenquelle errechnet. Dabei kann es sich um eine Eimerprobe handeln, die über der Bordwand eines Schiffes entnommen wurde; in diesem Fall werden die Art des Eimers und die Eimerisolierung berücksichtigt, sofern vorhanden. In diesem Fall wird der Standort des Thermometers in Bezug auf den Motor berücksichtigt, und so weiter. Anhand der Daten, die zu jeder Messung vorliegen, wird eine Reihe möglicher „Realisierungen“ der Verzerrungen erstellt, und der Mittelwert dieser hypothetischen Verzerrungen wird ausgewählt, um eine „verzerrungskorrigierte“ Anomalie zu berechnen. Die sich ergebenden verzerrungskorrigierten tatsächlichen Temperaturwerte werden in Abbildung 2 gemittelt und als „tatsächliche“ Temperatur in Grad Celsius in hellgrüner Farbe dargestellt. Die rohen Anomalien ohne Bias-Korrektur sind in Abbildung 2 als dunkelblaue Linie dargestellt. Interessant ist, dass die verzerrungskorrigierte Ist-Temperatur eine andere Form hat als die endgültige Kernanomalie oder die unkorrigierte Anomalie. Ich bin mir nicht sicher, was das zu bedeuten hat.
Da die meisten der zur Berechnung der SST verwendeten Messungen beweglich sind (Schiffe und driftende Bojen) und sie alle unterschiedliche Verzerrungen und Messmethoden haben, die sich im Laufe der Zeit ändern, ist die Erstellung einer kohärenten und konsistenten SST-Aufzeichnung der globalen Durchschnittstemperatur eine Herausforderung.
ERSST v. 5
Die am stärksten verarbeitete Schätzung der globalen Ozeantemperaturen ist die ERSST v. 5 Rekonstruktion. Wir haben keine Zwischendaten wie bei der HadSST-Rekonstruktion, aber wir haben die Beschreibung des Prozesses von Boyin Huang und anderen (Huang et al. 2017). Wie der HadSST-Prozess beginnt auch ERSST v. 5 mit dem ICOADS v. 3-Datensatz. Das ERSST-Team durchläuft dann einen Prozess, bei dem die Beobachtungen validiert werden, wobei diejenigen verworfen werden, die den Qualitätskontrollen nicht entsprechen, die Daten auf Verzerrungen hin korrigiert werden, Quervergleiche mit Nachbarn durchgeführt werden und Ausreißer ausgeschlossen werden. Dabei werden die ARGO-Daten direkt verwendet und nicht wie beim HadSST-Team ARGO als Validierungsdatensatz genutzt. In ERSST werden die ARGO-Beobachtungen mit dem 6,8-fachen Gewicht der Schiffsbeobachtungen gewichtet.
Die Abdeckung in der Fläche
Das ERSST-Verfahren nutzt die HadSST-Daten zur Lokalisierung der Eisbedeckung. Wenn eine Gitterzelle zu 90 % oder mehr mit Eis bedeckt ist, wird die SST in der Gitterzelle auf -1,8 °C gesetzt. Die Teilbedeckung wird linear zwischen dem rekonstruierten Wert der Gitterzelle und -1,8°C interpoliert (Huang, et al., 2017). Da -1,8 °C die Temperatur ist, bei der Meerwasser gefriert, ergibt dies einen gewissen Sinn, aber unter Eiskappen gibt es Strömungen und die Temperatur der Meeresoberfläche unter dem Eis beträgt eindeutig nicht einheitlich -1,8 °C. Ihre Annahme ist eine spekulative Übervereinfachung, wenn wir versuchen, die Erwärmung der Oberfläche in der Größenordnung von 0,1 °C/Dekade zu schätzen.
Ihr Rekonstruktionsprozess umfasst sowohl Interpolation als auch Extrapolation. Durch diese Annahmen ist das rekonstruierte ERSST-Gitter vollständiger als das HadSST-Gitter, wie in Abbildung 3 dargestellt:
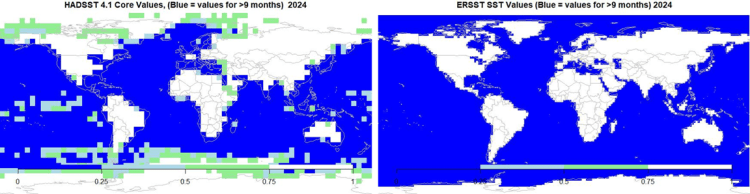
Abbildung 3. Die besetzten Gitterzellen sind für die Datensätze HadSST 4.1 und ERSST 5 eingefärbt. Die HadSST-Zellen sind 5×5 Grad groß und die ERSST-Zellen 2×2 Grad. In beiden Karten bedeutet blau, dass 10 oder mehr Monate Werte haben, hellblau, dass 6-9 Monate Werte haben, und grün, dass 3-5 Monate Werte haben. Eine weiße Zelle hat zwei Werte oder weniger. Beide Karten beziehen sich auf das Jahr 2024.
ERSST bietet ein sehr vollständiges Gitter. HadSST ist konservativer, verwendet aber immer noch Interpolation und einiges an Extrapolation, um ein möglichst vollständiges Raster zu erstellen. Man vergleiche diese beiden Karten mit der in Abbildung 4 gezeigten ICOADS-Karte der aktuellen Daten für 2024:
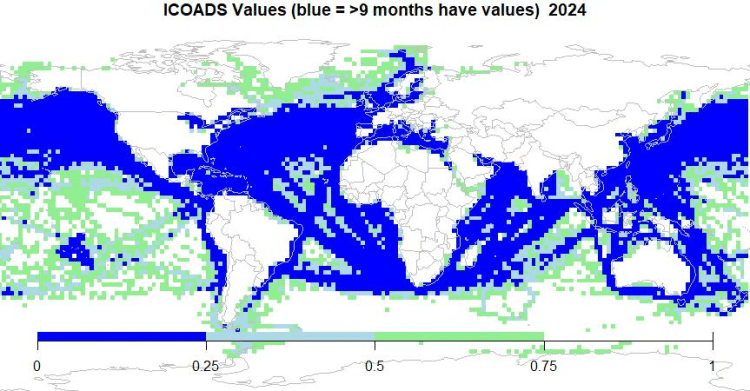
Abbildung 4. Eine Karte der 2×2 ICOADS-Besiedlungszellen für 2024. Das Farbschema ist das gleiche wie in Abbildung 3.
Die einfache ICOADS-Mitteltemperatur verwendet alle Werte, während sowohl HadSST als auch ERSST anomale Werte zurückweisen, so dass die ICOADS-Abdeckung, wie sie in Abbildung 4 dargestellt ist, so gut ist, wie sie nur sein kann, zumindest in Bezug auf die tatsächlichen Messungen.
Der Vergleich der Karten in Abbildung 3 und 4 zeigt uns einen der Gründe, warum die ICOADS-Durchschnittstemperatur in Abbildung 1 am höchsten und die ERSST-Temperatur am niedrigsten ist. Der ERSST-Durchschnitt enthält viele angenommene niedrige Werte unter dem Polareis, die in den ICOADS- und HadSST-Durchschnitten nicht als Nullwerte verwendet werden. Die Unterschiede zwischen HadSST und ICOADS sind zumindest teilweise auf die unterschiedliche Größe der Zellen zurückzuführen. Die ICOADS-Zellen haben eine Größe von 2×2 Grad und die HadSST-Zellen eine solche von 5×5. Dies entspricht einer Fläche von 49.000 km² bzw. 308.000 km² am Äquator. Die größere HadSST-Zellengröße ermöglicht es, kleinere Gebiete ohne Messungen in größere Zellen mit Werten zu integrieren. Mit anderen Worten, die größeren Zellen verteilen die vorhandenen Daten auf größere Gebiete.
Beobachtungen im Verlauf der Zeit
Bisher haben wir uns nur die Verteilung der Messwerte und die Endwerte für 2024 angesehen. Wie variiert die Datenmenge im Laufe der Zeit? Wir haben sowohl für ICOADS als auch für HadSST detaillierte Daten zu den Beobachtungen und haben sie in Abbildung 5 aufgetragen:
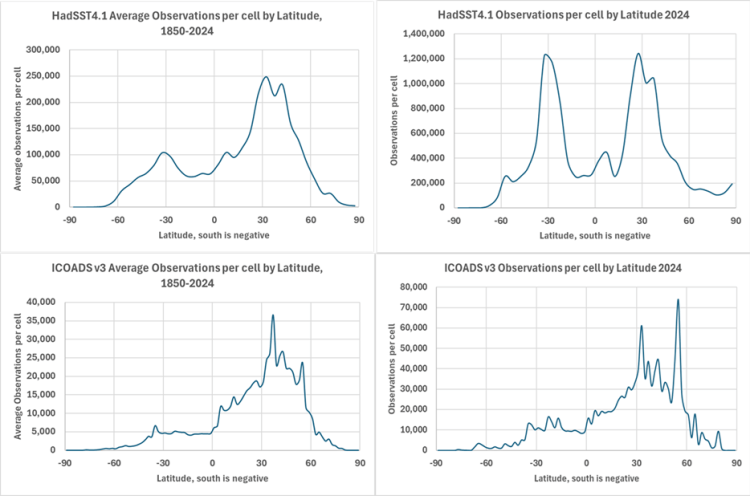
Abbildung 5. Gemeldete Beobachtungen nach Zellen für HadSST 4.1 und ICOADS v3. Dargestellt sind die Durchschnittswerte von 1850-2024 und für 2024. Die HadSST-Zellen sind 5×5 und die ICOADS-Zellen sind 2×2, was einen Teil des Unterschieds ausmacht.
Abbildung 5 zeigt, dass HadSST viel mehr Beobachtungen pro Zelle meldet als ICOADS, sogar mehr als aufgrund der größeren HadSST-Zellengröße zu erwarten wäre. Darüber hinaus meldet HadSST für den Breitengrad 30S genauso viele Beobachtungen wie für 30N für 2024, diese Beobachtungen sind im ICOADS-Datensatz für 2024 nicht enthalten. Die ICOADS-Daten werden nicht interpoliert oder manipuliert, daher sind die in der unteren Hälfte von Abbildung 5 gezeigten Beobachtungen real. HadSST interpoliert, extrapoliert oder füllt Zellen nicht in dem Ausmaß wie ERSST, aber sie tun offensichtlich etwas. Die Methoden, die zur Interpolation, Füllung und Extrapolation von Werten in HadSST verwendet werden, sind zum Teil in Rayner et al. beschrieben (Rayner et al., 2006). Vieles davon wird erreicht, wenn die anfänglichen Ein-Grad-Zellen zu den endgültigen Fünf-Grad-Zellen kombiniert werden.
Diskussion
Es ist offensichtlich, dass wir die globale durchschnittliche Meerestemperatur (SST) nicht mit der erforderlichen Genauigkeit kennen, um eine Erwärmungsrate von 0,1 °C pro Jahrzehnt zu ermitteln. Die Rohdaten (ICOADS) sind nicht gut mit den verarbeiteten Ergebnissen vergleichbar, wie in Abbildung 1 und 2 dargestellt.
Der einfache ICOADS-Mittelwert kommt den tatsächlichen Messungen am nächsten und wird daher bevorzugt. Ein Vergleich dieses (grün) und der um die Verzerrung korrigierten HadSST 4.1 Actual-Werte (hellblau) in Abbildung 6 mit den stärker verarbeiteten Standardanomalien zeigt, dass alle Schätzungen, ob Anomalien oder andere, vor 1990 und sogar danach fragwürdig sind.
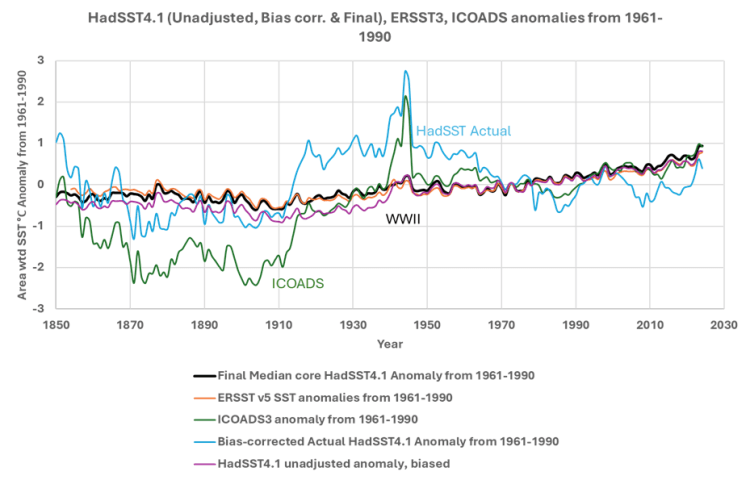
Abbildung 6. Die endgültige HadSST 4.1-„Kern“-Anomalie im Vergleich zu den in Anomalien umgewandelten ERSST-, ICOADS- und HadSST-Istwerten.
In Abbildung 6 werden die tatsächlichen Temperaturen von ERSST, ICOADS und HadSST 4.1 in Anomalien umgewandelt, indem ihre jeweiligen Mittelwerte für 1961–1990 von jedem Rasterzellenwert subtrahiert werden. Dies weicht vom üblichen Verfahren ab, bei dem jede Anomalie durch Subtraktion ihres individuellen Referenzmittelwerts von jedem Wert berechnet wird, bevor das Raster verarbeitet und gefüllt wird. Das übliche Verfahren wurde verwendet, um die dargestellte endgültige mittlere Kernanomalie von HadSST 4.1 in Abbildung 6 zu erstellen. Obwohl die anderen Anomalien unterschiedlich berechnet wurden, passt die ICOADS-Anomalie recht gut zu den ERSST- und endgültigen HadSST-Anomalien von Anfang der 1990er Jahre bis 2024.
Die um einen Bias korrigierten tatsächlichen Werte von HadSST, die in eine Anomalie umgewandelt wurden, stimmen nicht sehr gut mit den meisten anderen Anomalien überein, auch nicht nach 1990, was etwas verwirrend ist. Die Datenqualität über den Zweiten Weltkrieg (WWII) ist sehr schlecht, wie von Huang et al. erörtert. Kennedy et al. (2019) erörtern ebenfalls die Datenqualität für diesen Zeitraum, insbesondere den starken Abfall am Ende des Krieges, und führen dies auf eine große Veränderung in den von der Weltflotte erfassten Gebieten zurück. Ein Teil des plötzlichen Abfalls nach dem Krieg könnte auch auf eine Veränderung der Verfahren zu Schiffsmessungen zurückzuführen sein. Diese Anomalie ist in den meisten Datensätzen verborgen, weil die Anomalien in den meisten Datensätzen berechnet werden, bevor die Verarbeitung beginnt, wodurch der gemessene Sprung und Abfall der tatsächlichen SST maskiert wird. Wenn man die Erde durch ein Mikroskop betrachtet, kann man manchmal die Berge übersehen. Die Originalarbeiten enthalten keine Diagramme der tatsächlichen Temperatur, aber das Problem mit den Daten aus dem Zweiten Weltkrieg ist in den Bias-Diagrammen von Kennedy et al. (2019) in ihren Abbildungen 6, 7, 8, 9, 10 und 13 zu sehen.
Auch die Übereinstimmung der geschätzten Anomalien ist vor 1912 gering, was hauptsächlich auf eine unzureichende Stichprobenauswahl zurückzuführen ist. Die ICOADS-Beobachtungen vor 1912 überschreiten in der Regel nie 5000 und erreichen zwischen 30°N und 45°N ihren Höhepunkt mit nur 9000 Beobachtungen. Zwar gibt es gute Gründe für alle in diesem Beitrag identifizierten Probleme und für alle von den HadSST- und ERSST-Teams vorgenommenen Korrekturen, doch bedeutet dies nicht, dass sie die richtige Antwort erhalten.
Daher war die globale durchschnittliche Meerestemperatur (SST), die wichtigste Komponente der globalen durchschnittlichen Temperatur, vor Anfang der 1990er Jahren weitgehend unbekannt, und selbst nach 1990 bestehen Zweifel. Die Zweifel am SST-Durchschnitt und die Zweifel an der Landaufzeichnung, zusammen mit der sehr geringen Erwärmung seit Beginn des 20. Jahrhunderts (etwa ein Grad), wecken, zumindest meiner Meinung nach, erhebliche Zweifel an den Schätzungen der modernen globalen Erwärmung. Ich bezweifle nicht, dass die Welt seit 1900 im Durchschnitt wärmer ist, aber ich glaube nicht, dass wir das Ausmaß der Erwärmung mit Sicherheit kennen. Ich glaube auch nicht, dass wir den Trend oder die Trends unbedingt richtig einschätzen. Ist ein Teil des „Buckels“ des Zweiten Weltkriegs real? Ich glaube nicht, dass wir das wissen.
References
Huang, B., Thorne, P. W., Banzon, V. F., Boyer, T., Chepurin, G., Lawrimore, J. H., . . . Zhang, H.-M. (2017). Extended Reconstructed Sea Surface Temperature, Version 5 (ERSSTv5): Upgrades, Validations, and Intercomparisons. Journal of Climate, 30(20). doi:10.1175/JCLI-D-16-0836.1
Kennedy, J. J., Rayner, N. A., Smith, R. O., Parker, D. E., & Saunby, M. (2011). Reassessing biases and other uncertainties in sea surface temperature observations measured in situ since 1850; 1. Measurement and sampling uncertainties. Journal of Geophysical Research, 116. Retrieved from https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2010JD015218
Kennedy, J. J., Rayner, N. A., Smith, R. O., Parker, D. E., & Saunby, M. (2011b). Reassessing biases and other uncertainties in sea surface temperature observations measured in situ since 1850: 2. Biases and homogenization. J. Geophys. Res., 116. doi:10.1029/2010JD015220
Kennedy, J., Rayner, N. A., Atkinson, C. P., & Killick, R. E. (2019). An ensemble data set of sea-surface temperature change from 1850: the Met Office Hadley Centre HadSST.4.0.0.0 data set. JGR Atmospheres, 124(14). Retrieved from https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2018JD029867
Rayner, N. A., Brohan, P., Parker, D. E., Folland, C. K., Kennedy, J. J., Vanicek, M., . . . Tett, S. F. (2006). Improved Analyses of Changes and Uncertainties in Sea Surface Temperature Measured In Situ since the Mid-Nineteenth Century: The HadSST2 Dataset. J. Climate, 19, 446-469. doi:10.1175/JCLI3637.1
Link: https://andymaypetrophysicist.com/2025/04/08/what-is-the-global-average-sst/
Übersetzt von Christian Freuer für das EIKE

















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Hier tagesaktuell die Entwicklung der Oberflächentemperatur der Meere.
Laut allgemeinem Narrativ wäre die Durschnittstempertur auf der Erde ohne Atmosphäre -18Grad Celsius. Durch den Treibhauseffekt der Atmosphäre steigt die Durchschnittstemperatur auf ca 15 Grad Celsius. Wie schafft es die durchschnittlich 15 Grad warme Atmosphäre die Ozeane auf durchschnittlich 21 Grad zu erwärmen?
Ich denke, dass ist irgend so ein Ding mit Physik, Herr Kneifel
Aha, und welches Ding sollte das sein?
Silke Kosch, ich hab da was passendes mit Physik:
https://de.sci.physik.narkive.com/i19J65lU/ist-die-hoelle-exotherm-oder-endotherm
„aber ich glaube nicht, dass wir das Ausmaß der Erwärmung mit Sicherheit kennen. Ich glaube auch nicht, dass wir den Trend oder die Trends unbedingt richtig einschätzen.“
Angesichts der vielen Messungenauigkeiten offenbar ein realistisches Resumee. Das nicht so ganz einfach nachzuvollziehen ist, aber trotzdem informativ!
Ceterum censeo, die «Berechnung» der «Welt-Durchschnitts-Temperatur» auf ein halbes Grad C genau, bzw. überhaupt, ist ein Verstoss gegen die elementaren Prinzipien der mathematischen Statistik! Versucht es doch zuerst mit der Durchschnitts-Temperatur eurer eigenen Wohnung!
Wenn man noch ein paar Zahlen zusammensucht, kann man sich ein schönes Rätsel basteln:
Die globale Oberflächentemperatur der Meere beträgt grob 22°.
Die Temp. der Ozeane sinkt mit zunehmender Tiefe gen 1° in 4000m Tiefe: https://eike-klima-energie.eu/2020/12/01/wassertemperatur-der-ozeane-aktualisierung/
Die Oberflächentemp. in Europa beträgt 6,03° lt: https://eike-klima-energie.eu/2025/04/11/europa-erlebt-den-waermsten-maerz-seit-beginn-der-aufzeichnungen-oder-seit-125-002-jahren-oder-so/
Die Temperatur des Planeten erhöht sich mit zunehmender Tiefe, es wurden in 14km 300° gemessen: https://de.wikipedia.org/wiki/Innerer_Aufbau_der_Erde
Ich hab hier schon mal gepostet, dass in allen Planeten außer Merkur und Mars, die zu klein sind, ein Reaktor brennt und schwere Elemente in leichte zerlegt, welche dann die Atmosphäre bilden. Der Venus bleibt nur CO2, weil der Sonnenwind alles Leichtere verbläst.
Die dabei freiwerdende Energie speist ein Feld. Mit diesem Feld wechselwirkt Materie, die mit dem Feld in Resonanz treten kann. Bei allen Prozessen treten Verluste in Form von Wärme auf.
Wasser hat eine Oberflächenspannung. Weil an der Oberfläche im übertragenen Sinn eine Bindungsmöglichkeit ins Leere ragt, hält sich das Molekül bei seinesgleichen stärker fest. Das erschwert Flucht durch Verdunstung erheblich. Da braucht es schon einen kräftigen Tritt, dass das Molekül aus seiner Gemeinschaft rausfliegt, wo es so wohlig geschaukelt wurde. Diesen Tritt gibt das Feld aus dem Zentrum. Die Oberflächenspannung verhindert die erneute Eingemeindung des Moleküls, das unter Abgabe von Energie erst kondensieren muss, um als Tropfen wieder eintauchen zu können.
Jedes verdunstete Molekül vermindert den Druck in der gesamten Wassersäule darunter, was Temperaturabfall bedeutet. Da Tiefseewasser ungefähr nur alle 1.000 Jahre ausgetauscht wird, werden die Tiefseebecken trotz der großen Hitze in relativ geringer Distanz bis auf 1°C runtergekühlt!
Also 300° Differenz auf weniger als 10 km Basalt oder Granit, mit einer Wärmedurchgangszahl von 2.8, wobei die Zeit mit rund 1.000 Jahren einzusetzen ist.
Das Energiefeld wechselwirkt mit der Wasseroberfläche, die Ozeane sind wärmer als die Kontinente, die geringere Wasserbedeckung haben. Aber dafür haben die Kontinente mehr Fläche durch Pflanzenbewuchs. Wachsen die Pflanzen im Winter nicht, wird’s wegen der geringeren Verdunstungsfläche noch kälter.
Das Leben basiert auf dieser Energie, erst wenn wir sie kennen, können wir überhaupt die Erde verlassen. Wer diese Energie nutzbar macht, hat nie mehr Probleme mit Wärmegewinnung auf der Erde.
Das ist das Rätsel.
Gemittelte Temperaturen zur Globalen Temperatur gemacht – Unfug.
Gemittelte historische (nicht vorhandene) Temperaturen zur globalen Temperatur gemacht – Unfug zum Quadrat, oder?
Gemittelte Temperaturen, auch mit Globaltemperaturen bezeichnet, sind das goldene Kalb der Klimakirche.
Schon gar nicht kann man aus so gerechneten Temperaturen in °C Erwärmung in Ws ableiten.
Ob den Mittlern der Meeres-Temperaturen schon aufgefallen ist, dass die unzähligen unterschiedlichen Zonen auch ganz unterschiedliche Tiefen von 0,01km bis 10km haben? –
Auch ja, das wird ja alles durch Adjustierungen in Großrechnern ähnlich Glaskugeln berücksichtigt.
Wichtig ist nur, dass die so adjustierten Ergebnisse einzig auf menschengemachtes CO2 zurück zu führen sind und darauf Steuern erhoben und die Menschen gängelt werden können.
Das ist falsch.
Richtig ist: Die Veränderung der globalen Meeresoberflächentemperatur ist eine sehr wichtige Komponente der globalen durchschnittlichen Temperatur.
Auch falsch!
Wie kann das eine falsch sein ohne das das andere nicht auch falsch ist?
Man nehme eine Münze, der Eine setzt auf Kopf, der Andere auf Zahl. Der Dritte kommt und behauptet, dass die Münze eine illegale Nachprägung sei.
Geht auch gar nicht anders. Werfen Sie vor POlitikern eine Münze mit Wert in die Luft.
Sie wird niemals den Boden erreichen…