von Untitled (call me Stephen)
Wie genau sind unsere historischen Temperatur-Aufzeichnungen?
Im Jahr 2021 brachte Bugatti den Chiron Super Sport 300+ auf den Markt. Die Bezeichnung „300+“ kommt daher, dass es sich um das erste Auto mit Straßenzulassung handelt, das Geschwindigkeiten über 300 km/h erreicht, obwohl die Serienmodelle elektronisch auf 271 km/h begrenzt sind.
Der Wagen kann in rund 40 Sekunden auf seine Höchstgeschwindigkeit von 490 km/h beschleunigen und in weniger als 15 Sekunden aus dieser Geschwindigkeit zum Stillstand kommen.
Der Tunnel im Dubliner Hafen wurde am 20. Dezember 2006 eröffnet. Technisch gesehen handelt es sich um zwei 4,5 km lange Tunnel, einen für jede Verkehrsrichtung.
Die Wände des Tunnels sind hart, im Gegensatz zu oberirdischen Autobahnen, die flexible Sicherheitsbarrieren haben. Ein Aufprall auf die Wände bei hohen Geschwindigkeiten wäre nicht nur für die Unfallbeteiligten tödlich, sondern könnte auch die strukturelle Integrität des Tunnels beschädigen.
Um die Verkehrsteilnehmer dazu zu bewegen, sich an die Geschwindigkeitsbegrenzung von 80 km/h zu halten, wurden Kameras zur Überwachung der Durchschnittsgeschwindigkeit installiert. Ein solches Kamerasystem besteht aus mindestens zwei Kameras (idealerweise aber mehr), die über die Region verteilt sind, in der die Geschwindigkeitsbegrenzung durchgesetzt werden soll.
Die billigste Variante wären zwei Kameras an jedem Tunnel, eine am Anfang und eine am Ende. Wenn der Zeitstempel Ihres Fahrzeugs beim Passieren der zweiten Kamera weniger als 202,5 Sekunden nach dem Passieren der ersten Kamera liegt, haben Sie die 4,5 km mit einer Durchschnittsgeschwindigkeit von mehr als 80 km/h zurückgelegt, was einen Strafzettel und Punkte für Ihren Führerschein zur Folge hat.
Besser wäre es, wenn mehr als zwei Kameras entlang des Tunnels verteilt wären, um zu verhindern, dass ein rücksichtsloser und idiotischer Chiron Super Sport 300+ Fahrer folgendes versucht…
– Fahren Sie mit einer rollenden Startgeschwindigkeit von 80 km/h in den Tunnel ein.
– Geben Sie Gas und erreichen Sie die Höchstgeschwindigkeit von 490km/h nach etwa 33,5s
– Halten Sie die Höchstgeschwindigkeit für etwa 1,5s.
– Bremse hart auf 30km/h über 3,5s
– Halten Sie die Geschwindigkeit von 30km/h für die restlichen 164 Sekunden der Fahrt.
Da dies genau 202,5 Sekunden dauert, ergibt sich bei nur zwei installierten Kameras pro Tunnel im Dubliner Hafentunnel eine Durchschnittsgeschwindigkeit von 80 km/h, obwohl die Geschwindigkeit des Autos zwischen 30 km/h und 490 km/h schwankte!
„Stephen, was genau haben der Bugatti Chiron Super Sport 300+ und der Dubliner Hafentunnel mit dem Vergleich der Temperaturen von gestern und heute zu tun“, höre ich Sie fragen. Bitte bleiben Sie dran. Ich hoffe, dass es Sinn macht, wenn Sie das Ende erreichen.
Das Thermometer ist eine relativ junge Erfindung. Während Galilei bereits 1603 mit Thermoskopen herumspielte, dauerte es bis 1724, als Daniel Gabriel Fahrenheit seine Thermometerskala vorschlug, bevor sich die Idee einer standardisierten Temperaturskala durchsetzte. Dass René-Antoine Ferchault de Réaumur und Anders Celsius 1732 und 1742 unterschiedliche und konkurrierende Normen vorschlugen, dürfte niemanden überraschen, der mit der Funktionsweise von Normen vertraut ist.
Leider konnte sich Réaumur mit seiner Wahl von 80 Grad zwischen Gefrier- und Siedepunkt von Wasser nicht durchsetzen.
Der größte Teil der Welt verwendet heute die Celsius-Skala, allerdings mit umgekehrten 0°C- und 100°C-Punkten gegenüber Anders‘ ursprünglichem Vorschlag. Nur die Vereinigten Staaten, die Bahamas, die Kaimaninseln, Palau, die Föderierten Staaten von Mikronesien und die Marshallinseln verwenden noch Fahrenheit.
Unsere frühesten tatsächlichen Temperaturmessungen, vor allem die aus der Zeit vor 1732, beruhen darauf, dass die Menschen entweder die ursprünglich verwendeten Thermometer später durch andere ersetzt oder ihre eigene Wahl der Referenz dokumentiert haben.
Es dauerte auch eine Weile, bis die Menschen herausfanden, wie sie die Temperatur messen konnten. Bei den meisten frühen Messungen handelte es sich um Innenraummessungen in unbeheizten Räumen, die einmal pro Tag aufgezeichnet wurden. Schließlich fand man heraus, dass das Thermometer zur Messung der Außentemperatur im Freien und im Schatten stehen musste.
Erst 1864 schlug Thomas Stevenson einen standardisierten Instrumentenschutz vor, und nach Vergleichen mit anderen Schutzvorrichtungen wurde 1884 sein endgültiger Entwurf für die Stevenson-Wetterhütte veröffentlicht.
Auch wenn wir heute über Leute lachen, welche die Außentemperatur mit einem Thermometer in einem unbeheizten Raum gemessen haben, weil der Raum eine große Wärmekapazität hat, d. h. es eine Weile dauert, bis er sich aufheizt und abkühlt, ist eine Messung in einem Raum pro Tag gar nicht so schlecht, um die durchschnittliche Außentemperatur zu messen.
Wenn man das Thermometer an einem gut belüfteten Ort im Freien aufstellt, z. B. in einer Stevenson-Wetterhütte, ändert sich die Temperatur sehr viel schneller. Wenn Sie die Durchschnittstemperatur messen wollen, muss man über den Tag und die Nacht verteilt mehrere Messungen vornehmen.
1780 erfand James Six ein Thermometer, das die Höchst- und Tiefsttemperaturen seit der Rückstellung festhielt. Da es jedoch auf Quecksilber zur Bewegung der Markierungen angewiesen war, konnte es bei niedrigen Temperaturen Probleme geben. Um 1790 hatte Daniel Rutherford Entwürfe für getrennte Minimum- und Maximum-Thermometer entwickelt, die mit Alkohol bzw. Quecksilber arbeiteten und eine größere Genauigkeit der beiden Messwerte ermöglichten.
Es sollte bis in die 1870er Jahre dauern, bis Minimum- und Maximumthermometer in großem Umfang zur Erfassung der Temperaturschwankungen eingesetzt wurden. Die längste Temperaturaufzeichnung, die Central England Temperature History, basiert zum Beispiel auf Beobachtungen für eine Vielzahl von Stunden vor 1877, wobei danach tägliche Tiefst- und Höchsttemperaturen verwendet wurden.
Meteorologen verwenden die täglichen Minimal- und Maximaltemperaturen, um die tägliche Durchschnittstemperatur zu schätzen, indem sie einfach den Durchschnitt der Minimal- und Maximaltemperaturen bilden. Dies wird als Taxn bezeichnet und die Formel lautet: Taxn=(Tmax+Tmin)/2.*
[*Anmerkung des Übersetzers: Das ist so nicht ganz richtig. Zumindest in Deutschland wurde die Mitteltemperatur steit den 1950er Jahren nach der Formel T07 + T13 + 2xT21/4 ermittelt. Mit der Einführung automatischer Sensoren wurden dann die stündlichen Temperaturwerte durch 24 geteilt. Am Institut für Meteorologie der Freien Universität Berlin wurden diese Mittelwerte mehrere Jahre lang parallel ermittelt. Die entsprechende Veröffentlichung war jedoch nicht mehr auffindbar. – Ende Anmerkung]
Verstehen Sie mich nicht falsch, wenn Sie nur die täglichen Minimal- und Maximaltemperaturen haben, ist die Mittelung der beiden die beste Schätzung, die Sie machen können, aber es ist nicht die tägliche Durchschnittstemperatur, die Tavg genannt wird, die Sie erhalten, wenn Sie die Temperatur idealerweise mehr als 20 Mal in gleichmäßigen Abständen über den 24-Stunden-Zeitraum messen und alle diese Ergebnisse mitteln.
Hier kommen der Bugatti Chiron Super Sport 300+ und der Dubliner Hafentunnel wieder ins Spiel. Wenn ich Ihnen sage, dass die Höchstgeschwindigkeit des Bugatti im Tunnel 490 km/h betrug und er nie langsamer als 30 km/h fuhr, würden wir bei Anwendung des Algorithmus der Meteorologen zu dem Schluss kommen, dass er im Durchschnitt mit (490+30)/2=260 km/h unterwegs war. Wir wissen jedoch von früher, dass es möglich ist, dass diese beiden Grenzwerte eine Durchschnittsgeschwindigkeit von 80 km/h ergeben.
Wenn man die Minimal- und Maximalgeschwindigkeiten im Tunnel bei 30km/h und 490km/h belässt, kann man eine Durchschnittsgeschwindigkeit zwischen 71km/h und 332km/h erreichen. Die von den Meteorologen ermittelte Durchschnittsgeschwindigkeit von 260 km/h liegt zwar in diesem Bereich, aber die Spanne ist recht groß.
Um ein weiteres Beispiel dafür zu geben, wie das Verfahren der Meteorologen zu einer Schätzung führen kann, die ein ganzes Stück daneben liegt: Nach Angaben des Irish Central Statistics Office [CSO] verdienten die obersten 1 % der Arbeitnehmer im Jahr 2022 mindestens 3 867 € pro Woche. Dagegen verdiente das untere 1 % der Arbeitnehmer höchstens 92 € pro Woche. Der durchschnittliche Wochenverdienst lag bei 856 € pro Woche, und nur 27 % der Arbeitnehmer verdienten mindestens diesen Betrag, wobei der mittlere Wochenverdienst 671 € betrug.
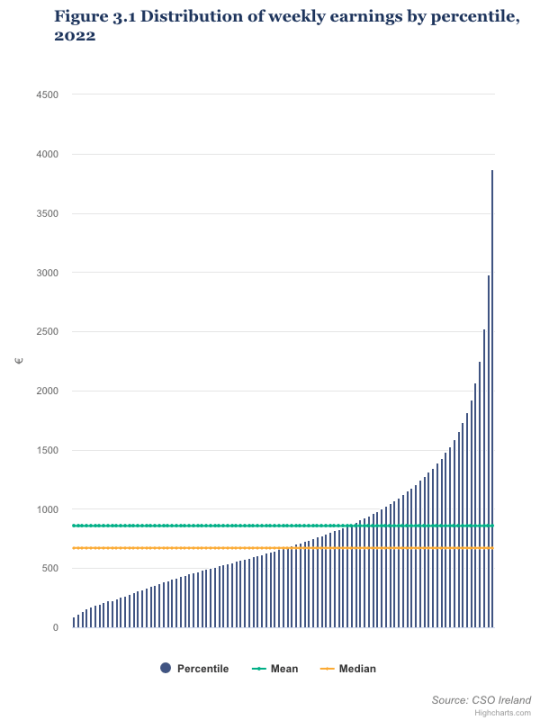
Quelle: CSO
Wenn wir den Durchschnitt von 3867 € und 92 € nehmen, sind das 1980 € pro Woche. Weniger als 6 % der Erwerbstätigen erhielten mindestens 1980 € pro Woche, so dass der Durchschnitt der Meteorologen bei der Schätzung des Einkommens oder der Durchschnittsgeschwindigkeit eines Bugatti im Hafentunnel ziemlich weit daneben liegt.
In den 1970er Jahren wurde es mit dem Aufkommen billiger Computer möglich, die Temperaturmessung zu automatisieren. Ein Computer hat keine Wahl: Wenn wir ihm sagen, er soll die Temperatur jede Stunde oder alle 5 Minuten messen, egal ob es regnet oder schneit, wird die Messung aufgezeichnet. Da die meisten Wetterstationen zwischen 1990 und 2010 auf automatische Messungen umgestellt haben, können wir jetzt die tatsächliche Durchschnittstemperatur, Tavg, messen.
Das Valentia Observatory liegt 1 km westlich von Cahirciveen, Co Kerry, und in diesem Gebiet wurde eine Wetterstation betrieben, die einige Temperaturaufzeichnungen für 1850-51 und kontinuierliche tägliche Min-Max-Aufzeichnungen seit Mitte Januar 1872 enthält. Die historischen Datensätze wurden sorgfältig transkribiert und sind bei Met Éireann erhältlich: 1850-1920 und 1921-1943. Im Jahr 1944 unternahm Met Éireann etwas Ungewöhnliches: Sie begannen, die Temperatur stündlich zu messen. Ob Regen oder Sonnenschein, Schneeregen oder Schnee, die fleißigen Mitarbeiter von Met Éireann gingen zur Wetterstation und zeichneten die Temperatur auf. Zwischen Januar 1944 und April 2012, als die Station durch eine automatische Station ersetzt wurde, wurden nur 2 Stunden ausgelassen. Der Datensatz ab 1944 ist auf der Website der irischen Regierung verfügbar: tägliche Zusammenfassung (einschließlich Mindest- und Höchsttemperatur) und stündliche Messungen.
Da sich die Messungen der Minimum- und Maximum-Thermometer und die 24 stündlichen Messungen für Valentia überschneiden, können wir überprüfen, wie groß die Differenz zwischen Tavg und Taxn ist, um zu sehen, wie genau das Verfahren der Meteorologen zur Schätzung der Durchschnittstemperatur aus Tmin und Tmax ist.
Das erste Diagramm zeigt die Differenz Tavg-Taxn für jeden Tag seit dem 14. Januar 1944 in Form von blauen Punkten. Überlagert wird der gleitende 1-Jahres-Durchschnitt durch eine rote Linie. Wenn Sie sich für die Statistik interessieren, ist Tavg in Valentia im Durchschnitt um 0,17ºC höher als Taxn (Standardabweichung 0,53, N=29339, min=-2,20, max=3,20).
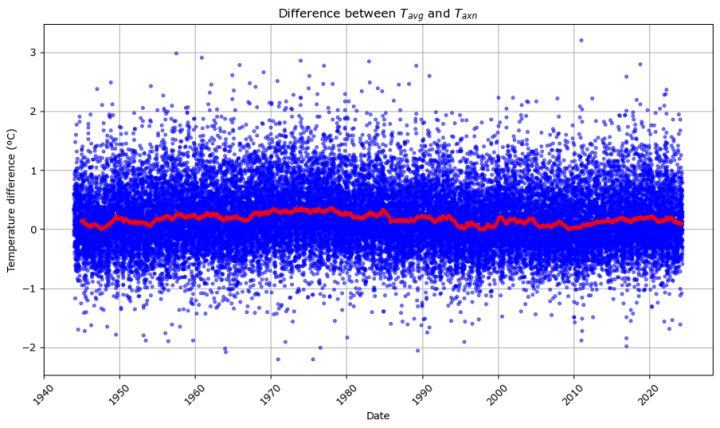
Quelldaten Copyright © Met Éireann und lizenziert zur Wiederverwendung unter CC-BY-4.0. Mathematische Analyse, Transformationen und visuelle Darstellung von Stephen Connolly.
Wenn wir nur den gleitenden Durchschnitt betrachten, sehen wir, dass die Beziehung nicht konstant ist. In den 1970er Jahren war die Durchschnittstemperatur zum Beispiel durchschnittlich 0,35 ºC höher als die meteorologische Schätzung, während es in den späten 1940er, 1990er und 2000er Jahren Gelegenheiten gab, bei denen die meteorologische Schätzung etwas höher war als die tatsächliche tägliche Durchschnittstemperatur.
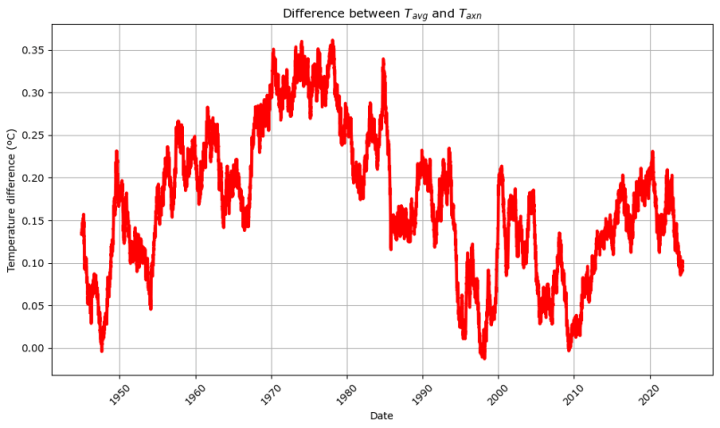
Quelldaten Copyright © Met Éireann und lizenziert zur Wiederverwendung unter CC-BY-4.0. Mathematische Analyse, Transformationen und visuelle Darstellung von Stephen Connolly.
Es ist wichtig zu betonen, dass diese mehrjährige Variabilität sowohl unerwartet als auch faszinierend ist, insbesondere für diejenigen, die Temperaturanomalien untersuchen. Abgesehen von der mehrjährigen Variabilität haben wir jedoch durch das Auftragen von fast 30.000 Datenpunkten auf die x-Achse vielleicht eine mögliche Erklärung dafür versteckt, warum die blauen Punkte typischerweise eine Streuung von etwa ±1ºC aufweisen… Ist die Streuung von ±1°C eine saisonale Variabilität?
Der kürzeste Tag des Jahres auf Valentia ist der 21. Dezember mit einer Tageslänge von etwa 7h55m. Der längste Tag des Jahres ist der 21. Juni mit einer Tageslänge von 16h57m. Am kürzesten Tag des Jahres hat die Sonne nur wenig Zeit, um die Luft aufzuheizen, und die meiste Zeit ist es dunkel, so dass wir davon ausgehen, dass Wärme verloren geht. Daher erwarten wir, dass die Durchschnittstemperatur im Winter näher an der Tiefsttemperatur liegt als im Sommer.
Wir können die jahreszeitlichen Auswirkungen auf die Differenz zwischen Tavg und Taxn überprüfen, indem wir uns eine zeitabhängige Korrelation ansehen. Da nicht jeder mit dieser Art der Analyse vertraut ist, zeige ich Ihnen zunächst die zeitabhängige Korrelation von Tavg mit sich selbst:
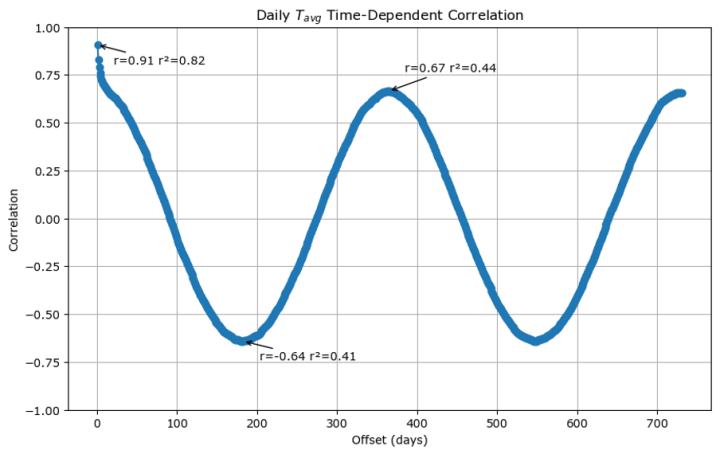
Quelldaten Copyright © Met Éireann und lizenziert zur Wiederverwendung unter CC-BY-4.0. Mathematische Analyse, Transformationen und visuelle Darstellung von Stephen Connolly.
Die x-Achse gibt an, wie viele Tage zwischen den Messungen liegen, und die y-Achse ist der Pearson-Korrelationskoeffizient, bekannt als r, der misst, wie ähnlich die Messungen im Durchschnitt aller Daten sind. Ein Pearson-Korrelationskoeffizient von +1 bedeutet, dass die Veränderungen in der einen Variable genau mit den Veränderungen in der anderen übereinstimmen, ein Koeffizient von -1 bedeutet, dass die Veränderungen genau entgegengesetzt sind, und ein Korrelationskoeffizient von 0 bedeutet, dass die beiden Variablen keine Beziehung zueinander haben.
Der erste Punkt auf der x-Achse steht für einen Abstand von 1 Tag zwischen den durchschnittlichen Temperaturmessungen.
Die einfachste Wettervorhersage ist die folgende:
„Morgen wird das Wetter im Wesentlichen so wie heute“
Der r-Wert von +0,91 für den Abstand von einem Tag veranschaulicht die Genauigkeit der trägsten Wettervorhersage und deutet darauf hin, dass sie für die Durchschnittstemperatur zu etwa 82 % richtig ist.
Bei einem Abstand von einem halben Jahr ergibt sich ein r-Wert von -0,64, der besagt, dass in sechs Monaten 41 % der durchschnittlichen Tagestemperatur als das Gegenteil der heutigen Temperatur erklärt werden können.
Im Abstand von einem Jahr beträgt der r-Wert 0,67, was bedeutet, dass 44 % der heutigen Durchschnittstemperatur als saisonal für diese Jahreszeit erklärt werden können. Das bedeutet, dass die einfachste Wettervorhersage nur 38 % besser erklärt als die saisonale Vorhersage.
Sie sehen sehr ähnliche Graphen, wenn Sie die zeitabhängige Korrelation von Tmax, Tmin oder Taxn betrachten, wobei die 1-Tages-r-Werte bei 0,90, 0,81 bzw. 0,90 liegen und die saisonale Schwankung etwa -0,6 bis +0,6 für 6 Monate und 1 Jahr beträgt.
Das obige Schaubild zeigt uns im Grunde, was zu erwarten ist, wenn etwas stark saisonabhängig ist.
Was passiert, wenn wir die zeitabhängige Korrelation von Tavg-Taxn darstellen? Nun, man erhält dies:
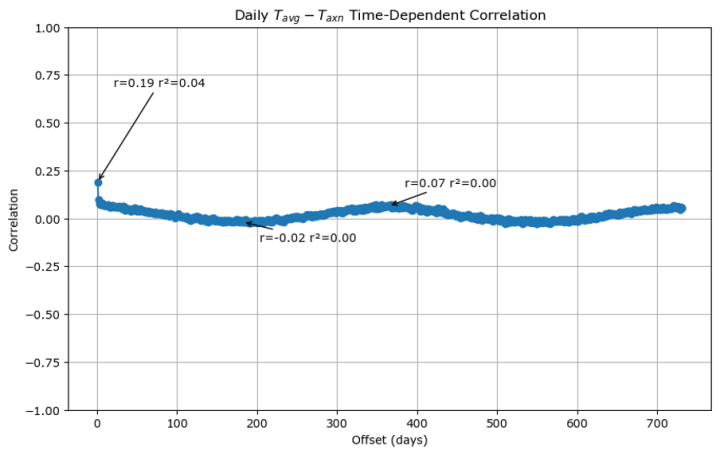
Quelldaten Copyright © Met Éireann und lizenziert zur Wiederverwendung unter CC-BY-4.0. Mathematische Analyse, Transformationen und visuelle Darstellung von Stephen Connolly.
Die 1-Tages-Korrelation beträgt 0,19, was bedeutet, dass etwa 4 % des heutigen Korrekturfaktors zwischen Tavg und Taxn vorhergesagt werden können, wenn wir den gestrigen Korrekturfaktor kennen. Die Saisonalität ist sogar noch schlechter, der Korrelationskoeffizient für 6 Monate beträgt -0,02 und der Korrelationskoeffizient für 1 Jahr +0,07.
Dies beantwortet unsere frühere Frage… Die Streuung von ±1°C ist keine saisonale Variabilität.
Das bedeutet, dass, wenn wir nur Taxn kennen, Tavg überall ±1°C betragen könnte.
Hier ist ein weiteres Diagramm, um dies zu veranschaulichen. Die x-Achse ist Tavg und die y-Achse ist Taxn. Wenn die durchschnittliche Tagestemperatur höher ist, ist natürlich auch die durchschnittliche Tiefst- und Höchsttemperatur höher und wir erhalten eine gerade Linie mit der Steigung 1, aber die Dicke der Linie stellt die Unsicherheit der Beziehung dar. Wenn wir also wissen, dass Taxn bei 15°C liegt, können wir aus diesem Diagramm schließen, dass Tavg wahrscheinlich zwischen 13,5°C und 16,5°C liegt.
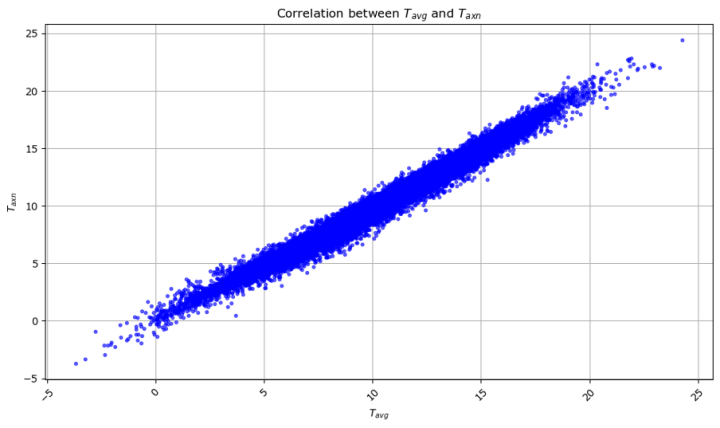
Quelldaten Copyright © Met Éireann und lizenziert zur Wiederverwendung unter CC-BY-4.0. Mathematische Analyse, Transformationen und visuelle Darstellung von Stephen Connolly.
Da die meisten Wetterstationen bis vor kurzem nicht stündlich aufzeichneten, sind die meisten unserer historischen Temperaturdaten in der Taxn-Form und nicht in der Tavg-Form. Das bedeutet, dass, wenn Valentia repräsentativ ist, die vergangenen Temperaturaufzeichnungen nur auf ±1°C genau sind. Wenn Ihnen jemand sagt, dass die Durchschnittstemperatur in Valentia am 31. Mai 1872 11,7 °C betrug, dann wissen wir das einfach nicht. Mit 95-prozentiger Wahrscheinlichkeit lag sie irgendwo zwischen 10,6ºC und 12,7ºC, und wir haben keine Möglichkeit, den genauen Wert herauszufinden, so wie die Kenntnis der Höchst- und Mindestgeschwindigkeiten des Bugatti im Hafentunnel nicht wirklich viel über seine durchschnittliche Geschwindigkeit aussagt.
In diesem letzten Diagramm zeigen die blauen Punkte den durchschnittlichen Taxn jedes Jahres in Valentia seit 1873 mit vertikalen Fehlerbalken, die das 95%-Konfidenzintervall anzeigen. Die roten Punkte zeigen den durchschnittlichen Tavg-Wert für jedes Jahr ab 1944, wobei die Fehlerbalken die jährlichen Schwankungen anzeigen. Das Blau, das unter dem Rot hervorsticht, zeigt den Unterschied zwischen der von den Meteorologen geschätzten Durchschnittstemperatur und der tatsächlichen Durchschnittstemperatur, selbst auf der Skala eines Jahresdurchschnitts:
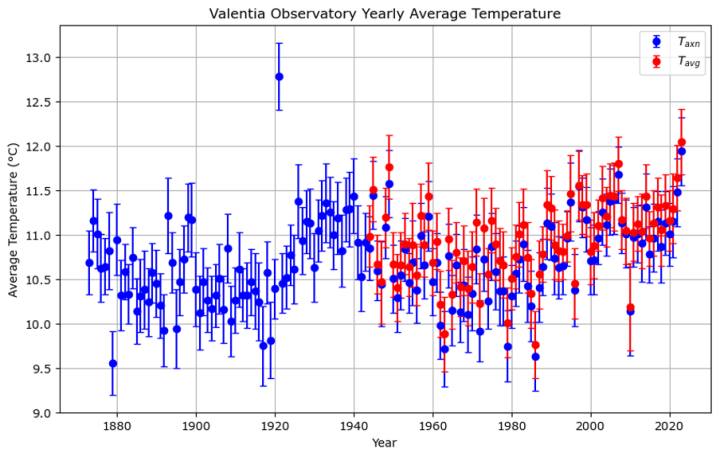
Quelldaten Copyright © Met Éireann und lizenziert zur Wiederverwendung unter CC-BY-4.0. Mathematische Analyse, Transformationen und visuelle Darstellung von Stephen Connolly.
Das Valentia Observatory ist eine der besten Wetterstationen der Welt. Seit der Umstellung auf automatisierte Stationen in den 1990er Jahren können wir nun genaue Durchschnittstemperaturen ermitteln.
Dank der akribischen Arbeit der früheren und heutigen Mitarbeiter des Valentia Observatory und von Met Éireann verfügen wir über 80 Jahre an Daten, die einen Vergleich der alten Schätzmethoden mit den tatsächlichen Durchschnittswerten ermöglichen.
Die Schlussfolgerung?
Unsere historischen Temperaturaufzeichnungen sind weit weniger genau, als wir einst glaubten.
Link: https://wattsupwiththat.com/2024/06/01/comparing-temperatures-past-and-present/
Übersetzt von Christian Freuer für das EIKE
















Wenn an einem Meßpunkt über 24 Stunden irgend ein Temperaturgang herrscht, kann man daraus zwar mathematisch nach verschiedenen Regeln Mittelwerte bilden, aber das ist dann keine Temperatur mehr, sondern ein Rechenwert. Wie tückisch so ein Vorgang ist, erkennt man am folgenden Beispiel: Wenn man 8°C und 10°C mittelt, ist das Ergebnis 9°C. Wenn man 2°C und 16°C mittelt, ist das Ergebnis auch 9°C. Was also sagt ein Mittelwert 9°C über das konkrete Temperaturgeschehen aus?
Wenn man schon Mittelwerte bildet, dann muß zumindest der betrachtete Ort konstant bleiben. Aber einen einzigen Mittelwert über ein ganzes Jahr über einen ganzen Planet zu bilden, ist sowohl logischer als auch physikalischer Unsinn, weil es um Energie geht und Energie nicht in °C meßbar ist. Temperatur ist intensiv, Energie ist extensiv.
In der „wissenschaftlichen Klimatologie“ werden grundsätzliche Fragen wie diese selten bis nie behandelt. Oder kennt wer eine Definition, wie die Klimatologen die aktuelle „Weltmitteltemperatur“ bestimmen, die ja angeblich bereits um ca. 1,5°C höher sein soll als der Vergleichswert „Vorindustriell“? Aber auch wie der Vergleichswert Vorindustriell bestimmt wurde und für welchen Zeitpunkt er gilt, ist nicht definiert. Oder kennt wer den konkreten Wert „Vorindustriell“ und wieso er und genau er als Referenz angenommen wird?
„Oder kennt wer eine Definition, wie die Klimatologen die aktuelle „Weltmitteltemperatur“ bestimmen….“
Aber Herr Strasser, das ist doch das bestgehütete Geheimnis der Klima-Pseudowissenschaft, Sie sollen doch nicht mitdenken, sondern glauben!
Selbst ein Rahmstorf muss dafür seine gehätschelte Greta befragen, weil er durch seine eigenen Programme nicht mehr durchblickt. Und wenn er selbst merkt, dass jegliche Temperaturmittelung totaler physikalischer Schwachsinn ist, rettet er sich auf eine Hütte auf einem Berg und misst dann deren Höhe aus, ohne zu wissen auf welchem Berg er ist und ohne zu wissen, wie hoch der Berg selbst ist. Solche Beispiele kennzeichnen doch das wirkliche Genie.
Reicht Ihnen das nicht, vom größten Wissenschaftler aller Zeiten, herangezüchtet von einem Selbstverbrenner Schellnhuber, zu erfahren, wie einfach es ist, Temperaturen zu mitteln und darüber hinaus Temperatur-Anomalien zu bestimmen? – Packen wir das Ganze am Besten unter „künstliche Intelligenz“, echte ist es ja nun einmal wirklich gar nicht. Das heißt nicht, dass man damit nicht irgendwie seinen Lebensunterhalt zusammenbekommt!
Wir haben also keine genauen Temperaturdaten früherer Epochen, d.h. wir haben keine genauen Klimadaten früherer Epochen.
Wer also die Hoheit über Temperturschätzungen erringt, der erringt die Hoheit über die Klimadatenauswertung.
Wer sodann mit gemittelten Globaltemperaturen, also Unfugtemperaturen, den Diskurs bestimmt, ist am Ziel und kann sich Gründer einer neuen Religion nennen, oder?
Temperatur ist eine von Menschen erschaffene Ersatzgröße, die unter bestimmten Umständen in einer Größe in °C oder K etwas angeben kann, was in einem homogenen und eingeschwungenem System einen Rückschluss auf den Energiegehalt dieses System erlauben kann. Eine Tasse Tee ist nicht warm, weil sie eine Temperatur hat, sondern weil sie eine Energie beinhaltet, aus der lediglich eine Temperatur abgeleitet werden kann. Temperatur ist eine geschaffene Messgröße, keinesfalls eine Wirkgröße.
Mit diesem Grundverständnis ergibt sich Folgendes für den Wärmeausgleich zwischen einem warmen und einem kalten Körper, die thermisch aneinander gekoppelt werden:
Der Wärmefluss von warm nach kalt ergibt sich nicht aufgrund eines Temperaturunterschiedes, sonst könnte er nur in Systemen stattfinden, wo mit entsprechenden Messgeräten, die von Menschen geschaffen wurden, Temperaturen gemessen werden können. Das ist für den Rest des Universums auszuschließen, dennoch wirkt die Physik auch dort ohne Ausnahme entsprechend.
Der Wärmefluss von warm nach kalt bis zum Ausgleich (Ruhe) wird also nicht durch die Temperatur gesteuert, sonst müssten der vormals kältere Körper und der vormals wärmere Körper sich irgendwann zurufen können: „Stopp, aufhören mit dem Energiefluss von warm nach kalt, wir haben jetzt beide die gleiche Temperatur“. Da die Körper selbst keine Temperatur kennen, können sie sich auch nichts zurufen, was zu einer Beendigung des energetischen Ausgleichsprozesses führt. (Mit „zurufen“ ist hier ein Informationsaustausch gemeint.)
Der Ausgleich funktioniert also unbestreitbar mit einem Mechanismus, der sich nicht an Temperaturen orientiert. Und er funktioniert auch, wenn sich die Massen der beiden Teilsysteme unterscheiden.
Ohne auf die Physik dieses thermodynamischen Vorgangs tiefer einzugehen, lässt sich eines ganz sicher ableiten, Temperaturen oder gar gemittelte Temperaturen sind für diese Ausgleichsprozesse weder erforderlich noch hilfreich, noch spielen sie überhaupt eine Rolle. Schon allein, weil sie außer von bestimmten Vertretern auf dieser Erde im gesamten restlichen Universum gar nicht existent sind und zu irgendetwas benötigt werden.
Wer immer noch Temperaturen, Temperaturmittelwerte oder gar Globaltemperaturen als Basis für Erderwärmung oder Erdabkühlung heranzieht und dies in kunstvollen Rechnungen als physikalisch zulässig verteidigt, möge sich einmal intensiv damit auseinandersetzen, warum das gesamte Universum energetische Ausgleichsprozesse seit dessen Existenz erfolgreich durchführt, ohne Temperaturen, deren Mittelwerte oder auf die Erde bezogen Globaltemperaturen zu kennen und überhaupt zu benötigen. – Eine lohnenswerte Aufgabe, die nur zu einem einzigen Ergebnis führen kann: Temperaturmittelwerte oder Globaltemperaturen sind rein zu gar nicht zu gebrauchen, es sei denn, man hat Freude daran, ein hochkomplexes thermisches Ausgleichssystem mit einer einzigen Zahl zu beschreiben, was schon deshalb unsinnig ist, weil es sich ja nicht um ein einfach beschreibbares eingeschwungenes System handelt, sondern eben um ein hochkomplexes System, welches aus Millionen jeweils unterschiedlichen Einzelsystemen gebildet ist.
Besonders niederträchtig ist, dass man eine Temperatur gar nicht messen kann. Ein Quecksilberthermometer reagiert nicht auf irgendeine Temperatur, sondern reagiert mit der Ausdehnung seiner Substanz auf einen neuen energetischen Status. Erst danach wird von Menschenhand ein ablesbarer Temperaturwert in Form einer Skala erzeugt. Das gilt analog auch für andere „Temperaturmesssysteme“, die über energetische Veränderungen Widerstands- oder z. B. Spannungsänderungen bewirken.
Sehr geehrter Herr Mechtel,
es fällt mit schwer, einen Bezug zu meinem Artikel zu erkennen. Es ging dabei weniger um Messtechnik, sondern um den Missbrauch anzeigbarer Messgrößen (Temperatur), die nur in Ausnahmefällen bei exakter Systembeschreibung und im eingeschwungenen Zustand in Bezug auf die im System vorhandene Wärmeenergie einen Schluss zulassen.
Wer diese bedingungslosen Erfordernisse ignoriert und dann mit gemittelten Temperaturen in einem falschen und unzulässigen Umkehrschluss eine Globaltemperatur heranzieht, um daraus eine Erderwärmung oder Erdabkühlung daraus abzuleiten, mag ja die von ihm erdachten Rechenoperationen richtig ausführen. Dennoch wird verkannt, dass der Ansatz vom Grunde her falsch ist und damit das Ergebnis lediglich eine aussagelose Zahl ist, die mit Physik nichts mehr zu tun hat.
Um überhaupt etwas präsentieren zu können, was nicht schon allein dem Wärme- oder Kälteempfinden der Menschheit entgegensteht, sind eben die vielen (unbekannten) Adjustierungen und Homogenisierungen erforderlich, die natürlich – wie bei einem politischen Programm – gut und nicht nachprüfbar begründet werden.
Dabei erhebt sich noch die Frage, warum sich niemand dieser Pseudowissenschaftler für den Temperatursprung 1987 / 1988 interessiert und eine plausible Erklärung präsentiert, ob es sich um Messfehler, Rechenfehler, Adjustierungsfehler oder ein globales Erdbeben mit globaler Energiefreisetzung handelt. – Oder kam z. B. für eine sehr überschaubare Zeit plötzlich eine zweite Sonne ins Spiel, die kein Mensch bemerkt hat?
Um die Wärmeleitung zu berechnen, sind in der Regel vier Schritte notwendig1:
Wie man sieht, hantiert man nicht mit der Differenz der Wärmeinhalte der beiden Enden, sondern mit der Differenz der Temperaturen. Ganz ähnlich das Ohm’sche Gesetz: Der el. Strom ergibt sich aus der Spannungsdifferenz multipliziert mit der el. Leitfähigkeit. Temperatur und Spannung sind keine Energien, sondern Potentiale, die bestimmen, in welche Richtung der Energiestrom fließt.
Der Menschheit ist bisher nichts besseres eingefallen, als die Temperaturen zu messen, um eine Aussage über kalt oder warm zu treffen. Würde man stattdessen Wärmeinhalte angeben, woher auch immer man die nimmt, dann könnte kein Mensch etwas damit anfangen.
Ganz anders der Energiegehalt und Energiefluss von Nahrung, z.B. Schokolade: Der Energiefluss wird von Appetit und Essverhalten gesteuert und kommt ganz ohne Temperaturen und el. Spannung aus…
Ich finde es immer wieder ernüchternd, was so genannte „gebildete Menschen“ der thermodynamischen Größe der Temperatur (Zustandsgröße) zuschreiben bzw. nicht zuschreiben.
Es ist metrologisch unmöglich, die Temperatur über die mittlere Energie von Teilchen oder gar über Entropieänderungen und Wärmemengen/-energien zu bestimmen, da niemand weiss, wie man diese Größen mit einer vernünftigen Genauigkeit und Methode messen könnte. Die Temperatur ist als skalare systemeigene makroskopische Größe bereits definiert, bevor man sie mit mikroskopischen Begriffen verknüpft und lange bevor man Änderungen der Gesamtentropie und/oder Gesamtenergie abschätzen kann.
Zum Beispiel: Die Temperaturen zweier unterschiedlich großer Körper (Systeme) im „Wärmekontakt“ werden sich spontan immer nur annähern. Das thermische Gleichgewicht (Spezialfall vom thermodynamischen Gleichgewicht) ist erreicht, wenn beide Körper dieselbe Temperatur haben. Die Begriffe Entropie, Wärmemenge/-energie, Wärmekapazität, Masse usw. werden dafür nicht benötigt. Die Temperatur als systemeigene Größe ist nicht an die Größe vom System und die Stoffeigenschaften gebunden.
+ PTB: Themenschwerpunkt Temperatur
https://oar.ptb.de/files/download/310.20070399.pdf
Siehe auch:
+ PTB: Wie viel Energie steckt in der Temperatur?
https://oar.ptb.de/files/download/310.20160207.pdf
Auszug:
Die für die Verteilung der charakteristische Größe ist darin die mittlere mikroskopische thermische Energie kT, die mit der Proportionalitätskonstanten k linear mit der Temperatur wächst. Durch Festlegung ihres Wertes wird in Zukunft das Kelvin direkt mit der Energieeinheit Joule verknüpft. Streng genommen wäre also gar keine eigene Temperatureinheit mehr notwendig, allerdings müssten dann alle Thermometer Joule anzeigen. Das ist aus vielen Gründen nicht praktikabel und durchsetzbar.
Wie formulierte es mein ehemaliger Professor für Angewandte Physik: „Die Temperatur (Energiestärke bzw. „Wärmestärke“) entspricht einer Zustandsgröße der ursächlichen energetischen Prozesse auf der betrachteten Längen- und Zeitskala.“
„+ PTB: Wie viel Energie steckt in der Temperatur?“
Gibt es irgendeine Erkenntnis, dass in der Temperatur eine von Null verschiedene Energie „steckt“?
Ich antworte mal auf die präzise Frage genauso präzise.
Es gibt noch die so genannte „Nullpunktsenergie“, die sich beim absoluten Temperaturnullpunkt ergeben soll, wenn man annimmt, dass die „quanten-theoretischen Betrachtungen“ der Realität entsprechen.