In meinem vorherigen Beitrag über die multiple Regression bekannter Sonnenzyklen im Vergleich zu HadCRUT5 [in deutscher Übersetzung hier] habe ich einfach die Sonnenzyklen, ENSO und Sonnenflecken in den Regressionsmixer geworfen und das Ergebnis mit verschiedenen Modellen verglichen, die CO₂ enthalten. vor der Lektüre dieses Beitrags sollten man den vorherigen Beitrag lesen, da sich ein Großteil dieses Beitrags auf die darin enthaltenen Informationen stützt. Es handelte sich um eine sehr einfache statistische Analyse, die zeigen sollte, dass die Schlussfolgerung des IPCC, wonach der Anstieg von CO₂ und anderen Treibhausgasen für die Erwärmung von 1,1 °C seit 1850-1900 „verantwortlich“ ist, wahrscheinlich falsch ist. Die Differenz zwischen dem HadCRUT5-Durchschnitt von 1850-1900 und dem von 2018-2023 (bis zum gesamten Jahr 2022) beträgt 1,18 °C, d. h. sie sagen, dass im Wesentlichen die gesamte Erwärmung seit dem 19. aufgrund menschlicher Einflüsse vonstatten ging. Die in diesem Beitrag beschriebenen Analysen zeigen, dass sie sich ihrer Schlussfolgerung nicht sicher sein können, haben sie doch überzeugende Beweise dafür ignoriert, dass Veränderungen der Sonne zumindest einen Teil der Erwärmung verursacht haben.
Wir haben gezeigt, dass verschiedene statistische Kombinationen bekannter Sonnenzyklen mit HadCRUT5 genauso gut oder manchmal sogar besser als Änderungen der CO₂-Konzentration korrelieren. Die Art und Weise, wie die Sonne unser Klima beeinflussen könnte, ist unbekannt. Der IPCC betrachtet nur die direkte Auswirkung der sich ändernden Gesamt-Sonneneinstrahlung (oder TSI) direkt auf die Erde, als ob die Sonne eine Glühbirne über einem Blatt Papier wäre, aber das kann nicht stimmen. Der Klimaeffekt der solaren Veränderungen während eines einzigen 11-jährigen Sonnenzyklus‘ [1] ist fast eine Größenordnung größer als die Veränderung der Sonneneinstrahlung ausmachen kann.
In letzter Zeit wurden große Fortschritte bei der Modellierung und dem Verständnis des solaren Dynamos gemacht. Die Modellierung vieler wichtiger Elemente bei der Entstehung von Sonnenzyklen liegt jedoch nach wie vor außerhalb unserer Möglichkeiten. Wir wissen nur, dass ihre Auswirkungen auf das Klima der Erde viel größer sind als die Änderung der von der Sonne während des Zyklus‘ empfangenen Energie. Wir können den Zusammenhang zwischen den bekannten (aber schlecht verstandenen) Sonnenzyklen und dem Klimawandel untersuchen, aber wir können die beteiligten Prozesse nicht erklären.
Wie zusätzliches CO₂ die Erdoberfläche erwärmen kann, ist bekannt, aber die Klima-Sensitivität [2] für CO₂ ist nicht bekannt. Jüngste veröffentlichte Schätzungen der Empfindlichkeit reichen von nahezu Null bis über 5°C/2xCO₂ (2xCO₂ bedeutet eine Verdoppelung der CO₂-Konzentration). Der IPCC behauptet, dass das vom Menschen erzeugte CO₂ und andere menschliche Aktivitäten die gesamte (oder im Wesentlichen die gesamte) jüngste Erwärmung verursacht haben. Dies ist Spekulation. Wir wissen nicht, inwieweit sich CO₂-Veränderungen auf das Klima auswirken können, und wir können die großen beobachteten Auswirkungen nicht durch solare Veränderungen erklären [3] – wie können wir also wissen, dass die gesamte beobachtete Erwärmung auf CO₂ und menschliche Aktivitäten zurückzuführen ist? Der Vorteil der CO₂-Hypothese besteht darin, dass der Prozess bekannt ist, aber da das Ausmaß des Effekts nicht genau berechnet werden kann, ist er quantitativ genauso unbekannt wie der solare Effekt, den der IPCC eindeutig unterschätzt. [4]
In diesem Beitrag werden wir uns die Korrelation zwischen Sonnenaktivität und HadCRUT5 genauer ansehen und auf einige der vielen Kommentare zu meinem vorherigen Beitrag eingehen. Erstens Überanpassung.
Überanpassung
Die solaren Zyklen werden nicht verstanden, können aber in Studien mit kosmogenen Isotopen beobachtet werden, die zur Dokumentation der sehr langen Hallstatt- (oder Bray-Zyklus, 2400 Jahre, ±200 Jahre) und Eddy-Zyklen (1000 Jahre ±30 Jahre) verwendet wurden. Diese beiden langen Zyklen korrelieren mit den bedeutendsten Klimaereignissen der Geschichte, der Bray-Zyklus mit dem griechischen Dunklen Zeitalter (~ 1200 bis 800 v. Chr.) und dem frühen Teil der Kleinen Eiszeit (~ 1300 bis 1600, als Hallstatt-Tiefpunkt nehmen wir 1470 an). Der Eddy-Zyklus korreliert mit der mittelalterlichen Warmzeit (~ 950 bis 1250), dem letzten Teil der Kleinen Eiszeit (~ 1500 bis 1816, wir peilen 1680 als Eddy-Tief an) und der modernen Warmzeit (~ 1940 bis ~ 2005) [5].
Die kürzeren Zyklen sind klimatisch nicht so bedeutsam, aber dennoch spürbar. Sowohl die „Pause“ in der Erwärmung als auch die kühle Periode um 1910 korrelieren gut mit dem Feynman-Zyklus, und die kühlere Periode von 1945 bis 1976 im frühen Teil des modernen Sonnenmaximums korreliert mit dem Pentadenkadenzyklus. Alle diese Zyklen sind für den instrumentellen Zeitraum in Abbildung 1 zusammen mit HadCRUT5 aufgetragen:
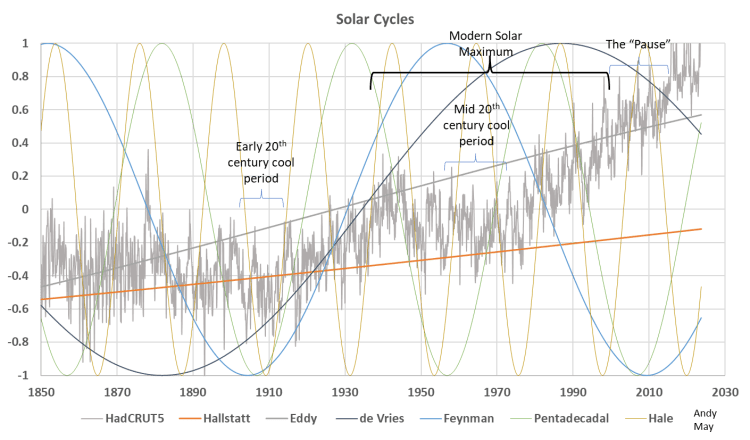
Abbildung 1. Die bekannten Sonnenzyklen, aufgetragen für die instrumentelle Ära zusammen mit der HadCRUT5-Aufzeichnung der globalen Temperatur.
Wie einige in den Kommentaren zu meinem letzten Beitrag anmerkten, wird die multiple Regression bei so vielen Zyklen immer eine vernünftige Anpassung an fast alles finden, was nach oben tendiert. Außerdem sind alle Zeitreihen, einschließlich HadCRUT5, stark autokorreliert. Die Zyklen sind an den solaren Tiefst- oder Höchstständen verankert, wie in den Veröffentlichungen von Ilya Usoskin (2016 und 2017) [6] oder Joan Feynman (2014) beschrieben. [7] Der 22,1-jährige Hale-Zyklus ist Anfang 2020 während des solaren Minimums des Zyklus 24 verankert. Es wurde vorgeschlagen, dass der de Vries-Zyklus eine Schwebungsperiode zwischen dem Hale-Zyklus und der 19,86-jährigen Umlaufbahn der Sonne um das Baryzentrum des Sonnensystems ist; [8] diese Konfiguration stimmt mit dieser Hypothese überein.
Wie in Abbildung 2 zu sehen ist, stützt sich diese Regression hauptsächlich auf die quasi-linearen Hallstatt- und Eddy-Zyklen. Frank Stefani hält nichts von dieser Idee und ist der Ansicht, dass nur die besser dokumentierten Feynman- und de Vries-Zyklen und Log(CO₂) benötigt werden, um den Zeitraum von 1850 bis heute zu modellieren. Dies ist möglich, denn Log(CO₂) ist ebenfalls eine quasi-lineare Reihe und ähnelt den Eddy- und Hallstatt-Reihen (siehe den ersten Beitrag), so dass alle drei einander ersetzen können, ein Argument, das nicht so bald durch Beobachtungen ausgeräumt werden wird.
Da der Sonnendynamo nicht vollständig verstanden ist [9], haben wir keine andere Wahl, als die beste Regression dieser Zyklen auf HadCRUT5 als unser Sonnenmodell zu wählen. Mir ist klar, dass Regressionen auch mit anderen Konfigurationen der Zyklen möglich sind, aber wir haben eine solide Grundlage für diese Konfiguration. Die Regression ist in Abbildung 2 dargestellt:

Abbildung 2. Ein multiples Regressionsmodell von HadCRUT5, das nur die bekannten Sonnenzyklen verwendet. Die Koeffizienten (Gewichte) für jeden der Zyklen sind aufgelistet, die Regressionsstatistiken sind in den Kästen angegeben. Der Rückgang der globalen Temperaturen von 1944 bis 1976 wird nicht sehr gut modelliert, ansonsten leistet das Modell gute Arbeit.
Da die Eingabezyklen und HadCRUT5 autokorreliert sind, sind die dargestellten Regressionsstatistiken (insbesondere R²) gegenüber der Realität überhöht. Experimente zeigen, dass die meisten Zykluskonfigurationen zu R²-Werten über 0,8 führen würden, obwohl einige weit darunter liegen. Dieser R²-Wert von 0,83 ist nicht großartig, aber er ist das Beste, was mit diesen Zyklen erreicht werden kann, und das ist es, was wir wollten.
Auf diese Weise haben wir eine einzige Variable zur Vorhersage des Sonnenzyklus geschaffen. Der Grund für die Zyklen ist nur sehr unzureichend bekannt. Dies ist eine statistische Übung, und es ist die beste Übereinstimmung dieser Prädiktoren mit HadCRUT5, aber das ist alles, was wir sagen können.
Als Nächstes fügen wir weitere Variablen hinzu, die sich in unserer Residual- und Teilregressionsstudie als signifikant erwiesen haben. Dabei handelt es sich um den Nino-3.4-Index und den Logarithmus zur Basis 2 der CO₂-Zeitreihe oder „Log(CO₂)“. Seltsamerweise führte die Hinzufügung der Nino 3.4-Reihe, zumindest statistisch gesehen dazu, dass die Sonnenfleckenreihe zu einem unbedeutenden (etwa 1 %) Zusatz in der Regression wurde. Infolgedessen konnte die Sonnenfleckenreihe nicht in die Regression aufgenommen werden, und die Nino-3.4-Reihe war immer mit über 10 % signifikant. Dies könnte auf die von Warren White und seinen Kollegen in Scripps beschriebene Auswirkung des Sonnenzyklus auf die Temperaturen im oberen Ozean zurückzuführen sein [10]. Abbildung 3 zeigt die Regression mit hinzugefügtem Nino 3.4:
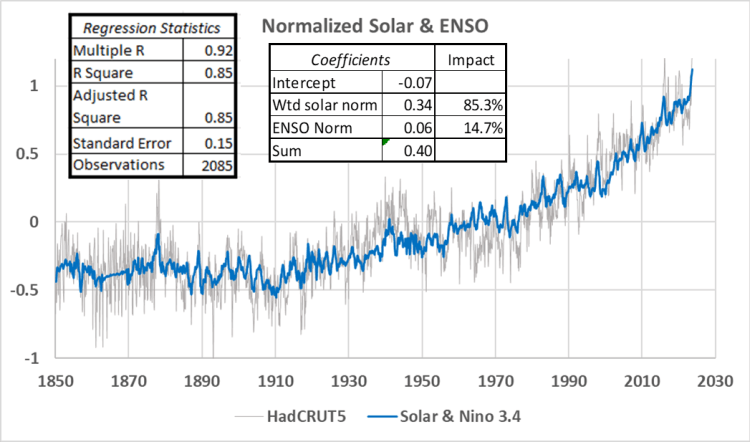
Abbildung 3. Hinzufügen von ENSO (Nino 3.4) zur zusammengesetzten Sonnenfunktion. Die Eingaben sind normalisiert, um die Koeffizienten vergleichbar zu machen. Die Abkühlungsperiode in den frühen 1960er Jahren ist immer noch nicht sehr gut modelliert.
Die Hinzufügung von Nino 3.4 zur zusammengesetzten Sonnenreihe erhöht das R² auf 0,85, aber die Koeffizienten deuten darauf hin, dass die Hinzufügung von Nino 3.4 mit 15 % zwar signifikant, aber gering ist. Nino 3.4 ist mit oder ohne Sonnenflecken ein Zusatz von etwa 15 %. Die normalisierten Koeffizienten zeigen, dass statistisch gesehen 85 % der Regression auf die kombinierte Sonnenreihe und 15 % auf Nino 3.4 zurückzuführen sind.
Die Eingangsreihen in diesen Diagrammen (Abbildungen 3, 4 und 5) sind alle normalisiert [11], so dass die Koeffizienten vergleichbar sind und zum Vergleich des relativen Einflusses der Eingangsreihen auf das Modell verwendet werden können. Abbildung 4 zeigt das Ergebnis, wenn Log(CO₂) hinzugefügt wird:
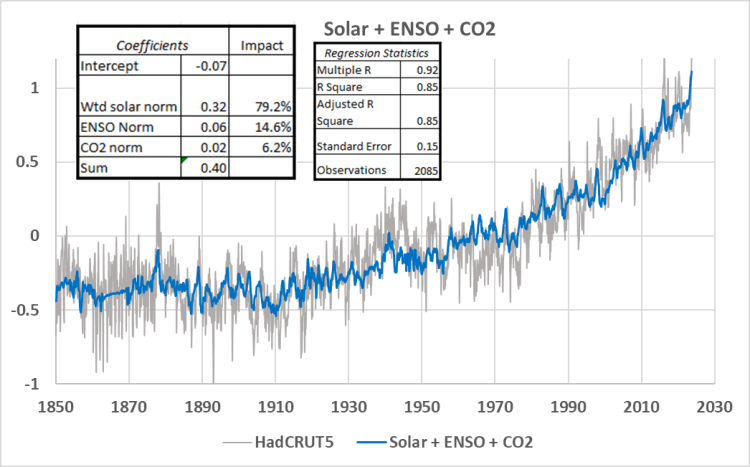
Abbildung 4. Die Regression, wenn Log (CO₂) hinzugefügt wird. Die Eingaben sind normalisiert, damit die Koeffizienten vergleichbar sind.
Aus Abbildung 4 geht hervor, dass die Hinzufügung von Log(CO₂) das R² nicht wesentlich verändert und auch das Regressionsmodell kaum verändert. Die Koeffizienten zeigen, dass die kombinierte Sonnenreihe statistisch gesehen 79 % zum Modell beiträgt, ENSO bleibt mit 15 % unverändert, und Log(CO₂) trägt nur 6 % bei. Abbildung 5 schließlich zeigt das Modell, das nur aus Log(CO₂) und der kombinierten Sonnenreihe erstellt wurde.
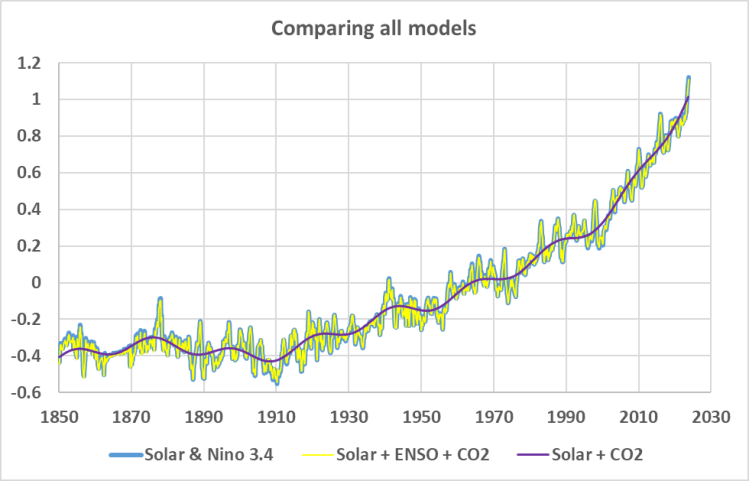
In Abbildung 5 ist das R² auf 0,83 gesunken, die solare Zeitreihe liefert 87 % des Ergebnisses, und Log(CO₂) liefert nur 13 %. Abbildung 6 vergleicht die Regression unter Verwendung der kombinierten Solar- und Nino 3.4 mit einer Regression unter Verwendung der kombinierten Solar-, Nino 3.4 und Log(CO₂). Wie man sieht, sind sie nicht genau gleich, aber fast gleich:

Abbildung 6. Die Modelle mit der kombinierten Sonnenkurve, ENSO und CO₂ im Vergleich zu Solar und ENSO allein. Obwohl es sich um exakte Überlagerungen zu handeln scheint, sind sie leicht unterschiedlich. Die Vermutung liegt nahe, dass CO₂ nicht zur Regression beigetragen hat.
Abbildung 7 fügt die kombinierte Solar- und Log(CO₂)-Reihe in das Diagramm ein. Es wird nun deutlich, dass die Kombination der Sonnenzyklen zu einem Prädiktor zusammen mit ENSO das beste Regressionsmodell zur Vorhersage von HadCRUT5 ergibt. Wie die Sonnenzyklen im Solardynamo entstanden sind, ist unbekannt, aber wenn unsere kombinierte Sonnenzyklusreihe korrekt ist, sind die großen Sonnenzyklen die dominierende Kraft hinter der jüngsten Erwärmung.
Diese Analyse ist kein Beweis dafür, dass die solare Variabilität die Hauptursache des jüngsten Klimawandels ist. Sie zeigt lediglich, dass aus einer Kombination bekannter und gut dokumentierter Sonnenzyklen ein statistisch signifikantes Modell der HadCRUT5-Durchschnittstemperaturreihen erstellt werden kann. Der physikalische Grund für diese beobachteten Sonnenzyklen ist unbekannt, obwohl es viele plausible Hypothesen gibt, die sie erklären könnten [12].
Alle derzeit möglichen Prozesse zeigen, dass die Sonne als Generator eines Wechselstromfeldes mit einer Periode von etwa 22 Jahren wirkt. Die längeren Modulationen sind nur unzureichend verstanden. Beobachtungen und Näherungswerte zeigen, dass die Sonne sowohl über kurze als auch über lange Zeiträume schwankt, was zu einer Änderung der Sonnenleistung und damit zu Klimaänderungen auf der Erde führt. Was ist die treibende Kraft für die solaren Veränderungen? Sie scheinen von den komplexen Flüssigkeitsbewegungen im Sonneninneren abzuhängen, die wiederum von der wechselnden Gravitationswirkung der umkreisenden Planeten beeinflusst werden könnten, aber all dies ist unklar [13]. Das von uns beschriebene Modell ignoriert diese ganze Komplexität und befasst sich nur mit den beobachteten Zyklen. Wir haben ein sehr einfaches statistisches Modell erstellt, aber in letzter Zeit wurden aufwändigere und kreativere Sonnenmodelle mit multipler Regression veröffentlicht, von denen im Folgenden einige kurz zusammengefasst werden.
Stefani, 2021
Frank Stefani verwendet eine doppelte Regression zur Modellierung der globalen Meerestemperaturen (HadSST.4) mit dem aa-Index [14] der Sonnenvariabilität und Log(CO₂). Der aa-Index ist ein zuverlässiger Indikator für die Sonnenleistung und korreliert gut mit der Sonnenfleckenzahl (siehe hier für weitere Informationen). Stefani prüft die Regressionsparameter viel ausführlicher als wir hier. Er verwendet sein Modell auch zur Vorhersage der Temperatur im nächsten Jahrhundert. Seine Vorhersagen zeigen eine geringere Erwärmungsrate für das kommende Jahrhundert. Er verwendet sein Modell, um eine Klimasensitivität von 0,6 bis 1,6°C/2xCO₂ zu berechnen, die viel niedriger ist als die im letzten Bericht des IPCC (AR6 [15]) angegebene. Stefanis Werte stehen jedoch im Einklang mit anderen, auf Bobachtungen basierenden Schätzungen der Klimasensitivität [16] (Link).
Scafetta, 2023
Scafetta konstruiert multiple Regressionsmodelle, die den solaren Antrieb, die Auswirkungen von Vulkanausbrüchen und Log(CO₂) berücksichtigen. Er ahmt die Modellergebnisse des IPCC nach, indem er deren Annahmen verwendet, obwohl er eine geringere Klimasensitivität von 1,4 bis 2,8°C/2xCO₂ errechnet. Unter realistischeren Annahmen sinkt die Klimasensitivität auf 0,9 bis 1,8°C/2xCO₂, was mit der obigen Schätzung von Stefani übereinstimmt. Scafetta regressierte auf HadSST4, HadCRUT4 und HadSST3 sowie HadCRUT5 und kam zu ähnlichen Klimasensitivitäten. Sein Modell berücksichtigt eine verzögerte Reaktion aufgrund der Pufferung der absorbierten Sonnenstrahlung durch den Ozean. Um die Möglichkeit einer städtischen Verzerrung zu berücksichtigen, wurden einige von Scafettas Regressionsstudien nur mit Datensätzen zur Meerestemperatur durchgeführt. Seine Studie zeigt, dass nur 20 % des solaren Einflusses auf die globalen Temperaturen auf eine erhöhte Strahlung zurückzuführen sind. Andere Faktoren wie die Modulation der kosmischen Strahlung, solarbedingte Veränderungen der atmosphärischen/ozeanischen Zirkulation oder andere Prozesse sind wahrscheinlich wichtiger. Diese letztgenannten Prozesse und andere solare Verstärker sind in den IPCC-Klimamodellen nicht programmiert, weshalb sie möglicherweise den klimatischen Einfluss der Sonne unterschätzen. (Link)
Soon, et al, 2023
Soon et al. führten eine Regressionsstudie der solaren, vulkanischen und menschlichen Einflüsse auf zwei Datensätze der nördlichen Hemisphäre durch, einen mit ländlichen Temperaturen und einen mit einer Mischung aus ländlichen und städtischen Datensätzen [17]. Diese Arbeit ist eine Erweiterung der früheren Solar/CO₂-Regressionsstudie von Soon und Kollegen [18]. Sie verwendeten zwei Datensätze für den solaren Antrieb, den vom IPCC empfohlenen TSI-Datensatz [19] und einen anderen, der im AR6 ignoriert wurde [20]. Sie stellten fest, dass die Wahl der Temperatur- und des solaren Antriebsdatensatzes einen großen Unterschied im Ergebnis der Studie ausmacht. Die Temperatur- und TSI-Datensätze sind alle möglich, keiner ist besser oder schlechter als der andere, aber wie viel Erwärmung auf menschliche Aktivitäten oder die Natur zurückzuführen ist, hängt von den verwendeten Datensätzen ab. Dies lässt Zweifel an der Schlussfolgerung des IPCC aufkommen, dass der Mensch die gesamte oder fast die gesamte jüngste Erwärmung verursacht hat. (Link)
Es ist wichtig zu berücksichtigen, dass es in städtischen Gebieten wärmer ist als im Umland und dass städtische Gebiete im letzten Jahrhundert weltweit schnell gewachsen sind und zuvor ländliche Wetterstationen umgeben haben. Dies lässt Zweifel an den Erwärmungstrends aufkommen, die mit kombinierten ländlichen/städtischen Datensätzen ermittelt wurden. Darüber hinaus gibt es keine endgültige Aufzeichnung der Sonneneinstrahlung (TSI), es gibt sowohl TSI-Datensätze mit niedrigem als auch mit hohem Trend, und es gibt keine Möglichkeit, festzustellen, welcher davon korrekt ist, da die entsprechenden Aufzeichnungen zu kurz und ungenau sind. Eine korrekte Studie würde daher beide Daten verwenden, wie es Soon et al. tun. Soon et al. fanden heraus, dass 85 % der Erwärmung zwischen 1850 und 2018 durch solare und vulkanische Einflüsse erklärt werden können, wenn man ihren „nur ländlichen“ Datensatz verwendet.
Stefani et al. 2023
Die Regression wird in dieser Arbeit nicht verwendet, ist aber hier von Interesse, weil die Autoren den Sonnenzyklus (Schwabe) und den Hale-Zyklus mit dem de Vries-Zyklus (oder Suess-Zyklus) über eine 193-jährige Schwebungsperiode [21] zwischen dem 22,14-jährigen Hale-Sonnenzyklus und der 19,86-jährigen Umlaufbahn der Sonne um das Baryzentrum des Sonnensystems verbinden [22]. Sie stellen fest (wie viele andere auch), dass der de Vries-Zyklus wahrscheinlich für den Abstand von 190 bis 210 Jahren zwischen den solaren Grand Minima während der Tiefpunkte des Hallstatt-Bray-Zyklus verantwortlich ist. Das jüngste Beispiel sind die Wolf-Spörer-Maunder-Minima zwischen etwa 1300 und 1715 mit dem zugehörigen Bray-Tief um 1500 (diese Werte sind den in meinem obigen Modell verwendeten sehr ähnlich). Sie stellen auch fest, dass der de Vries- und der Bray-Hallstatt-Zyklus in gewisser Weise miteinander verbunden sind, oder zumindest scheint der de Vries-Zyklus durch den Hallstatt-Bray-Zyklus moduliert zu werden. (Link)
Schlussfolgerungen
Diese verschiedenen Studien zur multiplen Regression beweisen nichts, sie sind nicht einmal ein richtiger Beweis für irgendetwas. Aber sie zeigen, dass die Annahme des IPCC, die Sonne habe keinen Einfluss auf die beobachtete Erwärmung seit 1750, fragwürdig ist. Sie zeigen auch, dass der von ihnen gewählte TSI-Datensatz und ihre Annahme, die einzige Auswirkung einer sich verändernden Sonne sei die Menge der Strahlung, die die Erde empfängt, fragwürdig ist. Sowohl White als auch Haigh haben festgestellt, dass es im Klimasystem der Erde Verstärker gibt, die die Auswirkungen solarer Veränderungen um das Vierfache [23], vielleicht sogar um das Zehnfache erhöhen [24], doch dies wird vom IPCC ignoriert. Der IPCC muss noch einmal zur Schule gehen und AR6 überarbeiten, einschließlich aller Forschungsergebnisse, die er beim ersten Mal ignoriert hat.
I acknowledge the generous help from Dr. Frank Stefani and Dr. Willie Soon, but any errors in the post are mine alone.
Download the bibliography here.
Download the supplementary data here, it includes R code, data, and Excel spreadsheets to make all the figures in this post.
- The Schwabe Cycle. ↑
- Verschiedene Autoren beziehen sich auf die Gleichgewichts-Klimasensitivität (ECS), die vorübergehende Klimareaktion (TCR), die effektive Klimasensitivität (ECS). Es gibt eine verwirrende Anzahl von Möglichkeiten, die Wirkung von CO₂ auf das Klima zu messen, siehe hier und hier für eine Diskussion. Um diese Verwirrung zu vermeiden, werden wir uns in diesem Beitrag nur auf die „Klimasensitivität“ beziehen. ↑
- (Lean, 2017) ↑
- (White, Dettinger, & Cayan, 2003) ↑
- (Usoskin I. , 2017) ↑
- (Usoskin, Gallet, Lopes, Kovaltsov, & Hulot, 2016) and (Usoskin I. , 2017) ↑
- (Feynman & Ruzmaikin, 2014) ↑
- (Stefani, Stepanov, & Weier, 2021) and (Stefani, Horstmann, Klevs, Mamatsashvili, & Weier, 2023) ↑
- (Stefani, Stepanov, & Weier, Shaken and Stirred: When Bond Meets Suess–de Vries and Gnevyshev–Ohl, 2021) ↑
- (White, Dettinger, & Cayan, 2003) ↑
- They are normalized by subtracting their respective means and dividing by their standard deviation. The model is not affected, but the coefficients become comparable when this is done. ↑
- (Charbonneau, 2022) ↑
- (Charbonneau, 2022) and (Stefani, Horstmann, Klevs, Mamatsashvili, & Weier, 2023) ↑
- The aa index data used was from NOAA, the British Geological Survey, and from (Nevanlinna & Kataja, 1993) ↑
- (IPCC, 2021) ↑
- (Christy & McNider, 2017), (Wijngaarden & Happer, 2020), (Lewis & Curry, 2018), (Lewis N. , 2022), and other examples in (Stefani, Stepanov, & Weier, 2021). Also see Tables 1 & 2 here. ↑
- (Soon W. , et al., 2023) ↑
- (Soon, Connolly, & Connolly, 2015), see also the summary here. ↑
- TSI is total solar irradiance. The IPCC assumes that the increase or decrease in solar output is the only warming or cooling effect the Sun has on Earth’s climate. This is hotly debated, as there are recognized amplifiers in the climate system (Haigh, 2011). ↑
- (Hoyt & Schatten, 1993) ↑
- When two waves with dissimilar frequency interact, they cause an alternating constructive and destructive interference that is called “beating.” More here. ↑
- The solar system barycenter is the center of mass of the solar system, which moves with the planets. The Sun moves about this barycenter in a complex orbit. More here. ↑
- (White, Dettinger, & Cayan, 2003) ↑
- (Haigh, 2011) and (Lean, 2017) ↑
Link: https://andymaypetrophysicist.com/2023/11/25/climate-CO₂-and-the-sun/
Übersetzt von Christian Freuer für das EIKE

















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Zu Martin Rohde am 5. Dezember 2023 um 19:54
Sie beachten nicht dass THE-Berechnungen für das Strahlungsgleichgewicht gemacht werden, und dafür gilt auch – all inclusive am Boden – das ECS. Transient kann man mit etwa 69% rechnen. Und die Temperatur aus einem Strahlungsmittelwert (im vereinfachten Strahlungmodell) liefert bei S^0,25 – soweit die Kelvin-Abweichungen des weitaus größten Teils der Erdoberfläche nur ± im Prozentbereich liegen – einen recht guten Mittelwert (im isothermen Fall wird der Mittelwert sogar exakt). Und die tatsächliche Temperatur interessiert uns meist garnicht, sonden eher das Delta, und das berechnet sich ja zu deltaT=deltaS/S/4*T, wobei für deltaS bei CO2-Verdoppelung die Gegenstrahlung (bei clear sky) am Boden eingesetzt wird, also z.B. 3,7•390/240 oder ggf. noch mit ln(C/Co)/ln(2) multipliziert. Danach kommen noch Korrekturen für Wolken, Wasserdampf, Feedback, Feuchtkonvektion.
Drastische Mängel der Klimamodelle: Eine Abweichung von ±15° C möglich
https://www.epochtimes.de/panorama/wissen-genial/fehleranalyse-zeigt-unzuverlaessigkeit-globaler-temperaturprognosen-klimamodelle-abweichung-a3012168.html
Viele Fragezeichen. Da sind doch die Alarm-„Forscher“ die großen Schlaumeier, die mit dem „monokausalen“ anthropogenen CO2, zwar vollkommen ungewiss, maximalen Wahnsinn erzeugen. Und nichts einfacher als das: Potsdämlich Alarm-Verdummte gibt es viele! Hat zwar keinen Einfluss auf das Klima, Gott sei Dank. Dafür ruinieren Klima- und Energiewende-Politiker Land und Menschheit, ferngesteuert durch die Potsdamer Alarm-Zombies. Was in Zeiten der Klima-Alarm-Verdummung als „erfolgreiche Wissenschaft“ gilt.
Herr May, Ihre Aussage „Der Klimaeffekt der solaren Veränderungen während eines einzigen 11-jährigen Sonnenzyklus ist fast eine Größenordnung größer als die Veränderung der Sonneneinstrahlung ausmachen kann“ stimmt in etwa wenn man die Sekundäreffekte (i.w. Wolkenbedeckung) berücksichtigt, welche ca. den Faktor 5 ergeben. Wenn man einen Feedback-Faktor 1,5 dazunimmt, kommt man auf 7,5. Und wie zusätzliches CO₂ die Erdoberfläche durch Gegenstrahlung erwärmen kann, ist bekannt, aber dass die Klima-Sensitivität für CO₂ nach mehr als 40jähriger Forschung noch unbekannt sein soll, ist ein Märchen. Mit MODTRAN wird z.B. „all inclusive“ mit Wolken (unterhalb derer CO2 weitgehend wirkungslos ist), mit Wasserdampf, Feedback und US-Standardatmosphäre die Verdoppelungssensitivität ECS zu etwa 0,6 Grad berechnet (1/5 vom „best guess“ des IPCC).
„Und wie zusätzliches CO₂ die Erdoberfläche durch Gegenstrahlung erwärmen kann, ist bekannt,“
Oh Herr,
laß Hirn regnen!
Herr Dietze hat Recht. Die Gegenstrahlung ist klar gemessen worden. Daran gibt es keine Zweifel.
Da ist nichts „gemessen“, da ist gemäß MODTRAN „gerechnet“
Mach den Spiegel-Test!
Ja. Bitte.
„Und wie zusätzliches CO₂ die Erdoberfläche durch Gegenstrahlung erwärmen kann, ist bekannt, …“
Aha, und wie berechnet sich das?
Wie viele Watt/qm strahlt die Oberfläche ab, z. B. bei 27°C, und wie viele Watt Gegenstrahlung treffen auf diesen Quadratmeter? Und um wie viele °C meinen Sie, daß sich diese 27°C dann konkret dadurch erwärmen?
Genau das ist die spannende Frage. Meine Antwort: 0,0
Herr Strasser, bekanntlich bewirkt jede CO2-Verdoppelung an TOA für clear sky einen „Strahlungsantrieb“ von 3,7 W/m². Wenn Sie diesen – im Strahlungsmodell – mit 1/Eps=390/240 auf den Boden herunterrechnen und bei 288 K deltaT=deltaS/390/4*T rechnen, erhalten Sie den Basiswert +1,11 Grad. Mit Berücksichtigung von Wolken, Wasserdampf, Feedback und Feuchtkonvektion werden es (wie z.B. auch bei MODTRAN) etwa +0,6 Grad. Übrigens ist nach Dr. Roth auch die Sonnenstrahlung Gegenstrahlung. Und jede absorbierte Strahlung (W/m² hat keine Temperatur) führt dem absorbierenden Boden zusätzlich Energie zu, welche in Wärme umgesetzt wird. Im Gleichgewicht kann die Bodentemperatur mit (SummeS/Sigma)^0,25 berechnet werden.
Bitte Quelle angeben. Mir ist das nicht bekannt und ist auch mit einer Berechnung wie spectralcalc oder Modtran nicht nachvollziehbar.
Das ist falsch, das jeder absorbierten Energie eine Emittierte gegenuebersteht und nur die Differenz die Waerme bestimmt die beim Koerper verbleibt oder weggeht.
Herr Schulz, toll mit welcher Ahnungslosigkeit Sie sich hier outen! Der Strahlungsantrieb ist ein Grundparameter von IPCC, der aus dem CO2-Spektrum (Integration line by line) für die Bodenemission von Dr. Keith Shine berechnet wurde, siehe z.B. auch https://www.fachinfo.eu/dietze2018.pdf oder http://www.eike-klima-energie.eu/wp-content/uploads/2016/11/Dietze_Klimasensitivitaet_ECS-4.pdf oder Wikipedia.
Dass jeder absorbierten Energie eine emittierte gegenübersteht, entspringt Ihrer Phantasie. Emittiert wird im Gleichgewicht die Summe der absorbierten W/m², woraus sich nach S-B ja auch die Temperatur ergibt. Die Differenz der W/m² die im Körper verbleibt oder weggeht, ist dann Null.
Herr Dietze ist es ok, das ich sie nach einer anderen Quelle Frage und nicht ihrer eigenen Arbeiten?
Meines Erachtens haben sie nicht das thermodynamische Grundwissen, wie sie in ihren Schlusssaetzen dokumentieren und Wikipedia glaube ich an der Stelle wenn wir von einem „Strahlungsantrieb“ reden auch nicht.
Ich werde nach „Dr. Keith Shine“ Arbeit suchen.
„Herr Schulz, toll mit welcher Ahnungslosigkeit Sie sich hier outen!“
…sagt der Master of Perpetuum -Mobiles!
LOL
Peter Dietze am 4. Dezember 2023 um 14:30
„Emittiert wird im Gleichgewicht die Summe der absorbierten W/m², woraus sich nach S-B ja auch die Temperatur ergibt.„
Also Wärmeleitung existiert nicht? Die Erdoberfläche steht im Strahlungsgleichgewicht? Die Erde hat keine Ausgleichstemperatur, insofern ist eine Umkehrung der SB-Gleichung unzulässig, da weder Wärmeleitung noch Konvektion noch Verdunstungskühlung erfasst werden. Per SB können Sie nur feststellen, wie viel Energie bei einer bekannten Bodentemperatur momentan abgestrahlt wird, aber niemals, welche Temperatur sich durch Einstrahlung einstellen wird. Und dabei auch bitte Emmissionsfaktor und Albedo berücksichtigen, die Erde ist kein schwarzer Körper.
Herr Rohde, ich schrieb: „Im Strahlungsmodell erhalten Sie [für CO2-Verdoppelung, am Boden] den Basiswert +1,11 Grad. Mit Berücksichtigung von Wolken, Wasserdampf, Feedback und Feuchtkonvektion werden es (wie z.B. auch bei MODTRAN) etwa +0,6 Grad“. Sie erwarten doch von mir nicht etwa ein Klimamodell mit Berücksichtigung aller kleinen Details mit mehr als 100 Mannjahren an Programmierarbeit?? Hier geht es doch um die grundsätzliche Physik des THE sowie die groben Fehler des IPCC. Alles was Sie meinen, besser zu wissen und vermissen, können Sie doch gern als Korrektur zum vereinfachten globalen Strahlungsmodell berechnen – und vergessen Sie nicht die Solaraktivität, Wolken, Erdrotation, Jahreszeiten, Winde, Meeresströmungen und die globalen Mittelwerte.
Peter Dietze am 5. Dezember 2023
Herr Dietze,
ich stelle fest, dass sich aus einer Einstrahlungsleistung keine Temperatur berechnen lässt, so lange der bestrahlte Körper seinen Ausgleichszustand nicht erreicht hat. Dieser ist bei der Erde noch lange nicht erreicht, allein die Ozeane haben noch eine riesige Aufnahmekapazität und die solare Einstrahlung dringt tief in dieses Medium ein. Sie fordern mich dann auf, genauere Berechnungen anzustellen. Kann ich nicht, denn solange die Energieflüsse im System Erde nicht vollumfänglich erfasst sind, kann das niemand. Wer allerdings mit wie auch immer gebildeten Mittelwerten in eine Formel mit 4. Potenz einsteigt, beschreitet einen mathematisch falschen Rechenweg.