Thomas E. Shula
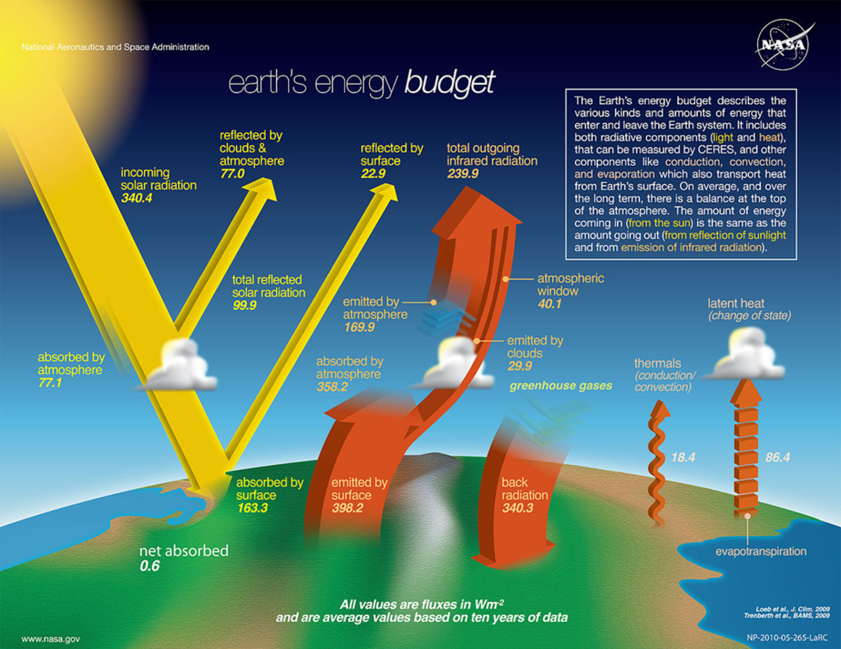
Die nachstehende, von der NASA veröffentlichte Abbildung ist ein Beispiel von vielen, die versuchen, die verschiedenen Faktoren des „Energiehaushalts“ der Erde zu veranschaulichen. Die gelben Pfeile auf der linken Seite stellen die einfallende Sonnenstrahlung dar. Sie wird zum Teil von der Atmosphäre absorbiert, zum Teil von Wolken und der Atmosphäre in den Weltraum reflektiert, zum Teil von der Erdoberfläche reflektiert, und etwas weniger als 50 % wird von der Erdoberfläche absorbiert und in Wärme umgewandelt. Auf der rechten Seite zeigen die roten Pfeile die Wege, auf denen die Energie von der Erdoberfläche in den Weltraum transportiert wird, wie es der Treibhauseffekt postuliert. Dieses Modell des „Energiebudgets“ ist die Grundlage für Klimamodelle, die versuchen, die Auswirkungen der vermuteten anthropogenen globalen Erwärmung (AGW) durch Treibhausgase vorherzusagen.
Diagramm mit freundlicher Genehmigung der NASA
Wie der Absatz im NASA-Diagramm besagt, besteht „im Durchschnitt und auf lange Sicht ein Gleichgewicht an der Obergrenze der Atmosphäre“.
Die mit den einzelnen Pfeilen im Diagramm verbundenen Werte sind die entsprechenden Energieflüsse in Watt/m². Diese Werte werden auf unterschiedliche Weise abgeleitet, von denen einige für diese Darstellung relevant sind und im Folgenden beschrieben werden. Diese Werte werden in Klimamodellen verwendet und können sich im Laufe der Entwicklung der Modelle ändern, wenn auch in der Regel nicht wesentlich. Einige typische Werte aus einem NASA-Dokument finden Sie auf Seite 16 hier [1]. Bestimmte Annahmen führten zur Entwicklung der Treibhausgastheorie.
Eine der Schlussfolgerungen, die auf der Seite Erdtemperatur ohne Treibhausgase – Energieerzeugung [2] erläutert werden lautet, dass die Erde ohne Treibhausgase etwa 33 °C kühler wäre, was im Wesentlichen einer Durchschnittstemperatur nahe dem Gefrierpunkt entspricht. Dies ist das Ergebnis der Behandlung der Erde und ihrer Atmosphäre als schwarze Körper nach dem Stefan-Boltzmann-Gesetz, wie in diesem Video [3] aus einem Online-Kurs über Klimamodellierung erläutert wird.
Im Diagramm des Energiehaushalts gibt es vier rote Pfeile, die dem (durchschnittlichen) langwelligen (Infrarot-)Strahlungsfluss entsprechen. Sie lauten wie folgt:
● 398,2 Watt/m² langwellige Strahlung, die von der Oberfläche aufsteigt
● 18,4 Watt/m² aufsteigend durch Konduktion/Konvektion
● 86,4 Watt/m² aufwärts durch Evapotranspiration
● 340,3 Watt/m² langwellige Strahlung, die aus der Atmosphäre als Rückstrahlung nach unten abfließt.
Nach dem Treibhauseffekt ist es die abwärts gerichtete Rückstrahlung, die die Wärme in der Atmosphäre „einfängt“ und die Erde warm hält.
Für die Zwecke dieser Darstellung werden wir nur die ersten beiden Komponenten betrachten, da wir die Beziehung zwischen aufsteigender langwelliger Strahlung und Leitung/Konvektion an der Erdoberfläche untersuchen werden. Nach dem oben erläuterten Modell entsprechen 398,2 W/m² etwa 95,5 % des gemeinsamen Wärmetransports und Konduktion/Konvektion etwa 4,5 % des gemeinsamen Wärmetransports.
Wie können wir dies messen? Wir wissen, dass es drei Mechanismen für den Transport von Wärmeenergie gibt: Leitung, Konvektion und Strahlung. Man muss ein Experiment entwerfen, mit dem man den Anteil des Wärmeverlusts durch Strahlung gegenüber dem Wärmeverlust durch Leitung und Konvektion feststellen kann. Zufälligerweise gibt es ein gängiges Instrument, das seit über 100 Jahren verwendet wird und genau dies ermöglicht.
Das Pirani-Messgerät
Das Pirani-Messgerät (Dieses Bild wurde mit Genehmigung von MKS Instruments, Inc. (Andover, MA) zur Verfügung gestellt).
Das moderne Pirani-Messgerät wird zur Messung des Vakuums im Bereich von 760 Torr bis 10-4 Torr verwendet, obwohl einige Geräte für die Messung höherer Drücke bis zu 1000 Torr ausgelegt sind. Es wurde 1906 von Marcello Pirani, einem deutschen Physiker bei Siemens & Halske erfunden und wird seit über 100 Jahren in einer Vielzahl von Anwendungen eingesetzt. Das Funktionsprinzip des Messgeräts ist einfach. Im Inneren des Messgeräts befindet sich ein Glühfaden, der erhitzt und auf einer konstanten Temperatur gehalten wird. Die Energie, die in den Glühfaden fließt, wird über den Strom, der durch ihn fließt, gesteuert. Die Energie kann auf vier Arten von der Glühwendel abgeleitet werden:
● Gaskonduktion
● Konvektion von Gas
● Strahlung
● Endverluste (d. h. Wärmeleitung von der Glühwendel zu ihrer Trägerstruktur).
Die Abstrahlungs- und Endverluste sind konstant und können gemessen werden, indem im Inneren des Messgeräts ein ausreichendes Vakuum erzeugt wird, so dass die Verluste durch Leitung und Konvektion vernachlässigbar sind. Wenn Gas in das Gehäuse eingeleitet wird, wird dem Heizfaden durch Leitung und Konvektion Wärme entzogen. Die zur Aufrechterhaltung der Temperatur des Glühfadens erforderliche Eingangsleistung hängt davon ab, wie viel Energie durch Leitung und Konvektion durch das Gas abgeführt wird. Zusammenfassend lässt sich sagen, dass das Pirani-Messgerät die relativen Beiträge zum Wärmetransport durch Strahlung gegenüber Leitung/Konvektion als Funktion des Gasdrucks für ein Objekt (in diesem Fall die Glühwendel) angibt, das auf einer konstanten Temperatur gehalten wird. Wie im Absatz vor dem obigen Bild erwähnt, ist dies genau die Messung, die wir suchen.
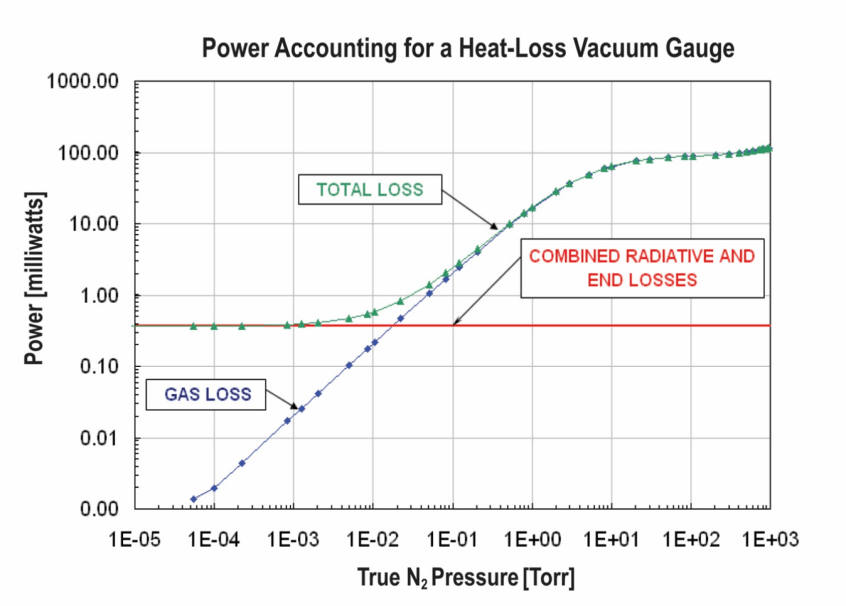
Die Ansprechkurve für ein typisches Messgerät ist in der nächsten Abbildung dargestellt. Beide Abbildungen sind in der von MKS Instruments herausgegebenen technischen Notiz „Introduction to Vacuum Pressure Measurement“ zu finden, und das in der Abbildung dargestellte Messgerät ist ein konvektionsverstärktes Pirani-Messgerät von MKS Instruments.
Dieses Bild wurde mit Genehmigung von MKS Instruments, Inc. (Andover, MA) zur Verfügung gestellt.
Die rote Linie im Diagramm stellt die (konstanten) Gesamtstrahlungs- und Endverluste von etwa 0,4 mW dar. Die blaue Linie stellt den Leistungsverlust nur durch das Gas dar, und die grüne Kurve, die an den beiden Enden abflacht, stellt den Gesamtverlust dar, d. h. die gesamte Energiezufuhr, die erforderlich ist, um die Temperatur des Glühfadens in Abhängigkeit vom Druck aufrechtzuerhalten. Bei atmosphärischem Druck, 760 Torr, beträgt die zur Aufrechterhaltung der Temperatur des Glühfadens erforderliche Leistung 100 mW. Da die Strahlungs- und Endverluste 0,4 mW betragen, bedeutet dies, dass der Wärmetransport durch das Gas 99,6 % beträgt, wobei nur 0,4 % auf Strahlungs- und Endverluste zurückzuführen sind. Dies sollte nicht überraschen, denn alle Gasmoleküle können Wärme durch Leitung und Konvektion transportieren, nicht nur der winzige Teil, der die so genannten „Treibhausgase“ ausmacht.
Wir können auch den Fall eines Vakuumdrucks von 10 Torr betrachten, was einer Höhe von etwa 33.000 m über dem Meeresspiegel entspricht. In diesem Fall sind etwa 60 mW Leistung erforderlich, um die Temperatur des Glühfadens aufrechtzuerhalten, so dass das Gas immer noch für etwa 99,3 % des Wärmetransports verantwortlich ist, während Strahlungs- und Endverluste nur 0,7 % ausmachen. Mit zunehmender Höhe ist ein größerer Anteil des Wärmetransports auf die Strahlung zurückzuführen, und so kehrt die gesamte Wärme in der obersten Atmosphäre schließlich in den Weltraum zurück. Der Übergangspunkt, an dem die Gasverluste gleich den Strahlungs- und Endverlusten sind, liegt bei etwa 200 milliTorr (0,02 Torr), was einer Höhe über 76.000 m entspricht. Das Ansprechverhalten des Pirani-Messgeräts ist unabhängig von dem Gehäuse, in dem es sich befindet, oder dem Fehlen eines solchen. Würde man ein „nacktes“ Pirani-Messgerät in eine Höhe bringen, in der der Atmosphärendruck 10 Torr beträgt, wäre das Ansprechverhalten dasselbe, als wäre es an ein Vakuumsystem mit einem Druck von 10 Torr angeschlossen. Es wurden Pirani-Messgeräte in vielen verschiedenen Größen und Konfigurationen hergestellt, einige mit Strahlungsverlusten in der Größenordnung von 0,1 % bei normalem Atmosphärendruck[4].
Der Faden im Pirani-Messgerät entspricht der Oberfläche der Erde. Die Gasmoleküle stoßen mit der Oberfläche zusammen und absorbieren Energie, wodurch sich ihre effektive Temperatur erhöht (Wärmeleitung). Eine „Blase“ dieses wärmeren Gases steigt dann im Verhältnis zu dem kühleren Gas um sie herum auf, während das kühlere Gas zur Oberfläche sinkt und den Zyklus ständig wiederholt (Konvektion). Dies kühlt die Oberfläche ab und wird durch die Reaktion des Pirani-Messgeräts perfekt veranschaulicht. Diejenigen, die sich mit Hochtemperaturprozessen in Vakuumsystemen beschäftigt haben, und zweifellos auch viele andere, wissen dies sehr gut. Der Autor kann nur darüber spekulieren, warum dies nicht früher berücksichtigt wurde.
Schlussfolgerungen
Das Pirani-Messgerät bietet eine Methode zur Messung der relativen Beiträge von Strahlung und Leitung/Konvektion zum Wärmetransport in einer gasförmigen Umgebung als Funktion des Drucks. Bei Drücken, die für die untere Atmosphäre (Troposphäre + Stratosphäre) relevant sind, macht die Strahlung weniger als 1 % des Wärmetransports nach oben aus. Damit wird die Existenz dieser Strahlung in der unteren Atmosphäre nicht widerlegt, es wird lediglich experimentell nachgewiesen, dass ihr Anteil am Aufwärtswärmetransport unbedeutend ist.
Anhand des Funktionsprinzips des Pirani-Messgeräts wurde nachgewiesen, dass der Aufwärtswärmetransport durch Strahlung eine unbedeutende Rolle für den Wärmetransport bei Atmosphärendruck von der Oberfläche in die obere Stratosphäre spielt. Der Treibhauseffekt, wenn es ihn denn gibt, beruht auf dem Aufwärtstransport von Wärme durch Strahlung in der unteren Atmosphäre. Daher spielt der Treibhauseffekt, wenn er denn existiert, eine unbedeutende Rolle für den Wärmetransport und damit auch für die Energiebilanz der Atmosphäre.
Heutige Klimamodelle beruhen auf Energiebilanzmodellen, wie sie im NASA-Diagramm zu Beginn dieses Beitrags dargestellt sind. Aus dem NASA-Diagramm und ähnlichen Diagrammen aus anderen Quellen geht klar hervor, dass die Grundannahme dieser Modelle darin besteht, dass die Strahlung die Hauptursache für den Aufwärtswärmetransport in der unteren Atmosphäre ist. Da die Strahlung für den Aufwärtswärmetransport in der unteren Atmosphäre unbedeutend ist, beruhen diese Modelle auf einer falschen Annahme und sind daher ungültig. Da die Modelle im Allgemeinen dazu dienen, die Theorie der anthropogenen globalen Erwärmung aufgrund des Treibhauseffekts zu stützen, gibt es keine wissenschaftlichen Beweise für den Treibhauseffekt oder die anthropogene globale Erwärmung.
[Hervorhebung vom Übersetzer]
Die Strahlungsenergie, die die Erde von der Sonne absorbiert, trifft mit Lichtgeschwindigkeit ein. Die Erde verliert die Wärme mit einer Geschwindigkeit, die durch Konvektion in einem Prozess angetrieben wird, den wir „Wetter“ nennen. Das Wetter ist der chaotische Prozess, bei dem die Erdatmosphäre ständig versucht, ein thermisches Gleichgewicht zu erreichen, was ihr jedoch nie gelingt. Die Konvektion findet ständig statt, aber die Geschwindigkeit, mit der Wärme durch Konvektion transportiert wird, ist VIEL langsamer als die Lichtgeschwindigkeit. Das bedeutet, dass die Wärmeenergie die Erde langsamer verlässt als sie ankommt, und deshalb ist die Erde wärmer, als es das Stefan-Boltzmann-Gesetz vorhersagt.
Anhang: Wie konnte die „Klimawissenschaft“ das so falsch einschätzen?
Die beiden grundlegenden Annahmen, die zum Treibhauseffekt führen, sind, dass 1) der primäre Mechanismus, durch den die Erdoberfläche Wärme verliert, die Strahlung ist, und dass 2) auf der Grundlage des Stefan-Boltzmann-Gesetzes die Temperatur der Erdoberfläche 33 K kühler sein sollte, als wir es beobachten.
Das Stefan-Boltzmann-Gesetz (SBL) definiert einen Schwarzen Körper (ein idealisiertes Objekt, das in der Natur nicht existiert) mit den folgenden Merkmalen
1. Er existiert in einer Umgebung von 0 K, d. h. in einem perfekten Vakuum.
2. Er befindet sich im Gleichgewicht mit seiner Umgebung.
3. Es ist ein perfekter Absorber von Strahlung.
Mit bestimmten Anpassungen, wie z. B. dem Emissionsgrad, bietet die SBL eine bequeme Möglichkeit, die Temperatur eines Objekts auf der Grundlage seiner emittierten Strahlung auch in nicht idealen Umgebungen zu messen. Dies gilt beispielsweise für die Schätzung der Temperatur von Sternen und für die Verwendung von Infrarotkameras zur Erkennung von „Hot Spots“. Man muss jedoch bedenken, dass sich nur der „idealisierte“ schwarze Körper streng nach der SBL verhält.
Die Erde und ihre Atmosphäre erfüllen keine der Bedingungen der SBL. Außerdem ist es üblich geworden, die obige Bedingung Nr. 1 zu ignorieren. Wenn man die Definition eines Schwarzen Körpers nachschlägt, wird die Bedingung 0 K (perfektes Vakuum) oft nicht erwähnt. Dies hat in der Regel nur geringe Auswirkungen, wenn es um Temperaturmessungen mit optischen Verfahren geht, ist aber für das Verständnis der Dynamik der Wärmeübertragung, z. B. unter irdischen Bedingungen, äußerst wichtig.
Dies wird in Klimamodellen nicht berücksichtigt. Es wird angenommen, dass bei einer Oberflächentemperatur von 288 K die von der Oberfläche nach oben abgestrahlte Leistung 398 Watt/m² beträgt und dass es sich dabei ausschließlich um langwellige IR-Strahlung handelt. Dann muss diese aufsteigende Strahlung mit der „Rückstrahlung“ „ausgeglichen“ werden, um ein „Strahlungsgleichgewicht“ in der Atmosphäre zu erreichen.
Die Realität sieht jedoch ganz anders aus. Bei einer Temperatur von 288 K beträgt der Photonenfluss (unter der großzügigen Annahme, dass alles bei einer Wellenlänge von 15 Mikrometern liegt, um die Anzahl der IR-aktiven Photonen zu maximieren) etwa 3 X 10^²² Photonen/Sek-m². Das ist eine Menge Photonen, und wenn sich die Oberfläche in einem perfekten Vakuum befände, wäre dieser Strahlungsfluss die einzige Möglichkeit für die Oberfläche, Energie abzugeben.
[Hervorhebung im Original]
Aber wir haben eine Atmosphäre. Bei Standardtemperatur und -druck hat die Luft einige sehr interessante Eigenschaften. Sie ist viel dichter als wir uns normalerweise vorstellen.
Durchschnittliche Molekulargeschwindigkeit ca. 470 m/sec (1050 mph, Überschall auf der Makroebene)
Frequenz der Molekül-Zusammenstöße (jeder mit jedem) ca. 7.000.000.000 Zusammenstöße/Sekunde (7 Ghz)
Mittlere freie Weglänge etwa 70 nm (etwa 1/10 der Wellenlänge des sichtbaren Lichts)
Häufigkeit der Kollisionen mit einer idealen ebenen Oberfläche ca. 3 X 10^27 Kollisionen/sec-m²
[Alle Hervorhebungen im Original]
Um dies ins Verhältnis zu setzen, ist die letzte Zahl recht nützlich. Die durchschnittliche Oberfläche eines erwachsenen Menschen beträgt etwa einen Quadratmeter. Das bedeutet, dass jede Sekunde etwa 100 Pfund Luftmoleküle mit einer Durchschnittsgeschwindigkeit von etwa 1050 mph auf jeden von uns treffen. Noch wichtiger ist, dass dies angesichts des Photonenflusses bei 288 K bedeutet, dass für jedes potenziell emittierte Infrarot-Photon etwa 100.000 Luftmoleküle mit der Oberfläche kollidieren. Da der Energietransfer durch Kollisionen das Gleichgewicht an der Oberfläche verändert, indem Energie durch Leitung abgeführt wird, ist es wahrscheinlich, dass der tatsächlich emittierte Photonenfluss noch geringer ist. Wenn man davon ausgeht, dass die Strahlungsübertragung der primäre Mechanismus für die Aufwärtswärmeübertragung an der Erdoberfläche ist, würde das bedeuten, dass ein einziges IR-Photon mehr Energie übertragen würde als 100.000 Molekülkollisionen. Diese Zahlen beziehen sich auf eine vollkommen glatte, ebene Oberfläche. Der tatsächliche Oberflächenbereich auf atomarer Ebene kann viel größer sein.
[Hervorhebung im Original]
Es liegt auf der Hand, dass die Grenzfläche zwischen der Erdoberfläche und der Atmosphäre auf atomarer Ebene ein extrem chaotischer Ort ist. Dies erklärt, was wir in der Funktionsweise des Pirani-Eichmaßes sehen, wie im Hauptteil dieser Arbeit erläutert.
References:
[1] Kelly, Schmidt, et al, GISS-E2.1: Configurations and Climatology
[2] Earth Temperature without GHGs – Energy Education
[3] (224) Climate Dynamics Lecture 02 Energy and the Earth System – YouTube
[4] Fabrication of thermal‐based vacuum gauge – Jung – 2014 – Micro & Nano Letters – Wiley Online Library
Link: https://wattsupwiththat.com/2023/04/18/a-novel-perspective-on-the-greenhouse-effect/
Übersetzt von Christian Freuer für das EIKE
Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"@ Thomas Heinemann
Da die ANTWORTEN-Funktion nicht möglich ist, schreibe ich einen neuen Kommentar.
Sehr geehrter Herr Heinemann!
Danke für Ihre sehr detaillierten Ausführungen – nun habe ich verstanden, wie der Treibhauseffekt gemeint ist. Sie haben damit aber auch gezeigt, dass es keinen menschengemachten Klimawandel aufgrund von CO2 gibt, da nach Ihren Angaben die CO2-Konzentration keine Rolle spielt!
Sie schreiben: „System A besteht nur aus einer Erdoberfläche …
System B ist wie A hat aber einen Absorber A zwischen der Erde und dem Weltall …
… ergibt sich E1 = 2 x J = 2 x E (aus System A). D.h. die Abstrahlungsleistung der Erdoberfläche E1 ist im System B doppelt so hoch wie im System A. Der Treibhauseffekt basiert grundsätzlich auf diesem Effekt …“
Es geht also anscheinend nur darum, dass die Wärmestrahlung der Erdoberfläche von CO2 komplett absorbiert und dann aber nur zur Hälfte ins Weltall abgestrahlt wird. Bei einer CO2-Konzentration von 280 ppm um 1850 war eine bestimmte Höhe HA der Atmosphäre nötig, um CO2 vollständig zu absorbieren. Bei einer aktuellen Erhöhung auf 430 ppm wäre dann HA also nur ca. 65 % so hoch und bei einer Verdopplung eben nur halb so hoch, aber dies hätte doch keine Auswirkung auf die Temperatur. Das würde eine Klimasensitivität = 0° C bedeuten.
wErner Schulz schrieb am 05/05/2023, 00:30:48 in 322820
Die beiden Aussagen beziehen sich auf verschiedene Vorgänge.
Im ersten Beispiel wollte Herr Heinemann das möglichst nahe an die Vorstellungen von Herrn Keks annähern. Daher richtete sich der Behälter von selbst auf (Die Isolation quasi masselos und die Teilchen bewegten sich quasi alle in einem Viertelkreis um das eine Ende der Box und richteten die Box auf) und die benötigte Energie für die Höhenänderung der Teilchen wurde der inneren Energie entnommen.
Da das schwer vorstellbar ist, wechselte er auf das beispiel mit dem Kran, der die Box aufrichtet und die dafür nötige Arbeit liefert.
Warum dann Ihr Widerspruch, nachdem Herr Heinemann den Kran zum Anheben eingeführt hat?
Die Luft bewegt sich nicht von allein nach oben. Sie wird durch Auftrieb aufgrund von Erwärmung angehoben.
In der Troposphäre – Ja, die innere Energie ändert sich, sie wird kleiner. Allerdings wird sie kleiner, weil das Paket beim Aufsteigen Arbeit verrichten muss – Volumenarbeit.
Haben sie nicht gerade Herrn Keks recht gegeben?
Herr Schulz glaubt, jede aufgerichtete Luftsäule sei eine Troposphäre.
WErner Schulz schrieb am 6.5.2023, 22:20:06 in 323091
Nein. Könnten Sie vielleicht erklären, wie Sie darauf kommen?
Soweit ich weiss, positioniert sich Herr Keks gegen die die Moeglichkeit einer Isothermen Atmosphaere bei Wirkung einer Gravitation.
Alles was sie gesagt haben, hoert sich danach an, das Herr Keks recht hat.
Und wenn wir davon ausgehen, das die Arbeit zum Aufsteigen von Luft aus der Inneren Energie kommt, dann denke ich haben sie Herrn Keks recht gegeben.
Oder haben sie noch vergessen etwas zu sagen oder darzustellen?
Werner Schulz schrieb am 09/05/2023, 23:07:33 in 323423
Gehen Sie einfach noch,mal zum Anfang zurück (26. April 2023 um 10:18 ). Dann sehen Sie, dass ich gesagt habe, dass sich der Temperaturgradient „aus dem Zusammenspiel von Wärmeleitung, Wärmestrahlung und Konvektion“ ergibt. Damit bin ich laut Herrn Keks entweder ahnungslos oder verlogen. In dem Kommentar, in dem sie eine Übereinstimmung mit Herrn Keks sehen, habe ich wieder auf Konvektion und die damit verbundene Volumenarbeit als Ursache hingewiesen. Bei Herrn Keks wäre die Ursache lediglich die Umwandlung kinetischer in potentielle Energie und es ist immer noch fraglich, warum es in seiner Vorstellung bei einem bestehenden Temperturgradienten nicht zu einem Wärmefluss von warm nach kalt kommen sollte.
Interessant ist allerdings, dass er neuerdings „Absorption von eingehender/ausgehender Strahlung, freiwerdende Latenzwärme, Konvektion etc.“ als „Störgrößen, welche lokal den isentropen Gradienten beeinflussen.“ einführt. Wie gr0ß ist denn dann der Anteil der Störgrößen am Gradienten?
Herr keks hat eingesehen, dass er falsch liegt und ist abgetaucht. Wer glaubt, dass potentielle Energie nur aus innerer Energie entstammen kann, muss eben einsehen, dass dies allgemein nicht zutrifft.
Seine Behauptung, dass eine Luftsäule, die senkrecht aufgerichtet wird, dadurch oben kühler und unten wärmer wird, ist keks wohl doch zu obskur.
Übrigens, es sollte klar sein, dass beim Aufrichten der Luftsäule im Schwerefeld durch den Kran die gesamte Arbeit in potentielle Energie übergeht. Da sich die Temperatur nicht ändert, ist diese gleichzeitig auch die Wärmemenge, die hinzugefügt wird. Der Wirkungsgrad dieser Kranarbeit an der Luftsäule ist natürlich null.
Bitte noch mal durchdenken!
Wenn sie Arbeit von draussen reinstecken, dann muss sich die Temperatur nicht aendern? Abgesehen davon das sie scheinbar die Innere Energie erhoehen?
Aber wenn sie den Behaelter in einem Schwerefeld aufrichten, ist die Dichte dann oben genau so wie unten? In einem komprimierbaren Medium? Wie wirkt sich das auf die Temperaturen aus? Wird die Luft unten verdichtet? Was denken sie? Denken sie schon?
Werner Schulz am 9. Mai 2023 um 23:15
wollen Sie jetzt die Arbeit in Erhöhung der inneren Energie verwenden oder zum Aufrichten gegen das Gravitationsfeld? Oder wollen Sie beides gleichzeitig?
Im 2. Versuch fügen wird dem Behälter nur soviel Energie in Form von Arbeit zu, wie fürs Aufrichten gebraucht wird. Woher bekommen Sie dann noch die Energie für eine Temperaturerhöhung in der stehenden Luftsäule?
Herr keks schweigt dazu, er hat seinen Fehler eingesehen.
Ich schrieb hydrostatisches Gleichgewicht. Wie verläuft dann vertikal die Dichte in Luft konstanter Temperatur? Sollte man wissen.
Da war bei mir ein Fragezeichen, das sollte eher eine Aussage sein.
Und wo ist der Behaelter in der Atmosphaere?
Werner Schulz am 13. Mai 2023 um 0:21
Im 2. Versuch fügen wird dem Behälter nur soviel Energie in Form von Arbeit zu, wie fürs Aufrichten gebraucht wird. Woher bekommen Sie dann noch die Energie für eine Temperaturerhöhung in der stehenden Luftsäule?
Also, Sie behaupten wie Herr keks, die Luft müssen beim Aufrichten unten wärmer als oben sein. Wo kommt die Energie dafür her, wenn ihr von außen keine Energie zur Erhöhung der inneren Energie zugeführt wird, sondern nur die porentielle Energie füs Aufrichten?
Wenn Sie das nicht erklären können, ist Ihre Behauptung unbegründet. Das ist klar, oder?
Also, ein langer, dünner, masseloser, quaderförmiger Behälter mit Luft gefüllt wird am Boden aufgerichtet, sodass die lange Seite in die Höhe ragt – von waagrecht zu senkrecht. Sie wissen schon.
Herr Heinemann,
sie scherzen:
Sie können also Arbeit in einen masselosem Behälter stecken, schaffen es aber nicht die Frage zu beantworten, was im „Behaelter‘ passiert, obwohl die Natur es ihnen aufzeigt?
Und wer sagt die Luft muss insgesamt wärmer werden? Wie wäre es, wenn sie es so sortieren wie Herr Marvin Müller?
Immerhin dürfte die Hauptmasse der Luft zu Boden rutschen und ein natürliches Dichteprofil annehmen. Nein?
Könnte ja sein oben wird kälter und unten wärmer?
Wenn ja warum?
natuerlich, die Arbeit wird in vollstaendig in Waerme umgewandelt (Wirkungsgrad Null) aber nichts erwaermt sich.
Abgesehen davon bleibt nichts fuer das Aufrichten des Behaelters uebrig!
Falls sie Physiker sind, dann sicherlich keiner der sein Fach versteht. Oder sind sie Astrophysiker? Die haben keine Wirkung, darum auch der Wirkungsgrad Null!
Ich wußte es, dass dies Gestuß auslöst. Dass Wärmezufuhr nicht unbedingt die innere Energie und damit die Temperatir erhöht ist die Einstiegserkenntnis in die Thermodynamik. Siehe 1. HS.
„Herr keks hat eingesehen, dass er falsch liegt und ist abgetaucht. “
Heinemännchen,
ich habe besseres zu tun als ständig auf irgendwelche Scheinargumente von selbsternannten Füsiggern zu antworten.
Aufgrund des um sich greifenden Klima-Terrors wollte ich mich über den sogenannten Treibhauseffekt informieren und habe mir „Klimawandel: Dokumentationen von Terra X zum Thema CO2 (Ursachen, Folgen und die Rolle des Menschen)“ auf YouTube (https://youtu.be/DvZmf7UqfTo) angesehen. Ich habe das so verstanden, dass die durch kurzwellige Strahlung aufgewärmte Erdoberfläche mittels Infrarotstrahlung versucht, diese Wärme wieder abzustrahlen, dies aber durch CO2 teilweise verhindert wird, da dieses Treibhausgas diese Strahlung aufnimmt und in alle Richtungen – also auch wieder auf die Erdoberfläche zurück – strahlt. Ab Minute 0.53 wird ein Versuch von Professor Borrmann präsentiert, wo eine heiße Oberfläche eines Erdmodells durch ein nach oben offenes transparentes Gefäß mit Luft Wärme abstrahlt, die dahinter mit einem IR-Sensor gemessen wird. Dann füllt er mit einem Schlauch CO2 ein und der Zeiger wandert auf Null, was beweist, dass die Wärmestrahlung absorbiert wird. Aber der Versuch zeigt nicht, dass CO2 in alle Richtungen abstrahlt, sondern das Gegenteil, da ja überhaupt keine Strahlung mehr beim Sensor ankommt. Borrmann hätte doch die Gegenstrahlung auf der anderen Seite messen müssen – oder wäre da auch nichts angekommen? Was passiert mit der absorbierten Energie nun, die kann doch nicht verloren gehen? Bitte um Information, warum diese Experimente so schlecht durchgeführt werden. Danke
Das ist eine gute Beobachtung, die zu tiefen Diskussionen gefuehrt hat und die Frage steht im Raum, ob die Absorption auch die Abstrahlung beweist.
Dazu waere zu vermerken, das die Absorption auf gewissen Wellenlaengen begrenzt ist, aber die Strahlung kann von einem Koerper mit einer unbestimmten Temperatur kommen, waherend die Abstrahlung der Eigentemperatur des Gases entsprechen muss.
@Michael Kunerth
Zitat: Was passiert mit der absorbierten Energie nun, die kann doch nicht verloren gehen?
Richtig, die geht auch nicht verloren, sie wird teilweise in thermische Energie umgewandelt und teilweise wieder emittiert, nur ist das nicht die Absicht hinter diesen Demonstrationen.
Sie haben den ganzen Witz dabei völlig übersehen. In der Luft, die bei den beiden Demonstrationen am Anfang verwendet wird, ist bereits die reguläre CO2 Konzentration enthalten.
Um die Dramatik zu erhöhen, leitet man jetzt CO2 bis ca. 90% in die Küvette bzw. das Rohr ein. Jetzt stellt sich noch die Frage, in welchen Wellenlängen-Bereich mißt der Sensor eigentlich?
Es geht in diesen beiden Demonstrationen nur um den Effekt der Totalabsorption bei einer entsprechenden Konzentration zwischen Strahlungs-Quelle und Empfänger. In der Atmosphäre gilt für CO2 (15 µm-Bande) L0 = 2314 ppm·m/x und für die Transmission T = I/I0 = e^(-l/L0).
Bei einer CO2 Konzentration in der Küvette von x = 900000 ppm (90%) ist L0 = 0,0026 m = 2,6 mm, d.h., bei einer Weglänge der Strahlung von l = 3*L0 = 7,8 mm wird die Strahlung bereits zu 95% absorbiert.
Ich nenne das schlich und einfach – Volksverdummung!
Mfg
Werner Holtz
Danke für Ihre Antwort (gilt auch für Werner Schulz)! Den Witz mit der bedrohlich treibhausgasverunreinigten Luft habe ich tatsächlich nicht gesehen :-). Die Formeln mit der Transmission habe ich leider nicht verstanden – mein letzter Physikunterricht war in den 70ern des vorigen Jahrhunderts, als man übrigens noch Angst vor einer neuen Eiszeit hatte.
Sie schreiben: „Richtig, die geht auch nicht verloren, sie wird teilweise in thermische Energie umgewandelt und teilweise wieder emittiert, nur ist das nicht die Absicht hinter diesen Demonstrationen.“ Das war ja meine Hauptfrage, warum dieses Experiment so schlecht gemacht ist. Man hätte doch einen Temperaturmessfühler in den transparenten Behälter platzieren können, um so die Umwandlung in thermische Energie zeigen zu können – was passiert dann? Erwärmte Gase haben doch ein niedrigeres spezifisches Gewicht und steigen auf? Die Konvektion spielt doch eine große Rolle, nehme ich an. Und die Emission – ist die in der gleichen oder einer anderen Frequenz wie die aufgenommene Strahlung? Warum hat Borrmann nicht die Gegenstrahlung gemessen? Würde sie sich überhaupt eignen, den erwärmten Bodenring zusätzlich zu erhitzen? Oder nur dazu, dass sie sich weniger schnell abkühlt, wie es in der Nacht ja möglich wäre? Da hätte er die Lampe abschalten und bei verschiedenen CO2-Konzentrationen die Zeit der Abkühlung messen müssen.
Wenn diese Demonstration zur Volksverdummung beigetragen haben soll, so ist dies misslungen, denn erst dadurch beginnt man sich zu wundern, warum nicht diese relativ einfachen Messung durchgeführt worden sind. Und überhaupt – den IPCC gibt es seit 35 Jahren und es gibt trotzdem noch kein einziges Experiment, das den Treibhauseffekt stichhaltig nachweisen konnte?
Die sogenannte Gegenstrahlung erwärmt nichts. Wie sie sagen, sie verhindert nur Wärmeverlust durch Strahlung. Und weiter wie sie feststellen gibt es noch die Konvektion, die die Wärme anstatt durch Strahlung transportiert.
Werner Schulz am 9. Mai 2023 um 22:17
Sie glauben also, dass atmosphärische Gegenstrahlung auch ohne Absorption möglich ist?
B) ergibt sich der Treibhauseffekt trivial deduktiv aus der Absorptionseigenschaft von CO2 und der Physik
Ja, denn Gegenstrahlung (= thermische Strahlung) aus dem Gas ist gemäß Kirchhoffschen Strahlungsgesetz gegeben, sobald Absorption im Gas erfolgt. Das ist trivial deduktiv und Physik.
Nein, Woran wollen sie das Ablesen? Ich habe doch gesagt, wie es ist.
Die Sache ist recht einfach:
A) kann man trivialerweise die Erde nicht zum Experimentemachen ins Labor stecken
B) ergibt sich drr Treibhauseffekt trivial deduktiv aus der Absorptionseigenschaft von CO2 und der Physik
C) dient das Experiment nur dazu zu zeigen, dass CO2 Infrarot absorbiert und damit die Vorausetzung für B) erfüllt.
Ah ja, die Absorption. Das mit der Gegenstrahlung also nicht?
Werner Schulz am 7. Mai 2023 um 15:37
Sie glauben also, dass atmosphärische Gegenstrahlung auch ohne Absorption möglich ist? Worauf basiert denn Gegenstrahlung, Ihrer Meinung nach?
Die ganze Erde in ein Labor zu packen kann doch nicht notwendig sein, um den Treibhauseffekt nachzuweisen. Es wäre doch schon ein Anfang gewesen, wenn Borrmann wenigstens die Gegenstrahlung gemessen hätte. Hier wäre es auch interessant, in welcher Frequenz und Intensität diese stattfindet. Absorption bedeutet doch Aufsaugen – wenn es sich um die selbe Frequenz und Intensität handeln würde, wäre es doch eher eine Kombination aus Reflexion und Streuung? Eine Überprüfung der Oberflächentemperatur wäre auch nicht so schwierig gewesen – ob die zunimmt oder ob die Abkühlung verzögert wird. Besteht vielleicht die Angst, dass der Treibhauseffekt doch nicht so ganz wissenschaftlich stimmig ist?
Woran wollen sie das Ablesen? Sie haben doch gesagt das:
Wenn sie Absorption so herausstellen, dann schliessen sie die Gegenstrahlung als Ursache einer Erwaermung aus, oder nicht?
Die sogenannte Gegenstrahlung ist ein unphysikalischer Begriff der davon ablenken soll das elektromagnetische Strahlung eine normale Eigenschaft von Materie ist. Das manche Gase nicht mit IR Strahlung reagieren ist das ungewoehnliche und die Frage steht im Raum, welche Auswirkungen hat das!
Das Wort „Gegen“ wurde eingefuehrt, um vorzugaukeln, das es eine Wirkrichtung gibt, die scheinbar nur in Richtung Erdboden eine Wirkung hat. Dabei kann jedes Raumvolumen in der Atmosphare in alle Richtungen strahlen und jeder Abstrahlung in Richtung Erdboden aus diesem Volumen steht auch eine gleichstarke Abstrahlung in Richtung All zur Seite.
Falls sie spezifisch interessiert sind und den Temperaturgradienten berucksichtigen wollen, da die Temperatur mit der Hoehe abnimmt und es je nach Raumvolumen zu einem Unterschied kommt wenn man die Strahlung nicht auf einen bestimmte Temperatur bezieht . . . , tun sie das. Dann kommen sie aber um die Frage nicht herum, warum es diesen gibt! Vielleicht mitteln sie einfach die Temperaturen . . .!
Ist die Temperatur im Mittel in der gesamten Atmosphaere vielleicht – 18 Grad C? Was denken sie?
Was ich auch schon immer mal wissen wollte, wenn CO2 bei 15 Grad C. in seinen Bandlinien ungefaehr 100 W/m2 abstrahlen kann, und sich die Bandlinien mit denen vom Wasser ueberdeckt, wo kommen eigentlich die durchschnittlich 324 W/m2 im KT Diagram her? Das heisst die Atmosphaere strahlt mit ueber 80% der Strahlstaerke eines Schwarzkoerpers der Temperatur von 15 Grad C.
Gute Frage, ja worauf eigentlich!
Michael Kunerth am 9. Mai 2023 um 21:28
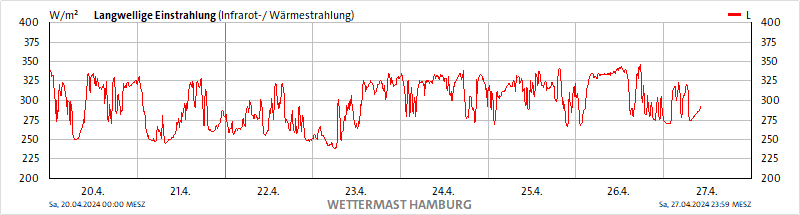
Messungen der „Gegenstrahlung“ (downwelling longwave radiation) finden Sie jede Menge im Netz, als Energiefluss in ganzen oder spektral aufgelöst. Hier z.B. eine Messung des Wettermastes Hamburg:
Ein Experiment, dass den Zusammenhang zwischen der Konzentration infrarotabsorbierender Gase und der Änderung der Temperatur zeigt, finden Sie sogar hier auf Eike:
Vielleicht beantwortet das einige Ihrer Fragen …
Michael Kunerth am 9. Mai 2023 um 21:28
Über kurze Strecke findet jedoch eine geringe Änderung der Wärmestrahlungsdichten statt. Damit ist auch die Gegenstrahlung, welche ja nichts weiter als die thermische Abstrshlung des Treibhausgases ist, schlecht von der sich damit überlagernden thermischen Strahlung der Wandungen des Labors zu unterscheiden. Die beiden ergeben in Summe ja das Planckspektrum (wenn die Wand ein schwarzer Strahler ist) und Wand und Gas gleiche Temperatur haben.
Bei der Erde hat man keine Wand im Hintergrund, das Weltall da strahlt vernachlässigbar im IR.
Schoenes Beispiel! Und wenn man die Faehigkeit einschaetzen will, wie warm es in einem Zimmer wird, dann messe ich die Strahlung von der Wand und dann berechne ich die Heizleistung als Wert W/m2 und addiere diese Zahl und die Strahlungsleistung der Wand und dann kriege ich die Temperatur.
Und der Fakt das mit einer duennenWand bei gleicher Heizleistung die Temperaturen im Inneren geringer sind, als bei einer dickern Wand, wie wird das erklaert?
Ach so man kriegt ja in einem waermeren Zimmer eine hoehere Strahlung von der Wand. Ach so! Und die Ursache ist?
Im RP-Energie-Lexikon habe ich unter „Perpetuum Mobile zweiter Art“ Folgendes gefunden:
„Das gleiche Gesetz würde auch verletzt, wenn Wärme von einem Medium niedrigerer Temperatur auf ein Medium mit höherer Temperatur übertragen würde, ohne dass zusätzlich Exergie aufgewandt werden müsste (etwa als Antriebsenergie einer Wärmepumpe). Würde dies gelingen, könnte man damit ein Haus allein mit Hilfe von Umgebungswärme heizen, beispielsweise auch in dunkler kalter Nacht. Eine solche Maschine könnte man außerdem auch mit einer Wärmekraftmaschine verbinden, die dann auch mechanische Energie liefern würde.“
Trifft das nicht auch beim Treibhauseffekt zu? CO2 ist ja eindeutig ein Medium niedrigerer Temperatur und die Erdoberfläche ein Medium höherer Temperatur – was wäre dann beim Treibhauseffekt die Exergie?
Herr Kunerth,
Nein, sonst gäbe es ihn ja nicht.
Sie vergessen, dass die Sonne scheint. Der Treibhauseffekt benötigt nicht nur eine Treibhausatmosphäre, sondern auch die Zufuhr niederentroper Sonnenenergie, die liefert den Großteil der Exergie.
Michael Kunerth am 11. Mai 2023 um 20:53
Demonstration des Treibhauseffektes und des 2. HS an zwei einfachen Systemen.
System A besteht nur aus einer Erdoberfläche, die Sonnenstrahlung der Leistungsmenge J absorbiert. Im Gleichgewicht gilt, dass die als Abwärme abgestrahlte Leistung von der warmen Oberfläche E gleich ist wie die absorbierte Sonnenstrahlung, es gilt also J = E. Sei die Erdoberfläche schwarz, dann ist die Temperatur der Erdoberfläche TE alleine durch J (=E) bestimmt.
System B ist wie A hat aber einer Absorber zwischen der Erde und dem Weltall. Der Absorber ist voll für die Sonnenstrahlung durchlässig, absorbiert aber die Wärmestrahlung der Erdoberfläche E1 vollständig. Wir betrachten wieder den Gleichgewichtszustand, in dem sich zeitlich nichts ändert. Der Absorber nimmt eine Temperatur an. Intuitiv ist klar, dass die Temperatur des Absorbers TA (ebenso wie die der Erdoberfläche) u.a. auch von der Sonnenstrahlungsleistung abhängt. Denn wenn J=0 ist, sind beide Systeme bei TE1=TA=0 K im Gleichgewicht. Wenn J steigt, so steigen auch TE1 und TA.
Der Absorber ist ebenso wie der Rest im Vakuum und kann daher seine Wärmeenergie nur per Wärmestrahlung abgeben. Dies passiert zu beiden Seiten hin gleichartig. Seine Abstrahlungsleistung sei F. Da der Absorber E1 komplett absorbiert, gelangt nur die Wärmestrahlung des Absorbers F ins All.
Im Gleichgewicht stellt sich folgendes ein. a) die ins Weltall abgestrahlte Leistung F = J. b) da der Absorber seine Leistung komplett vom Boden bekommt und in beide Richtungen gleichartig abstrahlt, gilt F + F = 2 x F = E1.
Damit ergibt sich E1 = 2 x J = 2 x E (aus System A). D.h. die Abstrahlungsleistung der Erdoberfläche E1 ist im System B doppelt so hoch wie im System A. Der Treibhauseffekt basiert grundsätzlich auf diesem Effekt. Wenn Erdoberfläche und Absorber schwarze Strahler sind, so ergeben sich die Temperaturen aus ihren Abstrahlungsleistungsdichte. Es gilt damit TA = TE < TE1.
Sehen Sie hierin einen Verstoß des 2. HS der Thermodynamik? Doch hoffentlich nicht.
Michael Kunerth am 11. Mai 2023 um 20:53
Demonstration des Treibhauseffektes und des 2. HS an zwei einfachen Systemen.
System A besteht nur aus einer Erdoberfläche, die Sonnenstrahlung der Leistungsmenge J absorbiert. Im Gleichgewicht gilt, dass die als Abwärme abgestrahlte Leistung von der warmen Oberfläche E gleich ist wie die absorbierte Sonnenstrahlung, es gilt also J = E. Sei die Erdoberfläche schwarz, dann ist die Temperatur der Erdoberfläche TE alleine durch J (=E) bestimmt.
System B ist wie A hat aber einer Absorber zwischen der Erde und dem Weltall. Der Absorber ist voll für die Sonnenstrahlung durchlässig, absorbiert aber die Wärmestrahlung der Erdoberfläche E1 vollständig. Wir betrachten wieder den Gleichgewichtszustand, in dem sich zeitlich nichts ändert. Der Absorber nimmt eine Temperatur an. Intuitiv ist klar, dass die Temperatur des Absorbers TA (ebenso wie die der Erdoberfläche) u.a. auch von der Sonnenstrahlungsleistung abhängt. Denn wenn J=0 ist, sind beide Systeme bei TE1=TA=0 K im Gleichgewicht. Wenn J steigt, so steigen auch TE1 und TA.
Der Absorber ist ebenso wie der Rest im Vakuum und kann daher seine Wärmeenergie nur per Wärmestrahlung abgeben. Dies passiert zu beiden Seiten hin gleichartig. Seine Abstrahlungsleistung sei F. Da der Absorber E1 komplett absorbiert, gelangt nur die Wärmestrahlung des Absorbers F ins All.
Im Gleichgewicht stellt sich folgendes ein. a) die ins Weltall abgestrahlte Leistung F = J. b) da der Absorber seine Leistung komplett vom Boden bekommt und in beide Richtungen gleichartig abstrahlt, gilt F + F = 2 x F = E1.
Damit ergibt sich E1 = 2 x J = 2 x E (aus System A). D.h. die Abstrahlungsleistung der Erdoberfläche E1 ist im System B doppelt so hoch wie im System A. Der Treibhauseffekt basiert grundsätzlich auf diesem Effekt. Wenn Erdoberfläche und Absorber schwarze Strahler sind, so ergeben sich die Temperaturen aus ihren Abstrahlungsleistungsdichte. Es gilt damit TA = TE < TE1.
Sehen Sie hierin einen Verstoß des 2. HS der Thermodynamik? Doch hoffentlich nicht.
Thomas Heinemann am 12. Mai 2023 um 9:10
Michael Kunerth am 11. Mai 2023 um 20:53Demonstration des Treibhauseffektes und des 2. HS an zwei einfachen Systemen.
Der Übergang von A nach B kann so passieren. Der Absorber wäre zunächst weg und sei 0 K kalt. Die Erde sei zunächst im Zustand A. Der Absorber würde nun plötzlich vor die Oberfläche gebracht und schirmt damit die Abstrahlung der Erdoberfläche ins All ab.
Intuitiv und quantitativ ist klar, dass die Oberfläche dann wärmer wird, denn die von der Sonne unverändert an der Oberfläche absorbierte Energie kann nicht mehr im gleichen Maße ins All abgestrahlt werden. Es erwärmt sich aber der Absorber aufgrund der von der Oberfläche angelieferten Energie. Das neue Gleichgewicht stellt sich bei höherer Temperatur der Oberfläche ein = Treibhauseffekt.
Michael Kunerth am 3. Mai 2023 um 0:25
Sie meinen zwischen der Küvette mit CO2 und dem schwarzen Streifen um den Globus. Das wäre dann die richtige Messtelle, um den Treibhauseffekt zu messen, denn ohne CO2 war der schwarze Streifen 80 °C warm. Mit CO2 in der Küvette sollte diese Temperatur noch weiter steigen, wenn das System ins Strahlungsgleichgewicht mit der Lampeneinstrshlungsleistung ginge.
Der Punkt ist hier, dass man hier kaum einen Effekt messen könnte, denn dazu ist das System nicht „dicht“ genug (Energie geht nicht alleine durch Strahlung verloren) und zudem bildet sich quer zur Küvette kaum ein Gradient aus, der bewirken würde, dass zimmerseitig weniger durch aus der Küvette gestrahlt würde als globusseitig eingestrahlt wird. Dies ist aber der Witz beim Treibhauseffekt. Die Küvette ist zu dünn und der Temperaturunterschied beträgt höchstens Zimmertemperatur gegen 80°C.
Sie müssen sich klarmachen, dass es zu keinem Treibhauseffekt kommt, wenn das CO2 gleichwarm ist wie die Globusfläche.
Nein, natürlich nicht. Es ist ja gerade das wesentliche beim Treibhauseffekt, dass die einseitig absorbierte Leistung wieder komplett und in alle Richtungen abgestrahlt wird.
Herr Heinemann,
lesen sie heimlich bei „Klimaleugnern“ mit?
Ist das nicht das Argument das man fuer den Boden, die Einstrahlung aus der Atmosphaere und Konvektion postulieren muss?
Wie was zu duenn? Was soll das heissen, was macht dick oder duenn denn aus?
Ist das eine Anspielung auf die Frage warum eine dicke Wand besser isoliert als eine duenne? Oder wie was!
Sie sind ja doch ein patenter Kerl der selber nachdenkt! Glueckwunsch.
Obwohl, eigentlich liegen sie falsch, was sie sagen kann nicht stimmen.
WErner Schulz am 27. April 2023 um 23:54
Ich rede nicht von der gesamten Erde, sondern vom Klimasystem.
Ich überlasse es Ihnen, was Sie einsetzen. .
Generell gilt jedoch in der Physik und Technik: die Abschätzung ist immer unumgänglich.
Einmal, um sich nicht in unwesentlichen Details zu verirren und den Wald vor Bäumen nicht zu sehen und so nie den Zustand der Unsicherheit oder Verwirrung zu entrinnen. Also einfach deshalb, um Klarheit und Kontrolle zu erlangen.
Zum zweiten, um effektiv zu sein. Sich Gedanken über den Boden zu machen, ja, können Sie machen. Aber machen Sie es einfach, es reicht ja, abzuschätzen, wieviel der Boden im Vergleich zum Ozean an Wärmekapazität hat. Die Tiefsee berücksichtigen Sie einfach so, indem sie einfach die Temperaturerhöhung in Abhängigkeit von verschiedenen Tiefen ausrechnen. Da sehen Sie ja schon.
Sehen sie, da ist genau der Fehler. Die Klimawissenschaft muss diese Aufgabe angehen. Wenn sie es nicht hat, dann fehlt ein wichtiges Teil im Puzzle.
Sie sprechen von einer Abschaetzung, wo gibt es diese denn? Wollen sie sich auf mich verlassen? Ich dachte ich habe keine Ahnung?
Sie sind doch derjenige der sich mit Physik auskennt und Klimamodelle erklaeren koennen will.
Wofuer reicht das? Was macht man mit dem Wissen?
Nur das wir uns klar sind, die Temperatur nimmt mit der Tiefe ab.
Nach all dem was sie geschrieben haben, kann ich nur so zusammenfassen:
1. Sie koennen eine Energiemenge ausrechnen die von der Sonne kommt
2. Sie haben keine Angabe gemacht wieviel Energie das System verlaesst
3. Sie wissen nicht wieviel Temperaturerhoehung die eingetragene Energie bedeutet, weil sie weder die effektive Masse, noch den Waermeinhalt bestimmen wollen oder koennen. Das ueberlassen sie Forenmittgliedern, von denen sie sagen, das sie Physik nicht verstehen.
Am Ende haben sie eine Rechnung gemacht, die sie nicht weiterfuehrt ohne das sie ihr Klimasystem ordentlich definieren.
Wie definieren sie es also?
WErner Schulz am 30. April 2023 um 10:44
Sie können meine Abschätzung gerne übernehmen:
Das Klimasystem, um das es hier geht, ist das, in welchem Klimaänderungen im Laufe von einigen Jahrzehnten stattfinden. Das umfasst den Raum der festen Erde bis in eine Tiefe von höchstens 100 m. Den Ozean können wir bis h=700 m ansetzen, aber h variabel halten. Da der Kubikmeter Wasser von der Größenordnung gleiche Wärmekapazität wie fester Erdkörper, reicht die Abschätzung für eine wasserbedeckte Erde. Die Wärmekapazität dieses Klimasystems „Weltozean“ ist dann C = 4200 J/kg/K * O * 1030 kg/m3 * h = 2,2e+21 J/K/m * h, wobei O die Erdoberfläche ist.
Laut NASA-Diagramm bekommt das Klimsystem dE = 9,66e+21 J ein jedem Jahr an Wärmeenergie zugeführt, dies habe ich Ihnen schon berechnet (überprüfen Sie es). Der Zusammenhang zwischen Erwärmung dT unseres Klimasystems und der Wärmeenergie E (Mittelstufe) ist: dE = C*dT. Damit folgt dT = 9,66e+21 J / (2,2e+21 J/K/m * h) = 4,4 K/m /h.
Lassen wir den Wärmeeintrag so 100 Jahre laufen. In der Zeit ist die Deckschicht und darunter bis 700 m vermischt. Damit ergibt sich eine Erwärmung von 4,4 K/m/Jahr * 100 Jahre / 700 m = 0,6 K. Dies ist etwa die Größenordnung des beobachtbaren Klimawandels der letzten 100 Jahre. Die beobachtbare Erwärmung ist etwas größer, da unser C großzügig nach oben abgeschätzt wurde.
Mit anderen Worten: der im NASA Energiediagramm (dto. KT 2009) ausgewiesene jährliche Zuwachs an Wärmeenergie ins Klimasystem erklärt (per Abschätzung bis auf einen Faktor der Größenordnung 1) die beobachtare Erwärmung des Klimasystems.
Danke fuer die Rechnung.
Stehen diese Werte irgendwo bei der NASA? Also ist das Klimasystem so definiert wie sie sagen?
Kann es auch sein das jemand die 0.6 W/m2 anhand der vermeintlichen Temperaturzuhnahme ausgerechnet hat, so wie sie es hier in der Gegenrechnung dargestellt haben?
Was mich aber mehr interessiert, laut ihnen wird also Boden und Luft und Erde alles gleichzeitig waermer.
Wie sieht dazu das neue Diagram aus und wie verteilen sich die Waermestroeme?
Wenn der Boden eine hoehere Temperatur hat, verschiebt sich die Wellenlaenge der Abstrahlung weg von den Absorptionsbanden von CO2. Ich gehe davon aus das etwas mehr Waerme in den Weltraum durch das Atmosphaerische Fenster geht. Vielleicht macht das auch nichts aus, aber sicherlich kommt auch mehr Strahlung aus der Atmosphaere, die wird ja auch waermer.
Ihre Zahlen muss ich noch pruefen. Welchen Radius haben sie genommen? Und welche Flaeche fuer die Ozeane?
Sie haben leider eine Fehler in ihrer Berechnung wegen einer falschen Zahl der Erdoberrflaeche in ihrem vorhergehenden Beitrag. Da sie mit dem falschen Wert von 9,66e+21 Joule im Jahr weiter gerechnet habe, ist ihre gesamte Rechnung falsch. Verwunderlich allerdings, das sie genau das Ergebnis kriegen, wie es gewuenscht ist. Zufall? Oder nicht geprueft?
Werner Schulz am 1. Mai 2023 um 23:19
Heißt das, dass Sie endlich verstanden haben, dass die 0,6 W/m2 für die Erwärmung zuständig sind? Ich hoffe, Sie kommen in Zukunft nicht mehr mit der Gegenstrahlung u.ä. als Ursache der Erderwärmung an…
Wenn Sie es detaillierter abschätzen wollen, so machen Sie nur. Mir reichte die Größenordnung. Sie sehen ja daran schon die Konsistenz im Rahmen dessen.
Tun Sie das.
PS das NASA Diagramm stellt den Zustand ermittelt über die letzten Jahrzehnte dar. Der Rest ist klar.
Aha, woher wollen Sie das wissen? Wie groß ist denn dieser angeblich falsche Wert? Den müssen Sie doch vorliegen haben, wenn Sie eine solche Beschuldigung tätigen.
Herr Heinemann,
sie werden sicher noch antworten wegen dem Fehler mit der Flaeche.
Sie fragen ob ich einsehe, das die 0.6 W/m2 die Erwaermung verursachen.
Das kann ich leider nicht.
Ich habe ein Problem mit der Logik. Wenn die 0.6 W/m2 in den Boden gehen, wie erwaermt sich dann die Atmosphaere?
Die Waermestroeme in der Atmosphaere sind doch ausgeglichen?
Da kann sich also nichts erwaermen! Koennen sie das erklaeren? Wie gesage, wenn sich das Klimasystem erwaermt, dann doch bitte Boden und Atmosphaere.
Wie Herr Marvin Mueller weiter unten richtig bemerkt hat, haben sie mit der Flaeche doch richtig gerechnet aber eine ungewoehliche Notatation angegeben, die ich nicht so benutze.
Ich bitte sie sie um Verzeihung. Ich nehme an sie haben die Rechnung trotzdem noch mal geprueft?
Die Frage besteht, wie sich die Atmosphaere erwaermt, wenn der Restwaermestrom nur in einen Teil des Klimasystems geht?
Werner Schulz am 2. Mai 2023 um 18:27
Sie meinen, weil die Zahl im Diagramm am Boden steht? Diese Zahl benennt jedoch den Wärmeeintrag ins Klimasystem, welches ja ständig – wie man im Diagramm sieht – Energie zwischen den Teilsystemen austauscht. Die Zahl müssen sie sich als verteilt im Klimasystem vorstellen, wobei die Aufteilung der Energie so erfolgt, dass die Luft und die nahen Boden- und Ozeanschichten diese aufnehmen und sich erwärmen mit der Zeit tiefere Schichten des Klimasystems erfasst werden.
Da darf ich hoefflichst widersprechen. Die Waerme geht in den Boden. Die Waermestroeme der Atmosphaere sind ausgeglichen. Wenn eine Verteilung da waere mueeste auch die Atmosphaere ein negatives Defizit aufweisen. Tut sie aber nicht.
Werner Schulz am 3. Mai 2023 um 13:22
Dürfen Sie, aber wie so oft, liegen Sie auch hier falsch.
Sieht nicht so aus, wenn man nachrechnet. Die 0,6 W/m2 sind das Defizit zwischen Ein und Ab an der TOA.
Herr Heinemann,
sie sagen:
Es ging um die Atmosphaere. An der TOA sehen sie nur das gesamte Klimasystem.
Das hat zwei Teilbereiche: Atmosphaere und Boden. Laut Nasa gibt es nur einen Ueberschuss im Boden. Was sie an der TOA sehen ist nicht die Atmosphaere.
Es bleibt dabei, die Atmosphaere hat ausgeglichene Waermestroeme und kann so nicht waermer werden.
Werner Schulz am 4. Mai 2023 um 11:12
Ich habe Ihnen bereits erklärt, dass Ihre Behauptumg falsch ist und warum.
Das waere dann ihre Behauptung.
Fakt ist, das sie auf das Gesamtsystem an der TOA ablenken, waehrend es darum geht der Ueberschuss fuer das Gesamtsystems nur zu einem Teilsystem fliesst, waherend das anderes, also die Atmospharee sich scheinbar ohne aenderung des Waermezuflusses erwaermen soll.
Bitte erklaeren. Meinetwegen noch mal, aber bitte dann richtig.
keks am 28. April 2023 um 14:09
Verlogen kaum. Es ist ganz einfach, Ihr Fehler liegt bei der Annahme, dass jedes Molekül egal bei welcher Höhe dieselbe Energie haben müsse und diese bei Vertikalbewegung konstant bleiben müsse. Dies ist jedoch eine falsche Interpretation des Energieerhaltungssatzes. Der besagt nur, dass die Gesamtenergie des Systems konstant bleibt. Die Energien der einzelnen Moleküle verteilen sich jedoch nach einer Boltzmann (Maxwell-) Verteilung. Das ist elementare Thermodynamik.
Nehmen Sie einen mehrere Kilometer langen Behälter voll 20°C warmer Luft. Der Behälter ist von der Umgebung isoliert und liegt auf dem Boden.
Er wird plötzlich aufgerichtet. Ihre Behauptung ist nun, dass die Luft im oberen Teil kühler sein müssen als die untere und der vertikale Temperaturverlauf dem isentropen Gradienten entspräche. Für die isentrope Beziehung zwischen einem Luftmolekül unten und oben besteht aber kein Grund. Es besteht auch kein Grund, dass die Moleküle alle dieselbe Eneegie haben müssen. Im Gegenteil: die Thermodynamik ist die Physik der Fluktuationen (statistische Physik): bei gegebener Temperatur des Gases verteilen sich die Energien der einzelnen Moleküle des (klassischen) Gases gemäß der Boltzmannschen Verteilung. Im Schwerefeld bedeutet dies, dass das Gas im Behälter eine unabhängig von der Höhe konstante Temperatur annimmt und die Dichte des Gases nach oben hin abnimmt. Die potentielle Energie, die das Gas im senkrechten Behälter bekommt, wird der inneren Energie entnommen. Das Gas im senkrechten Behälter ist also kühler als vorher aber überall gleich.
Wenn Teile im System unterschiedliche Temperaturen hätten, so würde dies gemäß dem 2. HS zu einem Wärmefluß führen, der die Temperaturen angleicht und zum thermischen Gleichgewichtszustand führte. Die Entropie des Systems wäre dort maximal.
Ein isoliertes Systen wie von Ihnen beschrieben mit Temperaturgradienten widerspricht dem 2. HS.
Herr Heinemann,
dieses aufrichten des Behälters, wird dabei Arbeit verrichtet und wenn ja, wie gehen sie damit in ihrem Gedankenmodel um?
Sie sagen:
Richtet sich der Behaelter von allein auf?
Uebrigens da es ihr Model ist, koennen sie keine Angabe dazu machen was Herr Keks dazu zu sagen hat.
waere sicherlich besser formuliert als: Ich denke sie meinen!
Das waere auch positiver fuer sie, weil sie sagen, das sie denken!
Es ist auf jeden Fall positiv fuer uns! Danke!
„Im Schwerefeld bedeutet dies, dass das Gas im Behälter eine unabhängig von der Höhe konstante Temperatur annimmt und die Dichte des Gases nach oben hin abnimmt.“
Heinemännchen,
an welcher Baumschule willst du Physik studiert haben???
Energieerhaltung bezieht sich nicht auf ein Volumen, sondern auf die darin enthaltene Masse.
Entropie verteilt sich gleichmäßig im Raum
Die „Temperatur“ ist ein Maß für die E(kin).
Gemäß Energieerhaltung fällt E(kin) mit steigendem E(pot).
Beim Aufrichten deines Behälters verrichtest du Arbeit. Wo kommt die Energie her und wo geht sie hin???
Wäre die Geschwindigkeitsverteilung „oben“ wie die am Boden, würde die Atmosphäre ständig an Masse verlieren, da sich die Luftmoleküle ins All verdünnisieren würden. Dies trifft aber nur für H und He zu, da deren Brown’sche Geschwindigkeit am Boden über der Fluchtgeschwindigkeit liegt.
Damit, Heinemännchen, gilt das Gesagte nicht nur für den Scheinphysiker Müller, sondern auch für dich!
besso keks am 30. April 2023 um 12:44
Richtig lesen: der Behälter ist wie beschrieben isoliert (abgeschlossen). Masse und Energie bleiben also erhalten.
Ihnen ist also nicht mal klar, dass die Luftdichte im Behälter nach oben abnimmt?
Nun, das ist der Punkt, den Sie nicht verstehen. Sie behaupten also, jedes Molekül hat dasselbe E(kin)? Richtig ist, dass zwischen der MITTLEREN E(kin) und der Temperatur ein Zusammenhang besteht. Die Folgerung, dass gleichzeitig jedes Molekül dieselbe kinetische Energie hat, ist falsch. Merke: Thermodyamik ist Statistische Physik.
Die Arbeit ist natürlich die potentielle Energie, die fürs Aufrichten des Behälters aufgewandt werden muss. Diese wird wie geschrieben der inneren Energie des Gases entnommen.
„Energieerhaltung bezieht sich nicht auf ein Volumen, sondern auf die darin enthaltene Masse.“
Das bezieht sich nicht auf das mißglückte Behälterbeispiel
„Die „Temperatur“ ist ein Maß für die E(kin).“
Natürlich bezieht sich das auf den Durchschnitt des Assembles.
„Beim Aufrichten deines Behälters verrichtest du Arbeit. Wo kommt die Energie her und wo geht sie hin???
Die Arbeit ist natürlich die potentielle Energie, die fürs Aufrichten des Behälters aufgewandt werden muss. Diese wird wie geschrieben der inneren Energie des Gases entnommen.“
Aha…
Welche „innere Energie“ und wie geht das???
besso keks am 1. Mai 2023 um 14:07
Was soll es dann? Für uns ist nur wichtig, dass das Gas im Behälter isoliert ist und damit die Gesamtenergie konstant ist.
Schön. Wenigstens da herrscht Konsens.
Unter innerer Energie U versteht man in der Physik die thermische Energie, für unser ideales Gas gilt dU = Cv × dT, wobei Cv die isochrone Wärmekapazität ist, dT die Temperaturänderung.
Der wesentliche Punkt ist, dass die Dichte (ebenso der Druck) des Gases im thermischen und hydrostatischen Gleichgewicht mit der Höhe gemäß der Boltzmannverteilung (diese ist grundlegend in der Thermodynamik) abnimmt, wobei die Temperatur überall gleich ist.
Herr Schulz am 1. Mai 2023 um 18:58
Egal, so geht’s noch einfacher: drehen Sie den Behälter mit einem geeigneten Kran in die Senkrechte und lassen die Energiemenge der Luft unverändert im isolierten Behälter. Der Kran liefert also die Arbeit, die das Aufrichten erfordert und dabei in die Erhöhung der potentiellen Energie der Luft (und des Behälters) verwandelt wird.
Zur Erinnerung, das Thema ist: Herrn keks wird erklärt, dass auch in einem Behälter mit Luft im Schwerefeld thermisches Gleichgewicht herrscht, wenn überall die Temperatur dieselbe ist und nicht, wenn es oben kälter als unten ist.
Herr keks geht davon aus, dass die Luft mit dem Aufrichten oben kühler und unten wärmer wird, weil beim Aufrichten obere Luft eine höhere potentielle Energie annimmt. Letzeres ist zwar richtig. Aber die Ausbildung eines Temperaturgradienten und das „weil“ sind falsch.
„Unter innerer Energie U versteht man in der Physik die thermische Energie,“
Nicht nur!
Die Größe innere Energie
„Der wesentliche Punkt ist, dass die Dichte (ebenso der Druck) des Gases im thermischen und hydrostatischen Gleichgewicht mit der Höhe gemäß der Boltzmannverteilung (diese ist grundlegend in der Thermodynamik) abnimmt, wobei die Temperatur überall gleich ist.“
Darüber, Heinemännchen, solltest du nochmals nachdenken!
Warum soll die Dichte gemäß der Boltzmannverteilung abnehmen???
„Zur Erinnerung, das Thema ist: Herrn keks wird erklärt, dass auch in einem Behälter mit Luft im Schwerefeld thermisches Gleichgewicht herrscht, wenn überall die Temperatur dieselbe ist und nicht, wenn es oben kälter als unten ist.“
Jaja, Heinemännchen, schon gut, du mußt mir nichts erklären.
Die Natur kennt aber nur energetische Gleichgewichte und keine ausschließlich thermischen Gleichgewichte.
Mit thermischen Gleichgewichten zu hantieren macht im Schwerefeld nur auf der Ebene Sinn.
Wo willst du Physik studiert haben???
besso keks am 2. Mai 2023 um 13:33
… gehen dann in die spez. Wärmekapazität cv ein, innere (thermische) Energie dU = cv ×dT. Wie erklärt.
Seien Sie doch mal ehrlich-Sie haben keine Ahnung was die Boltzmannverteilung ist und Statistische Physik kennen Sie auch nicht. Sie haben nichts zu bieten.
Mit anderen Worten bei Ihnen ist es jetzt schon soweit, dass es nicht nur mehr oben kälter sein soll, sondern, dass der Behälter im Schwerefeld gar keine Temperatur hat.
Wenn ich also vom Erd- ins Dachgeschoß gehe, wird mein Kaffee nicht nur kalt, sondern hat gar keine Temperatur mehr.
Das erinnert an den Physikprofessor, der meinte wenn er einen Behaelter mit Luft hochhebt, das die Lufttemperatur sich ja nicht aendert, und deshalb ist es oben nicht kaelter als unten.
Daher die Frage an sie, was erwarten sie von der Temperatur im Inneren? Sie stecken Arbeit rein. Wie wirkt sich das aus?
Schon zu Ende gedacht?
Herr Heinemann,
bitte nicht so einen Unsinn schreiben.
1. Potentielle Energie in der Masse der Luft und des Behaelters entsteht durch das Aufrichten.
2. Kintetische Energie muss aufgewendet werden.
3. Die Energie kann nicht aus der Inneren Energie kommen, sonst wuerde sich der Behaelter selber aufrichten koennen. Abgesehen davon wuerde die Luft oder der Behaelter nicht kaelter werden, wenn sie innere Energie entnehmen? Geben sie damit Herrn Keks nicht recht, der sagt, das die Luft in der Atmosphaere durch den Aufstieg innere Energie in potentielle Energie umwandelt? Und da gibt es keinen Behaelter und keinen Heinemann der die Luft anhebt, das macht die wirklich von allein.
Wo wollen sie also mit der Diskussion hin? Hoffentlich zur Wahrheit!
„Wo wollen sie also mit der Diskussion hin? Hoffentlich zur Wahrheit!“
Aber Herr Schulz
Für Menschen wie Heinemännchen ist Wahrheit nur ein inhaltsleerer Begriff.
Solche Leute sind von ideologischer Verblendung und politischem Machtstreben getrieben.
Es geht darum anderen den eigenen Willen aufzuzwingen.
„Wahrheit“ ist den Faschisten letztlich nur ein kleines Übel
WErner Schulz am 2. Mai 2023 um 18:32
Wie schon gesagt, die Arbeit wird zu Steigerung der potentiellen Energie, die steigt beim Senkrechtstellen, verwendet, die innere Energie bleibt hingegen gleich. Sie müssen sich mal wieder mehr Zeit zum sorgfältigen Lesen nehmen.
Dann sind sie der Einzige der Potentielle Energie nicht zur Inneren Energie rechnet?
Oder der Einzige der Arbeit an einem System verrichten kann, ohne dessen Energieinhalt zu veraendern?
Der Einzige der den Satz von der Erhaltung der Energie nicht verstanden hat oder nicht weiss was innere Energie ist?
Werner Schulz schrieb am 04/05/2023, 10:58:23 in 322773
In der ersten Minute des Videos gibt es folgenden Satz zu hören: „Wenn du diesen Behälter auf einen Regal stellst, erhöht sich seine potentielle Energie aufgrund der Wechselwirkung des Behälters mit der Erde. Seine innere Energie jedoch nicht.“ Haben Sie sich das Video überhaupt angesehen oder haben Sie es nur nicht verstanden?
„Dann sind sie der Einzige der Potentielle Energie nicht zur Inneren Energie rechnet?
Oder der Einzige der Arbeit an einem System verrichten kann, ohne dessen Energieinhalt zu veraendern?
Der Einzige der den Satz von der Erhaltung der Energie nicht verstanden hat oder nicht weiss was innere Energie ist?“
Der Kerle hat nie im Leben einen Abschluß für Physik an einer ordentlichen Universität – oder er lügt
Werner Schulz schrieb am 04/05/2023, 10:58:23 in 322773
In der ersten Minute des Video erfährt man folgendes: „Wenn du diesen Behälter auf einen Regal stellst, erhöht sich seine potentielle Energie aufgrund der Wechselwirkung des Behälters mit der Erde. Seine innere Energie jedoch nicht.“ Haben Sie sich das Video überhaupt mal angesehen? Oder haben Sie einfach nur nicht verstanden, was da mitgeteilt wird?
Wir haben zwei Aussagen von Herrn Heinemann:
und
Finden sie den Widerspruch? Was ist es denn nun?
Paaren sie das mit der zweideutigen Anwendung des Begriffes „Potentielle Energie“ in meinem Link, weil es steht ja da:
Und sie haben den Salat. Ich gebe ihnen Recht das das Video und auch im Text sagt, das sich die Innere Energie nicht aendert wenn man den Behaelter nach oben stellt, aber man muss das im Bezug auf das System sehen.
Der Punkt ist ja genau der, wenn sie den Behaelter von „aussen“ anheben, dann muss sich die Innere Energie auch nicht aendern. Anders ist es in der Atmosphaere, das gibt es nichts was diese von aussen anfasst und anhebt. Aendert sich die Innere Energie aufgrund des Lagewechsels von Luftpaketen oder bleibt sie gleich?
wErner Schulz schrieb am 05/05/2023, 00:30:48 in 322820
Die beiden Aussagen beziehen sich auf verschiedene Vorgänge.
Im ersten Beispiel wollte Herr Heinemann das möglichst nahe an die Vorstellungen von Herrn Keks annähern. Daher richtete sich der Behälter von selbst auf (Die Isolation quasi masselos und die Teilchen bewegten sich quasi alle in einem Viertelkreis um das eine Ende der Box und richteten die Box auf) und die benötigte Energie für die Höhenänderung der Teilchen wurde der inneren Energie entnommen.
Da das schwer vorstellbar ist, wechselte er auf das beispiel mit dem Kran, der die Box aufrichtet und die dafür nötige Arbeit liefert.
Warum dann Ihr Widerspruch, nachdem Herr Heinemann den Kran zum Anheben eingeführt hat?
Die Luft bewegt sich nicht von allein nach oben. Sie wird durch Auftrieb aufgrund von Erwärmung angehoben.
In der Troposphäre – Ja, die innere Energie ändert sich, sie wird kleiner. Allerdings wird sie kleiner, weil das Paket beim Aufsteigen Arbeit verrichten muss – Volumenarbeit.
besso keks am 4. Mai 2023 um 18:35 und
werner Schulz
Herr Schulz, Sie müssen ihr Zitat komplett lesen und dann korrekt zitieren. Wenn Sie das machen, sehrn Sie, dass Ihr Zitat mich bestätigt. Die hier gewonnene potentielle Energie im äußeren Schwerefeld zählt nicht zur inneren Energie.
Herr keks,
Im zweiten Experiment, in dem der Kran die Arbeit am System verrichtet, wird ihm aber Energie zugeführt. Diese Arbeit wird aufgewandt, um die Luft anzuheben, also in potentielle Energie verwandelt und offensichtlich nicht, um die innere Energie zu erhöhen, also die Luft zu erwärmen. Merke: die Gesamtenergie enthält die Summe aus innerer und potentieller Energie in äußeren Feldern!
„oder ist ein verlogenes A…och“ und „Heinemännchen“
hey, bro, peace man! Du Krümelmoster mit dem kleinen Schw… Geh, doch mal in die Baumschule, da lernste vielleicht gepflegten Umgang mit Mitmenschen. Haste wohl in Deiner Ferkelstube nicht mitbekommen!???
Weil aus dramaturgischen Gründen mein letzter Hinweis an Herr Heinemann der Zensur zum Opfer fiel ,jetzt mal ein Versuch den Unterschied von Leistung und Energie im physikalischen Sprachgebrauch zu erläutern.
Vor 150 Jahren ist in der internationalen Physik festgelegt,die aktuelle Wärmemenge eines Körpers wird Wärme genannt und als Energie bezeichnet.
Energie ist im physikalischen Sinne eine reine Bilanzgröße.Für die Beschreibung physikalischer Vorgänge daher unbrauchbar.
Der Begriff Leistung in der Physik ist zur Beschreibung des physikalischen Vorgangs besser geeignet.Sinnvoll ist eine Aufteilung in Potenzial und Stromstärke.Und hier hadert die Physik mit sich selbst.Für die elektromagnetische Welle ist es sehr anschaulich formuliert.Kommt bei den Wanderbewegungen allerdings die Masse ins Spiel,wird es nicht konsequent formuliert.
Bei der Wärme wird es dann letztendlich zum gedanklichen Problem.
Machen Sie den Selbstversuch!!
Das Potenzial der Wärme ist die Temperatur.Die Stromstärke für die Wärmewanderung ist nicht definiert.Und selbstgebaute Brücken sind verboten.
Es scheint für einige ein Problem zu sein, daß es potentielle, kinetische, elektrische, chemische und thermische Energie gibt, wenn ich nichts übersehen habe. All diese Energien haben die identische physikalische Einheit Joule, haben aber trotzdem unterschiedliche Eigenschaften. Das einzige, was sie eint, ist, daß einen idealen Prozeß vorausgesetzt, sie 1:1 ineinander überführbar sind.
Der Begriff „Energiefluß“ ist semantisch irreführend, weil er Dynamik vorgaukelt, in Wirklichkeit aber ganz banal eine Leistung der Dimension Watt ist. Es kann natürlich ein dimensionsloser Faktor daraus werden, wenn man z. B. die kWh/24h ermittelt. Dann kürzen sich die h heraus und über bleibt kW x 1/24.
Herr Peters,
Sie haben eine komische Sicht auf die Physik. Physikalische Größen werden im Experiment oder in Beobachtungen als geeignetes Maß für physikalische Phänomene gefunden. Durch weitere Forschung findet sich ggf. auch eine anschauliche Korrespondenz. So weiß man heute, dass die Stromstärke proportial ist zur Anzahl von Elementarladungen ist, die pro Sekunde fließen. Und man weiß, dass das elektrische Potential bzw. deren Differenz Spannung proportial zur potentiellen Energie ist, welche eine Ladung im elektrischen Feld erfährt.
Ich hoffe, Ihnen ist klar, dass die „Aufteilung in Potenzial und Stromstärke“ nicht willkürlich möglich ist. Die elektrische Energie ergibt sich z.B. durch Vergleich mit der mechanischen Arbeit, die man aufwenden muss, um eine Ladung im elektrischen Feld zu verschieben.
Diese Sichtweise auf Leistung und Energie im physikalischen Sinne mag Sie verwundern.Darum bemühe ich ein praktisches Beispiel.
In einem Kernkraftwerk wird im Reaktor eine Wärmeleistung von 3000 MW erzeugt.
1000 MW sind als Elektrische Leistung nutzbar in Potenzialen Ihrer Wahl.
2000 MW sind Wärmeleistung mit einem Potenzial von (40+273) Kelvin.Ich kenne niemand,der auf die Idee käme,die 2000 MW Wärmeleistung in elektrische Energie umzuwandeln.
Daher ist es mehr als irreführend,einfach nur mal so eine Umrechnung über die Zeit zu machen.
Anschaulich wird es wenn die verbliebene Wärmeleistung aus dem Dampf des Turbinenkreislaufes über einen Kondensator an die Umgebung abgeführt wird.(Kühlturm oder Temperaturerhöhung eines Fließgewässers).Dabei ist das Potenzial wenige Kelvin,dafür aber sehr große Stromstärke!!
Zu allem Übel kommt dann noch der Wirkungsgrad dazu.In der Regel ist es noch zusätzliche Wärme.Temperaturbestimmung fast unmöglich.
Ich nehme an, Sie meinen hier elektrisches Potential. Na und? Was hat die Größe elektrische Spannung/Potential mit Energie zu tun? Da sie verschiedene physikalische Größen sind, ist hier nichts zum wundern.
Ja, das geht thermodynamisch bekanntlich auch nicht komplett (Entropie). Auch wenn Anergie nicht in elektrische Energie umgewandelt werden kann, ist sie trotzdem Energie (Wärme).
Mein Einwand war ja die aufgeworfene Frage,was unter Leistung im physikalischen Sinne zu verstehen ist.
Die Erklärung von Prof.Puschner ist ja sehr allgemein verständlich,wenn man denn will.
Weil aber in dem Diagramm der NASA von Watt/m² die Rede ist,habe ich mal dazu einige Bemerkungen aus meiner Sicht gemacht.
Da fällt mir auf,dass Sie die Physik eben anders verstehen.
Wenn es für Sie egal ist,mit welchem Potenzial die Leistung erbracht wird,was soll dann noch eine Bilanzierung über die Energie??
Ferdinand Peters am 28. April 2023 um 19:28
Dafür findet man in der Physik eine Definition, die man einfach verstehen muß. Das ist alles. Weder Herr Puschner noch Sie demonstrieren durch Ihr sinnlos ausuferndes Philosophieren, dass Sue den Stoff beherrschen.
Es gibt von physikalischer Sicht NULL Probleme mit dem Diagramm. Jeder, der Problem damit nennt, hat das Diagramm entweder nicht verstsnden oder heuchelt Probleme.
Ich verstehe Physik so wie hunderte meiner Industriekollegen, die ebenfalls Physiker oder Ingenieur sind. Es gibt keinen darunter, die mit Watt/m² ein Problem hätte.
Ihre Frage ist auch ohne Ihre Unterstellung sinnlos, denn offensichtlich ist Ihnen der Begriff Potential nicht klar. Der wird vielfach in der Physik in völlig verschiedenen Sinn gebraucht, aber wesentlich hier ist, dass es auch Energien gibt, die nicht aus einem enger benutzen Begriff des Potentials stammen, aus sog. nichtkonservativen Kräften. Aber solange Sie nicht wissen, welchen Potentialbegriff Sie hier meinen, ist Ihre Behauptung sinnlos.
Raten Sie mal, warum sowohl die Ladung, als auch die Wärme als physikalische Größe den Buchstaben Q haben.. Bei beiden ergibt die Ableitung nach der Zeit den Strom: I = Q_punkt = dQ/dt. Bei beiden ergibt sich über ein ohmsches Gesetz ein Widerstand. Bei der Strahlung mag das anstrengender sein, das die Potentialdifferenz T2^4 – T1^4 ist, aber auch dort lässt sich ein Wärmefluss beschreiben.
Und erneut wieder der Unfug mit einer 33K kälteren Erde ohne THE. 15 Grad am Erdboden und -18 Grad Abstahlungstemperatur der Erde ins All ergeben die 33K.
Aber wir wissen ja alle längst, es gibt nur eine Tagerde und Druck und Volumenarbeit erklären alles …
Wären Leistung und Energie identisch, hätten beide die selbe physikalische Dimension.
Weil das aber eben nicht der Fall ist, hat Leistung die Dimension Watt und Energie oder Arbeit die Dimension Joule oder Wattsekunde Ws oder auch kWh.
Die weiter unten genannte Dimension Joule/s = Ws/s = W, ist also keine Energie sondern Leistung ohne Zeitbezug.
Energie oder Arbeit hat also immer einen Zeitbezug, eine „Momentanarbeit“ oder „Momentanenergie“ existiert nicht. Es ist aber natürlich richtig, daß es ohne Leistung keine Arbeit oder Energie gibt. Und weil die Zeit normalerweise von selbst vergeht, sich so also aufintegriert, wird aus wirkender Leistung eine zeitproportionale Energie.
Ein Windrad mit 3 MW Leistung erzeugt also nur dann Energie, wenn es sich dreht und über die Zeit Energie abgibt. Wenn es also 24 Stunden voll läuft, erzeugt es 72 MWh. Wenn es aber steht, ist die verfügbare Leistung immer noch 3 MW, aber die Energie ist Null.
stefan strasser schrieb am 24/04/2023, 01:02:39 in 321782
Niemand behauptet, dass die identisch sind.
Darüber besteht auch Einigkeit.
Wer behauptet denn, dass das Energie wäre? Es wird immer wieder klargestellt, dass das entweder ein Energiefluss oder eine Leistungsangabe ist.
Und hier sehen Sie das genau falsch herum. Energie und Arbeit existieren auch ohne einen Bezug auf die Zeit. Wenn Sie einen Gegenstand hochheben, verrichten Sie Arbeit und erhöhen die potentielle Energie des Gegenstandes. Dabei ist es für die Arbeit egal, wie schnell Sie den Gegenstand hochgehoben haben – sie müssen nur die Höhe und die Gewichtskraft wissen. Die potentielle Energie existiert einfach, bis sie in eine andere Energieform umgewandelt wird, z.B. in kinetische Energie durch fallenlassen … Die innere Energie eines Körpers existiert auch ohne Zeitbezug, im Energieerhaltungssatz haben sie keinen Zeitbezug.
Leistung und Energiefluss hingegen können nicht ohne Zeitbezug existieren – daher haben sie den Bezug auf direkt in der Einheit: Energie pro Zeit bzw. Arbeit pro Zeit …
Das ist gerade falsch. Leistung/Energiefluss ist eine aus Arbeit/Energie und Zeit abgeleitete Größe. Sie brauchen zur Bestimmung der Arbeit keine Zeit. Die brauchen Sie nur, wenn Sie bei einer gegebenen Leistung/Energiefluss die Arbeit/Energie bestimmen wollen …
[1] Sie könnten vielleicht argumentieren, dass auch Arbeit und Energie abgeleitete Größen sind mit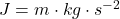
– aber dann hätte beide Größen einen Zeitbezug und Leistung mit 
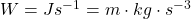sogar noch einen stärkeren …
Sehr richtig, dem Wärmeinhalt ist die Zeit egal. Je nachdem wieviel Energie im Körper ist, so ergibt sich die Temperatur.
Deshalb muss man bei einer Energiebilanz den Wärmeinhalt vorher und nachher angeben.
In Joule wenn’s geht. Und eben nicht in Watt oder W pro Quadratmeter.
Und wenn wir bei dem Beispiel bleiben mit dem Anheben. Wenn eine Masse Luft angehoben wird, spielt es keine Rolle wie schnell das passiert, sondern nur das es passiert? Wie wirkt sich das dann auf den Energieinhalt aus, mit steigender Höhe aber geringerer Dichte?
Werner Schulz schrieb am 24/04/2023, 18:55:19 in 321870
Wenn abgesehen vom Anheben nichts anderes passiert ist es egal, wie schnell das passiert.
Sie kennen die Antwort auf diese Frage – genauer gesagt mindestens ein Werner Schulz kennt die Antwort auf diese Frage. Warum teilen Sie nicht einfach mal Ihr Wissen statt immer nur Fragen zu stellen?
#321917
Danke Herr Mueller,
suchen sie also keine Antworten? Wollen sie einfache Fragen nicht beantworten?
Reicht ein Wort vielleich? Lapserate?
Ist diese physiklaisch dargestellt? Erklaert sie den Temperaturgradienten in der Atmosphaere?
Wollen sie nicht Antworten? Warum?
Werner Schulz schrieb am 26/04/2023, 07:09:11 in 321978
Ich bin ständig dabei, Ihre Fragen zu beantworten. Es bleibt nur nichts hängen und ich bin mir nicht sicher, was die Ursache dafür ist.
Die Lapsrate ist lediglich die Angabe der Temperaturabnahme mit der Höhe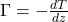
, sie kann also den Gradienten nicht erklären. Die Temperaturänderung ergibt sich aus dem Zusammenspiel von Wärmeleitung, Wärmestrahlung und Konvektion. Könnten Sie in einem Artikel über die Lapsrate nachlesen, wenn Sie das wissen wollen würden …
„Die Temperaturänderung ergibt sich aus dem Zusammenspiel von Wärmeleitung, Wärmestrahlung und Konvektion.“
Müller,
es gibt zwei Möglichkeiten
1. du lügst
2. du hast keine Ahnung
Welch, glaubst du, halte ich für wahrscheinlicher?
Mindestens ein Marvin Mueller hat behauptet die Temperatur der Oberflaeche ist von der Strahlung abhaengig.
Ist das der gleiche der nun sagt:
???
Werner Schulz schrieb am 26/04/2023, 20:39:38 in 322075
Wo sehen Sie da einen Widerspruch? Vor allem, wenn Sie berücksichtigen, dass auch in dem anderen Statement Konvektion vorkam: „1964er Manabe Papier .. Dort wurde doch klar, dass sich die Temperatur am Boden und in der Atmosphäre durch Strahlung ergibt und diese Temperatur durch Konvektion und latente Wärme reduziert wird. “
Sie demonstrieren hier wieder schön, was passiert, wenn man Ihre Fragen beantwortet. Da wird nicht der Inhalt diskutiert, sondern es werden scheinbare Widersrpüche konstruiert … Das „mindestens ein“ können Sie bringen, wenn ich anfange, mir selbst permanent zu widersprechen oder beliebige Positionen zu vertreten …
besso keks schrieb am 26/04/2023, 14:20:04 in 322041
Was Sie glauben ist nicht wichtig. Die Frage ist eher, welcher Fall der richtige ist. Erklären Sie doch einfach, warum sich die Temperatur mit der Höhe ändert und wenn Sie das plausibel erklären können, ohne Wärmeleitung, Wärmestrahlung und Konvektion zu betrachten – dann räume ich gerne ein, dass ich keine Ahnung habe …
„Erklären Sie doch einfach, warum sich die Temperatur mit der Höhe ändert und wenn Sie das plausibel erklären können, ohne Wärmeleitung, Wärmestrahlung und Konvektion zu betrachten – dann räume ich gerne ein, dass ich keine Ahnung habe …“
Schwerefeld, E(pot)
Wie oft muß man das noch sagen???
In einem Schwerefeld kann es über die Höhe keine Isothermie geben!
besso keks schrieb am 27.4.2023, 16:59:32 in 322136
Und das Schwerefeld verändert sich an der Tropopause (dort bleibt die Temperatur trotz sich ändernder Höhe konstant) und kehrt sich in der Stratosphere sogar um (dort steigt die Temperatur mit zunehmender Höhe wieder)? Wie passt das zu Ihrer persönlichen Sicht?
Marvin Müller am 27. April 2023 um 9:32
Man braucht, um Temperaturänderung mit der Höhe zu erklären, keine Wärmeleitung, Wärmestrahlung oder Konvektion! Es ergibt sich ganz einfach aus der Energieerhaltung. Wenn es in einem gewissen Raumvolumen auf 100 m Seehöhe eine Temperatur T1 hat und man dieses Raumvolumen auf 1100 m Seehöhe hebt, dann ist der Rauminhalt aufgrund des dort herrschenden niedereren Drucks wesentlich größer als auf 100 m. Vergleiche die Größe des Heliumballons beim Stratosphärensprung von Felix Baumgartner am Boden und oben in Absprunghöhe.
Es verteilt sich also die Energie=Wärme einmal auf ein geringes Volumen und dann auf ein wesentlich größeres, was daher eine niederere Temperatur T2 ergibt. Weil die Energie bleibt konstant, drückt man dieses Volumen wieder nach unten, wird es auch wieder wärmer, siehe auch Föhnwinde.
Natürlich kann es zusätzlich auch noch andere energetische Effekte geben, aber der Basiseffekt ist die Energieerhaltung.
stefan strasser schrieb am 28/04/2023, 08:00:54 in 322176
Wodurch geschieht das Anheben des „Raumvolumens“? Nicht durch Konvektion?
Und wie entstehen die Bedingungen für Konvektion? Nicht dadurch, dass der Boden durch Sonnenstrahlung erwärmt wird und die oberen Schichten durch Abstrahlung gekühlt werden und dadurch ein Gradient entsteht, der zu Konvektion führt?
Und die Temperatur sinkt auch nicht aufgrund der Volumenänderung sondern aufgrund der dafür nötigen Arbeit – siehe Gay-Lussac-Versuch, bei dem sich das Volumen ändert, ohne dass sich die Temperatur ändert …
Wollen Sie nicht doch nochmal in ein Physikbuch schauen und Ihr Wissen auffrischen? Das ist zum grossen Teil Schulwissen …
„Und das Schwerefeld verändert sich an der Tropopause (dort bleibt die Temperatur trotz sich ändernder Höhe konstant) und kehrt sich in der Stratosphere sogar um (dort steigt die Temperatur mit zunehmender Höhe wieder)? Wie passt das zu Ihrer persönlichen Sicht?“
Das paßt sehr gut, da ja nur das Grundgerüst des Temperaturgradienten durch die Isentropie bestimmt wird.
Daneben gibt es Störgrößen (Absorption von eingehender/ausgehender Strahlung, freiwerdende Latenzwärme, Konvektion etc.), welche lokal den isentropen Gradienten beeinflussen.
Daher nochmal:
wer behauptet, daß in einem Schwerefeld der vertikale Temperaturgradient den Bedingungen der Isothermie folgt, hat entweder keine Ahnung oder ist ein verlogenes A…och!
Marvin Müller am 28. April 2023 um 9:56
Sorry, ich habe aus Ihrem Text Konvektion irrtümlich mitkopiert, war mein Fehler. Eigentlich sollte nur Wärmeleitung und Wärmestrahlung ausgenommen werden. Meine Erklärung an sich ist deshalb natürlich nicht falsch.
Wärmere Luft ist leichter als kühlere, deshalb steigt sie auf und damit verteilt sich die vorhandene Wärme auf ein immer größer werdendes Volumen, was gem. Energieerhaltung zu einer Abkühlung führen muß.
Werner Schulz am 24. April 2023 um 18:55
Fürs Klimasystem der Erde liest sich diesen aus dem NASA-Diagramm im Artikel ablesen: der Wärmeinhalt der Erde steigt offensichtlich nach der Angabe im Diagramm gegenwärtig um 9,66e+21 Joule im Jahr, am 1. Januar 2013 war er um diesen Betrag höher als am 1.1.2012, z.B.
Ah ja,
um wieviel Grad C erwaermt eine solche Waermemenge die Erde?
Muss man dazu nicht erst mal den Waermeinhalt der Erde kennen?
Wie hoch ist der?
Werner Schulz am 26. April 2023 um 7:20
Das dürfen Sie bitteschön selber ausrechnen. Die Anleitung dazu habe ich bereits xmal gepostet.
Tip: Wärmekapazität vom Klimasystem ist von der des Weltmeeres dominiert, die spez. Wärmekapazität von Wasser ist einfach zu finden, elementare Geometrie zur Berechnung der Masse des klimawirksamen Meereswassers nutzen. Mittelschulphysik ergibt die zur Änderung des Wärmeinhalt gehörige Temperaturänderung im Klimasystem.
HErr Schulz, man erwartet Ihr Ergebnis für die Temperaturerhöhung, welches aus der nun bekannten Änderung des Wärmeinhalts resultiert.
Oder haben Sie den Klimawandel über die Energiezunahme alleine verstanden?
Reicht das? Immerhin sprachen wir vom Waermegehalt der ganzen Erde! Sie kommen mit dem Klimasystem. Wieviel Bodenschicht wollen sie mit einrechnen?
Tiefmeere gehoeren dazu? Was soll ein Klimawirksames Meerwasser sein?
Was ist Mittelschulphysik?
Ich habe jetzt erkannt, dass strasser und Prof Puchner glauben, die Kennzeichnung eines Energiewandlers mit Angabe einer Leistung sei betrügerisch. Wenn eine Glühbirne ungenutzt in der Verpackung liegt, auf der 100 W steht, die Birne aber in der Stunde nicht 100 Wh Energie abgibt, sondern nur rumliegt aber mit der Kennzeichnung 100 W protzt, so sei das Betrug.
Was sie so alles feststellen.
Aber das mit der Glühbirne ist nur der kleine Betrug
Der grosse passiert bei der Angabe von installierter Leistung bei den unsteten Erzeugern.
Na Licht schon an?
Ist der Käufer nicht einfach nur zu blöd, der meint, eine 100 W Birne würde diese Leistung schon in der Packung schon ohne Stromanschluß leisten?
Vielleicht auch nur der, der solche Fragen stellt!
100 W bedeutet für eine 220 V-Birne, daß sie einen Strom von 2,2 A fließen läßt. Wenn man die Birne einschaltet, wird also eine Leistung von 100 W benötigt, sie zu betreiben und pro Sekunde, die sie brennt, entsteht „Arbeit“ von 100 Ws oder 100 Joule. Nach einer Stunde brennen sind es 1 Wh oder 0,001 kWh. Dabei werden ca. 5% dieser Arbeit in Lichtenergie umgewandelt und 95% in Wärmeenergie.
Die Kommentare von Heinemann belegen offen sein wirres Verständnis bezüglich physikalischer Einheiten.
stefan strasser am 26. April 2023 um 7:55
Nö, weniger als 0,5 A.
Thomas Heinemann schrieb am 28/04/2023, 12:50:12 in 322211
Sie müssen schon mit der Strasserschen Physik rechnen, da gilt offensichtlich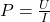
…
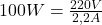meine Eselsbrücke von vor 45Jahren: „Watt ist VAtt“
W=VA
insofern: 100W=220V*0,45A
Sorry, sowas kommt offenbar vor, wenn man mit knapp 39°C Fieber Kommentare abgibt.
Natürlich ist P=UxI …
„Energie und Arbeit existieren auch ohne einen Bezug auf die Zeit.“ wird behauptet.
Aha, und welche Dimension hätte so eine Energie oder Arbeit dann?
Eines ist natürlich klar, wenn Arbeit einmal geleistet ist, also Leistung mal Zeit stattgefunden hat, dann ist das Ergebnis davon natürlich existent, nur ist das nicht die Arbeit, sondern eben das Ergebnis der Arbeit!
Wenn ich also einen Haufen Erde von a nach b schaufle, geschieht die Arbeit während der Zeit des Schaufelns. Danach ist die Arbeit erledigt, ihr Nachweis ist aber, daß der Haufen an einer anderen Stelle liegt. Nach dem Ende des Schaufelns vergeht zwar die Zeit weiter, aber es gibt keine weitere Leistung mehr, es findet also keine Arbeit mehr statt.
Heinemann und Müller geben also wieder einmal ein typisches Zeugnis ihrer physikalischen Einfältigkeit ab.
Köstlich. Verraten Sie mir auch, ob es im 1. HS der Thermodynamik (Energieerhaltungssatz) nun um die Erhaltung der Energie oder um die Erhaltung des Ergebnisses der Energie geht? Ist Joule die Einheit für Arbeit resp. Energie oder ist Joule die Einheit für das Ergebnis der Arbeit resp. Energie ?
Sagten sie nicht das sie Physiker sind?
Es scheint doch eher sie sind Theologe!
stefan strasser schrieb am 25/04/2023, 09:30:40 in 321900
Das kann man doch einfach nachschlagen. Wenn ich mich recht entsinne wird Arbeit im Physikunterricht als Arbeit = Kraft mal Weg –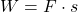
mit den Einheiten 
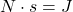eingeführt. Es werden später verschiedene andere Formen von Arbeit eingeführt, aber das Prinzip ist immer das gleiche – kein Bezug zur Zeit. Dieser kommt erst, wenn man die Leistung bestimmen will, wenn man die geleistete Arbeit durch die für die Arbeit benötigte Zeit teilt …
Marvin Müller schrieb am 25.4.2023, 13:38:00 in 321921
Das sollte natürlich
– Newtonmeter – sein …
Müller und Heinemann
Es ist müßig mit Ihnen beiden zu diskutieren. Es gibt ein eindeutiges Merkmal in der Physik, und das ist die physikalische Einheit einer Größe.
Wenn also nicht bestritten wird, daß die Einheit von Energie/Arbeit das Joule ist, was sich zusammensetzt aus Leistung (Watt) mal Zeit (Sekunden), also Ws, verwundert es, wenn so jemand gleichzeitig starrsinnig behauptet, Energie/Arbeit hätten keinen Zeitbezug. So könnte man auch die Quadratur des Kreises behaupten.
Natürlich steigt die potentielle Energie eines Steines, wenn man ihn höher hebt. Aber das höher Heben benötigt Zeit. Die potentielle Energie, die dem Stein zugeführt wird, beinhaltet also die Leistung, die erforderlich ist, ihn höher zu heben und die Zeit, wie lange er gehoben wurde. Was daran ist unklar? Wenn der Stein dann stabil weiter oben liegt, tritt keine Arbeit bzw. Energie mehr auf. Energie oder Arbeit entsteht erst wieder, wenn der Stein erneut seine Höhe verändert, was wieder gleichzeitgen Bezug zu Leistung und Zeit hat.
Mehr ist dazu eigentlich nicht zu sagen. Gute Nacht!
stefan strasser schrieb am 25/04/2023, 23:30:58 in 321961
Da heben Sie Recht. Und diese Einheiten sind für Arbeit/Energie Joule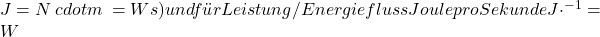
. Sie lassen sich nur dadurch verwirren, dass man für Leistung eine extra Einheit Watt mit 
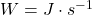eingeführt hat und daher für Energie/Arbeit auch Ws schreiben kann. Werfen Sie einfach einen Blick auf die SI-Einheiten, dann sehen Sie, was woraus abgeleitet wird:
Aber vielleicht wäre es viel einfacher, wenn Sie sich erinnern, wie mechanische Arbeit in der 6. Klasse in Physik eingeführt wurde. Bei der Formel Arbeit ist Kraft mal Weg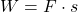
kann man eigentlich nichts missverstehen.
Welche Angaben benötigen Sie zur Bestimmung der Änderung der potentiellen Energie in dieser Situation? Ein Schüler der 6. Klasse (?) würde Ihnen sicherlich sagen, dass Sie nur die Gewichtskraft und die Höhe brauchen. Das ist reine Physik, da sollte es doch eigentlich keine Missverständnisse geben. Vielleicht ein paar Aufgaben zur Arbeit rechnen …
Der Nachteil an LaTex – man sieht das Resultat nicht sofort. Der Text sollte heissen: „Und diese Einheiten sind für Arbeit/Energie Joule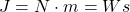
und für Leistung/Energiefluss Joule pro Sekunde 
. “ …
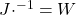#Thomas Heinemann am 23. April 2023 um 13:56
Danke für die Weitergabe Ihrer einleuchtenden Erkenntnis, es tut mir leid, dass ich nicht die Ihnen genehme Wortwahl getroffen habe. Dennoch finde ich es aufopfernd, dass Sie den Anwalt von Herrn Ketterer spielen. Haben Sie schon mit Ihm gesprochen, ob er auch so allergisch gegen meine Zeilen reagiert hat? – Wäre doch einmal eine kleine Aufgabe. – Aber vielleicht wollen Sie sich ja auch nur einfach abreagieren.
Sollte ich da einen wunden Punkt getroffen haben? Um verstanden zu werden, drücken Sie sich einfach klar aus.
Jedenfalls ist es klar, das sich weder die Begriffe noch die Gesetze der Physik durch politisches Geplänkel ändern. Wenn Sie das anders sehen, tut es mir leid. Ebenfalls ist klar, dass es keine Debatte um den physikalisch wohldefinierten Begriff Leistung braucht, nur weil Politiker ihn in den Mund nehmen, ohne zu wissen, was er bedeutet.
#Thomas Heinemann am 23. April 2023 um 18:07
„Um verstanden zu werden, drücken Sie sich einfach klar aus.“
Ist das jetzt ein Befehl, oder soll das eine Bitte sein, bei der Ihnen einfach nur die Höflichkeit mangels geübten Umgangs damit abhanden gekommen ist?
Zu Ihrem restlichen Geschreibsel passt rein gar nicht, was ich geschrieben habe und was Sie glauben kommentieren zu müssen. Haben Sie wohl im Übereifer der Selbstdarstellung etwas verwechselt, soll ja vorkommen.
Herr Puschner,
Hier ist kaum der Ort, Befehle zu erteilen, denn wir machen dies hier ja alles nur zum Zeitvertreib.
Ich bitte Sie also. Und möglicherweise liegt meine forsche Art daran, dass ich mir grundsätzlich nicht vorstellen kann, wieso ein Ingenieur ernsthaft Probleme bei den Begriffen Energie, Energiefluss, Leistung und Leistungsdichte hat. Ich fühle mich verschaukelt. Meine einzige Erklärung ist bislang, dass der Schuh bei Ihnen eigentlich woanders drückt, was Sie jedoch nicht erklärt haben. Daher die Bitte um Aufklärung.
Frage an den Inschenör:
Was ist Leistung?
#M. F. Ketterer am 23. April 2023 um 9:24
=>Was ist Leistung?
Eine ganz einfache Antwort, zu der es keiner physikalischen Kenntnisse bedarf: Leistung ist nicht Energie, sonst wäre eine Vokabel zu viel definiert worden. Wer das nicht auseinanderhalten will oder kann, ist in den Kreisen unserer ehemaligen Bundeskanzlerin als angebliche Physikerin gut aufgehoben, sie kann es, wie die meisten Politiker, auch nicht.
Eine 100W Glühlampe in der Schublade wandelt noch keine Energie, sie bleibt trotz der Leistung(sfähigkeit) 100W dunkel und Sie brauchen auch nicht deren mögliche Arbeit (Energie) bezahlen, solange sie ihre Leistung nicht für eine bestimmte Zeit angeschlossen am Netz zur Energiewandlung nutzt.
Aber warum haben Sie die Frage überhaupt gestellt? Die Zukunft bringt uns doch eine ganz neue und viel bessere Physik, sie wird per Gesetz beschlossen, und dann ist sie gültig. Für die kommende Generation eine totale Erleichterung, muss sie sich doch nicht mehr mit dem Ohmschen Gesetz, den Kirchhoffschen Regeln, oder gar Maxwellschen Feldgleichungen auseinandersetzen.
Wer in Zukunft 100% „Erneuerbare“ per Gesetz durchbringt, für den ist Flaute auf dem Meer für ein Segelschiff dadurch zu beheben, dass man einfach 1000 Segelschiffe bei Flaute auf das Meer setzt. Auch wenn Sie den Schwachsinn erkennen, Herr Habeck wird das durch Gesetz einfach zu neuer genialer Politphysik umdrehen.
Zurück zur Frage: Leistung wird erst dann zur Energie, wenn die Zeit als Faktor hinzukommt, sich also Ws oder Joule ergeben. Mit W oder Joule/s kann man eben gerade nicht Energie beschreiben. Sie werden in der Regel auch nicht für Ihre Leistungsfähigkeit bezahlt, wenn Sie diese nicht entfalten. Wenn Sie sie entfalten, nennt man das Arbeit (Energie), dafür werden Sie in der Regel bezahlt.
Hm, sollen Ihre Andeutungen darauf hinemweisen, dass Ihnen der Begriff „installierte Leistung“ missfällt, da 100 W installierte Leistung nicht 100 W Leistung ist?
Das macht die Begriffe Leistung und Energie jedoch nicht problematisch! Als Physiker und für die Physik ist im übrigen der falsche oder unprofessionelle Gebrauch physikalischer Begriffe irrelevant.
„Als Physiker und für die Physik ist im übrigen der falsche oder unprofessionelle Gebrauch physikalischer Begriffe irrelevant.“
Na toll
…für Physiklehrer ist anscheinend der korrekte Gebrauch deutscher Rechtschreibung irrelevant ;-)…
Leistung zur Energie ist das gleiche wie eine Geldrate zum Geld.
Wenn sie Ihr Geld auf dem Konto zaehlen, welche Einheit nehmen sie dann? Euro oder Euro pro Tag?
Haben sie schon mal ne Bilanz gesehen die keinen Geldwert angibt und alles nur in Raten?
Wie sagte Friedrich Hebbel: „Es ist unglaublich, wieviel Geist in der Welt aufgeboten wird, um Dummheiten zu beweisen.“
Lesen Sie hier (ab Seite 10): G. Falk, W. Ruppel, Energie und Entropie – Die Physik des Naturwissenschaftlers. Eine Einführung in die Thermodynamik, 1976
https://books.google.de/books?id=rKimBgAAQBAJ&pg=PA12&lpg=PA12&dq=energiestrom+definition&source=bl&ots=vkO3y41yzi&sig=ACfU3U1U669IIrN5EskDF4Ze4ZcSm7-_9A&hl=de&sa=X&ved=2ahUKEwiYhq3Qjo72AhXjgv0HHU_DAW04WhDoAXoECBkQAw#v=onepage&q=energiestrom%20definition&f=false
Zusammenfassung:
+ Leistung (Energiestrom) P -> Prozessgröße – entspricht einer Wirkung, die in einem Prozesszeitraum bewirkte Energieänderung.
+ Energie E -> Zustandsgröße – entspricht einem Potential.
Energie kann somit nicht mit einer Leistung gleichgesetzt werden. Man kann die Leistung oder den Energiestrom P als energie-analoge Größe betrachten, dabei gilt für ein System nach dem Erhaltungssatz der Energie für die Energieänderung Pi = ∆Ei/∆t und Pa = ∆Ea/∆t, damit kann die Energiebilanz wie folgt forumliert werden: Pi = Pa -> ∆Ei/∆t = ∆Ea/∆t. Entscheidend ist also der Prozesszeitraum, in der die Energieänderung stattfindet.
+ Energiestrom = Leistung [J/s = W] – Korrekt müsste es Energiestromstärke P = ∆E/∆t heißen, die eine extensive Größe ist.
Der Energiestrom = Leistung P ist die abgeleitete Größe: P = E/t = F·s/t. Demzufolge stellt der Energiestrom = Leistung P in Jolue pro Sekunde oder Watt diejenige Energie E in Joule dar, die während der Prozesszeit t dem System zu- oder abfließt bzw. ausgetauscht wird.
+ (Flächen-) Energiestromdichte = (Flächen-) Leistungsdichte [J/(s·m²) = W/m²]
Die Energiestromdichte = Leistungsdichte j ist eine vektorielle intensive Prozessgröße (Ausgleichsgröße) der vektoriellen Geschwindigkeit v = ∆s/∆t von einem „Energiepaket“ der Energiedichte ∆E/∆V = ∆E/(A·∆s): j = ∆E/∆V·v = ∆E/(A·∆s)·v = ∆E/(A·v·∆t)·v = ∆E/(A·∆t).
Die Differential-Schreibweise für die Flächenstromdichte ist: dP = j·dA. Die vektorielle Flächenstromdichte j ist die charakteristische intensive Größe für den Strom der mengenartigen extensiven Systemgröße dP. Das vektorielle Flächenelement dA ist in diesem Fall die extensive Größe. In jedem Fall ist die gesamte Energieströmung an jeder Stelle des Raumes auf die Flächen- und Zeiteinheit bezogen, ein bestimmter endlicher Vektor. Die vektorielle Flächenstromdichte j ist somit eine vektorielle intensive Transport-Prozessgröße, also die sich ausgleichende Größe.
Mfg
Werner Holtz
Bravo!
„Wie sagte Friedrich Hebbel: „Es ist unglaublich, wieviel Geist in der Welt aufgeboten wird, um Dummheiten zu beweisen.““
Ein kluger Mann!
Christian Friedrich Hebbel (* 18. März 1813 in Wesselburen, Dithmarschen; † 13. Dezember 1863 in Wien)
Man sieht, es war früher nicht alles besser…
„Bei einer Temperatur von 288 K beträgt der Photonenfluss (unter der großzügigen Annahme, dass alles bei einer Wellenlänge von 15 Mikrometern liegt, um die Anzahl der IR-aktiven Photonen zu maximieren) etwa 3 X 10^²² Photonen/Sek-m². Das ist eine Menge Photonen,“
Na, wieviel Photonen wären es denn nur im 15 Mikrometerbereich?
Und weiter , wieviel CO2 und H2O Moleküle sind im 1. Kubikmeter Luft über dem Boden?
Schon im ersten Kubikmeter Luft über dem Boden, wird alles absorbiert und in kintische Energie umgewandelt – kann man messen, über die Temperatur ohne grossen Auffwand – 2 oder 3 Glasscheiben über dem strahlenden Boden in verschieden Höhen befestigen und deren Temeperatur messen!
Alles ganz einfach – ohne komplexen Gleichungan ala Kramm!
Peter Puschner, Prof. Dr.-ing. schrieb am 21.4.2023, 16:34:28 in 321546
Vielleicht könnten Sie dieses Argument mal anhand der Wärmeleitung prüfen. Die ist an Material gebunden und der Wärmestrom hat die Einheit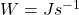
bzw. die Wärmestromdichte 
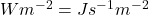. Wärmestrom ist Joule pro Sekunde, da steckt also die Energie drin …
#Marvin Müller am 22. April 2023 um 13:13
=> Wärmestrom ist Joule pro Sekunde, da steckt also die Energie drin …
Nein, in Watt oder Joule/s steckt gerade nicht Energie drin, sondern schlicht Leistung. Energie steckt in Ws oder Joule!
Peter Puschner, Prof. Dr.-ing. schrieb am 22.4.2023, 16:36:04 in 321648
Wollen Sie wirklich sagen, dass bei Wärmeleitung keine (Wärme-)Energie fliesst? Dass da nicht Energie von warm nach kalt fliesst? Dass da nicht X Joule pro Sekunde von warm nach kalt fliessen?
Zur Erinnerung: Klima ist die Geschichte des Wetters. Seine wahrscheinliche Veränderung für wenige Tage liefert der Wetterbericht! –
Alles andere besorgen Wahrsager mit Glaskugel, Kaffeesatz. oder „Modellen“!
Man fragt sich, wieso wir früher darauf gekommen sind. Es ist so offensichtlich, das Prinzip Thermoskanne: Bei der Thermoskanne wird die Wärmeleitung und die Konvektion unterbunden, es bleibt der Wärme nur die Strahlung, um sich aus der Flüssigkeit in der Kanne in die Umgebung zu übertragen. Das funktioniert aber nicht. Die Wärme eines Körpers überträgt sich eben durch Strahlung nur sehr schlecht in die umgebende Atmosphäre. Damit bricht aber auch das Kartenhaus der CO2-bestimmten Erdoberflächentemperatur zusammen.
Eine Übertragung der Pirani-Messung auf die Erde ist unzulässig, wie bereits Dr. Ullrich angemerkt hat, da als Wärmequelle absichtlich ein dünner Heizdraht mit einer sehr kleinen Oberfläche verwendet wird.
Herrn Shula‘s Schlussfolgerung „Die IR-Strahlung sei für den Aufwärtswärmetransport in der unteren Atmosphäre unbedeutend“ ist völliger Unsinn, was leicht zu widerlegen ist, wenn man sich die nächtliche Strahlungsinversion ansieht. Nach Sonnenuntergang kühlt sich der Boden durch IR-Strahlung schneller ab als die bodennahe Luftschicht, was Konvektion als mächtigen, alternativen Wärmetransport ausschaltet. Jetzt gibt es nur noch Strahlungskühlung (Abkühlung des Bodens) und Wärmeleitung (Übertragung der Boden-Temperatur auf die Luft), wodurch eine Temperatur-Inversion (eine stabile Temperaturschichtung) von einigen hundert Metern entsteht. Diese geringe Distanz markiert den Wirkungsbereich der Wärmeleitung in der Atmosphäre. Bodeninversion tritt insbesondere bei winterlichen Hochdruckwetterlagen und niedrigen Temperaturen auf und wenn eine fehlende Wolkendecke (mit ihrer „ominösen“ Gegenstrahlung) die IR-Ausstrahlung des Bodens begünstigt.
Wann hört der Unsinn auf, dass nur IR-Strahlung Wärme ist. Es sind alle Bestandteile der Atmosphäre Wärmeträger. Das ergibt sich auch eindeutig aus dem Planckschen Strahlungsgesetz.
Die Strahlungskonstante des Stefan-Boltzmann-Gesetzes zu missbrauchen ist Betrug.
Es geht darum die Transportmechanismen zu trennen. Elektromagnetische Strahlung, Wärmeleitung des Gases und Konvektion des Gases. Plank ist nur für die Strahlung zuständig. Sie müssen das unterscheiden!
Es geht darum nicht nur CO2 ist Wärmestrahlungsträger.
Ihre Unkenntnis ist frappant. Das Plancksche Strahlungsgesetz bezieht sich ausschließlich auf Strahlung (Photonen) und damit offensichtlich nicht auf alle Bestandteile der Atmosphäre. Warum heißt es wohl so?
Frage an Leite mit Physikkenntnissen (typische Übungsaufgabe): A) wie hoch ist die thermische Energiedichte u (Joule/m3) eines thermischen Strahlungsfeldes, welches eine Temperatur von 15 °C hat? Man leite u aus dem Planchen Strahlungsgesetz ab und vergleiche mit der thermischen Energiedichte von Luft desselben Temperatur.
B) man expandiere ein Strahlungsfeld, welches einen Hohlraum ausfüllt, indem der Hohlraum ins Vakuum expandiert. Wird dabei Arbeit verrichtet? Wie lautet der 1. Hauptsatz der Thermodynamik fürs Strahlungsfeld?
Wer die Aufgaben korrekt löst, bekommt ein CO2 Zertifikat.
Halten wir also fest das IR nicht allein Wärme ist, oder Wärme durch IR übertragen wird, und daher müssen immer auch Konvektion und Wärmeleitung in die Beschreibung der Wärmeflüsse mit einbezogen werden. Das trifft besonders auf die Schnittstelle Atmosphäre und Erdoberfläche zu und führt dazu daß die einseitige Berücksichtigung nur von IR Strahlung nicht die Temperatur vorgeben kann, da sensible, latente und die minimale Wärmeleitung – aka Wärme zurückhalten, die Temperatur mitbestimmen.
So ist es und es kommen weitere Komponenten hinzu. Die Aufgaben A und B von Herrn Heinemann sind irrelevant, da sie zunächst ein geschlossenes System Luft definieren müssten. Da bleibt kaum noch eine Schnittmenge zum offenem System Atmosphäre übrig. Die Ergebnisse wären so aussagekräftig wie: Die Klassenstärke beträgt 23,7 Schüler. Diese Angabe ist „richtiger“ als irgendeine gemittelte Temperatur der Erde.
Herr Hanass,
Ihnen traue ich keine Lösung zu. Die Lösung ergibt sich aus meiner gestellten Fragestellung und nicht aus Ihren Bemerkungen.
Im übrigen, zu Ihrem
Wollen Sie dies nicht selber nun korrigieren, nachdem Sie Ihren Fehler eingesehen haben?
Werner Schulz schrieb am 23/04/2023, 07:06:28 in 321690
Aber das ist Wissen der 60er Jahre, das niemand in Frage stellt. Sie sehen genau diese Energieflüssen im of kritisierten Kiel/Trenberth Diagramm (ausser Wärmeleitung, die so gering ist, dass man sie vernchlässigt). Welchen Punkt wollen Sie also hier machen?
Ich will das seit 60 Jahren, aber scheinbar nicht allen bekannten, Wissen unterstreichen, das Strahlung nicht die Temperatur der Oberflaeche bestimmt.
Werner Schulz schrieb am 24/04/2023, 19:52:33 in 321878
Wenn man sich überlegt, dass die Sonne unsere primäre Energiequelle ist und ihre Energie über Strahlung bei uns ankommt und Energie auch nur über Strahlung wieder von der Erde weggeht – dann ist das eine … interessante Aussage.
Habe ich gerade das 1964er Manabe Papier mit einem anderen Werner Schulz diskutiert oder waren Sie das? Dort wurde doch klar, dass sich die Temperatur am Boden und in der Atmosphäre durch Strahlung ergibt und diese Temperatur durch Konvektion und latente Wärme reduziert wird. Da ist Ihre Aussage zumindest (bewusst?) irreführend wenn nicht gar bewusst falsch.
Sie sind echt ein Sprachkúnstler.
Wie sie gerade richtig gesagt haben. Bestimmt dir Konvektion die Temperatur. Da sich die der Strahlung gar nicht erst einstellt.
Hm, dagegen spricht, dass die Kontrollrechnung mit Hilfe der Wärmeleitfähigkeit von Gasen nur einen relativ kleinen Beitrag der Wärmeleitung zum Wärmetransport liefert – ähnlich wie im NASA-Diagramm. Mögliche Ursache: Die strahlende Oberfläche im Pirani-Messgerät ist sehr klein im Vergleich zum umgebenden Gasvolumen. Etwa so, als würde man die Erde durch einen Punktstrahler ersetzten.
@Dr. Roland Ullrich
So sehe ich das auch. Die Aufteilung der Flüsse zwischen Abstrahlung und Konvektion hängt u.a. stark von der Geometrie ab, und deshalb kann man die Gegebenheiten in der Pirani-Sonde nicht eins zu eins auf Erde und Atmosphäre übertragen. Diese Sonde ist dafür auch gar nicht gedacht, sondern sie ist eigentlich ein Messgerät für Gasdrücke.
Auszug aus dem Artikel
Nach der üblichen Berechnung wären das -18°C, was nicht nahe des Gefrierpunktes von Wasser, sondern -18°C darunter entspricht…;-) Naja, Übersetzungsproblem vielleicht?
Schon falsch. Es ist anderes herum. Die Energiebilanz ergibt sich aus dem Klimamodell.
Klimamodelle berechnen das Klima aus first principles. Dazu gehört lediglich die Solarkonstante und die geographische Verteilung der Albedo (wobei heutige Geosystemmodelle selbst die berechnen), das übrige sind Naturgesetze der Physik und Materialkonstanten. Daraus berechnet sich Wetter und deren Statistik ist das berechnete Klima. Die Energiebilanz ergibt sich damit ebenfalls automatisch.
„das übrige sind Naturgesetze der Physik und Materialkonstanten.“
Hm.
Ein paar hundert Millionen Dollar zur Vorbereitung des größten Betrugs aller Zeiten sollten auch noch Erwähnung finden…
Ach Herr Heinemann,
schon die grundlegende Betrachtung der abgestrahlten Leistung ist grob falsch. Da wird -wie auch immer- einer Durchschnittstemperatur der Erde gebildet und diese dann benutzt, um eine durchschnittliche Strahlungsleistung zu berechnen. Dummerweise steht in der SB hinten T hoch 4, also eine steile Parabel. Somit müssen zuerst die einzelnen Strahlungsleistungen für jeden Punkt der Erde im Tages- und Jahresgang ermittelt werden, erst dann kann eine durchschnittliche Strahlungsleistung berechnet werden. Allerdings nur unter Berücksichtigung des für die jeweils gemessene Temperatur gültigen Emmissionsfaktors. Die „Durchschnittsleistung aus Durchschnittstemperatur“ – Geschichte haut Ihnen jeder halbwegs fähige Messtechniker um die Ohren.
Martin Rohde schrieb am 21.4.2023, 21:51:38 in 321580
Was dabei rauskommt, können Sie in „Earth’s Global Energy Budget„, Trenberth et. al. 2009 nachlesen, im Kästchen „SPATIAL AND TEMPORAL SAMPLING“. Die Abweichung ist im einstelligen W/m^2 …
Was jedoch nichts an der Tatsache ändert, dass der benutzte Rechenweg falsch ist. Und wenn ich das richtig sehe, sollen ja etwa 3 W/qm für die globale Erwärmung zuständig sein.
Martin Rohde am 21. April 2023 um 21:51
Herr Rohde, Sie antworten auf meinem Beitrag, in dem ich erklärt habe, warum diese Ihre Behauptung falsch ist. Was soll man davon nun halten?
Herr Heineman,
die Energiebilanz ergibt sich also aus den Klimamodellen? Da stellt sich die Frage, welche Energiebilanz für die Erstellung der Klimamodelle benutzt wird. Nennt sich Zirkelschluss, beweist also rein gar nichts. Der große Fehler der gezeigten Energiebilanzen ist die Anwendung des Gleichzeitigkeitsprinzips. Spätestens, wenn Sonnenstrahlung auf die Meere trifft, ist es vorbei mit der Gleichzeitigkeit, da die Strahlung so bis zu 100 Meter in das Medium eindringt. Oder wird es dunkel, sobald man unter Wasser ist? Somit erwärmt sich die Wasseroberfläche sehr langsam, die Abstrahlung der Energie erfolgt über einen langen Zeitraum auf entsprechend niedrigerem Niveau. Hier kommt die Parabel wieder ins Spiel. Die korrekte Frage zur Erdtemperatur muss folgerichtig nicht heissen: „Wie warm wäre eine Erde ohne Atmosphäre?“, sondern: „Wie warm wäre eine Erde ohne Wasser?“
Sie können selbst leicht in Excel nachrechnen, dass Ihre Behsuptung falsch ist. Ohne Atmosphäre trifft die Sonnenstrahlung direlt auf die Erde, ein Teil wird reflektiert, der Rest absorbiert. Die Dolarkonstante betrrät 1368 W/m2. Rechnen sie breiten-und längengradaufgelöst (von mir aus auch mit plausiblen ortsaufgelösten Albedowerten) die örtlich auf der Erdoberfläche absorbierte Sonnenstrahlung über 1 Jahr summiert aus. Diese Energie pro Flächenelement Ihres Längen- und Breitengradnetzes muß dann im stationären Gleichgewicht derselben Energie der Temperaturstrahlung entsprechen, die die Erde thermisch direkt ins All abstrahlt. Wenn Sie aus dieser Temperaturverteilung im Längen- und Breitengradnetz den globalen Mittelwert bilden (Ihren „T^4-Parabelfehler“ umgehen Sie damit), so liegt der unter Garantie niedriger als die Erdoberfläche in Wirklichkeit hat. Ihre Erde ohne Atmophäre ist kühler.
Ihr Modell eines Klimas ohne Atmosphäre ist sehr unrealistisch.
Herr Heinemann,
sie schiessen auf Strohmaenner.
Herr Rohde hat nichts von einem Klima ohne Atmosphaere erzaehlt.
Martin Rohde am 22. April 2023 um 18:33
wie ich bereits schrieb macht man seit ca. 100 Jahren ( Simpson 1928?) Energiebilanzen des Klimasystems aus Messwerten.
Seitdem man mit 3D globalen gridaufgelösten Zirkulationsmodellen das Klimasystem auch im Computer aus first principles berechnen kann (etwa ab den 80igern), kann man selbstverständlich aus diesen Berechnungen ebenfalls Energiebilanzen ableiten und mit der des realen Klimas vergleichen.
Es wird aber nicht vorausgesetzt, dass an jeden Punkt der Erdoberfläche gleichzeitig dieselben Werte vorliegen, wenn Sie dies unter Gleichzeitigkeitsprinzip verstehen. Warum fällt es Ihnen so schwer, diese unzutreffende Annahme abzulegen? Es ist für heutige Klimamodelle kein Aufwand, das Computerwetter mit Schrittweiten von Stunden über Jahrzehnte zu rechnen und damit den Sonnenstand in jedem grid-Punkt entsprechend seiner physikalischen Zeit im Computer korrekt zu berechnen. Ebenso werden die physikalischen Prozesse entsprechend ihrer Differentialgleichungen schrittweise numerisch integriert. Zeitliche Verzögerungen, die Sie ansprachen, ergeben sichdann automatisch aus den physikalischen Modellgleichungen. Die morgentlich Erwärmung und der Tagestemperaturgang in den grid-Punkte wird in Klimamodellen berechnet, und zwar so, wie es in der Realität auch ist, denn dies ergibt sich aus den Differentialgleichungen, z.B. Wärmeleitungsgl. des Bodens und der Energiebilanz am Boden individuell im jedem grid-Punkt. Ob Sie wollen oder nicht, heutige Klimamodell ist längst nicht so primitiv wie Sie es darstellen. Für die Vorstellung Ihres Klimamodells bräuchte man nicht mal einen Computer.
#Thomas Heinemann am 21. April 2023 um 17:38
Schon falsch. Es ist anderes herum. Die Energiebilanz ergibt sich aus dem Klimamodell.
Da stimme ich zu! Aber nur bis „anders herum„. Denn dann kommt für die Klimamodellierer die sog. Global-Temperatur ins Spiel. Und die gibt weder wirklich noch physikalisch, egal, wie aufwendig das Klimamodell rechnet. Energien, um sie zu bilanzieren, werden an keiner Stelle erfasst. Man wünscht sich nur, dass unerlaubte Rechnungen stimmen.
Ein Beispiel aus der Nasa-Energiebilanz im Artikel (läuft mit jeder Zahlenangabe dort genauso). Die langjährig und globale gemittelte absorbierte Sonneneinstrahlung an der Erdoberfläche ist mit 163,3 W/m2 angegeben. Die Erdoberfläche O beträgt 510e+12 m2. Wieviel Energie Es hat die Erdoberfläche in t = 5 Jahren absorbiert? t = 5 Jahre = 157,788e+6 s. Ergebnis: Es = 163,3 W/m2 × 510e+12 m2 × 157,788e+6 s = 2,63e+24 Joule.
Laut Wiki hat die Erde
Gesamtfläche Erde 510.000.000 km²
Meine Umrechnung ergibt:
510.000.000 km² = 5.1E+14 m2
In einem weiteren Beitrag errechnen sie mit diesem Fehler eine angeblich richtige Zahl.
Das finde ich seltsam. Bei Folgefehlern keine Punkte fuers Endergebnis.
Die Bruecke wuerde bei ihnen zusammenbrechen.
WErner Schulz schrieb am 01/05/2023, 23:13:45 in 322552
Sie kommen auf den gleichen Wert wie Herr Heinemann. Wo ist das Problem? Scheitert es an der Rechnung mit Exponenten?
Danke Herr Mueller,
ich schiebe es auf eine ungewoehliche Notation.
Wer bitte schreibt : 510 * 10 12 anstatt 5.1 *10 14
Na wenigstens hat sich der Fehler geloest!
WErner Schulz schrieb am 2.5.2023, 18:38:17 in 322656
Was ist denn an 510 Billionen ungewöhnlich?
Aber unabhängig von der Darstellung – wenn Sie ein wenig mehr Zeit für das Verstehen aufwenden würden, würden solche Dinge nicht passieren …
Danke Herr Mueller,
nicht jeder beschaeftigt sich hier hauptberuflich mit dem Thema!
Koennen sie den Widerspruch erklaeren, warum laut Nasa Diagram sich nur der Boden erwaermt aber nicht die Atmosphaere?
„Die mit den einzelnen Pfeilen im Diagramm verbundenen Werte sind die entsprechenden Energieflüsse in Watt/m²“
In Watt/m² kommt Energie nicht vor, auch wenn die Vokabel Energieflüsse benutzt wird. Watt steht für Leistung und m² für Fläche, es lässt sich damit also bestenfalls eine Leistungsdichte beschreiben.
Man bekommt die Dimension Energie auch nicht mal soeben da hinein, da hierzu nämlich die Dimension Zeit eingebracht werden müsste. Und das passiert eben genau erst dann, wenn die Strahlung mit ihrer Dichte auf ein Objekt einwirkt, und zwar nicht in der Zeit 0, sondern in einer von 0 verschiedenen Einwirkzeit.
Wenn die NASA mit Strahlungsdichten operiert und ihr buntes Kunstwerk mit „earth’s energy budget“ tituliert, stellt sich doch die Frage, wen sie damit ansprechen will. Physiker scheiden jedenfalls aus. – Also ist es bestenfalls schlechte Unterhaltung!
Ich bin Physiker, verstehe das Diagramm und bestätige, dass sowohl Name als auch Inhalt physikalisch und meteorologisch korrekt ist. Zudem sehen das ca. 3000 Meteorologen und 50.000 Physiker in D. genauso, wieviel Fachleute dies weltweit zusammen sind und die letzten hundert Jahre seit Bestehen dieses Diagrammes zusammengekommen sind, kann man abschätzten, ebenso ist dieses Diagramm in der wissenschaftlichen Literatur zu finden.
Der Zusammenhang zwischen Energie und Leistungsdichte ist offensichtlich trivial. Das Diagramm stellt die stationären Leistungsdichten j dar, die Leistungen ergeben sich durch Multiplikation mit der Erdoberfläche O. Die Energiebilanz stellt die Energien dar, die in einem bestimmten festen Zeitraum t fließen. Da stationären Bedingungen gelten, ist der Zusammenhang zwischen Energie E und Leistung äquivalent, da sie proportional sind: E = j × O × t, Proportionalitätsfaktor O×t. Das Diagramm ist also vollständig geklärt.
Es ist sehr mutig von Ihnen,sich auf Eike so zu bekennen.
Für mich als Pädagogik-Historiker würde noch brennend interessieren,wann Ihnen das Abiturzeugnis ausgehändigt wurde.
Herr Peters, mein Abitur, Diplom und Promotion in Physik liegen einige Jahrzehnte zurück. Alles weit vor Bologna.
…. dann beschreiben Sie doch einmal ganz kurz, wie man von der Leistungsdichte zum Energiefluss kommt. Muss doch mathematisch möglich sein. Oder genügt schon die Namensgebung?
Benutzen sie immer als Bezug die gesamte Erdoberfläche? Oder geht das nur für einen einzigen Tag?
Was ist mit einem halben Tag? Oder zwei Tagen? Welche Fläche setzen sie ein?
Die 390 W/m² Bodenstrahlung hat als Ursache die 340 W/m² aus der Gegenstrahlung die sich wiederum aus der Bodenstrahlung speist… 🤦♀️. Ein sich selbst erwärmendes System, nicht vereinbar mit den HS der Thermodynamik, um das als Unsinn zu erkennen braucht man kein Messgerät….
…wenn das System abgeschlossen wäre.
Da das Klimasystem offensichtlich nicht abgeschlossen ist, liegen Sie falsch. Die Sonne verdirbt Ihnen Ihre Behauptung.
Bitte Sinn machen!
Ich vermisse den recht erheblichen Einfluss von Konvektion als Folge von Absorption bei den „Klimagasen“
Das ganze Modell so wie dargestellt ist einfach nur Mist und wird so ähnlich in unseren Schulen gelehrt. Achselzucken bei einem Physiklehrer , „wenn es so vom Bildungsministerium vorgegeben ist muss es wohl stimmen“
Die Konvektion spielt offensichtlich eine Rolle, Sie müssen nur nach rechts ins Energiebilanzdiagramm im Artikrl oben gucken.
Wer mit einem energetischen Fließgleichgewicht beginnt, wenn er Zustandsänderungen der Erde erklären will, hat bereits verloren. Um das zu erkennen genügt ein Blick auf den dominanten Energiespeicher, auf die Ozeane:
Der Durchfluss absorbierter Solarenergie erhöht die Wassertemperatur gegenwärtig zweifellos von etwa 30 K auf 287±16 K. Das ist nur möglich, wenn es „im Mittel“ etwa 200 Jahre (Größenordnung!) dauert, bis die diskontinuierlich absorbierte Solarwärme aus den Ozeanen wieder in den Weltraum abfließt. Dazu einige Anmerkungen, die Niemand zur Kenntnis nimmt.
https://de.scribd.com/document/391176117/Erderwarmung-Treibhauseffekt-und-Zeit-CO2-ist-klimaneutral
Ich habe ein Paar Fragen:
1/ Die Erde bekommt laut THE -Theorie 163,3W/m2
2/ Wie kann es sein, dass die Erde 398,2W/m2 emitiert? Wo ist diese Energie entstanden?!
3/ Gut, die Erde strahllt 398,2W/m2 – und jetzt passiert ein Wunder: THE-Gase strahlen 340,2W/m2 zurück zu Erde!Ich nehme ann, dass Strahlung jedes Teilchen rundumm wirkt, dass heisst, diese 340,2W/m2 müssen nur ein kleineren Teil des Gesamten Strahlung der THE-Gasen sein!
4/ Wo endet diese „Reststrahlung“ und wie gross ist?! Und wo ist die Quelle dieser Energie?!
5/Ich halte diese THE-Zirkus für Scheinbescheftigung überdurschnitlich erhobenen „Wissenschaftler“ : sie müssen doch Probleme finden, welche dann nur sie lősem kő(e)nnen.
6/ Bei 162,3W/m2 würd KEINE Photovolteikanlage funktionieren..
Peter Zinga
zu 1) Richtig ; zu 2) Die Ozeane haben die Energie gespeichert; zu 3) Nicht TG, sondern Wasser und Eis Aerosole besorgen die Rückstrahlung zum Ausgleich der Energiebilanz des Wasser der Ozeane
https://de.scribd.com/document/413528852/Atmospha-risches-Kohlendioxid-tra-gt-nicht-zur-Erwa-rmung-bei
zu 4) Es gibt keine Reststrahlung; zu 5) Die z. B. am Wettermast Hamburg kontinuierlich gemessene energetische Rückkopplung des atmosphärischen Treibhauseffektes ist Fakt und nicht Phantasie! zu 6) Die Solarzellen funktionieren immer dann, wenn die lokale Intensität der Solarstrahlung hinreichen groß ist, z.B. bis zu 1,6 kW/m^2 mittags am Äquator bei wolkenfreien Himmel.
„Die z. B. am Wettermast Hamburg kontinuierlich gemessene energetische Rückkopplung des atmosphärischen Treibhauseffektes ist Fakt und nicht Phantasie!“
Gemessen mit Geräten, welche ausschlißlich im offenen atm. Fesnster „messen“
LOL
“ Die Solarzellen funktionieren immer dann, wenn die lokale Intensität der Solarstrahlung hinreichen groß ist, z.B. bis zu 1,6 kW/m^2 mittags am Äquator bei wolkenfreien Himmel.“
Es müssen nich gerade 1,6kW/m2 sein, bei uns in Tschechien sind es durchschnitliche cca 600W/m2 ,aber auch das sind 3 mal mehr, als die 163 W/m2. Und, entschuldigen Sie mir, wann und wie kőnnte Ozean so viel Energie einsparen, wie kőnnten Einsparnisse hőhere sein, als Einkommen? Verraten Sie mir es, ich werde es gerne im meinem Haushalt praktizieren.Und jetz ernst: ich bin der Meinung, dass die Sonne mit voller Kraft Sonnenseite der Erde aufheizt und die Erde diese Energie während des Tages speichert, um sie Nachts auszugeben. Wer auf 163W/m2 glaubt, mus auch einnehmen, dass sich die Erde mit unendlichen Geschwindigkeit dreht. Nur im diesen Falle kann im jedem Moment jeder Stück der Erde von der Sonne angestrallt werden.
P.s.: Hamburger Mast misst nur das, was in Richtung Erde strahlt -und einige hier diskutierte würden auch das bestreiten.
Was meinen sie eigentlich mit „energetischer Rueckkopplung“
Das die Energie, die aus der Atmosphaere kommt eigentlich von der Oberflaeche stammt? Oder das die Waerme auf der Erde aus der Atmosphaere stammt?
Das erstere ist meines Erachtens nach richtig. Wenn das so ist, ist die Temperatur der Atmosphaere von der Oberflaechentemperatur abhaengig oder anders herum?
Peter Zinga am 21. April 2023 um 13:45
Die Erdoberfläche. Der Wert ist aus Messwerten ermittelt.
Die entsteht aus der Summe der anderen Energien an der Erdoberfläche, wie sich durch Nachrechnen ergibt.
3/-5/ sind unverständlich
Wer will die gesamte Erdoberfläche mit PV Anlagen belegen?
Warum beantworten Sie 1) und 6) nicht einfach und klar:
Der Wert 163,3W/m² ist ein Durchschnittswert für die gesamte Erdoberfläche und das gesamte Jahr. Somit gibt es auch Gebiete bzw. Zeiten, wo sich der Betrieb einer PV-Anlage lohnt.
…weil es eben auch Gebiete und Zeiten gibt, wo der Wert unter dem Durchschnittswert liegt
„Da die Strahlung für den Aufwärtswärmetransport in der unteren Atmosphäre unbedeutend ist, beruhen diese Modelle auf einer falschen Annahme und sind daher ungültig. Da die Modelle im Allgemeinen dazu dienen, die Theorie der anthropogenen globalen Erwärmung aufgrund des Treibhauseffekts zu stützen, gibt es keine wissenschaftlichen Beweise für den Treibhauseffekt oder die anthropogene globale Erwärmung.“
So ist es!
Mein Glasscheiben -Experiment liefer viel einfacher und billiger den Beweis!
3 Glasscheiben über dem „idealen, schwarzen Boden“ positioniert, in 3 verschiedenen Höhen
(ca 10 cm , 50 cm und 120 cm) , natürlich nicht übereinander sondern seitlich verschoben, zeigen genau wo eine Wirkung der Erdstrahlung noch ist und wo nicht mehr!
Mit einer 4. Glasscheibe und paar Wärmelampen, kann mn den angeblichen „Treibhauseffekt“ sogar simulieren – mit ca 330 W bestrahlt wird sie sehr schell warm – siehe hier stimmt Stefan + Boltzmann noch!
Dei unterste Glasscheibe wird so warm , wie der Boden! (Manche sehen hier einen „Wärmestau“ am Wirken- dem ist nicht so, was der gleiche Versuch mit eienem Glasstreifen mit ca 40 mm Breite beweisen tut!
Und die oberste?
Wird nur so warm , wie die Luft, auch erst nach ca einer Stunde!
Die resultierenden Temperaturen kann man alle messen, aber auch das Gefühl der Hand reicht aus, um diese Differenzen zu fühlen!
Somit bleibt nach wie vor die Frage offen, wie kann man das komplexe Klimageschehen mit einer, für alle verständlichen Sprache, erklären?
Wenn ich Kindern erkläre, wie der 2. Hauptsatz der Thermodynamik funktioneiert, kapieren das auch die jüngsten, nur ein Herr Dietze nicht!
Ein Eiswürfel wird niemals das Getränk erwärmen, in das er geschüttet wird!
Und so ist es mit der eiskalten Atmopshäre, dei angeblich dei Erde stark erwärmt!
Und was passiert wenn, mehr CO2 in der Atmosphäre sich befindet (bodennah)?
Nix, denn ein Quadratmeter Erdboden strahlt im 15 Mikrometer CO2 Absorptionband, gerade mal 18 W/m2 ab!
Somit spielt das Mehr an CO2 Molekülen hier keine Rolle mehr!
Auch dazu eine kleine Analogie:
„Ein Bauer hat eine Kuh und eine Melkmaschine!, Dei Kuh produziert pro Jahr ca 10.000 Liter Milch.
Da kommt ein sehr pfiffiger Vertreter und will dem Bauer eine 2. Melkmaschine verkaufen mit folgendem Argument:“ Bei 2 Melkmaschinen wirst du 20.000 Liter Milch produzieren!“
Ja, in der Klimapolitik glauben das sogar studierte Leute!
Es stimmt tatsächlich – Wissen kann Dummheit nicht verdrängen!
MfG
„Es stimmt tatsächlich – Wissen kann Dummheit nicht verdrängen!“
Ist so, lieber Herr Ordowski
Am NASA-Modell ist so ziemlich alles falsch, was dargestellt ist. Der wichtigste Fehler ist schon die künstliche Aufteilung der Sonnenenergie auf die gesamte Oberfläche, also die Annahme einer permanenten Rundumbestrahlung der Erde mit 1/4 der Solarkonstante.
Betrachtet man die rotierende Bestrahlung, so wie sie wirklich ist, lösen sich alle „Effekte“ in Luft auf und alles funktioniert genau so, wie es gem. der bekannten Physik sein muß. Die Wirklichkeit beweist auch, daß eine wichtige Komponente die Energiespeicherung speziell in den Ozeanen ist, wo die Wassertemperatur über 24 Stunden an einem konkreten Ort belgt, welche Energien wie wirken.
Experimente wie das beschriebene von Pirani arbeiten natürlich auch nach den Regeln der Wirklichkeit und können damit ebenfalls simulieren, daß gemachte Modellannahmen im TK96-NASA-Modell falsch sind. Und auch, daß dieses Modell den 2. HS vollkommen auf den Kopf zu stellen versucht, merken die Verfechter dieser Theorie offenbar nicht.
Die „Ursünde“ der modernen Klimatologie ist der religionsartige Glaube an diese Trenberth/Kiehl Darstellung. Man sieht zwar auf den ersten Blick, daß sie unphysikalisch ist, trotzdem hat sie sich zum allgegenwärtigen „Quasistandard“ entwickelt. Vermutlich weil sie so schön bunt ist …
Vermutlich weil sie so schön bunt ist … Genau, vielleicht fehlen noch ein paar Blümchen, damit schon die Kindergartenkinder angesprochen werden.
Toller Artikel, sein Fazit ist: Bei gleichem Luftdruck wäre die Erdatmosphäre in etwa genauso warm wie jetzt, egal aus welchen Gasen die Atmosphäre besteht.
Kohlendioxid trägt zur Erwärmung bei, aber nicht durch einen Treibhauseffekt, sondern durch Wärmekonvektion, d.h. Berührung der Erdoberfläche, Aufnahme der Wärme und Verteilung der Wärme in der Luft. Verdoppelt man die Konzentration von CO2 auf 800 ppm, so ändert sich gar nichts, denn der Sauerstoffanteil nimmt um 400 ppm ab, was vollkommen unbedeutend ist.
„Bei gleichem Luftdruck wäre die Erdatmosphäre in etwa genauso warm wie jetzt, egal aus welchen Gasen die Atmosphäre besteht“
Ist so nicht ganz richtig. Denn erst die IR-aktiven Gase erlauben es der Atmosphäre, Energie an den Weltraum abzugeben. Somit wäre eine Atmosphäre ohne Treibhausgase deutlich wärmer.
stefan strasser schrieb am 21/04/2023, 05:19:00 in 321488
Wenn Sie das mal rechnerisch zeigen könnten, wäre das schön. Sie argumentieren (gefühlt seit Jahren) dafür, dass man mit der Wärmekapazität rechnen sollte, zeigen aber nie, wie diese Rechnung aussehen würde und welche Temperatureen sich bei Ihnen laut Rechnung einstellen würden. Andere, die diese Art Rechnung wirklich durchgeführt haben (Kramm, Spencer, Dietze, ich, …) kommen zu anderen Ergebnissen als Sie. Da Sie Ihre Rechnung aber nie präsentieren, kann man auch nie prüfen, warum unterschiedliche Ergebnisse herauskommen …
Zitat: Andere, die diese Art Rechnung wirklich durchgeführt haben (Kramm, Spencer, Dietze, ich, …) kommen zu anderen Ergebnissen als Sie.
Witz komm raus, du bist umzingelt. Diese Rechnungen kann mal alle mit einer Plausibilitätsprüfung der physikalischen Gegebenheiten falisfizieren.
Mfg
Werner Holtz
Werner Holtz schrieb am 21.4.2023, 17:44:31 in 321554
Ich wäre an dieser Falsifizierung interessiert.
Schöner, nein sehr schöner Artikel!
Über einen Satz sollte man aber nochmal nachdenken:
„Die Konvektion findet ständig statt, aber die Geschwindigkeit, mit der Wärme durch Konvektion transportiert wird, ist VIEL langsamer als die Lichtgeschwindigkeit. Das bedeutet, dass die Wärmeenergie die Erde langsamer verlässt als sie ankommt, …“
Und darüber besonders:
„…und deshalb ist die Erde wärmer, als es das Stefan-Boltzmann-Gesetz vorhersagt.“
denn daß die Strahlungstemperatur der Erde eine physikalisch nichtssagende Größe ist sollte nach gefühlt hundert Artikeln und tausend Foristenbeiträgen jedem klar sein
Und der Mond, wenn auch aus anderen Gründen, deutlich kälter.
..denn daß die Strahlungstemperatur der Erde eine physikalisch nichtssagende Größe ist sollte nach gefühlt hundert Artikeln und tausend Foristenbeiträgen jedem klar sein.
Sind Sie da so sicher? Warten Sie ab bis Kosch und Co als bezahlte Foristen ihnen widersprechen werden.
Leider verstehe ich den Satz auch bei längerem Nachdenken nicht: Wenn die Wärmeenergie die Erde langsamer verlässt als sie ankommt, müsste es doch ständig immer wärmer werden und nicht nur wärmer sein als SB vorhersagt.
Warum? Das Gleichgewicht entsteht eben später und dieser Zeitverzug hat die innere Wärme der Atmosphäre zur Folge.
Admin.: Der Zeitverzug in der Atmosphäre zählt Stunden und Tage, im Wasser der Ozeane dagegen Jahrzehnte und Jahrhunderte. – Daher ist die Atmosphäre „kalt“ und das Wasser der Ozeane „warm“. Am Land „dazwischen“ ist es dagegen „wechselhaft.“ – Ein Hurra für die „mittleren“ Temperaturen“, die es nirgendwo gibt!!
Es ging mir darum darzustellen, dass letztendlich die Erde per Abstrahlung im Gleichgewicht mit der Einstrahlung ist. Dass die gespeicherte Wärme der Ozeane dabei eine große Rolle spielt, ist klar.
Herr Wolff, ich kann Ihnen nur zustimmen mit den 2/3 Meeresbedeckung die wir haben. Es gibt noch Dutzende und mehr Beispiele, wie im Zusammenspiel mit Atmosphäre und Sonneneinstrahlung Energie lange Zeit zurückbleibt, bis sich wieder ein Gleichgewicht einstellt. Denken wir an Wärmeperioden im Sommer mit hohen Temperaturen und Sonneneinstrahlung. Die Häuser und Gemäuer heizen sich über Tage stark auf, man kann die Wärmestrahlung als auch die warme Luft sehr gut wahrnehmen, es raubt einem den Schlaf in der Nacht ohne Klimagerät. Es kommt nun eine abrupte Abkühlung mit Gewittern und Regen, aber die Gemäuer haben die Wärme in sich und es dauert je nach Witterung noch Tage, bis innen wieder normale Temperaturen herrschen, auch wenn man innen mit der kälteren Luft öfter lüftet, das Gemäuer wärmt diese wieder auf, eine gewisse Zeit. Also, die Sonne und die warme Luft, deren Energie letzlich aber auch von der Sonne stammt, haben die Häuser erwärmt, und nach plötzlichen Temperatursturz dauert es rel. lange bis sich die Temperatur wieder mit der Umgebung eingependelt hat. Was ist das anderes als Energiespeicherung? Und das geht m.E. ganz ohne sog. Klimagase (ausgenommen vielleicht Wasserdampf), nur mit einer Atmosphäre. Das beschriebene ist ja auch genau das Problem der Wärmeinseln, Städte, Siedlungen mit viel Straßen, Asphalt, unbegrünten Flächen heizen sich immer stärker auf als Wald und Flur, desgleichen dauert die Abkühlung und Anpassung umso länger, künstliche, menschliche Energiespeicher die die Sonnenenergie länger speichern als die umgebende Natur, die sich schnell anpasst, das sind tatsächliche Probleme statt irgendwelche marginalen CO2 Konzentrationen und sog. Klima-Spurengase!
Wie kann ein Gleichgewicht entstehen, solange die Wärmeenergie die Erde langsamer verlässt als sie ankommt? Oder ist das „später“ (wann später?) nicht mehr der Fall?
Stellen wir uns nun eine Badewanne mit einem Zulauf und einem Ablauf vor. Wenn der Zulauf genauso groß ist wie der Ablauf, bleibt der Wasserstand konstant. Wird der Zulauf verstärkt oder der Ablauf verringert, erhöht sich der Wasserstand, während umgekehrt bei Verringerung des Zulaufs oder Verstärkung des Ablaufs der Wasserstand sinkt. Logischerweise gilt: Je größer die Differenz zwischen Zulauf und Ablauf, desto stärker verändert sich der Wasserstand.
Vergleichen wir nun die Badewanne mir unserem Planeten. Dabei sei der Zulauf der Energiezufluss durch die Sonneneinstrahlung, der Wasserstand der Energiegehalt der Atmosphäre und der Ablauf die Abstrahlung ins Weltall. Solange die Einstrahlung gleich der Abstrahlung ist, bleibt der Energiegehalt konstant. Ist die Einstrahlung größer als die Abstrahlung, erhöht sich der Energiegehalt und umgekehrt. Logischerweise gilt: Je größer die Differenz zwischen Einstrahlung und Abstrahlung, desto stärker verändert sich der Energiegehalt.
„Wie kann ein Gleichgewicht entstehen, solange die Wärmeenergie die Erde langsamer verlässt als sie ankommt?“
Das, Herr Ermel, ist auch mein Problem mit diesem Satz.
In der Realität wird 12h eingestrahlt und 24 h abgestrahlt. Das hat aber nix mit „langsam“ zu tun, sondern mit „Stärke“
Langsam ist der Transport der Energie innerhalb der Atmosphäre hin zu Abstrahlhöhen. Allerdings ist die Konvektionsgeschwindigkeit nur ein Faktor, der andere ist die Energiemenge pro Kubikmeter. Der Energiefluß innerhalb der Atmosphäre entspricht dem Energiefluß der Abstrahlung +/- Zwischenspeichereffekten
F. Ermel: Besso Keks – “
„Wie kann ein Gleichgewicht entstehen, solange die Wärmeenergie die Erde langsamer verlässt als sie ankommt?“
Ob Ihnen das hilft? : Ein Ofen, ein Wohnzimmer, ein variabler Fensterspalt der die Wärme langsamer oder schneller abfließen lässt, um den jeweils gewünschten Gleichgewichtszustand einzustellen.
Übrigens, die Wassertemperatur der Ozean ändert sich bekanntlich im Tagesverlauf nicht.
@Herr Ermel und herr Keks
„Wie kann ein Gleichgewicht entstehen, solange die Wärmeenergie die Erde langsamer verlässt als sie ankommt? Oder ist das „später“ (wann später?) nicht mehr der Fall?“
Tja, wenn man vergißt, dass in der Stefan+Boltzmann Formel auch die Fläche vorkommt, dann hat man ein Problem! Es wird immer nur eine hälfte der Erde beschienen, aber dei gesamte oberfläche strahlt immer ab!
Bei Stefan+ Boltzmann wird immer wieder unterschlagen oder auch vergessen, dass es immer um zwei Temperatur haltenden Körper geht!
So muß man beide Temperaturen in die Formel einsetzen, erst dann kann man sehen ob es zur einer resultierenden Strahlung in eine Richtung geht!
Haben beide Körper die gleiche Temperatur, ist dei Wirkung der Strahlungsflüsse gleich 0.0!
Bezognen auf das System Erde Atmosphäre ergibt sich immer ein Strahlungsfluß von der Warmen Erde zur kalten Atmosphäre – braucht man den 2. hauptsatz der Tehrmodynamik gar nicht strapazieren!
Also ganz einfach – wer immer noch Zweifel hat, der informiere sich über die Messung der CO2 Konzentration in der Luft!
Es wird über die Absorptionsfähigkeit des CO2 Moleküls gemessn, nicht über seine Emittierbarkeit!
Warum wohl?
Und immer wieder dei Frage an alle THE Gläubigen, warum wird die Lufttemperatur in ca 2 Meter Höhe gemessen???
MfG
Der Zeitverzug ist die Zeit die die Waerme braucht durch die Atmosphaere durchzugehen.
Was Herr Ermel meint ist, das wenn es eine Storgroesse gibt, die die Waerme davon abhaelt, dann muss diese entweder laufend wirken, mit der von Herrn Ermel angegebenen Wirkung, oder sie existiert nur einmal und dann ist die Frage wie ein solch labiles System existieren kann. Dann wuerde jede Wolke das Klima aendern koennen.
@ Ulrich Wolff:
„Ob Ihnen das hilft? : Ein Ofen, ein Wohnzimmer, ein variabler Fensterspalt der die Wärme langsamer oder schneller abfließen lässt, um den jeweils gewünschten Gleichgewichtszustand einzustellen.“
Leider nicht wirklich. Nehmen wir an, die Leistung des Ofens ist konstant und wenn der Fensterspalt 1 cm offen ist, stellt sich eine Temperatur von 20° C ein, während bei einem 2 cm geöffneten Fensterspalt 15° C vorherrschen. Wenn ich Sie richtig verstehe, meinen Sie nun, dass bei einem 2 cm geöffneten Fensterspalt der Wärmeabfluss größer ist als bei einem 1 cm geöffneten und sich dementsprechend eine niedrigere Temperatur einstellt. Meiner Meinung nach kann sich aber nur eine konstante Temperatur einstellen, wenn Wärmezufluss und Wärmeabfluss genau gleich sind. Der Wärmeabfluss hängt aber nicht nur von der Breite des Fensterspalts ab, sondern auch von der Differenz zwischen Innen- und Außentemperatur. Der Wärmeabfluss ist also in beiden Fällen genau gleich und entspricht dem Wärmezufluss. Öffnet man den Fensterspalt von 1 auf 2 cm, erhöht sich zunächst der Wärmeabfluss, bis die Temparatur so weit gefallen ist, dass ein neues Gleichgewicht entsteht und der Wärmeabfluss dem Wärmezufluss entspricht.
Richtig. Q=Konstant.
Die Temperaturen sind unterschiedlich weil es mehrere Waermetransportmoeglichkeiten gibt.
Wenn durch Konvektion mehr Waerme abgefuehrt wird, dann wirkt sich die Wandisolieruing weniger stark aus. Bei einer Wand laesst man die Strahlung aussen vor, das man davon ausgeht, das sich Innenraum und Wand im Strahlungsgleichgewicht befinden. Die Isolierung der Wand wird vornehmlich durch Waermeleitung dargestellt.
Wenn Fenster und Dach geschlossen bleiben erziehlt man die hoechste Temperatur im Innenraum.
Eigentlich sehr einfach. Da in der Atmosphaere freie Konvektion herrscht, passt sich der Gradient der Isolierung Atmosphaere an das Konvektionsgleichgewicht an, nicht an das Strahlungsgleichgewicht.
Und bei einem Raum ohne Fenster offen, passt sich die Temperatur an die Waermeleitung durch die Wand an, auch nicht an das Strahlungsgleichgeiwcht.