von Kip Hansen
Ein Hauptergebnis der Temperaturdaten, das von USCRN produziert wird, ist die Durchschnittstemperatur-Anomalie für das gesamte Netzwerk über seine gesamte Länge von etwa 17 Jahren. Sie wird aktuell hier bei WUWT im Abschnitt Referenzseiten als „ Oberflächentemperatur, US. Climate Reference Network, 2005 to present ” dargestellt:
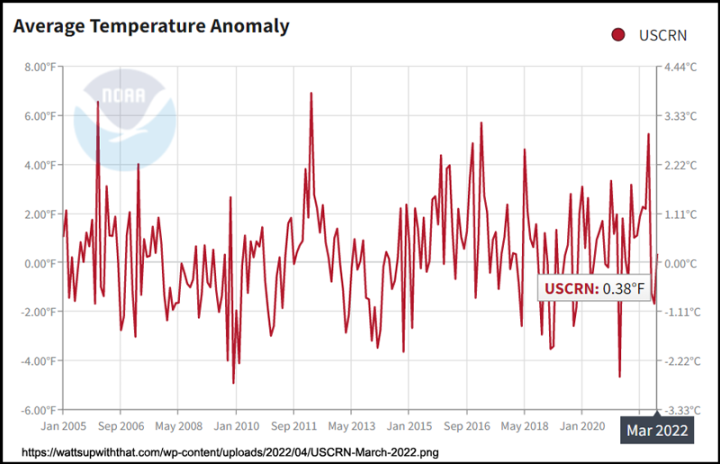
Jetzt würden viele Leute gerne anfangen, Trendlinien herauszufinden und uns zu sagen, dass die Anomalie der US-Durchschnittstemperatur entweder „steigt“ oder „sinkt“, und wie schnell sie das tut.
Aber fangen wir mit einem pragmatischeren Ansatz an und fragen zuerst: „Was sehen wir hier?“
Ich schlage Folgendes vor:
- Wie groß ist die Bandbreite über den dargestellten Zeitraum (2005-2022)?
Vom höchsten bis zum niedrigsten Wert liegt der Bereich bei etwa 11 °F oder 6 °C. Dieser Bereich stellt keinen Anstieg oder Abfall der Metrik dar, sondern die Variabilität (natürlich oder erzwungen). Schauen Sie sich den Unterschied zwischen dem Hoch Ende 2005 und dem Tief Anfang 2021 an. Wenn diese Grafik unbeschriftet gewesen wäre, hätte ich sie als halbchaotisch identifiziert.
Nun, für mich ist es schwer zu sagen. Seltsamerweise scheint die Anomalie etwas über „0“ zu laufen – was uns sagt, dass die Basisperiode für die Anomalie aus einer anderen Zeitperiode stammen muss. Und es ist so, dass USCRN einen Basiszeitraum von 1981-2010 für „0“ verwendet, wenn es diese Anomalien berechnet, der Basiszeitraum liegt nicht innerhalb des Zeitbereichs dieses hier dargestellten Zeitreihen-Datensatzes.
Wir können jedoch Excel nutzen, uns mathematisch mitzuteilen, wie der Trend über den gesamten Zeitraum ist.
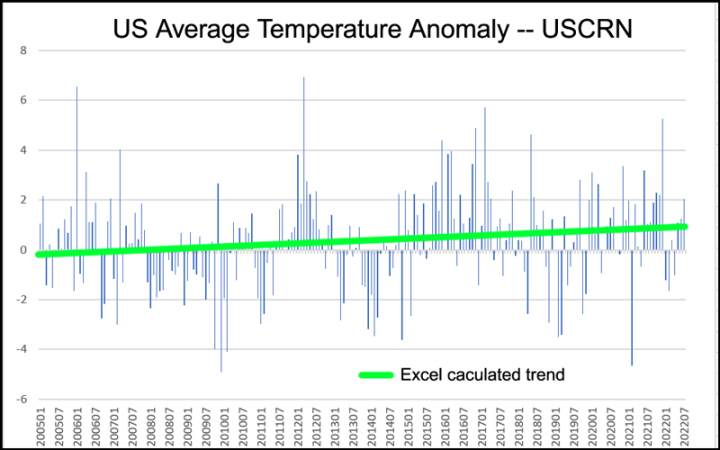
So, jetzt wissen Sie es. Oder tun Sie nur so? MS Excel sagt, dass die Anomalie der USCRN-Durchschnittstemperatur im Laufe von 17 Jahren um etwa 0,6 °C (1 °F) nach oben tendiert.
~ ~ ~
Jetzt kommt der SPASS!
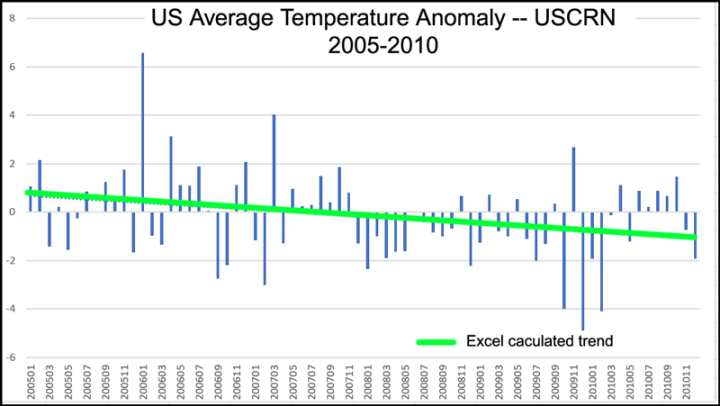
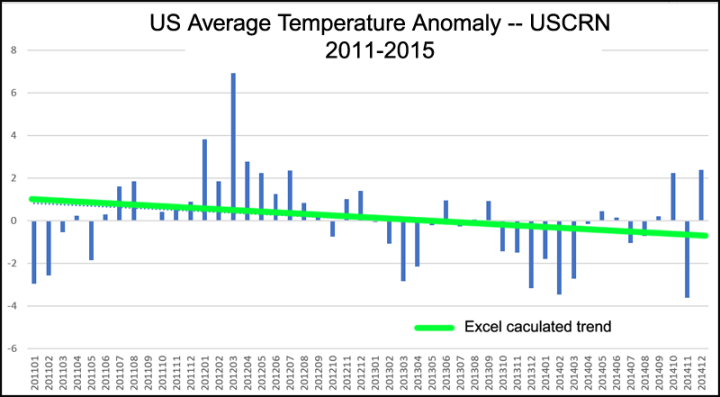
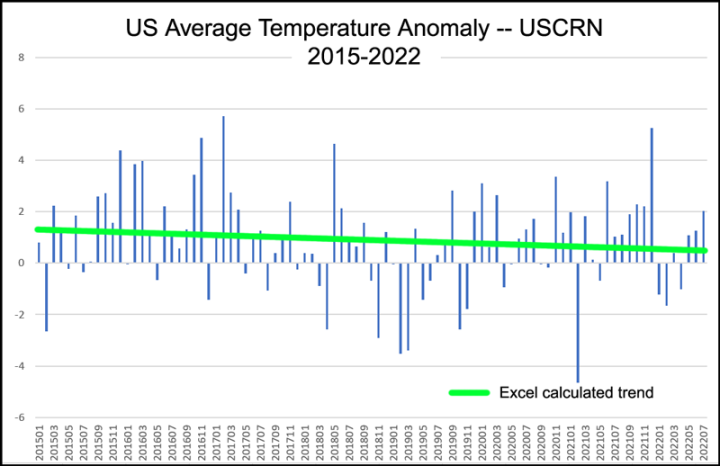
Ich habe willkürlich Zeitintervalle von fünf Jahren ausgewählt, da sie etwa 1/3 des gesamten Zeitraums ausmachen. Drei 5-Jahres-Trends (der letzte, etwas länger), die alle abwärts gerichtet sind, ergeben zusammen ein Diagramm mit aufwärts gerichtetem Trend, wenn sie in Datumsreihenfolge aneinandergereiht werden.

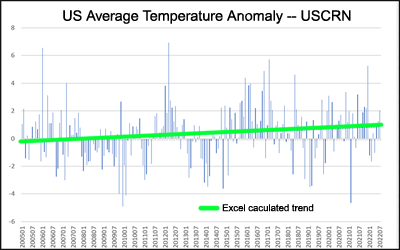
Lektionen, die wir lernen können:
- Verwenden Sie keine kurzen Zeiträume, wenn Sie Trends in einer Zeitreihe bestimmen. Trends sind immer empfindlich gegenüber Start- und Enddaten.
- Dieses Phänomen ähnelt in gewisser Weise dem Simpson -Paradoxon : „…. ist ein Phänomen in Wahrscheinlichkeit und Statistik, bei dem ein Trend in mehreren Datengruppen auftritt, aber verschwindet oder sich umkehrt, wenn die Gruppen kombiniert werden.“
„In seinem 2022 erschienenen Buch Shape: The Hidden Geometry of Information, Biology, Strategy, Democracy and Everything Else argumentiert Jordan Ellenberg , dass Simpsons Paradox falsch benannt ist:“
„Paradox“ ist eigentlich nicht der richtige Name dafür, weil es keine Einschränkung gibt, sondern nur zwei verschiedene Arten, über dieselben Daten nachzudenken. … Die Lehre aus Simpsons Paradoxon besteht nicht darin, uns zu sagen, welchen Standpunkt wir einnehmen sollen, sondern darauf zu bestehen, dass wir sowohl die Teile als auch das Ganze im Auge behalten.“ [die Quelle ]
- Es erinnert an andere Datensätze, die den Trend (oder sogar das Trendzeichen) ändern, wenn sie in unterschiedlichen Zeiträumen betrachtet werden – der Anstieg des Meeresspiegels kommt mir in den Sinn, wobei die kurze Satellitenaufzeichnung behauptet, doppelt so hoch zu sein wie die jahrhundertelange SLR-Rate der Gezeitenpegel. [surface level rate]
- Warum sollte man sich Trends ansehen, die über verschiedene Zeitskalen offensichtlich nicht zuverlässig sind? Das ist eine philosophische Frage. Kann ein längerer Trend real sein, wenn alle kürzeren Komponenten des Trends das entgegengesetzte Vorzeichen haben? Können sich drei kürzere Abwärtstrends zu einem längeren Aufwärtstrend summieren, der in der realen Welt anwendbar ist? Oder ist es nur ein Artefakt der gewählten Zeitskala? Oder ist das Gegenteil der Fall? Sind drei kürzere Abwärtstrends echt, wenn sie sich zu einem Aufwärtstrend addieren? (Wenn ich „echt“ sage, meine ich nicht nur mathematisch korrekt – sondern physikalisch korrekt.)
- Haben wir es hier mit einer Simpson-ähnlichen Verirrung zu tun? Kann man daraus etwas Wichtiges lernen? Beide Ansichten sind gültig, aber das scheint unwahrscheinlich.
- Oder ist das, was wir hier sehen, nur ein Versuch, einen kurzen, sehr variablen Datensatz zu einem realen Trend zu zwingen? Machen wir uns etwas vor mit der Interpretation der USCRN-Durchschnittstemperaturanomalie als einen Aufwärtstrend – wenn die physikalische Realität ist, dass dieser ziemlich kurze Datensatz besser einfach als „hochgradig variabel“ beschrieben werden sollte?
# # # # #
Kommentar des Autors:
Ich hoffe, dass einige Leser diese Kurznotiz interessant finden und sie zu tieferem Nachdenken anregen könnte als: „ …. der Durchschnitt und sein Trend müssen stimmen – sie sind einfach Mathematik“.
Viele Metriken von CliSci werden auf einer künstlich zugewiesenen Zeitskala von „seit dem Beginn des modernen Industriezeitalters“ betrachtet, die normalerweise als Ende des 19. Jahrhunderts interpretiert wird, ungefähr 1860 bis 1890. In ihrem kürzlichen Interview bei Mind and Matter hält Judith Curry dies buchstäblich für „kurzsichtig“ besteht darauf, dass für viele Metriken ein viel längerer Zeitraum in Betracht gezogen werden sollte.
Ich hoffe, ich habe Zeit, Ihren Kommentaren nachzugehen, ich versuche, alle zu beantworten, die ausdrücklich an mich gerichtet sind.
Danke fürs Lesen.
https://wattsupwiththat.com/2022/08/17/fun-with-trends/
Übersetzt durch Andreas Demmig
















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Was mich stets stört, ist dieses dämliche Ami-Fahrenheit, ein völlig veraltetes Temperaturmaß. Bin mal gespannt, wann auch noch Reaumur aus der Mottenkiste geholt wird. Im 21. Jahrhundert sollte es doch möglich sein, Celsius b.zw. Kelvin für die Abweichungen zu verwenden. Ansonsten aber ein guter Beitrag.
Völlig richtig, Herr Kämpfe,
aber bedenken Sie bitte, dass der „Durchschnitts-Amerikaner“ nur diese Grad Fahrenheit kennt. In meiner Zeit in den USA habe ich in meiner Umgebung immer wieder die dumme Frage gestellt, warum man nicht zur Celsius-Skala wechselt. Viel einfacher – alles mal zehn.
Es war ein Kampf gegen Windmühlen. In dieser Hinsicht sind die Amis offenbar genauso lernresistent wie hierzulande. Der Autor Kip Hansen wollte seine Landsleute erreichen, und leider ist es immer noch so, dass es wohl nur so geht. In Kanada beispielsweise ist Grad Fahrenheit völlig out! (Da gibt es auch keine Meilen o. Ä. mehr)
Anmerkung: In meinen Übersetzungen nenne ich grundsätzlich nur in Grad Celsius umgerechnete Werte.
MfG
Interessant! Sagt aber auch viel über den Unsinn aus, bei einer natürlichen Variabilität von etwa 6 Grad C sich mit Trends von wenigen Zehntelgrad pro Dekade verrückt zu machen und verbindliche globale Obergrenzen wie 1,5 Grad seit der Kleinen Eiszeit auszugeben. Was schon von den Asiaten, auch ohne Mitwirken des Westens, locker überschritten wird (was sie dürfen und auch tun), falls man dem CO2 den behaupteten Einfluss auf die globalen Temperaturen zugesteht und die Temperaturen weiter steigen sollten. Was viel über den Geisteszustand unserer Politiker verrät.
Danke für den interessanten Beitrag.
Meinung: Daten werden oft nicht vorbehaltslos, sondern mit einem bestimmten Ziel durchforstet und ausgewertet. Man betreibt sogenanntes Data-Mining, auch um bestimmte eigne Thesen zu beweisen bzw. fremde Thesen zu widerlegen. Gern gemacht in der Finanzpornografie, und zwar genauso wie im obigen Artikel analysiert. Es werden Daten in Zeitabschnitten gesucht, die ins eigene Konzept passen, und sodann im Verkaufsprospekt präsentiert, weil man Geld verdienen will und muss.
Die Theorie sagt, dass man in jedem genügend großen Datensatz, abschnittsweise Beweise für die These und die Antithese finden kann.