Hans Jankowiak
Vorbemerkung
Diese Betrachtung benutzt den AR 5 der WG I des IPCC. Im Abfassungszeitraum war
- der AR 6 der WG I noch nicht erschienen
- die im Internet verfügbare Fassung der WG I trägt den Hinweis (auf gut deutsch)
„Vorabzug; nicht zitieren, als Quelle anführen oder verteilen“
- das Thema – CH4 im Vergleich zu CO2 – wird im AR 6 auf alle drei WG verteilt
Methan – CH4 84 mal wirkungsvoller als Kohlenstoffdioxyd – CO2 ??
So finden wir diese Zahl häufig in Berichten, wenn es um die Rettung der Welt vor dem bösen „anthropogenic global warming“ geht und das CO2 nicht allein dazu herangezogen wird sondern als nächster Begleiter das Methan – CH4.
Woher kommt diese Zahl? Wie und wer hat sie nach welcher Formel, nach welchem ggf. empirischen Verfahren ermittelt?
Der erste Blick geht in die Wikipedia.
In der deutschen Fassung [1] finden wir den Wert 84 unter Methan → Umweltrelevanz → Treibhauspotenzial.
In der englischen Fassung [2] finden wir einen anderen Wert – nämlich 72 – unter Methane → Occurrence → Atmospheric methane.
Nanu, wieso gibt es zwei unterschiedliche Werte für den selben Sachverhalt? Herrschen in Deutschland und dem Rest der Welt zwei unterschiedliche physikalische Naturgesetze?
Der Weg zur Klarstellung beginnt in den Hinweisen der Wiki`s, woher dieser entsprechende Wert stammt.
Die deutsche Wiki bezieht sich auf den IPCC, AR5-WGI von 2013, die englische Wiki benutzt den Wert aus AR4-WGI von 2007, schreibt selbst aber als Fußnote „AR5“ – also ein „Druckfehler“.
Trotzdem; zwei unterschiedliche Werte für ein und das selbe Gas? Haben sich die physikalischen Gesetze in den 6 Jahren Zwischenzeit geändert?
Nein, die Erleuchtung liegt verborgen in den Definitionen.
Doch zunächst werfen wir einen ersten Blick auf den AR5-WGI [3] des IPCC, Chapter 8,dort 8.7 – Emission Metrics .
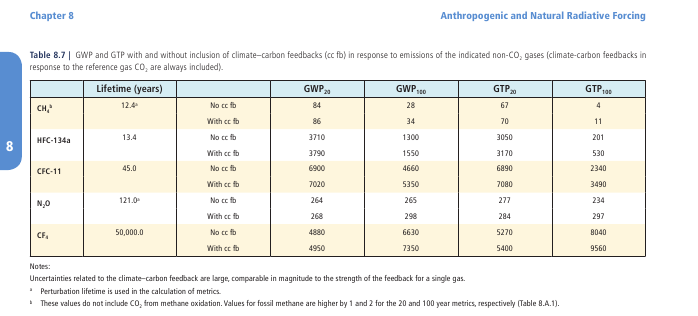
Dort finden wir in Table 8.7 auf Seite 714 die Zahl 84 für CH4 in der Spaltenbezeichnung „GWP20 “
Aber in der selben Tabelle finden wir noch Werte in drei weitere Spalten für CH4, nämlich
den Wert 28 in der Spaltenbezeichnung „GWP100 “, den Wert 67 in der Spaltenbezeichnung „GTP20“ und den Wert 4 in der Spaltenbezeichnung „GTP100 “.
Des Weiteren finden wir diese Werte näher erläutert auf Seite 731, Apendix 8.A in
Table 8.A.1 mit der Überschrift „Lifetimes, Radiative Effencies and Metric Values“
Als Beispiel die Spaltenbezeichnung „GWP 20-year“ Davor steht die Spaltenbezeichnung „AGWP 20-year“. Die Dimensionsangabe lautet hier (W m-2 yr kg-1).
Wir finden dort für CO2 den Wert 2,49 e-14 und für CH4 den Wert 2,09 e-12. Berechnet man diese Werte und setzt sie ins Verhältnis zueinander, so ergibt sich für CH4 zu CO2 ein Verhältniswert von 12,84 zu 2,07 – also rund 6!!!!!! und nicht 84!!! wie in der Zeile Methane aufgeführt.
Also müssen für den Wert 84 noch weitere Einflüsse wirken als in den Tabellen für die allein stehende Verhältniszahl ausgedrückt wird.
Der Pfad der Erkenntnis führt weiter durch den Dschungel der Definitionen, denn der IPCC nutzt für sein Wirken ihm höchst eigene Definitionen, die in den klassischen physikalischen Lehrwerken über Thermodynamik nicht vorkommen oder dort anders – nämlich wissenschaftlich – ausgedrückt sind.
Verfolgen wir als Beispiel die o.g. Spaltenbezeichnungen „GWP 20-year “und
„AGWP 20-year“
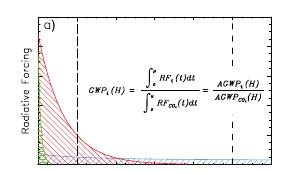
GWP steht für Global Warming Potential und ist gem. Absatz 8.7.1.2 definiert als
„as the time-integrated RF due to a pulse emission of a given component, relative to a pulse emission of an equal mass of CO2 (Figure 8.28a and formula).“
Die Zahl 20 steht für einen Betrachtungszeithorizont von 20 Jahren und der Bezugswert – der Vergleichswert – ist der Wert für CO2!
AGWP steht für Absolute Global Warming Potential und ist das bestimmte Integral von RF über den Zeithorizont, hier z.B. 20 Jahre.
Nun muss man jedoch erst noch einen Abstecher in den 8 SM – dem Supplementary Material zum Chapter 8 [4] – in den Abschnitt 8.SM.11.1 machen, denn dort steht die gleiche Formel unter der Nummer (8.SM.6) für dieses bestimmte Integral, das auch in
Figure 8.28 a genannt wird.
Was bedeutet jedoch RF(i) in der Formel?
In dieser Formel steht RFi und nicht RF – ohne i – und wird definiert „is the radiative forcing due to a pulse emission of a gas i given by RFi = AiRi where Ai is the RFi per unit mass increase in atmospheric abundance of species i (radiative efficiency (RE)), and Ri is the fraction of species i remaining in the atmosphere after the pulse emission.“
Diese Definition ist also eine andere als in Box 8.1 auf Seite 665:
RF steht dort für Radiative Forcing und ist definiert als „as it was in AR4, as the change in net downward radiative flux at the tropopause….“
ERF steht dort für Effective Radiative Forcing und ist definiert als „is the change in net TOA downward flux ….“
Im bestimmten Integral z.B. für das CO2 muss der Ausdruck RFCO2 also eine integrierbare Funktion f(t) aufweisen. Diese Funktion wird unter der Nummer (8.SM.10) bezeichnet als
und enthält ein mathematisches Summenzeichen und ist keine kontinuierliche Form ebenso wie die Lösungsformel (8.SM.11) des bestimmten Integrals
ein mathematisches Summenzeichen enthält, also im Grunde auch keine kontinuierliche Form aufweist.
Darum steht auch als Erläuterung der Formeln (8.SM.10) und (8.SM.11) :
„The decay of a pertubation of atmospheric CO2 following a pulse emission at time t is usually approximated by a sum of exponentials“. (Hervorhebung durch Verfasser)
Wie so oft so auch hier: Beim IPCC muss man auf das „Kleingedruckte“ achten, um eine Klarheit in den Zielen des IPCC zu erreichen!!
Und mit diesem „freundlichen Hinweis“ des IPCC ist das Zwischen-Ende der Fahnenstange, das IPCC-Bermuda-Dreieck für den Wert 84 erreicht
Ich werde versuchen, im Teil 2 dem „Rätsel 84 “ auf andere Weise bzw. mit weiteren Schritten näher zu kommen.




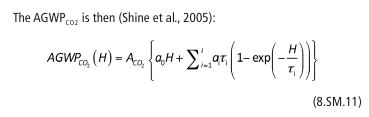















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Methan – 84 mal wirkungsvoller als Kohlenstoffdioxyd ??
Hallo Leute,
Auf diese Wahnsinnsfaktoren von 20, 82 usw. kommt man nur, wenn man sowohl das CO2 als auch das Methan um dengleichen Betrag in ppm(!) erhöht (z.B. 10 ppm). Allerdings ist Methan über 200 (ca. 1.8 ppm) mal seltener in der Atmosphäre ist als CO2 (ca. 400 ppm).
Ein sinnvoller Vergleich der „Klimaschädlichkeit“ zwischen den beiden Gasen wäre viel eher der, wenn man den Einfluß beider bei z.B. Verdoppelung der Konzentration vergleichen würde, denn Methan kann nie die Konzentration von CO2 erreichen.
Dabei kommt für Methan bei einer Standardatmosphäre anstatt 20 oder 84 nur ein Faktor von 0.16i relativ zu CO2 heraus!
Die Wahnsinnszahlen sind also nicht falsch, aber völlig irrelevant!
Dann noch zu den furzenden Kühen im Bild: Immer wieder werden als böse anthropogene Methanquellen die furzenden Kühe und Reisfelder gebrandmarkt.
Dabei zeigen Satellitenmessungen z.B: bei der ESA „Erste Animationen der Treibhausgasverteilung – mit Envisat SCIAMACHY-Daten“ (dort ist eine Animation für 2003 zu sehen), daß die ganz großen Methanerzeuger nicht die Kühe sondern die borealen Wälder im Spätsommer sind, offensichtlich, wenn die Pflanzen das Absterben beginnen.
Dann furzen die Bakterien ohne den Zwischenwirt „Kuh“.
MfG
G.Wedekind
Danke!
Im Grunde ist die Zahl 84 sehr interessant. Weiß jemand wie groß die Leckrate von Biogasanlagen ist?
Wenn man beim CO2-Wert (2,49 e-14) das „e“ nicht wie der Autor als die Konstante e = 2,7 sondern wie auf jedem Taschenrechner als Zehnerexponent betrachtet (also 2,49 mal 10 hoch -14) und das dann beim CH4 genau so macht, erhält man als Quotient der beiden Werte die Zahl 84 – Rätsel gelöst.
Es sieht so aus. Aber die Physik, die dahinter steht, habe ich trotzdem nicht verstanden. Vielleicht bringt es Teil 2.
Schaue ich mir meinen Taschenrechner an, dann unterscheidet er zwischen 10 hoch x und e hoch x. Was dem Verfasser des Artikels recht gibt. Alarmforschern („Klimaforschern“) traue ich hingegen den dümmsten Blödsinn zu, wie sie ihn seit Jahrzehnten produzieren. Ihre größte Leistung ist, eine einfältige Pastorentochter zu verdummen, die seitdem Billionen für Klima-Blödsinn verplempert. Die dumme und unfähige Ursula macht dies in der EU. Die noch einfältigere Swenja ist derweil als Umweltministerin in Wartestellung. Und die Dümmsten von allen sind die Karlsruher Verfassungsrichter, auf dem Niveau von Greta und Luisa.
Dr. Roland Ullrich schrieb am 5. September 2021 um 0:50
Ahhh… Ich hatte mich (in meinem nicht veröffentlichten Kommentar) gefragt, was der Autor denn an den Zahlen noch berechnen will, bevor er sie ins Verhältnis setzt. Er hat also
gerechnet.
Wie kommt man darauf? Die Schreibweise e-12 für 10^-12 ist doch eigentlich uralt und bei den Einheiten sieht man, dass die Exponenten korrekt schreiben können …