Würden Sie ein solches Angebot tatsächlich annehmen?

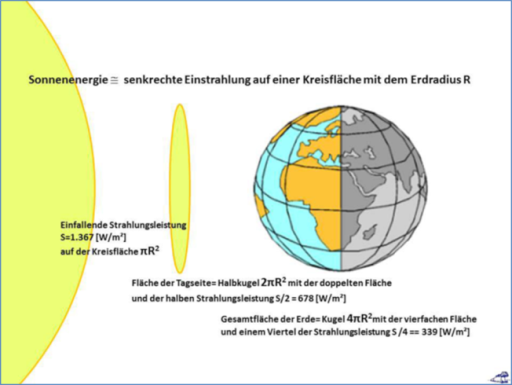
Vielleicht würden Sie die Funktionsweise eines solchen Turbobräuners auf das Prinzip eines Hähnchengrills zurückführen, dessen Leistung man einfach auf das ganze Hähnchen inklusive seiner Rückseite herunterrechnet. Und daher könnten Sie zu der Erkenntnis gelangen, dass die Wirkung einer doppelt so großen direkten Strahlungsleistung Ihrer Gesundheit nicht ganz zuträglich wäre. Und genauso berechnet man jetzt umgekehrt einen viel zu geringen Wert für die tatsächliche „natürliche“ Temperatur unsere Erde. Man verteilt nämlich einfach die tatsächliche spezifische Strahlungsleistung der Sonne auf der Tagseite unserer Erde rechnerisch über die gesamte Erdoberfläche, also auch auf deren Nachtseite. Dabei kommt man fälschlicher Weise auf eine „theoretische Globaltemperatur“ von (-18°C) und behauptet, die Sonne sei gar nicht stark genug, um mit ihrer direkten Einstrahlung die gemessenen Temperaturen auf unserer Erde zu erzeugen. Als Erklärung für die Differenz zur sogenannten „gemessenen globalen Durchschnittstemperatur“ (NST) von ca. (15°C) postuliert man dann eine ominöse „atmosphärische Gegenstrahlung“, die konstruktionsbedingt jede Differenz zu einer beliebigen NST erklären kann, weil sie quantitativ lediglich an der sogenannten „Abstrahlungstemperatur“ von (-18°C) „festgemacht“ ist. Damit schaltet man dann eben mal den natürlichen Klimaantrieb aus, dessen Einfluss in den vergangenen 420.000 Jahren immerhin um ca. +3°C/-9°C geschwankt hatte. Mit diesem „Hähnchentrick“ beweist man also einen vorgeblich „natürlichen atmosphärischen Treibhauseffekt“ als alleinigen Antrieb unseres Klimageschehens, denn man muss ja immer nur die „Gegenstrahlung“ passend nachjustieren. Die direkte spezifische Strahlungsleistung der Sonne kann auf unserer Erde im äquatorialen Zenit aber eine Maximaltemperatur von bis zu ca. 120°C erzeugen. Abzüglich des durchschnittlich reflektierten Anteils und durch eine Mittelung über die gesamte Erdoberfläche ergeben sich nach herkömmlicher Rechnung aber lediglich -18°C.

Bezogen auf einen Hähnchengrill, bei dem man ebenfalls die Leistung des Heizstrahlers auf das gesamte Hähnchen inklusive seiner Rückseite herunterrechnet, würde das den Unterschied zwischen einem gegrillten (120°C) und einem tiefgefrorenen (-18°C) Hähnchen ausmachen.
(Aus meinem Buch „Mehr geht nicht“ mit Änderungen und Ergänzungen.)

Also, je nachdem, ob man sich auf die tatsächlich bestrahlte Fläche beschränkt oder ob man, wie beim Hähnchen, „aufgrund der Rotation“ fälschlicherweise unbestrahlte Flächen in diese S-B-Inversion einbezieht, kommt man für unsere Erde zu ganz unterschiedlichen „theoretischen“ Temperaturen, von denen nur eine richtig sein kann. Und beim THE-Paradigma wird ohne weitere Erklärung der planare solare Poynting Vektor (Einstrahlung) gegen einen radialen terrestrischen Poynting Vektor (Abstrahlung) ausgetauscht, indem einfach nur mit Beträgen gerechnet wird. Bei meinem hemisphärischen S-B-Modell wird dagegen bei der solaren Einstrahlung auf der Tagseite der Erde der solare Zenitwinkel berücksichtigt.

Definition: Als Temperaturgenese sei derjenige Prozess bezeichnet, mit dem der Vektor (Betrag&Richtung) der Strahlstärke von der solaren Einstrahlungsrichtung zur terrestrischen Abstrahlungsrichtung hin verändert wird. Es ist in einer physikalischen Betrachtung nicht statthaft, die Richtung eines Vektors zu unterdrücken und nur mit seinem Betrag zu rechnen.

ERGO: Mein hemisphärisches S-B-Modell ist das einzige Modell für die Temperaturgenese auf unserer Erde, das die „gemessene“ Realität von etwa 15°C widerspruchsfrei abbilden kann.

Abbildung 1: Das hemisphärische S-B-Modell für die Temperaturgenese auf unserer Erde

Das hemisphärische S-B-Modell kann als vieljährige Durchschnittsbetrachtung unserer realen Erde die räumlichen und zeitlichen Abhängigkeiten der solaren Einstrahlung abbilden und erfasst damit qualitativ alle drei räumlichen Dimensionen und die Tages-/Jahreszeit bei der Temperaturgenese.

Das Modell einer „Erde ohne Atmosphäre“ orientiert sich am Mond

Die hemisphärische S-B-Inversion ist nicht auf eine ominöse „Erde ohne Atmosphäre“ anwendbar, aus der sich dann ein „natürlicher atmosphärischer Treibhauseffekt herleitet. Nur zur Erinnerung, Klima kommt aus dem Griechischen und bedeutet ‚Krümmung/Neigung [des Sonnenstandes]‘ – und eine solche Neigung des Sonnenstandes gibt es nachts nun einmal nicht. Der unvoreingenommene Betrachter kann das schon daran erkennen, dass der Lichtschutzfaktor der – selbstverständlich nur am Tage – benutzten Sonnencreme üblicherweise umgekehrt proportional zur geographischen Breite des jeweiligen Einsatzortes ist. Eine solche „Erde ohne Atmosphäre“ entspricht übrigens viel eher dem Mond, dessen Tagestemperatur mein hemisphärischer S-B-Ansatz (hier und hier) ganz hervorragend abbilden kann. Dabei ist zu beachten, dass, abweichend von der Situation auf dem Mond, auf der Erde das S-B-Temperaturäquivalent niemals erreicht wird. Denn mit der örtlichen Erwärmung beginnen hier unmittelbar auch Konvektion und Verdunstung, durch die fortlaufend Energie in die globalen Zirkulationssysteme abgeführt wird.

Also noch mal zur Erinnerung der Unterschied zwischen dem S-B-Gesetz und einer S-B-Inversion:

Das Stefan-Boltzmann-Gesetz: Temperatur (primär) => Spezifische Strahlungsleistung (sekundär)

Formel: S=P/A=SIGMA T4

In Worten: Ein schwarzer Körper mit einer gegebenen Temperatur T (>0K) in [K] strahlt zeitgleich eine durch das S-B-Gesetz fest verknüpfte Strahlungsleistung [W] über seine gesamte Oberfläche „A“ in [m²] aus. Die Abstrahlung erfolgt in Richtung der Flächennormalen. Das S-B-Gesetz enthält weder nicht strahlende Flächen „B“ noch Zeit [s] oder zeitlich abgeleitete Mittelwerte [J/s].

Jede Berechnung einer Temperatur (sekundär) aus einer bestimmten Strahlungsleistung (primär) stellt eine Inversion (Strahlung=>Temperatur) des Stefan-Boltzmann-Gesetzes dar, die nur zulässig ist, wenn alle genannten Randbedingungen des S-B-Gesetzes strikt 1:1 erfüllt werden:

Die Stefan-Boltzmann-Inversion: Spezifische Strahlungsleistung (primär) => Temperatur (sekundär)

Formel: T=(S/SIGMA)1/4

In Worten: Eine gegebene spezifische Strahlungsleistung [W/m²] beleuchtet einen (schwarzen) Körper mit einer Oberfläche „A“ in [m²] und erzeugt dort zeitgleich ein über das S-B-Gesetz fest verknüpftes Temperaturäquivalent in T [K], und zwar strikt abhängig vom Einfallswinkel der Strahlungsleistung auf die Fläche „A“. Eine Stefan-Boltzmann-Inversion darf weder unbeleuchtete Flächen „B“ noch Zeit [s] oder zeitlich abgeleitete Mittelwerte [J/s] enthalten.

Die PHYSIKALISCHE Gleichzeitigkeit im Stefan-Boltzmann-Gesetz: Die Zeit „t“ ist NICHT im S-B-Gesetz enthalten. Daher müssen alle mathematischen Prozesse im Zusammenhang mit S-B (S-B-Berechnung, S-B-Inversion) unmittelbar zeitgleich erfolgen.

Die fehlerhafte Durchschnittsberechnung: In einem physikalischen T4-Gesetz folgt eine Durchschnittsberechnung nicht der ursprünglichen Funktion, Beispiel:
0 W/m² entsprechen nach dem S-B-Gesetz -273 °C und 470 W/m² entsprechen 28 °C. Der daraus gemittelte Temperaturwert von etwa -122,5 °C für einen Strahlungsdurchschnitt von 235 W/m² entspricht aber keineswegs der diesem Strahlungswert direkt zugeordneten S-B-Temperatur von -19°C.

Im Stefan-Boltzmann-Gesetz ist der Rechenweg nicht austauschbar:

PHYSIK(=MEAN@S-B-Inversionen[W/m²]) # MATHEMATIK(=S-B-Inversion@MEAN[J/m²s])

In jede Gleichung können Sie ohne Veränderung der mathematischen Lösung beliebige Größen einfügen, solange diese gleichzeitig im Zähler UND Nenner auftauchen, also zum Beispiel:

(Lichtgeschwindigkeit/Lichtgeschwindigkeit) oder (Gewicht der Erde/Gewicht der Erde) oder (Sekunde/Sekunde) oder…

Wenn Sie also auf Ihrem Rechenweg zwischendurch die spezifische Leistung mit Sekunden multiplizieren (=Arbeit [s*W/m²=J/m²]) und am Ende wieder durch Sekunden teilen (Leistung [J/m²s=W/m²]), macht das der Mathematik gar nichts; anders ist es mit der Physik, denn die ist hinterher nicht mehr dieselbe. Denn in der Physik muss der Gegenstand der Betrachtung physikalisch anwesend sein. Beim S-B-Gesetz selbst ist das ganz profan, weil der Schwarzkörper eine ganz konkrete Temperatur besitzt und daher die gleichzeitige spezifische Strahlungsleistung über seine gesamte Fläche „A“ konstant ist. Bei der S-B-Inversion darf dagegen ein Temperaturdurchschnitt nur aus den UNMITTELBAR GLEICHZEITIGEN S-B-Ortstemperaturen berechnet werden, eine MITTELBARE Durchschnittsbildung über die zeitliche Summation/Integration der spezifischen Strahlungsleistung mit nachfolgender S-B-Anwendung ist dagegen nicht erlaubt.

Unbeleuchtete Flächen und zeitliche Ableitungen haben in einer S-B-Inversion nichts zu suchen.

AUFFORDERUNG: Die Faktor4-Tag=Nacht-THE-Fraktion möge den PHYSIKALISCHEN Beweis erbringen, dass das Stefan-Boltzmann-Gesetz (S=P/A=SIGMA T^4) Flächen (B) enthält, die NICHT zur Strahlungsleistung (P) des Schwarzkörpers beitragen.

 

 

ERGEBNIS: Es gibt im streng „gleichzeitigen“ Stefan-Boltzmann-Gesetz keine Flächen (B), die nicht zur Strahlungsleistung (P) des Schwarzkörpers beitragen. Daher sind auch keine unbeleuchteten Flächen (B) in einer „gleichzeitigen“ S-B-Inversion erlaubt. Physikalisch „gleichzeitig“ bedeutet übrigens auch nicht, dass unterschiedliche „Gleichzeitigkeiten“ in einer einzigen S-B-Berechnung aufaddiert und gemittelt werden dürften…

Die „zweite Sonne“ im hemisphärischen S-B-Modell sind die Ozeane

Und jetzt betrachten wir einmal, wie sich die Flächen (A=beleuchtet) und (B=unbeleuchtet) auf die sogenannte „gemessene globale Durchschnittstemperatur“ von 14,8°C auswirken. Diese Durchschnittstemperatur NST kann über ihren 24h-Verlauf nur ganz minimal schwanken. Schließlich soll dieser Wert aus weltweit zeitgleich ermittelten Temperaturen berechnet werden und bildet deshalb für jeden Zeitpunkt des 24h-Tages einen globalen Tag&Nacht-Durchschnitt ab. Die Tagseite (A) und die Nachtseite (B) der Erde sind an diesem Durchschnittswert also gleichberechtigt beteiligt. Lediglich die unterschiedliche geographische Verteilung von Land- und Ozeanflächen und deren Position zum aktuellen Stand der Sonne dürften einen merklichen Einfluss auf den globalen tages- und jahreszeitlichen Temperaturdurchschnitt ausüben.

Die Nachtseite unserer realen Erde erhält in der erlebten Realität also keinerlei Sonneneinstrahlung, hat aber trotzdem keine Mond-Temperatur von etwa minus 200°C. Denn die Nachttemperatur hängt im Wesentlichen von der Wärmespeicherfähigkeit des passiv bestrahlten Himmelskörpers ab. Und auf der Erde wird der Nachtseite die erforderliche Wärme von ihrer kombinierten Luft-Wasser-Heizung aus den globalen Zirkulationen (Atmosphäre und Ozeane) zur Verfügung gestellt. Allein die Ozeane, die zwei Drittel unserer Erdoberfläche bedecken, enthalten ein Wärmeäquivalent von etwa 50.000 24h-Tagen Sonneneinstrahlung, und diese Wärmespeicher werden wiederum fortwährend durch die solare Einstrahlung auf der Tagseite unserer Erde „aufgeladen“. In der nachfolgenden Abbildung ist die jahresdurchschnittliche Oberflächentemperatur der Ozeane dargestellt, also der Durchschnitt zwischen Tag und Nacht sowie Frühling, Sommer, Herbst und Winter auf beiden jahreszeitlichen Hemisphären:

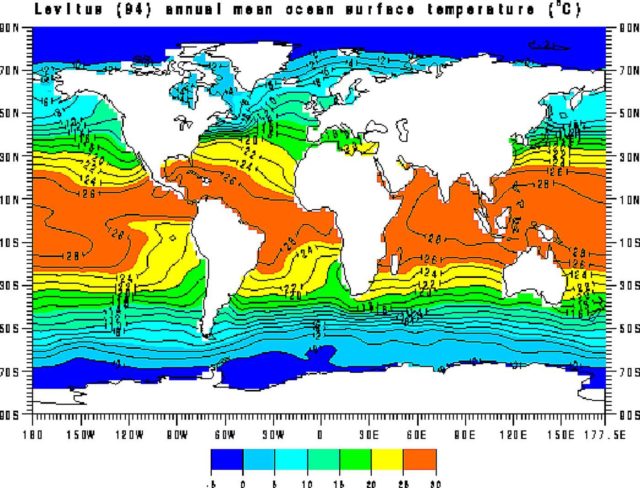
Abbildung 2: “Annual Mean Ocean Surface Temperature” based on observed data up until 1994 (NASA)

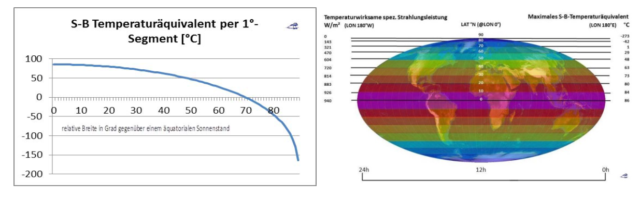
Diese Ozean-Daten repräsentieren also schon einmal zwei Drittel der „gemessenen“ globalen Ortstemperaturen. Die mittlere jährliche Oberflächentemperatur der Ozeane liegt bis etwa 70° nördlicher und südlicher geographischer Breite zwischen 0°C – 30°C und fällt erst jenseits davon auf bis zu -5°C ab; ein globaler Durchschnitt dürfte also in etwa bei der NST von ca. 15°C kumulieren. Dieser Verlauf bestätigt mein hemisphärisches S-B-Modell, das den 0°C-Durchgang des tagseitigen S-B-Temperaturäquivalentes ebenfalls bei etwa 70° nördlicher und südlicher geographischer Breite berechnet, wie die nachfolgende Abbildung beweist:

Abbildung 3: Das breitenabhängige S-B-Temperaturäquivalent im Äquinoktium

Links: Das vom Zenitwinkel abhängige tagseitige S-B Temperaturäquivalent für 1°-Segmente zwischen 0° und 90° nördlicher und südlicher Breite in [°C]

Berechnungsschema:

Lotrechter Sonnenstand auf dem Äquator,
Berechnung des S-B-Temperaturäquivalents aus der lokalen solaren Einstrahlung auf Mantelringen von 1° Breite mit dem Radius ri und dem Zenitwinkel i nach der Formel:

Der Grenzwert (n->oo) für die Summation über alle Segmente „n“ zwischen 0° und 90° nördlicher und südlicher Breite auf der Tagseite der Erde ergibt sich als meine Korrektur der Integrallösung von G&T (2009) zu 2 x 144,15K = 288,3K = 15,15°C

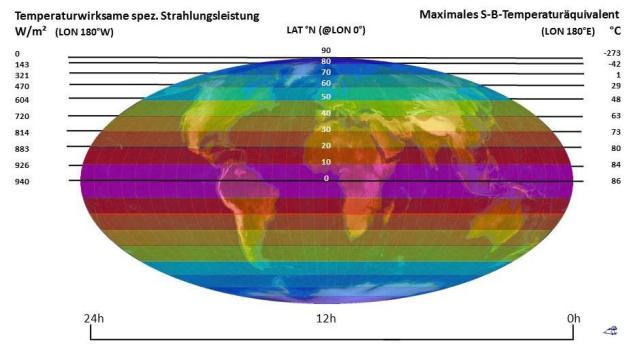
Rechts: Das maximale breitenabhängige S-B-Temperaturäquivalent über den 24h-Tag

Und nun erkläre bitte irgendein Anhänger der ominösen „Erde ohne Atmosphäre“, wie die globale Nachttemperatur in meinem hemisphärischen S-B-Modell für die reale Erde auch nur auf -18°C oder sogar auf Mond-Temperaturen von ca. -200°C absinken sollte. Die NASA-Abbildung der jährlichen mittleren ozeanischen Oberflächentemperatur weist vielmehr nach, dass die Ozeane genügend Wärme enthalten, um die Nachttemperaturen über die Umgebungsgleichung des S-B-Gesetzes nicht unter ihr eigenes Temperaturniveau absinken zu lassen (Ozean=>Atmosphäre=>Land). Denn schließlich tragen die dort abgebildeten Durchschnittstemperaturen nicht nur zu zwei Dritteln zur globalen Durchschnittstemperatur bei, nachts/im Winter/in höheren geographischen Breiten erfolgt aus diesem Wärmereservoir auch noch ein stetiger Wärmefluss vom Meer zum Land (hier Punkt 6). Auf dem Hamburger Bildungsserver Klimawandel heißt es unter „Ozean im Klimasystem“ bestätigend, Zitat mit Hervorhebungen:
„Zwischen Ozean und Atmosphäre herrscht ein ständiger Energie-/Wärmeaustausch: Energie wird immer an das Subsystem gegeben, welches gerade weniger Energie besitzt. Im Sommer/ am Tag ist der Ozean kälter als die Atmosphäre, da diese sich schneller durch die höhere solare Einstrahlung erwärmt. Es wird also Wärme von der Atmosphäre in den Ozean transportiert, der diese speichert. Auch im Winter/ in der Nacht reagiert der Ozean nur sehr langsam auf die viel geringere Einstrahlung. Während die Atmosphäre schon wieder stark abgekühlt ist, ist in der oberen Schicht des Ozeans noch viel Wärme gespeichert und erwärmt somit die über ihm liegende Atmosphäre. Der Ozean dämpft also den Einfluss der Sonneneinstrahlung, sodass Landgebiete in Meeresnähe im Winter eher wärmer, im Sommer kühler als meerferne Gebiete sind. Sie zeigen somit einen schwächeren Jahresgang. Analoges gilt für Tag- und Nachttemperaturen.“

ALSO: „Energie wird immer an das Subsystem gegeben, welches gerade weniger Energie besitzt“, und dieser Energietransfer wird durch die S-B-Umgebungsgleichung beschrieben:

DELTA S = SIGMA (T4 – T04)
An dieser Stelle bietet es sich an, auch gleich noch das viel diskutierte Jacken-Paradoxon aufzulösen. Wenn es draußen kalt ist, dann ist die Umgebungstemperatur T0 niedrig, nehmen wir mal 273K; Ihre Körpertemperatur beträgt dagegen 310K. Ihr Körper strahlt also mit DELTA S = SIGMA (3104K – 2734K) und Sie frieren. Wenn Sie jetzt eine Jacke anziehen, erwärmt sich deren Innenseite durch Ihre Körpertemperatur, sagen wir einmal auf 305K, das ist also Ihre neue Umgebungstemperatur. Ihr Körper strahlt dann nur noch mit DELTA S = SIGMA (3104K – 3054K) und Sie frieren nicht mehr, weil Ihr Körper durch die Jacke besser gegen den Wärmeverlust isoliert ist. Die Jacke erhöht also Ihre Körpertemperatur nicht, sondern verhindert lediglich dass Sie auskühlen. Anders ist es, wenn Sie in dieser Jacke Sport treiben. Dann produziert Ihr Körper mehr Wärme, als durch diese Jacke abgeleitet werden kann und Sie fangen an zu schwitzen. Da hilft dann nur noch eine dünnere Jacke, die schlechter isoliert…

Die hemisphärische S-B-Inversion ist ein qualitatives 3D&T-Modell unserer Erde

Da nun einmal die tagseitige solare Einstrahlung als Primärquelle für die Temperaturgenese auf unserer Erde anzusehen ist, stellt die hemisphärische S-B-Inversion ein realistisches 3D&T-Modell unserer Erde dar. Dieses Modell erklärt die Temperaturgenese, die Nachttemperatur und die globale Abstrahlung widerspruchsfrei zu den Hauptsätzen der Thermodynamik, wie die drei nachfolgenden Abbildungen belegen:

Tagseitige Einstrahlung @2PIR² und Temperaturgenese: Die hemisphärische Temperaturgenese folgt dem Sonnenstand auf der Tagseite der Erde:
S0*(1-ALBEDO) * COS(örtl. Zenitwinkel der Sonne)

Abbildung 4: Maximales breitenabhängiges S-B-Temperaturäquivalent im Äquinoktium.

Die Temperatur auf den Landmassen der Nachtseite unserer Erde kann nicht unter die Temperatur der globalen Wärmespeicher absinken und wird durch die S-B-Umgebungsgleichung DELTA S=SIGMA(T4-T04) beschrieben:
Die globalen Wärmespeicher unserer Erde (@T0) verhindern ein Mond-ähnliches Absinken der Nachttemperaturen auf unserer Erde. Der nächtliche Abstrahlungsverlust der Landoberfläche (@T) wird durch Advektion und Kondensation kompensiert.

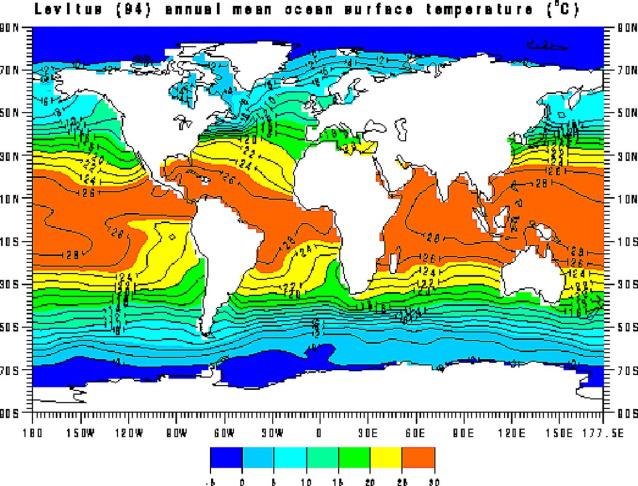
Abbildung 5: “Annual Mean Ocean Surface Temperature” based on observed data up until 1994 (NASA).

Globale Abstrahlung @4PIR²:

Der Energiefluss bei der Abstrahlung (@4PIR²) vom Warmen (Erdoberfläche@390W/m²) zum Kalten (Abstrahlungshöhe@235W/m²) gehorcht den Hauptsätzen der Thermodynamik.

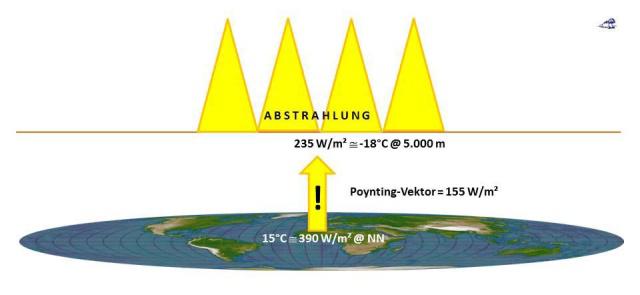
Abbildung 6: Die Richtung des Poynting-Vektors im globalen Abstrahlungsmodell (@4PIR2). Mit perspektivisch angepasster Mollweide-Projektion (Copyright L. Rohwedder – Lizenz CC BY-SA 3.0)

QED: Mein hemisphärisches S-B-Modell geht vom prinzipiellen Unterschied zwischen Tag und Nacht aus und erfordert keinen „natürlichen atmosphärischen Treibhauseffekt“ zur Erklärung der terrestrischen Temperaturgenese. Dieses S-B-Modell liefert vielmehr ein qualitatives Bild von den räumlichen und zeitlichen Veränderungen, die unser globales Klimageschehen bestimmen. Das hemisphärische S-B-Modell wäre also eine einmalige Möglichkeit, die Position der Klimarealisten in der Auseinandersetzung um unserer aller Zukunft zu stärken und die gesamte CO2-Klimahysterie ad absurdum zu führen; meinen damaligen Ausführungen ist also nichts hinzuzufügen…

Das Treibhaus-Paradoxon macht die Nacht zum Halbtag – den Tag aber leider auch…

Aber GLAUBEN Sie mir bitte ja nichts, schon gar nicht mein hemisphärisches S-B-Modell. PRÜFEN Sie vielmehr alles sehr sorgfältig, und widerlegen Sie mein S-B-Modell, indem Sie den wissenschaftlichen Nachweis über eine eindeutige physikalische Tag&Nacht-Gleichheit führen. In der nachfolgenden Tabelle können Sie noch einmal die Unterschiede der beiden konkurrierenden Modelle überprüfen:

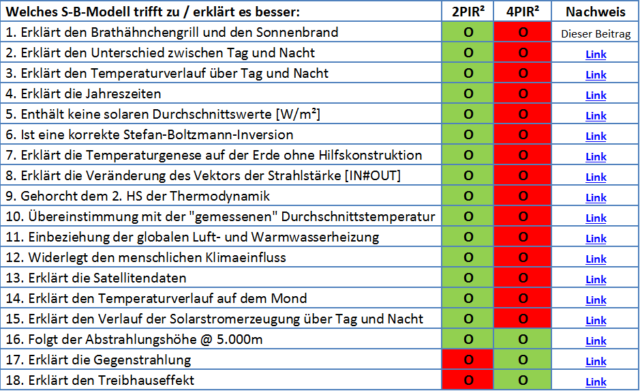
Tabelle 1: Direkter Vergleich der konkurrierenden S-B-Modelle für die Globaltemperatur mit meiner Bewertung – können Sie hier vielleicht einen Vorteil für das 4PIR2-THE-Paradoxon erkennen?

2PIR² = Das hemisphärische S-B-Modell 4PIR² = Das THE-Tag=Nacht-Flacherdeparadigma
[Hinweis von Admin: Die in der Tabelle in der rechten Spalte genannten Links konnten im EIKE-Editor nicht übernommen werden. Sie folge hier entsprechend der Numerierung links.

Links: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18.

Ende Hinweis]

Die tatsächliche Abfolge von Tag und Nacht im realen Leben entspricht nicht dem 4PIR2-Tag=Nacht-THE-Halbdunkel, sondern spiegelt vielmehr das Kindergarten-Alltagswissen, nachts sei es dunkler als draußen. Von daher müsste jeder Betrachter erkennen können, dass unsere Sonne ausschließlich am Tage (@2PIR2) Arbeit (=Leistung*Zeit) zu verrichten gewillt ist und nachts (ebenfalls @2PIR2) einfach streikt. Der Ausgangspunkt der herkömmlichen THE-Ableitung, die „-18°C-S-B-Globalinversion“ ist also definitiv falsch, weil sie mit der Tag&Nacht-Realität auf unserer Erde nichts zu tun hat und erst durch das Kunstprodukt „THE“ wieder an diese Realität anzuschließen vermag. Wer also meinen hemisphärischen 2PIR2-Ansatz ablehnt, der möge sich gerne etwas ganz Neues ausdenken; der 4PIR2-Tag=Nacht-THE-Ansatz kann es jedenfalls wirklich nicht sein. Es ist schon sehr erstaunlich, dass der astronomische Gebrauch des Stefan-Boltzmann-Gesetzes für aktiv leuchtende Sterne einstmals kritiklos auf einen passiv bestrahlten Planeten wie unsere Erde übertragen worden ist. Es ist noch erstaunlicher, dass mehr als drei Jahrzehnte intensiv alimentierte Klimaforschung den Unterschied zwischen Tag und Nacht nicht erkannt haben will. Am erstaunlichsten aber ist, dass selbst bei den sogenannten Klimarealisten eine überwiegende Mehrheit diese fehlerhafte S-B-Inversion hochemotional verteidigt.

 

image_pdfBeitrag als PDF speichernimage_printBeitrag drucken