Das Zitat oben von Stefan Rahmstorf am 12.2.18[1] ist ein Beispiel zur Behauptung warum Anomalien genauer sind als die ihnen zugrunde liegenden Absolutwerte. Er hat bis heute nicht begriffen, dass er in diesem Beispiel Absolutwerte misst und diese als Anomalien ausgibt. Klimaanomalien werden jedoch nicht gemessen, sondern aus den Absolutwerten mit all ihren Fehlern berechnet. Und da gilt nun mal das Gesetz von der Fehlerfortpflanzung. Er betreibt also – bewusst oder unbewusst- Etikettenschwindel.
Teil 1 hier und Teil 2 hier
Anomalien und sprunghafter Fehler
Machen wir dazu die Probe aufs Exempel, indem wir einen Anomalienverlauf aus einem (künstlichen) sinusförmigen Temperaturverlauf von 1850 bis 2009 erzeugen. Blau sei der Anomalienverlauf ohne Fehler. Die Anomalie verläuft fast eben, wie die blaue Trendlinie anzeigt. Ab 1940 wird nun ein Fehler von + 1 K eingefügt. Gemäß Rechenanweisung w.o. wird dann aus beiden Werten für alle Jahre (x) die Differenz gebildet. Ab 1940 hebt sich der Fehler auf. Beide Verläufe gehen ineinander über. Vor 1940 jedoch wird allein durch den Rechenprozess die Temperaturanomalie um 1 k abgesenkt. Wir sehen, die Annahme von vorhin gilt nur für die Zeit nach 1940. Vorher nicht. Lässt man Excel eine Trendgerade durch diese Werte legen, dann sehen wir, dass sich beide erheblich unterscheiden.
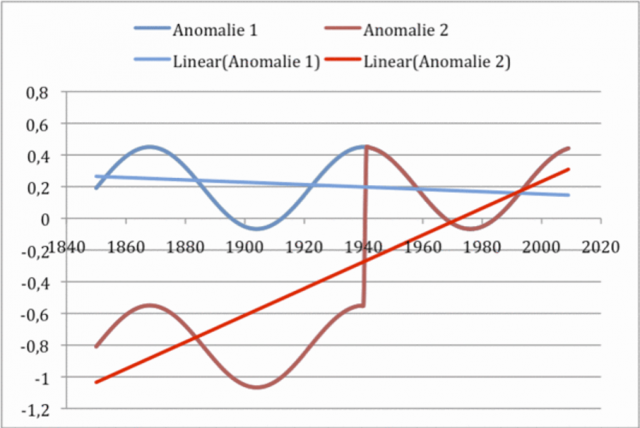
Abbildung 8 Ein systematischer Fehler von + 1 K tritt ab 1940 sprunghaft auf, weil z.B. die Station neu gestrichen wurde. Von dieser Veränderung sind das „Station Normal“ wie alle aktuellen Werte ab 1940 betroffen. Ab 1940 gleicht sich der Fehler aus, vorher aber nicht. Der Trend verschiebt sich.
Daran ändert sich auch nichts, wenn wir den Eintritt des Fehler auf später verlegen. Wie das nächste Bild zeigt. Dort werden die Kurven Anomalie 1 und 3 genannt.
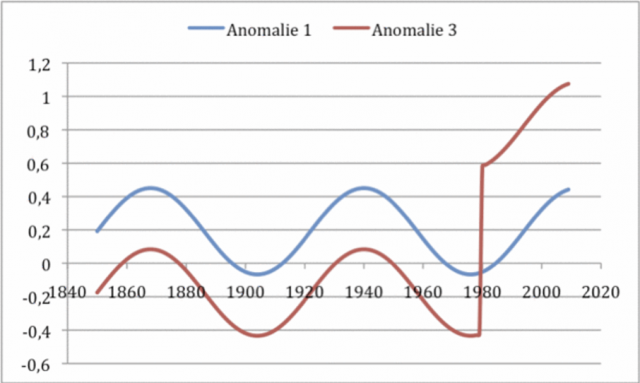
Abbildung 9 Ein systematischer Fehler von + 1 K tritt jetzt 1980 sprunghaft auf, weil z.B. die Station neu gestrichen wurde. Von dieser Veränderung sind das „Station Normal“ zur Hälfte und alle aktuellen Werte ab 1980 betroffen. Der Fehler gleicht sich nicht mehr aus, weder vorher noch nachher. Der Trend verschiebt sich.
Auch hier hebt sich der Fehler nicht auf, sondern ist weiter voll vorhanden und wirksam, natürlich erst, nachdem er auftritt. Der Unterschied zum ersten Beispiel ist, dass nun überhaupt keine „wahre“ Temperaturanomalie mehr gezeigt wird, sondern nur noch die fehlerbehaftete Summe.
Schleichender Fehler
Genauso entwickelt sich das Ergebnis, wenn man anstatt (oder zusätzlich) einen schleichenden Fehler in den zuvor fehlerfreien Verlauf einbringt. Ich habe das in der folgenden Abbildung getan. Dort wurde von Anfang an ein schleichender systematischer Fehler von +0,1 K/Dekade eingebracht, wie er z.B. vom städtischen Wärmeinseleffekt hervorgerufen werden kann.
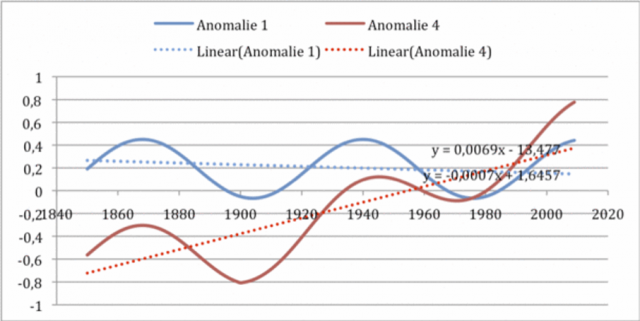
Abbildung 10 Ein systematischer Fehler von + 1 K tritt schleichend ab Beginn auf, weil z.B. die Station altert. Von dieser Veränderung sind das „Station Normal“ entsprechend seinem linearen Anteil ebenso wie alle aktuellen Werte von Anfang an betroffen. Der Fehler gleicht sich nicht mehr aus, weder vorher noch nachher. Der Trend verschiebt sich.
Wir sehen einen schön ansteigenden Verlauf (zuvor war er fast gerade) – verursacht allein durch den schleichenden systematischen Fehler- z.B den UHI. Nur kann jetzt überhaupt nicht unterschieden werden, ob ein systematischer Fehler vorliegt, oder ob sich die Umgebungstemperatur z.B. durch den Treibhauseffekt erhöht hat.
Man könnte nun beanstanden, dass die Fehlergröße in diesen Beispielen etwas hoch gewählt wurde. Dem ist aber nicht so, wie die zahlreichen Untersuchungen z.B. von Watts (http://www.surfacestations.org/) zeigen. Denn Fehler dieser Art gab und gibt es zahlreich. Sie werden durch Stationsverlegungen, Thermometertausch, Änderung der Farbbeschichtung der Station, Änderung des Algorithmus für die Berechnung des Mittelwertes u.v.a. mehr eingebracht. Es wäre nun vielleicht möglich den Anstieg im obigen Beispiel als Ausreißer zu erkennen, weil er einmalig und sprunghaft -wenn auch konstant- auftritt, und ihn durch entsprechende Rechnungen zu kompensieren. Das geschieht aber nur sehr, sehr selten, weil sich bei den abertausenden von Datensätzen der Vergangenheit kaum jemand diese Mühe macht, bzw. machen kann
Kein Fehlerausgleich möglich
Eine Korrektur unterbleibt hauptsächlich deswegen, weil man die Binsenweisheit (siehe Brohan et al 2006) von zuvor glaubt, dass sich der Fehler bei Anomalienbildung von selbst ausgleicht. Das ist aber, wie wir gesehen haben, grottenfalsch!
Eine Korrektur unterbleibt aber auch in den allermeisten Fällen deshalb, weil die dazu erforderlichen sog. „Metadaten“ fehlen und auch nicht mehr herbeigeschafft werden können. Diese beschreiben die Umgebungsbedingungen, Maßnahmen, Algorithmen und vieles anderes, was in und um die Station über den Zeitraum passiert ist. (Siehe dazu bspw. Harrys Read Me Files des Meteorologen und Programmierers bei der CRU Harry: „HARRY_READ_Me.txt.“ z.B. hier . Diese ist 274 Seiten lang. Die dazugehörige Datenbasis enthält über 11.000 Dateien aus den Jahren 2006 bis 2009[2])
Allgemein gilt daher, die Annahme, dass sich bei Anomalienbildung die Fehler aufheben, ist nur dann richtig, wenn der gemeinsame, gleich große und richtungsgleiche Fehler vor dem Beginn der untersuchten Zeitspanne eintritt und dann so bleibt. In unserem Falle also vor 1850. Das liegt jedoch weder in unserem Ermessen, noch haben wir davon Kenntnis, sondern es wird allein durch die Realität bestimmt. Deshalb kann festgehalten werden, dass diese simple Fehlerkorrekturmethode in aller Regel nicht anwendbar ist. Angewendet wird sie aber von so gut wie allen -auch IPCC- Klimatologen trotzdem.
Zusammenfassung
In der Statistik ist es eine gängige Methode Werte von div. Variablen mit Referenzwerten eben dieser Variablen zu vergleichen, um auf diese Weise bei eventuellen Abweichungen u.U. Ähnlichkeiten im Verlauf oder sogar Hinweise auf mögliche Ursache und Wirkungsbeziehungen zu bekommen. Allerdings muss man sich immer im Klaren darüber sein, wie sehr diese Methode von den Randbedingungen abhängt. Es wird gezeigt, dass eine schlichte Anomalienbildung keineswegs ausreichend ist, um schwer bestimmbare variable oder konstante systematische Fehler herauszurechnen. Im Gegenteil, man müsste in jedem Fall diese Fehler bestimmen, sie quantifizieren und einordnen, um sie dann evtl. mehr oder weniger gut rechnerisch ausgleichen zu können. In der Klimatologie ist diese Einschränkung in Bezug auf die Schwächen der Anomalienbildung offensichtlich nicht nur nicht bekannt, sondern wird auch – auf den ersten Anschein hin- negiert.
Der berühmte Physiker und Nobelpreisträger Dick Feynman würde sagen: „Sie halten sich selbst zum Narren“. Nur so lässt sich erklären, dass auch hochangesehene Forscher diese simplen Zusammenhänge oft nicht beachten. Ihre Ergebnisse sind dadurch entsprechend falsch und damit unbrauchbar, bzw. mit wesentlich größeren Fehlern (Unsicherheiten) behaftet als angegeben.
Anhang.
Zur behaupteten Genauigkeit
Die berechnete Globaltemperatur im letzten Jahrhundert hat sich, gemäß Aussage des Intergovernmental Panel of Climate Change (IPCC) um ca. 0,6 ° bis 0,7° C erhöht, wie uns im Bericht TAR 2001(Third Assesment Report) mitgeteilt wurde. Um diese Aussage treffen zu können, müssen Veränderungen über lange Zeiträume mit einer Genauigkeit von < 1/10 °C ermittelt, erfasst, dokumentiert und verdichtet werden. Das englische Klimazentrum CRU (Climate Research Unit) -siehe Abbildung 1- zeigt sogar einen Anstieg von 0,8 °C mit einem Vertrauensintervall bei 95% von -0,09 bis +0,11 °C (Jahr 1905) bis ± 0,08 ° (Jahr 2005.).[3]
Dem steht aber entgegen, dass selbst bei Verwendung der bestgewarteten Messstationen und von gut trainierten Meteorologen so genau wie möglich abgelesenen Temperaturwerte, diese nur die Bestimmung von Tagesmittelwerten mit einer von Genauigkeit ± 2 bis ± 3 K erlauben. Zitat des Meteorologen und Statistikers Jürgen Pelz
Jürgen Pelz: „Anmerkungen zur Prüfung von Daten und Ergebnissen von Modellrechnungen unter Verwendung der Statistik und der ,Informationstheorie“ Beilage zur Berliner Wetterkarte vom 7.12.1995; S. 5
„Will man beispielsweise die Tagesmitteltemperatur auf ± 0.1 K genau ermitteln, darf der Abstand der Messungen nicht grösser als 15 Minuten sein. Genügt eine Genauigkeit von ± 2 bis 3 K, reichen die Klimatermine.“ [Pelz, 1995b][4]
Trotzdem behaupten die Wissenschaftler der Climate Research Unit (CRU) der University von East Anglia, welche die CRU Hadley Reihe produzieren[5]: „How accurate are the hemispheric and global averages? Annual values are approximately accurate to +/- 0.05°C (two standard errors) for the period since 1951. They are about four times as uncertain during the 1850s, with the accuracy improving gradually between 1860 and 1950 except for temporary deteriorations during data-sparse, wartime intervals. Estimating accuracy is a far from a trivial task as the individual grid-boxes are not independent of each other and the accuracy of each grid-box time series varies through time (although the variance adjustment has reduced this influence to a large extent). The issue is discussed extensively by Folland et al. (2001a, b) and Jones et al. (1997). Both Folland et al. (2001a,b) references extend discussion to the estimate of accuracy of trends in the global and hemispheric series, including the additional uncertainties related to homogenity corrections.”
[1] Quelle: „Verwirrspiel um die absolute globale Mitteltemperatur“ https://scilogs.spektrum.de/klimalounge/verwirrspiel-um-die-absolute-globale-mitteltemperatur/ (hier)
[2] Details entnommen aus ‚Botch after botch after botch‘ Leaked ‚climategate‘ documents show huge flaws in the backbone of climate change science By LORRIE GOLDSTEIN (hier)
[3] Diese Darstellung der Zeitreihe der mittleren Globaltemperatur kommt auf vielfältige Weise in öffentlichen Berichten des IPCC AR 4 vor. So z.B. Im Summary for Policymakers SPM auf Seite 19, In den FAQ´s des Berichtes der Workung Group 1 Fig. 3.1 auf S 104. In der Technical Summary des Berichtes der Working Group 1 (WG1-TS) als Fiure TS.6 auf Seite 37 usw.
[4] Pelz, J b (1995) Anmerkungen zur Prüfung von Daten und Ergebnissen von Modellrechnungen unter Verwendung der Statistik und der Informationstheorie. Beilage zur Berliner Wetterkarte 7.12.1995
[5] Quelle http://www.cru.uea.ac.uk/cru/data/temperature/#datter (hier)
Für alle die diese Arbeit am Stück lesen wollen hier das pdf dazu Die schwierige nimmer endende Fehlerdiskussion
















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"„Er hat bis heute nicht begriffen, dass er in diesem Beispiel Absolutwerte misst und diese als Anomalien ausgibt.“ (zum Rahmstorf-Blog)
Nicht nur das!
Messen kann man nämlich nur meßbare Werte. Die Temperaturwerte, um die es hier geht, sind aber nicht meßbar, sondern es sind Rechenergebnisse! Und ich möchte einmal den „Meßaufbau“ sehen, mit der man Differenzen von Rechenergebnissen „messen“ kann, deren Basiswerte aus verschiedenen Jahrhunderten stammen …
Sehr geehrter Herr Limburg,
wäre es vielleicht möglich, die internen Verweise im Artikel mit tatsächlichen URLs zu unterfüttern? Manch geneigter Leser mag verlockt sein, sich an den Referenzen zu versuchen. Hoffend auf baldige Abhilfe verbleibt meine Wenigkeit
mfG
H.Lodsch
Offensichtlich waren einige der links nicht mehr erreichbar. Soweit möglich habe ich die aktuellen noch erreichbaren unterlegt. Mit freundlichen Grüßen
M.L.
Sehr geehrter Herr Limburg,
ich bin jetzt etwas enttäuscht, weil ich auf die Stelle gewartet habe, wo mit den Trivialitäten Schluss ist und dann endlich die Punkte kommen, über die man diskutieren kann.
Natürlich verursachen Stationswechsel und andere Änderungen Fehler bei Verwendung der Rohdaten. Aber niemand berechnet ja Differenzen von Rohdatenzeitreihen. Die meisten Arbeitsgruppen verwenden homogenisierte Daten, Best macht das nicht, die setzen auf Kriging.
Schleichende Effekte wie Wärmeinseleffekt sind ebenfalls bekannt. Statt damit zu langweilen, dass es das gibt, wäre interessanter gewesen zu diskutieren, wie man versucht, diese Effekte zu quantifizieren und zu korrigieren.
Ausgangspunkt der letzten Diskussion war ja, warum Anomalien präziser gemessen werden können als absolute Temperaturmittel. Da hat mich besonders enttäuscht, dass der Elefant im Raum nicht mal Erwähnung fand, nämlich:
Man stelle sich vor, man hat eine Messtation im Tal, eine auf eine Berg. Der Unterschied in den absoluten Temperaturen ist wegen der Höhenabhängigkeit groß, die Mittelung wegen dieser Abhängigkeit schwierig. Die Erwämung dagegen (die Anomalie) ist dagegen über viel größere, regionale Bereiche, praktisch dieselbe.
Glauben Sie, Sie hätten etwas entdeckt, was der Wissenschaft bislang unbekannt ist? Glauben Sie, Sie könnten alle Verfahren der Temperaturreihenbestimmung widerlegen? Dann beteiligen Sie sich an der wissenschaftlichen Diskussion:
Reichen Sie ein Paper ein. Leute, die gängige Meinungen über Bord werfen konnten, sind dadurch Berühmtheiten geworden.
Danke für Ihre Eindrücke, und wirklich, wirklich, wirklich, es tut mir schrecklich leid, dass ich so einen profunden Fachmann wie Sie es sind gelangweilt habe. Mea Culpa! Mea maxima culpa.
Und auch dass ich Ihr tolles Berg- und Tal Beispiel nicht gebracht hatte, den Elefant im Raum wie sie ihn zu nennen pflegen, tut mir schrecklich leid. Ich hatte zwar darüber berichtet, dass die Bildung von Anomalien durchaus das Erkennen ähnlicher Trends ermöglicht, habe das aber wohl so gut im Text versteckt, dass Sie diesen Hinweis nicht entdecken konnten. Auch das meine alleinige Schuld. Leider kann man daraus nicht den Schluss ziehen, dass Anomalien genauer sind als ihre Komponenten.
Im übrigen hatte ich schon des öfteren auf diesen link verwiesen, peer reviewed, wie verlangt.
Es ist natürlich meine Schuld, dass Ihro Gnaden da noch nicht reingucken konnten. Auch dafür bitte ich nachträglich um Entschuldigung. Wie konnte ich nur den Nürnberger Trichter vergessen und auf eigene Überprüfung hoffen.
Auch hatte ich des öfteren auf die grundlegenden Arbeiten von Dr. Pat Frank verwiesen. siehe hier, hier und hier.“ Auch, dass Sie die übersehen haben, ist natürlich meine Schuld.
Beste Grüße
Ihr untertänigster
M.L.
Herr Limburg,
Sie schreiben:
„Auch hatte ich des öfteren auf die grundlegenden Arbeiten von Dr. Pat Frank verwiesen. siehe hier, hier und hier.“ Auch, dass Sie die übersehen haben, ist natürlich meine Schuld.“
Doch, ich hatte dort kommentiert, mein dort benutzter Name funktionierte damals aber plötzlich nicht mehr. Merkwürdig, dass solche technischen Fehler mmer nur bei Leuten passiert, die anderer Meinung sind als Sie. Aber Sie versichern ja regelmäßig, es gibt keine Zensur. Woran liegt es?
PS:
Wer etwas mitzuteilen hat von wissenschaftlichem Wert, der würde etwas besseres finden als E&E. Kein Wissenschaftler liest, was dort erscheint.
Aber trotzdem meine Glückwünsche zu Ihrem Erfolg dort, das Peer Review war sicherlich ganz schön hart 😉
Ich würde aber lieber über Inhalte sprechen als zu streiten, ich versuche das nochmals:
Wenn ihr Ziel ist, den Anbietern von Temperaturzeitreihen Fehler nachzuweisen, dann müssen Sie schon das kritisieren, was diese tun. Jeder kennt die Problematik der Verwendung von Rohdaten, man verwendet daher homogeniserte Daten. Diese Problematik verursacht durch Stationsänderungen etc. zeigen Sie hier schön auf, dafür ein Lob.
Nun wundert mich folgendes:
Hier klingt es immer so, als sei die Verwendung von Rohdaten der Goldstandard und die Eindämmung der beschriebenen Fehler durch homogenisierte Daten wird hier wörtlich oft „Betrug“ genannt. Wie passt das zusammen?
Ich erinnere mich an eine Arbeit von Lüdecke et al., publiziert in einem namhaften Journal, wo Spektralzerlegung von 5 langen Temperaturzeitreihen durchgeführt wurden. Von den Rohdaten übrigens, trotz Standort- und Instrumentenwechseln.
Wie passt das zusammen? Sie kritisieren immer nur die, die um diese Fehler wissen und die diese Fehler angehen, sind das nicht die falschen Adressaten ihrer Botschaft?
Sie weichen aus, Herr Löffler, zur Sache kommt von Ihnen nichts.
Und Ihre (abwertende) Meinung zu E&E ist eigentlich auch nicht von Interesse.
Zur Arbeit von Lüdecke et al.
Wie ich in meinen Vorträgen ausführte und auch in manchen meiner Beiträge zum Thema, handelt es sich bei den von mir untersuchten systematischen Fehlern um statische oder semistatische Einflüsse, d.h. sie treten schleichend auf (Beispiel: Alterung) oder sprunghaft (Beispiel Standortwechsel, Neuanstrich etc.) und verbleiben dann so.
Lüdecke et al untersuchten periodische Änderungen und die bilden sich ab, weil sie sich den Mittelwerten überlagern, vergleichbar wie eine Amplitudenmodulation. Sowohl bei den errechneten Mittelwerten, als auch beim umhüllenden Unsicherheitsband. Daher kann eine solche Studie zu nützlichen Erkenntnissen kommen, jedenfalls in Bezug auf Periodendauern, weniger auf die Höhe der Amplitude.
Bravo Herr Wolfgang Löffler1,
sehe ich genauso. Mehr als billiges Zweifelsähen kommt hier nicht, wer Fakten fordert, wird angemscht und abgesägt. Selbst einfachste wissenschaftliche Tatsachen werden dämonisiert.
@Sverre Petersen 1. Mai 2020 um 16:39
Wahrscheinlich haben auch Sie keine Ahnung von der Messerei und der Statistik, sonst würden Sie nicht solche Formulierungen wählen.
Zweifel und damit das „Zweifelsäen“ sind bitter nötig, weil die Kritik der Messreihen auf wissenschaftlicher Basis bei den Klimahysterikern nicht erfolgt. Bei den Temperaturen sind die eigentlichen Thermometer nicht mal das größte Problem bei den messtechnischen Unsicherheiten, sondern die Anwendung bzw. die Bedingungen „drumherum“. Ein berührend messendes Thermometer misst immer nur die eigene Temperatur, selbst das scheint Ihnen nicht klar zu sein.
Ich selbst halte als Messtechniker mit über 40 Jahren sehr praktischer Erfahrung auch nichts von den „Homogenisierungen“, weil die fast immer sehr subjektive Einschätzungen zur Basis haben, da kann man zu viel in die gewünschte Richtung manipulieren. Bei WI-Effekten oder anderen Einflüssen z.B. auf die Messhüttten (Farbe, Pflegezustand usw.) weiss man zwar die Richtung der Verfälschungen, aber niemals den genauen Wert, erst recht nicht nach 100 Jahren. Was man recht sicher weiß, dass die Messunsicherheit wesentlich größer ist als laienhaft vermutet. Und damit sind die ganzen Klimamodellierungen wertlose Computerspiele ….
Herr Petersen,
sie meinen vereinfachte unwissenschaftliche Behauptungen werden daemonisiert!
Sie haben sich aus unerfindlichen Gründen nicht zu der Behauptung von Herrn Loeffler geäußert, wo er behauptet das:
„….Anomalien präziser gemessen werden können als absolute Temperaturmittel.“
Betrachten sie das wissenschaftliche Tatsache?
Herr Loeffler,
koennen sie bitte eine wissenschaftliche Arbeit nennen und verlinken die bestätigt, das sich die Temperaturen im Tal genau so verhalten wie die Temperaturen auf dem Berg?
Solch eine Arbeit sollte auch in der Lage sein die Höhe der Abweichungen darzustellen. Davon auszugehen, das es keine gibt, so wie sie, ist unwissenschaftlich und fahrlässig.
Gleiche Arbeiten sollte es geben über verschiedene Regionen, vielleicht mit einem engeren standardisierten Messnetz, um zu bestätigen, was sie sagen das:
„Die Erwärmung dagegen (die Anomalie) ist dagegen über viel größere, regionale Bereiche, praktisch dieselbe.“
Sie sollten, ordentlich und sorgfältig recherchieren und äußern. Dieser Satz bezeugt das sie immer noch nicht wissen worum es geht und wo ihre Denkfehler anfangen:
„Ausgangspunkt der letzten Diskussion war ja, warum Anomalien präziser gemessen werden können als absolute Temperaturmittel.“
NEIN!
Anomalien werden nicht gemessen.
Anomalien werden aus gemessenen Temperaturen errechnet.
Temperaturmittel werden auch nicht gemessen, diese werden auch berechnet.
Das einzige was gemessen wird sind Temperaturen.
Sie sollten Ihre Aussagen noch mal mit den obigen Fakten abgleichen. Vielleicht ergibt sich ja dann eine sinnvolle Diskussion. Bisher jedenfalls haben sie keinen ordentlichen Beitrag geleistet.
Sie haben völlig recht.
Wenn Begriffe wahllos durcheinander geworfen werden, dann können nur (höflich gesagt) Missverständnisse daraus erwachsen.
Gestatten Sie mir noch eine Ergänzung zum Thema Homogenisierung:
„Über Land werden manche ermittelten Zeitreihen, sofern möglich, auf Inhomogenitäten untersucht. Findet man Inhomogenitäten, und dies setzt erhebliches detektivisches Gespür, Geduld, Können und Zeit voraus, d.h. signifikante Abweichungen, die systematische Fehler vermuten lassen, dann müssen diese Zeitreihen korrigiert (im meteorologischen Sprachgebrauch „homogenisiert“) werden bevor sie weiter verarbeitet werden können. D.h. sie werden als absolute Werte mit den Werten einer als fehlerfrei angesehenen Zeitreihe verglichen, d.h. voneinander abgezogen. Stimmen beide Zeitreihen dann 1:1, d.h. ohne den gesuchten Fehler überein, bleibt als Restterm dieses Vergleiches nur der Fehler in seinem Verlauf übrig. Er kann dann zur Korrektur verwendet werden. Stimmen beide nicht exakt überein, und das ist der Normalfall, bleibt eine Restdifferenz zusätzlich zum Fehler übrig und verfälscht mehr oder weniger stark das Ergebnis. Dieses wird aber in der Praxis oft nicht erkannt. Es kann schwerlich unterschieden werden, was Signal bzw. was Fehler ist. Die Konsequenz daraus ist, dass in diesem Fall mit der Homogenisierung der fehlerhaften Zeitreihe Größe und Verlauf der Referenzzeitreihe aufgeprägt wird. Ihre Bestimmung wird damit wertlos. Das evtl. vorhandene Signal verschwindet.
Quelle meine Diss. Seite 80-81.
Wer diese Aussage widerlegen möchte kann dies hier gern versuchen.
Und auch das sollte jedem zu denken geben:
“ Der Klimatologe und CRU Programmierer Ian „Harry“ Harris, unter dem Namen „Harry“ bekannt geworden, war beauftragt, die Datensätze der historischen Daten der WMO in einem dazu zu schreibenden Programm auszuwerten. Er äußerte in seinen Anmerkungen zu seinen Programm-Codes schwerste Bedenken bezüglich die Qualität der zu bearbeitenden WMO Datensätze und schrieb dazu u.a. in seine Programmcodes zur Berechnung der globalen Temperaturzeitreihe:
“[The] hopeless state of their (CRU) database. No uniform data integrity, it’s just a catalogue of issues that continues to grow as they’re found…I am very sorry to report that the rest of the databases seem to be in nearly as poor a state as Australia was. There are hundreds if not thousands of pairs of dummy stations, one with no WMO and one with, usually overlapping and with the same station name and very similar coordinates. I know it could be old and new stations, but why such large overlaps if that’s the case? (241)….“But what are all those monthly files? DON’T KNOW, UNDOCUMENTED. Wherever I look, there are datafiles, no info about what they are other than their names. And that’s useless …“ (Page 17)- „It’s botch after botch after botch.“ (18)-„The biggest immediate problem was the loss of an hour’s edits to the program, when the network died … noexplanation from anyone, I hope it’s not a return to last year’s troubles … This surely is the worst project I’veever attempted. Eeeek.“ (31)- „As far as I can see, this renders the (weather) station counts totally meaningless.“ (57)- „COBAR AIRPORT AWS (data from an Australian weather station) cannot start in 1962, it didn’t open until1993!“ (71)- „You can’t imagine what this has cost me — to actually allow the operator to assign false WMO (WorldMeteorological Organization) codes!! But what else is there in such situations? Especially when dealing with a’Master‘ database of dubious provenance …“ (98)- „So with a somewhat cynical shrug, I added the nuclear option – to match every WMO possible, and turnthe rest into new stations … In other words what CRU usually do. It will allow bad databases to passunnoticed, and good databases to become bad …“ (98-9).
Damit wird nachvollziehbar klar, dass die damit befassten Wissenschaftler sehr viel Fleiß und auch Improvisation und Intuition in die Bearbeitung der zu behandelnden historischen, lücken- – und fehlerhaften Datensätze stecken mussten. Umso erstaunlicher ist die proklamierte Genauigkeit der Aussagen.“
Quelle ebenda S 54/55
Mit freundlichen Grüßen
M.L.
Danke Herr Limburg,
mir sind diese Unzulänglichkeiten von Daten sehr wohl bekannt. Beruflich beschäftige ich mich sowohl mit Temperaturmessungen und deren Auswertung als auch mit großen Datensätzen aus unterschiedlichen Quellen.
Danke an dieser Stelle für ihre unermüdliche Arbeit und Aufklärung.
Gern geschehen.
Wenn es nicht auch noch Spaß machen würde, hätte ich ob der allgemeinen Ignoranz die mir immer wieder entgegenschlägt, siehe so manche Kommentare, schon längst aufgegeben.
Mit freundlichen Grüßen
M.L.
Herr Schulz
„Sie sollten, ordentlich und sorgfältig recherchieren und äußern. Dieser Satz bezeugt das sie immer noch nicht wissen worum es geht und wo ihre Denkfehler anfangen:“
Fällt Ihnen etwas auf? Sie bitten mich um Quellen, es sind also Sie selbst, der nicht recherchiert hat. Bei mir ist das etwas anders: Sie können davon ausgehen, dass ich nur darüber schreibe, wo ich informiert bin.
Das grundlegende Paper zu absoluten mittleren Temperaturen ist von Jones et al. 1999: https://www.st-andrews.ac.uk/~rjsw/papers/Jones-etal-1999.pdf
Auf der GISS-Seite gibt es Material mit weiteren Links.
Über welche Räume sind Anomalien vergleichbar und representativ?
Das haben die Leute von GISS in einem paper untersucht. Auf der GISS-Seite finden Sie das, ich suche jetzt nicht für Sie heraus.
Name und Erscheinungsjahr wird Herr Limburg sicherlich sofort nennen können, er ist ja schließlich der großartige Experte.
PS:
Es gibt ein „technisches“ Problem. Ich versuche mal einen neuen Namen, vielleicht klappt es ja jetzt.
Herr Loeffler,
danke fuer den Link zum Jones Papier.
Auf Seite 5 finden sie den folgenden Satz:
„we can calculate the average large-scale SE in a similar manner to the calculation of the large-scale average temperature anomalies.“
Dort steht also, das Anomalien berechnet werden. Punkt!
Das Paper beantwortet meine Frage nicht. Ich fragte nach einer Untersuchung die beweist, das eine lineare Interpolation wirklich anwendbar ist. Jones benutzt Zeit und Raeumlich Lineare Interpolation. Und das fuer massiv grosse Gebiete, die keine Temperaturmessstellen haben. Allein die Anwendung der linearen Methode ist kein Beweis, das diese Methode richtig ist.
Und dann schauen sie mal Figure 3 an. Das sind Isolinien. Wie kommt man von spaerlichen Messungen auf Isolinien? Im Ozean! Ich bitte sie! Dort gibt es keine festen Temperaturmessstellen.
Faehrt der Dampfer mit dem Wetter mit, benutzt man seine Daten nitt!
Hallo Herr Tengler, Sie verfügen nicht über die Voraussetzungen, über meine Person ein Urteil zu bilden. Die Messfehler bei meteorologischen Temperaturmessungen sind bekannt.
Aber die Autoren in der hier verlinkten Links vermögen es nicht, von diesen Fehlern ausgehend eine nachvollziehbaren mathematisch- methodische Beweiskette zu konstruieren, um damit unzweifelhaft zu belegen, warum die von CRU, GISS, WMO, u.a. angegebenen Fehlerangaben bei der globalen Anomalie zu eng seien. Es bleibt nur bei unzusammenhängendem Gefasel.
Man muss nicht nur lesen können, sondern auch verstehen können. Am letzteren mangelt es offensichtlich bei Ihnen.
Machen Sie sich nichts draus. Dieses Schicksal teilen Sie mit Millionen unserer Landsleute.
Gut, vielleicht verstehe ich Sie auch nicht.
Bei meiner Suche nach Substanziellem in Ihren Schriften fiel mir Ihre Abbildung der Abweichungen der unterschiedlichen Tagesmittelmethoden auf die Monatsmittel auf. Je nach Tagesmittelungsmethode können dann die Monatsmittel des gleichen Rohdatensatzes um einige Zehntelgrad abweichen, am stärksten ist der Unterschied zwischen der Tagesmittel = (Max+Min)/2 Berechnung und der Tagesmittelberechnung aus den 24 Stundentemperaturen von zwischen 0,5 und 1 Grad im Monatsmittel.
Nun besteht das Problem, dass von einigen alten Stationsaufzeichnungen z.B. in den USA nur Monats- oder Tagesmittel berechnet nach der Formal Tagesmittel = (Max+Min)/2 überliefert sind. Diese „Min-Max-Monatsmittel“ sind daher nicht vergleichbar mit Monatsmitteln aus 24 Stundentemperaturen und Monatsmitteln aus 24 Stundentemperaturen sind nicht überliefert.
Stimmen Sie mir nun zu, daß mit der obigen Ermittlung der Differenzen in den Monatsmitteln nach den verschiedenen Methoden an heutigen Stationen eine Korrektur für die alten abgeleitet werden kann und damit die Monatsmittel in die heutige 24 Stundenmethode umrechnen kann?
Dies ist nicht exakt möglich, aber den Restfehler kann man großzügig (also unter Annahme extremer Auswirkungen der täglichen Temperaturkurven) abschätzen und er ist geringer als die so angebrachte systematische Korrektur. Somit sind die alten Daten mit den heutigen – zumindest was die Methode der Tagesmittelbildung angeht- vergleichbar gemacht worden.
Nein, das kann man nicht. Das könnte man nur dann, wenn alle anderen Randbedingungen gleich und vor allem bekannt gewesen wären. Sie sind aber beides nicht. Außerdem wurde das m.W.n auch nicht versucht.
Das bedeutet, dass sie für einen systematischen Fehler sorgen, den ich in Algrorithmusfehler getauft habe und dessen Größe ich in dieser Arbeit versucht habe zu quantifizieren.
„..um damit unzweifelhaft zu belegen, warum die von CRU, GISS, WMO, u.a. angegebenen Fehlerangaben bei der globalen Anomalie zu eng seien.“
CRU,GISS,WMO verwenden die gleichen Messdaten von Wetter-Stationen. Diese deckten bzw. decken die Oberfläche nicht gut ab. Diesen Fehler kann man schlecht abschätzen wenn man keine Daten hat. In dieser Hinsicht sind Satelliten-Daten, die eine bessere Flächen-Abdeckung haben, eine wertvolle Ergänzung.
„Aber die Autoren in der hier verlinkten Links vermögen es nicht, von diesen Fehlern ausgehend eine nachvollziehbaren mathematisch- methodische Beweiskette zu konstruieren, um damit unzweifelhaft zu belegen, warum die von CRU, GISS, WMO, u.a. angegebenen Fehlerangaben bei der globalen Anomalie zu eng seien.“
Haben Sie sich einmal die Fehlerangabe von CRU angeschaut? Sie finden sie unter
https://www.metoffice.gov.uk/hadobs/hadcrut4/data/current/time_series/HadCRUT.4.6.0.0.monthly_ns_avg.txt
Für 202002 geben sie als Anomalie 0,999 und ein Unsicherheit-Intervall von 0,867..1,137, also +/- 0,14 °C an. Allerdings ist dies kein globales Mittel da nicht die ganze Oberfläche abgedeckt ist.Wie viele Mess-Stationen gibt es im Inland von Grönland, bzw. nördlich von 85°N? Im Inland der Antarktis gibt es auch sehr wenige Stationen. Amundsen Scott ist eine viel besuchte Forschungsstation mit Flugfeld.
Addendum:
Vergleich: Gistemp 202002 1,25 °C (1951-1980), Wert bezogen auf (1961-1990) 1,139 °C. Dies liegt schon außerhalb des von CRU angegebenen Unsicherheit-Intervalls.
Vergleichs-Daten von Berkeley Earth bzw. Cowtan and Way liegen nicht vor. Neuere Daten von HADCRUT 4.6 liegen nicht vor.
„Schleichende Effekte wie Wärmeinseleffekt sind ebenfalls bekannt. Statt damit zu langweilen, dass es das gibt, wäre interessanter gewesen zu diskutieren, wie man versucht, diese Effekte zu quantifizieren und zu korrigieren.“
Wärmeinsel-Effekte kann man nicht korrigieren, das ist eine Verfälschung von gemessenen Temperaturen. Ich bin sehr skeptisch bei den verschiedenen Verfahren
fehlende Daten von nicht besiedelten Gebieten durch Extrapolation von Daten aus besiedelten Gebieten zu gewinnen. Häufig verwendet man Ozean-Temperaturen um
Land-Temperaturen zu schätzen. Das geht schief.
Hallo Herr Limburg,
In ihrer E&E Arbeit S118 Fig 2 sieht man doch, wie die Monatsmittel der Station Puchheim von einer Tagesmittelmethode in die andere umgerechnet werden müssen. Der Zeitraum von 9 Jahren ist lang genug, um für diese Station und benachbarte Stationen monatliche Korrekturen für die historischen Daten anbringen zu können, um diese auf eine vergleichbare Tagesmittelmethode umzurechnen.
1. Das ist richtig, gilt aber zunächst mal nur für diese Station.
2. Damit ist es nur ein Hinweis, wie groß die Unterschiede schon bei dieser gut gepflegten Station sind, gelten also zunächst mal nicht für andere Stationen, mit einer Einschränkung, er ist sehr wahrscheinlich für den Rest der Welt größer.
2. Um sie weltweit zu verwenden, bräuchten sie die Randbedingungen vorher und nachher, die Sie nicht haben. Das ist ja die Krux. Schauen Sie sich die HARRY Readme Dateien an.
4. Und weil das so ist addiert sich zu jeder Mittelwertbildung eben dieser Unsicherheit dazu.
„historischen, lücken- – und fehlerhaften Datensätze stecken mussten. Umso erstaunlicher ist die proklamierte Genauigkeit der Aussagen.“
Ja, aber was Sie da verknüpfen basiert nur auf emotionalen Eindrücken. Der mathematische Nachweis fehlt nach wie vor.
Was ist denn der korrespondierende Fehler, der sich aus dem Zitat dieses Harrys ergibt? Aus der Prosa müssen Sie einen Fehlerbeitrag bestimmen, sonst bleibt das Zitat nur eine emotionale und qualitativ wertlose Aussage.
Zudem lassen sich die Tagesmittelkorrekturen schon auf mit Unsicherheitsgrenzen auf vergangene Klimate und benachbarte Stationen anwenden (punkt 3 +4). Bedenken Sie, dass die Differenzen aus den täglichen Temperaturverläufen bedingt sind. Diese zeigen ein weitgehend stations- und zeitstationäres Spektrum. D.h. die Zusammenhänge bei Puchberg sind im Rahmen von meteorologisch plausibel abschätzbaren Genauigkeiten auch an anderen Stationen und zu vergangenen Zeiten anwendbar! Weltweit nicht, aber zumindest in der gleichen Klimazone. Aber neben der Station puchberg gibt es ja weltweit noch viel mehr, die eine solche Umrechnung historischen daten zulassen, es sind alle, die heute über mehrere Jahre stündlich und min max aufzeichnen, denn diese liefern automatisch auch ihre eigene Korrektur ihrer verschiedenen Tagesmittel nach 24 stunden methode gegen min+max/2 und Mannheimer Stunden.
1. Warum vermengen Sie eigentlich ständig die Themen? Die ganze Serie beschäftigt sich mit den Qualiätsmängeln historischen Temperaturdaten und Sie kommen mit den modernen 24 Stundenmessungen. Was soll das?
2. Sie spekulieren, dass sich die Tagesmittelkorrekturen auch auf vergangene Klimate anwenden lassen könnten, weil es neben Puchberg noch andere Stationen etc. etc. etc. gäbe.
Statt zu spekulieren, dass es so sein könnte, nennen Sie doch bitte Ross und Reiter und zitieren Belege, Quellen, papers wo das versucht wurde. Oder – wenn Sie denn schon keine finden – dann machen Sie es doch bitte selber, denn so schwer kann das ja nicht sein, wenn Sie Ihren eigenen Worten glauben.
Hallo Herr Limburg,
die historischen Daten kann man ja nur auf die neuen 24 Stunden methode umrechnen, indem man Zusammenhang zwischen den Ergebnissen der verschiedenen Methoden kennt. Den bekommt man aus den vornehmlich moderneren Daten, die Ergebnisse mit beiden Methoden zulassen. Dieser zusammenhang besteht auch für die historischen Daten (in meteorologisch plausibel abschätzbaren Grenzen)!
Aus der „Eichung“ des Umrechnungsmechanismus mit rezenten Daten erfolgt die Umrechnung der historischen Daten. Ist doch klar, anders geht es ja nicht!
Dass dieser zusammenhang grundsätzlich besteht, folgt daraus, dass das historische Wetter tägliche Temperaturverläufe hatte, die in der Form nicht grundsätzlich anders waren als heute. Und da die Unterschiede in den Tagesmittelmethoden nur bedingt sind durch das Spektrum der Tagesverläufe, sind die beobachtbaren Unterschiede ein (in meteorologisch plausibel bestimmbaren Grenzen) ein auch historisch zutreffendes Charakteristikum der Station und benachbarter Stationen. Ich gehe davon aus, daß Sie auch schon selbst festgestellt haben, daß dieser von ihnen genannte „Algorithmusfehler“ an verschiedenen Stationen vergleichbare Größe und Systematik hat und damit als „universelle“ Korrektur verwendet werden kann.
Dann machen Sie das bitte und wenn Sie fertig sind, dann melden Sie sich bitte.
Herr Petersen,
wenn ich sie richtig verstehe, denken sie das man mit den heutige 24 Stunden Daten, den Verlauf von historischen Aufzeichnungen eichen kann oder sollte.
Fuers Erstere haben sie das Problem klimatische Aenderungen von systematischen Fehlern zu Unterscheiden. Um den Fehler zu kennen, muessen sie also die klimatische Aenderung kennen. Diese wiederumg versuchen sie aus den Temperaturmessungen herrauszulesen.
Da beisst sich die Katze in den Schwanz. Aber sie sind jetzt schlauer. Endlich wissen sie wie die Klimafolgeforschung das Problem praktisch geloest hat.
Die geht naemlich davon aus, das CO2 fuer einen Temperaturanstieg verantwortlich ist. Damit sind alle Temperatursteigerungen in den historischen Daten erklaerbar und man kann davon ausgehen, das die Fehler unbedeutend und deshalb nicht interessant sind.
Ich denke sie sollten ihre Meinung auch bei der Klimafolgenforschung kund tun. Bitte berichten sie ueber die Antwort.
Ich bin ja berufsmäßig seit über 40 Jahren mit der Temperaturmessung als Hersteller bzw. durch Kalibrierungen „liiert“. Wenn ich daran denke, welche „Kopfstände“ nötig sind, ein DAkkS-Labor für Temperatur im betreffenden Temperaturbereich fit zu machen und zu halten, um 50 mK Unsicherheit bescheinigen zu dürfen oder als Hersteller die üblichen Fehlergrenzen der Sensoren glaubhaft seinen Kunden gegenüber nachzuweisen, dann muss man ganz einfach sagen, dass bei den betreffenden Leuten entscheidende Zusammenhänge völlig unklar sind bzw. Schule und Studium nicht nur kostenlos, sondern umsonst.
Die „alten“ meteorologischen Glasthermometer hatten meist eine 0,2 K – Teilung. Der halbwegs geübte Ableser schafft durchaus die 50 mK zu schätzen. Frühere Versuche in Eichämtern haben gezeigt, dass sehr gute Leute, deren Hauptaufgabe die Kalibrierung war, auch die Zwanzigstel zwischen den Teilstrichen reproduzierbar ablesen konnten (in unserem Fall 10 mK). Ich traue mir heute noch die Zehntel zwischen den Teilstrichen zu.
Das ist aber nur die Ablesung! Zu jedem Thermometer gab es einen Werkprüfschein, meist mit Korrekturangaben alle 10 Grad. Dabei durfte von Punkt zu Punkt nur eine bestimmte Änderung der Korrektur auftreten. Bevor also aus einer Ablesung eine Temperatur wird, sind gemäß der Kalibrierdaten Korrekturen anzubringen. Wie konsequent wurde das gemacht??? Wie wurden die Thermometer messtechnisch überwacht? Wurde z.B regelmäßig am Eispunkt gemessen, um Driften zu erkennen? Wurden die Einsatzfristen zwischen Nachkalibrierungen eingehalten? Wurde überhaupt nachkalibriert?
Für die heutigen elektrischen Fühler und die Folgetechnik trifft übrigens das gleiche „Primborium“ für die Richtighaltung und Rückführbarkeit zu! Nur weil der Mensch nicht mehr ablesen muß, wird es nicht automatisch genauer oder sicherer.
Aus meiner Erfahrung sind also für die üblichen meteorologischen Temperaturmessungen kaum bessere Messunsicherheiten als ± 1 K zu erwarten. Die Anomalienbildung sind tatsächlich nur mathematische Spielchen die aus messtechnischer Sicht verboten sind, wenn man daraus eine Verringerung von Fehlern erwartet.
Danke, Herr Tengler für dieses Lehrstück aus der praktischen Messtechnik. BG M.L.
Das Messen von Temperatur-Abweichungen soll ja nach der Potsdamer Lehre viel genauer sein als das Messen absoluter Größen!
Temperaturabweichungen entsprechend der Rahmstorfschen Hütte auf dem Berg kann man nicht messen. Ein Maßband kann man am Fundament der Hütte anlegen und von da aus die Hüttenhöhe bis zum Dachfirst bestimmen.
Es gibt kein Thermometer, dem man eine Temperatur aus der Vergangenheit beibringen kann, damit es dann nur die Differenz zur Gegenwart misst und anzeigt.
Das Hüttenbeispiel von Rahmstorf zeigt, mit welcher Hinterlist dieser Mann die Menschen hintergeht.
Absoluter Schwachsinn und eine Unmöglichkeit, Temperatur-Anomalien zu messen. Das sind reine Computerspiele, die aber unter Irrtumserregung als Messungen verkauft werden.
Und dieses Lügengebilde wird dann auch noch als angeblich besonders genau dargestellt. Schande über derartige sog. Wissenschaftler. Sie ziehen die seriöse Wissenschaft vorsätz-lich in den Dreck!
OBER-„RABULIST“ Rahmstorf zieht doch nur Strippen in einem politisch einge-„richteten“ SYSTEM – mal „Rabulistik“ auf Wiki lesen 😉
Hallo Herr Schulz,
„Fuers Erstere haben sie das Problem klimatische Aenderungen von systematischen Fehlern zu Unterscheiden.“
Hallo, hier geht es weder um klimatische Änderungen noch um systematische Fehler, sondern um die Umrechnung von historischen Daten auf eine einheitliche Methode des Tagesmittels, hier als 24 Stundenmittel. Die unterschiedlichen Tagesmittel sind ja nicht als systematischer Fehler gegenüber einer „Sollmethode“ zu sehen.
„Ich denke sie sollten ihre Meinung auch bei der Klimafolgenforschung kund tun. Bitte berichten sie ueber die Antwort.“
Was ich schreibe ist nicht neu, sondern wird in der Klimaforschung seit Beginn an praktiziert… Wenn es inzwischen vielfältige Verfahren in der Klimatologie bzw. Statistik dazu gibt.
Denken Sie aber nur mal, woher die Mannheimer Stunden kommen: Schon 1780 war den Meteorologen klar, dass man mit den drei Ablesezeitpunkten und der gewählten Gewichtung 1-1-2 eine praktikable Approximation für den (eigentlich gesuchten) Mittelwert der Tagestemperaturkurve bekommt. Integrieren von kontinuierlichen Messkurven über den Tag ging damals eben noch nicht. Also schuf man sich damit ein einfaches Regressionsverfahren zur näherungsweisen Bestimmung.
Heute ist es natürlich mit EDV ein Kinderspiel, das Tagesmittel per 3 oder n Ablesepunkten und Regression mit denselben besser zu approximieren.
Hallo Herr Limburg, die Aufgabe, Ihre beanstandeten Mängel in den Fehlerrechnungen von zitierten Klimawissenschaftlern auch tatsächlich zu quantifizieren, haben Sie selbst.
Ich versuche Ihnen nur klar zu machen, daß die Differenzen durch verschiedene Tagesmittelmethoden nicht als Fehler zu werten sind, wenn diese Differenzen durch Korrekturen („geeicht“ mit heutigen Daten) der historischen Daten reduziert werden. Ihr „Algorithmusfehler“ ist signifikant (aber freilich nicht perfekt) behebbar.
Sie machen nichts klar, Sie spekulieren.
Suchen Sie nach Literatur, die Ihre Spekulation beweist, oder machen Sie es selbst.
Sie werden feststellen, dass Sie nicht die Metadaten haben, die Ihnen sagen welche Verfahren wo, wann wie oft etc. eingesetzt. Und das ist nur ein systematischer Fehler von vielen, die sich im Nachhinein nicht mehr korrigieren lassen. D
as sagt z.B. -wenn ich es richtig in Erinnerung habe – Tom Karl oder Petersen, bei ihren durchaus ehrenwerten Versuchen diese Fehler zu definieren, ihre Größe und ihre Richtung für eine mögliche Kompensation zu bestimmen.
Hallo Herr Limburg,
gucken Sie mal in Tabelle 1 in A SIMPLE METHOD FOR ESTIMATING DAILY AND MONTHLY MEANTEMPERATURES FROM DAILY MINIMA AND MAXIMA
https://rmets.onlinelibrary.wiley.com/doi/pdf/10.1002/joc.1363
Die Autoren kommen an anderen Stationen zu ähnlichen Beziehungen zwischen den unterschiedlichen Tagesmittelmethoden wie Sie in E&E in Fig 2 und 3.
Ihr „Algorithmusfehler“ ist also (bedingt) behebbbar bzw. reduzierbar.
So ergibt sich das Monatmittel historischer Daten nach der heutigen 24 Stundenmethode aus den historisch verfügbaren Daten, die das Tagesmittel nach = das (Tmax+Tmin)/2 berechnet haben als
Monatsmittel (24 Std) = Monatsmittel (Min-Max) minus 0,24-0,3 K
(siehe Ihre Fig 3 und im obigen paper Tabelle 1 bias bei Tavg.).
Der „Algorithmusfehler“ ist dann von 0,3 K auf 0,05 K (Unsicherheit der Umrechnung zwischen 0,24 und 0,3 K) oder so reduziert worden.
Ähnlich die Umrechnung Mannheimer Stunden etc.
Dazu benötigt man keine Metadaten, denn wie und wo die Station die historischen Daten gemessen hat, ist unwichtig, man rechnet nur die Temperaturmittel nach damaliger Methode auf die heutige Methode am originalen Standort um.
Bei Anomalien entfällt der „Algorithmusfehler“ sowieso, denn da interessieren konstante Differenzen ja eh nicht.
1. Bitte und zum letzten Mal, zeigen Sie Arbeiten, bei denen die lokalen Temperaturdaten für die weltweite Verdichtung, nach Ihren Ideen korrigiert wurden.
2. Sie haben meinen Beitrag zu den Zeitreihen aus Anomalien nicht gelesen oder verstanden.Konstante Fehler fallen nur raus, wenn sie vor Beginn der Messreihe entstanden sind. Das gilt aber nicht für die angewendeten Algorithmen, die wurden oft mitten drin geändert. Und das müssen Sie wissen, sonst klappt das nicht.
Hallo Herr Limburg,
nur um Missverständnisse zu vermeiden:
mir ist klar, dass viele historische Temperaturreihen schlecht dokumentiert sind und einen Haufen Probleme bereiten, wenn man daraus Informationen zum Temperaturverlauf er Vergangenheit gewinnen möchte. Aus diesem Grund ist der Fehlerbereich um die globale Anomalie dort auch größer als heute.
Natürlich ist es klar, dass ein nicht dokumentierter Wechsel in der Tagesmittel-Methode eine Inhomogenität in der Reihe erzeugt und es historische Reihen gibt, die man nicht mehr auf Tagesmittel der absoluten Temperatur nach der 24 Stunden Methode korrigieren kann, weil nicht klar ist, nach welcher Methode damals die Tagesmittel berechnet wurden. Aber es gibt eben auch überlieferte Reihen, mit denen man das kann.
Die ganze Diskussion um die Reduzierung des „Algorithmusfehlers“ entfällt allerdings, wenn man sowieso nur Anomalien betrachtet. Gerade deswegen
sind Anomalien auch vergleichbarer als absolute Reihen, denn egal welche Tagesmittelmethode Sie nehmen: die Reihen zeigen den selben Trend! Immer natürlich vorausgesetzt, dass die Reihe homogen ist. Aber das ist ein anderes Thema.
zu Ihrer 1.: Ich kenne keine Veröffentlichung, die nun Monatsmittel nach verschiedenen Tagesmittelmethoden umrechnet. Das liegt wohl daran, dass die meisten eben gleich nur Anomalien betrachten, wo ein konstanter bias keine Rolle spielt.
Wenn Sie allerdings absolute Temperaturreihen haben wollen – das war ja Ihre Anfrage, müssen Sie dies betrachten.
Mich alleine interessiert, aus welcher Fehlerrechnung nun herauskommt, dass das Fehlerband der globalen Temperaturanomalie heute (schmal) wie historisch (breiter) von HADLEY, GISS, WMO etc. zu gering wäre. Es gibt meines Wissens keine konkrete Berechnung dazu, die auf ein anderes Resultat käme. In Ihren verlinkten papern betrachten Sie ja nur Teilbeiträge der Fehler aber die Integration in einen daraus resultierenden Fehler in der globalen Anomalie fehlt.
Sie wollen oder sie können es nicht begreifen.
Es geht um die Fehlerfortpflanzung.
Die Fehler (es geht hier vor allem um systematische Fehler) verschwinden eben nicht, wenn man aus den Werten, egal welchen Anomalien bildet, sondern bleiben da, addieren sich mit der berühmten Quadratwurzel aus der Summe Ihrer Quadrate, und haben ein um ein bis zwei Größenordnungen höheres Gewicht als vorher.
Es sei denn, Sie hätten sie zuvor einzeln oder als Gruppe sauber isoliert, ihre Größe und Richtung und die Zeit wann und wie lange sie aufgetreten sind, bestimmt und sie dann gegen gerechnet – also korrigiert.
Das ist aber nur in wenigen Sonderfällen geschehen. Die Gründe sind nachvollziehbar, aber tun eigentlich nichts zur Sache. Beim weitaus größten Teil der Daten ist das eben nicht geschehen.
In jeder anderen naturwissenschaftlichen Disziplin nimmt man diese Situation zur Kenntnis und umhüllt dann die Anomalie oder die Zeitreihe davon, mit einem Unsicherheitsband, das die Größe der Fehler wiedergibt. Nur in der „Klimaforschung“ passiert das nicht. Stattdessen weicht man auf Wahrscheinlichkeitsbetrachtungen aus, und bestimmt irgendwelche Sigmawerte. Das ist aber ein ganz anderer Ponyhof.
Natürlich kann man versuchen Vergleichsmessungen und deren Ergebnisse auf frühere Daten übertragen. Das wird aber ganz selten so gemacht. Wenn Sie also wollen dann machen Sie das bitte. Es genügt ein moderner Computer, ein bisschen Programmierpraxis, eine Menge Know How und viel, viel Zeit. Nur zu!
Wenn Sie damit fertig sind kommen Sie wieder. Und wenn dann alles stimmt, was Sie so herausgefunden haben, dann kriegen Sie einen Orden.
Meine Aufgabe und auch die Dissertation war, diese Mängel herauszuarbeiten, sie zu quantifizieren sowie eine grobe Abschätzung zu erstellen, über die Mindestgröße. Die finden Sie dort, ebenso wie in meinem Vortrag. Meine Aufgabe war nicht, diese Aufgabe den Klimaforschern abzunehmen, dazu gab es weder die Möglichkeit, noch die Notwendigkeit.
Das ist mein letzter Wort in dieser Angelegenheit.
„Meine Aufgabe und auch die Dissertation war, diese Mängel herauszuarbeiten, sie zu quantifizieren sowie eine grobe Abschätzung zu erstellen, über die Mindestgröße.“
Das war doch die Dissertation, mit der Sie durchgefallen sind.
Mir scheint, Sie werden nie begreifen, wo Ihre Fehler lagen.
Sie sind zwar unwissend oder bewusst lügend, aber pampig. Passt zusammen.
Wahr ist, dass die Universität die Ablehnung meiner Dissertation zurück genommen hat, und sich für Ihr Verhalten mir gegenüber, bzw. dem ihrer Gremien entschuldigen musste.
M.L.
Danke (auch an G. Wedekind), das ist aufschlussreich. Daraus folgt, dass auch nicht-adjustierte und Wärmeinsel-ferne Landmessdaten, die es in den USA von Messstationen an z.T. entlegenen Standorten gibt, nicht viel mehr leisten können. Gewisse Fehler bleiben und alle 15 Minuten wird dort aufgrund der entlegenen Standorte mit Sicherheit nicht gemessen. Wohl eher wird die ein oder andere Messung ausfallen…
Wieder einmal wird klar, auf welch „soliden“ Beinen diese „Klimaforschung“ steht. Hinzu kommen deren höchst fragwürdige Klimamodelle samt ewig falscher und übertriebener Alarmprognosen – KlimaGate und Mann’schem Hockey Stick-Betrug vervollständigen das ziemlich unerfreuliche Bild! Doch die Klimakatastrophen-Hörigen schlucken alles, was diese Alarmisten-Truppe produziert – mit Ratio hat das nichts mehr zu tun.
Hallo,
Fehler wie in den Abbildungen 8 bis 10 sind ja nicht auszuschließen. Bevor Klimadaten weiterverarbeitet werden sie daher auf Homogenität geprüft. Die Verfahren sind bekannt. Wieso sollten die Autoren, die damit globale Mitteltemperaturen berechnen, das nicht wissen? Es ist anzunehmen, daß die nur homogenisierte Reihen verarbeiten bzw. die Homogenisierung selbst vornehmen.
Ihre Annahme trügt leider. Lesen Sie bitte die angegebene Literatur. Hier finden Sie noch viel mehr, https://www.eike-klima-energie.eu/publikationen/michael-limburg/.
Admin schrieb am 30. April 2020 um 12:56:
Eine oberflächliche Suche nach entsprechender Literatur liefert schnell z.B. den in Teil 1 von mir verlinkten Artikel zur paarweisen Homogenisierung in GHCN oder zum Artikel: „Homogenization of Temperature Data – An Assessment“ in dem steht:
Das deckt sich mit der Anmerkung von Sverre Petersen. Die Bildung von Anomalien soll die in Abbildung 8 bis 10 dargestellten Fehler nicht beseitigen. Dass die das nicht können, damit haben sie recht. Dafür werden andere Methoden angewendet.
1. Welche?
2. Bitte Quellen zu den RAW Data. Keine Meinungen.
Hallo Herr Müller,
die Antwort vom admin (Hr. Limburg?) ist in der Tat widersprüchlich. Der link dort führt u.a. zur Diss. Limburg. Dort wird klar zitiert:
Dissertation_5-4-2bLit_01.pdf
S.15, Fußnote 17
Das wird auch in Zukunft schwierig bleiben, denn das für die Originaldatensätze verantwortliche britische Hadley Center schrieb kürzlich in einer mail (http://rogerpielkejr.blogspot.com/2009/08/we-lost-original-data.html ) an Prof. R. Pielke (12.8.09). „We are not in a position to supply data for a particular country not covered by the example agreements referred to earlier, as we have never had sufficient resources to keep track of the exact source of each individual monthly value. Since the 1980s, we have merged the data we have received into existing series or begun new ones, so it is impossible to say if all stations within a particular country or if all of an individual record should be freely available. Data storage availability in the 1980s meant that we were not able to keep the multiple sources for some sites, only the station series after adjustment for homogeneity issues. We, therefore, do not hold the original raw data but only the value-added (i.e. quality controlled and homogenized) data.“ Mit anderen Worten, die Originaldatensätze sind verschwunden und somit der Forschung nicht mehr zugänglich
Und S. 44
Bewertung der amerikanischen Messstationen auf S. 2845 „…One thousand two hundred twenty-one homogeneity adjusted stations in the United States were computed using a different technique. These are high quality rural stations taken directly from the U.S. Historical Climatology Network (U.S. HCN; Easterling et al.1996a), a sister project to GHCN. These data were adjusted using a metadata approach as part of the creation of the U.S. HCN and their adjusted time series were directly incorporated into GHCN. For climate analysis confined to the United States, the U.S. HCN is the preferred dataset because its stations are well distributed, mostly rural stations that were selected based upon their location and their station history metadata.“ (Hervorhebungen vom Autor)
Hier steht doch, daß z.B. das Hadley Center quality controlled and homogenized Temperatur-Datensätze verwendet. Und Stationsdaten im das GHCN sind auch homogeneity adjusted.
Dann noch Tabelle S. 70
1 Fehlerbenennung: Instrumentenfehler 0,1 – 0,2 °C, Maßnahme zur Fehlerbewertung: Keine, von gelegentlichen Ausnahmen abgesehen
2 Fehlerbenennung: Ungleiche, nicht regelkonforme Aufstellung von Wetterhütten, veränderte Landnutzung, UHI 1-5 °C Maßnahme zur Fehlerbewertung: Wenige bekannt, sehr aufwendige Homogenisierung, Metadaten w.w. kaum bekannt, Pauschale Korrekturen im 0,1°C Bereich
Auch in seiner Tabelle gibt er zu, dass Homogenisieren eine Methode der Klimaforscher ist.
Dann noch S. 29
Zusätzlich muss die Homogenität, der Messungen gesichert sein. Homogenisierung bedeutet, die Messungen müssen von nicht-klima bestimmten Einflüssen bereinigt sein, und die Messverfahren und -regime müssen für die Vergleichszeiten und -flächen standardisiert sein. All diese Voraussetzungen waren aber in frühen historischen
Phasen nicht gegeben, die erzielbare Messgenauigkeit betrug lt. Schönwiese damals nur ca. 1° C.
Also wieder die Bestätigung, daß homogenisiert wird. Wo Schönwiese das schreibt und ob sich dieses Zitat auf die Behauptung anwenden läßt, läßt sich nicht prüfen, denn die genaue Quelle wird nicht genannt.
Auch Limburg muss daher davon ausgehen, daß die Klimaleute homogenisierte Reihen verarbeiten bzw. die Homogenisierung selbst vornehmen und daher die in den Abbildungen skizzierten Fehler den Klimatologen sowohl bekannt sind und durch Datenaufbereitung gerade eliminiert werden sollen.
Das hat doch niemand bestritten. Nur muss man die ganze Geschichte kennen, die Homogenisierung ist der verständliche aber verzweifelte Versuch, Fehler, die in den Nachbarstationen mit Sicherheit vorgekommen sind, auf Verdacht zu kompensieren.
Auch nach Bekanntwerden der Watt´schen Ergebnisse hat die US Wetterbehörde versucht, die offensichtlichen Fehler per Homogenisierung zu mindern, bzw. auszumerzen. Das ging aber meistens schief, weil sie die Vergleichsdaten gar nicht haben.
Sie sollten sich mit dieser Frage ausführlicher beschäftigen.
Mit freundlichen Grüßen
M.L.
Hallo Herr Limburg,
also Sie meinen, Homogenisierung ist notwendig, kann aber nicht mit der notwendigen Genauigkeit erreicht werden, um in eine Fehlerangabe von wenigen Zehntel Grad bei der globalen Temperaturanomalie zu resultieren?
Aber wo ist diese Rechnung, der Beweis?
Die von Ihnen beschriebenen Fehlerquellen sind ja Klimaleuten bekannt. Statt also Bekanntes ausführlich zu beschrieben und mit ausgewählten Einzelzitaten zu schmücken, sollten Sie mal lieber Ihre Entdeckung darlegen, und mathematisch beweisen, warum die Fehlerangaben falsch sind. All diese Leute geben in ihren papern Fehlerquellen an, Sie zitieren die ja. Aber es fehlt bei Ihren Ausführungen der Beweis, daß die Leute trotz quantitativer Angaben zu Fehlerquellen und der Angabe eines resultierenden Fehler die Fehlerrechnung falsch machten.
Dazu müsssen Sie die Prozess der Datenverarbeitung der Temperaturreihen wie ihn Brohan, Jones, Hansen und andere gemacht haben, selbst im Detail nachvollziehen und zeigen, an welchen Stellen genau diese etwas falsch machten.
Es nützt aber nichts, dass den Klimaleuten die Fehlerquellen bekannt sind, wie Sie schreiben, was sie im übrigen in fast allen Fällen nur dem Typ nach sind. Denn sie kennen oft nicht die wirkliche Art, die Größe und die Richtung dieser Fehler. Und haben auch keinerlei Chancen diese bei den historischen Daten nachträglich zu bestimmen. Dazu fehlen so gut wie sämtliche Metadaten.
Und genau das ist ja das Problem. Den Text aus HARRY READ.Me haben Sie offensichtlich nicht gelesen, oder nicht zur Kenntnis genommen.
Und genau deswegen wurde ja die Homogenisierung erfunden.
Sie können sich gerne die umfangreiche Beweisführung in meiner Dissertationsschrift z.b. ab S 141 anschauen. Vorab nur eine Fußnote daraus.
Zum Thema der Homogenisierung: Aus „Klimarekonstruktion der instrumentellen Periode – Probleme und Lösungen für den Großraum Alpen“ Reinhard Böhm Zentralanstalt für Meteorologie und Geodynamik, Wien S. 6 ….Problem, an dem alle entsprechenden mathematisch-statistischen Methoden leiden, die ja in ihrem Kern auf demselben Grundprinzip beruhen: Man berechnet Differenz- oder Quotientenreihen hochkorrelierter Nachbarreihen, testet sie auf abrupte Sprünge, die statistisch signifikant sind, und eliminiert diese unter der Annahme der angenommenen zeitlichen Stationarität der Differenzen (Quotienten). Da üblicherweise alle Reihen irgendwann nicht- klimatologische Sprünge haben, gilt es noch das Problem der Zuordnung zu lösen, welche der Reihen die infizierten und welche die Referenzreihen für ein betrachtetes Subintervall mit einer Sprungstelle sind. Das kann man mit statistischen Wahrscheinlichkeitsüberlegungen abklären, indem man in regionalen Subgruppen von typischerweise 10 Reihen alle Reihen mit allen anderen testet. Die sich ergebende Entscheidungsmatrix (typischerweise 10*10) liefert dann recht eindeutige Ergebnisse, wenn die Sprünge nicht alle zur selben (ähnlichen) Zeit erfolgen.
Und Seite (12)- 156: Das oft gehörte Argument, dass bei Verwendung genügend vieler Einzelreihen die Inhomogenitäten in der Mittelreihe als „random effect“ verschwinden würden, ist nicht zutreffend. Es gibt sehr wohl systematische Inhomogenitäten, die auch größere Gebiete betreffen“
Und dazu muss man wissen, dass das Projekt „Histalp“ über die Klimaentwicklung der Alpen ein höchst anspruchsvolles, aufwendiges, langfristiges und teures Projekt war, dass nur in wirklich gut bestückten Regionen, die perfekt gewartete Stationen aufwiesen, durchgeführt werden konnten. Unmöglich – wie HARRY das so verzweifelt beschreibt- das nachträglich für die restliche Welt durchzuführen.
Das gilt auch für den „Goldstandard“ USA
Zitat aus meiner Fehlertabelle S 137 (und das ist nur eines von mehreren Beispielen)
siehe NOAA CRN Class 2 same as Class 1 with the following differences. Surrounding vegetation less than 25 centimeters. Artificial leating soure es within 30 meters. No shading for a SUfi elevation greater than 5°.Referenz US
Fehlerart Grob, Systematisch Selten berücksichtigt, Homogenisierung aufwendig, lücken- und fehlerhaft. S. Beispiele D ́aleo Central Park New York [D’Aleo, 2008 #18863]
Herr Petersen,
Das es Homogenisierung der Daten gibt ist bekannt. Wie wirksam diese ist, sei eine andere Frage. Oder auch wofür man diese nutzen kann.
Hier ein kleines Praxisbeispiel in Englisch. Da sie auch in Englisch zitieren lasse ich das mal so stehen:
https://ipa.org.au/publications-ipa/bureau-cooling-the-past-to-declare-record-heat
Es geht um die ACORN-SAT version 2, Temperatur Database und entsprechende „Homogenisierungen“.
Vielleicht interessant dann auch dieser Artikel:
https://jennifermarohasy.com/2019/02/changes-to-darwins-climate-history-are-not-logical/
Man muss leider aufmerksam verfolgen was wirklich passiert.
Das Herr Rahmstorf unrecht hat kann man mit diesem Absatz feststellen:
„Das Zitat oben von Stefan Rahmstorf am 12.2.18[1] ist ein Beispiel zur Behauptung warum Anomalien genauer sind als die ihnen zugrunde liegenden Absolutwerte. Er hat bis heute nicht begriffen, dass er in diesem Beispiel Absolutwerte misst und diese als Anomalien ausgibt. Klimaanomalien werden jedoch nicht gemessen, sondern aus den Absolutwerten mit all ihren Fehlern berechnet. „
Sehr geehrter Herr Limburg
Ich stimme Ihnen voll zu.
Die behautptete Genauigkeit in der Globaltemperaturmessung von +-0.05 Grad C entspricht der A b l e s e g e n a u i g k e i t von guten Thermometern in der Meteorologie (siehe Hupfer e.a. „Witterung und Klima, Eine Einführung in die Meteorologie und Klimatologie“). Diese Temperatur in der Meßhütte hat aber zunächst nichts mit der „klimatisch relevanten“ Außentemperatur zu tun.
Am problematischsten sind natürlich die Änderungen in der Umgebung der Meßstelle, und hier besonders der Stadtinseleffekt (UHI), der auch noch eine logarithmischer Abhängigkeit von der Einwohnerzahl hat. Demnach sind besonders kleine wachsende Städte kritisch.
Nimmt man eine typische Formel (nach Hupfer z.B. die „Kanadische Formel“, u=3.5 m/s), dann ist für eine Zunahme der Einwohnerzahl von 10000 der maximale UHI-Effekt:
– in einer Kleinstadt von 10000 Einwohnern 0.58 Grad C
– und bei einer Großstadt von 100 000 Einwohnern für die selbe Zunahme 0.08 Grad C.
Ein mittlerer UHI_Effekt kann mit etwa einem Drittel dieses Wertes abgeschätzt werden.
Ausgerechnet die kleinen Städte, die meistens noch als ländlich „rural“ angesehen werden, zeigen also bei ihrem Wachstum die größten UHI-Effekte.
Die Definition von „rural“ von Phil Jones e.a in in seinem Artikel „Assessment of urbanisation effects in time series of surface air temperatures over Land“, auf den sich das IPCC bezieht, ist völlig daneben. Als schlimmstes Beispiel sind hier nur die chinesischen Städte angegeben:
„Eastern China: Rural < 0.1 million (after statistics 1984)."
– sind 0.1 Million Einwohner wirklich noch "rural"??
– und wie stark sind gerade in China diese Städte seit 1984 gewachsen?
Man kann nur festhalten: Seine Behauptung ebenda "It is unlikely, that … could increase the overall urban bias above 0.050C during the twentieth century." ist geradezu abenteuerlich!
Fazit ist, daß gerade bei den Bodenmessungen die nichtklimatischen Einflüsse unmöglich herauszukorrigieren sind, und daß sie für Klimaanalysen genaugenommen nicht taugen. Am besten läßt man die Finger davon.
MfG
G.Wedekind