Der sogenannte „natürliche atmosphärische Treibhauseffekt“ ist die Basis aller Befürchtungen über eine menschengemachte Klimakatastrophe, weil dieser sich durch den technischen CO<sub>2</sub>-Ausstoß der Menschheit angeblich noch weiter verstärken und zu einer globalen Selbstverbrennung führen soll. Für einen solchen „natürlichen atmosphärischen Treibhauseffekt“ gibt es unterschiedliche Modelle, einen experimentellen Ansatz und zwei Widerlegungen. In Teil 1 wurden die unterschiedlichen Thesen/Antithesen vorgestellt, die nachfolgend einzeln diskutiert werden.
MEINE ARGUMENTATION zu THESE (1):
Der Ansatz (1) ist grundlegend FALSCH, weil er über eine Gleichsetzung von Tag und Nacht die STRENGE PHYSIKALISCHE GLEICHZEITIGKEIT im Stefan-Boltzmann-Gesetz verletzt. Mit der Solarkonstanten (S0=1367 W/m²), der Erdalbedo (ALPHA=0,3) und der temperaturwirksamen Strahlungsleistung (Seff = S0*(1-ALPHA) = 940 W/m²) ergibt sich für die Netto-Strahlungsbilanz der Erde:
(IN = 940 W/m² * π R2) = (OUT = 235 W/m² * 4 π R2) @ NST (= 14,8 °C)
Das bedeutet, die Temperaturgenese der Erde erfolgt ausschließlich auf ihrer Tagseite mit (940 W/m² * cos Phi), und die Abstrahlung erfolgt mit durchschnittlich 235 W/m² über ihre gesamte Oberfläche. Und das alles geschieht im Strahlungsgleichgewicht der Klimadefinition (>30 Jahre) bei einer vorgeblich „gemessenen“ konstanten Globaltemperatur NST, in deren Berechnung bereits die tatsächlich gemessene Nachttemperatur eingegangen ist.
Ansatz (1) ignoriert den Unterschied zwischen Tag und Nacht und setzt einfach den Wert für die durchschnittliche globale Abstrahlung in das Stefan-Boltzmann-Gesetz ein. Durch diese globale Mittelung wird aber die temperaturwirksame spezifische Flächenleistung der solaren Einstrahlung verfälscht. Und die daraus abgeleitete „natürliche“ Temperatur der Erde von minus 18°C erfordert wiederum einen „natürlichen atmosphärischen Treibhauseffekt“ von 33°C, um die Differenz zur vorgeblich gemessenen Globaltemperatur NST zu erklären.
Selbst in der Ableitung einer Strahlungstransfergleichung wird unter impliziter Einbeziehung einer Nachttemperatur von minus 273°C die vorgebliche „S-B Gleichgewichtstemperatur“ (Teq = -18°C) als globale Mittelung der temperaturwirksamen solaren Einstrahlung über die gesamte Erdoberfläche benutzt. Und damit führt dieser Ansatz rekursiv auf seine eigene Randbedingung einer globalen „Faktor4-Mittelung“ zurück.
Vielmehr kann man sich physikalischen Randbedingungen des Stefan-Boltzmann-Gesetzes auch so vorstellen, dass die die Temperaturgenese auf unserer Erde ausschließlich dort erfolgt, wo Strahlung GLEICHZEITIG Temperatur erzeugen kann. Bei einer Betrachtung der Temperaturgenese muss man sich also auf die tatsächlich beleuchtete Tagseite unserer Erde beschränken.
BEWEISFÜHRUNG zu (1.1) – Die Erde wird als ein selbstleuchtender Stern betrachtet (Dietze):
Für einen selbst leuchtenden Stern kann man tatsächlich eine S-B-Inversion durchführen, beispielsweise für die Sonne, indem man die spezifische Strahlungsdichte (Solarkonstante) vom Erdbahnradius auf die Oberfläche der Sonne zurückrechnet und darauf das S-B-Gesetz anwendet; dabei bleibt die spezifische Strahlungsleistung auf den jeweils betrachteten Flächen zeitgleich konstant.
Die Erde ist aber kein selbst leuchtender Stern, bei dem man die einfallende Strahlungsleistung der Sonne über die gesamte Oberfläche mitteln könnte; dazu bräuchte es nach These (1.1) vielmehr zwei Sonnen mit halber Strahlkraft, jeweils eine auf der Tagseite und eine auf der Nachtseite der Erde. Denn die Temperaturgenese findet ausschließlich auf der solar bestrahlten Seite der Erde statt, und zwar tageszeit-, breiten- und jahreszeitabhängig. Die Einbeziehung der Nachtseite der Erde in eine Berechnung mit dem Stefan-Boltzmann-Gesetz ist damit physikalisch naiv und hat dieselbe Relevanz wie eine Einbeziehung der Fläche des Experimentiertischs in die Ergebnisrechnung des Stefan-Boltzmann-Experiments – solche unbeleuchteten Flächen haben mit dem S-B-Gesetz nämlich überhaupt nichts zu tun.
BEWEISFÜHRUNG zu (1.2.1) – Die Klimawirksamkeit von Treibhausgasen (Krüger):
TREIBHAUSGASE: Den sogenannten „Treibhausgasen“ (THG), hauptsächlich Wasserdampf, Kohlenstoffdioxid und Methan, wird vom IPCC eine aktive Temperaturwirksamkeit in [W/m²] zugemessen. Diese Zuordnung ist aber grundsätzlich falsch, weil solche Gase keine aktive Strahlungsquelle darstellen. IR-aktive Gase absorbieren zwar passiv Infrarotstrahlung, können eine solche Strahlung aber ohne externe Quelle gar nicht aus eigener Kraft erzeugen. Es handelt sich vielmehr um eine Art „energetischen Staffellauf“ – und damit entfällt auch ein zusätzlicher energetischer Beitrag dieser THG zum sogenannten Treibhauseffekt.
SATELLITENMESSUNGEN: Der Beweis eines atmosphärischen Treibhauseffektes durch Satellitendaten besteht lediglich aus einem VERGLEICH zwischen der theoretischen IR-Abstrahlung der Erde und den vorgeblich von Satelliten „gemessenen“ Spektren, denen ganz erhebliche Rechenprozesse hinterlegt zu sein scheinen: Die veröffentlichten NIMBUS-IR-Spektren überdecken einen deutlich größeren Wellenlängenbereich, als es die dort gemessenen IR-Intervalle hergeben (Fußnote *1). Und beim AERI-Spektrometer werden offenbar lediglich Interferenzsignale für konkrete IR-Intervalle gemessen und über eine Fourier-Transformation spektral analysiert. Daraus wird dann anscheinend im Abgleich mit Vergleichs-Schwarzkörpern ein IR-Gesamtspektrum berechnet (Fußnote *2).
Das abschließende KO-Kriterium für die These (1.2.1): Das vorgelegte IR- Beweisspektrum für diese These zeigt eindeutig globale rechnerische Mittelwerte aus dem konventionellen S-B-Ansatz und stellt daher keine beweiskräftigen Messerwerte dar. Vielmehr bedeutet die exakte Einhaltung der durchschnittlichen THE-Eckwerte (240+150=390) W/m² in dem vorliegenden IR-Spektrum ein eindeutiges KO-Kriterium für die These (1.2.1).
Bei dem IR-Spektrum@70km handelt es sich nicht etwa um echte IR-Messwerte, sondern um ein wohlmeinendes handwerkliches Zirkelkonstrukt. Dieses konstruierte F-Wort-Spektrum kann keinerlei eigene Beweiskraft für einen „natürlichen atmosphärischen Treibhauseffekt“ entwickeln, weil es nämlich umgekehrt rein rechnerisch aus dieser THE-Hypothese abgeleitet worden ist.
Fußnoten zu den „gemessenen“ IR-Spektren (bei tieferem Interesse sei der Google-Übersetzer empfohlen):
*1) Das Nimbus 3 Satellite Infrared Spectrometer (SIRS) misst laut NASA 8 Intervalle, Zitat: „… in seven spectral intervals in the carbon dioxide band (11 to 15 micrometers) and one interval in the atmospheric window centered at 11.1 micrometers“.
*2) Nach dem AERI Handbook scheint es bei solchen Messungen eine Art vergleichendes Dataprocessing zu geben, Zitat mit Hervorhebungen (7.3.1 Theory): „Two blackbody sources, one at ambient temperature and the other at 330K are used to calibrate the instrument. The two sources are used to determine the slope and offset, which define the linear instrument response at each wavenumber. (see reference 1) The AERI views these two blackbodies every two minutes. Magnitude of the difference between these blackbody spectra is then formed to compute the responsivity and offset for the instrument.“
BEWEISFÜHRUNG zu (1.2.2) – Experimenteller Nachweis des „natürlichen atmosphärischen Treibhauseffektes“ (Schnell):
Kernaussage (1.2.2-1): Mit Bezug auf eine abgewandelte Umgebungsgleichung des Stefan-Boltzmann-Gesetzes wird hier der Umgebungstemperatur T0 eine „Gegenstrahlung“ zugeschrieben. Aber anders als beim Stefan-Boltzmann-Gesetz, das eine Umgebung von 0 Kelvin voraussetzt, strahlt ein Schwarzer Körper (T) in einer erwärmten Umgebung (T0) lediglich mit einer verminderten Leistung nach der S-B Umgebungsgleichung DELTA S (=P/A) = SIGMA (T4 – T04). Es handelt sich hierbei physikalisch also eindeutig um eine verminderte Abstrahlung des Schwarzen Körpers und nicht um eine „Gegenstrahlung“ seiner Umgebung.
Die Verminderung der Strahlungsleistung eines Schwarzen Körpers mit (T) in einer Umgebung von (T0>0K) stellt also keinerlei physikalischen Beweis für eine „Gegenstrahlung“ dar, sondern folgt lediglich den bekannten physikalischen Gesetzen.
Kernaussage (1.2.2-2): Um welchen Effekt es sich bei der von Dr. Schnell experimentell festgestellten Temperaturwirkung von CO2 handeln könnte, vermag der Autor nicht zu beurteilen.
Nach den HS der Thermodynamik muss die erforderliche Energie jedenfalls irgendwo herkommen, denn das CO2-Molekül ist nicht in der Lage, aus sich selbst heraus Energie zu erzeugen.
BEWEISFÜHRUNG zu (1.3) – Variable Abstrahlungshöhe der Erde (Heller):
Die „atmosphärische Rückstrahlung“ soll angeblich die Erdoberfläche mit zusätzlich 150 [W/m²] erwärmen, ein kälterer Körper (240 W/m²) erwärmt also fortlaufend einen wärmeren (390 W/m²). Für These (1.3) liegen verschiedene Konformitätsbehauptungen mit den HS der Thermodynamik vor.
Diese Gegenstrahlung bedient sich exakt der konventionellen Stefan-Boltzmann Herleitung von (240 W/m² entspricht -18°C) und (390 W/m² entspricht 15°C) mit einer Temperaturdifferenz von 33 Grad. Aber die Hauptsätze der Thermodynamik schließen ein Perpetuum Mobile jeglicher Art grundsätzlich aus, da hilft auch die Hilfskonstruktion einer „variablen Emissionshöhe“ nicht weiter.
Weiterhin entkoppelt sich das Modell einer „variablen Emissionshöhe“ ausgerechnet von der globalen Durchschnittstemperatur, der es eine grundsätzliche globale Abstrahlung bei minus 18°C entgegensetzt, ohne deren zwingende Relevanz nachgewiesen zu haben. Die „variable Emissionshöhe“ bei minus 18°C stellt damit lediglich eine Rekursion auf den konventionellen S-B-Ansatz selbst dar. Und durch eine „vollautomatische“ Anpassung der Emissionshöhe „deckelt“ dieses Modell alle inneren Widersprüche des konventionellen S-B-Ansatzes (1).
Insbesondere sperrt dieses Modell die tatsächliche Temperaturgenese auf der Tagseite unserer Erde und die nachgewiesenen paläoklimatischen Temperaturschwankungen aus seiner Betrachtung aus.
Umgekehrt wird allerdings ein Schuh daraus: Wenn der gesamte „Körper ERDE“ in der hohen Atmosphäre bei minus 18°C mit 235 W/m² in den Weltraum abstrahlt, dann entspricht die vorgeblich durchschnittlich 14,8°C warme Erdoberfläche zunächst einem S-B-Strahlungsäquivalent von 390 W/m². Gegenüber der hohen Atmosphäre mit minus 18°C ergibt sich damit nach der Umgebungsgleichung des S-B-Gesetzes [Delta S = Sigma * (T4-T04)] aber ein Delta-Wärmefluss vom Wärmeren (Erdoberfläche) zum Kälteren (hohe Atmosphäre) von lediglich 155 W/m²:
(@NST = 14,8°C&390W/m²) 155 W/m² => (@T@70 = -18°C&235W/m²) 235 W/m² => Weltraum
Damit folgt die bekannte Differenz von [Delta S = 155 W/m²] exakt den HS der Thermodynamik und hat gar nichts mit einem „Treibhauseffekt“ oder einer „Gegenstrahlung“ zu tun, sondern ist allein den jeweils behaupteten Ortstemperaturen (T=14,8 °C) und (T0 = -18°C) geschuldet.
MEINE ARGUMENTATION zu THESE (2) – Breitenabhängige Mittelung der solaren Einstrahlung über Tag und Nacht (Kramm et al.):
Dieser Ansatz ist zwar „etwas anders“ als (1), aber auch NICHT richtig. Denn er verletzt durch eine breitenabhängige globale Mittelung ebenfalls die die STRENGE PHYSIKALISCHE GLEICHZEITIGKEIT im Stefan-Boltzmann-Gesetz.
BEWEISFÜHRUNG (2.1): Eigenartig ist, dass Kramm et al (2017) hier mit einem dünnen „Multilayer“ als Modell für unseren „Wasserplaneten“ Erde arbeiten. Diese (begrenzte) Slab-Speicherung bewirkt nämlich lediglich eine leicht verzögerte Abstrahlung, die sich vordergründig allerdings erheblich auf die Ortstemperatur auswirkt, weil die ersten 2 W/m² im S-B-Gesetz bereits ein Temperaturäquivalent von ca. 70 Kelvin liefern.
Aber allein die in den OZEANEN gespeicherte Energie (=Arbeit=Leistung*Zeit) entspricht einer Abstrahlungsleistung unserer Erde von etwa 120 JAHREN bei (IN=OUT@NST). Ein konservativer Vergleich des Wärmeinhalts der Ozeane mit der täglichen und jährlich global eingestrahlten Sonnenenergie zeigt, dass deren Einfluss auf die globale Temperaturgenese nicht vernachlässigt werden darf:
(Tag = 1,05*10^22 Joule) << (Jahr = 3,85*10^24 Joule) << (Ozeane > 4,59*10^26 Joule)
Die Ozeane enthalten also ein Energieäquivalent von etwa 50.000 Tagen Sonneneinstrahlung oder 100.000-mal die notwendige Energie, um auf der Erde eine vergleichbare Nachtabkühlung wie auf dem Mond zu verhindern. Die Interaktion der Ortstemperatur mit den globalen Wärmespeichern Atmosphäre und Ozeanen ist ein wesentlicher Mechanismus in der Temperaturgenese auf unserer Erde, der bei Kramm et al. (2017) lediglich durch eine (begrenzte) Slab-Speicherung in Analogie zum Mond berücksichtigt wird.
Zur Darstellung des Jahresverlaufs eines breitenabhängigen S-B-Temperaturäquivalentes: Kramm et al. (2017) stellen in Abbildung 22 den breitenabhängigen 24-Stunden-Durchschnitt der solaren Einstrahlung und dessen S-B-Temperaturäquivalent dar. Die Problematik einer solchen 24-stundendurchschnittlichen solaren Strahlungsleistung hatte ich in meinem EIKE-Artikel „Noch ein paar Fragen zum ‚natürlichen‘ atmosphärischen Treibhauseffekt“ vom 23. Juni 2017 anhand einer vergleichbaren Abbildung von Dennis L. Hartmann ausführlich erläutert; insbesondere lässt ein solcher Strahlungsdurchschnitt keinesfalls die Berechnung eines S-B-Temperaturäquivalentes zu. Der korrekte breitenabhängige Jahresverlauf des maximalen S-B-Temperaturäquivalentes ist weiter oben unter THESE (4) abgebildet und bestätigt die globale Klimaküche zwischen den Wendekreisen.
Es ist daher äußerst befremdlich, wenn Kramm et al. (2017) in Abbildung 22a aus einem solchen rechnerischen 24-Stunden-Strahlungsdurchschnitt ein S-B-Temperaturäquivalent ableiten, bei dem sich die globalen Temperatur- und Strahlungsmaxima wegen der Tageslängen im Polarsommer zwangsläufig auf der Polkalotte der jeweiligen Sommerhemisphäre konzentrieren. Die dermaßen fehlerhaft ermittelten Temperaturen liegen folglich im Jahresverlauf um den Äquator zwischen 220K und 240 K und steigen zum jeweiligen Pol der Sommerhemisphäre stark an. Grund dafür ist, dass die temperaturwirksame solare Einstrahlung zwischen den Wendekreisen im 24-Stunden-Durchschnitt praktisch halbiert wird, und sich in diesem Modell von Kramm et al. (2017) die globale „Klimaküche“ dadurch fälschlicherweise von der Äquatorzone zwischen den Wendekreisen auf den geographischen Pol der Sommerhemisphäre verschiebt.
BEWEISFÜHRUNG (2.2): Kramm et al. (2017) umschiffen die Problematik der terrestrischen Temperaturgenese, indem sie in ihrer Kernaussage (2.2) einfach die primäre Wirkungskette (Strahlungsflüsse = Ursache) und (lokale Temperaturen = Wirkung) umkehren. So kommen Kramm et al. (2017) schließlich zu dem Ergebnis, Zitat: „Based on our findings, we may conclude that the effective radiation temperature yields flawed results when used for quantifying the so-called atmospheric greenhouse effect.“ (S. 283 Ende vorletzter Absatz)
Der unparteiische Google-Übersetzer sagt: „Aufgrund unserer Ergebnisse können wir den Schluss ziehen, dass die effektive Strahlungstemperatur bei der Quantifizierung des sogenannten atmosphärischen Treibhauseffekts zu fehlerhaften Ergebnissen führt.“
Das Problem dieser Aussage ist wiederum, dass Kramm et al. gar nicht versucht hatten, den atmosphärischen Treibhauseffekt an einem realistischen Modell der Erde zu quantifizieren, sondern an ihrem nachweislich der BEWEISFÜHRUNG zu (2.1) unzureichenden „Multilayer“-Mond-Modell.
MEINE ARGUMENTATION zu THESE (3) – Globale Stefan-Boltzmann-Integration (Gerlich&Tscheuschner):
Der von Gerlich und Tscheuschner aufgezeigte Widerspruch (33°C # 144°C) ist analog zu dem gängigen „Faktor4“-Ansatz für einen „natürlichen atmosphärischen Treibhauseffekt“ innerhalb dieses Modells (1) korrekt abgeleitet worden.
Damit haben Gerlich&Tscheuschner den „natürlichen atmosphärischen Treibhauseffekt“ widerlegt.
Allerdings ist diese Widerlegung aus dem global gemittelten Modell (1) heraus erfolgt und daher kann dieses Ergebnis nicht auf die reale Erde angewendet werden. Denn lediglich die Tagseite der Erde (2PIR2) darf im Strahlungsgleichgewicht zwischen Sonne und Erde mit dem Stefan-Boltzmann-Gesetz betrachtet werden. Von daher hätte diese Lösung von Gerlich and Tscheuschner (2009) auf die Tagseite der Erde (2PIR2) beschränkt bleiben müssen.
BEWEISFÜHRUNG (3): Die physikalische Globaltemperatur Tphys von Gerlich and Tscheuschner (2009) beträgt -129 °C, respektive 144,15 K für die gesamte Erdoberfläche (4PIR2). Mit dem Stefan-Boltzmann-Gesetz darf aber lediglich die Tagseite der Erde (2PIR2) im Strahlungsgleichgewicht zwischen Sonne und Erde betrachtet werden. Von daher muss diese Lösung von Gerlich and Tscheuschner (2009) auf die Tagseite der Erde (2PIR2) reduziert werden.
Korrektur Weber für die Integrallösung von G&T: Lösung G&T * 4πR2 / 2πR2 = 2 * Lösung G&T
Folglich verdoppelt sich die Lösung von Gerlich and Tscheuschner für die physikalische Temperatur auf Tagseite der Erde zu
Tphys-korr = 288,3 °K oder 15,15 °C (Korrektur Weber für Lösung G&T)
und bestätigt damit wiederum meinen hemisphärischen Stefan-Boltzmann-Ansatz.
MEINE ARGUMENTATION zu THESE (4) – Hemisphärischer Stefan-Boltzmann-Ansatz (Weber):
Hier muss sich der interessierte Leser ein eigenes Urteil bilden, weil es sich um meinen eigenen hemisphärischen Stefan-Boltzmann-Ansatz handelt. Zwecks Arbeitsentlastung der EIKE-Redaktion finden Sie nachfolgend einige Kommentarvorschläge zum Ankreuzen:
O U. Weber, Fachrichtung Science Fictíon – unklar bleibt, warum EIKE einen derartigen Quark veröffentlicht!
O Alles was Sie hier schreiben ist völlig falsch, das hatte ich Ihnen schon vor 2 Jahren in meiner E-Mail nachgewiesen.
O Der „Geophysiker“ Weber verbreitet nun schon zum 14. Mal seinen Quatsch hier auf EIKE und hat den Faktor 4 immer noch nicht verstanden.
O Sie vergessen völlig, dass sich die Erde dreht. Und das so schnell, dass sich der größte Anteil der Erdoberfläche mit Überschallgeschwindigkeit nach Osten bewegt.
O Sie haben da einen Rechtschreibfehler in Ihrem Text. Wenn Sie einen so simplen Fehler machen, muss alles andere auch falsch sein.
O Zum fremdschämen, Herr Weber ist einfach nur peinlich.
O Die Anwendung des Stefan-Boltzmann-Gesetzes auf die Erde ist absurd.
O Was der Autor schreibt ist völliger Unsinn, ich habe das deshalb HIER mal einfach verständlich erklärt…
O Man kann doch nicht eine spezielle Situation der Anwendung des Stefan-Boltzmann Gesetzes herzuziehen, um die Physik der Erde umzukrempeln.
O Sie behaupten also, die Erde sei eine Scheibe und die Sonne scheint auch nachts.
Diese Liste bitte ausdrucken, einen passenden Kommentar ankreuzen, den Zettel zusammenknüllen und dann wegwerfen – Sie werden Sich danach sofort erleichtert fühlen. Die in diesem Beitrag zitierten Protagonisten dürfen selbstverständlich gleich mehrere Kommentare ankreuzen…
BEWEISFÜHRUNG (4): Ich darf an dieser Stelle zunächst nochmals darauf hinweisen, dass das mathematische Gleichheitszeichen im Stefan-Boltzmann-Gesetz die physikalische Randbedingung der GLEICHZEITIGKEIT impliziert.
Ein weiteres Argument für meinen hemisphärischen S-B-Ansastz ist die nachfolgende Abbildung „Jahresmittel des Energiehaushaltes der Atmosphäre und seiner Komponenten in Abhängigkeit von der geographischen Breite“ nach Häckel, die das Jahresmittel der advektiven Energieströme auf unserer Erde zeigt:
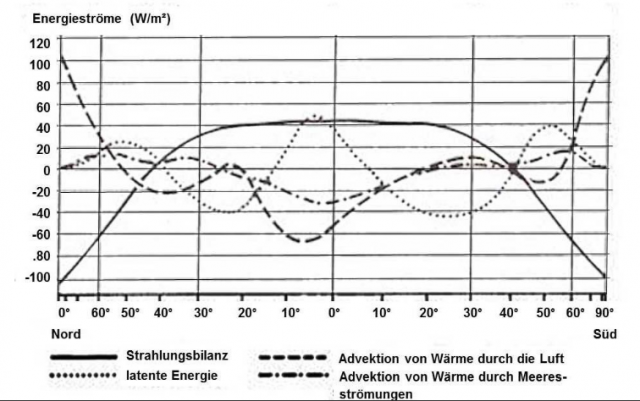
Abbildung: „Jahresmittel des Energiehaushaltes der Atmosphäre und seiner Komponenten in Abhängigkeit von der geographischen Breite“ nach HÄCKEL, H. (1990): Meteorologie. – 8. Aufl. 2016; Stuttgart (Verlag Eugen Ulmer), ISBN 978-3-8252-4603-7)
Diese Abbildung zeigt auf Basis einer globalen Energieabstrahlung von 235 W/m² den im Jahresdurchschnitt von den globalen Zirkulationen aus den äquatorialen Regionen in mittlere und höhere geographische Breiten hinein verfrachteten Wärmestrom. Tatsächlich dürften diese Beträge im jeweiligen Winterhalbjahr der mittleren und höheren Breiten noch deutlich höher ausfallen als der Jahresdurchschnitt selbst. Da die Betrachtung der globalen Abstrahlung über die Umgebungsgleichung des Stefan-Boltzmann-Gesetzes in meinem hemisphärischen S-B-Ansatz ebenfalls auf einer durchschnittlichen globalen Abstrahlung von 235 W/m² beruht, reiht sich diese Abbildung von Häckel widerspruchslos in diese Argumentation ein.
Denn damit ist der Nachweis erbracht, dass die hemisphärisch ermittelten Einstrahlungsdefizite im jeweiligen Winterhalbjahr der mittleren und höheren Breiten aus dem horizontalen Wärmetransport der globalen Zirkulationen abgemildert werden.
In Teil 3 werden die Erkenntnisse zu den einzelnen Thesen/Antithesen und das Ergebnis dieser Analyse vorgestellt.
















Dazu möchte ich kurz die Stefan-Boltzmann-Strahlungswelt verlassen: Der Energieaustausch zwischen den CO2-Molekülen erfolgt durch mechanische Stöße und/oder Strahlung und zwar statistisch gleich verteilt in alle Richtungen, wobei dann kein oder allenfalls nur ein geringer Energienettotransport stattfindet:
Keine Vorzugsrichtung = kein Treibhauseffekt
Soweit es dabei einen geringen Energienettotransport von warm nach kalt gibt, so erfolgt er übereinstimmend mit dem zweitem Hauptsatz dadurch, dass relativ höhere mechanische Anregungsenergie kT/2 (T Temperatur, k Boltzmann-Konstante) an kältere Nachbarn weitergegeben wird. Bei der IR-Strahlung handelt es sich aufgrund der diskreten, konstanten Anregungsniveaus um die Weitergabe von stets etwa gleichgroßen Strahlungs-/Energiequanten. Gerlich und Tscheuschner sehen es etwas komplizierter – aber mit gleichem Resultat: Die IR-Strahlung trägt wenig zur Erwärmung der Atmosphäre bei.
Und die Erdoberfläche, überwiegend im Gleichgewicht mit der Umgebung, spielt in diesem „Temperaturgewusel“ mit. Wenn die These von der dramatisch erhöhten Abstrahlung durch Rückstrahlung richtig wäre, dann müsste man bei all den Myriarden Mikro-Stößen ebenfalls die herausnehmen, die mit der Erdoberfläche wechselwirken, und sie auch dem „Energierückfluss“ zuschlagen und der Erdoberfläche als Folge eine nochmals erhöhte Energieabgabe zuschreiben, das ganze dann noch als Endlos-Folge – ein m.E. sinnloses Unterfangen.
Abkühlung bzw. Energieabgabe an den Weltraum ist nur mittels IR-Strahlung möglich, die, was die Gase der Atmosphäre anbelangt, nur durch Klimagase erfolgt. Ab einer gewissen Höhe entweicht die IR-Strahlung ungehindert in den Weltraum.
Oberhalb der Troposphäre wird in den letzten Jahrzehnten mit Satelliten eindeutig eine Abkühlung gemessen. Was stimmig ist: Das vermehrte CO2 sorgt für mehr Energieabstrahlung/Abkühlung in der oberen Atmosphäre.
Die Konsequenz wäre, dass zu der derzeitigen Erderwärmung, sofern man der ganzen Temperaturmesserei samt Manipulationen überhaupt noch trauen will, das anthropogene CO2 weniger beiträgt als selbst von den meisten Skeptikern angenommen wird. Möglicherweise überwiegt sogar ein Kühleffekt. Und der verbleibende Treibhauseffekt der Atmosphäre wird durch alle Player bewirkt (von Konvektion über Molekülstöße bis hin zur IR-Strahlung), die allesamt zu der Abkühlung zwar beitragen, sie aber, weil nicht beliebig wärmeleitfähig, zugleich auch verlangsamen.
Wenn man die IR-spektroskopischen Satellitenmessungen betrachtet, erkennt man allerdings in den Spektralbereichen, in denen die Klimagase absorbieren, eine deutliche Verminderung der Abstrahlungsintensität – also genau das Gegenteil? Wie korrekt ist diese Interpretation, wie auch Herr Weber hinterfragt? Sind diese Einbuchtungen bei korrekter Interpretation der Strahlungskurven nur eine Folge eines kälteren (und höheren) Ursprungsortes? Wenn diese Strahlungsdiagramme zur Bestätigung des Treibhaus-Effektes taugten, warum wird dieses Argument nicht häufiger benutzt?
Natürlich hätte die Richtigkeit meiner Überlegung, wie bei allen „Treibhausleugnern“, zur Folge, dass die allermeisten der heutigen Berechnungen obsolet würden…
Zu 1.1. Herrn Dietze: Ich bewundere, dass Herr Dietze es schon vor langer Zeit schaffte, mittels analytischer Rechnung eine (relativ kleine) CO2-Klimasensitvität von 0,6 Grad zu ermitteln. Ein Wert, dem sich die neueren Klimamodelle immer mehr annähern. Wenn da nicht meine jüngsten Zweifel an den Strahlungs- (und Rückstrahlungs-) Modellen wären…
Zu „Temperaturgenese“: Die Annahme eines Schwarzen Strahlers ist oftmals fragwürdig, insbesondere wenn es sich um Gase handelt. Aber auch die Nachtseite strahlt (ohne Sonne) in den Weltraum ab, solange sie nicht auf – 273,15 Grad C abgekühlt ist.
Ansonsten ist der Hemisphärenansatz sehr verlockend, er rechnet gewissermaßen den Treibhauseffekt weg. Da musste erstmal ein Gerlich kommen, um den Klimatologen zu zeigen, wie man ein einfaches Doppelintegral ausrechnet. Ergebnis: -144 anstatt -18 Grad C ohne angeblichen Treibhauseffekt!! Die –18 Grad C „ohne Treibhausgase“, überall zu lesen, sind wohl definitiv eine Luftnummer!
Und im Hemisphärenansatz dann logischerweise die Temperaturverdoppelung der -144 Grad C. Auch sind auf der Taghalbseite dann alle Player, auch die Sonne, anwesend. Doch ist damit die nächtliche Abkühlung nicht verschwunden, sie belastet mit einem dicken Minus die Tagseite, vor allem in den Morgenstunden spürbar. Allerdings müsste ich jetzt erst nochmals nachforschen, wie Herr Weber diesen Aspekt konkret behandelt.
Zu 1.2.1 Herr Krüger: Wo verbleibt die Differenz zwischen 390 und 240 W/m2? Nochmals Rückstrahlung zu Erde?? Vollständiger Verbrauch für den Antrieb des Wettergeschehens?
Zu 1.2.2 Dr. Schnell: Respekt vor der experimentellen Arbeit und den vielen, sicherlich meist korrekten Darlegungen. Aber auch ich habe letzte Zweifel, was tatsächlich gemessen wurde. Trotz sorgfältig durchdachter Anordnung gibt es prinzipielle Einschränkungen wie die Gefäßgrenzen, zumeist abweichende Gaskonzentrationen verglichen mit der realen Atmosphäre sowie die gasspezifischen Einflüsse von Wärmeleitfähigkeit und Wärmekapazität. Auch stimmt, soweit ich mich erinnere, ein Teil der Ergebnisse nicht mit der üblicherweise berichteten Temperatur-Wirksamkeiten der verschiedenen Klimagase überein.
Zu 1.3. Dr. Heller: Ich habe Zweifel an den – 18 Grad C und an der Wirkung der Treibhausgase generell (siehe oben).
Zu 2.2 Herr Kramm et al: Nach meinem Gefühl wird ein wichtiger Teilaspekt angesprochen. Interessant wären Ergebnisse, die die Auswirkungen auf die Globaltemperatur sichtbar machen.
Zu 4 siehe weiter oben unter 1.1
Weil es Leute mit abstrusen Ideen gab und gibt, die ein komplexes System in einfache Berechnungsformeln packen und damit erklären will.
Hier muß das System selbst erstmal vereinfacht werden und unzählige Klammerrechnungen müssen herausgekürzt werden. Am Ende stehen Ergebnisse die mit der Realität nicht viel gemein haben.
Satire:
Ich habe gerade 500 m vom Haus entfernt ein Lagerfeuer entzündet. Alle IR- aktiven Moleküle im direkten Umfeld des Feuers bis hin zum Haus nehmen zusätzliche Energie, mit der 4. Potenz abnehmend zur Entfernung zum Feuer auf und geben diese in alle Richtungen wieder ab. Warum wird es im Haus nicht wärmer? Habe ich vergessen Fenster und Türen zu öffnen, oder nimmt mir das Feuer durch Absorbtion der Rückstrahlung seiner eigenen Energie mir die Wärme weg und wird selbst heisser? Oje was für eine Katastrophe! Dem Feuer droht die Selbstverbrennung oder bin ich mit Schuld weil ich atme, rauche und Fleisch esse, an diesem ganzen Dilemma.
Mit freundlichen Grüßen!
Christian Möser
Zimmerer
1. 940 W/m² @ Kreisfläche = 235 W/m² @ Kugelfläche – Gesamt-Energiebilanz am TOA
Die 940 W/m^2 Energiestromdichte wirken nicht auf einer Kreisfläche, sondern auf die Hemisphäre. Die Formulierung ist so nicht korrekt. Die 940 W/m^2 ist die eingehende hemisphärische Energiestromdichte vom isotrop-homogenen Flächenstrahler Sonne und die 235 W/m^2 ist die ausgehende Energiestromdichte vom isotropen Strahler Erde.
Korrekt müsste man das wie folgt formulieren: 940 W/m² @ pi = 235 W/m² @ 4*pi
Das „@ Fläche“ besser „@ Raumwinkel“ bezieht sich auf den Strahler (Emittent, Strahlungsquelle), nicht auf den Absorber.
Die eingehende Energiestromdichte vom Erdsystem wäre damit S*(1 – A) = 1361*(1 – 0,296) = 958 W/m^2. Die sphärische Albedo A bezieht sich auf eine sphärische Objektfläche, die Anwendung auf eine andere Form der Objektfläche ist nicht zulässig.
Die Berechnung mit S*(1 – A) @ Kreisfläche(Absorber) ist somit falsch.
2. AERI-Instrument in NIMBUS Satelliten?
Ein AERI-Instrument (Atmospheric Emitted Radiance Interferometer) wird für oberflächen-gestützte Emissionsspektren benutzt. In den NIMBUS Satelliten kommt eine so genannte ERB-Apparatur zum Einsatz, und kein AERI-Instrument.
Siehe: H. L. Kyle, J. R. Hickey, P. E. Ardanuy, H. Jacobowitz, A. Arking, G. G. Campbell, F. B. House, R. Maschhoff, G. L. Smith, L. L. Stowe, T. Von der Haar, „The Nimbus Earth Radiation Budget (ERB) Experiment: 1975 to 1992,“ Bulletin of the American Meteorological Society, Vol. 74, Issue 5, May 1993, pp. 815-830,
URL: http://journals.ametsoc.org/doi/pdf/10.1175/1520-0477%281993%29074%3C0815%3ATNERBE%3E2.0.CO%3B2
3. (Tag = 1,05*10^22 Joule) << (Jahr = 3,85*10^24 Joule) < 4,59*10^26 Joule)
Wo kommen nur immer diese unsinnigen Werte her, die von keine einzigen Messung abgesichert sind.
Am Tag liefert die Sonne rund 1361 W/m^2*(1 – 0,3)*[(5,1*10^14 m^2 * 24h)]/2 = 5,8*10^18 Wh = 2,1*10^22 J/d an Energie für das Erdsystem.
Daten unter: https://www.ngdc.noaa.gov/mgg/global/etopo1_ocean_volumes.html und https://www.nodc.noaa.gov/OC5/indprod.html
Der Oberflächenschicht-Energiegehalt (O = 3,619*10^14 m^2) der Weltmeere im Jahresmittel beträgt ungefähr 9,1*10^23 J. Die jährliche Verdunstungsrate beträgt etwa 5,25*10^17 kg und auf den Oberflächen-Anteil der Weltmeere bezogen von 3,7*10^17 kg, wobei dies einer Energie von 9,2*10^23 J entspricht. Der Volumen-Energiegehalt (V = 1,335*10^18 m^3) der Weltmeere im Jahresmittel liegt bei ca. 1,5*10^27 J.
An der Oberflächenschicht der Erde kommt im Jahresmittel eine Energie der Sonne von ca. 7,2*10^24 J an. Ca. 70% der Erd-Oberfläche sind von Wasser bedeckt, damit ergibt sich im Jahresmittel ein Energie-Eintrag von ca. 0,7*7,2*10^24 J – 9,2*10^23 J – 9,1*10^23 J = 3,2*10^24 J. Damit würde der Volumen-Energiegehalt der Weltmeere durch die oberflächliche Energie-Abgabe und -Zufuhr nach ca. 500 Jahren ausgeglichen. Auf dieser Basis würde ein Austauschzyklus rund 1000 Jahre dauern. Der Ausgleichszyklus von ca. 500 Jahren hat noch zwei Unter-Zyklen, einmal den Tiefenwasser-Ausgleichszyklus nach etwa 120 Jahren (Austauschzyklus ca. 240 Jahre) und den oberflächenschicht-nahen Ausgleichszyklus nach ca. 30 Jahren (Austauschzyklus ca. 60 Jahre).
Siehe (Bild 2): https://kaltesonne.de/klima-zyklen-und-ihre-extrapolation-in-die-zukunft/
Der oberflächenschicht-nahe Ausgleichszyklus von ca. 30 Jahren ist mit den TSI-Schwankungen der Sonne verknüpft, die sich nach etwa 25-30 Jahren bemerkbar machen.
Mfg
Werner Holtz
Das sind die Zahlen mit denen man das Klimasystem der Erde erklaeren kann.
Es ist nicht unbedingt falsch wenn Herr Weber annimmt das die 940 W/m2 auch auf der Hemisphaere wirken.
Die Solarkonstante ist eine Strahlstaerke. Und diese berechnet sich einzig und alleine aus der Abstrahltemperatur auf der Sonne und dem Abstandsgesetz. Die Veringerrung der Solarkonstante auf die 940 W/m2 ergibt sich aus der atmosphaerischen Absorption von Solarenergie 15% angenommen und Wolkenalbedo 15% angenommen. Bei direkter Einstrahlung ohne Wolken messes sie sogar mehr. Wenn man ein Spektrum der Einstrahlung an den Polen nimmt oder am Aequator, stellt man fest, das mindestens die 940 W/m2 immer noch gegeben sind. Erst bei der Aufteilung der Energie ueber die bestrahlte Flaeche ergibt einen geringeren Betrag von verteilten Watt pro Quadratmeter. Halten sie eine Flaeche Rechtwinklig zur Sonneneinstrahlung an den Polen oder auf deutschen Breitengeraden und auf dieser Flaeche kommen wieder mindestens 940 W/m2 an.
Heute Abend freu ich mich schon auf den 3. Teil
1. Was würde hier auf der Kommentarplattform von EIKE wohl geschehen, wenn ich die Strahlungsbilanz so schreiben würde, wie Sie sie für richtig halten also:
940 W/m² @ pi = 235 W/m² @ 4*pi ???
2. Meine Aussage zu den IR-Spektren war, Zitat: „Der Beweis eines atmosphärischen Treibhauseffektes durch Satellitendaten besteht lediglich aus einem VERGLEICH zwischen der theoretischen IR-Abstrahlung der Erde und den vorgeblich von Satelliten „gemessenen“ Spektren, denen ganz erhebliche Rechenprozesse hinterlegt zu sein scheinen:…“ – und für diese Aussage hatte ich zwei Beispiele aufgeführt.
Ich kann nach Ihren Ausführungen jetzt also ganz sicher davon ausgehen, dass in der von Ihnen genannten ERB-Apparatur im Gegenteil KEINE „erheblichen Rechenprozesse hinterlegt“ sind, um die betreffenden IR-Spektren zu erzeugen???
3. Sie fragen, „Wo kommen nur immer diese unsinnigen Werte her, die von keine einzigen Messung abgesichert sind“. Das kann ich Ihnen sagen, ich hatte mit erlaubt, diese Werte zu BERECHNEN. Und schon wenn ich meinen Tag-Wert (= 1,05*10^22 Joule) mit Ihrem Tag-Wert (= 2,1*10^22 J/d) vergleiche, dann springt mich ein Faktor „2“ und die Vermutung an, dass einer von uns einen Fehler gemacht haben könnte – und meinen Wert habe ich eben überprüft…
Und am Ende bezweifeln Sie dann, dass der Energiegehalt der Ozeane GRÖSSER als 4,59*10^26 Joule ist, OBWOHL Sie selbst dafür 1,5*10^27 angeben???
Meine Frage an Sie: Herr Holtz, was wollen Sie damit eigentlich bewirken???
1. Strahler1 @ Raumwinkel vom Strahler1 = Strahler2 @ Raumwinkel vom Strahler2 -> 940 W/m² @ pi = 235 W/m² @ 4*pi
2. ERB-Apparatur vs AERI-Instrument
Sie scheinen nicht in entfernsten den Unterschied zwischen diesen beiden Geräten zu kennen. Welche „erheblichen Rechenprozesse“ meinen Sie? Ein völlig sinnfreies Geschwätz.
3. (Tag = 1,05*10^22 Joule) << (Jahr = 3,85*10^24 Joule) < 4,59*10^26 Joule)
Das ist absolutes Wischiwaschi. Damit kann keiner etwas anfangen.
Mfg
Werner Holtz
Ihr Ärger darüber, dass Sie meine Fragen nicht beantworten konnten, ist menschlich verständlich.
Aber warum beschädigen Sie Ihre eigene Reputation mit der finalen Aussage „Das ist absolutes Wischiwaschi. Damit kann keiner etwas anfangen“, nachdem Sie diesem „Wischiwaschi“ vorher längliche Ausführungen und Gegenrechnungen gewidmet hatten, die Sie in der Folge nicht aufrechterhalten konnten???
Diesbezügliche Beiträge von mir wurden bei EIKE gelöscht bzw. diffamiert,
so z.B. von Professor Dr. Gerhard Kramm:
– …, dass Sie Ihren Geschirrschrank von einem Experten auf Vollstaendigkeit ueberpruefen lassen. …
– Lernen Sie also zunaechst einmal die Grundlagen der Geophysik und der Meteorologie. …
– Was glauben Sie eigentlich, wer Sie sind? …
– Ihre Excel-Berechnungen sind wertlos. Auch ist Ihre Interpretation vollkommen falsch. …
Auch mein Beitrag in einem Tscheuschner-Video wurde gelöscht…
https://tinyurl.com/y35b6ga6
Ihr Excelsheet hat keine Qualitaet und laesst in keiner Weise den Schluss zu, das Uli Weber und Ralf D. Tscheuschner sich irren!
Wie wollen sie das denn begruenden?
Und in der Begruendung nehmen sie Trennberth mit seinen gemittelten Strahlungsleistungen und vergleichen das mit echten Messungen?
Im uebrigen koennen sie die Gegenstrahlung nicht mit Ihren IR-Thermometer bestimmen. Es sollte Ihnen klar sein, das sie keine Aufloesung der Strahlungsbaender damit haben. Sie brauchen sich deshalb ueberhaupt nicht wundern warum sie bei Wolken etwas messen. Die sind graue Strahler auf die Ihr IR anspricht.
Wie man im 1. Teil dieser Serie sehen kann, entspricht der Messbereich eines IR-Thermometers ziemlich genau dem atmosphärischen Fenster und – glauben Sie mir: Dem IR-Thermometer ist es egal, ob die Gegenstrahlung von Wolken, blauem Himmel, Klimagasen oder Engelspfürzen kommt.
Wie man im 1. Teil dieser Serie sehen kann, entspricht der Messbereich eines IR-Thermometers ziemlich genau dem atmosphärischen Fenster und – glauben Sie mir: Dem IR-Thermometer ist es egal, ob die Gegenstrahlung von Wolken, blauem Himmel, Klimagasen oder Engelspfürzen kommt.
Wie erklaeren sie den Umstand, das sie in der Atmosphaere im Bereich des Atmosphaerischen Fensters etwas messen koennen? Das ist ja gerade der Bereich in dem NICHTS strahlen sollte.
Wenn es das doch tut, dann sind es wohl Engelspfürze. Damit koennen sie einen Treibhauseffekt nachweisen?
Ich hatte mal bei Ihrem kleinen Excelfile reingeguckt. Die Dokumentation von dem was sie gemacht haben war schlecht praesentiert, um es gelinde auszudruecken. Wenn sie Ihre Mittelungen mal erlaeutern wollen, bitteschoen.
Da ich alle Messungen auf meinem Grundstück gemacht habe, ist es eine zeitliche Mittelung.
Die gemittelte Sonneneinstrahlung von 161W/m² (Trenberth) teilt sich wie folgt auf:
– Latenter Wärmefluss: 80 W/m^2
– sensibler Wärmefluss: 17 W/m^2
– Nettoabsorbtion: 1W/m²
– Nettoabstrahlung im Infrarotbereich: 63 W/m^2
Diese 63W/m² werden vom der Erdoberfläche abgestrahlt und im wesentlichen von der Wolkendecke und anderen Klimagasen (O3, CO2, …) im Strahlungsfenster teilweise reflektiert. Sie müssen deshalb erneut abgestrahlt werden und genau das ist der Treibhauseffekt! Details siehe unten in meinem ExcelSheet bei „Rechenaufgabe zum Treibhauseffekt“.
Wie haben sie denn bitte den Sensiblen, Latenten und Strahlungswaermefluss gemessen?
Wie haben sie die Sonneneinstrahlung gemittelt? Haben sie die Nachtstunden mit einbezogen? Trenberth macht das so.
Sie haben auf Ihrem Grundstueck gemessen, machen aber globale Angaben?
Wie kommen sie auf 63 W/m2 Nettoabstrahlung?
Klingt verdaechtig nach Trenberth.
Ohne ihre Messungen weiter zu erlaeutern, ist ihre Erklaerung wertlos.
Und falls sie meine Meinung hoeren wollen, wenn der Beweis so einfach waere, dann haette man schon was gehoert.
Eine Nettabstrahlung im Infraroten macht auch nichts waermer. Sollte ihnen klar sein. Alles minus was sie da angeben.
Siehe ggf. auch
http://www.peter-boesche.de/klimaluege
auf meiner HP.
also koennen sie weder Angaben zur Konvektion oder zur Wasserverdampfung machen, haben genausestens die Strahlstaerken gemessen, womit eigentlich? Und sie haben das Stahlungsdiagram von Trenberth als Grundlage genommen?
Da kann ja nichts mehr schief gehen.
Trenberth hat ja nur den sogenannten Treibhauseffekt mit diesem Diagram defienert, also muessen zwanglaeufig Ihre Berechnungen zum selben Ergebnis kommen!?
Das ist aber keine Wissenschaft. Ihre Berechnungen bestaetigen scheinbar lediglich was Trenberth sagt, weil sie sich auf ihn beziehen.
Wundern sie sich bitte nicht wenn ihnen das keiner als Beweis abnimmt. Es ist keiner!
mfg Werner
Uerspruenglich sollte das CO2 ja herhalten die Eiszeiten zu erklaeren. Da CO2 ein excellentes Kuehlmittel in der Atmosphaere ist, werden wir aber wohl bald hoeren muessen, das mehr CO2 eine Kaltzeit, die ja ach so katastrophal ist, hervorruft.
Es lebe die Katastrophe!
…. rechnet man nicht mittlerweile (seit 2016?) in bestimmten *Klimamodellen* mit variablen (temp.bereichsabhängigen???) Co2- Sensitivitäten, damit die Modelle auch backwarts möglichst funktionieren?
Wäre doch das Vorgeschlagene quasi durch die Hintertür.
(..irgendeiner Veröffentlichung hatte ich das entnommen, weiss aber nicht mehr, wo… wäre ggfs. für Bestätigung und evtl. Link dankbar)
beide Größen aus dem CERES-Datensatz zwischen 20003 und 201905 berechnen und die Differenz graphisch darstellen. Zwischen 20003 und 201502 betrug THE 33,75 +/- 0,05 °C. Während des El Ninos 2015/2016 stieg THE an und liegt im Zeitintervall 201503 – 201905 bei 33,94 +/- 0,06 °C.
THE verändert sich offensichtlich in Stufen, die durch El Nino-Ereignisse getriggert werden. Der Zeitraum ist leider recht kurz, so dass diese Folgerungen eher als spekulativ einzuordnen sind. Jedenfalls trägt in der hier diskutierten Definition des Treibhaus-Effektes nicht nur die Atmosphäre, sondern auch die Erwärmung des tiefen Ozeans zum THE bei.
https://docplayer.org/27469048-Der-atmosphaeren-effekt.html
Ich bin kein Naturwissenschaftler und aus Faulheit zum Googeln habe ich das aus dem Kopf geschrieben, Quelle kann ich aber nachreichen.
N.B. Der Effekt ist eigentlich immer Null da es keine physikalisch plausible Begründung für eine Erderwärmung durch CO2 gibt.
Damit ist für mich der „Käse“ gegessen. Dennoch wird dieser Tage der „Kipp-Punkt“ durch die Fernsehlandschaft getrieben. Als „Beweis“ gelten abrupte Klimaänderungen der Vergangenheit (die ja eigentlich gerade den menschlichen Einfluss ad absurdum führen). Jetzt ist es der Permafrostboden, wenn der taut…
Meine tägliche Katastrophe gib mir heute!
Gase strahlen in ihren Absorbtionsbanden gemäß des Absorptionsgrades=Emissionsgrades entsprechend ihrer Temperatur ab.
„Den sogenannten „Treibhausgasen“ (THG), hauptsächlich Wasserdampf, Kohlenstoffdioxid und Methan, wird vom IPCC eine aktive Temperaturwirksamkeit in [W/m²] zugemessen. Diese Zuordnung ist aber grundsätzlich falsch, weil solche Gase keine aktive Strahlungsquelle darstellen.“
Zunächst einmal muss die Energie für eine Abstrahlung der IR-aktiven Gase ja irgendwo aufgebracht werden. Erklären Sie mal, welche Energie die Strahlung der IR-aktiven Gase verursacht und wie sich dadurch die Temperatur der Atmosphäre erhöhen soll. Dabei können Sie auch gleich die Frage der Admin vom 2. Dezember 2019 um 18:35 Uhr aus Teil 1 beantworten, ich zitiere:
„So klingt es auch sehr nachvollziehbar. Danke. Und diese Temperatur von – 18 ° in 5000 m Höhe lässt sich ziemlich genau nach der adiabatischen Höhenformel berechnen, wenn man als Ausgangswert 15 °C am Boden annimmt. Was bleibt da noch für den Treibhauseffekt übrig?“
Und dann wäre da noch das ominöse IR-Spektrum aus Ihrem Artikel „Grundlagen des Treibhauseffektes für EIKIANER“ (2016). Sie hatten in Ihrem Kommentar vom 3. Dezember 2019 um 13:34 Uhr nämlich nur meine Kritik zitiert und ganz zufällig „vergessen“, Ihr ominöses Diagramm zu verteidigen. Es steht also die Frage im Raum, wo dieses Diagramm herkommt und was es zeigt, nämlich konkrete IR-Meßwerte oder lediglich eine Werbegraphik für den THE.
Hic rhodus hic salta, Herr Krüger, jetzt ganz ohne „hätte, könnte, wollte“ einfach mal „Butter bei die Fische“: Datum der Messung, Ort der Messung, Autor und Titel der Veröffentlichung und Link zur Veröffentlichung!
=> Und hier geht’s zum Notausgang, Zitat von ScienceFiles (https://tinyurl.com/yxs657jo:„Ambushologie, deren Vorgehensweise man in drei Schritte unterteilen kann:
1. Eine große Klappe riskieren und verbal um sich schlagen.
2. Wegrennen und verstecken.
3. Bei Entdeckung: Keine große Klappe mehr riskieren und versuchen, sich zu wegzudrücken.“
Je wärmer das Gas, desto mehr Wärme strahlt es auch in seinen Emissionsbanden ab.
THG behindern daher die direkte Wärmeabstrahlung des Erdbodens ins All.
Das zeigt auch das Diagramm. Entsprechende Diagramme finden sie über google, wenn Sie Wärme-Abstrahlungssprektrum der Erde eingeben. Die Erde strahlt aufgrund der THG und Wolken nun mal weniger Wärme ins All ab, als es der warme Erdboden bei ungehinderter Ausstrahlung tun würde.
Herr Weber, es sollte doch klar sein, dass die Gasstrahlung nicht vom warmen Erdboden direkt ins All geht, sondern aus größeren Höhen, wo es entsprechend kälter ist? Dadurch geht am Erdboden halt weniger Wärme verloren. Die Folge davon sollte selbsterklärend sein.
sie sagen:
„dadurch geht am Erdboden halt weniger Wärme verloren.“
Man kann sie auch noch hundertmal darauf hinweisen, das die Waerme dann eben nicht durch Strahlung sondern durch Konvektion und Latente Waerme von der Oberflaeche abgefuehrt wird. Sehr effektiv uebrigens.
Ihre Aussage ist so wie sie sie da haben FALSCH.
Waerme geht eben nicht nur durch Strahlung verloren.
Ihre Ignoranz in der Hinsicht ist ausgezeichnet hoffnungslos.
„Bei dem IR-Spektrum@70km handelt es sich nicht etwa um echte IR-Messwerte, sondern um ein wohlmeinendes handwerkliches Zirkelkonstrukt. Dieses konstruierte F-Wort-Spektrum kann keinerlei eigene Beweiskraft für einen „natürlichen atmosphärischen Treibhauseffekt“ entwickeln, weil es nämlich umgekehrt rein rechnerisch aus dieser THE-Hypothese abgeleitet worden ist.“
Mit IR-Skeptrometern, die zwischen 1-100 Mikrometer messen, können Sie das Wärmeabstrahlungsspektrum der Erde ab 70 km Höhe und egal wie weit von der Erde entfernt messen. Da messen Sie 240 W/m2, die die Erde ins All abstrahlt und das entspricht nun mal -18°C Strahlungstemperatur der Erde.
Diese Temperatur finden sie in der Atmosphäre in einer Höhe von 5.000-6.000 m vor. Deshalb spricht man hier von der mittleren Abstrahlungshöhe, aus der die Erde ihre Wärme im Mittel ins All abstrahlt.
Kann man alles messen.
Am Erdboden haben Sie hingegen rund 15°C.
Das ist alles.
Und was liegt näher, als für die (mittlere) Grenze des Systems Erde mit Atmosphäre (die ist ja nun mal da [ausgeborgtes Zitat]), den mittleren Luftdruck zu wählen?
Sie messen die 15 Grad und alle anderen muessen diese als statistisches Mittel erst errechnen. Uebrigens bei mir sind es gerade 21 Grad draussen, muss an der Erdueberhitzung liegen.
Alles schon zu spaet!
Jo!
Auch sind wir alle längst verschmort.
Wir wissen es blos nicht weil wir so dumm sind nicht mal diesen ach so einfachen Treibhausblödeleffekt zu begreifen…
Die ganze Diskussion hier ist ein Witz!
-CO2 strahlt bodennah nicht
-die behauptete Gegenstrahlung in Höhe von 330W/qm existiert nicht
-die „Meßdaten“ im CO2-Absorptionsspektrum sind keine
-die „gemessenen“ Temperaturdaten werden nach Bedarf hin gebogen
-usw.
Ein Treibhauseffekt wäre dann gegeben, wenn sich der Boden aufgrund einer wie auch immer gearteten Gegenstrahlung erwärmen würde.
Dafür gibt es nicht den geringsten Beweis.
Wohl aber würde ein Effekt dieser Art den Regeln geltender Physik widersprechen.
Das Ganze ist von G/T, K/D, Kramm längst nachvollziehbar widerlegt.
Wer daran zweifelt, muß G/T, Kramm etc. widerlegen.
Tut aber niemand – warum wohl?
Also:
das TH-Gefasel ist Dummquatsch – von Anfang an bis heute.
Offenbar kann man damit aber viel Geld verdienen…
Bitte erläutern!!!
https://www.youtube.com/watch?v=R181kCfttW0
Dr. Kramm besucht ab und zu mal diese Blogs bei Eike.
Zum Beispiel hier:
https://www.eike-klima-energie.eu/2010/05/21/klimaforscher-weist-den-brief-zurueck-mit-dem-255-fachfremde-wissenschaftler-die-erwaermungsthese-stuetzen/
16 Fragen zum Klimawandel an die Abgeordneten des Deutschen Bundestages.
Aufgrund eines behaupteten Klimanotstandes sollen neue Gesetze erlassen werden. Diese schreiben uns unsere Art zu leben vor, haben nachteilige Umweltfolgen und können zur Deindustrialisierung Deutschlands führen. Das bedeutet den Verlust von Wohlstand und sozialer Sicherheit. Regierung und Parlament veranlassen somit gezielt eine Senkung des Lebensstandards und gefährden damit Arbeitsplätze, Alterssicherung und soziale Hilfen in Notfällen. Dann sollten unsere gewählten Vertreter zumindest nachweisen, dass sie den zugrunde liegenden Sachverhalt vollständig verstehen und die Konsequenzen durchdacht haben. Wir stellen daher 16 Klimafragen an die Abgeordneten des Deutschen Bundestages. Wer sich den Fragen anschließen möchte, zeichnet bitte online hier. Jeder wahlberechtigte deutsche Staatsbürger kann mitmachen.
https://www.klimafragen.org/#initiative
Bitte hier nur unter vollem Klarnamen posten, siehe Regeln.
Moment, werden Sie sagen – das geht doch nicht ! Dann schauen Sie sich bitte an, was Prof. Rahmstorf dazu schreibt:“Vorallem Wasserdampf und CO2-Moleküle absorbieren einen Teil der von der Erde abgegebenen Strahlung, und strahlen dann selber die Energie wieder in alle Richtungen ab. Ein Teil der Strahlungsenergie kommt damit wieder auf die Erde zurück.“ (Quelle: http://www.pik-potsdam.de/~stefan/leser_antworten.html)
Sie können natürlich auch zwischen den Fensterscheiben in den Hohlraum CO2 einblasen, wenigstens im Winterhalbjahr, das man im Sommerhalbjahr wiederum durch Luft ersetzt. Auch beim Autoreifen würde die IR-Strahlung des Erdbodens angenehm warme Reifen ergeben, die auf der Straße den Schnee wegschmelzen.
Dieses Beispiele ist ein Anschauungsstück für die ausbeuterische Gier des Kapitals, auf dessen Seite, wieder einmal, der Profit liegt.Der Bonze im Haus hat abgepresste 16° während die Ausserhausigen nur über 8° verfügen, von dem noch die Hälfte dem Innerhausigem abgeben werden muß; und der somit über dann 20°verfügt.Die Investition von 4° zieht er, Steuerneutral, von der Klimasteuer ab. Es wird Zeit für eine Umkehr.Die Besteuerung der CO2 Emissionen ist nur der erste Schritt. Der Klimasozialismus fordert daher die alleinige Wärmeabgabe des wärmeren Körpers an den kälteren unterpriviligierten.Obwohl dies von den Leugnern als Tatsache dargestellt wird, ist es doch nur ein Ablenkungsmanöver; und es wurde klar gezeigt, daß die Verhältnisse andersrum liegen.
Satire Ende (falls es Niemand bemerkt haben sollte)
Und ich bin so dumm und heize!
Dabei muß ich nur die Gegenstrahlung rein lassen…