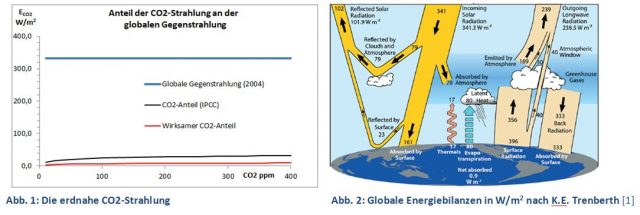
Dabei ist selbst dieser kleine Wert immer noch zu hoch. CO2 ist nicht der einzige Strahler der Atmosphäre. Wasserdampf, die nicht sichtbaren Aerosole und vor allem die Wolken sind weitere Akteure der atmosphärischen Gegenstrahlung, die sich gegenseitig kontrollieren und verringern (Abb. 21). Es ist bereits bekannt, dass sich die CO2– und Wasserdampf-Strahlungen teilweise überlagern, was in feuchter Luft den CO2-Beitrag verringert [6], [7]. Die Wechselwirkung mit den Wolken/Aerosolen ist ein weiterer, weitaus wirksamerer Dämpfer der CO2-Wirkung. Würde das IPCC auch diese Strahlungskonkurrenten berücksichtigen, wäre der tatsächliche CO2-Treibhauseffekt rund 10 W/m2 oder 3 % der globalen Gegenstrahlung (Abb. 1, rote Kurve).
Bei einem so geringen CO2-Anteil muss man sich schon fragen, ob das Klima wirklich von CO2 bedroht wird und wie die atmosphärische Gegenstrahlung überhaupt zu verstehen ist. Das Prinzip von Vorder- und Hintergrundstrahlung ist ein neuer Ansatz, die Aktionen verschiedener atmosphärischer Strahlungsquellen besser zu verstehen. Dieses Anliegen zieht sich wie ein roter Faden durch die Publikationsreihe „Experimentelle Verifikation des Treibhauseffektes“. Im Folgenden wird eine CO2-StrahlungsforCO2 , ausgehend von J. Stefans Erkenntnissen [8] und auf der Grundlage der eigenen Laborexperimente, Schritt für Schritt abgeleitet. Danach ergibt sich eine weitaus geringere CO2-Wirkung als vom IPCC angenommen (Kap. 4, Seite 9).
-
Einführung
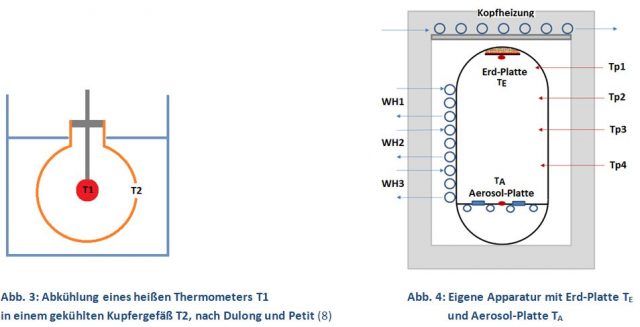
Anfang des 19. Jahrhunderts suchten verschiedene Forschergruppen einen mathematischen Zusammenhang zwischen Temperatur und IR-Strahlung eines Körpers. Unter anderen Dulong und Petit, die die Abkühlung eines heißen Thermometers (200 – 300 °C) in einem kalten Vakuumgefäß verfolgten (Abb. 3) [9]. Sie entwickelten eine einfache Formel, die hinreichend genau die zeitliche Abkühlung des Thermometers wiedergab. Die Gleichung versagte jedoch, wenn wesentlich heißere Körper, wie die der Sonne, berechnet werden sollten.
Josef Stefan überprüfte die Versuche von Dulong und Petit und anderer Forschergruppen und konnte rein empirisch Gl. 1 ermitteln, womit die Wärmeübertragung P paralleler Oberflächen, auch bei sehr hohen Temperaturen, berechnet werden konnte [8]. Stefan brauchte den sogenannten Strahlungsaustauschgrad „E“ für blanke, also reflektierende Oberflächen (Emissionsgrad ε << 1). Geht man aber von einer Schwarz-Körper-Strahlung mit ε = 1 aus, wird auch E = 1 und wir haben mit Gleichung Gl. 2 den Vorläufer des Stefan-Boltzmann-Gesetzes (Gl. 3) vor uns, das von Ludwig Boltzmann 1884, einem Schüler von Stefan, theoretisch abgeleitet wurde [10].
Mit Gl. 2 legt Stefan die Grundlage für die Berechnung des Treibhauseffektes. Die Abkühlung des Thermometers (Energieverlust) hängt sowohl von der Temperatur T1 als auch von T2 ab, also von der Differenz zwischen Ausstrahlung des Thermometers und Gegenstrahlung der Kupferwand.
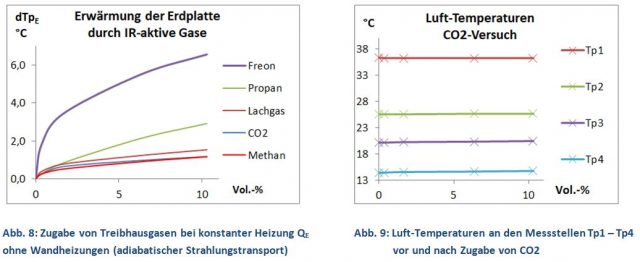
Will man den CO2-Treibhauseffekt nach Gl. 2 experimentell untersuchen, benötigt man zwei schwarze Flächen mit einem ausreichenden Temperaturunterschied (T1 >> T2). Die eigene Apparatur mit einer warmen Erd- und einer kalten Aerosol-Platte erfüllt diese Voraussetzung. Der Versuchsaufbau (Abb. 4) zeigt eine große Ähnlichkeit mit dem Kupfergefäß von Dulong und Petit, nur dass der Abstand zwischen Erd- und Aerosol-Platte vergrößert wurde. Dadurch entsteht nicht nur ein Luftraum für die potentielle Zugabe von IR-aktiven Gasen, sondern auch eine dritte Strahlungsfläche, die Seitenwand, die einen wesentlichen Einfluss auf die Gegenstrahlung hat. Um das zu verstehen, wird ein sehr einfaches Schema der Gegenstrahlung vorgestellt, das mit roten (warm = TV) und blauen (kalt = TH) Farben Strahlungsquellen unterschiedlicher Temperaturen angibt.
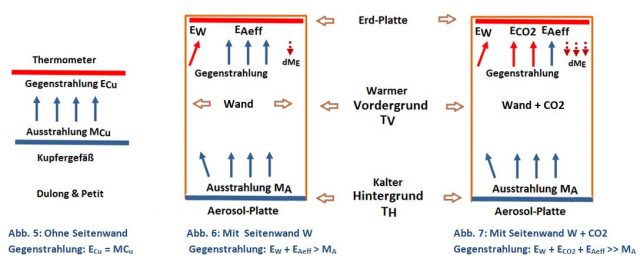
Abbildungen 6 und 7 zeigen die Veränderung der Gegenstrahlung, wenn zur warmen (rot) und kalten (blau) Fläche in Abb. 5 eine dritte Strahlungsquelle, die Seitenwand und CO2, hinzukommt. Aus Sicht der Erd-Platte haben wir jetzt zwei Gegenstrahler, die als warmer Vordergrund (TV, Seitenwand und CO2) und kalter Hintergrund (TH, Aerosol-Platte) definiert werden. Seitenwand und CO2 absorbieren einen Teil der Aerosol-Platten-Strahlung (blaue Pfeile) und emittieren dafür eigene, energiereichere Strahlungen (rote Pfeile), entsprechend ihrer höheren Temperatur TV (Abb. 6, 7). Der Eingriff von CO2 hat vier Konsequenzen:
A: Erd-Platte: CO2 erhöht die Gegenstrahlung (2 rote anstelle von 2 blauen Pfeilen). Dadurch kommt es zu einer verringerten Energieabgabe (Gl. 2) und es entsteht ein Wärmestau, wodurch sich die Erd-Platte solange erwärmt, bis Energieverlust und -gewinn wieder gleich sind (Abb. 8). CO2 entnimmt die für die Strahlung erforderliche Energie ihrer Umgebung (siehe Punkte C und D). CO2 ist kein zusätzlicher Wärmeinput für die Erde. Vergleichbar mit der Corioliskraft handelt es sich hier um eine Scheinwirkung.
B: Aerosol-Platte: Nicht alle Photonen der Aerosol-Platte erreichen die Erd-Platte (1 blauer Pfeil in Abb. 7). Dieser Bruchteil ist die effektive, von der Vordergrundstrahlung verdeckte, Strahlung der Aerosol-Platte EAeff [11]. Im Hintergrund ist die Aerosol-Platten-Ausstrahlung MA jedoch ständig als latente Strahlung vorhanden.
C: Luft-Temperatur: Die Seitenwand und CO2 verlieren Energie, da ihre Emission EW bzw. ECO2 (rote Pfeile) größer als ihre Absorption (blaue Pfeile) ist, wodurch sich der Luftraum abkühlen müsste.
In einem bereits publizierten Demonstrations-Experiment [12], [11] wurden unter adiabatischen Bedingungen (ohne Wandheizung) die Auswirkungen von CO2 (und anderen Treibhausgasen) untersucht. Dabei wurde eine deutliche Erwärmung der Erd-Platte beobachtet, während innerhalb der Röhre, an den Messstellen Tp1 – Tp4, die Temperaturen konstant blieben (Abb. 8 und 9). Die Konstanz der Luft-Temperatur erklärt sich durch den Ausstrahlungsanstieg dME der wärmer gewordenen Erd-Platte (braune gestrichelte Pfeile, Abb. 6 und 7), wodurch Erwärmungs- und Abkühlungseffekte gleich groß sind.
D: Energiebilanzen: Bei adiabatischer Versuchsdurchführung müssen Heizung QE (Input) und die auf die Aerosol-Platte übertragene Energie (Output) gleich groß sein (Energieerhaltungssatz), unabhängig von CO2. Um diese Gleichheit herzustellen, kann die trockene Erdoberfläche bei einem Wärmestau durch Treibhausgase mit einer Temperatur-Erhöhung reagieren (Abb. 8, Gl. 2). Ozeane und Feuchtgebiete können bei einem Wärmestau auch ohne IR-Strahlung die überschüssige Wärme durch Verdunstung von Wasser auf eine Wolkenschicht übertragen. Diese Wasser-Flächen würden sich nur wenig oder gar nicht erwärmen. Der CO2-Treibhauseffekt würde dann eine Abkühlung der Atmosphäre bewirken. Ließe sich das beweisen, würde es die CO2-Wirkung auf den Kopf stellen und die Wasserdampf-Rückkopplung ad absurdum führen! Eine experimentelle Untersuchung hierzu steht noch aus.
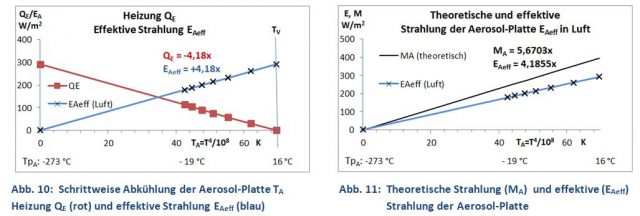
Die Existenz einer effektiven Aerosol-Platten-Strahlung EAeff nach Punkt B) ließ sich experimentell beweisen (Abb. 10 und 11). Grundlage ist Gl. 4, die aussagt, dass bei konstanter Temperatur der Erd-Platte TE (im thermisches Gleichgewicht) Energieverlust (Ausstrahlung ME) und Energiezufuhr (Gegenstrahlung EA + EW und Heizung QE) gleich groß sind. Wenn bei diesem Experiment (in Luft, ohne IR-aktive Gase) die Aerosol-Platte stufenweise abgekühlt wird, verringert sich die effektive Gegenstrahlung EAeff. Damit TE konstant bleibt, muss nach jedem Abkühlungsschritt die Heizung QE erhöht werden. Trägt man QE über die Temperatur der Aerosol-Platte (als T4/108) auf, erhält man als Trend eine Gerade (rot) mit dem Anstieg dQE/dTAeff = -4,18 (Abb. 10).
In Gl. 4 sind ME und EW Konstanten, da ihre Temperaturen annähernd konstant bleiben. Heizung QE und die effektive Strahlung EAeff sind Variable und haben nach Gl. 4 den gleichen Anstieg aber ein umgekehrtes Vorzeichen.
Der Anstieg dieser Geraden EAeff beträgt 4,18 und ist kleiner als die σ-Konstante (5,6703), die Stefan empirisch ermittelt hatte (Abb. 11, schwarze Gerade). Das Verhältnis beider Zahlen 4,18/5,67 = 0,74 zeigt die Schwächung der Aerosol-Platten-Strahlung durch die im Vordergrund agierende Seitenwand, oder vereinfacht ausgedrückt, nur 74 % der Photonen der Aerosol-Platte erreichen die Erd-Platte [11]. Das Verhältnis von EAeff/MA definiert den effektiven Emissionsgrad der Aerosol-Platten-Strahlung εAeff.
Wenn Vorder- und Hintergrund die gleiche Temperatur (TV = TH) haben, ist QE = 0 (Abb. 10). Da man eine Gerade mit nur zwei Punkten konstruieren kann, lässt sich der Anstieg sogar aus einem einzigen Heizungswert QE mit der Bedingung TV > TH durch QE/dT ermitteln (Einpunktkalibrierung). Diese Technik ist die Grundlage für die Bestimmung der CO2-Emissionsgrade (Kap. 2).
Das Abkühlungsexperiment zeigt, dass die Wirkung einer Vordergrundstrahlung EV anhand der Heizung QE ermittelt werden kann. Voraussetzung ist eine Temperaturdifferenz zwischen warmem Vorder- und kaltem Hintergrund, denn bei gleicher Temperatur (TV = TH) ist QE = 0. Oder mit anderen Worten: Der Treibhauseffekt lässt sich nur vor einem kalten Hintergrund experimentell nachweisen. An dieser Anforderung sind alle bisherigen Labor-Experimente von Al Gore bis Wood gescheitert. Anstelle des Treibhauseffektes wurden andere physikalische Effekte (Verhinderung der Konvektion, Wärmeleitung oder Thermalisierung) beobachtet [13], [14], [15].
1.1 CO2-Emissionsgrade
Feste und flüssige Stoffe lassen sich durch einen durchschnittlichen Emissionsgrad ε charakterisieren, der nur durch die Art ihrer Oberfläche, glänzend oder rau/matt, beeinflusst wird. Bei Gasen ist das grundsätzlich nicht möglich, da ihre Strahlung auch von der Anzahl ihrer Teilchen (Masse) abhängig ist. Zur Charakterisierung der Teilchenzahl kann man Konzentrationsangaben (ppm oder Vol.-%) verwenden, solange Temperatur, Druck und Volumen konstant sind. Bei der Erd-Atmosphäre ist das aber nicht der Fall. Die CO2-Teilchenzahl /m3 nimmt jedoch mit steigender Höhe stark ab. Um die Experimente auf die CO2-Strahlung der Atmosphäre übertragen zu können, werden zunächst aus den Versuchs-Konzentrationen (Vol.-%) mit Hilfe der idealen Gasgleichung die Anzahl der CO2-Moleküle n (mol), die sich zwischen den 1,11 m entfernten Erd- und Aerosol-Platten bei einem Strahlungs-Querschnitt von 1 m2 befinden, ermittelt (Gl. 5).
Um die CO2-Strahlung zu ermitteln, wird die CO2-Konzentration schrittweise erhöht und die Heizung QE solange verringert, bis die Erd-Platte exakt wieder die Start-Temperatur von +16,1 °C erreicht hat. Die veränderte Heizung QE zeigt dann die durch CO2 verursachte Strahlungsverstärkung an. Da diese Verstärkung aber nur bei einer bereits vorhandenen, möglichst geringen Hintergrundstrahlung messbar ist, wird die Aerosol-Platte auf eine möglichst konstante Temperatur von -15 °C abgekühlt. Da die CO2-Strahlung auch von der CO2-Temperatur abhängt, muss der gesamte Luftraum eine einheitliche Temperatur haben (isotherme Versuchsbedingungen). Diese Aufgabe übernehmen die Wandheizungen WH1 bis WH3.
Die CO2-Emissionsgrade lassen sich aus dem effektiven Emissionsgrad der Aerosol-Platten-Strahlung εAeff(n) berechnen, da Vordergrundstrahler die effektive Strahlung des Hintergrundes verändern, wie in Kap. 1 abgeleitet wurde (Abb. 11). Dazu wird zunächst ein erster Wert (für n = 0, ohne CO2) nach Gl. 6 ermittelt. Aus diesem Startwert wird dann der Emissionsgrad der Seitenwand εW bestimmt.
Die Zugabe von CO2 verringert die effektiven Emissionsgrade der Aerosol-Platte εAeff(n), da jetzt zur Strahlung EW die CO2-Strahlung hinzukommt, was aus der jeweiligen Heizung QE(n) berechnet wird (Gl. 7).
Da Seitenwand und CO2 die gleiche Temperatur haben, tauschen sie untereinander keine Energie aus und können sich auch nicht gegenseitig schwächen, solange die Summe εW + εCO2 < 1 ist. Es wird deswegen angenommen, dass εW während eines Versuches konstant bleibt. Die CO2-Emissionsgrade εCO2(n) werden aus den effektiven Emissionsgraden εAeff(n)und dem Emissionsgrad εW nach Gl. 7 berechnet.
Die experimentelle Bestimmung der CO2-Emissionsgrade mit der Versuchs-Apparatur hat gegenüber Rechenmodellen den großen Vorteil, dass sie alle Aspekte der komplexen CO2-Strahlung (Einfluss der Rotationslinien, Luft-Temperaturen, Überlagerung mit der Wolken-Strahlung usw.) einschließt.
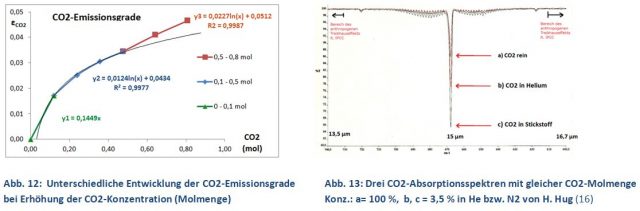
Die grafische Auswertung der CO2-Emissionsgrade zeigt keinen einheitlichen Trend (Abb. 12). Der Verlauf der CO2-Strahlung wird durch drei unterschiedliche Trendlinien (Y1, Y2 und Y3) charakterisiert. Auf den ersten Blick ein unbefriedigendes Ergebnis, aber dann entpuppt sich das Diagramm als eine Überraschung und eine kleine Sensation:
Trotz der sehr einfachen Apparatur lassen sich die Trendlinien Y1 und Y2 als das Ergebnis von Schwingungen (Y1) und Rotationen (Y2) des CO2-Moleküls interpretieren!
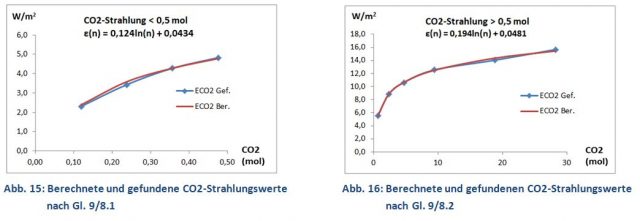
Die Trendlinien geben die Strahlungsmöglichkeiten des CO2-Moleküls wieder. CO2 kann bei einer bestimmten Wellenlänge (Linie) keine höhere Strahlungsdichte erzeugen kann als ein Schwarz-Strahler bei gleicher Temperatur und Wellenlänge. Erreicht die CO2-Strahlung einer bestimmten Wellenlänge den maximalen Wert, spricht man von einer Sättigung dieser Linie. Nun ist die CO2-Valenzschwingung bei 15 µm wesentlich intensiver als die nach außen abflachenden CO2-Rotationslinien (Abb. 13). Schon nach der ersten CO2-Zugabe von 0,1 mol (1 Vol.-%, 2.500 ppm) ist die 15 µm Linie gesättigt und lässt sich behelfsmäßig durch eine lineare Funktion Y1 berechnen (behelfsmäßig, da zwei Datenpunkte zu wenig für eine korrekte Beschreibung sind). Der weitere Verlauf bis zu einer Molmenge von 0,5 mol CO2 folgt aber sehr gut einer logarithmischen Funktion (Gl. 8.1). Dieser Verlauf von Y2 ist das eigentliche Ziel der Untersuchung. Hiermit lässt sich die weitere Progression der atmosphärischen CO2-Strahlung auch oberhalb der derzeitigen 400 ppm ausrechnen.
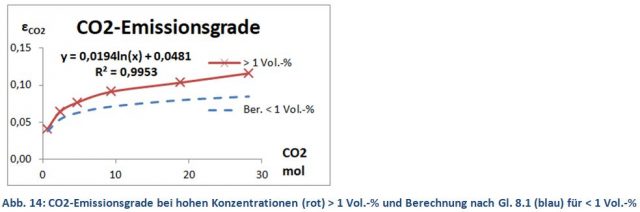
Oberhalb von 1 Vol.-% (0,5 mol) endet der bis dahin logarithmische Verlauf der CO2-Emissionsgrade und es tritt eine unerwartete Zunahme der CO2-Strahlung mit der Trendlinie Y3 (rote Kure) auf. Ein Phänomen, das sich sehr gut reproduzieren ließ und bei allen untersuchten Treibhausgasen bei hohen Konzentrationen gefunden wurde. Ein Kontrollexperiment oberhalb von 1 % bis zu 60 Vol.-% CO2 (30 mol) zeigt erneut einen logarithmischen Trend, nunmehr über den gesamten Bereich und mit einem etwas höheren Korrelationsfaktor (Gl. 8.2 und Abb. 14). Der auffällige Anstieg zwischen Y2 und Y3 konnte als Konzentrationseffekt geklärt werden. Da dieser Mechanismus sehr viel über die Strahlung der Treibhausgase aussagt, wird diesem Effekt ein eigenes Kapitel gewidmet.
1.2 Der CO2-Konzentrationseffekt
Heinz Hug hatte bei der Bestimmung der CO2-Absorption mit einem FT-IR-Spektrometer beobachtet, dass bei gleicher CO2-Menge die Extinktion in Verdünnung mit IR-inaktiven Gasen (Helium bzw. Stickstoff) größer ist als beim reinen CO2 (Abb. 13) [16]. Um den Effekt zu verstehen, muss man wissen, dass CO2-Moleküle elektromagnetische Strahlung nur absorbieren, wenn sie sich im sogenannten Grundzustand befinden. Bei der IR-Bestrahlung werden die CO2-Moleküle aber in den angeregten Vibration/Rotations-Zustand versetzt. Die Energieaufnahme (Schwächung des IR-Lichtes) würde nach kurzer Zeit zum Erliegen kommen, wenn alle CO2-Moleküle in den angeregten Zustand übergegangen sind. Dass das nicht der Fall ist liegt daran, dass die angeregten CO2-Moleküle nach sehr kurzer Zeit (Relaxationszeit) wieder in den Grundzustand zurückfallen und die aufgenommene Energie entweder durch Emission eines Photons oder durch Thermalisierung (Energieübertragung auf IR-inaktive Gasmoleküle oder die Küvettenwand) wieder abgeben. Letztendlich entsteht ein Gleichgewicht von angeregten und nicht angeregten Molekülen, was durch die Inertgase beeinflusst wird. Die Intensität einer Absorption ist demnach nicht nur von der formalen CO2-Konzentration, sondern auch von diesem Anregungs-Verhältnis abhängig, was H. Hug durch sein Konzentrations-Experiment nachgewiesen hat.
Der angeregte Zustand kann jedoch auch durch Kollisionen der Gasmoleküle erfolgen. Auch ohne elektromagnetische Bestrahlung befindet sich dadurch ein Teil der CO2-Moleküle im angeregten Zustand. Der Konzentrationseffekt findet seine Erklärung in der Art der Molekülkollisionen. In großer Verdünnung durch IR-inaktive Gase stoßen die CO2-Moleküle ausschließlich mit den Inertgasen zusammen. Dabei wird die kinetische Energie entweder vom CO2 oder vom Inertgas aufgenommen. Mit steigender CO2-Konzentration steigt aber die Wahrscheinlichkeit, dass zwei CO2-Moleküle kollidieren, was ihre Anregungschance erhöht. Oder mit anderen Worten, mit steigender CO2-Konzentration steigt die Zahl der angeregten CO2-Moleküle: A) durch die Zunahme der Konzentration (Anzahl der CO2-Moleküle) und B) durch die höhere Anregungschance. Die angeregten CO2-Moleküle können durch eine spontane bzw. induzierte Emission in den Grundzustand zurückfallen und die freiwerdende Energie in Form von Photonen abgeben, was die höhere CO2-Emission mit der Trendlinie Y3 (Abb. 12) erklärt. Die quantitative Auswirkung des Konzentrationseffektes zeigt Abb. 14 als Abstand zwischen blauer (gemessener) Kurve für hohe CO2-Konzentrationen und rote Strichpunktkurve (gerechnet) für kleine CO2-Konzentrationen.
Zusammenfassend lässt sich feststellen, dass bei CO2-Konzentrationen > 1 Vol.-% die Zahl der angeregten CO2-Moleküle überproportional ansteigt, was bei den Absorptionsspektren zu einer Schwächung der Absorption (Abb. 13), aber bei den CO2-Strahlungs-Experimenten (Abb. 12) zu einem Anstieg der Emission führt.
Was bedeutet diese Erkenntnis? Auf das atmosphärische CO2 ist der Effekt nicht anwendbar, da hier die Konzentration mit rund 0,04 Vol.-% weit unterhalb der kritischen Schwelle von 1 Vol.-% liegt. Im Folgenden wird deswegen der CO2-Emissionsgrad nur mit Formel 8.1 berechnet. Beim Wasserdampf, der in der erdnahen Atmosphäre bis zu 4 Vol.-% erreichen kann, könnte ein Konzentrations-Effekt von Bedeutung sein.
2. Die CO2-Strahlungsformel
Die CO2-Emissionsgrade wurden aus den experimentell ermittelten CO2-Strahlungen unter Einbeziehung der Temperaturen für den Vorder- und Hintergrund ermittelt. Es liegt deswegen nahe, diese Prozedur einfach umzudrehen und die effektive CO2-Strahlung aus den mol-abhängigen CO2-Emissionsgraden εCO2(n) mit den Temperaturen für den Vorder- und Hintergrund zu berechnen. Dabei ist die CO2-Strahlung ECO2 der tatsächliche, wirksame CO2-Beitrag zur Bestrahlung der Erde von 1 m2, die sogenannte Strahlungsverstärkung einer bereits vorhandenen Hintergrundstrahlung. Die effektive CO2-Strahlung hängt von der CO2-Temperatur, CO2-Molmenge und der Temperatur der Wolken/Aerosole ab. Wird die CO2-Strahlung ohne Hintergrund (TH = 0) gerechnet, bedeutet ECO2 die theoretische, maximal mögliche CO2-Strahlung.
Diese empirisch abgeleitete Gleichung ist nahezu identisch mit Stefans Gl. 2 für den Wärmeverlust des heißen Thermometers, nur dass jetzt noch die CO2-Emissionsgrade εCO2(n) hinzugekommen sind. Mit den Gleichungen 9/8.1 bzw. 9/8.2 lassen sich jetzt die CO2-Strahlungen der Labor-Experimente berechnen. Berechnete und gemessene Werte zeigen eine gute Übereinstimmung (Abb. 15 und 16).
Die Relativität der CO2-Strahlung, also die Strahlungsverstärkung einer bereits vorhandenen Hintergrundstrahlung, wird in Gl. 9 durch die Temperaturdifferenz TV (CO2) und TH (Wolken/Aerosole) ausgedrückt. Dabei ist TV die Luft-Temperatur der erdnahen Luftschicht und TH ist die Strahlungstemperatur der Wolken/Aerosole (in Kelvin), die sich mit einem Pyrgeometer im atmosphärischen Fenster bei rund 10 µm messen lassen. Bei tiefen Wolken oder bei Nebel, wenn TH = TV ist, wird der Ausdruck (TV4/108 – TH4/108) null und CO2, egal in welcher Konzentration, verliert seinen Treibhauseffekt.
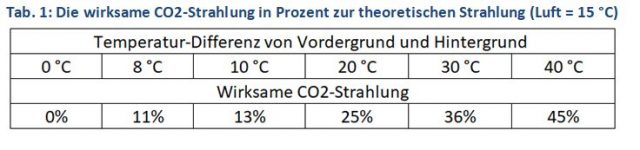
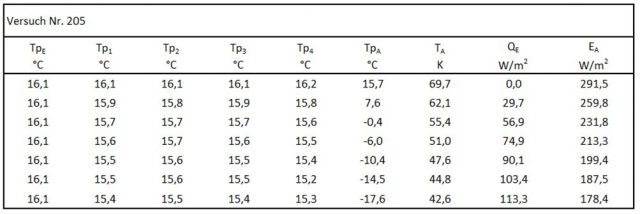
Messungen der Hintergrund- und Luft-Temperaturen in Berlin (2016 bis 2017) ergaben bei wolkenfreiem Himmel einen Temperaturunterschied von 40 °C und bei bedecktem Himmel 8 °C [12]. Natürlich sind diese Messungen nicht repräsentativ für die Erde, aber sie geben eine Vorstellung mit welcher Minderung der theoretischen CO2-Strahlung zu rechnen ist, wenn eine Hintergrundstrahlung berücksichtigt wird (Tab. 1).
2.1 Die atmosphärische CO2-Strahlung
Klimatologen berechnen die atmosphärische CO2-Strahlung mit komplizierten Rechenmodellen, wobei zunächst viele Hundert Linien eines hoch aufgelösten CO2-Spektrums bewertet werden (Abb. 17). Anschließend werden mit den Temperaturen von Troposphäre, Tropopause und Stratosphäre Strahlungsgleichgewichte dieser gewichteten Linien berechnet. Ein gewaltiger Aufwand, den Normalbürger weder verstehen noch nachvollziehen können. Vielleicht aus diesem Grunde haben Ramaswamy et al. [2] mit den erhaltenen Werten für die CO2-Gegenstrahlung eine einfache Beziehung zwischen CO2-Konzentration und -Strahlung, dem sogenannten Strahlungsantrieb dF, aufgestellt (Gl. 10). Das Konzept des Strahlungsantriebes geht von der These aus, dass sich die Welt in einem sensiblen, thermischen Gleichgewicht befindet, das schon durch kleinste Veränderungen, durch eine Kraft (dF) aus dem Gleichgewicht gebracht werden kann. Eine leicht messbare Veränderung ist die CO2-Konzentration, die seit 1750 (Beginn der Industrialisierung) kontinuierlich von 278 bis auf heutige 400 ppm zugenommen hat. Mit Gl. 10 wird nun nach Ramaswamy die zusätzliche CO2-Strahlung dieser Konzentrationszunahme berechnet.

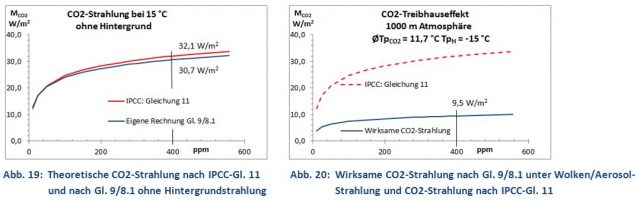
Die Rechnung verschleiert jedoch die absolute CO2-Strahlung und den tatsächlichen CO2-Anteil an der globalen Gegenstrahlung, die sich jedoch wie folgt aus Gl. 10 ableiten lassen. Hierzu wird der Strahlungsantrieb dF für die CO2-Konzentrationen von 278 bis 400 ppm nach Gl. 10 ausgerechnet und als ln(c/278) in einem Excel-Diagramm aufgetragen (Abb. 18). Mit Hilfe der Trendlinie wird für x = 0 (278 ppm CO2) ein Wert von minus 30,108 erhalten. Damit kann man die CO2-Strahlung für das Jahr 1750 zu 30,11 W/m2 ermitteln. Durch Addition dieses Wertes zu Gl. 10 erhält man Gl. 11, mit der sich nun die absolute CO2-Strahlung berechnen lässt. Danach erzeugen 400 ppm CO2 eine Gegenstrahlung von 32,1 W/m2 (30,11 + 1,95) oder 9,6 % der globalen Gegenstrahlung von 333 W/m2 (Abb. 1, 19).
Kiehl und Trenberth geben für CO2 einen Anteil an der Gegenstrahlung (ohne Wolken) von 9 bis 26 % an [17]. Die kleinere Zahl steht für die Mischung von CO2 mit anderen Treibhausgasen und die größere Zahl für reines CO2. Die Angabe von 9 % CO2 deckt sich mit obiger Rechnung nach IPCC-Gleichung 11, aber sie führt auch zu einem Konflikt, da mit diesem kleinen CO2-Wert die Gegenstrahlung von die 333 W/m2 nicht erklärt werden kann. Für Wasserdampf geben die gleichen Autoren einen Anteil von 36 – 70 % an. Rechnet man mit den kleineren Zahlen (9 und 36 % für Gasmischungen), haben Wasserdampf und CO2 nur einen Gesamtanteil von 45 % an der atmosphärischen Gegenstrahlung. 55 % oder 183 W/m2 stammen demnach nicht von diesen Treibhausgasen, sondern von den Wolken/Aerosolen (und einigen Spurengasen). Ein eklatanter Widerspruch zu dem angeblichen Wolken-Treibhauseffekt von nur 30 W/m2 [3].
Nun lässt sich die CO2-Strahlung ja auch mit der experimentell gefundenen Gl. 9/8.1 berechnen. Bei einer Rechnung unter Normalbedingen aber ohne Hintergrund (siehe weiter unten) erhält man eine Strahlungskurve (blau), die mit der IPCC-Kurve (rot) erstaunlich gut übereinstimmt (Abb. 19, Tab. 2). Die gute Übereinstimmung ist eine weitere Bestätigung, dass 400 ppm CO2 bei 15 °C tatsächlich nur eine Strahlung von 31 – 32 W/m2 erzeugen, wenn die Wolken/Aerosol-Strahlung ausgeklammert wird.
Berücksichtigt man jedoch die Strahlung der Wolken/Aerosole, kommt es zu einer weiteren Verminderung der wirksamen CO2-Strahlung von 32 auf nunmehr 9,5 W/m2 (3 % der globalen Gegenstrahlung). Man erhält diesen Wert, wenn in Gl. 9/8.1 für den Hintergrund eine realistische Temperatur von -15 °C (statt -273 °C, ohne Hintergrund) eingesetzt wird. Diese Minderung der CO2-Strahlung entsteht dadurch, da CO2 die gleichen Wellenlängen nutzt, die auch Wolken/Aerosole aussenden, wodurch eine vorzeitige Sättigung eintritt. Die gemeinsame Strahlung regelt sich nach dem Prinzip der Vorder- und Hintergrundstrahlung. Demnach erhält die Erde auch ohne Treibhausgase bereits durch die Hintergrundstrahlung der Wolken/Aerosole eine Gegenstrahlung von rund 275 W/m2 [4]. Die Anwesenheit von CO2 (32 W/m2) und Wasserdampf (0,36 ∙ 333 = 120 W/m2) als Vordergrundstrahler führt zu einer Überlagerung mit der bereits vorhandenen Hintergrund-Strahlung und zu einer Verstärkung durch CO2 und H2O (orange, blau), wodurch die Gegenstrahlung nur um 58 W/m2 auf nunmehr 333 W/m2 ansteigt (Abb. 21). Das Energieschema widerlegt die These eines fragilen Gleichgewichtes. Jede Veränderung eines IR-Strahlers führt zu einer Gegenreaktion der anderen Strahlungsquellen und deutet auf ein robustes Strahlungssystem hin.
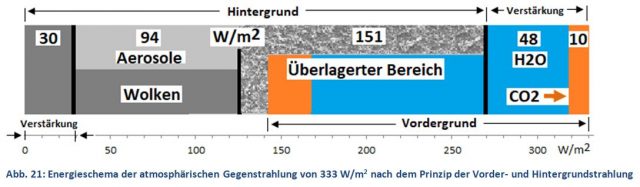 So ist der scheinbar geringe Wolken-Treibhauseffekt nur eine Verstärkung der Aerosol-Strahlung um 30 W/m2, während der größte Teil der Wolken-Strahlung im überlagerten Bereich verborgen ist. Mit dieser Überlegung lässt sich auch das Wolken/IR-Gas-Paradoxon lösen.
So ist der scheinbar geringe Wolken-Treibhauseffekt nur eine Verstärkung der Aerosol-Strahlung um 30 W/m2, während der größte Teil der Wolken-Strahlung im überlagerten Bereich verborgen ist. Mit dieser Überlegung lässt sich auch das Wolken/IR-Gas-Paradoxon lösen.
Das Wolken/IR-Gas-Paradoxon [11]: Bei Messungen der atmosphärische Gegenstrahlung wurde gegensätzliches gefunden:
A) Bei unterschiedlichen Luftfeuchten: Wolken dominant (Wasserdampf hatte geringen Effekt) [18].
B) Bei klarem und bewölktem Himmel: Wasserdampf dominant (Wolken hatten geringen Effekt) [5].
Der Widerspruch löst sich auf, wenn berücksichtigt wird, dass bei Variation einer atmosphärischen Strahlungsquelle (Wasserdampf, Bewölkungsgrad) nicht ihre Strahlung, sondern nur ihre Strahlungsverstärkung gemessen wird.
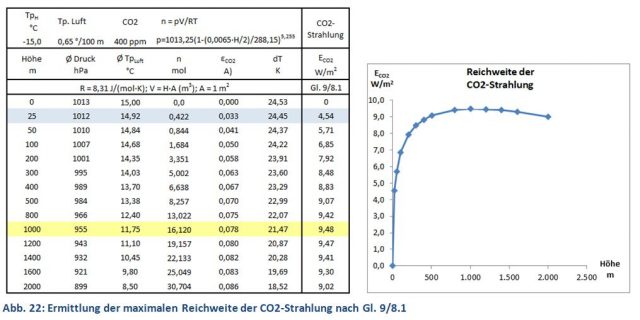
Die folgenden Rechnungen zur atmosphärischen CO2-Strahlung nach Gl. 9/8.1 sind Überschlagsrechnungen, mit denen die Laborversuche auf die Atmosphäre übertragen werden. Zunächst benötigt man die Reichweite der CO2-Strahlung, das ist die Schichtdicke, die gerade noch zu einer Strahlungsverstärkung der Erdoberfläche beiträgt. Hierzu werden schrittweise Luftschichten von 25 bis 2.000 m Dicke analysiert. Benötigt werden Druck, Temperatur und CO2-Molmenge dieser Schichten, die sich aus der barometrischen Höhenformel, einem Temperatur-Gradient von 0,65 K/100 m Höhe und der idealen Gasgleichung ergeben. Temperatur und Druck werden als Mittelwert einer Schicht angesehen. Die Strahlungs-Temperatur des Hintergrundes wurde, mangels bekannter Werte, willkürlich mit minus 15 °C angenommen. Mit diesen Daten wird nun nach Gl. 9/8.1 die CO2-Strahlung jeder Schicht (bezogen auf Höhe = 0) berechnet. Luftschichten über 1.000 m tragen demnach nicht mehr zur Erhöhung der CO2-Strahlung bei, was hauptsächlich durch den Rückgang der Temperaturdifferenz dT = (TV4/108 – TH4/108) verursacht wird. Bemerkenswert ist auch der 50%-Wert, der bei rund 25 m liegt und die kurze Reichweite der CO2-Strahlung unterstreicht (Abb. 22).
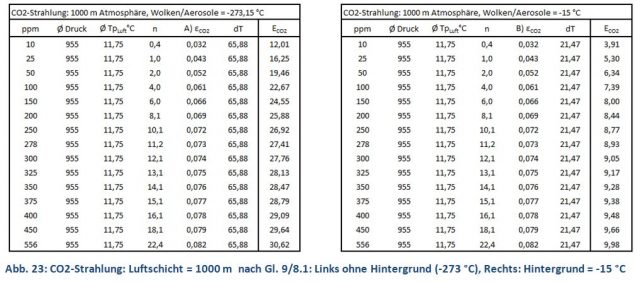
Mit der ermittelten Reichweite von 1.000 m und den dazugehörenden Druck- und Temperatur-Werten wurden die konzentrationsabhängige CO2-Strahlung ohne Hintergrund (Abb. 18, 23) und die CO2-Strahlungsverstärkung (Abb. 1 und 19) berechnet.
-
Anhang- Experimentelle Daten
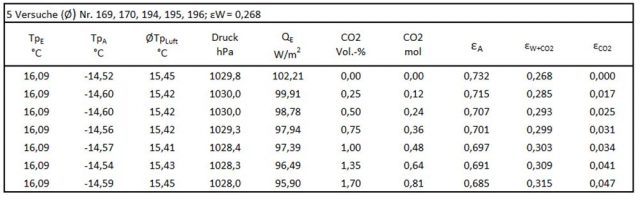
Die Ermittlung der CO2-Emissionsgrade ist schwieriger als die einfache Demonstration des Treibhauseffektes (Abb. 8). Nach jeder Zugabe von CO2 wird die Spannung für die Heizung QE solange verringert, bis die Start-Temperatur der Erd-Platte von 16,09 °C gerade wieder erreicht ist. Da das System von Heizung und Temperatur-Messung eine gewisse Trägheit besitzt, wird das Mittel von zwei Messungen im Abstand von 0,01 bis 0,02 Volt gebildet, die beide eine Temperatur von 16,09 °C ergeben. Die Versuche wurden 3 bis 5-mal wiederholt und als Durchschnittswert gewertet.
Die Erd-Platte hat einen Durchmesser von 16,7 cm und eine Fläche AE= 219,04 cm2. Die Heizung QE der Erd-Platte wird durch Multiplikation mit 45,654 auf einen Quadratmeter AE= 1 m2 umgerechnet. Der Abstand zwischen Erd- und Aerosol-Platte beträgt 1,11 m. Die Molmenge bezieht sich somit auf fiktives Volumen von 1,11 m3.
-
-
CO2-Emissionsgrade bis 0,8 mol (1,7 Vol.-%).
-
-
-
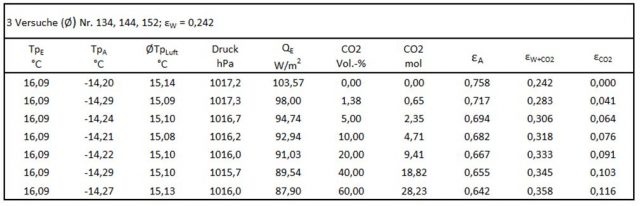
CO2-Emissionsgrade bis 28,2 mol (60 Vol.-%)
-
-
-
Effektive Strahlung EA in Luft
-
Literaturverzeichnis
[1] K. E. Trenberth et al., „EARTH’S GLOBAL ENERGY BUDGET,“ 19 Juli 2008. [Online]. Available: https://www.klimamanifest-von-heiligenroth.de/wp/wp-content/uploads/2016/09/Trenberth_Jones_Treibhauseffekt_TFK_bams_2009_15Grad_390Watt_SBG_gelbMark.pdf
[2] V. Ramaswamy et al., „Radiative Forcing of Climate Change,“ März 2018. [Online]. Available: https://www.ipcc.ch/site/assets/uploads/2018/03/TAR-06.pdf .
[3] „Wolken im Klimasystem,“ 23 Oktober 2017. [Online]. Available: http://wiki.bildungsserver.de/klimawandel/index.php/Wolken_im_Klimasystem .
[4] M. Schnell, „2. Mitteilung: Die Hintergrundstrahlung der Wolken und Aerosole,“ 2018 Juni 2018. [Online]. Available: https://www.eike-klima-energie.eu/2018/06/03/experimentelle-verifikation-des-treibhauseffektes/ .
[5] „Atmosphärische Gegenstrahlung,“ 24 Mai 2009. [Online]. Available: https://de.wikipedia.org/wiki/Atmosph%C3%A4rische_Gegenstrahlung .
[6] E. Roth, „Welchen Einfluss hat CO2 auf das Klima?,“ 02 Juli 2013. [Online]. Available: http://www.energie-fakten.de/pdf/2013-07-roth.pdf .
[7] P. Dietze, „Berechnung der CO2-Klimasensitivität,“ 19 Oktober 2016. [Online]. Available: https://www.eike-klima-energie.eu/wp-content/uploads/2016/11/Dietze_Klimasensitivitaet_ECS-4.pdf .
[8] J. Stefan, „Über die Beziehung zwischen der Wärmestrahlung und der Temperatur.,“ SB der Ak. d. Wiss. Wien, Math. Physikal. Kl. 79, 1879, S. 391-428, Wien, 1879.
[9] P. Dulong, Annales de chim. de phys, Bde. %1 von %2VII. Seite 225 – 264 und 337 – 367,, 1817.
[10] „Stefan-Boltzmann-Gesetz,“ 26 September 2018. [Online]. Available: https://de.wikipedia.org/wiki/Stefan-Boltzmann-Gesetz .
[11] M. Schnell, „Experimentelle Verifizierung des Treibhauseffektes,“ 12. Internationale Klima- und Energiekonferenz (IKEK-12), München, 2018.
[12] M. Schnell, „3. Mitteilung Labor-Experimente zur Demonstration des CO2-Treibhauseffektes,“ 17 Juli 2018. [Online]. Available: https://www.eike-klima-energie.eu/2018/07/17/experimentelle-verifikation-des-treibhauseffektes-2/ .
[13] N. S. Nahle, „Repeatability of Prof. Robert Wood’s 1909 Experient on the Theory of the Greenhouse,“ 05 Juli 2011. [Online]. Available: http://www.biocab.org/experiment_on_greenhouses__effect.pdf .
[14] A. Watts, „Replicating Al Gore’s Climate 101 video experiment shows that his „high school physics“ could never work as advertised,“ [Online]. Available: https://wattsupwiththat.com/2011/10/18/replicating-al-gores-climate-101-video-experiment-shows-that-his-high-school-physics-could-never-work-as-advertised/?cn-reloaded=1 .
[15] S. Sirtl, „Absorption thermischer Strahlung durch atmosphärische Gase. Experimente für den Physikunterricht,“ 12 November 2010. [Online]. Available: https://docplayer.org/18989667-Absorption-thermischer-strahlung-durch-atmosphaerische-gase.html .
[16] H. Hug, „Der anthropogene Treibhauseffekt – eine spektroskopische Geringfügigkeit,“ 20 August 2012. [Online]. Available: https://www.eike-klima-energie.eu/2012/08/20/der-anthropogene-treibhauseffekt-eine-spektroskopische-geringfuegigkeit/ .
[17] „Treibhauseffekt,“ 16 Januar 2019. [Online]. Available: Literatur\Treibhauseffekt Wikipedia.pdf.
[18] F. Albrecht, Untersuchungen über den Wärmehaushalt der Erdoberfläche in verschiedenen Klimagebieten, Bd. VIII, Berlin: Julius Springer, 1940.
Diesen Beitrag gibt es auch als PDF auf Deutsch
Experimentelle Verifikation des Treibhauseffektes – Die erdnahe CO2-Strahlung
und auf Englisch
Experimental verification of the greenhouse effect – The near-Earth CO2 radiation



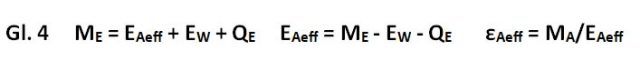
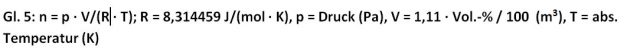
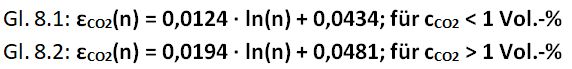
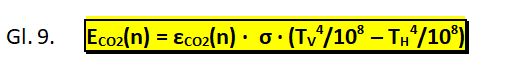
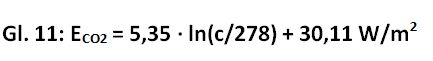















Sie schreiben: „Mit ein wenig Logik und Mathematik lässt sich aus den IPCC-Angaben die aktuelle CO2-Strahlung zu rund 32 W/m² (10% der globalen Gegenstrahlung, Abb. 1, schwarze Kurve) ermitteln.“
Das kann ich nicht nachvollziehen. Meiner Meinung nach geht der IPCC und der Mainstream der Klimaforscher von einer noch viel geringeren Gegenstrahlung durch CO2 aus. Begründung:
Der Mainstream der Klimaforschung geht davon aus, dass der Strahlungsantrieb des anthropogenen CO2 ungefähr 1,8 Wm^-2 beträgt. Hierzu z.B.
https://www.ipcc.ch/site/assets/uploads/2018/02/WG1AR5_Chapter08_FINAL.pdf
>“Using the formula from Table 3 of Myhre et al. (1998), and see Supplementary Material Table 8.SM.1, the CO2 RF (as defined in Section 8.1) from 1750 to 2011 is 1.82 (1.63 to 2.01) W m–2.“
Bei 130 ppm anthropogen und 410 ppm Gesamt-CO2 sind das
1,8 Wm^-2 * 410ppm/130ppm = 5,68 Wm^-2 für das gesamte CO2, also viel weniger als die von Ihnen angegebenen 32 Wm^-2.
Der Mainstream der Klimaforscher sieht außerdem in dem Artikel von Feldman und Collins, 2015, mehr oder weniger einen Beweis, dass die CO2-Hypothese zutrifft. Hier ein Link zum Artikel:
http://asl.umbc.edu/pub/chepplew/journals/nature14240_v519_Feldman_CO2.pdf
Es heißt dort im Text unter Bezug auf zuvor genannte Quelle des IPCC:
>“Radiative transfer models calculate that the increase in CO2 since 1750 corresponds to a global annual mean radiative forcing at the tropopause of 1.82 +/- 0.19Wm^-2 (ref.2).“
Feldman und Collins messen über ein Jahrzehnt bei klarem Himmel und einer Zunahme von 22 oder 23 ppm CO2 (widersprüchliche Angaben im Artikel) 0,2 Wm^-2:
>“Here we present observationally based evidence of clear-sky CO2 surface radiative forcing that is directly attributable to the increase, between 2000 and 2010, of 22 parts per million atmospheric CO2. […] The time series both show statistically significant trends of 0.2 Wm^-2 per decade (with respective uncertainties of +/-0.06 Wm^-2 per decade and +/- 0.07 W m^-2 per decade) and have seasonal ranges of 0.1–0.2 Wm^-2 . […] We focus here on clear-sky flux changes because models predict most of the CO2 surface forcing to occur under clear-sky conditions 15. “
15. Stephens, G.L. et al. An update on Earth’s energy balance in light of the latest global observations. Nature Geosci. 5, 691–696 (2012).
Betrachten wir die Messungen und Aussagen mal etwas genauer: Feldmann und Collins (F&C) messen also über ein Jahrzehnt eine Zunahme der Rückstrahlung bei klarem Himmel von 0,2 Wm^-2 bei einer Zunahme der CO2-Konzentration von 369 (oder 370) auf 390 ppm.
Dies entspricht bei einem anthropogenen Anteil von ca. 130 ppm am derzeitigen Wert von 410 ppm Gesamt-CO2 einem Strahlungsantrieb von 0,2 Wm^-2 * 130ppm/22,5ppm = 1,15 Wm^-2.
Hierbei bezieht sich der von F&C ermittelte Wert aber nur auf einen klaren Himmel. Er muss also deutlich nach unten korrigiert werden, um ihn mit dem Wert von 1,8 Wm^-2 vergleichen zu können, den das IPCC genannt hatte. Wir haben also schon im Mainstream eine Diskrepanz um einen Faktor von ca. 2 bis 3. Und gemäß der Messungen von F&C eine aktuelle Gegenstrahlung des Gesamt-CO2 von etwa 0,2Wm^-2 * 410ppm/22,5ppm = 3,64 Wm^-2 (nota bene bei KLAREM HIMMEL).
Also noch einmal die Frage zu Beginn: Wie kommen Sie auf 33 Wm^-2 und was halten Sie von dem durch F&C ermittelten Wert von 3,6 Wm^-2?
mfg
Roland Köster
https://www.ipcc.ch/site/assets/uploads/2018/03/TAR-06.pdf
>“The new best estimate based on the published results for the radiative forcing due to a doubling of CO2 is 3.7 Wm^−2, which is a reduction of 15% compared to the SAR. The forcing since preindustrial times in the SAR was estimated to be 1.56 Wm^−2; this is now altered to 1.46 Wm^−2 in accordance with the discussion above.“
Der von mir aus den Mars-Daten berechnete Extinktionskoeffizient führt übrigens zu einem Strahlungsantrieb von 1,43 Wm^-2 für das Gesamt-CO2 von 410 ppm bei klarem Himmel.
Dieser Wert führt zu 0,279 Wm^-2 bei durchschnittlich bedecktem Himmel. Das lässt sich in eine direkte Temperaturerhöhung umrechnen. Wenn die Luft über dem Erdboden 288K warm ist, beträgt die vom Boden emittierte Strahlung I gemäß 5,67E-8 * 0,989 * T^4 = 385,789 m^-2. Einer Strahlung von 386,068 m^-2 entspricht eine Temperatur von 288,052K. Die direkte Wirkung des anthropogenen CO2 entspricht also einer Temperaturerhöhung von 0,052K.
Diese Emission (0b nun größer oder kleiner) klingt – wie die des Wasserdampfes von einem Maximum an der Erdoberfläche ausgehend – konzentrations- und temperaturabhängig nach oben ab.
Die Wasser- und Eispartikel darüber absorbieren und wandeln auch den Energiefluss aller „Wärmestrahlung in Wärme“ und emittieren Energie temperaturabhängig als Wärmestrahlung in den Raumwinkel von 360 Grad, also auch als Energiefluss der sog. Gegenstrahlung zurück zur Materie an der Erdoberfläche. – Daher kann eine Interaktion von CO2 und Wasserdampf die Größe des Rückfluss von Energie aus der Atmosphäre nicht beeinflussen!!!! Als Folge ist die geliebte https://de.scribd.com/document/372778420/Klimasensitivita-t-des-CO2-eine-Seifenblase
Die Wirkung einer energetischen Rückkopplung ist in der Physik sehr gut bekannt! Den Zustand und die Temperatur der Materie an der Erdoberfläche, ihre Enthalpie, bestimmt daher das Produkt aus der Größe des gesamten Zuflusses von Energie und ihrer Speicherzeit. („Die obere Schranke der durch Rückkopplung erzielbaren „Erwärmung“ ist daher leider die Emissionstemperatur der Sonne.“) – Man nennt das alles auch: http://de.scribd.com/doc/144664169/Treibhauseffekte
Sogar ein Goebbels hat übrigens die „energetische Rückkopplung“ mit seiner sog. „Propagandaorgel“ im Großversuch nachgewiesen!!
Schauen Sie hier: https://tinyurl.com/y98bm8v8
ja danke, Herr Weber, der Ozeanpuffer als thermostatheizungsfunktion ist an sich bekannt. Die Erklärung der ominösen 33 grad ist auch interessant. Also THE reine Fiktion, da zu marginal, um spürbare Effekte zu haben. Was mich auch wundert, ist, dass, selbst bei diesem unsäglichen Beginn 1850 rum, als grad sehr kalte Phase war (vgl. mit Temp.messungen ab 1700 aus Nordeuropa-Paris, London…, kann für welweite Aussage durch Eisbohrkerne sicher bestätigt werden…) nun trotz Datenmanipulation, Meßpunktwechsel, Wärmeinseleffekte, Meßmethodik und-gerätewechsel, Milliarden mehr an Menschen, der gewaltigen Industrie, etc., nicht mal ein lumpiges Grad mehr nachweisbar ist. Und wenn man wie Herr Limburg sich mit Fehlergrößen auskennt, ist klar, dass selbst Nutzung ( ebenfalls nicht fehlerfreier) Satellitendaten ( in jüngerer Zeit) es nicht erlauben. mit 10-tel !!! grad als WELTWEITEN Durchschnitt zu hantieren. unseriös. Also sind die Tendenzen und Schwankungen eigentlich nicht der Rede wert bei all diesen Änderungen, es bleibt nur die fade Feststellung, dass es sich um eine politisch gewollte Indoktrination zur Umsetzung der Globalistenziele auf Kosten der verführten und verdummten Masse handelt… und dank Lücken-/Lügenmedien halten sie leider (noch) den Kurs.
Ich musste jede Menge Steuerzeichen aus Ihrem Text entfernen. Bitte anderen Editor/Browser verwenden.
Ja, bisher kein Problem.
Die Effektivtemperatur Teff wurde ursprünglich für Stern-Atmosphären definiert, bei denen der gesamte Energietransport über die Stern-Atmosphäre in den Weltraum stattfindet (Annahme: Isotropie). Bei Planeten ist das jedoch anders, hier findet ein Teil des Energietransportes direkt von der Planeten-Oberfläche ins Weltall statt.
Man unterscheidet bei Planeten die Effektivtemperatur und die planetare Effektivtemperatur. Bei den aktuellen Gegebenheiten der Erde ergibt sich eine Effektivtemperatur von Teff = 242K (+/- 1K) und eine planetare Effektivtemperatur von Teff,p = 255K (+/- 2K).
Bei Betrachtungen die nur die Erd-Atmosphäre betreffen, muss man mit der Effektivtemperatur von Teff = 242K arbeiten.
Die Definition der Effektivtemperatur Teff (laut Eddington):
Die Effektivtemperatur Teff charakterisiert den wesentlichen Teil der Energie, die über die Stern-Atmosphäre unter Annahme der Isotropie in den Weltraum abgegeben wird.
Eddington-Barbier Relation (Annahme: Isotropie): T(tau)^4 = 3/4*Teff^4*[tau + 2/3]
Für die Erde:
+ bei der optischen Dicke tau = 2/3 ist T(tau=2/3) = Teff
+ bei der optischen Dicke tau = 2 erhält man die atmosphärische Oberflächen-Temperatur T(tau=2) = 287,8K
+ bei der optischen Dicke tau = 0 erhält man die atmosphärenlose Oberflächen-Temperatur T(tau=0) = 203,5K
Folgende „Temperaturen“ sind für die Strahlung von Körpern definiert:
+ Effektivtemperatur Teff – Temperatur desjenigen äquivalenten schwarzen Körpers, der pro Einheitsfläche die gleiche Gesamtenergie ausstrahlt.
+ Strahlungstemperatur TStr – …, der im beobachteten Spektralbereich [endliches dλ] pro Einheitsfläche die gleiche Energie ausstrahlt.
+ Schwarze Temperatur TSchw – …, der bei einer bestimmten Wellenlänge pro Einheitsfläche die gleiche Energie ausstrahlt.
+ Farbtemperatur TF – …, der im beobachteten Spektralbereich den gleichen Verlauf der Intensität zeigt.
+ Gradationstemperatur TG – …, der bei einer bestimmten Wellenlänge die gleiche Steigung des Intensitätsverlaufs zeigt (= Grenzfall von TF für dλ -> 0).
+ Wiensche Temperatur TW – aus dem Maximum der Intensitätsverteilung nach dem Wienschen Gesetz.
Alle anderen „Temperatur-Namensgebungen“ für die Strahlung, wie Abstrahlungstemperatur oder Emissionstemperatur oder Strahlungsgleichgewichtstemperatur usw. gibt es nicht, sind also der Phantasie der Schreiber entsprungen.
Die Effektivtemperatur Teff ist keine Temperatur im eigentlichen Sinne, sondern ein Maß für die Gesamtenergie. Der Übergang Teff -> TStr entspricht dem Übergang der bolometrischen Magnitude zur visuellen Magnitude m(bol) -> m(vis) und TSchw ist ein Grenzfall von TStr für dλ -> 0. Auch die Strahlungstemperatur TStr ist nur ein formales Maß für die Energie.
Zum Beispiel die Sonne:
Die Effektivtemperatur der Sonne (L = 4pi*r^2*F(r); F(r) = sigma*T^4 -> L = 4pi*r^2*sigma*Teff^4) beträgt Teff = 5800K, die Strahlungstemperatur dagegen TStr = 6050K. Die Synchrotronstrahlung der Magnetfeld-Erscheinungen der Sonne ist dabei nicht berücksichtigt.
Die Effektivtemperatur kann nur im thermodynamischen Gleichgewicht mit der thermodynamischen Temperatur gleichgesetzt werden.
Die Energieverteilung in horizontaler Richtung durch die fluiden Elemente auf der Erde ist sehr effizient. Der Atmosphären- und Oberflächen-Effekt ist somit ein Energieverteilungs-Effekt über die fluiden Komponenten der Erde, wobei ca. 57% auf die Atmosphäre und ca. 43% auf die Ozeane im hundertjährigen Mittel bei der aktuellen Gestalt der Erde entfallen.
Mfg
Werner Holtz
Sehr geehrter Herr Klaus Mager,
es ist wirklich interessant,sich über diese Vergleichspunkte mal etwas genauer zu unterhalten.
Dabei werden Sie feststellen,das eine verfeinerte Betrachtung ihre Tücken hat.Es ist der Mühe wert.
Man muss sich nicht unbedingt vor einem Tensor verneigen,um diesem Märchen vom Treibhauseffekt auf die Spur zu kommen.
Schreiben Sie mal welche 2 Stationen Ihnen da ins Auge gefallen sind.
Falls Sie noch interessiert sind?!
Es wurden Messungen mit dem Atmospheric Emitted Radiance Interferometer (AERI) in den verschiedenen Klimazonen durchgeführt und eine Abschätzung vom mittleren Emissionsverhalten im oberflächen-nahen Bereich der Atmosphäre vorgenommen.
Funktionsweise siehe: Atmospheric Emitted Radiance Interferometer. Part II: Instrument Performance – Knuteson et al., 2004
Die Abschätzung ergab für die hemisphärische Energieflußdichte der Emission im oberflächen-nahen Atmosphären-Bereich für die gasförmigen Anteile unter Standard-Bedingungen und wolkenlosen Himmel im Mittel 130 – 142 W/m^2 (32-36 W/m^2 CO2 und 98-106 W/m^2 Wasserdampf, Ozon u.a.). Zuzüglich des Wasserdampf-Gehaltes bis zum Taupunkt, erhält man eine mittlere hemisphärische Energieflußdichte der Emission im oberflächen-nahen Atmosphären-Bereich bei Standard-Bedingungen von 102 – 238 W/m^2. Betrachtet man noch den Flüssig-Wasser-Anteil (Wolken, Nebel usw.) ergibt sich im Mittel eine Größe von 204 – 408 W/m^2. Weshalb der „Sprung“ vom Flüssig-Wasser-Anteil so groß ist, erklärt sich durch den „Freiheitsgrad-Gewinn“ (gasförmig: f=12; flüssig: f=18) beim Übergang der Dampf- bzw. Gasphase in die Flüssigkeitsphase.
Die Überlagerungs- und Verschiebungs-Effekte (Fugazitäts-Faktor) der Spektren bei den AERI-Messungen werden hauptsächlich durch die folgenden drei atmosphärischen Elemente hervorgerufen, der so genannte Liquid/Ice Water Path (LWP/IWP), der Precipitable Water Vapor (PWV) Wert und die Windgeschwindigkeit. Für Messungen der reinen gasförmigen Anteile der Atmosphäre sollten diese drei Größen möglichst kleine Werte haben (LWP < 5 g/m^2, PWV < 0,5 mm und Windstille). Ganz ausschließen lassen sich diese Überlagerungs- und Verschiebungs-Effekte aufgrund der natürlichen Gegebenheiten jedoch nicht.
Die sogenannte „Gegenstrahlung“ ist das Ergebnis aus der Energiebilanz-Erhaltung der solaren Einstrahlung. Einen wie auch immer gearteten „atmosphärischen Treibhauseffekt“ gibt es nicht, dieser würde gegen die Bilanzerhaltung der Energie verstossen – So einfach ist das!
@ Hr. Schnell
zu 1.2 Der CO2-Konzentrationseffekt
Dieser Effekt begründet sich nicht durch eine Anregung durch Stoß, sondern durch Kollisionsabsorption oder kollisionsinduzierte Absorption. Diese Form der Energieaufnahme tritt aber nicht nur bei CO2-CO2 Kollisionen auf, sondern auch mit anderen Molekülen wie N2 oder O2 (größerer Relativ-Geschwindigkeit als CO2). Hierbei werden stoß-induzierte Dipolübergänge erzeugt, welche eine deutlich stärkere Absorption bewirken. Da die Absorption durch Stöße hervorgerufen wird, spielt die Dichte eine entscheidende Rolle.
Zitat: … oder durch Thermalisierung (Energieübertragung auf IR-inaktive Gasmoleküle oder die Küvettenwand)
Definition: Die Thermalisierung beschreibt die Vorgänge in Körpern, die das thermische Gleichgewicht durch Wechselwirkungen erreichen. Die Thermalisierung wird von allen temperatur-ändernden Prozessen bestimmt. Zur Thermalisierung gehören folgende Prozesse: Stoß-, Ionisations-, Absorptions- und Emissionsprozesse.
Mfg
Werner Holtz
Sie haben richtig erkannt, dass „der THE die Abkühlung verzögert und damit zweifellos ggf. die Erwärmung verstärkt!“
MfG
„zweifellos gegebenenfalls“ Gehts noch?
Wenn sie einen Koerper der 30 Grad C warm ist, innerhalb einer Stunde oder in zwei Stunden abkuehlen lassen, dann war der Koerper doch nur 30 Grad C warm.
Mit Ihrer generalisierten Aussagen wollen sie vom globalen Geschehen auf die lokalisierte Moeglichkeit der Wolkenbedeckung umschwenken.
Welche Schluesse wollen sie im Zusammenhang mit Wolken auf den THE ziehen?
Lieber Herr Schulz.
hier etwas zum Einlesen auch für Anfänger:
http://de.scribd.com/doc/144664169/Treibhauseffekte
https://de.scribd.com/document/372778420/Klimasensitivita-t-des-CO2-eine-Seifenblase
MfG
das sind mir zu viele Effekte. Sind das mehrere oder nur einer?
Was ist ein Anfaenger? Einer der nicht mal ein Gewaechshaus mit sinnvollen Worten beschreiben kann?
Habe nur einmal das Wort Konvektion gefunden.
Das reicht nicht in dem Zusammenhang.
Wie kann man was erkennen, was es nicht gibt???
THE: wie definiert?
„Die Abkühlung“: von was? Oberfläche? Atmosphäre?
„Verzögert“: Wie? Tagsüber? Nachts? Wird es deshalb im anderen Teil des Tages wärmer?
„Wärmer“: Wo?
hier noch einmal die Antworten auf Ihre permanent wiederholten Fragen:
http://de.scribd.com/doc/190496647/Angst-auf-Objektsuche-wahlt-Klimawandel-und-Energiewende
MfG
@Wolff nein, da Sie sicher auch ab und an früh aufstehen, werden Sie feststellen, Treibhaus Erde hat kein Dach, bei uns ist es daher früh um 5 meist am kühlsten, die Verzögerung reicht nicht für Restwärme zum Aufheizen.punkt. Als nennenwerter Speicher ist nur Erde und Ozean zu betrachten, aber Ozean regelt ja dann über Verdunstung, dass es nicht aufheizt. Und Wüste geht jede Nacht auf nahe 0!° runter, also wovon sprechen wir nun? Die Luft hat nur geringe direkte durch Strahlung bedingte Aufnahmemöglichkeiten, aber diese werden ja auch bei Sonnenaufgang schon in Anspruch genommen mit dem Anteil infrarot des einfallenden Lichts, so dass es erst leicht verzögert warm wird auf Erde und abends später kühler , als zum Zeitpunkt, wenn Sonne untergeht, aber bei CO2 ist auch dass nicht messbar. Es ist nunmal ein Spurengas und kann nix bewirken außer gutes Pflanzenwachstum.
Lieber Herr Mager,
Sie irren! – Bis in die Tropopause hinein übernehmen Wasser- und Eispartikel die Aufgaben der Verglasung des Gärtner Treibhauses, seines Daches:
Reflexion von Solarstrahlung, Emission von Wärmestrahlung, sammeln aller Energieflüsse der Wärmestrahlung, Konvektion, Kondensation und Wärmeleitung und ihre Wandlung in Wärme!
Meine Empfehlung: Hin und wieder das Schreiben durch Lesen unterbrechen. http://de.scribd.com/doc/144664169/Treibhauseffekte
MfG
Sehr geehrter Herr Dr. Schnell,
in Ihrem Artikel stellen Sie in den Erläuterungen zu den Gleichungen (1) – (3) falsche inhaltliche und physikalische Zusammenhänge her, Zitat:
„Mit Gl. 2 legt Stefan die Grundlage für die Berechnung des Treibhauseffektes. Die Abkühlung des Thermometers (Energieverlust) hängt sowohl von der Temperatur T1 als auch von T2 ab, also von der Differenz zwischen Ausstrahlung des Thermometers und Gegenstrahlung der Kupferwand.“
Diese Aussage enthält gleich drei Fehler:
Sie schreiben Ihre Gleichungen 1 und 2 Josef Stefan [8] zu und stellen diese in den Kontext einer Wärmeübertragung zwischen parallelen Oberflächen. In den Sitzungsberichten der Kaiserlichen Akademie der Wissenschaften in Wien ist in Band 079 (1879) aber keine solche Arbeit von Stefan auffindbar.
Bei Ihrer Gleichung 2 handelt es sich vielmehr um eine sehr eigenwillige Interpretation der Umgebungsgleichung des Stefan-Boltzmann-Gesetzes unter Vermeidung der spezifischen Strahlungsleistung (S = P/A).
Implizit erfordert Ihre Schreibweise (P = SIGMA A T1hoch4 – SIGMA A T2hoch4) daher exakt gleich große Oberflächen (A) für den Schwarzkörper und seine Umgebung – und verlässt damit eindeutig den vorgegebenen physikalischen Kontext (Körper<<Umgebung).
Mit Bezug auf die Umgebungsgleichung des Stefan-Boltzmann-Gesetzes schreiben Sie der Umgebungstemperatur T2 nun willkürlich eine „Gegenstrahlung“ zu. Aber anders als beim Stefan-Boltzmann-Gesetz (Ihre Gleichung 3), das eine Umgebung von 0 Kelvin voraussetzt, strahlt ein Schwarzer Körper (T1) in einer erwärmten Umgebung (T2) lediglich mit einer verminderten Leistung nach der S-B Umgebungsgleichung DELTA S (=P/A) = SIGMA (T1hoch4 – T2hoch4).
Es handelt sich hierbei physikalisch also eindeutig um eine verminderte Abstrahlung des Schwarzen Körpers und nicht um eine „Gegenstrahlung“ seiner Umgebung!
Die Verminderung der Strahlungsleistung eines Schwarzen Körpers mit (T1) in einer Umgebung von (T2>0K) stellt also keinerlei physikalischen Beweis für eine „Gegenstrahlung“ dar, sondern folgt lediglich der bekannten Umgebungsgleichung des Stefan-Boltzmann-Gesetzes. Die implizite Definition Ihrer „Gegenstrahlung“ ist demnach physikalisch eindeutig falsch, wie das nachfolgende Beispiel verdeutlichen mag:
Sie brühen sich einen Tee auf und holen ein Eis aus dem Tiefkühler. Dann werden Sie gestört und stellen nach Stunden fest, dass beide jetzt die Zimmertemperatur angenommen haben. Weder fällt also die Temperatur Ihres Tees auf 0 Kelvin, noch wurde das geschmolzene Eis durch eine unerwartet aufgetretene „Gegenstrahlung“ erwärmt. Vielmehr haben sich beide lediglich an ihre Umgebungstemperatur „angepasst“ – und diese Umgebungstemperatur hat sich wegen der extrem unterschiedlichen Größenverhältnisse (Körper<<Umgebung) praktisch nicht verändert.
Ich stelle also zusammenfassend fest: Die reduzierte Strahlungsleistung eines Körpers (T1) in einer erwärmten Umgebung (T2) wird physikalisch eindeutig über die Umgebungsgleichung des Stefan-Boltzmann-Gesetzes beschrieben. Diese Verminderung der Strahlungsleistung hat demnach physikalisch überhaupt nichts zu tun mit einer sogenannten „Gegenstrahlung“ oder einem angeblichen „Treibhauseffekt“, die beide auf einer unbewiesenen Energievermehrung zusätzlich zur globalen Energiebilanz basieren und damit den 2. Hauptsatz der Thermodynamik verletzen.
Wenn also die Umgebungsgleichung des Stefan-Boltzmann-Gesetzes tatsächlich die theoretische Grundlage für Ihre „Verifikation des Treibhauseffektes“ darstellen sollte, dann ist dieses Vorhaben physikalisch eindeutig als gescheitert zu betrachten.
Mit freundlichen Grüßen
P.S.: Hier finden Sie noch einige Informationen zur S-B Umgebungsgleichung https://tinyurl.com/y9vz6hgw
———————————-
Bis hier gelesen und sofort aufgehört!
Und ewig grüßt das Murmeltier!
Jeder Mensch, der seinen gesunden Menschenverstand einschaltet, wird sofort sehen, dieses IPCC Bildchen mit der Darstellung der angeblichen Energieströme ist ein Witz!
Wer das Ernst nimmt, zeigt nur, dass er keinen Humor hat!
Einen „Treibhauseffekt“ gibt es nicht – ansonsten hätten sich die klugen Menschen längst etwas einfallen lassen, um diese angebliche Atmosphären-Strahlung von ca 333 W/m² zu nutzen!
Für die angebliche 161 W/m² Sonnenstrahlung pflastert man ja auch die halbe Welt zu!
Jo!
zwar habe ich ein Ingenieurdiplom, Ihre vier Arbeiten in der Thematik durchzulesen, und zu begreifen, würde mir Wochen, wenn nicht Monate dauern.
Könnten sie Ihre Ergebnisse in 10-20 Sätzen zusammenfassen? Sie fangen zwar mit einer Kurzfassung an, was diesem Zweck dienen sollte. Trotzdem ist es für mich nicht nachvollziehbar. Schlüsselpunkt Ihrer Argumentation sollte das linke Bild der Abbildung 1 sein.
Sehe ich das richtig, die Ergebnisse Ihrer Arbeiten ergeben hier die rote Linie? Oder ist die rote Linie unabhängig von Ihren Arbeiten entstanden? Wenn ja, aufgrund wessen Berechnungen?
Was heißt diese rote Linie auf exakte Zahlen übersetzt?
Wie beeinflussen Ihre Ergebnisse das rechte Bild dieser Abbildung?
Welche Konsequenzen haben Ihre Arbeiten für das IPCC-Modell?
Könnten Sie dieses rechte Bild mit den richtigen Zahlen hier veröffentlichen?
Ich erwarte eine Aussage von Ihnen, etwa, daß die Erhöhung des CO2-Gehaltes der Atmosphäre auf x ppm nur eine Temperaturerhöhung von y Grad C bewirkt (statt des von der IPCC behapteten z Grad C).
Und noch etwas:
Berücksichtigen Sie, daß die CO2-Moleküle der Atmosphäre auch von den IR-Strahlen ex Sonne angeregt werden? Zumal sie eine höhere Strahlungsleistung haben, als die IR-Strahlen ex Erde. Das heißt nämlich für mich, daß die Erhöhung der CO2-Konzentration der Atmosphäre eine Abkühlung zur Folge hat.
Sehe ich das richtig?
Zum Glueck ist die Laenge auch damit verbunden einige Schwierigkeiten des Messaufbaues darzulegen.
Da alle Stoffe, ausser strahlungs-inaktiven Gasen, immer elektromagnetische Strahlung abgeben kann man in den Messaufbauten nur schwer feststellen wo die Strahlung wirklich herkommt: Ob vom Gas oder der dahinterliegenden Wand.
Deshalb wird gesagt, dass man die Messung am Besten vor einem nichtstrahlenden Hintergrund machen sollte. Durch Analyse des Spektrums kann man vielleicht sagen wo die Strahlung herkommt, das ist aber in dem Versuchsaufbau nicht gegeben. Oder ist es?
Was mich interessiert ist im Rahmen des Abkühlungsexperiments:
Dabei wird die Heizung heruntergedreht weil die Ausgleichstrahlung vom CO2 kommt.
Die verringerte Heizleistung soll Ausdruck sein fuer die Gegenstrahlung.
Da diese Strahlung auch auf die Aerosolplatte gerichtet ist, muesste diese sich dann aber erwaermen.
Frage ist, wie hoch ist die dazu erforderliche Kuehlleistung und wie aendert sie sich, um den kalten Hintergrund zu erhalten? Welche Schluesse kann man daraus ziehen?
Bei den Grünen ist der Autor nun aber ein Held, und vielleicht spekuliert er auf einen gut dotierten Job in Potsdam.
Einige Kommentatoren sprechen wenigstens schon mal von Wärmekapazitäten.
Andere von der Entropie als physikalische Zustandsgröße ,die den Wärmetransport beschreibt.
Was noch fehlt sind die entsprechenden Speicher,damit man mal eine Überschlagsrechnung machen kann.Die Verfeinerung kann in einem nächsten Schritt erfolgen,wenn erkennbar wird,es macht noch einen Sinn.
Nehmen wir an,die Luftsäule von 1 Quadratmeter Grundfläche hat eine Masse von 10000 Kilogramm.Dann sind die 100 Kg Wasser und sonstige zwar wichtig.Für die Beschreibung des Speichers fallen Sie vorerst nicht ins Gewicht.
Die entscheidende Idee: alle Wärme,die nicht über IR-Strahlung die Erde verlässt,wird in diesem Speicher dafür sorgen,dass er wärmer wird.
Der andere Speicher wird als Oberflächenspeicher identifiziert.Das ist der Erdboden und die Ozeane.
Diese Speicher lassen sich als lineare oder exponentielle Speicher beschreiben.
Das geschieht analog,wie bei einem RC-Glied. Das ist in der Grundstruktur das ganze Geheimnis.
Wenn man dann noch mit etwas Geschick den Netzknotensatz von Kirchhoff einbindet,ist das Grundgerüst fertig.
Die Erde wurde von der Landvermessern in Breitengrade unterteilt.Und jeder Breitengrad-Bereich erfüllt eine spezifische Funktion.Das ist aber vorerst Zukunftsmusik,wenn das Grundgerüst nicht verstanden,beschrieben und berechnet ist.
Sie sollten ernsthaft versuchen Fehler in den Annahmen, Arbeitshypothesen und Mess-Ergebnissen und deren Interpretation zu finden, statt Plattitüden zu verbreiten.
Oh je. „Wärmestau“ durch CO2. Gemessen in einem geschlossenen Gefäß. Das Gärtnertreibhaus lässt grüssen. Temperaturerhöhung bei konstanter Insolation, der erste Hauptsatz der Thermodynamik wird verletzt. Und dass der „trockene“ Erdboden natürlich über Konvektion und nicht über Strahlung seine Wärme abgibt wird einfach unterschlagen! Ich lade den Autor des Beitrags ein am 21 Juni in einem ir-durchlässigen Kasten auf trockenem Boden in der Mittagssonne zu sitzen, während ich auf einem Stuhl daneben sitze (Wodd Experiment). Wir beide sind dann in Sachen Strahlungsbilanz in exakt der selben Situation. Mal sehen wer als erster umfällt…..
Für die Einladung 100 Punkte. Wenn Sie dann noch einen Kasten übrig hätten…
Den könnten Sie dann mit Helium füllen und Herrn Schnell darüber philosophieren lassen, dass Edelgase jetzt auch schon zu den Treibhausgasen gehören, bevor er vom Stuhl kippt.