Fangen wir also am Anfang an, nämlich an der Obergrenze der Atmosphäre TOA. Die von der TOA nach unten strahlende Solarenergie für die nördliche und die südliche Hemisphäre sieht so aus:

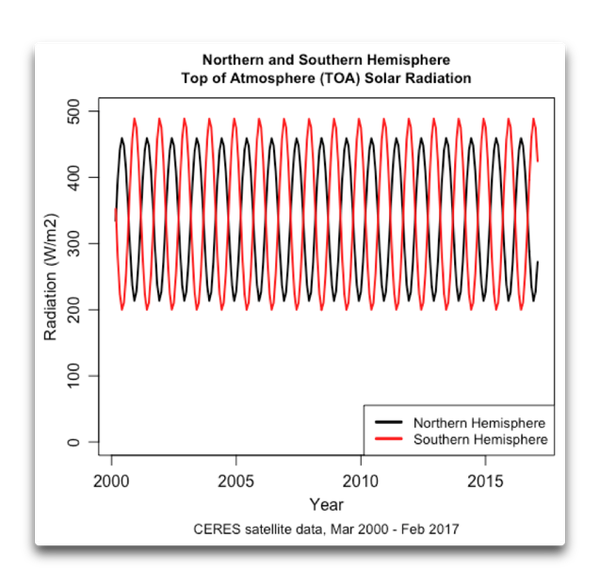
Abbildung 1: Von der TOA nach unten strahlende Sonnenenergie, gemittelt über 24 Stunden an 7 Tagen der Woche [24/7] über die gesamte Erdoberfläche.

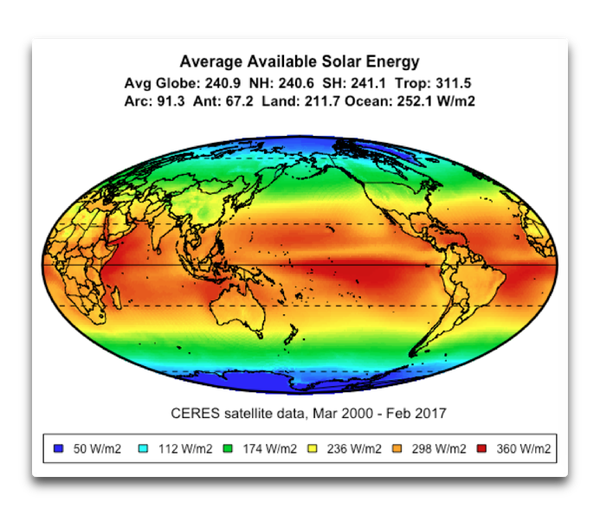
Allerdings kommt diese Energie nicht vollständig unten an. Vieles davon wird ins Weltall zurück reflektiert. Also nahm ich mir die CERES-Solardaten vor und subtrahierte die reflektierte Solarstrahlung. Die nach oben strahlende Solarenergie an der TOA wird reflektiert von Wolken, Aerosolen, Erde, Pflanzen, Eis und Ozeanen. Die von der TOA nach unten minus der von unten zur TOA reflektierten Solarenergie ist die zur Erwärmung des Planeten zur Verfügung stehende Energiemenge. Die Menge verfügbarer Solarenergie rund um die Welt sieht so aus:

Abbildung 2: Karte der globalen Verteilung der verfügbaren Solarenergie. Hierbei handelt es sich um verbleibende Solarenergie nach Abzug der Albedo-Reflektion des einfallenden Sonnenlichtes zurück ins Weltall.


Hatte ich erst einmal die verfügbare Energie, entfernte ich die jahreszeitlichen Variationen. Dabei handelt es sich um die Änderungen, welche sich Jahr für Jahr wiederholen. Die Eliminierung dieser wiederkehrenden Signale hinterlässt lediglich die geringen Variationen, die unregelmäßigen Änderung der reflektierten Strahlungsmenge geschuldet sind. (Es gibt auch eine sehr geringe, auf Sonnenflecken bezogene Variation der einfallenden Solarstrahlung von etwa einem Viertel eines W/m² auf der 24/7-Grundlage. Sie geht in die folgenden Berechnungen mit ein, macht aber praktisch keinen Unterschied).

Hier also ein erster Blick auf die Menge der verfügbaren Energie, welche die große planetenweite Wärmemaschine am Laufen hält, die wir Klima nennen, unterteilt für die beiden Hemisphären:

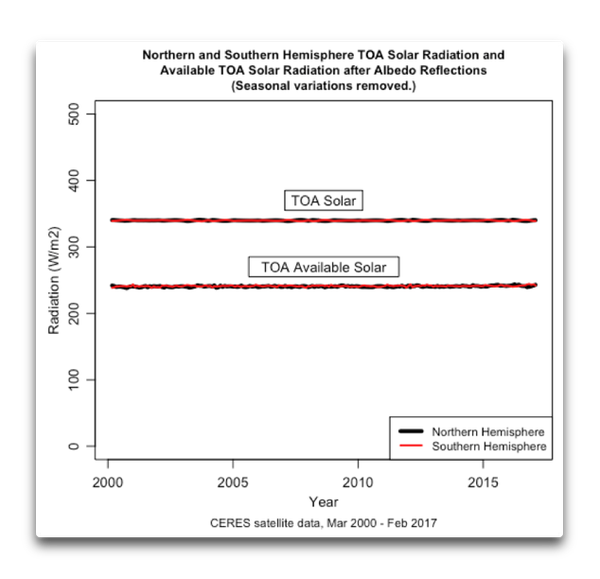
Abbildung 3: Solarenergie an der TOA und verfügbare Solarenergie nach [Entfernung der] Albedo-Reflektionen. Die Solarenergie macht etwa 340 W/m2 aus, wovon etwa 100 W/m2 wieder in den Weltraum reflektiert werden.

Dabei darf man nicht vergessen, dass die in das Klimasystem eintretende Energiemenge nach Albedo-Reflektionen eine Funktion hoch variabler Eis-, Schnee- und Wolkenverhältnisse ist … und trotzdem gibt es nur sehr geringe Variationen, sowohl räumlich als auch zeitlich. Jahr für Jahr gleichen sich Wolken, Eis und Schnee praktisch aus, auf beiden Hemisphären … warum?

Wie man oben erkennt, liegt die auf beiden Hemisphären verfügbare Solarenergie so nahe beieinander, dass ich die die Südhemisphäre repräsentierende Linie dünner zeichnen musste als die für die Nordhemisphäre, damit man beide erkennt. Um die beiden separat zu betrachten, müssen wir uns hinein zoomen, das Ergebnis davon zeigt Abbildung 4:

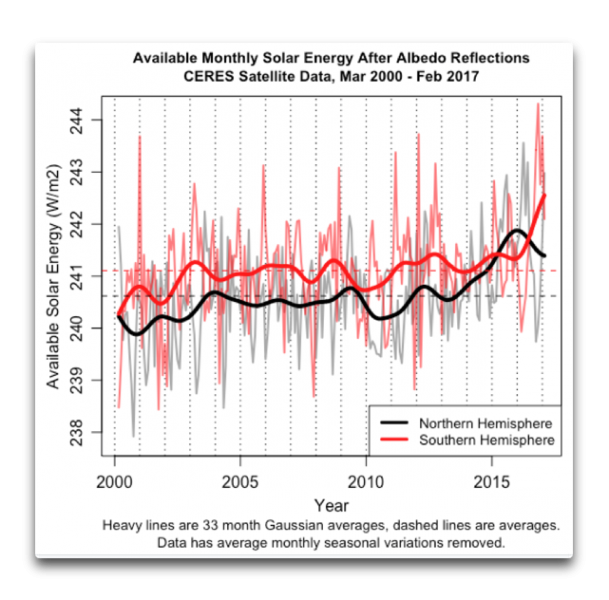
Abbildung 4: Verfügbare Solarenergie an der TOA ohne Albedo-Reflektionen, nördliche und südliche Hemisphäre.


Augenblicklich bemerkte ich einige Merkwürdigkeiten in dieser Graphik. Eine davon ist, dass trotz der großen Unterschiede zwischen der Nordhemisphäre (mehr Landfläche, viel Eis und Schnee in mittleren und hohen Breiten) und der Südhemisphäre (mehr Ozeanfläche, kaum Festland oder Eis/Schnee in mittleren Breiten) die Menge der mittleren einfallenden Energie innerhalb ½ W/m² liegt (NH = 240,6 W/m²; SH = 241,1 W/m², schwarze und rote gestrichelte horizontale Linie.

Zweitens, die Verhältnisse auf beiden Hemisphären sind allgemein parallel. Sie nahmen zu von 2003 bis 2004, blieben auf einem Niveau von 2013 bis 2014 und nahm dann wieder zu.

Drittens, es zeigt sich eine offensichtliche zeitliche Verschiebung zwischen den beiden Hemisphären. Zuerst dachte ich an die entgegen gesetzten Jahreszeiten … aber dann fiel mir ein, dass es in den Daten keine jährlichen Signale mehr gibt. Und ich vergewisserte mich, dass es auch kein Sechs-Monate-Signal mehr in den Daten gab. Nicht nur das, sondern auch – bis etwa 2011 lief die Südhemisphäre der Nordhemisphäre voran, aber danach lieft die Nordhemisphäre wieder voran. Warum?

Ich liebe die Freuden einer settled Wissenschaft …

In jedem Falle wollte ich jetzt die Variationen der verfügbaren Energie vergleichen mit den Variationen der Temperatur an der Erdoberfläche. Nun enthalten die CERES-Daten keine Oberflächen-Temperaturen. Allerdings gibt es darin einen Datensatz der von der Oberfläche nach oben gehenden Strahlung, welche manchmal „Strahlungstemperatur“ genannt wird, weil sie zur vierten Potenz der Temperatur variiert. Abbildung 5 zeigt die monatlichen Änderungen der von der TOA nach unten gehenden Solarstrahlung im Vergleich mit der von der Oberfläche nach oben gehenden Strahlung:

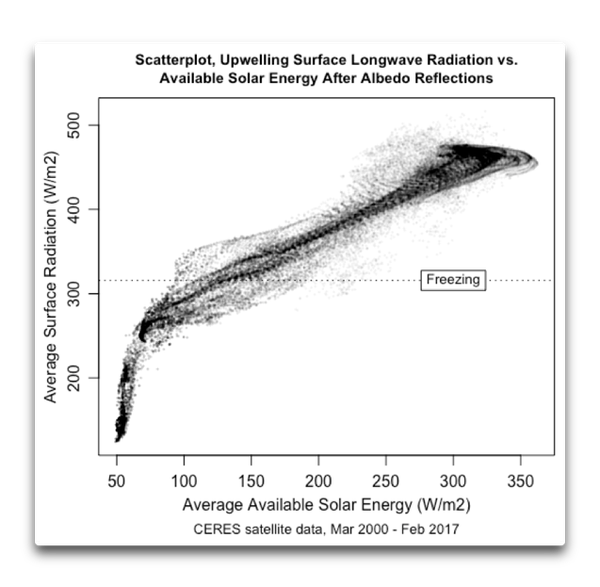
Abbildung 5: Scatterplot, Oberflächen-Strahlungstemperaturen (ausgehende langwellige Strahlung) im Vergleich mit der mittleren, an der TOA verfügbaren Solarenergie. Jeder Punkt steht für die Situation in einem 1° mal 1°-Gitternetz, welches den gesamten Planeten überspannt. Es befinden sich also 64.800 Punkte in der Graphik.


Was sagt uns dieser Scatterplot nun? Offensichtlich hängt das, was vor sich geht, von der Temperatur ab … und vielleicht weiteren Parametern. Um das verständlicher zu machen, möchte ich die gleichen Daten zeigen, aber getrennt nach Hemisphäre und getrennt zwischen Festland und Ozean. Hier zeige ich die vermutlich erhellendste Graphik bzgl. des Festlandes auf der Südhemisphäre:

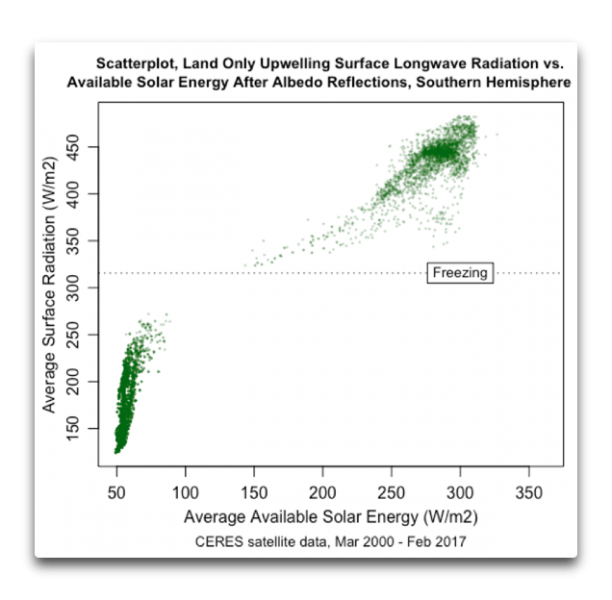
Abbildung 6: Scatterplot, Strahlungstemperaturen der Südhemisphäre, nur Festland vs. mittlere verfügbare Solarenergie an der TOA


Rechts erkennt man die südlichen Gebiete von Afrika und Südamerika … und links die Antarktis. Man kann eindeutig die unterschiedlichen Reaktionen ausmachen, die auftreten bei Temperaturen im Minus-Bereich und im Plus-Bereich.

Als Nächstes kommt hier die gleiche Darstellung für die Nordhemisphäre:

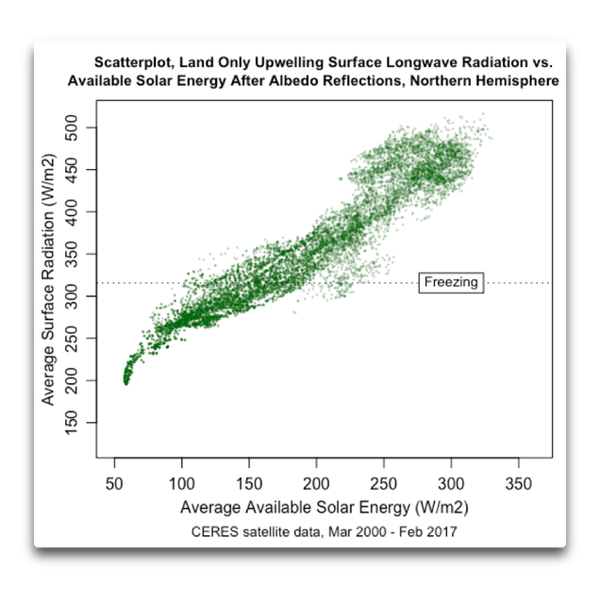
Abbildung 7: Scatterplot, Strahlungstemperaturen der Nordhemisphäre, nur Festland vs. mittlere verfügbare Solarenergie an der TOA


Nirgendwo auf der Nordhemisphäre kühlt sich das Festland so stark ab wie in der Antarktis. Teilweise liegt das daran, dass sich der Südpol auf dem Festland und dort auf einem hoch gelegenen Plateau, der Nordpol dagegen in einem Meer befindet.

All dies zeigt, dass die Reaktion der Planetenoberfläche auf zunehmende Sonneneinstrahlung teilweise eine Funktion der Temperatur ist. Je niedriger die mittlere Temperatur, umso mehr reagiert das System auf zunehmende Sonneneinstrahlung.

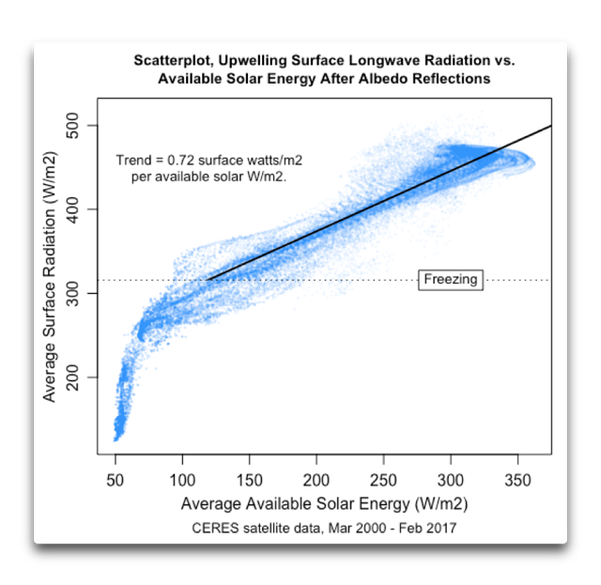
Damit im Hinterkopf zog ich noch einmal Abbildung 5 heran und berechnete die Neigung in dem Teil der Welt, der im Mittel nicht gefroren ist. Das Ergebnis dieser Berechnung zeigt Abbildung 8:

Abbildung 8: Wie in Abbildung 5 einschließlich des Trends der nicht gefrorenen Gebiete des Globus‘.


Diese Graphik fand ich nun höchst eigenartig, und zwar aus folgendem Grund: Der Treibhauseffekt ist der Grund, dass die Oberfläche des Planeten wärmer ist als man aus der einfachen Berechnung auf der Grundlage der Menge Sonnenstrahlung, welche die Erde trifft, erwarten würde. Grund hierfür ist die Absorption der ausgehenden langwelligen Strahlung, und wenn sie strahlen, geht etwa die Hälfte der Strahlung in den Weltraum, die andere Hälfte zurück zur Erde. Als Folge davon ist die Erde wärmer als sie es anderenfalls wäre.

Falls der „Treibhauseffekt“ – eine schlechte Etikettierung – zu 100% perfekt wäre für jedes zusätzliche, in das System einfallende W/m² Sonnenlicht, würde die Oberfläche zwei W/m² abstrahlen – ein W/m² des Sonnenlichtes und ein W/m² der Einstrahlung aus der Atmosphäre. Auf der Grundlage des Verhältnisses der einfallenden Strahlung und der Strahlung von der Oberfläche können wir sagen, dass der Gesamt-Multiplikations-Faktor des perfekten Treibhauses 1,0 wäre (hier habe ich mehr dazu geschrieben).

Natürlich ist der Multiplikations-Faktor in der realen Welt geringer. Wir kennen den langzeitlichen mittleren Multiplikations-Faktor des Planeten. Wir können ihn berechnen, indem wir die mittlere ausgehende langwellige Strahlung von der Oberfläche durch die mittlere verfügbare Solarenergie dividieren. Die mittlere ausgehende langwelligen Strahlung macht 398 W/m² aus und die mittlere verfügbare Sonnenenergie 240 W/m². Daraus ergibt sich ein Treibhaus-Multiplikations-Faktor von 398/240 = 1,66.

Und da haben wir die Merkwürdigkeit: der mittlere Multiplikations-Faktor in Abbildung 8 beträgt 0,72, also deutlich weniger als 1,0. Weil dieser Multiplikator kleiner als eins ist, würde dies implizieren, dass es auf der Erde viel kälter ist als es in Wirklichkeit der Fall ist…

Wie können wir diesen offensichtlichen Widerspruch erklären? Für mich ist es ein Beweis für etwas, das ich schon viele Jahre lang gesagt habe, nämlich: Die Sensitivität der Temperatur an der Erdoberfläche auf die Menge der einfallenden Strahlung ist keine Konstante, wie es von Mainstream-Klimawissenschaftlern vertreten wird. Stattdessen ist es eine Funktion der Temperatur. Bei Temperaturen über dem Gefrierpunkt nimmt die ausgehende Strahlung um etwa drei Viertel eines W/m² zu für jedes zusätzlich einfallende W/m² der Sonnenstrahlung.

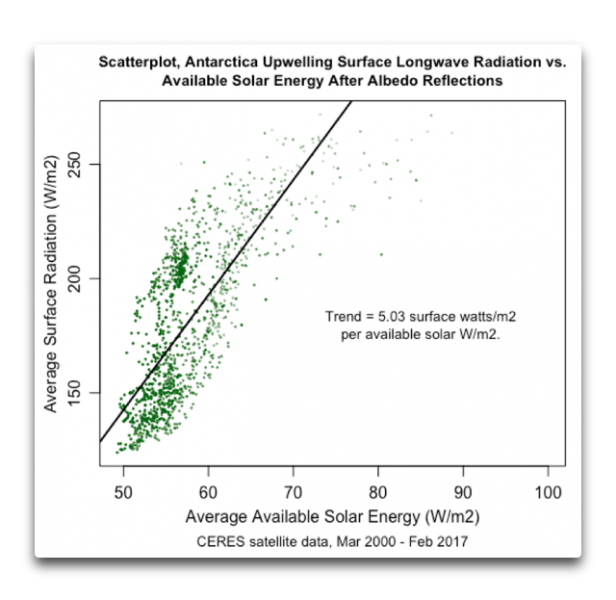
Aber wenn es ziemlich kalt ist, wie es in der Antarktis der Fall ist, reagiert die Oberflächen-Temperatur viel stärker auf Änderungen der einfallenden Strahlung. Die Situation in der Antarktis ist Folgende:

Abbildung 9: Wie in Abbildung 8, aber für die Verhältnisse in der Antarktis


Man beachte, dass diese Sensitivität nicht eine Folge des Abschmelzens von Festlands-Eis in der Antarktis und sich die damit ändernde Albedo ist. Fast die gesamte Antarktis ist das ganze Jahr über gefroren.

Wir können aber noch auf eine andere Art und Weise auf diese Situation schauen. Die Abbildungen 5 bis 9 zeigen die langfristigen Verhältnisse, im Grunde eine Steady-State-Situation, belegt durch die 68.400 Gitterzellen von 1° mal 1°, welche die Oberfläche des Planeten ausmachen. Anstatt dieses langfristige Mittel zu betrachten, können wir aber auch betrachten, wie sich die Dinge mit der Zeit ändern. Abbildung 10 zeigt die zeitliche Änderung der Temperaturanomalie über den Zeitraum der CERES-Satelliten-Beobachtungen im Vergleich zur Anomalie der mittleren Sonnenenergie an der TOA:

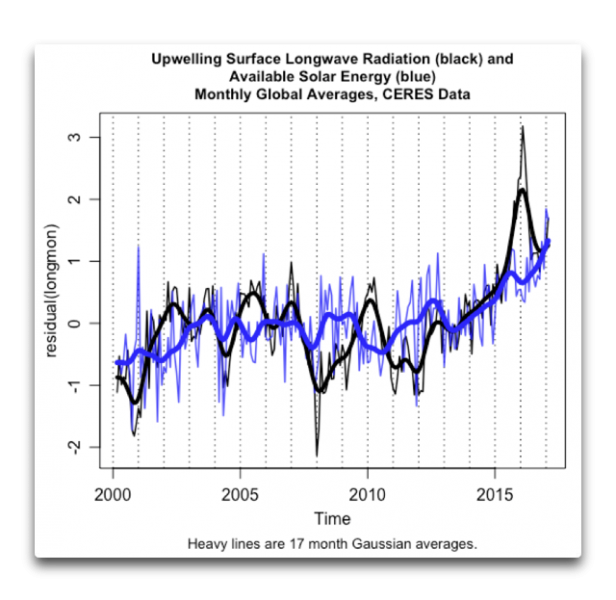
Abbildung 10: Monatliche langwellige Strahlung von der Oberfläche und mittlere Sonneneinstrahlung an der TOA.


Man erkennt, dass es abgesehen von Sprüngen der Oberflächenstrahlung während der warmen El Nino-Jahre von 2009/10 und 2016/17 eine enge Relation gibt mit dem verfügbaren Sonnenschein. Eine Kreuz-Korrelations-Analyse (hier nicht abgebildet) verifiziert, dass es keine zeitliche Verzögerung gibt zwischen Änderungen des solaren Eingangssignals und der Reaktion der Oberfläche.

Wir können auch die Natur der kurzfristigen Relation zwischen diesen beiden Variablen bestimmen mittels eines Scatterplots wie hier in Abbildung 11:

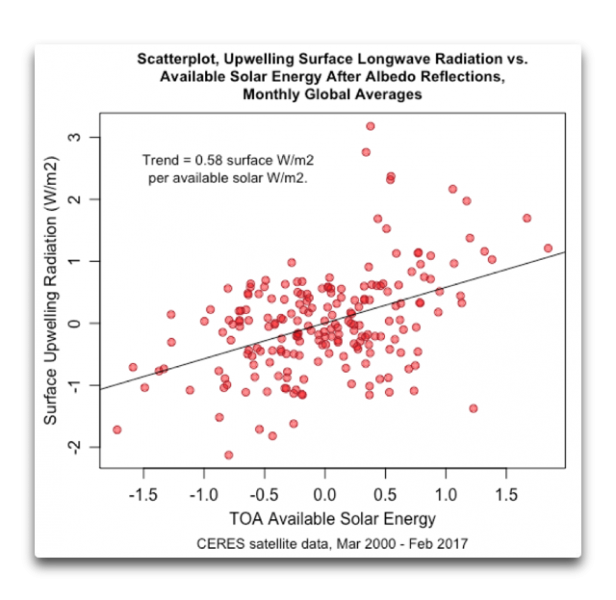
Abbildung 11: Scatterplot, monatliche Mittelwerte der an der TOA verfügbaren Sonnenstrahlung und der ausgehenden langwelligen Strahlung von der Oberfläche.


Wie zu erwarten war, ist der Trend in den monatlichen Änderungen der kurzfristigen Daten kleiner als das längerfristige Gitterzellen-Mittel in Abbildung 8 (0,58 vs. 0,72 W/m² Oberflächen-Änderung pro W/m²-Änderung der solaren Einstrahlung).

Schlussfolgerungen:

● Alles in allem besteht die Reaktion der nicht gefrorenen Oberfläche auf zunehmende solare Einstrahlung in einer mittleren Zunahme der ausgehenden langwelligen Strahlung von etwa 0,7W/m² für jede Zunahme der verfügbaren Solarenergie um 1 W/m².

● Unterhalb des Gefrierpunktes nimmt diese Reaktion mit abnehmender Temperatur zu, bis die Reaktion bei den typischen Antarktis-Temperaturen zwischen -20°C und -60°C etwa 5 W/m² für jede Zunahme der Solarenergie um 1 W/m² beträgt.

● Mittels der Stefan-Boltzmann-Gleichung ergibt sich eine Änderung der Temperatur an der Oberfläche bei einer Änderung der langwelligen Ausstrahlung um 1 W/m² von etwa 0,2°C pro W/m² bei 0°C bis 0,16°C pro W/m² bei etwa 30°C.

● Bei einer gegebenen Änderung der einfallenden Solarstrahlung von 0,7 W/m² würde dies zu einer Temperaturänderung im nicht gefrorenen Teil des Planeten von 0,11°C pro zusätzlichem W/m² bei 30°C und einer Erwärmung von 0,4°C bis 0,6°C pro zusätzlichem W/m² bei 0°C führen.

● Die geschätzte Rückstrahlung bei einer Verdoppelung des CO2-Gehaltes beträgt 3,7 W/m². Dies würde zu einer Erwärmung von 0,4°C bis 0,6°C führen, falls die Sonneneinstrahlung um 3,7 W/m² zunehmen würde, abhängig von der Temperatur an der Oberfläche.

● Und schließlich als Randbemerkung: die mittlere Änderung der von der TOA nach unten gehenden totalen Sonneneinstrahlung TSI infolge einer Änderung der Sonnenflecken-Aktivität ist von einer Größenordnung von 0,26 W/m² von Spitze zu Spitze. Allerdings stehen nur etwa 240/340 = 70% davon zur Verfügung, der Rest wird zurück ins Weltall reflektiert. Setzt man die Relation von 0,72 W/m² Änderung an der Oberfläche pro jedem zusätzlichen W/m² der an der TOA verfügbaren Sonnenenergie an sowie eine maximale Temperaturänderung pro Watt von 0,16°C pro W/m², würde dies eine maximale Auswirkung von 0,26 X 240/340 X 0,72 X 0,16 = 0,02°C aus jener Änderung der TOA-Strahlung ausmachen…

——————————————

DATA: This is all done with the CERES satellite TOA and Surface datasets, which are available here under the heading:

Energy Balanced and Filled (EBAF)
Climate Data Record (CDR) of monthly TOA fluxes and consistent computed surface fluxes and clouds suitable for analysis of variability at the intra-seasonal, inter-annual, and longer time scales.
Link: https://wattsupwiththat.com/2018/05/05/symmetry-and-balance/
Übersetzt von Chris Frey EIKE

image_pdfBeitrag als PDF speichernimage_printBeitrag drucken