Meine Antwort auf Roy Spencers Kommentar, geschrieben auf seinem Blog drroyspencer.com, wurde inzwischen 1400 mal angeklickt, und die drei vorherigen Artikel wurden jeweils über 1000 mal, über 350 mal und über 750 mal angeklickt. Anderswo hat ein notorisch jähzorniger skeptischer Blogger auf die Frage, ob er zu unserem Ergebnis einen Kommentar schreiben will, geantwortet, er lasse sich nicht dazu herab, etwas so Einfaches zu diskutieren. Einfach ist es. Wie kommt man bloß darauf, dass es keine Klima-Rückkopplungs-Prozesse auf die große Emissionstemperatur gibt, jedenfalls nicht im gleichen Ausmaß, wie sie auf die geringe Erhöhung jener Temperatur reagieren, verursacht durch das Hinzufügen nicht kondensierender Treibhausgase in die Atmosphäre? Das ist ein einfacher Punkt. Aber einfach heißt nicht notwendigerweise falsch.
In diesem Beitrag wird die Mathematik hergeleitet, was weder einfach noch intuitiv, wenngleich auch nicht besonders komplex ist. Wie in Beiträgen zuvor möchte ich einige Fragen aus Kommentaren zu jenen Beiträgen beantworten. Wie zuvor akzeptieren wir ad interim, ad argumentum oder ad experimentum alle Ergebnisse der offiziellen Klimatologie – es sei denn, wir können nachweisen, dass diese Ergebnisse falsch sind.
Führen wir doch einfach ein simples Gedankenexperiment durch. Dabei kehren wir das Modell von Lacis et al. (2010) um. Lacis hatte herausgefunden, dass das Klima, nachdem man alle nicht kondensierenden Treibhausgase aus der Atmosphäre entfernt hatte, ein neues Gleichgewicht erreicht hätte. Dann wäre die Erde ein Schneeball oder ein Wasserplanet mit einer Albedo von 0,418, was eine Emissionstemperatur von 243,3 K impliziert. Kraft dieses Experimentes sollten wir folglich annehmen, dass es im Jahre 1800 keine Treibhausgase in der Atmosphäre gab. Für all jene, die mit wissenschaftlicher Logik nicht vertraut sind: Damit ist nicht gesagt, dass es im Jahre 1800 wirklich keine Treibhausgase gab.
Lacis zufolge soll die globale mittlere Temperatur 20 Jahre nach Entfernung aller nicht kondensierenden Treibhausgase aus der Atmosphäre auf 253 K sinken. Während der folgenden 30 Jahre soll die Temperatur um lediglich ein weiteres K zurückgehen auf 252 K oder 8,7 K über der Emissionstemperatur. Folglich erreicht die Temperatur in Lacis‘ Modell bereits nach 50 Jahren ihr neues Gleichgewicht.
Eine Frage, die nur Wenige in den bisherigen Beiträgen beantwortet haben, und keiner davon überzeugend, lautet: Aus welcher Quelle stammen diese zusätzlichen 8,7 K, wenn es doch keine nicht kondensierenden Treibhausgase als Antrieb gab? Unsere Antwort lautet, dass Lacit implizit die Existenz einer Rückkopplungs-Reaktion auf die Emissionstemperatur von 243,3 K eingeräumt hat, wenngleich dieser Wert viel zu klein ist, um realistisch zu sein. Viel zu klein deshalb, weil wie im vorigen Artikel gezeigt, Lacis die Temperaturdifferenz von 45,1 K zwischen der impliziten Emissionstemperatur von 243,3 K bei der spezifizierten Albedo von 0,418 einerseits und der heutigen globalen Mitteltemperatur andererseits von 288,4 K (ISCCP, 2018), wie folgt zuordnet: Rückkopplungs-Reaktion auf die Emissionstemperatur 252 – 243,3 = 8,7 K. Direkt von natürlich vorkommenden, nicht kondensierenden Treibhausgasen angetriebene Erwärmung (288,4 – 252)/4 = 9,1 K, und bei Anwendung der Rückkopplungs-Reaktion von 0,75 nach Lacis aus den nicht kondensierenden Treibhausgasen 27,3 K: insgesamt 45,1 K. Diese asymmetrische Zuordnung der Differenz zwischen Emissionstemperatur und gegenwärtiger Temperatur impliziert, dass die Rückkopplungsreaktion von 8,7 K auf die Emissionstemperatur lediglich 3,6% von 243,3 K ausmacht, während die Rückkopplungs-Reaktion von 27,3 K auf die Treibhaus-Erwärmung 300% der 9,1 K ausmacht. Später wird formell nachgewiesen, dass diese implausible Zuordnung irrig ist.
Es ist nützlich zu unterscheiden zwischen der vorindustriellen Lage im Jahre 1850 (dem ersten Jahr der HadCRUT-Reihe, dem längsten globalen Temperatur-Datensatz) und der industriellen Ära. Wir wollen annehmen, dass die gesamt globale Erwärmung vor 1850 natürlichen Ursprungs war. In jenem Jahr lag die Temperatur um etwa 0,8 K unter dem heutigen Wert von 287,6 K (HadCRUT4) oder um 44,3 K über der Emissionstemperatur. Lacis‘ Aufteilung der 44,3 K wäre also 8,7 K; 8,9 K und 26,7 K.
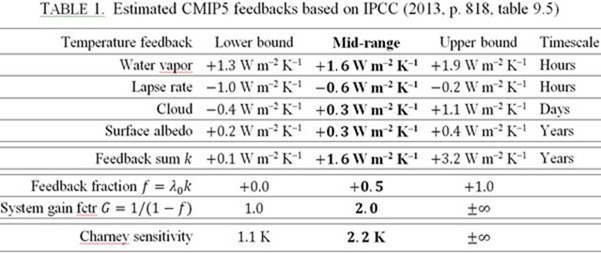
Nehmen wir einmal an, dass Lacis recht hatte damit, dass die direkt getriebene Erwärmung durch Hinzufügen der natürlich vorkommenden, nicht kondensierenden Treibhausgase 8,9 K betragen hatte. Lassen wir das Experiment ab 1850 umgekehrt laufen, können wir den Rückkopplungs-Anteil berechnen, der implizit in Lacis‘ Modell steckt nach der Korrektur, um eine ordentliche Rückkopplungs-Reaktion auf die Emissionstemperatur zuzulassen. Bevor wir das tun sei an die gegenwärtig vom IPCC verwendete Liste der Rückkopplungen erinnert, die relevant für die Ableitung sowohl der kurzlebigen als auch der Gleichgewichts-Sensitivitäten sind:
Die vom IPCC gewählte Luxus-Rückkopplungs-Summe [high-end feedback sum] impliziert eine Charney-Sensitivität irgendwo zwischen minus unendlich und plus unendlich pro CO2-Verdoppelung. Kein wirklich gewaltiges Ergebnis nach 30 Jahren und der Ausgabe von hunderten Milliarden Steuerzahler-Dollar. Die Rückkopplungssumme des IPCC in der Mitte der Bandbreite impliziert eine mittlere Charney-Sensitivität von nur 2,2 K und nicht die in den früheren IPCC-Berichten genannten 3,0 bis 3,5 K; und auch nicht die 3,3 K der CMIP3 und CMIP5-Modelle. Da ist es keine Überraschung, dass das IPCC im Jahre 2013 zum ersten Mal keine mittlere Schätzung der Charney-Sensitivität genannt hat.
Keine der vom IPCC gelisteten Rückkopplungen ist vom Vorhandensein irgendwelcher nicht kondensierender Treibhausgase abhängig. Daher wären alle diese Rückkopplungs-Prozesse in unserer Welt um das Jahr 1800 ganz ohne derartige Gase präsent. Um eine Rückkopplungs-Reaktion zu induzieren, so irgendein Rückkopplungs-Prozess präsent ist, bedarf es als einzige Notwendigkeit einer Temperatur, d. h. die Emissionstemperatur. Da Rückkopplungs-Prozesse präsent sind, ist eine Rückkopplungs-Reaktion unvermeidlich.
Die Emissionstemperatur hängt von lediglich drei Größen ab: Einstrahlung, Albedo und Emissivität. Man begeht kaum einen Fehler, falls man die Emissionstemperatur wie gewöhnlich als Einheit betrachtet. Damit beträgt die Emissionstemperatur bei der heutigen Einstrahlung von 1364,625 W/m² und einer Lacis-Albedo von 0,418: [1364,625(1 – 0.418) / d / (5,6704 x 10–8)]0.25 = 243.3 K. Dies steht in Übereinstimmung mit der fundamentalen Gleichung des Strahlungstransports, wobei d das Verhältnis ist zwischen dem Gebiet der sphärischen Oberfläche der Erde zu ihrem großen Kreis = 4 ist. Genauso läge die Emissionstemperatur bei der heutigen Albedo von 0,293 bei 255,4 K. Dieser Wert wird allgemein in der Literatur zur Klimasensitivität genannt.
Der Grund, warum die offizielle Klimatologie bis jetzt der Rückkopplungs-Reaktion auf die Emissionstemperatur nicht das angemessene Gewicht verliehen hat (oder besser, überhaupt kein Gewicht) ist, dass man eine entartete Form der Null-Dimensions-Modell-Gleichung verwendet hat, die da lautet ΔTeq = ΔTref / (1 – f ), wo die Gleichgewichts-Sensitivität ΔTeq nach Berücksichtigung von Rückkopplungen gleich ist dem Verhältnis der Referenz-Sensitivität ΔTref zu (1 minus Rückkopplungs-Anteil f). Das Rückkopplungs-Loop-Diagramm (unten) räumt der Emissionstemperatur keinen Raum ein und daher auch nicht irgendeiner Rückkopplungs-Reaktion.
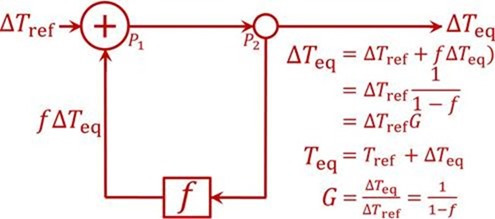
Der Rückkopplungs-Loop in der von der offiziellen Klimatologie verwendeten Null-Dimensions-Modell-Gleichung ΔTeq = ΔTref / (1 – f )
Diese entartete Form der Null-Dimensions-Modell-Gleichung ist angemessen, wenn nicht sogar ideal, um Gleichgewichts-Sensitivitäten abzuleiten unter der Voraussetzung, dass zunächst eine Rückkopplungs-Reaktion auf die Emissionstemperatur zugelassen wird. Dennoch finden es viele Kommentatoren empörend, dass die offizielle Klimatologie eine so einfache Gleichung anwendet, um die Gleichgewichts-Sensitivitäten zu diagnostizieren, welche zu prophezeien von den komplexen Zirkulations-Modellen erwartet wird. Einige wenige haben versucht zu leugnen, dass diese Gleichung angewendet wird. Allerdings haben Hansen (1984), Schlesinger (1985), das IPCC (2007, p. 631 fn.), Roe (2009), Bates (2016) und einige andere Größen diese Gleichung angewendet:
f = 1 –Tref / Teq = 1 – (TE + ΔTB) / TN
= 1 – (255,4 + 8) / 287,6 = 0,08. (4)
Jetzt wollen wir beweisen, dass die Form dieser diagnostischen Gleichung, wie sie von der offiziellen Klimatologie angewendet wird, das offizielle Intervall der Charney-Sensitivitäten ergibt, wenn man die offiziellen Werte eingibt. Das IPCC (2013, Abb. 9.43) erwähnt Vial et al. (2013), der den CO2-Antrieb ΔQ0 diagnostiziert hat, ebenso wie den Planck-Parameter λ0 und die Rückkopplungs-Summe k bei einer abrupten Vervierfachung der CO2-Konzentration in 11 CMIP5-Modellen via des linearen Regressions-Verfahrens in Gregory (2004). Vial gibt die mittlere Schätzung kmid der Rückkopplungs-Summe aus 11 CMIP5-Modellen als 1,57 W/m²K an mit der Implikation fmid = kmidλ0 = 0,49 und der 2σ-Grenzen von f als fmid ± 40%, d. h. 0,49 ± 0,20.
Der implizite CO2-Antrieb ΔQ0, in welchen schnelle Rückkopplungen mit eingehen, betrug 4,5 W/m² im Vergleich zu den 3,5 W/m² in Andrews 2010. Die Referenz-Sensitivität ΔTS, von Vial mit 1,41 K bewertet, lag um 20% über der mittleren Schätzung der CMIP5-Modelle von 1,1 K. Verwendet man diese Werte erweist sich die Version der von der offiziellen Klimatologie herangezogenen Null-Dimension-Modell-Gleichung als gut kalibriert. Sie ergibt eine Charney-Sensitivität ΔT auf 3,3 (2,0; 4,5) K, fast genau inhaltsgleich mit vielen veröffentlichten offiziellen Intervallen der CMIP3 und CMIp5-Modelle (Tabelle 2):
Aus dieser erfolgreichen Kalibrierung folgt, dass obwohl die von der Gleichung vermuteten Rückkopplungen linear, einige aber auch nicht linear sind, sie immer noch die Gleichgewichts-Sensitivitäten korrekt aufteilt zwischen der erzwungenen Erwärmung und der Rückkopplungs-Reaktion. Im Besonderen reproduziert sie das von den CMIP5-Modellen projizierte Intervall der Charney-Sensitivitäten, welche Nicht-Linearitäten berücksichtigen. Die Kalibrierung bestätigt nicht, dass der Modellwert f ≈ 0,7 für den Rückkopplungs-Anteil oder ihr Intervall der Charney-Sensitivitäten korrekt ist. Sie bestätigt jedoch, dass die Gleichung mit den offiziellen Werten von f die offiziellen, von den komplexen CMIP-Modellen veröffentlichten Prognosen der Charney-Sensitivität bestätigt. Und das, obwohl keinerlei Berücksichtigung der großen Rückkopplungs-Reaktion auf die Emissionstemperatur erfolgte.
Die offizielle Klimatologie adjustiert ihre Modelle so lange, bis sie das Klima der Vergangenheit reproduzieren. Folglich wurden die Modelle so frisiert, dass sie der Differenz von 33 K Rechnung tragen zwischen der Emissionstemperatur von 255,4 K und der heutigen Temperatur von 288,4 K. Man hatte hypothetisiert, dass ein Drittel der 33 K der direkt getriebenen Erwärmung geschuldet war seitens natürlich auftretender, nicht kondensierender Treibhausgase, und die anderen zwei Drittel bis drei Viertel waren die Rückkopplungs-Reaktion auf diese direkte Erwärmung. Folglich haben sie hypothetisiert, dass der Rückkopplungs-Anteil zwei Drittel bis drei Viertel der Gleichgewichts-Sensitivität ausmacht: d. h. dass f irgendwo zwischen 0,67 und 0,75 liegt.
Als einen ersten Schritt zur angemessenen Berücksichtigung der Rückkopplungs-Reaktion auf die Emissionstemperatur kann die Version der offiziellen Klimatologie der Null-Dimension-Modell-Gleichung überarbeitet werden, um die Delta-Eingangs- und -Ausgangssignale durch absolute Werte zu ersetzen, welche lediglich Änderungen der Temperatur sind. Man beachte, dass die korrekte Form jedweder Gleichung, welche natürliches Auftreten (oder jedwede Naturgesetzte) beschreibt, absolute Werte sind: Die Anwendung von Deltas ist nur zulässig, falls die Delta-Gleichungen korrekt abgeleitet sind aus der absoluten Gleichung. Demzufolge sollte ΔTeq = ΔTref / (1 – f ) werden zu Teq = Tref / (1 – f ). Das überarbeitete Rückkopplungs-Loop-Diagramm sieht so aus:
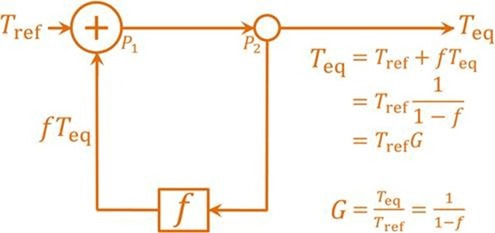
Nach Amendierung, um Delta-Eingangs- und -Ausgangssignale durch absolute Werte zu ersetzen, wird die offizielle Version der Null-Dimension-Modell-Gleichung zu Teq = Tref / (1 – f ).
Um f bei bekannter Referenz- und Gleichgewichts-Temperatur zu berechnen, kann diese überarbeitete Gleichung umgeschrieben werden zu f = 1 – Tref / Teq. In dem umgekehrten Lacis-Experiment setzt sich die Referenz-Temperatur Tref vor der Rückkopplung zusammen aus Emissionstemperatur TE und der zusätzlichen Temperatur ΔTE = 8,9 K. Diese ist die direkte Erwärmung bei Hinzufügen der natürlich auftretenden, nicht kondensierenden Treibhausgase in die Luft. Folglich gilt: Tref = TE + ΔTE = 243.3 + 8.9 = 252.2 K. Die Gleichgewichts-Temperatur Teq ist einfach die Temperatur des Jahres 1850, nach 50 Jahren des umgekehrten Lacis-Experimentes. Dann ist f = 1 – Tref / Teq = 1 – 252.2 / 287.6 = 0.123, also nur ein Fünftel bis ein Sechstel des Wertes der offiziellen Klimatologie. Ursache dieser Differenz ist, dass wir anders als die offizielle Klimatologie die Rückkopplungs-Reaktion auf die Emissionstemperatur korrekt berücksichtigen.
Weiter. Wie viel der Differenz von 35,4 K zwischen Tref = 252,2 K und Teq = 287,6 K geht zurück auf die Rückkopplungs-Reaktion auf die Emissionstemperatur TE = 243,3 K und wie viel macht die Rückkopplungs-Reaktion auf die direkte Treibhausgas-Erwärmung ΔTE = 8.9 K aus? Man nehme einfach das Produkt von jedem Wert, und f / (1 – f) = 0,14. Folglich: 243,3 x 0,14 = 34,1 K und 8,9 x 0,14 = 1,3 K. Dass dies die korrekte Aufteilung ist, beweisen wir mittels der Standard-Mainstream-Form der Null-Dimension-Modell-Gleichung, die in allen dynamischen Systemen universell ist außer Klima. Die Mainstream-Gleichung separiert anders als die degenerierte Form der Klimawissenschaft explizit das Eingangssignal (bei Klima die Emissionstemperatur von 255,4 K) von jeder Verstärkung ( wie etwa die Erwärmung um 8,9 K durch Hinzufügen der nicht kondensierenden Treibhausgase zur Atmosphäre).
Die Mainstream-Null-Dimension-Modell-Gleichung lautet Teq = Tref μ / (1 – μβ), wobei Tref das Eingangssignal ist (hier: die Emissionstemperatur); μ = 1 + ΔTref / Tref der Verstärkungsfaktor, der jedwede Verstärkung von Tref repräsentiert wie etwa jenen, die verursacht wird durch die Präsenz der natürlich vorhandenen, nicht kondensierenden Treibhausgase; β ist der Rückkopplungs-Anteil; μβ ist der Rückkopplungs-Faktor, äquivalent zu f in der gegenwärtigen Version der offiziellen Klimatologie; und Teq ist die Gleichgewichts-Temperatur bei Re-Equilibration des Klimas, nachdem alle Rückkopplungen kürzer als ein Jahrzehnt wirksam geworden sind.
Der Rückkopplungs-Loop für diese korrigierte Form der Null-Dimension-Modell-Gleichung sieht so aus:
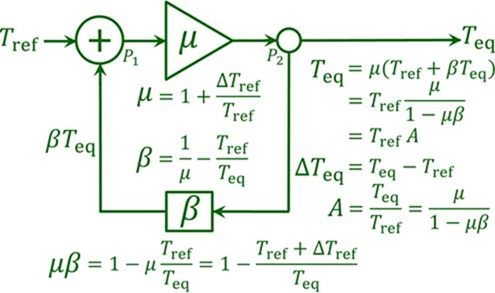
Das Rückkopplungs-Loop-Diagramm der Standard-Null-Dimension-Modell-Gleichung Teq = Tref μ / (1 – μβ)
Ein Vorteil der Anwendung dieser Form der Null-Dimension-Modell-Gleichung der Mainstream-Wissenschaft ist, dass sie explizit und separat das Eingangssignal Tref berücksichtigt und jede Verstärkung desselben via dem gain factor μ im Verstärker. Daher ist es nicht mehr möglich, entweder Tref oder die Rückkopplungs-Reaktion zu ignorieren oder zu gering zu bewerten, wozu es kommen muss, solange der Rückkopplungs-Anteil β ungleich Null ist.
Weiter unten wird nachgewiesen, dass die Aufteilung der Differenz von 35,4 K zwischen Tref = 252,2 K und Teq = 287,6 K im Jahre 1850, was wir aus unserem Gedankenexperiment zuvor abgeleitet haben, tatsächlich die korrekte Aufteilung ist. Beginnt man mit der Mainstream-Gleichung, führen wir zur rechten Zeit den direkten oder open-loop gain factor μ = 1 + ΔTref / Tref ein. Der Rückkopplungs-Faktor μβ, also das Produkt aus dem direkten oder open-loop gain factor μ und dem Rückkopplungs-Anteil β, hat genau die Form, welche wir angewendet haben, um unseren Rückkopplungs-Anteil f abzuleiten als 1 – (243,3 + 8,9) / 287,6 = 0,123. Dies bestätigt, dass unsere Aufteilung korrekt war.
Man beachte im Vorübergehen, dass f in der offiziellen Klimatologie sofort der Rückkopplungs-Anteil und der Rückkopplungs-Faktor ist, nimmt doch die offizielle Klimatologie an, dass der direkte oder open-loop gain factor μ = 1 ist. In der Praxis führt diese einzelne Hypothese die offizielle Klimatologie in die Irre, weil die Verstärkung der Emissionstemperatur, getrieben durch die Präsenz der nicht kondensierenden Treibhausgase, nur ein kleiner Anteil jener Temperatur ist.
Für uns war jedoch die Annahme vernünftiger, dass die Temperatur von 287,6 K im Jahre 1850 vor jedem potentiellen Einfluss des Menschen eine Gleichgewichts-Temperatur war. Wir wissen, dass sich die Welt während der 168 Jahre seit 1850 um nur 0,8 K erwärmt hat. Die offizielle Klimatologie ordnet diese gesamte Erwärmung dem Menschen zu, nicht der Natur.
War es sinnvoll von uns, mit der impliziten Emissionstemperatur von Lacis von 243,3 K anzufangen, welche die spezifizierte Albedo 0,418 auf einer Wasser-Erde beim Fehlen nicht kondensierender Treibhausgase reflektiert? Warum fingen wir nicht mit Pierrehumbert (2011) an, welcher sagte, dass eine Schneeball-Erde eine Albedo von 0,6 aufweisen würde, was eine Emissionstemperatur von 221,5 K impliziert? Rechnen wir mal. Der Rückkopplungs-Anteil f = μβ würde dann zu 1 – (221,5 + 8,9) / 287,6 = 0,20.
Folglich wäre der mittlere Rückkopplungs-Anteil einer Schneeball-Erde im Jahre 1850 0,20; derjenige von einer Wasser-Erde in jenem Jahr 0,12 und bei der heutigen Albedo 0,293 mit einer impliziten Emissionstemperatur von 255,4 K. Es ergibt sich 1 – (255,4 + 8,9) / 287,6 = 0,08. Damit begannen wir auch unsere Reihe. Man bemerkt, dass beim Schmelzen der großen Eisschilde die Dominanz der Albedo-Rückkopplung unaufhaltsam geringer wird, während der Rückkopplungs-Anteil mit der Zeit sinkt.
Obwohl die Albedo-Rückkopplung bis jetzt dominiert haben mag, was ist mit der größten aller heutigen Rückkopplungen, der Wasserdampf-Rückkopplung? Die Clausius-Clapeyron-Gleichung impliziert, dass der von der Atmosphäre eingenommene Raum bei Erwärmung derselben fast exponentiell mehr Wasserdampf enthalten kann, aber nicht muss. Wentz (2007) kam zu dem Ergebnis, dass die Gesamt-Säule Wasserdampf pro 1 K Erwärmung um etwa 7% zunimmt. Lacis (2010) kam aufgrund dieser Zuwachsrate zu der Aussage, dass falls man die nicht kondensierenden Treibhausgase aus der heutigen Atmosphäre entfernt und die Temperatur um 36 K, also von 288 auf 252 K sinken würde, sich etwa 10% des heutigen Wasserdampfes in der Atmosphäre befinden würde, also: 100% / 1.0736 = 9%.
Obwohl die Zunahme der Wasserdampf-Säule mit Erwärmung folglich als exponentiell angesehen wird, ist der daraus folgende Rückkopplungs-Antrieb jedoch in etwa logarithmisch (genau wie der direkte CO2-Antrieb logarithmisch ist). Was noch mehr zählt ist, dass ein substantieller Anteil der daraus folgenden Rückkopplungs-Reaktion ausgeglichen wird durch eine Reduktion der Rückkopplung des geringer werdenden vertikalen Temperaturgradienten. Demzufolge ist die Wasserdampf/lapse rate-Rückkopplung in etwa linear.
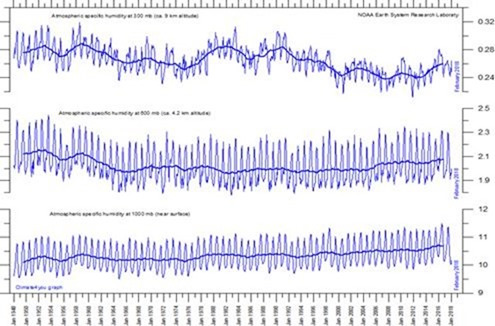
Während des Zeitraumes der NOAA-Aufzeichnungen der spezifischen Feuchtigkeit in drei verschiedenen Druckniveaus (oben) erfolgte eine globale Erwärmung von 0,8 K. Wentz hätte eine Zunahme des Wasserdampfes um etwa 5,5% erwartet. Tatsächlich fand sich nahe der Erdoberfläche, wo sich der meiste Wasserdampf befindet, ein Trend der spezifischen Feuchtigkeit mit etwa diesem Wert. Aber die Reaktion der Wasserdampf-Rückkopplung in niedrigen Höhen ist gering, weil die Luft alles andere als bereits gesättigt ist.
Allerdings sank die spezifische Feuchtigkeit mit der Höhe, wo die Luft trockener ist und zunehmender Wasserdampf die einzige in Frage kommende Quelle von Erwärmung ist. Das bestätigt die Nicht-Existenz des prophezeiten „Hot Spots“ in mittlerer Höhe der Atmosphäre über den Tropen, welcher angeblich durch zunehmenden Wasserdampf-Gehalt entstehen sollte. Also gibt es kaum Beweise dafür, dass die Temperatur-Reaktion auf einen gestiegenen Wasserdampf-Gehalt und die korrespondierende Verringerung der lapse rate nicht linear ist. Andere Rückkopplungen sind nicht groß genug, um einen großen Unterschied auszumachen, selbst wenn sie nicht linear sind.
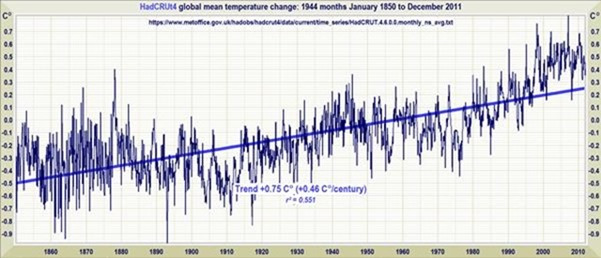
Unser Verfahren prognostiziert eine Erwärmung von 0,78 K von 1850 bis 2011. Beobachtet worden waren 0,75 K.
Ein Kommentator hat sich darüber beklagt, dass der Planck-Parameter (die Quantität, mit der ein Strahlungsantrieb in W/m² multipliziert werden muss, um in eine Temperaturänderung konvertiert zu werden) weder konstant noch linear ist: stattdessen sei er die erste Ableitung einer Relation zur vierten Potenz, die fundamentale Gleichung des Strahlungstransports. Hier müssen wir eine kleine Berechnung durchführen. Übernimmt man die gewöhnliche harmlose und vereinfachende Hypothese der konstanten Einheit Emissivität ist die erste Ableitung, d. h. die Änderung ΔTref der Referenztemperatur pro Einheitsänderung ΔQ0 der Dichte des Strahlungsflusses einfach Tref / (4Q0), und das ist linear.
Eine einfache Approximation, um breitenabhängige Variationen des Planck-Parameters zu integrieren ist es, das Schlesinger-Verhältnis anzuwenden: d. h. das Verhältnis der Temperatur TS zum Vierfachen der Flussdichte Q0 = 241,2 W/m² in der Emissionshöhe. Bei den 255,4 K, welche ohne Rückkopplungen und Treibhausgase vorherrschen würden, wäre der Planck-Parameter 255,4 / (4 X 241,2) = 0,26 K/Wm². Bei der heutigen Temperatur von 288,4 K ist der Planck-Parameter 288,4 / (4 X 241,2) = 0,30. Da ist nicht sehr viel Nichtlinearität.
Es ist daher sinnvoll anzunehmen, dass so etwas wie der mittlere Rückkopplungs-Anteil 0,08; abgeleitet aus dem Experiment, in welchem man der Atmosphäre nicht kondensierende Treibhausgase hinzufügt, weiterhin vorherrschen wird. Falls das so ist, beträgt die Gleichgewichts-Erwärmung, die man aus dem anthropogenen Antrieb der 2,29 W/m² während der industriellen Ära bis 2011 (IPCC 2013, Abb. SPM.5) erwarten kann, 2,29 / 3,2 / (1-0,08) = 0,78 K. Und tatsächlich zeigt der Trend der linearen Regression kleinster Quadrate im Datensatz der globalen mittleren Temperatur von HadCRUT4 von 1850 bis 2011 eine Erwärmung um 0,75 K.
Aber warum zeigen die Temperaturmessungen der ARGO-Bojen dann ein „Strahlungsenergie-Ungleichgewicht“, was auf mehr Erwärmung in der Pipeline hindeutet, sondern dass die enorme Wärmekapazität der Ozeane diese für jetzt absorbiert hat?
Eine Möglichkeit ist, dass die ganze Erwärmung seit 1850 anthropogenen Ursprungs ist. Nehmen wir an, dass das Strahlungs-Ungleichgewicht bis 2010 0,59 W/m² betragen hat (Smith 2015). Die Erwärmung hat dann 2,29 – 0,59 = 1,70 W/m² in den Weltraum abgestrahlt. Die Gleichgewichts-Erwärmung sowohl durch anthropogene als auch durch natürliche Antriebe bis 2011 kann damit um 34,8% größer gewesen sein als die während der industriellen Ära gemessene Erwärmung von 0,75 K: d. h. 1,0 K. Falls 0,78 dieser 1 K anthropogenen Ursprungs wäre, dann gibt es nichts, um zu verhindern, dass die restlichen 0,22 K natürlichen Ursprungs sind, geschuldet der internen Variabilität. Dieses Ergebnis ist tatsächlich konsistent mit dem vermeintlichen „Konsens“, dass über die Hälfte der jüngsten Erwärmung anthropogenen Ursprungs ist.
Die Implikation für die Charney-Sensitivität – d. h. die Gleichgewichts-Sensitivität bei einer verdoppelten CO2-Konzentration – ist geradlinig. Den Modellen zufolge beträgt der CO2-Antrieb 3,5 W/m² pro Verdoppelung. Teilt man dies durch 3,2, um dem heutigen Planck-Parameter Rechnung zu tragen, konvertiert sich dieser Wert zu einer Referenz-Sensitivität von 1,1 K. Dann ist die Charney-Sensitivität 1,1 / (1 – 0,08) = 1,2 K. Und das ist die Grundlinie. Nicht die 3,3 K Schätzung der CMIP5-Modelle. Nicht die 11 K von Stern (2006). Nur 1,2 K pro CO2-Verdoppelung. Und das liegt weit unterhalb allem, weswegen man sich Sorgen machen muss.
Keiner der Einwände gegen unsere Ergebnisse hat sich als substantiell erwiesen. Als Beispiel seien hier Yahoo-Antworten angeführt (sogar noch unzuverlässiger als Wikipedia) mit der folgenden herrlich albernen Antwort auf die Frage „hat Monckton einen grundlegenden Fehler entdeckt?“
Damit treibt der Fragesteller das folgende unsinnige Argument vor sich her:
1. Falls ich die Temperatur von 255,4 K auf der Erde ohne Treibhausgase heranziehe und die 8 K mit Treibhausgasen dazu addiere, erhalte ich eine Temperatur von 263,4 K.
2. Was ich sagen will: diese Total-Temperatur (anstatt lediglich des Treibhausgas-Effektes) führt zu einer Rückkopplung. Und falls ich dies anwende, erhalte ich eine Rückkopplung von 1 – (263,4 / 287,6) = 0,08.
Das Problem: Wie kann die Temperatur des Planeten (255,4 K) ohne Treibhausgase dann zu einer Rückkopplung führen? Die Rückkopplung ist den Gasen selbst geschuldet. Man kann nicht argumentieren, dass die Rückkopplung und in der Folge die höhere Temperatur infolge der Treibhausgase tatsächlich der Temperatur des Planeten ohne die Treibhausgase geschuldet ist! Was er gemacht hat ist, dass er die Grundlinie, auf der die Zunahme und die Rückkopplung fußt, herangezogen hat und diese dann als Grundlinie der Quelle von Zunahme und Rückkopplung angewendet hat.
Also, ich fürchte, das ist totaler Unsinn …
Der von Yahoo Answers begangene Fehler liegt in der falschen Annahme, dass „die Rückkopplung den Gasen selbst geschuldet ist“. Nein: man muss unterscheiden zwischen den kondensierenden Treibhausgasen einerseits (eine Änderung des Wasserdampfgehaltes der Atmosphäre ist ein Rückkopplungs-Prozess) und den nicht kondensierenden Treibhausgasen andererseits wie etwa CO2 (fast alle Änderungen der Konzentration nicht kondensierender Treibhausgase sind Antriebe). Alle in Tabelle 1 gelisteten Rückkopplungs-Prozesse wären präsent sogar beim Fehlen irgendeines der nicht kondensierenden Treibhausgase.
Ein weiterer Einwand ist, dass die offizielle Klimatologie vielleicht die Rückkopplungs-Reaktion auf die Emissionstemperatur berücksichtigt. Diesem Einwand kann rasch begegnet werden. Hier ist die typische eingestampfte und verschleiernde Definition einer „Klima-Rückkopplung“ vom IPCC (2013):
Klima-Rückkopplung: Eine Wechselwirkung, bei der eine Änderung in einer Klima-Quantität eine Änderung in einer zweiten verursacht, und die Änderung in der zweiten Quantität ultimativ zu einer zusätzlichen Änderung in der ersten Quantität führt. Bei einer negative Rückkopplung wird die Änderung abgeschwächt durch die Änderungen, die sie verursacht; eine positive Rückkopplung ist eine solche, in welcher die initiale Änderung verstärkt wird. In diesem Zustandsbericht wird oft eine engere Definition angewendet, in welcher die Klima-Quantität, welche sich ändert, die globale mittlere Temperatur ist, was wiederum Änderungen des globalen Strahlungshaushaltes verursacht. In jedem Falle kann die initiale Änderung entweder externen Ursprungs sein oder als Teil der inneren Variabilität daher kommen.
Diese IPC-Definition schließt also explizit jedwede Möglichkeit einer Rückkopplungs-Reaktion aus auf eine zuvor herrschende Temperatur wie die 255,4 K Emissionstemperatur, welche auf der Erde beim Fehlen jedweder Treibhausgase und Rückkopplungen herrschen würde. Aus diesem Grunde dachte Roy Spencer, dass wir falsch lagen.
Unser einfacher Punkt bleibt: wie kann ein unbelebter Rückkopplungs-Prozess wissen, wie man zwischen der Eingangs-Emission der Temperatur von 255,4 K und weiteren 9 K unterscheidet, der sich aus dem Hinzufügen nicht kondensierender Treibhausgase zur Atmosphäre ergibt? Wie kann dieser Prozess wissen, dass er auf Ersteres schwächer reagieren sollte als auf Letzteres? Oder, falls man der IPCC-Definition folgt, auf Erstere überhaupt nicht und auf Letztere extravagant? Trotz einiger wackerer Versuche seitens der wahrhaft Gläubigen, alles zu komplizieren, ist am Ende unser Punkt so einfach – und in unserer Eingabe unwiderlegbar.
Link: https://wattsupwiththat.com/2018/04/06/looping-the-loop-how-the-ipccs-feedback-aerobatics-failed/
Übersetzt von Chris Frey EIKE



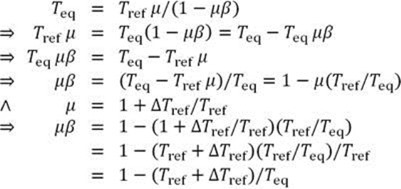















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Bei diesen Abschätzungen der CO2-Sensitivität sollte man übrigens immer im Hinterkopf behalten, dass meist implizit angenommen wird, dass der Temperaturanstieg menschlichen Ursprungs ist. Roy Spencer (der gerade zitiert wurde), hat einen Artikel darüber geschrieben (was ist denn mit der Link-Funktion hier los? Die klappt nicht unter Android):
http://www.drroyspencer.com/2018/02/diagnosing-climate-sensitivity-assuming-some-natural-warming/
Sehr interessanter Artikel, der mich wohl noch länger beschäftigt.
Ein kleiner Übersetzungsfehler:
müsste
heißen.
Nein, das ist schon richtige übersetzt. Es werden ja Extremsituationen betrachtet.
Im Original steht aber:
Stimmt. werden wir ändern.
Auch hier finden sich lediglich mathematische Spielereien, denen – wie auch beim IPCC et. al. – jeder Bezug zum realen Zustand des menschlichen Lebensraums fehlt.
Welche Gase lassen wohl im Bereich der Tropopause durch Emission von Wärmestrahlung die Temperaturen den Erdball umspannend knapp unter -50 Grad C absinken? – CO2 und Wasserdampf sind es dort mangels Masse nicht! – Kommen dort (und darunter) etwa andere Quellen als Eis und Wasser für die Emission in den Weltraum und für die wohltuende energetische Rückkopplung in Frage? – Warum könnte sich denn der Beitrag von Eis und Wasser nicht gegenläufig ändern, wenn sich darunter die Menge „angeblicher Treibhausgase“ ändert?
Klimasensitivität des CO2, eine Seifenblase!
Anthropogener Klimawandel
Und wieder wird einmal mehr lediglich die Grundlage des für viele sehr kostspieligen und für einige profitablen „Energiewende Quarks“ breit getreten!!!
Es steht immer der Vorbehalt drin, dass die CO2 Hypothese ansonsten korrekt ist.
„Es steht immer der Vorbehalt drin, dass die CO2 Hypothese ansonsten korrekt ist.“
Das ist nicht relevant! – Mathematische Spielereien sind es schon deshalb, weil der Zustand den menschlichen Lebensraumes aus einer Reihe anderer Gründe nicht mathematisch dargestellt werden kann. – Den täglichen Beweis dieses einfachen Sachverhaltes liefert das „wahrscheinliche Wetter für einige Tage“.
Unter dem Aspekt, dass man mit den Richtern und vor allem den Geschworenen in Kalifornien die CO2 Hypothese nicht diskutieren kann.
Daher muss die Strategie dort eine ganz andere sein, als z.B. auf einem wissenschaftlichen kongress.
Andreas Demmig schrieb am14. APRIL 2018 UM 20:47
Das ganze ist aber auch als Beitrag bei einem Journal eingereicht worden. Es geht also nicht nur um die Verhandlung, bei der der Amicus Brief eingereicht wurde …
„Es steht immer der Vorbehalt drin, dass „die“ CO2 Hypothese ansonsten korrekt ist.“
PS. Zur Präzisierung:
1. Die Hypothese, dass CO2 zur energetischen Rückkopplung beiträgt, wurde (qualitativ) bewiesen.
2. Trivial ist, dass der vom CO2 geleistete Beitrag zur energetischen Rückkopplung für andere Quellen nicht mehr verfügbar ist.
3. Trivial ist daher auch, dass nur eine Erfassung aller Quellen Aussagen zur Wirkung der energetischen Rückkopplung und zu ihren Änderungen liefern kann.
Insoweit ist auch die praktizierte Verwendung des sog. „radiative forcing“ irreführend.
„1. Die Hypothese, dass CO2 zur energetischen Rückkopplung beiträgt, wurde (qualitativ) bewiesen.“
Wo?
Wie?
Wann?
Durch wen?
Lieber Herr Keks,
die Antworten auf Ihre Fragen finden sich u. a. in den „gesammelten Werken“ des IPCC. (Lediglich die gegenläufigen Wirkungen hat man dort leider übersehen.)
In Erwartung des Angebots für den „Gegenstrahlunshähnchengrill“,
MfG
Lieber Herr Wolf,
Sie schreiben „wurde (qualitativ) bewiesen.“
Da wir alle wenig Interesse daran haben, die „gesammelten Werke“ des IPCC zu durchforsten, wäre ich Ihnen für eine kurze Schilderung des „qualitativen“ Beweises sehr verbunden.
MfG
„Qualitativ“ können das Modellchen und Messungen durchaus, „quantitativ“ geht leider nicht, weil sich der Zustand des menschlichen Lebensraums bekanntlich nicht mathematisch darstellen lässt! – Endlich kapiert?
Lieber klecks,
Merke: Wer lesefaul ist, bleibt dumm!
MfG
Ulllrich Wolv
„„Qualitativ“ können das Modellchen und Messungen durchaus…“
Echt?
Welches Modellchen denn?
Das von Al Görechen???
Und welche „qualitative“ Messung gibt es denn?
Von wo?
Und von wann?
Von wem? Mit was???
„Merke: Wer lesefaul ist, bleibt dumm!“
Ich lese Ihre Postings und versuche dabei meinen Restverstand zu bewahren…
Schwer zu lesen und nachzuvollziehen. Mehr Struktur bitte!
Carsten
—
Die Menschen schufen die Götter nach ihrem Bilde
„Die Menschen schufen die Götter nach ihrem Bilde“
Danke, zutreffende Aussage!
Hat sich daran irgendwas geändert? Soweit ich weiss, ist Spencer immer noch der Meinung, dass Monckton falsch liegt. Seine Begründung ist hier „Climate F-Words“ nachzulesen …
Und was denken Sie darüber, Herr Müller?