In einer neuen begutachteten wissenschaftlichen Studie, veröffentlicht im vorigen Dezember (2017) im Journal Earth Sciences sagt ein Student der Wissenschaft und des Ingenieurswesens an der Federation University (Australien) namens Robert Holmes, dass er vielleicht den Schlüssel gefunden habe, um uns verstehen zu lassen, wie Planeten mit einer dichten Atmosphäre (wie die Erde) eine bestimmte Temperatur von 288 K (Venus 740 K, Jupiter 165 K) „konstant“ [fixed] halten können, ohne dass ein planetarischer Treibhauseffekt oder Änderungen des atmosphärischen CO2-Gehaltes nötig sind.
Das ,Gedankenexperiment‘ Treibhauseffekt
Die vielleicht grundlegendste Konzeptualisierung in der Klimawissenschaft ist das „Gedankenexperiment“, mit dem man sich vorstellen kann, welche Temperatur auf der Erde vielleicht herrschen würde, falls es keinen Treibhauseffekt oder keine Atmosphäre gibt.
„Die Größe des Treibhauseffektes wird oftmals als die Differenz geschätzt zwischen der tatsächlichen globalen Temperatur und der Temperatur, die auf dem Planeten herrschen würde ohne jede atmosphärische Absorption, aber mit genau der gleichen planetarische Albedo, rund 33°C. Dies ist mehr ein ,Gedankenexperiment‘ als ein messbarer Zustand, aber es ist eine nützliche Grundlinie“.
Vereinfacht kann die global gemittelte Temperatur mit 288 K angegeben werden. Im „Gedankenexperiment“, in welchem eine imaginäre Erde keine Atmosphäre hätte (und folglich auch keine Treibhausgase absorbieren und die Wärme von der Oberfläche wieder emittieren kann), betrüge die Temperatur nur 255 K. Die Differenz zwischen der Temperatur auf der realen und der imaginären Erde ohne Atmosphäre beträgt 33 K, was bedeutet, dass es auf der Erde viel kälter (und diese damit unbewohnbar) wäre ohne die Gegenwart der Treibhausgase, welche die hypothetische „Wärmefalle“ bilden.
Von jenen 33 K Treibhauseffekt leiten sich der Vorstellung zufolge 20,6 K aus Wasserdampf-Teilchen in der Atmosphäre ab (1000 bis 40.000 ppmv), während man 7,2 K der „natürlichen“ (oder vorindustriellen) atmosphärischen CO2-Konzentration von 200 bis 280 ppm zuschreibt (Kramm et al., 2017).
Als „Gedankenexperiment“ fehlt es der entscheidenden Rolle der Erwärmung durch Wasserdampf-Teilchen und der CO2-Konzentrationen an Validierungen in der realen Welt. Zum Beispiel enthalten die Ozeane der Erde bereits 93% der Wärmeenergie des Planeten (Levitus et al., 2012), und bis heute gibt es keine physikalischen Messungen in der realen Welt, die zeigen, wie viel Erwärmung oder Abkühlung variierenden CO2-Konzentrationen geschuldet ist über einer Wasserfläche mit Volumen-Inkrementen von parts per million (0,000001). Konsequenz: Der CO2-Treibhauseffekt ist eine hypothetische, modellbasierte Konzeptualisierung.
Und während der letzten Jahre sind viele wissenschaftliche Studien veröffentlicht worden, welche nicht nur die Grundlagen des hypothetischen Treibhauseffektes auf der Erde in Frage stellen, sondern auch die Rolle von Treibhausgasen auf anderen Planeten mit dichten Atmosphären (wie der Venus) (Hertzberg et al., 2017, Kramm et al., 2017, Nikolov and Zeller, 2017 , Allmendinger, 2017, Lightfoot and Mamer, 2017, Blaauw, 2017, Davis et al., 2018). Die hier behandelte Studie von Holmes könnte vielleicht die jüngste derartige Studie sein.
,Extrem genaue‘ planetarische Temperatur-Berechnungen mit der Druck-Dichte-Massen-Formel
Holmes argumentiert, dass die mittlere Temperatur von 8 planetarischen Körpern mit dichten Atmosphären (0,1 bar oder mehr) präzise mit „extremer“ Genauigkeit vermessen werden kann – mit einer Fehler-Bandbreite von lediglich 1,2% – mittels Anwendung einer Formel, die von der Kenntnis von drei Parametern abhängt: 1) des mittleren atmosphärischen Drucks an der Oberfläche, 2) der mittleren atmosphärischen Dichte an der Oberfläche und 3) der mittleren molaren Masse der oberflächennahen Atmosphäre.
Holmes zog die Werte der abgeleiteten Druck/Dichte/Masse für jeden planetarischen Körper heran. Dann berechnete er mit diesen Zahlen die Temperaturen der Planeten.
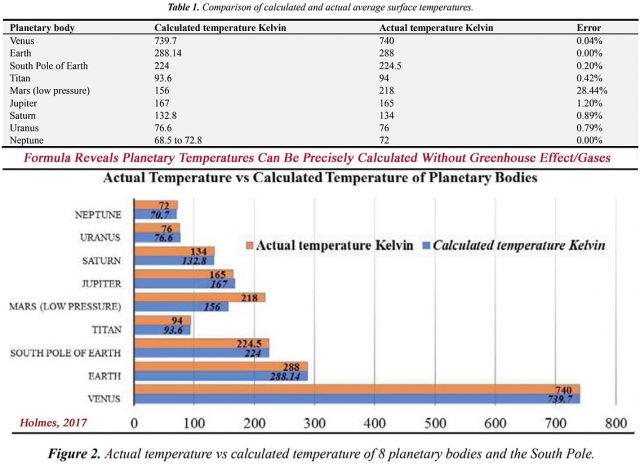
Die berechnete Temperatur der Venus ergab sich mit dieser Formel zu 739,7 K. Die gemessene Temperatur dort beträgt 740 K. Dies zeigt, dass die Genauigkeit der Formel für die Venus eine Fehlerbandbreite von lediglich 0,04% aufweist.
Mit den Werten von Druck/Dichte/Masse auf der Erde errechnet sich mit Holmes‘ Formel eine Temperatur von 288,14 K. Die gemessene Temperatur der Erde beträgt 288 K, passt also genau.
Die berechnete Temperatur auf dem Saturn beträgt 132,8 K. Die gemessene Temperatur dort beträgt 134 K – eine Fehlerbandbreite von nur 0,89%.
Die eindrucksvolle Genauigkeit der Formel wird in der folgenden Zusammenstellung illustriert (Tabelle 1 und Abbildung 2):
Atmosphärischer Druck/Dichte und Temperatur nahe der Oberfläche
Zum größten Teil ist die Dichte einer Planetenatmosphäre eine primäre Bestimmungsgröße von deren Temperatur. Planeten mit dichten Atmosphären sind wärmer, solche mit dünnen Atmosphären kälter. Je weiter man sich von der Oberfläche entfernt, umso geringer sind Druck und Gravitation und umso kälter wird es. Und umgekehrt.
„Im Allgemeinen ist die Atmosphäre eines Planeten umso dünner, je schwächer dessen Gravitation ist. Ein Planet mit schwacher Gravitation neigt dazu, weniger Masse zu haben und mehr seiner Atmosphäre in den Weltraum entweichen zu lassen. Folglich hängt die Dichte einer Atmosphäre von der Stärke der Gravitation ab. Beispiel: Die Gravitation des Planeten Jupiter ist 318 mal stärker als die der Erde, und folglich ist die Atmosphäre viel dichter als die irdische Atmosphäre. Die Gravitation wird umso schwächer, je weiter man von einem Planeten entfernt ist, und darum wird die Atmosphäre an der Oberfläche am dichtesten sein“.
Eine mühelose Illustration der Effekte des atmosphärischen Luftdrucks auf die Temperaturen eines Planeten wie die Erde kann man im Grand Canyon im Südwesten der USA finden. Der nördliche Rand liegt etwa 305 Meter höher als der südliche Rand. Interessanterweise ist es auch am nördlichen Rand rund 5°C kälter als am südlichen Rand – geschuldet dem Einfluss des atmosphärischen Drucks und der Gravitation. Am Grund des Canyons ist es rund 11 bis 14°C wärmer als an den oberen Rändern. Dieser erhebliche Temperaturgegensatz ist völlig unabhängig von irgendwelchen Treibhausgas-Konzentrationen an beiden Stellen, und es hängt auch nicht vom Sonnenlicht ab. Es ist der Unterschied in der Gravitation, welcher die Wärmedivergenz erzeugt.
„Höhe über NN und Jahreszeit bestimmen die mittleren Temperaturen im Grand Canyon. Die mittlere Höhe der oberen Ränder am südlichen Ende beträgt etwa 2100 m ü. NN, am nördlichen Ende etwa 2400 m ü. NN. Je höher, desto kälter. Zu jeder gegebenen Zeit wird es am nördlichen Ende rund 4 bis 5 Grad kälter sein als am südlichen Ende. … Direkt am Grund des Canyons kann es rund 11 bis 14°C wärmer sein als auf den jeweiligen oberen Rändern“.
Sensitivität bzgl. Änderungen der CO2-Konzentration „extrem gering“
Holmes weist darauf hin, dass die Implikationen seiner präzisen Berechnung planetarischer Temperaturen unabdingbar zu der Schlussfolgerung führen, dass es keinerlei Treibhauseffekten oder Existenz von Treibhausgasen bedarf, um eine hypothetische „Wärmefalle“ zu erzeugen. Stattdessen, so schreibt er, „können planetarische Körper mit dichten Atmosphären nicht durch den ,Treibhauseffekt‘ bestimmt werden, sondern höchstwahrscheinlich durch Auswirkungen von Strömungsdynamik und namentlich adiabatischer Autokompression“.
Der Effekt schließt die Möglichkeit aus, dass CO2 ein vorherrschender Klimatreiber ist.
Tatsächlich beträgt Holmes‘ Berechnung der CO2-Klimasensitivität (bei einer Verdoppelung von 0,03% auf 0,06%) -0,03°C.
Wie er in seiner Schlussfolgerung offensichtlich untertrieben schreibt: „Diese Klimasensitivität ist schon so gering, dass es unmöglich ist, sie in der realen Atmosphäre aufzuspüren oder zu messen“.
Molare-Masse-Version der Gasgleichung für ideale Gase weist auf eine sehr geringe Klimasensitivität
Introduction
Hier wird ein einfaches und zuverlässiges Verfahren gezeigt, mit dem man die mittlere atmosphärische Temperatur nahe der Oberflächen planetarischer Körper berechnen kann, welche an der Oberfläche einen atmosphärischen Druck von über 10 kPa (eine dichte Atmosphäre mit 0,1 bar oder mehr) aufweisen. Dieses Verfahren erfordert eine Gaskonstante und Kenntnis von lediglich drei Parametern: 1) des mittleren atmosphärischen Drucks an der Oberfläche, 2) der mittleren atmosphärischen Dichte an der Oberfläche und 3) der mittleren molaren Masse der oberflächennahen Atmosphäre. Die angewendete Formel ist eine molare Version der Zustandsgleichung für ideale Gase.
Hier wird gezeigt, dass die Informationen in diesen drei Gas-Parametern allein ein extrem guter Prädiktor für Temperaturen auf Planeten mit einem atmosphärischen Druck über 10 kPa sind. Dies zeigt, dass alle Informationen über die effektive plus die oberflächennahe atmosphärische Temperatur auf Planeten mit dichten Atmosphären automatisch von diesen drei Gas-Parametern festgelegt wird.
Diese Formel erweist sich nicht nur als viel genauer als jedes andere bisher angewendete Verfahren, sondern ist auch viel einfacher zu berechnen. Man braucht keinen Input von Parametern, die man früher als essentiell erachtete: solare Einstrahlung, Albedo, Treibhausgasgehalt, ozeanische Zirkulation und Wolkenbedeckung neben vielen Weiteren.
Damit wird hier gezeigt, dass kein einzelnes Gas anomale Auswirkungen auf atmosphärische Temperaturen hat, die stärker sind als bei jedem anderen Gas.
Kurz gesagt: Es kann keinen 33°C-,Treibhauseffekt‘ auf der Erde geben oder irgendwelche signifikanten ,Treibhauseffekte‘ auf irgendwelchen anderen planetaren Körpern mit einer Atmosphäre von über 10 kPa.
Die Formel: Ein ,extrem genauer Prädiktor‘ planetarischer Temperaturen
Die hier vertretene Hypothese lautet, dass im Falle der Erde die Sonneneinstrahlung die ,ersten‘ 255 K liefert – in Übereinstimmung mit der Schwarzkörper-Gleichung (11). Adiabatische Auto-Kompression liefert die ,übrigen‘ 33 K, so dass die bekannte und gemessene mittlere globale Temperatur von 288 K erreicht wird. Diese ,anderen‘ 33 K können nicht dem Treibhauseffekt geschuldet sein, weil wenn das doch so wäre die molare-Masse-Version der Gleichung für ideale Gase dann nicht herangezogen werden könnte, um planetarische Temperaturen genau zu berechnen, wie es hier eindeutig mit dieser Gleichung möglich ist.
Es ist offensichtlich, dass sich mit dieser einfachen Gleichung die ,Oberflächen‘-Temperaturen vieler planetarer Körper in unserem Sonnensystem genau berechnen lassen (Abbildung 2).
Dies gilt besonders für Körper, deren Atmosphären dicht genug sind, um eine Troposphäre entstehen zu lassen (d. h. einen atmosphärischen Druck über 10 kPa oder 0,1 bar aufweisen). Dazu zählen: Venus Erde, Jupiter, Saturn, Titan, Uranus und Neptun. Alle für diese Planeten berechneten Temperaturen liegen innerhalb einer Fehlerbandbreite von 1,2% bzgl. den von der NASA gemessenen ,Oberflächen‘-Temperaturen (außer beim Mars, der hier ausgeschlossen ist: sein atmosphärischer Druck ist viel geringer als 10 kPa). Diese Genauigkeit wird erreicht ohne Anwendung der Stefan-Boltzmann-Schwarzkörpergleichung und ohne die Einbeziehung von Termen für Parameter wie TSI-Niveau, Albedo, Wolken, Treibhauseffekt oder adiabatische Auto-Kompression. Alles was man braucht, um die oberflächennahe Temperatur genau zu berechnen, ist die relevante Gaskonstante und die Werte der drei variablen Gas-Parameter.
Die Implikationen: CO2-Klimasensitivität (-0,03°C) ist ,extrem gering‘
Ein paar Überlegungen hinsichtlich der Einfachheit und Genauigkeit dieser Ergebnisse werden einem unvoreingenommenen Menschen die offensichtlichen Implikationen dieser Arbeit vor Augen führen – als da wären, dass die residualen oberflächennahen Temperaturen auf planetaren Körpern mit dichten Atmosphären nicht durch den ,Treibhauseffekt‘ bestimmt werden können (residual bedeutet hier den Unterschied zwischen den Ergebnissen aus der Stefan-Boltzmann-Gleichung und der tatsächlichen Temperatur). Stattdessen sind dafür höchstwahrscheinlich Effekte durch Strömungsdynamik, namentlich adiabatische Autokompression ursächlich.
Eine weitere Implikation führt direkt zu der Schlussfolgerung, dass die Klimasensitivität bei einer beispielsweisen Verdoppelung der atmosphärischen CO2-Konzentration augenblicklich Auswirkungen zeigen müsste und auch extrem gering wäre. Diesem Szenario zufolge kann die Klimasensitivität bzgl. CO2 kaum anders sein als durch das Hinzufügen irgendeines anderen Gases in ähnlicher Quantität.
Vor allem die hier gezeigten Formeln 5 (und 6) schließen jedwede Möglichkeit komplett aus, dass ein Treibhauseffekt von 33°C von der Art, wie er vom IPCC in dessen Berichten kolportiert wird (23), in der realen Atmosphäre überhaupt existieren kann. Grund hierfür ist, dass das IPCC in seinen Berichten schreibt, dass eine Zunahme des atmosphärischen CO2-Gehaltes um 0,03% (300 ppm), also eine Verdoppelung, zu einem globalen Temperaturanstieg von ~3°C führen muss (mit einer Bandbreite von 1,5°C bis 4,5°C, was sich seit 1990 kaum geändert hat) (24). Das ist die so genannte ,Klimasensitivität‘. Dass diese Größenordnung der Erwärmung durch eine so geringe Änderung des Gasgehaltes verursacht wird, ist nach der Molaren-Masse-Version der Zustandsgleichung für ideale Gase ausgeschlossen.
Rechnung für eine Verdoppelung des CO2-Gehaltes seit vorindustrieller Zeit von 0,03% (300 ppm):
Berechnete Temperatur nach einer Verdoppelung des CO2-Gehaltes auf 0,06% ≈ 288,11 K.
Klimasensitivität bzgl. CO2 ≈ 288,14 – 288,11 ≈ -0,03 K.
Die Änderung wäre tatsächlich extrem klein und schwierig genau abzuschätzen und würde eine Größenordnung von -0,03°C aufweisen. Das ist einhundert mal kleiner als die ,wahrscheinliche‘ Klimasensitivität von 3°C, wie sie vom IPCC in seinen Berichten genannt ist, und vermutlich auch mit umgekehrtem Vorzeichen (Abkühlung). Aber selbst diese geringe Zahl wäre wahrscheinlich schon die maximale Änderung. Werden nämlich fossile Treibstoffe verbrannt, welche das CO2 emittieren, wird auch atmosphärischer Sauerstoff (O2) verbraucht, was dieses Gas in der Atmosphäre reduziert – und was jede durch zusätzliches CO2 erzeugte Temperaturänderung ausgleicht. Die Klimasensitivität ist bereits so gering, dass es unmöglich ist, sie in der realen Atmosphäre aufzuspüren oder zu messen, selbst vor irgendeiner Berücksichtigung des Verbrauchs atmosphärischen Sauerstoffs.
Übersetzt von Chris Frey EIKE
Anmerkung der Redaktion: Dieser Beitrag wird wieder heftige Kontroversen auslösen. Und das ist im Sinne der Wissenschaft. Als Anregung mag dieser Artikel von Willis Eschenbach dienen der sich mit dem Verhalten des idealen Gases in Bezug auf die Ergebnisse des Autors bezieht.

















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Nachdem ich mir das diesem Artikel zugrundeliegende Dokument angesehen habe, muß ich leider feststellen, daß es sehr trivial ist: es besteht aus: a) einer Anwendung des idealen Gasgesetzes b) einer Anwendung der isentropen Kompression durch Druckanstieg bei Verringerung der Höhe.
zu a) Die Bedingungen auf der Venusoberfläche wurden durch die Sonden mit Druck- und Temperatursensoren bestimmt. Ich nehme an, daß für eine gesonderte Messung der Dichte der Venusatmosphäre kein Raum in der Sonde vorhanden war, so daß die Dichte aus den Druck- und Temperaturwerten bestimmt wurde. eine gesonderte Messung der Dichte hätte eine „Abmessung“ eines Volumens und der Bestimmung der Masse des Volumens erfordert.
zu b) die Temperaturerhöhung in einem Bergwerksschacht wird dahingehend richtig beschrieben, daß ein substantielle Luftvolumen in die Tiefe gebracht wird und sich dabei durch isentrope Kompression erwärmt. Leider gelingt die Übertragung auf Venusverhältnisse nicht, da die „Randbedingung oben“ nicht fixiert wurde. Diese entspricht den Bedingungen an der Erdoberfläche vor dem Herunterbringen des Luftvolumens, dort sind aber die Randbedingungen bekannt.
Trotzdem verdient der Gedanke eine Weiterverfolgung, da die Venustemperatur als „Beweis“ eines natürlichen Treibhauseffektes sehr oft genannt wird.
Bei weiterer Betrachtung kam mir ein Gedanke:
Die Venusatmosphäre ist für das (dem Menschen) sichtbare Licht – also auch für die wichtigsten Anteile des Sonnenlichtes – undurchlässig. Das zeigt schon ein Blick durch ein Amateurteleskop, während man/frau/div Details der Marsoberfläche sehen kann (wie jetzt gerade) bleibt die Venus ein weißer Ball. Die für einen „Treibhauseffekt“ notwendige Absorption der Sonnenstrahlung muß in den Wolken passieren, statt auf der (festen) Oberfläche.
Wikipedia schreibt: „Dass die Atmosphäre der Venus von außen völlig undurchsichtig ist, liegt nicht an der großen Masse und Dichte der Gashülle, sondern hauptsächlich an einer stets geschlossenen Wolkendecke. Diese befindet sich mit ihrer Unterseite in einer Höhe von etwa 50 km und ist rund 20 km dick.“ https://de.wikipedia.org/wiki/Venus_(Planet)
D.h. in dieser Schicht finden die Absorptions- und Rückstrahlungsvorgänge statt. Dort ist es aber ca – 100°C kalt und der Druck liegt bei 0,1 bis 1 bar. Ein Venusluftpaket, welches von dieser Höhe zur Oberfläche transportiert würde, erwärmte sich aufgrund der isentropen Kompression.
Herr Ulrich,
sehr weise Gedanken haben sie da!
mit freundlichen Grüßen
Werner
My latest climate paper, (published 26th December, 2019) shows in a completely different way that there cannot be any troposphere warming effect from any so-called ‚greenhouse gases‘ such as CO2.
The paper compares atmospheric temperatures of three planetary bodies at 1atm of pressure, and proves that this temperature is ONLY dependent on solar insolation, neither greenhouse gases nor albedo have any effect.
It is easily possible to calculate Earth’s surface temperature from Venus or Titan without knowing anything at all about Earth’s atmospheric composition;
http://www.sciencepublishinggroup.com/journal/paperinfo?journalid=161&doi=10.11648/j.earth.20190806.15
To cite;
Robert Ian Holmes. On the Apparent Relationship Between Total Solar Irradiance and the Atmospheric Temperature at 1 Bar on Three Terrestrial-type Bodies. Earth Sciences. Vol. 8, No. 6, 2019, pp. 346-351. doi: 10.11648/j.earth.20190806.15
First, I recommend my latest climate paper;
Holmes, R. I. (2018). Thermal Enhancement on Planetary Bodies and the Relevance of the Molar Mass Version of the Ideal Gas Law to the Null Hypothesis of Climate Change. Earth, 7(3), 107-123.
Here is a final proof that the greenhouse effect does not exist in any thick atmosphere (one of >10kPa).
Postulates;
• The Ideal Gas Law is correct.
• The same external conditions such as insolation and auto-compression prevail.
My papers show that for a GHE to occur in a convecting atmosphere (one of >10kPa), a large anomalous change must happen in the density, pressure or both.
No anomalous changes of this magnitude have been seen in any planetary atmospheres.
This is not really a surprise, since anomalous changes are actually forbidden by the ideal gas law and its derivatives like the molar mass version, which treat all gases equally.
To provide the proof in excruciating detail;
Different concentrations of gases at the same or at different times can provide the same temperature or different temperatures;
BUT – the same concentrations of gases cannot provide different temperatures at different times. The formula T = P M / R ρ forbids it.
This fact disproves the greenhouse gas hypothesis, as it is presented by the IPCC*.
*Because there is said to exist a time delay to reach ‘equilibration’, due to the (ECS) climate sensitivity to CO2 being in the range of 1.5C – 4.5C.
The IPCC reports state that if there was a sudden doubling in the atmospheric greenhouse gas CO2, the greenhouse effect from this would operate slowly, causing an eventual ~3c of warming over centuries to millennia.
Therefore the claim is that the temperature would rise significantly over time, with the same prevailing atmospheric gas concentrations, and there would be no rapid equilibration, as the Ideal Gas Law demands. This represents a terminal conflict between the IPCC’s greenhouse effect and the molar mass version of the ideal gas law.
Therefore the climate sensitivity to, for example, a doubling of atmospheric CO2, must be close to zero. This means that essentially, there is no GHE.
Best Regards
Dr Robert Ian Holmes
Da hat einer gar nichts verstanden.
Natürlich ist es ein Zirkelschluss.
Man stelle sich eine schwarze Erde ohne Wasser mit einer Heliumatmosphäre vor.
In Abwesenheit einer Sonne kühlt das System immer weiter ab.
Die Druckwerte aus der barometrischen Höhenformel gelten nur für eine bestimmte
Temperatur. Wann man diese Temperatur spektrometrisch ermittelt, ergibt sich
natürlich ein Zirkelschluss.
Bitte hier nur unter vollem Klarnamen posten, siehe Regeln.
Ich sehe hier keine Zirkelschluß.
Der Druck auf der Planetenoberfläche hängt nicht von der Temperatur ab, sondern von der Masse der Atmosphäre und der Gravitation.Im Sommer bei 30° herrscht der selbe Druck wie im Winter bei -30°.
Ist die Zusammensetzung der Atmosphäre, deren räumliche Ausdehnung und deren Druck bekannt, kann auf die molare Masse geschlossen und die Temperatur ermittelt werden.
Eine kalte Erde ohne Sonne hat keine Atmosphäre, auch keine aus Helium!
Das FS3 veröffentlichte diese logische Überlegung bereits 2012 und führte sie als Idee genau aus. Es ist schön, wenn immer mehr Menschen die Indoktrinierung hinter dem Klimaschwindel verstehen lernen und wieder Geld für wirkliche Wissen-Schafft aufgewendet wird, statt für politische Fake-Science.
Das Märchen vom „Treibhauseffekt“ auf der Venus …
https://farsight3.wordpress.com/2015/11/02/8ung-2-11/
FS3
Bitte hier nur unter vollem Klarnamen posten, siehe Regeln.
Zum Vorwurf des Zirkelschlusses hat sich Holmes (mittlerweile PhD) geäußert:
„The fact is that the Gas Law does not care about the chemical composition of a gas. This means that there are no ‘special’ gases which exist that can cause an anomalous change in any of the three gas parameters. This is also clear from measurements in the solar system, which prove no anomalous changes are taking place, no matter what the concentration of GHG is.
Example; Earth has 2.5% GHG, Venus has 96.5% GHG. Yet there is no anomalous changes to the gas parameters on Venus due to this massive difference in the atmospheric GHG content; The temperature of a planetary body in space varies with the fourth-root of the power incident upon it, meaning that the temperature of Venus at 1atm (Tv) should be the fourth-root of 1.91 times the temperature on Earth at 1atm (Te). Venus receives 1.91 times the solar insolation of Earth.
Tv=∜1.91 x Te
Earth temperature at 1atm = 288K
Venusian temperature at 1atm = 340K
The fourth root of 1.91 is 1.176
288 x 1.176 = 339K“
Mit anderen Worten: Die Energiezufuhr durch die Sonne ist in den Variablen (Druck, Dichte etc.) inhärent. Wenn noch ein Treibhausgasmechanismus hinzugefügt würde, würde diese Gleichung nicht mehr funktionieren. Da die Gleichung jedoch unabhängig vom Anteil der Treibhausgase korrekte Ergebnisse liefert, kann ein Einfluss etwaiger Treibhausgase auf die globale Durchschnittstemperatur ausgeschlossen werden.
Das klingt für mich logisch. Oder mache ich einen Denkfehler?
Hier noch ein Link zu einer Diskussion darüber: https://culturalanalysis.net/2019/01/14/the-zeller-nikolov-climate-controversy/
Nur nimmt man die Treibhausgase und deren Wärmeabstrahlung weg, bleibt von der Theorie nicht mehr viel übrig. Der verbleibende Stickstoff und Sauerstoff können keine Wärme abstrahlen und es entsteht eine nahezu isotherme Atmosphäre ohne Temperatur-Gradienten. Die Gravitation und der Druck können da alleine nichts ausrichten.
„Der verbleibende Stickstoff und Sauerstoff können keine Wärme abstrahlen und es entsteht eine nahezu isotherme Atmosphäre ohne Temperatur-Gradienten. Die Gravitation und der Druck können da alleine nichts ausrichten.“
Das ist Blödsinn pur.
Die Atmosphäre ist vom Grunde her isentrop und nicht isotherm.
Nehmen Sie das doch endlich mal zur Kenntnis.
… und das ist sie, weil alle betrachteten Planeten infrarot-aktive Gas in ihrer Atmosphäre haben. Was auch immer die Theorie hinter der Gleichung sein soll, sie scheint vorauszusetzen, daß die Atmosphäre für die Wärmestrahlung der Planetenoberfläche intransparent ist. (Ist das der Grund, warum sie nicht für die dünne Mars-Atmospäre taugt?)
„… und das ist sie, weil alle betrachteten Planeten infrarot-aktive Gas in ihrer Atmosphäre haben.“
Quatsch!
Der Zwang zur Isotropie hat mit Strahlung nichts zu tun.
Daß sich aus der Isotropie keine Isothermie ergibt, liegt an der Schwerkraft und an der damit verbundenen potentiellen Energie, welche die kinetische Energie über die Höhe substituiert.
Es ist doch ganz einfach. In diesem Fall strahlt die Oberfläche direkt in den Weltraum.
Addendum: Die Frage ist welche Temperatur die isotherme Atmosphäre ohne Treibhaus-Gase annimmt. Bei 90 K wird Sauerstoff, bei 77 K Stickstoff flüssig. Die Atmosphäre ist aber kein Reinraum. Die Aerosole bestimmen dann wohl die Temperatur.
1.) Alleine eine kleine Überschlagsrechnung zeigt die Absurdität der Treibhausargumentation:
70% der Erdobefläche sind bekanntlich Ozean mit einer durchschnittlichen Tiefe von ca. 3800 m. Ich setze jetzt die mittlere Wassertemperarur mit nur 4°C , das sind 277K, an. Umgelegt auf die gesamte Erdoberfläche sind dann 0,7 x 3,8 x 10^6 x 4,187 x 278 = 3,10 x 10^9 kJ/m2 Energie allein in den Ozeanen mindestens gespeichert.
Die Atmosphäre hat ein Gewicht von ca. 10000 kg/m2 (=Normalluftdruck). Die Temperatur in der Troposphäre beträgt im Mittel ca 15 – (15 – -55 )/2 = -20°C, das sind 253 K. Die darin gespeicherte Energie beträgt dann ca. 1 x 10^4 x 1,01 x 253 = 2,56 x 10^6 kJ/m2
Das heisst, allein in den Ozeanen (3,1 x 10^9 kJ/m2) ist ca. tausend mal soviel Energie als in der Atmosphäre (2,56 x 10^6 kJ/m2) gespeichert. Wenn sich jetzt in der Atmosphäre ein Bestandteil um 0,01% ändert wirkt sich das auf den Energiehauhalt der Erde wie stark aus?
2.) Wenn sich jemand auf das Stefan Boltzmann Gesetz beruft und meint eine Erhöhung von CO2 würde die Temperatur in der Atmosphäre erhöhen, sagt er damit gleichzeitig, dass sich die Abstrahlung der Erdatmosphäre in den Weltraum auch erhöhen muss (höhere Temperatur => höhere Strahlung).
Nachdem aber niemand behauptet, dass im gleichen Zuge mehr Wärmeeinstrahlung durch die Sonne erfolgen wird, verschiebt sich somit ja die „Strahlungsbilanz“ der Erde (es wird gleich viel Energie eingestrahlt aber wegen der höheren Atmosphärentemperatur mehr Energie ausgestrahlt!) und es muss folglich auf der Erde langfristig kälter werden.
Klar, mehr Masse in der Atmosphäre, mehr Wärmeleitung nach aussen! Dadurch auch Wärme also Temperatur? (geht der Wärmetransport schneller?) in der Atmosphäre, aber eben kein Treibhauseffekt, dass es sich mehr und mehr erwärmt, die Umgebung des Planeten Erde kühlt diesen dann halt schneller ab.
Ich frage mich, warum dieser bare Unsinn von Holmes (2017) von EIKE uebernommen wurde.
Die Zustandsgleichung fuer ideale Gase ergibt sich aus der kinetischen Theorie idealer Gase, auf der die Definition der Temperatur beruht. Kein Wunder, dass Holmes bei den entspchenden Annahmen hinsichtlich Luftdruck und -dichte eine Temperatur von 288 K erhaelt.
Man nennt das im allgemeinen „gi – go“, was fuer “ garbage in – garbage out“ steht.
Hier ein Beispiel, wie absurd man zitiert wird. Es wird behauptet:
„Von jenen 33 K Treibhauseffekt leiten sich der Vorstellung zufolge 20,6 K aus Wasserdampf-Teilchen in der Atmosphäre ab (1000 bis 40.000 ppmv), während man 7,2 K der „natürlichen“ (oder vorindustriellen) atmosphärischen CO2-Konzentration von 200 bis 280 ppm zuschreibt (Kramm et al., 2017).“
Nur sind das die Zahlen, die von Kondratyev & Moskalenko (1984) stammen, die sich auf eine effektive Strahlungstemperatur einer Erde ohne Atmosphaere von 255 K beziehen. Kramm et al. (2017) haben diese Werte zitiert und nachgewiesen, dass diese Werte nicht stimmen koennen, und zwar weil die effektive Strahlungstemperatur von 255 K die falsche Bezugsgroesse ist.
Interessant ist dass Prof. Kramm gegenüber dem Fall ohne Atmosphäre, aber mit Erdrotation und Bodenwärmeflüssen, einen Treibhauseffekt von 288-220,7 K = 67,3 anstatt 33 Grad berechnet hat. Dabei sind die 220,7 K noch um 18,8 Grad zu hoch weil die Albedo fehlt, womit sein TE etwa 86 Grad wird.
Dass er – weil die Gegenstrahlung keine zusätzliche Energiequelle ist und sie „kälter“ ist und so wegen des 2.HS den Boden vermeintlich nicht wärmer machen kann – fälschlich auf der Nichtexistenz eines TE besteht, scheint ihn nicht zu stören.
@Dietze
Jetzt wird es komplett lächerlich!
Einen „Treibhauseffekt“ ohne Atmosphäre????
Mich wundert es nicht, wenn sich die „Klimaalarmisten“ über, nicht nur diese, Äußerungen kapputlachen!
@Dietze,
Sie schrieben
„Interessant ist dass Prof. Kramm gegenüber dem Fall ohne Atmosphäre, aber mit Erdrotation und Bodenwärmeflüssen, einen Treibhauseffekt von 288-220,7 K = 67,3 anstatt 33 Grad berechnet hat. Dabei sind die 220,7 K noch um 18,8 Grad zu hoch weil die Albedo fehlt, womit sein TE etwa 86 Grad wird.“
Wo habe ich etwas davon geschrieben? Offensichtlich sind Sie unfaehig, irgend etwas korrekt zu zitieren.
Die effektive Strahlungstemperatur einer Erde ohne Atmosphaere von 255 K, die zur die zur Quantifikation des sog. atmosphaerische Treibhauseffekt herangezogen wird, beruht auf Annahmen, die vollkommen realitaetsfern sind. Das haben bereits Gerlich & Tscheuschner (2009) nachgewiesen.
Was Sie zur Albedo schreiben, ist falsch. Die lokale Albedo ist abhaengig von der lokalen Zenitdistanz der Sonne. Wenn man dieses beruecksichtigt, was Kramm et al. (2017) sowohl im Falle des Mondes als auch im Falle einer Erde ohne Atmosphare getan haben, dann ergibt als Quotient zwischen der global gemittelten reflektierten solaren Strahlung und der global gemittelten einfallenden solaren Strahlung ein Wert von 0,178. Wenn Sie mit 0,3 argumentieren wollen, der zur Berechnung der effektiven Strahlungstemperatur einer Erde ohne Atmosphaere von 255 K herangezogen wird, dann ignorieren Sie, dass dieser Wert nur fuer das System Erde-Atmosphaere gilt.
Dazu heisst es selbst in der Fussnote 1 der Stellungnahme der Deutschen Meteorologischen Gesellschaft zu den Grundlagen des Treibhauseffektes von 1999:
„Dabei ist eine planetare Albedo von 30 %, wie sie fuer das System Erde/Atmosphaere gilt, angenommen worden, d. h. die dem System zugefuehrte Sonnenenergie ist genauso gross wie in Wirklichkeit. Nimmt man eine realistische Albedo der Erdoberflaeche von 15 % an, so ergibt sich fuer die mittlere Erdoberflaechentemperatur ein Wert von -5,5° C.“
Die effektive Strahlungstemperatur einer Erde ohne Atmosphaere von 255 K, die zur die zur Quantifikation des sog. atmosphaerische Treibhauseffekt herangezogen wird, beruht auf Annahmen, die vollkommen realitaetsfern sind.
Was hier ausgerechnet wird ist doch eine Temperatur für eine glatte Fläche, die 30% der Strahlung reflektiert und in einem Winkel von 15° von der Sonne beschienen wird. Dann verteilt sich ein m^2 auf 4 m^2. Die Erde sieht also so aus, wie bei den Nachrichten das Bild hinter dem Sprecher. Auf dem Planeten, auf dem wir leben, und auf allen Himmelskörpern im gesamten Universum, die um einen Stern kreisen, ist es völlig ausgeschlossen, dass überall die gleichen Temperaturen herrschen. Wenn dann ein nichtlinearer Zusammenhang mit einer anderen Größe vorliegt, T^4, ist die Rechnung sinnlos und grenzt an Hirntod. Wenn das Leben auf der Erde auf diesen Blödsinn eingestellt wäre und nur mit Temperaturen 15°C +- 2° zurecht käme, wäre die Erde ein toter Planet. Es tut mir leid, für mich bedeutet Naturwissenschaften, mit den Mitteln der Wissenschaft, die Natur zu beschreiben. Dazu gehört ein Modell zu erstellen, was die Temperaturen vorhersagt, die auch nachweislich gemessen werden können.
Ich habe letztens mal aus Spass vorgerechnet, welche Temperatur die Erde hätte, wenn sie eine Scheibe wäre. Ist zwar immer noch bescheuert, aber näher an der Wirklichkeit als diese ‚gesicherte‘ Wissenschaft. Eine Scheibe hat nämlich zwei Seiten, also wird es auch mal Nacht; ein sehr häufiger Zustand, der der Klimakirche völlig unbekannt ist. Ich habe bis jedenfalls immer nur Klimaschemata gesehen (das sind die Bildchen mit den vielen lustigen Pfeilen) auf denen immer die Sonne scheint.
Meine Rechnung war: aus den 240 W ergibt x 4 = 960. Diese verteilt sich auf einer Scheibe natürlich nur auf die halbe Oberfläche. Aus 480 W folgt 303 K. Für die Nachtseite erhält man natürlich 0, mit der kosmischen Hintergrundstrahlung 2 Kelvin. Und schon vergibt eine Temperatur von (305/2) rund 152 Kelvin.
Ich weiß nicht, wie oft man diesen Blödsinn fortsetzen muss, bis erwachsene Menschen begreifen, dass Mathematik nur dann etwas mit Naturwissenschaft zu tun hat, wenn sie so genau wie möglich beschreibt, was wirklich passiert.
Meiner Meinung nach würden Naturwissenschaftlicher Modelle erstellen, die die 100 Grad Temperaturunterschied, der nun mal genau so real ist wie der Klimawandel, auch berücksichtigen.
Wenn wir in der achten Klasse auf die Idee gekommen wären, bei Potenzfunktionen mit Mittelwerten herumzuspielen, hätte es eine 5 nach der anderen gegeben.
Die in dieser Studie enthaltenen Aussagen und Zusammenhänge sind zunächst verblüffend und erscheinen genial, beim näheren Hinschauen entpuppen sie sich jedoch als lapidar und völlig ungeeignet, die Existenz eines Treibhauseffektes auszuschließen.
Laut Formel 6 ist Temperatur eines Gases durch die 3 Parameter Druck, Dichte und molare Masse eindeutig bestimmt. Das ist ein aus der Theorie des idealen Gases abgeleiteter allgemeiner Zusammenhang, der überall besteht wo Gas (mit Mindestdruck) vorkommt.
Diese Aussage ist so allgemein, dass sie für die Erde völlig unabhängig von der solaren Strahlung oder der Wolkenbedeckung immer zutrifft. Weil die molare Masse als stabil angesehen werden kann, befinden sich nur noch Druck und Dichte in einem Wechselspiel mit den Temperaturveränderungen.
Die Formel sagt aber nichts über die Ursache der Temperaturveränderung aus. Die Ursache kann und muss sogar außerhalb der wechselwirkenden Parameter liegen. Nimmt z.B. die Solarstrahlung zu, so wird es auf der Erde wärmer, entstehen mehr Wolken (Svensmark) wird es kälter. Und falls es tatsächlich einen THE geben sollte, dann trägt dieser selbstverständlich auch zur Erwärmung der Erde bei, so als ob die Sonne stärker und/oder öfter scheinen würde. Die Formel stimmt in jedem Fall.
Ich stelle fest, dass es mehrere Ursachen für eine Temperaturerhöhung gibt, und immer bildet die Formel den Zusammenhang zwischen den 4 Gasparametern korrekt ab. Die Ursache der Temperaturveränderung wird hingegen nicht durch die Formel abgebildet sondern nur deren Auswirkung!
Mit dieser Erkenntnis ist es aber nun vermessen, diese Formel für die Berechnung der CO2-Klimasensitivität zu benutzen, so wie Holmes es tut. Er bildet damit nur den verschwindend kleinen Teil (-0,03K) ab, den der Eintrag an zusätzlichem CO2 direkt über die 3 Gasparameter bewirkt. Dabei kann er aber nicht ausschließen, dass CO2 über einen weiteren Mechanismus (THE) die globale Temperatur zusätzlich erhöht.
Eine Widerlegung der Treibhaushypothese ist dieser Beitrag also nicht.
„Eine Widerlegung der Treibhaushypothese ist dieser Beitrag also nicht.“
Welche Treibhaushypothese ist gemeint? Es gibt meines Wissens keine allgemein anerkannte! Gerlich/Tscheuschner haben in ihrer Falsi-Arbeit alleine 14 verschiedene Versionen geprüft und keine einzige als physikalisch haltbar bewertet.
Wer also von Hypothesen spricht, sollte einen Link auf jene Version angeben, der er anhängt.
@stefan strasser
Auch wenn ich Holmes These,
ablehne, so heißt das nicht, dass ich mich andererseits für eine der angebotenen Treibhaushypothesen entscheiden muss. Ich bin mir nicht sicher, wie man die Differenz von 33K zwischen dem globalen S-B-Ansatz und der real gemessenen Erdmitteltemperatur, zutreffend erklären und beweisen kann.
Im Sinne der Wahrheitsfindung nach dem Ausschlussverfahren halte ich es jedoch für notwendig, auch Thesen entgegenzutreten, die jegliche Treibauseffekte für nicht existent erklären wollen. Darunter fallen diese hier und der „hemisphärische S-B-Ansatz“ von Herrn Uli Weber. Dies tue ich, weil ich sie für falsch halte und nicht, weil ich Anhänger irgendeiner Treibaushypothese bin.
Der globale S.B.-Ansatz ist eben Unsinn. In Richtung von Leistung auf Temperatur gilt er nur für den real nicht existenten Schwarzen Strahler.
Daß die Rechnung Unsinn produziert, sieht man ganz klar, wenn man statt mit mathematisch falsch gebildeten Mittelwerten mit Istwerten für reale Punkte der Oberfläche reehnet.
Wenn man also rechnet, daß die reale Albedo z. B. 15% ausmacht, wie etwa durchschnittlich für Wasser angegeben, bleiben von der Solarkonstante noch 1162 W/m² erwärmend über. Gemäß Stefan-Boltzmann Formel P(ᴛ) = ?·A·?⁴ ergibt das eine Temperatur von 378,4 K oder 105,2°C für einen Quadratmeter Wasserfläche dieser Albedo und Sonne im Zenit. Das hieße, das Wasser würde mehr als kochen. Für die Situation unbeschienen käme man auf nahe dem absoluten Nullpunkt. Allein diese Beispiele zeigen, daß die Aussage „in guter Näherung“ für die Erde als Schwarzer Strahler von P nach T falsch ist.
Der Begriff Wärme – Joule [kg*m²/s²], und nur die produziert Temperatur, kommt in dieser ganzen Rechnung überhaupt nicht vor!
In Ihrem Post waren jede Menge Steuerzeichen, die ich löschen musste. Bitte anderen Browser oder Texteditor verwenden.
@stefan strasser
Ihre Rechenbeispiele zeigen keineswegs die Unsinnigkeit oder Unanwendbarkeit des S-B-Gesetzes, denn auf dem Mond herrschen solch krasse Temperaturunterschiede, sondern nur die Notwendigkeit von Wärmespeicherung und Wärmzirkulation auf der Erde. Hier muss mit idealisierten Mittelwerten gerechnet werden, sonst resultieren unrealistische Ergebnisse.
Die Wärmemenge in Joule (=Ws) beschreibt die eingestrahlte Leistung (W) über einen gewissen Zeitabschnitt (s). Da im gleichen Zeitraum (Tag, Jahr) die Wärme absorbiert und auch wieder abgestrahlt wird, ist eine Rechnung mit Leistungen (W) (bzw. Leistungsdichten W/m^2) durchaus sinnvoll, denn die Zeiten kürzen sich weg.
„Hier muss mit idealisierten Mittelwerten gerechnet werden, …“
Wenn eine Modellrechnung nicht mit der Wirklichkeit übereinstimmt, ist die Modellrechnung falsch! Das ist so sicher, wie das Amen im Gebet!
@Egbert Krause, für dieses Kürzen verletzen Sie caeteris paribus, vom Absorber (e.g. Wasser, Ozeane, etc) und Emitter (e.g. Gase, Atmosphäre, etc), nicht wahr. Der Mond (Emitter ≈ Absorber) ist nicht unser Wetterplanet (Emitter ≇ Absorber).
P.S. typischer Einsteinjünger Fehler: indem alles Unberücksichtigte gleich 1 gesetzt wird, soll ein angeblich Mögliches ausgerechnet werden. Sehen Sie das ex falso sequitur quodlibet nicht.
@Alwin Bruno
Tja, wer schon glaubt, die Erde ist immer im thermischen Gleichgewicht, dem ist nicht mehr zu helfen!
Wie sieht es denn im Frühjahr auf der Nordhalbkugel aus? Wieviel Energie wird denn benötigt, um Eis und Schnee zu schmelzen? Wieviel Energie wird benötigt um die Böden u. Wasser auf sommerliche Temperaturen zu bringen?
Schon etwas von spezifischen Wärmen gehört?
Und wie sieht die Tag – Nacht – Energiebilanz aus?
Der größte Denkfehler kommt zustande, wenn man annimmt, aus der täglichen Energiemenge der Sonne, die die Erde erreicht, auf die tatsächliche Erdtemperatur schließen zu können!
Wir wissen genau, wieviel Energie notwendig ist , um 10 Liter Wasser um 10 Grad C zu erwärmen – wissen wir dann wie warm oder kalt das Wasser im Kochtopf ist????
Niemals!
Danke für die sympathische Stellungnahme. Erfrischend arroganz- und aggressionsfrei bei gleichzeitigem Sachverstand…
Das klingt etwas nach Schulnoten. Ein gute Näherung ist für mich, wenn die Näherung für die weitere Aussagen ausreichend ist. Eine sehr gute Näherung, wenn die Näherung besser ist als ich für die weiteren Aussagen benötige.
Man hat jedoch nicht die Gasdichte gemessen, sondern sie wird mit Hilfe der idealen Gasgleichung berechnet. Dies wird auch auf der Erde so praktiziert. In die Dichte der Atmosphäre gehen aber nicht nur Gase ein, sondern auch Schwebeteilchen. Deren Beitrag wird offensichtlich vernachlässigbar.
Korrektur: In meinem Beitrag erhält man für die Korrektur der Venus-Atmosphäre nicht 9 K, sondern 15 K. Deshalb müssen aber nicht alle Temperaturmessungen auf der Venus korrigiert werden, sondern die Veröffentlichung von Herrn Holmes, der die Venus-Temperatur aus der Gasdichte berechnet hat.
@Herrn P. Berberich 13. Februar 2018 um 9:45
Zitat: „Ein gute Näherung ist für mich, wenn die Näherung für die weitere Aussagen ausreichend ist.“
Sie betreiben Wissenschaft und kein Okkultismus. Wie wollen Sie „ausreichend“ bewerten – Wer definiert das? Die Gültigkeits-Grenzen einer Theorie, gibt die Theorie und die gewonnenen empirischen Referenzen vor, und nicht Ihre subjektive „ausreichende“ Bewertung.
Zitat: „Man hat jedoch nicht die Gasdichte gemessen, sondern sie wird mit Hilfe der idealen Gasgleichung berechnet.“
Nein, das ist nicht richtig – Wo haben Sie das her? Die Venera-Sonden hatten ein Densitometer (Gas Density Gauge) an Bord. Keine Gasdichte rho = m/V(T,p) kann direkt gemessen, wegen der Abhängigkeit zur Temperatur und Druck. Andere Methoden der Messung der Atmosphärendichte sind mit dp/dz = -g*rho = -p*M*g/[R*T] und/oder über die Staupunkt-Druckmessung (Aero-Braking) p(St) = p + rho*v^2 und/oder mit der Aerodrag Gleichung m*a = 1/2*rho*Cd*A*v^2 und/oder über die Schallgeschwindigkeit usw..
Mfg
Werner Holtz
Herrn Werner Holtz 17.2.2018 11:27
Praktisches Beispiel: Ich suche eine einfache Formel um das Temperaturprofil auf der Erdoberfläche in Abhängigkeit von Jahreszeit, Breiten-, Längengrad und Höhe zu beschreiben. Welches einfache Rechenverfahren schlagen Sie vor? Die Ansätze sollten besser sein als die von North 1981 „Energy Balance climate models“ verwendeten. Ein Vergleich von Rechnung und Messung (HADCRUT 4.6) für North 1981 ergibt ein monatliches Mittel von R² = 0,78 Global, R² = 0,67 NH, R²= 0,81 auf der SH.
Warum kompliziert – wenn doch alles ganz einfach ist?
——–Isolierkanne – Warum Vakuum und nicht CO2 ?——–
https://www.facebook.com/EOCO2/
Wegen der Konvektion
Bauschaum genügt
Carsten
Ich habe eine einfache Formel gefunden:
LWSout= c1*ASRS+c2*LWSin ,(1)
ASRS= absorbed solar radiation surface, LWSin = LWSurface in, LWSout= LWSurface out. Aus LWSout folgt dann die Oberflächen-Temperatur Ts nach dem SB-Gesetz: LWSOut= SB-Konstante*Ts^4 (epsilon=1).Die Parameter c1 und c2 kann man durch einen Fit von (1) mit ASRS und LWSIn (aus CERES-Datensatz, All sky) an LWSOut (aus Ts HADCRUT 4.6) ermitteln. Für 2016 erhält man z.B. c1= 0,0404 und c2= 1,114. Das so berechnete Ts weicht im monatlichen Mittel an jedem Punkt nur um SDR= +/- 4 °C vom gemessenen ab (R²= 0,93).
Dies ist kein Klima-Modell, sondern eine empirische Formel. Meine Interpretation: LWSOut hängt nur wenig von ASRS ab, da dieser Beitrag nur die direkte Emission ins Weltall beschreibt. Der größte Anteil von ASRS wird von Oberfläche an die Atmosphäre abgegeben und von der Atmosphäre wieder emittiert. c2 ist größer als 1, da Ts höher ist als die Temperatur der Atmosphäre. Die Formel kommt ohne Wärmekapazität, Winde oder Aufwinde aus. Dies folgt aus der starken lokalen Kopplung von Atmosphäre und Oberfläche. Der lokale Energieaustausch geht aber nicht nur über Wärmestrahlung, sondern hauptsächlich über sensible und latente Wärme. Die Wärmestrahlung ist nur der Indikator.
Um zu erkennen, dass der sogenannte „Treibhauseffekt“ physikalischer Unsinn ist, braucht man nicht unbedingt weitreichendes klimatisches Fachwissens, es reicht schon, sich des Hausverstandes zu bedienen und ein paar grundlegende physikalischen Gesetzmäßigkeiten und Zusammenhänge zu kennen!
Die Atmosphäre ist als Gasmaterie den physikalischen Gesetzmäßigkeiten, in diesem Fall insbesondere denen der Thermodynamik, unterworfen.
Ihre thermisch aktiven Anteile („Treibhausgase“) absorbieren Wärme sowohl aus der Sonneneinstrahlung als auch aus der geringen von der Erdoberfläche abgegebenen langwelligen Wärmeabstrahlung und erwärmen sich dadurch ein wenig und in der Folge auch die umgebende Atmosphäre.
Zur Klarstellung sei erwähnt, dass erstens ca. 45% der Solarstrahlung im langwelligen Bereich liegt und zweitens der größte Teil der durch Sonneneinstrahlung auf der Erdoberfläche erzeugten Wärmeenergie durch Wasserverdunstung, Konduktion und Konvektion „entsorgt“ wird. Nur ca. 15% der gesamten von der Erdoberfläche abgegebenen Wärmeabgabe erfolgt als Strahlung die für „Treibhausgase“ absorbierbar ist!
Nun zu den thermisch inaktiven Atmosphärenanteile N2, O2 und Arg, die ca.99,9 % der Atmosphärengesamtmenge ausmachen! Diese erhalten wie schon erwähnt von der Erdoberfläche ausgehend große Mengen Wärmeenergie durch Wasserverdunstung, Konduktion und Konvektion. Sie werden aber auch etwas von den spärlich vorhandenen Treibhausgasen erwärmt, die ihre in den unteren Schichten der Troposphäre absorbierte Wärme größtenteils durch direkte Molekülstöße an sie abgeben. Weil es dort hohe Moleküldichte gibt, ist das die bevorzugte physikalisch Art der Wärmeübertragung und nicht Strahlung wie fälschlicherweise behauptet wird.
Unsere Atmosphäre ist also physikalisch gesehen, ein gigantischer Wärmespeicher, der zwar einerseits direkt und indirekt permanent von der Sonne aufgeheizt wird, aber andererseits auch permanent von ihrem oberen Rand aus durch Wärmeabstrahlung an das Weltall abge-kühlt wird! Das ist eine unbestrittene Tatsache, ohne die der Planet schon längst den Hitzetod gestorben wäre. Diese Tatsache wird in der „Klimadiskussion“ leider weitgehend verschwiegen, vermutlich deshalb, weil diese permanente Abkühlung ausschließlich durch thermisch aktive Gase, also die „Treibhausgase“ erfolgen kann, was in eklatantem Widerspruch zur Behauptung steht, „Treibhausgase“ würden zu einer katastrophalen Klimaerwär-mung führen! Korrekterweise ist zu erwähnen, dass ein geringer Teil der Kühlung auch durch Strahlung von der Erdoberfläche aus erfolgt. Diese Strahlung ist aber für „Treibhausgase“ nicht absorbierbar (Atmosphärisches Fenster) und somit für die „Treibhausthese“ irrelevant.
Nachdem also aufgezeigt wurde, dass und warum die Atmosphäre ein gigantischer Wärmespeicher ist und da Temperatur ein Maß für den Wärmeinhalt einer Materie ist, sollte erkennbar sein, dass unsere „Globaltemperatur“ von ca. 15°C in der Nähe der Erdoberfläche nichts anderes ist, als eben eine Maßzahl für die in dieser Atmosphärenschicht enthaltene Wärmeenergie und dass das mit Strahlung unmittelbar nicht das geringste zu tun hat!
Dipl. Ing. Axel Stolz
A-6370 Kitzbühel
@ Axel Stolz
Sehr gut, genau so ist es!
http://thumulla.com/home/ein_gedankenexperiment_zum_klima_auf_der_erde.html
Carsten
Sehr geehrter Herr Stolz! Endlich stoße ich mal auf einen Kommentator, der auf einen Punkt hinweist, der ständig übersehen wird: das Gros der Atmosphäre besteht aus Gasen, die Wärme weder als Strahlung absorbieren noch emittieren können (und zwar bekanntermaßen: bereits Tyndall hat vor gut 160 Jahren hierzu die Empirie geliefert), diese Gase nehmen aber geleitete Wärme am Boden auf, woraus – so muss man annehmen – ein permanenter Konvektionsprozess entsteht, so lange der Boden erwärmt wird. Folge ist in der Tat eine Atmosphäre, die einen „gigantischen Wärmespeicher“ darstellt (wenn auch, verglichen mit den Weltmeeren, einen kleinen)! Man muss sich doch auch die grundsätzliche Frage stellen, wieso die Erde mit gasförmiger Hülle umgeben ist – von Gasen (O2, N2), die erst oberhalb von minus 190-180 Celsius-Grad ihren Siedepunkt erreichen! Bei Temperaturen wie im freien Weltraum wären das Flüssigkeiten oder Festkörper, wenn sie nicht irgendwie erwärmt werden können. Dass sie gasförmig sind, wird einfach als selbstverständlich hingenommen! Ihre Temperatur am Boden, die uns das Leben ermöglicht, muss also direkt damit zusammenhängen, dass sie Wärme bereits aufgenommen haben und diese auch behalten. Die adiabatische Temperaturabnahme mit der Höhe spiegelt dann lediglich die abnehmende Dichte dieser wärme-haltenden Gase wieder.-
Offenbar ist der Vorgang der Erwärmung durch direkten Kontakt mit anschließender Konvektion so „unspektakulär“, dass man ihn so vernachlässigt hat. Er dürfte auch schwer messbar und quantifizierbar sein, denn sicherlich hängt er auch stark von der Rauigkeit des Bodens ab und ist sehr chaotisch. (Im Internet stieß ich auf ein Buch über Planetenatmosphären, wo in dem Modell der atmosphärischen Temperaturbildung – ganz nach dem Muster des „Treibhauseffekts“ – der Term „Konvektion“ komplett weggelassen war!)
Stattdessen hat man sich den Kopf darüber zerbrochen, wie man sich die reale Temperatur konstruieren könne, indem man bei einer atmosphärelosen Erde anfängt und dann alles nur auf die Strahlung abstellt! Wäre es nicht ein sinnvollerer Ansatz gewesen, von den bekannten Phänomenen auszugehen?: Es gibt eine Atmosphäre, und die zeigt die Fähigkeit, Wärme festzuhalten (auch in der Polarnacht verliert die Atmosphäre nicht so viel Wärme, dass sie unter den Kondensationspunkt der Hauptgase fällt!); sie setzt sich aus verschiedenen Gasen zusammen, deren unterschiedliches Verhalten in bezug auf Infrarotstrahlung längst bekannt ist. Damit hätte man eine Art „Treibhaus“ beschrieben, auch wenn dieser Vergleich ja bekanntlich sachlich falsch ist – das aber nicht auf den danach bezeichneten Gasen beruht, sondern gerade auf den in bezug auf thermische Strahlung inerten Gasen! Der „Treibhaus“-Begriff ist somit eine Halbwahrheit, weshalb er auch so schwer zu korrigieren ist – aber vollkommen verkehrt ist leider seine Erklärung.- Hier steckt der erste Denkfehler.
Der weitere Fehler bestand dann darin, dass man sich auch über die Konsequenzen dieser Situation keine Klarheit verschuf: Sauerstoff, Stickstoff, Argon, die keine Wärmestrahlung aufnehmen können, aber geleitete Wärme, sind auch unfähig, sich in Richtung Weltraum ständig wieder zu kühlen, weil das nur durch Infrarotstrahlung möglich ist! Also müsste eigentlich die Atmosphäre ständig wärmer werden – wird sie aber nicht.- Es ist geradezu paradox, wie selbstverständlich über diesen Punkt hinweggegangen wird. Die Atmosphäre kühlt sich permanent, indem sie Infrarotstrahlung abstrahlt – das kann man ja schließlich mit Satelliten detektieren!
Aber wie kann sie das bei 99% strahlungsunfähigen Gasen? Wer oder was leistet diese Abstrahlung? Das ist bekannt: Einzig und allein jene Gase, die zu Unrecht in Verruf geraten sind, „klimaschädigende Treibhausgase“ zu sein, geradezu das krasse Gegenteil der tatsächlichen Gegebenheiten: sie kühlen permanent die übrige Atmosphäre, d.h. sie nehmen ihr letztlich die Wärme wieder ab; und das kann auch gar nicht anders sein. An allererster Stelle leistet das natürlich der Wasserdampf (der seltsamerweise von der „Klimapolitik“ ausgespart wird trotz seiner geradezu „gefährlichen“ Gehaltsschwankungen in der Atmosphäre von fast null bis in den Prozentbereich – es wäre auch einfach absurd und aussichtlos, Wasserdampf zum „Klimakiller“ zu deklarieren und durch ein noch zu treffendes „Pariser Wasserdampfabkommen“ künstlich regulieren zu wollen); dann das Kohlendioxid, ferner die kleinen Piccoloflöten u. Triangel in dem ganzen Orchester, Methan, Stickoxide usw. (all jene Gase, die Moleküle mit einem Dipolmoment darstellen).
Der dritte Schritt wäre dann gewesen, sich zu klarzumachen, dass sich je nach dem atmosphärischen Anteil des Kohlendioxids sicherlich etwas verändert in der Menge absorbierter – und in Bodennähe sofort thermalisierter – Strahlung, sowie in größerer Höhe die Menge der durch dasselbe Gas abgestrahlten Wärme, dass aber auf jeden Fall bei einer Zunahme der CO2-Konzentration nicht nur die Absorption steigen sollte (beachte aber die Sättigung und die logarithmische Beziehung Konzentration-Absorption), sondern vermutlich gleichsinnig damit auch die Abstrahlung, denn der CO2-Anteil ist bis in beträchtliche Höhe derselbe und homogen (Angabe: bis ca. 80 km Höhe) – was übrigens auch darauf hinweist, wie intensiv und permanent die Durchmischung der unteren Atmosphäre ist.
Hält man aber beide Funktionen des CO2 in der Atmosphäre zusammen – statt sich für die eine zu interessieren und die andere zu vergessen -, dann fällt die ganze CO2-Debatte über die angeblich die Gesamtexistenz des Lebens gefährdende Klimawirkung eines leicht zugenommenen CO2 in sich zusammen wie ein kalt gewordenes Soufflee.
(Wir haben ja noch nicht einmal die magische Verdoppelung jenes – wirklich unangefochtenen? – Anfangsgehalts von 280 ppm erreicht, bei der der volle Betrag der Erwärmung gemäß der Klimasensitivität erreicht sein müsste – wenn man sich nur einig wäre, welcher Wert: 1°, 2°? Oder nur 0.5, 0.2, 0.1°? Erreicht sind bisher nur ein Plus von ~120 ppm. Die 560 ppm liegen noch in weiter Ferne. Ob sie je erreicht werden?)
(Auch dies ist ja an sich nicht unbekannt: es gab Erdzeitalter mit einem Vielfachen des heutigen CO2-Wertes: wieso ist damals das gesamte Leben nicht ausgelöscht worden und die Erde „im Fieber zugrunde gegangen“?)…
Leider hat sich die Atmosphärenphysik nicht folgerichtig entwickelt: statt die Tyndall´schen Erkenntnisse über Gase sorgfältig anzuwenden (heute durch das Modell der möglichen Bindungsschwingungen bei Molekülen mit Dipolmoment erklärt, die bei unpolaren Molekülen nicht vorkommen), spann man die früheren Spekulationen von einem „Treibhaus“ der Atmosphäre weiter (de Saussure, um 1780) und verfolgte Fouriers Vermutung weiter, dass die Atmosphäre die „helle“ Sonnenstrahlung durchlasse, die „dunkle“ vom Boden ausgehende Wärmestrahlung aber „festhalte“. Damit war der Blick bereits einseitig auf die Strahlungsvorgänge fixiert, und das Mikrogeschehen der Wärmeleitung mit anschließender Konvektion sowie ständig kompensativem Nachfließen kälterer Luft direkt am Boden (mit den Augen in der Regel nicht wahrgenommen) entfiel der Aufmerksamkeit, trotz seiner makroskopischen Tragweite. Der verhängnisvolle weitere Weg bis zur politisch hochaufgeladenen „Treibhausdebatte“ und einem größenwahnsinnigen Weltvorhaben der „Klimarettung“ durch globale CO2-Reduzierung wurde durch Svante Arrhenius´ Aufsatz: ‹On the Influence of Carbonic Acid in the Air Upon the Temperature of the Ground› (Philosophical Magazine 41, 237-276) asphaltiert, in dem er den ‹Treibhauseffekt› des CO2 sogar zu beziffern versuchte. Empirisch nachgewiesen wurde das nie, was er errechnete, seine Kritiker hat man trotzdem überhört. Dennoch erfüllt diese Rechnerei mit dem gekünstelten „Strahlungsgleichgewichtsmodell ohne / mit Atmosphäre“ heute Tausende von Seiten in Lehr- und populären Büchern, Fachaufsätzen, Doktorarbeiten und amtlichen Veröffentlichungen, sowie endlose Blogdiskussionen seit Jahren, die regelmäßig in gehässigem Streit enden.
Eines kommt dabei völlig zu kurz: die schlichten Grundtatsachen der Wärmephysik der Atmosphäre – Wärmeleitung (trotz „schlechter“ Leitfähigkeit der Gase, was durch ihre Beweglichkeit kompensiert wird), Konvektion (+ Evaporation, Transpiration u. die Phasenübergänge des Wassers), Absorption und Emission, Thermalisierung, Kühlung.- Wie wackelig hier die elementarsten Grundkenntnisse sind, zeigt sich darin, dass manche meinen, wenn von „Wärmestrahlung“ die Rede sei, müsse diese auch immer und überall wärmend wirken – egal, um welche Temperaturen es sich handelt. Das ist der weitere Denkfehler, der hinter der Idee der „Gegenstrahlung“ / back radiation steckt – durch die der Boden noch einmal erwärmt werden soll von der Strahlung, die er bereits abgegeben hat und die in größerer Höhe z.B. von CO2 absorbiert und zur Hälfte wieder in Richtung Boden emittiert wird – vergessen wird aber: das geschieht bei wesentlich niedrigeren Temperaturen entsprechend der Höhe, in der das stattfindet. Diese „Wärmestrahlung“ kann den Boden nicht noch einmal erwärmen (wenn es um Reflexion an einer Wolkenunterseite [Tröpfchen oder Eiskristalle] geht, handelt es sich um einen anderen Vorgang: der kann tatsächlich die Abkühlung bremsen, was der Unterschied zwischen bewölktem und sternklarem Himmel in Winternächten deutlich lehrt). Aber eine Rückstrahlung homogen verteilten Kohlendioxids in 10 km Höhe kann den Boden nicht „rückerwärmen“. Jede „Wärmestrahlung“ eines offenen Kühlschranks mit ihrer der Temperatur entsprechenden Wellenlänge beweist uns das. Durch sie wird die Küche nicht erwärmt.
Dass diese einfachen, aber gravierenden Denkfehler im „Treibhausmodell“ nicht bemerkt wurden, bevor man darauf einen Wolkenkratzer von klimatologischen Folgerungen hochzog, der nun wiederum mit weitreichendsten wirtschaftspolitischen Konsequenzen und „Transformationsplänen“ verkettet ist und diese stabilisieren muss, wie er seinerseits von ihnen (wider den gesunden Menschenverstand) stabilisiert wird, wobei auch noch die Klimasimulationen für 80 Jahre im Voraus „vorauseilend-beweisend“ postuliert werden (ein weiterer Denkfehler: gekoppelte nichtlineare Prozesse in Vielzahl sind nicht vorausberechenbar), scheint unglaublich. Wenn es auch kein Einzelfall ist: falsche Paradigmen gibt es auch in anderen Wissenschaftsbereichen – so sind aber Paradigmen leider sehr zählebig, da nicht die unwiderlegbare Evidenz, sondern vielmehr soziologische und psychologische Kräfte sie am Leben halten; man denke an den Widerstand der Schulgeologie gegen Alfred Wegeners Ideen von „wandernden Kontinenten“ ab 1912: noch ganze 50 Jahre hielt diese fixistische Front gegen den verspotteten „Nichtgeologen“ Wegener – bis Anfang der 1960er Phänomene entdeckt wurden, die sogar die sukzessive Entstehung von Ozeanböden und eine passive Bewegung von Kontinenten nahelegten. Heute kann man über den Fixismus lächeln.- Wann wird sich der klimatologische Treibhaus-Fixismus bequemen, die für „vernachlässigbar“ gehaltenen Details atmosphärischer Mikrovorgänge und ungleichartiger Gas-Strahlungswechselwirkungen genauer ins Auge zu fassen?
Im Moment dominiert nicht der sachbezogene Streit in der Klimawissenschaft selbst, sondern die Politisierung von Begriffen, die sachliches Denken vernebelt und emotional aufwühlt, und der moralische Einfluss populistischer Politiker, die in der „CO2-Gefahr“ vor über 30 Jahren eine Riesenchance für ein zugkräftiges und vor allem äußerst „nachhaltiges“ Dauerthema entdeckten: die „Klimarettung“ durch erzwungene CO2-Reduzierung. Damit kann die Politik das Versagen auf anderen, einst viel wichtigeren Gebieten vergessen machen: Armut und Hunger, schreiende Ungerechtigkeiten im eigenen Lande, inhumane Kriege vor Europas Haustür trotz Existenz eines „UN-Sicherheitsrates“, gewaltige Müllprobleme (Kunststoffverseuchung der Weltmeere), weiterhin durch Brandrodung schrumpfende Regenwälder und Artenauslöschung u.v.a.m. Nun gibt es nur noch ein Zentralthema, das auf einer einzigen All-Erklärung basiert: wir müssen CO2 reduzieren, weil dies zu einer angeblich linear fortschreitenden Erwärmung der Erde führt (selbst darin steckt noch ein physikalischer Denkfehler) – dann wird wieder alles gut.
Michael Kalisch, Diplombiologe, 72076 Tübingen
Bitte kürzer fassen! Unbedingt!
@Admin
Betrachten Sie die Kommentare von Herrn Stolz und Kalisch einfach als eigenständige Beiträge hier im Forum, die das Thema umfassend erläutern, dann passt auch die Länge. Scnr.
Nein! Ich finde es hervorragend so…
Alternativ könnte dieser Kommentar als Bericht auf EIKE veröffentlicht werden…
Hallo Herr Kalisch,
schöne Zusammenfassung –
Sie haben als Biologe mehr Ahnung von Physik als viele der sog. „Physiker“.
Glückwunsch!
Sehr geehrter Herr Kalisch, darf ich Ihren Kommentar unter Quellenangabe verwenden?
Das können Sie gerne. Darf ich fragen, wofür?
Danke. Für meinen Blog.
Sehr geehrter Herr Stolz, darf ich Ihren Kommentar unter Quellenangabe verwenden?
Sehr geehrter HerrPoost,
selbstverständlich dürfen sie!
Grüße, Axel Stolz
Danke. Den Beitrag werde ich hier verlinken.
Ich meine, Willis Eschenbach bringt es hier ganz ohne Schock auf den Punkt.
Ideale Gase verhalten sich nun mal so!
https://wattsupwiththat.com/2018/02/06/ideal-gases/
Diese Diskussion, man sieht es schon an der Anzahl der Beiträge, ist das eigentliche Herzstück der Klimadiskussion; CO2 (wie andere strahlungsaktive Gase) kühlt die Erde, es erwärmt sie nicht! Das ist natürlich Häresie. Ein Weltbild (Klimakirche) ist auf dem Dogma der CO2 Klimaerwärmung aufgebaut, praktisch alle gesellschaftlich relevante Gruppen richten ihr Heilsbestreben danach aus. Und jetzt das, die Welt steht für diese Leute auf dem Kopf. Es ist so wie seiner Zeit mit Charles Darwin, der Mensch ist nicht Gottgleich sondern mit dem Affen verwandt. Das braucht seine Zeit ehe sich die Klimakirche der Physik beugen wird.
Nie wird sie sich beugen, NIE!
Das Problem der Menschen ist nicht die Dummheit, es ist die Sturheit.
Klimaleugner, Holocaustleugner, Gottesleugner…
Carsten
—
„Herr Trump war noch nicht im Amt, seine Präsidentschaft schien sogar in den Sternen zu stehen, als aus England aus allen Dreckschleudern auf ihn geschossen wurde.“
Willy Wimmer, Staatssekretär a. D.
Allen die beim Treibhauseffekt an die adiabatische Gasgleichung glauben, sei gasagt dass diese hier NICHT anwendbar ist. Die Atmosphäre ist ein zum Weltraum offenes System über das der solar beheizte Boden Wärme und Strahlung abgibt. Die Zunahme der Temperatur nach unten ist NICHT durch den Druck bedingt, sondern entsteht einfach durch den Gradienten beim Energietransport nach oben.
Wenn statischer Druck dauernd Wärme erzeugen würde, könnten wir doch unsere Wohnungen mit Pressluftflaschen heizen!
Der von Nikolov und Zeller berechnete TE von 90 Grad ist genauso unsinnig wie der von 144 Grad, den Prof. Gerlich – allerdings für eine nicht rotierende Erde mit 0 K auf der Nachtseite – als globalen Mittelwert ohne Atmosphäre berechnet hatte (obwohl er wegen des 2.HS einen TE für nicht existent hielt). Da die 33 Grad auf einem stark vereinfachten quasi isothermen (also schnell rotierenden und gut Wärme umverteilenden) Erdmodell beruhen, ist auch dringend davon abzuraten, den extrem langsam rotierenden Mond zum Vergleich für die Erde zu benutzen.
Da irren Sie. Bitte folgende Definition beachten:
Ein offenes System ist ein System, das mit seiner Umgebung sowohl Masse als auch die Prozessgrößen Arbeit und Wärme austauschen kann.
Ein geschlossenes System kann keine Masse, aber trotzdem Wärme/Arbeit mit seiner Umgebung austauschen.
Die Atmosphäre ist ein geschlossenes thermodynamisches System.
Und das mit der Pressluftflasche haben Sie auch nicht verstanden. Die Wärme die am Kühler der Kompressors an die Umgebung abgegeben wird entspricht genau der Wärme die der Umgebung beim Entspannen das Gases wieder entnommen wird.
Ein Wunder gibt es nur in der Klimakirche, da wo der Erdboden sich durch die „Gegenstrahlung“ erwärmt, deren Ursache der Erdboden selbst ist….
In erster Näherung mögen Sie Recht haben, aber ein Blick auf Meteoritenkrater lässt Zweifel an Ihrem Argument aufkommen.
MfG
Ketterer
Herr Ketterer, wollen Sie die Definition eines im thermodynamischen Sinne offenen Systems widerlegen?
Adiabatische Verhältnisse gelten nur in aufsteigenden Gasblasen. Es stellen sich deshalb die bekannten Verhältnisse ein.
Herr Dietze, Sie wissen nicht, wovon Sie schwadronieren.
Wenn ich das richtig sehe, kann der sogenannte Treibhauseffekt bisher nur ungenügend erklärt werden. Aus diesem Grund gibt es EIKE. Die ominösen 33 K hervorgerufen fast einzig und allein durch H2O und CO2 können das gar nicht schaffen.
Auf http://hockeyschtick.blogspot.de/ ist eine Studie veröffentlicht, die genau den gleichen Ansatz hat wie Holmes. Ned Nikolov und Karl Zeller behandeln dort ebenfalls den adiabatischen Wärmetransport.
Mich hat die Arbeit überzeugt, da sie empirisch total passt.
Der „Treibhauseffekt“ ist ja eine an sich schon irreführende Bezeichnung und hier ist das beste Argument warum das so ist. Wärme allein adiabatisch.
Wie kommt es z.B., dass es Sommertags in München 30°C ist und zur gleichen Stunde am 1000 m höher gelegenen Eibsee eine geringere Temperatur gemessen wird. Wir sagen klar liegt ja auch 1000 m höher. So klar ist das aber gar nicht. Nimmt man jedoch das adiabatische Faktum erklärt es sich ganz einfach. Geringere Anzahl von Luftmolekülen bewirkt geringeren Druck und damit geringere kinetische Energieabgabe durch Einstrahlung der Sonne. Ein Hoch auf den Schöpfer, der das Raumschiff Erde geschaffen hat.
Hier eine Googleübersetzung des Abstracts.
Eine aktuelle Studie hat gezeigt, dass der natürliche Treibhauseffekt der Atmosphäre um die 90 K oder etwa 2,7 mal stärker ist als in den vergangenen 40 Jahren angenommen. Eine thermische Verstärkung von solch einer Größe kann nicht mit der beobachteten Menge an austretender infraroter langwelliger Strahlung erklärt werden, die von der Atmosphäre absorbiert wird (d. H. & Ap; 158 W m-2), was eine erneute Untersuchung der zugrundeliegenden Greenhouse-Theorie erfordert. Wir präsentieren hier eine neue Untersuchung der physikalischen Natur des atmosphärischen thermischen Effekts unter Verwendung eines neuartigen empirischen Ansatzes zur Vorhersage der globalen mittleren jährlichen oberflächennahen Gleichgewichtstemperatur (GMAT) von felsigen Planeten mit verschiedenen Atmosphären. Unsere Methode nutzt Dimensional Analysis (DA), angewendet auf eine geprüfte Menge von beobachteten Daten von sechs Himmelskörpern, die eine breite Palette von physikalischen Umgebungen in unserem Sonnensystem darstellen, dh Venus, Erde, Mond, Mars, Titan (ein Mond des Saturns), und Triton (ein Mond von Neptun). Zwölf von DA vorgeschlagene Beziehungen (Modelle) werden durch nichtlineare Regressionsanalysen untersucht, die dimensionslose Produkte aus Sonnenstrahlung, Treibhausgaspartialdruck / -dichte und Gesamtdruck / -dichte als treibende Variablen und zwei Temperaturverhältnisse als abhängige Variablen beinhalten.
@Günter Ossa
Sie schreiben:
„Wie kommt es z.B., dass es Sommertags in München 30°C ist…..“
Ja, messen Sie Sonneneinstrahlung, wahrscheinlich über 1.000 W/m² – dann können sie die Bodentemperaturen messen, und je nach Absorptionsgrad der Oberfläche, könne Sie feststellen, alles „paßt schooo!“ – ganz ohne „Treibhauseffekt“ – hier können Sie mit den S-B Formeln rechnen!
„Die ominösen 33 K hervorgerufen fast einzig und allein durch H2O und CO2 können das gar nicht schaffen.“
Ja, das ist Unsinn. Es ist die innere Energie der Atmosphäre. Eine Strahlungsisolation gibt es nicht, solange es Konvektion gibt, die Wärme WESENTLICH stärker transportiert als die Strahlung in der Atmosphäre.
1. Zum Thema Zirkelschluss:
Wenn man bei einem Planeten unseres Sonnensystems die (vermeintliche) Klimawirksamkeit eines seiner Atmosphärenbestandteile „abschaltet“ oder auch „erhöht“, gleichzeitig aber Masse, Teilchenzahl und Dichte konstant ließe, so würde die o.g. Formel versagen.
Woher „weiß“ die Formel nun aber, das sie exakt bei den gegebenen und extrem unterschiedlichen Gehalten an „Klimagas“ genau so funktioniert und das sie dabei keinerlei Kenntnisse über die chem. Zusammensetzung dieser Atmosphäre haben muss, um diese exakten Vorhersagen machen zu können ? Schwarze Löcher werden z.B. auch nur durch wenige Parameter vollständig beschrieben (Informationsparadoxon) und auch da könnte man beliebig viele zusätzliche Parameter einfordern, die sich „irgendwie“ so ausgleichen, dass deren Nicht-Notwendigkeit nach außen nur fälschlich suggeriert wird.
So funktioniert Physik aber nicht denn wenn eine einfachere Theorie die Realität genauso beschreibt wie die komplexere dann gilt die einfachere.
2. Erklärung der „Boring Billion“
Diese Theorie wäre auch eine verblüffend einfache Erklärung für das Rätsel der über 1 Mrd. Jahre konstanten und konstant hohen Temperaturen auf der Erde trotz der (deutlich) schwächeren Sonne: Ein Atmosphäre konstanter Masse dehnt sich mit steigender Solarstrahlung exakt proportional aus und bewirkt ganz zwanglos die gesuchte, hochgenaue negative Rückkopplung völlig unabhängig von deren chem. Zusammensetzung.
3. Erklärung für (große) Eiszeiten
Z.B. die „Große Sauerstoffkatastrophe“ ließe sich damit auch durch reine Massenverschiebung zwischen Atmosphäre und Oberfläche erklären: CO2 (Gehalt damals geschätzte 10%) wird durch O2 (Cyanobakterien) ersetzt und der gesamte atmosphärische Kohlenstoff landet im Boden/Wasser, was einen enormen Masseverlust der Atmosphäre darstellen würde (O2 hat nur ca. 72% der Masse von CO2), der wiederum (gemäß obiger Formel) zur Abkühlung führen würde, die dann durch konsekutive Verschiebung von Wasserdampf in die Meere (plus Vereisung) zur eskalierenden Abkühlung führen würde, bis Vulkane wieder genügend Masse in die Atmosphäre pumpen können, um das wieder rückgängig zu machen.
Ich denke, der Artikel ist peinlich…ähnlich der Ökogläubigen überwindet man die Grenzen der Naturwissenschaft. Die Realität ist zu komplex um mit einer einfachen Formel wiedergegeben werden.
Meines Erachtens sind die Schätzungen zur CO2 Sensitivität des Erdklimas sind in der Regel stramme Annahmen. Der Treibhauseffekt der Atmosphäre ist sehr komplex. Es gibt zahlreiche unterschiedliche qualitative Abschätzungen. Hauptunterschied ist die Wirkung der Wolken. Eine Quantifizierung des Treibhauseffekts, der Wirkung der Treibhausgase, oder gar eine Quantifizierung einer möglichen Temperaturerhöhung bei einer Zunahme des Spurengases CO2 in der Atmosphäre wäre wissenschaftlich sehr, sehr herausfordernd. Man könnte dies analog der Reaktorphysik über eine Montecarlo Simulation mit Wirkquerschnitten der Moleküle für Strahlen, verschiedenen repräsentativen Oberflächen, Breitengraden, Wetter, Jahreszeiten, Schwankungen der Klimagasanteile, zusammen mit einer Berechnung des Wärmetransports vornehmen.
1. Die „Oberflächentemperatur“ hängt von der Sonneneinstrahlung und dem Abstand zur Sonne ab.
2. Die Oberflächentemperatur der Erde hängt vom Albedo ab, sprich dem Anteil der reflektierten Sonneneinstrahlung. Es wäre sehr anspruchsvoll den Albedo genau abzuschätzen, da sich dieser von Tag zu Tag ändert (Wolken, Schnee..)
3. Das IPCC schätzt den Albedo auf 0,3. Das IPCC errechnet daraus eine „Globale Durchschnittstemperatur“ der Erde von -18C°, entsprechend einem Treibhauseffekt von 33 °C. Gem. Jinan Cao beruht dieser Wert auf einer falschen Annahme hinsichtlich der Oberfläche des Körpers Erde, korrekt wäre es zum Teil die Atmosphäre (und Wolken) als Oberfläche und daraus folgend deren Temperatur als Oberflächentemperatur anzunehmen. Daraus ergeben sich ein niedrigerer Albedo und damit ein geringerer Treibhauseffekt als in den Klimamodellen angenommen.
4. Die Wärmeabstrahlung ergibt sich gem. des Stefan Bolzmann Gesetzes. Die Rückstrahlung eines Körpers (der Erde) mit der 4. Potenz einer Temperaturerhöhung P = Ϭ * A * T4 mit Ϭ = 5,67 * 10 -8 W/m2/K4
Eine Rechnung mit einer durchschnittlichen Abstrahltemperatur von 15°C ist nicht statthaft, da die heisseren Teile der Erde, z.B. Sahara, überproportional zur Abstrahlung beitragen.
5. Die Abstrahlung ist erfolgt in einem weiten Wellenlängenspektrum im IR Bereich. Ein Teil der Abstrahlung erfolgt über ein atmosphärisches Fenster, andere Wellenlängen werden von H2O/CO2 nahe der Bodenoberfläche absorbiert. Ein erheblicher Anteil des Wärmetransports von der Erdoberfläche erfolgt über den Wasserdampf.
Holger Narrog
Wenn er das alles liest, fragt sich der bescheidene Physiker: „Verhalten sich etwa das Wetter und seine Statistik Klima tatsächlich stationär?“ – Denn, an 71% der Erdoberfläche sollen Ozeane bei einer mittleren Tiefe von 3700 Metern angeblich Wasser enthalten, dessen Temperatur den Bereich von 270 K und 300 K niemals verlässt, richtig? – Ohne Solarstrahlung von 0,24 kW/m^2 würde die Temperatur auf 30 K absinken, richtig? -Dann lässt also der Durchfluss von etwa 0,24 kW/m^2 (etwa 200 kcal/h) die Enthalpie jeder solcher Wassersäulen von 1 m^2 Oberfläche um 9,25 x 10^8 kcal (Temperatur um 250 K) ansteigen, richtig? – Das funktioniert jedoch nur dann, wenn die Zeit zwischen Absorption und Emission in den Weltraum (die Verweilzeit der Solarenergie (9,25 x 10^8 kcal / 200 kcal/h = 4,6 x 10^6 h bzw.) etwa 530 Jahre beträgt, richtig?
Die Oberfläche der Ozeane verliert einen Energiefluß von etwa 480 W/m^2, den die Gegenstrahlung etwa hälftig dann ausgleicht, wenn sich die Entapie des Wassers nicht ändert, richtig? – (Bitte beachten, dass unterschiedliche Spektren unterschiedliche Eindringtiefen der Energieflüsse und damit unterschiedliche Verweilzeiten zur Folge haben!)
Ob wohl die Speicherzeit der Solarenergie tatsächlich eine Naturkonstante sein kann? Einstein hätte sicher Zweifel, oder?
@Ulrich Wolff, gutes Stichwort stationär. Die Eingangswerte in Klima“berechnung“ sind vermittels Abstraktionitis befreit (mittlerisch gemittelte Mittelwerte) von Funktions- u. Phasenstakt der Maschine. Also kann keine Maschine erkannt werden und Jedermann streitet über ersatzweise Kobolde die das unverstandene Klima takten, nicht wahr.
Nicht eine der Komponenten einer Atmosphärischen Dampfmaschine (Wassertransport entgegen Gravitation, Arbeit durch Unterdruck, trotz ganz schwachem Dampfkesseldruck, etc) kann aus gemittelten Mittelwerten wissenschaftlich bestimmt werden, und/oder zeigt wissenschaftlich behandelbaren Funktions- u. Phasenstakt; hobgoblins everywhere.
Ein klassischer Zirkelschluß. Wenn ich eine Zustandsfunktion mit 4 Variablen habe und davon 3 messe (Dichte, molare Masse, Druck), kann ich die vierte (Temperatur) ausrechnen. Dabei gewinne ich keine Informationen darüber, wie das System diesen Zustand erreicht hat oder warum es in diesem Zustand ist.
Schlimm finde ich, dass diese Arbeit das Peer-Review-Verfahren durchlaufen ist, ohne abgewiesen zu werden. Schande über die Referees.
Das hat nichts mit Treibhauseffekt oder Rückstrahlung zu tun, darüber lässt sich aus dieser „Arbeit“ keine Aussage treffen. Es ist mißglückte Mittelstufenphysik.
Viele Grüße,
Ernst Flemm
Das ist mit anderen Worten genau meine Aussage. Danke.
H.Otte
@ Ernst Flemm: peer reviewed ist nicht gleich peer reviewd – leider… siehe:
https://de.wikipedia.org/wiki/Science_Publishing_Group
Dies ist wohl eine Faschingsveröffentlichung in Analogie zur Faschingsvorlesung. Die zentrale Formel der Veröffentlichung von Holmes ist das ideale Gasgesetz Gl. 5: T= p/(R*rho/M) mit Temperatur T, Druck p, Gasdichte rho und Molekül-Massenzahl M. Dies ist die Basis eines Gas-Thermometers. Holmes hat rho, M und p anderen Veröffentlichungen entnommen und daraus die Temperatur an der Oberfläche berechnet. Ich bezweifele dass ortsaufgelöste Messungen der Gasdichte an Planeten-Oberflächen wie z.B. der Venus existieren.
An der Venus-Oberfläche beträgt der Druck der CO2-Atmosphäre 92 bar. Ich bezweifele dass das ideale Gasgesetz hier noch eine gute Näherung ist. Bei 1,023 bar und 0°C ist das Molvolumen von CO2 22,256 l/mol und damit etwa 0,7% kleiner als das einen idealen Gases 22,414 l/mol. (Daten für 740K und 92 bar habe ich leider nicht).
Ich vermute ich dass die zitierten Quellen die Gasdichte nicht gemessen, sondern näherungsweise mit Hilfe des idealen Gas-Gesetzes berechnet haben. Dies führt dann zur guten Übereinstimmung.
Siehe hier:
https://tu-freiberg.de/fakult2/angph/forschung/hb/hb_atmosphaereneffekt2005.pdf
Kapitel 5
Anmerkungen. aus 2010:
Kein CO2 Treibhauseffekt in der Venusatmosphäre
@Herrn P. Berberich 10. Februar 2018 um 15:30
Dazu brauchen Sie den Realgasfaktor oder Kompressibilitätsfaktor.
Siehe: http://www.unternehmensberatung-babel.de/berechnungen/realgasfaktor.php
Wenn Z = 1 (ideales Gas), kann man die thermische Zustandsgleichung der idealen Gase verwenden. Bei Z > 1 überwiegen die Abstoßungskräfte (schwer kommprimierbar) und bei Z < 1 die Anziehungskräfte (leicht kommprimierbar) (siehe: Lennard-Jones-Potential).
Der Realgasfaktor für die Venus-Atmosphäre bei 92bar und 740K beträgt Z = 1,022577519.
Da sich der Realgasfaktor der beiden gasförmigen Haupt-Komponenten unter den Bedingungen der Venus-Atmosphäre an der Oberfläche um den Wert von 1,0000 bewegen, sowie das molare Volumen sich gering unterscheidet (Vm(CO2): 0,0006725209 m^3/mol; Vm(N2): 0,0006946616 m^3/mol), kann man in guter Näherung die Gesetzmäßigkeiten eines idealen Gases anwenden.
Mfg
Werner Holtz
Gute Näherung ist ein vager Begriff. Der von Ihnen angegebene link verwendet die sog. „Redlich Kwong Soave-Näherung“. Ich habe die Van der Waal-Gleichung (VdW) benutzt. Wenn Gasdichte, Druck und und die molukulare Masse der Venus-Atmosphäre an der Oberfläche durch Messung bekannt wären, so würde sich durch Anwendung von VdG gegenüber der Idealen Gas-Gleichung eine Temperaturänderung von 2% ergeben.Das sind immerhin 9 K. In der Tabelle 1 von Herrn Holmes würde dies schon auffallen. Bei der Angabe der mittleren Gas-Dichte auf der Venus ist eine Genauigkeit von 2% wohl ausreichend. Interessant wäre die akademische Frage, wie eine Venus-Sonde die Gasdichte messen könnte. Ich würde eine Viskositätsmessung vorschlagen.
@ Herrn P. Berberich – 12. Februar 2018 um 12:21
Zitat: „Gute Näherung ist ein vager Begriff.“
Nein, nicht in der Thermodynamik – Das hat mit dem „Redistribution Factor“ zu tun.
Eine gute Nährung bedeutet, dass die maximale Abweichung im Bereich von +/- 5% liegen kann. Von einer sehr guten Näherung spricht man, wenn die maximale Abweichung im Bereich von +/- 3% liegt.
Zitat: „Wenn Gasdichte, Druck und und die molukulare Masse der Venus-Atmosphäre an der Oberfläche durch Messung bekannt wären, …“
Es gibt doch Messungen von den Venera – Venus Lander Missionen. Man hat Druck, Temperatur, Windgeschwindigkeit und Beschleunigungs-Größen gemessen.
+ Auszug: Venera – Venus Lander Missionen (an der Oberfläche):
Venera 09 – Temperatur: 728 K (Sonnenstand 33°) ; Druck: 90 atm
Venera 10 – Temperatur: 737 K (Sonnenstand 27°) ; Druck: 91 atm
Venera 13 – Temperatur: 738 K (Sonnenstand 35°) ; Druck: 89,5 atm
Venera 14 – Temperatur: 743 K (Sonnenstand 35°) : Druck: 93,5 atm
Einfach mal googlen nach: „venera measurement“
Mfg
Werner Holtz
Die Gaszustandsgleichung läßt vermuten, es gäbe eine allgemeingültige Beziehung zwischen den einzelnen Parametern. Daß dies nicht der Fall ist, erkennt man an einer Preßluftflasche. Bei Druckerhöhung steigt der Druck und die Dichte, Volumen bleibt gleich ebenso Gaskonstante und molare Masse. Die Temperatur im Inneren wird im eingeschwungenen Zustand aber nicht von der Außentemperatur abweichen. Die Gültigkeit der Formel hängt also von weiteren Bedingungen ab, die man vollständig kennen und berücksichtigen muß.
Wikipedia dazu: „Die Gleichung stellt den Grenzfall aller thermischen Zustandsgleichungen für verschwindende Dichte ρ → 0 {\displaystyle \rho \rightarrow 0} dar, das heißt für verschwindenden Druck bei genügend hoher Temperatur. In diesem Fall kann man das Eigenvolumen der Gasmoleküle und die Kohäsion – die anziehende Kraft zwischen den Molekülen – vernachlässigen.“ Auch die Erkenntnisse der kinetischen Gastheorie wären hier wohl zu berücksichtigen.
Hier wird von dem australischen Physik-Studenten Robert Holmes die erhöhte Bodentenperatur mit dem Atmosphärendruck (!!) berechnet. Dass statischer Druck keine Dauer-Wärme erzeugt, hat dieser Herr (und auch EIKE) noch nicht gespannt.
Wenn dem so wäre, hätten wir nämlich ein energieerzeugendes Perpetuum Mobile und könnten auch Schwerkraft-Kraftwerke bauen wo z.B. durch den Druck und die Hitze, die ein Gewicht von 5000 t in einem Zylinder erzeugt, dauernd eine Dampfturbine angetrieben wird.
Der Treibhauseffekt, der am Boden real insgesamt nur 0,6 Grad pro CO2-Verdoppelung beträgt, entsteht durch IR-Absorption in der Atmosphäre und Gegenstrahlung (Energietransport von kalt nach warm). Dies widerspricht NICHT dem 2.HS, da dieser nur für NETTO-Flüsse gilt.
Siehe hier:
https://tu-freiberg.de/fakult2/angph/forschung/hb/hb_atmosphaereneffekt2005.pdf
Kapitel 5
http://www.schmanck.de/hb_klimakatastrophe2006.pdf
Kapitel 4
Leider lassen sich Wetter, seine Statistik Klima und der atmosphärische Treibhauseffekt nicht mathematisch darstellen. Dazu die folgenden Anmerkungen:
Treibhauseffekte
Der Traum vom anthropogenen…
Was haben die „Treibhauseffekt-Diskussion“ und ein „Kropf“ gemeinsam? Beide sind überflüssig und sinnlos.
Sehr geehrter Herr Dietze,
Sie scheinen sich da besser auszukennen, ich hätte da eine Frage, die Sie mir sicherlich beantworten können:
Wieviel Gesamtenergie ist im CO2 und in den anderen Gasen der Erdatmosphäre gespeichert?
liebe Grüsse
Franz Jäger
@ P. Dietze
Zum 2. HS wäre zu sagen, daß er nicht für Flüsse sondern für Wärme definiert ist. Wäre das mit den Nettoflüssen der Fall, erhebt sich die Frage, wie dann die Erdoberfläche zu den Treibhausgasen strahlen soll, geht doch der Hauptfluß „netto“ immer von der Sonne zur Erde. Und auf welche geheimnisvolle Weise die Treibhausgase nach Sonnenuntergang ihre Fähigkeit verlieren, die Erde rückzuerwärmen, bliebe in dieser Denkweise als Frage ebenfalls stehen?
Herr Dietze,
lernen Sie erst einmal die Grundlagen der Physik der Atmosphaere.
Da kommt bei mir leider keine Schockstimmung auf. Der Inhalt ist physikalischer Nonsens. Warum?
Wenn man mit dem Gasgesetz aus den Messwerten von Druck, Molmasse und Dichte die Temperatur berechnet, muss man beachten, dass in der Dichte die Temperatur bereits implizit enthalten ist. Es sollte also keine Freude oder Verwunderung aufkommen, wenn man die „richtige “ Temperatur herausbekommt. Die Berechnung der Sensitivität ist dadurch natürlich auch wertlos.
Anders gesagt: wenn eine andere Temperatur herrschen würde, dann würde man auch eine andere Dichte messen und entsprechend eine andere Temperatur bekommen, da die Dichte von der Temperatur abhängig ist.
mit freundlichen Grüßen
H. Otto
Nach ihrer Logik ist die Bestimmung der Fallbeschleunigung auf der Erde durch eine Masse aus 10 m Höhe auch nur physikalischer Nonsens, da diese ja auch schon in der Formel drin ist. Merken Sie was? Die Begründung der bodennahen Erdtemperatur durch adiabatische Kompression ist physikalisch plausibel WEIL sich dabei Theorie UND Messung decken. Die Erklärung via „Gegenstrahlung“ hingegen ist nicht vereinbar mit den HS der Thermodynamik und auch empirisch (Strahlungsfrost) widerlegt.
Der Unterschied zwischen Druck und Kompression muss hier hoffentlich nicht erläutert werden, oder?
MfG
Ketterer
http://www.schmanck.de/hb_klimakatastrophe2006.pdf
Kapitel 4
Dieses Paper liegt die außerhalb der Grenzen des akademischen Ordens. Die Konsequenzen für Klimastrologie und Pseudo(leer)bücher sind unerträglich. Der Messenger muss diskreditiert werden, kein Ad Hominem zu schade. Nur die Keplers des Ordens dürfen eine Ratio ausrechnen (πr² / 2πr), egal wofür die Zahl steht /sarc.
Zitat: Klimasensitivität bzgl. CO2 ≈ 288,14 – 288,11 ≈ -0,03 K.
Wer bei den vier Grundrechenarten schon einen Fehler macht, dem ist nicht zu trauen. Nach Adam Riese oder dem Milchmädchen ist das Ergebnis:
… CO2 ≈ 288,14 – 288,11 ≈ +0,03 K
Mfg
Werner Holtz
Zitat aus dem Text:„Im Allgemeinen ist die Atmosphäre eines Planeten umso dünner, je schwächer dessen Gravitation ist“
===================
Die Masse des Planeten Venus (4,867 × 10^24 kg) ist geringfügig niedriger als die der Erde (5,972 × 10^24 kg)
Fakt ist, dass die CO2-Atmosphäre der Venus viel mehr Masse (90mal höherer Druck) hat als die Lufthülle der Erde.
Wie passt das zur obigen Aussage?
Ist es nicht viel mehr so, dass nicht nur die Masse also Anziehungskraft des Himmlskörpers ausschlaggebend ist, sondern auch die Zusammensetzung der Atmosphäre; Die obige Aussage ist irgendwie nicht akzeptabel. Ein „schweres Gas“ (CO2 ist schwerer als Erdluft) „haftet“ eher an einer Oberfläche als leichtere Gase. Eine Atmosphäre mit z.B. Helium, Methan oder H2 wäre schon lange verflogen in den Weiten des Alls. Oder irre ich mich da?
Willis Eschenbach:
Dang … “adiabatic auto-compression” as a permanent energy source. Is it patented yet?
Dazu mindestens 558 Kommentare.
Nun, man kann es auch einmal anders sehen: Man nehme die Erde, die eine trockene Atmosphäre aus Stickstoff und Sauerstoff hätte, round about im Verhältnis 80/20, und an der Oberfläche hätte sie den uns bekannten Druck von 1 atm. Nach den Annahmen des „Treibhauseffekts“ hätte diese Erde eine Oberflächentemperatur von – 18 °C. Jetzt fügen wir dieser Atmosphäre ca. 1 % Wasserdampf zu. Was wird passieren? Mit der Argumentation des „Treibhauseffekts“ würde sich die Erde um gut 20 Grad erwärmen, also auf schwache 2 °C. Noch ein wenig „CO2“, und wir landen bei „gemütlichen“ +15 °C. Aha! Wie sieht noch einmal geschwind das Phasendiagramm von Wasser aus?
Zur Venus: Leider hat bis heute dort keine Sonde lange genug überlebt, aber basierend auf einem Oberflächendruck von 100 atm kann es m.E. nur bedeuten, dass die Venus vulkanisch recht aktiv ist.
Es gibt so viele total spannende Fragestellungen, aber denen geht ja niemand nach, weil angeblich das Geld fehlt.
Ich mache mir keine Illusionen und zitiere, was mir Gerhard Gerlich in unserem letzten Gespräch, als er schon krank war, dies aber nicht wusste, sagte: „Dieser Betrug wird niemals aufhören!“. Egal, was passiert: Haben wir mal einen (zu) warmen Tag, war es der menschengemachte Klimawandel. Ist es einmal zu kalt, war es entweder die natürliche Variabilität, oder es wird eben kälter, weil es wärmer wird. Das, was wir aktuell in der „Klima-Diskussion“ erleben, ist ein Lehrbeispiel dafür, was passiert, wenn die Politik ihre Ziele durchsetzen will und via „divide et impera“ willfährige Wissenschaftler (?) als Erfüllungsgehilfen rekrutiert. Von den „Qualitätsmedien“ will ich in diesem Zusammenhang gar nicht erst reden.
Was ist mit Gerhard Gerlich?
Dass Prof. Gerhard Gerlich vor ein paar Jahren gestorben ist, wissen Sie bestimmt. Dem gleichnamigen Sohn geht es gut.
Haben Sie sich mit ihrer Ableitung nicht von hinten durch die Brust ins Auge geschossen?
Ihre Formel (6) T = P*M/(R*rho) oder T = P/((R/M)*rho) ist nichts anderes als die ganz normale Gasgleichung mit (R/M), der speziellen Gaskonstanten des betreffenden Gases.
Geben Sie sich jetzt den bekannten Bodendruck P und die bekannte Bodendichte rho vor, dann kommt notwendigerweise die Bodentemperatur T heraus. Nichts anderes haben Sie gemacht. Mit einem Treibhauseffekt o.ä. hat das überhaupt nichts zu tun.
MfG
G.Wedekind
„Holmes argumentiert, dass die mittlere Temperatur von 8 planetarischen Körpern mit dichten Atmosphären (0,1 bar oder mehr) präzise mit „extremer“ Genauigkeit vermessen werden kann – mit einer Fehler-Bandbreite von lediglich 1,2% – mittels Anwendung einer Formel, die von der Kenntnis von drei Parametern abhängt: 1) des mittleren atmosphärischen Drucks an der Oberfläche, 2) der mittleren atmosphärischen Dichte an der Oberfläche und 3) der mittleren molaren Masse der oberflächennahen Atmosphäre.“
Was für ein Bluff! Wenn Holmes Druck, Dichte und molare Masse an der Oberfläche des Planeten kennen will, muß er diese Größen messen. Dann kann er mittels der allgemeinen Gaszustandsgleichung daraus die Temperatur an der Oberfläche des Planeten berechnen, aber viel einfacher wäre es doch, die Temperatur gleich zu messen. Eine Erklärung dafür, weshalb diese Temperatur abweicht von der Temperatur der Planetenoberfläche, wenn dieser keine Atmosphäre hätte, gibt dieses Verfahren nicht.
Und was sollen die Angaben von Oberflächentemperaturen der großen Gasplaneten Jupiter, Saturn, Uranus und Neptun? Diese Planeten bestehen zum größten Teil aus Gas und haben einen kleine feste Kerne, deren Oberflächentemperaturen meines Wissens noch nie gemessen werden konnten und die mit Sicherheit weit höher sind als die von Holmes angegebenen Temperaturen.
Im Übrigen wäre die mittlere Oberflächentemperatur der Erde ohne Atmosphäre (und dann notwendigerweise auch ohne Meere) deutlich niedriger als die überall angebenen -18°C. Für die Strahlungsbilanz ist nämlich nicht die über die Oberfläche gemittelte Temperatur wichtig, sondern die über die Oberfläche gemittelte 4. Potenz der Temperatur. Wenn dann die Temperatur über die Oberfläche nicht konstant ist, dann ist die korrekt aus der Strahlungsbilanz ermittelte mittlere Temperatur deutlich niedriger als die unter der Annahme ermittelte, daß die Strahlung über die gesamte Oberfläche mit einer konstanten Temperatur erfolge. Die mittlere Oberflächentemperatur einer Erde ohne Atmosphäre wäre nahe der des Mondes von -55°C.
Machen Sie das bei Hinzunahme der Atmosphäre auch, was kommt dann bei angenommen gleich angewandtem Ansatz dabei heraus?
Ich muss einerseits zustimmen. Holmes Formel liefert nur die Antwort auf die Frage: Wie funktioniert ein Heißluftballon? Und die Substanz des Ansatzes entspricht der Füllung eines solchen Ballons.
„Die mittlere Oberflächentemperatur einer Erde ohne Atmosphäre wäre nahe der des Mondes von -55°C.“
Nein, mit Verlaub, das wäre sie nicht.
1. Wird ein Fehler der schon im Artikel zitiert wird wiederholt. Ohne Atmosphäre wäre die Albedo weit niedriger, weil dann halt auch keine Wolken sein könnten. Also wäre die theoretische Temperatur weit höher.
2. Wären auch ohne Atmosphäre die Temperaturen auf der Erde weit gleichmäßiger, weil es ja erstens Ozeane gibt und zweitens und vor allem, weil der Tag halt nur 24h dauert. Natürlich könnte man jetzt weiterspinnen und fragen was passiert, wenn die Ozeane alle einfrieren usw. Lassen wir zumindest dynamische Momente mal außen vor..
3. Ist die Sache mit der 4.Potenz natürlich richtig, aber es gehört in die andere Richtung gerechnet. Also ausgehend von der beobachteten Oberflächtemperatur eine logarithmische Mittelung durchführen. Alles andere hat wenig Sinn, denn ich muss ja die Ungleichverteilung berücksichtigen, und die kann ich nicht theoretisch ermitteln, sondern nur empirisch erfassen.
Wenn man etwa weiß, dass der Mond mit der Sonne im Zenith durchschnittlich ca. 390°K erreicht (es gibt noch heißere Stellen, etwa Krater die wie Parrabolschüsseln wirken), dann kann ich damit schon die relevante logarithmische Durchschnittstemperatur ermitteln.
Wenn ich im Schreiben von mathematischen Formeln etwas begabter wäre, würde ich die Formel auch gleich mitliefern. So aber löse ich die Aufgaben halt in Excel. Jedenfalls wird sich dann die Oberflächentemperatur T = SIN(Alpha)^0,25*390 bestimmen lassen, mit Alpha = 90 für die Sonne im Zenith, und Alpha = 0 für die Sonne am Horizont.
Wenn man das Durchrechnet ergibt sich für die Tagseite eine logarithmische Durchschnittstemperatur von 327,2K. Das kann man dann mit der Schattenseite kombinieren (ich nehme mal einfach 90K dafür an, das spielt in dem Fall keine große Rolle), und schon ergibt sich ein Schnitt von 275,6K.
Bedenkt man jetzt noch, dass die Oberfläche des Mondes nicht eben ist, er also mehr Oberfläche besitzt als eine theoretische Kugel mit gleichem Radius, dann wirkt sich das auf die Temperatur aus. Würde die ABweichung zB. 4% betragen, dann müsste allein deshalb die beobachtete Temperatur um 1% niedriger sein. Korrigiert man diesen Faktor, dann ergäben sich beispielsweise 278,3K.
So ein Ergebnis ist doppelt interessant. Erstens entspricht es praktisch exakt der Temperatur eines perfekten Schwarzkörpers auf dieser Position, zweitens bedeutet es jedenfalls einen starken Treibhauseffekt wo keiner existieren kann. Und dieser Umstand allein falsifiziert die TH-Theorie.
Herr Schaffer, schauen Sie einfach mal hier:
https://www.eike-klima-energie.eu/2017/07/02/beweist-die-temperatur-des-mondes-den-hemisphaerischen-stefan-boltzmann-ansatz/
Ja, kenn ich schon. Ich verstehe nach wie vor nicht wirklich, was Sie damit sagen wollen. Die Vorstellung man dürfe sich nur an der Tagesseite orientieren halte ich für Unfug. Das mag am Mond funktionieren, weil halt die Nachtseite kaum Strahlung emittiert, gilt aber nicht für die Erde. Und somit lässt daraus nichts über den THE ableiten.
Interessant und relevant ist vielmehr das was ich oben ausgeführt habe. Der Mond erreicht anscheinend (so es Daten hierzu gibt) ziemlich exakt die Temperatur eines perfekten Schwarzkörpers (knapp 279K). Es gibt also einen THE wo keiner sein kann. Noch einfacher und eindeutiger lässt sich das viele weitere Himmelskörper zeigen, etwa Ceres, Enceladus, Pluto usw. Und das hat sehr wohl Beweiskraft.
Nebst natürlich dem rießigen Bock den das TH-Modell bei der Verbuchung von Wolken geschossen hat..
https://www.fischundfleisch.com/leitwolf/ein-ganz-bloeder-fehler-der-treibhauseffekt-43471
Aber um das zu verstehen, werden Sie mir den Gefallen erwidern müssen den jewiligen Text auch zu lesen!
Die Formel (ich verstehe nicht = halte ich für Unfug) ist keine Basis für eine ernsthafte Diskussion.
@U. Weber
Es ist schön, dass Sie weiterhin hier kommentieren.
Ich möchte Sie noch um eine Reaktion auf meine Widerlegung Ihres „hemisphärische S-B Ansatzes“ bitten:
https://www.eike-klima-energie.eu/2017/11/26/rueckblick-ein-jahr-hemisphaerischer-stefan-boltzmann-ansatz/
Wirklich nur ausnahmsweise und auch nur aus Mitleid dafür, dass Sie offenbar bis heute Ihren grundlegenden Fehler nicht selbst erkannt haben, mich mit etwas widerlegen zu wollen, das ich gar nicht behauptet hatte. Sie haben dort nämlich eine ganz neue Hypothese aufgestellt, die zur Hälfte aus meinem hemisphärischen S-B Ansatz (für die Tagseite) und zur anderen Hälfte aus dem S-B Temperaturäquivalent für 0 W/m² (Ihr Ansatz für die Nachtseite) bestand.
Ihre vorgebliche „Beweisführung“ liegt also außerhalb meiner hemisphärischen S-B Hypothese, denn ich habe nirgendwo eine Temperatur von -273°C für die Nachtseite der Erde postuliert. Zitat aus dem damals von Ihnen kommentierten Artikel: „Und schließlich wurde auch noch gezeigt, dass die Abkühlung auf der Nachtseite der Erde über die Umgebungsgleichung des Stefan-Boltzmann-Gesetzes erfolgt.“
In dem dort verlinkten Artikel heißt es dann wiederum, Zitat mit Hervorhebung:
„4. ERKENNTNIS: Mit der Umgebungsgleichung des S-B Gesetzes ist jetzt das einzige Manko der hemisphärischen S-B Ableitung geheilt, nämlich das Fehlen einer Erklärung für das Verhalten der örtlichen Nachttemperatur.“
Sie hatten sich mit Ihrem Kommentar vom 13. Dezember 2017 also selber widerlegt.
Sehr geehrter Herr Krause,
ich denke nicht, dass Weber jemals behauptet hat, dass die beiden von Ihm gezeigten Ansätze in irgend einer Form richtig sind. Er wollte lediglich rekonstruieren und demonstrieren wie durch eine historische falsche Anwendung des S_B Gesetzes die ominösen 33 °C Treibhauseffekt in die Welt gesetzt wurden. Die von Weber gezeigte globale Berechnung wurde mir schon in den 60-zigern im Gymnasium präsentiert und der Protest dagegen vom Physiklehrer niedergebrüllt.
Im heimsphärischen Ansatz versucht Weber zu demonstrieren, wie die 15°C Erddurchschnittstemperatur berechnet wurden, nicht gemessen. Wohlgemerkt Ende des 19. Jahrhunderts, als es noch keine zigtausend Messstationen gab.
Es handelt sich hier also um physikalische Polizeiarbeit. Rekonstruktion des Verbrechens, leider noch ohne Spuren zum Täter.
Mit freundlichem Gruß
B.B.
@B. Bauernhirn
Haben Sie schon einmal etwas von einem „Kachelofeneffekt“ gehört?
Früher gab es diese Öfen in fast jeder Wohnung! Man hat tagsüber geheizt, ziemlich pünktlich, gegen 20 Uhr, damit aufgehört. Der Ofen war am nächsten Morgen immer noch warm! Wer hat ihn denn über Nacht erwärmt??? Die Rückstahlung des Zimmers???
Vielleicht hilft ja hier weiter, wenn wir uns einmal mit den spezifischen Wärmen und Wärmespeichern auseinandersetzen !
@U. Weber
Danke für Ihre Antwort.
Bitte verzeihen Sie, dass ich Ihre Ausführungen ergänzt habe. Dies tat ich nur, weil Sie unvollständig waren.
Sie schreiben im Originalartikel:
„Der hemisphärische S-B Ansatz hat damit nicht nur den „natürlichen“ atmosphärischen Treibhauseffekt widerlegt, sondern die gemessene MITTELTEMPERTUR DER ERDE von etwa plus 15 Grad Celsius wurde über die Umgebungsgleichung des S-B-Gesetzes auch als die „natürliche“ DURCHSCHNITTSTEMPERATUR UNSERER ERDE identifiziert.“
Sie behaupten also, eine Mitteltemperatur für die gesamte Erde berechnet zu haben, was aber gar nicht zutrifft.
Sie haben die gesamte zur Verfügung stehende Strahlungsleistung auf nur eine Hemisphäre verteilt, was rechnerisch natürlich zu einer erhöhten Mitteltemperatur dieser einen Hemisphäre führen muss.
Diese Temperatur dürfen Sie aber nicht mit der GLOBALEN Mitteltemperatur gleichsetzen und damit die dunkle Hemisphäre unter den Tisch fallen lassen.
Frage: Woher kommt bei Ihrem Ansatz die Strahlungsleistung für die Nachtseite, die die Nachttemperatur über 0K hält?
Müssten Sie diese nicht von der Bilanz der Tagseite abziehen?
Zu Ihrer „4. Erkenntnis“ gelangen Sie, indem Sie in Frage stellen, dass das Umgebungsniveau unserer Erde 0K beträgt.
Stattdessen berufen Sie sich auf den „Wärmeinhalt der globalen Zirkulationen als unmittelbar wirksame Wärmespeicher unserer Erde“.
Aber woher kommt diese Wärme wenn nicht von der Tagseite?
Na also, es ist die innere Energie der Atmosphäre! Das ist mir schon lange klar.
Daß die Seehöhe neben der Bestrahlungsstärke einen Einfluß auf die Temperaturen hat, weiß jeder Bergsteiger.
Extreme sind z. B. Badwater -85 müM als heißester Ort in den USA (ca. 35°N) und Mount Everest mit 8848 müM (ca. 28°N). An beiden Orten ist der Betrag durch Sonnenstrahlung vergleichbar, die Temperatur jedoch eher nicht. Druck und Dichte sind unterschiedlich, molare Masse und Strahlung vergleichbar.
Oder anders ausgedrückt…ein Gas, das zu 0,039% in der Atmosphäre vorhanden ist, kann auch nur einen, in dieser Größenordnung habenden Effekt, aufweisen. Also wenn überhaupt, dann nur eine „Erwärmung“ um 0,039 Grad.
So wird es sein,
(Sarkasmus An)
und da Ozon in noch kleinerer Menge vorhanden ist kann es nur 0,0039% des UV-B filtern.
(Sarkasmus Aus)
Neu ist das nicht! Genau diese Begründung der bodennahen Erdtemperatur kann man bei Thieme und Hebert schon vor 12 Jahren nachlesen….
https://tu-freiberg.de/fakult2/angph/forschung/hb/hb_atmosphaereneffekt2005.pdf
http://real-planet.eu/atmoseff.htm
Schockierend ist höchstens dass diese Zusammenhänge längst bekannt sind, von der Klimakirche aber konsequent unterdrückt wurden….
Also bin ich mit meiner (simplifizierten) Überlegung (als E-Techniker und nicht Atmosphärenphysiker) nicht so daneben gelegen. In ca. 5-5,5 km Höhe („Mitte der Atmosphäre“ ~0,5 bar) ca. 255 K, durch Druckerhöhung (adiabatischer Temperaturgradient) ca. 33 K wärmer!
Das ist der ganze Atmosphäreneffekt.
@Martin Pecka
Genau das ist es. Die Gleichgewichtstemperatur aus Einstrahlung und Ausstrahlung liegt mit Atmosphäre in einer größeren Höhe als ohne Atmosphäre. Die Atmosphäre hat aber einen Druck- und einen Temperaturgradienten. Unterhalb der Gleichgewichtshöhe kommen die 33°C bis zur Oberfläche zusammen. Traurig ist, daß selbst die Kritiker nur sehr langsam verstehen, was los ist.
Es ist die innere Energie der Atmosphäre und NICHT die Strahlungsisolation. Diese gibt es nicht!
http://thumulla.com/home/ein_gedankenexperiment_zum_klima_auf_der_erde.html
Carsten
—
Denken ist schwerer als man denkt
Rantanplan
ABER! Das Ding kommt mir halbgar vor, kein Bezug zur Temperatur erkennbar.
ABER! Das Ding kommt mir halbgar vor. Die Planetentemperatur fehlt.
Eine logische Erklärung, nur die 33 K sind dabei unsinnig bzw. gelten nur für ein Modell, bei dem die Erde mit einheitlicher Oberflächenstruktur gleichmäßig von allen Seiten beschienen wird.
Nichts befindet sich im Gleichgewicht bei einem rotierenden, von der Sonne beschienenen Planeten mit unterschiedlicher und sich an jeder Stelle der Gleichgewichtshöhe ständig ändernder Albedo. Die Temperaturen reichen von (ca) -50 bis +50 °C. An keiner Stelle ist die Temperatur konstant, schon gar nicht herrscht ein Mittelwert.
Bei soviel Abweichungen der realen Erde vom Modell fragt man sich, wozu das Modell überhaupt gedacht wird.
Schock Studie? Muß ich einmal wieder lächeln!
Schon der Versuch, auf der Tagseite der Erde (sonnenbeschienen) einen „Treibhauseffekt“ zu lokalisieren, scheitert!
Oft genug hier dargestellt!
Und nachts?
Siehe 2. HS der Thermodynamik!