Zugegeben es ist kein besonders spannendes Thema, wenn man nicht gerade ein Statistiker, Mathematiker oder ja, besonders engagierter Klimaforscher ist. Ich muss auch gestehen, dass mich erst der auch in diesen Kreisen bekannte Willis Eschenbach auf die Verknüpfung dieser Themen gebracht hat, der ein Meister darin ist, dass Offensichtliche zu hinterfragen. Er zeigt dabei häufig genug auf, dass das Offensichtliche nicht das Wahre und schon gar nicht das Wirkliche ist.
In der Klimatologie wird aus guten Gründen sehr oft mit Korrelationen gearbeitet. Diese werden gesucht, berechnet, verglichen, mit vermuteten Ursachen unterlegt, oft aber auch beides miteinander verwechselt, um der Beantwortung der schwierigen Frage näher zu kommen: Was steuert unser Klima? Oder – genauer – was steuert unsere Temperatur? Da Klimatologen es oft nicht unter „Weltklima“ machen – dabei es tunlichst unterlassen diesen Begriff zu definieren – muss die Frage lauten: Was steuert unsere Welttemperatur? Die einfachste Antwort müsste lauten: Nichts! Denn, da es eine Welttemperatur nicht gibt, kann sie auch nicht gesteuert werden! So einfach!
Damit würde man aber keine Forschungsmilliarden loseisen, der Politik kein 2°C-Ziel einreden und die (westliche) Welt nicht in Angst und Schrecken versetzen können. Also wird eine Welttemperatur per definitionem frei geschaffen. Sie soll der arithmetische Durchschnitt aller lokalen Jahresdurchschnittstemperaturen sein und die sollten zuvor möglichst genau und gleichmäßig über den Globus verteilt gemessen werden.
Nun wissen wir aus vielfältigen Berichten, dass dies zwar oft behauptet wird, man aber in der Realität weit davon entfernt ist, eine gleichmäßige Abdeckung zumindest für die Vorsatellitenzeit jemals erreicht zu haben. Und was die terrestrischen Stationen anbelangt, ist dieser Zustand nicht besser, sondern eher schlechter geworden. Zwar behauptet das britische Met. Office1 ungerührt auf seiner Website: „Die Untergruppe von Messstationen ist gleichmäßig über den Globus verteilt und gibt einen faire Übersicht über die Mitteltemperaturen in globalem Maßstab über Land“. Nun, dass das die Übertreibung des Jahrhunderts – wenn nicht Jahrtausends – ist, pfeifen inzwischen die Spatzen von den Dächern. Die Verteilung der einbezogenen Messstationen ist weit davon entfernt, gleichmäßig und/oder gleichförmig über den Erdball, oder auch nur die Landfläche, verteilt zu sein.
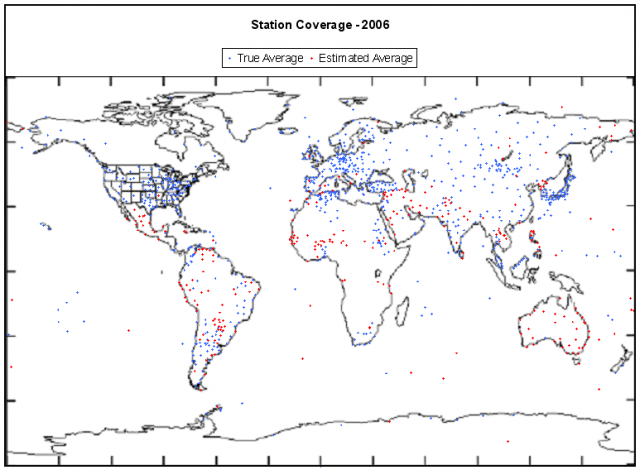
Abbildung 1: Verteilung der einbezogenen GHCN Messstationen 2006. Blau dargestellt mit kontinuierlicher Messung, rot mit diskontinuierlicher Messung.
Aber, die Frage sei erlaubt: Wie kommen die wackeren Wissenschaftler vom Met. Office zu dieser ebenso falschen wie naiven Behauptung? Nun, hier kommen vermutlich die oben erwähnten Korrelationen2 ins Spiel. Sie beziehen sich evtl. auf einen grundlegenden Aufsatz des damals noch jungen, aber schon sehr aggressiven Klimaforschers James Hansen und seines Kollegen Lebedeff aus dem Jahre 1987. Hansen ist auch derjenige, der 1988 dem amerikanischen Senat bei drückend heißem Wetter und unter tatkräftiger Mithilfe seines Kumpels – des Politprofis Al Gore – die Nachteile der künftigen vermutlich katastrophalen Erwärmung näherbrachte.
In einem Aufsatz von 1987 3 im damals noch angesehenen JOURNAL OF GEOPHYSICAL RESEARCH durften die Autoren „peer reviewed“ verkünden, dass es dank ihrer Forschung möglich sei, aus der Not eine Tugend zu machen. Nämlich aus der Not keine flächenmäßig ausreichende Abdeckung mit Klimamessstationen zu haben, die Tugend, diese auch gar nicht zu brauchen. Und nur weil man nun die Vorzüge von Korrelationen für unbekannte Trends einzusetzen imstande sei.
In der Zusammenfassung des Aufsatzes steht:“..Wir zeigen, dass die Temperaturen von Messstationen mittlerer und hoher Breite über 1000 km miteinander hoch korreliert sind. Bei Stationen in niederer Breite fällt die Korrelation mit der Entfernung stärker ab“ Und etwas später ebenda: “.. Fehlerabschätzungen basieren in Teilen auf Studien wie genau die derzeitigen Stationsverteilungen in der Lage sind Temperaturänderungen in einem globalen Datensatz zu repoduzieren, die von einem dreidimensionalen GCM (General Circulation Model) mit realistischer Variabilität erzeugt wurden.“ In diesem hochtrabenden, etwas sehr verschwurbelten Satz steht also im Klartext:“ Wir haben eine Fehlerabschätzung (in Teilen? Welche Teile?) gemacht, indem wir die Ergebnisse mit Modellen, die „realistische“ Temperaturvariationen zuvor errechnet hatten, verglichen haben.“ Also nix mit Realitätsvergleich, nix mit Überprüfung der Daten der einbezogenen Stationen, sondern stattdessen Überprüfung mit Modellen! Der künftige modellverliebte Kurs der Klimaforschung des IPCC wurde hier schon vorgezeichnet.
Und so sah das Ergebnis dann auch aus. Dank der großzügigen 1000 km Regel, die im Text dann nochmals auf noch großzügigere 1200 km Radius erweitert wurde, schaffte man
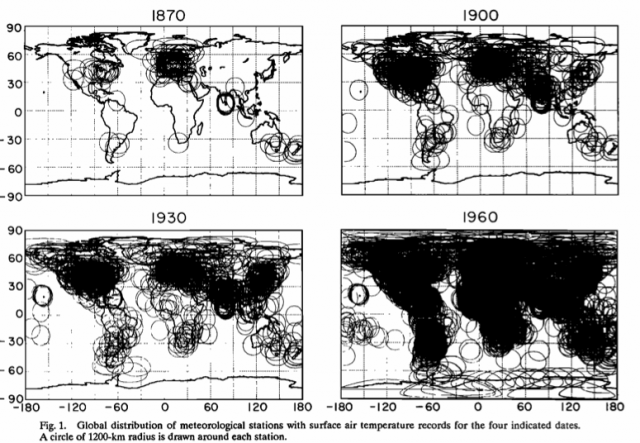
Abbildung 2: Verteilung der einbezogenen GHCN Messstationen nach Hansen & Lebedeff von 1870 bis 1960 sowie deren postulierte Abdeckung
das Kunststück aus einer unvollständigen auf die Nordhalbkugel bezogenen Abdeckung eine weltweite zu machen. Die Welt wurde überall schwarz. Dabei meint man, dass es genüge wenn in mittleren und hohen Breiten ein „mittlerer“ Korrelationskoeffzient von 0,5 nicht unterschritten wird und (nur noch) von 0,33 in niederen Breiten. Mit diesem trefflichen Handwerkszeug ausgestattet und abgesichert durch „präzise“ Vergleiche mit Modellrechnungen der damaligen Modelle (GCM´s) wurde die Welttemperatur bzw. ihre Abweichung vom gedachten Normal, die Anomalie und deren Trend bestimmt.
Diese Methode wird vom GISS unter seinem Chef James Hansen und seinem Nachfolger Gavin Schmidt bis heute angewendet und niemand in der IPCC Klimatologenbranche hat bisher öffentlich Zweifel an diesem überaus groben und unbestimmten, daher oft falschen Verfahren4 angemeldet.
Jüngst erst wieder in einer Studie über die Temperaturentwicklung in der Arktis. Auch dort wurden die wenigen Messstationen am Rand der Arktis benutzt, um die Temperaturtrends der ganzen Arktis zu berechnen. Und die steigen natürlich.
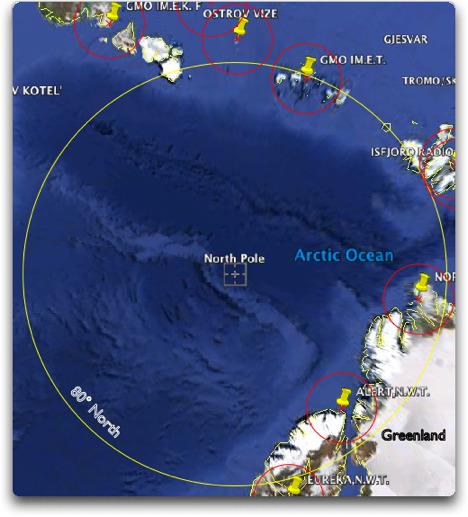
Abbildung 3 Satellitendarstellung der Arktis mit Nordpol und nächstgelegenen Messstationen. Die Kreise um die Stationen haben einen Durchmesser von 250 km! Der 80 ° Breitenkreis hat ca. einen Radius von 1200 km. Also wie von Hansen et al 1987 vorgeschlagen
Und hier die Temperaturtrends, die das GISS veröffentlicht, obwohl es dort keine Messstationen gibt.
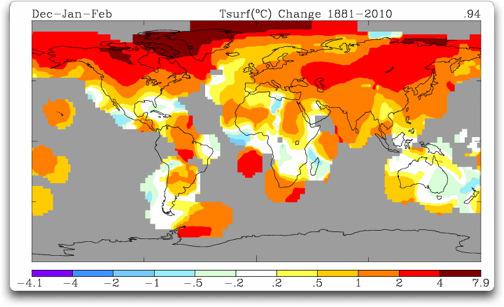
Abbildung 4 GISS Darstellung der Temperaturtrends weltweit von 1881-2010, Man beachte die braune Färbung im Norden am Pol – dort wo es keine Messstationen gibt.
Der Ingenieur Willis Eschenbach hat sich von dieser „schwarzen Kunst“ nicht beeindrucken lassen und sich die Frage gestellt, inwieweit sich denn aus Korrelationen stichhaltige Trends ableiten lassen, oder umgekehrt. Er zeigte sich darüber verwundert, wie man Temperaturen und deren Trends für weite Teile der Welt berechnen kann, wo es keinerlei Temperaturmessstationen gibt.
Wie immer geht er die Sache grundsätzlich an und erzeugt zuerst beliebige Trends, errechnet deren Korrelationen und geht dann weiter zu natürlichen Temperaturverläufen und deren Anomalien und Trends sowie Korrelationen.
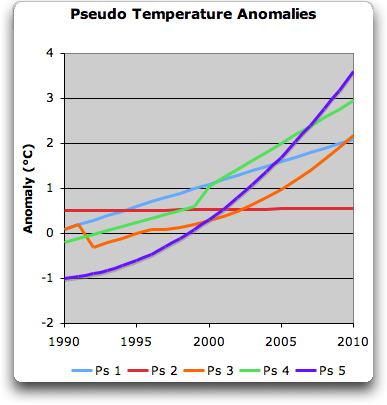
Wir sehen sie in Abbildung 5:
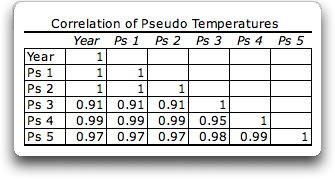
Die zugehörigen Korrelationen sehen wir in der folgenden Tabelle:
Allen gemeinsam ist, dass die Korrelation sehr hoch ist. Keine ist kleiner als 0,9!
Wir erinnern uns: Die Korrelation die Hansen & Lebedeff noch zuließen lagen bei > 0,5 in mittleren und hohen Breiten und nur noch 0,33 in niederen Breiten. Es fällt aber jetzt schon auf, dass diese sehr hoch korrelierten Pseudotemperaturen doch sehr, sehr verschieden (mehrere Grad Unterschied) und trotzdem hoch korreliert sind. Und (nicht nur) Eschenbach 5 folgert daraus:
„.Die unausweichliche Folgerung daraus ist, dass hohe Korrelationswerte zwischen Temperatur-Historien nicht bedeuten, dass deren Trends sich ähneln.
In Ordnung, ich kann schon hören, was Sie denken: „Ja, stimmt, für einige imaginäre kurze 20-jährige Pseudo-Temperatur-Historien kann man einige wilde Daten finden, die unterschiedliche Trends aufweisen. Doch was ist mit den realen 50-jährigen Temperatur-Historien, wie sie Hansen und Lebedeff benutzten?“
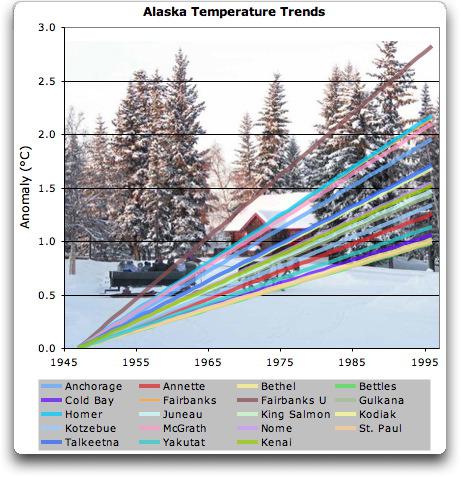
Abbildung 7: Natürliche Trends in Alaska mit Korrelationen zwischen 0,51 bis 0,94 im Mittel 0,75 bezogen auf Anchorage
Gut, dass diese Frage kommt … hier sind neunzehn 50-jährige Temperatur-Historien von Alaska. Alle korrelieren mit Anchorage höher als 0,5 (max 0.94, min 0.51, Durchschnitt 0.75).
Man sieht, die Trends rangieren von etwa einem Grad in 50 Jahren bis nahe drei Grad. Trotz dieser riesigen Spannweite (ca. 300%) bei den Trends haben alle eine gute Korrelation (größer +0,5) mit Anchorage. Das zeigt klar, dass eine gute Korrelation zwischen den Temperatur-Historien nichts aussagt über deren korrespondierende Trends.
Was ergibt sich daraus?
Hansen und Lebedeff lagen richtig damit, dass die jährlichen Temperatur-Historien von weit auseinander liegenden Messstationen dazu neigen, gut korreliert zu sein. Allerdings lagen sie nicht richtig mit ihrer Meinung, dass dies für die Trends der gut korrelierten Temperatur-Historien gälte. Deren Trends können völlig ungleich sein. Im Ergebnis ist die Extrapolation von Trends aus einer bis zu 1200 km entfernten Messstation ein unzulässiges Verfahren ohne jegliche mathematische Basis.
Soweit der pfiffige, misstrauische Willis Eschenbach. Er unterzieht dann gleich die kühnen Angaben des GISS über die Temperaturerhöhung der Arktis einer kritischen Betrachtung.(http://wattsupwiththat.com/2010/03/25/gisscapades/#more-17728) Denn dort wird so gut wie nirgends gemessen: „Macht nichts sagen die GISS Leute: Wo keine Temperaturen bekannt sind, erfinden wir eben welche“ Richtige seriöse Klimaforschung sollte anders aussehen.
Meint
Michael Limburg EIKE
1 Met Office(Quelle: http://www.metoffice.gov.uk/corporate/pressoffice/2009/pr20091205.html) …The subset of stations is evenly distributed across the globe and provides a fair representation of changes in mean temperature on a global scale over land.
2„Korrelation“ ist ein mathematisches Maß für die Ähnlichkeit (Wikipedia spricht allgemeiner von Wechselbeziehungen) zweier Datenzeitreihen. Sie rangiert von „null“, d. h. keine Ähnlichkeit, bis plus oder minus “eins”, d. h. sehr ähnlich. Ein negatives Vorzeichen verändert die Ähnlichkeit nicht, aber wenn der Wert eines Datenbestandes nach oben geht, nimmt der andere ab.
3 HANSEN, JAMES LEBEDEFF, SERGEJ (1987) Global Trends of Measured Surface Air Temperature. JOURNAL OF GEOPHYSICAL RESEARCH 92:13345 13372.
4 Damit sind nicht die Klimarealisten, Ross McKittrick, MacIntyre, Watts um nur diese zu nennen, gemeint. Die schießen seit Jahren gegen diese zu grobe und zu falschen Schlüssen führenden Methode
5 Quelle mit vielen weiteren Beispielen und Anmerkungen hier: http://wattsupwiththat.com/2010/03/25/gisscapades/#more-17728
















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Wo liegt den der Korrelationskoeffizient von Globaltemperatur und CO2, mal abgesehen von den Messungenauigkeiten? Für die Jahre 1945-1975 dürfte er sogar leicht negativ sein, für die Jahre 2000-2015 nahe bei Null. Gibt es überhaupt Zeiträume, in denen eine signifikante Korrelation besteht?
Da ist es wieder, das Wort „Anomalie“ mir geht das, persönlich total ab.
Einen Mittelwert X über einen Zeitraum Y als „Normal“ zu definieren finde ich zumindest nicht schlüssig, bei einem chaotischen System wie dem Klima (Wetter).
Aber das ist ja dass, was von der AGWler- Gemeinde gern veranstaltet wird.
Oh Herr lass wieder ordentliche Wissenschaft Raum greifen!
Und wenn wir auf jeden Quadratkilometer (theoretisch) der Erdoberfläche eine Messstation hätten und wir die „Erdmitteltemperatur“ statistisch korrekt bestimmen könnten…
Was sagt sie aus….. genau nichts!
Der Pearson-Korrelationskoeffizient zweier linear ansteigender Groessen ist definitionsgemaess immer Eins, wie elementar aus der Definition (z.B. Korn und Korn 1968) sichtbar ist. Insofern sind die Beispiele von Eschenbach in Abb. 6 trivial und werden der Analyse von Hansen & Lebedeff (1987) nicht gerecht. Dort geht es uebrigens um raeumliche Korrelationen und deren Nuetzlichkeit zur Ableitung von Temperaturanomalien und Klimatrends. Es lohnt sich durchaus, die Originalarbeit zu lesen, bevor Urteile gefaellt werden. Da der Autor Limbach aber jede Klimawirksamkeit von CO2 in der Atmosphaere ausschliesst, verstellt er sich jeden realistischen Blick auf die Wirklichkeit.
Lieber Hr. Müller,
es reicht nicht, sich mit den Feinheiten der Statistik auszukennen. Um beurteilen zu können, ob eine Korrelation eine Kausalität bestätigt, muss man die Vorgänge in der Atmosphäre, Hydrosphäre und Biosphäre wirklich kennen. Und schon daran hapert es. Die Kohlenstoffkreisläufe sind sehr komplex und gekoppelt und hängen von einer Vielzahl von Parametern ab. „Einfaches“ Beispiel: Wie erklären Sie z.B. Snowball Earth bei 6.000 bis 8.000 ppm CO2?
Mfg
@Fred Mueller:
Natuerlich impliziert eine hohe Korrelation nicht automatisch einen Ursachen-Wirkung-Zusammenhang. Das Beispiel der Snowball Earth taugt allerdings als Gegenbeispiel wenig: Es handelt sich um eine Hypothese ohne klare Kenntnisse fuer die atmosphaerischen Bedingungen damals. Keiner weiss, wie hoch vor einer Milliarden Jahren die CO2-Konzentration der Erde war. Heute sehen wir dagegen eine klare Korrelation des Anstiegs des atmosphaerischen CO2 und der globalen Temperatur, ueber eine Zeitspanne von ca. 150 Jahren. Da gibt es auch einen klaren physikalischen Mechanismus der Infrarot-Strahlungsuebertragung in der Atmosphaere, der diese Korrelation erzeugen kann. Das ueberzeugt mich, auch beim zugegeben komplexen System der atmosphaerischen Prozesse.
Lieber Hr. Mueller,
Meinen Sie das ernst? Falls ja, sind Sie hier ziemlich allein auf weiter Flur. Die Erde hatte ursprünglich eine CO2-reiche Atmosphäre mit geringen Sauerstoffanteilen, die erst durch pfanzliche Fotosynthese ihre heutige Zusammensetzung erhielt.
Mfg
Sehr geehrter Herr Mueller,
Ihr Bezug auf Abb 6.zeigt, dass Sie nicht wissen, was eine linear steigende Funktion ist. Wenn sie bei der Analyse von Hansen von „raeumlicher Korrelation“ reden, zeigen Sie auch, dass Sie keinerlei Ahnung von Geometrie haben. Ergo ist ihr gesamter Post mathematisch sinnlos! Sie verkörpern damit die klassische Verbindung zwischen Dummheit und Arroganz.
Man sollte allerdings die Möglichkeit nicht ausschließen, dass Sie bewusst Unsinn schreiben und nur ein klassischer Troll sind. Ihr abschließender Satz deutet stark in diese Richtung.
Mit überaus freundlichen Grüßen
Sie meinen wohl, Sie seien besonders schlau mit Ihrem xxxxxx (Merkel/Kemfert) Gefasel!
Herr Limburg schliesst überhaupt garnichts aus, lediglich wird zu guter Recht massiv bezweifelt, daß 4% menschlich emittiertes co2 das chaotische System Atmosphäre und damit das „Klima“ (30 Jahre Wetter), unter völliger Ignoranz des Faktors Sonne, beeinflussen soll, das s.g. AGW aka church of global warming! Selbst kleine Kinder von 5-6 Jahren verstehen das sofort, mit einem simplen Experiment: setzen Sie sie im Sommer morgens, mittags & abends auf eine Steintreppe oä, die Sonneneinstrahlung genossen hat; und am nächsten Tag noch einmal. JEDES Kind kapiert: die Hitze wurde durch den Kernreaktor (hoch einige Millionen) SONNE generiert, die Abkühlung über Nacht durch das Fehlen dieses „Ofens“, der das Leben erst möglich macht, genau wie das Pflanzenfutter co2. Photosynthese usw, kennen Sie???…
Solch differenziertes Denken scheint Ihnen aber offensichtlich in diesem Leben nicht mehr möglich, dazu benötigt es halt höher entwickelte Denkstrukturen, durch die Sonne (leider nur einem kleinen Teil der Menschheit) zum Leben erweckt! 😉
Nun zu DDR Zeiten gab es in Ostdeutschland neben zahlreichen offiziellen Messstellen noch unzählige lokale Messstellen, die von „Bürgerbeobachtern“ betreut und gewartet wurden. Das gab es m.W. im ganzen Ostblock. Einige solcher Stationen arbeiten noch heute . Es wäre interessant, an diese Daten ranzukommen…..Es gab auch schon früher „extrem“ Wetter. So der Winter 78/79 mit viel Schnee an Neujahr oder der extrem milde 82 wo Weihnachten die Kirschbäume blühten. Oder der heiße Sommer 67? wo die Elbe bei Dresden fast ausgetrocknet war.
Ich war 34 Jahre Bauer. Hab solche und solche Jahreszeiten erlebt. Was mir jedoch scheint ist,das die relative Menge der Niederschläge zurückgegangen ist. Man spricht von etwa 10 %. Was aber nur selten erwähnt wird, ist das die Menge der verwertbaren Niederschläge, also das was z.B Pflanzen zur Verfügung steht und letztlich ins Grundwasser absickert nur noch etwa 70 % beträgt. Weil mehr Niederschlag oberflächlich abläuft…. Nun weiß ich nicht , wie verlässlich diese Prozentzshlen sind. Sie sind mir aus Beitragen hängen geblieben. Wäre interessant ,dem mal auf den Grund zu gehen. Man kann zwar offizielle Zahlen ( unter Schwierigkeiten!) abrufen, aber der Sache traue ich nicht ganz……..
Sehr geehrter Herr Limburg,
imtext steht, daß hansen zusammen mit Al Gore den Betrug bei der Senatsanhörung gemacht hat. Wenn ich recht erinnere, war es nicht Al Gore (dem wäre das auch zu zutrauen) sondern der demok. Senator Tim Wirth.
Sie haben tlw. recht. Gore hat das zusammen mit Timothy Wirth gemacht. So meine Kenntnis.
——————-Die Lebenserwartung————————
———-CO2 läßt die Lebenserwartung steigen !!!——-
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
“ In Europa lag die Lebenserwartung um 1820 bei etwa 36 Jahren.“
———————————
„In Deutschland ist die Sterblichkeit seit 1871 im Mittel um 0,8 % jährlich zurückgegangen. In den Jahren von 1994 bis 2004 hat sich dieser Trend zur Erhöhung der Lebenserwartung verstärkt; in diesem Zeitraum sank die Sterblichkeit sogar um zwei Prozent jährlich!“
————————————————————————-
„Im Jahr 2015 betrug die durchschnittliche Lebenserwartung neugeborener Jungen 77 Jahre und 9 Monate (2010: 77 Jahre und 4 Monate). Die entsprechende Zahl für neugeborene Mädchen lautete 82 Jahre und 10 Monate (2010: 82 Jahre und 6 Monate“
——————————————
(Verheiratete leben etwas länger, als andere, habe ich noch nicht genauer untersucht – könnte aber auch etwas mit dem CO2 zu tun haben.Eine sehr wahrscheinliche Ursache:
Verheiratete Küssen sich öfters, atmen dann den Atem des Partners ein, in diesem ist das CO2 sogar mit ca 4 % dabei.
In der Atmosphäre nur ca 0.04 % !!!)
————————————————————————–
CO2 in der Atmosphäre steigt – die Lebenserwartung auch!!
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
Hier kann man ganz genau sehen, da besteht eine Korrelation – die Kausalität liegt doch auf der Hand! ????
————————————————————————-
Somit stellt sich uns die Frage, wollen wir in einer etwas wärmeren Welt
auch etwas länger Leben, oder in einer kälteren, kürzer?
Legt man die CO2 Kurve darüber, sieht man es passt!
Hier die Graphik:
https://de.wikipedia.org/wiki/Lebenserwartung