Damit wird klar, dass alle bisherigen globalen Mittel-Temperaturzeitreihen für den Ihnen zugedachten Zweck der Signalanalyse und ggf. Zuordnung von pot. Ursachen (detection and attribution problem) unbrauchbar sind.
Hinzu kommt die Tatsache, dass diesen Zeitreihen weitere Unsicherheiten anhaften, die aus der Fülle der unvermeidbaren und rückwirkend auch unkorrigierbaren systematischen Fehler entstehen, die wohl ihrem Typ nach bekannt sind aber weder von Richtung und Größe her im Einzelnen bestimmbar sind. Die Vergangenheit ist endgültig vorbei. Die daraus resultierende Unsicherheit liegt bei mindestens± 1 bis ± 2 K. Mit den in der Arbeit ermittelten zufälligen Fehlern ergibt sich eine gesamte minimale Unsicherheit von mindestens bei ± 1,5 bis ± 2,5 K. Daraus folgt, dass keine vernünftige Signalanalyse aus diesen Reihen möglich ist. Die Signale verschwinden im Fehlerrauschen.
Auszug aus einem paper von M. Massah, H. Kantz
Mittelwerte über einen Zeitraum, ein Standardwerkzeug bei der Analyse von Umweltdaten, sind stark von langfristigen Korrelationen betroffen. Die Stichprobengröße, um wie gewünscht ein kleines Vertrauensintervall zu erhalten, kann dramatisch größer sein, als für nicht korrelierte Daten. Wir präsentieren quantitative Ergebnisse für kurz- und langfristige korrelierte Gauss’sche stochastische Prozesse. Mit diesen berechnen wir Vertrauensintervalle für zeitliche Mittelwerte von Temperaturmessungen.Temperatur-Zeitreihen zeichnen sich bekanntlich dadurch aus, dass sie langfristig mit Hurst-Exponenten größer als ½ korreliert sind. Multidekadische Zeit-Mittelwerte werden routinemäßig bei den Studien zum Klimawandel herangezogen. Unsere Analyse zeigt, dass Unsicherheiten derartiger Mittelwerte genauso groß sind wie für ein einzelnes Jahr mit nicht korrelierten Daten.
Kernpunkte
● Im Falle des Vorhandenseins langfristiger Korrelation konvergieren zeitliche Mittelwerte sehr langsam als eine Funktion der Stichprobengröße.
● Wir zeigen, wie man Fehlerbalken berechnet für begrenzte zeitliche Mittelwerte von langfristig korrelierten Daten.
● Die Unsicherheit in einem 30-jährigen Temperatur-Mittelwert in Potsdam beträgt plusminus 0,5°C und in Darwin plusminus 0,4°C.
Einführung
Ein allgemein angewandtes und sehr leicht anzuwendendes Werkzeug bei der Analyse einer Zeitreihe ist es, Mittelwerte aus Einzelwerten zu berechnen. Klimawandel beispielsweise wird zuerst analysiert mittels zeitlicher Mittelwerte meteorologisch relevanter Größen (Temperatur, Niederschlag) über 20 oder 30 Jahre, um interdekadische Fluktuationen heraus zu mitteln. Und dies, obwohl Klimawandel ein sehr komplexes Phänomen mit vielen Facetten ist. Wesentlich detailliertere Studien sind durchführbar und dürften viele weitere Details enthüllen, welche jedoch viel schwerer zu verstehen und viel schwieriger zu integrieren sind in eine allgemeine Perspektive. Daher sind Mittelwerte über die Zeit ein essentielles Werkzeug zum Verständnis von Klimawandel und werden es auch bleiben.
Der präzise Mittelwert einer Stichprobengröße ist abhängig von den Details der Stichprobe und variiert folglich von Stichprobe zu Stichprobe, die alle mit dem gleichen Prozess zustande kommen. Falls der Prozess stationär ist, konvergieren derartige Mittelwerte mit zunehmender Größe der Stichprobe und werden unabhängig von den Details der gewählten Stichprobe. Nur dann repräsentieren sie eine Systemeigenschaft anstatt einer Stichproben-Eigenschaft.
Thema dieser Studie ist die Frage, wie langsam eine solche Konvergenz ablaufen kann, d. h. wie weit ein Mittelwert über ein begrenztes Zeitfenster vom asymptotischen Limit entfernt sein kann. Wir machen dies speziell im Hinblick auf die allgemeine Praxis, ein Zeitfenster von 30 Jahren heranzuziehen, um Klima zu quantifizieren.
Kurz gesagt, wir untersuchen Zeit-Mittelwerte von Zeitreihen-Daten:
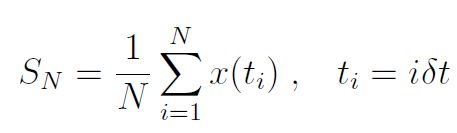
Für stationäre ergodische [was das ist? Siehe hier bei Wikipedia! Anm. d. Übers.] Prozesse konvergiert SN im Limit N → ∞ zu einem gut definierten Wert, dem Ensemble-Mittel. In der Praxis ist N endlich, und wir wollen untersuchen, wie nahe SN ist als eine Funktion von N. Dies kann man mittels des Konzeptes eines Konfidenz-Intervalls ausdrücken.
Ein Vertrauensintervall von r% ist definiert als das größte Intervall innerhalb der Bandbreite einer Zufallsvariable (hier: SN), und zwar dergestalt, dass deren Wert innerhalb der r%-Wahrscheinlichkeit liegt (Wahrscheinlichkeit = r = 100). Allgemein gebräuchliche Vertrauensintervalle sind Wahrscheinlichkeiten für 95%, 99% und 99,9%. Oftmals wird das Statement invertiert: Ist ein geschätzter Wert irgendeiner Quantität gegeben, liegt dessen wahrer Wert (als Ensemble-Mittel der unbekannten zugrunde liegenden Wahrscheinlichkeits-Verteilung) mit der Wahrscheinlichkeit r = 100 innerhalb des r%-Vertrauensintervalls um den geschätzten Wert. Folglich werden Vertrauensintervalle herangezogen, um die statistischen Schätzfehler zu quantifizieren und als Fehlerbalken darzustellen.
Wir werden die N-Abhängigkeit von Vertrauensintervallen analysieren und damit das Tempo der Konvergenz von SN zu μ für zwei Klassen korrelierter Gauss’scher Prozesse. Während kurzfristige Korrelationen einer einfachen Korrektur der Stichprobengröße bedürfen im bekannten 1/√N-Verhalten, führen langfristige Korrelationen zu einer wesentlich langsameren Abnahme statistischer Fehler. Auf der Grundlage dieser Ergebnisse werden wir dann Vertrauensintervalle berechnen für zeitliche Mittelwerte gemessener Temperatur-Zeitreihen. Derartige Daten repräsentieren mit einer gewissen Approximation Gauss’sche stochastische Prozesse mit langfristigen Korrelationen. Wir berechnen die Vertrauensintervalle der zeitlich gemittelten Temperaturen als eine Funktion der Länge des Zeitfensters. Die Fehlerbalken von 30-Jahre-Mittelwerten dieser Daten sind größer als die eines 1-Jahr-Mittelwertes identischer, unabhängig voneinander verteilter Daten (iid). Das 95%-Intervall von Potsdam beträgt ±0,5°C und von Darwin ±0,4°C. Wir folgern daraus, dass unser Wissen über das wahre Klima erheblich weniger präzise ist als man naiv erwarten könnte, kann aber präzise quantifiziert werden.
Auswirkungen langfristiger Korrelationen (LRC) auf statistische Schätzungen sind zu einer Quelle immer stärkerer Bedenken vieler Forscher geworden. Mittels eines Verfahrens mit der Bezeichnung Detrended Fluctuation Analysis (DFA) wurde in einer großen Anzahl von Veröffentlichungen die Existenz von LRC in vielen Datensätzen gezeigt: bei den Temperaturdaten und auch in vielen anderen meteorologischen Zeitreihen wie etwa Abflussmengen von Flüssen, in physiologischen und ökonomischen Daten. Bei der Abschätzung von Trends und der Anwendung von Extremwert-Statistiken und der clustering von Extremereignissen wurden LRCs als Gründe für Abweichungen vom statistischen Standardverhalten ausgemacht. Im Zusammenhang mit Klimawandel hat die Bedeutung geschätzter Trends beim Vorhandensein von LRCs in der Vergangenheit viel Aufmerksamkeit erregt. Unser Schwerpunkt hier, namentlich die Analyse der Auswirkungen von LRCs auf Vertrauensintervalle für zeitliche Mittel ist technisch und konzeptuell weniger schwierig als die oben erwähnten Arbeiten, aber eine Methodik zur Bestimmung dieser [Auswirkungen] liegt noch nicht vor. Eine numerische Analyse exponentieller Korrelationen wurde durchgeführt, und die allmähliche Konvergenz von Mittelwerten begrenzter Stichproben bei Vorhandensein eines langen Gedächtnisses ist in der statistischen Literatur bereits erwähnt worden.
Wir beenden diese Einführung mit einer Interpretation der oben erwähnten Fehlerbalken. Klimadaten werden nicht mittels Gauss’scher stochastischer Prozesse erzeugt, sondern Gauss’sche Modelle sind dafür manchmal gute Datenmodelle. Quantifiziert man den „Zustand“ des Klimas mit einer Zeitreihe, interpretieren wir das beobachtete Signal als stochastische (plus jahreszeitliche) Fluktuationen rund um einen gegebenen festen Wert. Falls diese Fluktuationen weißes Rauschen wären, würden Zeitreihen über diese zu Null konvergieren wie der Term 1/√N. Falls diese Fluktuationen LRCs wären, würden sich ihre Zeit-Mittelwerte viel langsamer entspannen [relax], und wir haben größere Schwierigkeiten, die wirklichen Abstufungen zu bestimmen. Vergleicht man unterschiedliche Zeitfenster unabhängig davon, wie sich kleine Fluktuationen heraus mitteln, würden wir Änderungen des Mittelwertes als Änderung des wahren Klimas fehlinterpretieren. Für Temperaturen ist die Annahme von LRC Gauss’scher Fluktuationen über ein Hintergrundsignal sehr realistisch und bietet einen Weg, die Schätzfehler des wahren „Klimazustandes“ zu bestimmen.
…
Zusammenfassung und Ergebnisse
(Hervorhebungen von EIKE Redaktion) Wir haben einen theoretischen Rahmen diskutiert, der es uns erlaubt, die Vertrauensintervalle zeitlicher Mittelwerte für kurz- und langfristig korrelierte Messdaten zu berechnen. In der Praxis müssen die folgenden drei Schritte erfolgen:
●Konstruktion der Reihe von Anomalien oder, allgemeiner, die Sequenz so stationär wie möglich machen.
●Forschen nach langfristigen Korrelationen, z. B. mittels einer DFA, und Berechnung des Hurst-Exponenten.
●Während die asymptotische Abnahme des Fehlerbalkens ∝ NH−1 des Fehlerbalkens sein wird, kann dessen Vor-Faktor [pre-factor] bestimmt werden mittels Berechnung der Standardabweichungen der Verteilung von zeitlichen Mittelwerten über viele kurze Daten-Sequenzen als Funktion der Sequenz-Länge sowie der zu diesen passenden asymptotischen Abnahme.
Folglich ist das Fitting eines ARFIMA-Modells nicht erforderlich, und auch Nicht-Gauss’sche Daten können auf diese Weise bearbeitet werden. Die theoretischen Grundlagen basieren auf einem Gauss’schen Datenmodell. Für stark nicht-Gauss’sche Daten wie Niederschlag oder Windgeschwindigkeit ist ein solches Modell ungeeignet, aber das Verfahren kann angewendet werden und führt zu einer groben Fehlerschätzung, was nützlich ist, da selbst für stark asymmetrische Daten die Verteilung zeitlicher Mittelwerte SN zu einer Gauss-Verteilung tendiert bei einem großen Zeitfenster N.
Im Einzelnen fanden wir, dass die 95%-Vertrauensintervalle für 30-Jahre-Mittelwerte der Temperatur in Potsdam (und in Darwin) fast genau so groß (oder sogar noch größer) sind als der gesamte Erwärmungseffekt der letzten 100 (50) Jahre. Obwohl die physikalischen Konsequenzen zunehmender Treibhausgas-Konzentrationen unanfechtbar sind, zeigt diese Arbeit, dass eine quantitative Abschätzung des Klimawandels mittels gemessenen Daten immer noch eine Herausforderung ist. Die für Potsdam und Darwin gezeigten Ergebnisse gestatten es mit geringer, aber endlicher Wahrscheinlichkeit, sowohl das Fehlen von Klimawandel als auch eine Erwärmung bereits über 1°C anzunehmen, und ohne die letzten 5 Jahre mit Daten zeigt die gleiche Analyse eine noch viel geringere Signifikanz für Erwärmung.
Ein anonymer Begutachter wies uns darauf hin, dass es sehr interessant wäre, den externen Antrieb der globalen Mitteltemperatur der Erde aus gemessenen Temperatur-Fluktuationen heraus zu arbeiten innerhalb eines linearen, stochastischen Modells der Energiebilanz mit Langzeitgedächtnis. Unabhängig von Themen wie der Frage, ob eine additive Aufspaltung in kurzfristige Wetter-Fluktuationen und langzeitliche Treiber überhaupt sinnvoll wäre, läge die eindeutige Schwierigkeit bei einem solchen Unterfangen in der Tatsache, dass Zeitreihen über korreliertes Rauschen sich nicht so zu Null mitteln, wie es bei weißem Rauschen der Fall wäre. Da haben wir es: die Auswirkungen von LRCs auf die Unsicherheiten der Mittelwerte müssen berücksichtigt werden.
Der gesamte Beitrag ist als PDF hier einsehbar:
Übersetzt von Chris Frey EIKE
Anmerkungen der EIKE Redaktion.
Mit dieser grundlegenden Arbeit wird die fast allen Temperaturzeitreihen zugrunde gelegten Annahme, dass sich die zufälligen Fehler mit 1/Wurzel ihrer Anzahl ausgleichen, widerlegt. Ein unteres Limit ist bei dieser Art von Zeitreihen nicht unterschreitbar. Dieses Limit ist größer als die gesamte vermutete Änderung im letzten Jahrhundert.
Damit ist deutlich, dass alle bisherigen globalen Mittel-Temperaturzeitreihen für den Ihnen zugedachten Zweck der Signalanalyse und ggf. Zuordnung von pot. Ursachen (detection and attribution problem) unbrauchbar sind.
Hinzu kommt die Tatsache, dass diesen Zeitreihen weitere Unsicherheiten anhaften, die aus der Fülle der systematischen Fehler entstehen, die wohl ihrem Typ nach bekannt sind, aber weder in Richtung noch in Größe her im Einzelnen bestimmbar sind. Die Vergangenheit ist endgültig vorbei.
Die aus dieser Fehlerart resultierende Unsicherheit liegt mindestens bei ± 1 bis ± 2 K. Mit hoher Wahrscheinlichkeit aber noch viel höher.
Mit den oben ermittelten Fehlern ergibt sich eine gesamte minimale Unsicherheit von mindestens bei ± 1,5 bis ± 2,5 K.
Daraus folgt, dass keine vernünftige Signalanalyse aus diesen Reihen möglich ist. Die Signale verschwinden im Fehlerrauschen
Weiterführende links hier

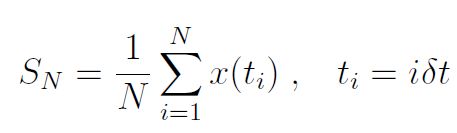














1. die wie auch immer errechneten Temperaturen und der Anomalien sind im thermodynamischen sinne keine Temperaturen sondern irgendwelche Zahlenwerte.
2. Es ist das Verdienst dieser Arbeit gezeigt zu haben, daß der statistische Fehler dieses Zahlenwertes eben nicht gegen null konvergiert, wie die AGW-Truppe immer behauptet. Dazu kommen dann noch die systematischen Fehler (siehe die Dissertation von Herrn Limburg).
3. der Satzteil: „Obwohl die physikalischen Konsequenzen zunehmender Treibhausgas-Konzentrationen unanfechtbar sind“ ist falsch, weil völlig unphysikalisch. Es gibt keinen experimentellen Nachweis für den behaupteten Effekt. Abgesehen davon, ist dieser nicht eindeutig definiert (siehe dazu G. Kramm).
In einem gerade erschienen Report von J. Christy, J. D’Aleo und J. Wallace „On the existence of the Tropical Hot Spot“
wird gezeigt, daß dieser nicht existiert. Eine Theorie, wenn man die AGW-Vermutung einmal so nennen will, ist gescheitert, weil die von ihr gemachte Vorhersage über die Existenz des THS nicht eingetroffen ist.
Möglicherweise haben die Autoren diesen Satz ja nur geschrieben, damit ihr Paper veröffentlicht wurde.
4. In einer gerade erschienen Veröffentlichung von Gallo und Xian wird gezeigt, wie massiv die Temperaturmeßstation durch umgebenden Beton und asphalt beeinflußt werden.
MfG
Daraus zwei Sprüche zur Statistik und Schätzungen:
“ … Wie Benjamin Disraeli vor langer Zeit ausführte, gibt es Menschen, die die Statistik
benutzen wie ein Betrunkener einen Laternenpfahl: als Stütze statt zur Erleuchtung.“
“ Je schwächer die verfügbaren Daten, auf die man seine Folgerungen stützt, um so höher die Genauigkeit, die man angeben muß, um den Daten Glaubwürdigkeit zu verleihen.“
Statistik und Wahrheit:
„Kein Test, der auf der Wahrscheinlichkeitstheorie beruht, kann für sich genommen etwas Nutzbringendes über das Wahr oder Unwahr einer Hypothese aussagen.“
Neyman J, Pearson E (1933) Phil Trans R Soc A, 231:289-337