Jinan weist nach, dass diese Zahlen, wiederholt als „Fakten“ dargestellt, nichts weiter sind als eine falsche Anwendung der Stefan-Boltzmann-Gleichung. Falls die Erde kein perfekter Schwarzkörper ist, sondern eine Emissivität von 0,7 aufweist (wie Satelliten belegen), dann betrüge die Temperatur an der Oberfläche des Planeten ohne irgendeinen Treibhauseffekt nicht -18°C, sondern lediglich 5°C. Dies würde bedeuten, dass die gesamte, dem Treibhauseffekt geschuldete Erwärmung nur etwa 10°C beträgt und nicht eindrucksvolle 33°C wie von den üblichen Verdächtigen behauptet. Es bedeutet, dass der Treibhauseffekt viel weniger wichtig ist als dargestellt.
Der direkte Anstieg um 1,1°C, der nach einer Verdoppelung des CO2-Gehaltes ohne Rückkopplungen prophezeit wird, müsste ebenfalls neu berechnet werden. Diese Studie versucht nicht, das zu tun, aber falls Jinan recht hat, wäre auch diese Zahl deutlich niedriger. Jinan betrachtet, wie diese Zahl hergeleitet worden ist. Dr. David Evans hat ihm geholfen und auch die Einführung zu der Studie geschrieben. Diese folgt als Nächstes. – Jo Nova
Introduction von Dr David Evans
Die Stefan-Boltzmann-Gleichung beschreibt, wie viel Strahlung (Energie) ein Körper wie z. B. ein Planet oder eine Luftschicht abgibt. Sie taucht extensiv in der Klimawissenschaft auf, vor allem bei einfachen Berechnungen des mittleren Energieflusses, strahlt doch die Erde Wärme in den Weltraum ab als infrarote Strahlung.
Die Stefan-Boltzmann-Gleichung wird angewendet, um bekannte Patentlösungen der Klimadebatte zu erhalten wie etwa „ohne Treibhausgase wäre es 33°C kälter“ und „die direkte Auswirkung (also ohne Rückkopplungen) einer Verdoppelung des CO2-Gehaltes würde die Temperatur um 1,1°C steigen lassen“. In der Physik ist diese Gleichung Standard. Jeder Physiker oder Wissenschaftler kann sie auf Strahlung von der Erde anwenden; dafür reichen schon sehr rudimentäre Kenntnisse der Klimawissenschaft aus. (Es gibt hier kein Geheimwissen der Klimawissenschaft, die Gesetze von Arithmetik und Physik sind völlig ausreichend).
Jinan Cao seziert mit klinischer Präzision viele dieser Anwendungen der Stefan-Boltzmann-Gleichung und kommt zu dem Ergebnis, dass sie sehr schlampig angewendet worden ist. Glaubt jemand, dass die Anwendung seitens der Klimawissenschaft für eine Unter- oder Übertreibung der Rolle von CO2 sorgen? Jinans Beitrag ist trotz seiner theoretischen Natur nicht schwierig.
Diese Studie wird einige Leute sehr verärgern und verdient eine faire Würdigung. Sie zeigt valide Standpunkte auf und stellt die Anwendungen der SB-Gleichung in Frage, die irgendwie unbefriedigend sind.
Die heutigen Klimawissenschaftler werden versuchen, diese Kritik ins Lächerliche zu ziehen, und zwar mit den Worten, dass ihre eigenen Modelle sehr viel weiter entwickelt und genauer sind als die groben 0-D-Modelle, auf die man bei der Anwendung der SB-Gleichung zurückgreift. (Ein 0-D-Modell betrachtet die Erde als einen Punkt mit Null Dimensionen. Ein 1-D-Modell betrachtet eine Dimension, entweder Höhe in der Atmosphäre oder Breitengrad. Ein 3-D-Modell berücksichtigt die Erde als ein Gebilde mit Länge, Breite und Höhe.).
Aber hierbei gibt es zwei Probleme. Das erste Problem ist die Kompetenz: Wir wissen nicht, was innerhalb dieser Modelle vor sich geht. Wir haben also nur die Versprechungen der Modellierer, dass sie alles richtig gemacht haben. Die Modelle sind zu undurchsichtig und stehen für eine genaue Untersuchung seitens der Öffentlichkeit nicht zur Verfügung. Das Motto der Royal Society lautet, niemandes Versprechungen zu glauben. Das zweite Problem ist, dass die heutige klimawissenschaftliche Gemeinschaft eine Gewohnheit an den Tag gelegt hat, Dinge zu übertreiben bis hin zu Todesdrohungen. Wie also könnten sie mit Themen umgehen, die so unabdingbar für ihre Finanzierung sind wie die Bedeutung von Treibhausgasen für unser Wohlergehen?
Allgemeine Fehler bei der Anwendung der Stefan-Boltzmann-Gleichung
Jinan Cao
1. Introduction
Klimawissenschaftler machen häufig methodische Fehler bei ihrer Anwendung der Stefan-Boltzmann-Gleichung.
Diese Gleichung ist einfach: ein Schwarzkörper mit Oberflächentemperatur T emittiert Energie pro Zeiteinheit und Flächeneinheit; J ist die Dichte des Energieflusses:

Wenn das Stefan-Boltzmann-Gesetz auf das Erde-Atmosphäre-System angewendet wird, machen Klimawissenschaftler oftmals einen oder mehrere der folgenden Fehler:
i) Ein Koeffizient ε im Bereich 0 bis 1, Emissivität genannt, sollte die Gleichung rechts multiplizieren, aber nicht bei der Anwendung auf Körper, die keine Schwarzkörper sind;
ii) Die falsche Spezifizierung der „Oberfläche“ und der „Oberflächen-Temperatur“ des Erde-Atmsphäre-Systems;
iii) die falsche Spezifizierung, ob eine Luftschicht ein einzelnes Objekt oder ein Cluster von Objekten ist oder nicht.
Diese Fehler können leicht offengelegt werden mittels der Untersuchung vieler Statements (und Verfahren), die gegenwärtig in der Klimaforschung am populärsten sind:
1) Der Treibhaus-Erwärmungs-Effekt von 33°C für die Erde
2) Die Oberflächenstrahlung von 390 W/m² des Energiehaushaltes der Erde
3) Die 1°C-Sensitivität ohne Rückkopplungen, und
4) die Formel für Emission durch eine Luftschicht.
2. THEORETISCHE ANALYSE
2.1 Der 33°C-Treibhauseffekt für die Erde
Wiederholt wurde gesagt, dass die mittlere Temperatur der Erde um 33°C niedriger liegen würde als heute, falls es keinen Treibhaus-Erwärmungseffekt geben würde (1 bis 5). 33°C = 15°C – (-18°C). Die -18°C ergeben sich aus der Gleichung des Strahlungsgleichgewichtes zwischen der Einstrahlung von der Sonne und der Ausstrahlung der Erde:
![]()
Dabei ist r der Radius der Erde, a (alpha) ist die Albedo der Erde, und S0 (= 1368 W/m²) ist die Solarkonstante, die die Dichte der einfallenden Sonnenstrahlung repräsentiert. Das Symbol ε steht für die Emissivität der Erdoberfläche.
In vielen aktuellen Arbeiten der Klimaforschung fehlt dieses ε, oder es wird gleich 1 gesetzt. Setzt man die Werte von a = 0,3 und ε = 1 in die Gleichung (2) ein und löst diese nach T auf, ergibt sich:
(3): (K) @ 255 (K) @ -18°C
Bei der Gleichsetzung von ε = 1 nehmen wir jedoch an, dass die Erdoberfläche die eines Schwarzkörpers ist, was sie niemals ist. Falls ε nicht 1 ist, sondern 0,9; 0,8; 0,7 oder 0,6 würde sich T ergeben zu -11,4°C, -3,6°C, 5,5°C oder 16,5°C. Das Ergebnis von -18°C ist einfach einem Verfahrensfehler geschuldet. Tatsächlich kann die Emissivität der Erde mit ε ≈ 0,7 angesetzt werden, ermittelt aus Satellitendaten der Ausstrahlungs-Spektren.
Die Temperatur an der Erdoberfläche, wie sie an den globalen Wetterstationen gemessen wird, liegt um 15°C (≅ 288 K). N2 und O2 machen etwa 99% der Luft aus. Beide sind buchstäblich transparente Elemente. Diese 15°C nahe der Erdoberfläche ist einfach eine andere physikalische Quantität, die nicht herangezogen werden kann, um davon minus 18°C zu subtrahieren. Weiße und transparente Elemente emittieren gar nichts, ganz gleich welche Temperatur sie haben.
Dieser Fehler beruht auf einem Missverständnis des Wortes „Oberfläche“, welches ein symbolisiertes Konzept des Stefan-Boltzmann-Gesetzes ist. Falls es keine Atmosphäre gibt, bedeutet der Terminus Oberfläche Land und Wasser auf der Erdoberfläche, und T repräsentiert die mittlere Temperatur der Bodenfläche. Falls es doch eine Atmosphäre gibt, die fast durchweg aus Stickstoff und Sauerstoff besteht, ist die Oberfläche immer noch die Bodenfläche und T immer noch die mittlere Temperatur der Bodenfläche, egal welche Temperatur die Luft hat. Grund hierfür ist, dass Stickstoff und Sauerstoff nicht radiativ sind (buchstäblich ε = 0 für Transparent- und Weißkörper). Multipliziert man etwas mit 0, kommt immer 0 heraus.
Wenn wir das gesamte Erde-Atmosphäre-System als ein Objekt identifizieren, ist dessen Oberfläche und die Oberflächen-Temperatur nicht mehr direkt verbunden, sondern weisen unterschiedliche Werte auf für unterschiedliche Strahlungs-Wellenlängen. Über die Absorptionsbänder von Wasserdampf und Kohlendioxid (d. h. das Absorptionsband 15 μm für CO2), ist die Oberfläche eine Luftschicht ab der Obergrenze der Atmosphäre (TOA) mit einer Dicke gleich der Absorptionstiefe, während die „Oberflächen-Temperatur“ die mittlere Temperatur von CO2-Molekülen ist innerhalb dieser Luftschicht (≅ -50°C). Genauso kann man die Oberfläche und die Oberflächen-Temperatur für jedwedes andere Absorptionsband radiativer Gase entdecken. Für die übrigen Bänder sind Oberfläche und Oberflächen-Temperatur an der Bodenfläche und deren mittlere Temperatur (≅ 12°C).
2.2 Die Strahlung von 390 W/m² im Energiehaushalt der Erde
Abbildung 1 erscheint auch im AR 4 des IPCC als eine Abschätzung des jährlichen und globalen mittleren Energie-Gleichgewichtes (8 bis 13).
Wir untersuchen die Strahlung von der Bodenfläche der Erde von 390 W/m², welche als korrespondierend mit einer Schwarzkörper-Emission betrachtet wird, p, bei 15°C mittels der Stefan-Boltzmann-Gleichung:
(4): ![]()
Erstens, die Bodenfläche der Erde ist niemals ein Schwarzkörper. Die Emissivität für die Bodenfläche der Erde ε↓g ergibt sich aus Gleichung (4).
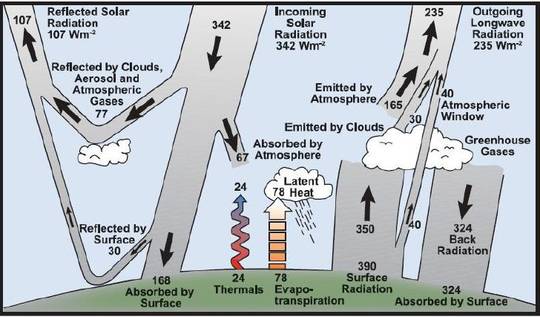
Abbildung 1: Diagramm des Energiehaushaltes der Erde laut IPCC-Bericht AR 4 (2007).
Zweitens, es wurde eine mittlere Temperatur nahe der Oberfläche von 15°C angesetzt. N2 und O2 emittieren buchstäblich gar nichts, egal bei welcher Temperatur. T in Gleichung 4 muss die Temperatur der Bodenfläche der Erde sein, nämlich 285,04 K (11,89°C) (6, 7). Diese wurde berechnet aus ausgehenden spektroskopischen Messungen und Simulationen. Die Strahlung von der Bodenoberfläche ergibt sich dann zu:
(5): 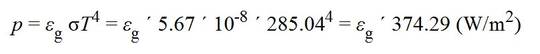
Die Emissivität der Bodenfläche der Erde ε↓g dürfte kaum nahe 1,0 liegen. Schwarzkörper ist eine Abstraktion eines physikalischen Konzeptes; kaum eine Substanz ist auf der Erde ein schwarzer Körper.
Man kann leicht verstehen, warum die Bodenoberfläche der Erde die 324 W/m² niemals vollständig absorbieren wird, weil sie eben keine Schwarzkörper-Oberfläche ist. Da diese beiden Bilder falsch sind, muss man viele andere Bilder am Emissionsbaum der Erde in Frage stellen.
2.3 Die 1°C-CO2-Klimasensitivität ohne Rückkopplungen
Es ist in der gegenwärtigen Klimaforschung weithin akzeptiert, dass eine Verdoppelung von CO2 aus sich selbst heraus eine Treibhaus-Erwärmung um 1°C auslöst, bekannt unter CO2 non-feedback climate sensitivity oder direkte Klimasensitivität von CO2. Bei der Debatte geht es um Rückkopplung; eine positive Rückkopplung wird zu einer höheren, eine negative zu einer niedrigeren Klimasensitivität führen.
Schauen wir einmal, wie dieses Statement abgeleitet worden ist. Die vom Erde-Atmosphäre-System pro Zeit- und Flächeneinheit emittierte Energie (Strahlungsfluss alias Antrieb), F, ergibt sich aus:
![]()
Die Ableitung von F unter Beachtung von T ergibt sich zu:
![]()
Daraus folgt:

Gleichung 8 wurde dahin gehend interpretiert, dass sie zeigt, wie viel Erwärmung DT sich für jedes Antriebs-Inkrement ergibt. Falls sich der CO2-Gehalt verdoppelt, wurde DT mittels einer spektroskopischen Untersuchung mit 3,7 W/m² berechnet. Setzt man DF = 3,7 W/m², T = 255 K in Gleichung 8 ein, ergibt sich Gleichung 9:
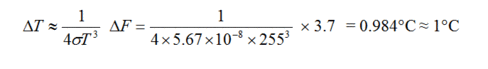
Die Ableitung einschließlich der Emissivität ergibt:
![]()
Nutzt man den Vorteil der Beziehung zwischen T und S0 in Gleichung (2), erhält man:
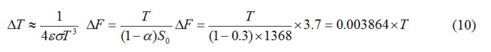
Setzt man T = 255 K in Gleichung 10 ein, erhält man das gleiche Ergebnis von 0,985°C. Man beachte, dass DT abhängig ist von der Emissivität ε via T, obwohl ε nicht einmal explizit in Gleichung 10 auftaucht. Falls ε gleich 1,0; 0,9; 0,8; 0,7 oder 0,6 wäre, ergäbe sich T jeweils zu -18°C, -11,4°C, -3,6°C, 5,5°C oder 16,5°C (wie oben) und würde nach Gleichung (10) jeweils 0,98°C, 1,01°C, 1,04°C, 1,07°C oder 1,11°C ergeben.
Der Fehler, der sich aus dem Weglassen der Emissivität ergibt, kann folglich nicht größer als 10% sein; es handelt sich in diesem Falle mehr um eine Verfahrensfrage. Das Problem ist jedoch, dass die Temperatur T eine physikalische Quantität aufweist, die sich von der mittleren Temperatur der Erde nahe der Oberfläche T↓air (h) unterscheidet, welche zum größten Teil die Temperatur von N2 und O2 ist. Diese beiden sind buchstäblich transparente Körper, die nichts emittieren, gleich welche Temperatur sie haben. Das Symbol H steht für die Höhe, die nahe der Oberfläche fast 0 ist. Um die direkte Klimasensitivität von CO2 abzuschätzen, muss man die Beziehung zwischen DT↓air (h) ~ DF und nicht DT ~ DF ermitteln. Es gibt Wärmeaustausch-Prozesse unabhängig von der Verbindung zwischen diesem T und T↓air (h).
2.4 Die Formel für Emission einer Luftschicht
Von Zeit zu Zeit wird die Atmosphäre repräsentiert durch eine (oder mehrere) Luftschichten für die Klima-Modellierung (8). Man betrachte eine gegebene Luftschicht mit Temperatur Ta und Bodenfläche S wie in Abbildung 2 gezeigt. In der gegenwärtigen Klimaforschung wird die Stefan-Boltzmann-Gleichung direkt angewendet, um σTa 4 zu erhalten für die emittierte Energiefluss-Dichte der Luftschicht. Sie wird einfach nur behandelt wie eine Scheibe eines festen Objektes.
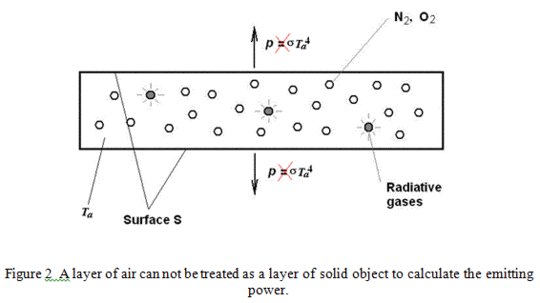
Wie oben diskutiert, emittieren N2 und O2 bei keiner Temperatur irgendetwas. Nur die radiativen Gase in der Luftschicht emittieren. Man wird leicht erkennen, dass 1) nur die Temperatur der radiativen Spezies relevant ist und nicht die mittlere Temperatur der Luftschicht – unterschiedliche Gase können unterschiedliche Temperaturen aufweisen wegen ihrer unterschiedlichen Strahlungseigenschaften; 2) kein Gas ein Schwarzkörper ist, nicht einmal die radiativen Gase.
Es gibt hier einen fundamentalen methodischen Fehler. Weil die emittierenden Spezies so wenig in der Luft enthalten sind, kann eine gegebene Luftschicht nicht als ein einzelnes Objekt identifiziert werden, auf das man das Stefan-Boltzmann-Gesetz anwenden könnte (streng genommen das Planck’sche Gesetz). Das korrekte Verfahren wäre es, jedes einzelne radiative Molekül als ein Objekt zu identifizieren, dass gemäß seiner Temperatur und radiativen Bänder emittiert, was zur Bildung eines Clusters von Objekten innerhalb der Luftschicht führt. Wie viel die Luftschicht emittiert, muss berechnet werden mittels Aufsummierung der gesamten Strahlungsenergiedichte, die von jedem individuellen molekularen Objekt auf der Oberflächen-S emittiert wird. Das Prinzip der formulation wird im folgenden einfachen Beispiel erklärt:

Stellen wir uns eine Luftschicht vor, die n kleine, sphärische Graukörper-Objekte enthält mit einheitlichem Radius r, Emissivität ε und einheitlicher Temperatur T. Dabei ist der Abstand eines jeden Objektes zu einem gegebenen Punkt auf der Oberfläche der Luftschicht L↓i, wobei i von 1 bis n reicht wie in Abbildung 3 gezeigt. Auf der Oberfläche eines jeden individuellen Objektes muss die Emissions-Flussdichte (Energie pro Gebiets- und Zeiteinheit) der Stefan-Boltzmann-Gleichung folgen, d. h. ε σT↑4. Die Flussdichte nimmt mit dem Abstand von ![]() ab. Daher ergibt sich die Gesamt-Flussdichte an einem gegebenen Punkt auf der Oberfläche der Luftschicht zu:
ab. Daher ergibt sich die Gesamt-Flussdichte an einem gegebenen Punkt auf der Oberfläche der Luftschicht zu:
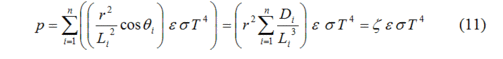
wobei

ein weiterer Koeffizient ist (0 < ζ <= 1), der in der gegenwärtigen Klimaforschung fehlt. Man beachte, ζ = 0 für n = 0, und ζ nähert sich 1, wenn n ausreichend groß genug ist in einem gegebenen Volumen. Dieser Koeffizient gilt auch für die Planck’sche Verteilungs-Funktion.
Gleichung (11) zeigt, dass die Flussdichte sehr stark abhängt von der Anzahl von Objekten innerhalb der Luftschicht. Falls die radiativen Objekte innerhalb der Luftschicht nicht dicht genug sind, wird der Summenterm nur einen sehr kleinen Teil ausmachen. Eine exakte mathematische Beschreibung kann entlang dieser Linie erfolgen, wird aber in diesem Beitrag nicht verfolgt.
Download the full paper here 8 page PDF with References
Anmerkung des Übersetzers: Hierzu gab es viele Kommentare, von denen einer besonders bemerkenswert ist. Dieser soll hier noch in der Übersetzung angefügt werden. Es handelt sich um Kommentar # 19:
Michael Hammer
Zu diesem Thema habe ich in der Vergangenheit schon viele Beiträge geschrieben. Ich stimme einigen, aber nicht allen Behauptungen von Jinan zu.
Erstens, die Warmisten leiten die -33°C her unter der Annahme einer Albedo der Erde von 0,3, was Jinan auch erwähnt. Allerdings muss man sich vor Augen führen, dass das meiste dieser Albedo den Wolken geschuldet ist, welche [aus] Wasserdampf [entstanden] sind. Ohne Treibhausgase, d. h. ohne Wasserdampf würde die Albedo der Erde mehr jener des Mondes gleichen (0,12). Daher wäre die empfangene Strömung höher (390 * .88), was zu einer Oberflächentemperatur von 279 K oder +6°C führen würde.
Nun argumentiert Jinan, dass die Oberflächen-Emissivität viel geringer als 1 ist, tatsächlich mehr 0,7 – hergeleitet aus der Albedo. Dem kann ich nicht zustimmen, stammt doch die Albedo von der Reflektion sichtbaren Lichtes durch Wolken. Die flüssige Wasseroberfläche, die 70% der Erdoberfläche umfasst, hat im thermischen Infrarot eine Emissivität von etwa 0,96, was tatsächlich sehr nahe 1 liegt. Festland kann eine etwas geringere Emissivität aufweisen, aber selbst dort hat eine von Vegetation überzogene Oberfläche im thermischen Infrarot eine hohe Emissivität.
Jinans Punkt ist, dass wir jede Wellenlänge separat betrachten müssen, und hier bin ich total und absolut anderer Ansicht. Dies ist m. E. ein fundamentaler Fehler, den die Warmisten begehen, wenn sie über eine äquivalente Strahlungshöhe reden. Im atmosphärischen Fenster ist die Atmosphäre transparent, und die Emission stammt direkt von der Oberfläche (oder von der Wolkenobergrenze, wo Wolken liegen). Bei Absorptions-Wellenlängen von Treibhausgasen ist die Atmosphäre dicht, und die Emission stammt direkt von der Obergrenze der Treibhausgas-Säule, genau wie Jinan sagt, und wie er korrekt feststellt, liegt die Temperatur des Gases in dieser Höhe näher bei -50°C (im Grunde die Tropopause), aber mit Sicherheit nicht bei +14°C. Falls irgendjemand hier Zweifel hegt, fordere ich denjenigen auf, sich das Emissionsspektrum der Erde zu betrachten, wie es sich aus dem Weltraum darstellt (NIMBUS Satellit).Bei diesen Wellenlängen ist die Emissivität der Atmosphäre genau 1. Dies ergibt sich daraus, dass die Emissivität immer gleich der absorptivity ist. Falls die Gassäule all die Energie absorbiert, die von der Oberfläche ausgestrahlt wird, hat sie eine absorptivity von 1 und folglich auch eine Emissivität von 1.
Der Abschnitt 2.4 von Jinan ist derjenige, mit dem ich am wenigsten übereinstimme. Es ist nicht erforderlich, die Emission eines jeden Moleküls separat zu betrachten. Eine Luftschicht, die dick genug ist, um alle Energie zu absorbieren, die als Ganzes unterhalb der Schicht abgestrahlt wird, hat eine Emissivität von 1 (natürlich bei jener Wellenlänge) und kann als Schwarzkörper-Strahler bei jener Wellenlänge behandelt werden (was heißt, dass man das Planck’sche Gesetz anwenden kann, welches die emittierte Energie bei einer bestimmten Wellenlänge definiert, aber NICHT das Stefan-Boltzmann-Gesetz, welches die Emission eines Objektes definiert, welches ein Schwarzkörper bei allen Wellenlängen ist).
Was die Sensitivität bzgl. einer Verdoppelung des CO2-Gehaltes betrifft: wir wissen, dass es eine logarithmische Beziehung zwischen der Treibhausgas-Konzentration und der zurück gehaltenen Energie gibt. Wir wissen, wie viel Energie das CO2 gegenwärtig zurück hält einfach durch Betrachten des Emissionsspektrums der Erde, wie es der NIMBUS-Satellit sieht. Ohne CO2 läge die Emissions-Temperatur bei etwa 14,7 Mikron bei dem Wert an der Oberfläche von +14°C anstatt bei -50°C, wie es in Wirklichkeit der Fall ist. Wir können entweder das Planck’sche Gesetz über die Bandbreite der Absorption der Wellenlänge integrieren, oder wir können graphisch die Reduktion in der Fläche unter der Kurve des Emissionsspektrums betrachten, um zu dem Ergebnis von 27 W/m² zu kommen. Wir kennen auch den Gesamt-Absorptionsgrad der CO2-Säule bei 280 ppm, also etwa 2000 abs. Das repräsentiert 10 bis 11 Verdoppelungen von dem Punkt an, an dem die Mittellinie gesättigt ist (von wo die logarithmische Beziehung beginnt). Der Effekt einer CO2-Verdoppelung ist also 2,7 W/m² (ich war immer gegen die Zahl von 3,7 W/m² der Warmisten). Meine Berechnung ignoriert die Auswirkung von Wolken. Falls man diese berücksichtigt, verringert sich die Zahl von 2,7 W/m², weil es an der Wolkenobergrenze kälter ist als an der Oberfläche. Daraus folgt, dass die Emission in dem Weltraum ohne CO2 geringer als eine Oberflächen-Temperatur von 14°C implizieren würde.
Alles in allem stimme ich den meisten, aber nicht allen Punkten zu, die Jinan hier aufstellt, aber meine Schlussfolgerungen stimmen mit seinen in der Tat überein.
Übersetzt von Chris Frey EIKE

















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"#1 bis #96 (ff): Mir ist noch Niemand begegnet, der
1. den Zustand der Atmosphäre mathematisch darstellen könnte, der
2. den Zustand der Atmosphäre durch Messung erfassen könnte und der
3. noch nicht bemerkt hättet, dass es aus der Atmosphäre ständig Süßwasser regnet (oder schneit, oder hagelt)!
Haben Sie andere Kontakte?
#93 – „Paulchen Panther“, merke: – Bodennahes CO2 absorbiert (bei 15µm) Wärmestrahlung, wandelt sie wahlweise in Wärme oder zerstreut sie in „alle Winde“!
„Wir wissen nicht, was innerhalb dieser Modelle vor sich geht.“
Das ist nicht richtig. Man weiß sehr genau, was da in den „Modellen“ passiert. Deshalb kann man die ja auch tunen. Es gibt da genug Stellschrauben, an denen gedreht werden muß (und kann), bis der Output zufriedenstellend ist. Das problem ist aber nach wie vor die Auflösung und die Darstellung der Orographie. Mit einer Auflösung von 1,875 ° (T63) sind die Modelle noch viel zu grob für die Kleinskaligen Prozesse. Damit stimmt auch nicht mehr das Modellwetter mit der Realität überein. Die Niederschläge sind beispielsweise durchweg um 30% zu niedrig … .
#93: Dr.Paul sagt:
„was die erdnahe Strahlung von CO2 betrifft,
orientiere ich mich nach wie vor z.B. an dieser MESSUNG:
http://tinyurl.com/cvrssgr
das sind immer noch 0,0 bei 15µm (CO2)
und beachten Sie wie hoch das so bleibt,
mehr als 5000m!“
Lieber Herr Dr. Paul,
ich bin da wohl ein wenig Politiker.
Aber ein Kompromiss (auch wenn die Physik keine macht) an der Stelle tut nicht weh und ändert nichts, aber auch gar nichts am Ergebnis:
Die Behauptung, CO2 würde den Boden um 33°C erwärmen, entbehrt jeder Grundlage.
MfG
P.S.
Heute Abend sehr schöner Bericht auf ARTE zum Thema Kernenergie, allerdings vom französischen Teil von ARTE…
#93: Dr.Paul sagte am Dienstag, 20.09.2016, 21:12:
„#90:Werther besso keks, (fast) immer voll auf Ihrer Seite, was die erdnahe Strahlung von CO2 betrifft, orientiere ich mich nach wie vor z.B. an dieser MESSUNG: http://tinyurl.com/cvrssgr
das sind immer noch 0,0 bei 15µm (CO2) und beachten Sie wie hoch das so bleibt, mehr als 5000m!“
Lesen Sie auch den Text zu den Diagrammen? Es geht um Infrarot-Astronomie und die Diagramme zeigen, wieviel der Infrarotstrahlung von Sternen auf der Erde bzw. in der Höhe der Sofia detektiert werden können: (https://goo.gl/JXbcPG) „Die folgende Abbildung zeigt einerseits, wieviel Prozent der elektromagnetischen Strahlung in den jeweiligen Spektralbereichen tatsächlich am Erdboden ankommt und somit beobachtbar ist. In der typischen Flughöhe von SOFIA von etwa 13 Kilometer kann andereseits der großteil der Infraroten Strahlung detektiert werden.“ Es geht also um ein Signal, dass von entfernten Sternen ausgeht und naheliegenderweise am Erdboden nicht mehr zu erkennen ist. In großer Höhe jedoch schon noch. Das ist keine Aussage darüber, ob Co2 in Bodennähe strahlt, oder nicht …
#90:Werther besso keks,
(fast) immer voll auf Ihrer Seite,
was die erdnahe Strahlung von CO2 betrifft,
orientiere ich mich nach wie vor z.B. an dieser MESSUNG:
http://tinyurl.com/cvrssgr
das sind immer noch 0,0 bei 15µm (CO2)
und beachten Sie wie hoch das so bleibt,
mehr als 5000m!
Selbst von einer Wolke, die thermisch auch nach unten strahlt kommt nichts von 15µm unten an.
Warum das so sein muss, ist auch bekannt.
mfG
#89 Mein Schreibcomputer wurde offenbar von einem Klimaschwindler programmiert, daher wurde aus „energetisch“ automatisch „energisch“.
#91 Für die Windmacher: Die Luft der Troposphäre über dem Äquator beobachtet erfreut, wie sich die Erde darunter unnötig beeilt.
#89: Ulrich Wolff ein Glück dass die Tropopause nicht noch die Flugzeuge einsperrt.
In den Lehrbüchern steht eher, dass hier viel weniger Luftwiderstand existiert, ob Sie´s glauben oder nicht AUCH für die Luft selbst.
Googeln Sie mal unter jetstream,
da werden Geschwindigkeiten bis über 600km angegeben.
Dagegen wurde erdnah auch nicht ganz unten die höchste Windgeschwindigkeit in der Schweiz mit 285 km/h auf dem Jungfraujoch in der Nacht vom 26. auf den 27. Februar 1990 während des Orkans Wiebke gemessen.
mfG
#87: P. Dietze sagt:
Sehr geehrter Herr Dietze,
Ihr Post ist direkt an Herrn Kramm gerichtet,
da er bislang nicht geantwortet hat ein paar Anmerkungen meinerseits.
„Daß Sie die physikalische Tatsache bestreiten, daß ein Schwarzkörper im Strahlungsgleichgewicht seine Temperatur erhöht wenn die Be- und Abstrahlung zunimmt (womit Sie S-B für falsch halten), ist doch absurd“
Der Boden ist nicht im „Strahlungsgleichgewicht“. Das ist er NIE!
Eine Temperaturänderung des Bodens ist eine Funktion der ZU- und ABgehenden ENERGIEflüsse.
Diese sind: LEITUNG/KONVEKTION, LATENZWÄRME und STRAHLUNG.
Beispiel Wasseroberfläche:
Die (tagsüber) hohe Sonneneinstrahlung wird nur zu einem sehr geringen Anteil in Erwärmung des Wassers umgesetzt, ein hoher Anteil der Energie geht in Verdunstung (Latenzwärme) und bedingt damit sogar einen Kühleffekt an der Oberfläche.
75% der Erdoberfläche ist mit Wasser bedeckt…
„Die quasi isotherme IR-Schwarzkörper-Modellkugel Erde hat also bei T=288K und S=391 W/m² eine Klimasensitivität von 0,184 K/(W/m²) – und mit einem realen Strahlungsantrieb von insgesamt ~3,3 W/m² am Boden“
Woher kennen Sie die 3,3W/qm???
„Sie behaupten ja auch (fälschlich nach Clausius), daß Wintermäntel, also Wärmedämmungen, sowie auch Gegenstrahlung beheizte Körper nicht wärmer machen, es also einen TE nicht gibt.“
Die Gegenstrahlung durch CO2 ist die thermische Eigenstrahlung von CO2 aus der c.a. 1m dicken atmosphärischen Bodenschicht.
Unmeßbar wenig!
Siehe auch die Arbeiten zur „Prantl“-Schicht,
in der die bodennahen Energieflüsse dargelegt werden.
Das Wort „Gegenstrahlung“ kommt dort nicht vor.
„daher sind auch für das 2-Grad-Ziel – ganz im Gegensatz zu Paris – definitiv 2820 ppm anstatt nur 445 zulässig!“
Da es keine Korrelation und keinen mathematischen Zusammenhang zwischen CO2 und Bodentemperatur gibt, sind sowohl 445 ppm als auch 2820 ppm falsch bzw. irrelevant.
MfG
PS.: Die Existenz der Tropopause mit Temperaturen, die sowohl nach oben, als auch nach unten ansteigen, lässt mich tatsächlich vermuten, dass Wasser und Eis die Atmosphäre kühlen, den Planeten wärmen und CO2 und Wasserdampf schlicht („energisch“) einsperren, oder gibt es etwa die Tropopause überhaupt nicht?
Es ist immer wieder lustig, dass derartige Artikel geschrieben werden und noch lustiger, dass vorgeblich intelligente Menschen darüber diskutieren.
Das Wetter ändert sich. Wir modellieren eine „Prediction of first kind“ und erhalten eine wahrscheinliche Veränderung für eine ganzen Woche!!!
Das Klima ändert sich. Wir wissen das, aber nicht wie. – Der Fachmann auf diesem Gebiet definiert stolz (als Abhilfe?) die erforderliche „Prediction of second kind“. – Das war’s denn, oder?
Selbst der „einfachste Physiker“ wird niemals abstreiten, dass CO2 und Wasserdampf an diskreten Wellenlängen Wärmestrahlung in alle Richtungen emittieren. (Man kann das sogar punktuell messen!) Er weiß auch, dass die Dichte dieser Gase mit der Höhe abnimmt.
Ihm ist ebenfalls gut bekannt, dass sich der Wasserdampf mit zunehmender Höhe zu Wasser und Eis wandelt, (in diesem Zustand) alle von unten eintreffenden Energieflüsse einsammelt und gleichzeitig „Tropfen für Tropfen und Partikel für Partikel“ als Wärmestrahlung in alle Richtungen emittiert.
Wenn es allerdings den von CO2 und Wasserdampf emittierten Energieflüssen
gelingen würde, dieser Falle zu entgehen, könnte sogar eine Änderung ihrer Menge die Energiebilanz der Materie an der Erdoberfläche verändern.
Amen!
@#83 gkramm
„Alles, was Sie behaupten, ist falsch. Ihre Formel, die Sie staendig wie warmes Bier anbieten, kann man nur als hanebuechenen Unsinn bewerten… Jemand, der mit hohen oder niedrigen Werten fuer die Kliamsensitivitaet argumentiert, streitet sich allenfalls um des Kaisers Bart. Mit Physik hat das nichts zu tun“
Daß Sie die physikalische Tatsache bestreiten, daß ein Schwarzkörper im Strahlungsgleichgewicht seine Temperatur erhöht wenn die Be- und Abstrahlung zunimmt (womit Sie S-B für falsch halten), ist doch absurd – denn dieser Zusammenhang ist ja genau die „Klimasensitivität“. Egal welche vermeintlich zu verwerfenden Energiebilanzmodelle Sie in der Literatur gefunden haben, die S-B-Formel S=Sigma*T^4 kann nach T differenziert werden und ergibt dann dS/dT=4*Sigma*T^3 und mit T^3=S/(Sigma*T) ergibt sich dT=dS/S/4*T. Dies gilt trotz T^4 recht genau für kleine Änderungen von S, wie sich durch Beispiele auch leicht nachweisen läßt.
Die quasi isotherme IR-Schwarzkörper-Modellkugel Erde hat also bei T=288K und S=391 W/m² eine Klimasensitivität von 0,184 K/(W/m²) – und mit einem realen Strahlungsantrieb von insgesamt ~3,3 W/m² am Boden ergibt sich für jede CO2-Verdoppelung ein deltaT von ~0,6 Grad. Genau diese beiden Werte sind doch im Grunde der wissenschaftliche Streitgegenstand beim ganzen Treibhausthema, und daher sind auch für das 2-Grad-Ziel – ganz im Gegensatz zu Paris – definitiv 2820 ppm anstatt nur 445 zulässig!
Daß Sie als Atmospärenphysiker behaupten, das habe mit Physik nichts zu tun, ist nicht zu fassen. Sie behaupten ja auch (fälschlich nach Clausius), daß Wintermäntel, also Wärmedämmungen, sowie auch Gegenstrahlung beheizte Körper nicht wärmer machen, es also einen TE nicht gibt. Und so kritisieren Sie – bar jeglicher Physik – erfahrungsgemäß niemals selbst den absurdesten physikalischen Unsinn – soweit Sie den Verfasser als TE-Leugner eingestuft haben. Dafür diffamieren Sie aber geradezu krankhaft jede physikalisch korrekte Aussage von Fachleuten, die einen TE für existent halten – sebst einen real sehr geringen. Damit konterkarieren Sie alle
Bemühungen, gegen den Unsinn Klimaschutz und Dekarbonisierung anzugehen.
@ #83 gkramm
Betr.: MODTRAN
Modtran ist: „The MODTRAN® [1][2] (MODerate resolution atmospheric TRANsmission) computer code is used worldwide by research scientists in government agencies, commercial organizations, and educational institutions for the prediction and analysis of optical measurements through the atmosphere.“
Man kann das, was die Leute mit MDTRAN veranstalten, um etwas zu beweisen auch Zirkelschluß oder Scheinkorrelation nennen. Sie wissen ja das mit den Störchen und den Babies.tT
@#77 Thomas Milz
Diesen Beitrag kann man nur als grotesk bezeichnen. Sie haben die vereinfachte Strahlungsmodellierung mit der quasi isothermen (rotierenden und speichernden) Schwarzkörperkugel sowie Stefan-Boltzmann offensichlich garnicht verstanden, glauben aber, daß die Modellierer total blöd sind.
„Das Märchen vom Treibhauseffekt: Der eintreffende solare Flux wird fälschlich durch einen Faktor 4 geteilt, wodurch die Sonnenenergie über den gesamten Planeten als durchschnittlich dämmriges Zwielicht verteilt wird. Im Endeffekt verwandelt die Klimawissenschaft unseren rotierenden Globus in eine flache, mit Eis bedeckte Scheibe, indem schlichtweg der wärmende und kühlende Prozess von Tag und Nacht verworfen wird .. Weil das GHE-Standardmodell die Erde so behandelt, als käme das Sonnenlicht überall auf der Erde auf einmal an, kann kein Teil des Planeten mehr als ein viertel des tatsächlichen Werts der eintreffenden solaren Energie empfangen. Die Klimawissenschaftler begehen dann einen weiteren schweren Fehler bei den Zahlen: sie setzen die Energieflussdichte der eintreffenden Leistung mit der ausgehenden Leistung gleich“
Gerade die Tatsache dass die solare Energieflussdichte (abzüglich 30% Albedo) durch den Geometriefaktor 4 dividiert wird, da die abstrahlende Kugelfläche viermal so groß ist wie die effektiv bestrahlte, beweist doch daß im Modell eine Kugel benutzt wird! Eine Schwarzkörper-Scheibe (senkrecht zur Sonnenstrahlung) würde – wenn sie hinten isoliert ist – ohne Albedo bei 1364 W/m² die „Orbit-Temperatur“ von 120 Grad annehmen. Ohne Isolation wäre der Geometriefaktor 2 und die Temperatur bei 782 W/m² dann 69 Grad.
Wie Sie sehen, ist die Division der Energieflussdichte völlig korrekt, und im Strahlungsgleichgewicht muss selbstverständlich die eintreffende Leistung mit der ausgehenden Leistung gleichgesetzt werden, da sich ja sonst der Körper dauernd erwärmen oder abkühlen würde. Auch dass die speichernde Erde so behandelt wird, als käme das verringerte Sonnenlicht überall auf der Erde auf einmal an, ist korrekt.
Stellen Sie sich eine Elektrospeicherheizung mit 8 kW vor, die stündlich jeweils nur 1/4 h eingeschaltet ist, aber die Wärme ziemlich gut speichert. Da sie dann im Mittel 2 kW abgibt kann man eine Dauerbeheizung mit 2 kW annehmen und entsprechend stellt sich auch die Raumtemperatur ein. Bei einem Mittelwert von 240 W/m² ergibt sich im Weltraum im Gleichgewicht nach S-B tatsächlich 255 K (-18 Grad), soweit 30% Albedo und keine Gegenstrahlung angenommen wird.
Oje @54 Ullrich sagt: „Ich habe Ihnen mal den Begriff Hypothese aus Wikipedia hier kopiert“
Leser Ullrich, als emsiger Klimahysteriker weiss immer noch nicht, dass Wikipedia bezüglich Wissenschaftstheorie und vieler anderer wissenschaftlicher Inhalte vollkommen unmassgeblich ist. Ziemlich oft werden Artikel dort von unmassgeblichen, schlecht ausgebildeten, manchmal sogar vollkommen fachfremden Personen verbrochen, die nur eines wirklich auszeichnet: absolut betonverbohrte und überfanatisierte Rechthaberei bezüglich ihrer grün-kommunistischen Glaubensinhalte. Diese Leute hängen den grosteskesten Verschwörungstheorien an, wie zum Beispiel, dass die Ölindustrie die Klimarealisten finanziert.
#79: P. Dietze sagt:
„Interessant dass MODTRAN am Boden für CO2-Verdoppelung einen Strahlungsantrieb von 3,8 W/m² berechnet, was bei 288 K nach der Formel deltaT=deltaS/S/4*T einen TE von 0,7 Grad ergibt – und auch ein Hinweis darauf ist dass der IPCC-clear-sky-Wert an TOA eher nur ~2,5 statt 3,7 W/m² betragen sollte. Hiermit wird auch klar, dass die umstrittenen 33 Grad bei den Berechnungen überhaupt keine Rolle spielen.“
Alles, was Sie behaupten, ist falsch. Ihre Formel, die Sie staendig wie warmes Bier anbieten, kann man nur als hanebuechenen Unsinn bewerten.
Was Sie nicht begreifen, ist die Tatsache, dass das Konzept der Klimasensitivitaet auf dem globalen Energiebilanzmodell von Schneider & Mass (1975) beruht. Das belegen auch die Arbeiten von Robert E. Dickinson (1985), „Climate sensitivity“, und Berger & Tricot (1986), „Die Modellierung des Spurengaseinflusses auf das Klima“. (Ich habe Ihnen schon vor Jahren diese beiden Arbeiten zukommen lassen.) Das Energiebilanzmodell von Schneider & Mass (1975) beruht ebenfalls auch einer globalen Temperatur. Es ist aus physikalischen und mathematischen Gruenden zu verwerfen. Ein falsches Modell liefert im allgemeinen nur falsche Ergebnisse.
Jemand, der mit hohen oder niedrigen Werten fuer die Kliamsensitivitaet argumentiert, streitet sich allenfalls um des Kaisers Bart. Mit Physik hat das nichts zu tun.
@ #80 Dr. Bayerl alias Paul
Was wollen Sie eigentlich? Der Mann hat sich als „Urgrüner“ (Das sind die, die Pädophilie und Päderastie erlauben wollten) geoutet, allerdings unfreiwillig.
Er kennt sich halt nicht mit den Methoden der empirischen Sozialforschung aus.
Sehr geehrter Herr Dr. Kramm
Damit Sie mich nicht, für an die Treibhausbefürworterwelt, verloren halten, habe ich mir den PDF Artikel „ Rettung vor den Klimarettern“ durchgelesen, wo der TE als ein Irrtum dargelegt wird.
Auch ihr geehrter Name ist unter den Wissenschaftlern zu finden ,bei denen sich der Autor für ihre Mitarbeit und fachlichen Beiträge bedankte
mit freundlcihen Grüßen
S.Bernd
#74: Herr Jan Dirk Ullrich, das inakzeptable an Ihrem Diskussionsstil ist Ihre Weigerung auf Gegenargumente überhaupt einzugehen, oder sich gar zu beschweren, dass überhaupt jemand wagt Gegenargumente zu äußern.
Nun wurden Sie schon 2mal mit dem Satz:
„Sums or averages over the individual temperatures in the field are not temperatures. Neither are they proxies for internal energy.“
konfrontiert, der eigentlich aus Ihrem eigenen Hinweis auf eine Arbeit aus 2006 stammt.
Dieser Satz zerschmettert lediglich die vorgetragene Basis für eine korrekte Berechnung der hypothetischen Strahlenflüsse der „Treibhaus-Künstler“ ebenso wie die Wunschvorstellung eines Strahlungsgleichgewichts auf der Erdoberfläche.
Aber bei diesem politischen Program überschlägt man sich ja geradezu mit Pseudophysik, wie z.B. Herr Dietze in grober Unhöflichkeit von Ignoranz an hier schon abgeschlossenen Themen wie seiner „Hin-und-her-Strahlung“ ohne Strahlungsquelle immer wieder aufs neue unter Beweis stellt.
So soll Erkenntnisfortschritt des Mitlesers brutal blockiert und torpediert werden.
mfG
@#4 G. Wedekind
Interessant dass MODTRAN am Boden für CO2-Verdoppelung einen Strahlungsantrieb von 3,8 W/m² berechnet, was bei 288 K nach der Formel deltaT=deltaS/S/4*T einen TE von 0,7 Grad ergibt – und auch ein Hinweis darauf ist dass der IPCC-clear-sky-Wert an TOA eher nur ~2,5 statt 3,7 W/m² betragen sollte. Hiermit wird auch klar, dass die umstrittenen 33 Grad bei den Berechnungen überhaupt keine Rolle spielen.
Im Strahlungsmodell wurde von MODTRAN die US-Standardatmosphäre zugrunde gelegt, und da spektroskopisch gerechnet wird, ist davon auszugehen dass hierbei Folgendes nicht berücksichtigt wird
– CO2 ist unter Wolken (IR-Schwarzstrahler) wirkungslos
– am Boden wird durch Hin- und Herstrahlung der Strahlungsantrieb um den Faktor 390/240=1,6 erhöht
– ein (gegenüber IPCC reduziertes) Wasserdampf-Feedback fehlt. Wasserdampf-Überlappung ist jedoch enthalten
– der Transport-Bypass – i.w. durch erhöhte tropische Feuchtkonvektion – fehlt
Plausible Abschätzungen dieser Korrekturen ergeben am Boden einen Strahlungsantrieb von ca. 3,3 W/m², womit die Verdoppelungssensitivität etwa 0,6 Grad wird (1/5 von IPCC). Dieser Wert deckt sich mit den Berechnungen von Prof. Harde.
#70: S.Bernd:
Lernen Sie endlich, dass voellig falsche Vergleiche und voellig falsche Konzepte nichts Vernuenftiges liefern. Mit solchem Unfug werden die Wissenschaften und das Ingenieurwesen bis auf die Fundamente zerstoert.
Das Märchen vom Treibhauseffekt
Der eintreffende solare Flux wird fälschlich durch einen Faktor 4 geteilt, wodurch die Sonnenenergie über den gesamten Planeten als durchschnittlich dämmriges Zwielicht verteilt wird. Im Endeffekt verwandelt die Klimawissenschaft unseren rotierenden Globus in eine flache, mit Eis bedeckte Scheibe, indem schlichtweg der wärmende und kühlende Prozess von Tag und Nacht verworfen wird.
Mit anderen Worten modellieren die Klimatologen die Erde als einen Planeten bestehend aus einer desolaten flachen Scheibe, auf dem der Sonnenschein immerwährend eiskalt ist und flüssiges Wasser und Wasserdampf unmöglich sind. Anschließend korrigieren die Modellierer ihren Fehler durch Einflicken eines “33 Grad Dingsda”, das sie den Treibhauseffekt nennen.
Weil das GHE-Standardmodell die Erde so behandelt, als käme das Sonnenlicht überall auf der Erde auf einmal an, kann kein Teil des Planeten mehr als ein viertel des tatsächlichen Werts der eintreffenden solaren Energie empfangen.
Die Klimawissenschaftler begehen dann einen weiteren schweren Fehler bei den Zahlen: sie setzen die Energieflussdichte der eintreffenden Leistung mit der der ausgehenden Leistung gleich (was keine Erfordernis des Gesetzes über den Erhalt der Energie (LCE) ist).
Wir sehen also wie jeder sogenannte Treibhausexperte irgendwie bei einem durchschnittlichen Modelleintrag von 240 J/s/m2 solarer Leistung ankommt. Dies liefert eine äquivalente Temperatur von ungefähr –18 Grad Celsius (255K oder -0.4F).
Doch ein Heilmittel ist zur Hand. Wenn wir die Erde als eine Kugel behandeln (so dass Nacht und Tag existieren), können wir plötzlich alles mit Standard-Physik erklären. Es zeigt sich nämlich, dass uns der Tag die +33 Grad C fehlende Temperatur gibt, weil er im Durchschnitt nur die Hälfte der Erde abdeckt (das ist der doppelte Effekt der Zahlen der GHE-Modellierer).
Um es zusammenzufassen sind die sich selbst widersprechenden und eigentümlichen zweidimensionalen Modelle orthodoxer Klimawissenschaft widerlegt. Sie zeigen, dass die Modelle entlarvt sind, weil die Erde fälschlich als ein flacher, kalter, von Zwielicht beschienener Planet modelliert wurde. Aber von dem Moment an, in dem die Erde korrekt als eine dreidimensionale Kugel modelliert wird, trifft die gesamte ankommende Sonnenenergie nur eine Hemisphäre auf einmal, was wiederum dazu führt, dass die Klimazahlen ohne Erfindung irgendeines unphysikalischen Treibhaus-Effekts ansteigen.
#71: gkramm sagte am Freitag, 16.09.2016, 17:22:
„#64: Marvin Müller:
Sie muessen schon den Beitrag von Connolley lesen, um zu verstehen, was Halpern meinte.“
Habe ich jetzt Ihnen zuliebe nochmal gelesen (hatte ihn gestern vor meiner Antwort schon gelesen). Aber das hat nichts an meiner Sicht geändert, dass er sich über einige Diskussionteilnehmer amüsiert (siehe z.B. das vorangegangene „Oh goody, new pinatas. The Weasel has all the luck.“ um auch mal einfach so ohne Kontext was zu zitieren). Wenn sich da was ändern sollte, müßten Sie schon etwas konkreter werden.
@ #73
Daß die gesetzliche Sperrzone zu Recht geschaffen wurde ist wissenschaftlich erwiesen. Diese Leute sind eine Gefahr für die Gesundheit anderer.
Für mich allerdings nicht. Mit HIV kann unsreins nicht infiziert werden.
Mit Homophobie hat das alles nichts zu tun, denn der Begriff wurde von den Gefährdern selbst geschaffen, um Diskriminierung behaupten zu können. Was diese Leute aber nicht davon abhält andere zu gängeln, diskriminieren und zu gefährden.
@J. Ehlig – #66
Komisch, wenn Sie erwähnen das die Temperatur etwas mit der inneren Energie zu tun hat bleibt das Forum hier ruhig. Erwähnen das andere könnte man fast glauben einen Mord begangen zu haben. Aber so ist das wohl, es kommt nicht darauf an was jemand sagt, sondern wer etwas sagt.
@T.Heinzow – #58
Nein nicht wirklich. Nach Ihrem homophoben geschreibsel #26, der sogar zensiert werden musste, traue ich Ihnen nichts mehr zu.
Hallo Herr Keks, Sie haben völlig Recht. Herr Dietze sollte sich einmal die 3 Teile des Artikels Chaos und Klima von hansen zu Gemüte führen. Vielleicht hilft das ja.
MfG
#64: Marvin Müller:
Sie muessen schon den Beitrag von Connolley lesen, um zu verstehen, was Halpern meinte.
Sehr geehrter Herr Dr. Kramm #62
Ist meine Meinung, daß ein irdisches Treibhaus, aka Gewächshaus, eine gute Sache ist, absurd oder der Vergleich zwischen dem sogenannten atmosphärischen Treibhaus und dem irdischen? Wohl letzteres.
Ich denke, entscheidend ist, wie mit dem „Fiktum“ umgegangen wird, welche Ideologie es für seine Zwecke nutzt.Sind die Schlüsse, die eine „CO2 ist Böse“- Fraktion daraus zieht, real? Zumal ja die über 900 fach gewichtigere Rolle des Wasserdampfs außer acht gelassen wird. Wenn unbestreitbar nachgewiesen würde, daß kein atmosphärisches Treibhaus existiert, würde es dennoch weiter als Phantom in den Köpfen herumspuken. Wer weiß, vielleicht ist es sogar akut der Fall.
Ich denke es gibt Wichtigeres als den „Klimawandel“ zu bekämpfen. Mit einem Bruchteil der Gelder die dafür bereitgestellt werden, könnte der Hunger in der Welt vermindert werden (Nicht die Hungernden, aber das ist die eigentliche Absicht, siehe: Bevölkerungsschrumpfung)
mit freundlichen Grüßen
S. Bernd
#67: P. Dietze sagt:
„Das gilt für das vereinfachte quasi isotherme Strahlungsmodell wobei 38,5% der thermischen Bodenabstrahlung gegengestrahlt werden, was im Gleichgewicht – ohne Verletzung des 2.HS – durch „Strahlungsdämmung“ zu einer Temperaturanhebung am Boden von -18 auf +15 Grad führt.“
Gaga-Physik a la Dietze.
Schließen Sie sich Ketterer an, dann sind Sie schon zu dritt…
#65: J. Ehlig sagt:
am Freitag, 16.09.2016, 01:34
@ #44: F.Ketterer:
CO2 ist genau so wenig ein Festkörper wie O2 oder N2…
#################
Fast überall 😉
Weißköerstrhaung war für mich eher eine Sache der Reflektion. Aber danke man lernt nie aus.
Feste „Weißkörper“ gibt es also nicht (Im IR) nur solche die leicht grau sind.
EIKE sollte sich schämen, solch blamablen Unsinn zu den 33 Grad TE am Boden zu veröffentlichen. Die Albedo von 0,3 gilt i.w. für kurzwelliges Sonnenlicht welches von Wolken reflektiert wird – ohne Temperatureffekt. Diese Albedo dann als Eps=0,7 für IR-Emission am Boden mit Stefan-Boltzmann zu verwenden und damit quasi die solare Albedo hinweg zu kompensieren um damit statt -18 dann +5 Grad zu berechnen ist doch grotesk! Und niemand scheint es zu bemerken…
Der TE entsteht durch die IR-Absorption und thermische Re-Emission der Atmosphäre in Richtung Erdboden. Bezogen auf das Verhältnis 390 W/m² am Boden (bei 288 K und Eps ~1 gemäß S-B und Messung) und 240 W/m² oben beträgt das global-mittlere Eps für IR damit 0,615. Das gilt für das vereinfachte quasi isotherme Strahlungsmodell wobei 38,5% der thermischen Bodenabstrahlung gegengestrahlt werden, was im Gleichgewicht – ohne Verletzung des 2.HS – durch „Strahlungsdämmung“ zu einer Temperaturanhebung am Boden von -18 auf +15 Grad führt.
Man hat der Eindruck daß hier vom Autor sowie vielen Kommentatoren die physikalischen Grundlagen der Basis-TE-Modellierung immer noch nicht verstanden sind und bei EIKE offenbar jeder seine Irrtümer und Mißverständnisse ungeprüft veröffentlichen darf und Verwirrung stiften kann. Der ewige Laien-Streit um die fiktiven 33 Grad, die ja nach S-B für eine quasi isotherme (gut speichernde, gut Wärme umverteilende und genügend schnell rotierende) Schwarzkörper-Erde mit 30% Albedo im Vergleich zwischen den Fällen ohne und mit Gegenstrahlung entstehen (*nicht* ohne und mit Atmosphäre!), ist völlig irrelevant. Die 33 Grad dienen nur dazu, Laien den TE zu erklären, werden aber von der Fachwelt garnicht benutzt um den TE (strahlungsphysikalisch) beim CO2-Anstieg zu quantifizieren.
Auch der Vergleich mit Temperaturwerten an der Oberfläche des um den Faktor 28 langsamer rotierenden atmosphärelosen Mondes (Kramm #41 und #42) der uns weismachen soll daß die Anwendung von S-B auf Mittelwerte auch am Erdboden völliger Unsinn sind, ist grotesk. Wegen des T^4-Gesetzes treten natürlich bei extrem großen Strahlungs- und Temperaturschwankungen große Fehler auf. Der T-Mittelwert wird dann deutlich zu niedrig (Höldersche Ungleichung). Schwanken jedoch die absoluten Temperaturen für den größten Teil der Erdoberfläche nur um etwa +/- 5%, so können mit Strahlungsmittelwerten durchaus Temperaturmittelwerte mit einer Genauigkeit von ~2 Promille berechnet werden, was sich einfach nachweisen läßt. Und es geht ja auch nicht um absolute Mittelwerte, sondern nur um TE-bedingte geringfügige Änderungen hiervon…
Hallo Herr Ulrich,
versuchen Sie doch einmal, den Sinn dieses Satzes zu verstehen, ohne danach zu fragen, wer ihn geschrieben hat:
„Sums or averages over the individual temperatures in the field are not temperatures. Neither are they proxies for internal energy.“
Und wenn Sie mit dem Inhalt klar gekommen sind, dann denken Sie mal über die Konsequenzen nach.
@ #44: F.Ketterer:
CO2 ist genau so wenig ein Festkörper wie O2 oder N2…
#53: Jan Dirk Ullrich sagte am Donnerstag, 15.09.2016, 14:05
„@gkramm – #49
Worauf wollen Sie hinaus? Auf den Punkt mit „FWIW microwave radiation is strongly absorbed by molecules with dipole moments….“ oder „Eli thinks he will apologize to Gerlich, Tscheuner and Kramm…“, nicht wirklich, oder?“
Herr Kramm denkt anscheinend. Eli wollte sich für seine Kritik entschuldigen. Liest man den ganzen Thread, kann man auch zu einer anderen Sicht kommen. Da traben zwei anscheinend völlig unbedarfte in den Thread und stellen sich nach Meinung der an der Diskussion Teilnehmenden völlig dumm an. Im Angesicht dieser Teilnehmer sagt Eli, er denke darüber nach, sich dafür zu entschuldigen, die drei genannten für „the greatest possible box of rocks“ gehalten zu haben. Es ging anscheinend noch schlimmer … Wie man daraus einen Rückzieher konstruieren kann … Und wer das auch noch glaubt …
#55: Jan Dirk Ullrich sagt:
„Die glauben mal im vorbeilaufen einer anderen Berufsgruppe zu erklären was sie alles falsch machen.“
Herr Ulrich,
Klima ist Statistik.
Aus diesem Grund heißt das Studienfach ja auch Meteorologie.
Statistische Kenntnisse haben viele, insbesondere auch Wirtschaftswissenschaftler.
Beide, „Klimawissenschaft“ und Wirtschaftswissenschaft sind empirische Wissenschaften:
man wertet Vergangenheitsdaten aus und versucht daraus zu lernen.
Insofern habe ich kein Problem damit, wenn
Personen mit Kenntnissen in Statistik an der „Klimadiskussion“ beteiligen.
Genauso wie ein Ingenieur wie ich an der Diskussion beteiligen kann, wenn es um grundlegende physikalische Effekte handelt.
„Ich nenne ihnen einen „Klimawissenschaftler“ der an den Müll glaubt, nein besser. Der von der Richtigkeit der Ergebnissen seiner Arbeit überzeugt ist. Stefan Rahmsdorf.“
Das glauben Sie doch hoffentlich selbst nicht.
Herr Rahmsdorf vertritt die Interessen der Versicherungsbranche, die sich mit der Klimalüge eine goldene Nase verdienen will.
#56: S.Bernd sagt:
„Unabhängig davon, ob es so was wie ein atmosphärisches Treibhaus überhaupt gibt oder nicht, ist so ein Gewächshaus, Vorbild des atm. Treibhauses, eine gute Sache.“
Was Sie behaupten, ist absurd. Gerade die Wirkung eines realen Treibhauses hat mit dem fiktiven atmosphaerischen Treibhauseffekt ueberhaupt nichts zu tun. Die Unterdrueckung der Vermischung der im Treibhaus erwaermten Luft mit der das Treibhaus umgebenden Luft spielt beim sog. atmosphaerischen Treibhauseffekt ueberhaupt keine Rolle, denn solche Vermischungsprozesse werden ueberhaupt nicht beachtet. Es wird ja noch nicht einmal beachtet, das etwa ein Drittel der vom System Erde-Atmosphaere absorbierten solaren Strahlung auf die Atmosphaere entfallen.
#57: Lutz Herrmann:
Rahmstorf ist fachfremd und hat von der Physik der Atmosphaere keine Ahnung. Seine Vorstellungen zum Strahlungstransport sind absurd. Und einfaeltige Besserwisserei ist keine akademische Disziplin.
#53: Jan Dirk Ullrich:
Offensichtlich begreifen Sie gar nichts. Sie begreifen ja noch nicht einmal, dass Halpern aka Eli Rabett, auf den Sie sich berufen wollten, mittlerweile einen Rueckzieher gemacht hat. Von daher ist es muessig zu versuchen, Ihnen weitere Begruendungen zu liefern, warum das gesamte Konzept der effektiven Strahlungstemperatur einer Erde ohne Atmosphaere vollkommen sinnlos ist. Die detaillierte Begruendung ist im uebrigen bei Kramm & Dlugi (2011), „The atmospheric greenhouse effect and its climatic impact“ zu finden.
Es existiert kein empirischer Befund, dass das Konzept der effektiven Strahlungstemperatur fuer eine Erde ohne Atmosphaere richtig ist. Die Annahmen, auf denen dieses Konzept beruht, sind bei weitem nicht erfuellt. Hinzu kommt, dass dieses Konzept, wenn es auf unseren Mond angewendet wird, sowohl empirisch als auch theoretisch-numerisch widerlegt wird. Damit ist es zu verwerfen, egal was Rahmstorf, Schmidt und sonstige Kardinaele der Church of Global Warming verbreiten.
Auf Richard Feynman geht folgendes Zitat zurueck:
„In general we look for a new law by the following process. First we guess it. Then we compute the consequences of the guess to see what would be implied if this law that we guessed is right. Then we compare the result of the computation to nature, with experiment or experience, compare it directly with observation, to see if it works. If it disagrees with experiment it is wrong. In that simple statement is the key to science. It does not make any difference how beautiful your guess is. It does not make any difference how smart you are, who made the guess, or what his name is – if it disagrees with experiment it is wrong. That is all there is to it.“
Es ist an der Zeit, diese simple Wahrheit zu begreifen.
„McKitrick ist Wirtschaftswissenschaftler und kann mal eben allen Klimawissenschaftlern sagen was sie falsch machen“
Klimawissenschaftler haben oft über Einstein und Quanten promoviert, sind dann aber in die Statistik abgebogen, ohne jedoch mit der Community viel zu tun zu haben. Da ist McKitrick auch nicht weiter entfernt.
@ #54 Wikipedia-Gläubiger
Nehmen Sie ernsthaft an, daß ich Ihren geposteten Quatsch durchlese? Wikipedia ist wissenschaftlich nicht zitierfähig.
„Was macht ein Stefan Rahmsdorf falsch was ein Isaac Newton, auf dessen Axiomen die Mechanik beruht, oder ein Charles Darwin richtig gemacht haben?“
Eine wirklich gute Frage. Ein Newton hat bestimmt für die Erdbeschleunigung keine zwei Werte gelten lassen, sondern das Dingelchen erstmal bestimmt. Rahmsdorf verlässt sich auf das IPCC wenn’s um die Emissivität vom CO2 geht, obwohl die da draussen experimentell schon oft sehr viel niedriger bestimmt wurde. Okay, damit isser immer noch besser dran als Dr. Paul, der sie strikt auf 0 setzt, weil er Absorptionsbanden nicht versteht.
Was macht ein Schellnhuber falsch was ein Isaac Newton, auf dessen Axiomen die Mechanik beruht, oder ein Charles Darwin richtig gemacht haben?
Dessen Methode ist ganz einfach. Er behauptet, einen funktionalen Zusammenhang gefunden zu haben. Kein Gesetz. Nur ein Zusammenhang. Dessen Konstanten werden aus Daten schnell bestimmt und dann fortgeschrieben. Fertig. Das mache ich auch beruflich. Kundenvorlieben aus Daten mit Neuronetzen oder Gevatter Bayes. Nur verkaufe ich es nicht als Gesetz. Und niemand würde mir glauben, dass das für die nächste Eiszeit auch greift.
Unabhängig davon, ob es so was wie ein atmosphärisches Treibhaus überhaupt gibt oder nicht, ist so ein Gewächshaus, Vorbild des atm. Treibhauses, eine gute Sache. Nun werden dessen positive Eigenschaften ins Gegenteil verkehrt.Da wird der Schutzengel zum Belzebul.Aus Gut wird Böse aus Weiß wird Schwarz! Verwerflich an der Sache ist die Umkehrung einer natürlichen Einrichtung, die dem Schutz dient, ins negative, um Ängste zu schüren und überflüssige Maßnahmen zu rechtfertigen.
Es gibt nichts Neues unter der Sonne und dazu zählt auch der Klimawandel.Viele Male wiederholte er sich, ohne markante negative Auswirkungen; und ist nun scheinbar in eine Phase eingetreten, wo er für den Fortbestand, vieler Menschen , Tier und Pflanzen gefährlich werde. Der Deutsche darauf ausgerichtet möglichst viele Versicherungen zu haben, wegen der Möglichkeit, „es könne ja mal so ein Fall eintreten“ glaubt an die Notwendigkeit der von der Politik bechlossenen Maßnahmen und verschafft sich so ein ruhiges Gewissen.
An Hand des kohledioxidspeichernden Minerals Goethit konnte ein Konzentration von bis zu 6000 ppm CO2 in der Vergangenheit festgestellt werden.Klimarekonstruktionen ergaben aber, daß sich die Temperaturen nicht von den heutigen unterschieden .Einzig den seinerzeitigen größeren Pflanzen war der höhere Anteil an der Luftzusammensetzung geschuldet.Ob die Pflanzen nun mehr Wärme(Sonne) oder CO2 benötigen, müßte sich experimentell feststellen lassen. Ich tippe auf CO2 als notwendiger, als Wärme oder Sonnenlicht.
@besso keks – #51
Herr keks!
Sie kommen doch aus dem Hochbildungsland Bayern, wie bitte schön passt Ihre Antwort:
„Ich glaube nicht, daß es einen ernsthaften „Klimawissenschaftler“ gibt (so es diese Form von „Wissenschaft“ überhaupt gibt, der den Treibhausmüll glaubt. Insofern macht dieser Kreis nichts „falsch“, sondern es wird schlicht und einfach nur GELOGEN.“
zu meiner Feststellung, dass kritiklos Kommentare und Äußerungen von fachfremden Personen hingenommen werden. Die glauben mal im vorbeilaufen einer anderen Berufsgruppe zu erklären was sie alles falsch machen. Wo ist da der Zusammenhang.
Ich nenne ihnen einen „Klimawissenschaftler“ der an den Müll glaubt, nein besser. Der von der Richtigkeit der Ergebnissen seiner Arbeit überzeugt ist. Stefan Rahmsdorf.
Was macht ein Stefan Rahmsdorf falsch was ein Isaac Newton, auf dessen Axiomen die Mechanik beruht, oder ein Charles Darwin richtig gemacht haben?
@T.Heinzow – #52
Zitat: „Sie liefern keine Beweise für ihre Hypothesen.“
Ich habe Ihnen mal den Begriff Hypothese aus Wikipedia hier kopiert:
Hypothese:
Eine Hypothese ist eine in Form einer logischen Aussage formulierte Annahme, deren Gültigkeit man zwar für möglich hält, die aber bisher nicht bewiesen bzw. verifiziert ist. Die Hypothese muss anhand ihrer Folgerungen überprüfbar sein, wobei sie je nach Ergebnis entweder bewiesen bzw. verifiziert oder widerlegt werden würde. Bei der Formulierung einer Hypothese ist es üblich, die Bedingungen anzugeben, unter denen sie gültig sein soll.
1.) Wo habe ich in #50 eine Hypothese aufgestellt? Bitte zeigen Sie mir das!
2.) Wenn ich Beweise mitgeliefert hätte, wäre es keine Hypothese mehr, siehe oben in der Definition
Ich habe nur festgestellt das es hier in diesem Forum eine sehr ambivalente Umgangsweise mit Personen gibt, die sich zum Thema Klima äußern, obwohl das von Ihrer Ausbildung her nicht ihr Fachgebiet ist, sonst hätten Sie ja Klimawissenschaften oder ähnliches studiert, oder dass diese Personen in der Vergangenheit durch Veröffentlichungen zum Thema aufgefallen sind, die in der Fachwelt ernsthaft diskutiert wurden. Als Beleg für meine Feststellung habe ich auf den Artikel mit dem BDI verwiesen.
Ein Wirtschaftswissenschaftler hat für mich erst einmal keine Kompetenz in Sachen Naturwissenschaften, von der Ausbildung her. Sollte er sich dennoch genötigt fühlen zu naturwissenschaftlichen Themen ein Paper zu veröffentlichen, ok. Dann müsste ich dieses Paper erst lesen und mir dann ein Urteil bilden. Das gilt natürlich auch in die andere Richtung.
Zitat: „Die Propagandisten (sog. Klimawissenschaftler – obwohl „Klima“ ein lokales statistisches Konstrukt ist) verstoßen gegen das wesentlichste Prinzip jedweder Wissenschaft:“
Das ist eine Behauptung von Ihnen, das Klimawissenschaftler so etwas tun. Können Sie das Beweisen, Sie haben mich ja auch aufgefordert Beweise zu liefern, unsinniger Weise für eine Hypothese. Dann müssten Sie Beweise liefern für Ihre Behauptung. Können Sie das?
@gkramm – #48
Das ist leider keine Antwort. Ich hatte ja wirklich gedacht Sie könnten etwas inhaltliches beisteuern. Zumal Sie ja in Ihrem Disput mit Ferdinand Peters so sehr auf Ihre wissenschaftlichen Erfolge hingewiesen haben.
Zu #49
Worauf wollen Sie hinaus? Auf den Punkt mit „FWIW microwave radiation is strongly absorbed by molecules with dipole moments….“ oder „Eli thinks he will apologize to Gerlich, Tscheuner and Kramm…“, nicht wirklich, oder?
Ein Mann mit Ihrer Bildung sollte doch in der Lage sein mit einfachen klaren Sätzen zu sagen was er sagen will. Ohne Nebelkerzen und Andeutungen in Worthülsen und Füllsätzen versteckt.
@ #50
Klar kann man das als Wiertschaftswissenschaftler. Die Propagandisten (sog. Klimawissenschaftler – obwohl „Klima“ ein lokales statistisches Konstrukt ist) verstoßen gegen das wesentlichste Prinzip jedweder Wissenschaft:
Sie liefern keine Beweise für ihre Hypothesen.
#50: Jan Dirk Ullrich sagt:
„McKitrick ist Wirtschaftswissenschaftler und kann mal eben allen Klimawissenschaftlern sagen was sie falsch machen, ohne Kritik?“
Ich glaube nicht, daß es einen ernsthaften „Klimawissenschaftler“ gibt (so es diese Form von „Wissenschaft“ überhaupt gibt,
der den Treibhausmüll glaubt.
Insofern macht dieser Kreis nichts „falsch“, sondern es wird schlicht und einfach nur GELOGEN.
@Dr.Paul – #46
Und wunderbar erklärt welche Fehler gemacht wurden sieht man hier: http://tinyurl.com/jhnweq8
Aber ist schon witzig, im Beitrag „Bundesverband der Industrie (BDI) ist komplett zu den Klimaalarmisten übergelaufen: Nach der Devise – If you cant beat them join them“ heißt es „Keiner der Autoren verfügt über naturwissenschaftliche Kompetenz – aber alle über eigensüchtige Motive“. Hier wird kritisiert das fachfremde Personen sich äußern, McKitrick ist Wirtschaftswissenschaftler und kann mal eben allen Klimawissenschaftlern sagen was sie falsch machen, ohne Kritik?
#45: Jan Dirk Ullrich:
Lesen Sie bitte, was Joshua Halpern aka Eli Rabett in 2014 schrieb (siehe goo.gl/FrGHKs)
Eli Rabett
http://rabett.blogspot.com
2014/02/19
FWIW microwave radiation is strongly absorbed by molecules with dipole moments (basically an asymmetric distribution of charge). Water has a humongous dipole moment and absorbs strongly. Most plastics have very small dipole moments and absorb hardly at all.
Eli thinks he will apologize to Gerlich, Tscheuner and Kramm for thinking that they were thegreatest possible box of rocks. Maybe not.
Manche Leute sind halt noch lernfaehig.
#45: Jan Dirk Ullrich:
Ich beschaeftige mich nicht mit barem Unsinn.