Update 25.9.12
Aufgrund der überaus aktiven Diskussion hat Dr. Hug seinen Artikel nochmals überarbeitet, evt. schlecht verständliches verständlicher dargestellt und evtl. fehlendes ergänzt. Sie finden den vollständigen aktualisierten Beitrag als pdf im Anhang
Zusammenfassung: Ganz offensichtlich wird die Wirkung des anthropogenen Treibhauseffekts weit überschätzt, denn insbesondere der CO2-Treibhauseffekt war bis auf unbedeutende, spektroskopisch begründbare Restbeträge („Peakflanken“) bereits zu Zeiten Goethes ausgereizt. Wegen des weitgehenden „Sättigungseffekts“ ist der anthropogene Anteil der Treibhausgase für die gegenwärtige Klimaänderung von untergeordneter Bedeutung. Vielmehr geht die Varianz der Erdoberflächentemperatur mit der Wolkenbedeckung einher, die wiederum von der Fluktuation des solaren Magnetfelds abhängt. Dabei hat eine größere Wolkenbedeckung des Globus in etwa die gleiche Auswirkung wie Vulkanasche nach einem Ausbruch. Der Einfluss der Wolkenbedeckung lässt sich mit den Klimamodellen des IPCC nur äußerst unzulänglich abbilden. Klimamodelle sind auch deshalb ein spektroskopisches Artefakt, weil sie mit gewillkürten Flusskorrekturen arbeiten müssen, deren Beträge den des anthropogenen Treibhauseffekts um ein Vielfaches übersteigen.
1. Was ist unter dem Begriff „Sättigung“ des Treibhauseffekts zu verstehen?
Klimaforschung ist eine in Politik gegossene Naturwissenschaft. Da beide Handlungsfelder nicht von einander zu trennen sind, gab es im Vorfeld von Rio92 in den unter Einfluss der Politik agierenden Medien ein flächendeckendes Meinungsbombardement über die kommende Klimakatastrophe.
Unter dem Eindruck der Medienhype versuchte man als Naturwissenschaftler in den neunziger Jahren etwas über die spektroskopischen Grundlagen des propagierten Klima-Harmagedons in den allgemein gelesenen Periodika zu erfahren – und biss auf Granit. Weder in „Nature“ noch in „Science“ oder in „Scientific American“ (deutsch „Spektrum der Wissenschaft“) erschien ein informativer Artikel über den grundlegenden spektroskopischen Mechanismus des „Treibhauseffekts“ und dessen Grenzen (Emissionsspektren des Erdkörpers, Strahlungstransport, Anwendung des Planckschen-Strahlungsgesetzes auf die Besetzung von Schwingungsrotationsbanden bei CO2, Integration über dem Halbraum zur Berechnung des „Treibhauseffekts“ einer Stoffmengenportion von CO2, Festlegung und Definition der als normal geltenden Mitteltemperatur (288 K) im Rahmen einer Konferenz usw.). Auch Roger Revelle, der den späteren US-Vizepräsident Al Gore am College mit der Treibhausgastheorie bekannt machte, publizierte hierzu keine brauchbare Information [2]. Es war fast so, als hätte man Angst, die Karten aufzudecken.
Da man von den allgemein gelesenen Wissenschaftsjournalen im Stich gelassen wurde und die Propagandawalze in dem Medien unaufhörlich trommelte, möchte man als Chemiker erfahren, ab welchen CO2-Gehalt der Treibhauseffekt aus spektroskopischen Gründen unter realistischen Annahmen ausgereizt ist. Dies insbesondere, wenn man beruflich mit der Quantifizierung von Analyten mittels spektroskopischer Methoden befasst ist und weiß, dass es immer einen Konzentrationsbereich gibt, ab dem die Messstrahlung nahezu komplett absorbiert wird. Es verhält sich ähnlich wie beim Eintropfen von schwarzer Tinte in ein Wasserglas. Je mehr man zufügt, desto mehr des einfallenden Lichts wird absorbiert bis die Absorption schließlich vollständig ist (Transmission t = 0).
Ganz irreführend war ein Aufsatz von 1984 in der Mitgliederzeitschrift der Gesellschaft deutscher Chemiker, den so genannten „Blauen Blättern“ [5]. In dieser Veröffentlichung, auf die ich weiter unten zurückkomme, wird die „Rolle der treibhauswirksamen Spurengase“ mit Hilfe von Transmissionsspektren erläutert. Ein deutlicher Hinweis, dass es beim Treibeffekt um die atmosphärische spektrale Strahldichte (vereinfacht Emission) durch atmosphärische Spurengase geht, wird nur unterschwellig beschrieben. Angeregt durch die Literaturstelle [5], unternahm ich Messungen zur Transmission (bzw. Absorption oder Extinktion) in einer Gasküvette, um festzustellen, inwieweit der Treibhauseffekt des CO2 „ausgereizt“ ist.
Wird durch Treibhausgase beispielsweise 35 % der vom Erdboden ausgehend Strahlung bei einer bestimmten Wellenlänge in einer bestimmten Höhe absorbiert, dann ist die Absorption (früher A) a = 0,35 (bzw. a = 35 %) Die Transmission (früher T) beträgt t = 0,65 bzw. t = 65 %.
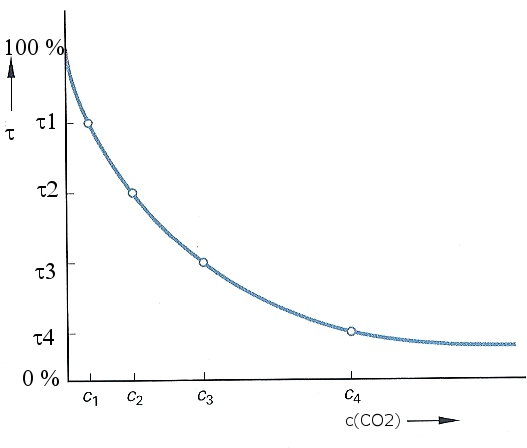
Da die Absorption von IR-Strahlung („Wärmestrahlung“) quantitativ dem Bouguer-Lambert-Beer-Gesetz (eine e-Funktion) folgt, sollte es eine „fließende Grenze“ geben, ab der bei zunehmender Konzentration des Absorbers keine wesentliche Steigerung der Absorption a erfolgt bzw. die Transmission t gegen Null geht (Bild 1).
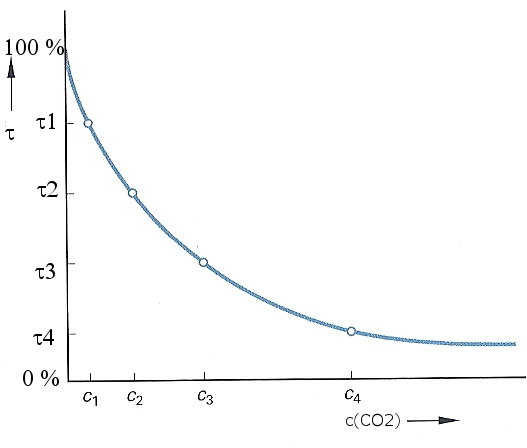
Bild 1: Transmission und Konzentration
Die Betrachtung der Transmission t zur Abschätzung des anthropogenen Treibhauseffekts ist nicht vollkommen falsch, weil nämlich die „Emissionsfähigkeit“ der Treibhausgasmoleküle mit der Absorptionsfähigkeit gemäß dem Kirchhoffschen Strahlungsgesetz korreliert. Deshalb sollte es einen („fließenden“) Konzentrationsbereich geben, ab dem der atmosphärische Treibhauseffekt CO2 nicht mehr nennenswert ansteigt. Ich bezeichne dies als „Sättigung“, die es, wenn man in immer kleineren Kleinigkeiten kramt, tatsächlich nicht gibt. Nicht ganz korrekt aber anschaulich verhält es sich mit der „Sättigung“ ähnlich wie mit dem Grenzwert einer geometrischen Reihe. Beispiel:
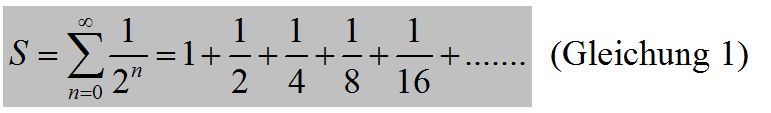
Für eine solche geometrische Reihe gilt:
![]()
Dabei ist a1 das Anfangsglied und q der Quotient zweier aufeinander folgender Glieder (q¹1). In der obigen geometrischen Reihe ist a1 = 1 und q = 0,5 (z. B. ¼ : ½ = 0,5). Setzt man jetzt beispielsweise n = 11 resultiert
![]()
und für n = 12 erhält man:
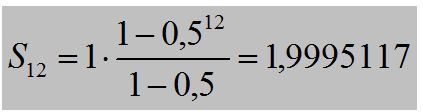
Der Zuwachs zwischen S11 auf S12 beträgt: DS = 1,9995117 – 1,9990234 = 2,777 . 10-4 entsprechend 0,014 %. Bezeichnet man den Grenzwert dieser arithmetischen Reihe als „vollständige Sättigung“ (S¥ = 2), dann ist der Betrag von S12 nur noch um
![]()
von dieser vollständigen „Sättigung“ entfernt.
Natürlich beruht der Treibhauseffekt auf der Emission von IR-Strahlung durch atmosphärische Spurengase und nicht auf der Absorption bzw. der Transmission von IR-Strahlung durch dieselben. Weil aber
– erstens IR-aktive Spurengase gemäß dem Kirchhoffsche Strahlungsgesetz genau so emittieren wie sie absorbieren,
– kann zweitens der „Sättigungscharakter“ des Treibhauseffekts in einfacher Näherung mit Hilfe des Bouguer-Lambert-Beer-Gesetzes abgeschätzt werden.
Nun basiert dieses Gesetz nicht wie oben auf einer geometrischen Reihe sondern auf einer e-Funktion, die als Potenzreihe gegen Null konvergiert (vgl. a. Bild 1).
![]()
Angenommen für eine Absorptionsbande des CO2 wird für eine bestimmte CO2-Konzentration in einer bestimmten Höhe willkürlich der Zahlenwert x = 8 eingesetzt, dann resultiert
![]()
Werden die Bedingungen gleich gehalten und lediglich die CO2-Konzentration verzehnfacht, erhält man
![]()
Man kann das Spiel beliebig weiter machen und gelangt schnell an die Grenzen eines Taschenrechners und später auch an die eines Supercomputers ( ![]() . Anschaulich gesprochen heißt das, die tatsächliche „Sättigung“ wird erst in einer reinen CO2-Atmosphäre mit unendlicher Schichtdicke erreicht. Erst dann ist die Transmission formal t = 0 und die Absorption a = ¥. Das ist natürlich Unsinn, aber orthodoxe Anhänger der Treibhausgastheorie können immer argumentieren, es gibt auch bei stetig steigenden CO2-Gehalt keine Sättigung des Treibhauseffekts und damit ein endloses Diskussions-perpetuum-mobile in Gang halten.
. Anschaulich gesprochen heißt das, die tatsächliche „Sättigung“ wird erst in einer reinen CO2-Atmosphäre mit unendlicher Schichtdicke erreicht. Erst dann ist die Transmission formal t = 0 und die Absorption a = ¥. Das ist natürlich Unsinn, aber orthodoxe Anhänger der Treibhausgastheorie können immer argumentieren, es gibt auch bei stetig steigenden CO2-Gehalt keine Sättigung des Treibhauseffekts und damit ein endloses Diskussions-perpetuum-mobile in Gang halten.
Nebenbei bemerkt hatte 1995 der englische Chemiker Jack Barrett in der Spectro Chimica Acta auf die bereits längst gegebene „Sättigung“ der Treibhauseffekts hingewiesen und damit eine heftige Kontroverse ausgelöst [3, 8, 9, 10, 11]. Der damalige Chairman und spätere Co-Chairman des IPCC, Sir John Houghton, rief Barrett nach Erscheinen der Publikation an und verlangte, er solle seine Veröffentlichung zurückziehen. Außerdem verständigte Sir Houghton die Leitung des Imperial Colleges, an dem Barrett damals arbeitete. Diese untersagte ihm umgehend unter Androhung von Konsequenzen weitere kritische Veröffentlichungen zum Treibhauseffekt [35].
2. Der Treibhauseffekt
Fälschlicherweise wird oftmals angenommen, der Treibhauseffekt sei mit der Absorption von Infrarotstrahlung (IR-Strahlung) durch atmosphärische Spurengase (CO2, CH4, Wasserdampf u. a.) identisch. Durch strahlungslose Deaktivierung der angeregten Moleküle („Thermalisierung“) würde sich die Luft erwärmen und ihre Wärmeenergie auf die Erdoberfläche übertragen. Ähnlich wie eine heiße Flüssigkeit die Wandung eines Behälters durch Wärmeübertragung erhitzt. Der Treibhaushypothese nach verhält es sich genau umgekehrt: Die Erdoberfläche wird fast ausschließlich durch Bestrahlung erwärmt und die Atmosphäre nimmt ihre Wärmeenergie durch direkten Kontakt mit dem Erdboden auf.
Die Bestrahlung der Erdoberfläche setzt sich aber aus zwei Teilen zusammen:
1. Die direkte Solareinstrahlung (abhängig von der Wolkenbedeckung)
2. Strahlung durch den atmosphärische Treibhauseffekt (im wesentlichem ausgereizt)
Die Existenz einer atmosphärischen Gegenstrahlung, die den Treibhauseffekt charakterisiert, lässt sich zwar leicht nachweisen, aber bereits die Größenordnung des natürlichen Treibhauseffekts kann nur berechnet werden und die ihm zugeschriebene Auswirkung auf das Klima entzieht sich vollkommen der Verifikation [20]. Im gleichen Maß entziehen sich Klimacomputermodelle vollkommen der Falsifikation. Man kann mit ihnen jegliche Entwicklung prophezeien, ohne je befürchten zu müssen, gegenwärtig widerlegt zu werden.
Zum Verständnis des CO2-Treibhauseffekts ist zunächst einmal die „ganz normale“ Infrarot-Absorption atmosphärischer Spurengases zu betrachten [2]. Da IR-aktive Verbindungen mit mehr als zwei Atomen meist verschiedene Absorptionsbanden bzw. Emissionsbanden besitzen, muss geklärt werden, welche der Absorptions-/Emissionsbande des CO2 von Bedeutung ist. Hierüber geben Satellitenspektren Auskunft [4].
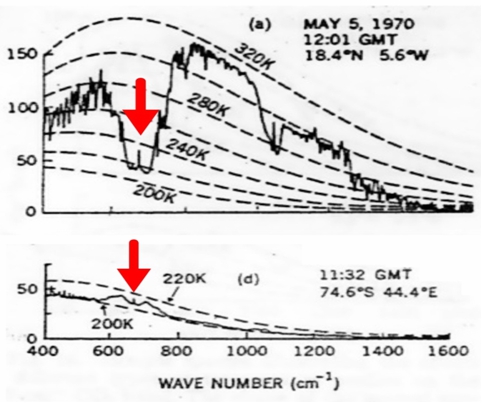
Bild 2: Satellitenspektren, oben über der Sahara, unten über der Arktis
Die gestrichelten Linien im Bild 2 sind die idealen Planck-Strahlungskurven der Erdoberfläche berechnet bei unterschiedlichen Temperaturen in K. Die „gezackte Linien“ repräsentieren neben der ungehinderten Emission der Erdoberfläche die Emissionsgraphen der atmosphärischen Treibhausgase. Die stets offenen Strahlungsfenster liegen bei 800 – 1000 cm-1 und 1050 – 1300 cm-1. Die roten Pfeile im Bild 1 kennzeichnen die ν2-Bande um 15 μm (667 cm-1). Deshalb ist nur diese relativ schwache Bande von Bedeutung und nicht die wesentlich stärkere n3-Bande um 4,2 μm (2349 cm-1). Außerdem erkennt man, die Atmosphäre emittiert tatsächlich IR-Strahlung („Treibhauseffekt“). Dies sieht man ganz deutlich im Satellitenspektrum über der Arktis (unteres Spektrum im Bild 2). Die Bodentemperatur beträgt dort nämlich ca. 200 K (-73 °C), während die Atmosphäre in etwa 10 km Höhe eine höhere Temperatur von ca. 210 K (-63 °C) aufweist. Dies ist ein erster Hinweis darauf, dass der den IPCC-Computermodellen zugrunde liegende Strahlungstransport die Verhältnisse nicht korrekt beschreibt. Es handelt sich vielmehr um einen Energietransport infolge der natürlichen Konvektion. Dabei steigt wärmere Luft unter Abkühlung auf und gibt ihre Energie oberhalb einer Höhe von 10 km als „ungestörte Emission“ ins Weltall ab.
Die im Bild 2 deutlich erkennbaren Strahlungsfenster, die bei wolkenfreien Himmel stets offen sind, veranlassen einige Skeptiker zu argumentieren, selbst wenn es einen Treibhauseffekt gäbe, könne dieser nicht die behauptete Erwärmung der Erdoberfläche verursachen, weil die Auskühlung durch die Strahlungsfenster mindest so groß wie die Wirkung des Treibhauseffekts.
Andere Skeptiker sagen, weil „klimawirksame“ Spurengase wie CO2 usw. IR-Strahlung nicht nur absorbieren sondern im gleichem Maße auch emittieren (Kirchhoffsches Strahlungsgesetz), besitzen „Treibhausgase“ eine kühlende und keine erwärmende Wirkung. Dies beweisen u. a. die im Bild 2 mit rotem Pfeil markierten Maxima des Emissionsspektrums von CO2, der die Abgabe von Strahlungswärme ins Weltall präsentiert. Die gleichen Skeptiker sagen, gäbe es wirklich einen Treibhauseffekt, müsste die Oberfläche der Arktis (200 K) auf die Temperatur erwärmt werden, die in ca. 10 km Höhe herrscht (210 K). Außerdem verstoße der Treibhausgaseffekt gegen den 2. Hauptsatz der Thermodynamik, weil kältere, höher gelegene Luftschichten nicht dem wärmeren Erdboden durch „Rückstrahlung“ erwärmen können (vgl. Temperaturgradient im Bild 10).
3. Eigene Messungen
Weil, wie eingangs erläutert, in den allgemein gelesenen wissenschaftlichen Journalen keine auch nur annähernd brauchbare Information zur Spektroskopie des Treibhauseffekts veröffentlicht wurde, habe ich die Absorption des Kohlendioxids einmal in einem Industrielabor und einem Hochschullabor gemessen und die Transmission einzelner Banden, so weit sie erfassbar waren, auf die Atmosphäre hochgerechnet.
Ein Teil der Messungen (vgl. Bild 4) wurden mittels einer 10-cm-Küvette mit IR-durchlässigem Fenster durchgeführt, die mit synthetischer CO2-freier und wasserfreier Luft gefüllt war. Danach wurde mit einer Mikroliterspritze CO2 zugegeben, so dass 357 ppm CO2 zugegen waren (CO2-Konzentration von 1993). Weiter wurden soviel Wasser zugefügt, bis 2,6 % Wasserdampf vorlagen. Als IR-Strahlungsquelle diente ein Globar, ein elektrisch auf 1000-1200 ºC geheizter Siliziumkarbid-Stab mit nachgeschaltetem variablen Interferenzfilter. Nach der Aufnahme dieses Spektrums wurde mit CO2 aufgestockt, so dass 714 ppm enthalten waren. Die Messung erfolgte zum einem FT-IR-Spektrometer „Bruker IFS 48“.
Um den Einfluss von Fremdgasen zu überprüfen wurde reines CO2 und CO2 in Gegenwart von He sowie N2 bei 1020 mbar mit einem Perkin Elmer System 2000 FT-IR-Spektrometer gemessen. Bild 3 zeigt das Ergebnis. Im Strahlengang des Spektrometers befand sich jedes Mal die gleiche Anzahl an CO2-Molekülen. Reines CO2, das die niedrigste Absorption hat, wurde bei einer Schichtdicken von 0,35 mm gemessen. Die anderen in einer 10-cm-Küvette in Gegenwart von He (mittlere Absorption) und Stickstoff (größte Absorption).
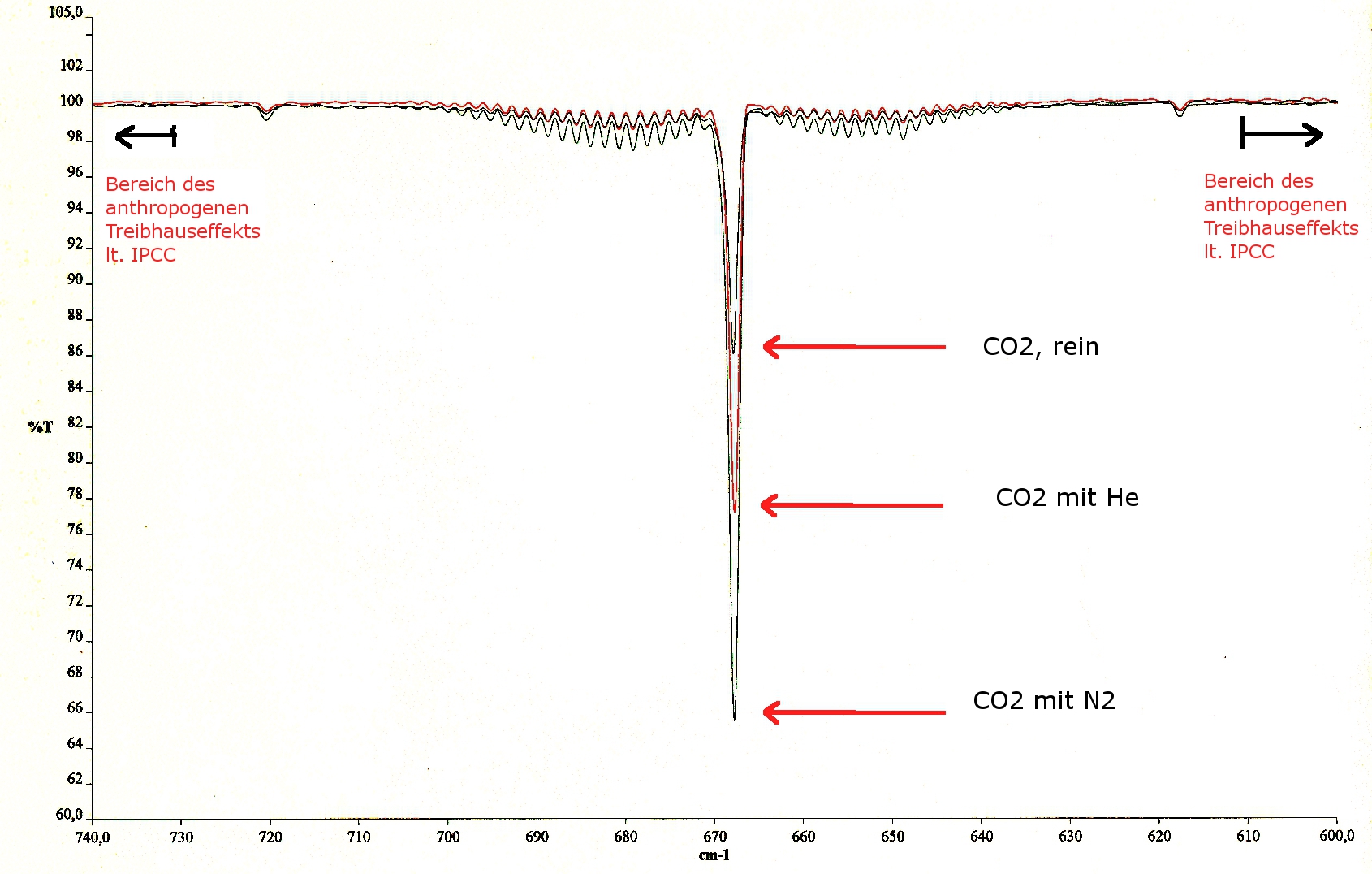
Bild 3: Spektrum von CO2 (rein) und in Gegenwart von He sowie N2
Deutlich erkennbar ist, dass in bodennahen Schichten angeregte CO2-Moleküle durch strahlungslose Deaktivierung (Thermalisierung“) in den Grundzustand zurückkehren. Ähnlich wie es Jack Barrett in seiner Spectro Chimica Acta-Publikation 1995 feststellte.
Der Bereich, der nach IPCC-Angaben den zusätzlichen – anthropogenen – Treibhauseffekt präsentiert, ist durch Pfeile im Bild 3 kenntlich gemacht. Nun kann man argumentieren, wählt man eine Küvette mit einer Länge von 1 000 m findet man an den Rändern mehr „klimawirksame“ Absorptions-/Emissionsbanden. Dies insbesondere, wenn man eine Wegstrecke vom Erdboden bis zur Tropopause (ca. 10 000 m) wählt. Wie gesagt, das Diskussions-perpetuum-mobile lässt sich endlos in Gang halten.
3.1 Auswertung der eigenen Messungen
Bild 4 zeigt das unbearbeitete Spektrum der 15 µm-Bande für 357 ppm CO2 und 2.6% H2O.
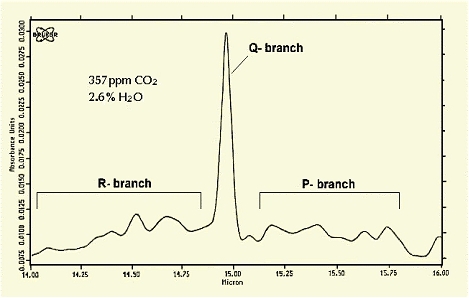
(Bild 4: Unbearbeitetes Spektrum der 15 µm-Bande (ν2-Bande)
Deutlich sind wie im Bild 3 der R– (ΔJ = + 1) und der P– (ΔJ = – 1) sowie der Q-Zweig (ΔJ = 0) der n2-Bande zu erkennen. Der Extinktionskoeffizient im Maximum (ΔJ = 0) ergab sich zu:
e = 20,2 m2 mol-1 (ν2 bei 667 cm-1)
Um die Absorption zu berechnen, wurde der durchschnittliche CO2-Gehalt der Atmosphäre mit c = 1,03.10-3 mol/m3 angenommen. Setzt man die oben gemessenen molaren Extinktionen nebst der Konzentration und der Schichtdicke der Troposphäre (h = 10 km = 104 m) in das Lambert-Beer’sche-Gesetz ein, so erhält man eine Extinktion (Formelzeichen nach DIN: A) von
A(n2) = 20,2 m2 mol-1 × 1,03.10-3 mol/m3 × 104 m = 208
Dies bedeutet, dass die Transmissionen in der Mitte der Absorptionsbande bei den um 1997 gegebenen 357 ppm CO2 bei T(n2) = 10-208 liegt (Bild 5).
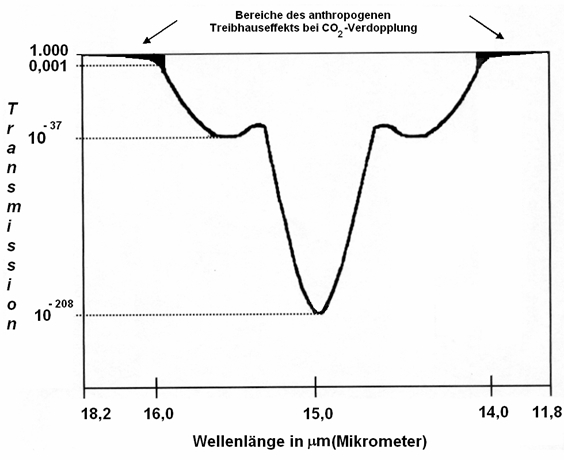
Bild 5: Spektrales Auswertungsschema
Dies ist ein extrem geringer Transmissionswert, der eine Steigerung des Treibhauseffektes bei Verdopplung des klimawirksamen Spurengases in diesem Bereich vollkommen ausschließt.
Setzt man den molaren Extinktionskoeffizient e für die n2-Bande sowie die Volumenkonzentration in mol/m3 (357 ppm CO2) in das Lambert-Beersche-Gesetz ein und nimmt eine Schichtdicke von 10 m an, resultiert eine Extinktion von
A = 20,2 m2 mol-1 × 0,0159 mol/m3× 10 m = 3,21
Dies entspricht einer Transmission von T = 10-3.21 = 0,6 Promille. Mit anderen Worten: Bereits nach 10 m absorbiert die Q-Bande 1 – T = 99,94% der IR-Strahlung.
Bei der Absorption an den Peakflanken ist die Extinktion naturgemäß kleiner. Deshalb stellt das IPCC 1990 fest, die Schwingungsrotationsbanden im mittlerem Bereich der 15 mm-Bande seien so gut wie gesättigt („saturated“), weshalb sie zum „Treibhauseffekt“ bei weiter erhöhter Konzentration kaum beitragen. Aber: „The effect of added carbon dioxide molecules is, however, significant at the edges of the 15 µm band, and in particular around 13,7 and 16,3 µm [14]“. D. h. Der vom IPCC als gefährlich eingestufte anthropogene Treibhauseffekt soll vor allem auf IR-Banden des Kohlendioxids unterhalb von 625 cm-1 bzw. auf oberhalb von 729 cm-1 beruhen [vgl. a. 36]. Was diese Aussage bedeutet, erkennt man am Besten, wenn man sich das Bild 3 noch einmal anschaut. Abgesehen davon stützen sich IPCC-Forscher auf eine vollkommen unbedeutende Oberschwingung des CO2 bei 9,6 mm, die, wie bei Oberschwingungen üblich, 15 bis 30mal schwächer ist als die zugehörige Grundschwingung. Hinzu kommen noch andere „Treibhausgase“ wie N2O, CH4 usw., auf die ich hier nicht eingehen kann. Selbst das Schwefelhexafluorid (SF6), das u. a. zur Füllung von Autoreifen verwendet wurde, damit die Fahrzeuge leiser dahinrollen, musste vor Jahren der befürchteten Klimakatastrophe weichen.
Natürlich existieren diese o. g. „edges“ um 15 mm, denn die Rotationsquantenzahl J geht von J = + 1 bis J = + ¥ und von J = – 1 bis J = – ¥. Bedauerlicherweise werden aber die „ungesättigten Bereiche“ des 15 mm-CO2-Spektrums an den Rändern immer schwächer.
Da die Besetzung (NJ/NJ=0) der Rotationsschwingungsniveaus der Boltzmann-Verteilung (Gleichung 4)
| (B = Rotationskonstante, J = Rotationsquantenzahl, h = Planck-Konstante, c = Lichtgeschwindigkeit, k = Boltzmann-Konstante, T = thermodynamische Temperatur) |

gehorchen, sind bei hohen Rotationsquantenzahlen (J) zu einem gegebenen, fixen Zeitpunkt („Momentaufnahme“) nur sehr wenige CO2-Moleküle vorhanden, die in diesem Bereich absorbieren und entsprechend dem Kirchhoffschen Strahlungsgesetz emittieren („Treibhauseffekt“). Wie schwach die Banden besetzt sind, kann man anhand folgender HITRAN-Daten überprüfen [6]:
| Wellenlänge | Absorptionskoeffizient pro Molekül in10-22 cm-1/(molec . cm2) |
| 13,5 mm (= 741,7 cm-1) | 76 |
| 15,0 mm (= 666,7 cm-1) | 79 452 (Bandenmitte) |
| 12,5 mm (= 797,3 cm-1) | 46 |
Um die Absorption an den Peakflanken abzuschätzen, wurde bei den eigenen Messungen als Arbeitshypothese angenommen, die Extinktion soll sich bei Verdopplung des CO2-Gehalts um die Größenordnung A = 3 (t = 10-3) erhöhen. Hierzu wurde das Gesamtintegral der Banden bis zu den auslaufenden Enden des R- und P-Zweiges bei A = 0 ermittelt (s. Bild. 5). Anschließend wurden die digital abgespeicherten Spektren ab einer Extinktion, die dem Wert A = 3 (Gesamtweg Erdboden-Troposphäre) entsprachen bis zu den auslaufenden Enden (A = 0) des R- und P-Zweiges integriert.
Da die Messwerte nur schwer reproduzierbar waren, wurden sämtliche Messungen 30mal wiederholt, so dass die „edges„ annähernd erfasst werden konnten. Diese „edges„ begannen beim P-Zweig bei 14,00 µm und beim R-Zweig bei 15,80 µm und liefen jeweils bis zur Grundlinie A = 0. IPCC lässt die Banden an den Rändern bei 13,7 und 16 µm beginnen und an der „HITRAN-Erfassungsgrenze“ enden [14]. Den eigenen Messungen nach ergaben sich für die n2-Bande:
| 15 µm-Bande | 357 ppm | 714 ppm |
| Gesamtintegral 624,04 cm -1 von 703,84 cm -1 | 0,5171/cm | 1,4678/cm |
| Summe der Flanken-Integrale | 1,11.10-4/cm | 9,79.10-4/cm |
Tabelle: 15 µm-Bande (Gesamtintegral und Flankenintegrale A = 0 bis A = 3)
Natürlich lassen sich Extinktionen nicht mit dem Planckschen-Strahlungsgesetz kombinieren. Das ist auch gar nicht die Absicht. Aber der aus daraus abschätzbare relative Zuwachs bei Verdopplung des CO2-Gehalts ist entscheidend. Er entspricht der Differenz der Flankenintegrale bei 714 ppm und 357 ppm im Verhältnis zum Gesamtintegral bei 357 ppm.
(9,79.10-4/cm – 1.11.10-4/cm) / 0,5171/cm = 0,17 %
Wie bereits erwähnt, es handelt sich nur um eine Abschätzung und nicht um einen exakten Messwert. Dennoch macht er deutlich, auf welch geringfügigen Größen sich die seinerzeit im Spiegel (33/1986) prophezeite „Klimakatastrophe“ stützt.
3.2. Kritik der eigenen Messungen
Obwohl die oben angegebenen Messwerte relativ ungenau sind, hatte ich sie seinerzeit veröffentlicht, weil
– erstens jeder Chemiker und nicht direkt mit der Klimaforschung befasste Physiker, wohl wissend um die Eigenschaften IR-aktiver Spurengase, unter Eindruck der Medienhype davon ausgehen musste, dass eine Verdopplung des atmosphärischen CO2 zu einer erheblichen Steigerung (eventuell sogar Verdopplung) des Treibhauseffekts führen sollte. Ich jedenfalls und ca. 30 Chemiker aus Industrie und Hochschule hatten nach meiner eigenen ca. 20 Jahre zurückliegenden Rundfrage in etwa mit einer Verdopplung des Treibhauseffekts bei 100 % mehr CO2 gerechnet.
– Zweitens die Geringfügigkeit des anthropogenen Treibhauseffekt bei der Information der Medien durch die direkt damit befassten „Klimamodellierer“ vornehm verschwiegen wurde. So etwas aber „gehört Sonntags auf den Tisch.“
Interessanterweise werden meine Messergebnisse auch durch die Aussage des Nobelpreisträges Paul Crutzen gestützt. Dieser schrieb1993 in einem Lehrbuch [21]: „Es gibt bereits so viel CO2 in der Atmosphäre, dass in vielen Spektralbereichen die Aufnahme durch CO2 fast vollständig ist, und zusätzliches CO2 spielt keine große Rolle mehr.“ Demnach ist der Treibhauseffekt auch nach Aussage dieses Nobelpreisträgers nahezu „gesättigt“. Man kann es auch so ausdrücken: Ein Treibhaus heizt sich bestenfalls geringfügig (Spureneffekt!) stärker auf, wenn man das normale Fensterglas gegen ein zehn Zentimeter dickes Panzerglas austauscht!
Die zur Messung verwendeten FT-IR-Spektrometer werden im Chemie- und Pharmabereich sowohl in der Industrie als auch an den Hochschulen mit großem Erfolg eingesetzt (vgl. Bild 3 und 4). Sie besitzen aber nur einen Spiegelweg von 5…15 cm. Dies ergibt eine Auflösung der IR-Banden von 0,2…. 0,07 cm-1. Da die „ungesättigten“ Spektralbereiche ungewöhnlich schwache IR-Banden betrifft, benötigt man Spektrometer, die eine Auflösung von 0,0004 cm-1 erbringen [6]. Hierzu muss man ein FT-IR-Spektrometer bauen, das theoretisch über einen Spiegelweg von 2.500 cm (25 m!) verfügt. Nur dann lassen sich die äußerst schwachen IR-Banden messen, auf die sich die Klimamodellierer des IPCC stützen. Es sind Banden, mit einer „Absorptionsstärke“ von nur 0,05 % der 15 mm CO2-Hauptbande!
Die üblicherweise in der Industrie und Hochschulforschung verwendeten FT-IR-Spektrometer mit geringerer Auflösung kosten je nach Ausstattung zwischen 4 000 bis 10 000 Euro. Ein FT-IR-Spektrometer, wie das Bruker IFS 125 HR, mit denen man die Akkuratesse der HITRAN-Datenbank erreichen kann, kostet mindest 125 000 Euro. Ein Industriechemiker, der eigenmächtig ein solches Gerät beispielsweise zur Strukturaufklärung organischer Moleküle anschaffen würde, müsste mit seiner sofortigen Kündigung rechnen. Und das zu recht! Geräte dieser Art sind nur dann sinnvoll, wenn man Spureneffekte messen möchte. Deshalb findet man die Geräte vor allem in Instituten, die sich im Auftrag der Politik mit atmosphärischen Ultraspuren beschäftigen. Das Geld hierfür stammt vom Steuerzahler.
4. Vergleich mit den offiziellen Daten des IPCC
Nimmt man die offiziellen Zahlen (IPCC), dann beträgt der „natürliche“ Treibhauseffekt“ 324 W/m2 [22, 23]. Bei Verdopplung des CO2 (100 % Steigerung!) wird nach Übereinkunft („best guess“) angenommen, dass sich der Strahlungsantrieb um 3,7 W/m2 erhöht [23, 24]. Im Bild 6 sind die Verhältnisse dargestellt.
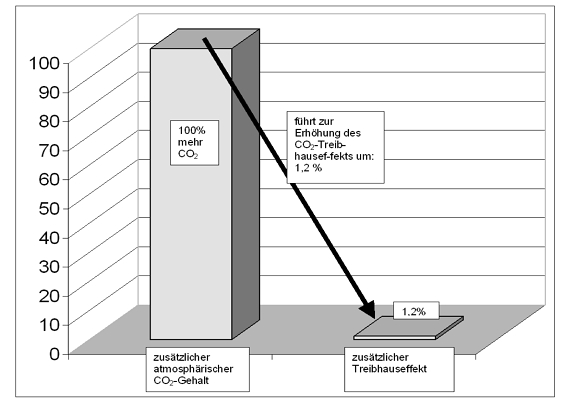
Bild 6: Prozentuale Erhöhung des Treibhauseffekts bei Verdopplung des atmosphärischen CO2-Gehalts gemäß der offiziellen Angaben des IPCC
Auch das Bild 6 belegt die oben beschriebene weitestgehende Sättigung, denn die Steigerung des Treibhauseffekts bei CO2-Verdopplung beträgt nur geringfügige 1,2 %. Dies ist in der Klimaforschung bekannt. Deshalb wird versucht, den „Sättigungscharakter mit dem Argument zu entkräften, das Klima sei ein so empfindliches System, dass es bereits von kleinsten Änderungen des Strahlungsantriebs aus dem Gleichgewicht gebracht werden kann. So wird behauptet, die Abkühlung zwischen 1930 und 1970 sei durch die Staubbelastung der Industriegesellschaft verursacht. Dies ist falsch. Die Abkühlung war durch das geänderte Magnetfeld der Sonne verursacht, wie aus dem Bild 15 (rot eingekreist) hervorgeht.
Neben der HITRAN-Datenbank kann zur Berechnung des allgemeinen und anthropogenen Treibhauseffekt das von der US-Airforce und der Fa. Spectral Sciences Incorporated entwickelte MODTRAN-Programm genutzt werden, dem sich auch die Forscher des IPCC bedienen. David Archibald hat mit Hilfe des MODTRAN-Programms der Universität Chikago [37] die Abhängigkeit der Erdoberflächentemperatur vom atmosphärischen CO2-Gehalt berechnet. Das verblüffende Ergebnis zeigt das Bild 7.
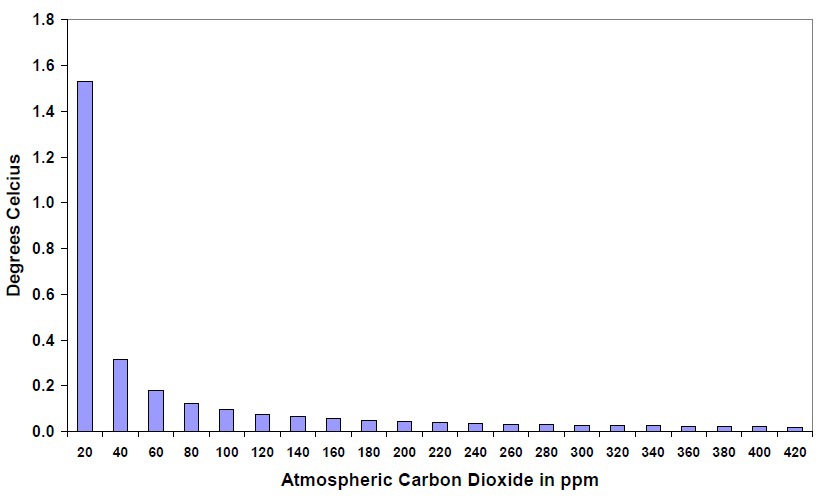
Bild 7: Wirkung des CO2 und Anstieg der mittleren Erdtemperatur
Der höchste Anstieg der mittleren Erdoberflächentemperatur wird von 20 ppm CO2 bewirkt. Danach fällt der Einfluss des CO2 rapide ab. Dies verwundert nicht, denn der Einfluss der „edges“ wird bei höherem CO2-Gehalt immer geringer. Nicht zuletzt deshalb war der CO2-Treibhauseffekt bereits zu Goethes Zeiten weitgehend ausgereizt.
5. Erdoberflächentemperatur, Treibhauseffekt und CO2-Konzentration
Zur Berechnung der irdischen Oberflächentemperatur ohne Treibhausgasatmosphäre wird allgemein und nicht nur von den IPCC-Forschern eine einfache Gleichung benutzt, die auf dem Stefan-Boltzmann– Gesetz beruht.
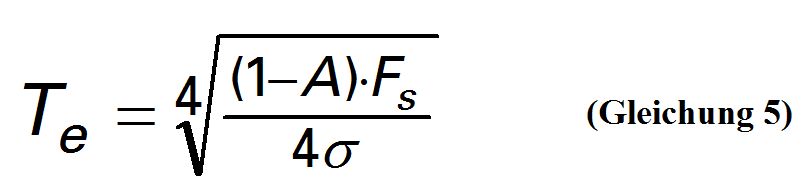
A ist dabei die Albedo – das durchschnittliche „Rückstrahlvermögen“ der Erde (nicht mit der Extinktion A verwechseln!). Sie wird mit A= 0,3 angenommen. Tatsächlich existierten in der Vergangenheit auch andere Angaben. Die Solarkonstante, die in Wirklichkeit gar nicht so konstant ist, hat den Wert Fs = 1368 W/m2. Weiterhin enthält die Gleichung die Stefan-Boltzmann-Konstante s = 5,67 . 10-8 W.m-2.K-4.
Rechnet man mit diesen Angaben, so resultiert für die Oberflächentemperatur der Erde:
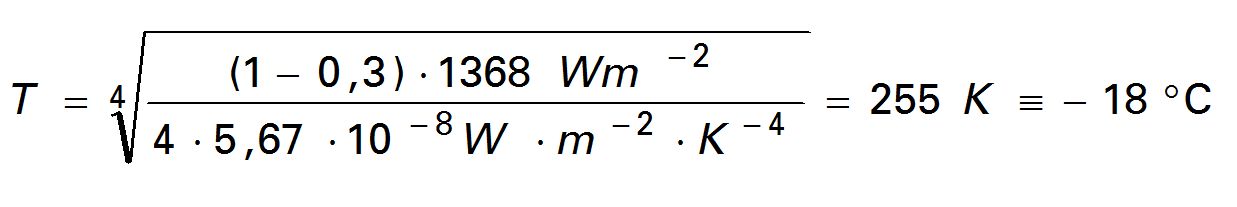
Das Ergebnis ist fragwürdig. Die Erde ist nämlich kein wasserloser Gesteinshaufen im Weltall. Sehr wahrscheinlich liegt die irdische Mitteltemperatur ohne Treibhausgase um einiges höher! Aber bleibt man zunächst einmal dabei, dann beträgt die spezifische Ausstrahlung der Erdoberfläche bei dieser Temperatur (Formelzeichen M nach DIN 5031, Teil 1):
M1 = (1-0,7) . 0,25 . 1368 W/m2 = 239 W/m2
Für die Klimanormalperiode bezeichnet, hat man sich vor Jahren unter Konsensbildung auf eine Mitteltemperatur von + 15 °C (T = 288 K) geeinigt. Benutzt man jetzt das „unveränderte“ Stefan-Boltzmann-Gesetz
![]()
und berechnet damit die spezifische Ausstrahlung der Eroberfläche erneut, resultiert:
![]()
Folglich erhöht der „natürliche“ Treibhauseffekt, mit einer hypothetische Erwärmung von DT = 288 K – 225 K = 33 K (33 °C), die spezifische Ausstrahlung der Erdoberfläche um
DM = M2 – M1 = 390,0 W/m2 – 239,0 W/m2 = 151 W/m2
Wie bereits oben erläutert, wird bei Verdopplung des CO2 (100 %ige Steigerung) ein zusätzlicher Strahlungsantrieb von 3,7 W.m-2 angenommen (anfänglich gab IPCC 4,2 W.m-2 an, die Größenordnung entzieht sich der Falsifikation und beruht auf Konsens – „best guess“!).
Nimmt man die besagten 3,7 W.m-2, dann steigt die spezifische Ausstrahlung der Eroberfläche von 390,0 W.m-2 auf 393,7 W.m-2. Setzt man diesen Wert in die Stefan-Boltzmann-Gleichung (Gleichung 6) ein, resultiert als Erdoberflächentemperatur:
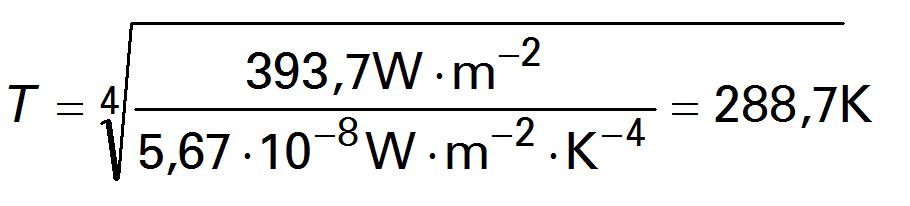
Demnach erhöht sich die Temperatur bei CO2-Verdopplung (100 % mehr CO2!) von 288,0 K auf 288,7 K. Das entspricht gerade einmal DT = 288,7 K – 288,0 K = 0,7 K (0,7 °C) und nicht mehr. Die Klimamodellierung hätte keinerlei politische Beachtung gefunden, wenn man nicht die Hypothese der Wasserdampfverstärkung in die Diskussion eingebracht hätte. Diese lässt sich jedoch glücklicherweise falsifizieren, wie im nächsten Absatz dargelegt wird.
6. Die Wasserdampfverstärkung
Da eine Erwärmung von lediglich 0,7 °C bei 100 % mehr CO2 zu wenig erscheint, hat man sich vor Jahren darauf geeinigt, dass diese geringfügige Temperaturerhöhung gemäß der altbekannten Clausius-Clapeyronschen-Gleichung deutlich mehr Wasser aus den Ozeanen verdunsten lasse. Weil Wasserdampf ein Treibhausgas ist, fällt deshalb Temperaturerhöhung durch CO2 wesentlich höher aus. Originalton IPCC [25]: „Der ‚Wasserdampf-Feedback’ ist nach wie vor der durchweg wichtigste Rückkopplungseffekt, der die von den allgemeinen Zirkulationsmodellen als Reaktion auf eine CO2-Verdopplung vorhergesagte globale Erwärmung verursacht.“ Wenn dies richtig ist, muss besonders in einer kälteren Periode, während der die direkte Solarstrahlung nicht so viel Wasser verdunsten lässt, dennoch der Wasserdampfgehalt (Balken in Bild 8) über den Ozeanen parallel mit dem atmosphärischen CO2-Gehalt ansteigen (rote Strich-Punkt-Linie in Bild 8). Dies ist eindeutig nicht der Fall ist, wie das Bild 8 belegt [32]. Deshalb können sich die Klimamodellierer auf keinen Fall auf den durchaus einleuchtenden, hypothetischen Wasserdampfverstärkungsmechanismus berufen, der eine viel zu große Temperatursteigerung prophezeit.
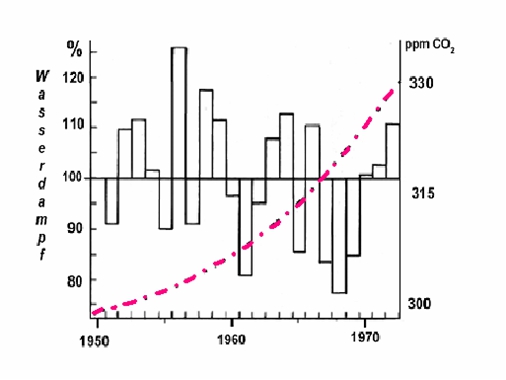
Bild 8: Prozentuale Abweichung des Wasserdampfgehalts über dem Atlantik [s. a. 34]
Um Missverständnissen vorzubeugen: Mit der Prozentangabe im Bild 8 ist natürlich nicht die relative Luftfeuchte gemeint, die niemals höher als 100 % sein kann, sondern vielmehr die Abweichung des Wasserdampfgehalts nach oben und nach unten um den Messwert von 1950. So liegt der absolute Wasserdampfgehalt 1956 um 25 % höher als 1950. 1968 liegt der Wasserdampfgehalt um ca. 45 % niedriger, obwohl der CO2-Gehalt weiter angestiegen ist! Auch wenn der Zeitraum relativ kurz gewählt ist, so belegt er eindeutig, dass die Wasserverdunstung über den Ozeanen nicht mit dem steigenden CO2-Gehalt korreliert. Die Wasserdampfverstärkung, auf denen sämtliche Vorhersagen der Klimamodelle beruhen, existiert nicht.
7. Die Strahlungstransportgleichung
Bei der Berechnung des Treibhauseffekts wird ein „Schicht- oder Kaskadenmodell“ zugrunde gelegt nach dem innerhalb der Atmosphäre eine ständige Absorption (I) und Emission (L) stattfindet. Diesem fiktiven Strahlungstransport liegt die Schwarzschild-Gleichung zugrunde, die ursprünglich entwickelt wurde, um das Verhalten von Atomen in einer Sternenatmosphäre zu beschreiben [12]. Bei einem infinitesimalen Weg dz, dem Absorptionskoeffizienten sa und der Teilchenzahl n gilt hierfür im lokalen thermodynamischen Strahlungsgleichgewicht (LTE):
![]()
Die Größe L ist hierbei die Strahldichte (vgl. DIN 5031, Teil 1), welche die Emission gemäß der temperaturabhängigen Planck-Strahlungsgleichung angibt.
Dass innerhalb der Atmosphäre ein Strahlungstransport stattfindet, meint man belegen zu können, indem man die gemessenen Satellitenspektren mit den berechneten vergleicht. Das Ergebnis ist verblüffend, wie das Bild 9 belegt.
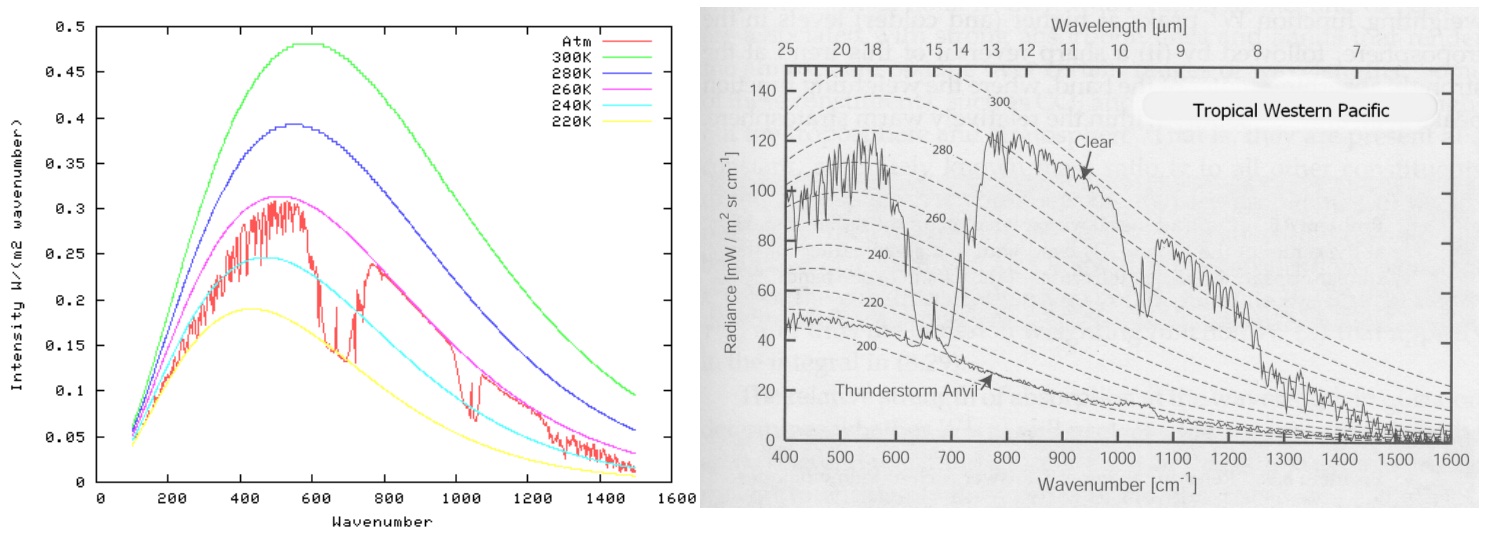
Bild 9: Links das gemessene Emissionsspektrum der Erde (Satellitenspektrum); rechts das mit Hilfe der Strahlungstransportgleichung berechnete Emissionsspektrum
Das lokale thermodynamische Strahlungsgleichgewicht (LTE) begründet man mit dem Kirchhoff’schen Gesetz der Wärmestrahlung. Danach ist das Emissionsvermögen eines Körpers genau so groß wie sein Absorptionsvermögen. Das Ganze hat nur einen Haken. Es existiert kein „Strahlungsenergieerhaltungssatz“, wie er bei diesem Mechanismus stillschweigend vorausgesetzt wird. Tatsächlich setzt man bei der „nachvollziehenden“ Berechnung der Satellitenspektren das gemessene atmosphärische Temperaturprofil in die Plank-Strahlungsgleichung ein, wie im Bild 10 gezeigt.
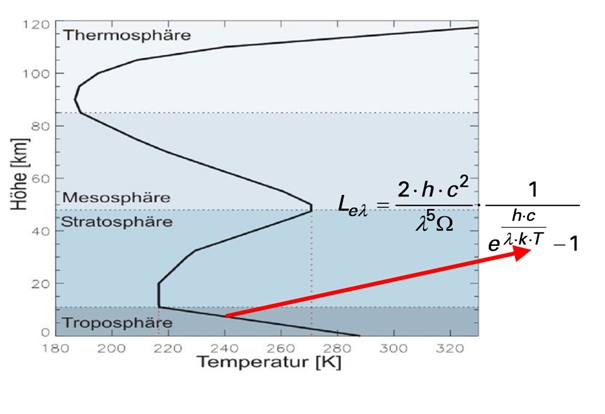
Bild 10: Strahlungstransport, Planck-Gleichung und gemessener Temperaturgradient
Zur Erinnerung: Beim Treibhauseffekt geht es auch um den Temperaturgradienten („Temperaturprofil“), den die Atmosphäre im Kontakt mit dem Erdboden unter adiabatischer Expansion annimmt. Lässt man sich dies durch den Kopf gehen, dann wird das Ergebnis – die Temperatur bzw. der Temperaturgradient – in die Planck-Gleichung eingesetzt (vgl. Bild 10), um dann daraus das temperaturabhängige Emissionsspektrum der Atmosphäre und des Erdkörpers zu erhalten (vgl. auch Bild 2). Deshalb ist die Übereinstimmung der im Bild 10 gezeigten Spektren kein Beweis für den Strahlungstransport innerhalb der Atmosphäre. Es ist vielmehr ein Beweis, dass man im Kreis herumrechnet und sich dann über den mathematisch „bewiesenen“ Treibhauseffekt im Sinne eines Strahlungsenergieerhaltungssatzes freut. Natürlich kann man auch die gemessene Emission innerhalb einer Schicht (Strahldichte L) in die Planck-Gleichung einsetzen, um dann die Temperatur zu erhalten. Auch dann wird im Kreis herum gerechnet.
Experimentelle Untersuchungen und die allgemein akzeptierte Theorie belegen eindeutig, dass die Molekülfluoreszenz anders funktioniert wie die Atomfluoreszenz, bei der die absorbierte Strahlung zu 100 % wieder emittiert wird. Dies geschieht in einem Atomabsorptionsspektrometer (AAS-Gerät), mit dem man in der Instrumentellen Analytik Metalle in Proben quantifiziert (z. B. Cd in einer Bodenprobe).
Das LTE setzt eine „100%ige Molekülfluoreszenz“ voraus, die nicht existiert – auch nicht im IR-Bereich (vgl. a. Bild 3) [26, 27]. Während angeregte Atome nur unter Emission von Strahlung in den Grundzustand zurückkehren können, erfolgt die Relaxation bei Molekülen wegen der Rotations- und Schwingungsfreiheitsgrade meist strahlungslos gemäß den Prinzipien des Jablonski-Diagramms [28]. Deshalb reichte es eigentlich vollkommen aus, wenn man den „theoretischen“ Treibhauseffekt ohne jegliche Absorption nur mit der – temperaturabhängigen – Planck-Gleichung beschreibt, die man mit den jeweiligen Bandenstärken „klimawirksamer“ Spurengase und der „Anzahl IR-aktiver Moleküle in einem Luftvolumen“ multipliziert. Berücksichtigung man den Raumwinkel, erhält man die thermische Emission der Atmosphäre innerhalb eines Halbraums.
Fazit:
Dass eine atmosphärische Wärmestrahlung gemäß dem Planck-Gesetz gegeben ist, ist eine Selbstverständlichkeit. Solange aber ein atmosphärisches Temperaturprofil (oben kälter – unten wärmer) existiert, und die Konvektion erheblich zum Energietransport beiträgt, solange ist die Hypothese, im offenen System der Atmosphäre wird die Energie einer erdbodennah absorbierten IR-Strahlung mittels Strahlungstransport von unten nach oben weitergereicht, falsch. Es gibt nämlich keinen „Strahlungsenergieerhaltungssatz“. Vielmehr übertragen angeregte „erdbodennahe Treibhausgasmoleküle“ ihre Energie im Wesentlichen auf die nicht IR-aktiven Hauptbestandteile des Atmosphäre (N2 und O2).
Interessanterweise wird die Strahlungstransportgleichung angewandt, wenn man das Abkühlungsverhalten großer Glaskörper mittels Modellierung kontrollieren will, etwa bei der Herstellung von Spiegelteleskopen. Dies funktioniert sehr gut. Weil es nämlich in einer erstarrten Glasschmelze bei 600 K keine Konvektion gibt!
8. Was Klimamodelle nicht können
Klimamodelle sind Computeralgorithmen (sprich: „Rechenvorschriften“, welche die meinungsabhängigen Vorgaben der Programmierung widerspiegeln) und nicht die Realität. Weil die Komplexität des Klimageschehens gegenwärtig und auch in absehbarer Zukunft mit keinem Computer realitätsorientiert erfassbar sein dürfte, handelt es sich mehr um politische Instrumentarien, denn um exakte Naturwissenschaft.
8. 1 Die Flusskorrekturen
Der Hypothese nach soll der „natürliche“ Treibhauseffekt den Globus um 33 °C aufheizen. Irrigerweise wird dabei angenommen, die Erde, die zu 70 % mit Wasser bedeckt ist, würde sich ähnlich verhalten wie der vollkommen wasserlose Mond. Nimmt man an, nur die ersten 10 m Wassertiefe der Ozeane würden die mittlere Erdtemperatur thermostatisch regeln, ergibt die Rechnung, dass die Ozeane im Temperaturbereich von –18 °C bis +15 °C eine Energiemenge von 1,57.1018 MJ speichern. Hierzu die Gegenrechnung: In 24 Stunden werden durch den irdischen Treibhauseffekt 1,43.1016 MJ umgeschlagen [23]. Der gesamte natürliche Treibhauseffekt macht somit nur 0,9 % der Energie aus, die in den Ozeanen bei einer Wassertiefe bis zu 10 m gespeichert ist. Die Folge sind erhebliche Schwierigkeiten bei der Kopplung atmosphärischer Zirkulationsmodelle („General Circulation Atmospheric Models“) mit ozeanischen Zirkulationsmodellen („General Circulation Oceanic Models“). Diese Probleme lassen sich nur mit Hilfe so genannter „Flusskorrekturen“ überwinden, deren Beträge, wie das Bild 11 belegt, um ein Vielfaches größer sind als der anthropogene Treibhauseffekt. Die rechte Säule in Bild 11 stellt den Strahlungsantrieb des CO2 bei Verdopplung dar. Danach ist allein schon die 100 W/m2-Flusskorrektur zur Kopplung Ozeanoberfläche-Atmosphäre rund 27-mal (!) größer als der anthropogene Treibhauseffekt bei CO2-Verdopplung (3,7 W/m2).

Bild 11: Anthropogener Treibhauseffekt (rechte kleine Säule) im Verhältnis zu den bei der Klimamodellierung angewandten Flusskorrekturen
Es soll nicht unerwähnt bleiben, dass von einschlägigen Instituten in neuerer Zeit verlautbart wird, man benötige keine Flusskorrekturen mehr. Tatsächlich kommen Klimamodelle nach wie vor nicht ohne sie aus.
8. 2 Die Wolkendichte
Bei der Abschätzung des Strahlungsantriebs der Wolken kommen Klimamodelle zu äußerst unterschiedlichen Ergebnissen. So findet das „Bureau of Meteorology Research Center“ (BMRC) von Australien, dass die Wolken eine Abkühlung von ca. 1 W/m2 erbringen, während das Labaratoire de Météologie Dynamic (LMD) aus Frankreich meint, Wolken würden eine Erwärmung von ca. 1,7 W/m2 bewirken (Bild 12). Auch das ist beachtenswert!
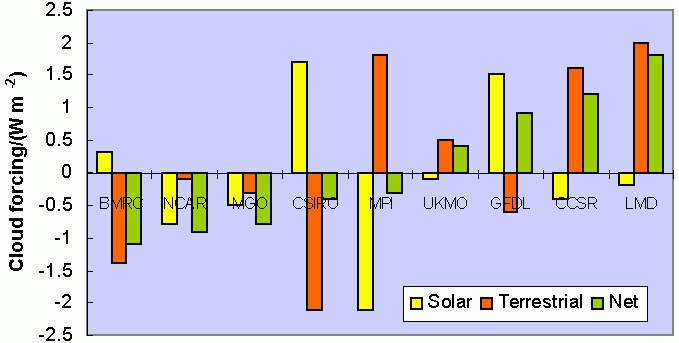
Bild 12: Strahlungsantrieb der Wolken mit unterschiedlichen Klimamodellen gerechnet
8. 3 Modellabhängige Parameter
In der bereits mehrfach zitierten Veröffentlichung von Hermann Flohn [5] stellt dieser in einer Graphik den globalen Temperaturanstieg gemäß einschlägiger Computermodellierungen vor (Bild 13). Flohn referiert in dem Aufsatz den Stand der Klimamodellierung von 1984, auf der wenig später in geringfügig verbesserter Form der Erdumweltgipfel Rio92 basierte.
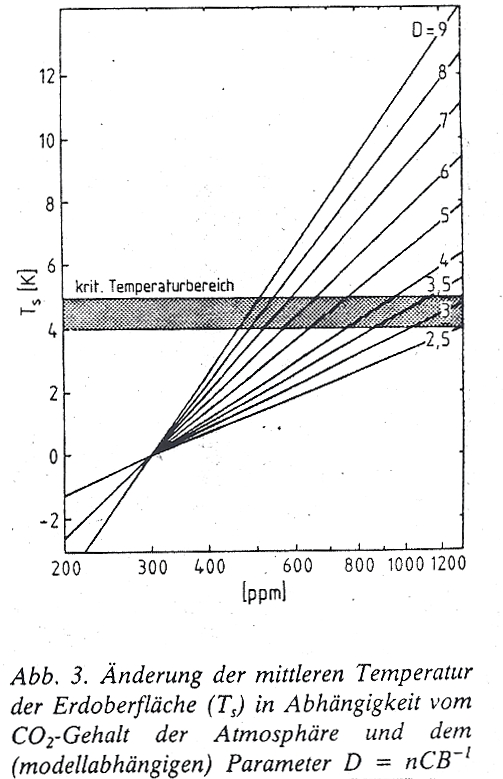
Bild 13: Mittlere Erdbodentemperatur und modellabhängiger Parameter
Interessant ist bei dem einfachen Modell, das Flohn referiert, der modellabhängige Parameter „D“, der die Steigung der jeweiligen Geraden angibt.
![]()
Je größer D ist, desto stärker fällt der Temperaturanstieg aus. Die Größe n ist das Verhältnis der mit Unsicherheit belasteten Strahlungsbilanz aller Spurengase zur Strahlungsbilanz von CO2:
![]()
B und C bezeichnet Flohn vornehm als „Sensitivitätsparameter“, die u. a. natürlich die Wasserdampfverstärkung berücksichtigen (B= 1,8 W . m . K-1, C = 6,5 W . m . K-1). Flohn gibt für die Parameter einen Unsicherheitsfaktor von ca. 20 % an. D. h. je nach dem, wie n, B und C gewählt werden, resultieren im Computer (!) dramatischere oder weniger dramatischere Klimaänderungen. Dass es heute ausgefeiltere Modelle gibt, daran zweifle ich nicht, aber so lange der Wasserdampfverstärkungsmechanismus in ihnen enthalten ist, so lange sind höchste Zweifel angebracht.
8. 4 Die Vergangenheit
Weiterhin versagen Klimamodelle bei der Reproduktion der Vergangenheit. So können sie bis heute nicht die im Bild 14 gezeigte Abkühlung zwischen 1930 und 1975 ohne Zuhilfenahme von Kunstgriffen (atmosphärischer Staubeintrag durch die Industriegesellschaft!) nachvollziehen. (Die tatsächliche Ursache des ungewöhnlichen Verlaufs zeigt Bild 15.)
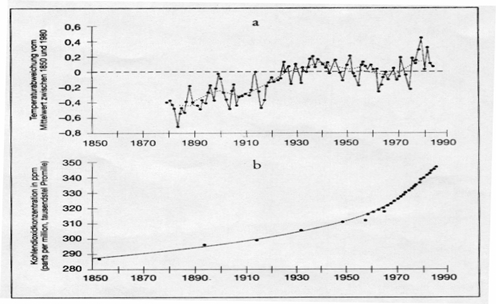
Bild 14: CO2-Gehalt und Temperaturverlauf
Im Sachstandsbericht des IPCC von 2001 tauchte noch eine Kurve auf, die das römische und das mittelalterliche Klimaoptimum zeigte, Zeiten, die mindestens so warm waren wie heute. So wurde Grönland 875 vom Wikinger Erik „der Rote“ Thorvaldsson besiedelt, der Bischof von Trondheim konnte damals seinen eigen Wein ernten und es existierten hochgelegene Gebirgsdörfer, die während der kleinen Eiszeit aufgegeben wurden und heute infolge des Gletscherrückgangs wieder auftauchen. Das stört. Deshalb kursierte in IPCC-Kreisen die Formulierung „We have to get rid of the Medieval Warm Period“. Dem wurde nachgekommen. 1999 veröffentlichte Michael E. Mann et al. Die berühmte Hockeystick-Kurve [1], in der sämtliche vorindustriellen Erwärmungsperioden „weggebügelt“ waren und die Gegenwart als wärmste Periode seit dargestellt wurde. Stephen McIntyre und Ross McKittrick haben die Studie inzwischen gründlich widerlegt [38]. U. a. konnten fast beliebige Zahlen in den Mann benutzte Programm eingesetzt werden, immer resultierte ein „Hockeystick“.
9. Die Alternative
Da treibhausgasfixierte Computer-Klimamodelle nicht nur im Zeitraum zwischen 1930 bis 1970 versagen sondern auch die kleine Eiszeit (14. bis 18. Jh.) und das mittelalterliche Klimaoptimum (11. – 13. Jh.) nicht nachbilden können, muss es einen anderen entscheidenden Mechanismus geben.
Sehr viel spricht dafür, dass dies die Wolkendichte ist, die von der kosmischen Strahlung beeinflusst wird, wie der Direktor des Centre for Sun-Climate Research des Danish National Space Center, Henrik Svensmark, seit Jahren betont [39]. Die kosmische Strahlung besteht überwiegend aus Protonen, die als Echo des Urknalls in unser Sonnesystem eindringen. Gelangen diese positiv geladenen Kernbausteine in die Atmosphäre, so führen sie über einen noch nicht restlos geklärten Mechanismus zur Kondensation von Wasserdampf – Wolken entstehen. Erhöht sich bei höherer Solaraktivität das Magnetfeld der Sonne, dann werden die Protonen stärker abgeschirmt. In der Folge entstehen weniger Wolken und die einfallende Sonnenstrahlung kann die Erdoberfläche (Ozeanoberflächen!) stärker erwärmen. Deshalb folgt der globale Temperaturverlauf der Schwankung des solaren Magnetfelds (Bild 15).
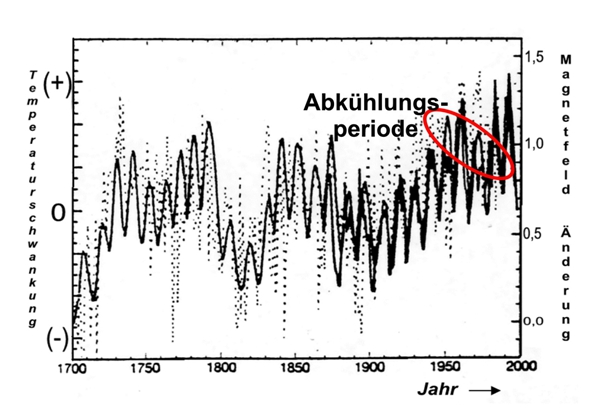
Bild 15: Solares Magnetfeld und Globaltemperatur [29, abgewandelt]
Wie Messungen zeigen, war im übrigen die Solaraktivität seit dem Jahr 850 noch nie so hoch wie nach 1940 [30]. Auch im Wärmehaushalt der Weltmeere macht sich die wolkenbedeckungsabhängige Schwankung der solaren Einstrahlung stärker bemerkbar. Somit dürfte der anthropogene Treibhauseffekt eine kleine, aufgesetzte Größe auf einer natürlichen Klimaschwankung sein.
Abgesehen davon erscheint die unter Punkt 5 (Gleichung 5) vorgerechnete Temperatur von – 18 °C, welche die Erde ohne Treibhausgase angeblich hätte, viel zu niedrig angesetzt sein. Sie entspricht aber der offiziellen Doktrin, die – und das muss betont werden – eine Hypothese ist. Weil, wie bereits hervorgehoben, die Erde kein wasserloser Gesteinshaufen im Weltall ist, sondern zu 70 % mit Wasser bedeckt ist, muss die direkte Absorption im nahen Infrarotgebiet (NIR) und die sehr verzögerte Strahlungsemission von Ozeanwasser stärker berücksichtigt werden.
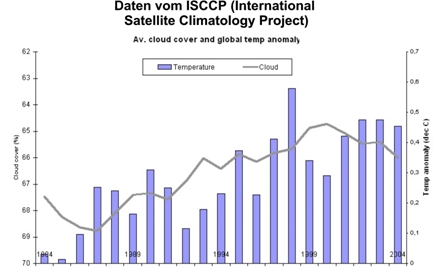
((Bild 16: Wolkenbedeckung (Wolkendichte) und globale Temperatur))
Aus dem Bild 16 geht hervor, dass sich die globale Wolkenbedeckung zwischen 1986 und 2000 von 69 % auf 65 % reduzierte (linke Ordinate, „fallend“ aufgetragen). Parallel hierzu stieg die globale Mitteltemperatur (rechte Ordinate, „steigend“ aufgetragen).
Während die Temperaturschwankungen in der Sahara im Tagesverlauf ohne weiteres bis zu Dd = 50 °C betragen können, verhalten sich Meere wesentlich träger. Der Gesamtwärmeumsatz (Wärmeenergie nicht Wärmeleistung!) eines Meeres ist die Summe vieler Größen:
Qges = (QS – QA) – QK – QV – QT + QC + QE + QF + QR
QS = im Meer absorbierte Sonnen- und Himmelsstrahlung (= „Treibhauseffekt“)
QA = effektive Ausstrahlung
QK = „fühlbarer“ Wärmeübergang Luft-Wasser
QV = latenter Wärmeübergang Luft-Wasser (Verdunstung, Kondensation)
QT = Wärmetransport durch Strömung
QC = chemisch-biologische Prozesse
QE = Wärmezufuhr aus dem Erdinnern
QF = Reibungswärme
QR = radioaktiver Zerfall
Da die Speicherfähigkeit des Wassers erheblich über der von Gesteinen liegt, ist es ausgeschlossen, dass sich die Erde bei einer Trägheit des Systems Wasser-Luft nachts schlagartig um 50 °C herunterkühlen. Denn insbesondere die Abstrahlungsleistung dQA/dt unterscheidet sich wegen der wesentlich höheren Wärmespeicherungsfähigkeit von Meerwasser deutlich von jener der Sahara. Gemäß der Stefan-Boltzmann-Gleichung (Gleichung 6) hängt nämlich die spezifische Ausstrahlung der Erdoberfläche mit der Temperatur unmittelbar zusammen. Je höher die letztere ist, desto größer ist auch die Abstrahlung.
Aus der obigen Aufzählung geht aber hervor, dass der Energiegehalt des Meerwassers auch auf der Wärmezufuhr aus dem Erdinnern, auf chemisch-biologischen Prozessen, auf radioaktiven Zerfall und auf Reibungswärme beruht. Die Größe QF (Reibungswärme) in der obigen Aufzählung hängt von der Windgeschwindigkeit ab. Wie H. Volz auf einer Tagung der Bayerischen Akademie der Wissenschaften berichtete, differiert die spezifischen Ausstrahlung bei den Windstärken 0 und 7 in einer Größenordnung von DM = 11,1 W/m2 [31]. Die Ein- und Ausstrahlungsbilanz geht aber von einer ruhenden See aus. Addiert man diese Größe zur spezifischen Ausstrahlung bei 15 °C, so erhält man:
M = 239,0 W/m2 + 11,1 W/m2 = 250,1 W/m2
Eingesetzt in die Gleichung 2 resultiert für die Temperatur T = 257,7 K (- 15,3 °C). Diese Temperatur liegt um 2,7 °C höher, als die besagten – 18 °C. Die Treibhausgase erhöhen dann die Mitteltemperatur nicht um 33 °C sondern „nur“ um 30,3 °C, insofern die These richtig ist, wonach die „normale“ Mitteltemperatur der Erde + 15 °C beträgt. Wie hoch war diese eigentlich während des mittelalterlichen Klimaoptimums (11. – 13. Jh. ) und während der „kleinen Eiszeit“ (14. bis 18. Jh)?
Ein weiteres kommt hinzu. Etwa 50 % der Sonneneinstrahlung, die den Erdboden erreicht, ist Wärmestrahlung (nahes und mittleres IR). Diese wird vom Meerwasser absorbiert. Die strahlungsfixierte Treibhausgastheorie saldiert nur die Einstrahlung und Ausstrahlung im Tagesverlauf als könnten sich die Weltmeere auf der Nachtsseite schlagartig auf – 18 °C abkühlen. Die Trägheit der Ozeane ist aber mit einer Relaxationszeit bis zu 200 Jahren sehr hoch. Folglich dürfte die mittlere globale Gleichgewichtstemperatur der Ozeane ohne atmosphärische Treibhausgase eher um + 4 °C (Wasser höchster Dichte am Grunde eines zugefrorenen Gewässers) denn bei – 18 °C liegen.
Als ich vor einiger Zeit einmal mit einem ehemaligen Leiter eines Klimarechenzentrums korrespondierte und ihn fragte, wie hoch die irdische Mitteltemperatur ohne Ozeane anzusetzen sei aber mit dem gegenwärtigen atmosphärischen Treibhausgasgehalt, erhielt ich zur Antwort, dies sei eine interessante Frage, die man aber bislang nicht durchgerechnet habe.
Zusammenfassung
· Der anthropogene Treibhauseffekt ist im wesentlichem ausgereizt, wie die Messung der Transmission von IR-Strahlung belegt. Eine globale Klimakatastrophe ist daher selbst bei einer CO2-Verdoppelung nicht zu erwarten.
· Die Steigerung des Treibhauseffekt von 324 W . m-2 auf um 327,7 W . m-2 bei 100 % mehr CO2 ist eine 1,2 %ige Geringfügigkeit (s. Bild 6), die man nur mit Hilfe des hypothetischen Wasserdampfverstärkungsmechanismus künstlich vergrößern kann.
· Zweifellos enthält die Atmosphäre gemäß der Clausius-Clapeyronschen-Gleichung mehr Wasserdampf, wenn es wärmer wird. Jedoch lässt sich der hypothetische Wasserdampfverstärkungsmechanismus, ohne den die Klimamodelle nicht auf die politisch erwünschten Temperatursteigerungen kommen, in der Realität nicht nachzuweisen. Weil sich somit der atmosphärische Wasserdampfgehalt nicht an der Konzentration der Treibhausgase orientiert, erhöht sich die globale Mitteltemperatur bei 100 % mehr CO2 bestenfalls um 0,7 K (0,7 °C). Natürlich lassen sich genügend „Computermodellierungen“ anstellen, die eindeutig beweisen, dass die Wasserdampfverstärkung als positive Rückkopplung den CO2-Treibhauseffekt verstärkt.
· Computerklimamodelle kommen u. a. deshalb zu falschen Ergebnissen, weil der hypothetische Wasserdampfverstärkungsmechanismus vollkommen überwertet wird.
· Der atmosphärische Temperaturgradient beruht auf einem Energietransport und nicht auf einem Strahlungstransportmechanismus mit dem fiktiven LTE. Deshalb wird der atmosphärischen Rückstrahlung – dem Treibhauseffekt – eine zu große Bedeutung zugemessen.
· Klimamodelle müssen mit – gewillkürten – Flusskorrekturen arbeiten, deren Größenordnung den des anthropogenen Treibhauseffekts um ein Vielfaches übertreffen. Im anderen Fall „hat (man) als Modellierer … die Wahl, entweder ohne Flusskorrektur mit einem unrealistischen Klimazustand zu operieren, oder die Flusskorrektur mit ihren Schwächen zu akzeptieren, dafür aber ein realistisches Klima zu erhalten.“ [33]
· Die Abbildung des Klimas in der Vergangenheit mit Computeralgorithmen gelingt nicht ohne massive Korrekturgrößen.
· Die globale Mitteltemperatur ohne Treibhauseffekt dürfte um einiges höher als bei 255 K (-18 °C) liegen.
· Das Klima hängt stärker von der Variation der Wolkenbedeckung ab als vom Gehalt atmosphärischer Treibhausgase.
· Das IPCC ist eine politische Organisation, die sich eines Wissenschaftlergremiums bedient, um volkspädagogische Lernziele durchzusetzen.
Abschließend möchte ich die Leser darauf aufmerksam machen, dass dem gegenwärtigen CO2-Gehalt je nach Literaturstelle ein unterschiedlicher Temperatureffekt zugeordnet wird. In dem von von J.T. Houghton herausgegebenen Buch „The Global Climate“ geben Kondratjew und Moskalenko 7,2 K an [15]. Die Autoren zitieren sich dabei selbst [16]. Besorgt man sich das in Kyrillisch geschriebene Buch und schaut auf der angegebenen Seite nach, so findet man keinerlei Information darüber, wie Kondratjew und Moskalenko auf die o. g. 7,2 K kommen. Andererseits scheint man sich doch recht sicher zu sein, denn die Angaben der Autoren werden gerne zitiert [17]. Allerdings gibt es Widersprüche, denn K.P. Shine [18] gibt einen anderen Wert an, nämlich 12 K und R. Lindzen [19] geht davon aus, dass dem CO2 nur etwa 5% des natürlichen Treibhauseffekts zuzuordnen sind. Das wären 1,65 K und damit weniger als ein Viertel des bei IPCC benutzten Werts von 7,2 K.
Literatur
[1] Michael E. Mann, Raymond S. Bradley und Malcolm K. Hughes (1999): Northern Hemisphere Temperatures During the Past Millennium: Inferences, Uncertainties, and Limitations, in: Geophysical Research Letters, Vol. 26, No. 6, S. 759–762
[2] R. Revelle, Scientific American, 247, No.2, Aug. 1982, 33-41
[3] J. Barrett, Spectrochim. Acta Part A, 51, 415 (1995)
[4] R.A. Hanel et al. Journal of Geophysical Research, 77, 2629-2641 (1972)
[5] H. Flohn, Nachr. Chem.Tech.Lab, 32, 305-309 (1984)
[6] L.S.Rothman et al., Appl.Opt. 26, 4058 (1987)
[7] H. Hug, Chemische Rundschau, 20. Febr., S. 9 (1998)
[8] P. S. Braterman, Spectrochim. Acta Part A, 52, 1565 (1996)
[9] K. Shine, Spectrochim. Acta Part A, 51, 1393 (1995)
[10] J. Houghton, Spectrochim. Acta Part A, 51, 1391 (1995)
[11] R. S. Courtney, Spectrochim. Acta Part A, 53, 1601 (1997)
[12] R. P. Wayne, Chemistry of Atmospheres, Oxford University Press,
2nd. Edition, 44-49 (1991),
[13] Murry L. Salby, Fundamentals of Atmospheric Physics, Academic Press, 198-257 (1996)
[14] Climate Change 1990. The IPCC Scientific Assessment, p. 49
[15] K.Ya. Kondratyev, N.I. Moskalenko in J.T.Houghton, The Global Climate, Cambridge
Universitiy Press, 225-233 (1984)
[16] K.Ya. Kondratyev,N.I. Moskalenko, Thermal Emission of Planets, Gidrometeoizdat,
263 pp (1977) (Russisch)
[17] C.D. Schönwiese, Klimaänderungen, Springer-Verlag Berlin Heidelberg, p. 135 (1995)
[18] K. P. Shine, A. Sinha, Nature 354, 382 (1991)
[19] R. S. Lindzen, Proc. Nat. Acad. of Sciences, 94, 8335 (1997)
[20] R. Raschke, R. Hollman, Strahlungsübertragung in der Atmosphäre, Modellierung und Messung, Preprint zum CO2-Kolloquium der DECHEMA in Frankfurt/Main am 11.10.2001
[21] T. E. Graedel, Paul J. Crutzen, Chemie der Atmosphäre, Spektrum Akademischer Verlag, Heidelberg, Berlin, Oxford 1993, S. 414
[22] IPCC, Climate Change 2001, Chap. 1.2.1 Natural Forcing of the Climate System
[23] J. T. Kiehl, K. E. Trenberth, Bull. Amer. Meteor. Soc., 78 (1997) 197
[24] IPCC, Climate Change 1994, Radiative Forcing of Climate Change and Evaluation of the IPCC IS92 Emission Scenarios, Cambridge University Press, S. 174
[25] IPCC, Climate Change 2001, Working Group I: The Scientific Basis. Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panal on Climate Change, Chap. 7.2.1.1
[26] H. Hug, Energy & Environment, 11, 631, (2000)
[27] N. D. Coggeshall and E. L. Saier, J. Chem. Phys., 15, 65, (1947), Fig. 1
[28] Matthias Otto, Analytische Chemie, Wiley-VCH Verlag, Weinheim (2000), S. 280 ff
[29] S. Solanki, M Schüssler, M Fligge, Nature, 408 (2000) 445
[30] I. G. Usoskin, S. K. Solanki, M. Schüssler, K. Mursula, K. Alanako, Phys. Rev. Let., 91 (2003) 211101-1
[31] Rundgespräche der Kommission für Ökologie, Klimawandel im 20. und 21. Jahrhundert: „Welche Rolle spielen Kohlendioxid, Wasser und Treibhausgase wirklich?“ Bayerische Akademie der Wissenschaften, Verlag Dr. Friedrich Pfeil, Müchen, April 2005, S. 93
[32] Wasserdampfgraphik nach H. Flohn, BdW 12/1978, S. 132
[33] U. Cubasch, Phys. Bl. 51 (1995) 269
[34] H. Hug, Die Angsttrompeter, Signum Verlag, München, 2006, S. 227
[35] Privatmitteilung Jack Barrett, 2001 und 2012
[36] E. Raschke et al., Chemische Rundschau, 23. Okt., S. 9 (1998)
[37] http://www.davidarchibald.info/papers/Failure%20To%20Warm.pdf
[38] Stephen McIntyre, Ross McKitrick, Geophysical Research Letters, Vol. 32, L03710, 5PP., 2005
[39] Henrik Svensmark, A&G, February 2007, Vol. 48, p 1.18
Heinz Hug, für EIKE; Wiesbaden August 2012















meinen Sie nur weil Sie auf einmal beschlossen haben sich über die Vorgänge in diesem Sonnensystem Gedanken zu machen muss der Rest der Menschheit auch wieder bei 0 anfangen? Und nein, in Kernkraftwerken findet keine Kernfusion statt.
Sie wollen zwanghaft eine Konstante herstellen und diese als „allgemeinverbindlich“ darstellen. Aber beim „Klima“ gibt es KEINE KONSTANTE, weil die Sonne,Kosmos,Natur NICHT KONSTANT sind. Auch die durchschnittliche Erdtemperatur ist eine mathematische Konstante, die ich so nicht stehen lassen kann! Beim „Klima“ handelt es sich um das Wechselspiel von Warm/Kalt. Im Sommer ist es eben wärmer, weil die Erde ihren „Po“ näher an die Sonne reckt. Und im Winter streckt die Erde diesen wieder weiter weg von der Sonne. Somit ist eine durchschnittliche Temperatur von 15 Grad einfach nur ein Wert ohne Aussagekraft. Bestens geeignet für div. Computersimulationen und Angsmärchen aber eben nicht Realitätsnah.
Zum Verständnisgewinn hilft es Ihnen auch nicht weiter, wenn Sie sich dem Selbstdenken verweigern, in dem Sie mich als Schriftsteller darstellen wollen. Laufen Sie doch nicht irgendwelchen CO2 Werten hinterher. In der Größenordnungen/Liga in der sich „Klima“ abspielt, ist CO2 ein „nicht vorhandenes“ Gas.
Kennen Sie das, oder kommt Ihnen folgendes Szenario als möglich vor?
In einer Gemeindeversammlung erklärt ein Netzbetreiber (Elektroenergieversorgung), dass durch die Region unbedingt einen Leitung neu oder umgebaut (220kV->380kV) werden muss. Die „Experten“/Wissenschaftler des Netzbetreibers erklären umfangreich die Gründe und warum kein Kabel und dies und das. Und dann kommt einer aus dem Publikum und sagt einfach: „Aber ich habe Angst davor.“ Da können Sie als „Experte einpacken“. Dem werden Sie mit noch so viel sachlichen Argumenten nicht beikommen.
Scheint Ihnen so ein Szenario für möglich. Ja? Dem ist auch ständig so.
Und nun betrachten Sie bitte Ihren Beitrag #329! Fällt Ihnen da auch eine gewisse Parallelität auf. Mir schon. Ich finde den hier mittlerweile inflationär gebrauchte Begriff „Nullsatz“ ziemlich verwirrend. Heißt er
1. ich habe keine Ahnung, was du da schreibst, ich verstehe es einfach nicht;
2. das kenne ich einfach schon, es ist für mich nichts Neues, ergo null Information; oder
3. ich kann gegen Ihr Wissen nicht argumentieren, weil ich Ihnen intellektuell das Wasser nicht mal bis zur Gürtellinie reichen kann, also versuch ich Sie einfach anders verbal anzugehen?
na, mal wieder Gleitzeit? Und nix bessere zu tun als Nullsätze zu formulieren?
Das muss doch einer bezahlen.
Erst einmal: Sie hätten ruhig Danke sagen können, dass ich Ihre Zahlen korrigiere. Mehr war mein Beitrag eigentlich nicht.
Und warum hat der Mars keine dünne Atmosphäre? Wie dick ist sie denn und wie dick ist die der Erde? Was verstehen Sie unter dick/dünn? Die Höhe, der Druck, die Dichte oder die Gravitationskraft.
Die Masse an CO2 ist auf dem Mars ist etwa 10 mal so groß wie auf der Erde. Und jetzt glauben Sie, dass das allein der Grund ist, dass …ja was eigentlich? Das der Treibhauseffekt auch 10 mal so groß sein muss? Wo steht der lineare Zusammenhang? Also mir fällt grad mal einer mit der 4. Potenz ein. Allerdings ist da die „Ausgangstemperatur“ (=Strahlungsgleichgewichtstemperatur) mit entscheidend, die ja schon wohl baim Mars deutlich geringer ist.
Ich möchte mich jetzt damit nicht befassen, finde nur Ihre Vorgehensweise mir gegenüber abstoßend. Sie werfen einfach mal ein paar Zahlen um sich und wenn man die korrigiert wird man auch noch angebellt. Sie können ja mal eine Berechnung äquivalent zur Berechnung in der Erdatmosphäre machen (wobei ich nicht weiß, ob das so einfach geht bei einer quasi fast nicht existenten Marsatmosphäre). Und – bitte – erst dann kommen Sie wieder. Alles andere ist Kaffeesatzleserei.
„Niemand misst auf der Erde eine „Gegenstrahlung“ in Höhe von 340 W/m² aus IR-aktivierbaren Spurengasen.“
Träumen/leugnen Sie weiter.
Wenn sich mal die Tabelle aus http://tinyurl.com/dy4ejc6 anschauen, dann stellen Sie fest, dass Sie allein mit der Sonneneinstrahlung (abhängig von der mittleren Entfernung der Planeten zur Sonne) selbst zusammen mit dem Albedo des Planeten nicht auf die gemessenen Durchschnittstemperaturen kommen. Ich hoffe, Sie sehen ein, dass da ganz allgemein ausgedrückt, noch eine Komponente des Planeten mit reinspielt. Es wird schnell offensichtlich, dass das mit der Atmosphäre zusammenhängen muss. Wenn Sie dem zustimmen können, wäre tatsächlich der Bildungsauftrag von EIKE mal halbwegs gelungen.
„Die Sonne sendet nicht nur Strahlen ins Sonnensystem hinaus sondern die Sonne hält auch unser Sonnensystem mit ihrer großen Masse in Bewegung und somit auch die Erde. Also treibt nicht nur die „Sonnenenergiestrahlung“ unser Erdklima an sondern auch die „Gravitationsenergiebewegung“. Diese Bewegungsenergie hat auch Einfluss auf alle anderen Planeten in unserem Sonnensystem und diese Planetenbewegungen haben dann auch wieder indirekten Einfluss auf die Erde und somit auf das Klima in From von Wind/Wellen. Weiterhin sollte man sich auch immer im klaren sein, dass die Sonne auch für unsere Erdatmospähre verantwortlich ist. Photosynthes ohne Sonne? Sauerstoff ohne Photosynthese? Sauerstoff ohne CO2? CO2 schädlich…warum?“
Herr Hofmann, mit Interesse lese ich da, was Sie schreiben und bewundere ihre Phantasie, neue Erklärungsmodelle zu schaffen. Ganz ehrlich, das ist ein schöpferischer Prozess, zudem selbst Schriftsteller manchmal nicht in der Lage sind. Aber leider kann ich Ihnen nicht viel Hoffnung machen, dass die Gravitationsenergiebewegung-Idee ein wirklicher Erklärungsansatz in der Physik ist bzw. einer werden könnte. Bewegungen werden nur über ein Bezugssystem gemessen. Wir selbst bekommen von der Geschwindigkeit der Erde, die von der Sonne aus beobachten kann oder vom Zentrum der Milchstraße nichts mit. Ob wir uns mit 100 km/h von der Sonne aus betrachtet bewegen oder mit 100.000 km/h hat auf den Wind/Wolken bei uns keinen Einfluß. Etwas anderes ist es bei der Erdrotation, siehe Corioliskraft.
Sie müssen generell keine Angst hier haben, dass einige AGW-Anhänger in Wirklichkeit die Finsternis anbeten und Feinde der Sonne sind. Die Bedeutung unseres Sternes kennt jeder. Deshalb muss man es auch nicht als Ketzerei abstempeln, wenn man von Dingen hier berichtet, die NEBEN der Sonne auch Einfluß auf Wetter und Klima nehmen. In diesem Sinne mal Nana Mouskouri zitiert: „Guten Morgen, Sonnenschein
Nein du darfst nicht traurig sein.“
Niemand misst auf der Erde eine „Gegenstrahlung“ in Höhe von 340 W/m² aus IR-aktivierbaren Spurengasen.
Noch einer mit „so wenig Atmosphäre“…
Sehen Sie sich einmal die Partialdrücke an! Auf der Erde soll ja der Anstieg von 340 ppm auf 600 ppm die Katastrophe auslösen.
Was lesen wir in Ihrer Quelle: …Dieser Effekt ist bereits beim Mars trotz seiner dünnen CO2 Atmosphäre bereits 8 K…
Der Witz dabei ist, die „dünne CO2 Atmosphäre“ mit einem Partialdruck von 608 Pa ca. 16 mal grösser ist als auf der Erde (36 Pa). Wie soll denn da der Anstieg von 380 ppm auf vielleicht 600 ppm eine „Klimakatastrophe“ auslösen? Die weiteren Erklärungsversuche in dem Buch kann man sich sparen, denn schon bald taucht die famose „Gegenstrahlung“ von 340 W/m² auf – bei jemandem der die Partialdrücke nicht versteht kein Wunder. Ihre Quelle ist für die Tonne.
„Herr Hader, im Gegensatz zu Ihrer Selbstdarstellung als grosser Experte des anthropogenen Klimawandels, muss ich Ihre Einbildung hier einmal gerade rücken.“
Nun, ich bin der Meinung, da muss ich bei Ihnen was gerade rücken.
Ein Studium erfolgreich abzuschließen, Dissertation als Fortsetzung, heißt, dass man zwei Dinge kann (können soll).
1.) Fachmann auf seinem Gebiet sein.
2.) Die Methodik der Aneignung neuen Wissens auf dem eigenen und auf artfremden Gebiet zu beherrschen.
Die Argumentation, dass man devot und katzbuckelnd die Meinung von Fachleuten übernehmen soll, nur weil man dieses Fachgebiet nicht studiert hat, erinnert mich an den Untertanengeist des Diederich Heßling aus Heinrich Manns Roman „Der Untertan“.
Sicherlich habe ich Sie mit diesen Vergleich überfordert, denn Sie haben sicher nicht deutsche Literatur studiert. Ich übrigens auch nicht, hatte aber eine sehr gute Schulbildung, bei der sehr viel Wert auf breites Allgemeinwissen gelegt wurde.
Gruß Holger Burowski
„Strahlungsgleichgewichtstemperatur“
Noch eine Ergänzung: die durchschnittliche Oberflächentemperatur bei einem Himmelskörper ohne treibhausgashaltige Atmosphäre liegt erheblich unter der Strahlungsgleichgewichtstemperatur (Höldersche Ungleichung). Siehe z.B. den Mond, der keine Atmosphäre hat.
Deswegen wird beim Mars durch den Treibhauseffekt die Oberflächentemperatur nicht nur um 8 K erhöht.
MfG
Wenn Sie „Klima“ verstehen wollen, dann konzentrieren Sie sich auf DIE SONNE als den einzig wahren Ausgangspunkt! Mit dem Gas CO2 können Sie weder „Klima“ verstehen noch steuern!
Die Sonne sendet nicht nur Strahlen ins Sonnensystem hinaus sondern die Sonne hält auch unser Sonnensystem mit ihrer großen Masse in Bewegung und somit auch die Erde. Also treibt nicht nur die „Sonnenenergiestrahlung“ unser Erdklima an sondern auch die „Gravitationsenergiebewegung“. Diese Bewegungsenergie hat auch Einfluss auf alle anderen Planeten in unserem Sonnensystem und diese Planetenbewegungen haben dann auch wieder indirekten Einfluss auf die Erde und somit auf das Klima in From von Wind/Wellen. Weiterhin sollte man sich auch immer im klaren sein, dass die Sonne auch für unsere Erdatmospähre verantwortlich ist. Photosynthes ohne Sonne? Sauerstoff ohne Photosynthese? Sauerstoff ohne CO2? CO2 schädlich…warum?
Und wie dominant „Die Sonne“ ist, zeigt sich schon daran, dass wir „Planet Erde“ das Glück haben genau in dem richtigen Abstand zur Sonne unsere Kreise ziehen zu dürfen. Einige Millionen KM zu nahe an der Sonne oder zu weit weg von der Sonne, und wir hätten ein ganz anderes Leben bzw. kein Leben in der uns heute jetzig bekannten gelebten Form. Unsere Atmosphärenzusammensetzung hängt unweigerlich mit dem Abstand/Umlaufbahn um die Sonne zusammen.
Also Hr. Hader, wenn Sie Klimawissenschaftler spielen wollen, dann lassen Sie die alberne „Treibhaustheorie“ fallen und beschäftigen Sie sich mit dem Thema „SONNE“. In der Kernphysik hat man schon längst das Energiepotential der Sonne entdeckt. Die Kernkraftwerke sind ein Produkt dieser Forschung. Die Energiemechanismen der Sonne in einen Menschenmaßstab (Kernkraftwerke) gebracht und damit zum Wohle und Fortschritt des Menschen beigetragen. Und in diesem Zusammenhang denkend sind Solarmodule eine Rückschritt gegenüber Kernkraftwerken. Das gleiche gilt übrigends auch für Windmühlen!
So, ich hoffe ich hab mal wieder einige nachdenkliche Punkte angesprochen..
wenn man die Geegnstrahlung in der Erdatmosphaere empirisch nachweisen will, so misst man empirisch in der Erdatmosphaere. Diese Messungen verleugnen Sie!
Mit Daten der Marsatmosphaere kann man schlecht empirisch etwas widerlegen, was man auf der Erde vermutet.
Dieser erneute Betrugsversuch ist ja noch billiger als der erste mit dem verleumderisch falschen Zitat.
@ #304: Dr.Paul sagt am Donnerstag, 27.09.2012, 19:08
„der Physiker Ebel meint also auch, dass es am Mt.Everest deshalb so kalt ist, weil „von unten“ warme Luft nach oben kommt?“
Nein, in der Höhe ist es deshalb kalt, weil der Druck in einem Luftpaket beim Aufsteigen abnimmt (um so höher, um so niedriger der Druck) und die Ausdehnungsarbeit beim adiabatischen Aufsteigen dem Wärmeinhalt des Luftpaketes entnommen wird – das bedeutet Absinken der Temperatur.
Also es ist am Mt.Everest nicht deshalb kalt, weil warme Luft von unten aufsteigt, sondern weil warme Luft beim Aufsteigen adiabatisch abkühlt.
Es zeigt sich wieder: Hinter dem Bestreiten des Treibhauseffektes steckt nur Demagogie, kein Fachwissen – bestenfalls rudimentäres Fachwissen um die Demagogie scheinbar zu „unterfüttern“.
MfG
„Man sieht also, dass Sie [Herr Hader] vom Klima überhaupt nichts verstehen, dafür aber umso tiefere Überzeugungen haben, die von keinem Fachwissen getragen sind.“
Herr Zuber, woher haben Sie Ihr „Fachwissen“ um alles besser zu wissen, als Fachleute?
MfG
irgendwas mach ich falsch, wenn Sie mich immer noch lieb finden. Ich stelle hier keine weiteren Spekulationen über ihre Vorlieben an.
Und fachliche Äußerungen können Sie mit ihrer vollkommenen Unwissenheit eh nicht beurteilen.
Daher auch mal wieder dieser Nullsatzkommentar.
Und von Ihnen lasse ich mir das Spekulieren über Diskutanten wie Sie und Co. nicht verbieten.
Das ist einfach zuviel Mist um von einem Privaten verzapft zu werden.
@ #301: D. Glatting sagt am Donnerstag, 27.09.2012, 11:23
„den eigentlich jeder naturwissenschaftlich gebildeter Laie als solchen erkennen kann.“
Einstein hat in zwei wesentlichen Punkten sich trotz seiner wissenschaftlichen Größe geirrt – einmal bei den nicht gleichzeitig beliebig genau meßbaren dualen Größen Ort und Impuls (Heisenbergsche Unschärferelation) auf dem Solvay-Kongreß 1927 und bei der Verschränkung von Teilchen (EPR-Experiment 1935), wo erst John S. Bell 1964 zeigen konnte, daß Einstein sich geirrt hatte.
Ein zusammenfassendes Zitat ( http://tinyurl.com/dxvg2y6 ), daß zeigt, daß nicht
@ #301: D. Glatting sagt am Donnerstag, 27.09.2012, 11:23
„die AGW Physiker hahnebüchenden Blödsinn erzählen“,
sondern Sie:
„Sie [die Widersprüche, bzw. scheinbar hahnebüchender Blödsinn – JE] entstehen, weil unser Verstand und unsere Sprache, mit denen wir unter anderem auch Philosophie treiben, sich nicht im täglichen Umgang mit einzelnen Atomen, Elementarteilchen und Strahlungsquanten entwickelt haben, sondern aus der Alltagserfahrung mit makroskopischen Objekten. Wenn man Modelle aus der Makrowelt zur Beschreibung der Mikrowelt heranzieht, darf man sich über Widersprüche – insbesondere zwischen dem Wellen- und dem Teilchenbild – nicht wundern.“
Zu dem ganzen Buch siehe http://tinyurl.com/9chnrdx Schon die dort verlinkten Einleitung, Inhaltsverzeichnis und die Rezensionen könnten Ihnen helfen, Ihren Hochmut abzulegen und anzuerkennen, daß Physiker auf dem modernen Kenntnisstand keine „hahnebüchenen Blödsinn erzählen“, wie Sie fälschlich behaupten.
Wenn Ihnen etwas unverständlich erscheint, fragen Sie nach – die meisten werden versuchen, Ihnen das für Sie Unverständliche zu erklären. Ein Hochmut von Ihnen ist da wenig hilfreich.
MfG
„Es kommt dort generell weniger Energie von der Sonne als bei uns an. D.h. der planetare Treibhauseffekt ist in absoluten Zahlen ausgedrückt deutlich geringer, als wenn bei der selben Atmosphäre mehr Sonnenenergie auftrifft.“
Dass die Temperatur von der Sonneneinstrahlung abhängig ist, erkennt man eigentlich schon im Kindergartenalter,
aber der „Treibhauseffekt“? Herr Hader? welcher „Treibhauseffekt“? Ich dachte der ist vom CO2 abhängig?
Oder passiert das nur auf der Erde durch den Menschen? Mit den 0,04% CO2?
Und wenn es sogar CO2 Wolken gibt, die können doch wie ein schwarzer Körper strahlen!
Es scheint also mit CO2 KÄLTER zu sein als ohne!
Sie kennen doch sicher ihren viel zitierten Treibhausmodellprediger den „Wissenschaftler“ Trendberth, da strahlt das CO2 wesentlich STÄRKER ALS DIE SONNE!
Auch auf der Venus müsste es eigentlich ca 100k heißer sein, Sie erinnern sich doch warum, auch ohne CO2. Gar nicht auszudenken wie heiß dann mit CO2, wenn es einen „CO2-Treibhauseffekt“ denn überhaupt gäbe!
Ises aber NICHT
Auch auf der Erde kann man einen solchen NICHT nachweisen.
Oder können Sie, Herr Hader?
Ich würde mal mit der Korrelation anfangen.
mfG
Um Ihr eigenes Interesse zu befriedigen: Es ärgert mich keineswegs, daß von dem Avatar Baecker keine Veröffentlichungen zu finden sind, denn genau das bestätigt die reale Nichtexistenz der Fiktion, die Sie mit Herr Baecker anreden. Ärgern tu mich über mich selber, weil ich diese Kunstfigur der AGW-Propaganda eine zeitlang ernst genommen habe und für diskussionsfähig hielt. Und über die unsichtbaren Hintermänner, die mit dieser äußerst unsauberen Methode die hiesigen Leser zu täuschen versuchen. Denen gehört das Handwerk gelegt. Die Chimäre Baecker ist nur eine Spur, die zu diesen Gaunern führen wird. Herr Mappus hat ja inzwischen erfahren, daß das Netz nicht so schnell vergisst. Die Gauner werden das auch noch merken. Der Avatar mit dem eingebauten Größenwahn ist doch uninteressant und Dr.Paul,bzw Greg House haben mit der Rosstäuscherei durch Unbekannte nun garnichts zu tun,
MfG
Michael Weber
Ich muss Sie aber leider in einer Sache korrigieren, ich bin weder ein Experte des anthropogenen Klimawandels, noch gebe ich mich als solcher aus. Mein Wissen speist sich aus zahlreichen mitgelesenen Diskussionen, Übersichtsvorträgen und -artikel (Herr Heß hatte einige wirklich lesenswerte hier genannt, auch die von Prof.Lüdecke sind zu nennen) und durch Gespräche mit Arbeitskollegen, die Physik studiert haben. Nur mal so am Rande gefragt, mit wem reden Sie persönlich über solche Fachthemen und von wem holen Sie sich auch mal Rat ein?
Es ist nett von Ihnen, dass Sie hier nochmal Werbung für meine Diss machen, die übrigens weiterhin recht preiswert käuflich erhältlich ist. Bitte nicht falsch verstehen, ich habe Herrn Zuber nichts angeboten, dass er diese Werbung machen soll. ;o) Wünschenswert wäre wirklich nur, wenn Sie, Herr Zuber, tatsächlich soviel Respekt vor akademischen Abschlüssen und Arbeiten hätten, wie sie hier im Forum immer vorgeben. Aber das können Sie natürlich gleich bei Prof.Kramm nachholen. Übrigends das Versehen von Herrn Baecker, dass er mich als Physiker einstufte ist nun wirklich alter Kuchen. Dieses Missverständnis auf seiner Seite war damals nach ein paar Stunden geklärt gewesen.
Das Thema Ihrer Dissertation war:
„Data Mining auf multidimensionalen und komplexen Daten in der industriellen Bildverarbeitung“
Mit folgender Zusammenfassung des Inhalts:
„Inaugural-Dissertation zur Erlangung der Doktorwürde der Naturwissenschaftlich-Mathematischen Gesamtfakultät der Ruprecht-Karls-Universität Heidelberg. Die in den letzten Jahrzehnten gestiegene Komplexität in der industriellen Fertigung, der Anstieg der zu erreichenden Qualität und das Streben nach geringen Produktionskosten führen zu erhöhten Anforderungen in der Qualitätssicherung bezüglich dem Aufwand, der Effizienz und der Fehlerfreiheit. Um diesen Erfordernissen gerecht zu werden, kommen zunehmend Verfahren der industriellen Bildverarbeitung und des maschinellen Lernens zum Einsatz. Diese Arbeit beschreibt einen Entwurf und dessen Realisierung von Methoden des Data Minings in der industriellen Bildverarbeitung. Der Schwerpunkt liegt in der Detektion von Fertigungsfehlern. …“
—————————–
Man sieht also, dass Sie vom Klima überhaupt nichts verstehen, dafür aber umso tiefere Überzeugungen haben, die von keinem Fachwissen getragen sind.
Sie sind eine sehr herbe Enttäuschung für den Leser NicoBaecker, der Sie für einen Physiker hält und Sie generös wie einen Ziehsohn behandelt.
http://tinyurl.com/dy4ejc6
Strahlungsgleichgewichtstemperatur: 217K
mittlere Oberflächentemperatur: 225K
Das macht einen Unterschied von etwa 8K aus. Was wäre beim Mars noch zu erwähnen? Es kommt dort generell weniger Energie von der Sonne als bei uns an. D.h. der planetare Treibhauseffekt ist in absoluten Zahlen ausgedrückt deutlich geringer, als wenn bei der selben Atmosphäre mehr Sonnenenergie auftrifft. Hinzu kommen heftige Staubstürme, die die Atmosphäre intransparent für ein großes Frequenzspektrum macht. Erst vor einigen Jahren entdeckte man 80km über der Marsoberfläche Wolkenformationen aus gefrorenen CO2-Partikeln, die ebenfalls eine Intransparenz erzeugen und die Oberflächentemperaturen um bis zu 10K verringern können (http://tinyurl.com/cexfy2p).
Leider fehlt arbeitenden Menschen die Zeit, jeden Mist den Sie, Ebel, Baecker und Co. verzapfen auseinander zu nehmen.“
Lieber Herr Glatting, ich habe einen Vollzeit-Job. Millionen von Deutschen, bei denen das ebenfalls zutrifft, haben Zeit sich an Diskussionen und anderen Internetaktivitäten zu beteiligen, naturwissenschaftlich gebildet sind auch sehr viele von denen. Daran kann es eigentlich nicht liegen, warum so wenige „gebildete Laien“ den angeblichen Unsinn öffentlich widerlegen. Ich schreibe hier in diesem Forum seit gut einem Jahr mit, aber ich sehe hier immer nur dieselben wenigen Leute, die sich fachlich äußern.
„Wer bezahlt euch eigentlich alle?
Die Grünen Sie und die SED Ebel? Baecker wird vom PIK, also vom Steuerzahler, finanziert?“
Sie merken nicht mal, wie lächerlich Sie sich mit solchen Spekulationen machen. Ich habe einen Arbeitgeber, der mich für meine Arbeit vorort bezahlt und nicht für meine Internetaktivitäten in meiner Freizeit. Vielleicht ist Ihnen ja schon aufgefallen, dass ich mich hier nicht mittags oder nachmittags an Diskussionen beteilige, wo normalerweise andere Berufstätige ihrer Arbeit nachgehen (Schichtarbeiter und Leute in Bereitschaft mal ausgenommen). Ich bin eher eine Eule und froh einen Arbeitgeber zu haben, der Gleitzeit ermöglicht, so dass ich auch mal ’nen Vormittag zu Hause verbringen kann und ins Internet schaue. Über Ihren beruflichen Status hingegen wissen wir hier gar nichts.
dass es am Mt.Everest deshalb so kalt ist,
weil „von unten“ warme Luft nach oben kommt?
Im übrigen ist Ihr Beitrag lächerlich,
weil Sie genau das, was ich geschrieben habe sinngemäß wiederholen und das als Richtigstellung deklarieren wollen.
Wer soll Sie noch ernst nehmen?
mfG
Sie haben die beiden Zahlen verwechselt. Der Mars hat eine Strahlungsgleichgewichtstemperatur von 217K (wo sie wohl 210 gefunden haben?)und eine mittlere Temperatur an der festen Oberfläche von 225K. Die Differenz ist sehr gering aber bei sowenig Atmosphäre nicht verwunderlich. Erde ist 255K zu 288K und bei der Venus ist trotz deutlich größerem Albedo als bei Erde und Mars der Unterschied extrem hoch.
Ich hoffe Ihre Verwunderung hat sich damit erledigt.
Mars (Erde in Klammern)
Bodendruck : 640 Pa (101.300 Pa)
CO2 Anteil: 95% (0,038%)
CO2 Partialdruck: 608 Pa (36 Pa)
Eff. Einstrahlung: 125 W/m² (239 W/m²)
Strahlungsgleichgewichtstemperatur: 226 K
Messwerte ergeben eine Mittlere Temperatur von ~ 210K
Ups, wo ist er denn, der Treibhauseffekt aus der CO2 Gegenstrahlung auf dem Mars?
weil die AGW Physiker hahnebüchenden Blödsinn erzählen, den eigentlich jeder naturwissenschaftlich gebildeter Laie als solchen erkennen kann.
Leider fehlt arbeitenden Menschen die Zeit, jeden Mist den Sie, Ebel, Baecker und Co. verzapfen auseinander zu nehmen.
Wer bezahlt euch eigentlich alle?
Die Grünen Sie und die SED Ebel? Baecker wird vom PIK, also vom Steuerzahler, finanziert?
Dr.Paul und Greg House geben nicht vor der GröPhaZ zu sein.
„“Die Jahreszeiten habe nicht ich ins Spiel gebracht.“
Sie vergessen wohl den Threat
anthropogener-treibhauseffekt-zu-schwach-fuer-klimakatastrophe
Erinnern Sie sich mal an ihre Postings #61, #66 und #75. Sowie meine Postings und #64, #72, #84.“
Sie wissen also nicht mal, was Sie selbst geschrieben haben. In Ihrem Posting #84 haben Sie von Jahreszeiten gefaselt, vorher war nicht von Jahreszeiten die Rede.
@ #294: D. Glatting sagt am Mittwoch, 26.09.2012, 13:50
„Insbesondere in ihrem Posting #75 mit
“Noch Zahlen zur Adiabatik: 1 Monat dauert etwa 2,6*10^6 s.““
Wollen Sie etwa bestreiten, daß ein Monat so viele Sekunden hat? Oder wollen Sie die Vertikalzirkulation bestreiten? Oder dauert Ihnen ein Kreislauf der Vertikalzirkulation zu lange? Sie müssen schon schreiben, welchen Unsinn Sie meinen!
Nächster Unsinn:
@ #294: D. Glatting sagt am Mittwoch, 26.09.2012, 13:50
„Nach der Quantenmechanik gilt definitiv kein Absorption ist gleich Emission“
Unter Absorption und Emission versteht man die Intensitäten – und die sind auch nach Kirchhoff nicht immer gleich. Also hat sich am Sachverhalt durch die Quantenmechanik nichts geändert. Es kann natürlich sein, daß Sie nicht in der Lage sind, zwischen „Absorption und Emission“ und „Emissionskoeffizient und Absorptionskoeffizient“ zu unterscheiden. Das zeigt aber nur Ihr mangelndes Wissen, keine falsche Darstellung von mir.
Aber noch eine Ergänzung, die schon vor der Quantentheorie bekannt war – der statistische Charakter der Entropie (Boltzmann). Aber „Emissionskoeffizient und Absorptionskoeffizient“ sind der statistische Mittelwert vieler Absorptions- und Emissions-Vorgänge.
#282: Ebel sagt am Dienstag, 25.09.2012, 19:16
„Die waren doch bis jetz immer der Meinung, das Emissionskoeffizient und Absorptionskoeffizient gleich sind – also wo absorbiert wird, wird auch emittiert.“
MfG
Michael Weber
setzen Sie sich lieber mal mit der Bildung(Allgemeine Unwissenheit) von Herr Hader auseinander bevor Sie über andere Diskuttanten schwadronieren.
was ist denn das schon wieder für ein Ablenkungsmanöver?
Nach der Quantenmechanik gilt definitiv kein
Absorption ist gleich Emission
Genauso wenig wie man aus der Beobachtung, dass die Atmosphäre wohl weitgehend zweigeteilt ist, die Wirkung von geringfügigen Variationen des Spurengases CO2 auf die Globaltemperatur (was das immer sein mag) beschreiben kann.
“Die Jahreszeiten habe nicht ich ins Spiel gebracht.“
Sie vergessen wohl den Threat
anthropogener-treibhauseffekt-zu-schwach-fuer-klimakatastrophe
Erinnern Sie sich mal an ihre Postings #61, #66 und #75. Sowie meine Postings und #64, #72, #84.
Insbesondere in ihrem Posting #75 mit
“Noch Zahlen zur Adiabatik:
1 Monat dauert etwa 2,6*10^6 s.“
Betrachten Sie hier monatliche Zeiträume um ihre kruden Thesen zu belegen? Da ist man doch nicht mehr weit von Jahreszeiten und damit der Ekliptik entfernt.
Versuchen Sie es doch gleich mit Eingeweide lesen oder den Vogelflug zu interpretieren. Da kann man Ihnen wenigstens nicht widersprechen. Ihren Physikkenntnissen schon.
„Ich verstehe deshalb nicht, warum so viele Klimaskeptiker trotzdem auf diesen Zug aufspringen und in Lehrbüchern der Meteorologie stehende Aussagen als falsch hinstellen wollen. Dann wird man erst recht nicht von einer Vielzahl von Physikern und Meteorologen noch ernst genommen.“
Ich verstehe das schon. Das sind Leute, die sowieso nicht ueber Bildung verfuegen ud im Rahmen ihrer Moeglichkeiten ist damit eine differenzierte Betrachtung nicht moeglich. Damit bleibt ihnen nur, bei der Verleugnung bis zu den basics zurueckzugehen, da ihnen konkretere Anknuepfungspunkte fehlen. Ich hatte den Eindruck, Herr Pesch laege mit dem Bildungsniveau etwas ueber DrPaul. Nach seinen letzten Beitraege, muss ich aber feststellen, dass der offenbar nicht mal ueber ein technisches Studium verfuegen kann und auch vor Betrug nicht zurueckschreckt.
„seit Kirchhoff (1860) ist ein bisschen Erkenntnis ins Land gegangen. Die Quantenmechanik zum Beispiel.“
Und seit Clausius ist noch ein bißchen mehr Zeit ins Land gegangen, seit Stefan-Boltzmann etwas weniger. Aber grundlegende Erkenntnisse sind gleich geblieben, sie wurden durch die weiteren Erkenntnisse nur mehr untermauert.
Mit der Quantentheorie ist das Stefan-Boltzmann-Gesetz besser untermauert, mit Atomtheorie (Boltzmann), Quantentheorie usw. wurde Clausius stärker (Entropie) untermauert.
Ein schönes Beispiel der Untermauerung ist Schwarzschild, der schon 1906 den Wärmestrom durch die Sonne richtig beschrieben hat, aber von einer unbekannten Quelle sprach, die den ständigen Wärmestrom vom Kern der Sonne liefert – heute wissen wir, daß es die Kernfusion ist.
Auch Kirchhoff ist heute besser untermauert, als es 1860 war.
@ #284: D. Glatting sagt am Dienstag, 25.09.2012, 20:10
„Eigentlich würde ich Sie jetzt gerne (rhetorisch natürlich) fragen, ob Sie auch den Grund für die Jahreszeiten kennen.“
Die Jahreszeiten habe nicht ich ins Spiel gebracht.
MfG
„Davon abgesehen ist Ihre Bemerkung ausnahmsweise formal richtig, weil real ZUSÄTZLICH zu diesem Gradienten noch Wärmetransport vor allem durch Konvektion stattfindet. Das Wesen dieser Konvektion kann allerdings nicht in einer einseitigen Wärmetransportrichtung nach oben liegen, sonst würde unten ja irgendwann keine Luft mehr übrig bleiben,“
Paul, können Sie nicht lesen? Hader schreibt nur vom Wärmetransport nach oben und zum damit verbundenen Luftaustauch schreibt er
@ #275: S.Hader sagt am Dienstag, 25.09.2012, 10:57
„Es findet aber ein ständiger Luftaustausch statt.“ Die Wärmetransportrichtung ist also nur nach oben, aber der Luftaustausch ist geschlossen als Zirkulation, weil eben oben die Wärme abgegeben wird, wie Hader richtig schreibt:
@ #275: S.Hader sagt am Dienstag, 25.09.2012, 10:57
„Beim Aufstieg nach oben gibt es seine Wärme ab.“
Also nichts mit „irgendwann keine Luft mehr übrig bleiben“ was Sie unterstellen – in der Absicht zu täuschen?
Wegen des Wärmetransport wird tatsächlich der adiabatische Temperaturverlauf modifiziert – eine Abschätzung liefert für die Temperaturdifferenz zwischen Oberfläche und Tropopause eine zusätzliche Temperaturdiffernz von ca. 2K bei einer Gesamttemperaturdifferenz von ca. 70K.
MfG
„Zur Wiederholung:
Während angeregte Atome nur unter Emission von Strahlung in den Grundzustand zurückkehren können, erfolgt die Relaxation bei Molekülen wegen der Rotations- und Schwingungsfreiheitsgrade meist strahlungslos gemäß den Prinzipien des Jablonski-Diagramms.“
Sie vergessen bloß, daß durch Kollisionen auch angeregte Moleküle entstehen – und das ist eben zwangsläufig und deckt sich deshalb mit Kirchhoff.
Und das können Sie auch bei Einstein nachlesen ( http://tinyurl.com/5rw3szr ).
@ #285: Dr.Paul sagt am Dienstag, 25.09.2012, 20:42
„etwa zwischen 40 und 60 Km näherungsweise angenommen werden kann, so daß die Emission dort nur von der lokalen Temperatur abhängig ist“
Sie sollten mal Milne lesen ( http://tinyurl.com/3kh76mv ). Zwar steht dort nicht in welcher Höhe das LTE (oder Ihr LTG) anzunehmen ist, aber falsch ist Ihre Aussage trotzdem. In Oberflächennähe ist die Dichte der angeregten Zustände wegen der vielen Kollisionen fast nur durch die Gastemperatur bestimmt (LTE). In Höhen zwischen 40 und 60 Km kommt relativ zum Kollisionsterm der Streuterm immer stärker ins Spiel, der in Höhen über 60 km immer mehr bestimmend wird. Der Streuterm wird deshalb immer bestimmender, weil die Kollisionen immer seltener erfolgen und demzufolge ein durch Absorption angeregter Zustand immer häufiger abgeregt wird durch Emission statt durch Kollision – es ist also genau dem entgegengesetzt, was Sie fälschlich annehmen. Wenn eben die Emission vorwiegend von Molekülen erfolgt, die durch Strahlung angeregt wurden (Streuterm) und nicht durch Kollisionen, wird die Dichte der angeregten Zustände nicht mehr durch die Gastemperatur, sondern durch die ankommende Strahlung bestimmt.
MfG
weil die Höhe auf dem Mt.Everest permanent Wärme aus der Tiefe erhält, wird es dort oben so kalt???
Und OHNE diese permanent Wärmezufuhr wäre es auf dem Mt.Everest viel wärmer, so warm wie „bei uns“.“
Nicht Wärmezufuhr, sondern Luftzufuhr aus tieferen Schichten. Diese Luft hat sich durch den Aufstieg in die höheren Schichten abgekühlt. Gleichzeitig gibt es auch eine Luftzufuhr in umgekehrter Richtung in tiefere Schichten. Alles soweit bekannt. Würde in irgendeiner Form die Zirkulation verhindert werden, erwärmt sich die Luft auf dem Mt.Everest genauso bei Sonnenschein, wie bei uns im Tiefland. Nur kann man diesen Luftaustausch unmöglich bei einem offenen Planeten stoppen, von daher sind die Überlegungen rein theoretischer Natur.
„Sie tun mir wirklich leid Herr Hader,
offenbar ist ihnen auch nicht bekannt, dass auf dem tibethanischen Hochplteau (>4500m) Permafrost herrscht, also eine Durchschnittstemperatur unter 0° C. 🙂 „wie bei uns“.“
Da sollten Sie sich wirklich mal informieren, denn Tibet ist davon abgesehen eine interessante und für uns Europäer eine sonderbare Region, die oft mit Überraschungen verbunden ist. Zunächst einmal existiert auf der Hochebene von Tibet nur zum Teil ein Permafrostboden. Den Wechsel kann man u.a. mit der Lhasa-Bahn erleben. Es gibt dort zahlreiche Gebiete und Städte, die einen Jahresdurchschnitt von 6-8°C haben. Zum Vergleich, Deutschland hat momentan einen Durchschnitt von etwas mehr als 9°C, entsprechend gibt es auch Regionen hierzulande, die darunter liegen. Nur die Temperaturunterschiede sind in der Hochebene von Tibet extremer. Der wärmste Januar in Lhasa z.B. hatte +6,8°C (Berlins wärmster Januar hatte +2°C), aber auch Durchschnittswerte für den Januar von unter -10°C sind möglich (in Berlin nie unter -3°C).
So weit, so gut, Herr Pesch.
„Luft dehnt sich bei Erwärmung aus, wird bezogen auf die Volumeneinheit leichter als die umgebende, auch darüberliegende, kühlere Luft, und steigt deshalb auf. Gegebenenfalls absorbierte Wärme wird durch Luftmassenaustausch abgeführt.“
Und wohin, wenn man fragen darf?
„Ebenso wie jene Wärme, die der Luft durch Konvektion zugeführt wird. Es kommt somit zur Abfuhr der absorbierten Wärme durch Aufsteigen der erwärmten Luft. Dieser Vorgang ist übrigens auch unter dem Begriff Thermik geläufig. Beim Aufsteigen der Luft sinkt gleichzeitig durch Ausdehnung infolge Druckabnahme deren Temperatur, so daß sich keine Erwärmung einstellt.“
Wollen Sie damit ausdrücken, dass die aufgewärmte Materie in der Atmosphäre keine Bewandnis hat, weil durch das ständige Ausdehnen der Luftmassen und das Auf- und Absteigen die Energie sich dort sowieso verliert? Mit derselben Begründung könnte man auch behaupten, dass eine doppelt so starke Sonneneinstrahlung zu keiner Temperatursteigung in der Atmosphäre führen würde, weil die Wärme sowieso durch den ständigen Luftmassenaustausch abgeführt wird.
„Wegen der einheitlichen Temperatur innerhalb kleinster Gasvolumina in der Luft und der mit der Höhe rückläufigen Temperatur ist es ausgeschlossen, daß es z. B. durch CO2-Anteile zu einer Rückübertragung der von der Erde oder erdnäher liegenden Schichten abgehenden Wärmeabstrahlung wieder zur Erde hin kommen kann.“
Herr Pesch, jeder Körper emittiert Wärmestrahlen. Deshalb gibt es Wärmestrahlen in alle möglichen Richtungen. Entscheidend sind die Nettobilanzen. Was soll denn mit den Wärmestrahlen passieren, die von den Luftschichten Richtung Erdboden emittiert werden? Werden die alle(!) vorher abgefangen?
Vielleicht hilft ja ein Blick in ein Meteorologie-Buch (Seite 13, erster und zweiter Absatz): http://tinyurl.com/d5z8ckp
#279: „Die Strahlungseigenschaften der Spurengase sind wichtig für die Kühlung der Atmosphäre, aber ein Aufheizen duch das CO2 ist weder theoretisch noch empirisch begründbar. Egal was der IPCC an politisch gewünschtem Unsinn auch von sich geben mag, die „Klimakatastrophe“ durch CO2 ist und bleibt ein Hirngespinst.“
Sie scheinen da zu übersehen, dass selbst die Korrektheit des natürlichen Treibhauseffektes alleine eine „Klimakatastrophe“ nicht zwingend macht. Es ist deshalb gar nicht notwendig, den Treibhauseffekt abzustreiten, um den Anstieg von mehr als 2 Grad bis 2100 anzuzweifeln oder angestrebte politische Maßnahmen schlecht zu finden. Ich verstehe deshalb nicht, warum so viele Klimaskeptiker trotzdem auf diesen Zug aufspringen und in Lehrbüchern der Meteorologie stehende Aussagen als falsch hinstellen wollen. Dann wird man erst recht nicht von einer Vielzahl von Physikern und Meteorologen noch ernst genommen.
Davon abgesehen ist Ihre Bemerkung ausnahmsweise formal richtig,
weil real ZUSÄTZLICH zu diesem Gradienten noch Wärmetransport vor allem durch Konvektion stattfindet. Das Wesen dieser Konvektion kann allerdings nicht in einer einseitigen Wärmetransportrichtung nach oben liegen, sonst würde unten ja irgendwann keine Luft mehr übrig bleiben,
sondern es sind die bekannten kreisförmigen Konvektionszellen, bei denen in der Bilanz selbstverständlich ebensoviel Luft herunterkommen muss, wie vorher aufgestiegen ist, in der Regel gleichzeitig, aber an unterschiedlichen Orten, meteorologisch bekannt als Hochdruck- und Tiefdruckgebiete. Was die Atmosphäre grob gesprochen am Tag kühlt, gibt sie nachts der Erde wieder (unvollständig) zurück.
Deshalb ist es am Tag kälter als am Mond und nachts wärmer.
Ihre Vorstellungen vom Mt Everest sind allerdings geradezu abenteuerlich und eines Dr.rer.nat nun wirklich unwürdig.:
Original Hader, Dr.rer.nat!
„Würde es keinen Luftaustausch mit tieferen Schichten geben, dann erwärmt sich die Luft genauso wie bei uns. Es findet aber ein ständiger Luftaustausch statt. Warme Luft in tieferen Schichten dehnt sich aus. Beim Aufstieg nach oben gibt es seine Wärme ab.“
Sie meinen also tatsächlich,
weil die Höhe auf dem Mt.Everest permanent Wärme aus der Tiefe erhält, wird es dort oben so kalt???
Und OHNE diese permanent Wärmezufuhr wäre es auf dem Mt.Everest viel wärmer, so warm wie „bei uns“.
Sie tun mir wirklich leid Herr Hader,
offenbar ist ihnen auch nicht bekannt, dass auf dem tibethanischen Hochplteau (>4500m) Permafrost herrscht, also eine Durchschnittstemperatur unter 0° C. 🙂 „wie bei uns“.
Mein Rat, auch einem „Freund“ wie Ebel nicht alles glauben.
Den adiabatischen Gradient hat er nicht verstanden.
Er weis nicht was Gravitation ist und er kennt nicht die Gasgesetze.
Das hat alles NICHTS mit Konvektion zu tun.
mfG
auch ich gratuliere, Herr Ebel.
Es ist erstaunlich wie sachlich und ohne größere Emotionen sie Leuten begegnen, welche sie oft wüstest beschimpfen, wie ein angeblicher Dr. der Volksmusik (Paul), der nicht mal weiß, wann der Herbst beginnt. Bei solchen Dilletanten die Fassung bewahren, spricht für ihr Wissen, insbesondere „Stehgreifwissen“.
Danke für ihre schönen Ausführungen, wenngleich sie mir noch zwei, drei Fragen schuldig sind, aber die kommen wieder…!
Zur Wiederholung:
Während angeregte Atome nur unter Emission von Strahlung in den Grundzustand zurückkehren können, erfolgt die Relaxation bei Molekülen wegen der Rotations- und Schwingungsfreiheitsgrade meist strahlungslos gemäß den Prinzipien des Jablonski-Diagramms.
In der Luft bei 1bar und 269K kann man Teilchendichte, Geschwindigkeit und mittlere Weglänge leicht ausrechnen. Die mittlere freie Weglänge der Luft ergibt sich bei diesen Bedingungen zu 68 nm. Räumlich betrachtet, hat der eine Stoß eine Auswahl von ca. 8000 Teilchen und nur mit einen einzigen Teilchen erfolgt der Zusammenstoss. Die mittlere Zeit zwischen den Kollisionen in der Luft beträgt ca. 10^-10 Sekunden, bei der Schwingungsanregung dagegen ca. 10^-5 – 10^-4 Sekunden.
Kirhoff gilt dagegen per definitione bei einem Strahlungsgleichgewicht, das selbstverständlich zwischen Erde und Atmosphäre niemals existiert.
Alles schon mehrfach erleutert.
Herr Wille hat uns in der Vergangenheit hier plausiebel dargelegt, dass ein LTG (lokales thermodynamisches Gleichgewicht) erst in einer Höhe wesentlich größerer Molekülabstände etwa zwischen 40 und 60 Km näherungsweise angenommen werden kann, so daß die Emission dort nur von der lokalen Temperatur abhängig ist und Ihr Kirchoff oder SB auch bei Gasen zur Anwendung kommen kann.
Wir müssen uns hier nicht mit allen möglicherweise und in verschiedenen Höhen strahlungsfähigen Spurengasen beschäftigen und sollten uns wegen der aktuellen physikalisch unhaltbaren AGW-Ideologie der Übersicht halber auf das CO2 beschränken.
Und hier gibt es nun mal die bekannten SELEKTIVEN BANDEN dieses Moleküls. Und es gibt die Infrarot-photometrischen Messungen der atmosphärischen Transparenz (Luftdurchlässigkeit) für diesen Strahlenfrequenzanteil.
Und der beträgt in der Troposphäre bis zu ihrem Oberrand praktisch 0.
Deshalb kann eine CO2-Gegenstrahlung auf der Erdoberfläche keinen messbaren Temperatureffekt entfalten.
Dazu im Gegensatz ist der Abstrahlungseffekt (=Kühlung) in den Weltraum nun wirklich nicht zu leugnen.
mfG
seit Kirchhoff (1860) ist ein bisschen Erkenntnis ins Land gegangen.
Die Quantenmechanik zum Beispiel. Und da kommt es darauf an welche Zustände besetzt sind und wie die Übergangkoeffizienten zu den niedrigeren Zuständen sind.
Dazu wurde einiges (andere sagen ziemlich viel) gemessen.
Wer aus der Existenz der Jahreszeiten die Existenz der vertikalen Zirkulation und daraus den “Treibhauseffekt“ ableitet ist mit dieser Physik, die sich überhaupt nicht dem dialektischen Materialismus unterordnen will natürlich total überfordert.
Eigentlich würde ich Sie jetzt gerne (rhetorisch natürlich) fragen, ob Sie auch den Grund für die Jahreszeiten kennen. Aus ihrer bisherigen Begründung des “Treibhauseffektes“ müsste jetzt eigentlich die Ekliptik für den verheerenden Einfluss des CO2 auf die Bewohnbarkeit der Erde sein.
Seit Kirchhoff (1860) wurde auch ein Kommunismus erdacht und in Diktaturen umgesetzt. Die Realität hat hier genauso gezeigt, dass dieser Schwachsinn ein Irrweg ist. Genauso wird es dem “Treibhauseffekt“ ergehen. Alles was Sie noch dazu beitragen können ist sich zu blamieren!
Machen sie weiter!
Die Diskussion dreht sich um die Temperaturschichtung der Troposhäre. An der Tropopause ist die Wettergrenze, alles Wetter und somit auch das Klima, beschränkt sich auf die Troposphäre. Eine Betrachtung der Atmosphäre oberhalb der Tropopause ist für die Klimadiskussion unerheblich.
„Das CO2 absorbiert in dieser Höhe nur, aber es strahlt nicht.“
Gratulation. Erst Sie korrigieren Kirchhoff (1860) weil die Physiker in den vergangenen 150 Jahren nicht bemerkt haben, daß Kirchhoff Unrecht hat!
Die waren doch bis jetz immer der Meinung, das Emissionskoeffizient und Absorptionskoeffizient gleich sind – also wo absorbiert wird, wird auch emittiert.
MfG
„Eine Rückstrahlung der von der Erdoberfläche abgehenden Wärmeabstrahlung wieder zur Erde hin wäre ausschließlich durch Reflexion möglich“
Wenn Sie denn definieren würden, was Sie unter „Wärmeabstrahlung“ verstehen, könnte man vielleicht Ihren Ausführungen folgen.
Und das hier ist Quatsch: 2In der Lufthülle der Erde sinkt auf Grund des mit der Höhe abnehmenden Druckes die Temperatur kontinuierlich, bei trockener Luft um 1oC je 100 m Höhe, unter üblichen atmosphärischen Bedingungen (feuchte Luft) um etwa 0,7oC je 100 m Höhe. Oben ist es also kälter als unten.“
Was ist feuchte Luft oder trockene Luft in Ihrer Vorstellungswelt?
Und daß es oben immer „kälter“ ist, ist auch eine Fiktion. Schon mal was von Inversion, Peplopause, Tropopause gehört?
„Betrug ist die Behauptung es gäbe eine „Gegenstrahlung“ in Höhe von 324 W/m²!“
Wenn Sie meinen, und Messungen verleugnen, dann betrügen Sie eben nicht nur andere, sondern auch sich selbst.
Betrug ist die Behauptung es gäbe eine „Gegenstrahlung“ in Höhe von 324 W/m²! aus IR-angeregten Spurengasen zur Begründung der Temperatur der Erdoberflâche von 288 K. Die Temperaturschichtung der Troposphäre hat praktisch nichts mit dem CO2 Gehalt zu tun und somit kann auch eine Freisetzung von CO2 durch menschliche Aktivitäten keine Klimaveränderung hervor rufen. Das sind die Fakten, wie Sie aus der Thermodynamik abzuleiten sind. Die Strahlungseigenschaften der Spurengase sind wichtig für die Kühlung der Atmosphäre, aber ein Aufheizen duch das CO2 ist weder theoretisch noch empirisch begründbar. Egal was der IPCC an politisch gewünschtem Unsinn auch von sich geben mag, die „Klimakatastrophe“ durch CO2 ist und bleibt ein Hirngespinst.
Erklären Sie mir lieber, warum Sie hier betrügen
und Ihre physikalisch falsche Meinung als Zitat aus einem Lehrbuch von v Storch et al. darstellen?
Dann würde es mich noch interessieren, warum man eigentlich jedem persönlich hier schreiben muss, dass die IR-Strahlung aus der Atmosphäre nicht durch Reflexion zum Boden gelangt, sondern dass es sich um thermische Strahlung handelt und diese in alle Richtungen abgestrahlt wird?
in ihrem Posting behaupten Sie quasi, dass die Oberflächentemperatur eines Planten nicht von der Größe seiner Atmosphäre abhängt. Hat das ihnen Herr Ebel (Innerhofer, Baecker, Dr. Mayer, Marvi Müller, Alex alias Fischer, etc) erklärt? Oder entsprang das ihrer eigenen omnipotenten Ahnungslosigkeit.
Jetzt noch mal zur Klarstellung. Ein paar ppm mehr CO2 führen zur Katastrophe aber auf 2/3 der Atmosphäre könnte man locker verzichten.
Und jemand mit so einer Nullahnung ist aber vehementer Verfechter der „Treibhausthese“ nach der wir alle in der Hölle schmoren, wenn wir weiter soviel CO2 produzieren.
Ich habe keine Ahnung was Sie einwerfen. Aber Sie sollten damit aufhören.
Eine Rückstrahlung der von der Erdoberfläche abgehenden Wärmeabstrahlung wieder zur Erde hin wäre ausschließlich durch Reflexion möglich, ähnlich der Wirkung der Alu-Folie unter der Wärmeisolierung in unseren Dächern. Reflexion gibt es jedoch durch das in der Lufthülle (unterste ca. 25 km der Atmosphäre) gleichmäßig verteilte CO2 nicht. Reflexion, wie Brechung, dies ist aus der Strahlenoptik bekannt, tritt nur an Grenzschichten von Stoffen unterschiedlicher optischer Dichte oder an Phasengrenzen eines Stoffes oder Stoffgemisches (fest-flüssig, flüssig-gasförmig, fest-gasförmig) auf, so z.B. an Wassertropfen oder Eiskristallen in/an der feuchten Luft, an der Grenze Luft-Wasser, nicht aber innerhalb von homogenen Stoffen, wie z. B. Gase und Gasgemische (Luft), Wasser, Glas.
Die Absorption von Strahlungsenergie innerhalb der Lufthülle, verursacht von Bestandteilen wie CO2, führt nun aber keineswegs zu einer Erwärmung. Die Gründe hierfür sind weitgehend bekannt und können wie folgt zusammengefaßt werden:
In der Lufthülle der Erde sinkt auf Grund des mit der Höhe abnehmenden Druckes die Temperatur kontinuierlich, bei trockener Luft um 1oC je 100 m Höhe, unter üblichen atmosphärischen Bedingungen (feuchte Luft) um etwa 0,7oC je 100 m Höhe. Oben ist es also kälter als unten.
Wenn innerhalb der Atmosphäre Wärmeabstrahlung der Erde absorbiert wird, erwärmt sich die absorbierende Materie. Der für einen Ruhezustand der Luftschichten notwendige und gegebenenfalls zuvor bestandene vertikale Verlauf von Temperatur, Volumen und Druck wird gestört. Luft dehnt sich bei Erwärmung aus, wird bezogen auf die Volumeneinheit leichter als die umgebende, auch darüberliegende, kühlere Luft, und steigt deshalb auf. Gegebenenfalls absorbierte Wärme wird durch Luftmassenaustausch abgeführt. Ebenso wie jene Wärme, die der Luft durch Konvektion zugeführt wird. Es kommt somit zur Abfuhr der absorbierten Wärme durch Aufsteigen der erwärmten Luft. Dieser Vorgang ist übrigens auch unter dem Begriff Thermik geläufig. Beim Aufsteigen der Luft sinkt gleichzeitig durch Ausdehnung infolge Druckabnahme deren Temperatur, so daß sich keine Erwärmung einstellt.
Voraussetzung für jede Art der Wärmeübertragung ist stets, daß der Absender wärmer ist, also eine höhere Temperatur ausweist als der Empfänger. Die durch Strahlung übertragbare Wärme ist dabei proportional der Differenz der jeweils 4. Potenzen der Temperaturen des aussendenden und des empfangenden Ortes. Wegen der einheitlichen Temperatur innerhalb kleinster Gasvolumina in der Luft und der mit der Höhe rückläufigen Temperatur ist es ausgeschlossen, daß es z. B. durch CO2-Anteile zu einer Rückübertragung der von der Erde oder erdnäher liegenden Schichten abgehenden Wärmeabstrahlung wieder zur Erde hin kommen kann.
Die dünne Luft alleine ist nicht die Ursache für die tiefen Temperaturen auf dem Mt.Everest. Würde es keinen Luftaustausch mit tieferen Schichten geben, dann erwärmt sich die Luft genauso wie bei uns. Es findet aber ein ständiger Luftaustausch statt. Warme Luft in tieferen Schichten dehnt sich aus. Beim Aufstieg nach oben gibt es seine Wärme ab. Wenn man Gas spontan ausdehnen lässt, so gibt es Wärme ab. Da wird Ihnen niemand widersprechen. Nur ist das kein ewiger Prozess. Sobald die Wärmeübertragung in Gang kommt, wird auch das dünnere, kältere Gas wieder aufgewärmt. Auf dem Mt.Everest scheint es, als wenn die Luft dort ewig kalt bleibt, in Wirklichkeit findet aber ein ständiger Luftaustausch statt, wo immer wieder kalte, ausgedehnte Luft von unten nachkommt. Würden Sie diesen Prozess stoppen, erwärmt sich auch dort allmählich die Luft. Die geringere Dichte wird dazu führen, dass die Tag-Nacht-Unterschiede extremer werden, als Extrembeispiele kann man hierfür den Mond oder den Merkur nennen. Im Schnitt führt eine dünnere Atmosphäre aber zu ähnlichen Durchschnittstemperaturen. Wenn man mal die Hochebene von Tibet nimmt, sieht man was passiert, wenn der Luftaustausch mit niedrigeren Luftmassen eingeschränkt ist. Die Durchschnittstemperaturen ähneln nämlich dann fast denen unserer Breiten. Mit anderern Worten, der Mt.Everest ist deshalb so kalt, weil es Luftschichten gibt, die tausende Meter unterhalb liegen. Wäre alles auf dem Niveau vom Mt.Everest, aber mit demselben Luftdruck wie heute auf diesem Berg, dann würde hauptsächlich der Sonnenstand über die Temperaturen bestimmen.
„p.s. es hindert Sie kein Mensch, ihre Luftdruckexperimente durchzuführen.“
Schon passiert. :o)
MfG
S.Hader
Die adiabatische Druck und Temperaturverteilung hat per definitione NICHTS mit Bewegungen von Lufmassen zu tun, die diesen Gradienten natürlich überlagern können,
sondern nur mit der Masse des Gases und der Gravitation.
Sie existiert also uneingeschränkt auch bei totaler Windstille.
Es ist auf dem Mt.Everest auch bei totaler Windstille erheblich kälter, weil die Luft dort in dieser Höhe dünner ist.
Der niedrige Luftdruck ist NICHT eine Folge von Konvektion.
mfG
p.s. es hindert Sie kein Mensch, ihre Luftdruckexperimente durchzuführen.
Ich würde bei hohem Druck einen KFZ-Mechaniker fragen.
„Von Storch et al. bestätigen in [14], daß der Ansatz der „Gegenstrahlung “ willkürlich gewählt und damit nicht im geringsten durch Messung verifiziert ist. Dieser Ansatz ist getroffen worden, um beobachtete Temperaturen in einem angewendeten Energiebilanzmodell rechnerisch reproduzieren zu können, was ohne Einbeziehung einer solchen „Gegenstrahlung“ bei dem genutzten (hypothetischen) Energiebilanzmodell nicht gelänge. Es handelt sich bei der „Gegenstrahlung“ also keinesfalls um eine gemessenene, es ist vielmehr eine frei erfundene Größe.
[14] von Storch, H., Güss, S., Heimann, M., Das Klimasystem und seine Modellierung, Springer-Verlag, Berlin Heidelberg New York, 1999, S. 83″
Oha, ein manifester Betrug von Ihnen!!
Diese als Zitat („“) gekennzeichnete Stelle gibt es in dem Buch gar nicht. Außerdem unterschlagen Sie frechdreist, was in dem Buch sonst noch steht (siehe links zun den Seiten 82-87, das haben Sie den Lesern doch glatt verschwiegen…: http://tinyurl.com/VStorch-etal-p82, http://tinyurl.com/VStorch-etal-p84, http://tinyurl.com/VStorch-etal-p86).
An der Textstelle S. 83 fällt der Begriff „Gegenstrahlung“ nicht. Und außerdem steht da unten auf der Seite 83 nun (kontrollieren Sie das Zitat in den links)
„Es ist aber möglich, mit Daten aus Meßkampagnen am Boden und vom Satelliten aus zu prüfen, ob der Ansatz konsistent (also widerspruchsfrei) mit den Beobachtungsdaten ist.“
Und dann wird betont, dass es sich bei dem Modell um ein EBM handelt und im nächsten Kapitel 4.3. ab S. 85 geht es um weiterentwickelte „physikalisch orientierte Modelle“, in denen man (S. 86 oben) „mehrere übereinanderliegende Atmosphärenschichten betrachtet“, bei denen für jeder dieser Schichten die Energiebilanz angesetzt wird, und „jeder Schicht Temperatur, Wärmekapazität und auf- und abwärtsgerichtete Strahlungsflüsse zugeordnet“. Der abwärtsgerichtete Strahlungsfluss im IR ist die Gegenstrahlung!
Ihr billiger Täuschungsversuch gegen die Leser ist aufgeflogen!
„Die Erde kann Wärme abstrahlen und die Spurengase H2O und CO2 können ihre Anregungsenergie auch abstrahlen – allerdings nur in großen Höhen, also bei hinreichend geringer Dichte der Luft!“
So wie ich Sie (und andere, die diese beliebten wissenschaftlich falschen Behauptungen bringen) verstehe, machen Sie eine Unterscheidung zwischen der Abstrahlung einer Gasatmosphäre ins Weltall und der Abstrahlung von einem Teil der Gasatmosphäre zu einem anderen bzw. der Abstrahlung zum Boden. Anscheinend lassen Sie sich von der Vorstellung leiten, dass ein Molekül in einer dichten Gasatmosphäre öfter inelastische Stöße macht und somit die für strahlende Abregung und damit Emission weniger Moleküle zur Verfügung stehen also in der dünneren Atmosphäre oben.
Es ist richtig, dass inelastische Stöße unten häufiger stattfinden. Aber Sie übersehen (bzw. ignorieren es vorsätzlich-?), dass die Moleküle trotzdem im thermischen Gleichgewicht mit dem Strahlungsfeld sind, und das bedeutet, dass abregende und anregende strahlenden Uebergaenge sich das Gleichgewicht halten. Ihre Vorstellungen kommen bei nicht-thermischen Strahlungsquellen vor, spielt aber in der unteren Atmosphaere keine Rolle.
“ Meinen Link nach Prof. Hebert noch immer nicht gelesen?“
Doch, aber ich kenne das alles schon aus den Lehrbüchern, aus denen der Herr die Abbildungen her hat. Zu den hier gefragten physikalischen Vorgängen schreibt er aber nichts.
„Messgrössen?? Das hat noch nie jemand gemessen, die „Gegenstrahlung“ ist nichts als eine willkürlich Bilanzgrösse!“
Das ist falsch, suchen Sie mal im Eike-Archiv unter dem link Hamburger Wettermast. Da wird online die aktuelle Gegenstrahlung bei Hamburg gemessen.
Fazit: Atmosphärendruck und Vertikalzirkulation können den Boden NICHT wärmen!
Antwort:
Föhnwetterlagen sind also auch nur Einbildung?
„Dann machen wir mal folgendes Gedankenexperiment:“
Lieber Herr Dietze – Sie ahben zwar schon eine Menge Kenntnisse zum Treibhauseffekt – aber trotzdem noch große Defizite.
In der Stratosphäre herrscht kaum Vertikalzirkulation, nur in der Troposphäre ist die Vertikalzirkulation gradientenbestimmend. Genau so, wie die Tropopausenhöhe bei zunehmender Treibhausgaskonzentration zunimmt, nimmt sie bei geringerer Treibhausgaskonzentration ab. Ganz ohne Treibhausgase liegt die Tropopause fast auf der Erdoberfläche auf – die Konvektion entfällt also wegen fehlender Troposphäre und Ihr Gedankenexperiment entbehrt jeder Grundlage.
Mit der Verlagerung der Tropopause ist noch eine weitere veränderung verbunden – um so höher die Tropopause, um so kühler wird die Stratosphäre. Also auch umgekehrt, um so niedriger die Treibhausgaskonzentration, um so wärmer die Stratosphäre.
Summa summarum: Der größte Teil der Atmosphäre ist etwa so warm, wie das wärmste Gebiet der Erdoberfläche und der größte Teil der Erdoberfläche ist kühler und die Durchschnittstemperatur ist deutlich unter -18°C. Die warme Atmosphäre und die kühle Oberfläche sind durch eine Inversionsschicht getrennt, die sehr stabil ist und schlecht wärmeleitend: http://tinyurl.com/8hvacxn
„Bei Temperaturinversionen nimmt die absolute Temperatur mit zunehmender Hoehe zu. Was wir dann haben, wird als thermisch sehr stabil bezeichnet. … Unter solchen thermischen Bedingungen ist ein turbulenter Waermefluss kaum noch nenenswert (falls er ueberhaupt noch zu messen ist)“
Also Ihr Gedankenexperiment geht vollkommen fehl:
@ #270: P. Dietze sagt am Montag, 24.09.2012, 11:06
„Höchst blamabel – … insbesondere aber für den Physiker Ebel sowie für jene „Thermodynamiker“ die das Adiabatik-Gasgesetz ohne Verstand anwenden.“
Sagen wir mal lieber „Höchst blamabel“ für Herrn Dietze, der den Treibhauseffekt nur halb verstanden hat, aber Schiedsrichter spielen will.
MfG
„Atmosphärengase die schnell zur Oberfläche zirkulieren, erwärmen sich durch Kompression, während umgekehrt die bei Zirkulation natürlich auch vorhandene Aufwärtsströmung durch Druckabnahme sich abkühlt“
Aha, Atmosphärendruck und Vertikalzirkulation wärmen den Boden.. Dann machen wir mal folgendes Gedankenexperiment: Die Erdatmosphäre bestehe aus solar- und IR-transpatentem N2, und wir haben wegen der Vertikalzirkulation einen Temperaturgradienten – oben kalt und unten warm. Die Frage ist nur, wie warm wäre es denn am Boden?
Antwort: -18 °C !! Wäre es nämlich wärmer, würde der Boden MEHR als die 240 W/m² – die er von der Sonne erhält – in den Weltraum abstrahlen und wir hätten ein energieerzeugendes Perpetuum Mobile. Höchst blamabel – nicht nur für Herrn Pesch #263 – insbesondere aber für den Physiker Ebel sowie für jene „Thermodynamiker“ die das Adiabatik-Gasgesetz ohne Verstand anwenden. Fazit: Atmosphärendruck und Vertikalzirkulation können den Boden NICHT wärmen!
„Das was Sie, Herr Pesch, als Ergebnis erwarten, dürfte klar sein. Das was rauskommen wird, dürfte dagegen …“
Dazu auch ein erweitertes Diagramm: http://tinyurl.com/86z7np7
Das die dickere Venus-Troposphäre mit ihrem nahezu konstanten Temperaturgradienten (die Temperturgradienten auf Erde und Venus sind ähnlich) durch die Vertikalzirkulation zu einer höheren Bodentemperatur führt, sollte eigentlich klar sein. Atmosphärengase die schnell zur Oberfläche zirkulieren erwärmen sich durch Kompression, während umgekehrt die bei Zirkulation natürlich auch vorhandene Aufwärtsströmung durch Druckabnahme sich abkühlt.
Interessanter sind Erd- und Venustropopause: Zwar hat die Erdtropopuase einen höheren Gesamtdruck (ca. 200mbar), aber der Partialdruck des CO2 ist mit ca. 0,16 mbar vergleichbar mit dem Tropopausengesamtdruck der Venus, die eine fast reine CO2-Atmosphäre hat.
Interessant ist auch die Temperatur der Venustropopause (niedriger als Erdtropopause trotz größerer Sonnennähe). Bei der beobachteten Zunahme der CO2-Konzentration auf der Erde verschieben Partialdruck und Tropopausentemperatur in Richtung Venustropopause.
MfG
#258: „S.Hader, Sie meinten sicher bestätigt;
wie selbst in der AGW-freundlichen „nature“ lesen kann, die haben Sie doch sicher als Pflichtlektüre abonniert.
http://tinyurl.com/cjvx4s7“
Nein, die habe ich nicht abonniert. Hier eine Fassung, die man auch ohne Account lesen kann:
http://tinyurl.com/cwoq7ze
„p.s. was ist denn so schwer zu verstehen an meinen Ausführungen?“
Sehr häufig sind es ihre unpräzisen Aussagen. Da wird gerne mal etwas als wärmer bezeichnet, ohne zu konkretisieren, ob es sich dabei auf die Maximal- oder Durchschnittstemperaturen bezieht. Im konkreten Fall bei #229 gibt es hingegen keine Verständnisschwierigkeiten. Die Aussagen dort sind nur einfach falsch. :o) Was Sie nun mit dem Nature-Artikel beweisen wollen, dürften vermutlich nicht mal Ihre Fans genau wissen.
@Gerald Pesch,
#263: „Die Temperatur der Venus ist durch den Bodendruck bestimmt, nicht durch irgendwelche „Gegenstrahlung“ aus dem CO2.“
Wenn dem tatsächlich so ist, dann ließe sich das mit einem einfachen Experiment nachprüfen. Das dürfte auch für Dr.Paul interessant sein und wer das Wood-Experiment schon kennt, wird wohl Gefallen daran haben. Man baut einfach Glaskästen, die mit Luft gefüllt sind und dem Sonnenlicht ausgesetzt werden. Dabei genügen schon zwei Kästen, einer wird mit Normaldruck betankt und beim zweiten wird ein Überdruck erzeugt. Die Kästen sollen dasselbe Volumen besitzen. Wahlweise kann man statt Überdruck auch einen Unterdruck erzeugen. Das weitere Vorgehen kann man sich fast schon denken, man vergleicht die Temperaturen über den Tag. Das was Sie, Herr Pesch, als Ergebnis erwarten, dürfte klar sein. Das was rauskommen wird, dürfte dagegen Physik-Interessierte nicht überraschen. :o)
MfG
S.Hader
Sie geben hier also offen zu, dass Sie nicht einmal das Bratpfannenbeispiel verstehen.
Peinlich, peinlich 🙂
mfG
„Es ist die Tarnkappe von Leuten, die ihre eigene Reputation nicht mit dem Unsinn verbunden sehen wollen, den Sie aus AGW-Gründen verbreiten wollen.“
Wie kommt es dann, daß Leute ohne Trankappe das Gleiche sagen:
– Stefan 1879 – http://tinyurl.com/bvfp7od S. 411 (tatsächlich 1879 – also vor über 130 Jahren).
– Einstein 1916 – http://tinyurl.com/5rw3szr
– Prof. Kramm – http://tinyurl.com/ccqxz7q
– Schwarzschildt – 1906 http://tinyurl.com/KarlSchwarzschild-1906
– Goody/Yung 1995 – http://tinyurl.com/RGoody-Yung-p22 , http://tinyurl.com/GoodyYung-p46
– Kondratyev 1969 – http://tinyurl.com/Kondratyev-p36
MfG
deswegen poste ich hier auch so sparsam.
Klaus Plöger
Ich frage mich grade, ob eine Bratpfanne oder ein Gewächshaus besser zur Veranschaulichung des Treibhauseffektes dient. Was meinen Sie?
Manchmal ist es schwer die Quantenphysik mit einem Nudelholz zu erklären. Manchmal spielt die Physik unserer Logik auch einen Streich. Zum Beispiel bei der Relativitätstheorie. Viele kennen Sie, aber nur eine Handvoll verstehen Sie auch. Oder (besser zum Klima): warum fällt das Wasser aus einer Wolke nicht einfach runter?
Wie Sie sehen Herr Dr. Paul: Man kann nicht immer auf Hausfrauenart die Physik erklären. Versuchen Sie es dann bitte auch nicht. Oder was glauben Sie: Ist ein Liter trockenes oder ein Liter feuchtes (z.B. gesättigtes) Wasser schwerer (bei gleichem Druck)?
Die Temperatur der Venus ist durch den Bodendruck bestimmt, nicht durch irgendwelche „Gegenstrahlung“ aus dem CO2.
http://tinyurl.com/6ur7fnm
…nach den primaeren Messgroessen thermische Bodenstrahlung und atmosphaerische Gegenstrahlung aufgeschluesselt.
Antwort:
Messgrössen?? Das hat noch nie jemand gemessen, die „Gegenstrahlung“ ist nichts als eine willkürlich Bilanzgrösse!
Von Storch et al. bestätigen in [14], daß der Ansatz der „Gegenstrahlung “ willkürlich gewählt und damit nicht im geringsten durch Messung verifiziert ist. Dieser Ansatz ist getroffen worden, um beobachtete Temperaturen in einem angewendeten Energiebilanzmodell rechnerisch reproduzieren zu können, was ohne Einbeziehung einer solchen „Gegenstrahlung“ bei dem genutzten (hypothetischen) Energiebilanzmodell nicht gelänge. Es handelt sich bei der „Gegenstrahlung“ also keinesfalls um eine gemessenene, es ist vielmehr eine frei erfundene Größe.
[14] von Storch, H., Güss, S., Heimann, M., Das Klimasystem und seine Modellierung, Springer-Verlag, Berlin Heidelberg New York, 1999, S. 83
Schwachsinn. Jeder Planet mit Gasatmosphäre emittiert aus seiner Atmosphäre thermische Strahlung. Gucken Sie sich Messungen an!
Antwort:
Bestreitet ja auch niemand. Meinen Link nach Prof. Hebert noch immer nicht gelesen?
Abb. 4: IR-Emissionsspektren der Erdatmosphäre über (a) – der Sahara, (b) – dem Mittelmeer und (c) – über Antarktika (nach HANEL, 1972; BOLLE, 1979)
Die eingezeichneten Schwarzkörperkurven nach Planck zeigen Temperaturniveaus bei 320 K, 260…280 K und 220 K an. Die Strahlungsquellen sind:
– Im IR-Fenster (8…13 ?m) die Sahara mit einer Bodentemperatur von ca. 45 oC,
– im Bereich der H2O-Rotationsbande (? > 15 ?m, Abb. 3) der Wasserdampf mit t ? 10 oC, also in einem Höhenniveau um 4000 m und
– bei 15 ?m das CO2 (t ca. –50 oC) im Höhenbereich um 10000 m.
Wir erkennen: Die Erde kann Wärme abstrahlen und die Spurengase H2O und CO2 können ihre Anregungsenergie auch abstrahlen – allerdings nur in großen Höhen, also bei hinreichend geringer Dichte der Luft!
Sie überfordern den Avatar Baecker restlos. Das Kunstwesen weiss nicht, was eine Bratpfanne ist, da es sich nur virtuell manifestiert. Es ist die Tarnkappe von Leuten, die ihre eigene Reputation nicht mit dem Unsinn verbunden sehen wollen, den Sie aus AGW-Gründen verbreiten wollen. Das macht der Avatar Baecker. Es ehrt Sie, daß Sie gegen den Unsinn vorgehen, aber es würde den Mitlesern sehr helfen, wenn Sie die reale Nichtexistenz Ihres Gegenübers deutlich machen. Das zeigt nämlich, daß die übergroße Mehrzahl der Wissenschaftler weder den sachlichen Unfug noch die politische Zielsetzung(große Transformation) der unbekannten Hintermänner des Avatars mitträgt.
MfG
Michael Weber
Es genügt für die Richtigkeit der Bemerkung von Herrn Pesch also lediglich die Alltagserfahrung einer Bratpfanne auf der Heizplatte mit und ohne Wasser darin.
Oder haben Sie schon einmal eine rot glühende Bratpfanne mit Wasser darin gesehen?
mfG
wie selbst in der AGW-freundlichen „nature“ lesen kann,
die haben Sie doch sicher als Pflichtlektüre abonniert.
http://tinyurl.com/cjvx4s7
mfG
p.s. was ist denn so schwer zu verstehen an meinen Ausführungen?
damit Sie wissen, was Sie zu widerlegen haben, hier die Strahlungstransportgleichung in unterschiedlichen Lehrbüchern. In keinem dieser Lehrbücher sind die von Ihnen postulierten Gültigkeitskriterien genannt. Goody Yung und Kondratyev verwenden sie zur Berechnung des Strahlungstransports in der Erdatmosphäre, Karl Schwarzschild wendet sie für Analoges in der Sonnenatmosphäre an.
Goody/Yung, Seite 22
http://tinyurl.com/RGoody-Yung-p22
Goody/Yung, Seite 46
http://tinyurl.com/GoodyYung-p46
Kondratyev, S. 36
http://tinyurl.com/Kondratyev-p36
Karl Schwarzschild 1906
http://tinyurl.com/KarlSchwarzschild-1906
dF/dz = (B-F)/L
Wie man leicht sehen kann folgt daraus als Grenzfall das bekannte Lambert-Beerschen Gesetz:
dF/dz = -F/L, wenn die Plancksche Strahlungsquelldichte B gegenüber der einfallenden Strahlungsdichte F vernachlässigbar ist. Das ist z.B. für die Extinktion sichtbaren Lichts bei Raumtemperatur der Fall, bei der Sonne trifft dies wiederum nicht zu. Für IR-Strahlung bei Raumtemperatur muss man die volle Gleichung nehmen, es sei denn die einfallende IR-Strahlung F hat eine viel höhere Strahlungsdichte als die thermische B (z.B. IR-Laser).
Hat das Medium längs des Weges konstante Temperatur, ist also dB/dz = dB(T(z))/dz = dB/dT*dT/dz = 0, wegen dT/dz = 0, d.h. B(z) = B0 und ist die Anfangsbedingung F(0) = B0, so ist die Lösung F(z) = B0. D.h. unabhängig von der Absorptionslänge ist die Strahlungsdichte konstant gleich dem Anfangswert. Das ist natürlich klar, denn längs des Weges wird gleich viel emittiert wie absorbiert. Dies sieht man auch an einem Spektrum von thermischen Na-D-Linien, die durch eine kontiniuerliche Flamme gehen. Ist die Flamme kälter, so sieht man die Na-D-Linien in Absorption im kontinuierlichen Spektrum der Flamme, ist die Flamme wärmer, so sieht man die Na-D-Linien in Emission. Wenn beide thermischen Quellen gleiche Temperatur haben, so sieht man keine Linien mehr im kontinuierlichen Spektrum, da F(z)_NaD konstant ist.
Sie schrieben in #242:
„Will man experimentell innerhalb von Gasen eine Energieabgabe einzelner Gasmoleküle durch Strahlung erreichen, so müssen entweder die Gase in erheblicher Verdünnung, praktisch in vakuum-ähnlichen Druckzuständen vorliegen, oder aber die dem Gas zugeführte und dann wieder abzugebende Leistung muß beträchtliche Leistungsdichten erreichen. Unter Bedingungen der unteren Atmosphäre, also im Luftraum bis rd. 25 km Höhe, gibt es weder die eine noch die andere Voraussetzung für das Auftreten quantenphysikalischer Reemission empfangener Wärmestrahlung einzelner Moleküle.“
Schwachsinn. Jeder Planet mit Gasatmosphäre emittiert aus seiner Atmosphäre thermische Strahlung. Gucken Sie sich Messungen an!
“
Energiebilanzen siehe meinen Link zu der Arbeit von Prof. Hebert.
Eine Gegenstrahlung gibt es da nicht.“
Bei Prof. Hebert wird auf die Energiebilanz von Kiehl Trenberth referenziert. Fuer die Energiebilanz reicht es auch, wenn man nur die Differenz der thermischen Strahlungsstroeme bilanziert, in KIehlTrenberth sind die eben noch nach den primaeren Messgroessen thermische Bodenstrahlung und atmosphaerische Gegenstrahlung aufgeschluesselt. Denn die 66 Wm-2 IR-nettoverlust des Bodens ermittelt man ja durch globale Mittelung der thermischen Abstrahlung der Bodenflaeche minus dem glibalen Mittel der Gegenstrahlung.
„Aus der Wärmelehre ist aber auch bekannt, daß Energie im wesentlichen dann über Strahlung abgegeben wird, wenn die anderen Wege zur Energieabfuhr, nämlich Konvektion (Wärmeübergang) und Wärmeleitung, nicht oder nicht in ausreichendem Maße genutzt werden können.“
Waermetransport durch Konvektion findet in der unteren Atmosphaere auch zusaetzlich statt, dies widerspricht nicht der Schwarzschildschen Strahlungstranportgleichung. Sie argumentieren jedoch nur ueber Extremfaelle, in denen der Strahlungstransport dominiert. Der Strahlungstransport in der unteren Erdatmosphaere ist nun nicht Groessenordnungen groesser als der konvektive Anteil, aber nun auch nicht Groessenordnungen kleiner. Wenn Sie keine quantitative Therorie haben, die man den Ergebnissen gemaess dem Lehrbuch GoodyYung und anderer meteorologischen Literatur gegenueber stellen kann, ist Ihre Argumention als nicht bewertbare Spekulation zu verwerfen, zumal Sie keine wissenschaftlichen Beweise anfuehren koennen, die GoodyYung widerspraechen.
Das liegt schlicht daran, dass hier der Kühleffekt deutlich überwiegt, weil dadurch auch die Transparenz für Sonnenlicht deutlich vermindert wird, also die Wirksamkeit der eigentlichen treibenden Wärmequelle für die Erdoberfläche.“
Sehr geehrter Dr.Paul, Ihre Behauptungen werden schon allein durch die Existenz des Planeten Venus und der dort herrschenden Temperaturen in Oberflächennähe widerlegt.
Als wenn letzteres hier von Bedeutung wäre.
Klimawandel
Der Treibhauseffekt
Hauptverursacher: Kohlendioxid
Die als Treibhauseffekt bezeichneten physikalischen Prozesse in der Erdatmosphäre sind absolut notwendig für das Leben auf unserem Planeten. Derzeit beträgt die durchschnittliche Temperatur an der Erdoberfläche etwa plus 15 Grad – ohne den natürlichen Treibhauseffekt läge sie bei lebensfeindlichen minus 18 Grad. Die Stärke des „wärmenden“ Treibhauseffektes hängt davon ab, wie hoch die Konzentration bestimmter Gase, sogenannter Treibhausgase, in der Atmosphäre ist. Auf der Venus zum Beispiel bewirkt eine Atmosphäre, die zu 96 Prozent aus Kohlendioxid besteht, die Aufheizung unseres Schwesterplaneten auf bis zu 470 Grad Celsius.
Die Wirkungsweise des Treibhauseffektes lässt sich am besten, wie es der Name schon sagt, mit den aus dem Gartenbau bekannten Gewächshäusern erklären. Ihre Glas- oder Folienhüllen lassen fast die gesamte Sonnenstrahlung ungehindert passieren, verhindern jedoch, dass die vom Treibhaus empfangene Wärme wieder nach außen entweichen kann. Sie wird an der Glasschicht festgehalten. Deshalb sind in Gewächshäusern selbst an frostigen Wintertagen bei Sonnenschein ohne künstliche Beheizung wachstumsfördernde Temperaturen anzutreffen.
Das ist so wissenschaftlich wie das Horoskop in der Fernsehzeitschrift!!
Die Venus (Schwesterplanet!!!, vom CO2 vergewaltigt…) ist so heiß wegen dem „vielen CO2“ und das CO2 in der Troposphäre wirkt analog zum Gärtnertreibhaus! Mit solchen Märchen werden die Leute gefüttert damit die „große Transformation“ der Gesellschaftsumbauer vom PIK auch genügend demütige Anhänger findet. Keine Ahnung, wer bei „Wetter Online“ verantwortlich ist für solche Ökopropaganda auf Kindergartenniveau, aber mit Meteorologie hat das nichts mehr zu tun.
Ach Herr Dietze, dass Ihre Modelle entweder am 1. Hauptsatz oder am 2. Hauptsatz sterben, hat Herr Roesicke Ihnen doch schon dargelegt. Es bringt nichts wenn ich jetzt wieder von vorne anfange….
Die Strahlungstransportformel ist auf die Troposphäre nicht anwendbar. Die Gründe habe ich Ihnen genannt.
“ Womit begründet man die 350 W?“
Ist physikalisch bereits geklaert.
Wenn Sie glauben, dieser Wert waere Null, so zeigen Sie mal Ihre Energiebilanz, die ohne diesen Term den Energieerhaltungssatz erfuellt.
Antwort:
Energiebilanzen siehe meinen Link zu der Arbeit von Prof. Hebert.
Eine Gegenstrahlung gibt es da nicht.
erklaeren Sie Ihren Denkfehler einfach Richard Goody, warum die Strahlungstransportformel nicht richtig sein sollte, in GoodyYung steht sie eben so, wie ich sie oben notiert und geloest habe, und das, trotzdem die Quantenphysik in seinem Lehrbuch zugrundegelegt wurde. Fragen Sie mal, wie es sein kann, dass 4 Generationen Physiker nicht gemerkt haben, dass Karl Schwarzschilds Arbeiten zum Strahlungstransport falsch sind, und melden Sie sich zum Nobelpreis an.
„Nichts ist im Lot.“
Meine rechnung schon. Oder habe ich mich etwa verrechnet?
“ Womit begründet man die 350 W?“
Ist physikalisch bereits geklaert.
Wenn Sie glauben, dieser Wert waere Null, so zeigen Sie mal Ihre Energiebilanz, die ohne diesen Term den Energieerhaltungssatz erfuellt.
„Nichts ist im Lot.. Und da dreht es sich, das perpetum mobile der Klimakirche mit dem man jede beliebige Temperatur am Erdboden einstellen kann – bei konstanter Insolation!!“
Nein, alles ist ok – bloß haben Sie die Gegenstrahlung energetisch mißverstanden. Lassen Sie einfach mal das Flußbild von Trenberth weg und denken Sie sich im Strahlungsmodell eine für Sonnenlicht (abzüglich Albedo) transparente Atmosphäre. Dann wird der Boden (im Mittel) mit 240 W/m² beheizt. Er hat 288 K und emittiert 390 W/m². Davon werden 300 W/m² in der Atmosphäre absorbiert. Je 150 W/m² werden dann thermisch nach unten und oben re-emittiert.
Dann kommen oben heraus: 390-300+140=240 W/m² und der Boden erhält 240(Sonne)+150(Gegenstrahlung)=390 W/m², also genau soviel wie er auch wieder emittiert. Ihre Vermutung daß sich per Gegenstrahlung jede beliebige Temperatur am Erdboden einstellen kann, beruht auf einem Mißverständnis. Die Absorption von 300 W/m² ist durch den derzeitigen THG-Gehalt mitsamt Wolken bedingt und keinesfalls beliebig.
Angenommen, die Absorption steigt um 4 W/². Dann steigt die Bestrahlung des Bodens um 2 W/m² und dessen Temperatur zunächst um 2/390/4*288=0,37 °C. Die Abstrahlung steigt um 2 W/m² und die Gegenstrahlung weiter um 2*150/390=0,77 W/m² usw. Es ergibt sich eine geometrische Reihe mit dem Endwert 0,37*1/(1-150/390)=0,6 °C.
„wird ggf. die durch Absorption von Strahlung aufgenommene Energie unverzüglich in die Form Wärme transformiert und ebenso schnell durch Konvektion und Leitung an die unmittelbare Umgebung abgegeben.
Ihre Strahlentransportkaskade gibt es nicht.“
Sie sollten sich mal etwas gründlicher mit Strahlungsphysik und Kirchhoff befassen.
Z.B. Einstein http://tinyurl.com/5rw3szr oder sich eine Bemerkung von Prof. Harde S. 34 oben zu Gemüte ziehen: „In den Spektralbereichen, in denen eine starke Absorption der Eingangsstrahlung auftritt, emittiert die Atmosphäre eben auch besonders intensiv.“
MfG
PS: Das die Abstrahlung den Umweg über den Wärmeinhalt des Gases macht, ist für die Wirkung unerheblch. Es wird sogar mehr abgestrahlt, als absorbiert wird, weil auch konvektiv herantransportierte Wärme abgestrahlt wird.
„Es ist eine Frechheit, wie Sie sich hier aufführen und so tun, als wären Sie eine Klimakapazität.“
Es ist schon ein Witz, wie Sie ohne ausreichende Kenntnisse in Physik und Klima hier etwas beurteilen wollen. Leute die etwas mehr Ahnung als Sie haben, schreiben z.B. ( http://tinyurl.com/8eqoh75 ):
„Lieber Herr Ebel, … Aber mal ungeachtet aller technischer Detaildiskussion: in Ihrem grundlegenden Punkt haben Sie natürlich Recht, dass es nicht nur den einen von mir genannten Grund für die Stabilität der Stratosphäre gibt, insofern war mein kurzer Einwurf zu simpel. Wir freuen uns über kompetente Leser, die (oft mit erheblich mehr Zeit, als wir darauf verwenden können) Zusammenhänge näher erläutern – auch wenn es für die Mehrheit der Leser eines Blogs wahrscheinlich dann manchmal doch recht technisch wird.“
Und für Sie sind offensichtlich meine Aussagen zu technisch, weil Ihnen das nötige Wissen fehlt und Sie sich auch nicht bemühen, solches Wissen zu erwerben.
Und in einem Paper der peer-Review-Zeitschrift (International Journal of Modern Physics B Vol. 24, No. 10 (2010) 1309–1332), auf das G&T mit Rücknahme wesentlicher Punkte Ihrer „Falsification …“ geantwortet haben („Reply …“) steht: „We wish to express our special thanks to Jochen Ebel who has analyzed one of the German versions of GT09 in detail.“ [Wir wünschen unseren besonderen Dank an Jochen Ebel auszudrücken, der eine deutsche Version von GT09 im Detail analysiert hat.]
Sie sollten sich also schon etwas besser über meine Kompetenz informieren, bevor Sie hier Ihren Schwachsinn sowohl physikalisch als auch menschlich ablassen.
Auch wenn Sie meine Fachpublikationen im Netz nicht finden, sagt das etwas über Ihre Fähigkeiten zur Suche aus, nicht etwas über meine Fähigkeiten.
Sie spielen sich hier auf, als könnten Sie meine fachlischen Fähigkeiten beurteilen – aber das, was Sie schreiben, ergibt nur ein Urteil über Ihre Fähigkeiten.
Und noch etwas ist interessant und betrifft nicht nur Sie: Leute, die umfangreiche Kenntnisse haben, stören sich nicht daran, daß ich in der DDR aufgewachsen bin – nur Leute, die mir fachlich nicht das Wasser reichen können, ersetzen ihre mangelnde fachliche Kompetenz durch Beleidigungen (politisch und menschlich) – Ihre Beleidigungen quittierte z.B. der Admin mit „Bitte mäßigen Sie sich! mfG Admin“
MfG
….sind die Strahlungsleistungsdichten F(z) vom Boden bis 30 km Höhe eingezeichnet, die sich durch die lokale thermische Strahlung der Atmosphäre und ihrem Transport durch fortwährende Emission und Absorption durch Treibhausgase ergeben.
Denkfehler!
Es ist bekannt, daß Strahlung mittels der Quantenphysik erklärt werden kann. Aus der Wärmelehre ist aber auch bekannt, daß Energie im wesentlichen dann über Strahlung abgegeben wird, wenn die anderen Wege zur Energieabfuhr, nämlich Konvektion (Wärmeübergang) und Wärmeleitung, nicht oder nicht in ausreichendem Maße genutzt werden können. Letzteres trifft insbesondere für das Vakuum bzw. vakuum-ähnliche Zustände zu, z. B. bei der Übertragung der Sonnenenergie durch das All.
Will man experimentell innerhalb von Gasen eine Energieabgabe einzelner Gasmoleküle durch Strahlung erreichen, so müssen entweder die Gase in erheblicher Verdünnung, praktisch in vakuum-ähnlichen Druckzuständen vorliegen, oder aber die dem Gas zugeführte und dann wieder abzugebende Leistung muß beträchtliche Leistungsdichten erreichen.
Unter Bedingungen der unteren Atmosphäre, also im Luftraum bis rd. 25 km Höhe, gibt es weder die eine noch die andere Voraussetzung für das Auftreten quantenphysikalischer Reemission empfangener Wärmestrahlung einzelner Moleküle. In diesem Bereich wird ggf. die durch Absorption von Strahlung aufgenommene Energie unverzüglich in die Form Wärme transformiert und ebenso schnell durch Konvektion und Leitung an die unmittelbare Umgebung abgegeben.
Ihre Strahlentransportkaskade gibt es nicht.
Nichts ist im Lot. Womit begründet man die 350 W? Mit den 324 W aus der „Gegenstrahlung“. Womit begründet man die 324 W der „Gegenstrahlung“? Mit den 350 W aus der terrestrischen Strahlung…..
Und da dreht es sich, das perpetum mobile der Klimakirche mit dem man jede beliebige Temperatur am Erdboden einstellen kann – bei konstanter Insolation!!
http://tinyurl.com/ca6deqk
„Die Absorptionslänge der semigrey atmosphere beträgt am Boden 5500 m und nimmt mit der Höhe proportional zur Luftdichte ab“
Fehler, das ist anders rum, die Absorptionslaenge nimmt umgekhrt proportional zur Luftdichte rho ab, der Absorptionskoeffizient prop. zu, also in meiner Rechnung gilt
L(rho(z)) = L*rho(z)/rho(0)
Dies ist nur eine Naeherung, die nur den wesentluchen Effekt beruecksichtigt, dass die Dichte der Absorber beruecksichtigt, dass deren Spektrallinienform sich noch etwas aendert, ist nicht beruecksichtigt, ebenfalls nicht, dass Wasserdampf anders als anderen wellmixed Treibhausgase mit der Hoehe abnimmt. Das kann man mal genauer einbauen, aendert am grundsaetzlichen Kurvenverlauf von F aber nichts.
dF/dz = (B-F)/L,
wobei L die Absorptionslänge der Atmosphäre im IR ist („semigrey“) und B die Plancksche Strahlungsquelldichte. In dem Diagramm (http://tinyurl.com/8d5ycge) sind die Strahlungsleistungsdichten F(z) vom Boden bis 30 km Höhe eingezeichnet, die sich durch die lokale thermische Strahlung der Atmosphäre und ihrem Transport durch fortwährende Emission und Absorption durch Treibhausgase ergeben. Nach oben gerichtete thermische Strahlung Fu (blau) nimmt vom Boden von 390 W/m2 bis in 30 km Höhe auf 240 W/m2 ab. Dies ändert sich auch bei größeren Höhen kaum noch und mit dieser Strahlungsdichte gibt die Erde die Energie ins All ab. Die Gegenstrahlung Fd (grün) nimmt von Null am Rand zum Weltall auf hier 213 W/m2 am Boden zu (weniger als in Realität weil die Wasserdampfkonzentration stärker mit der Höhe fällt als die Luftdichte). Der Treibhauseffekt ist also wie in echt 390-240=150 W/m2. Als Temperaturprofil (rot) wurde die Standardatmosphäre genommen. Die Absorptionslänge der semigrey atmosphere beträgt am Boden 5500 m und nimmt mit der Höhe proportional zur Luftdichte ab (das trifft in Realität v.a. wegen Wasserdampf nicht ganz zu). Diese Wert wurde durch Ausprobieren erhalten, bis zu den 15 °C am Boden auch die im Mittel real zu beobachtenden 240 W/m2 ins Weltall abgegeben werden.
Durch Treibhausgaszugabe erniedrigt sich die Absorptionlänge (im Beispiel um 5% auf 5225 m).Damit dann wieder dieselbe Strahlungsleistung wie vorher (240 W/m2) ins Weltall abgegeben werden, erhöht sich die Troposphärentemperatur (und Boden) um 2,3 °C, die Stratosphäre kühlt um -1,9 °C ab, die Tropopause steigt um 350 m (siehe Kurven mit Bezeichnung „2“).
„Zählen wir mal:
Solare Einstrahlung: 342 W
Albedo: -107W
Emission durch die Atmosphäre: -165W
Wolken: -30W
Atmosphärisches Fenster: -40 W
Für die 324 W der imaginären „Gegenstrahlung“ bleibt nichts übrig. “
Hallo, geht’s noch? Was machen Sie für einen Schwachsinn? Das ist leistungsbilanz am Oberrand der Atmosphäre und besagt nur, dass durch diese Fläche in beide Richtungen gleich viel geht, was klar ist, denn eine 2D Fläche kann keine Energie aufnehmen. Das brauchen wir nicht!
Sie sollen die Ströme (Pfeile) zusammenzählen, die in die Atmosphäre gehen und dort dissipieren (Pfeilende dort) und so der Atmosphäre die Energie zuführen, die Sie nicht gefunden haben!!! Kapiert?
Ich sehe da von unten am Erdboden
thermals: 24
evapotranspiration: 78
surface radiation 350 (von den 390 vom Boden werden 40 ja nicht in Luft absorbiert, die gehen durchs atm. Fenster ins Weltall)
und von Richtung Weltall nur der in der Luft absorbierte Anteil Sonnenstrahlung 67.
Der Rest der Sonnenstrahlung wird an Wolken reflektiert oder durch die Luft zum Boden transmittiert (und dort wieder absorbiert und reflektiert)
Macht also in Summe als input für die Atmosphäre:
78+24+350+67 = 519. Also alles im Lot.
welche den TE der Atmosphäre nicht verstehen können.
Nun, schaut euch einfach das Wasser an. Man nehme einen Ozean und weiß, dass IR Strahlung in den oberstend Schichten bereits vollständig absorbiert wird. Anders kann Sonnenlicht einige Meter vordringen. Aber, erwärmt sich auch nur eine ganz dünne Schicht, blockiert diese bereits den Strahlungsfluss aus der Tiefe markant und somit bleibt das ganze Volumen darunter wärmer, als wenn diese dünne , wärmere Schicht nicht da wäre. Eigentlich alles pipi einfach, wenn man 1+1 zusammenzählen kann…
Doch, zählen Sie im Kiehl Trenberth Diagramm einfach die in die Atmosphäre einströmenden Leistungsdichten zusammen. Es geht genau so viel rein wie raus.
Antwort:
Zählen wir mal:
Solare Einstrahlung: 342 W
Albedo: -107W
Emission durch die Atmosphäre: -165W
Wolken: -30W
Atmosphärisches Fenster: -40 W
Für die 324 W der imaginären „Gegenstrahlung“ bleibt nichts übrig.
„Aber eine Leistungsdichte. Wenn Sie eine elektrisch beheizte Platte von 1 m² haben, die zu einer Seite 195 Ws emittiert und zur anderen Seite 324 Ws. Wie viel Energie muss dann das Kabel bringen? 519 Ws.“
Völlig richtig.
„Und diese Energie steht der Troposphäre gar nicht zur Verfügung.“
Doch, zählen Sie im Kiehl Trenberth Diagramm einfach die in die Atmosphäre einströmenden Leistungsdichten zusammen. Es geht genau so viel rein wie raus.
Dennoch verwechseln Sie zwei physikalische Größen, die die gleiche Einheit W/m2 haben. Das eine sind die Flussdichte durch eine berandenenden Oberflächen der Atmosphäre 195 und 324 W/m2. Die Summe beider ist die Leistung, die dem durch die berandenden Oberflächen eingeschlossenen Volumen durch Strahlung verloren geht bezogen auf die Querschnittsfläche des Volumens.
Auch Sie haben Ihr Unvermögen kundgetan, indem Sie die Energietransporte einer schneebedeckten Landschaft nicht bilanzieren konnten. Ich habe mich bereits mit Gleichungen rumgeschlagen, da waren Sie noch nicht einmal ein lütter Schieter.
Wenn Ebel ernst zu nehmen wäre, hätte er den Quatsch mit der Strahlung, die eine Temperatur hat, verfaßt.
Und ich habe Prügel kassiert, weil ich den Klimaalarmisten eine politische Farbe zugeordnet hatte. Heimatlose Ideologen nach dem Mauerfall.
Scheint so, dass ich da nicht so ganz neben der Realität liege.
Sie haben das immer noch nicht kapiert! Es werden 195 Wm-2 Richtung Weltall emittiert, das entspricht einer effektiven Temperatur von 242 K der Richtung Weltall emittiertenden Schicht, und 324 Wm-2 Richtung Boden, das entspricht 275 K Effektivtemperatur der Richtung Boden emittierenden bodenaeheren AtmosphaerenSchicht. Die Summe aus den beiden in entgegengesetzten Richtungen strahlenden Strahlungsdichten von 519 Wm-2 ist selber keine Strahlungdichte, Sie muessen schliesslich beruecksichtigen, dass es sich dabei um vektorielle Groessen handelt. Nun endlich kapiert?
Antwort:
Aber eine Leistungsdichte. Wenn Sie eine elektrisch beheizte Platte von 1 m² haben, die zu einer Seite 195 Ws emittiert und zur anderen Seite 324 Ws. Wie viel Energie muss dann das Kabel bringen? 519 Ws. Und diese Energie steht der Troposphäre gar nicht zur Verfügung. Die „Gegenstrahlung“ ist ein Verstoß gegen den 1. Hauptsatz; Energie kann nicht aus dem Nichts entstehen.
ist es nicht traurig, Heizow? Sie, der nicht mal die einfachste Gleichung versteht, geschweige den herleiten kann, beleidigen fortlaufend den Herrn Ebel. Nicht mal das Wasser können sie reichen und glauben sie mir, Ebel weiß ganz genau, wie man Strahlung und Temperatur in Verbindung zu bringen hat. Sie allerdings sind lernresistent und so werden sie auch nie verstehen, worum es eigentlich geht.
Sie sollten ihr eigenes Unvermögen nicht auf andere projizieren:
„wenn Sie schon nicht mal das vereinfachte Problem verstehen, wie wollen Sie dann die vollständigen Zusammenhänge verstehen?“
Nehmen Sie ernsthaft an, daß ich mir „Erklärungen“ von jemandem reinziehe, der behauptet Strahlung habe eine Temperatur?
Viele Fehler haben Sie ja schon selbst als „Vereinfachung“ genannt.
Der wichtigste fehlt noch: Es gibt keine Treibhausstrahlung von oben, die bis zur Erde reicht. Was thermalisiert wird kann nicht gleichzeitig strahlen.
Natürlich gibt es auch Strahlung von oben, die man aber nicht Treibhausstrahlung nennen kann, z.B. durch Wasser oder Aerosole.
Das liegt schlicht daran, dass hier der Kühleffekt deutlich überwiegt, weil dadurch auch die Transparenz für Sonnenlicht deutlich vermindert wird, also die Wirksamkeit der eigentlichen treibenden Wärmequelle für die Erdoberfläche.
Weiter haben Sie überhaupt nicht verstanden, was „Sättigung“ im Zusammenhang mit den CO2-Banden bedeutet, obwohl sie selbst von der Verkürzung der Absorbtionslänge reden.
Die Absorbtionslänge kann nur verkürzt werden, wenn eine BEGRENZTE Menge dieser Strahlungsanteile verfügbar ist. Ist das einmal absorbiert, ist die Sättigung erreicht, mehr gibt es nicht.
Anders ist es beider Emission in großer Höhe, die schlicht von der dort herrschenden Temperatur abhängt und eine Kühlung der Atmosphäre bedeutet, deren Ausmaß von der CO2Menge bestimmt ist.
Auf der Erdoberfläche kommt diese nicht mehr an bei der bekannten Transmission von 0.
Bei quantitativer Betrachtung ist der größte Fehler das Ignorieren des materiellen Wärmeübergangs, also der Kühleffekt der Erdatmosphäre für die Oberfläche. Deshalb wird es nicht so heiß wie auf der Mondoberfläche oder wie in den gut isolierten Solarkollektoren.
mfG
Leser Ebel, halten Sie gefälligst mal die Luft an mit Ihrer rotzfrechen Anmassung, Sie hätten wissenschaftlich auch nur irgendetwas Substantielles beizutragen. SIE HABEN WEDER EINEN HÖHEREN AKADEMISCHEN GRAD, WIE ZUM BEISPIEL EINEN DOKTORTITEL, PRIVATDOZENTENTITEL ODER PROFESSORENTITEL, NOCH HABEN SIE JEMALS AUCH NUR EINE EINZIGE WISSENSCHAFTLICHE PUBLIKATION VERFASST, auch Ihr Machwerk „Der Treibhauseffekt existiert doch“ ist eine einzige amateurhafte Peinlichkeit, sprachlich wie inhaltlich, und so ein Schmarren wäre nie und nimmer von irgendeiner Fachzeitschrift angenommen worden. Die Formulierungen, die sich da leisten haben mit akademischen, wissenschaftlchen Gepflogenheiten nichts, aber auch gar nichts zu tun!
Fazit: Sie sind eine absolute wissenschaftliche XXXXXX, niemand kennt Sie.
Sie sind in der Baubranche tätig und beschäftigen sich mit Themen wie Trockenlegung von feuchten Wänden, Kampf gegen Veralgungen von feuchten Bauten, und dergleichen mehr. Mit Wissenschaft haben Sie überhaupt nichts am Hut: Sie kennen wissenschaftliches Denken, Arbeiten, Publizieren nicht einmal vom Hörensagen. Sie haben NULL AHNUNG VON WISSENSCHAFTSTHEORIE, kennen nicht einmal die Prinzipien wissenschaftlicher Methodologie, kennen nicht den Unterschied zwischen wissenschaftlicher Hypothese, wissenschaftlicher Theorie, experimentellem Nachweis, etc., da Sie ja NOCH NIE WISSENSCHAFTLCH GEARBEITET HABEN, JA NICHT EINMAL EINE DISSERTATION VERFASST HABEN.
Sie sind bloss ein politischer Aktivist, als Mitglied der Partei „Die Linke“ und rühriger Voritzender der Basisorganisation Borkheide der Linken. Es ist eine Frechheit, wie Sie sich hier aufführen und so tun, als wären Sie eine Klimakapazität.
Michael Weber
„Betrachten Sie doch einmal das Diagramm von Kiehl und Trenberth! Dort werden 195 W/m² in das Weltall abgestrahlt und 324 W/m² als „Gegenstrahlung“ Richtung Erdboden um die Erdbodentemperatur von 288 K zu „erzeugen“. In der Summe sind das 519 W/m² Strahlungsleistung der Troposphäre!! Unmöglich, von daher gibt es die „Gegenstrahlung“ nur in der Phantasie der Klimaerwärmer.“
Sie haben das immer noch nicht kapiert! Es werden 195 Wm-2 Richtung Weltall emittiert, das entspricht einer effektiven Temperatur von 242 K der Richtung Weltall emittiertenden Schicht, und 324 Wm-2 Richtung Boden, das entspricht 275 K Effektivtemperatur der Richtung Boden emittierenden bodenaeheren AtmosphaerenSchicht. Die Summe aus den beiden in entgegengesetzten Richtungen strahlenden Strahlungsdichten von 519 Wm-2 ist selber keine Strahlungdichte, Sie muessen schliesslich beruecksichtigen, dass es sich dabei um vektorielle Groessen handelt. Nun endlich kapiert?
„Warum können Sie physikalische Zusammenhänge nicht korrekt formulieren und definieren?“
Ich kann schon, aber das wird dann ein umfangreiches Werk, zu lang für einen Beitrag hier. Aber das Hauptproblem ist ein anderes – wenn Sie schon nicht mal das vereinfachte Problem verstehen, wie wollen Sie dann die vollständigen Zusammenhänge verstehen?
@ #220: T. Heinzow sagt am Donnerstag, 20.09.2012, 16:36
„Was soll der Quatsch? Wenn B von T abhängig ist, dann schreiben Sie es gefälligst hin! Und Wenn T von h abhängig ist, dann schreiben Sie es noch dazu in die Gleichung. Kann ja wohl nicht so schwer sein, oder?“
Der Zuammenhang zwischen Quellstärke und Temperatur ist nichtlinear (Planckformel). Diese Planckformel für die Temperatur einzubauen, kompliziert die Betrachtung nur, ohne einen Gewinn an Verständlichkeit zu bringen.
@ #220: T. Heinzow sagt am Donnerstag, 20.09.2012, 16:36
„Haben Sie nie gelernt, wo man seine Randbedingungen und sonsigen einschränkenden Annahmen angibt?“
Sie verstehen ja noch nicht mal einfache Zusammenhänge, aber motzen rum.
MfG
„Schon mal was vom 1. Satz der Thermodynamik gehört?“
Der erste Hauptsatz ist der Energiesatz und liefert keine Temperaturen. Temperaturen haben etwas mit Entropie und dem II.HS. der TD zu tun.
@ #222: T. Heinzow sagt am Donnerstag, 20.09.2012, 19:38
„Aus dem Nichts bzw. Nichtselementen wird eine Temperatur.“
Wer eben kaum Ahnung von Physik hat, versteht die Aussagen zur Temperatur nicht.
MfG
Sie als „Gläubiger“ oder überführter Nullsatzschreiber und Forenstörer sollten es besser unterlassen, anderen „Glauben“ zu unterstellen:
„nicht vertraut sind und lieber so wie Heinzow glauben, dass über die Physik in der Schule oder dem Grundstudium schon alles gesagt wurde, was es zu sagen gibt, ist das Ihr Problem.“
Sie sind von mir der Falschaussage sauber überführt worden, und versuchen nun mit der Benennung von Lehrbüchern, die jeder im Netz finden kann, Kenntnisse (Sie wollen die zudem gelesen haben) und Fähigkeiten vorzutäuschen, die sie nicht haben.
„Das einzelne Photon hat keine Temperatur – aber die Richtungs- und Energie-Verteilung vieler Photonen liefert eine Temperatur.“
Aus dem Nichts bzw. Nichtselementen wird eine Temperatur.
Schon mal was vom 1. Satz der Thermodynamik gehört?
„Ihre sog. thermodynamische Temperatur der Strahlung, die aber weder mit der Quelle noch mit dem THE etwas zu tun hat, scheint nur eine akademische Scherzfrage eines overeducateten Physikers zu sein“
Ja, endlich haben Sie das auch mitgekommen!
Sehen Sie mal oben, da hat jemand behauptet, dass Strahlung keine Temperatur hat. Und dies haben wir durch Verweis auf die Physikliteratur widerlegt.
„Vielleicht sind Sie so gut und geben mir mal die thermodynamische Temperatur von el. Strom an.“
Ist doch oben schon gegeben: Die ist ebenfalls durch T=dU/dS gegeben. Differenzieren Sie die innere Energie der Leitungselektronen nach ihrer Entropie, fertig.
In der weitverbreiteten Näherung der Boltzmannschen Transportgleichung ist die Temperatur der Leitungselektronen in einem elektrischen Potential gleich der ohne Potential, m.a.W. hängt die Temperatur der Leitungselektronen also in 1. Näherung nicht vom Strom ab. Und i.a. ist diese Temperatur auch die des Festkörpers, denn die Leistungsbandelektronen stehen mit den Atomrümpfen auch bei Strom in 1. Näherung im thermischen Gleichgewicht.
Interessant sind die Fälle, wo das nicht so ist, in hohen elektrischen Feldern z.B.. Dann gibt’s „hot electrons“ und andere nette Effekte an denen Generationen von Physikern forsch(t)en.
„d.h. nicht ganz, weil die Druckverbreiterung in verschiedenen Höhen verschieden ist. Da es nur ums Prinzip geht, wird dieser Effekt vernachlässigt.“
Warum können Sie physikalische Zusammenhänge nicht korrekt formulieren und definieren?
„Die Strahlungstransportgleichung lautet in Druckkoordinaten mit der Strahlungsintensität I und dem Quellterm B, wobei der Quellterm nur von der Temperatur abhängt und wegen der unterschiedlichen Temperaturen in verschiedenen Druckhöhen von der Druckhöhe:
(2) kp * dI/dp = I – B“
Was soll der Quatsch? Wenn B von T abhängig ist, dann schreiben Sie es gefälligst hin! Und Wenn T von h abhängig ist, dann schreiben Sie es noch dazu in die Gleichung. Kann ja wohl nicht so schwer sein, oder?
„Da eine Wärmestrom W aufwärts stattfindet und keine weiteren Wärmequellen in der Atmosphäre angenommen werden, muß die Differenz zwischen Io und Iu konstant sein:“
Haben Sie nie gelernt, wo man seine Randbedingungen und sonsigen einschränkenden Annahmen angibt?
Fragen wir mal ganz doof: Um was für Athmosphäre handelt es sich denn, auf die Sie Ihre Gleichungen anwenden?
„Alles klar, deswegen soll der Berliner Nachthimmel auch zunehmend rot werden“
Stimmt – der Himmel schämt sich immer mehr, daß unter ihm Leute mit so dussligen Ansichten leben.
Mfg
Die Rechnung ist falsch, da die Strahlungsleistungsdichte nicht 519, sondern 519/2 beträgt, schließlich wird in ZWEI Richtungen abgestrahlt, gell?
Antwort:
Betrachten Sie doch einmal das Diagramm von Kiehl und Trenberth! Dort werden 195 W/m² in das Weltall abgestrahlt und 324 W/m² als „Gegenstrahlung“ Richtung Erdboden um die Erdbodentemperatur von 288 K zu „erzeugen“. In der Summe sind das 519 W/m² Strahlungsleistung der Troposphäre!! Unmöglich, von daher gibt es die „Gegenstrahlung“ nur in der Phantasie der Klimaerwärmer.
„Es gibt diese famosen „Gegenstrahlung“ nur in der Phantasiewelt“
Sie brauchen keine Gegenstrahlung verwenden, Sie haben dann nur Schwierigkeiten den Wärmestrom vom wärmeren Körper (Erdoberfläche) zum kühleren Körper (Atmosphäre) zu berechnen. Deshalb hat Stefan schon 1879 die Gegenstrahlung eingeführt – und die hat sich als Rechenmethode bewährt. Heute kann man sich mikrophysikalische Vorstellungen zur Gegenstrahlung machen – aber es bleibt dabei: die Wärme geht vom wärmeren zum kälteren Körper bzw. die Gegenstrahlung vom kälteren zum wärmeren Körper ist immer geringer als die Strahlung vom wärmeren zum kühleren Körper.
Können Sie soagr bei G&T in deren „Reply …“ nachlesen.
MfG
„Um die tatsächliche mittlere Temperatur der Erdoberfläche (T = 288 K = 15 oC) begründen zu können, braucht man am Erdboden eine Leistungsdichte von 390 W/m2. Diese „erzeugt“ man, indem man eine Gegenstrahlung aus der unteren Troposphäre von 324 W/m2 einführt, zu der die an der Oberfläche der Erde von der solaren Einstrahlung verbliebenen 66 W/m2 zu addieren sind. “
Das hört sich bei Ihnen an, als seien Physiker nur Buchhalter, die etwas beliebig erfinden, um eine Bilanz auszugleichen. Die Gegenstrahlung ist nicht aus teleologischen Gründen erfunden worden, sondern ist gemessener Fakt.
Ebenfalls wird gemessen, dass ein 15°C warmer Boden nicht 66 W/m2 an Wärmestrahlung abgibt, sondern eher 390 W/m2. Und das ist nicht überraschend, denn die Naturgesetze erklären die 390 W/m2. Um 66 W/m2 zu erklären, müssten Sie schon einen unrealistischen Emissionsgrad postulieren, der aber nicht mit dem gemessenen Wert übereinstimmt.
„a. Die Gesamtabstrahlung der Troposphäre ergibt sich incl. Gegenstrahlung zu 519 W/m2. Die zugehörige Strahlungstemperatur beträgt nach Gl.4 309 K (+36 oC).“
Die Rechnung ist falsch, da die Strahlungsleistungsdichte nicht 519, sondern 519/2 beträgt, schließlich wird in ZWEI Richtungen abgestrahlt, gell?
„b. Erhöht man die Strahlungsleistung des Erdbodens und der Gegenstrahlung um gleiche Beträge, so kann man leicht auch höhere Erdtemperaturen „einstellen“, z.B. mögen jeweils 100 W/m2 addiert werden: Dann stehen am Erdboden 490 W/m2 zur Verfügung. Daraus ergäbe sich ein Anstieg der Temperatur der bodennahen Luft auf 305 K (+32 oC) ohne jegliche Netto-Energiezufuhr!! “
Das ist zu ungenau:
Keine Netto-Energiezufuhr besteht dann im neuen stationären Gleichgewicht bei höherer Temperatur. Zum Erreichen dieses neuen Gleichgewichts bei höherer Temperatur müssen aber erstmal die Wärmekapazitäten „aufgeladen“ werden, dafür wird Energie aufgenommen.
Nach CO2-Verdopplung verbleibt durch die reduzierte thermsiche Abstrahlung ins Weltall
Netto zugeführte Sonnenenergie im System, die zur Ladung der Wärmekapazitäten führt und damit zur Erwärmung der bodennahen Atmosphäre. Mit der Erwärmung findet aber auch eine Erhöhung der thermsichen Abstrahlung statt, so dass der Nettoenergiebeitrag zur Sättigung kommt (Nettoleistungsbeitrag konvergiert zu Null) und sich damit ein neues stationäres Gleichgewicht bei höherer Temperatur einstellt.
„Es gibt diese famosen „Gegenstrahlung“ nur in der Phantasiewelt der Klimaalarmisten und der Gesellschaftsveränderer, die nach dem Ende des Kommunismus eine neue Ideologie brauchen.“
Der übliche Abschlußschwall.
Warum stellen Sie den nicht voran. Dann weiß ich gleich, dass Sie Müll schreiben.
„Sie gehen immer noch vom falschen Temperaturmaß aus. Die (thermodynamische) Temperatur der Strahlung ist nicht von dem zurückgelegten Weg von der Quelle abhängig. Siehe Plancks Arbeiten…
Hallo aufwachen!!! Es geht um die Temperatur der Strahlung, nicht des Absorbers derselben!!!! Die ist i.a. anders und ergibt sich aus den Überlegungen von Ihnen“
Ist ja nett daß Sie mir hinsichtlich der Bodenbilanz mitsamt wärmender CO2-Gegenstrahlung (und somit trotz 2.HS dem THE) zustimmen – obwohl Herr Pesch (#211) meint „es gibt diese famose ‚Gegenstrahlung‘ nur in der Phantasiewelt der Klimaalarmisten und der Gesellschaftsveränderer, die nach dem Ende des Kommunismus eine neue Ideologie brauchen“.
Ihre sog. thermodynamische Temperatur der Strahlung, die aber weder mit der Quelle noch mit dem THE etwas zu tun hat, scheint nur eine akademische Scherzfrage eines overeducateten Physikers zu sein – denn bestimmen läßt sich die Quelltemperatur meiner grünen Bande offenbar nicht. Außer Sie rechnen die einfach gemäß der Frequenz aus wie z.B. bei der Mikrowelle. Vielleicht sind Sie so gut und geben mir mal die thermodynamische Temperatur von el. Strom an. Ist das vielleicht die höchste Dampftemperatur der Kraftwerke die am Netz sind? Und was gilt dann für WKA und PV?
„Das einzelne Molekül hat keine Temperatur, aber eine Geschwindigkeit und Richtung. Erst der statische Mittelwert vieler Gasmoleküle bestimmt die Temperatur des Gases.“
Klar doch, der Einzelne ist schwach, die Masse ist stark 😉
Quasi, eine revolutionäre Situation in der Athmosphäre. Das CO2 Molekül ist fortschrittlich, unabhängig von seinem Bewusstsein, ob es will oder nicht 😉 . Die CO2 Moleküle werden geführt von der Vorhut der revolutionären CO2 Moleküle, der Partei des THE.
Alles klar, deswegen soll der Berliner Nachthimmel auch zunehmend rot werden 😉
„Nein, die Photonen der Strahlung haben keine Temperatur!“
Sie müssen unterscheiden zwischen einzelnen Photonen und Strahlung. Das einzelne Photon hat keine Temperatur – aber die Richtungs- und Energie-Verteilung vieler Photonen liefert eine Temperatur. Das ist analog Gasmolekülen. Das einzelne Molekül hat keine Temperatur, aber eine Geschwindigkeit und Richtung. Erst der statische Mittelwert vieler Gasmoleküle bestimmt die Temperatur des Gases.
Anmerkung: durch keine optischen Mittel (Linsen, Spiegel usw.) können Sie Strahlung so bündeln, daß in der Brennfläche eine höhere Temperatur als die Temperatur der Strahlung entsteht.
MfG
Zum besseren Verständnis erfolgt die Herleitung nicht mit der vertikalen geometrischen Höhe, sondern mit der Druckhöhe, da bei gleichen Druckhöhendifferenzen immer die gleiche Anzahl an Molekülen vorhanden ist und z.B. Temperaturänderungen nicht eingehen. Die Beziehung zwischen Druckhöhe und geometrischer Höhe ist durch die barometrische Höhenformel gegeben:
(1) dp/dh = – g * rho
Dementsprechend wird auch die Absorptionslänge als Druckhöhendifferenz kp gegeben. Weil bei gleichen Druckhöhendifferenzen immer die gleiche Anzahl an Molekülen vorhanden ist kp höhenunabhängig – d.h. nicht ganz, weil die Druckverbreiterung in verschiedenen Höhen verschieden ist. Da es nur ums Prinzip geht, wird dieser Effekt vernachlässigt.
Die Strahlungstransportgleichung lautet in Druckkoordinaten mit der Strahlungsintensität I und dem Quellterm B, wobei der Quellterm nur von der Temperatur abhängt und wegen der unterschiedlichen Temperaturen in verschiedenen Druckhöhen von der Druckhöhe:
(2) kp * dI/dp = I – B
Nun werden Vereinfachungen gemacht: Es wird angenommen, daß keine weiteren Wärmequellen in der Atmosphäre sind (wie z.B. UV-Heizung der Ozonschicht), der absorbierende Wellenlängenbereich schmal sei und die Absorptionskurve sei kein Voigtprofil, sondern ein Rechteckprofil (0 außerhalb, konstant innerhalb). Außerdem wird nicht die kugelförmige Strahlung betrachtet, sondern nur zwei Strahlungen eine nach oben (Io) und eine nach unten (Iu). Damit sind von (2) zwei Gleichungen zu betrachten (ohne Quellterm muß die Intensität in Ausbreitungsrichtung immer abnehmen):
(3) kp * dIo/dp = Io – B und – kp * dIu/dp = Iu – B
Da eine Wärmestrom W aufwärts stattfindet und keine weiteren Wärmequellen in der Atmosphäre angenommen werden, muß die Differenz zwischen Io und Iu konstant sein:
(4) Io – Iu = W ==> Io = Iu + W
Damit wird aus Gleichung (3):
(5) kp * d(Iu + W)/dp = Iu + W – B und – kp * dIu/dp = Iu – B
Da W unabhängig von p ist, verkürzt sich (5):
(6) kp * dIu/dp = Iu + W – B und – kp * dIu/dp = Iu – B
Werden die beiden Gleichungen (6) addiert, so wird:
(7) 0 = 2 Iu + W – 2 B ==> Iu = B – W/2
Gleichung (7) wird differenziert:
(8) dIu/dp = dB/dp
Gleichung (7) und (8) werden in Gleichung (3) eingesetzt:
(9) – kp * dB/dp = B – W/2 – B = – W/2 ==> dB/dp = W / (2 kp)
Gleichung (9) ist eine einfache Dgl. für B ist, die durch Integration gelöst wird:
(10) B = W * p / (2 kp)
Die Gleichung (10) erfüllt die Randbedingung, daß aus dem Weltraum keine Strahlung kommt. B (und damit die Temperatur) steigt nach unten (zunehmendes p) um so schneller, le kleiner die Absorptionslänge (entspricht kp) ist. Eine Sättigung ist auch bei beliebigen kp nicht vorhanden.
Die Gleichung beschreibt indirekt auch noch einen weiteren Sachverhalt: Da die Oberflächentemperatur bei dem konstant bleibenden Oberflächendruck (p0 = 1023 mbar) wegen höheren B (und damit höherer Temperatur) zunimmt, steigt die Strahlung in den Weltraum aus den Wellenlängenbereichen, wo keine Absorption stattfindet. Da aber die Gesamtabstrahlung gleich bleiben muß, sinkt W, da ja W ein Teil der Gesamtabstrahlung ist.
Durch die Vereinfachungen (im Wesentlichen nur 2 Strahlrichungen statt Strahlung in alle Richtungen) ist B = 0 am Oberrand der Atmosphäre und B nimmt linear mit steigendem p zu. Ohne die Vereinfachungen nimmt B am Oberrand der Atmosphäre einen Grenzwert an und B nimmt in komplizierter Weise zu.
Aber – und das ist das Wichtigste – die prinzipiellen Sachverhalte in der Atmosphäre sind richtig dargestellt. Nicht erwähnt ist das Einsetzen der Vertikalzirkulation, wenn der Temperaturgradient einen bestimmten kritischen Wert übersteigt. Durch diese Vertikalzirkulation steigt die Oberflächentemperatur nicht so stark an wie ohne Berücksichtigung der Vertikalzirkulation.
MfG
Um die tatsächliche mittlere Temperatur der Erdoberfläche (T = 288 K = 15 oC) begründen zu können, braucht man am Erdboden eine Leistungsdichte von 390 W/m2. Diese „erzeugt“ man, indem man eine Gegenstrahlung aus der unteren Troposphäre von 324 W/m2 einführt, zu der die an der Oberfläche der Erde von der solaren Einstrahlung verbliebenen 66 W/m2 zu addieren sind.
Die Begründung dieser „Gegenstrahlung“ führt zu Widersprüchen:
a. Die Gesamtabstrahlung der Troposphäre ergibt sich incl. Gegenstrahlung zu 519 W/m2. Die zugehörige Strahlungstemperatur beträgt nach Gl.4 309 K (+36 oC). Die mittlere Temperatur der Troposphäre liegt aber bei nur –20 oC in den Tropen und –30 oC in den Polar-gebieten (ROEDEL, 2000, S. 76).
b. Erhöht man die Strahlungsleistung des Erdbodens und der Gegenstrahlung um gleiche Beträge, so kann man leicht auch höhere Erdtemperaturen „einstellen“, z.B. mögen jeweils 100 W/m2 addiert werden: Dann stehen am Erdboden 490 W/m2 zur Verfügung. Daraus ergäbe sich ein Anstieg der Temperatur der bodennahen Luft auf 305 K (+32 oC) ohne jegliche Netto-Energiezufuhr!!
Es gibt diese famosen „Gegenstrahlung“ nur in der Phantasiewelt der Klimaalarmisten und der Gesellschaftsveränderer, die nach dem Ende des Kommunismus eine neue Ideologie brauchen.
„Nein, die Photonen der Strahlung haben keine Temperatur!“
Hören Sie doch auf mit Dogmen.
Anhand der obigen links sehen Sie, dass dies die Physik seit Planck, Wien und Einstein anders sieht. Und in den obigen Texten sowie in den links ist eindeutig beschrieben, woraus sich die Temperatur von Photonen ergibt, nämlich als T=dU/dS!
Wenn Sie mit der Thermodynamik auf dem Niveau des Physikhauptstudiums (siehe #161 meine Liste von Lehrbüchern dieses Niveaus: Kittel/Krömer, A. Sommerfeld, F. Reif, Callen, Landau/Lifschitz Theoretische Physik Band 5) nicht vertraut sind und lieber so wie Heinzow glauben, dass über die Physik in der Schule oder dem Grundstudium schon alles gesagt wurde, was es zu sagen gibt, ist das Ihr Problem.
„Die Quellen-Temperatur der in meinem Beispiel genannten ausgefilterten grünen Bande ist NICHT bestimmbar da dieselbe Bande von Körpern unterschiedlicher Temperatur ebenso emittiert wird.“
Hä, ja klar ist das möglich, ja und? Gleiches Spektrum heißt nicht gleiche Strahlungstemperatur. Verwechseln Sie die obige thermodynamische Temperatur der Strahlung NICHT mit den nicht-thermodynamischen Temperaturen, wie Helligkeitstemperatur, Effektivtemperatur etc. Sie stellen nur Strahlungsleistungsflüsse jedweder Strahlung (also auch nicht-thermischer) als äquivalente Temperatur eines Schwarzkörpers desselben Strahlungsleistungsflusses dar. Das ist so wie man den Luftdruck als mm Quecksilbersäule ausdrückt, also das Maß einer speziellen Messmethode für eine physikalische Größe als Einheit dieser Größe nimmt, der Luftdruck ist ja auch keine Länge. Verstanden?
„Und die Intensität hängt auch von der Entfernung ab, also kann durchaus eine schwache Bande von einem heißen Strahler stammen. „
Sie gehen immer noch vom falschen Temperaturmaß aus. Die (thermodynamische) Temperatur der Strahlung ist nicht von dem zurückgelegten weg von der Quelle abhängig. Siehe Plancks Arbeiten.
„Die erwärmende Wirkung beim absorbierenden Körper hängt lediglich von der Summe der Strahlungsleistungen in W/m² ab“
Hallo aufwachen!!! Es geht um die Temperatur der Strahlung, nicht es Absorbers derselben!!!! Die ist i.a. anders und ergibt sich aus den Überlegungen von Ihnen. Da stimme ich Ihnen zu. Aber das ist nicht das Thema, an dem Sie sich jetzt beteiligen wollen!
„..traegt thermische Strahlung die Temperatur der Strahlungsquelle“
Nein, die Photonen der Strahlung haben keine Temperatur! Die Quellen-Temperatur der in meinem Beispiel genannten ausgefilterten grünen Bande ist NICHT bestimmbar da dieselbe Bande von Körpern unterschiedlicher Temperatur ebenso emittiert wird. Und die Intensität hängt auch von der Entfernung ab, also kann durchaus eine schwache Bande von einem heißen Strahler stammen.
Die erwärmende Wirkung beim absorbierenden Körper hängt lediglich von der Summe der Strahlungsleistungen in W/m² ab – und das gilt ebenso für die CO2-Gegenstrahlung am Boden. Denken Sie z.B. an die Mikrowelle welche (rechnerisch) eine Temperatur von deutlich unter 1 K aufweist. Trotzdem kann man damit bei Raumtemperatur Speisen erhitzen. Auch Wellen von Fernsehsendern, denen eine noch tiefere Temperatur zugewiesen werden kann, werden von warmen Schaltkreisen im Empfänger aufgenommen, wobei sie selbstverständlich etwas zusätzliche Wärme erzeugen.
in 204 ist eine Erklaerung sprachlich verunglueckt, da steht
„Wie kommen Sie auf die absurde Idee, dass der Treibhauseffekt darauf basiere, dass CO2 die Photonendichte ändern würde? Wenn in die Strahlungstransportgleichung aus GoodyYung oder ThomasStames die Photonendichte substituiert, ergibt sich mit IR Absorption immer nach der Treibhauseffekt, lassen Sie sich das mal durch den Kopf gehen und praesentieren Sie hier Ihr Ergebnis.“
Wie man nach der Lektuere von ThomasStamnes, GoodyYung oder einem anderen Lehrbuch der Physik des atmosphaerischen Strahlungstransports weiss, ist die Strahlungstransportgleichung ein (nicht DAS, wie vielfach von Skeptikern unzulaessig simplifiziert behauptet wird!) Element zur quantitativen und qualitativen Erklaerung des Treibhauseffekts.
Fuer unsere Zwecke genuegt die Strahlungstransportgl der Form wie Gl 2.91 in GoodyYung. Wie man unschwer erkennen kann, kommt der einzige Beitrag von materiellen Absorbern in Form des Absorptionskoeffizienten in die Gleichung. Die Photonendichte bzw. die Photonenenergiedichte ist aber proportional zu einem ANDEREN Faktor in der Gleichung, und da Sie ja Thomas Stamnes verstanden haben, wissen Sie ja auch, welchen Faktor ich meine und erkennen selbst, dass es nicht der Absorptionskoeffizient ist. Da Sie ThomasStamnes verstanden haben und damit die Strahlungstransportgl., haben Sie Ihre obige Behauptung, dass CO2 die Photonendichte aendert, selber widerlegt. Qed.
@ #199: Heinz Hug sagt am Mittwoch, 19.09.2012, 15:17
„Erstens Cooperpaare haben etwas mit Supraleitfähigkeit zu tun.“
Und üben sich selbst in großer Ablenkung
@ #198: Heinz Hug sagt am Mittwoch, 19.09.2012, 15:13
„Hierzu erzählt man sich in Russland ein schönes Beispiel.“
Das ich Ihnen nichts Böses will, sondern es mir um die Wahrheit geht, hatte ich ja #24: Ebel sagt am Mittwoch, 22.08.2012, 15:53
einen großen Teil Ihrer Aussagen bestätigt und bei anderen Gelegenheiten Sie auch noch vor den Angriffen Dietzes in Schutz genommen, Ihre Messungen seien zu ungenau.
In einem nachfolgendem Beitrag werde ich noch mal eine vereinfachte Rechnung des Strahlungstransports mit nur je einem Vertiaklstrahl aufwärts und abwärts machen mit einem Kastenprofil der Absorption. Da wird das Prinzip deutlich und auch, daß es keine Sättigung geben kann.
MfG
Was hat das Bose-Einstein-Kondensat mit dem Treibhauseffekt zu tun?
NICHTS
Weder die Quantentheorie noch eine Strahlungstransportgleichung machen einen Treibhauseffekt, da die Transmission für die CO2 Bande in der unteren Atmosphäre 0 ist.
Das bedeutet 0 Photonen und 0 Strahlungstransport auf die Erdoberfläche durch CO2
Strahlung „trägt“ oder transportiert Energie, aber keine Temperatur, denn sie hat keine Wärme.
Wann lernen Sie das Student Baecker?
Ist doch hier schon mehrfach mit einfachen Worten erklärt worden.
mfG
Nun begeben Sie sich ganz ins Nirwana:
„Wie man oben und den dortigen Links nachlesen kann, traegt thermische Strahlung die Temperatur der Strahlungsquelle.“
Das Quatschometer befindet sich im Grenzbereich der Anzeigemöglichkeit.
„Hierzu stelle ich fest: Lässt man sich die letzte Antwort vom Avatar Nico Baecker durch den Kopf gehen, dann bedeutet das, dass es gar keinen Treibhauseffekt gibt, denn CO2 ändert die Photonendichte einer thermischen Strahlung nicht, wenn das zugegebene CO2 und die Hohlraumstrahlung die gleiche Temperatur haben.“
Wie kommen Sie auf die absurde Idee, dass der Treibhauseffekt darauf basiere, dass CO2 die Photonendichte ändern würde? Wenn in die Strahlungstransportgleichung aus GoodyYung oder ThomasStames die Photonendichte substituiert, ergibt sich mit IR Absorption immer nach der Treibhauseffekt, lassen Sie sich das mal durch den Kopf gehen und praesentieren Sie hier Ihr Ergebnis.
# 199
„Erstens Cooperpaare haben etwas mit Supraleitfähigkeit zu tun.“
Ja, und? wie man weiß sind Sie (quasi)bosonisch und zeigen daher eine Energieverteilung gemäß dem Planckgesetz, gleiches gilt für suprafluides He-4, oder sonstige Bose-Einstein-Kondensate.
„Zweitens zur Herleitung der Planck-Gesetzes benötigt es keine Bose-Einstein-Statistik.“
Planck wußte damals noch nicht, dass er mit seiner Besetzungsstatistik der Energie der elektromagnetischen Oszillatormoden (Quanten) genau die von Bosonen benutzte. Die Entdeckung dieser Teilchenklasse wurde schließlich durch Plancks Arbeit erst vorbereitet – Quantentheorie. Die Verallgemeinerung von Plancks Anwendung auf EM-Wellen erfolgte später (um 1924) durch Bose und Einstein. Das Planck-Gesetz ist daher nur eine Folge der Bose-Einstein-Statistik von Photonen, das „entwertet“ andere – eher historisch orientierte – Herleitungen keinesfalls, zumal ja das gleiche rauskommen muss.
Lieber Herr Dietze,
Wie man oben und den dortigen Links nachlesen kann, traegt thermische Strahlung die Temperatur der Strahlungsquelle.
@ #198: Heinz Hug sagt am Mittwoch, 19.09.2012, 15:13
„Hierzu erzählt man sich in Russland ein schönes Beispiel.“
@ #199: Heinz Hug sagt am Mittwoch, 19.09.2012, 15:17
„Zweitens zur Herleitung der Planck-Gesetzes benötigt es keine Bose-Einstein-Statistik.“
Da muß ich doch etwas zur Geschichte 1900 schreiben:
Planck hat sich viel mit Entropie beschäftigt. Die Wiensche Formel ergibt sich, wenn die zweite Ableitung der Entropie nach der Energie gleich Konstante durch Energie (e) ist. Die Raylieghsche Beziehung ergibt, daß die zweite Ableitung der Entropie nach der Energie gleich Konstante durch Quadrat der Energie (e²) ist.
Bei Versuchen beide Formeln zu vereinigen hat er „e“ und „e²“ durch „e(b + e)“ ersetzt. bei kleinen e ist die Klammer fast konstant (Wien) und bei großen e ist b fast ohne Bedeutung (Rayleigh). Bei geeignetem Wert von b entstand empirisch eine Formel, die die beobachteten Werte sehr gut beschreibt.
Aber Planck hat sich damit nicht zufrieden gegeben und hat gefunden, wenn man die Boltzmannsche Statistik geeignet modifiziert, wird die gefundene Strahlungsformel richtig beschrieben. Das für diese Statistik erst später der Name Bose-Einstein-Statistik angewandt wurde, ändert nichts daran, daß es eine Bose-Einstein-Statistik ist.
Aber Sie, Dr. Hug, haben die Wirkungskette des Treibhauseffektes nicht verstanden. Im Hohlraum herrscht Isothermie und Wärmetransport findet nicht statt. In der Atmosphäre (besonders wichtig in der Stratosphäre) findet ein strahlender Wärmetransport statt – und für Wärmetransport sind Temperaturdifferenzen erforderlich. Deshalb spielt die Absorption in der Troposphäre keine temperaturbestimmende Rolle. Siehe Wirkungsweise Treibhauseffekt hier: http://tinyurl.com/9q76abw
MfG
„Weiter oben habe ich ja selber geschrieben, wie man thermische Stragler experimentell realisiert.“
Relevanz = Null, deshalb ein weiterer Nullsatz.
„die Erklaerung thermischer Strahlung, die Sie brachten, kenne ich natuerlich auch.“
Sie verwechseln Definition mit Erklärung. Ein weiteres Indiz für Ihre Einordnung unter Avatar, Forenstörer … .
„Der Punkt ist alleine, dass diese Definition nichts darueber aussagt, ob Thermische Strahlung nur selber eine Temperatur hat.“
Und weiter geht es nach Handbuch: Dem ‚Gegner‘ etwas unterschieben, was er nicht behauptet hat. Sie haben behauptet, daß ‚thermische Strahlung‘ eine Temperatur hat. Und nun beweisen Sie das gefälligst! – Können Sie aber nicht –
Negativbeweise gibt es in der Wissenschaft nicht, insbesondere nicht in Rechtswissenschaft.
„Wenn Sie sich nun verweigern, sich darueber aufzuklaeren, so ist dies nicht mein Problem.“
Und wieder ein Nullsatz gepaart mit einer unsubstantiierten Unterstellung. Alles streng nach Handbuch.
Wie sagte es noch Herr Hug so zutreffend weiter unten: Und nun wetzen Sie ganz schnell wieder in die Bibliothek …
Ich füge hinzu: Sie müssen noch fleißig üben.
„Die höchst unerfreuliche Physiker-Debatte darüber ob Strahlung eine Temperartur ‚hat'“
Lieber Herr Dietze,
Strahlung hat keine Temperatur. Darüber debattieren Physiker auch nicht. Und was daran unerfreulich sein soll, ein paar Möchtegernwissenschaftler des Geschwafels und der Falschbehauptung zu überführen, erschließt sich mir nicht.
Nur deucht es mir, daß Sie nicht begriffen haben, worum es dabei geht, denn was soll der Quatsch mit: „ob ‚kältere‘ Gegenstrahlung additiv in die Bodenbilanz eingeht“?
Etwas, was keine Temperatur hat, kann auch nicht kälter oder wärmer sein.
„Strahlung ist ein Energiefluß in W/m² und kann nicht mit einer wärmeleitenden, temperaturübertragenden Verbindung verglichen werden, sondern eher mit elektrischem Strom – dem man auch keine Temperatur zuweisen kann.“
Soso, „Temperatur“ kann also „übertragen“ werden?
Präziseres Formulieren vermeidet solche Anfragen.
Das hier wäre korrekt gewesen:
‚Strahlung ist ein Energiefluß ohne Übertragungsmedium und kann nicht mit dem Energiefluß in einer wärmeleitenden Verbindung zweier unterschiedlich warmer Körper verglichen werden.‘
Dietze: „Fazit: Diese Physiker-Debatte hat mit dem THE-Problem nichts zu tun, ist sinnlos und sollte schleunigtst beendet werden.“
Ja, ganz furchtbar!! Wenn nicht ununterbrochen darüber diskutiert wird, was den Treibhausfanatiker Dietze am meisten umtreibt, wird er ganz nervös und fordert den sofortigen Abbruch ein untreibhaushaften Physikerdebatte. Ja, Herr Fanatiker Dietze, sind Sie denn in einem Ausmass treibhausfanatisch wie man sich dies bei halbwegs normalem Verstand überhaupt nicht ausmalen kann??
Lieber Herr Paul,
das Plancksche Gesetz folgt deduktiv aus der Bose-Einstein-Statisitk und ist bekanntlich fuer Bosonen gueltig, also z.B. Photonen, Helium4, Cooperpaaren, Gluonen, etc. Fuer Fermionen gilt die Fermi-Dirac-Statistik.
Von Euch Schlaumeiern hat keiner kapiert, dass das Planckgesetz ein Gesetz ueber die Thermodynamik von Photonen ist und mit der Materie gar nichts zu tun hat.
Offenbar hat das Hug auch nicht verstanden.
Dass ich das Planckgesetz sehr wohl verstanden habe, steht außer Frage. Nur der Avatar Nico Baecker scheint da etwas verwirrt zu sein.
Erstens Cooperpaare haben etwas mit Supraleitfähigkeit zu tun.
Zweitens zur Herleitung der Planck-Gesetzes benötigt es keine Bose-Einstein-Statistik. Es ist offensichtlich, dass Nico Becker darauf zurückgreift, um zu beeindrucken und damit ausdrücken, was für ein toller Kerl er ist. Alle anderen sind dumm, während er allein im Vollbesitz der wissenschaftlichen Wahrheit ist.
Liest man die verständlich geschriebenen Originalarbeiten von Max Planck um 1900 nach wie „Über das Gesetz der Energieverteilung im Normalspektrum“ oder „Entropie und Temperatur strahlender Wärme“, dann findet man nichts über die Bose-Einstein-Statistik. Kein Wunder, Arbeiten hierüber wurden erst um 1924 veröffentlicht, wobei es sich um Quantenstatistik handelt (Gerthsen: „quantenmechanisch begründbare Abzählverfahren“).
Nebenbei bemerkt, gibt es eine ganze Reihe von Herleitungen des Planck-Gesetzes.
Da wäre zunächst einmal Planck selbst. Er baut auf den Vorarbeiten von Otto Lummer und Ernst Pringsheim auf, die sehr sorgfältige Messungen „schwarzer Körper“ mit kleinen Öffnungen durchgeführt haben (Hohlraumstrahlung). Die Strahlungsentropie spielt bei ihm eine große Rolle.
Später kam Einstein hinzu, der weniger statistische Physik als Planck zur Ableitung benötigt. Einstein spricht von der Materie (nix mit Hohlraumstrahlung oder Entropie von „Resonatoren“ wie bei Planck). Einstein unterscheidet zwischen spontaner Emission und erzwungener Emission. Zur Beschreibung führt er eine kinetische Konstante „gamma“ für die Absorption und eine kinetische Konstante „beta“ für die Emission ein (s. u. a. Gerthsen/Vogel 19. Aufl., S. 572 ff). Neben Gerthsen findet man eine sehr verkürzte Darstellung der Temperaturstrahlung bei Rudolf Fleischmann „Einführung in die Physik“, S. 483 ff).
Eine etwas andere Ableitung des Planckschen Strahlungsgesetzes findet man bei W. J. Moore/D. Hummel, „Physikalische Chemie“, deGruiter 1986, S. 693. Diese Ableitung gefällt mir am besten. Aber das ist Geschmackssache.
So Herr Avatar Baecker, jetzt können Sie wieder in die Bibliothek wetzen und sich mit ihren Auftraggebern beraten. Ich werde nicht auf Sie weiter eingehen und erst recht nicht von Ihnen examinieren lassen.
Herr Ebel ist zweifellos ein ausgebildeter Dialektiker. Hierzu erzählt man sich in Russland ein schönes Beispiel. Kolchosbauern fragten ihren Priester: „Genosse Pfarrer, was ist Dialektik?“ Als Antwort brachte der Geistliche ein Gleichnis: „Zu mir kommen zwei Bauern, der eine ist sauber, der andere schmutzig. Ich biete ihnen ein Bad an. Wer von beiden wird ein Bad nehmen?“ „Der Schmutzige natürlich“, sagten die Bauern. „Nein“, antworte-te der Pfarrer, „der Saubere wird baden wollen, denn er ist gewohnt zu baden. Der Schmutzige legt keinen Wert auf ein Bad, weil er immer schmutzig ist.“ „Der Saubere nimmt also das Bad“, stellten die Bauern fest. „Nein, beide“, belehrte sie der Pfarrer, „der Schmutzige hat das Bad nötig, der Saubere ist gewohnt zu baden. Wer wird also baden?“ „Bei-de“, meinten die Bauern verdutzt. „Nein, keiner von bei-den“, schmunzelte der Pfarrer, „denn der Schmutzige ist ans Baden nicht gewöhnt, der Saubere hat es nicht nötig.“ Jetzt begehrten die Bauern auf: „Das kann kein Mensch verstehen; jedes Mal sagst du uns etwas anderes. Einmal ist es der Schmutzige, dann der Saubere, dann beide, dann keiner.“ „Seht ihr, das ist Dialektik“, lächelte der Pfarrer.
Genau so lässt es sich auch mit der PLanck-Gleichung hantieren. Einmal handelt es sich nur um die Entropie von Photonen ein andermal geht es um die Temperaturstrahlung erhitzter Körper (z. glühendes Hufeisen), dann kommt man auf die Hohlraumstrahlung, die auch ganz ohne Materie auskommt und am Schluss emittieren Treibhausgasmoleküle gemäß der Planck-Gleichung.
Offensichtlich haben Sie nicht gelernt, daß Beispiele zum Beweis untauglich sind. Lernen Sie definieren. Dann klappt es vielleicht mal mit dem Verständnis von Wissenschaft.
So, jetzt habe ich wieder etwas Zeit, denn die Handwerker sind nach der Renovierung wieder abgezogen. Ich möchte noch einmal den Disput mit Herrn Baecker aufgreifen.
Die Frage Nico Baeckers: „Ein Hohlraumstrahler ist zunaechst luftleer, die Wandungen werden auf 300 K konstant gehalten. Mit einer winzigen Sonde, die den Aufbau nicht stoert, wird die Photonendichte bzw. die Strahlungsdichte im Hohlraum bestimmt. Dann wird CO2 in den Hohlraum eingelassen und solange Energie nachgeregelt, dass alles wieder auf konstant 300 K ist. Erneute wird mit der Sonde gemessen. Frage: ergibt sich ein anderes Ergebnis?“
Antwort Heinz Hug: Natürlich erhöht sich die Photonendichte (Strahlungsdichte). Sie haben nicht nur einen Absorber/Emitter zugeführt sondern gleichzeitig die Energie so lange nachgeregelt, bis wieder 300 K erreicht sind.
Antwort Nico Baecker: Die Photonendichte erhöht (oder erniedrigt) sich mit dem Nachregeln selbstverständlich nicht!! Schließlich ist vor und nach dem Nachregeln die Temperatur der thermischen Strahlung konstant 300K! Und damit ist die Photonendichte auch konstant, nämlich die, die das Planckgesetz für 300 K angibt.
Wenn das CO2 schon vor Zugabe 300K hätte und auch sonst beim Einlassen keine thermodynamische Änderung (Druck etc. konstant) durchmacht, so ist auch keine Regelung mit Energiezu- bzw. abfuhr nötig, denn die Hohlraumstrahlung von 300K und das zugegebene CO2 von 300K sind dann bereits thermalisiert, und es ändert sich an der Photonendichte der thermischen Strahlung durch Zugabe von CO2 gar nichts!
Hierzu stelle ich fest: Lässt man sich die letzte Antwort vom Avatar Nico Baecker durch den Kopf gehen, dann bedeutet das, dass es gar keinen Treibhauseffekt gibt, denn CO2 ändert die Photonendichte einer thermischen Strahlung nicht, wenn das zugegebene CO2 und die Hohlraumstrahlung die gleiche Temperatur haben. Das wird besonders Herrn Dr. Wolfgang Thüne erfreuen, der seit Jahren bereits behauptet, es gibt gar keinen Treibhauseffekt.
Herr Becker, wissen das eigentlich Ihre Auftraggeber, die Sie angeschafft haben in einschlägigen Klimaskeptikerblogs, die Teilnehmer zu beleidigen?
So und jetzt können Sie wieder ausfällig werden. Ich werde Ihnen nicht mehr antworten.
„Sie waren nicht in der Lage den Begriff ‚thermische Strahlung‘ aus der Experimentalphysik zu definieren.“
Jeder Fachmann weiß, um was es sich handelt. Ich nehme mal ein analoges Beispiel:
Jeder weiß, was ein Tisch ist. Jetzt definieren Sie mal, was ein Tisch ist – und ich werde Ihnen jede Definition auseinandernehmen. Und trotzdem weiß jeder was ein Tisch ist.
MfG
Zu #119 W. Kinder:
„Die Frage unter #125 nach der „Grundlage für das Einführen des Terms (1-e/2) als Teiler“ beantwortet er in #128 nur mit „das finden Sie in jedem Paper zur Physik der Erde“. Abgesehen von der Behauptung „Dieses werden Sie mit Ihren physikalischen und mathematischen Kenntnissen wahrscheinlich niemals begreifen und nachvollziehen können“ warten wir bisher vergeblich auf ein Zitat bzw. eine Erklärung.“
Vielleicht ist ihm ja inzwischen doch aufgegangen, dass er keine vernünftige Erklärung für diesen Term hat. Folgt er der umstellung von Herrn Hess, hat er plötzlich eine „Energiquelle“ in seiner Formel, die er bisher als grössten phsyikalischen Blödsinn bezeichnet hat. Folgt er Ihrer Interpretation, hat der die Abstrahlung auf der sonnenabgewandten Seite vergessen.
Beides ist nicht besonders angenehm und vielleicht möchte er doch lieber den Mantel des Vergessens drüber breiten und hofft, dass es in Vergessenheit gerät.
Wenn allerdings Herr Bäcker Recht hat, dann sehen wir die Formel nochmal wieder, nachdem ausreichend Zeit verstrichen ist und keiner mehr dran denkt.
Die höchst unerfreuliche Physiker-Debatte darüber ob Strahlung eine Temperartur ‚hat‘ oder man ihr als Photonenfluß-Ensemble lediglich eine ‚zuordnen‘ kann, hat sich weit entfernt von dem eigentlichen treibhausrelevanten Problem ob ‚kältere‘ Gegenstrahlung additiv in die Bodenbilanz eingeht und somit eine zusätzliche Erwärmung des solar beheizten Erdbodens bewirkt oder nicht.
Strahlung ist ein Energiefluß in W/m² und kann nicht mit einer wärmeleitenden, temperaturübertragenden Verbindung verglichen werden, sondern eher mit elektrischem Strom – dem man auch keine Temperatur zuweisen kann. Bei der absorbierenden Oberfläche eines Körpers kommt es doch lediglich auf die Summe der Strahlungsleistungen an!
Man stelle sich vor, der Körper werde sowohl von einer Schwarzkörper-Quelle bestrahlt, als auch von einer Natriumdampf-Lampe, einer Leuchtstoffröhre sowie von einem starken Strahler dessen Filter nur die grüne Bande um 0,5 µm durchläßt. Da jeder Strahler eine andere Temperatur sowie ein anderes Spektrum und auch unterschiedliche Entfernung hat, ist für die Einstrahlung jegliche Temperaturzuordnung unmöglich.
Erst über die Körpertemperatur welche sich im Gleichgewicht aufgrund der Reflektivität, der IR-Emissivität sowie des Geometriefaktors (Kugel:4, Platte:2) einstellt, läßt sich eine äquivalente Temperatur für eine gedachte Schwarzkörper-Quelle in einer bestimmten Entfernung berechnen. Selbstverständlich kann die absorbierende Körperoberfläche nicht irgendwelche Spektralanalysen durchführen sowie Temperaturdifferenzen und Entfernungen ermitteln und dann ggf. – um dem eingebildeten 2.HS Genüge zu leisten – ‚kältere‘ Photonen abweisen. Fazit: Diese Physiker-Debatte hat mit dem THE-Problem nichts zu tun, ist sinnlos und sollte schleunigtst beendet werden.
Die Methode „haltet den Dieb“ zu rufen ist eine alte Ablenkungsmethode von Ganoven. Der Avatar Baecker bleibt vollkommen unabhängig von mir als Person ein Avatar. Das zeigen die Fakten, wenn man die Puzzleteile richtig sortiert. Und nur das habe ich gemacht. Ich finde es ethisch nicht in Ordnung ahnungslose Leser mit einer Kunstperson zu veräppeln wie es die AGW-Bewegung offensichtlich tut. Sonst hätte sich das Kunstwesen schon längst unter Lebendigen blicken lassen. Es war schon mal, wenn ich richtig erinnere, unter Kostenübernahme zu einer EIKE-Konferenz eingeladen, hat aber abgesagt „weil es was besseres zu tun hätte“ Die Beiträge von der Konferenz konnte es dann wieder prächtig kritisieren.Auch das ist ein Puzzleteil.
Und wenn Sie unbedingt „outen“ wollen machen Sie es einfach vor. Das nennt man Führung durch Vorbild. Denken Sie mal drüber nach, bevor Sie Forderungen stellen, die Sie selbst nicht erfüllen.
MfG
Michael Weber
„So werden Heizow, Paul und Co auch nie verstehen, warum sich die Erde erwärmen muss, auch wenn kein einziger CO2 Strahl aus x km Höhe je die Erde erreicht.“
Genau so ist es, schön dass du das nun selbst endlich kappierst hast.
Ein CO2-Strahl, der die Erde nicht erreicht,
kann sie auch nicht erwärmen.
Denn die Transmission – wenn du weist was das ist – für diese Strahlung in der unteren Atmosphäre ist GEMESSEN 0
http://tinyurl.com/cvrssgr
mfG
die Erklaerung thermischer Strahlung, die Sie brachten, kenne ich natuerlich auch. Und diese ist ja auch soweit richtig und reicht fuer Experimentalzwecke. Weiter oben habe ich ja selber geschrieben, wie man thermische Stragler experimentell realisiert.
Der Punkt ist alleine, dass diese Definition nichts darueber aussagt, ob Thermische Strahlung nur selber eine Temperatur hat.
Wenn Sie sich nun verweigern, sich darueber aufzuklaeren, so ist dies nicht mein Problem.
„ich folge hier nur der Temperaturdefinition wie man sie im Physikstudium in der Thermodynamikvorlesung im Hauptstudium lernt“
Und wieder ein Nullsatz.
Sie waren nicht in der Lage den Begriff ‚thermische Strahlung‘ aus der Experimentalphysik zu definieren. Sie waren auch nicht in der Lage korrekt zu formulieren, daß man der ‚thermischen Strahlung‘ eine Temperatur < Schwarzkörpertempearatur zuordnen kann. Und nun kommen Sie mit den Inhalten der Vorlesung 'Thermodynamik' daher, ohne konkret zu sagen, was da abgehandelt wird. "Die von mir genannten Lehrbuecher der Thermodynamik und statistischen Physik sind leicht zu bekommen. Wenn Sie darauf verzichten, ist das Ihr Bier." Was Sie in Ihrer Dummerhaftigkeit als bezahlter oder ehrenamtlicher Forenstörer, der gemäß Handbuch schreibt, nicht wissen, ist die Tatsache, daß ich "in der Stabi ein Sofa stehen habe", wie es mal jemand formulierte. Für mich besteht jedoch keine Veranlassung die Bibliothek in der Jungiusstr. aufzusuchen, um mich mit den wirren Behauptungen eines überführten Forenstörers oder Avatars zu beschäftigen, der noch nicht einmal den Begriff 'thermische Strahlung' definieren konnte.
ich folge hier nur der Temperaturdefinition wie man sie im Physikstudium in der Thermodynamikvorlesung im Hauptstudium lernt, wenn Sie dies nicht in der Schule oder Einfuehrungsvorlesungen gehoert haben, ist das Ihr Problem. Deswegen endet die Physik aber nicht an Ihrem Horizont, den Sie ja offenbar auch nicht durch adaequates Studium erweitern wollen. Die von mir genannten Lehrbuecher der Thermodynamik und statistischen Physik sind leicht zu bekommen. Wenn Sie darauf verzichten, ist das Ihr Bier.
„Sie wissen aber schon, dass sich das „auch“ darauf bezieht, dass die Herren an vieles glaubten AUCH bis hin zur Zwangsbeglückung des Menschen mit dem realexistierden Sozialismus.“
Genau das glaubten die nicht. Die kannten die Realitäten.
„Die DDR war kein demokratischer Staat. Ich sags nur mal vorsorglich, nicht das Sie da auf sprichwörtliche dumme Ideen kommen, ich hätte daran irgendwelche Zweifel gelassen.“
Wenn man Ihnen das abnehmen soll, müssten Sie DDR in Tütelchen wie folgt schreiben: „DDR“ oder sog. DDR.
Das wäre überzeugend gewesen.
„Und wenn Sie mit den Erklärungen hier nichts anfangen können“
Mit Ihrem Gemülle aufgrund von Copy and Paste, das Sie Erklärungen nennen, kann man in der Tat nix anfangen. Es hat mit dem Thema nix zu tun und dient nur der Vernebelung der Tatsache, daß Sie einen recht simplen Begriff aus der Experimentalphysik (1. und 2. Semester) nicht definieren können und Unfug in Nullsätzen zusammenschreiben, wie z.B. die Behauptung, daß ‚thermische Strahlung‘ eine Temperatur habe, anstatt korrekt zu schreiben, daß man der ‚thermischen Strahlung‘ eine Temperatur zuordnen kann, wobei Sie ja nicht wußten, wie ‚thermische Strahlung‘ definiert ist. Sie haben das in einem Nullsatz versucht zu kaschieren:
„der Begriff thermische Strahlung ist unmissverstaendlich in der Physik definiert und kennzeichnet ein Ensemble von Photonen im thermischen Gleichgewicht mit definierter Temperatur.“
Selten solch einen Quatsch gelesen.
Das nach Handbuch schreiben müssen Sie noch fleißig üben, wenn Sie sich mit Leuten anlegen wollen, die Physik studiert haben.
Und weiter geht es nach bei NicoBaecker nach Handbuch für Forenstörer. Nachdem er erwischt wurde, weder definieren zu können, was ‚thermische Strahlung‘ ist und er auch keinen Beweis erbringen konnte, daß Strahlung eine Temperatur hat (#134), schwenkt er nun um und versucht sich mit der Behauptung aus der Affäre zu ziehen, er hätte die Zuordnung gebraucht ( „wie Strahlung Temperatur zugeordnet wird.“).
Leider hat er gepennt, denn daß man Strahlung eine Temperatur zuordnen kann, was aber ungleich „Strahlung hat eine Temperatur“ ist, habe ich bereits in #172 geschrieben.
Lesen müßte man können und vor allen Dingen müßte man Physik verstanden haben, was bei NicoBaecker offensichtlich nicht der Fall ist. Sein Rückzugsgefecht entlarvt ihn endgültig als Forenstörer, der nach Handbuch schreibt und der gemäß der Darstellungen von M. Weber ein „Avatar“ ist.
Unterlassen Sie bitte Ihre dümmlichen Unterstellungen. Sie sind ja noch nicht einmal in der Lage eine korrekte Bilanz der Energieströme einer schneebedeckten Landschaft unter verschiedenen Randbedingungen zu erstellen.
Am besten wäre es, wenn Sie einmal anfangen. Sagen Sie kurz, wo sie diplomiert und wo und bei wem und mit welchem Thema Sie promoviert haben!
schau Nico, mit Heinzow, Paul usw. ist es so wie mit kleinen Kindern. Die fragen, Papa, besteht die Milchstraße aus Milch? Dann sagt man nein, dass ist wissenschaftlich bewiesen. Die sagen dann, aber da hat doch wer geschrieben, diese „Straße“ nennt sich Milchstraße, also muss da Milch sein. Dann versucht man zu sagen, ja aber das hat nichts mit dem heutigen Wissen zu tun und dann sagt das Kind vielleicht, wenn es alt geworden ist (siehe Kandidaten), beweise es.
Nun, wir können nun mal die Atmosphäre nicht in ein Labor packen und so den Kindern leichter zu zeigen, was funktioniert und was nicht, nur geben sich diese auch nicht zufrieden, wenn es wegen Verständnismängel eben nicht gelingt, Zusammenhänge zu verstehen.
So werden Heizow, Paul und Co auch nie verstehen, warum sich die Erde erwärmen muss, auch wenn kein einziger CO2 Strahl aus x km Höhe je die Erde erreicht. Das geht in deren Köpfe nicht rein, genau so wenig wie der Versuch, Kindern, die fest dran glauben zu beweisen, dass die Straße eben nicht aus Milch besteht.
Eigentlich kann man es aufgeben, es sind nämlich nicht die geringsten Fortschritte zu erkennen, auch wenn man sich noch so bemüht. Wie nennt man solche Kinder gleich…?
Michael Weber
Sie fragen nach Beweisen von physikalsichen Erkenntnissen, die 120 Jahre alt sind. In den historischen links ist es m.E. auch für Laien verständlich erklärt, wie Strahlung Temperatur zugeordnet wird.
Und wenn Sie mit den Erklärungen hier nichts anfangen können, so folgen Sie meinem Rat und besuchen ein Physikinstitut, welches Untersuchungen bei tiefen Temperaturen macht. Die Physiker erklären Ihnen möglicherweise nochmal, was Temperatur ist und wie die von Photonenensembles angegeben wird, wenn Sie nett fragen.
Und weiter geht NicoBaecker nach dem Handbuch für Forenstörer vor. Erst mal unsubstantiiert behasupten, ich hätte aus nem Lexikon zitiert, um von der eigenen Unfähigkeit Definitionen liefern zu können, abzulenken.
Und dann wird hinsichtlich einer Behauptung, die von ihm selbst stammt, ein Negativbeweis gefordert, obwohl die Beweislast beim Behaupter liegt, nämlich daß Strahlung eine Temperatur hat.
Anschließend werden dann wieder jede Menge Nullsätze produziert.
nun maulen Sie schon wieder rum und fordern von anderen, Allgemeinwissen von Physikern oder Mathematikern hier zu beweisen, sehen es aber als nicht noetig an, Die eigenen Behauptungen zu belegen. Ich glaube Ihnen ja, dass Ihr zitierte Satz aus einem Lexikon unter dem Stichwort thermische Strahlung steht. Nur steht da nichts ueber die Temperatur der Strahlung selber, sondern nur die experimentelle Realisierung solcher Strahlung. Ihre Behauptung, dass wegen des Lexikoneintrags Strahlung keine Temperatur haben koenne, ist Ihre Erfindung.
Nochmal zurueck zur urspruenglichen Behauptung von Ihnen, Sie behaupteten, Strahlung koenne keine Temperatur haben. Die historischen Links zu Planck und Wien belegen, dass diese Physiker Strahlung, monochromatisch bzw. einem Modenspektrum im gegenseitigen thermischen Gleichgewicht insgesamt, eine Temperatur zuordnen und dafuer eine eindeutige Beziehung in Form der Ableitung der Strahlungsentropie nach der Strahlungsenergie angaben, und damit der allgemeinen thermodynamischen Definition der Temperatur folgen.
Damit waere Ihre Behauptung wiederlegt, und seit dieser Zeit Ende 19 Jhdt ist die diese Sichtweise Lehrstoff im Physikstudium. Die Physiker wenden dies inzwischen auch fuer weitere Teilchensysteme an, die damals noch nicht bekannt waren, so fuer Elektronen, Phononen, Spinquanten etc.. Und da Sie so schoen unwissenschaftlich und unlogisch argumentieren, ja, ich haette diese Auflistung irgendwo rauskopieren koennen, z.B. aus meiner Diplom- oder Doktorarbeit, denn in beiden untersuchte ich experimentell die Eigenschaften von solchen Teilchensystemen wie beispielsweise solche wie oben aufgelistet in Abhaengigkeit von ihrer Temperatur!
Gehen Sie mal durch die Gaenge von eines Physikinstituts, vor dem draussen ein grosser Behaelter mit fluessigem Stickstoff steht und grosse Dewarbehaelter mit Gummiballons stehen, die trotz Fuellung leicht anzuheben sind. Dann sind Sie in einem Forschungsbereich, der Experimente bei tiefen Temperaturen bis 4 K runter macht. An den Waenden finden Sie dann Poster, auf denen Kurven in Abhaendigkeit von der Temperatur haengen. Da sehen Sie dann die Temperaturabhaegigkeit von Teilchensysteme,
deren Namen Sie noch nie gehoert haben.
ist in Süddeutschland eine ganz normale Anrede ohne ködeln, wie man an der Küste sagt. Die hat der Avatar B. nach einer Rüpelphase von mir übernommen. Ich finde es an der Zeit, das Kunstwesen Nico Baecker, das den Physik-Oberguru gibt, nicht nur als unfähig sondern als real nicht existent nachzuweisen. Das würde beweisen, daß die AGW-Seite seit Jahren mit unlauteren Mitteln versucht eine politische Entscheidung als
wissenschaftlich erforderlich zu verkaufen ohne überhaupt wissenschaftliches Personal zu haben, das für die schrägen Behauptungen seinen Namen und sein Gesicht hinhalten will. Einzige Ausnahme, der Data-miner Dr.rer.nat S. Hader, der allerdings selber seine Unfähigkeit unfreiwillig zugibt, indem er Daten anfordert, die mit seiner Qualifikation in 10 min leicht zu finden wären.
Interessant ist ja, daß „Herr Baecker“ seine reale Nichtexistenz auch hier nicht bestreitet. Das heißt, der virtuelle „Gröphaz“ kann seine Existenz in der Realität nicht beweisen. Da ähnelt er dem virtuellen Hot spot. Nicht messbar vorhanden! Soll er doch erst mal belegen, daß es ihn überhaupt gibt, bevor er Belege einfordert die er mangels Physis eh nicht lesen und verstehen kann. Avatare haben nun mal kein Hirn.
Und das sollte weiter herausgearbeitet werden.
MfG
Michael Weber
ich nehme an, Sie haben Ihr Zitat also einem Physiklexikon entnommen? Das aendert nichts daran, dass man im 6. Semester des Physikstudiums in der Thermodynamik die obige Beziehung zwischen innerere Energie, Entropie und Temperatur lernt, anhand zahlreicher Beispiele und Uebungsaufagben sich davon ueberzeugen kann, dass dieser Zusammenhang mit der heuristischen Temperturdefinition uebereinstimmt. Letztere wird haeufig ueber das Gasthermometer eingefuehrt, siehe z.B. dem aelteren Thermodynamiklehrbuch von Richard Becker.
Wenn Sie nun noch nie davon gehoert haben, dass jedes Ensemble von Teilchen, welches eine energieabhaengige Entropie hat, automatisch auch eine Temperatur hat und wenn Sie nicht wissen, dass elektromagnetische Strahlung einem Ensemble von Photonen entspricht, was ist das mein Problem? Sie werden einfach hinzunehmen haben, dass Physik aus etwas mehr als einem Schuelerlexikon der Physik besteht.
Nun machen Sie Planck also doch noch dumm.Lesen Sie doch erstmal meinen link zum historischen Artikel ueber Plancks Arbeit oder Planck im
Original. In der Txtstelle, die Herr Hess ueber Planck zitierte, ging es um die thermische Strahlung des Hohlraumstrahlers. Das koennen Sie verleugnen, wie Sie wollen, es aendert nichts an dieser Tatsache.
„Ulbricht und Honecker haben sich auch als Führer demokratischer Staaten verstanden.“
Besser hätte ich Ihre Intentionen und Ihre nichtvorhandene Verfassungstreue nicht ausdrücken können.
Das obige Zitat werde ich Ihnen hier stets vorhalten.
Typisch bezahlter oder ehrenamtlicher Forenstörer:
„geben Sie lieber an, wo Sie Ihre Definition der thermischen Strahlung her haben“
Fordern des Nachweises einer Quelle, obwohl eine Quellenangabe nicht notwendig ist, weil es sich um Allgemeinwissen handelt.
Pech für Sie:
Lesen mal in den Physiklexika nach, was da über ‚thermische Strahlung‘ oder ‚Wärmestrahlung‘ steht.
Da Sie aber mutmaßlich ein bezahlter oder ‚ehrenamtlicher‘ Schreiberling sind, dürfte Ihnen der Besuch einer adäquat ausgestatteten Bibliothek kaum möglich sein. Das ist in Ihrem Etat nicht drin.
Lesen Sie mal ganz genau:
„so besitzt jede nach allen Richtungen gleichmäßig monochromatische Strahlung, welche ein bestimmte Energiedichte u hat“
‚Thermische Strahlung‘, um die es hier geht, ist keine monochromatische Strahlung, das nur nebenbei.
Man kann der ‚thermischen Strahlung‘ eine Temperatur (< Schwarzkörpertemperatur) zuordnen, aber deshalb hat Strahlung noch keine Temperatur. Ebensowenig, wie Sie begriffen haben, daß die Methode des IPCC zu den FAQ 3.1 nichts mit dem Mittelwertsatz der Differentialgleichung zu hat, sind Sie in der Lage zu begreifen, daß es um die Definition des Begriffs 'thermische Strahlung' geht, die weder Sie, noch Ebel, Baecker oder Hader haben liefern können. Und wer, wie Sie, (Excel-)Tabellenkalkulationen als Beweis ansieht, aber nicht sauber mathematisch formulieren kann, was hinter der 'Tabellenkalkulation' steckt, kann nicht ernst genommen werden.
Mit Celsius kann man keine Strahlung messen.
Zumindest weis man jetzt, zu welchem Lager die Schreiber gehören, die der Strahlung selbst, nicht ihrer Quelle (oder ihrem Absorbtionsort) eine Temperatur andichten wollen.
Es sind die bezahlten Physikverdreher.
mfG
statt herumzumotzen, geben Sie lieber an, wo Sie Ihre Definition der thermischen Strahlung her haben und wieso diese nun Anlass waere, hier foermlich auszuflippen?
„Der Avatar Baecker (bzw sein Team) versucht gerade sich wissenschaftlich zu profilieren um seine politische Mission zu verdecken.“
Herr Weber,
das ‚Lieber‘ können Sie sich ersparen, denn Sie haben es nicht nötig, sich bei mir ‚anzuködeln‘, wie man an der Küste so sagt. Sie brauchen sich auch nicht auf die Schiene des Herrn NicoBaecker & Co. zu begeben, die versuchen sich ‚anzuködeln‘.
Wissenschaftlich (in Physik) kann sich ‚NicoBaecker‘ nicht profilieren, denn dazu fehlt ihm jegliches Grundwissen, welches Abiturienten eines math.-nat. Gymnasiums haben.
Was der Mann betreibt ist zusammenhangloses Copy & Paste:
„Nun ist Strahlung nichts weiteres als eine in der klassischen Physik gut zu verwendende Näherung für das Verhalten von bosonischen Ensembles der Quanten des elektromagentischen Feldes (Photonen). Diese Quanten können – wie alle Quanten – verschiedene Zustände bei verschiedenen Energien annehmen.“
Im Zusammenhang mit der Frage der Definition der ‚thermischen Strahlung‘ ein Nullsatz.
Jeder, der in eine gutsortierte Bibliothek geht, findet dort in Physiklexika und Büchern zu Experimentalphysik die Begriffsklärung: ‚thermische Strahlung‘ ist ein Synonym für ‚Wärmestrahlung‘ eines Körpers mit einer von Null Kelvin (-273,15.. °C) abweichenden Temperatur. Wobei ‚Wärmestrahlung‘ ein nicht exakter Begriff ist, denn in Abhängigkeit von der Temperatur strahlen Körper in allen Bereichen des elektromagnetischen Spektrums. Die mittlerweile von CO2-Fanatikern verbotene Glühbirne im sichtbaren Bereich.
NicoBaecker als Nullsatzschreiber oder Forenstörer zu überführen ist leicht, wenn er sich in Gebieten betätigt, wo seine Allgemeinbildung nicht ausreicht.
Im Fall der ‚thermischen Strahlung‘ war das allzu offensichtlich und ihn der Nullsatzschreiberei und der allgemeinen Laberei zu überführen.
Schon klar Herr Herr Heinzow, wir haben Ihr Nullsatz-Ranking schon verstanden. Zuerst kommt S.Hader, dann NicoBaecker gefolgt von Herrn Ebel. Es ist ja nur purer Zufall, dass es auch mit dem Ranking derjenigen Leute übereinstimmt, von denen sie sich am meisten angepisst fühlen. ;o) Wenn Sie da schon zu Mitteln der üblen Nachrede greifen müssen, sagt das wohl eher etwas aus, wie persönlich getroffen Sie sind.
„wenn Sie tatsächlich naturwissenschaftlich etwas drauf hätten, haben Sie aber nicht, könnten Sie locker erklären was die „thermische Strahlung“ ist.“
Wissen Sie, ob ich tatsächlich was naturwissenschaftlich draufhabe oder nicht, dass entscheiden zum Glück keine Dauerdoktoranden, sondern hierzulande immer noch kompetente Menschen in Universitäten und Hochschulen. Ob man naturwissenschaftlich arbeiten kann, weist man auch nicht in Diskussionsforen im Internet nach, sondern dort, wo man seine Diplome (heute Master) und Dissertationen ablegt und sich prüfen lässt. Sie können von mir aus gerne im Internet weiterhin der selbsternannte Wissenschafts-Checker bleiben und ihre Urteile über andere Arbeiten richten, eine Relevanz in der wirklichen Welt hat das nun wahrlich nicht.
„Und dann noch etwas. In einem anderen Thread haben Sie sich angemaßt die Einschränkung von Freiheiten mit dem Zweck und der Freiheitsbeschränkung auf anderen Feldern zu begründen. So haben Ulbricht und Honecker übrigens z.B. die „Mauer“ gerechtfertigt und selbstverständlich das Erschießen von Menschen auf dem Weg in die Freiheit.“
Ulbricht und Honecker haben sich auch als Führer demokratischer Staaten verstanden. Trotzdem heisst das nicht, dass die Demokratie eine schlechte Sache ist, sondern das sie für eigene Zwecke missbraucht wurde. So werden Freiheitseinschränkungen in der ganzen Welt mit z.T. albernen Argumenten begründet. Das heisst aber genauso wenig, dass jede Freiheitseinschränkung unsinnig ist. Letzteres war Inhalt meines Postings, auf welches Sie sich beziehen. Es liegt an uns, die Sinnhaftigkeit solcher Einschränkungen immer wieder aufs neueste zu prüfen. Pauschalurteile kann es da nicht geben. Wenn Sie daran etwas auszusetzen haben, dann kommentieren Sie es bitte auch dort, wo das Posting steht.
Sie haben völlig Recht.
Max Planck schreibt in seinem Buch: „Wärmestrahlung“ 5. Auflage auf S.90:
„Denn da s nur von u und v abhängt, so besitzt jede nach allen Richtungen gleichmäßig monochromatische Strahlung, welche ein bestimmte Energiedichte u hat, auch eine gaz bestimmte durch (117) gegebene Temperatur, und unter allen denkbaren Energieverteilungen ist die normale dadurch charakterisiert, dass die Strahlungen aller Schwingungszahlen die nämliche Temperatur haben.“
Die Gleichung (117) bei M. Planck ist die Gleichung von Herrn Bäcker in # 161.
Mit freundlichen Grüßen
Günter Heß
lesen Sie mal den verlinken Artikel http://tinyurl.com/PlanckEntropie
Da wird Ihnen klarer, dass Planck den verschiedenen Moden thermischer Strahlung auch Temperatur zuschriebt und dazu Formel (19) aus dem Essex paper Ebels heranzog ( 1/T = (d_part S/d_part U)| N,V.). Die Formel wird in meinem
link ebenfalls expliziert genannt. Die Schwarzkoerperstrahlung ist der von Planck behandelte Spezialfall, dass die Moden alle die gleiche Temperatur haben.
Die Definition der ‚thermischen Strahlung‘ lautet:
Def:
‚Thermische Strahlung‘ ist die von einem Körper mit einer Temperatur größer als 0 K emittierte elektromagnetische Strahlung (Wärmestrahlung).
Daß Sie solch eine simple Definition nicht hinkriegen, ist ein weiterer ernstzunehmender Hinweis auf einen bezahlten oder unbezahlten Forenschreiberling, der von Tuten und Blasen keine Ahnung hat, wie man an der Küste so sagt. Irgendjemand benutzte hier den Begriff ‚Avatar‘.
Nullsatzschreiben ist Ihre Spezialität:
„Das Spektrum dieser Strahlung ist dann – wie man in Lehrbüchern der Thermodynamik, z.B. Kittel/Krömer, Kap. 4, nachvollziehen kann – gegeben durch das Planck-Spektrum und wird experimentell durch die Strahlung eines Hohlraumstrahlers realisiert.“
denn was hat das mit der Defition des Begriffs ‚thermische Strahlung‘ zu tun? Und dann noch etwas: Schwarzkörperstrahlung ist Teil des Lehrstoffs der Experimentalphysik (bis zum Vordiplom). Diplom-Physiker wissen sowas, Netzjunkies nicht.
# 161
Sie schreiben:
„ich weiß ja nicht, was Sie da bewiesen haben wollen und ob dieser Beweis irgend etwas mit Physik zu tun haben möge.“
Das zeigt, daß Sie nicht wissen, was Sache ist oder daß Sie Nebelkerzen werfen, gemäß Handbuch für Forenschreiber.
Und dann schreiben Sie Nullsätze:
„Herr Ebel hat doch oben ein paper verlinkt. Das ist zwar nicht so einfach, aber trotzdem stehen da auch Gleichungen drin, die man auch im Lehrbuch findet. So gibt die Gln. (19) dort die allgemeine thermodynmaische Definition der Temperatur wieder: 1/T = (d_part S/d_part U)| N,V.“
Für die sprachliche und mathematische Formulierung einer Definition, hier ‚thermische Strahlung‘ benötigt man kein Paper und auch nicht Angabe eines Lehrbuches. Wären Sie tatsächlich Diplom-Physiker, wüßten Sie das und handelten entsprechend.
Was bezwecken Sie mit Ihren abstrusen Angaben, Behauptungen und „Zitaten“? Gemäß Handbuch für bezahlte und ‚ehrenamtliche‘ Forenschreiber bindet sowas die Kräfte der Gegner und verwirrt das meist ungebildete sonstige Publikum, welches sich informieren möchte.
Was Sie in #161 leisten, ist zusammenhangloses Copy and Paste und natürlich Nullsatzschreiberei:
„In der modernen Physik kann man so auch die Temperaturen von Spingittern, quantisierten Schallwellen, Cooperpaaren oder Quarks etc. angeben.“
denn eine „moderne Physik“ gibt es nicht. Nichtphysiker wissen das jedoch nicht.
Sie können es nicht und werden es wohl auch nie lernen, wie man etwas definiert:
Def:
‚Thermische Strahlung‘ ist die von einem Körper mit einer Temperatur größer als 0 K emittierte elektromagnetische Strahlung (Wärmestrahlung).
Sie werden es auch nicht mehr lernen, korrekt zu diskutieren, denn wenn Sie behaupten:
„Warum bestreiten Sie dann deren Aussagen?“
dann müssen Sie auch die Aussagen der Betroffenen beifügen und genau nachweisen, daß jemand genau diese ausdrücklich bestritten hat.
Alles andere ist Nullsatzschreiberei und Behaupten ins Blaue hinein.
Mein Tip:
Kaufen Sie sich ein gutes Lehrbuch der Experimentalphysik oder gehen Sie in die nächste Uni-Bibliothek. Da können Sie dann in den Lexika und Lehrbüchern nachlesen, was ‚thermische Strahlung‘ ist, nämlich ein anderer Begriff für den unglücklichen ‚Wärmestrahlung‘.
Und selbstverständlich hat die ‚thermische Strahlung‘ keine Temperatur. Das, was man machen kann, ist ihr eine Temperatur < der Schwarzkörpertemperatur zuordnen. Daraus dann zu machen, daß 'Strahlung' eine Temperatur habe, ist absurd. Eine solche Aussage dann Planck unterschieben zu wollen, ist m.E. eine Frechheit.
Der Avatar Baecker (bzw sein Team) versucht gerade sich wissenschaftlich zu profilieren um seine politische Mission zu verdecken. Wie immer versucht er die Diskussion von der eigentlichen Frage „Wie geringfügig ist die anthropogene Wirkung?“ abzulenken indem er allgemein über Temperatur doziert.Schenken Sie also dem Kunstwesen nicht zuviel Aufmerksamkeit.“Seine Virtualität“ B.sollte sich erst mal ausweisen bevor er als Person ernst genommen wird.
MfG
Michael Weber
http://tinyurl.com/PlanckEntropie
sollte selbsterklärend sein. Wenn nicht, fragen Sie die Physiker hier, was Sie daran nicht verstehen.
„Den Beweis, daß „Strahlung eine Temperatur hat“, haben Sie nicht geführt.“
ich weiß ja nicht, was Sie da bewiesen haben wollen und ob dieser Beweis irgend etwas mit Physik zu tun haben möge.
Herr Ebel hat doch oben ein paper verlinkt. Das ist zwar nicht so einfach, aber trotzdem stehen da auch Gleichungen drin, die man auch im Lehrbuch findet. So gibt die Gln. (19) dort die allgemeine thermodynmaische Definition der Temperatur wieder: 1/T = (d_part S/d_part U)| N,V.
Jedem Ensemble von N Teilchen oder sonstigen Einheiten im Volumen V, von dem man die Abhängigkeit der Entropie S des Ensembles von der inneren Energie U kennt, ist eindeutig eine Temperatur T zugeordnet.
Die Entropie ist per Definition die Zahl der bei der Energie U erreichbaren Zustände W: S = k*ln(W) (siehe Lehrbücher der Thermodynamik, z.B. Kittel/Krömer, Einleitung).
Wenn man also W in Abhändigkeit von U kennt, so ist die Temperatur definiert.
Nun ist Strahlung nichts weiteres als eine in der klassischen Physik gut zu verwendende Näherung für das Verhalten von bosonischen Ensembles der Quanten des elektromagentischen Feldes (Photonen). Diese Quanten können – wie alle Quanten – verschiedene Zustände bei verschiedenen Energien annehmen. Die Gesamtenergie U von N Quanten ist die Summe der Energie der N Quanten. Die Zahl der erreichbaren Zustände W ist im wesentlichen von der Wellenlänge und der Eigenschaft, dass Bosonen diegleichen Zustände mehrfach besetzen können.
Ergänzungen und mathematische Ausformulierung findet man in Hochschullehrbüchern der Thermodynamik und statistischen Physik, z.B. Kittel/Krömer, A. Sommerfeld, F. Reif, Callan, Landau/Lifschitz Theoretische Physik Band 5, …
In der modernen Physik kann man so auch die Temperaturen von Spingittern, quantisierten Schallwellen, Cooperpaaren oder Quarks etc. angeben.
unter „thermischer Strahlung“ versteht der Physiker Strahlung, die im thermischen Gleichgewicht untereinander steht, d.h. jeder Mode wird die gleiche Temperatur zugeordnet. Das Spektrum dieser Strahlung ist dann – wie man in Lehrbüchern der Thermodynamik, z.B. Kittel/Krömer, Kap. 4, nachvollziehen kann – gegeben durch das Planck-Spektrum und wird experimentell durch die Strahlung eines Hohlraumstrahlers realisiert.
„Was für ein Quatsch.“
Sie können sicher den Nachweis führen, daß meine Aussagen Quatsch sind oder?
MfG
„Den Beweis, daß „Strahlung eine Temperatur hat“, haben Sie nicht geführt. Können Sie auch nicht.“
Können schon, brauche ich aber nicht, da diese Beweise schon Wien und Planck geführt haben – und wie Sie selber schreiben: „Was Planck und Wien angeht, so habe ich keinerlei Veranlassung … mich [mit] diesen in irgendeiner Weise zu messen.“
Warum bestreiten Sie dann deren Aussagen?
MfG
Herr Ebel,
wieso können Sie nicht definieren, was „thermische Strahlung“ ist? Geht doch locker mit ein paar Worten, sagen wir mal 18 Worten. Muß wohl so Unter- bis Oberprima gewesen sein, wo ich mich zuerst mit Strahlung beschäftigt habe.
Was Planck und Wien angeht, so habe ich keinerlei Veranlassung – im Gensatz zu Ihnen – mich diesen in irgendeiner Weise zu messen.
Selbsternannte Weltökonomen und Leute, die meinen mit Subventionen könne man die Wirtschaft ankurbeln und Arbeitsplätze schaffen, sind viel bessere Ziele, den diese Typen sind genauso leicht zu widerlegen, wie Sie mit Ihren Nullsätzen:
„Auch wenn Sie meinen Beitrag „#137: Ebel sagt am Donnerstag, 13.09.2012, 22:23“ um 22:26 noch nicht gelesen haben konnten, veranlaßt mich Ihr Unsinn noch ein moderneres Paper zu nennen: Essex u.a.: How Hot is Radiation? [Wie heiß ist Strahlung?] http://tinyurl.com/9m4ustv oder „American Journal of Physics“ 71(2003), No. 10, 969 – 978.
Aber ich habe die Befürchtung, daß Sie mit Ihrem mindesten 120 Jahre alten Kenntnisstand der Physik diese Paper nicht verstehen können, da mit Hilbert-Räumen, Emsembles, Operatoren usw. gearbeitet wird.“
oder:
„Sie hatten fälschlich behauptet, Strahlung hätte keine Temperatur. Ich habe Ihnen nachgewiesen, daß Ihre Behauptung tatsächlich falsch ist – und Ihre Reaktion auf Ihren Fehler ist die Beschuldigung mit „Nullsätzen“. Also Ihr komisches Verständnis: Hängt den Boten, wenn die Botschaft richtig ist.“
Den Beweis, daß „Strahlung eine Temperatur hat“, haben Sie nicht geführt. Können Sie auch nicht.
Der Satz:
„Ich habe Ihnen nachgewiesen, daß Ihre Behauptung tatsächlich falsch ist.“
ist ein Nullsatz, denn einen Beweis haben Sie nicht geführt.
BTW: Die Beweistechniken habe ich ab der Obersekunda gelernt. Sie kennen das ja z.B. mit der vollständigen Induktion oder etwa nicht?
Denken Sie also nochmal darüber nach, wie man „thermische Strahlung“ definiert, bevor Sie rumpöbeln.
„Hier ging es aber um die Temperatur der Strahlung. Z.B. kann die Temperatur eines Laserstrahls weit über der Temperatur jedes Bauteils des Lasers liegen. Ein Wärmestrom kann als Vielteilchensystem betrachtet werden. Und über die Statistik eines Vielteilchensystem kann man eine Temperatur definieren“
Was für ein Quatsch.
Kriegen sie eigentlich Laberkilometergeld?
„Können Sie aber nicht, NicoBaecker und Ebel auch nicht. außer irgendwelchen Nullsätzen ist da nix gekommen.“
Herr Heinzow, ich ziehe vor Ihnen den Hut. Planck und Wien sind ja nur kleine Lichter gegenüber Ihnen.
MfG
Sie sind der Nullsatzschreiber in Perfektion. Und Sie sind als mutmaßlich bezahlter Forenschreiber überführt.
wenn Sie tatsächlich naturwissenschaftlich etwas drauf hätten, haben Sie aber nicht, könnten Sie locker erklären was die „thermische Strahlung“ ist.
Können Sie aber nicht, NicoBaecker und Ebel auch nicht. außer irgendwelchen Nullsätzen ist da nix gekommen. Wie denn auch, wenn der Auftrag „Stören“ lautet.
Und dann noch etwas. In einem anderen Thread haben Sie sich angemaßt die Einschränkung von Freiheiten mit dem Zweck und der Freiheitsbeschränkung auf anderen Feldern zu begründen. So haben Ulbricht und Honecker übrigens z.B. die „Mauer“ gerechtfertigt und selbstverständlich das Erschießen von Menschen auf dem Weg in die Freiheit.
Welch Geistes Kind Sie also sind, haben Sie damit perfekt demonstriert.
„Strahlungstemperatur“
Strahlungstemperatur und Temperatur der Strahlung sind zwei grundlegend unterschiedliche Sachverhalte. Unter der Strahlungstemperatur versteht man die von einem Körper ausgehende Strahlung, durch deren Messung man auf die Oberflächentemperatur des strahlenden Körpers schließen kann – und für diesen Begriff haben Sie Links gesetzt.
Hier ging es aber um die Temperatur der Strahlung. Z.B. kann die Temperatur eines Laserstrahls weit über der Temperatur jedes Bauteils des Lasers liegen. Ein Wärmestrom kann als Vielteilchensystem betrachtet werden. Und über die Statistik eines Vielteilchensystem kann man eine Temperatur definieren.
Ein Weg ist z.B. der folgende: Mit einer emittierten Strahlung wird Entropie abgestrahlt – z.B. durch die Richtungs- und Frequenzverteilung. Wenn die abgestrahlte Energie sich ändert, ändert sich auch die abgestrahlte Entropie. Die Ableitung der Entropie nach der Energie liefert den Kehrwert der Temperatur.
MfG
Sie sagen zu #150:
„Ihre Zitate sind korrekt, nun muessen Sie nur noch lernen, wie man diese auch richtig auf mein Gesagtes anwendet.“
richtig angewendet bedeutet, Ihr „Gesagtes“ ist falsch! Strahlung hat wirkliche keine Temperatur.
mfG
auch fuer Sie nochmal aufwachen, ich schrieb thermische Strahlung, fuer die gilt der Spezialfall Temperatur gleich Strahlungstemperatur und jeder Mode ist im thermischen Gleichgewicht mit einer anderen. Wenn man will, kann man auch sogar fuer ein Modenspektrum, welches paarweise nicht im Gleichgewicht iat, fuer jeden Mode eine thermodynamisch korrekt definieete Temperatur angeben, man muss dafuer nur wie z.b. in Ebels paper von Essex, die Entropieabhaengigkeit von der Energie bestimmen.
Ihre Zitate sind korrekt, nun muessen Sie nur noch lernen, wie man diese auch richtig auf mein Gesagtes anwendet.
Lieber Herr Ebel,
das Essex paper ist ok, ich habs verstanden, steht ja auch nichts revolutionierendes drin.
„Lieber Herr Heinzow, # 135
„Seit wann hat „Strahlung“ eine Temperatur? “
Hallo aufwachen: thermische Strahlung!!“
#137: Ebel sagt:
„@ #135: T. Heinzow sagt am Donnerstag, 13.09.2012, 18:43
„Seit wann hat „Strahlung“ eine Temperatur?“
Herr Heinzow, Ihre Physikkenntnisse sind auf dem Stand vor 1893 – also 120 Jahre zurück. Siehe z.B. http://tinyurl.com/9bchy7w“
=====================================================
„Strahlungstemperatur“ ist keine Temperatur der Strahlung. Strahlung hat keine Temperatur. Zum Begriff „Strahlungstemperatur“ hier nachlesen bitte: http://www.enzyklo.de/Begriff/Strahlungstemperatur. Zitat:
„1. Strahlungstemperatur
Ohne Korrektur, durch Messung der emittierten Strahlung eines Graukörpers (Emissionsgrad 1) abgeleitete scheinbare Temperatur.
Gefunden auf http://fe-lexikon.info/lexikon-s.htm
2. Strahlungstemperatur
die Temperatur, die ein schwarzer Körper hätte, wenn er die gleiche Lichtverteilung zeigte wie der jeweils untersuchte Körper (z. B. Fixsterne) . Sie ist ein ungefähres Maß für die wirkliche (bei Sternen nicht direkt messbare) Temperatur des Körpers.
Gefunden auf http://www.enzyklo.de/lokal/42303
3. Strahlungstemperatur
[radiation temperature] Die Temperatur, die ein Schwarzer Körper haben müsste, um einen grösseren, aber begrenzten Spektralbereichs eines Sterns anpassen zu können. Eine Spezialisierung auf eine Wellenlänge nennt man Schwarze Temperatur.
Gefunden auf http://astronomy.meta.org/infosys/ELisa/„
Sie schwafeln wieder nur und produzieren Nullsätze.
@ Ebel
Auch Sie produzieren überwiegend Nullsätze.“
Also sowas unoriginelles aus der Feder eines Ökonomen in Bezug auf naturwissenschaftliche Aussagen zu lesen, der über zehn Jahre vergebens versucht hat, erfolgreich seine Dissertation abzuschliessen und kaum eigene Fachartikel in Peer-review Journalen oder Konferenzen herausgebracht hat, muss man eigentlich schon als Auszeichnung ansehen.
„@ Ebel – Auch Sie produzieren überwiegend Nullsätze.“
Die Trauben sind zu sauer, sagte der Fuchs (Fabel von Äsop)
Sie hatten fälschlich behauptet, Strahlung hätte keine Temperatur. Ich habe Ihnen nachgewiesen, daß Ihre Behauptung tatsächlich falsch ist – und Ihre Reaktion auf Ihren Fehler ist die Beschuldigung mit „Nullsätzen“. Also Ihr komisches Verständnis: Hängt den Boten, wenn die Botschaft richtig ist.
MfG
„Allerdings hat die einfallende Nichtgleichgewichtsstrahlung i.a. keine Temperatur.“
Lesen Sie bitte Essex u.a.
MfG
Auch Sie gehören zu den Nulsatzschreibern.
Allerdings kommen Sie, Ebel und NicoBaecker nicht an diesen Nullsatzschreiber heran: »Die Applikation der Dialektologie im Bereich der Kulturraumforschung wie Volks- und Landeskunde basiert auf einer Adaption der diatopischen Betrachtungsweise und der damit verbundenen kartographischen Darstellungsverfahren sowie auf der hilfsdisziplinären Funktion dialektaler Erscheinungen im Rahmen kulturgeographischer Untersuchungen und führt generell zu einer Stützung kulturanthropologisch-geographischer Aussagen.«
„Kleine Ergänzung. Bei Gleichgewicht ist die Temperaturdefinition noch einfach, aber Essex u.a. behandeln u.a. auch die Temperatur einer Nichtgleichgewichtsstrahlung – wie auch Wien, der darauf hinwies, daß sogar ein Körnchen Schwarzkörper zur Gleichgewichtsstrahlung führt.“
In Arnold Sommerfelds altem Lehrbuch „Thermodynamik und statistische Physik“ leistet das „berühmte Kohlestäubchen“ auf der Innenseite des Hohlkörpers, dass eingefangene Strahlung jeglichen Spektrums mittels dem in allen Frequenzbreichen absorbierenden Köhlestäubchen mit der Zeit thermalisiert und sich im Hohlkörperinneren in thermische Strahlung mit Schwarzkörperspektrum umwandelt. Die Temperatur der sich ergebenden thermischen Strahlung ist allein durch die Gesamtenergie der Strahlung gegeben, die in den Hohlkörper einfiel (wenn die Wärmekapazität des Stäubchens als Null genommen wird und die Wandungen des Hohlkörpers ideal reflektieren). Ich nehme an, dies liegt letzten Endes Wiens Gedanke zugrunde. Allerdings hat die einfallende Nichtgleichgewichtsstrahlung i.a. keine Temperatur.
„Nullsätze sind Sätze, die ich auf Grund meiner fehlenden Fähigkeiten nicht verstehe.“
Sie schwafeln wieder nur und produzieren Nullsätze.
@ Ebel
Auch Sie produzieren überwiegend Nullsätze.
„der Begriff thermische Strahlung ist unmissverstaendlich in der Physik definiert und kennzeichnet ein Ensemble von Photonen im thermischen Gleichgewicht mit definierter Temperatur.“
Kleine Ergänzung. Bei Gleichgewicht ist die Temperaturdefinition noch einfach, aber Essex u.a. behandeln u.a. auch die Temperatur einer Nichtgleichgewichtsstrahlung – wie auch Wien, der darauf hinwies, daß sogar ein Körnchen Schwarzkörper zur Gleichgewichtsstrahlung führt.
MfG
Schreibt man die Kinder-Gleichung für die IR-Emission des Erdbodens Sb gemäss dem Muster
Sb = S*0,7/4 = Eps*Sigma*T^4 vom einfachen isothermen Erdmodell mit für Sonnenstrahlung S transparenter Atmosphäre sowie mit sb=Sigma entsprechend um, so ergibt sich aus
T(s) = [S*(1 – a – f)/(4*sb) * (1 – k/2)/(1 – e/2)]^1/4
die Gleichung S*0,7/(4*Sigma)/Eps = T^4
Das Eps (Bodenemission/Schwarzkörperemission = 0,967) mutiert also bei Herrn Kinder zu 1-0,967/2. Wie er zu diesem unsinnigen Ausdruck kommt, der natürlich in keinem Physikpaper zu finden ist und letztlich den THE wegzaubert, bleibt rätselhaft. Nicht nur die Subtraktion von 1, sondern auch die Halbierung lässt sich nicht erklären. Letztere ist wahrscheinlich darauf zurückzuführen dass Herr Kinder meinte, auf der Nachtseite der Erde werde kein IR emittiert – wozu diese aber 0 K annehmen müßte.
Die Frage unter #125 nach der „Grundlage für das Einführen des Terms (1-e/2) als Teiler“ beantwortet er in #128 nur mit „das finden Sie in jedem Paper zur Physik der Erde“. Abgesehen von der Behauptung „Dieses werden Sie mit Ihren physikalischen und mathematischen Kenntnissen wahrscheinlich niemals begreifen und nachvollziehen können“ warten wir bisher vergeblich auf ein Zitat bzw. eine Erklärung.
der Begriff thermische Strahlung ist unmissverstaendlich in der Physik definiert und kennzeichnet ein Ensemble von Photonen im thermischen Gleichgewicht mit definierter Temperatur.
„Auch das, was Sie „thermische Strahlung“ nennen, aber nicht definieren (können), hat keine Temperatur, denn Strahlung hat keine Temperatur, also auch nicht die jeweilige nach Wellenlänge benannte elektromagnetische Strahlung als Teilmenge.“
Auch wenn Sie meinen Beitrag „#137: Ebel sagt am Donnerstag, 13.09.2012, 22:23“ um 22:26 noch nicht gelesen haben konnten, veranlaßt mich Ihr Unsinn noch ein moderneres Paper zu nennen: Essex u.a.: How Hot is Radiation? [Wie heiß ist Strahlung?] http://tinyurl.com/9m4ustv oder „American Journal of Physics“ 71(2003), No. 10, 969 – 978.
Aber ich habe die Befürchtung, daß Sie mit Ihrem mindesten 120 Jahre alten Kenntnisstand der Physik diese Paper nicht verstehen können, da mit Hilbert-Räumen, Emsembles, Operatoren usw. gearbeitet wird.
MfG
„Seit wann hat „Strahlung“ eine Temperatur?“
Herr Heinzow, Ihre Physikkenntnisse sind auf dem Stand vor 1893 – also 120 Jahre zurück. Siehe z.B. http://tinyurl.com/9bchy7w
MfG
Lernen Sie doch erst mal korrekt zu formulieren.
Auch das, was Sie „thermische Strahlung“ nennen, aber nicht definieren (können), hat keine Temperatur, denn Strahlung hat keine Temperatur, also auch nicht die jeweilige nach Wellenlänge benannte elektromagnetische Strahlung als Teilmenge.
„Seit wann hat „Strahlung“ eine Temperatur? “
Hallo aufwachen: thermische Strahlung!!
„Schließlich ist vor und nach dem Nachregeln die Temperatur der thermischen Strahlung konstant 300K!“
Und Sie fragen Prof. Endres, natürlich gepaart mit einer unsubstantiierten Unterstellung: „mich würde interessieren, ob Sie inzwischen nachvollzogen haben, wie man den Entropiesatzes auf die Atmosphäre anwendet und damit einen Einwand gegen G&T nun physikalisch verstehen?“
Seit wann hat „Strahlung“ eine Temperatur?
„Es ging um das zugegebene CO2 und das Nachregeln der Temperatur, wodurch sich allein schon die Photonendichte (Strahlungsdichte) erhöht“
Das Nachregeln ist nur nötig, um sicherzustellen, dass nach Zugabe des CO2’s ins Behältnis wieder 300 K darin herrschen, das CO2 also die gleiche Temperatur hat, wie die Wandung und die thermische Strahlung der Photonen im Behälter. Die beim Nachregeln zu- oder abgeführte Energie „geht also nur aufs CO2“!
Die Photonendichte erhöht (oder erniedrigt) sich mit dem Nachregeln selbstverständlich nicht!! Schließlich ist vor und nach dem Nachregeln die Temperatur der thermischen Strahlung konstant 300K! Und damit ist die Photonendichte auch konstant, nämlich die, die das Planckgesetz für 300 K angibt.
Wenn das CO2 schon vor Zugabe 300K hätte und auch sonst beim Einlassen keine thermodynamische Änderung (Druck etc. konstant) durchmacht, so ist auch keine Regelung mit Energiezu- bzw. abfuhr nötig, denn die Hohlraumstrahlung von 300K und das zugegebene CO2 von 300K sind dann bereits thermalisiert, und es ändert sich an der Photonendichte der thermischen Strahlung durch Zugabe von CO2 gar nichts!
„Lieber Herr Becker, hätte ich das Gegenteil geschrieben, hätten Sie sich genau so geäußert.“
Eigentlich hatte ich tatsächlich nach Ihren Ausführungen weiter oben angenommen, Sie würden behaupten, die Photonendichte würde abnehmen. Denn ich interpretierte Ihre Vorstellungen, dass Sie annehmen, dass die IR-Absorption durch CO2 zu einem „Auslöschen“ von Photonen führt, denn Sie ignorieren oder wissen einfach nicht, dass im thermischen Gleichgewicht neben der Absorption von Photonen auch welche emittiert werden müssen, um das thermische Gleichgewicht aufrecht zu halten.
Aber mit meiner Vermutung, Sie wüssten nicht, dass thermische Strahlung selber ein thermodynamisches System mit Temperatur bildet, habe ich wohl richtig gelegen. Ihnen ist nicht klar, dass Hohlraumstrahlung entsprechend dem Planckschen Gesetz auch da ist, wenn der Raum nicht hohl ist, richtig?
Können Sie inzwischen meine Aufgabe über den Vergleich der Größenordnungen der Energiedichten (Luft vs. Photonen) lösen? Ist Ihnen nun klar, dass sich die Leistungsflussdichte aus Energiedichte mal Flussgeschwindigkeit ergibt? Und die ist für Photonen nun wie groß, hm…?
Außerdem scheinen Sie das Diagramm von GoodyYung mit der Strahlungsleistung der Sonne nicht verstanden zu haben. Ist da wirklich – wie Sie so kühn behaupten – die Gesamtleistung der Sonne abgebildet…mal nachgefragt, was sollte das für einen Sinn machen, auch den Teil der Leistung von der Sonne dort abzubilden, der auf der Erde gar nicht ankommt?
Hier noch zwei Fragen, die Sie leicht beantworten müßten, hätten Sie Physik Grundlagen oder GoodyYung, ThomasStamnes verstanden:
Wieviele thermische Photonen sind denn in einem Kubikzentimeter und wieviele CO2 Moleküle (bei 1bar und 300K)? Wieviele CO2 Moleküle kommen auf ein thermisches Photon? Und wie groß ist das Verhältnis der thermischen Energien von Photonen und CO2 Molekülen in diesem Kubikzentimeter?
„bis die Entropieproduktion durch Wärmeleitung die Entropieänderung dS gerade ausgleicht (erst dann ist das Fließgleichgewicht erreicht).“
Das zeugt von wenig Verständnis der Entropie. Die von verschiedenen Orten in den Weltraum abgestrahlte Energie ist genau so groß (im langzeitigen Mittel), wie die von der Erde absorbierte Energie. Die abgestrahlte Entropie hängt damit nur indirekt zusammen – gemäß dS = dQ/T. Wenn man noch die Entropie im Vakuum nimmt, kommt noch ein Vorfaktor hinzu, so daß gilt dS(Vakuum) = 4/3 dQ/T. Also die Abstrahlungstemperaturen bestimmen die Entropieproduktion und nicht umgekeht. Da die Strahlungstemperaturen unterschiedlich sind, ist die Entropieproduktion wegen der Konstanz des Integrals dQ wegen 1/T größer als bei einheitlicher Strahlungstemperatur.
Noch etwas zur Abstrahlung. Der Wärmestrom zwischen 2 Körpern ist um so geringer, je geinger die Temperaaturdifferenz ist. Wie man den Wärmestrom bei gegebenen Temperatrudifferenzen berechnet, ist eine Frage des Rechenganges, nicht der Physik – die Physik ist ganz eindeutig. Insofern ist die Frage Gegenstrahlung (existiert sie oder nicht), erwärmt sie oder nicht usw. ein Streit um des Kaisers Bart.
Zusammengefaßt siehe http://tinyurl.com/caokpo6
MfG
„Manche nennen den 2. Term auf der linken Seite Gegenstrahlung, Herr Kinder eben nicht, er nennt das Energieaustausch-Gleichgewicht“
Wahrscheinlich interpretieren Sie Herrn Kinder nicht richtig. Unter #119 ist sein e der Emissionsanteil der Oberfläche e = 0,967. Dieser ist auf die Sonneneinstrahlung bezogen. Wegen 1-e/2 geht er m.E. irrtümlich davon aus dass nur die als ruhend gedachte sonnenbeschienene Hemisphäre IR emittiert, und nicht auch die (dann weltraumkalte) Nachtseite – was mich an den von Prof. Gerlich berechneten absurden Temperaturmittelwert erinnert. Damit verdoppelt sich in etwa die Emisssion der Tagseite und entsprechend S-B erhöht sich deren Temperatur, welche Herr Kinder dann aber fälschlich für die gesamte globale Oberfläche – also auch für die nicht emittierende Nachtseite – angibt.
Wärmende Gegenstrahlung bestreitet doch Herr Kinder – also macht es sicher kaum Sinn, in einen Term seiner Gleichung eine Gegenstrahlung hineinzuinterpretieren, zumal die Gegenstrahlung nur 38,8 und nicht 50% ausmacht. Eigentlich sollte sich besser Herr Kinder, der ja die umstrittene Formel entwickelt hat, dazu äußern – aber ein Eingeständnis seines Fehlers können wir, die er für ziemlich blöd hält, wohl kaum erwarten.
#115: Herr NicoBaecker, Sie sind einfach nur unverschämt, von den „Bosonen“ haben Sie gesprochen und von den Materialeigenschaften ich, nämlich dem Unterschied von Gasen und festem oder flüssigem Körper.“
Sie haben in 76 behauptet, “ dass das Plancksche Strahlungsgesetz für „Gaskörper“ NICHT gültig ist und damit auch der emittierte Wärmestrom nicht proportional zu T^4 entsprechend dem Stefan-Boltzmann-Gesetz ist
und ich schrieb in 81 und 115 dass dies falsch ist. Denn das Plancksche StrahlungsGesetz folgt aus den Eigenschaften der Photonen und nicht der absorbierenden Materie. Das Plancksche StrahlungsGesetz kann daher fuer „Gaskoerper“ gar nicht falsch oder richtig sein, weil es keine Eigenschaften eines „Gaskoerper“s beschreibt, sondern von Photonen. Es folgt deduktiv aus der Statistik von Bosonen, zu denen auch Photonen als Teilchen mit ganzzahligem Spin gehoeren.
Die zwischen einem Koerper (ob Gas, fluessig oder fest) der Temperatur T und einem thermischen Strahlungsfeld der gleichen Temperatur T ausgetauschte thermische Strahlungsenergie ist nach dem Kirchhoffschen Gesetz nun proportional zu T hoch 4 und einem Materialparameter, dem Emissionsgrad, der von den Eigenschaften des Koerpers abhaengt, mit Photonen zu wechselwirken, naemlich seinen Absorptionslinien und deren Staerke.
Eine Abweichung vom T hoch vier Gesetz ist also nur moeglich, wenn der Emissionsgrad von T abhaengt, wenn nicht, so besteht die Proportionalitaet.
Lieber Herr Hess,
stimmt, die Formel wollte uns Kinder doch schon mal vor etwa einem Jahr unterjubeln. Ich hatte schon fest vergessen, dass es damals schon entlarvt wurde.
in einem groben globalen Strahlungsbilanz-Klimamodell wird der Strahlungsenergieaustausch zwischen Oberfläche und Atmosphäre durch zwei Terme bzw. Parameter beschrieben. Einen davon nennt man Gegenstrahlung.
ich habe nur die Gleichung von Herrn Kinder umgestellt:
„sb*T(s)^4 – sb*e/2* T(s)^4 = [S*(1 – a – f)/4* (1 – k/2)“
Links ist der Strahlungsenegieaustausch zwischen Oberfläche und Atmosphäre + Abstrahlung ins Weltall parametrisiert und Rechts die Einstrahlung in die Oberfläche. Manche nennen den 2. Term auf der linken Seite Gegenstrahlung, Herr Kinder eben nicht, er nennt das Energieaustausch-Gleichgewicht. Das ist ein freies Land. Er nennt ja auch die Entropie, Wärme. An der Physik ändert sich dadurch nichts.Im Kontext kann man das verstehen, nur nicht schließen, dass der Treibhauseffekt nicht existiert.
Mit freundlichen Grüßen
Günter Heß
=== zitat ===
@ #125: Marvin Müller sagt:
„Was ist nochmal die Grundlage für das Einführen des Terms (1-e/2) als Teiler?“
Also bitte, dass finden Sie in jedem Paper zur Physik der Erde. Ein bißchen Gedanken sollten Sie sich schon machen.
=== zitat ende ===
Na dann können Sie doch mal ein oder zwei Referenzen bringen.
Sie machen endlose Ausführungen zur Mittelung über Kreis/Kugel, die noch dazu in einer Verringerung der zur Verfügung stehenden Energie führen – aber zu einer von Ihnen eingeführten Erhöhung der Energie um den Faktor zwei kommt nichts? Das klingt nach Beweis durch Behauptung …
„Kreis- und Kugelflächenmittelung sind unnötig und beruhen auf Missverständnissen hinsichtlich des Erdmodells.“
Wieder so eine geistlose Phrase! Welches Erdmodell (witzig) verwenden Sie – Würfel, Tetraeder, Kegel?
Oh Mann, die Erde ist ein sphärischer Körper. Übrigens Messungen können dies bestätigen! Oder sind Sie schon so realitätsfremd?
„Sonderbar daß Sie Ihre 220 W/m^2 (statt 240) noch mit 0,9 multiplizieren und durch 1 – 0,967/2 = 0,5165 dividieren und hiermit die mittlere Strahlungsleistung fast verdoppeln. Somit erhöhen Sie die üblichen 255 K (-18 Grad) spielend auf 287 K (+14 Grad) und folgern prompt dass ein Treibhauseffekt nicht existiert. Solch hanebüchenen Unsinn glauben Sie doch wohl nicht im Ernst??“
Ihre Schlußfolgerung ist reinster Stuss! Die Strahlungsenergie-Änderung, die mit den beiden mittleren kontinuierlichen Temperaturen von T1=303K und T2=255K verbunden ist, beträgt dP = 5,67*10^-8*(303^4 – 255^4) = 238 W/m^2.
Da zeigt sich, dass Sie von dynamischen Systemen und Energieaustausch nicht die geringsten Kenntnisse haben. An der Energie, die von der Sonne kommt, können Sie nichts ändern. Ebensowenig an der Geometrie und den Eigenschaften der Erde, völlig egal ob sich Erde scnell oder langsam dreht. Jetzt müssen Sie nur noch die Dynamik aufgrund der Rotation berücksichtigen? Wie machen Sie das?
Dass die Verteilung innerhalb des Systems Erde (220 W/m^2) und die Abgabe an den Weltraum (238 W/m^2) über die Atmosphäre in der gleichen Größenordnung liegt und diese Verteilung zu den geringen Temperaturdifferenzen zwischen Tag- und Nachtseite führt, ist das entscheidende Merkmal dieses Planeten Erde. Die eigentliche Ursache liegt darin begründet, dass auf dem Planet Erde genügend Wasser vorhanden ist, und dieses Wasser FLÜSSIG und FLÜCHTIG ist.
Stehen keine anderen entropievergrößernden Prozesse zur Verfügung, steigt die Temperatur auf der Sonnen-Seite des Planeten solange an, bis die Entropieproduktion durch Wärmeleitung die Entropieänderung dS gerade ausgleicht (erst dann ist das Fließgleichgewicht erreicht). Ist die Temperaturdifferenz T1 – T2 hoch genug, kann diese Entropieproduktion mit der Entropieentsorgung aufgrund der Planeten-Rotation konkurrieren.
+ langsame Planeten-Rotation -> hohe Temperaturdifferenz im Fließgleichgewicht
+ schnelle Planeten-Rotation -> niedrige Temperaturdifferenz im Fließgleichgewicht
„Selbstverständlich strahlt die Erdoberfläche mehr ab, als ihr an Energie von der Sonne direkt zugeführt wird.“
Das ist der größte physikalische Unsinn! Wo ist die Energie-Quelle, die diese Energie erzeugt?
Wiederholung: Die Gegenstrahlung als eine eigene Energie-Quelle innerhalb der Atmosphäre zu bezeichnen, ist der Gipfel des physikalischen Unverständnis.
@ #125: Marvin Müller sagt:
„Was ist nochmal die Grundlage für das Einführen des Terms (1-e/2) als Teiler?“
Also bitte, dass finden Sie in jedem Paper zur Physik der Erde. Ein bißchen Gedanken sollten Sie sich schon machen.
@ #126: Günter Heß sagt:
„statt Mike‘s Trick gibt es jetzt den Kindertrick.“
Na ja, dass Sie das wieder nicht blicken, ist ja klar. Und eine Gegenstrahlung ist dort nicht enthalten, sondern ein Strahlungsaustausch-Gleichgewicht oder Energieaustausch-Gleichgewicht.
MfG
W. Kinder
„Im Grunde ist die Gegenstrahlung in der Formel:
„T(s) = [S*(1 – a – f)/(4*sb) * (1 – k/2)/(1 – e/2)]^1/4“
als sb*e/2* T(s)^4 parametrisiert. Herr Kinder nennt das nur anders. In seinem Modell geht etwa die Hälfte der emittierten Strahlung wieder als Gegenstrahlung zurück“
Ihre Vermutung scheint nicht zu stimmen denn Herr Kinder bestreitet doch mangels zusätzlicher Energiequelle eine erwärmende Gegenstrahlung (#119). Und es kommen nur etwa 38,8% der Bodenabstrahlung global als Gegenstrahlung zurück (Eps = 239/390 =0,612). M.E. wollte Herr Kinder mit 1-e/2 den Emissionsanteil der sonnenbeschienenen Hemisphäre berücksichtigen und hat damit – weil er so die IR-Emission der Nachtseite vergaß – die mittlere Abstrahlung verdoppelt. Ohne seine Korrekturzahlen hätte er das wohl auch gemerkt wenn S statt 240 auf 480 W/m² erhöht und damit T auf 303 K (+30 Grad) angestiegen wäre.
Die Kinder-Korrekturzahlen sind überflüssig und beruhen auf Missverständnissen hinsichtlich des Erdmodells. Die allgemein anerkannte Gleichung aus der T bestimmt werden kann, lautet 1364*0,7/4 = 239 W/m² = Eps*Sigma*T^4. Daraus ergibt sich T zu 288 K und ohne Eps zu 255 K. Die Differenz ist der Treibhauseffekt – der NICHT auf 1-e/2 sondern auf Eps als Maß für die behinderte IR-Emission zurückzuführen ist.
statt Mike‘s Trick gibt es jetzt den Kindertrick.
Im Grunde ist die Gegenstrahlung in der Formel:
„T(s) = [S*(1 – a – f)/(4*sb) * (1 – k/2)/(1 – e/2)]^1/4“
als sb*e/2* T(s)^4 parametrisiert. Herr Kinder nennt das nur anders. In seinem Modell geht etwa die Hälfte der emittierten Strahlung wieder als Gegenstrahlung zurück. Herr Kinder stellt also die Strahlungsbilanz mit Gegenstrahlung auf und zieht die Gegenstrahlung in die Klammer und behauptet dann der Treibhauseffekt existiert nicht.
Mit freundlichen Grüßen
Günter Heß
„Dieses werden Sie mit ihren physikalischen und mathematischen Kenntnissen wahrscheinlich niemals begreifen und nachvollziehen können.“
Da Sie mich so direkt ansprechen … Ja, Sie haben Recht, das kann ich mit meinen physikalischen Kenntnissen nicht nachvollziehen. Aber ich bin da offen für Neues. Was ist nochmal die Grundlage für das Einführen des Terms (1-e/2) als Teiler? Und warum nur e/2? Das ganze hat ja eine interessante Wirkung, (1-e) würde einen Faktor 30 einfügen, (1-e/2) nur noch einen Faktor 2.
Irgendwie wirkt das, als hätten Sie die Formel solange massiert, bis das von Ihnen gewünschte Ergebnis rauskommt. Es wäre also gut, wenn Sie mal die Begründung für die Einführung des Terms nahreichen könnten.
„Mit den Werten erhält man für die mittlere Temperatur der sphärischen Oberfläche aus der Strahlungs-Bilanz der sphärischen Erde:
T(s) = [1361*(1 – 0,3 – 0,0545)/(4*5,67*10^-8) * (1 – 0,19/2)/(1 – 0,967/2)]^1/4 = 287 K (+14°C)
Kurzum, der Treibhauseffekt ist nicht existent!“
Gratuliere zu Ihrer sensationellen Entdeckung dass es – im Gegensatz zu allen Strahlungsmodellen, -messungen und -berechnungen tausender Fachleute gar keinen THE gibt und Sie hier mit einer einzigen Zeile das ganze Kartenhaus des IPCC zum Einsturz bringen! Da wäre eigentlich ein Nobelpreis fällig oder wenigstens ein Ehrendoktor der Uni Entenhausen…
Betrachten wir die Erde als eine schnell rotierende, gut wärmeumverteilende und speichernde Schwarzkörperkugel, so können wir quasi Isothermie annehmen und global am Boden mit S-B rechnen. Der Einfangquerschnitt für Solarstrahlung ist eine Kreisfläche mit PiR², die Atmosphärenschicht ist für Sonnenstrahlung weitestgehend durchlässig, nicht jedoch für IR-Abstrahlung (Eps=0,612). Die Abstrahloberfläche der Kugel ist 4PiR², womit sich der Geometriefaktor 4 ergibt, dazu haben wir noch den Albedowert 0,3. Ihre übrigen Korrekturzahlen aus Kreis- und Kugelflächenmittelung sind unnötig und beruhen auf Missverständnissen hinsichtlich des Erdmodells.
Sonderbar daß Sie Ihre 220 W/m² (statt 240) noch mit 0,9 multiplizieren und durch 1 – 0,967/2 = 0,5165 dividieren und hiermit die mittlere Strahlungsleistung fast verdoppeln. Somit erhöhen Sie die üblichen 255 K (-18 Grad) spielend auf 287 K (+14 Grad) und folgern prompt dass ein Treibhauseffekt nicht existiert. Solch hanebüchenen Unsinn glauben Sie doch wohl nicht im Ernst??
Selbstverständlich strahlt die Erdoberfläche mehr ab, als ihr an Energie von der Sonne direkt zugeführt wird. Die Differenz wird von der Gegenstrahlung geliefert. Sie schreiben „DAS IST PHYSIKALISCHER UNSINN hoch 4! Wo hat die Erde eine Energie-Quelle, die diese „zusätzliche“ Energie produziert?“ Sie begreifen nicht dass Energiefluss (d.h. W/m²) und Temperatur nicht dasselbe sind. Bei guter Dämmung oder Gegenstrahlung kann auch mit weniger Heizenergie eine höhere Temperatur erreicht werden. Dazu bedarf es weder einer zusätzlichen Energiequelle noch Ihrer abstrusen Rechenakrobatik.
ich schildere das, was der Wettermast zeigt,
nichts anderes.
http://tinyurl.com/792ynwc
„immer mal wieder“ reicht leider nicht um daraus das Gegenteil zu machen mit dem Namen „Treibhauseffekt“.
mfG
Zitat:
3) konsequenterweise ist es am KÄLTESTEN bei maximaler langwelliger „Gegenstrahlung“, also bei Wolkenbedeckung, die die Erdrückstrahlung reflektieren kann, damit aber gemäß 2.HS die Erde trotzdem NICHT erwärmen kann.
Kälter ist es, weil aus dem gleichen Grund die viel größere Sonneneinstrahlung auf der Erde fehlt.
Schon wieder der gleiche Unsinn.
Ohne jetzt Gegenden strapazieren zu müssen, wo es bei Bewölkung meist viel wärmer ist, als ohne (Antarktis), trifft dies auch immer wieder mal für Hamburg meinetwegen zu. Speziell im Winter.
Aber mei, unserem Dr. der Nixwisserei jetzt auch das noch zu erklären, wäre wohl wieder extrem mühselig. Paul, mal doch mal die 2 Vekoren der Energieflüsse auf, addiere dann und guckst du, wie sich der Pfeil nach außen ändert.
Kühlt es weniger schnell ab, bleibt es länger wärmer, dass dürfte sogar Paul bereits aufgefallen sein und damit wird mal gaaaaaaanz sicher kein physikalisches Gesetz verletzt…:-)
nochmal zum Hamburger Wettermast:
http://tinyurl.com/792ynwc
Hier sieht man doch sehr schön:
1) die Höhe der Erdtemperatur ist ausschließlich von der Sonneneinstrahlung abhängig.
2) die Transparenz der Atmosphäre für Strahlung in dem zeitlichen Nachhinken der Temperatur der Atmosphäre gegenüber der Erde sowohl bei der Erwärmung, wie bei der Abkühlung.
3) konsequenterweise ist es am KÄLTESTEN bei maximaler langwelliger „Gegenstrahlung“, also bei Wolkenbedeckung, die die Erdrückstrahlung reflektieren kann, damit aber gemäß 2.HS die Erde trotzdem NICHT erwärmen kann.
Kälter ist es, weil aus dem gleichen Grund die viel größere Sonneneinstrahlung auf der Erde fehlt.
mfG
p.s. auch in dieser „Gegenstrahlung“ sind KEINE CO2-Banden enthalten! Das CO2 absorbiert in dieser Höhe nur, aber es strahlt nicht.
Und aus größerer Höhe kommt ganz besonders bei Wolkenbedeckung erst recht nichts auf der Erde an.
Ist doch nicht so schwer!
Sie ignorieren Fakten und machen Modellrechnungen.
Der Hamburger Wettermast misst KEINE CO2-Gegenstrahlung!
Wissen Sie das nicht?
Die Astronomen der Uni Stuttgart sind keine „Blödel“,
http://tinyurl.com/cvrssgr
sondern die Treibhausvertreter,
da sie falsche Modelle kreieren und sie noch als „Beweise“ werten.
mfG
„Differenz zwischen eingestrahlter Energie und abgestrahlter Energie gibt und das die Erdoberfläche mehr abstrahlt, als ihr an Energie von der Sonne direkt zugeführt wird. Diese Beobachtung wird im allgemeinen mit dem „Treibhauseffekt“ erklärt. Daher zog ich lax das Resumee, Sie hätten den Treibhauseffekt entdeckt.“
DAS IST PHYSIKALISCHER UNSINN hoch 4! Wo hat die Erde eine Energie-Quelle, die diese „zusätzliche“ Energie produziert?
Aus den Beoabachtungen folgt:
Vom der Sonne (als Flächen-Strahler) kommt eine Leistungsdichte von E(so) = 1361 W/m^2. Jetzt müssen aber die unterschiedlichen geometrischen Bedingungen bei der Einstrahlung und Ausstrahlung (Fläche, Hemisphäre und Sphäre) der Erde beachtet werden.
Die mittlere Einstrahlung auf die Zenith-Fläche beträgt: E(z) = E(so) * (1-a)/1 -> 360K (+87°C)
Die mittlere kontinuierliche hemisphärische Einstrahlung ist: E(h) = E(so) * (1-a)/2 -> 303K (+30°C)
Die durchschnittliche kontinuierliche sphärische Ausstrahlung beträgt: E(s) = E(so) * (1-a)/4 -> 255K (-18°C)
Man kann für die Hemisphären der Erde das Modell einer Absorptions-Kreisfläche (Schattenfläche) nicht anwenden, dazu muss die Strahlung der Sphäre vollkommen isotrop sein, die Symmetrie der Hemisphären muss vorhanden sein und die physikalischen Eigenschaften müssen sich monoton mit der Tiefe ändern. Für die Sonne sind diese Bedingungen in guter Näherung erfüllt, deshalb kann man die Sonne als Kreisflächen-Strahler annehmen. Für die Erde sind diese Bedingungen nicht erfüllt, damit sind einfache Flächen-Betrachtungen der Hemisphären ausgeschlossen.
Mathematisch betrachtet, ist die Kreisflächen-Mittelung nicht das gleiche wie die Kugelflächen-Mittelung. Man kann dies erkennen (Beispiel: Randverdunkelung der Sonne), indem man die Fläche von den Regionen eines Kreises oder einer Kugel mit |x| kleiner/gleich 1/2*r bestimmt. Für die Kreisfläche ergibt sich (pi/3 + sqrt(3)/2)*r^2, welches ca. 61% von der Gesamt-Kreisfläche ausmacht. Für eine Kugelfläche ergibt sich 2*pi*r^2, also genau 50% der Gesamtfläche der Kugel (Hemisphäre). Somit sind also bei der Kreisflächen-Mittelung die äquatorialen Regionen übergewichtet und die Pol-Regionen untergewichtet. D.h., man rechnet bei der Kreisflächen-Betrachtung mit einer höheren Energie, als die auf eine Hemisphäre bezogen. Aus den Mittelungen der Flächen kann man einen Kreisfläche/Hemisphären-Faktor f bezogen auf die Kugel bestimmen, er beträgt also f = (0,609 – 0,5)/2 = 0,0545.
Bei der Betrachtung der Strahlungs-Bilanz der sphärischen Erde mit einer kreisflächen-bezogenen Einstrahlung auf die Hemisphäre ergibt eine mittlere sphärische Oberflächen-Temperatur von:
T(s) = [S*(1 – a – f)/(4*sb) * (1 – k/2)/(1 – e/2)]^1/4
T(s) – Oberflächentemperatur
S – solarer Eingang (Solarkonstante) 1361 W/m^2
a – planetares Albedo a = 0,3
sb – Stefan-Boltzmann Konstante 5,67*10^-8
k – Adsorptionsanteil der Atmosphäre k = 0,19
e – Emissionsanteil der Oberfläche e = 0,967
f – Kreisfläche/Hemisphären-Faktor f = 0,0545
Mit den Werten erhält man für die mittlere Temperatur der sphärischen Oberfläche aus der Strahlungs-Bilanz der sphärischen Erde:
T(s) = [1361*(1 – 0,3 – 0,0545)/(4*5,67*10^-8) * (1 – 0,19/2)/(1 – 0,967/2)]^1/4 = 287 K (+14°C)
Kurzum, der Treibhauseffekt ist nicht existent!
Dieses werden Sie mit ihren physikalischen und mathematischen Kenntnissen wahrscheinlich niemals begreifen und nachvollziehen können.
MfG
W. Kinder
Es muss also heisen RICHTIG, Herr Dr.Paul
und nicht falsch.
mfG
„Hören Sie bitte mit Ihrem Strohhalm Alaska auf, wo die Luft wärmer ist als der Boden ist.
Und verdrängen Sie bitte nicht die Realität, dass die CO2- Banden – Transmission der Atmosphäre = 0 ist…Was das CO2 in dieser Höhe temperaturbedingt abstrahlt (SB) und was man vom Satelliten aus messen kann, kommt selbstverständlich ebensowenig auf der Erdoberfläche an“
Sie werden wohl als erleuchteter Allesbesserwisser bis ans Ende Ihrer Tage sämtliche anderen Wissenschaftler für Blödel halten weil Sie nicht begreifen dass Gegenstrahlung NICHT von 5% Spontanfluoreszenz aus der obersten Troposphäre stammt, sondern thermische Emission aus der untersten Troposphäre ist – gemäß Kirchhoff und Planck. Die in Barrow/Alaska gemessene Strahlung stammt nachweislich NICHT von einer Bodeninversion, und die Gegenstrahlung wird bekanntlich auch am Hamburger Wettermast gemessen.
Von der Bodenabstrahlung (390 W/m²) werden von der Atmosphäre insgesamt 300 W/m² absorbiert. Nach oben gehen (im Mittel bzw. Gleichgewicht) 390-300+150=240 W/m² heraus. Wenn nach unten NICHT 150 W/m² herauskämen, wie Sie behaupten, würde ja die Atmosphäre laufend wärmer obwohl der Boden -18 Grad kalt wäre. Beides widerspricht der Beobachtung und ist grottenfalsch. Selbst Prof. Kramm und Prof. Gerlich bestreiten nicht die Existenz der Gegenstrahlung am Boden, meinen aber wegen ihres 2.HS-Irrtums – sowie unter Verletzung von Stefan-Boltzmann und dem Energieerhaltungssatz – dass diese „Kaltstrahlung“ keine temperaturerhöhende Wirkung am Boden hat gegenüber dem Fall dass sie den Wert Null aufweist.
zählt die Troposphäre wohl nicht zur Erde, sondern zum All.
Wie sonst kommt man auf so „kosmische Gedanken“?
Hat sich der liebe Paul schon mal überlegt, aus welcher Höhe IR Strahlung von zB. Wasserdampf in den Tropen ins All entweicht und wie hoch diese Schicht im Mittel über zB. Deutschland liegt?
Wohl kaum.
Sollte er aber doch noch anfangen, mitzudenken, wird selbst ihm auffallen, wie peinlich sein Auftreten nun über Jahre schon war….
falsch, eben genau das nicht.
wie man leicht in Physikbuechern nachpruefen kann, folgt nach den Strahlunggesetzen, dass eine Abweichung der thermischen Gesamtabstrahlung vom T hoch 4 Gesetz nur dann vorliegen kann, wenn der Emissionsgrad temperaturabhaengig ist. Diese Abhaengigkeit ist durch die Materialeigenschaften der mit dem Photonenfeld wechselwirkenden Materie gegeben und hat nichts damit zu tun, dass Photonen Bosonen sind.
na,???
Sie bemühen sich vergeblich,
hier einfache Zusammenhänge verschleiern zu wollen. Das allerdings in unverschämten Ton,
was sagt nur ihre Freundin dazu?
Oder wird so ein Mist tatsächlich mit Geld bezahlt? Vielleicht sogar mit Steuergeldern?
also auch von mir?
Ich fordere Sie auf, etwas sachlicher zu werden für mein Geld!
mfG
Und verdrängen Sie bitte nicht die Realität, dass die CO2- Banden – Transmission der Atmosphäre = 0 ist.
Ein bischen Logik könnte Ihnen nicht schaden! Sie benötigen doch diese Totalabsorbtion auch für den „Treibhauseffekt“ ohne zu bedenken, dass diese Absorbtion für alle Richtungen durch die Atmosphäre wirken muss.
Noch einmal in den ca.10000 Höhe ist der CO2 Banden-Anteil der Erdrückstrahlung nicht mehr vorhanden, alles wurde auf dem Weg dorthin absorbiert. Das Wichtigste Fenster für die Erdabstrahlung liegt bei 10µm,
ausgerechnet dem Maximum der Rückstrahlung nach SB.
Was das CO2 in dieser Höhe temperaturbedingt abstrahlt (SB) und was man vom Satelliten aus messen kann,
komt selbstverständlich ebensowenig auf der Erdoberfläche an.
Hier wird also schlicht gelogen, dass sich die Balken biegen, auch von unserem kleinen Genie Baecker.
Das beschriebene zeigt eine Infrarot-Kamera von der Uni Stuttgart:
http://tinyurl.com/cvrssgr
Die „Gegenstrahlung“ für die beiden CO2 Banden bei 4,2µm (z.T. von der Sonne!!!) und um 15µm ist exakt 0.
Nichts davon kommt also auf der Erde an. Sie rechnen mit nicht existierenden Werten.
mfG
Nach allem was ich gelesen habe, kann auch der Svensmarkfaktor bestenfalls als sehr umstritten bezeichnet werden.
„Sollten Sie wirklich Ing. sein, bitte geben Sie umgehend Ihr Diplom zurück, wegen erwiesener Unfähigkeit! Und vorher fassen Sie noch an die Kühlrippen des Kompressors der die Pressluftflasche gefüllt hat, dann „erfühlen“ Sie auch die Wirkung der Gasgleichung. “
Ich glaube, Herr Dietze hat nichts dagegen, wenn Sie den ausgeschalteten Kompressor zusätzlich zur gefüllten Preßluftflasche ins Wohnzimmer stellen, um damit Heizkosten zu sparen…
„Hallo Herr Marvin Müller (#93)
Entschuldigung: Diese Äußerung in diesen Wortlaut haben Sie natürlich nicht getätigt.“
Auch nicht sinngemäß, aber lassen wir das.
‚Sie unterstellen mir ja auch: „Herr Kinder entdeckt den Treibhauseffekt :)“‚
Ich unterstelle Ihnen aber nicht, dass Sie das so gesagt haben. Was ich festgestellt habe, ist, dass Sie die Tatsache entdeckt haben, dass es eine Differenz zwischen eingestrahlter Energie und abgestrahlter Energie gibt und das die Erdoberfläche mehr abstrahlt, als ihr an Energie von der Sonne direkt zugeführt wird. Diese Beobachtung wird im allgemeinen mit dem „Treibhauseffekt“ erklärt. Daher zog ich lax das Resumee, Sie hätten den Treibhauseffekt entdeckt.
Aber wirklich interessant wäre ja mal, was denn nun Ihrer Meinung an der Betrachtung falsch sein soll:
– stimmt die Berechnung der einfallenden Sonnenenergie nicht? Wie gross ist denn die Differenz zu einem Ansatz mit einer Halbkugel? (Irgendie glaube ich mich zu errinnern, dass das im Kontext von Gehrlich und Tscheuschner mal ausgerechnet wurde und die Differenz minimal war)
– strahlt die Erde nicht von einer Kugelfläche ab?
„Dann bitte ich Sie aber gleichfalls, ihr Statement „Herr Kinder entdeckt den Treibhauseffekt :)“ zurück zunehmen.“
Ich hoffe, das ist mit obiger Erläuterung getan …
Und Gerald Pesch (#106) irrt gewaltig wenn er meint, „die Gesetze der Gasgleichung bestimmen die Bodentemperatur, das CO2 ist dabei unbedeutend“. Wenn er glaubt dass Druck laufend Wärme erzeugt, möge er sich doch eine Preßluftflasche (200 bar) ins Wohnzimmer legen um so die Heizkosten zu sparen.
Sollten Sie wirklich Ing. sein, bitte geben Sie umgehend Ihr Diplom zurück, wegen erwiesener Unfähigkeit! Und vorher fassen Sie noch an die Kühlrippen des Kompressors der die Pressluftflasche gefüllt hat, dann „erfühlen“ Sie auch die Wirkung der Gasgleichung.
„Herr Tietze wirkt schon etwas peinlich mit seiner nicht existierenden „Gegenstrahlung“ auf der Erdoberfläche, peinlich mit seiner grottenfalschen Herunterrechnung der Sonneneinstrahlung und konsequenterweise mit seinem hartnäckigen Ignorieren des mächtigen Kühleffektes der Atmosphäre für die Erdoberfläche. Er hat dazu dummerweise selbst mal als Ing., man sollte es nicht Glauben, das Beispiel der Solarkollektoren genannt, die noch besser als der Mond zeigen, wie stark diese Erdatmosphäre KÜHLT!“
Lese ich da richtig?? Meine „nicht existierende Gegenstrahlung“ wurde doch als thermische Emission der untersten Atmosphäre an der Forschungsstation Barrow/Alaska am Boden mit 43 W/m² gemessen! Und dazu ein „mächtiger Kühleffekt der Atmosphäre“ – ein Wunder dass wir nicht bei -28 °C leben müssen. Die nichtstrahlende N2/O2-Atmosphäre speichert allenfalls Wärme.
Das bedeutet dass sie tagsüber die Erwärmung verzögert und nachts die Abkühlung. Aber kühlen oder wärmen kann diese im Mittel NICHT. Und dass THG wegen der IR-Rückstrahlung zu Bodenerwärmung führen, dürfte unbestreitbar sein. Wenn Solarkollektoren, die Wasser von 60 Grad erzeugen, zeigen dass die Erdatmosphäre KÜHLT, sollte sich Dr. Paul mal ärztlich untersuchen lassen.
„Es geht um Energie-Betrachtungen in einem System, das unterschiedliche geometrische Bedingungen für den Eintrag und für den Austrag der Energie ausweist. Und das Pfannen-Beispiel können Sie sich an die Kniescheibe nageln“
Genau mein Pfannenbeispiel paßt doch bezüglich „geometrischer Bedingungen“: 1 kW, große Pfanne – bessere Kühlung – niedrigere Temperatur. Kleine Pfanne – schlechtere Kühlung – höhere Temperatur. Ihr Problem ist dass Sie analoge Beispiele nicht auf die Reihe bringen. Dann hätten Sie wenigstens die zusätzliche Erwärmung der Kochplatte bei IR-Rückstrahlung per Alufolie akzeptieren sollen – aber selbst das haben Sie mit Rücksicht auf Ihre treibhausfeindliche Physik-Scheinwelt ausgeblendet: Für Sie darf CO2 nicht ähnlich wirken wie eine Alufolie die IR zurückstrahlt und damit die Kühlung verschlechtert.
Weder CO2 noch Alufolie erzeugen zusätzliche Energie – aber beide wirken auf den Boden bzw. auf die Kochplatte so als ob, womit sich deren Temperatur erhöht. Selbst Prof. Kramm hat die („kältere“) Gegenstrahlung als additiven Term (W/m²) in seiner Bodenbilanz – aber dass sich damit zwangsläufig die Bodentemperatur erhöhen muss, will er partout nicht zugeben. Sie sollten endlich begreifen dass NICHT die Frage strittig ist ob der THE physikalisch existiert, sondern lediglich wie gering er ist.
Und Gerald Pesch (#106) irrt gewaltig wenn er meint, „die Gesetze der Gasgleichung bestimmen die Bodentemperatur, das CO2 ist dabei unbedeutend“. Wenn er glaubt dass Druck laufend Wärme erzeugt, möge er sich doch eine Preßluftflasche (200 bar) ins Wohnzimmer legen um so die Heizkosten zu sparen.
CO2 Moleküle reflektieren nicht, und unter den Bedingungen der Troposphäre reemittieren dies auch nicht (Stoßdeaktivierung). Ihre Überlegungen sind somit für die Tonne. Die Empirischen Beobachtungen sowohl bei Inversionswetterlagen wie auch bei Fönwetterlagen wiederlegen klar die „Gegenstrahlungstheorie“. Die Gesetze der Gasgleichung bestimmen die Bodentemperatur, das CO2 ist dabei unbedeutend.
Ich muss mich für ein paar Tage ausklinken, da ich anderweitig beschäftigt bin.
Aber noch einmal zu Inversionswetterlage. Ich fragte Herr Becker unter #34 zur Stabilität von Inversionslagen im Zusammenhang mit dem Strahlungstransport. Er antwortete unter #41: „Wieso sollten heutige GCM keine polare Inversionswetterlagen simulieren?“ Unter #59 habe ich mich vertippt. Es muss natürlich nicht heißen „Wo habe ich etwas über Inversion gesagt?“ sondern „Wo habe ich etwas über polare Inversion gesagt?“
So und jetzt noch mal die Frage an NicoBaecker, wieso löst sich trotz Strahlungstransport eine Inversionswetterlage (Warmluftschicht in 800 – 1200 m Höhe) erst nach Tagen auf? Das können Sie mit dem Strahlungstransport nicht beantworten. Deshalb ist das Prinzip mehr als fragwürdig!
Die richtige Antwort hat Herr Becker bereits unter #48 gegeben und Herr Pesch hat es auf den Punkt gebracht:
„Selbst bei einer Inversionswetterlage schafft es die „Gegenstrahlung“ aus der wärmeren!! Luftschicht nicht diese aufzulösen. Erst eine Durchmischung durch Konvektion beendet eine Inversionswetterlage. Die Temperaturschichtung der Troposphäre hat mit den Strahlungsmodellen der Klimaerwärmer nichts zu tun, diese ist definiert durch die Adiabate. Von daher, CO2 ist und bleibt ein harmloses Spurengas und das Ende der Welt durch dessen Freisetzung wird wohl nicht stattfinden.“
So ist es.
völlig richtig.
Herr Tietze wirkt schon etwas peinlich mit seiner nicht existierenden „Gegenstrahlung“ auf der Erdoberfläche, peinlich mit seiner grottenfalschen Herunterrechnung der Sonneneinstrahlung und konsequenterweise mit seinem hartnäckigen Ignorieren des mächtigen Kühleffektes der Atmosphäre für die Erdoberfläche. Er hat dazu dummerweise selbst mal als Ing., man sollte es nicht Glauben, das Beispiel der Solarkollektoren genannt, die noch besser als der Mond zeigen, wie stark diese Erdatmosphäre KÜHLT!
Ich hab da in den Prospekten mal nachgelesen, die Leistung dieser Absorber, die natürlich auch nach SB zurückstrahlen, aber zur Atmosphäre durch Vakuum (optimal) isoliert sind, gibt man mit der sog. Stagnationstemperatur an, also ohne Wärmeableitung, geht noch viel höher als auf dem Mond bei definierten (nur) 1000W/m², nämlich bis auf 300• Celsius bei den besten Absorbern.
Die Erde ist zudem sehr wenig gegen „Abstrahlung“ isoliert, was man besonders in Wolkenstein Nächten erlebt, aber dafür ganz exzellent diese NICHT strahlende Atmosphäre mechanisch durch das Vakuum des Welraums, weshalb es nicht so kalt werden kann wie auf dem Mond.
MfG
=== zitat ===
Marvin Müller (#80) bestätigte Herrn Kinder (#77) dass er mit der „wundersamen Vermehrung der Energie im System Erde/Atmosphäre von 151 W/m²“ den Treibhauseffekt entdeckt hat – dann aber meint er (#93), Herr Kinder habe recht mit „Die „Gegenstrahlung“ als eine eigene Energie-Quelle innerhalb der Atmosphäre zu bezeichnen, ist der Gipfel des physikalischen Unverständnis“.
Unter #94 habe ich dargelegt weshalb die Gegenstrahlung in bezug auf den Boden (wohlgemerkt NICHT für das Gesamtsystem Erde +Atmosphäre) intern wie eine zusätzliche Energiequelle betrachtet werden muss.“
=== ende zitat ===
Hmm, das war jetzt nicht als Kritik an Ihnen gemeint. Man bekommt oft vorgesetzt, das die nach unten gerichtete langwellige Infrarotstrahlung der Atmosphäre aus einer eigenen Energiequelle stammen müsse – einer Energiequelle wie die Sonne. Genau so habe ich die Aussage von Herrn Kinder verstanden und ihm daher zugestimmt, dass das Nonsens ist. Und ich war verärgert, dass er mir einen solchen Blödsinn unterschieben will. Hoffentlich hat er wenigstens die Größe, das einzuräumen.
Wenn man natürlich die Energiebilanz der Erdoberfläche aufstellen will, geht die nach unten gerichtete langwellige IR-Strahlung natürlich als Term ein, wie man sogar bei Herrn Kramm sehen konnte.
„bitte in Ihrer Scheinwelt nicht Energie bzw. (Strahlungs-)Leistung mit Temperatur gleichsetzen!“
Die Temperatur eines Systems ist ein Parameter, der im thermischen Gleichgewicht angibt, wie die Energien über die Energieniveaus der Mikrozustände verteilt sind. Es geht um Energie-Betrachtungen in einem System, das unterschiedliche geometrische Bedingungen für den Eintrag und für den Austrag der Energie ausweist.
Und das Pfannen-Beispiel können Sie sich an die Kniescheibe nageln.
MfG
W. Kinder
Entschuldigung: Diese Äußerung in diesen Wortlaut haben Sie natürlich nicht getätigt.
„Die Gegenstrahlung als eine eigene Energie-Quelle innerhalb der Atmosphäre zu bezeichnen, ist der Gipfel des physikalischen Unverständnis.“
Sie unterstellen mir ja auch: „Herr Kinder entdeckt den Treibhauseffekt :)“
Es geht um die Energie-Bilanz bei der Betrachtung einer kreisförmigen Eingangs-Absorptionsfläche (oder Schattenfläche) eines sphärischen Körpers.
Dass hat mit dem fiktiven „Treibhauseffekt“ erstmal gar nichts zu tun, nur ganz nebenbei bemerkt.
Dann bitte ich Sie aber gleichfalls, ihr scheinheiliges Statement „Herr Kinder entdeckt den Treibhauseffekt :)“ zurück zunehmen.
MfG
W. Kinder
„Bei den „Klimaerwärmern“ können aber IR-angeregte CO2 Moleküle aus Höhenlagen um -40°C den Erdboden erwärmen; durch „Gegenstrahlung“. Dass so ein Irrsinn propagiert wird, und als Grundlage zur Zerschlagung der Energieversorgung dient, ist nur schwer zu begreifen. Nachfolgende Generationen werden uns für verrückt erklären!“
Wenn es keine wärmende Gegenstrahlung gäbe – und die kommt NICHT aus Bereichen mit -40°C sondern ist i.w. thermische Emission aus der untersten Troposphäre – könnte niemals der Erdboden „irrsinnige“ 390 W/m² abstrahlen, also 150 W/m² mehr als die Sonne mit 240 W/m² liefert.
Marvin Müller (#80) bestätigte Herrn Kinder (#77) dass er mit der „wundersamen Vermehrung der Energie im System Erde/Atmosphäre von 151 W/m²“ den Treibhauseffekt entdeckt hat – dann aber meint er (#93), Herr Kinder habe recht mit „Die „Gegenstrahlung“ als eine eigene Energie-Quelle innerhalb der Atmosphäre zu bezeichnen, ist der Gipfel des physikalischen Unverständnis“.
Unter #94 habe ich dargelegt weshalb die Gegenstrahlung in bezug auf den Boden (wohlgemerkt NICHT für das Gesamtsystem Erde +Atmosphäre) intern wie eine zusätzliche Energiequelle betrachtet werden muss. Wenn Sie einen Spiegel vor das Objektiv eines Diaprojektors halten, brennt meist die Birne durch, obwohl der Spiegel keine zusätzliche Energiequelle ist. Die zurückgespiegelte bzw. zurückemittierte Strahlung behindert nämlich die Kühlung und wirkt somit quasi wie eine Wärmedämmung die zu einem „Wärmestau“ führt.
„Noch nie etwas vom Energie-Bilanzerhaltungssatz gehört?
Nur das was an Energie rein kommt (von der Sonne), kann verteilt werden.“
Den haben Sie in Ihrem #77 offensichtlich nicht auf die Reihe bekommen, indem Sie einfach mal ein paar Energieflüsse weggelassen und sich dann gewundert haben, dass das Kirchhoffsche Gesetz scheinbar nicht mit dem Eneergieerhaltungssatz zusammenpasst. Sie sind „genial“.
die „Null Aussage“!
1. ca. die Hälfte dieser „Werke“ ist jeweils komplett überflüssig. Die Herleitungen der physikalisch relevanten Formeln, das Beschreiben der selben usw. ist so was von alt und bekannt, dass man dem ganzen bestenfalls die Bezeichnung: der Odnung halber Fleißaufgabe, zumuten kann.
2. dann zeigen sie, völlig korrekt, dass es falsch Bezeichnungen für den THE gibt, wie „Reflexion von IR Strahlung usw., sie zeigen, dass es in der Literatur falsche Diagramme gibt (ohne Achsenbeschriftung usw) und begründen damit, dass es „diesen“ THE nicht gibt.
3. sie wissen, dass es die Gegenstrahlung gibt, haben diese sogar selbst gemessen. Sie wissen auch, dass heute „oben“ weniger IR raus kommt, als es sollte und verneinen jede Antwort auf die Frage, was hat das für Folgen?
4. G&T wie auch K&D sind zu feig od. sonst was um ein Ergebnis zu präsentieren. Welche Folgen hat eine Verdopplung des CO2 Gehaltes auf die Troposphäre? Gar keine??? Wir es kälter (hohoho), wärmer? oder ändert sich an der T gar nichts? Nur weil man oft nicht exakte Lösungen für die Differenzialgleichungen hat, heisst das noch lange nicht, dass man nicht ausreichend genau annähern kann. Auch die sg. Atmosphäregleichung ist eine Diff. Gleichung, welche nicht lösbar ist, dennoch schaffen es die sg. Wettermodelle den Zustand und die Entwicklung der Atmosphäre über einige Tage sehr gut zu berechnen. Nie exakt, oft aber mit erstaunlicher Genauigkeit über bis zu 2-3 Wochen.
Summarum, die Herren zeigen, was andere für Fehler machen, kommen gleichzeitig aber zu keiner eigenen Aussage, kein Ergebnis, nicht mal ne Abschätzung, nichts, na bravo!
„Es ging um das zugegebene CO2 und das Nachregeln der Temperatur, wodurch sich allein schon die Photonendichte (Strahlungsdichte) erhöht“
Das Nachregeln ist nur nötig, um sicherzustellen, dass nach Zugabe des CO2’s ins Behältnis wieder 300 K darin herrschen, das CO2 also die gleiche Temperatur hat, wie die Wandung und die thermische Strahlung der Photonen im Behälter. Die beim Nachregeln zu- oder abgeführte Energie „geht also nur aufs CO2“!
Die Photonendichte erhöht (oder erniedrigt) sich mit dem Nachregeln selbstverständlich nicht!! Schließlich ist vor und nach dem Nachregeln die Temperatur der thermischen Strahlung konstant 300K! Und damit ist die Photonendichte auch konstant, nämlich die, die das Planckgesetz für 300 K angibt.
Wenn das CO2 schon vor Zugabe 300K hätte und auch sonst beim Einlassen keine thermodynamische Änderung (Druck etc. konstant) durchmacht, so ist auch keine Regelung mit Energiezu- bzw. abfuhr nötig, denn die Hohlraumstrahlung von 300K und das zugegebene CO2 von 300K sind dann bereits thermalisiert, und es ändert sich an der Photonendichte der thermischen Strahlung durch Zugabe von CO2 gar nichts!
„Lieber Herr Becker, hätte ich das Gegenteil geschrieben, hätten Sie sich genau so geäußert.“
Eigentlich hatte ich tatsächlich nach Ihren Ausführungen weiter oben zu Ihren rudimentär und naiv durchdachten Vorgängen angenommen, Sie würden behaupten, die Photonendichte würde abnehmen. Denn ich interpretierte Ihr physikalisches Wirrwarr so, dass Sie annähmen, dass die IR-Absorption durch CO2 zu einem „Auslöschen“ von Photonen führt, denn Sie ignorieren oder wissen einfach nicht, dass im thermischen Gleichgewicht neben der Absorption von Photonen auch welche emittiert werden müssen, um das thermische Gleichgewicht aufrecht zu halten.
Aber mit meiner Vermutung, Sie wüssten nicht, dass thermische Strahlung selber ein thermodynamisches System mit Temperatur bildet, habe ich wohl richtig gelegen. Ihnen ist nicht klar, dass Hohlraumstrahlung entsprechend dem Planckschen Gesetz auch da ist, wenn der Raum nicht hohl ist, richtig?
Sie brauchen sich nicht zu beschweren, ich habe Ihnen ja die physikalisch richtige Antwort zuzüglich Erklärung geliefert. Wieder was dazugelernt. Jetzt antworten Sie in Zukunft hoffentlich richtig auf diese Frage 😉
“ Ich habe das sehr wohl verstanden, weshalb ich Ihnen Recht gebe. Anschaulich geht um die Thermodynamik (k x T-Term) von Photonen (h x f).“
Herr Hug, Physik besteht nicht daraus, Formeln abzuschreiben und irgendwas dazu zu fabulieren. Ihr Satz „es geht um…“ ist vollkommen sinnfrei.
Selbstverständlich können Sie natürlich auch nicht meine Aufgabe über den Vergleich der Größenordnungen der Energiedichten (Luft vs. Photonen) lösen, denn Ihnen ist nicht klar, dass sich die Leistungsflussdichte aus Energiedichte mal Flussgeschwindigkeit ergibt. Und die ist für Photonen nun wie groß, hm…?
Außerdem haben Sie das Diagramm von GoodyYung mit der Strahlungsleistung der Sonne nicht verstanden. Ist da wirklich – wie Sie so kühn behaupten – die Gesamtleistung der Sonne abgebildet…mal nachgefragt, was sollte das für einen Sinn machen, auch den Teil der Leistung von der Sonne dort abzubilden, der auf der Erde gar nicht ankommt?
Also nochmal meine Frage an Sie, ob Sie sich nicht reichlich selbst überschätzen, wenn Sie behaupten, das Buch verstanden zu haben aber schon an einem simplen Diagramm im Einleitungstext scheitern und nicht wissen, wie der Zusammenhang zwischen Energiedichte und Leistungsflussdichte ist…
Wenn ich Sie nun nach den anspruchvolleren Inhalten des Buches fragen würde, würden Sie natürlich behaupten, ich würde vom Thema ablenken wollen. Aber das Thema ist nunmal die Physik des Strahlungstransportes, es gibt kein anderes, das können Sie auch nicht durch Ihr Blabla über Sinn oder Unsinn von Klimaschutz etc. beantworten. Die Physik der Strahlung ist gegenüber Politik invariant, also bleiben Sie beim Thema und halten Sie sich an das, was ich geschrieben haben und überprüfen Sie das, anstatt sich einzureden, ich wolle Sie veräppeln.
Hier noch zwei Fragen, die Sie leicht beantworten müßten, hätten Sie Physik Grundlagen oder GoodyYung, ThomasStamnes verstanden:
Wieviele thermische Photonen sind denn in einem Kubikzentimeter und wieviele CO2 Moleküle (bei 1bar und 300K)? Wieviele CO2 Moleküle kommen auf ein thermisches Photon? Und wie groß ist das Verhältnis der thermischen Energien von Photonen und CO2 Molekülen in diesem Kubikzentimeter?
Ich wette, Sie antworten nicht oder nur ausweichend mit Blabla über Klimapolitik oder meine Motive. Jedenfalls bekomme ich von Ihnen keine konkrete Antwort auf die Fragen, und ich denke, es liegt daran, dass Sie einfach nicht fähig sind, diese zu beantworten.
Eine Strahlungsinversion betrifft in der Regel nur die unmittelbare Nähe zum Erdboden und wird daher auch als Bodeninversion bezeichnet. Sie wird durch die Abstrahlung und damit Abkühlung der Erdoberfläche hervorgerufen und tritt vor allem bei herbstlichen und winterlichen Hochdruckwetterlagen auf, da dann die Temperatur besonders niedrig ist und die fehlende Wolkendecke die nächtliche Auskühlung begünstigt.
Um die Zeit des täglichen Maximums der Lufttemperatur, also zwischen Mittag und drei Uhr, zeigt sich eine stark erwärmte Erdoberfläche, die die darüber befindliche Luft ebenso aufheizt. Aufgrund des dann in Bodennähe überadiabatischen Temperaturgradienten und der folglich labilen Atmosphärenschichtung kommt es zu einer Durchmischung der bodennahen Luftschichten über konvektive Prozesse. Mit zunehmender Tageszeit geht die Sonneneinstrahlung und damit die Erwärmung der Erdoberfläche jedoch zurück. Da die Strahlungsbilanz schließlich negativ wird, beginnt die Erdoberfläche und mit ihr die Luftschichten in Bodennähe auszukühlen. Dadurch entsteht schließlich in den Abendstunden eine zunächst schwache Inversion, wodurch der vertikale Luftaustausch praktisch unterbunden wird. Die im Tagesgang erzeugten wärmeren Luftschichten in größeren Höhen können den Erdboden dadurch nicht an der Auskühlung hindern, die immer weiter voranschreitet. Auch der meist schwächer werdende Wind trägt hierzu bei und verstärkt die Abkühlungstendenz.
Wärme Luftschichten in grosser Höhe können den Boden nicht an der Auskühlung hindern!!!!!!
Bei den „Klimaerwärmern“ können aber IR-angeregte CO2 Moleküle aus Höhenlagen um -40°C den Erdboden erwärmen; durch „Gegenstrahlung“. Dass so ein Irrsinn propagiert wird, und als Grundlage zur Zerschlagung der Energieversorgung dient, ist nur schwer zu begreifen. Nachfolgende Generationen werden uns für verrückt erklären!
Sie als Ausgeburt der multiplen Ahnungslosigkeit, haben vor langer Zeit die Begriffe „Dampferzeuger“ und „Turbine“
durcheinander geworfen. Und jetzt fordern Sie Dr. Paul auf, etwas zu quantifizieren, wovon Sie sowieso keine Ahnung haben.
Zeigen Sie hier erst mal, dass Sie zu etwas anderem als zu leeren Luftblasen fähig sind bevor Sie Konkretisierungen anfordern.
Oder anders gesagt: Auf Fragen von Trollen wie ihnen muss man nicht antworten.
Verstanden?
„Die Sonne trägt zu 99% am Energie-Haushalt der Erde bei. Die „Gegenstrahlung“ als eine eigene Energie-Quelle innerhalb der Atmosphäre zu bezeichnen, ist der Gipfel des physikalischen Unverständnis. Na ja, leben Sie weiter in Ihre Scheinwelt der pseudo-physikalischen Erklärungen“
Herr Kinder, bitte in Ihrer Scheinwelt nicht Energie bzw. (Strahlungs-)Leistung mit Temperatur gleichsetzen! Man kann auch mit geringer Leistung hohe Temperaturen erreichen. Sie bestreiten doch wohl nicht dass man mit einer Kochplatte bei 1 kW sehr unterschiedliche Temperaturen erreichen kann, je nachdem wie groß die Pfanne darauf ist (d.h. wie gut die Platte gekühlt wird). Und wenn Sie gar eine isolierende Asbestplatte auflegen, entsteht sogar Rotglut.
Die Temperatur erhöht sich auch dann wenn Sie die IR-Abstrahlung der Platte z.B. mit einer Alufolie zurückwerfen. Und damit wären wir bei der Gegenstrahlung, die tatsächlich wie eine zusätzliche Energiequelle betrachtet werden muss. Denn ohne die Folie (bzw. das CO2 in der Atmosphäre) gäbe es keine Rückstrahlung und die Abstrahlung ginge wirkungslos verloren.
Zu #91 Dr. Mayer: Link zu Regressionsanalysen von Baliunas et al., Solareinfluss ~60%, Svensmark-Faktor:
http://www.john-daly.com/fraction/fraction.htm
Hallo Marvin Müller (#80)
„Die „Gegenstrahlung“ als eine eigene Energie-Quelle innerhalb der Atmosphäre zu bezeichnen, ist der Gipfel des physikalischen Unverständnis.“
Da gebe ich Ihnen Recht. Aber wo habe ich eine entsprechende Aussage von mir gegeben? Oder anders gesagt – warum unterstellen Sie mir eine solche? Ich wäre Ihnen dankbar, wenn Sie das entweder mit einem Zitat belegen oder einräumen, sich da geirrt zu haben.
Es ging um das zugegebene CO2 und das Nachregeln der Temperatur, wodurch sich allein schon die Photonendichte (Strahlungsdichte) erhöht. Da es offensichtlich Ihre Aufgabe ist, Verwirrung zu stiften, mussten Sie natürlich antworten: „Ihre Antwort ist falsch und bestaetigt mich: Sie haben das Plancksche Gesetz nicht verstanden, und GoodyYung oder ThomasStamnes sind Lehrbuecher die angesichts Ihrer Luecken in der Grundausbildung zu schwierig sind. Lernen Sie die basics nochmal, dann merken Sie auch, was Sie bei ThomasStanmes alles nicht verstanden haben.“
Lieber Herr Becker, hätte ich das Gegenteil geschrieben, hätten Sie sich genau so geäußert. Das ist eine alte Diskussionstrategie. Egal, was der Gegener sagt, immer fleissig widersprechen. Den Rest Ihrer Antwort zu kommentieren ist witzlos, denn Ihre Argumentationstrategie zielt auf Schläge unter die Gürtellinie ab, weil Sie es nicht besser können. Sie betreiben nicht nur eine politisierte Physik, sondern scheinen möglicherweise auch eine politische Laufbahn anzustreben. Viel Glück.
„Von Euch Schlaumeiern hat keiner kapiert, dass das Planckgesetz ein Gesetz ueber die Thermodynamik von Photonen ist und mit der Materie gar nichts zu tun hat.
Offenbar hat das Hug auch nicht verstanden.“ Ich habe das sehr wohl verstanden, weshalb ich Ihnen Recht gebe. Anschaulich geht um die Thermodynamik (k x T-Term) von Photonen (h x f).
„halt Shader, erklären Sie zuerst mal warum man einen Dampferzeuger auch Turbine nennen kann. Diese Antwort steht schon viel länger aus.“
Also wenn Sie mit einer Turbine Dampf erzeugen, machen Sie irgendwas falsch. Wenn Sie unbedingt was mit Dampf haben wollen, nennen Sie die Turbine Dampfverbraucher.
Ansonsten, Literaturstelle: Physikbuch 8. Klasse/9.Klasse
Gruß Holger Burowski
@D.Glatting, was hat das bitte mit dem obigen Thema zu tun?
Empirie schlägt Theorie: Selbst bei einer Inversionswetterlage schafft es die „Gegenstrahlung“ aus der wärmeren!! Luftschicht nicht diese aufzulösen. Erst eine Durchmischung durch Konvektion beendet eine Inversionswetterlage. Die Temperaturschichtung der Troposphäre hat mit den Strahlungsmodellen der Klimaerwärmer nichts zu tun, diese ist definiert durch die Adiabate. Von daher, CO2 ist und bleibt ein harmloses Spurengas und das Ende der Welt durch dessen Freisetzung wird wohl nicht stattfinden.
Noch nie etwas vom Energie-Bilanzerhaltungssatz gehört?
Nur das was an Energie rein kommt (von der Sonne), kann verteilt werden. Die Sonne trägt zu 99% am Energie-Haushalt der Erde bei. Die „Gegenstrahlung“ als eine eigene Energie-Quelle innerhalb der Atmosphäre zu bezeichnen, ist der Gipfel des physikalischen Unverständnis.
Na ja, leben Sie weiter in Ihre Scheinwelt der pseudo-physikalischen Erklärungen.
MfG
W. Kinder
„Die Transmission der CO2 Banden in der Atmosphäre ist 0. bitte bei Wiki oder sonstwo nachsehen.“
Wie wäre es mal mit einer Referenz? So steht Ihre IMHO falsche Behauptung einfach nur so im Raum und wird vor allem durch Messungen, die sie selbst schon gesehen haben und die man auch im Artikel von Lüdecke/Link sehen kann, widerlegt.
„CO2 strahlt erst in größerer Höhe, ich hoffe, ich muss das nicht auch noch mal zum 1000sten mal erklären,“
Wenn Sie „erklären“ durch „behaupten“ ersetzen passt es. CO2 strahlt unabhängig von der Höhe Langwellig IR Strahlung ab. Nur kann die erst ab einer gewissen Höhe ins All entweichen und bis zu einer gewissen Höhe auch wieder den Erdboden erreichen. Das Ergebnis sind dann die Abstrahlungswerte, die Sie immer so munter zussammenaddieren, was eigentich nicht geht …
„Tatsache ist, dass nur etwa 1/4 der beobachteten Erwärmung seit 1860 auf CO2 zurückzuführen ist – also 0,19 Grad – obwohl die Menschheit seitdem etwa 450 Mrd. t C verbrannt hat.“
> Wenn thermische Energie durch CO2 seit 1860 nur 0,19 Grad verursacht hat, dann müssten 0,6 Grad durch andere Faktoren erklärkt werden, wenn Sie auch wie das IPCC von 0,8 Grad Steigerung ausgehen
Die Rechnung ist ziemlich einfach: Gemäß Regressionsanalysen von Baliunas et al. lag der Solareinfluß (einschließlich Wolken und Wasserdampf) bei knapp 60%. Die THG brachten 40%, davon macht CO2 etwa 60% aus. Also kann man dem CO2 (mitsamt Reduktionen und Feedbacks) allenfalls 1/4 des Temperaturanstiegs zuordnen. Wenn wir die Transienz – das derzeitige Erreichen von etwa nur 65% des Gleichgewichtswerts wegen thermischer Trägheit – berücksichtigen, wäre das durch CO2 bedingte deltaT im Gleichgewicht für heute 0,29 Grad. Rechnen wir nach Prof. Harde mit einer Verdoppelungssensitivität (all inclusive) von 0,6 Grad, so ergibt sich deltaT = 0,6* ln(395/280)/ln(2) = 0,3 Grad.
Paßt doch gut, oder? Ein grösserer CO2-Einfluß – wie er von IPCC behauptet wird – ist (soweit wir die Klimasensitivität als korrekt ansehen) durch die Beobachtung widerlegt.
„Tatsache ist, dass nur etwa 1/4 der beobachteten Erwärmung seit 1860 auf CO2 zurückzuführen ist – also 0,19 Grad – obwohl die Menschheit seitdem etwa 450 Mrd. t C verbrannt hat.“
Wenn thermische Energie durch CO2 seit 1860 nur 0,19 Grad verursacht hat, dann müssten 0,6 Grad durch andere Faktoren erklärkt werden, wenn Sie auch wie das IPCC von 0,8 Grad Steigerung ausgehen. Sie beschränken sich aussschließlich auf die durch thermische Strahlung verursachte Erwärmung am Boden. Das kann doch nicht alles sein?
So wie ich das verstehe, kann die thermische Auswirkung der direkten Sonnenstahlung nicht alleine an 0,6 Grad Steigerung seit 1850 verantwortlich sein. Umkehrschluss, es muss also neben dem CO2 weitere Rückkopplungen bzw. „Klimasensitivität“ geben. Zwingend logisch ist es dann, dass auch dem Treibhauseffekt ein Feedbackeffekt zugeordnet wird, wie groß oder klein der auch immer zu sein scheint.
Wenn wir aber von einer Klimasensitivität ausgehen, dann müssten sowohl CO2 genauso wie auch direkte Solareinstrahlung Rückkopplungen (Wasserdampf, Albedo, etc.) auslösen. D.h. zu den 0,19 müsste noch eine weitere Steigerung dazugekommen sein, genauso wie bei einer gestiegenen Solareinstrahlung.
Der Svensmark-Faktor wäre dann noch ein weiterer Faktor, da dieser vereinfacht gesagt ausgehend vom Magnetfeld der Sonne und der dadurch beeinflussten kosmischen Strahlung auf die Erde durch Wolkenbildung die am Boden ankommende Strahlung der Sonne modifiziert werden soll (und wohl auch der durch Wolken verursachte Treibhauseffekt?).
Einfach gedacht müsste das also so aussehen: CO2+Feedback+Sonne+Feedback(+Svensmark)=Steigerung insgesamt. Man hätte also nun die bekannten Zahlen einer Steigerung von insgesamt 0,8 Grad, den Anteil von CO2 von 0,19 Grad, einen unbekannten Feedback hierzu, einen unbekannten Anteil der direkten Sonneneinstrahlung und einen unbekannten Feedback auch dazu (plus unbekannte Höhe des Svensmark-Faktors).
Der Schlüssel zur Erkenntnis ist also Kenntnis von der Stärke der Rückkopplungen insgesamt. Soweit ich das verstanden habe, ist es genau das, was man mangels besserem Wissen mit Klimamodellen macht: Diese Modelle scheinen dann auch sowohl mit der Entwicklung aus der industriellen Phase als auch aus den Eiszeiten überprüft worden zu sein. Daraus dann das Fazit: Es muss mehr sein als nur die von Ihnen direkt dem CO2 zuschreibbaren 0,69 bzw. 1,1 Grad für die Zukunft. Soweit scheinen die Modelle doch eine relativ logische und solide Vorgehensweise zu haben.
Siehe dazu auch diesen Link:
http://tinyurl.com/d6vr2mk
Sie kritisieren, dass Wasserdampf (=temperatur abhängiger Grad an Wolkenbildung) mit dem Faktor 2,7 eingeflossen sei. Dagegen scheinen Sie den Svensmark-Faktor (=von kosmischer Strahlung abhängige Wolkenbildung) noch viel höher mit dem Faktor 4-5 ansetzen zu wollen. Das klingt für mich insgesamt also sehr unwahrscheinlich.
„Eingangs-Energie auf Kreisfläche: 1,215*10^17 W
Oberflächen-Energie auf sphärischer Fläche: 1,989*10^17 W
Welche wundersame Vermehrung der Energie im System Erde/Atmosphäre von 151 W/m^2!“
Das ist keine „wundersame Energievermehrung“, denn bekanntlich liefert die global gemittelte Einstrahlung 240 W/m² – d.h. 255 K für einen Schwarzkörper. Der Boden hat aber wegen der Gegenstrahlung von 151 W/m², also bei 391 W/m², eine mittlere Temperatur von 288 K. Man kann das in einem einfachen Strahlungsmodell auch so interpretieren dass die Erde ein EPS von 240/391=0,614 hat wenn man sich vorstellt, der Boden sei mit einer Folie beschichtet welche die kurzwellige Sonnenstrahlung zu 100% durchlässt, aber bei IR-Abstrahlung dieses EPS aufweist.
Dann hat alles seine Richtigkeit, denn es ergibt sich mit Stefan-Boltzmann S = 240 W/m² = EPS*Sigma*288^4
halt Shader, erklären Sie zuerst mal warum man einen Dampferzeuger auch Turbine nennen kann. Diese Antwort steht schon viel länger aus.
das Plancksche Gesetz folgt deduktiv aus der Bose-Einstein-Statisitk und ist bekanntlich fuer Bosonen gueltig, also z.B. Photonen, Helium4, Cooperpaaren, Gluonen, etc. Fuer Fermionen gilt
die Fermi-Dirac-Statistik.
Von Euch Schlaumeiern hat keiner kapiert, dass das Planckgesetz ein Gesetz ueber die Thermodynamik von Photonen ist und mit der Materie gar nichts zu tun hat.
Offenbar hat das Hug auch nicht verstanden.
„Na EIKE, kommt das TYPO3 wieder nicht mit größer/gliech zu recht.“
Das „groesser Zeichen“ beginnt ein html-Tag und darüber stolpert das Kommentar-Modul anscheinend.
„Der Ansatz mit der Kreisfläche ist physikalisch nicht korrekt. Auch mathematisch kann man das nachweisen, dass die Kreisflächen-Mittelung ist nicht das gleiche wie die Kugelflächen-Mittelung ist. …
Eingangs-Energie auf Kreisfläche: 1,215*10^17 W
Oberflächen-Energie auf sphärischer Fläche: 1,989*10^17 W
Welche wundersame Vermehrung der Energie im System Erde/Atmosphäre von 151 W/m^2!“
Herr Kinder entdeckt den Treibhauseffekt 🙂
Hallo Werter Herr Heinz Hug,
zu 5) Erdoberflächentemperatur, Treibhauseffekt und CO2-Konzentration
Der Ansatz mit der Kreisfläche ist physikalisch nicht korrekt. Auch mathematisch kann man das nachweisen, dass die Kreisflächen-Mittelung ist nicht das gleiche wie die Kugelflächen-Mittelung ist. Man kann dies erkennen, indem man die Fläche von den Regionen eines Kreis oder einer Kugel mit x größer/gleich 1/2*r bestimmt.
Die Sonnen-Energie auf eine Kreisfläche (absorbierte Energie) bezogen, ergibt: E(s) = 1361 W/m^2 * pi * R(erde) = 1,735*10^17 W
und unter Abzug der Albedo (a = 0.3) erhält man: E(e) = E(s)*(1 – a) = 1,215*10^17 W.
Berechnet man jetzt die Energie aus der mittleren globalen Oberflächentemperatur vom System Erde/Atmosphäre
erhält man: E(e) = 4*pi*R(erde) * sb * T(g)^4 = 5,1*10^14 * 5,67*10^-8 * 288^4 = 1,989*10^17 W.
Eingangs-Energie auf Kreisfläche: 1,215*10^17 W
Oberflächen-Energie auf sphärischer Fläche: 1,989*10^17 W
Welche wundersame Vermehrung der Energie im System Erde/Atmosphäre von 151 W/m^2!
MfG
W. Kinder
Sehr geehrter Herr Dr.Paul, quantifizieren Sie doch mal diese Abweichungen in ganz grober Form.
hinzu kommt, dass das Plancksche Strahlungsgesetz für „Gaskörper“ NICHT gültig ist und damit auch der emittierte Wärmestrom nicht proportional zu T^4 entsprechend dem Stefan-Boltzmann-Gesetz ist. Auch hier muss also mit Abweichungen gerechnet werden, was in der Praxis meist nicht geschieht.
Man kann einen selektiven Strahler nun mal nicht mit einem schwarzen Körper gleich setzen.
mfG
Die Transmission der CO2 Banden in der Atmosphäre ist 0. bitte bei Wiki oder sonstwo nachsehen.
Das gilt selbstverständlich für alle Richtungen.
CO2 strahlt erst in größerer Höhe, ich hoffe, ich muss das nicht auch noch mal zum 1000sten mal erklären,
deshalb kommen diese „CO2-Gegenstrahlen“ auf der Erdoberfläche NICHT an.
Das was an langwelligen Infrarotstrahlen die Atmosphäre passiert,
nennt man das FIR-Fenster
(auch LW für Long Wavelength) zwischen 8 und 14µm
bei 15µm ist dagegen, ich wiederhole, die Transmission 0
Es gibt noch andere Fenster (MIR etc.).
Und die Hitranspektren sind selbstverständlich kein Laborversuch für einen Treibhauseffekt Sie Dummkopf!
googeln sie einfach mal bei WOOD 1909.
Wer den Abkühlungseffekt der Atmosphäre am Tag und den Erwärmungseffekt in der Nacht ignoriert,
wird den Temperaturverlauf auf der Erdoberfläche selbstverständlich modellmäßig NIE hinbekommen,
ohne Strahlenphysik eklatant zu verletzen.
mfG
„Deshalb kann ich recht gut verstehen, wie die „Klimamodellierer“ mit ihren „sophisticated models“ (Originalton IPCC!!) tricksen: Möglichst unwidersprechbare Grundlagen der Physik „passend machen“ (LTE Atome = LTE Moleküle), dann alles so komplizieren, dass nur noch Adepten Details nachvollziehen können und schließlich alle „Modellierungsergebnisse“ in eine Zukunft projizieren, die kein Gegenwärtiger mehr erlebt.“
Exakt!
Sie beziehen sich auf NicoBaeckers (#63) Hohlraumstrahler und sagen, „die Frage kann beantwortet werden, die Differenz entspricht dem Kühleffekt des CO2. Das ist richtig. Die nachgeregelte Energie entspricht auch dem Kühleffekt des CO2, wenn man so will.
Lieber Becker,
Sie halten mich offensichtlich für einen Chemiker, der gerade einmal ein paar Grignard-Reaktionen zusammenstottern kann, der halbwegs auswendig weiß, wie man Recorcin (1,3-Dihydroxybenzol) synthetisiert und zur Not neben dem Lambert-Beer-Gesetz gerade noch die thermodynamisch kontrollierte Substitution von der kinetisch kontrollierten Substitution beim Naphthalin unterscheiden kann. Wenn er dann nicht nur die Formel Natriumchlorid richtig nennt sondern auch ein kubisch raumzentriertes Kristallgitter von einem kubisch flächenzentrierten Kristallgitter unterscheiden kann, dann ist Ihr Bild von einem Chemiker komplett. Sie halten diese Spezies für ziemlich schlicht.
Zu Ihrer Aufklärung: Es war in meiner Studienzeit nicht verboten, die Mathematik für Naturwissenschaftler I – IV zu hören und die zugehörigen Übungen zu lösen. Daher verwechsele ich nicht ein partielles Differential mit der abstrakten Zeichnung einer Schnecke nach Salvador Dalí.
Auch hatte ich u. a. Quantenchemie gehört. Deshalb schrecken mich weder Eigenwerte noch der Delta-Operator, Einstein-Koeffizienten oder der Nabla-Operator und ähnlicher Budenzauber. Auch unterscheide ich zwischen homogenen und inhomogenen Prozessen bei der Verbreiterung von Spektrallinien nebst zugehörigen Doppler-Verbreiterung, Lorentz-Funktion und Voigt-Funktion.
Deshalb kann ich recht gut verstehen, wie die „Klimamodellierer“ mit ihren „sophisticated models“ (Originalton IPCC!!) tricksen: Möglichst unwidersprechbare Grundlagen der Physik „passend machen“ (LTE Atome = LTE Moleküle), dann alles so komplizieren, dass nur noch Adepten Details nachvollziehen können und schließlich alle „Modellierungsergebnisse“ in eine Zukunft projizieren, die kein Gegenwärtiger mehr erlebt.
Wenn dann noch liest, was Cubasch, Santer und Hegerl drei Jahre nach dem Rio-Gipfel von 1992 schrieben, muss man einfach konstatieren, dass nur politische und journalistische Hohlraumstrahler einer solchen „Wissenschaft“ Glauben schenken können. Cubasch et al. schrieben: „Man hat als Modellierer also die Wahl, entweder ohne Flusskorrektur mit einem unrealistischen Klimazustand zu operieren, oder die Flusskorrektur mit ihren Schwächen zu akzeptieren, dafür ein realistisches Klima zu erhalten…… Wir wissen beispielsweise, dass die Wechselwirkungen zwischen den Wolken und dem Strahlungshaushalt kaum verstanden sind.“ Auch haben die Modellierer so genannte „Kaltstartprobleme“. Diese hängen damit zusammen, „dass man jegliche durch Treibhausgase verursachte Erwärmung, besonders im Ozean, vor 1985 nicht berücksichtigt.“ (Phys. Bl. 51, 1995, Heft 4, S. 269). Dazu empfehle ich noch einmal einen Blick auf das Bild 11 dieser Webseite.
Findet man dann bei Goody/Young auf S. 199 eine Graphik, bei der die „Fläche“ der „Blackbody Emission“ der Erde genau so groß ist wie die der Sonne, dann wird einem schwarz vor Augen. Die der Klimamodellierung zugrunde liegende Physik ist schon sehr tricky. So lügt man mit graphischen Darstellungen, ohne die Unwahrheit zu sagen. Schließlich hat man ja die Achsenbeschriftung weggelassen. Selbst die grundlegenden Lehrbücher, die der Klimamodellierung lassen einen aufmerken.
Mich wundert nicht, dass bei politischen Hohlraumstrahler-Köpfen die frohe Botschaften der Klimamodellierung als Grundlage der Suffizienzrevolution gut ankommen (Abschaffung des Glühobstes, Verzicht auf Fleischkonsum, weltweite Umverteilung des Wohlstands von Nord nach Süd).
zu 5) Erdoberflächentemperatur, Treibhauseffekt und CO2-Konzentration
Der Ansatz mit der Kreisfläche ist physikalisch nicht korrekt. Auch mathematisch kann man das nachweisen, dass die Kreisflächen-Mittelung ist nicht das gleiche wie die Kugelflächen-Mittelung ist. Man kann dies erkennen, indem man die Fläche von den Regionen eines Kreis oder einer Kugel mit |x|
“
Nur die gigantische Wärmespeicherung der NICHT strahlenden Atmosphäre schafft es…“
die da wäre???
Warum postest du eigentlich immer wieder den selben Quatsch? Eine handvoll „Freaks“ im www gibt dir scheinbar „Material“ und du, weil du den Unsinn nicht kapierst, wie denn auch, müllst Foren damit zu. Langsam wird es echt an der Zeit, dass du zumindest Versuche zeigst, verstehen zu wollen. Ebel & Co geben sich eh so Mühe, es auch Laien nahe zu bringen, einige wenige sind aber leider völlig aufnahmeresistent…
am Samstag, 01.09.2012, 09:19
Lieber Becker,
gestern schrieben Sie: „Ich bezweifle, dass Sie ThomasStamnes oder GoodyYung verstanden haben. Wenn Sie das haetten, so wuerden Sie diese einfache aus den zitierten Textstellen naheliegende Folgerung richtig beantworten koennen: Ein Hohlraumstrahler ist zunaechst luftleer, die Wandungen werden auf 300 K konstant gehalten. Mit einer winzigen Sonde, die den Aufbau nicht stoert, wird die Photonendichte bzw. die Strahlungsdichte im Hohlraum bestimmt. Dann wird CO2 in den Hohlraum eingelassen und solange Energie nachgeregelt, dass alles wieder auf konstant 300 K ist. Erneute wird mit der Sonde gemessen. Frage: ergibt sich ein anderes Ergebnis?“
Meine Antwort: Jetzt sind wir im spektroskopischen Kindergärtchen gelandet. So etwas lernt man in den ersten Stunden der „Spektroskopie für Chemiker“. Natürlich erhöht sich die Photonendichte (Strahlungsdichte). Sie haben nicht nur einen Absorber/Emitter zugeführt sondern gleichzeitig die Energie so lange nachgeregelt, bis wieder 300 K erreicht sind. Wenn Sie jetzt daraus schließen, ich würde die Strahlungstransportgleichung in der naiven Form (Moleküle verhalten sich wie Atome) akzeptieren, dann irren Sie sich.
Nun meine Gegenfrage: Wir nehmen wieder den Versuchsaufbau, in der von Ihnen beschrieben Form, fügen wieder eine Stoffportion CO2 zu und regeln die Temperatur nicht nach. Jetzt, lieber Herr Becker, bestätigen Sie mir bitte, dass sich die Strahlungsdichte ebenfalls wieder erhöht, denn CO2 ist eine eigene Energiequelle. Dann, lieber Herr Becker, akzeptiere ich, dass Sie Thomas/Stamnes oder Goody/Young richtig verstanden haben.
bekanntlich betraegt der Strahlungstransport zwischen Boden und Tropopause ca. 150Wm-2, der konvektive ca. 100 Wm-2. Beweisen Sie anhand der Angaben, dass der konvektive Transport mit ca. 1 cm pro Sec und der Kontinuitaetsgleichung, dass die Waermedichte der thermischen Strahlung deshalb um ca 10 Groessenordnungen kleiner sein muss, wie die Waermedichte der Luft, um die beobachtbare gleiche Groessenordung im Energiefluss zu transportieren.
„Frage: ergibt sich ein anderes Ergebnis? “
Die Frage kann beantwortet werden,
die Differenz entspricht dem Kühleffekt von CO2
mfG
„Und nehmen Sie und bitte auch Herr Hug zur Kenntnis, dass davon auch nichts mehr zurück auf der Erde ankommt. Die Gegenstrahlung auf der Erde „im 15 µm-Bereich“ ist exakt 0, das kann man leicht messen. Denn in diesem Bereich ist die Atmosphäre schlicht nicht transparent.“
Das reden Sie halt einfach Quatsch, den muss man nicht zur Kenntnis nehmen. Sie haben doch neulich sogar lobend das Diagram zur Kenntnis genommen, dass die auf der Erdoberfläche ankommende Langwellige IR-Strahlung darstellte? Haben Sie das schon wieder Verdrängt?
Und Sie haben doch auch die Ausführungen von Herrn Kramm aufmerksam verfolgt. Auch dort konnten Sie nachlesen, dass langwellige IR-Strahlung auf der Erdoberfläche ankommt und deshalb in die Energiebilanz der Erdoberfläche eingeht.
„Labormäßige Test werden ja merkwürdigerweise von allen Treibhausvertretern trikt abgelehnt,
sie könnten ja die Wahrheit an den Tag bringen.“
Die Hitran-Werte, auf die sich Herr Dietze bezieht, sind Laborwerte. Und sie konnten auch bei Herrn Hug lesen, dass man, wenn man die Werte in ein Strahlungs/Konvektionsmodell steckt, genau auf einen Temperaturgradienten kommt, wie er in der Atmosphäre zu finden ist. Erstaunlich ist nur, dass er sie trotzdem für falsch hält …
Sie vermischen Hypothese und Sachbeschreibung, wenn Sie von „Zurückhaltung von Abstrahlung im 15 µm-Bereich“ sprechen.
Das ist sachlich FALSCH, bestenfalls wilde Spekulation. Denn die Erde hält sich schlicht an ihre Abstrahlungstemperatur gemäß Physik, ist also nicht in irgend einer Weise zurückgehalten in ihrer Abstrahlung.
Und nehmen Sie und bitte auch Herr Hug zur Kenntnis, dass davon auch nichts mehr zurück auf der Erde ankommt. Die Gegenstrahlung auf der Erde „im 15 µm-Bereich“ ist exakt 0, das kann man leicht messen. Denn in diesem Bereich ist die Atmosphäre schlicht nicht transparent.
Und selbstverständlich existiert keine positive Wasserdampf-Rückkopplung,
sondern eine negative!
Siehe #62
Wer das abstreitet begibt sich wirklich auf Kindergartenniveau.
Der GEDANKLICHE Schritt von der selektiven Absorbtion einiger Gase in der Atmosphäre auf eine Erwärmung der Erdoberfläche zu schließen,
ohne sich auch nur ansatzweise Gedanken über die Eigendynamik dieser Atmosphäre zu machen,
kann man nur als unverbesserliche Scheuklappenideologie bezeichnen.
Nur die gigantische Wärmespeicherung der NICHT strahlenden Atmosphäre schafft es, am Tag die Erdoberfläche zu kühlen und nachts eine stärkere Abkühlung zu verhindern.
Die Dimensionen liegen dafür beim 10-100-fachen ihrer „berechneten“ pseudogenauen „Strahleneffekte“,
die sich damit gleichzeitig jeder Nachprüfung entziehen.
Labormäßige Test werden ja merkwürdigerweise von allen Treibhausvertretern trikt abgelehnt,
sie könnten ja die Wahrheit an den Tag bringen.
mfG
Wie Dr. Hug und ich gezeigt haben, bringt ein Strahlungsantrieb von 3,7 W/m² (der gemäß Strahlungsmodell die Hälfte der zusätzlichen CO2-Absorption ist und die Zurückhaltung von Abstrahlung im 15 µm-Bereich im Satellitentrichter am oberen Atmosphärenrand darstellt), gemäß Stefan-Boltzmann – in erster Näherung angewendet als zusätzliche Gegenstrahlung am Boden – 0,7 Grad für jede CO2-Verdoppelung.
Zu #45 Dr. Mayer:
„Haben Sie Wasserdampf-Rückkopplung mit einbezogen, oder ist das nur die zusätzliche Energie der CO2-Strahlung? Aus Ihren Äußerungen schließe ich, dass Sie diese Wasserdampf-Rückkopplung anders als Heinz Hug als gegeben sehen?“
Die 3,7 W/m² sind rein für CO2, ohne Wolken und ohne Wasserdampf. Wolkenbedeckung (die als IR-Schwarzkörper das CO2 darunter unwirksam macht) sowie Wasserdampf-Überlappung als Reduktion und Wasserdampf-Rückkopplung als Verstärkung müssen entgegen IPCC als Korrektur berücksichtigt werden. Sie können die 3,7 W/m² auch direkt aus dem Integral über den Satellitentrichter berechnen, das – wenn man die Wasserdampfüberlappung grafisch weglässt – 37 W/m² ergibt. 10% Erhöhung sind dann 3,7 W/m².
„Generell würde mich interessieren, mit welcher Begründung alle gängigen Klimamodelle so viel mehr Grad aus den (wohl größstenteils unbetrittenen?) 3,7 W/m² machen als Ihre 0,68 Grad, d.h. welche Faktoren sollen das sein? Ich bin bisher vom Wasserdampf und weiteren Verstärkern wie z.B. Albedo ausgegangen“
Am Boden ergeben sich wegen der Hin- und Herstrahlung letztlich 1,1 Grad. IPCC hat dann diesen Effekt i.W. durch eine stark übertriebene Wasserdampf-Rückkopplung (Faktor 2,7) „verschlimmbessert“ – daher „best guess“. Darin könnte auch etwas Eis-Albedo-Effekt enthalten sein. M.E. ist der wesentliche IPCC-Irrtum aber der, dass man den indirekten Solareinfluß (Verringerung der Wolkenbedeckung bei höherer Aktivität, den „Svensmark-Faktor“ 4-5) beharrlich außer Acht läßt und die beobachtete Erwärmung fälschlich i.w. dem CO2 mitsamt Wasserdampf-Rückkopplung anlastet. Tatsache ist, dass nur etwa 1/4 der beobachteten Erwärmung seit 1860 auf CO2 zurückzuführen ist – also 0,19 Grad – obwohl die Menschheit seitdem etwa 450 Mrd. t C verbrannt hat.
Eine Wasserdampf-Rückkopplung existiert selbstverständlich (ebenso wie eine leichte Erhöhung des CO2 durch Ozeanausgasung bei Erwärmung). Aber diese Effekte ergeben eine sehr schnell konvergierende geometrische Reihe und daher nur eine geringe Erhöhung – Wasserdampf ist ja auch weitgehend gesättigt. Herr Dr. Hug vermutet da irrtümlich einen „run away“ woraus er eine Nichtexistenz folgert. Sie kennen sicher den Wettlauf zwischen Achilles und der Schildkröte wo jeder, der die geometrische Reihe nicht versteht, zum falschen Schluß kommt dass Achilles die Schildkröte nie überholen kann.
ich bezweifle, dass Sie ThomasStamnes oder GoodyYung verstanden haben. Wenn Sie das haetten, so wuerden Sie diese einfache aus den zitierten Textstellen naheliegende Folgerung richtig beantworten koennen: Ein Hohlraumstrahler ist zunaechst luftleer, die Wandungen werden auf 300 K konstant gehalten. Mit einer winzigen Sonde, die den Aufbau nicht stoert, wird die Photonendichte bzw. die Strahlungsdichte im Hohlraum bestimmt. Dann wird CO2 in den Hohlraum eingelassen und solange Energie nachgeregelt, dass alles wieder auf konstant 300 K ist. Erneute wird mit der Sonde gemessen. Frage: ergibt sich ein anderes Ergebnis?
Wenn Sie die Frage nicht oder nur falsch beantworten koennen oder den Zusammenhang mit meiner obigen Kritik an Ihren Vorstellungen nicht sehen, haben Sie weder ThomasStamnes, GoodyYung noch den Vordiplomsstoff in
Thermodynamik eines Physikstudiums (Waermestrahlung, Planckgesetz, Kirchhoff) verstanden.
Zu GraedelCrutzen: Lesen Sie S. 414 ff nochmal genau durch. Da steht zum einen eine korrektere Beschreibung des radiative forcings als die von Ihnen zitierte spaetere Textstelle eine Seite weiter als auch, dass Wasserdampf-feedback bei den radiative forcings der dort gezeigten Treibhausgasen beruecksichtigt ist.
Wasserdampf entzieht bereits zu seiner Entstehung der Wasseroberfläche, oder der Erde oder der Pflanze Wärme, das ist nicht wenig.
Eine heiße Bodenfläche im Sommer bespritzt man mit Wasser, damit sie sich abkühlt.
Der entstandene Wasserdampf enthält diese LATENTE WÄRME und transportiert sie nach oben,
also weg von der Erdoberfläche,
weg von da,
wo die „globale Temperatur“ definiert ist.
Beim Aufsteigen wird es durch Luftverdünnung (Expansion) adiabatisch kälter und damit sinkt kontinuierlich die Kapazität der Luft Wasserdampf zu enthalten, es kommt physikalisch zwangsläufig wieder zur Kondensation,
so dass die Atmosphäre bei 3-4000 m praktisch wieder wasserdampffrei geworden ist zugunsten der Wolkenbildung.
Deshalb wird es natürlich nicht wärmer in der Atmosphäre, sondern der Abkühlungseffekt mit der Höhe ist etwas geringer als Differenz von trocken- und feucht-adiabatischem Höhengradient.
Es sind also physikalisch zwingend aus Wasserdampf Wolken geworden,
die ebenso physikalisch zwingend am Tag den größten Kühlungseffekt für die Erdoberfläche darstellen, den wir überhaupt kennen.
Es ist deshalb wirklich lächerlich,
von einer POSITIVEN Rückkopplung durch Wasserdampf zu sprechen.
Wasser muss wegen seinem bekannten Kreislauf in der Atmosphäre immer als ganzes betrachtet werden und hat selbstverständlich einen Kühleffekt für die bodennahe Temperatur,
das wird auch nicht durch ein bischen nächtliche Verlangsamung der der Erdabkühlung verhindert.
mfG
Lieber Herr Hug, können Sie hierzu etwas Ausführlicheres sagen, so daß auch ein einfaches Gemüt ihre Argumentation versteht – diese Rückkopplung ist ja schließlich der springende Punkt des AGW.
MfG
Lieber Herr Hug,
Vielen Dank für Ihre ausgezeichnete Beiträge!
Bezüglich den Bemerkungen von Baeckerchen müssen Sie sich nun wirklich nicht rechtfertigen, wir kennen unsere Pappenheimer. Konsequente Ignoranz hilft immer noch am besten.
Viele Grüße
Peter Georgiev
Ich beschrieb vorher (Heinz Hug #34), wie die absorbierte Strahlung zunächst in Wärme gewandelt wird (Stoßdeaktivierung) und dann dennoch sukzessive über einen Energietransportmechanismus ins Weltall abgestrahlt wird. Das schrieb ich: „Es handelt sich vielmehr um einen Energietransport infolge der natürlichen Konvektion. Dabei steigt wärmere Luft unter Abkühlung auf und gibt ihre Energie oberhalb einer Höhe von 10 km als „ungestörte Emission“ ins Weltall ab.“
Dies war die Antwort von Herrn Baecker: „Wohl kaum. Inversionen unterdruecken typischerweise die Konvektion, im unteren Falle von Bild 2 wird es bodennah entweder bewoelkt sein oder der Boden selber ist kaelter als die Luft oben. Die Emission des CO2 entspicht etwa der der gleichen Emissionshohe wie im Bild der Sahara.
Die Luft ist oben wohl kaum deswegen waermer, weil sie von unten erwaermt wird, das ist ja kompletter Schwachsinn, sondern, weil sie sich durch adiabatisches Absinken aufs Inversionsniveau erwaermt, wie es bei Hochdrucklagen typischerweise vorkommt.“
Wo habe ich etwas über Inversion gesagt? Wo steht etwas bei mir über den Mechanismus, den Sie zu recht als Schwachsinn bezeichnen? Sie bauen etwas auf, unterstellen dies, um dann kräftig draufzuhauen. Und noch einmal: Vokabeln wie „dumm“ oder „Schwachsinn“, benutzt man nur, wenn man sich nicht mehr anders zu helfen weiß.
Im übrigen haben Sie mit Ihrer Antwort #44 NicoBaecker“ zu „Heinz Hug #34“ nicht meinen Einwand entkräftet, dass die Aussage von Thomas/Stamnes:
„If inelastic cross sections were not much less than the elastic, there would be drastic consequences. Consider air at sea level, for which 10^9 collisons occur per second. If a signifcant fraction of these collisions were inelastic – leading to an eventual radiative loss of heat – the air would cool down almost instantaneously!“
auf einen Strahlungsenergieerhaltungssatz herausläuft. Noch einmal zum Mitschreiben: Die Autoren wollen nicht wahrhaben, dass die strahlungslose Deaktivierung angeregter CO2-Moleküle (u. ä.) durch ineleastische Stöße nicht zur sofortigen Abkühlung der Luft führe: „If inelastic cross sections were not much less than the elastic…..“ Alles ist Strahlung, Strahlung……. Wie die Strahlung dennoch ohne Verletzung des Energieerhaltungssatzes den Globus verlässt, habe ich weiter oben beschrieben.
Liebe Leser,
ich weiß, jeder, der den geheiligten und kanonisierten Treibhauseffekt in seiner unterstellten „Klimawirkung“ infrage stellt, bekommt es mit der heiligen Ökoquisition (Umweltministerium, UBA, PIK, IPCC, BUND…..) zu tun. Deshalb hat man auch Leute auf EIKE angesetzt und wird es auch weiter tun. Das ist sehr erfreulich, denn dann bleibt die Diskussion über strahlungsfixierte Klimamodelle in Gang. Genau betrachtet, gibt es keinerlei Beweis dafür, dass „Treibhausgase“ das Klima steuern.
Dass man es mit der Ökoquisition zu tun hat, belegt die Äußerung von NicoBaecker, der leider emotional wird und mich unter #43 der Dummheit bezichtigt. Das sollte er im Sinne einer sachlichen Auseinandersetzung nicht tun, denn damit kennzeichnet er sich als ein Mensch, dem die Argumente ausgegangen sind.
Nico Beckers Haupteinwand, mit dem er als Mitarbeiter der FU Berlin (AG Klimadiagnostik und Extremereignisse) belegen will, dass ich keine Ahnung habe, sind seine Einwendungen gegen meine verkürzte Definition des LTE (Schuster-Schwarzschild-Gleichung….). Natürlich weiß ich, wie das LTE genau definiert ist. Da müsste man mehr darüber schreiben. Nur möchte ich den Aufsatz, so weit es irgendwie geht, auch für die „schwäbische Hausfrau“ lesbar halten. Wer sich näher informieren will, kann das nachlesen:
http://www-star.st-and.ac.uk/~kw25/teaching/as4013/stellar/www/atmos5.ps.prn.pdf
http://www-star.st-and.ac.uk/~kw25/teaching/stars/LTE.pdf
http://zuserver2.star.ucl.ac.uk/~idh/PHAS2112/Lectures/Current/Part6.pdf
http://cc.oulu.fi/~jpoutane/teaching/TA07/TheorAstro6_handouts.pdf
http://bmif.unde.ro/docs/20101/pdf_final_11%20MHotinceanu.pdf
Interessanterweise erfährt man, dass das LTE eigentlich für hochangeregte Atome bzw. Plasmen in Sternatmosphären gilt und nicht für Moleküle (CO2, CH4….) innerhalb der irdischen Atmosphäre. Es geht also um Sternatmosphären, in denen locker Temperaturen von 6000 K herrschen. Hier ist das LTE angebracht und natürlich auch in einem ICP-OES gerät sowie der Flamme in einem AAS-Gerät. Es geht also nicht um Moleküle wie CO2 in der Atmosphäre. Trotzdem hat die Klimawissenschaft das LTE nebst Schuster-Schwarzschild-Gleichung (s. Gl. 7) gekapert. Dies geschah schon zu Zeiten von Manabe und Wetherald, die 1967 die ersten Ansätze zur Klimamodellierung mittels Computer entwickelten [Manabe, S., and R. T. Wetherald, 1967: Thermal equilibrium of the atmosphere with a given distribution of relative humidity. Journal of the Atmospheric Sciences, 24 (3), 241-259].
Auf einer der angegebenen Webseiten (http://www-star.st-and.ac.uk/~kw25/teaching/as4013/stellar/www/atmos5.ps.prn.pdf) wird die Gültigkeit des LTEs stark eingeschränkt: „But LTE makes calculations simple…“ So ist es.
Ich schrieb:
„Einige ältere, dispersiv arbeitende Zweistrahl-IR-Spektrometer hatten deshalb einen zweiten Chopper, mit dem die Eigenemission (…) der Probe während der Messung des Referenzstrahls vom Detektor weg gehalten wurde.“
Ihre Entgegnung „weghalten kann man die Eigenemission nicht, man kann sie nur rechnerisch eliminieren,“ beruht auf einen Missverständnis. Es geht darum, die Eigenemission der Probe vom Detektor (!) während der Messung des Referenzstrahls weg zuhalten. Also nicht darum, die Eigenemission „rechnerisch zu eliminieren“.
Lieber Herr Ebel, es freut mich, dass ich nicht der einzige bin, der die Wasserdampfverstärkung ablehnt. Der Meteorologe Prof. Lindzen vom MIT stellt ihre Wirkung ebenfalls infrage. Allerdings ebenfalls mit anderen Argumenten.
Sie schreiben: „ Obwohl ich aus anderen Gründen die Vereinfachung Wasserdampfrückkopplung ablehne (siehe konvektiver Temperaturgradient), ist Ihre Begründung nicht stichhaltig. Die positive Rückkopplung führt erst zu einem Kollaps, wenn die positive Rückkopplung stark genug ist. Ein Beispiel, was Sie vielleicht kennen, ist die akustische Rückkopplung, die zum Pfeifen führt. Das Pfeifen setzt erst ein, wenn der Lautstärkeregler am Verstärker über eine gewisse Grenze aufgedreht wird, vorher kommt es bestenfalls zum überproportinalen Ansteigen der Lautstärke.“
Mein Beispiel war lediglich als Metapher (!) gemeint und nicht als reales Szenario. Ihre Metapher kann allerdings auch nur teilweise stimmen, denn selbst bei der akustischen Rückkopplung kommt man wegen der Nichtlinearität der Verstärkerbauteile schwerlich die Schallstärke eines startenden Düsenjets erreichen (es sei den in Hongkong Island, wo die Chinesen in den sechziger Jahren mit ohrenbetäubenden Lautsprechern die Einwohner von den Segnungen des ach so gut gemeinten, menschlich warmherzigen Sozialismus überzeugen wollten).
Lieber Herr Becker,
Sie vermuten, dass ich meine Zweifel auf den Extinktionskoeffizienten des Q-Zweiges bei CO2-Verdopplung stütze. Das wäre in der Tat ein wenig schwach.
Erstens spreche ganz klar vom Emissionsverhalten der „Treibhausgase“.
Zweitens, und hier müssen Sie schon richtig lesen, beziehe ich mich eben nicht allein auf den Q-Zweig sondern auch auf Schwingungsrotationsbanden des P- und R-Zweiges, die ebenfalls weitestgehend ausgereizt sind. Das sehen Sie klar und deutlich am Spektrum im Bild 3, in dem ich den Petitessen-Charakter (!) der Banden gekennzeichnet habe, auf die sich die, den IPCC unterstützende, Klimamodellierung stützt. Sie sind eine Petitesse! Sagt man es noch deutlicher, so wird bei 100 % mehr CO2 der Treibhauseffekt um schwache 1,2 % erhöht.
Abgesehen davon kenne ich die Hypothese (!), dass sich der Temperaturgradient (vertikale Temperaturverteilung) bei höherem CO2-Anteil verschieben soll. Unten wärmer – oben kälter (John F. B. Mitchell, THE „GREENHOUSE“ EFFECT AND CLIMATE CHANGE, Reviews of Geophysics2, 7, 1 / February1989). Seien Sie versichert, ich kenne die ganze Geschichte. Natürlich habe ich auch, Goody and Young, Atmospheric Radiation: A theoretical basis, Oxford University Press 1989. Die habe ich natürlich gelesen und, Sie dürfen auch versichert sein, auch verstanden.
Gerade deshalb wende ich mich gegen die mit Steuer-Milliarden finanzierte Klimakatastrophenmodellierung (unlängst war nachzulesen, dass eine neu eingeführte Wasserkühlung eines Großrechners 250 000 Euro Stromkosten erspart). Wenn ich mich recht entsinne, waren es um 2005 international 50 Milliarden Dollar (Steuergelder!), die Politiker hierfür locker machten. Sehr viele Bürger wissen, mit welch verzweifelten Tricks, die anthropogene Klimaänderung im Computer herbeimodelliert wird. Nicht zuletzt deshalb, um Politikern ein Argument für ihr Glühbirnenverbot zu liefern.
Und dann unterstellen Sie mir, ich wisse nicht, was das „radiative forcing“ sei. Das müssen Sie auch dem Nobelpreisträger Crutzen vorwerfen. Er bezeichnet den Strahlungsantrieb als Verringerung der Infrarotabstrahlung der Erdoberfläche durch ein Treibhausgas (T. E. Graedel, Paul J. Crutzen, Chemie der Atmosphäre, Spektrum Akademischer Verlag, Heidelberg, Berlin, Oxford 1993, S. 414). Auf S. 415 seines Lehrbuches präzisiert er: „Der Strahlungsantrieb gibt die Erwärmung an, die aufgrund der Zugabe einer zusätzlichen Menge eines bestimmten Gases in der Atmosphäre erfolgte…“
Wenn das richtig ist, dann ist es nur allzu legitim, die 3,7 W/m2 bei CO2-Verdopplung „der Emission am Boden aufzuschlagen“ und dann mit Gl. 6 ohne Wasserverstärkungs-Zaubertricks die Temperaturerhöhung zu berechnen. So wie ich es getan habe: 100 % mehr CO2 = 0,7 °C mehr. Das ist alles.
im uebrigen sollte Gerlich Sich einfach mal bequemen statt irreale Annahmen fuer analytisch loesbare Gleichungen realistische Temperaturverteilungen ansetzen und den Vergleich zwischen den abgestrahlten thermischen Leistungen fuer verschiedene Temperaturverteilungen durchziehen. Dies wuerde dann zeigen, das Gerlichs Diskussion um des Kaisers Bart ginge und voellig irrelevant ist. Hier mal die Ergebnisse, die JEDER selber nachrechnen kann, der eine naturwissenschaftliche Ausbildung abgeschlossen hat.
Fall A: Eine Erde mit überall auf der Oberfläche konstanter Temperatur von 14,8°C hat eine Schwarzkörperabstrahlung von 389,8 W/m2.
Fall B: Eine Erde mit einer realistischeren Temperaturverteilung, die an den Polen – 42 °C, in 50° Breite 7,9 °C, am Äquator 26,0 °C beträgt, und im Mittel ebenfalls 14,8°C beträgt hat eine Schwarzkörperabstrahlung von 393,9 W/m2, diese Leistungsdichte würde von einer Erde mit konstanter Temperatur von 15,6 °C auch abgestrahlt.
Also beträgt der Effekt nur 0,8 °C, und zwar strahlt eine homogen mit dem Temperaturmittel temperierte Erde weniger ab als die mit der realistischeren Temperaturverteilung (Hölder). Der Unterschied ist im Vergleich zum Treibhauseffekt von 33 K vernachlässigbar.
Fall C: Erde mit Temperaturverteilung wie B im Tagesmittel, aber mit Tagesgang. Polen: -55 °C bis -29 °C, 50°: -5,1 °C bis +20,9 °C. Äquator: 13 °C bis 39°C. Globales Mittel wieder 14,8 °C. Schwarzkörperabstrahlung von 396 W/m2, was homogen einer äquivalenten Schwarzkörpertemperatur von 16,0 °C entspricht. Der Tagesgang macht also nochmal 0,4 °C aus, insgesamt zeigt eine Erde mit realistischer Temperaturverteilung und Tagesgang also 1,2°C höhere äquivalente Schwarzkörpertemperatur als das globale Temperaturmittel.
Merke: die thermische Strahlungsleistungsdichte einer Erde mit einer homogenen Temperaturverteilung, die dem globalen Temperturmittel entpricht, ist gemittelt ca. 6 Wm-2 geringerer als die der Erde mit der beobachtbaren Temperaturverteilung.
I.a.W. eine Erde mit homogener Temperaturverteilung muesste ca. 1,2 C (MERKEN!!!) kaelter sein, damit sie die gleiche thermische Strahlungsleistung am Boden abstrahlt wie bei der realen Erde beobachtet wird.
Die 1,2 C sind weit entfernt von den Differenzen, die Gerlichs analytischer Vergleich liefert, was zeigt, dass der Gerlichsche Vergleich eine ganz schlechte Naeherung an die Realitaet ist und nichts sinnvolles zur Diskussion betraegt.
Zur „Sättigung“
Die Infrarotfotographie einschliesslich der wirklich 50jaerigen militärischen Aufklaerung bestätigt eine Transmission der CO2-Bänden von 0, mehr geht wirklich nicht. Deshalb ist es FALSCH, von Gegenstrahlung zu sprechen, sie ist selbstverständlich ebenfalls 0!!!
Gruß
Von unterwegs
Paul
Ihr Zitat Gerlichs zeigt nur sein persoenliches Forscherdilemma, denn offenbar interessiert er sich nur fuer analytisch loesbare physikalische Probleme. Die sind aber selten und so abgegrast, dass man sie haeufig nur im Lehrbetrieb wiederfindet. Dass die Physik der Atmosphaere ebenso wie Gerlichs Forschungsgebiet der Plasmaphysik wie auch eigentlich jedes andere vitale Forschungsgebiet der Physik nicht alleine durch analytische Loesungen, sondern vor allem auch durch numerische Loesungen, also Modellierung, weiterkommt, ist nunmal Tatsache, und dass dabei Forscher wie Gerlich, die damit ein psychologisches Problem haben, dies dogmatisch ablehnen und damit keine neuen Beitraege zum Wissensfortschritt beitragen koennen, da die handvoll analytisch loesbaerer Gedankenmodelle, die sie nur akzeptieren, nur noch didaktischen Wert haben, ist nunmal eben Schicksal eines Forschers, der nicht mehr gefragt ist. Siehe das Zitat:
„Noch einmal Originalton Gerlich: Die gemittelten Temperaturen sind erheblich kleiner als die vierte Wurzel von der gemittelten vierten Potenz der absoluten Temperatur. Die Abstrahlung eines Körpers richtet sich aber nach der tatsächlichen Temperatur und nicht nach irgendwelchen Temperaturmittelwerten! Temperaturmittelwerte müssen immer aus gegebenen Temperaturverteilungen bestimmt werden und für diese Mittelwerte gibt es keine lösbaren theoretischen Modelle.“
„Keine loesbaren theoretischen Modelle“ ist daher falsch, es muss heissen „Keine loesbaren theoretischen ANALYTISCHEN Modelle“, denn numerische Klimamodelle gehen ja von Temperaturverteilungen auf, das Gerlichsche Problem beim Mitteln tritt bei der Klimamodellierung ueberhaupt nicht auf!!!!
„Ich vermute, dass die globale Mitteltemperatur ohne „Treibhauseffekt“ erheblich höher als -18 °C ist“
Dummerweise gibt es nur das eine Universum mit unseren Naturgesetzen, Eine Erde ohne Treibhauseffekt aber mit Wasser ist immer ein Gedankenexperiment, welches nicht zu realisieren ist, es sei denn, es gaebe eine experimentell realisierbare Situation, welche neben den heute gasfoermig auftretenden Treibhausgasen wie CO2 und Methan auch noch den Wasserdampf entfernte ohne Fluessigwasser zu entfernen, was schwer moeglichnist, ausserdem wuerden ja durch den Temperaturfall auch die Polargebiete mit gefrorenem Wasser wachsen, dies haette zudem auf die Albedo einen Einfluss, abgesehen von der absorbierenden Wirkung der Treibhausgase auf die Solarstrahlung.
Kurzum, es bleibt das Gedankenexperiment, und dabei ist die Frage der experimentellen Realisierbarkeit irrelevant, sonst waere es ja keines. Und ausserdem lassen sich sowieso keine Experimente mit der Erde von dem Umfange unternehmen, selbst das ungewollte vergleichsweise kleine des anthropogenen Treibhauseffekts „kostet“ ja 100 Jahre Industrieproduktion.
1.
Eine Berechnung stammt von Prof. Gerlich (Braunschweig). Der Physiker kommt aber nicht auf höhere Temperaturen sondern auf eine wesentlich niedrigere Temperatur. Er sagt, „dass ein solcher Mittelwert völlig ohne irgendeine physikalische Bedeutung ist, kann man am einfachsten dadurch zeigen, dass man die mittlere Temperatur für eine solche bestrahlte Kugel berechnet, wenn sich die Oberfläche in diesem so genannten Strahlungsgleichgewicht befindet.“ Unter Berücksichtigung des Einstrahlungswinkels kommt er sogar auf eine Mitteltemperatur von – 133 °. Also noch wesentlich weniger! Was richtig ist, will ich nicht entscheiden. Nur die simple Rechnung mit Gl. 5, wie es üblich ist, ist mit Sicherheit falsch. Gerlich rechnet im übrigen auch mit einer wasserlosen Erdkugel.
Noch einmal Originalton Gerlich: Die gemittelten Temperaturen sind erheblich kleiner als die vierte Wurzel von der gemittelten vierten Potenz der absoluten Temperatur. Die Abstrahlung eines Körpers richtet sich aber nach der tatsächlichen Temperatur und nicht nach irgendwelchen Temperaturmittelwerten! Temperaturmittelwerte müssen immer aus gegebenen Temperaturverteilungen bestimmt werden und für diese Mittelwerte gibt es keine lösbaren theoretischen Modelle. Damit ist wohl deutlich gezeigt, daß alle Berechnungen mit einem „mittleren Strahlungsbudget“ oder einer „Strahlungsbilanz“ nichts mit mittleren Erdtemperaturen zu tun haben.
Zum Nachlesen: http://www.ib-rauch.de/datenbank/vortrag-leipzig.html
„Nach oben nicht, weil kein Strahlungsaustrag wegen fehlender Treibhausgase nicht möglich ist.“
Ist ja putzig, wo sind sie denn hin die kleinen CO2 Killermoleküle? Pause ? Abgehauen? Republikflucht? Von Mutter Erde versteckt? 😉
„Ohne Treibhausgase fast keine Luftströmungen.“… diese Aussage ist für mich wirklich gar nicht nachvollziehbar. Der einfache Wechsel zwischen Tag und Nacht dürften ja wohl eine ganz wesentliche Ursache sein!?!“
Die Oberflächetemperatur folgt zwar dem Tag-Nacht-Wechsel, aber die Atmosphärentemperatur nicht. Solange Stellen an der Erdoberfläche wärmer als die Atmosphäre sind, wird die Atmosphäre erwärmt. Die eingetragene Wärme kann die Atmosphäre praktisch nicht verlassen: Nach oben nicht, weil kein Strahlungsaustrag wegen fehlender Treibhausgase nicht möglich ist. Nach unten nicht weil zwischen der größtenteils einheitlich warmen Atmosphäre und der meistens kühleren Erdoberfläche eine Inversionschicht ist. Eine Inversionsschicht besteht aus ruhuhender Luft – und ruhende Luft ist ein ganz schlechter Wärmeleiter.
Aber eine einheitlich warme Atmosphäre hat fast keine Luftströmung.
MfG
„Es handelt sich vielmehr um einen Energietransport infolge der natürlichen Konvektion. Dabei steigt wärmere Luft unter Abkühlung auf und gibt ihre Energie oberhalb einer Höhe von 10 km als „ungestörte Emission“ ins Weltall ab.“
Wohl kaum. Inversionen unterdruecken typischerweise die Konvektion, im unteren Falle von Bild 2 wird es bodennah entweder bewoelkt sein oder der Boden selber ist kaelter als die Luft oben. Die Emission des CO2 entspicht etwa der der gleichen Emissionshohe wie im Bild der Sahara.
Die Luft ist oben wohl kaum deswegen waermer, weil sie von unten erwaermt wird, das ist ja kompletter Schwachsinn, sondern, weil sie sich durch adiabatisches Absinken aufs Inversionsniveau erwaermt, wie es bei Hochdrucklagen typischerweise vorkommt.
ich will damit nicht ausschliessen, dass dies immer auch so per Begriffsdefinition ist. Ich nehme daher die Passage in 46, dass quenching thermodynamische Gleichgewicht stoert, zurueck.
„Die inelastischen Einfangsquerschnitte sind also viel kleiner als die elastischen und dazu muss man dann die zugehörige Fußnote (15) auf S. 128 lesen. Sie ist besonders interessant und lautet:
„If inelastic cross sections were not much less than the elastic, there would be drastic consequences. Consider air at sea level, for which 10^9 collisons occur per second. If a signifcant fraction of these collisions were inelastic – leading to an eventual radiative loss of heat – the air would cool down almost instantaneously!“
Da haben wir ihn, den „Strahlungsenergieerhaltungssatz“. Thomas und Stamnes behaupten tatsächlich, die erdbodennahe Luft würde sich sofort abkühlen, wenn angeregte „Treibhausgasmoleküle“ durch inelastische Stöße deaktiviert (Quenching) würden.“
Erstmal ist klar, dass Thomas und Stamnes diesen Effekt als nicht realistisch ansehen, denn die Voraussetzungen treffen ja in der realen Atmosphaere gar nicht zu, wie die Autoren ja selber schreiben. Zweitens setzt diese hypothetische Schlussfolgerung von Thomas und Stamnes KEINE unphysikalische Hypothese eines nach Ihren Worten postulieren „Strahlungsenergieerhaltungssatz“ voraus.
“ Ineleastische Stöße sind vom Übel – elastische Stöße sind gut – denn sie begründen den Treibhauseffekt im Sinne eines „Strahlungsenergieerhaltungssatzes“.“
Den Sinn verstehe ich nicht. Bei elastischen Stoessen behaelt das Moelkuel seine Energie, bei inelastischen aendert sich diese. Mit dem Strahlungsuebergaenfen hat dies unmittelbar gar nichts zu tun und mit dem Treibhauseffekt erst recht nicht.
“ Dies steht im Widerspruch zu meinem im Bild 3 gezeigten Messergebnis, aus dem klar hervorgeht, dass sich die Transmission eines CO2-haltigen Luftgemischs in Gegenwart von Begleitgasen, wie He oder N2, verringert. Die größte Transmission wird mit reinem CO2 gemessen, die mittlere stammt vom Gemisch CO2/He und die geringste vom Gemisch CO2/N2.“
An Ihrem Messergebnis ist nicht auszusetzen, nur ziehen Sie daraus Schlussfolgerung fuer den Treibhauseffekt, zu der Sie keine physikalische Begruendung liefern. Zeigen Sie doch endlich mal, in welchem quantitativen Zusammenhang Ihre Transmissionsmessungen mit der Differenz zwischen thermischen Strahlungsfluss zwischen TOA und Boden, d.h. dem Treibhauseffekt bzw. der vertikalen Temperaturverteilung hat. Da klafft eine logische Riesenluecke in Ihrer Argumentation.
Zur Mesungen, das ist nicht klar beschrieben, Ist immer gleich viel CO2 in der Kuevette u d wird nur N und He auf den Druck 1020 mbar zugefuehrt? Wenn ja, so ist das Ergebnis nicht ueberraschend. Wwas kommt raus, wenn 1020 mbar CO2 gemessen werden?
„Man kann es drehen und wenden, wie man will: Erdbodennah überwiegt im Vergleich zur IR-Emission der strahlungslose Übergang angeregter CO2-Moleküle in den Grundzustand durch ineleastische Stöße.“
Das ist doch klar, in Thomas Stamnes sind doch sicher die Raten zwischen strahlenden und nichtstrahlenden Uebergaengen angegeben. In Goody Yung steht es jedenfalls und demnach ist klar, dass
die nichtstrahlenden in der unteren Atmosphawre ueberwiegen. Das garantiert ja auch fuer die untere Atmosphaere die Anwendbarkeit der LTE Naeherung fuer die Quantifizierung des Strahlungstransports.
„Im übrigen ist die Stoßdeaktivierung („collisional deexitation, collisional quenching“
Quenching passiert bei LTE, also in der unteren Atmosphaere, selbstverstaedlich nicht. Quenching zerstoert per Definition ja das thermodynamische Gleichgewicht, denn dadurch wird die Besetzung der hoeheren Energieniveaus ja unter die Boltzmannverteilung gedrueckt.
“ Kühlt sich deshalb die Luft dadurch unmittelbar ab (cool down almost instantaneously)?“
Haeh, das war die Fussnote in ThomasStmnes fuer die nichtrealisierte Voraussetzung.
„Es gilt der Energieerhaltungssatz: Strahlungsenergie wird in kinetische Energie der Luftmoleküle gewandelt (vgl. thermodynamische Temperatur).“
Ja, klar, was sonst sollte bei LTE vorgehen…???? sie scheinen mit der Physik ueberfordert zu sein.
“ Aber dennoch verlässt die erdbodennah gewandelte Wärmestrahlung den Erdkörper wieder als Wärmestrahlung.“
Logisch, wie denn sonst…
“ Denn es gibt natürlich auch die Konvektion.“
Richtig, in der unteren Atmosphaere.
„Das gilt auch für die allseits bekannte „Earth’s Annual Global Mean Energy Budget“ von J. T. Kiehl and Kevin E. Trenberth, die für „thermals“ bzw. „evapotranspiration“ und „latent heat“ zusammen nur 102 W/m^2 gelten lassen, während die atmosphärische Rückstrahlung mit 324 W/m^2 angesetzt wird.“
Ja, beides Werte, die aus Messungen stammen. Das koennen Sie nicht leugnen.
“ Noch merkwürdiger wird es, wenn man sich das Bild 3 in meinem Beitrag anschaut und dann bei Kiehl/Trenberth erfährt, dass nur 40 W/m^2 durch das stets offene atmosphärische Strahlungsfenster („atmospheric window“) entweichen sollen bei einer gleichzeitigen Rückstrahlung („back radiation“) von 324 W/m^2.“
Das liegt daran, weil Sie den Zusammenhang zwischen Absorptionsspektrum und Strahlungstransport nicht begriffen ahben. Hohlen Sie das nach, auch wenn Sie seit Jahrzehnten daran arbeiten moegen, kann Sie keiner davon entbinden, die Wissenschaft erfordert dies an jeden eben. Das muessen auch Sie durch.
„Noch eine kleine Anmerkung zum Strahlungstransport: Es gibt Inversionswetterlagen. Wieso können diese über Tage und Wochen beständig über einem Fleck verbleiben, wenn doch wärmere Luftschichten in größerer Höhe mittels Strahlungstransport die kälteren erdbodennahen Luftschichten erwärmen müssten.“
Weils wolkig ist und Meteorologie nicht so einfach ist, wie Sie es sich vorstellen moechten.
Sie gehen im Ergebnis von 0,68 Grad am Boden aus, die aus den 3,7 W/m2 resultieren. Haben Sie Wasserdampf-Rückkopplung mit einbezogen, oder ist das nur die zusätzliche Energie der CO2-Strahlung?
Aus Ihre Äußerungen schließe ich, dass Sie diese Wasserdampf-Rückkopplung anders als Heinz Hug als gegeben sehen?
Generell würde mich interessieren, mit welcher Begründung alle gängigen Klimamodelle so viel mehr Grad aus den (wohl größstenteils unbetrittenen?) 3,7 W/m2 machen als Ihre 0,68 Grad, d.h. welche Faktoren sollen das sein? Ich bin bisher vom Wasserdampf und weiteren Verstärkern wie z.B. Albedo ausgegangen.
Ebel #29, „Ohne Treibhausgase fast keine Luftströmungen.“… diese Aussage ist für mich wirklich gar nicht nachvollziehbar. Der einfache Wechsel zwischen Tag und Nacht dürften ja wohl eine ganz wesentliche Ursache sein!?!
Sie schreiben im Fazit
„Dass eine atmosphärische Wärmestrahlung gemäß dem Planck-Gesetz gegeben ist, ist eine Selbstverständlichkeit. “
Dies gilt nur fuer Luft im thermodynamischen Gleichgewicht. Ok, nehmen wir an, dies sei fuer eine Luftsaule mit nach oben abnehmender Temperatur erfuellt. Sie schreiben dann weiter
„Solange aber ein atmosphärisches Temperaturprofil (oben kälter – unten wärmer) existiert, und die Konvektion erheblich zum Energietransport beiträgt, solange ist die Hypothese, im offenen System der Atmosphäre wird die Energie einer erdbodennah absorbierten IR-Strahlung mittels Strahlungstransport von unten nach oben weitergereicht, falsch.“
Aus Ihrem ersten Satz folgt nun zwingend, dass Ihr zweiter Satz falsch ist. Denn bei nach oben abnehmender Temperatur nimmt gemaess dem Planckschen Strahlungsgesetz, wenn man mal vereinfacht annimmt, dass der spektrale Absorptionskoeffizient hoehenunabhaengig ist, auch die thermische Strahlungsflussdichte L ab. Damit hat man einen vertikalen Gradienten in L und damit folgt mitnichten Ihre Schlussfolgerung, dass dI/dz gleich Null ist, d.h. der vertikale Strahlungstransport Null ist. Wie man aus der wissenschaftlichen Literatur unschwer erfahren kann, traegt die Konvektion nicht unerheblich beim vertikalen Energietransport bei. Aber der Strahlungstransport auch nicht. Der nicht-strahlungstransport durch Konvektion und latente Waerme zwischen Boden und Tropopause betraegt ca. 100 Wm-2, waehrend der Strahlungstransport die bekannten 150 Wm-2 betragen.
“ Es gibt nämlich keinen „Strahlungsenergieerhaltungssatz“.“
Den gilt es tatsaechlich nicht, weshalb erfinden SIE ihn dann?
“ Vielmehr übertragen angeregte „erdbodennahe Treibhausgasmoleküle“ ihre Energie im Wesentlichen auf die nicht IR-aktiven Hauptbestandteile des Atmosphäre (N2 und O2). “
Ja, das ist richtig, Das ist ja gerade die Basis fuer die physikalische Quantifizierung des Strahlungstransports in der unteren Atmsophaere, denn man setzt ja gerade lokales thermisches Gleichgewicht voraus, d.h. alle Luftmolekuele haben dieselbe Temperatur, nur so ist ja das Strahlungsfeld lokal auch thermisch und als Planckfunktion beschreibbar. Was denn sonst????
„Dennoch macht er deutlich, auf welch geringfügigen Größen sich die seinerzeit im Spiegel (33/1986) prophezeite „Klimakatastrophe“ stützt“
Wenn sich der Spiegel damals ueberhaupt auf wissenschaftliche Resultate stuetzte, so sicherlich nicht auf den Extinktionskoeffizienten des Q Zweiges bei CO2 Verdopplung, sondern auf die Effekte einer globalen Temperaturerhoehung um einige Grad aufgrund des durch CO2 Verdopplung resultierenden veraenderten Strahlungstransports und seinen Auswirkungen auf die vertikale Temperaturverteilung. Den Zusammenhang zwischen Extinktionskoeffizient und vertikaler Temperaturverteilung stellen Sie in Ihren Artikeln ueberhaupt nicht dar. Daher sind Ihre Folgerungen unbegruendet.
Ihr Kapitel 6 ist ein Beispiel fuer komplettes Fehlverstaendnis. Sie haben nicht mal kapiert, was radiative forcing ueberhaupt ist, wenn Sie sich wundern, dass das IPCC verschiedene Wette angibt ( das hat Sinn, wenn mans weiss) und wenn Sie dann auch moch so dumm sind, das radiative forcing der Emmissions am Boden aufzuschlagen, demostriert das sehr eindruecklich, dass Sie von der zugrundeliegenden Physik keine Ahnung haben.
„
Lieber Herr Hug,
vielen Dank für Ihre Antwort. Leider ist sie unbefriedigend. Ich hatte die Frage gestellt, woher die Energie für eine erwärmende Wirkung des Wasserdampfes auf die Wasseroberfläche kommt.
Sie schreiben als Antwort: „dass Wasserdampf ein IR-Emissionspektrum aufweist“.
Außerdem bringen Sie das Argument ein :“ Wenn Sie nicht glauben, dass IR-Absorber auch IR-Emitter sind …“
Vieles von dem, das Sie schreiben, sind reine Unterstellungen, manche sind unverständlich.
Natürlich weiß ich, dass Wasserdampf wie CO2 strahlen kann – in bestimmten Banden (Frequenzen). Und es ist ja auch bewiesen, dass sowohl Wasserdampf und auch CO2 an der Wärmeabgabe der Atmosphäre ins Weltall durch Abstrahlung beteiligt ist.
Insofern ist die Aussage „Wenn Sie nicht glauben, dass IR-Absorber auch IR-Emitter sind …“ voll am Thema vorbei.
Meine Kritik an der „Treibhaustheorie“ gründet sich vor allem darauf, dass Wärme nur in eine Richtung fließen kann, nämlich von warm nach kalt. Etwas anderes hat noch keiner beobachtet. Und auch wenn Strahlung in alle Raumrichtungen geht, wird damit nicht in jedem Fall Wärme übertragen – eine Konsequenz aus dem 2. HS der TD.
Bleibt aber noch die Frage zu klären, woher denn der Wasserdampf seine Energie hat, mit der er die Erdoberfläche zusätzlich erwärmen soll. Und da kommt nur die Sonne in Betracht, welche die Meere erwärmt und Wasser dabei verdunsten lässt. Nur dadurch und natürlich durch Kontakt mit warmer Luft und in geringem Maße durch Absorption von Strahlung (sowohl vom Boden als auch von direkter Sonnenstrahlung) kann der Wasserdampf Energie beziehen.
Alle diese Energie ist aber der Erdoberfläche entnommen (bzw. kommt dort nicht an), wobei diese gekühlt wird. Also selbst wenn der Wasserdampf Energie von der Erdoberfläche erhält, kann er nicht durch partielle Rückführung dieser Energie eine erwärmende Wirkung auf diese Erdoberfläche haben. Das wäre eine Erwärmung der Quelle mittels ihrer Senke und ist nach dem 2. HS ausgeschlossen.
Gegen Ihren Satz: „Deshalb sorgt bereits eine warme Wasseroberfläche dafür, dass die Luft darüber „energiehaltig“ genug ist, um die Emission von Wasserdampfmolekülen anzuregen.“ habe ich also überhaupt nichts einzuwenden. Nur werden diese Emissionen von anderen Molekülen sofort wieder fast vollständig absorbiert.
Ich erkenne keine erwärmende Wirkung des Wasserdampfes auf die Erd- oder Wasseroberfläche, sondern deren Kühlung (Verdunstungskälte) und die Erwärmung der Atmosphäre durch die Kondensation von Wasserdampf. Natürlich verhindert eine wärmere Atmosphäre die schnelle Abkühlung der Erdoberfläche, aber man darf dabei nicht unberücksichtigt lassen, dass die Erdoberfläche durch die Erwärmung der Atmosphäre gekühlt wird.
Um es auf den Punkt zu bringen: Bei konstanter Ein- und Ausstrahlung verteilt sich die Energie von der Sonne auf Erde und Atmosphäre. Geht mehr in die Atmosphäre (mehr Gegenstrahlung), erhält die Erdoberfläche weniger Energie. Eine Erwärmung der Erdoberfläche mittels „Treibhausgasen“ gibt es daher nicht.
Freundliche Grüße
M. Wehlan
Sie schreiben oben
„Dies ist ein erster Hinweis darauf, dass der den IPCC-Computermodellen zugrunde liegende Strahlungstransport die Verhältnisse nicht korrekt beschreibt“
Wieso sollten heutige GCM keine polare Inversionswetterlagen simulieren. Wenn Sie glauben, dass moderne GCM kein Konvektionsschema haben, so irren Sie. Ist aber kaum verwunderluch, denn ich nehme nicht an, dass Sie als Chemiker in der Lage sind, die implementierte Physik in eimem GCM zu verstehen.
„Ich persönlich bin davon überzeugt, dass die globale Mitteltemperatur ohne „Treibhauseffekt“ mit -18 °C viel zu niedrig angesetzt ist.“
Da irren Sie sich. Die globale Mitteltemperatur ist zu hoch angesetzt. Wenn eine strahlende Fläche (hier die Erdoberfläche) unterschiedliche Temperaturen hat, aber die Gesamtabstrahlung vorgegeben ist (hier durch die absorbierte Solarstrahlung), dann greift die Höldersche Ungleichung, die ergibt, daß die –18°C der obere Grenzwert der globalen Mitteltemperatur ist – dieser Grenzwert wird nur dann erreicht, wenn die Oberflächentemperatur einheitlich ist. Da aber die Oberflächentemperatur nicht einheitlich wäre, wäre auch die globale Mitteltemperatur erheblich niedriger als die –18°C.
@ #33: Heinz Hug sagt am Dienstag, 28.08.2012, 15:05
„Einige ältere, dispersiv arbeitende Zweistrahl-IR-Spektrometer hatten deshalb einen zweiten Chopper, mit dem die Eigenemission (…) der Probe während der Messung des Referenzstrahls vom Detektor weg gehalten wurde.“
Weghalten kann man die Eigenemission nicht, man kann sie nur rechnerisch eliminieren. Und die Eigenemission muß bei der Atmosphäre berücksichtigt werden (siehe z.B. #24: Ebel sagt am Mittwoch, 22.08.2012, 15:53). Beim Spektrometer benutzen Sie einen Globar oder sogar eine Laser, dabei ist die Äquivalenttemperatur der Meßstrahlung viel höher als die Temperatur des Meßobjekts.
Zumindest in der unteren Atmosphäre ist Gastemperatur in der gleichen Größe wie die Strahlungsquelle (Erdoberfläche), deshalb darf die Eigenemission nicht vernachlässigt werden. Die effektive Absorption ist die Absorption minus Eigenemission und die ist sogar negativ, denn emittiert wird nicht nur nach oben, sondern auch nach unten. Daß die effektive Absorption sogar negativ ist, zeigt sich z.B. darin, daß die konvektiv nach oben transportierte Wärme in Strahlung umgewandelt wird.
Wie groß die Eigenemission des Gases ist, hängt von dessen Temperatur ab. In der Tropopsphäre wird die Temperaturänderung nicht durch Änderung der Strahlungsverhältnisse bestimmt, sondern der Temperaturgradient wird durch die Expansion und Kompression der Luft infolge der Druckänderung bei Vertikalzirkulation bestimmt.
Die Strahlungseigenschaften sind erst in der Stratosphäre für den Temperaturverlauf bestimmend.
@ #22: Heinz Hug sagt am Mittwoch, 22.08.2012, 12:10
„Der zusätzliche Wasserdampf lässt als Treibhausgas noch mehr Wasser verdampfen usw. Merkt denn wirklich niemand diese Absurdität, den Unfug, der positiven Wasserdampfrückkopplung?“
Obwohl ich aus anderen Gründen die Vereinfachung Wasserdampfrückkopplung ablehne (siehe konvektiver Temperaturgradient), ist Ihre Begründung nicht stichhaltig. Die positive Rückkopplung führt erst zu einem Kollaps, wenn die positive Rückkopplung stark genug ist. Ein Beispiel, was Sie vielleicht kennen, ist die akustische Rückkopplung, die zum Pfeifen führt. Das Pfeifen setzt erst ein, wenn der Lautstärkeregler am Verstärker über eine gewisse Grenze aufgedreht wird, vorher kommt es bestenfalls zum überproportinalen Ansteigen der Lautstärke.
MfG
Zu Beginn muss ich Ihnen ein Lob aussprechen, Sie sind sehr umfangreich auf das Feedback der Leser eingangen. Das ist alles andere als selbstverständlich hier. Und wie man sieht, kommt man ganz ohne Beleidigungen und Diffamierungen aus, auch nicht selbstverständlich (leider).
Zu Ihren Entgegnungen.
„1. Wo hat die Natur einen limitierenden Faktor eingebaut? Wenn, dann ist es der Faktor, wenn alles Wasser auf dem Globus verdampft ist.“
Ein limitierender Faktor ist, dass ein Delta H2O in einer Atmosphäre mit wenig H2O eine höhere Wirkung besitzt, als wenn eine wasserreiche Atmosphäre vorhanden ist. Man muss quasi den H2O-Anteil stets verdoppeln, um ein konstantes Delta T zu bekommen. Ein weiterer limitierender Faktor ist das Stefan-Boltzmann-Gesetz. Die Energie, die ein schwarzer Strahler abstrahlt ist proportional zu T^4 (gilt auch für nicht-schwarze Strahler). D.h. der Sprung von 20 auf 21°C ist mit einer höheren Energieabgabe in Richtung Weltraum verbunden als der Sprung von 15°C auf 16°C. Für das positiv rückgekoppelte System wird es immer schwieriger den Temperaturanstieg aufrechtzuerhalten.
Das nur zwei Beispiele ohne Anspruch auf Vollständigkeit. Es gibt bezüglich dem Klima auch negative Rückkopplungen. Nehmen Sie nur die Eiszeit mit der Abdeckung größer Flächen mit meterhohen Eis- und Schneeschichten. Die Eis-Albedo-Rückkopplung führt dazu, dass je mehr Eis und Schnee auf der Erdoberfläche liegen, umso mehr Energie wird wieder Richtung Weltraum abgestrahlt und kühlt die Atmosphäre aus, weil dessen Albedo höher als der bisherige Durchschnitt liegt. Eine kältere Atmosphäre wiederum führt zu mehr Eis- und Schneeflächen usw. Auch hier ein Kreislauf, eben nur in die andere Richtung. Wieso sind in der Eiszeit die Temperaturen trotz negativer Rückkopplung nicht permanent gesunken, haben Sie sich das schon mal gefragt?
„2. Den „Klimamodellen“ in den Computern hat man einen limitierenden Faktor eingebaut, der die positive Wasserdampfrückkopplung limitiert.“
Das nehme ich jetzt mal zur Kenntnis, ohne das jetzt bestätigen oder negieren zu können.
„3. Und noch eins muss gesagt werden: Wenn der Wasserdampfverstärkungsmechanismus wirklich eine Berechtigung hat, dann hat er sie auch, wenn durch eine geringere Wolkenbedeckung sich das Ozeanwasser (am Äquator befindet sich die Wetter- und Klimaküche) erwärmt. Denn die Natur ist konsequent. Sie unterscheidet nicht, ob die zusätzliche Wärmeenergiezufuhr von der Rückstrahlung höherer „Treibhausgaskonzentrationen“ stammt oder bei geringerer Wolkenbedeckung von einer stärkeren Solareinstrahlung herrührt.“
Eine geringe Wolkenbedenkung heisst erstmal wärmere Tage und kältere Nächte. Ob dadurch aus den Ozeanen mehr Wasserdampf in die Atmosphäre gelangt, wäre zu klären. Vermutlich für Meteorologen gehört das zum Standardwissen, ich bin aber keiner.
„Tatsächlich kann man mit T^4 nicht so ohne weiteres die mittlere Temperatur einer an der Oberfläche inhomogenen (!) Erde (Wasser, Fels…) berechnen (!). Die besagten 33 °C, die man dem „Treibhauseffekt“ per Übereinkunft zuordnet, sind kein Messwert. Man müsste vielmehr aus einer Unzahl kleiner Flächeareale die mittlere Globaltemperatur (ohne „Treibhausgase“) unter Berücksichtigung des Sonneneinstrahlungswinkels berechnen. Ich persönlich bin davon überzeugt, dass die globale Mitteltemperatur ohne „Treibhauseffekt“ mit -18 °C viel zu niedrig angesetzt ist.“
==============================================
OK, die Berechnung der -18 °C ist falsch, das ist wunderbar. Aber wie kommen Sie darauf, dass es zu niedrig und nicht etwa zu hoch angesetzt ist? Gibt es Berechnungen dazu?
„Herr Wehlan ich weiß, dass Sie… Dabei verwenden Sie u. a. mit dem Argument, der „Treibhauseffekt“ verstößt gegen den zweiten HS d. Thermodynamik, weil eine kältere Atmosphäre die wärmere Erdoberfläche nicht erwärmen kann.“
=================================================
Was glauben Sie denn, Herr Hug, kann sie das und zwar durch die Strahlung/Gegenstrahlung? Und wenn ja, wer hat es experimentell bewiesen?
Sie Schreiben: „Die positive Rückkopplung wird nur aus dem Ruder laufen, wenn es in dem System keine limitierenden Faktoren geben würde. Wie ist denn zum Beispiel das Delta(H2O) vom Ausmaß, wenn man die Durchschnittstemperatur einmal von 15°C auf 15,5°C erhöht und dann von 17°C auf 17,5°C? Und hat der zusätzliche Wasserdampf in einer beispielsweise 2°C wärmeren und wasserreicheren Atmosphäre immer noch dieselbe Wirkung? Wenn die Wirkung des zusätzlichen Wasserdampfes immer mehr abnimmt, je mehr sich davon schon in der Atmosphäre befindet (so wie man es beim Treibhausgas CO2 mit dem logarithmischern Verlauf vermutet) und je wärmer die Atmosphäre schon ist, dann wird die positive Rückkopplung sich immer weiter abschwächen und die Temperatur in der Atmosphäre sich auf einem generell höheren Niveau bewegen.“
Dem Argument ist entgegenzuhalten.
1. Wo hat die Natur einen limitierenden Faktor eingebaut? Wenn, dann ist es der Faktor, wenn alles Wasser auf dem Globus verdampft ist.
2. Den „Klimamodellen“ in den Computern hat man einen limitierenden Faktor eingebaut, der die positive Wasserdampfrückkopplung limitiert.
3. Und noch eins muss gesagt werden: Wenn der Wasserdampfverstärkungsmechanismus wirklich eine Berechtigung hat, dann hat er sie auch, wenn durch eine geringere Wolkenbedeckung sich das Ozeanwasser (am Äquator befindet sich die Wetter- und Klimaküche) erwärmt. Denn die Natur ist konsequent. Sie unterscheidet nicht, ob die zusätzliche Wärmeenergiezufuhr von der Rückstrahlung höherer „Treibhausgaskonzentrationen“ stammt oder bei geringerer Wolkenbedeckung von einer stärkeren Solareinstrahlung herrührt.
Wenn Sie nicht glauben, dass IR-Absorber auch IR-Emitter sind, schauen Sie einmal bei H. Günzler, H. M. Heise (IR-Spektroskopie, VCH-Wiley 1996, S. 176) nach. Dort finden Sie zwar nicht das Emissionsspektrum von Wasserdampf aber das von Lanolin zugegeben bei 100 °C. Was man gut erkennt, ist zum einem die Emission und zum anderen das Prinzip des Wienschen Verschiebungssatzes. Wegen der relativ niedrigen Temperatur findet man oberhalb von 2000 cm^-1 (5 Mikrometer) keine Emissionsbanden. Also noch einmal zum mitschreiben:
IR-Absorber sind auch IR-Emitter. Herr Wehlan ich weiß, dass Sie nicht an eine, wie auch immer geartete IR-Emission, von CO2, H2O(g)… im Sinne des „Treibhauseffekts“ glauben. Dabei verwenden Sie u. a. mit dem Argument, der „Treibhauseffekt“ verstößt gegen den zweiten HS d. Thermodynamik, weil eine kältere Atmosphäre die wärmere Erdoberfläche nicht erwärmen kann.
Da müssen Sie etwas missverstanden haben. So und nicht anders habe ich das gemeint. Der thermodynamische Term steckt in der Maxwell-Boltzmann-Geschwindigkeitsverteilung, aus der letztendlich infolge der Stöße auch die temperaturabhängige (!) Boltzmann-Besetzung (Energie) der Rotationsschwingung-Banden folgt. Dies geht auch aus Thomas/Stamnes (Radiative Transfer in the Atmosphere and the Ocean“), S. 102 hervor. Ich wiederhole ihr Zitat: „Local thermodynamic equilibrium applies if the gas density is sufficiently high to ensure that the collisional lifetime of an exicted state t(coll) is much smaller then the radiactive lifetime t(rad). Dazu schreiben die Autoren auf S. 99 etwas über die typischen Einfangsquerschnitte und unterscheiden zwischen elastischen Stößen (10^-19 m^2) und inelastischen Stößen 10^-23 … 10^-25 m^2. Die inelastischen Einfangsquerschnitte sind also viel kleiner als die elastischen und dazu muss man dann die zugehörige Fußnote (15) auf S. 128 lesen. Sie ist besonders interessant und lautet:
„If inelastic cross sections were not much less than the elastic, there would be drastic consequences. Consider air at sea level, for which 10^9 collisons occur per second. If a signifcant fraction of these collisions were inelastic – leading to an eventual radiative loss of heat – the air would cool down almost instantaneously!“
Da haben wir ihn, den „Strahlungsenergieerhaltungssatz“. Thomas und Stamnes behaupten tatsächlich, die erdbodennahe Luft würde sich sofort abkühlen, wenn angeregte „Treibhausgasmoleküle“ durch inelastische Stöße deaktiviert (Quenching) würden. Ineleastische Stöße sind vom Übel – elastische Stöße sind gut – denn sie begründen den Treibhauseffekt im Sinne eines „Strahlungsenergieerhaltungssatzes“. Dies steht im Widerspruch zu meinem im Bild 3 gezeigten Messergebnis, aus dem klar hervorgeht, dass sich die Transmission eines CO2-haltigen Luftgemischs in Gegenwart von Begleitgasen, wie He oder N2, verringert. Die größte Transmission wird mit reinem CO2 gemessen, die mittlere stammt vom Gemisch CO2/He und die geringste vom Gemisch CO2/N2.
Im übrigen ist die Stoßdeaktivierung („collisional deexitation, collisional quenching“, lt. Thomas/Stamnes) ein uralter Spektroskopie-Hut. Dies bereits 1947 und davor – auch für den IR-Strahlungsbereich – beschrieben (vgl. Literaturstelle [27]). Man kann es drehen und wenden, wie man will: Erdbodennah überwiegt im Vergleich zur IR-Emission der strahlungslose Übergang angeregter CO2-Moleküle in den Grundzustand durch ineleastische Stöße. Kühlt sich deshalb die Luft dadurch unmittelbar ab (cool down almost instantaneously)? Nein! Es gilt der Energieerhaltungssatz: Strahlungsenergie wird in kinetische Energie der Luftmoleküle gewandelt (vgl. thermodynamische Temperatur). Aber dennoch verlässt die erdbodennah gewandelte Wärmestrahlung den Erdkörper wieder als Wärmestrahlung. Denn es gibt natürlich auch die Konvektion. Kalte Luft bleibt nicht unten! Je dünner aber die Atmosphäre wird, desto mehr überwiegt sukzessive der Strahlungsterm (L). Dies ersieht man aus der CO2-Bande im Bild 2 bei 667 cm^-1, die klar belegt, dass die Atmosphäre am Rand der Troposphäre im 15 Mikrometerbereich emittiert. Um nicht bewusst missverstanden zu werden: Natürlich emittiert CO2 auch erdbodennah IR-Strahlung nur nicht im gleichen Maße, wie es absorbiert.
Fazit: Insgesamt wird dem erdbodennahen „Strahlungsenergiegeschehen“ eine viel zu große Bedeutung zugeschrieben, während die anderen, thermodynamisch begründbaren, atmosphärischen Energieflüsse klein gerechnet werden. Sie erscheinen mehr als Anhängsel der atmosphärisch-terrestrischen Strahlungsbilanz. Das gilt auch für die allseits bekannte „Earth’s Annual Global Mean Energy Budget“ von J. T. Kiehl and Kevin E. Trenberth, die für „thermals“ bzw. „evapotranspiration“ und „latent heat“ zusammen nur 102 W/m^2 gelten lassen, während die atmosphärische Rückstrahlung mit 324 W/m^2 angesetzt wird. Noch merkwürdiger wird es, wenn man sich das Bild 3 in meinem Beitrag anschaut und dann bei Kiehl/Trenberth erfährt, dass nur 40 W/m^2 durch das stets offene atmosphärische Strahlungsfenster („atmospheric window“) entweichen sollen bei einer gleichzeitigen Rückstrahlung („back radiation“) von 324 W/m^2.
Noch eine kleine Anmerkung zum Strahlungstransport: Es gibt Inversionswetterlagen. Wieso können diese über Tage und Wochen beständig über einem Fleck verbleiben, wenn doch wärmere Luftschichten in größerer Höhe mittels Strahlungstransport die kälteren erdbodennahen Luftschichten erwärmen müssten. Nein, dem atmosphärischen Strahlungsgeschehen in damit dem „Treibhauseffekt“ wird eine viel zu große Bedeutung beigemessen.
Die Tatsache, dass Teilchen wie CO2 u. a. IR-Strahlung emittieren, ist allerdings kein Beweis dafür, dass der „Treibhauseffekt“ die ihm von IPCC-nahen Forschern und „Klimamodellieren“ zugeschriebene Größenordnung aufweist. Es ist noch nicht einmal ein Beweis dafür, dass der zu recht umstrittene Begriff der irdischen „Mitteltemperatur“ ohne „Treibhausgase“ von -18 °C durch den „natürlichen Treibhauseffekt“ um 33 °C auf + 15 °C angehoben wird.
Das ist aber eine ganz andere Wurmbüchse, die ich hier nur andeuten möchte. Prof. Gerlich (Braunschweig) hat insofern Recht, als die schlichte Anwendung des Stefan-Boltzmann-Gesetzes zur Berechnung der „mittleren Temperatur“ in der Art, wie ich es mit der Gleichung 5 gemäß der offiziellen Doktrin des IPCC (!) getan habe, kritisch zu sehen ist. Wie gesagt, ich referiere nur!! Tatsächlich kann man mit T^4 nicht so ohne weiteres die mittlere Temperatur einer an der Oberfläche inhomogenen (!) Erde (Wasser, Fels…) berechnen (!). Die besagten 33 °C, die man dem „Treibhauseffekt“ per Übereinkunft zuordnet, sind kein Messwert. Man müsste vielmehr aus einer Unzahl kleiner Flächeareale die mittlere Globaltemperatur (ohne „Treibhausgase“) unter Berücksichtigung des Sonneneinstrahlungswinkels berechnen. Ich persönlich bin davon überzeugt, dass die globale Mitteltemperatur ohne „Treibhauseffekt“ mit -18 °C viel zu niedrig angesetzt ist.
„Natürlich lassen sich Extinktionen nicht mit dem Planckschen-Strahlungsgesetz kombinieren. Das ist auch gar nicht die Absicht. Aber der daraus abschätzbare relative Zuwachs bei Verdopplung des CO2-Gehalts ist entscheidend. Er entspricht [mit 0,17%] der Differenz der Flankenintegrale bei 714 ppm und 357 ppm im Verhältnis zum Gesamtintegral bei 357 ppm.. Wie bereits erwähnt, es handelt sich nur um eine Abschätzung und nicht um einen exakten Messwert. Dennoch macht er deutlich, auf welch geringfügigen Größen sich die seinerzeit im Spiegel (33/1986) prophezeite ‚Klimakatastrophe‘ stützt“
Besten Dank, Herr Dr. Hug für Ihr umfangreiches Update. Aber auf so „geringfügige Größen“ hat sich seinerzeit der ‚Spiegel‘ mit dem Kölner Dom im Wasser gewiss nicht gestützt und Ihr 0,17% Extinktionszuwachs bei CO2-Verdoppelung ist keine Abschätzung sondern Ihr Messergebnis. Nimmt man großzügig an daß dieser Wert in etwa auch für den Absorptionszuwachs gilt und vergleicht mit den wesentlich exakteren (von mir integrierten) Werten von HITRAN (7,4/74 W/m² = 10%), so wird deutlich dass Ihr Wert leider um den Faktor 59 zu niedrig liegt.
M.E. liegt der große Fehler nicht so sehr an Ihrer geringen Auflösung (etwa Faktor 500), sondern einerseits an der m.E. gut um den Faktor 10^4 zu geringen Meßgenauigkeit – die Küvettenlänge war nur ca. 1/70.000 der äquivalenten Atmosphärendicke. Transmissionsunterschiede von z.B. 0.99999 und 0,99995 – siehe Ihr Bild 3 – die bei 10 cm (wegen der Potenzierung mit 70.000 gemäß Lambert-Beer für die Atmosphäre) entscheidend sind, lassen sich bei dieser Küvette auf keinen Fall mehr richtig messen. Man kann z.B. um den Faktor 5×10^5 genauer messen bei Spiegelwegen von 10 m und mit einem 5000-fachen CO2-Druck. Dieses Prinzip wurde ja bei HITRAN angewendet, dessen Akkuratesse Sie wenigstens für diejenigen bestätigen die eher Ihrer Messung vertrauen da sie argwöhnen, IPCC habe vielleicht – was definitiv nicht der Fall ist – die HITRAN-Daten zugunsten eines weit höheren Treibhauseffekts manipuliert.
Andererseits haben Sie versehentlich nur die Flankenfüße am Rand des gesättigten Bereichs (etwa 14-16 µm) mitgemessen – anstatt die vollen Flankenflächen weiter aussen wo der hauptsächliche Effekt bei CO2-Verdoppelung erst auftritt. Das ist m.E. der Hauptgrund weshalb Ihr Extinktionszuwachs viel zu klein wurde. Ihr molarer Extinktionskoeffizient 20,2 für den 15 µm-Peak bzw. die von Ihnen berechnete Schichtdicke von 10 m wo eine Extinktion von 3,21 oder Transmission von 0,6 Promille erreicht wird, hängt sehr stark von der Auflösung ab weil bei höherer Auflösung der Peak deutlich höher und schmaler wird. Sie sagen auch unter 3.2 dass Ihre Messwerte relativ ungenau sind – schließlich dienten sie eigentlich auch nur einer groben Überprüfung der IPCC-Behauptungen.
Prima finde ich dass Sie auch mit Zusatz von Wasserdampf, He und N2 gemessen haben wo in Bild 3 deutliche Unterschiede erkennbar sind. Bloß welche Auswirkung das auf Ihre 0,17% hatte, ist mir nicht klar geworden. Bild 4 finde ich nicht und 25.000 cm sind nicht 25 sondern 250 m. In Bild 6 zeigen Sie dass der IPCC-„Strahlungsantrieb“, der als Maß für den TE mit 3,7 W/m² etwa um den Faktor 60 höher ist als bei Ihnen, trotzdem nur geringfügige 1,2% (der aus einer Trenberth-Grafik stammenden „Gegenstrahlung“ von 324 W/m²) beträgt. In diesen 324 W/m² sind allerdings auch andere Rückflüsse (Konvektion und Niederschlag) sowie die Rückstrahlung sämtlicher THG enthalten. Allerdings unter #22 zu 3) haben Sie sich mit „diese Absurdität, den Unfug der positiven Wasserdampfrückkopplung“ verrannt. Dieser Effekt ergibt – ebenso wie die CO2-Ozeanausgasung bei Erwärmung – eine sehr schnell konvergierende geometrische Reihe – also keinen „run away“ der sich zu einer Widerlegung eignen würde.
Bezieht man den CO2-Verdoppelungszuwachs nur auf die CO2-Gegenstrahlung, so sind es etwa 10%. Die 3,7 W/m² würden am Boden allerdings nur 0,68 Grad ausmachen. Dass IPCC eine politische Organisation ist die unsere Umerziehung und ein globales Öko-Regime durchsetzen möchte, steht ausser Frage. So distanzierte sich z.B. der indische Umweltminister Ramesh von Pachauri und warf dem IPCC vor, man habe die Grenze zwischen Klimawissenschaft und Klimamissionierung (!) überschritten.
„Zu 3) Greg House. Ich habe mich sehr wohl entschieden. CO2 ist ein „Treibhausgas“ und Wasserdampf auch. So, jetzt spielen wir einmal die Szenerie durch. Mehr CO2 verursacht mehr atmosphärischen Wasserdampf. Der Wasserdampf erwärmt als Treibhausgas (Integration der IR-Emission über den Halbraum, Gradient, Tensor etc. ist alles bekannt) die Wasseroberfläche zusätzlich. Das bestreitet hoffentlich niemand. Jetzt geht es erst richtig los. Denn dadurch verdampft noch mehr Wasser, dessen Dampf wiederum den Ozean noch stärker aufheizt. Der zusätzliche Wasserdampf lässt als Treibhausgas noch mehr Wasser verdampfen usw. Merkt denn wirklich niemand diese Absurdität, den Unfug, der positiven Wasserdampfrückkopplung?“
==============================================
Herzlichen Glückwunsch, Herr Hug! Sie haben eben eine schöne Beweisführung „ad absurdum“ durchgeführt. Nicht dass Sie es so wollten, aber so ist es nun mal.
Nun was daraus folgt wissen Sie ja mit Sicherheit: richtig, daraus folgt, dass die Prämisse falsch ist!
Glauben Sie immer noch, dass Wasserdampf ein „Treibhausgas“ ist?
Der Erwärmungseffekt der NICHT STRAHLENDEN Atmosphäre beschränkt sich allerdings zeitlich auf die Nacht, also auf die „Durchschnittstemperatur“ und geht auf Kosten einer MÄCHTIGEN Abkühlung am Tag,
irgendwo muss die Energie ja herkommen,
das vergesst ihr Treibhauskünstler immer.
Ginge es dagegen nach der falschen Treibhaustheorie,
wäre es genau umgekehrt, denn Strahlen haben im Gegensatz zur Konvektion bekanntlich Lichtgeschwindigkeit:
Es müsste am Tag, wenn die Sonne scheint, WESENTLICH heißer sein,
HEIßER ALS AM MOND ohne „Treibhauseffekt“,
und in der Nacht geht diese „Gegenstrahlung“ gegen 0,
Sie wissen doch, die Sache mit der 4.Potenz.
oder nicht?
Diese einfachen Überlegungen zeigen, dass die „Treibhaustheorie“ falsch sein muss.
Herr Müller, man darf an die Sache halt nicht wie Sie rangehen, oder Fischer etc.,
dass man erst mal voraussetzt, es gäbe den Treibhauseffekt,
BEVOR man ihn vernünftig erklären kann.
mfG
p.s.
bitte beachten Sie,
dass ich „Gegenstrahlung“ in Gänsefüßchen schreibe,
denn die gibt es leider nicht da, wo die „Globaltemperatur“ definiert ist.
„Der Treibhauseffekt ist nicht notwendig, damit Luftströmungen entstehen.“
Ohne Treibhausgase fast keine Luftströmungen. Die Atmosphäre ist dabei fast einheitlich warm mit der höchsten Oberflächentemperatur, weil zwar Wärme in die Atmosphäre eingetragen werden kann, aber es praktisch keinen Weg für die Wärme gibt, die Atmosphäre zu verlassen. Nach oben in den Weltraum nicht, weil eine Abstrahlung nicht möglich ist. Nach unten nicht, weil eine dünne ruhende Inversionsschicht zwischen der größtenteils warmen Atmosphäre und der größtenteils kühleren Oberfläche ist. Eine ruhende Luftschicht ist aber ein ganz schlechter Wärmeleiter.
Aber fast ohne Temperaturgradient existieren fast keine Luftströmungen.
MfG
Gerade bei Wasserdampf ist es völlig klar, dass er im Rahmen des Wasserkreislaufs kühlt.
Und dieser Kreislauf wird allein durch den Tag/Nacht-Wechsel ständig in Gang gehalten.
Die beim Aufstieg obligatorische Wolkenbildung (Albedo) ist nur der bekannteste Effekt. Hinzu kommt nicht nur die Verdampfungskühlung bei der Entstehung sondern auch die Tatsache, dass ein wesentlicher Teil der H2O Absorbtionsbanden AUSERHALB des Erdrückstrahlungsspektrums der Erde liegt, also deutlich unter 4µm,
und damit im Bereich der solaren Infrarotstrahlung.
Nach der Treibhaustheorie müsste sich also eher die Sonne durch Wasserdampf der Erde erhitzen. 🙂
mfG
Soweit ich das bei den bisherigen Beiträgen und Artikeln über den Treibhauseffekt mitbekommen habe, wird genau Letzteres bestätigt. Nicht das CO2 direkt ist der Antreiber für mehr H2O in der Atmosphäre, sondern die Wärme. Das CO2 hat nur eine mittelbare Wirkung auf das H2O.
„Deshalb ist aus den Klima“modellen“ die Wasserdampfrückkopplung herauszunehmen.“
Warum das? Wenn es physikalisch richtig ist, dass eine höhere Temperatur allgemein zu mehr Verdunstungen und dadurch zu mehr H2O in der Atmosphäre führt und gleichzeitig dieses H2O ebenfalls wieder eine Erwärmung um einen gewissen Betrag nach sich zieht, dann müssen die Modelle diese Zusammenhänge auch abbilden.
„Zu 3) Greg House. Ich habe mich sehr wohl entschieden. CO2 ist ein „Treibhausgas“ und Wasserdampf auch. So, jetzt spielen wir einmal die Szenerie durch. Mehr CO2 verursacht mehr atmosphärischen Wasserdampf. Der Wasserdampf erwärmt als Treibhausgas (Integration der IR-Emission über den Halbraum, Gradient, Tensor etc. ist alles bekannt) die Wasseroberfläche zusätzlich. Das bestreitet hoffentlich niemand.“
Ohh ohh, warten Sie es ab, das kann noch lustig werden. ;o) Ich glaube eine Feststellung, die hier im Forum von niemanden bestritten wird, muss noch gefunden werden.
„Jetzt geht es erst richtig los. Denn dadurch verdampft noch mehr Wasser, dessen Dampf wiederum den Ozean noch stärker aufheizt. Der zusätzliche Wasserdampf lässt als Treibhausgas noch mehr Wasser verdampfen usw. Merkt denn wirklich niemand diese Absurdität, den Unfug, der positiven Wasserdampfrückkopplung?“
Die positive Rückkopplung wird nur aus dem Ruder laufen, wenn es in dem System keine limitierenden Faktoren geben würde. Wie ist denn zum Beispiel das Delta(H2O) vom Ausmaß, wenn man die Durchschnittstemperatur einmal von 15°C auf 15,5°C erhöht und dann von 17°C auf 17,5°C? Und hat der zusätzliche Wasserdampf in einer beispielsweise 2°C wärmeren und wasserreicheren Atmosphäre immer noch dieselbe Wirkung? Wenn die Wirkung des zusätzlichen Wasserdampfes immer mehr abnimmt, je mehr sich davon schon in der Atmosphäre befindet (so wie man es beim Treibhausgas CO2 mit dem logarithmischern Verlauf vermutet) und je wärmer die Atmosphäre schon ist, dann wird die positive Rückkopplung sich immer weiter abschwächen und die Temperatur in der Atmosphäre sich auf einem generell höheren Niveau bewegen.
Sie schreiben:
„Im übrigen habe ich das Buch von Thomas und Stamnes, „Radiation in the Atmosphere and Oceans“ gelesen und mich gewundert u. a., dass in der unteren Atmosphäre keine Deaktivierung durch ineleastische Stöße im Sinne des strahlungslosen Übergangs in den Grundzustand bei CO2 und Co. nicht existieren darf. Andernfalls gäbe es keinen Treibhauseffekt.“
Dann haben Sie das nicht richtig gelesen.
Thomas und Stamnes, „Radiation in the Atmosphere and Oceans“ schreiben in Kapitel 4:
„Local thermodynamic equilibrium applies if the Gas density is sufficient high to ensure that the collisional lifetime of an excited state tcoll is much smaller than the radiative lifetime. This condition is fullfilled in the Thermal IR (? > 3 ?m).
…nach kurzer Rechnung für 15 ?m schreiben T&S: „therfore wie would expect that LTE
exists in this band down to pressures of 0.01 – 0.1, which occurs near 75 km.“
Das haben sie wohl falsch verstanden, aber da steht, dass LTE für die 15 ?m Bände von Atmosphärendruck bis 0.01 mbar gilt. Also vom Erdboden bis weit in die Stratosphäre.
Und dass in der unteren Atmosphäre angeregte CO2 Moleküle sehr schnell inelastisch
durch Stöße in den Grundzustand abgeregt werden. Also genau das was Sie vermissen.
Wie schon gesagt Sie benutzen auch in ihrem Artikel den Begriff LTE nicht korrekt. Sie sollten daraufhin ihre Herleitung mal überprüfen. Thomas und Stamnes, „Radiation in the Atmosphere and Oceans ist da ein gutes Buch dafür.
Mit freundlichen Grüßen
Günter Heß
ich dachte doch tatsächlich einen Moment, du seist vernünftig geworden!
Wir waren nicht in der Antarktis, sondern in der Sahara!
Selbst in 4000 m Höhe wird es dort nicht -50°C
und benimm dich!
mfG
Sie haben richtig die Strahlungsübertragungsgleichung (Ihre Gleichung 7) genannt, die im Falle der Vernachlässigung des Quelltermes (L = 0) als Lösung das Bouguer-Lambert-Beer-Gesetz liefert. In der Atmosphäre sind aber etwa I und L von gleicher Größe, die Vernachlässigung ist also bei der Betrachtung der Atmosphäre unzulässig. Warum machen Sie es dann?
Bei Berücksichtigung von L ist die effektive Absorption viel geringer als bei L = 0.
In den Spektrometern wird I groß gegen L gewählt – und ggf. sogar noch L herausgerechnet.
Auch Ihre Vermutung, daß L unbedingt vorgegeben werden muß, ist unzuteffend. Der Temperaturverlauf kann auch mit der Strahlungstransportgleichung berechnet werden: Die Änderung von I beschreibt ob Wärme an die Atmosphäre abgegeben oder von der Atmosphäre entnommen wird. Die Temperatur ist so zu bestimmen, daß im Mittel über alle Wellenlängen und Winkel die Bilanz gleich 0 ist.
MfG
„Mehr CO2 verursacht mehr atmosphärischen Wasserdampf. Der Wasserdampf erwärmt als Treibhausgas (Integration der IR-Emission über den Halbraum, Gradient, Tensor etc. ist alles bekannt) die Wasseroberfläche zusätzlich. Das bestreitet hoffentlich niemand.“
Doch, ich bestreite das !
Woher kommt denn die Energie für erwärmende Wirkung des Wasserdampfes auf die Wasseroberfläche ? Das wurde niemals geklärt.
Da Wasserdampf selbst keine Energie erzeugen kann, muss die Energie aus der Wasserdampferzeugung stammen – also im Fall der Atmosphäre von der Sonne.
Gemäß Postulat des „Treibhaus-Effekts“ ist aber die Sonnenstrahlung konstant und Einstrahlung ist immer gleich Ausstrahlung.
Nun behaupten manche, dass die Energie aus der Zurückhaltung von Energie-Abgabe (Abstrahlung) stamme. Das ist aber unbewiesen – auch die Emissionsspektren der Erde lasen diese Schlussfolgerung nicht zu.
Im Gegenteil, die stratosphärische Kompensation beweist, dass die Erde ihre Energie immer ans Weltall abgibt, insbesondere nach einer Erwärmung der Meere, z.B. El Nino, (mehr Wasserdampf in der Atmosphäre) wird in der Höhe nicht weniger (wie manche vermuten) sondern mehr abgestrahlt.
Der Treibhaus-Effekt scheitert also schon aus Mangel an verfügbarer Energie.
Auch verursachen IR-aktive Gase keine Wärmedämmung. Selbst das Bundesbau-Ministerium hat festgestellt, dass das Treibhausgas SF6 die Wärmedämmung verschlechtert.
Richtig ist folgendes:
Eine höhere Sonneneinstrahlung führt zu mehr Wasserdampf und mehr Wasserdampf führt zu einer stärkeren Abstrahlung – andernfalls wären wir alle nicht hier, um zu diskutieren.
Freundliche Grüße
Dr. M. Wehlan
http://www.irs.uni-stuttgart.de/skript/RA1/RA1-SS060627_www.pdf
Curry and Schramm untersuchen die Wasserdampfrückkopplung über der Arktis (10jährige Zeitreihe)
http://curry.eas.gatech.edu/currydoc/Curry_JGR100.pdf
Bill untersucht die Änderung des troposhärischen Wasserdampf (thanks to Kevin Trenberth) und kommt zum Schluss, dass mehr Wasserdampf bei höherer Temperatur vorhanden ist (wer hätte denn das gedacht?)
http://curry.eas.gatech.edu/currydoc/Curry_JGR100.pdf
Zu 2) Herr Junkers, Sie wissen hoffentlich, dass sich die Weltmeere allein durch die Solareinstrahlung – auch ohne Treibhauseffekt – erwärmen (z. B. durch nahes Infrarot). Wo eine Erwärmung, da auch eine Konvektion und naturgemäß auch Wind. Der Treibhauseffekt ist nicht notwendig, damit Luftströmungen entstehen. Dann sollten Sie die Versuchsanordnung von Joule kennen. Danach wird mechanische Energie (Wind bewegt die Wellen) in Wärmeenergie gewandelt (Sie können den ersten HS der Thermodynamik in beliebigen Lehrbüchern der Physik, Physikalischen Chemie z. B. Heinz Hug, Physikalische Chemie, S. 118) nachsehen.
Zu 3) Greg House. Ich habe mich sehr wohl entschieden. CO2 ist ein „Treibhausgas“ und Wasserdampf auch. So, jetzt spielen wir einmal die Szenerie durch. Mehr CO2 verursacht mehr atmosphärischen Wasserdampf. Der Wasserdampf erwärmt als Treibhausgas (Integration der IR-Emission über den Halbraum, Gradient, Tensor etc. ist alles bekannt) die Wasseroberfläche zusätzlich. Das bestreitet hoffentlich niemand. Jetzt geht es erst richtig los. Denn dadurch verdampft noch mehr Wasser, dessen Dampf wiederum den Ozean noch stärker aufheizt. Der zusätzliche Wasserdampf lässt als Treibhausgas noch mehr Wasser verdampfen usw. Merkt denn wirklich niemand diese Absurdität, den Unfug, der positiven Wasserdampfrückkopplung?
Zu 6) Jörg Junkers. Glauben Sie wirklich, ich könne nicht zwischen Energie und Leistung unterscheiden? Nimmt man zu Gunsten der „Modellierer“ an, nur die ersten 10 m Wassertiefe der Ozeane würden die mittlere Erdtemperatur thermostatisch regeln, ergibt die Rechnung, dass die Ozeane im Temperaturbereich von –18 °C bis +15 °C eine Energiemenge von 1,57.1018 MJ speichern. Nebenbei bemerkt, beträgt die durchschnittliche Wassertiefe 3794 m und nicht 10 m. Nun die Gegenrechnung: Ein wasserloser Gesteinshaufen im Weltall, der sich einmal täglich um seine Achse dreht, wird wie ein Grillbraten am rotierenden Spieß, an der momentan der Sonne zugewandten Seite stark erhitzt und kühlt sich an der abgewandten Seite sofort wieder ab (Strahlungskühlung, Stefan-Boltzmann-Gesetz). Deshalb ist ein Ansatz von 24 Stunden zur Berechnung der Energie gerechtfertigt. In 24 Stunden werden durch den irdischen Treibhauseffekt 1,43.1016 MJ umgeschlagen (hier haben Sie die Umrechnung von Leistung in Energie). Der gesamte natürliche Treibhauseffekts macht somit nur 0,9 % der Energie aus, die in den Ozeanen bei einer Wassertiefe bis zu 10 m gespeichert ist. Nicht mehr! Weil dem so ist, ist die Kopplung atmosphärisch-ozeanischer Zirkulationsmodelle (AOGCM) äußerst schwierig. Das kleine bisschen Treibhauseffekt wird mit einem riesigen Wärmereservoir gekoppelt. Da braucht es schon Flusskorrekturen – unbedingt. Oder man man schafft die Flusskorrekturen ab und benutzt empirische Größen, die passend gemacht werden. Wie gesagt, die „Modellierer“ handeln im Auftrag der Politik – weltweit.
Im übrigen habe ich das Buch von Thomas und Stamnes, „Radiation in the Atmosphere and Oceans“ gelesen und mich gewundert u. a., dass in der unteren Atmosphäre keine Deaktivierung durch ineleastische Stöße im Sinne des strahlungslosen Übergangs in den Grundzustand bei CO2 und Co. nicht existieren darf. Andernfalls gäbe es keinen Treibhauseffekt.
Herr Müller, bitte beachten Sie den Zusammenhang. Kramm schrieb:
„Es fehlt eine eindeutige physikalische Definition, was denn dieser sog. atmsophaerische Treibhauseffekt beinhaltet.
Zu sagen, die globale Oberflaechentemperatur der Erde mit Atmosphaere ist hoeher als ohne Atmosphaere bzw. einer transparenten Atmosphaere ist im uebrigen trivial.“
mfg, M. Wehlan
wir messen aber auch so -50°C bei einem „Gasdruck“ von 1050 hPa und die Tageshöchstwerte werden oft nicht in den tiefsten Lagen der jeweiligen Region gemessen, sondern häufig hunderte Hm darüber im Tale.
Warum ist für Meteorologen einfach, dich würde auch das wieder überfordern, schätze ich.
Ok, man kann dir deine Absurditäten auch mit realen Beispielen nich austreiben.
Vielleicht könntest du ja mal versuchen, über deine „physikalisch akzeptierte“ Wissenschaft den selbst konstruirten Wahn herleiten und damit die Zustände der Atmosphäre beschreiben.
Wenn dir das auch nur ansatzweise gelingen würde, verspreche ich, dich nie wieder als jämmerlichen Laien hin zu stellen.
am Dienstag, 21.08.2012, 17:07
„#12: Marvin Müller , richtig.“
Da habe ich mir nun extra Mühe gegeben, das ganze aufs wesentlichen zu reduzieren und Sie schaffen das immer noch, das miszuverstehen. Die Aussage von Herrn Kramm steht im Gegensatz zu Ihrer. Oder rücken Sie jetzt plötzlich von Ihrer Aussage „Eine Erde OHNE Treibhausgase ist vermutlich wärmer nicht kälter.“ ab?
„#12: Marvin Müller
Herr Müller,
bitte reißen Sie bestimmte Äußerungen nicht aus dem Zusammenhang. Bei der Aussage von Kramm, dass etwas trivial sei, ging es nach meiner Erinnerung um …“
Sie brauchen da nicht Ihre Erinnerung bemühen, Sie können das einfach nachlesen. Da die Anmerkung gerade erst einen tag alt war, habe ich die Quelle nicht mit angegeben – hier ist sie: http://tinyurl.com/c5aozdn
„Also hat Kramm mitnichten behauptet, dass eine Erdoberfläche mit transparenter Atmosphäre kälter sei als eine mit IR-aktiven Gasen.“
Naja, formal gesehen haben Sie recht. Er schrieb das genau andersrum – er beschrieb, was wärmer ist. Das mag Ihnen nicht gefallen, aber das ist nun mal so. Wenn man so zwischend den Zeilen liest, scheint es ja noch andere Kommunikationskanäle zu geben. Vielleicht können Sie Herrn Kramm ja mal bitten, das klarzustellen, falls er das nicht so gemeint hat bzw. der Meinung ist, der Satz sei so allein stehend falsch. Ich zitier ihn prphylaktisch nochmal:
Gerhard Kramm: „Zu sagen, die globale Oberflaechentemperatur der Erde mit Atmosphaere ist hoeher als ohne Atmosphaere bzw. einer transparenten Atmosphaere ist im uebrigen trivial.“
es besteht am Tag ein viel mächtigerer Wärmefluss (direkte Wärmeleitung und Konvektion) in die Atmosphäre, als der Wärmefluss durch Strahlung (temperaturabhängige Erdrückstrahlung).
Dies erkennt man auch daran, dass die Erde auch an ihren heißesten Punkten keine Schance hat z.B. die hohen Temperaturen der Mondoberfläche zu erreichen.
Das kennen wir auch aus der Alltagserfahrung. Wenn sie ihre Hand 10 cm über eine rotglühende Herdplatte halten („sehr hohe Wärmestrahlung“???) passiert ihrer Hand kaum etwas, verglichen mit direktem Kontakt, der körperlichen Wärmeleitung.
Diese Wärme in der NICHT strahlenden Atmosphäre geht NIEMALS in den Weltraum verloren, weil dort ein „materieller“ Kontakt nicht mehr möglich ist.
Und nachts, wenn NUR die Erdoberfläche Wärme abstrahlen kann, kühlt sie stärker ab, als diese Atmosphäre
und es kommt zur Umkehr des Wärmeflusses von der Atmosphäre zur Erde.
Es sei denn …
… in dieser Atmosphäre existieren Gasanteile („Treibhausgase“),
die durch Wärmeleitung erhaltene Energie abstrahlen können,
abstrahlen IN DEN WELTRAUM.
Die SEEKTIVEN Banden im großen Spektrum der Infrarotstrahlung der Erde, in denen z.B. CO2 absorbieren und emittieren kann, kommen zwar nicht im Weltraum an (weil sie absorbiert werden),
aber logischerweise kommen auch diese CO2 Strahlen umgekehrt nicht auf der Erdoberfläche an.
Beides kann man unschwer messen!!!
Was also „oben“ in ca. 10km Höhe von CO2 abgestrahlt wird, stammt aus der Wärmeübertragung der Umgebungsmoleküle und nicht direkt aus der Erd-Oberfläche und ist mehr als das was die Erde selbst in diesen Banden emittieren kann, da die CO2 Moleküle ja immer wieder neu „angestoßen“ werden.
Deshalb kühlen diese „Treibhausgase“.
Bei Wasser ist das wegen der obligatorischen Wolkenbildung (Albedo) noch viel deutlicher.
Soweit in aller Kürze nur das Wichtigste.
Es ist also wirklich GROTTENFALSCH, aus thermodynamischer Sicht die dicke Atmosphäre, die am Tag mächtig KÜHLT (ohne diese Wärme zu verlieren) und in der Nacht genau so mächtig erwärmt, zu ignorieren.
mfG
Wenn überhaupt irgend etwas trivial sein sollte,
dann ist das die Klimawirksamkeit einer Atmosphäre.
Jede „Rechnung“, die die Anwesenheit einer Atmosphäre NICHT berücksichtigt, muss falsch sein,
selbstverständlich auch dann, wenn sie für Strahlung komplett transparent ist.
mfG
wie kommst du denn auf eine Temperatur von 15° in der Sahara?
Die Tag und Nacht-Schwankungen sind zwar sehr groß,
sagen wir 30°.
Wenn die Temperatur tags auf 60° steigt und nachts ist es 30°, dann ist das im Mittel immer noch 45°C aber nicht 15°.
Es gibt Teile im Süd-Ost, die gehen am Tag bis 80° mit Temperaturabfall von 50° nachts, das sind dann immer noch im Mittel 65°, hier geht der Wasserdampfanteil gegen 0%
so heiß ist es in den Tropen nicht, wegen Wolken.
Vergleichen kann man wegen dem Temperatureinfluss des Gasdruckes allerdings nur gleiche Höhenlagen,
also Gebirge gibt es sowohl in der Sahara wie in den Tropen.
Gruß
p.s. meine Logik ist wasserdicht
(nach langjähriger Übung,
mein richtiger Name ist Aristoteles :-))
Herr Müller,
bitte reißen Sie bestimmte Äußerungen nicht aus dem Zusammenhang. Bei der Aussage von Kramm, dass etwas trivial sei, ging es nach meiner Erinnerung um eine Definition für den fiktiven Treibhaus-Effekt – also darum, dass dieser angebliche Effekt nicht dadurch beschrieben werden kann, dass man meine, die Temperaturen … seien höher als ohne Treibhausgase.
Um einen physikalischen Effekt zu beschreiben, ist es immer nötig anzugeben, warum es diesen Effekt gibt, durch was er hervorgerufen wird und wie man dies überprüfen könne.
Also hat Kramm mitnichten behauptet, dass eine Erdoberfläche mit transparenter Atmosphäre kälter sei als eine mit IR-aktiven Gasen.
mfg, M. Wehlan
Worauf stützt sich die Vermutung das eine Erde OHNE Treibhausgase wärmer seien sollte? Und in Bezug auf welchen Wert wärmer: nach Boltzmann 255K oder nach Meßwerten 288K?
In wie weit ändert das vorhandensein (oder nicht-) einer Atmospäre das Albedo und welche Auswirkungen hat dies auf die Temperatur? Enceladus hat eine mit 75K eine tiefere Temperatur als der Saturn mit 134K bei einem Albedo von 0,47.
„#6: Auch Sie, verehrter Herr Jörg Junkers verwechseln offensichtlich den Effekt einer Atmosphäre (sowie anderer Wärmespeicher) mit einem theoretisch postulierten „Treibhauseffekt“, den kein seriöser Physiker bestätigen kann. Eine Erde OHNE Treibhausgase ist vermutlich wärmer nicht kälter.“
Dazu meint Gerhard Kramm:
„Zu sagen, die globale Oberflaechentemperatur der Erde mit Atmosphaere ist hoeher als ohne Atmosphaere bzw. einer transparenten Atmosphaere ist im uebrigen trivial.“
Das steht irgendwie im Gegensatz zu dem von Ihnen geäußerten …
LTE oder „Local Thermodynamic Equilibrium“ beschreibt einen Zustand in dem lokal die Energiezustände der Moleküle gemäß der Maxwell Boltzmann Verteilung besetzt sind.
LTE ist die Vorrausetzung dafür dass Sie das L in ihrer Gleichung 7 durch die Planckfunktion ersetzen dürfen.
Steht bei Thomas und Stamnes, Radiation in the Atmosphere and Oceans.
LTE bezeichnet nicht wie Sie in ihrem Artikel schreiben ein lokales thermodynamisches Strahlungsgleichgewicht. Das haben Sie falsch beschrieben.
Mit freundlichen Grüßen
Günter Heß
na immerhin hast zumindest du erkannt, dass das was ich in #1 angeführt habe, genau umgekehrt da zu stehen hätte.
Ich frage mich dabei auch, wie Leute ihre eigene Arbeit verbessern wollen und dann so nen groben Unfug übersehen können. Ist auch nicht der eizige, aber die Details sind hier offensichtlich eh wurscht.
Freilich hast du völlig recht, dass viel Energie vom Boden durch die Konvektion und durch den H2O Kreislauf sozusagen abgeführt wird und das enstpricht auch einer Abkühlung dort.
Diese quasi eindimesionale Ansicht hat aber nichts mit den Strahlungsflüssen zu tun und diese ergeben bei einer THE Anreicherung immer eine höhere Oberflächen T. Du hast recht, dass das Mehr an H2O in Dampf dann die Erwärmung dämpft, das Vorzeichen bleibt aber gleich. Erst, bzw. nur wenn die relative Feuchte nicht annähernd konstant bleiben sollte, es zu verstärkter Bildung von diversen Wolkenklassen kommt, kann sich das Vorzeichen in die von dir gedachte Richtung bewegen.
Deine Logik widerlegst du ja immer wieder selbst, wenn du die 25 Grad warmen Tropen mit den 17° warmen Subtropen vergleichst.
Ein astrologisch geläufiges wichtiges Temperaturkriterium ist dagegen die Albedo (messbar!), da Sie schon Astreroiden erwähnen. Der Saturn-Mond ENCELADUS z.B. hat eine solche von 0,99
mfG
Gegenstrahlung, Sättigung, Strahlungsantrieb, optische Dicke etc.
Ist doch ganz einfach: die angeblichen „Treibhausgase“ k ü h l e n.
Siehe Übergang von N2/O2-Atmosphäre auf einem Planeten ohne Wasser zu einer N2/O2-Atmosphäre mit Spuren von CO2.
Da kann der Effekt der IR-sensiblen Gase ganz leicht abgeschätzt werden.
Da braucht es keine Satellitenmessungen, keinen Plank und keine Strahlungstransportgleichung oder ähnlichen Müll.
für diesen Artikel. Damit wurden wohl alle Schwachsinnsargumente der AGW Anhänger pulverisiert.
Von den pseudophysikalischen Argumentationen eines gewissen Herr Dietz ganz zu schweigen. An dieser Stelle auch Dank an Herr Kramm.
Das mit dem Geheimdienst hat voll gepasst und der Absatz über das Handbuch des Fähnlein Fieselschweif war grenzgenial.
Ich konnte nicht mehr.
Noch mal Danke an Beide.
Zitat:
„Nimmt man an, nur die ersten 10 m Wassertiefe der Ozeane würden die mittlere Erdtemperatur thermostatisch regeln, ergibt die Rechnung, dass die Ozeane im Temperaturbereich von –18 °C bis +15 °C eine Energiemenge von 1,57.1018 MJ speichern. Hierzu die Gegenrechnung: In 24 Stunden werden durch den irdischen Treibhauseffekt 1,43.1016 MJ umgeschlagen [23]. Der gesamte natürliche Treibhauseffekt macht somit nur 0,9 % der Energie aus, die in den Ozeanen bei einer Wassertiefe bis zu 10 m gespeichert ist.“
Hier wird der Fehler begangen die Energie(menge) mit der Leistung (irdischer Treibhauseffekt) zu vergleichen. Über die Beziehung „Engergie gleich Leistung mal Zeit“ kann vielleicht berechnen wie lange es dauert -18°C kalte Ozeane auf 15°C zu erwärmen. 0,9% ist auch nicht der Anteil des gesamten natürlichen Treibhauseffektes sondern nur der eines Tages (24h wie Anfangs auch dargestellt) wirkt der Treibhauseffekt länger als 3 Monate (oder eben nicht) kommt eine Energie zusammen die etwa der Speicherkapazität entspricht.
erdnahe Asteroiden (NEOs) sind in der Regel „dreckige Schneebälle“ ihre Temperatur (ohne Atmosphere!) scheint also unter Null zu liegen. Von einer Erde ohne natürlichem Treibhauseffekt ist das Gleiche zu erwarten.
Man kann Wasserdampf physikalisch nicht isoliert betrachten, da er zwangsläufig einen Kreislauf durchläuft, der erst eine „Wetterrechnung“ ermöglicht.
Wasserdampf ist leichter als die übrigen Gase und unterstützt damit zusätzlich zur wichtigeren Wärmeexpansion die vertikale Zirkulation.
Mit der damit fallenden Temperatur sinkt die Sättigungsgrenze für Wasserdampf permanent (feucht-adiabatischer Temperaturgradient)
und spätestens in 3 bis 4 km Höhe ist aus Wasserdampf wieder Wasser (Wolken) geworden.
Also viel tiefer als der „Strahlungsbereich“ von CO2.
Der Wetter- oder Klimaeffekt von Wasser ist also durch diesen Kreislauf IMMER negativ bezüglich Temperatureinfluss. Für die „Natur“ natürlich positiv.
mfG
Bild 8 legt nahe das zwischen 1955 und 70 der Wasserdampfgehalt zurückgegangen ist. Bild 14a) und 15) weisen daraufhin das in diesem Zeitraum eine Abkühlung gegeben hat. Es gibt in diesem kurzen Zeitraum keine Korrelation zwischen CO2 und Wasserdampf, scheinbar aber eine Korrelation Wasserdampf und Temperatur. Wenn wie beschrieben CO2 die Erde um 0,7 Grad erwärmt, ist dann nicht auch damit zurechnen das der Wasserdampfgehalt ebenfalls steigt? Somit ein CO2-Wasserdampffeedback doch existiert, auch wenn die Zeiträume scheinbar größer als 20 Jahre sind. Gibt es Wasserdampfzeitreihen die länger als 20 Jahre sind?
Der anthropogene Treibhauseffekt ist im wesentlichem ausgereizt, wie die Messung der Transmission von IR-Strahlung belegt. Eine globale Klimakatastrophe ist daher selbst bei einer CO2-Verdoppelung nicht zu erwarten.
Die Steigerung des Treibhauseffekt von 324 W . m-2 auf um 327,7 W . m-2 bei 100 % mehr CO2 ist eine 1,2 %ige Geringfügigkeit (s. Bild 6), die man nur mit Hilfe des hypothetischen Wasserdampfverstärkungsmechanismus künstlich vergrößern kann.
Zweifellos enthält die Atmosphäre gemäß der Clausius-Clapeyronschen-Gleichung mehr Wasserdampf, wenn es wärmer wird. Jedoch lässt sich der hypothetische Wasserdampfverstärkungsmechanismus, ohne den die Klimamodelle nicht auf die politisch erwünschten Temperatursteigerungen kommen, in der Realität nicht nachzuweisen. …
Heinz Hug, für EIKE; Wiesbaden August 2012“
==================================================
Lieber Herr Hug, Sie müssen sich irgendwie entscheiden. Entweder ist Wasserdampf ein „Treibhausgas“, dann führt mehr Wasserdampf zu mehr „Treibhauseffekt“ bzw. mehr Erwärmung, oder er ist keines. Wenn Sie schon meinen, dass Verdoppelung des CO2 0,7C Erwärmung verursacht, warum soll dann Erhöhung der CO2-Konzentration Erwärmung verursachen, aber Erhöhung der Wasserdampf-Konzentration keine? Ich erkenne keine Logik hier.
Oder wird eine Erwärmung (aus welchem Grund auch immer) die Erhöhung der Wasserdampf-Konzentration in der Atmosphäre nicht verursachen? Warum denn?
Das Problem besteht darin, dass wenn Sie diesen unbewiesenen Treibhausunfug akzeptieren, dann ist es vorbei, dann hilft weder Ihre Sättigung-These noch Climategate noch „kalte Sohne“, die Liste ist nicht vollständig. Dass müssen einige „Skeptiker“ dringend begreifen. Man kann unter Umständen auch mit einem „Gegenunfug“ etwas erreichen, aber auf Dauer wird diese Strategie nicht funktionieren.
Bei der Betrachtung des natürlichen Treibhauseffektes sollte außerdem die „Eis-Albedo-Rückkopplung“ beachtet werden. Je kälter die Meere im Durchschnitt sind, desto mehr Eis sollte an den Polen vorhanden sein, desto höher ist das Albedo.
Ob die Relaxionszeit mit 200 Jahren sehr hoch oder sehr niedrig ist hängt von den betrachteten Zeiträumen ab. In einem Gleichgewicht sollte der Zeitraum keine Rolle spielen. Es ist also höchstens eine Frage der Zeit bis die Weltmeere die Gleichgewichtstemperatur annehmen.
(siehe Pkt. 6):
.“ Wenn dies richtig ist, muss besonders in einer kälteren Periode, während der die direkte Solarstrahlung nicht so viel Wasser verdunsten lässt, der Wasserdampfgehalt über den Ozeanen mit dem atmosphärischen CO2-Gehalt ansteigen.
???