Anmerklung von A. Watts: …Dies ist eine umstrittene Ausgabe, und während es eine wunderbare Sache wäre, falls es stimmte, sehe ich persönlich nicht, wie es auf irgendeine Weise den Energieerhaltungssatz (<a href= "http://en.wikipedia.org/wiki/Conservation_of_energy"target="_blank">hier</a>) überwinden könnte. Diese Ansicht wird auch von Anderen geteilt, wie aus der Einführung des Artikels unten hervorgeht. … Anthony WattsGrößenordnung des natürlichen ‚Treibhauseffektes’

  1. Einführung

Unsere jüngste Studie zur allgemeinen Klimatheorie löste intensive Diskussionen bei  WUWT und Tallbloke’s Talkshop aus. Die Blogger, aber auch zwei Online-Artikel von Dr. Ira Glickstein und Dr. Roy Spencer stellten viele wichtige Fragen. Nachdem wir uns durch die meisten Antworten hindurchgearbeitet hatten, wurde uns klar, dass weiterführende Ausführungen erforderlich sind. Wir präsentieren unsere Antwort in zwei separaten Artikeln, die die Schwerpunkte der Blogger ebenso ansprechen wie Schlüsselaspekte unseres neuen Paradigmas.

Beachten Sie bitte, dass Sie zum Verständnis dieser neuen Theorie Ihre Sichtweise ändern müssen! Wie Albert Einstein einmal sagte, ein neues Paradigma kann nicht innerhalb eines existierenden Gedankenexperiments verstanden werden; also werden wir durch das System [episteme], in dem wir leben, eingeschränkt. In dieser Hinsicht erfordert unser Konzept neue Definitionen, die exakte Ebenbilder in der aktuellen Treibhaustheorie haben können oder nicht. Zum Beispiel ist es für uns entscheidend, den Term Atmospheric Thermal Effect (ATE) einzuführen und zu verwenden, weil: a) der Term Greenhouse effect GE unvermeidlich irreführend ist aufgrund der Tatsache, dass die freie Atmosphäre nicht wirklich wie ein geschlossenes Treibhaus funktioniert, wenn man der konvektiven Abkühlung keine Grenzen auferlegt, b) ATE genau den physikalischen Sinn des Phänomens beschreibt, nämlich des Temperaturtreibers [temperature boost] an der Oberfläche infolge der Gegenwart der Atmosphäre, c) die Argumentation in Termen wie ATE im Gegensatz zum GE hilft, die Diskussion über den Strahlungstransport hinaus zu führen und d) der Term Atmospheric Thermal Effect keine zugrunde liegenden physikalischen Mechanismen impliziert.

Wir beginnen mit der unbestreitbaren Tatsache, dass die Atmosphäre zusätzliche Wärme auf der Erdoberfläche erzeugt, verglichen mit einer atmosphärefreien Umgebung wie auf dem Mond. Dies wirft zwei grundlegende Fragen auf: (1) Welche Größenordnung hat diese Zusatzerwärmung, d.h. ATE? und (2) wie macht die Atmosphäre das, d. h. welcher physikalische Mechanismus liegt ATE zugrunde? In dieser Antwort geht es um die erste Frage, da sie die Krux bei den Schwierigkeiten [des Verständnisses] der meisten Leute zu sein scheint, und die daher gelöst werden muss, bevor wir uns mit der übrigen Theorie befassen (siehe zum Beispiel Lord Monckton’s WUWT post).

  1. Die Größenordnung des irdischen atmosphärischen Thermaleffektes

Um ATE ordnungsgemäß zu evaluieren, bleiben wir dabei, dass man die mittlere Temperatur der Erde mit der Temperatur eines sphärischen Körpers ohne Atmosphäre mit gleichem Abstand von der Sonne vergleichen muss. Man beachte, dass wir uns gegenwärtig nicht mit der Zusammensetzung oder der Durchlässigkeit von Infrarotstrahlung befassen. Stattdessen versuchen wir einfach, den gesamten Effekt unserer Atmosphäre auf die thermische Umgebung der Oberfläche zu quantifizieren; also den Vergleich mit einem gleichermaßen beleuchteten luftleeren Planeten. Wir werden uns im Folgenden auf einen solchen Planeten als einen äquivalenten planetarischen Graukörper (PGB) beziehen.

Da die Temperatur proportional (in linearer Weise) zur internen kinetischen Energie eines Systems ist, ist es theoretisch absolut gerechtfertigt, mittlere globale Temperaturen zu verwenden, um ATE zu quantifizieren. Es gibt zwei mögliche Indizes, die man hierfür nehmen könnte:

  1. Die absolute Differenz zwischen der Mitteltemperatur der Erde (Ts) und der eines äquivalenten PGB (Tgb), d.h. ATE = Ts – Tgb; oder
  2. Das Verhältnis von Ts zu Tgb. Letzterer ist besonders attraktiv, weil er ATE normalisiert (standardisiert) mit Berücksichtigung der Solarstrahlung an der Obergrenze der Atmosphäre (TOA) und so den Vergleich ermöglicht von ATEs von Planeten, die mit verschiedenem Abstand um die Sonne laufen und verschieden große Mengen solarer Strahlung empfangen. Wir nennen dieses dimensionslose Temperaturverhältnis Near-surface Thermal Enhancement (ATEn) und kennzeichnen es durch NTE = Ts / Tgb. Theoretisch sollte NTE gleich oder größer als 1,0 sein (NTE ≥ 1.0). Man beachte bitte, dass ATEn eine Messung von ATE ist.

Es ist wichtig festzuhalten, dass unsere gegenwärtige GE-Theorie den ATE nicht durch Temperatur misst, sondern durch die Menge der absorbierten infraroten Strahlung. Obwohl Fachbücher oft erwähnen, dass die Erdoberfläche wegen des ‚Treibhauseffektes‘ unserer Atmosphäre um 18 K bis 33 K wärmer als der Mond ist, wird der tatsächliche Effekt der wissenschaftlichen Literatur zufolge durch die Menge der ausgestrahlten infraroten Strahlung gemessen, die durch die Atmosphäre absorbiert wird (siehe e.g. Stephens et al. 1993; Inamdar & Ramanathan 1997; Ramanathan & Inamdar 2006; Houghton 2009). Gewöhnlich wird sie als eine Differenz (seltener als ein Verhältnis) zwischen gesamten mittleren infraroten Strahlungsfluss an der Erdoberfläche und an der Obergrenze der Atmosphäre berechnet. Auf diese Weise definiert beläuft sich der mittlere GE Satellitenbeobachtungen zufolge auf 157 bis 161 W/m² (Ramanathan & Inamdar 2006; Lin et al. 2008; Trenberth et al. 2009). Mit anderen Worten, die aktuelle Theorie benutzt Einheiten des Strahlungsflusses anstatt Temperatureinheiten, um ATE zu quantifizieren. Diese Annäherung basiert auf der vorbedachten Absicht, dass der GE durch die Reduktion der Abkühlung durch die Rate der ins All abgestrahlten infraroten Strahlungsmenge funktioniert. Allerdings kann die Messung eines Phänomens mit einer vermuteten Grundlage anstatt durch manifeste Effekte eine Quelle erheblicher Konfusion und Irrtümer sein, wie unsere Studie zeigt. Folglich behaupten wir, dass die ordnungsgemäße Bestimmung des ATE von einer genauen Schätzung der mittleren Temperatur an der Oberfläche eines äquivalenten PGB (Tgb) abhängt.

  1. Abschätzung der Mitteltemperatur eines äquivalenten planetarischen Graukörpers

Es gibt zwei Möglichkeiten, Tgb zu bestimmen – eine theoretische, basierend auf den bekannten physikalischen Beziehungen zwischen Temperatur und Strahlung, und eine empirische durch Betrachtung von Messungen auf dem Mond als dem der Erde nächstgelegenen natürlichen Graukörper.

Dem Stefan-Boltzmann-Gesetz zufolge emittiert jedes physikalische Objekt mit einer Temperatur über dem absoluten Nullpunkt Strahlung, und zwar mit einer Intensität (I, W/m²), die proportional zur 4. Potenz der absoluten Temperatur des Objektes ist:

 

wobei ϵ die thermale Emissivität/Absorbtivität ist (0 ≤ ϵ ≤ 1 ) und σ = 5.6704×10-8 W/m². K-4  ist die Stefan-Boltzmann-Konstante. Bei einem theoretischen Schwarzkörper ist ϵ = 1,0, während bei realen festen Objekten wie Felsen normalerweise ϵ ≈ 0.95. Im Prinzip gestattet uns Gleichung 1 eine genaue Berechnung der Gleichgewichtstemperatur eines Objektes, wenn die Menge der durch das Objekt absorbierten Strahlung bekannt ist, d. h.

Die räumlich gemittelte Menge der vom System Erde-Atmosphäre absorbierten Solarstrahlung (Sα ̅̅̅, W/m²) kann aus der Gesamtsolarstrahlung TOA (Sα ̅̅̅, W/m²) und der planetarischen Albedo genau berechnet werden als

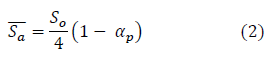
wobei der auf ein Flugzeug einfallende kurzwellige Fluss der TOA (W/m²) senkrecht zu den Sonnenstrahlen ist. Der Faktor ¼ dient dazu, den einfallenden solaren Strahlungsfluss von einer flachen Oberfläche auf eine Sphäre zu verteilen. Er ergibt sich aus der Tatsache, dass die Oberfläche einer Sphäre (4πR²) viermal größer ist als die Oberfläche einer Scheibe (πR²) mit gleichem Radius. Folglich erscheint es logisch, dass man die mittlere Temperatur der Erde ohne ATE aus dem Stefan-Boltzmann-Gesetz abschätzen kann, d. h.

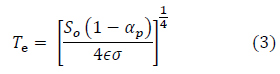
Hierin ist (TeK) bekannt als die effektive Emissionstemperatur der Erde. Setzt man typische Werte ein für S0 =W/m² und αp = 0,3 und ϵ  = 1,0 ergibt Gleichung (3) 254,6 K. Dies ist die Basis für den weithin zitierten Wert von 255 K (-18°C) als mittlere Temperatur auf der Erdoberfläche ohne Treibhauseffekt, d. h. als ob die Atmosphäre fehlt oder ‚vollständig transparent‘ für IR-Strahlung ist. Dieser Temperaturwert wird auch benutzt,, um die sog. Effektive Emissionshöhe in der Troposphäre zu definieren (bei etwa 5 km Höhe), von wo man vermutet, dass der Hauptteil der emittierten langwelligen Strahlung ins Weltall ausgeht. Da die mittlere Temperatur der Erde 287,6 K (+14,4°C) beträgt, schätzt die gegenwärtige Theorie die Größenordnung von ATE bei 287,6 K – 254,6 K = 33 K. Wie jedoch in anderen Studien gezeigt wurde, leidet diese Annäherung unter einem ernsten logischen Fehler. Wenn man die Atmosphäre entfernt (oder auch nur den Wasserdampf darin), würde daraus eine viel niedrigere planetarische Albedo resultieren, da Wolken dafür verantwortlich sind, dass die meiste kurzwellige Strahlung reflektiert wird. Folglich muss man eine andere Albedo (αp) in Gleichung 3 einsetzen, die die aktuelle Oberflächenreflektion allein quantifiziert. Eine Analyse des globalen Energiehaushalts der Erde von Trenberth et al. (2009) mit Hilfe von Satellitenbeobachtungen legt einen Wert αp≈ 0,12 nahe. Glücklicherweise ist dieser Wert ziemlich ähnlich der Albedo des Mondes von 0,11 (siehe Tabelle 1 in unserer  Originalstudie), so dass es uns möglich ist, den ATE der Erde unter Verwendung unserer Satelliten als passende PGB-Proxy zu evaluieren. Setzt man 0,12 in Gleichung 3 ein, ergibt sich ein Wert von Te = 269,6 K, welches gleichbedeutend mit einem ATE von lediglich 18 K ist (d. h. 287,6 – 269,6 = 18 K).

Zusammenfassend: die gegenwärtige Treibhaustheorie verwendet eine einfache Form des SB-Gesetzes, um die Größenordnung des irdischen ATE zwischen 18 K und 33 K zu schätzen. Die Theorie nimmt weiter an, dass die mittlere Temperatur des Mondes 250 K bis 255 K beträgt, trotz der Tatsache, dass die korrekte lunare Albedo (0,11) eingesetzt in Gleichung 3 etwa 270 K ergibt, d. h. eine um 15 bis 20 K höhere Temperatur! Außerdem, die Anwendung von Gleichung 3, um die mittlere Temperatur einer Sphäre zu berechnen, führt zu einem fundamentalen mathematischen Problem durch Hölders Ungleichheit zwischen nichtlinearen Integralen (u. a. Kuptsov 2001). Was bedeutet das? Hölders Ungleichheit gilt für gewisse nichtlineare Funktionen und legt fest, dass in solchen Funktionen die Verwendung eines arithmetischen Mittels für die unabhängige (Input-)Variable nicht einen korrekten Mittelwert der abhängigen (Output-)Variablen führt. Wegen einer nichtlinearen Beziehung zwischen Temperatur und Strahlungsfluss beim SB-Gesetz (Gleichung 3) und der Variation der absorbierten Strahlung mit der geographischen Breite auf einer Sphäre kann man nicht die mittlere Temperatur eines einseitig beleuchteten Planeten mit der Menge der räumlich gemittelten  absorbierten Strahlung, definiert durch Gleichung 2, genau berechnen. Hölders Ungleichheit zufolge wird die aus Gleichung 3 berechnete Temperatur immer signifikant höher sein als die aktuelle mittlere Temperatur auf einem luftleeren Planeten. Wir können diesen Effekt mit einem einfachen Beispiel illustrieren.

Nehmen wir zwei Punkte auf der Oberfläche eines PGB, P1 and P2, die sich beide auf exakt der gleichen geographischen Breite befinden (sagen wir 45°N), aber auf entgegengesetzter geographischen Länge, so dass P1 voll beleuchtet und gleichzeitig P2 vollständig beschattet ist, und umgekehrt (siehe Abbildung 1). Wenn der PGB in der gleichen Entfernung um die Sonne kreist wie die Erde und die Solarstrahlung die Wärmequelle darauf ist, dann würde die Gleichgewichtstemperatur am beleuchteten Punkt [T1 = 349,6 K]* betragen (unter Annahme eines solaren Zenitwinkels von θ = 45°), während die Temperatur am beschatteten Punkt T2 = 0 wäre (da er keine Strahlung erhält wegen cosθ < 0). Die mittlere Temperatur zwischen den beiden Punkten beträgt dann Tm = (T1 + T2)/2 = 174,8 K. Wenn wir allerdings versuchen, eine Mitteltemperatur aus der mittleren, an den beiden Punkten absorbierten Strahlungsmenge W/m² zu berechnen, erhalten wir 234,2 K. Klarer Fall, Te ist viel größer als Tm (Te ≫ Tm), was ein Ergebnis von Hölders Ungleichheit ist.

*Der Ausdruck in den eckigen Klammern fehlt im Original. Er wurde aus der Abbildung übertragen und eingesetzt. Es ist wohl von einem Versehen der Autoren auszugehen. A. d. Übers.

 

Abbildung 1: Illustration des Effektes von Hölders Ungleichheit bei der Berechnung der mittleren Temperatur auf der Oberfläche eines luftleeren Planeten. Details im Text.

Aus dem obigen Beispiel kann man das Ergebnis mitnehmen, dass zur Berechnung einer aktuellen mittleren Temperatur auf einem luftleeren Planeten eine explizite Integration des SB-Gesetzes über die Planetenoberfläche erforderlich ist. Dies impliziert, dass man erst die 4. Wurzel aus dem absorbierten Strahlungsfluss an jedem Punkt der Oberfläche ziehen muss und erst dann das sich daraus ergebende Temperaturfeld mitteln kann – und nicht zu versuchen, eine Mitteltemperatur aus einem räumlich gemittelten Strahlungsfluss zu berechnen wie in Gleichung 3.

Also brauchen wir ein neues Modell, das in der Lage ist, Tgb robuster vorherzusagen als Gleichung 3. Um diese abzuleiten übernehmen wir die folgende Argumentation. Die Gleichgewichtstemperatur an jedem Punkt auf der Oberfläche eines luftleeren Planeten wird bestimmt durch die einfallende Sonnenstrahlung und kann (unter der Annahme einer uniformen Albedo und bei Ignoranz kleiner Wärmebeiträge durch Gezeitenkräfte und inneren radioaktiven Zerfall) approximiert werden als:

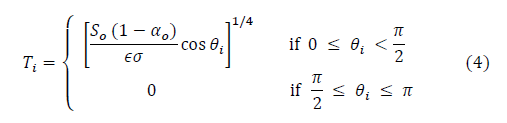
wobei [?]* der solare Zenitwinkel (Radiant) an dem Punkt ist, welches der Winkel zwischen den Sonnenstrahlen und der Achse senkrecht zur Oberfläche an diesem Punkt ist (siehe Abbildung 1). Bei Substituierung ergibt sich die mittlere Temperatur () des Planeten folglich aus dem sphärischen Integral von

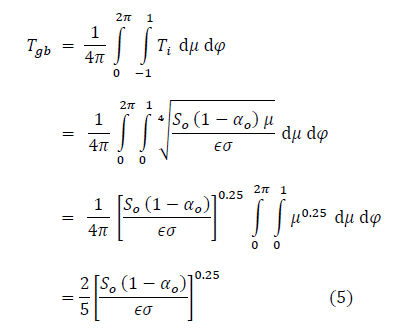
Vergleicht man die Endform von Gleichung 5 mit Gleichung 3 zeigt sich, dass Tgb << Te ist in Übereinstimmung mit der Hölder’schen Ungleichheit. Um den obigen Ausdruck physikalisch realistischer zu machen, fügen wir So eine kleine Konstante hinzu, Cs =0.0001325 W/m², so dass sich, wenn So = 0,0 ist, aus Gleichung 5 Tgb = 2.72 K ergibt (die nicht mehr reduzierbare Temperatur des freien Weltraums, also

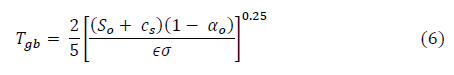
In einer aktuellen analytischen Studie hat Smith (2008) argumentiert, dass Gleichung 5 nur die mittlere Temperatur eines nicht rotierenden Planeten beschreibt und dass sich die mittlere Temperatur eines luftleeren Planeten der effektiven Emissionstemperatur nähert, falls die Rotation und die thermische Kapazität der Oberfläche explizit berücksichtigt werden. Es würde den Rahmen dieser Studie sprengen, den Trugschluss dieses Arguments mathematisch zu beweisen. Wir werden allerdings darauf hinweisen, dass eine Zunahme der mittleren Gleichgewichtstemperatur eines physikalischen Körpers immer die Zufuhr von Extra-Energie erfordert. Die Addition zusätzlicher axialer Rotation zu einem stationären Planeten mit einem Vakuum, bei dem es keine Reibung mit der äußeren Umgebung gibt, erzeugt nicht irgendeine Art zusätzlicher Wärme auf der Planetenoberfläche. Schnellere Rotation und/oder höhere thermische Trägheit des Bodens würde lediglich eine effizientere räumliche Verteilung der absorbierten Sonnenergie ermöglichen und würde damit die Gleichförmigkeit des resultierenden Temperaturfeldes über der gesamten Planetenoberfläche zunehmen lassen. Aber die mittlere Oberflächentemperatur könnte davon nicht beeinflusst werden. Folglich beschreibt Gleichung 6 korrekt (unter der Annahme gleichförmiger Albedo) die globale mittlere Temperatur von jedem luftleeren Planeten, ob er nun rotiert oder nicht.

Setzt man typische Werte für Erde und Mond in Gleichung 6 ein, d. h. So = 1362 W/m², αo = 0,11, and ϵ = 0,955, ergibt sich Tgb = 154,7 K. Diese Schätzung liegt um etwa 100 K unter der aus Gleichung 3 abgeleiteten konventionellen Schwarzkörpertemperatur und impliziert, dass der ATE der Erde (d. h. der GE) um ein Vielfaches größer ist als derzeit angenommen. Obwohl es mathematisch gerechtfertigt ist, erfordert ein  solches Ergebnis eine unabhängige empirische Verifikation wegen seiner tief greifenden Implikationen für die gegenwärtige GE-Theorie. Wie vorher schon gesagt, stellt der Mond einen idealen Proxy-PGB dar hinsichtlich seiner Position, seiner Albedo und der luftleeren Umgebung, mit der der thermische Effekt der irdischen Atmosphäre akkurat abgeschätzt werden kann. Also richten wir nun unser Augenmerk auf die jüngsten Temperaturbeobachtungen des Mondes.

  1. Das Lunar Radiometer Experiment von Diviner der NASA

Im Juni 2009 hat die NASA ihren Lunar Reconnaissance Orbiter (LRO) ins All geschossen, der (neben anderen Instrumenten) ein Radiometer mit der Bezeichnung Diviner an Bord hat. Die Aufgabe von Diviner ist es, die Temperatur der Mondoberfläche in bisher nicht erreichter Detaillierung zu kartographieren, und zwar durch Messungen in 7 IR-Kanälen, die eine Wellenlänge von 7,6 bis 400 μm umfassen. Diviner ist das erste zur Messung der gesamten Bandbreite der lunaren Oberflächentemperatur ausgelegte Instrument, von der wärmsten bis zur kältesten Stelle. Es schließt auch zwei solare Kanäle ein, die die Intensität der reflektierten Sonnenstrahlung messen, um auch eine Karte der lunaren kurzwelligen Albedo zu erstellen (weitere Details siehe die offizielle Website von Diviner, http://www.diviner.ucla.edu/).

Obwohl das Diviner-Experiment noch im Gange ist, wurde die Thermalkartierung der Mondoberfläche abgeschlossen, und die Daten sind online verfügbar. Aus zeitlichen Gründen hatten wir keine Gelegenheit, die Temperaturdaten von Diviner selbst für diese Studie zu analysieren. Stattdessen haben wir uns auf Informationen des Diviner Service Teams in wissenschaftlich begutachteten Veröffentlichungen und auf die Diviner website verlassen.

Die während der LRO-Übernahme gewonnenen Daten zeigen, dass der Mond eine der extremsten thermischen Umgebungen des Sonnensystems hat. Die Temperatur in niedrigen Breiten kann bis 117°C steigen, während sie in der langen Mondnacht bis -181°C zurückgehen kann; d. h. bis fast zum Siedepunkt flüssigen Sauerstoffs (Abbildung 2). Die per Fernerkundung gemessenen Temperaturwerte in der Äquatorregion korrelieren sehr gut mit den von der Apollo 15-Mission direkt gemessenen Temperaturdaten auf 26,1°N in den frühen siebziger Jahren (siehe Huang 2008). In den Polargebieten innerhalb dauerhaft beschatteter Gebiete in den großen Einschlagkratern hat Diviner sogar einige der kältesten jemals auf einem Himmelskörper registrierte Temperaturwerte gemessen, nämlich -238°C bis -248°C. Es ist wichtig zu beachten, dass Planetenwissenschaftler vor etwa 13 Jahren detaillierte Modelle der Oberflächentemperatur des Mondes und vom Merkur entwickelt haben (z. B. Vasavada et al. 1999). Diese Modelle wurden jetzt erfolgreich mit den Diviner-Messungen validiert (Paige et al. 2010b, Dr. M. Siegler an der UCLA, Personalkommunikation).

Was jedoch für unsere Diskussion am interessantesten ist, sind die mittleren Temperaturen in verschiedenen Breiten des Mondes, weil diese mit Temperaturen in ähnlichen Gebieten der Erde verglichen werden können, um die Größe von ATE zu evaluieren und unsere Berechnungen zu verifizieren. Abbildung 3 zeigt typische Tagesgänge der Temperatur auf der Mondoberfläche in vier geographischen Breiten (übernommen von Paige et al. 2010a).

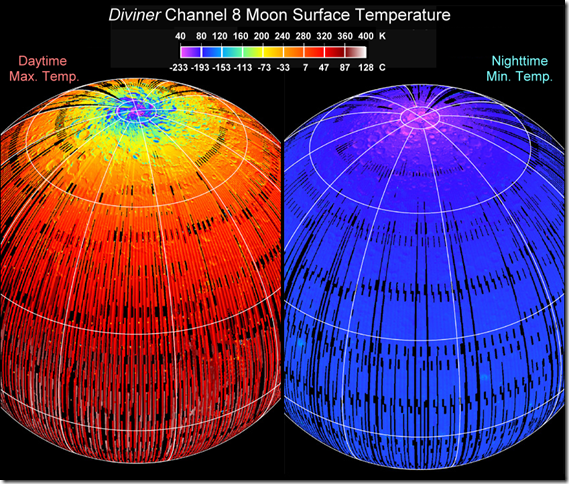
Abbildung 2 Thermalkarten der Mondoberfläche, basierend auf den Infrarotmessungen von Diviner, die die Temperaturfelder des täglichen Maximums und des nächtlichen Minimums zeigen (Quelle: Diviner Web Site)

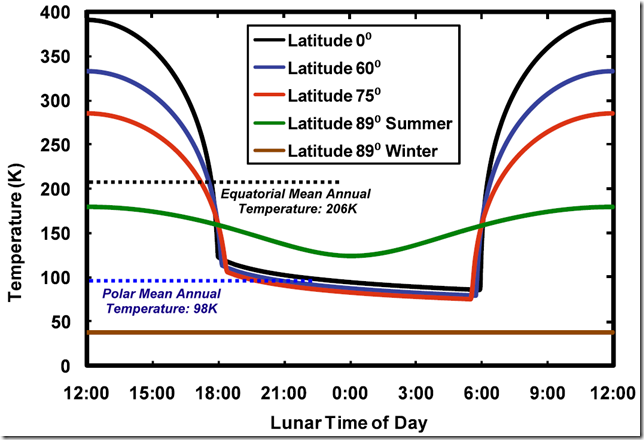
Abbildung 3: Typische Tagesgänge der Temperatur auf der Mondoberfläche in verschiedenen Breiten. Die lokale Zeit ist in Mondstunden dargestellt, die mit 1/24 eines Mondmonats korrespondieren. Auf einer Breite von 89° werden die Tagesgänge zur Sommer- bzw. Wintersonnenwende gezeigt (übernommen von Paige et al. 2010a). Gestrichelte Linien zeigen die Jahresmittel am Mondäquator und an den Polen.

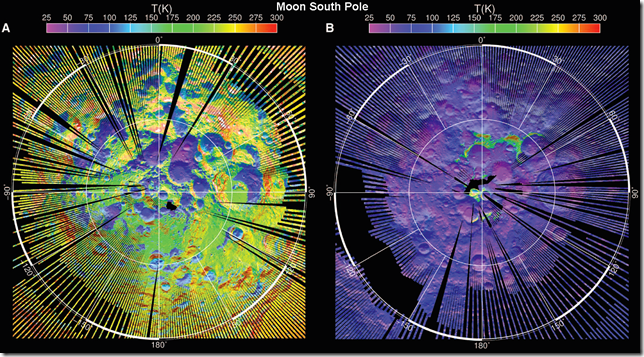
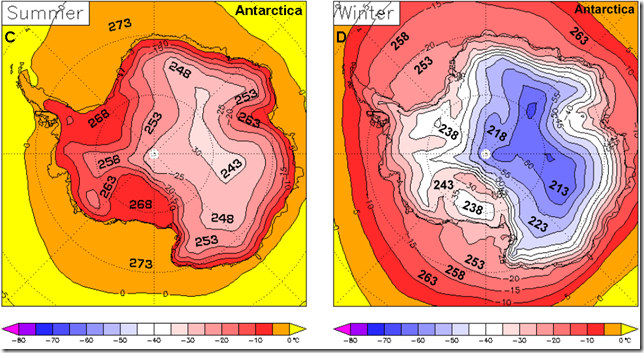
Abbildung 4: Die Temperaturkarten der Südpole von Mond und Erde: (A) Temperaturfeld tagsüber zur Zeit der stärksten Bestrahlung auf dem Mond; (B) Temperaturfeld nachts auf dem Mond; (C) mittlere Sommertemperatur in der Antarktis; (D) mittlere Wintertemperatur in der Antarktis. Die in Fettdruck gezeigten Zahlen in den Teilkarten (C) und (D) sind Temperaturwerte in °K. Die Teilkarten (A) und (B) wurden aus den Diviner Lunar Radiometer Experiment (Paige et al. 2010b) erzeugt. Die Verhältnisse in der Antarktis  stammen von Wikipedia (http://en.wikipedia.org/wiki/Antarctic_climate). Der Vergleich der Temperaturen zwischen dem Südpol des Mondes und der Antarktis legen für diesen Teil des Globus‘ eine thermische Auswirkung (enhancement) der Erdatmosphäre (d. h. ein „Treibhauseffekt“) von etwa 107 K im Sommer und 178 K im Winter nahe.

Die Abbildungen 4A und 4B zeigen die Temperaturverteilung am Südpol des Mondes während der stärksten Illumination am Tage und in der Nacht (Paige et al. 2010b). Da der Mond nur eine Achsenneigung von 1,54° und geringe Rotation aufweist, sind die mittleren täglichen Temperaturen ähnlich den monatlichen Temperaturmitteln. Diese Daten, zusammen mit den Informationen auf der Diviner Science webpage zeigen, dass die Mitteltemperatur an der Mondoberfläche von -175°C an den Polen bis -67°C am Äquator reicht. Das passt ziemlich gut zu unserer theoretischen Abschätzung von 154,7 K für die mittlere globale Temperatur nach Gleichung 6. In den kommenden Monaten wollen wir versuchen, die tatsächliche Mitteltemperatur des Mondes aus den Diviner-Messungen zu berechnen. Inzwischen zeigen die von den Planetenwissenschaftlern der NASA veröffentlichten Daten, dass der von der gegenwärtigen GE_Theorie übernommene Wert von 250 K bis 255 K als die mittlere Temperatur des Mondes weit übertrieben ist, da so hohe Temperaturmittel nicht an irgendeiner Breite des Mondes auftreten! Selbst am Mondäquator ist es 44 K bis 49 K kälter als nach dieser Schätzung. Dieser Wert ist deswegen ungenau, weil er das Ergebnis einer nicht zulässigen Applikation des Stefan-Boltzmann-Gesetzes auf eine Sphäre ist, wenn man von der falschen Albedo ausgeht (siehe die Diskussion in Abschnitt 2.1 oben)!

Genauso sind auch die auf der Website NASA Planetary Fact Sheet gezeigten mittleren globalen Temperaturen des Merkur (440 K) und Mars (210 K) nicht korrekt, da sie mit der gleichen Gleichung 3 berechnet wurden, die zum Ergebnis von 255 K für den Mond führte. Wir legen den Lesern nahe, diese Behauptung durch Anwendung von Gleichung 3 auf die Daten der Solarstrahlung (So) und der Albedo (bond albedo) (αo) zu verifizieren, die auf der Tatsachenseite (fact sheet) jedes Planeten gelistet sind, wobei ϵ = 1 gesetzt wird. Dies ist der Grund, warum wir in unserer Originalstudie den Wert von 248,2 K für den Merkur verwendet haben, da dieser Wert mit der theoretisch korrekten Gleichung 6 errechnet worden ist. Für den Mars haben wir Mittelwerte von Temperatur und Druck an der Oberfläche übernommen, die aus von dem Radio Science Team an der Stanford University erfragten regionalen Daten berechnet worden sind, und die aus Fernerkundungsdaten der Mars Global Surveyor-Raumsonde stammen. Ist es nicht merkwürdig, dass der Autor der Planetary Fact Sheet-Site der NASA, Dr. David R. Williams Gleichung 3 gewählt hat, um die mittlere Oberflächentemperatur des Mars‘ zu berechnen und die große Zahl direkter Messungen von hoher Qualität von dem Roten Planeten ignoriert hat!?

Also, welche reale Größenordnung hat der atmosphärische thermale Effekt (ATE) der Erde?

 

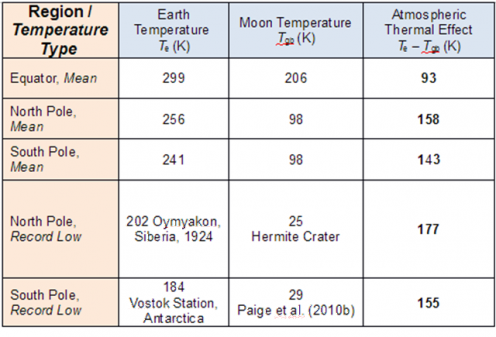
Tabelle 1: Geschätzter atmosphärischer Thermaleffekt für den Äquator und die Pole, basierend auf beobachteten Temperaturen auf der Erde und auf dem Mond unter Verwendung der Mondoberfläche als Proxy für den theoretischen Graukörper der Erde. Die Daten stammen von der Diviner’s Science webpage, Paige et al. (2010b), Abbildung 4 und von Wikipedia:Oymyakon.

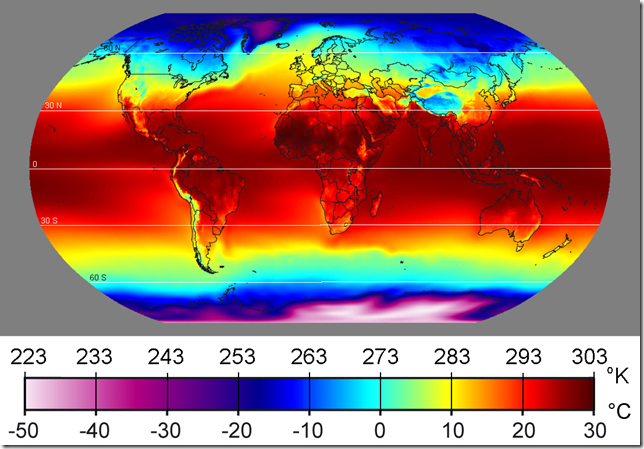
Abbildung 5: Die mittlere jährliche Temperatur der Erde nach Wikipedia (geographische Zonen: http://en.wikipedia.org/wiki/Geographical_zone).

Tabelle 1 zeigt beobachtete mittlere und rekordtiefe Temperaturen auf gleicher Breite von Erde und Mond. Der ATE ist berechnet als der Unterschied zwischen Erd- und Mondtemperaturen unter der Annahme, dass der Mond eine perfekte PGB-Proxy für die Erde ist. Abbildung 5 zeigt die globale Verteilung der mittleren Jahrestemperatur auf der Erde, um dem Leser zu helfen, einige der in Tabelle 1 gelisteten Werte visuell zu verifizieren. Die Ergebnisse dieses Vergleichs können wie folgt zusammengefasst werden:

Der atmosphärische thermale Effekt, derzeit als der natürliche Treibhauseffekt bekannt, variiert von 93 K am Äquator bis etwa 150 K an den Polen (letztere repräsentiert ein Mittel zwischen mittleren ATE-Werten am Nord- und Südpol, d. h. (158+143)/2 =150.5). Diese Spannbreite passt ziemlich gut zu unserer theoretischen Abschätzung von 133 K für den Gesamt-ATE der Erde, abgeleitet aus Gleichung 6, d. h. 287.6K – 154.7K = 132.9K.

Natürlich sind weitere Analysen der Diviner-Daten erforderlich, um eine präzisere Abschätzung der Mitteltemperatur an der Mondoberfläche abzuleiten und unsere Modellvorhersage zu verifizieren. Allerdings wird schon aus den veröffentlichten Messungen vom Mond deutlich, dass der weithin genannte Wert von 33 K für den mittleren ATE der Erde (GE) ausgesprochen in die Irre führt und falsch ist.

  1. Schlussfolgerung

Wir haben gezeigt, dass die Strahlungsintensität nach dem Stefan-Boltzmann-Gesetz fälschlich auf die Temperatur angewendet wurde (Gleichungen 1 und 3), um die mittleren Oberflächentemperaturen von Himmelskörpern einschließlich Mars, Merkur und Mond vorherzusagen. Infolge der Hölder’schen Ungleichheit zwischen nicht linearen Integralen liegt die mit Gleichung 3 ermittelte effektive Emissionstemperatur immer signifikant höher als die tatsächliche (arithmetische) Mitteltemperatur eines luftleeren Planeten. Dies macht die planetarische Emissionstemperatur Te aus Gleichung 3 physikalisch inkompatibel mit jeder gemessenen wirklichen Temperatur auf der Erdoberfläche oder in der Atmosphäre. Durch Verwendung einer geeigneten Integration des Stefan-Boltzmann-Gesetzes über eine Sphäre haben wir eine neue Formel abgeleitet (Gleichung 6), um die mittlere Temperatur eines planetarischen Graukörpers abzuschätzen (unter Mithilfe einiger Annahmen). Dann haben wir die nach dieser Formel berechnete Mitteltemperatur des Mondes verglichen mit aktuellen thermischen Beobachtungen durch das Diviner Radiometer Experiment der NASA. Die Ergebnisse zeigen, dass die Mitteltemperatur des Mondes wahrscheinlich sehr nahe dem Schätzwert nach unserer Gleichung 6 liegt. Gleichzeitig zeigen die Mondmessungen auch, dass die gegenwärtige Schätzung von 255 K für die lunare Oberflächentemperatur, die weit verbreitet in der Klimawissenschaft verwendet wird, unrealistisch hoch ist und außerdem demonstriert, wie ungeeignet Gleichung 3 für diesen Zweck ist. Das Hauptergebnis des Vergleichs Mond – Erde (unter der Annahme, dass der Mond eine perfekte Proxy für den Graukörper Erde ist) ist, dass der ATE der Erde, auch bekannt als der natürliche Treibhauseffekt, 3 bis 7 mal größer ist als gegenwärtig angenommen. Mit anderen Worten, die aktuelle GE-Theorie unterschätzt die tatsächliche Wärme durch die Atmosphäre um etwa 100 K! Ausgedrückt als relative thermische Größe (enhancement) wird der ATE zu NTE = 287.6/154.7 = 1.86.

Dieses Ergebnis wirft eine Frage auf: Wie kann eine so große thermische Wirkung (>80%) das Ergebnis einer Handvoll infrarot absorbierender Gase sein, die zusammen weniger als 0,5% der Gesamtatmosphäre ausmachen? Wir erinnern an unsere frühere Diskussion, dass Beobachtungen zufolge die Atmosphäre lediglich 157 bis 161 W/m² langwellige Strahlung von der Oberfläche absorbiert. Kann dieser geringe Fluss die Temperatur der unteren Atmosphäre um mehr als 100 K im Vergleich zu einer luftleeren Umgebung zunehmen lassen? Die offensichtliche Antwort lautet, dass der beobachtete Temperatursprung (temperature boost) nahe der Oberfläche nicht auf dieser atmosphärischen IR-Absorption beruhen kann! Folglich legen die Beweise nahe, dass die untere Troposphäre viel mehr kinetische Energie enthält, als der Strahlungsfluss allein bewirken kann. Die Thermodynamik der Atmosphäre wird durch die Gasgleichung festgelegt, die besagt, dass die kinetische Energie und die Temperatur eines Gasgemischs auch eine Funktion des Drucks ist (unter Anderem, versteht sich). Im Falle eines isobarischen Prozesses, bei dem der Druck konstant und unabhängig von der Temperatur ist, wie es auf der Erdoberfläche der Fall ist, ist es die physikalische Kraft des atmosphärischen Drucks allein, der in vollem Umfang die beobachtete thermische Wirkung (NTE) nahe der Oberfläche erklären kann. Aber dies ist Gegenstand unserer nächsten Studie… Bleiben Sie dran!

Ned Nikolov, Ph.D. und Karl Zeller, Ph.D.

  1. References

Inamdar, A.K. and V. Ramanathan (1997) On monitoring the atmospheric greenhouse effect from space. Tellus 49B, 216-230.

Houghton, J.T. (2009). Global Warming: The Complete Briefing (4th Edition). Cambridge University Press, 456 pp.

Huang, S. (2008). Surface temperatures at the nearside of the Moon as a record of the radiation budget of Earth’s climate system. Advances in Space Research 41:1853–1860 (http://www.geo.lsa.umich.edu/~shaopeng/Huang07ASR.pdf)

Kuptsov, L. P. (2001) Hölder inequality. In: Encyclopedia of Mathematics, Hazewinkel and Michiel, Springer, ISBN 978-1556080104.

Lin, B., P. W. Stackhouse Jr., P. Minnis, B. A. Wielicki, Y. Hu, W. Sun, Tai-Fang Fan, and L. M. Hinkelman (2008). Assessment of global annual atmospheric energy balance from satellite observations. J. Geoph. Res. Vol. 113, p. D16114.

Paige, D.A., Foote, M.C., Greenhagen, B.T., Schofield, J.T., Calcutt, S., Vasavada, A.R., Preston, D.J., Taylor, F.W., Allen, C.C., Snook, K.J., Jakosky, B.M., Murray, B.C., Soderblom, L.A., Jau, B., Loring, S., Bulharowski J., Bowles, N.E., Thomas, I.R., Sullivan, M.T., Avis, C., De Jong, E.M., Hartford, W., McCleese, D.J. (2010a). The Lunar Reconnaissance Orbiter Diviner Lunar Radiometer Experiment. Space Science Reviews, Vol 150, Num 1-4, p125-16 (http://www.diviner.ucla.edu/docs/fulltext.pdf)

Paige, D.A., Siegler, M.A., Zhang, J.A., Hayne, P.O., Foote, E.J., Bennett, K.A., Vasavada, A.R., Greenhagen, B.T, Schofield, J.T., McCleese, D.J., Foote, M.C., De Jong, E.M., Bills, B.G., Hartford, W., Murray, B.C., Allen, C.C., Snook, K.J., Soderblom, L.A., Calcutt, S., Taylor, F.W., Bowles, N.E., Bandfield, J.L., Elphic, R.C., Ghent, R.R., Glotch, T.D., Wyatt, M.B., Lucey, P.G. (2010b). Diviner Lunar Radiometer Observations of Cold Traps in the Moon’s South Polar Region. Science, Vol 330, p479-482. (http://www.diviner.ucla.edu/docs/paige_2010.pdf)

Ramanathan, V. and A. Inamdar (2006). The Radiative Forcing due to Clouds and Water Vapor. In: Frontiers of Climate Modeling, J. T. Kiehl and V. Ramanthan, Editors, (Cambridge University Press 2006), pp. 119-151.

Smith, A. 2008. Proof of the atmospheric greenhouse effect. Atmos. Oceanic Phys. arXiv:0802.4324v1 [physics.ao-ph] (http://arxiv.org/PS_cache/arxiv/pdf/0802/0802.4324v1.pdf ).

Stephens, G.L., A. Slingo, and M. Webb (1993) On measuring the greenhouse effect of Earth. NATO ASI Series, Vol. 19, 395-417.

Trenberth, K.E., J.T. Fasullo, and J. Kiehl (2009). Earth’s global energy budget. BAMS, March:311-323

Vasavada, A. R., D. A. Paige and S. E. Wood (1999). Near-surface temperatures on Mercury and the Moon and the stability of polar ice deposits. Icarus 141:179–193 (http://www.gps.caltech.edu/classes/ge151/references/vasavada_et_al_1999.pdf)

Link: http://wattsupwiththat.com/2012/01/22/unified-theory-of-climate-reply-to-comments/#more-55210

Übersetzt von Chris Frey für EIKE

image_pdfBeitrag als PDF speichernimage_printBeitrag drucken