Wir müssen einem ausführlichen Zitieren widerstehen, außer der Bemerkung, dass Keenan die Aufmerksamkeit des Leitautors dieser Studie Richard Muller selbst errungen hat, vor allem wegen eines Disputs darüber, was das einer Analyse vorausgehende Glätten einer Zeitreihe für deren Zuverlässigkeit bedeutet (das Glätten lässt sie übermäßig steigen). Muller sagt, dass es „mit Sicherheit Statistiker gibt, die dieser Art der Annäherung vehement widersprechen, aber es gab auch führende Statistiker, die dem Verfahren zugestimmt haben“.
Vehement dagegen bin auch ich! Die Gründe hierfür werden von Keenan und mir in den Links dargestellt, die Keenan in seinem Beitrag (hier, demnächst auf Deutsch bei EIKE) erwähnt hat. Außer dass ich Keenans Kritik zustimme – und diese ist umfangreich und fundamental – sage ich hier nichts weiter dazu. Stattdessen präsentiere ich meinen eigenen Kommentar zu der Studie „Berkeley Earth emperature averaging process.” Dieser Kommentar ist kein Duplikat von Keenans Kritik. Ich strebe keine Einfachheit oder erschöpfende Tiefe an.
Meine Kritik1
Ich stimme Keenan zu und sage, dass die Unsicherheitsbreite viel zu eng ist, während der generelle Punkt möglicherweise grob im Ungefähren liegt, mehr oder weniger, plus oder minus.
Die Autoren benutzen die Funktion
T(x,t) = θ(t) + C(x) + W(x,t).
Dabei ist x der Vektor der Temperaturen an Orten in der Fläche, t die Zeit, &theta() eine Trendfunktion, C() das räumliche Klima [the spatial climate], (integriert über die Erdoberfläche zu 0) und W() die Abweichung [the departure] von C() (integriert zu 0 über die Oberfläche oder die Zeit). Sie wird nur auf Landstationen angewendet. Nicht das gesamte Land, aber das meiste davon. Das Modell wird probabilistisch, wenn man betrachtet, wie eine individuelle Messung d(t) von einem Trend θ(), W(), einer „Messbasis“ plus einem „Fehler“ abhängt. Damit meinen sie nicht Messfehler, sondern die Restgröße des Standardmodells. Eigentliche Messfehler werden in diesem Teil des Modells nicht berücksichtigt.
Das Modell berücksichtigt eine räumliche Korrelation (wird als Nächstes beschrieben), ignoriert aber die Korrelation mit der Zeit. Es berücksichtigt die Höhe über NN, aber keine anderen geographischen Eigenheiten. Hinsichtlich des Zeitaspektes ist es ein einzelnes naives Modell. Die Korrelation mit der Zeit ist im wirklichen Leben wichtig und kann nicht ignoriert werden; daher wissen wir jetzt schon, dass die Ergebnisse des BEST-Modells zu sicher sein dürften. Das heißt, der Effekt, die Korrelation mit der Zeit zu ignorieren, erzeugt eine zu enge Bandbreite der Ungewissheiten. Wie sehr zu eng hängt von der (räumlichen) Natur der Zeitkorrelation ab. Je stärker diese in Wirklichkeit ist, umso mehr geht das Modell in die Irre.
Das Kriging-Verfahren (ein Standardverfahren, welches mit seinem eigenen Satz Standardkritiken kommt und von dem ich vermute, dass es dem Leser bekannt ist) wird benutzt, um nicht beobachtete räumliche Orte zu modellieren. Seine Korrelationsfunktion ist ein Abstandspolynom der 4. Ordnung (Gleichung 14). Vierte Ordnung, ja. Das stinkt nach einer handfesten Jagd, um dieses merkwürdige Wesen zu entdecken. Seine mittlere Passform zur Masse der blauen Punkte (Abb. 2) erscheint gut genug. Aber man höre auf, diese Punkte zu betrachten. Die Ungewissheit um die Passform ist gewaltig. Update, Korrektur: Ich meinte exponentiell eines Polynoms 4. Ordnung. Die übrige Kritik bleibt bestehen.
Das ist wichtig, weil die Autoren eine feste Korrelationsfunktion mit bestimmten Schätzungen verwendet haben. Sie sagen (S. 12), dass „weitere Feinheiten der Korrelationsfunktion wahrscheinlich Gegenstand zukünftiger Forschungen sind“. Das Problem ist, dass ihre über-sichere Schätzung dazu führt, dass die Gewissheit der finalen Modellergebnisse überschätzt wird. Keine Baysenianischen Techniken wurden während der Erzeugung dieses Modells verletzt, aber es wäre besser gewesen, wenn dies doch der Fall gewesen wäre.² Die Ungewissheit in dieser Korrelation muss absolut berücksichtigt werden. Da die Masse der blauen Punkte (Abb. 2) so enorm weit verteilt ist, ist die Ungewissheit sicherlich nicht insignifikant. Halten wir hier an und verstehen: Von dieser Korrelationsfunktion wurde angenommen, dass sie überall die gleiche ist, an jedem Punkt der Erdoberfläche, eine Hypothese, die mit Sicherheit falsch ist.
Update: Korrektur: Ich möchte diese letzte Feststellung als eine hauptsächlichen Kritikpunkt verstanden wissen. Wenn Sie eine Mine haben, in der an verschiedenen Stellen Mineralien gefunden werden und Sie deren Konzentration an Stellen schätzen möchten, an denen Sie bisher nicht gesucht haben, die aber innerhalb der Grenzen der Stellen liegen, die Sie untersucht haben, ist das Kriging-Verfahren das Ding. Ihre Mine ist wahrscheinlich irgendwie homogen. Die Landoberfläche der Erde ist nicht homogen. Zumindest ist sie durch riesige wassergefüllte Lücken unterbrochen, durch Berge und Wüsten und so weiter. Die gleiche Kriging-Funktion überall anzuwenden ist zu viel der Vereinfachung (was zu einer Über-Sicherheit führt).
Bezüglich der Messfehler (S. 15) wiederholen die Autoren die allgemeine falsche Auffassung, „dass die am breitesten diskutierte Auswirkung auf das Mikroklima das Potential für ‚städtische Wärmeinseln’ ist, was fälschlicherweise zu große Temperaturtrends an Stellen in Regionen führt, in denen eine städtische Entwicklung stattgefunden hat.“ Das ist keine reine Statistik, sondern schlechte Physik. Geht man davon aus, dass die Ausrüstung an den Stationen ordnungsgemäß funktioniert, sind diese Trends nicht „fälschlich“. Sie deuten auf die aktuelle ermittelte Temperatur hin. Als solche sollten diese Temperaturen nicht „korrigiert“ werden. Man schaue sich zur Erklärung diese Reihe an.
Um einen Aspekt eines geschätzten Messfehlers zu berücksichtigen, entwickeln die Autoren ein Verfahren, dem sie einen großen Namen geben: das „Skalpell“.
Unsere Methode besteht aus zwei Komponenten: 1) Aufteilung der Zeitreihe in unabhängige Fragmente zu den Zeitpunkten, wo es Beweise für eine abrupte Diskontinuität gibt und 2) die Wichtungen innerhalb der Anpassungsgleichungen zu justieren, um Unterschiede der Verlässlichkeit zu berücksichtigen. Der erste Schritt, die Aufzeichnungen zu Zeitpunkten offensichtlicher Diskontinuitäten zu unterbrechen, ist eine natürliche Erweiterung unserer Anpassungsprozedur, die die relativen Abstände zwischen Stationen bestimmt, eingerahmt von &bcirc [?] als eigentlichem Teil unserer Analyse.
Es ist unklar, inwieweit sich die Unsicherheiten in diesem Prozess durch die Analyse ziehen (gar nicht, so weit ich das sagen kann). Aber der Schritt zum Auseinanderbrechen ist weniger kontrovers als die Bewertungstechnik für „Ausreißer“. Ein Austauschfehler zum Beispiel bedeutet falsche Daten. Die Umkehrung des Vorzeichens eines Temperaturwertes bedeutet falsche Daten. Sehr große oder kleine Beobachtungen in den Daten können falsche Daten bedeuten oder auch nicht. Es gibt eine riesige Zahl von Aufzeichnungen, die ohne substantielle Kosten nicht alle von Hand untersucht werden können. Ein Prozess zur Abschätzung, ob eine Aufzeichnung falsch ist, ist wünschenswert: die verdächtig erscheinenden Punkte können von Hand gecheckt werden. Natürlich ist kein Verfahren perfekt, vor allem, wenn dieser Prozess mit historischen Temperaturmessungen durchgeführt wird.
Update Eine Veränderung des Stationsortes bringt keinen „Bias“ in die Aufzeichnungen dieser Station. Es wird daraus eine neue Station! Siehe auch die Reihen zur Homogenisierung der Temperatur hier, um hierzu mehr zu erfahren. Die Autoren haben ein paar Checks tatsächlich durchgeführt, z. B. haben sie wirklich merkwürdige Werte (alle Nullen usw.) entfernt, aber diese Säuberung scheint minimal. Stattdessen haben sie die Temperatur modelliert (wie oben) und die Beobachtung mit dem Modell verglichen. Jene Beobachtungen, die große Abweichungen vom Modell erkennen lassen, wurden herab gestuft und das Modell dann noch einmal gerechnet. Das Potential des Schummelns hier ist offensichtlich und auch der Hauptgrund für Verdächtigungen des Begriffes „Ausreißer“. Wenn die Daten nicht zum Modell passen, wirf sie raus! Am Ende bleiben nur die passenden Daten, welche – muss ich das wirklich sagen? – nicht die Gültigkeit des Modells beweisen. Egal wie, diese Prozedur wird die Unsicherheitsgrenzen des Modells verkleinern. Die Autoren behaupten, dass „erwartet“ worden ist, dass dieser Prozess etwa 1,25 bis 2,9% der Daten beeinflussen wird.
Der nächste Schritt zur „Korrektur” der Daten ist noch verdächtiger. Sie sagen: „In diesem Falle bewerten wir die generelle ‚Verlässigkeit’ der Aufzeichnung, indem wir die mittlere Übereinstimmung jeder Aufzeichnung mit dem erwarteten Feld &Tcirc;(&xtilde; , t) an der gleichen Stelle messen“. Zumindest die Verlässlichkeit wird mit beängstigenden Quoten benutzt. Und wieder hat dies die direkte Auswirkung, dass die aktuellen Beobachtungen in die Richtung des Modells gezogen werden, was die Ergebnisse zu sicher macht.
Zeigen die Ergebnisse auf den Seiten 24 und 25 alle aktuellen Änderungen? Das ist unklar. Liebe Autoren: Welcher Prozentsatz der Daten war betroffen von Entfernung von Rohdaten, Skalpell, das Herabstufen von Ausreißern und dessen Verlässlichkeit? 5%, 10% oder mehr? Und für welche Zeiträume waren diese Prozesse vorherrschend?
In Abschnitt 9, statistische Unsicherheit, bin ich ratlos. Sie nehmen jede Station und teilen sie wahllos in eine von 5 Gruppen ein, n = 1, 2, …, 5, und sagen: „ Dies führt zu einem neuen Satz von Temperaturzeitreihen hat-θn(tj)…. Da jede dieser neuen zeitreihen aus einem vollständig unabhängigen Stationsnetz erzeugt worden ist, können wir zu Recht deren Ergebnisse als statistisch unabhängig behandeln.“ Ich habe keine Ahnung, was das bedeutet. Die fünf Reihen sind mit Sicherheit nicht unabhängig im statistischen Sinne (weder räumlich noch zeitlich noch als Fallzahlen).
Die Prozedur versucht, die Unsicherheit der Schätzung abzuschätzen mit hat-θn(tj)— d. h. den Parameter und nicht die aktuelle Temperatur. Das behandeln der Fälle als unabhängig führt dazu, diese Unsicherheit zu unterschätzen. Aber schieben wir das alles mal beiseite und wenden uns dem zu, was wirklich zählt, die Unsicherheit in den Endergebnissen des Modells.
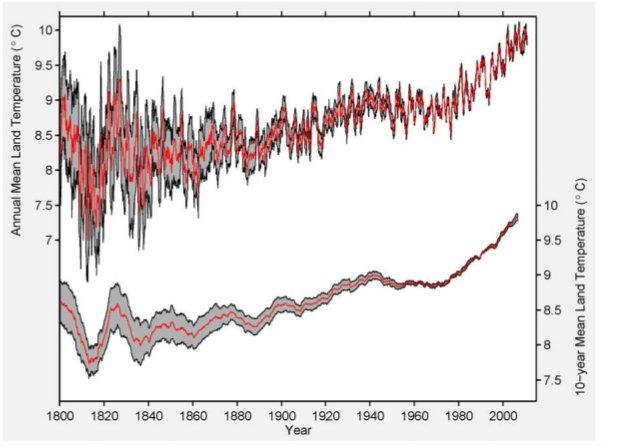
Abbildung 4b ist etwas irreführend – gut, dass es Abbildung 4a gibt – in der, sagen wir, im Jahre 1950 85% der Erdoberfläche nicht mit Thermometern bestückt waren. Dies ist eine Abdeckung in der Größenordnung einer Modellierung, nicht einer physikalischen Verteilung. Dies wird durch Abbildung 4a bewiesen, die zeigt, dass die physische Abdeckung der Räume abgenommen hat. Aber lassen wir das beiseite. Abbildung 5 ist der Schlüssel.
Dies ist nicht der Plot einer aktuellen Temperatur und es ist nicht ein Plot der Ungewissheit der aktuellen Temperatur. Es ist stattdessen ein Plot des Parameters hat-θn(tj) und der Unsicherheiten, die aus den oben beschriebenen Methoden herrühren. User von Statistiken haben die schlechte, um nicht zu sagen berüchtigte Angewohnheit, über Parameter zu sprechen, als ob sie über aktuelle Beobachtungsergebnisse sprechen. Die Sicherheit über den Wert eines Parameters ist aber nicht übertragbar auf die Sicherheit der Beobachtung. Lesen Sie diesen letzten Satz bitte noch einmal!
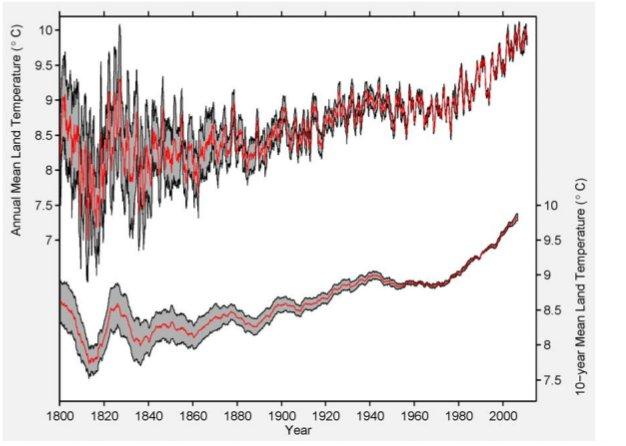
Abbildung 5: Ergebnis der Berkelely-Mittelungs-Methode nach Anwendung auf die monatlichen Daten des GHCN. Der obere Plot zeigt ein 12-Monats-Mittel nur von Landstationen und einer damit verbundenen Unsicherheit von 95% durch statistische und räumliche Faktoren. Der untere Plot zeigt das korrespondierende 10-Jahres-Mittel nur über Land und einer Unsicherheit von 95%. Dieser Plot korrespondiert mit dem Parameter ![]() in Gleichung 5. Unsere Plot-Konvention ist es, jeden Wert in die Mitte des Zeitintervalls zu legen, das er repräsentiert. Zum Beispiel wird das Mittel 1991 bis 2000 im dekadischen Plot bei 1995,5 gezeigt.
in Gleichung 5. Unsere Plot-Konvention ist es, jeden Wert in die Mitte des Zeitintervalls zu legen, das er repräsentiert. Zum Beispiel wird das Mittel 1991 bis 2000 im dekadischen Plot bei 1995,5 gezeigt.
Von Seite 26:
Wenn man die hier beschriebenen Verfahren anwendet, finden wir, dass die mittlere Landtemperatur von Januar 1950 bis Dezember 1959 8,849 +/- 0,041°C betragen hatte, und dass die Mitteltemperatur der jüngsten Dekade (Januar 2000 bis Dezember 2009) bei 9,760 +/- 0,096°C gelegen hatte. Die Trendlinie für das 20. Jahrhundert wird berechnet zu 0,733 +/- 0,096°C pro Jahrhundert. Dies liegt deutlich unter den 2,76 +/- 0,16°C pro Jahrhundert der globalen Erwärmungsrate über Land, die wir von Januar 1970 bis August 2011 beobachtet haben. (Alle hier und weiter unten erwähnten Unsicherheiten sind 95%-Intervalle für die kombinierte statistische und räumliche Unsicherheit). {Um HTML-Diskrepanzen zu vermeiden, habe ich das mathematische Symbol „+/-“ verwendet, so dass es lesbar bleibt}.
Man beachte, dass sie das Wort „Temperatur“ brauchen bei „wir finden, dass die mittlere Temperatur über Land…“ usw., obwohl sie hätten schreiben müssen „Modellparameter“. Von 1950 bis 1959 schätzen sie die Parameter „8,849 +/- 0,041°C“. Frage an die Autoren: Seid ihr sicher, dass ihr nicht 8,848 +/- 0,033°C gemeint habt? Wo liegt der Sinn in einer solchen dummen Überpräzision? Egal, von 2000 bis 2009 schätzen sie den Parameter als 9,760 +/- 0,041°C, ein Anstieg um 0,911 +/- 0,042°C“. Update: Diese Kritik wird den meisten unbekannt sein, selbst vielen Statistikern. Es ist eine Hauptquelle für Fehler (in der Interpretation); halten Sie inne, um das zu erkennen. Siehe dieses Beispiel hier!
Akzeptieren wir das für den Augenblick. Die Frage lautet dann, warum sie die fünfziger Jahre als Vergleich wählten und nicht die vierziger Jahre, als es wärmer war? Mögliche Antwort: weil der Vergleich mit den fünfziger Jahren die Änderung unterstreicht. Aber wir wollen hier nicht in die Politik abgleiten, also nichts für ungut, und ignorieren Sie auch die Hyperpräzision. Konzentrieren wir uns stattdessen auf die „+/- 0,033°C“, von dem wir inzwischen wissen, dass es nicht die Unsicherheit der aktuellen Temperaturmessung ist, sondern diejenige eines Modellparameters.
Falls alle Quellen der Über-Gewissheit, die ich (und Keenan) erwähnt haben, berücksichtigt werden, denke ich, dass diese Grenze der Unsicherheit mindestens doppelt so groß wäre. Dies würde eine Unsicherheit von mindestens +/- 0,66°C zur Folge haben, na und? Das ist immer noch wenig im Vergleich zu den 8,849°C (Intervall 8,783 – 8,915°C; und für 2000 bis 2009 beträgt es 9,678 – 9,842°C). Immer noch ein Sprung.
Aber wenn wir hierzu die Unsicherheit im Parameter addieren, so dass unsere Unsicherheitsgrenze bei der aktuellen Temperatur liegt, müssen wir erneut die Grenzen mit 5 bis 7³ multiplizieren. Dies bewirkt, dass die Grenze von 1950 bis 1959 bei mindestens 0,132, die für 2000 bis 2010 bei mindestens 0,410 beträgt. Die Intervalle betragen dann 8,519 – 9,179°C für die fünfziger Jahre und 9,350 – 10,170 jetzt. Immer noch eine Änderung, aber eine, die jetzt wesentlich weniger unsicher ist.
Da die Änderung immer noch nicht signifikant ist, könnte man sagen „na und?” Ich bin froh über diese Frage: man schaue auf die Grenzen der Jahre vor 1940, vor allem diejenigen vor 1900. Die Anwendung der oben erläuterten Änderungen verschieben diese Grenzen bis jenseits von gut und böse, was bedeutet, dass wir nicht mit irgendeinem Grad an Sicherheit sagen können, ob es jetzt wärmer oder kälter ist als vor 1940 und besonders vor 1900. Lesen Sie diesen Satz ebenfalls noch einmal bitte!
Und selbst wenn Sie bockig sein wollen und auf die Perfektion des Modells bestehen und Sie glauben, dass die Parameter real sind, decken schon viele der Unsicherheitsgrenzen vor 1880 gegenwärtige Temperaturen ab. Die Jahre um 1830 sind schon nicht „statistisch unterschiedlich“ zum Jahr 2008.
Einfacher ist es, hierzu Abbildung 9 zu betrachten, in welcher versucht wird, den Grad der Unsicherheit mit der Zeit zu zeigen. Alle Zahlen in diesem Plot sollten mit mindestens 5 bis 10 multipliziert werden. Und selbst danach haben wir immer noch nicht die größte Quelle der Unsicherheit berücksichtigt: das Modell selbst.
Statistiker sowie jene, die Statistiken verwenden, sprechen selten oder niemals von der Modellunsicherheit (das gleiche gilt für Klimatologen). Der Grund hierfür ist einfach: es gibt keine Kochrezepte, die automatische Messungen dieser Unsicherheit ergeben. Das kann auch nicht sein, weil der Wahrheitsgehalt eines Modells nur von außerhalb bewertet werden kann.
Und doch sind alle Ergebnisse abhängig vom Wahrheitsgehalt des Modells. Die Erfahrungen mit statistischen Modellen zeigen, dass sie oftmals zu sicher sind, vor allem, wenn sie komplex sind, wie es beim BEST-Modell der Fall ist (und welches annimmt, dass die Temperatur so sanft mit der geographischen Breite variiert). Nein, das kann ich nicht beweisen. Aber ich habe gute Gründe angegeben, warum man daran zweifeln sollte, dass das stimmt. Sie können auch weiterhin an die Gewissheit des Modells glauben, aber dies wäre nur ein weiteres Beispiel, dass Hoffnung über die Erfahrung triumphiert. Um wie viel, weiß ich nicht.
Update Weder in der BEST-Studie noch in meiner Kritik findet sich auch nur ein Wort dazu, warum sich die Temperaturen geändert haben. Niemand diskutiert nirgends, dass sie sich verändert haben. Siehe die Diskussion hier!
——————————————————————————————
1„Sagen Sie, Briggs, Sie sind immer dagegen. Sie sind doch so klug, warum führen Sie nicht Ihre eigene Analyse durch und enthüllen das alles?“ Gute Frage. Im Unterschied zu den Leuten beim BEST und anderen wie meinem Freund Gay habe ich keine Kontakte zu Big Green und auch keinen Sekretär, keine Juniorkollegen, keine Diplomanden, keine IT-Leute, Computerressourcen, Drucker, Kopierer, Büroutensilien Zugang zu einer Bibliothek, Zuwendungen für Reisen zu Konferenzen, Geld für Gebühren, Multimillionen Dollar Förderung, Multitausend Dollar Förderung, nicht einmal Multi Dollar Förderung. Alle meine Arbeit, die ich jemals im Bereich Klimatologie gemacht habe, war ehrenamtlich. Ich habe einfach keine Zeit und keine Ressourcen, um monatelange Anstrengungen zu unternehmen, die der Mühe wert sind.
²Die Autoren haben nur klassische Verfahren benutzt, einschließlich des Jackknife. Sie könnten, wenn sie dieser Philosophie folgen, die Ergebnisse durch erneutes Anbringen dieser Korrelationsfunktion urladen. *
[Diesen Satz habe ich inhaltlich nicht verstanden! A. d. Übers.]
³Dies ist, wie die Erfahrung zeigt, der Unterschied in vielen Modellen. Um den aktuellen Multiplikator zu ermitteln, müssten wir die ganze Arbeit noch einmal machen. Siehe hierzu Anmerkung 1!
Die Statistiken der BEST-Studie wurden mit Assistenz des bedeutenden (kein Sarkasmus) David Brillinger erstellt, obwohl er nicht als Ko-Autor in Erscheinung tritt. Charlotte Wickham war die Statistikerin und war Studentin bei Brillinger. „Charlotte Wickham ist Assistenzprofessorin im Department of Statistics an der Oregon State University. Sie legte 2011 ihre PhD-Prüfung in Statistik an der University of Berkeley ab”.
Weitere Veröffentlichungen des Autors William M. Briggs hier
Link zum Artikel (BEST), auf den sich diese Kritik bezieht: hier
Link zum Artikel von Keenan: hier
Übersetzt von Chris Frey für EIKE
Link zum Original: http://wmbriggs.com/blog/?p=4530
















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Die BEST- Studie
bewegt sich also auf dem Niveau des Hockeystick
Jackknife und Bootstrapping sind Resamplingmethoden in der Statistik und bedürfen als Fachworte keiner Übersetzung.