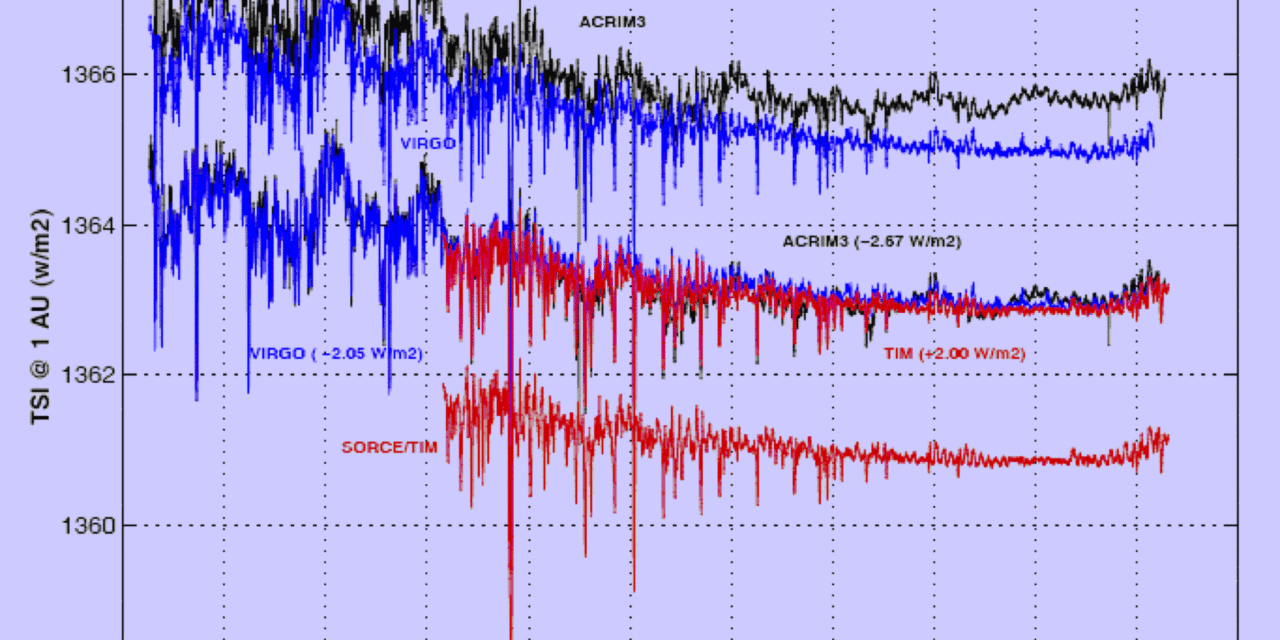
Dies impliziert, dass es ein Gleichgewicht gibt, was mit der Grundannahme eines optimalen Klimas des IPCC korrespondiert. Die totale solare Strahlungsintensität wird vom IPCC mit RFTSI = 1367W/m2 angegeben. Die folgende Graphik zeigt die Messungen von drei Satelliten: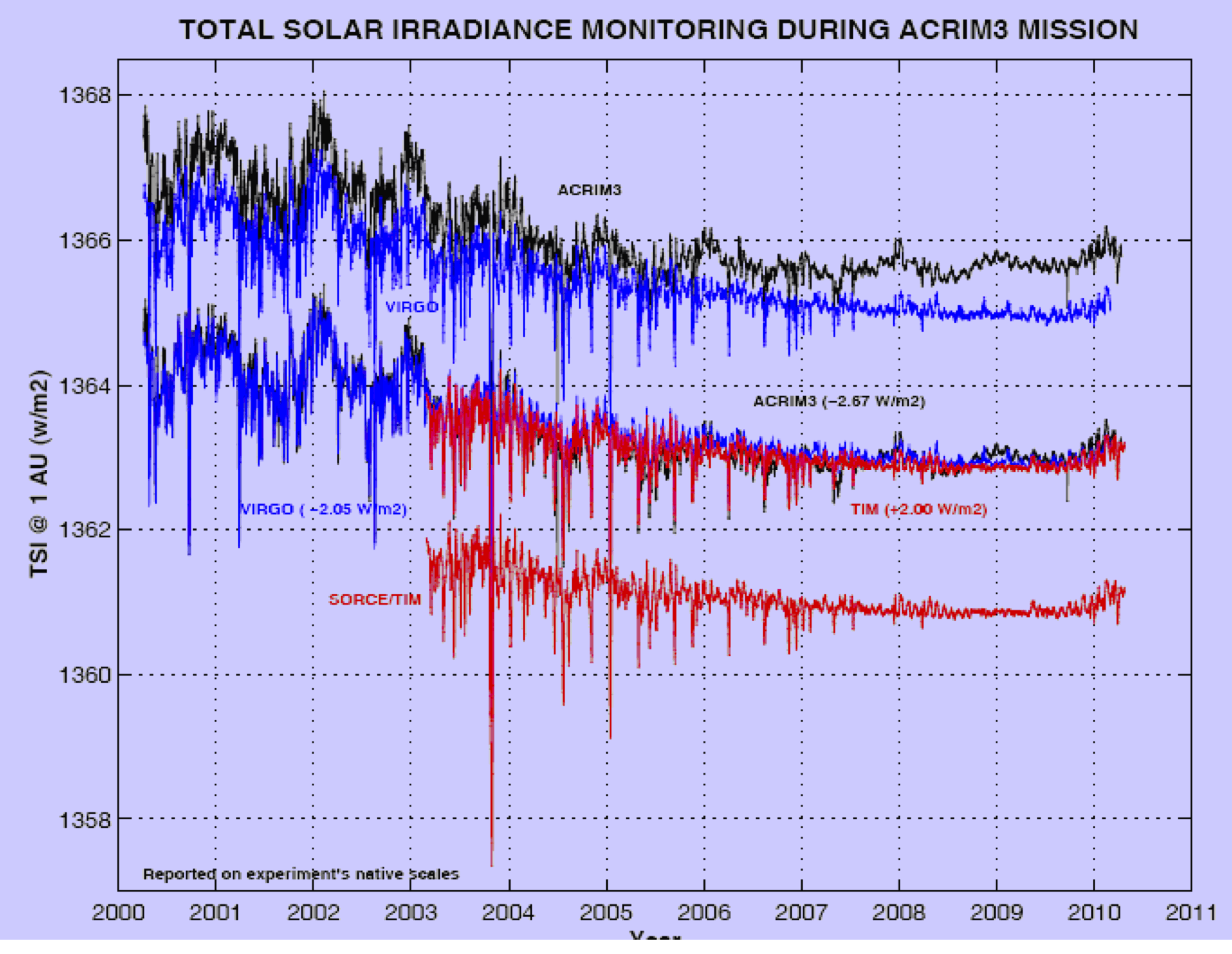 
Die Ursache für die 0.35% Differenz (?RFmeas = 4.8W/m2!) ist derzeit nicht verstanden.
Der IPCC sagt in seinem letzten Bericht:
“The differences in radiative forcing estimates between the present day and the start of the industrial era for solar irradiance changes and volcanoes are both very small compared to the differences in radiative forcing estimated to have resulted from human activities. As a result, in today’s atmosphere, the radiative forcing from human activities is much more important for current and future climate change than the estimated radiative forcing from changes in natural processes.” (Ch.2, p.137) Diese Behauptung werden wir näher betrachten.
Die Änderung der totalen solaren Strahlung seit 1750 wird vom IPCC abgeschätzt zu 0.12 (-0.06/ +0.18)W/m2 (Ch.2, Tab. 2.12). Dieser Wert liegt in der Größenordnung der relativen Änderung pro Dekade von Satellitenmessungen. ACRIM hat z.B. für die Zyklen 21-23 0.037% oder 0.5W/m2 gemessen. Der absolute Fehler liegt bei den Satelliten aber bei ± 3W/m2. Wie man allerdings ohne Satelliten in der Vergangenheit solch geringe Änderungen bestimmen konnte wird nicht erklärt. Zu einem völlig anderen Ergebnis kommen dagegen Solanki und Fligge (GRL 26 (1999) 2465). Ihre Rekonstruktion zeigt die nächste Graphik.
Sowohl die absoluten als auch die relativen Werte sind mehr als eine Größenordnung größer als die vom IPCC angegeben Werte.
Der durch das anthropogene CO2 verursachte Beitrag wird als RFCO2 = (1.66 ± 0,17) W/m2 bestimmt (Ch.2, Tab. 2.12). Im folgendem werden wir diesen Wert mit anderen Unsicherheiten vergleichen und damit seine Relevanz hinterfragen.
Kevin Trenberth, einer der führenden Autoren des IPCC, von dem der Satz „The fact is that we can’t account for the lack of warming at the moment and it is a travesty that we can’t.” stammt, hat einen neuen Artikel zum globalen Energiebudget publiziert (BAMS March 2009 311-323). Hier ist sein Flussdiagramm.
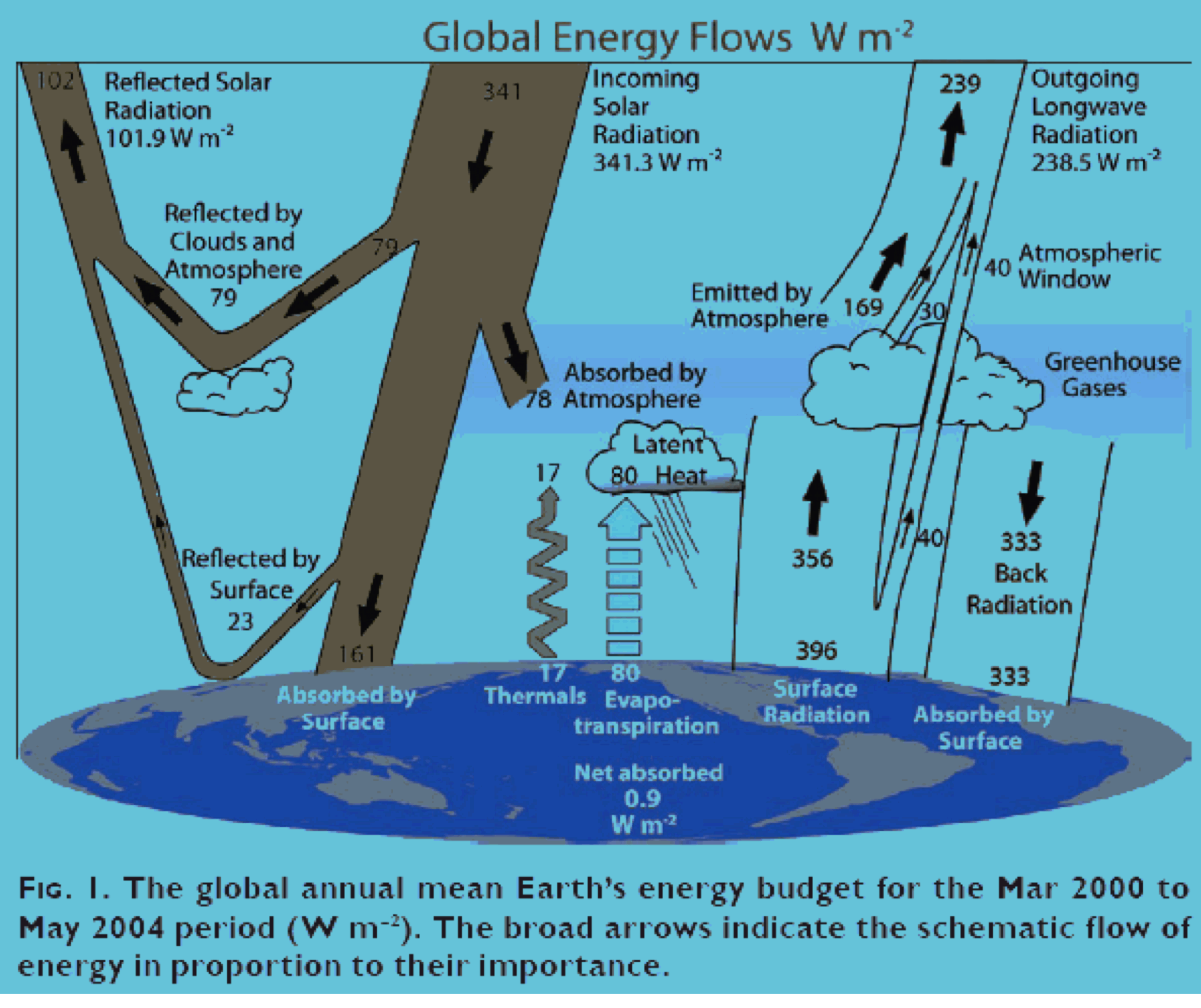
Die folgende Tabelle enthält die Unterschiede zu seiner früheren Publikation (J. Climate 10 (1997) 1771-1790).
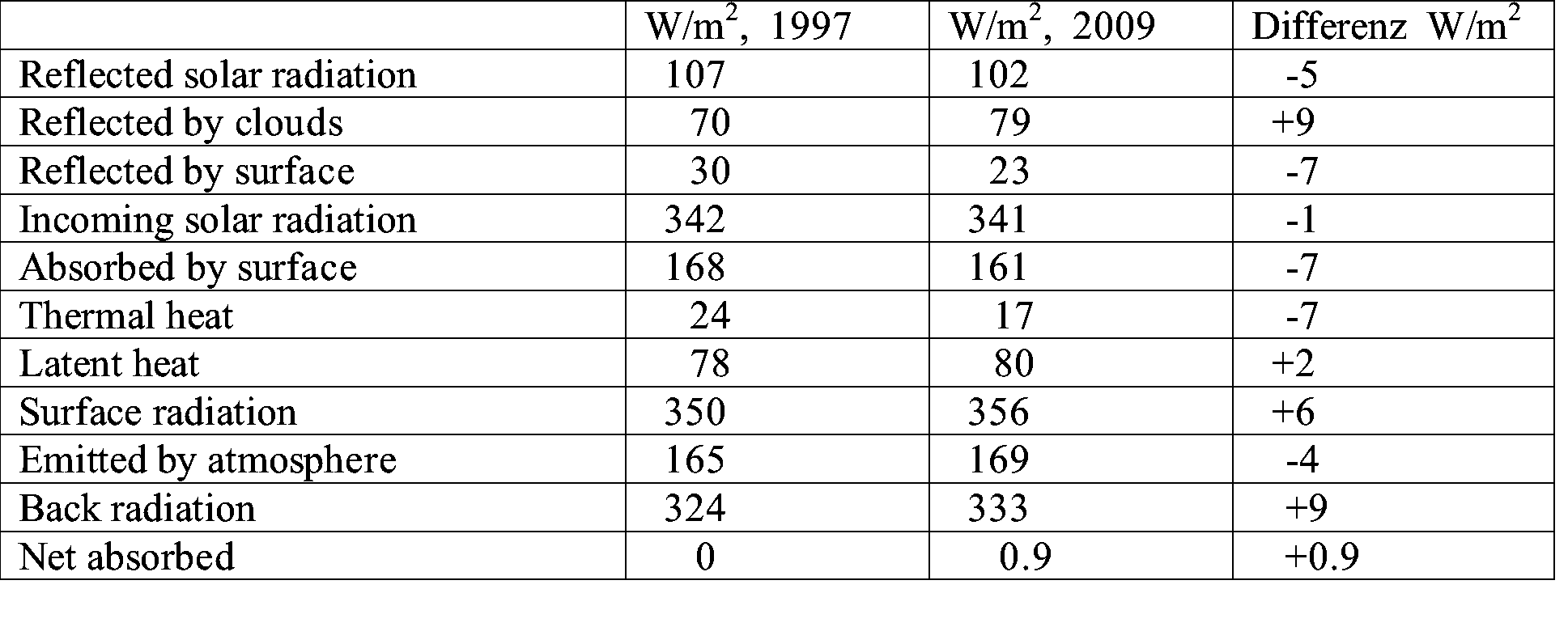
Das Problem besteht nicht darin, dass es Korrekturen bei den Werten gibt und dass viele Differenzen größer als die ominösen 1.66W/m2 sind, sondern in der Tatsache, dass diese Werte als Input in die Modellrechnungen eingehen. Selbst unter der unrealistischen Annahme, dass sich die Gewinne und Verluste gegenseitig kompensieren, bleibt eine Differenz von 5W/m2 (3-mal RFCO2) übrig (ohne Nettoabsorption, s. u.). Fehler wurden für die einzelnen Größen in obiger Tabelle noch nicht berücksichtigt. Bevor wir dazu kommen, soll erst noch eine andere Tabelle aus der Arbeit diskutiert werden.
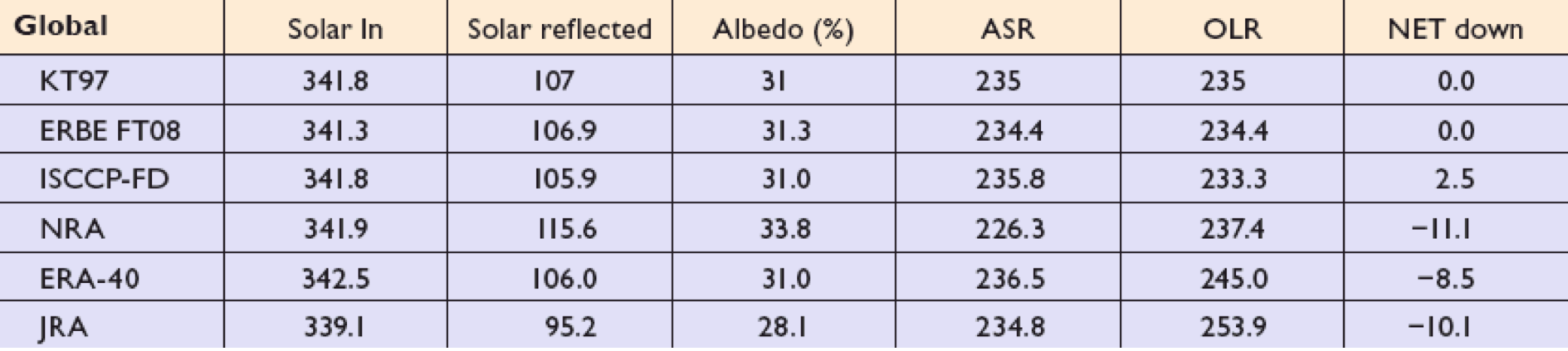
Kt97 steht für Trenberth, NRA, ERA und JRA für die amerikanische, europäische und japanische Klimaforschung und die restlichen zwei für Messungen. Bei der absorbierten Strahlung (ASR) beträgt die maximale Differenz 10.2W/m2 und bei der abgestrahlten Strahlung (OLR) 20.6W/m2. Wenn also der Unterschied bei der absorbierten Strahlung 6-mal größer als der anthropogene Beitrag ist, wie kann man dann mit Sicherheit dem letzteren einen Temperaturbeitrag zu ordnen. Obwohl die Autoren schreiben: „It is not possible to give very useful error bars to the estimates.“, geben sie an anderer Stelle einige Fehler an. Die Fehlerwerte beim Eintritt in die Atmosphäre werden zu ± 3% und die an der Oberfläche zu ? ± 10% abgeschätzt. Die 3 Prozent addieren noch einmal rund 10W/m2 zu den obigen 10.2W/m2 für die absorbierte Strahlung, was den anthropogenen Wert auf ein Zwölftel der Unsicherheit reduziert.
Verstehen kann man aber nicht, dass es über vier Jahre gemittelt eine Nettoabsorption geben soll. Wenn ein Körper mehr Energie absorbiert als er abgibt, dann muss seine Temperatur steigen und zwar so lange bis sich wieder ein Strahlungsgleichgewicht zwischen absorbierter und emittierter Energie einstellt. Aber vielleicht ist dies zu simpel gedacht.
Eine andere Diskrepanz findet man, wenn man sich die Emission betrachtet. Der IPCC verwendet für die Emission der Erde den Wert eins. Einen realistischeren Wert kann man aus der nächsten Graphik abschätzen (http://isccp.giss.nasa.gov/cgi-bin/browsesurft2).
Der Mittelwert ist ungefähr ?= 0.931 (0.70·92[Wasser] + 0.15·0.95 + 0.15·0.965 = 0.931). Für ? = 1 beträgt die abgestrahlte Intensität gemäß dem Stephan-Boltzmann Gesetz bei T = 288K I = 390.1W/m2. Nimmt man aber den realistischeren Mittelwert, ? = 0.931, so erhält man I = 363.2W/m2. Die Differenz ergibt sich zu 26.9W/m2, was 17-mal dem Wert für RFCO2 entspricht.
Die Behauptung des IPCC, dass der menschliche Einfluss viel bedeutender ist, als natürliche Änderungen, wird durch die Zahlen nicht unterstützt und muss als falsch eingestuft werden. Dies wird auch durch die letzte Graphik unterstützt, die eine klare Korrelation zwischen der totalen solaren Strahlung und den Sonnenflecken zeigt.
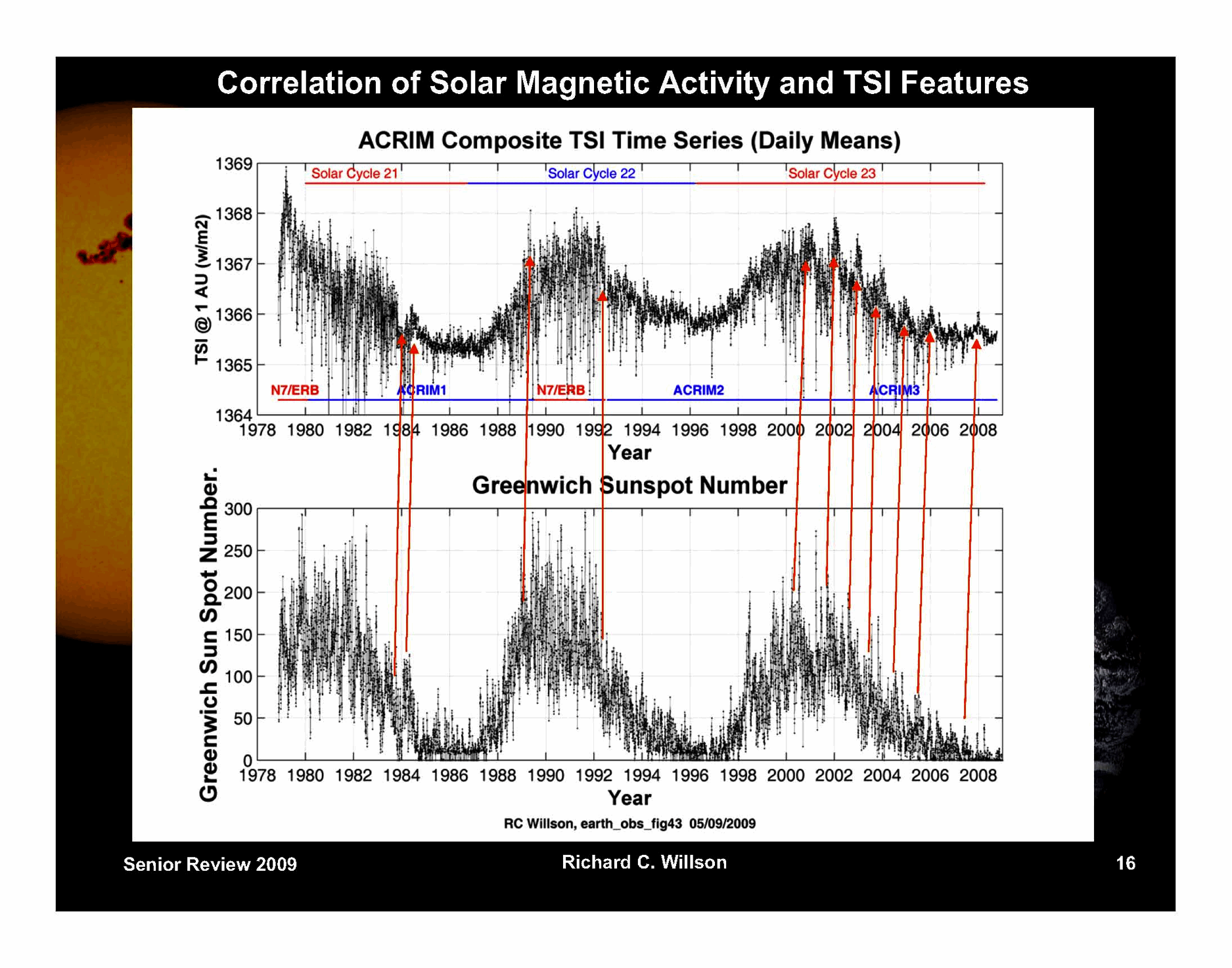
Folgerichtig kommen die Auswerter (http://www.acrim.com/) der Satellitenmessungen auch zu der folgenden Feststellung:
„The Earth’s weather and climate regime is determined by the total solar irradiance (TSI) and its interactions with the Earth’s atmosphere, oceans and landmasses. TSI proxies during the past 400 years and the records of surface temperature show that TSI variation has been the dominant forcing for climate change during the industrial era.”. (emphasis mine)
Dr. rer.nat. B. Hüttner (Diplom Physiker) für EIKE
Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Lieber Herr Fischer,
Ihre Definition wird vom IPCC nur für Wolken, das heißt für „cloud radiative forcing“ benutzt. Stattdessen definiert das IPCC die „radiative forcings“ immer gegen einen Referenzzustand 1750.
Im Grunde weicht das IPCC da von der Lehrbuchdefinition ab und definiert die „forcings“ als Differenzen. Das ist ein ähnliches Konzept wie das Verhältnis zwischen Reaktionswärmen und Bildungswärmen bei chemischen Reaktionen. Die Bildungswärmen sind gegen einen Referenzustand definiert und tabelliert. Die Summe über die Bildungswärmen ergibt für eine gegebene Reaktion die Reaktionswärme. Nur die Reaktionswärmen können im Experiment beobachtet werden.
Ihre Definition entspricht der Reaktionswärme, die IPCC Definition der Bildungswärmen.
Leider ist die Erde aber ein nichtlineares System, so dass die Summe der „radiative forcings“ nach der IPCC Definition nicht ohne weitere experimentelle Begründung linear gebildet werden darf. Insofern hat Herr Hüttner in #22 Recht, wenn das beobachtbare „radiatve forcing“ in ihrer Definition nur sehr ungenau bekannt ist und das System nichtlinear ist, dann ist die Zerlegung in Summanden nach der IPCC Definition experimentell nicht überprüfbar und willkürlich. Eine beliebige Kombination von Summanden erzeugt das gleiche Ergebnis. Um das tatsächliche „radiative forcing“ nach ihrer korrekten Definition in #21 aus den IPCC „difference radiative forcings“ zu berechnen müssen Wolkenbedeckung und andere Albedoänderungen seit 1750 als konstant angenommen werden oder für jedes Jahr bekannt sein.
Mit freundlichen Grüßen
Günter Heß
Mit freundlichen Grüßen
Günter Heß
Sehr geehrter Herr Kollege Fischer,
wenn man ein System mit einer Anzahl von Variablen hat von denen eine Variable eine kleine Störung aufweist, dann kann man eine kleine Änderung des Systems (Temperatur in unserem Fall) dieser Variablen nur dann eindeutig zuordnen, wenn alle anderen Variablen bekannt und konstant sind. Gibt es aber bei den anderen Variablen Fluktuationen, die sogar größer als die kleine Störung sind, dann ist es nicht mehr möglich zu sagen, dass eine Änderung des Systems durch die kleine Störung bewirkt wurde.
Vor einer weiteren Diskussion sollten Sie erst obige Aussage falsifizieren.
I agree, we disagree, Dr. Hüttner 😉
Vereinfacht formuliert beschreibt das radiative forcing (RF) die Differenz der ein- und ausgehenden Energieflüsse „top of atmosphere“ (TOA), also die Störung des Gleichgewichts. Diese Information genügt im Prinzip schon, um die Temperaturveränderung des Planeten zu beschreiben.
Wie die Störung nun zustandekommt bzw. was unterhalb von TOA, z.B. durch Rückstrahlung (meines Erachtens ein etwas unglücklicher Begriff) oder aus anderen Gründen, spielt dafür keine Rolle.
Die Zahlen der Tabelle beschreiben also diese „Nebensächlichkeit“. Anführungsstriche deshalb, weil Sie für die neue Gleichgewichtstemperatur von untergeordneter Bedeutung sind, sehr wichtig aber dann werden, wenn abgeschätzt werden soll, wann dieser neue Gleichgewichtszustand erreicht wird bzw. wie sich die Temperaturveränderung in der Atmosphäre bzw. am Boden verteilt.
MfG
sorry, aber den Fehler begehen Sie. Erstens, W/m2 sind Energie pro Fläche und Zeit und es ist egal, wie Sie die einzelnen Beiträge, forcing und was auch immer, benennen. Zweitens, die Theorie des Treibhauseffektes, wobei der Name irreführend ist, beruht darauf, dass ein Teil der abgestrahlten langwelligen Strahlung absorbiert und partiell zurückgestrahlt wird. Der anthropogene Beitrag sind die 1.67W/m2. Die Oberflächentemperatur wird durch die Summe der absorbierten Strahlung bestimmt. Also durch die von der Sonne kommende Intensität plus der natürlich rückgestrahlten (primär H2O) plus den 1.67W/m2. Wenn nun aber die Fehler bei der ASR und der OLR durch nicht exakt bekanntes Albedo und durch einen falschen Wert für die Emission von eins viel größer sind als die 1.67W/m2, dann könnte man den anthropogenen Beitrag auch negieren und trotzdem im Rahmen der Ungenauigkeiten die gleiche Temperaturverteilung, dies ist die Messgröße, in der Atmosphäre ausrechnen.
Sehr geehrter Dr. Hüttner,
„Soweit dürften wir einig sein. Der zweiten Tabelle können Sie aber entnehmen, dass es zwischen den einzelnen Modellen einen Unterschied von 20.6W/m2 gibt. Bei dieser Schwankung geht ein Beitrag von 1.67W/m2 einfach unter. Das gleiche Dilemma tritt bei der Emission auf.“
Auch hier begehen Sie denselben Fehler. Die Werte der zweiten Tabelle unterscheiden sich in ihren Angaben zur Albedo der Erde. Es ist sinnlos, die Differenz von Energieflüssen, beruhend auf verschiedenen Werten der Albedo, mit dam RF von CO2 zu vergleichen.
Nehmen Sie z.B. die japanischen Daten. Für diesen Ansatz mit der gewählten Albedo ist nun die Änderung der ausgehenden Strahlung entscheidend für die Temperatur. Verglichen mit der Situation vor ca. 50-100 Jahren ist das ungefähre Temperaturgleichgewicht durch Anstieg der CO2-Konzentrationen gestört worden, es kommt das CO2-forcing ins Spiel.
Dies gilt ebenso für jeden anderen Wert der zweiten Tabelle. Differenzwerte zwischen Modellannahmen mit dem RF der Treibhausgase zu vergleichen ist bestenfalls irreführend, aber wenig ergiebig.
Mir ist durchaus bewusst, dass das Konzept des radiative forcings eine Vereinfachung darstellt, die auch ihre Schwächen besitzt. Nur: Ihre Kritik zielt ins Leere.
MfG
Sehr geehrter Herr Kollege Fischer,
der beobachtete Temperaturanstieg von rund 0.8°C im 20. Jahrhundert wird vom IPCC dem anthropogenen radiative forcing zugeschrieben, welcher 1.67W/m2 beträgt. Die Größe der ausgehenden langwelligen Strahlung wird durch die Temperatur bestimmt. Soweit dürften wir einig sein. Der zweiten Tabelle können Sie aber entnehmen, dass es zwischen den einzelnen Modellen einen Unterschied von 20.6W/m2 gibt. Bei dieser Schwankung geht ein Beitrag von 1.67W/m2 einfach unter. Das gleiche Dilemma tritt bei der Emission auf.
„Wie landen Sie jetzt rein logisch bei ihrer Schlussfolgerung, dass TSI dominierend ist??“
Bitte genau lesen. Dies ist ein Zitat der NASA-Wissenschaftler, die die Satelliten betreiben.
Ihr Link http://tinyurl.com/35kz3m5 verweist auf eine Graphik zu der ich in einem früheren Bericht Stellung genommen habe. Ich darf zitieren: „Von den zwölf aufgeführten Größen wird der Kenntnisstand der Rückwirkungen acht mal (!) als sehr gering angegeben, ein mal als gering, zwei mal als mittelmäßig und ein mal als gut.
Im besten Fall versteht man also ein Viertel, aber trotzdem behauptet man, die Temperatur für 2100 ausrechnen zu können und, dies ist der entscheidende Punkt, daraus weittragende politische und ökonomische Schlussfolgerungen ziehen zu können.“
„Daß diese völlig verkehrt sein können, kann folgendem Beispiel entnommen werden.
Ramanathan, V; Ramana, M V; Roberts, G; Kim, D; Corrigan, C; Chung, C; Winker, D
NATURE – 448 (2007) 575-579
We found that atmospheric brown clouds enhanced lower atmospheric solar heating by about 50 per cent.
We propose that the combined warming trend of 0.25K per decade may be sufficient to account for the observed retreat of the Himalayan glaciers.
Was lernt man daraus? Der IPCC sagt, dass die Aerosole die globale Erwärmung um ~30% verringern, d.h. ohne Aerosole wäre es gemäß dem IPCC deutlich wärmer. Dies steckt als Annahme in den Modellen (-30%), gemessen wurde aber das Gegenteil (+50%). Bedenkt man, dass dies nur eine der schlecht verstandenen Rückwirkungen betrifft, da fragt man sich, was bleibt von der IPCC-Prophezeiung eigentlich übrig.“
Sehr geehrter Kollege Hüttner,
auch als Physiker habe ich ihre Gedankengänge nicht nachvollziehen können. Wie ich ihrem Kommentar an Herrn Bäcker entnehme, zweifeln Sie die Größe des radiative forcings (RF) von CO2 nicht an, meinen aber, dass dies relativiert wird durch die Differenzen der Werte in Trenberths Tabelle.
Sie unterliegen einem entscheidenden Denkfehler:
Nicht alles, was die Einheit W/m^2 hat, ist ein forcing!
Trenberths Diagramm ist eine vereinfachte und schematische Darstellung der Energieflüsse zwischen Erdoberfläche und Atmosphärenrand bzw. die Verteilung der Energieflüsse auf die verschiedenen Prozesse. Manche Tabellenwerte wie z.B. die latente Wärme sind überhaupt keine forcings, ebenso wie die Nettoabsorption.
Andere dagegen schon, wie z.B. die Reflexion an Wolken.
Da gibt nach der Tabelle Trenberth 1997 den Wert von 70 W/m^2 an, der jüngste Wert beträgt 79 W/m^2. Es ist mit Verlaub aber wenig ergiebig, die Veränderung von 9 W/m^2 mit einem forcing zu vergleichen. Sie vergleichen zwei Werte, die offenbar mit verschiedenen Methoden abgeschätzt worden sind. Notwendig wäre es, die Veränderung der Werte nach derselben Methode zu betrachten.
Kurz:
Ein Blick in den AR4 zum Thema radiative forcing wäre sinnvoll. Nirgendwo habe ich dort Trenberths Diagramm oder Tabelle gesehen, die forcings werden anders bestimmt und gemessen. Sie suggerieren in ihrem Artikel einen Zusammenhang, der nicht gegeben ist.
Die forcings und ihre Werte samt Fehlertoleranzen sind in folgender Abbildung dargestellt:
http://tinyurl.com/35kz3m5
Sie sehen, die Fehlertoleranzen der forcings sind allesamt kleiner als das CO2-Forcing.
Lehrreich auch die Entwicklung der forcings seit 1850, dargestellt in Fig. 2-23:
http://tinyurl.com/23y53q4
PS:
Ihr letztes Diagramm zeigt eine kaum überraschende Korrelation der Sonnenfleckenzahl mit der total solar irradiance (TSI). Wie landen Sie jetzt rein logisch bei ihrer Schlussfolgerung, dass TSI dominierend ist??
@ #10: NicoBaecker
Sie haben das Verständnisproblem. Nach den Prinzipien rationaler Problemlösungen ist es kein Kann sondern ein Muss, den CO2-RF zu vernachlässigen.
Die Dilettantenklatsche geht an Sie. Es reicht nicht etwas zu definieren und zu berechnen Man muss es auch messen können. Und dieser Effekt geht im Rauschen anderer Effekte unter. Damit ist es unsinnig diesen Effekt zu berücksichtigen wenn man in den anderen Messbaren Effekten noch Unsicherheiten hat. Wie war das mit dem Verständnis der Wolkenbildung? Was ist der größte Posten in der Energiebilanz? Klären Sie erst mal diese Fragen, bevor Sie mit so einem Fliegenschiss ankommen. So sind schon viele Thesen gescheiter. Und diese nun auch.
Und ihr Abschlusssatz ist wohl das Letzte. Wer widersetzt sich denn der Erkenntnis. Das sind doch wohl Sie und ihre AGW-Kirche. Hier in diesem Fall halten Sie die These für höherwertig als eine Messung. Das nenn ich Argwöhnen und lieber in Unwissenheit leben zu wollen und vor allem ist dies das Abstreiten von Erkenntnissen. Sie und ihre AGW-Kirche halten doch den Fortschritt auf indem Sie Märchen über das CO2 verbreiten und nützlicher Forschung das Geld entziehen.
Und das größte Ärgernis ist, dass diese Sekte ihren geistigen xxxxxxx via PIK direkt auf die MSM sprich n-tv.de setzen kann. Und dort kann man nicht über den wissenschaftlichen Gehalt der Meldungen diskutieren.
Sehr geehrter Herr Kollege Bäcker,
was soll die Polemik. Den Kernpunkt, dass denke ich schon, haben Sie doch verstanden. Für die Nichtphysiker unter uns möchte ich dies noch einmal kurz zusammenfassen. Beschränken wir uns auf die Annahme, dass die Temperatur determiniert ist durch die einzelnen Beiträge zur Strahlungsintensität (W/m2). Unsicherheiten, wie z. B. die Bedeckung durch Wolken und deren positiver oder negativer Beitrag, Fehlergrenzen bei den Treibhausgasen, sollen also unberücksichtigt bleiben. Die Strahlungsbilanz setzt sich somit aus mehreren Beiträgen, von dem ein kleiner, der anthropogene (1.67W/m2) ist, zusammen. Eine Änderung in der Summe der Beiträge bewirkt eine Änderung der Messgröße Temperatur. Nun ist es aber nicht möglich im Umkehrschluss zu sagen, dass sich die Temperatur durch den anthropogenen Beitrag geändert hat, wenn die Unschärfen der anderen Beiträge zum Teil viel größer als der anthropogene sind. Ein Ausweg bestände darin, wenn der anthropogene Beitrag ein charakteristisches Zeit- oder Frequenzsignal hätte, was auch bei der Temperaturänderung gesehen wird. Solch ein Nachweis ist mir auf der relativ kurzen Zeitskala von 200 Jahren nicht bekannt. Auf einer längeren Skala (400 000 Jahre) wurde dies kürzlich von Bershadskii (Journal of Cosmology, 2010, Vol 8, 1893-1905) für die Variation der Temperatur und des CO2 gezeigt. Beide werden aber durch außerirdische Phänomene verursacht.
Zu # 10 „Herrn Bäcker“…wieder einmal ein toller Beweis von Aroganz und Selbstherrlichlichkeit. Ich möchte mich keinesfalls in diese Diskussion einschalten aber wie Sie so etwas rüberbringen..Herr NB…ist schon einzigartig !
Erich Richter
#10: NicoBaecker
Wieso sind Sie nicht in der Lage, wenn Sie schon, auf durchaus unsoziale Art und Weise, Kritik äußern, diese auch zu begründen? Lediglich Worthülsen zu bemühen, die inhaltlich nichts aussagen, erwecken den Eindruck, dass es mit Qualifikation dazu nicht zum Besten steht!
Nach tiefgreifendem Durchdenken von #10 komme ich
zu dem Schluss, daß Dr.rer.nat. Baecker zugibt,daß das RF von CO2 so klein ist, dass es
locker im Fehlerbalken anderer Messungen unterzubringen ist. Der wissenschaftliche Fortschritt wird wohl von der Präzisierung dieser Fehlerbalken abhängen.
Michael Weber
Tja, Herr Baecker
Sie haben sich wieder perfekt an die Eschenbach-Blog-Regeln gehalten. Wer ad hominem argumentiert,verliert!
Michael Weber
Tja Herr Hüttner,
Sie sind auf einem gutem Wege und als Physiker sollten Sie eigentlich die Möglichkeiten haben, Ihre letzten Unklarheiten zu beseitigen und Ihre bislang dilettantischen Erklärungsversuche Ihrer persönlichen Diskrepanzen durch Klarheit und den Stand des wissenschaftlichen Erkenntnisse zu ersetzen. Dazu fehlt Ihnen jedoch die klare Artikulation Ihrer Verständnisprobleme. Sie werrden zugeben müssen, dass es nicht von besonders tiefgreifenden Durchdenken der SDachlage zeugt, wenn man wie Sie meint, die CO2-RF wäre zu vernachlässigen nur weil dieser Wert kleiner als der Messfehler anderen Energieflüsse ist.
Ich füchte jedoch, Ihnen ist das Argwöhnen durch Unwissen lieber als die Erkenntnis.
Dear Mr. Taylor,
what’s the point of your argumentation?
You argue, that 1,66 W/m^2 ist comparable small in regard to natural variability, but it’s increasing and big enough, to increase global temperature significantly.
And please take into account, that natural variability is not a radiative forcing according to the given definition.
0.12 W/m^2 is the long term change of TSI (divided by 4 by the way!), comparisons with short term fluctuations (solar cycles) are pointless.
Yours,
Norbert Fischer
@Norbert Fischer (#2)
Glauben Sie wirklich, dass Ihnen jemand auf Ihre Preisfrage antwortet? Wer es noch nicht weiß, kann das sehr gut selbst in Erfahrung bringen.
Es gab übrigens hier unter EIKE schon einen qualifizierten und vor allem sachlichen Informationsaustausch ohne widerwärtige Polemik zum RF und auch zu dem von CO2…!
P.S.: Es zeugt von jugendlichem Leichtsinn und jugendlicher Unreife und Blindheit, wenn im Voraus angenommen wird, dass der Rest der Welt unfähig ist, etwas Bestimmtes zu begreifen oder zu wissen und somit generell zu unterschätzen. Ein solches Herangehen fällt jedem früher oder später auf die eigenen Füße und gehört auch nicht zum Diskussionsstil ernsthafter Leute, glauben Sie `s, spricht ein „weiser Uhu“.
@Admin: „Bitte beim Thema bleiben, Herr Matthes.“
Leicht gesagt, lieber Admin.
Es ist schwer bis unmöglich, bei einem Thema zu bleiben, daß vermißt wird.
Stimmt doch so?
Wg. SEMI-OT, youtube-Text:
„Ein wirklich sehr aufschlussreicher Vortrag von Brigitta Zuber … auch noch über die Klimalüge!“
youtube.com/watch?v=IiWzU8Os9zQ
@NB
Wüsste nicht, das ich in diesen Thread schon kommentiert hätte……..wer derart vehement dem CO2 eine klimawirksame Schuld unterschieben will, sollte doch wenigstens in der Lage sein den richtigen Gesprächspartner zu zitieren,gelle.
Naja, warum Augenmerk auf Tatsachen legen, wo es doch gilt die Erde zu retten.
Heinz Eng
Sehr geehrter Herr Eng,
ich halte meinen Betrag schon für relevant.
Denn wenn der Autor Hüttner es so meint, wie ich ihn verstanden habe, dann schreibt er Unsinn.
Anfügen möchte ich noch, dass er die Definition des radiative forcings nicht verstanden hat. Die Definition beinhaltet ein Gleichgewicht in der Stratosphäre, dies ist aber keineswegs gleichbedeutend mit einem Temperaturgleichgewicht z.B. in Bodennähe (siehe die Erläuterungen im AR4).
Übersehen hat er auch, dass das radiative forcing des CO2 alleine aus Daten zur CO2-Konzentration der Atmosphäre gewonnen wird, und diese zweifelt ja nicht mal Eschenbach auf WUWT an. Jetzt hab ich’s verraten, der Preis ist damit aber futsch!
#1: Peter Taylor sagt:
„Excuse my Deutsche!!“
Geht klar; soooo viel besser ist mein English auch net.
___
Semi-OT
Ein brisantes Thema vermisse ich bei EIKE:
Chemtrails, neudeutsch „Geo-Engineering“.
Zum Einstieg für Unwissende empfehle ich den Vortrag von Brigitta Zuber,
einer glaubwürdigen, couragierten und offensichtlich intelligenten Frau.
Beeindruckend sind auch ihre Berichte, wie sie von offiziellen Stellen angelogen und für dumm verkauft wurde beim Versuch, Hintergrundinformationen zu erlangen.
Da wird massiv gemauert und verschleiert. WARUM??
Ich habe selten so einen klaren Sternenhimmel gesehen wie beim Vulkanasche-Flugverbot, tagsüber war der Himmel BLAU statt des üblichen verwaschen-milchigen bleus.
youtube.com/watch?v=IiWzU8Os9zQ
@#3: A. Heinz
Fischer macht seinen Job: Stänkern, desinformieren und versuchen, Diskussionen auf Nebenschauplätze abzulenken („Porno-Pachauri“). ‚Don’t feed the Troll.‘
Lieber Herr Fischer,
Ich fasse mal die wichtigsten Passagen ihres unglaublich sinnvollen Beitrags zusammen:
„Ich vermute“, „erschließt sich mir nicht“, „Vielleicht könnte der Autor nochmals erläutern, was er damit zum Ausdruck bringen möchte.“
Kurz: Sie haben keine Ahnung. Ist ein bisschen anmassend, dass „Preisfragen“ ausgerechnet von Ihnen kommen. Ausserdem sollten Sie, wenn Sie Ihr begrenztes Wissen schon unbedingt erweitern wollen, die Preisfragen nicht an die Leser, sondern an die Autoren richten.
Als Preis würde mir übrigens auf Anhieb einer einfallen. Dieser würde Ihnen jedoch nicht gefallen, da er etwas mit „Norbert Fischer“ und „Mund halten“ zu tun hat.
Ich vermute mal, der Autor ist einigen Missverständnissen aufgesessen:
Ist es möglich, dass er glaubt, das radiative forcing von CO2 wird aus Satellitendaten bestimmt? Für mich klingt das so beim Lesen des Artikels. Falls ja, ist es leider falsch (s. TAR)
Auch den Zusammenhang mit der Graphik von Trenberth und der angefügten Tabelle mit dem RF von CO2 erschließt sich mir nicht. Auch hier klingt es so, als würden diese Werte zur Bestimmung des RF benutzt, ich zitiere:
„Das Problem besteht nicht darin, dass es Korrekturen bei den Werten gibt und dass viele Differenzen größer als die ominösen 1.66W/m2 sind, sondern in der Tatsache, dass diese Werte als Input in die Modellrechnungen eingehen.“
Vielleicht könnte der Autor nochmals erläutern, was er damit zum Ausdruck bringen möchte.
Und nun die Preisfrage der Woche an alle EIKE-Leser:
Wie wird das RF von CO2 in Wirklichkeit bestimmt?
Nur ran, ich überlege noch an einem Preis.
Einverstanden! Bitte, sehen sie auch mein Buch – ‚Chill: a reassessment of global warming theory‘.
darein, gebe ich auch viele data fur RF/albedo/surface radiation, die klar machen dass AGW RF von 1.6 ist klein in vergleich zu naturale ‚variability‘ – circa 4x, deshalb, AGW = 20% maximum! Excuse my Deutsche!!