„Nicht der Kritiker zählt, nicht der Mann, der darauf hinweist, wie der Starke stolpert oder wo der Handelnde es besser hätte machen können.
Das Verdienst gebührt dem Mann, der tatsächlich in der Arena steht, dessen Gesicht von Staub und Schweiß und Blut gezeichnet ist, der sich tapfer bemüht, der sich irrt, der immer wieder zu kurz kommt, weil es keine Anstrengung ohne Fehler und Unzulänglichkeit gibt, der sich aber tatsächlich bemüht, die Taten zu vollbringen; der die große Begeisterung, die große Hingabe kennt; der sich für eine würdige Sache verausgabt; der im besten Fall am Ende den Triumph der hohen Leistung kennt, und der im schlimmsten Fall, wenn er scheitert, wenigstens scheitert, indem er Großes wagt, so dass sein Platz niemals bei jenen kalten und furchtsamen Seelen sein wird, die weder Sieg noch Niederlage kennen.“ – Theodore Roosevelt
Das Klima der Erde ist ein Energiefluss-System, das sich im Durchschnitt annähernd im Fließgleichgewicht befindet. Dabei ist die Energiemenge, die von jedem Teil des Systems aufgenommen wird, gleich der Energiemenge, die von diesem Teil des Systems verloren geht. Wäre dies nicht der Fall, würden sich die betroffenen Teile ständig entweder erwärmen oder abkühlen.
Und das trifft auf die Erdoberfläche zu. Sie verliert im Grunde so viel Energie, wie sie gewinnt, und deshalb war die Temperatur der Erde im 20. Jahrhundert mit einer Genauigkeit von weniger als einem Prozent stabil.
Zu Beginn dieser Ausführungen möchte ich darauf hinweisen, dass nicht der gesamte, von der Oberfläche absorbierte Energiestrom in Temperatur umgewandelt wird und durch Wärmestrahlung verloren geht. Ein Teil des Energiestroms geht als „fühlbare“ Wärme, d. h. als Wärme, die wir spüren können, durch Wärmeleitung in die Atmosphäre und Konvektion von der Oberfläche weg verloren. Ein anderer Teil geht als „latente Wärme“ verloren, d. h. als Wärme, die durch Verdunstung an der Oberfläche verloren geht. Nach diesen Verlusten heizt die verbleibende Energie die Oberfläche auf und geht als langwellige, aufsteigende Strahlung von der Oberfläche verloren.
Abbildung 1 zeigt die relativen Mengen an Energie, die von der Oberfläche absorbiert werden und verloren gehen:
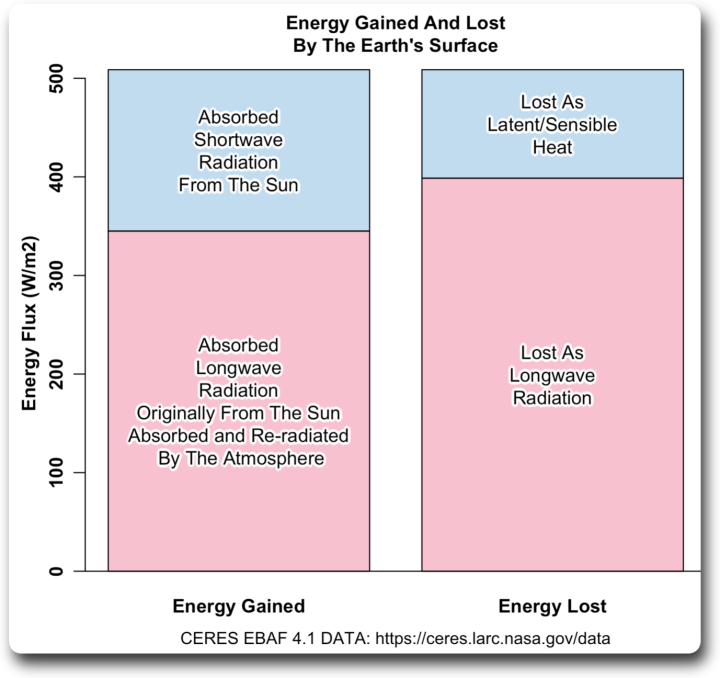
Abbildung 1. Energiehaushalt der Erdoberfläche mit Energiegewinn (lang- und kurzwellige Strahlung) und Energieverlust (langwellige Strahlung und latente/fühlbare Wärme). Da sich der Planet in einem stabilen Zustand befindet, sind Gewinne und Verluste etwa gleich groß.
Nehmen wir nun an, dass wir die Temperatur der Erde um 1°C erhöhen wollen. Wie viel zusätzlicher Energiefluss ist erforderlich, um diesen neuen, wärmeren Dauerzustand aufrechtzuerhalten?
Nun, da im Gleichgewichtszustand die Gewinne gleich den Verlusten sein müssen, brauchen wir so viel Energiefluss wie die zusätzliche Energiemenge, die bei der neuen höheren Temperatur abgestrahlt wird. Anhand der so genannten „Stefan-Boltzmann-Gleichung“ können wir berechnen, dass wir mindestens 5,5 Watt pro Quadratmeter (W/m²) zusätzlichen Energiestrom benötigen, um einen schwarzen Körper bei der Erdtemperatur um ein Grad Celsius anzuheben. (Es handelt sich um ein Minimum, da der prozentuale Anteil der latenten/sensiblen Wärmeverluste mit steigender Temperatur leicht zunimmt, aber das können wir bei dieser Analyse ignorieren).
Aus Abbildung 1 geht jedoch auch hervor, dass nur etwa 78 % des absorbierten Energiestroms in Temperatur umgewandelt wird und als Strahlung verloren geht. Einschließlich der latenten/sensiblen Wärmeverluste benötigen wir also 5,5 / 0,78 ≈ 7 W/m² an zusätzlichem Gesamtenergiefluss, der von der Oberfläche absorbiert wird, um die Oberflächentemperatur um ein Grad zu erhöhen.
Betrachten wir nun die gängige IPCC-Position, dass eine Verdoppelung des CO2 die abwärts gerichtete langwellige Strahlung an der „Oberseite der Atmosphäre“ (TOA) um 3,7 W/m² erhöhen wird. Das bedeutet, dass bei einer sofortigen Verdopplung des CO2 die Menge der Langwelle, die den Planeten am oberen Ende der Atmosphäre verlässt, um 3,7 W/m² reduziert wird.
Und diese zusätzlichen 3,7 W/m² an absteigender Strahlung durch die CO2-Verdoppelung sollen laut IPCC die Temperatur um 3°C erhöhen.
Unterm Strich? Nach Angaben des IPCC sind nur ~ 1,2 W/m² zusätzlicher TOA-Antrieb erforderlich, um die Temperatur um 1°C zu erhöhen.
Hier ist also die ernsthafte Frage, auf die ich im Titel anspielte …
Wie wird aus einem CO2-Antrieb von 1,2 W/m² an der Oberseite der Atmosphäre auf mysteriöse Weise ein zusätzlicher Oberflächen-Energiefluss von 7 W/m², den wir brauchen, um die Erde um 1°C zu erwärmen?
[Hervorhebung im Original]
Die IPCC-Leute fuchteln mit den Händen und spielen vage auf die „Wolkenrückkopplung“ und die „Wasserdampf-Rückkopplung“ an, die das abwärts gerichtete IR von der Oberseite der Atmosphäre zum abwärts gerichteten IR an der Oberfläche erhöhen.
Dies würde jedoch voraussetzen, dass die Rückkopplung das ursprüngliche Signal um einen Faktor von fast sechs verstärkt … und soweit ich weiß, führt schon ein Rückkopplungsfaktor von mehr als eins zu einem Runaway.
Meine Frage bleibt also bestehen:
Welche geheimnisvolle Kraft verwandelt die 1,2 W/m² CO2-TOA-Antrieb, der Antrieb, der laut IPCC die Oberflächentemperatur um 1°C ansteigen lässt, in die 7 W/m² absorbierten Energieflusses an der Oberfläche, der tatsächlich notwendig ist, um die globale Temperatur um 1°C anzuheben?
[Hervorhebung im Original]
Alle ernsthaften Antworten sind willkommen.
Fußnote: Die Vorstellung, dass die Wolkenrückkopplung positiv ist, ist ziemlich unwahrscheinlich. Erstens besagt das Prinzip von Le Chatelier, dass, wenn ein dynamisches Gleichgewicht (ein stationärer Zustand wie das Klima) durch eine Änderung der Bedingungen gestört wird, sich die Position des Gleichgewichts verschiebt, um der Änderung entgegenzuwirken und ein Gleichgewicht wiederherzustellen.
Außerdem wird die Behauptung einer positiven Netto-Wolkenrückkopplung durch die CERES-Daten widerlegt. Hier ist der Netto-Wolkenstrahlungseffekt (CRE) im Vergleich zur Temperatur für jede einzelne Gitterzelle dargestellt:
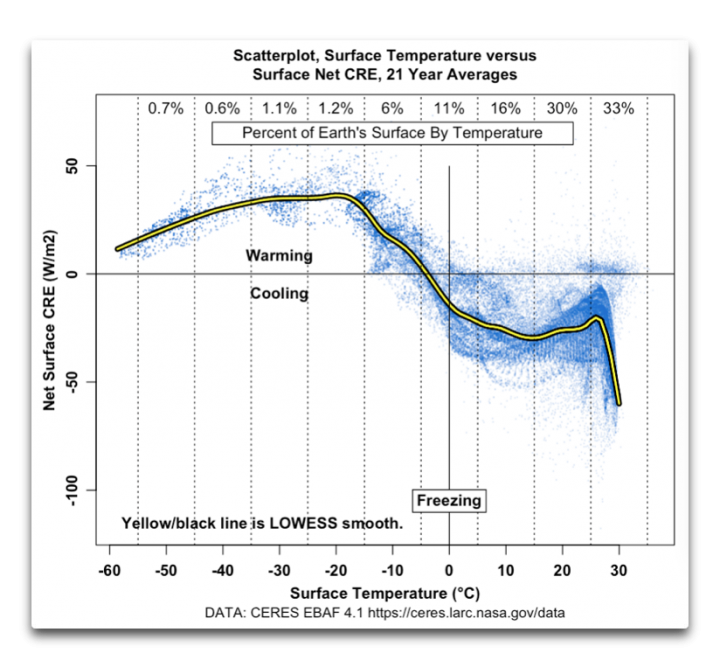
Abbildung 2. Netto-Wolkenstrahlungseffekt (CRE). Dies ist die Veränderung der abwärts gerichteten Strahlung in W/m², wenn Wolken vorhanden sind. Sie umfasst sowohl den lang- als auch den kurzwelligen Effekt. Unterhalb der horizontalen Linie ist der Nettoeffekt kühlend.
Die Steigung der gelben Linie zeigt die Richtung der Wolkenrückkopplung an. Wenn es mit steigender Temperatur mehr abkühlt (negative Rückkopplung), geht die Steigung nach rechts hinunter. Ist die Rückkopplung positiv, d. h. kühlt sie bei steigender Temperatur weniger ab, steigt die Steigung nach rechts.
In den Tropen, die etwa 40 % des Planeten ausmachen, ist die Rückkopplung extrem negativ, die Steigung verläuft fast senkrecht. Und von -15°C bis 15°C, weitere 33% des Planeten, ist die Rückkopplung ebenfalls negativ.
Es sieht also nicht so aus, als ob die Antwort auf meine Frage „Wolkenrückkopplung“ lautet.
Hinweis: Wie in meinen beiden vorangegangenen Beiträgen untersuche ich die Verzweigungen und die Mathematik des Treibhauseffekts. Wenn Sie der Meinung sind, dass der Treibhauseffekt gegen physikalische Gesetze verstößt, lesen Sie meine beiden Beiträge „Menschen auf Glasplaneten“ (hier) und „Das stählerne Treibhaus“ (hier). Und wenn Sie nach der Lektüre immer noch der Meinung sind, dass der Treibhauseffekt nicht existiert, dass die abwärts gerichtete Strahlung nicht existiert oder dass sich die Strahlungsenergieflüsse nicht addieren, dann gehen Sie bitte. Gehen Sie nicht wütend weg, Sie können die Kommentare gerne weiter lesen … aber dies ist NICHT der Thread, um über die abwärts gerichtete Strahlung oder den Treibhauseffekt zu diskutieren. Diese Themen neigen dazu, den Thread in eine unsinnige Endlosdiskussion zu verwandeln, die zu nichts führt, und daran bin ich nicht interessiert. Bitte verschieben Sie diese und ähnliche Themen in einen anderen Thread.
Ich bin an einer ernsthaften Antwort auf meine Frage interessiert, wie das funktionieren soll, wie 1,2 W/m² am TOA in 7 W/m² an der Oberfläche umgewandelt wird und woher diese zusätzliche Energie angeblich kommt.
MATH: Die Änderung der Strahlung bei einer Temperaturänderung von 1°C eines Objekts ist durch das Differential der Stefan-Boltzmann-Gleichung gegeben:
wobei c die Temperatur in Grad und epsilon der Emissionsgrad ist. In einem stationären Zustand, in dem die durchschnittlichen Verluste gleich den durchschnittlichen Gewinnen sind, ist dies auch die Menge an zusätzlicher Energie, die erforderlich ist, um die Temperatur des Objekts um 1 °C zu erhöhen. Wie bei dieser Art von Analyse üblich, und weil der Emissionsgrad der Erde irgendwo über 0,95 liegt, verwende ich der Einfachheit halber epsilon = 1.
Link: https://wattsupwiththat.com/2022/09/05/a-serious-question/
Übersetzt von Christian Freuer für das EIKE

















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"„Wie wird aus einem CO2-Antrieb von 1,2 W/m² an der Oberseite der Atmosphäre auf mysteriöse Weise ein zusätzlicher Oberflächen-Energiefluss von 7 W/m², den wir brauchen, um die Erde um 1°C zu erwärmen?“ Was soll ein CO2-Antrieb TOA denn antreiben? TOA ist praktisch Vakuum. Da ist nichts zum Antreiben vorhanden. Die 1,2 W/m² sind das Strahlungsungleichgewicht TOA, also ASR-OLR. Das globale Strahlungsungleichgewicht variierte 2021 saisonal zwischen 9,1 W/m² (Feb) und -7,8 W/m² (Juli) infolge der schwankenden solaren Einstrahlung. (CERES EBAF). Im jährlichen Mittel 2021 erhält man 1,7 W/m². Das Mittel 2001-2021 beträgt 1,0 W/m². Ursache des Ungleichgewichts: OLR eilt ASR nach. Die Verzögerung beträgt nur 1-2 Monate. Das jährliche Mittel von 1,2 W/m² rührt von den langen Relaxationszeiten der absobierten Solarstrahlung her, die in den tiefen Ozean wandert.
Energiebilanzen kann man nur für Grenzflächen aufstellen. Die Erdoberfläche ist so eine Grenzfläche.
TOA ist keine Grenzfläche, weil nicht feststellbar ist, wo genau TOA überhaupt ist. Und TOA ist auch keine Strahlungsquelle. TOA wird ausschließlich von Strahlungen durchstrahlt, in Richtung Erde annähernd gerichtet, in entgegengesetzter Richtung hochdiffus.
Es gibt keine Regel, die fordert, daß eine virtuelle Gegend im Raum energetisch ausgeglichen je Quadratmeter von irgendwelchen Strahlen durchstrahlt wird. Die Strahlung ab Sonne TOA kann man gut messen, weil sie gerichtet ist. Die Strahlung der Erde TOA kann man nicht messen, jedenfalls nicht durch Satelliten. Satelliten können nur Strahlung messen, die auf gerader Linie von der Oberfläche zum Meßinstrument strahlen. Das ist ein minimaler und auch leistungsmäßig nicht relevanter Anteil der diffusen Gesamtstrahlung.
Wer energetische Schieflagen in Energiebilanzen vermutet, hat irgend eine Komponente übersehen und sucht Dinge, die es nicht gibt.
M.E. gibt es nur eine Lösung: Die Atmosphäre, Wasserdampf, Verdunstung, Niederschläge führen nicht zu einer Verstärkung der spektroskopischen Erwärmung („THE“), wie der IPCC unermüdlich behauptet, sondern aufgrund des Kühleffekts zu einer Abschwächung (was ich immer wieder hier poste). Was zu einer Rückkopplung < 1 führt – etwa 0,5. Und was dann auch den (niemals beobachteten) runaway-Effekt zuverlässig verhindert. Oder anders ausgedrückt: Das CO2 müsste demnach nicht verdoppelt, sondern vervierfacht werden, um die Temperatur um ca. 1 Grad zu erhöhen.
Wie erklärt Herr Eschenbach, dass die sogenannte Rückstrahlung aus der Atmosphäre ungefähr doppelt so hoch ist wie die initial empfangene kurzwellige Solarstrahlung?
Zur Erinnerung:
1. Die einzige Energiequelle der Erde ist die Sonne.
2. Die Strahlung der Sonne trifft auf die Oberfläche im Tagesmittel mit einer durchschnittlicher Stäke von ca. 145 Watt/m2 ( unter Berücksichtigung von Reflektion/Absorbtion der Atmosphäre/ Erde; Albedo). Die Energiegenese durch Sonneneinstrahlung findet dabei ausschließlich währende des Tages statt.
3. Die eintreffende Sonnenstrahlung erwärmt die Oberfläche, wobei jede Art von Oberfläche sich nach ihren Materialeigenschaften unterschiedlich erwärmt (Sand, Asphalt, Wiese, Moor, Meer etc.)
4. Jeder erwärmte Gegenstand kühlt sich ggü. der Umgebung ab. An der Erdoberfläche finden parallel die Abkühlungsvorgänge Leitung/Konvektion, Verdunstung und Abstrahlung statt.
5. Soweit Wärmeenergie der Oberfläche dieser schon durch Leitung und Konvektion entzogen wurde, d. h. kühler wurde, steht diese nicht mehr für die Entwicklung von langwelliger Strahlungsenergie zur Verfügung. Die Abstrahlung der Oberfläche richtet sich ausschließlich nach ihrer Temperatur und wird durch nichts behindert, auch nicht durch IR-Aktive Gase! Diese verlangsamen allenfalls die Abstrahlung ins All.
6. Ein Teil der Strahlung geht durch das Atmosphärische Fenster direkt ins All (Anmerkung: laut Ramanathan et al, Climate-Chemical Reactions,und Enquete-Bericht der Bundesregierung von 1988 gelangen 70 bis 90 Prozent der Abstrahlung von der Erdoberflächeund von den Wolkendurch das Atmosphärische Fenster direkt in den Weltraum!). Ein weiterer Teil der Strahlung wird thermalisiert, d.h. er erwärmt Sauerstoff und Stickstoff und unterfällt damit der Konvektion ( ja, es gibt auch Rückanregungen von IR-Aktiven Gasen durch Stoß, aber angesichts des quantitativen Verhältnisses von absorbierenden und nicht absorbierenden Molekülen in der Luft ist die Rückanregung deutlich seltener als die Thermalisierung).
7. Nach all dem dürfte die von der Erde ausgehende langwellige Strahlungsenergie, die noch von IR-Aktiven Gasen absorbiert UND im Raumwinkel 360 Grad re-exmittiert wird ganz erheblich unter den im Tagesschnitt liegenden 145 Watt/m2 liegen.
8. Die langwellige Strahlung in der Atmosphäre hat ihren Ursprung immer an der strahlenden Erdoberfläche. Die sogenannte Rückstrahlung, was immer da auch gemessen wird, ist immer von der Strahlung der Erde abgeleitet. Sie kann nie mehr oder größer sein als die Strahlung, von der sie ausgeht bzw. von der sie abgeleitet ist. Welcher geniale Verstärkungsmechanismus ist da in der Atmosphäre am Werk, der die Abstrahlungsleistung von im Schnitt deutlich unter 145Watt/ m2 auf eine Gegenstrahlungsleistung von ca. 350Watt/m2 verstärkt (Absorbtion und Re-Emission???). Die die es behaupten, behaupten es nur und können es nicht erklären!
9. Die Atmosphäre ist keine eigenständige Energiequelle!
10. Die Strahlung, die nicht gleich ins Weltall geht, bahnt sich sukzessive ihren Weg an den Rand der Atmosphäre, bis sie letztendlich über die Re-Emmission IR-AktiverGase ihren Weg ins All findet.
11. Die Atmosphäre ( einschließlich des Anteils der langwelligen Strahlung, der nach erfolgter Absorbtion re-exmittiert wird und bis auf die Oberfläche zurückstrahlt erwärmt die Oberfläche NICHT ZUSÄTZLICH über die initiale Erwärmung durch die Sonne hinaus. Die Atmosphäre hat jedoch den Effekt, die fortwährende Abkühlung der Oberfläche zu verlangsamen.
12. Im Übrigen gehen wohl auch die Klimamodelle nicht mehr davon aus, dass die Erde von dem immer wieder herangezogenem Gegenstrahlungskaftwerk aufgeheizt wird. In ernsthaften Kreisen wird meines Wissens nach ein Treibhauseffekt nur noch im Zusammenhang mit der Erhöhung der effektiven Abstrahlungshöhe der Outgoing Longwave Radiation durch eine Erhöhung der Konzentration von IR-Aktiven Gasen diskutiert. Das hat mit den Vorstellungen vom Treibhaus und Gegenstrahlung nichts mehr zu tun.
Er vertraut den Mittelwerten, und die erklären nicht die Physik, sondern verfälschen sie.
Tom Oelschläger am 12. September 2022 um 11:04
Geht es bei der Frage um die Erklärung der Werte oder stellen Sie die Werte selbst in Frage?
Falls letzteres, könnten Sie sich Werte von Wetterstationen ansehen, so zeigt der Hamburger Wettermast momentan eine langwellige Einstrahlung zwischen 350W/m² und 375W/m² bei einer maximal möglichen mittleren Einstrahlung von etwa 261W/m² wenn die Sonne komplett auf den Boden wirkt (bzw, 183W/m² bei 0,3 Albedo bzw, noch weniger, wenn man die Absorption in der Atmosphäre berücksichtigt). Da ist die langwellige Infraroteinstrahlung aus der Atmosphäre auch größer als die Einstrahlung durch die Sonne …
Oder Sie könnten sich die Werte von Ceres ansehen, mit den Herr Eschenbach arbeitet …
Zitat: Oder Sie könnten sich die Werte von Ceres ansehen, mit den Herr Eschenbach arbeitet …
Was?! CERES kommt aber auf völlig andere Werte! Siehe die nette Animation:
+ Placing the Recent Hiatus Period in an Energy Balance Perspective (CERES)
https://svs.gsfc.nasa.gov/13557
Immer diese „Willi-Beiträge“, wobei der Schreiber meistens an den physikalischen und mathematischen Herausforderungen scheitert.
Unter der folgenden Web-Adresse findet man noch weitere nette Animationen:
+++ NASA Home – Scientific Visualization Studio
https://svs.gsfc.nasa.gov/Gallery/index.html
+ Zonal Climate Anomalies / Temperature Anomalies
https://svs.gsfc.nasa.gov/4978
+ Historical Atlantic Multidecadal Oscillation (AMO)
https://svs.gsfc.nasa.gov/4895
Mfg
Werner Holtz
Werner Holtz schrieb am 13/09/2022, 01:17:48 in 300018
Die Herausforderung hier scheint zu sein, den Inhalt des Artikels zu erfassen und dann zu erkennen, dass die verlinkte Ceres-Animation etwas anderes darstellt. Während Willis Eschenbach über Mittelwerte und Ungleichgewichte an TOA und Oberfläche redet, zeigt die Ceres-Animation der Ein- und Abstrahlung die monatlichen Ungleichgewichte. Im Sommer wird mehr Energie aufgenommen als abgegeben, im Winter mehr Energie abgegeben, als aufgenommen. Die Animation der akkumulierten Energie zeigt, dass im Ceres-Intervall mehr Energie aufgenommen als abgegeben wurde. Wie entnimmt man diesen Animationen, dass Ceres auf „auf völlig andere Werte kommt“? Das wird wohl das Geheimnis von Herrn Holtz bleiben. Das errinnert mich irgendwie an seinen Vergleich der Abstrahlung am Boden in Köln(?) im Januar mit der Abstrahlung an TOA in einem südamerikanischen Hochplatau einer Wüste im Juli(?)…
Zitat: Während Willis Eschenbach über Mittelwerte und Ungleichgewichte an TOA und Oberfläche redet …
Wer Augen im Kopf hat, kann das in der Animation erkennen (Pause-Button). Aber ich weiß ja, das Sie sich für die Realität nicht interessieren.
Zitat: … bei einer maximal möglichen mittleren Einstrahlung von etwa 261W/m² wenn die Sonne komplett auf den Boden wirkt (bzw, 183W/m² bei 0,3 Albedo bzw, noch weniger, wenn man die Absorption in der Atmosphäre berücksichtigt …
Wer solch einen groben Unfug schreibt, bewegt sich in völlig fantastischen Welten jenseits der messbaren Ergebnisse.
Mfg
Werner Holtz
Werner Holtz am 13. September 2022 um 16:48
Nehmen wir doch einfach mal ein Bild aus der Animation:
Man sieht die Werte für jeden „einzelnen Ort“. Wie entnimmt man dieser Grafik (bzw. den vielen Grafiken für die einzelnen Monate), dass Ceres etwas völlig anderes zeigt, als Willis Eschenbach schreibt? Gibt es jemanden, der beim Betrachten die Werte über Fläche und Zeit mitteln kann?
Es wäre überzeugender, wenn Sie die messbaren Werte genannt hätten. Sie schreiben nicht mal, ob meine Angaben zu hoch oder zu niedrig sind …
@M.Müller
Zitat: Wie entnimmt man dieser Grafik (bzw. den vielen Grafiken für die einzelnen Monate), dass Ceres etwas völlig anderes zeigt, als Willis Eschenbach schreibt?
Am besten nehmen Sie den Monat März und/oder September (Ich hoffe, Sie wissen warum!?), dann erhält man nach der Abschätzung der orthographische Projektion einen mittleren Tags-Wert (24h) der „Absorbed Solar“ von 370 ± 10 W/m².
Willi schreibt irgend etwas von 160 W/m² in seiner Abbildung 1.
Zitat: Es wäre überzeugender, wenn Sie die messbaren Werte genannt hätten.
Und Sie begehen denselben Fehler wie Willi, und schreiben Werte hin, die auf jedem Fall keine Messwerte sind.
Um es auf den Punkt zubringen:
Zeigen Sie mir eine Messung (Ich betone Messung – Es schwirren genügend Satelliten da oben rum, die das Messen.) egal von welchem Satelliten, der diese Werte – „… 261 W/m² wenn die Sonne komplett auf den Boden wirkt (bzw, 183W/m² bei 0,3 Albedo bzw, noch weniger …“ – zu mindestens im Ansatz verdeutlicht.
Mfg
Werner Holtz
Bitte nicht wundern, dass keine Reaktion auf Ihren Kommentar erfolgt. Die Moderation möchte die Diskussion an dieser Stelle anscheinend beenden, da sie keinen weiteren Kommentar von mir erlaubt.
Korrekt
Sehr geehrter Herr Müller,
ich habe schon erwartet, dass Sie die von mir gestellte Frage nicht beantworten werden. Offenbar haben Sie auch keine Erklärung dafür, wie i der Atmosphäre aus einer Ausstrahlung von 145 W/m2 eine Gegenstrahlung von 350 W/m2 wird.
Ihr Verweis auf den Hamburger Klimaturm und dessen Messungen befriedigt mich nicht, denn dieses Messergebnis beantwortet ja nicht die Frage nach dem Mechanismus des Entstehens. Was da als einheitlicher Strahlungsfluss Gegenstrahlung gemessen wird, müsste mal genau untersucht werden. Haben Sie schon mal einen Gedanken daran verschwendet, dass es sich dabei um die diffuse Hin- und Herstrahlung der ursprünglichen Outgoing Longwave im bodennahen Bereich zwischen IR-aktiven Molekülen auf ihrem Weg an den Rand der Atmosphäre handeln könnte? Und dass diese Strahlung energetisch keine über die initiale Erwärmung durch solare Einstrahlung hinausgehende Rolle bei der Erwärmung der Oberfläche spielt? Energetisch leistet die sogenannte Rückstrahlung keinen Beitrag zur Erwärmung der Oberfläche, denn soweit in ihrem Rahmen tatsächlich langwellige Strahlen auf die Oberfläche zurückfallen und diese erwärmen, reagiert die Oberfläche sofort wieder mit den Abkühlungsmechanismen (insbesondere erhöhter Abstrahlung), so dass das Ganze energetisch ein Nullsummenspiel ist.
Mit der Verlangsamung der Abstrahlung habe ich übrigens das Auf und Ab des Anteils der Outgoing Longwave gemeint, die nicht direkt durch das Atmosphärische Fenster ins All geht, sondern in vielen Schritten von IR-aktiven Gasen absorbiert und re-emmitiert wird und sich „langsam“ nach oben arbeitet und schließlich ganz abgestrahlt wird.
Bei Ihrer Fokussierung auf 390 W/m2 Strahlung am Boden bitte ich um Mitteilung, an welcher Meßstation diese 390W/m2 gemessen werden.
Ich bin eher der Ansicht, dass Sie Ihren Fokus auf Erwärmung ausschließlich durch Strahlung überdenken und differenzieren sollten zwischen Temperatur der Oberfläche und Temperatur der bodennahen Luftschichten.
Die Oberfläche wird durch die Sonne erwärmt und die bodennahe Luft durch die Oberfläche, aber die Oberfläche wird nicht durch die Luft erwärmt.
Die Temperatur der bodennahen Luft ergibt sich darüber hinaus aus dem Luftdruck der über ihr liegenden Luftsäule. Die Funktion des konvektiv- adiabatischen Prinzips ist Ihnen ja bekannt und ich gehe nicht davon aus, dass Sie bestreiten wollen, dass Gas unter Druck eine höhere Temperatur annimmt. Es ist in der Natur ja nicht ungewöhnlich, dass eine Temperaturerhöhung durch andere Prozesse als Strahlung erfolgt (z.B. Erwärmung der Luft durch Leitung/ Phasenveränderungen von gasförmig zu flüssig).
Ihre Ausführungen zu Ramanathan et al sind nicht überzeugend. Haben Sie sich schon mal vor Augen geführt, welche Temperaturspanne der Bereich von 7 bis 13 Mikrometern umfaßt? Ich habe das einmal ausgerechnet und das Ergebnis ist, dass bei 7 Mikrometern das Strahlungsmaximum von 141 Grad C und bei 13 Mikrometern das Strahlungsmaximum von minus 50 Grad C liegt. Wenn man jetzt die Planck- Kurven für alle zwischen diesen Werten liegenden Temperaturen über den Bereich des Atmosphärischen Fensters legt, wird man feststellen, dass die Masse der auf der Erde real vorkommenden Temperaturen mit dem Großteil ihres Strahlungsspektrums in das Atmosphärische Fenster fällt. Bezeichnenderweise liegt das Strahlungsmaximum der sog. Globalen Durchschnittstemperatur von 15 Grad C exakt im Zentrum des Atmosphärischen Fensters bei 10 Mikrometern. Der Strahlungsverlust durch das Fenster dürfte bei klarem Himmel tatsächlich die den 70 bis 90 % der Gesamtstrahlung liegen. Was das für das Thema Gegenstrahlung bedeutet dürfte auf der Hand liegen.
Ich bitte Sie noch einmal um eine Erklärung des Prozesses der bewirkt, dass die initiale Erwärmung der Oberfläche durch ca. 145W/m2 Incoming Solar Radiation, die ihrerseits eine Ausstrahlung langwelliger Strahlung bewirkt, in der Atmosphäre eine Verstärkung auf ca. 350 W/m2 erfährt, die dann wieder auf die Oberfläche zurückstrahlt.
Der Verstärkungsprozess muss ja noch viel gewaltiger sein, denn bei der Rückstrahlung kommt unten ja aufgrund der Abstrahlung im Raumwinkel 360 Grad nur die Hälfte an.
Ich bin auf Ihre umfassende Erklärung zum Nutzen aller gespannt. Die Anwendung des Prinzips würde uns von allen Energiesorgen befreien.
T.oelschläger am 13. September 2022 um 18:21
Bevor ich mich an einer Antwort versuchen wollte, wollte ich erst mal ein paar Dinge klären, die ich als Fakten bezeichnen würde (Messwerte, korrekte Text-Zitate, …). Wenn über Fakten keine Einigkeit erzielt werden kann, hat eine Diskussion über das warum keinen Sinn.
Bevor man sich über das Warum Gedanken machen kann, muss man erst mal darüber einig sein, was beobachtet wird. Daher meine einfache Frage.
Eine Veränderung des Drucks führt bei gleichbleibendem Volumen zu einer Veränderung der Temperatur.
Das ist die falsche Frage. Die richtige Frage ist, wieviel Energie in diesem Bereich abgestrahlt wird. Wenn Sie sich einen Graphen aus einem Artikel über Happers Veröffentlichung ansehen, dann sehen Sie, dass das atmosphärische Fenster nur ein kleiner Teil des Spektrums ist und dort nicht 70%-90% der vom Boden insgesamt abgestrahlten Energie rausgehen.
Aber hier höre ich auf. Die einfache Antwort auf Ihre Frage wäre gewesen, dass die höhere Temperatur und damit die höhere Abstrahlung vom Boden und aus der Atmosphäre einfach dadurch entstehen, dass die Sonne den Boden und die Atmosphäre erwärmt und die Atmosphäre die abfliessene Energie und damit die Abkühlung verringert. Im Ergebnis führt das zu höheren Temperaturen. Die Verringerung der abfliessenden Energie können Sie sich im Papier von Happer ansehen, Figure 7. Experimentell können Sie die Erhöhung der Temperatur bei Vorhandensein von Treibhausgasen im Experiment von Herrn Schnell sehen.
#300151
Auch heute ist diese Aussage falsch. Wie sie im KT Diagram oder anderen sogenannten Energiebilanzen leicht sehen koennen gibt es keine Verringerung der Abfliessenden Energie.
Diese Bilanzen zeigen, das was ins System reingeht ist auch das was rausgeht.
Das wird sogar so gemessen, wie sie in unzaehligen Hinweisen darauf bestanden haben. Rein wie raus!
Ich habe sie auch darauf hingewiesen, das die Erhoehung der Temperatur nur dann erfolgt, wenn sie den Waermestrom als konstant betrachten. Es geht dann darum wie dick die Isolierung ist.
Wenn sie die Dicke gleich lassen fuert eine Verringerung des Waermestromes zu einer Abkuehlung.
Der Treibhauseffekt ist eine Funktion der Dicke der Atmosphaere und wie lange die Waerme von der Oberflaeche ausgehend zum Abstrahlungshorizont „braucht“.
Lieber Herr Müller,
ich habe den Eindruck, dass Sie dass Konzept der zusätzlichen Erwärmung der Oberfläche durch die Gegenstrahlung bzw. langwellige Einstrahlung verstanden haben. Ich habe nach wie vor ein Problemdamit zu verstehen, wie aus ca. 145Watt/m2 durchschnittlicher solarer Einstrahlung , die den Boden erwärmt, der dann wieder entsprechend seiner Temperatur abstrahlt in der Atmosphäre eine Gegenstrahlung von ca. 350 Watt/m2 entstehen kann, die ihrerseits in gleicher Weise wie Solarstrahlung am Tage und in der Nacht die Oberfläche erwärmt. Es steht doch fest, was von der Sonne kommt und das was von der Sonne kommt, geht auch wieder. Aber erklären Sie mir bitte, wie dieser enorme Energiezuwachs von der Atmosphäre bewerkstelligt wird.
Tom Oelschläger schrieb am 13/09/2022, 03:52:06 in 300021
Die erste Frage wäre, ob Sie die gemessenen Werte für realistisch halten oder denken, die wären gefälscht:
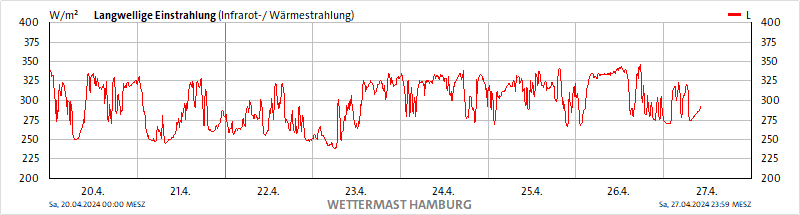
Wenn Sie denken, die 350W/m² bis 375W/m² am 9.9. wären nicht echt, kann man hier aufhören.
Für den Erdboden werden für diesen Zeitpunkt zwischen 16°C und 18°C ausgewiesen. Bei 15°C und einer Emissivität von .984 würde ein Körper etwa 384W/m² emittieren, was größer als die langwellige Einstrahlung ist. Klingt das auch noch plausibel?
Wenn am Erdboden im Mittel 390W/m² emittieren werden, ins All aber nur noch 240W/m² abgestrahlt werden – warum ist das dann Ihrer Meinung nach eine Verlangsamung der Abstrahlung („Diese verlangsamen allenfalls die Abstrahlung ins All.“) und nicht eine Verringerung der Abstrahlung ins All?
Diese Aussage „(Anmerkung: laut Ramanathan et al, Climate-Chemical Reactions gelangen 70 bis 90 Prozent der Abstrahlung von der Erdoberfläche und von den Wolken durch das Atmosphärische Fenster direkt in den Weltraum!).“ ist falsch. Der Text des Papiers lautet: „1.4.1 Radiatively active gase … This spectral region is referred to as the atmospheric“window,“ since in this region the atmosphereis relatively transparent. In the 7- to 13-µm region, roughly 70-90% of the surface and cloud emission escapes to space. Consequently, pollutants with strong absorption features in the 7- to 13-µm region are quite effective in enhancing the greenhouseeffect.“ Dort steht also, dass im Bereich des atmosphärischen Fensters 70%-90% der Abstrahlung direkt ins All geht, nicht generell 70%-90% der gesamten Abstrahlung. Fügt man Gase hinzu, die in diesem Fenster absorbieren (und es damit verkleinern), verstärkt man den Treibhauseffekt besonders effektiv.
Wenn diese Punkte geklärt sind, könnte man denke ich diskutieren, warum eine Verringerung der abgegebenen Energie zu einer höheren Temperatur führen kann …
Herr Oelschlaeger.
es geht denke ich nicht darum zu verstehen, wo die Leistungen herkommen.
1. Entspricht die Abgestrahlte Leistung nicht der Waermeleistung, da man die eingestrahlte Leistung kennen muss
2. ergeben sich die Leistungen entsprechend der Temperatur. Was man also verstehen muss, ist, warum die Temperaturen so sind, wie sie sind.
Die Atmosphaere bezieht den Grossteil der Waerme von der Oberflaeche. Und der Grossteil wird durch Latente Waerme und Konvektion uebertragen.
Im theoretischen Fall ist der Waermefluss durch Strahlung an der Grenze Oberflaechen und Atmosphaere Null, wenn beide die gleiche Temperatur haben und wir nur die Bandbreiten betrachten in denen beide Koerper strahlen und von einer sehr geringen Absorptionsdicke in der Atmosphaere augehen.
Damit uebertraegt dann Strahlung genausoviel Waerme wie die Waermeleitung.
Da aber die Atmosphaere nicht so ideal ist, gibt es auch einen Waermestrom von der Oberflaeche in die Atmosphaere.
Autor versucht, mit eigenen Waffen den Gegner zu fechten…
Ich persőnlich-als gelernte Laie -stimme eher Herrn Strasser.
Wissenschaft ist keine Glaubensfrage und auch keine Abstimmung von persönlichen Ansichten. Wissenschaft kann nur durch Wissenschaft bestätigt oder widerlegt werden.
@Bernd Palmer, es gibt keine Wissenschaft. Sie meinen etwas völlig anderes, das haben Sie aber nicht schreiben können, wohl weil Sie es bis heute nicht verstanden haben. ++ Und in Ihrer „Wissenschaft“ gibt es sehr viel Glauben, nur wird darüber nicht offen gesprochen. ++ Sie belieben zu scherzen und foppen dabei sich selbst. ++ Ich empfehle die Lektüre von Richard Feynman, bspw.. ++ Es gibt Daten und Interpretationen. Sehr viele Interpretationen in Ihrer „Wissenschaft“ sind purer Glaube. Jemand der in seinem Leben dieses extrem wichtige Thema noch nicht berarbeitet haben will, darf sich nicht Wissenschaftler nennen. ++ Sie dürfen nicht vergessen, Grundlage allen Wissens ist die wahre Aussage. Unsere Gegner bestreiten jedoch genau das und machen fröhlich Wissenschaft. Gemäß der Ansicht unserer Gegner ist das Wissenschaft was die Mehrheit entscheidet, meint. Und was die Mehrheit „denkt“, „denken“ soll, wird von wenigen (sehr reichen, bösartigen) Kriminellen kontrolliert. Die menschenverachtenden gottlosen Linken, Atheisten, haben zig falsche „Definitionen“ von Wahrheit entworfen, um die Massen zu betrügen. Der Multikulturalismus ist dabei jeden gültigen Wahrheitsbegriff zu zerstören um sich künstlich am Leben zu unterhalten. ++ Je früher Sie Ihr „Goldenes Kalb“ (Wissenschaft) platt machen, desto vernünftiger, besser für Ihr eigenes Denken. ++ Es gibt keine Wissenschaft. Niemand wird Ihnen zu Hilfe eilen, wenn Sie die mal brauchen sollten, als Verteidigerin. Niemand.
„Nehmen wir nun an, dass wir die Temperatur der Erde um 1°C erhöhen wollen.“
Man kann die Temperatur der Erde nicht um 1°C erhöhen. Die sog. Erdtemperatur, auch Global-Temperatur genannt, ist ein Mittelwert, mit dem man außer der Betrachtung der Zahl nichts weiteres anfangen kann.
Man kann die Temperatur von unzähligen einzelnen Schwarzkörpern durch Strahlung erhöhen und die so erreichten zusätzlichen Einzel-Energien summieren, um sich die Konsequenz erhöhter Strahlung anzusehen. Wer will, kann dann von den unzähligene Einzeltemperaturen der unzähligen Schwarzkörper einen neuen Mittelwert bilden, der aber nicht einmal zu einem Vergleich mit einem vorher ermittelten Mittelwert taugt. Dazu dürften sich die unzähligen einzelnen Schwarzkörper nämlich in Masse und thermischem Verhalten nicht verändert haben, also eine Erde im „eingefrohrenen“ Stillstands-Modus. So etwas können sich grüne Ideologen vorstellen, ernsthafte Physiker nicht. Es widerspricht dem dynamischen und niemals statischen Geschehen im gesamten Universum.
Dieser irrige Umgang mit Mittelwerten ist der Grundsatzfehler in den Betrachtungen des IPCC und der vermeintlichen Physik-Könner in Potsdam – egal wie laut ein Rahmstorf um sich schlägt oder mit wie vielen Gretas er sich umgibt.
Die Frage ist falsch. Denn es ist grundsätzlich die gleiche Frage, wie die Frage, wie die Atmosphäre 240 W/m2 ins All abgibt aber der dann Boden 390 W/m2 nach oben abstrahlt. „Woher kommt die „zusätzliche Energie“ von 390-240?“ Wer die Frage stellt, hat die Energiebilanz der Erde nicht verstanden.
Er
Fußnote: Die Vorstellung, dass die Wolkenrückkopplung positiv ist, ist ziemlich unwahrscheinlich. Erstens besagt das Prinzip von Le Chatelier, dass, wenn ein dynamisches Gleichgewicht (ein stationärer Zustand wie das Klima) durch eine Änderung der Bedingungen gestört wird, sich die Position des Gleichgewichts verschiebt, um der Änderung entgegenzuwirken und ein Gleichgewicht wiederherzustellen.
Wenn positive Rueckkopplung vorlaege, waere das System instabil und wuerde immer schneller werdend vom bisherigen Zustand wegwandern. Dies konnte weder in der letzten Zeit noch fuer fruhere Phasen beobachtet werden. Positive Rueckkopplung geht meistens schief, zb Rueckkopplungspfeifen wird nur durch Leistung des Verstaerkers begrenzt, Resonanzkatastrophen sind auch schon genug aufgetreten, zB beim Einstuerzen von Bauwerken durch pos. Rueckkopplung. Einigen AKW-Typen wird so ein instabiles Verhalten nachgesagt (Temp-Erhoehung bewirkt weitere, schnellere Temp-Erhoehung), was nur durch staendiges Nachregeln ausgeglichen weden kann, das auch schnell genug sein muss. (Entspicht einem umgekehrten Pendel).
Die Beobachtung schliesst also eine positive Rueckkopplung aus, da diese dann schon laengst aufgetreten waere, zb bei sehr viel hoeherem CO2-Gehalt in frueheren Zeiten.
Versuch einer Antwort: Liegt es an den unterschiedlichen Temperaturniveaus?
TOA: 255 K. Um auf 256 zu kommen, braucht es 3.8 W/qm zusätzlich.
Erdboden: 288 K. Um auf 289 zu kommen, braucht es 11 W/qm zusätzlich. Alles vereinfacht gerechnet mit epsilon = 1 und ohne sonstige Flüsse.
Die Frage, die hier gestellt wird, ist, wie funktioniert ein Perpetuum Mobile?
Eine Antwort darauf hat bisher noch niemand geben können. Daher besteht die Überzeugung, es gibt kein Perpetuum Mobile! Unterstützt durch die Erkenntnis, Energie kann sich aus sich selbst nicht vermehren, wie es auch der 1. HS der Thermodynamik klar besagt.
Es ist keine Erklärung des sog. natürlichen THE bekannt, die aus Sicht der Energiebilanz ausgeglichen wäre. Warum wohl?