Der Verfasser stellt dort eine einfache Energiebilanz an der Erdoberfläche auf und umgeht damit die komplizierten und großenteils unverstandenen Vorgänge in der Atmosphäre und in den Ozeanen. Dabei ist hervorzuheben, dass sich das irdische Leben in einer extrem dünnen Grenzschicht an der Erdoberfläche abspielt, während die Atmosphäre mit der Höhe rasch lebensfeindlicher, dünner und kälter wird. Gleichzeitig hat die Erdoberfläche eine deutlich größere Wärmespeicherkapazität als die umgebende Atmosphäre. Wobei sich die Atmosphäre in der Grenzschicht im ständigen Wärmeaustausch und Temperaturausgleich mit der Erdoberfläche befindet. Ein Ansatz, dem hier in etwas geänderter und verallgemeinerter Form gefolgt wird.
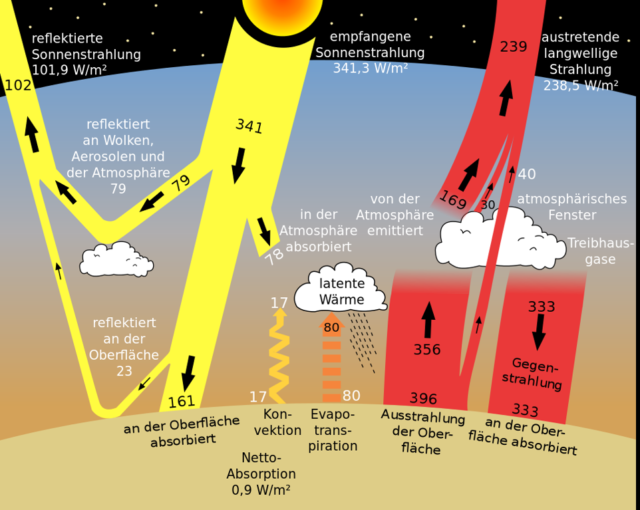
Das nachfolgende Strahlungsdiagramm nach Trenberth-Kiehl beinhaltet zwar ein physikalisch merkwürdiges Phänomen, nämlich die Generierung einer starken Gegenstrahlung in der Atmosphäre, die ausschließlich nach unten strahlt. Doch findet man in der Grafik recht detaillierte Zahlenangaben:
Gemäß obiger Grafik besteht an der Erdoberfläche ein Gleichgewicht aus eingestrahlter Sonnenenergie (So) und wieder abgegebener Energie in Form von Verdunstung (Evap), Infrarotstrahlung (Erad) und Konvektion (Kon).
Dieses Gleichgewicht wird um einen zunächst unbekannten Antrieb („forcing“) X erweitert:
So + Evap + Erad + Konv + X = 0
Der Antrieb X kann dabei unterschiedliche Ursachen haben – am geläufigsten ist der zusätzliche Strahlenantrieb durch vermehrtes CO2. Der Sonnenanteil So bleibt in dieser Bilanz konstant – Änderungen bei der Einstrahlung, z.B. durch veränderte globale Bewölkung, sind im Antrieb X enthalten. Ist der Antrieb X von Null verschieden und die Kühlterme Erad, Evap und Konv ändern sich monoton mit der Temperatur, dann stellen sich Gleichgewicht und Temperatur neu ein. Aus der neuen Gleichgewichtsbilanz erhält man dann die Temperaturänderung ΔT = T – T0, abhängig vom Antrieb X. To ist dabei die global gemittelte Ausgangstemperatur mit 15 ºC bzw. 288 K. Für den Startwert T = T0 gilt X = 0.
Zu der Erwärmung der Erdoberfläche tragen bei:
Sonne:
Gemäß obiger Grafik beträgt die an der Erdoberfläche im Mittel absorbierte Sonneneinstrahlung (So), abzüglich 0,9 Watt/m2 Nettoabsorption:
So = 160 Watt/m2
Zusätzlicher Antrieb X:
Wenn man den Antrieb X ausschließlich einem CO2-Anstieg zuschreibt, dann gilt:
X = 5,35 ⋅ ln (C/Co) [Watt/m²] mit der atmosphärischen CO2-Dichte C
Dieser „Strahlungsantrieb“ entsteht der Theorie zufolge durch spektroskopische Absorption und Emission bei den Resonanzlinien des Spurengases CO2, was in diesem Wellenlängenbereich den Energietransport verlangsamt und was vorwiegend in der dichteren, unteren Atmosphäre geschieht. Die logarithmische Abhängigkeit in der Formelbeziehung für X ist Folge der spektroskopischen Sättigung des CO2 in der Atmosphäre. Der Strahlungsantrieb wächst dabei mit zunehmendem CO2 immer langsamer. Wobei die Verdoppelung der CO2-Dichte C einen zusätzlichen Strahlungsantrieb von X= 3,7 Watt/m2 generiert. Was einer Temperaturerhöhung von 1,1 Grad (einige Autoren nennen etwas höhere Werte) entspricht und als CO2-Klimasensitivität definiert ist.
Zusätzlich gibt es positive Rückkopplung oder Verstärkung, z.B. durch vermehrten Wasserdampf, das bedeutendste Klimagas. Aber auch negative Rückkopplung oder Abschwächung des Strahlungsantriebs, z.B. durch Überdeckung der Absorptionsfenster von CO2 und Wasserdampf, Abkühlung durch vermehrte Wolkenbildung und Aerosole sowie weitere Wechselwirkungseffekte in einer komplizierten, großenteils unverstandenen Atmosphäre spielen eine Rolle.
Man kann sich den Temperaturanstieg der letzten 150 Jahre auch mit natürlicher (Rück-)Erwärmung seit der Kleinen Eiszeit erklären, wie es schon bei früheren Kalt- und Warmzeiten der Fall war – ganz ohne anthropogenes CO2. Wobei allerdings die Ursachen für die damaligen Temperaturänderungen nicht bekannt sind. Auch urbane Wärmeinseleffekte, Landnutzungsänderungen, Energiefreisetzung durch die Menschen, wahrscheinlich auch der Flugverkehr und natürliche periodische Einflüsse (z.B. ozeanische Oszillationen und variierende Sonneneinstrahlung, verstärkt durch den Svensmark-Effekt) tragen bei.
Die Behauptung von Alarmforschern ist falsch, man könne sich den neuzeitlichen Temperaturanstieg nur mit anthropogenem CO2 erklären.
Die Bezeichnung „X“ wird deshalb gewählt, weil der Antrieb X einer black box ähnelt, deren Inhalte man nicht genau kennt.
Wasserdampf-Rückkopplung:
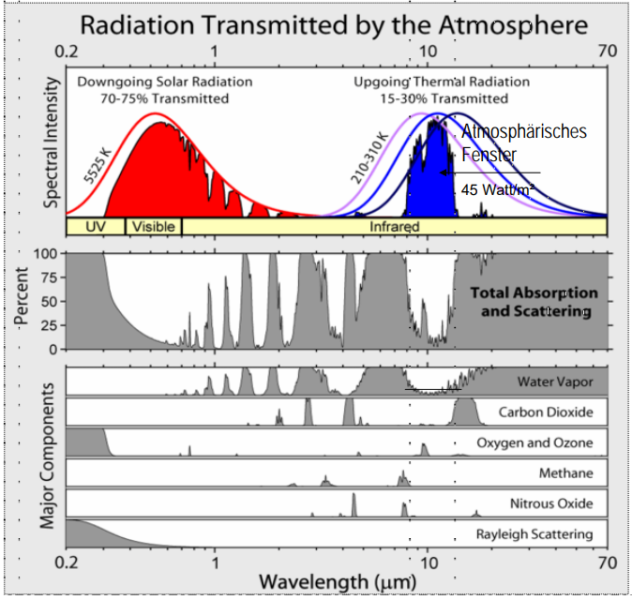
Die Rückkopplung durch zusätzlichen Wasserdampf wird in der Bezugsveröffentlichung aus nachfolgender Grafik für die spektroskopische Transmission in der Atmosphäre ermittelt:
Folgt man der zitierten Arbeit, trägt der Wasserdampf etwa 8 Watt/m2 zum Strahlungsantrieb bei – offensichtlich geschätzt anhand des atmosphärischen Fensters und der Reduktion der durchgehenden Strahlung (nach Trenberth-Kiel 40, in der Bezugsarbeit 45 Watt/m²) durch Wasserdampfabsorption und -streuung. Aufgrund von 7,5 Prozent mehr Wasserdampf pro 1 Grad Temperaturerhöhung wird demnach das Infrarot-Fenster um jeweils 0,6 Watt/m² weiter verkleinert. Was in diesem Modell der (positiven) Wasserdampf-Rückkopplung ΔR entspricht:
ΔR = 8 . (1,075 ΔT – 1) Watt/m2 mit ΔT = T – T0
Die Genauigkeit des Ansatzes soll hier nicht weiter hinterfragt werden. Von der Größenordnung her gehört ΔR zu den kleineren Beiträgen der Oberflächenbilanz. Außerdem ist die positive Wasserdampfrückkopplung ΔR ein Antrieb und in der eingangs aufgestellten Bilanz im Antrieb X mit enthalten. In den üblichen Klimamodellen verstärkt ΔR den Infrarot-Strahlungsantrieb der Klimagase und trägt dort zur Erhöhung der Klimasensitivität bei.
Kühlung der Erdoberfläche:
Verdampfung/Verdunstung:
Die in dem Strahlungsdiagramm (ganz oben) aufgeführte, relativ große Verdunstungswärme von 80 Watt/m2 lässt sich aus Niederschlagsmenge und spezifischer Verdunstungswärme offenbar recht gut ermitteln – weil sämtlicher Wasserdampf als Niederschlag und Tau zur Erde zurückkehrt.
Die Verdunstung von Wasser entzieht der Erdoberfläche Energie und transportiert diese in die höheren Atmosphärenschichten. Dort wird die Energie durch Kondensation (Wolkenbildung) wieder abgegeben und ins Weltall abgestrahlt. Durch das Abregnen der Wolken wird der Wasserkreislauf geschlossen. Für die Stabilität des Klimas ist von großer Bedeutung, dass die Verdunstungswärme stark abhängig von der Oberflächen-Temperatur der Erde ist. Diese Tatsache lässt sich an den Niederschlägen ablesen. Wir wissen, dass die Niederschläge dort am höchsten sind, wo die meiste Wärme von der Erdoberfläche abgeführt werden muss – am Äquator. Wir wissen auch, dass die Niederschläge auf der Erde mit der Erwärmung der letzten 100 Jahre zugenommen haben. Mit durchschnittlich 80 Watt/m² liefert die Verdunstung etwa 50 Prozent des Wärmetransports von der Erdoberfläche Richtung äußere Atmosphäre. Eine höhere Oberflächentemperatur führt zwangsläufig zu einer stärkeren Verdunstung weil Dampfdruck und Aufnahmefähigkeit der Luft für Wasserdampf ansteigen. Bereits ein Grad Erwärmung erhöht die Verdunstung und damit den Wärmetransport um 7,5 %. Bezogen auf den gesamten Wärmetransport von 80 Watt/m² sind das immerhin 6,0 Watt/m² zusätzlicher Kühleffekt an der Erdoberfläche. Die Verdunstung stellt also ein starkes Dämpfungsglied gegen Änderungen des Klimas dar.
Der Wärmetransport durch Verdunstung und dessen Zunahme mit der Temperatur bestimmen das Ergebnis maßgeblich. Für den Dampfdruck von Wasser lässt sich die Zunahme von etwa 7,5 % bei einem Grad Erwärmung verifizieren – z.B. hier. Bei der engl. Wikipedia heißt es: „The rate of evaporation in an open system is related to the vapor pressure found in a closed system.“ Aber was bedeutet „related to“? Lassen sich die Angaben in der Bezugsveröffentlichung bestätigen?
Hilfreiche Zahlen bietet nachfolgende Pool-Tabelle, vermutlich durch Messungen ermittelt. Man sieht dort gut, wie die verdunsteten Wassermengen mit der Temperatur zunehmen, in der Regel sogar um etwas mehr als 7,5%. Dabei ist RH die Relative Luftfeuchtigkeit und DEW PT der Taupunkt, Temperaturen in Fahrenheit.
Die Temperaturschritte von 2 ºF entsprechen jeweils 1,112 ºC. 68 ºF entsprechen 20 ºC und 86 ºF 30 ºC.
Dabei ist zu beachten, dass in den Tropen und in den Regenwäldern das meiste Wasser verdunstet. Auch steigt durch Wellengang und Wind die Verdunstung deutlich an – nach folgender Tabelle bis zu einem Faktor zwei.
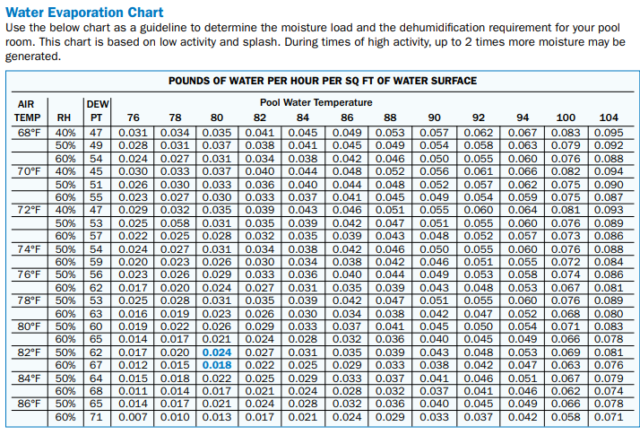Hingegen dürfte über den 29% Landfläche die Verdunstung niedriger sein, regional abhängig von Bodenfeuchte und Bewaldung. Eine mittlere Zunahme von Verdunstung und Wärmetransport um 7,5% je 1 ºC Temperaturerhöhung, wie in der Bezugsarbeit angenommenen, scheinen realistisch.
Als Formelbeziehung erhält man damit:
Evap = 80 ⋅ 1,075 ΔT Watt/m2
Evap ist dabei die Verdunstungswärme, ΔT = T – T0.
In der Bezugsveröffentlichung wird der Spezialfall ΔT = 1ºC behandelt.
Strahlung:
Folgt man der Strahlungsbilanz in der ersten Grafik oben, dann werden netto 63 Watt/m2 vom Boden abgestrahlt und davon etwa 40 Watt/m2 direkt in den Weltraum (in der Bezugsarbeit 45 Watt/m2). Die restlichen 23 Watt/m2 nehmen den „Umweg“ über die Atmosphäre. Entscheidend ist aber für die Betrachtung hier, wie viel Strahlung die Erdoberfläche verlässt.
Durch einen veränderten Antrieb X ändert sich die Temperatur T = T0 + ΔT und somit auch die Wärmeabstrahlung Erad mit der 4. Potenz von T:
Erad = 63 · (T/T0)4 Watt/m²
Konvektion:
Konvektion ist der Transport thermischer Energie durch fühlbare Wärme der Luftmassen. Der Antrieb sind Dichteunterschiede. Wird die Erdoberfläche wärmer, verstärkt sich die Thermik und transportiert mehr Energie in Richtung höhere Atmosphäre. Der Anteil der Konvektion am Wärmetransport ist mit knapp 11 Prozent (gemäß TK-Grafik) gering und dürfte gemäß folgender Beziehung mit der Temperatur zunehmen:
Konv = 17 · (1 + ΔT/T0) Watt/m2 mit ΔT = T – T0 und T0 = 288 K
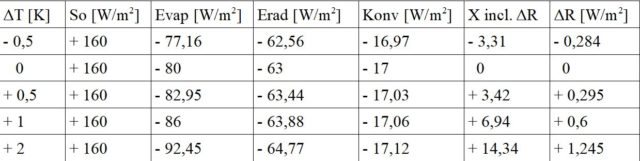
Naheliegend wäre jetzt, in die Oberflächenbilanz die oben aufgeführten Formelbeziehungen einzusetzen, um so die Beziehung zwischen X und ΔT auszurechnen. Einfacher und anschaulicher geht es, wenn man in nachfolgender Tabelle zeilenweise die Änderungen von X und ΔT vergleicht.
Bilanz
Eine Änderung des Antriebs X führt zu einer Temperaturänderung ΔT = T – T0 in der ersten Spalte. Mit der sich ändernden Temperatur T ändern sich auch die Kühleffekte. Es stellt sich ein neues Gleichgewicht ein, die Bilanz ist wieder ausgeglichen. Dabei kommen für den Antrieb X neben Klimagasen auch andere, z.T. natürliche Erwärmungsursachen in Betracht. Berechnet wird X aus der (negativen) Summe von So, Evap, Erad und Konv in der jeweiligen Tabellenzeile. Grundsätzlich sind auch negative Antriebe X möglich mit Temperaturrückgängen wie in der ersten Tabellenzeile, wie sie z.B. infolge bevorstehender solarer Minima eintreten könnten.
In der Bezugsarbeit wurde eine niedrige Klimasensitivität von 0,58 ºC ermittelt.
Was folgt daraus?
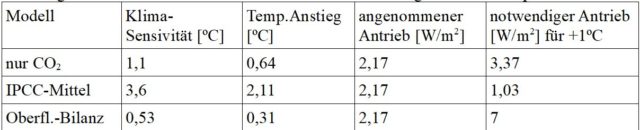
1) Man sieht in der Tabelle, dass der Antrieb X um ca. 7 Watt/m2 wächst für jeweils 1 Grad Temperaturerhöhung. Dabei erkennt man: Mit steigender Temperatur T = T0 + ΔT wachsen die verursachenden Antriebe X schneller als die zugehörigen Temperaturanstiege. Ein runaway-Effekt bei den Temperaturen ist deshalb nicht zu befürchten.
Bei spektroskopischer Erwärmung nur durch CO2 beträgt bei CO2-Verdoppelung der CO2-Antrieb 3,7 Watt/m2. Was in den bisherigen Klimamodellen einer Temperaturerhöhung bzw. CO2-Klimasensitivität von 1,1 Grad entspricht. Im Oberflächenmodell steigen bei einem gleichgroßen Antrieb die Temperaturen nur um 0,53 Grad – hauptsächlich als Folge der Verdunstungskühlung.
Was recht gut mit der Bezugsarbeit übereinstimmt. Berücksichtigt man ferner, dass X alle natürlichen und anthropogenen Antriebe mit enthält, dann ist eine Klimasensitivität von 0,53ºC sehr niedrig und zu vernachlässigen. Umgekehrt gilt genauso: Eine (utopische) Dekarbonisierung wird die Temperaturen kaum beeinflussen. In der Bezugsarbeit wird auf weitere Arbeiten verwiesen, die ähnlich niedrige Ergebnisse für die Klimasensitivität ermitteln.
Zur Erinnerung: Der IPCC gibt für die CO2-Klimasensitivität eine Spanne von 1,6 bis 5,6 Grad C an, aber nur mit einer Wahrscheinlichkeit von 66%. Was um eine Größenordnung höher ist.
In den letzten 150 Jahren sind die globalen Temperaturen offenbar um 1 Grad gestiegen. Das CO2 in der Atmosphäre dabei um knapp 50%, was einem CO2-Antrieb von 2,17 Watt/m2 entspräche. Dazu eine Vergleichstabelle für diesen Antrieb und den Auswirkungen auf die Temperaturen:
Bei der Rechnung gemäß Oberflächenbilanz ist noch viel Raum für weitere Antriebe wie z.B. Wasserdampf-Rückkopplung oder andere, nicht-anthropogene Antriebe. Das anthropogene CO2 alleine reicht für 1 Grad Temperaturerhöhung hier bei weitem nicht. Während der IPCC mit positiver Wasserdampf-Rückkopplung rechnet und diesen Wasserdampf-Zusatzantrieb der CO2-Klimasensitivität zuschlägt – nur das anthropogene CO2 ist alleiniger Übeltäter! Und mit seinen Computer-Klimamodellen viel zu hohe Temperaturen errechnet. Halbwegs passend wird es nur, wenn der IPCC die niedrigeren Klima-Sensitivitäten am unteren Rand seines Unsicherheitsbereichs verwendet. Auch gibt es kaum Platz für natürliche Antriebe, deren Existenz der IPCC im Wesentlichen bestreitet.
So spricht für das Oberflächenmodell unter anderem, dass die Temperaturprognosen des IPCC meist zu hoch liegen. Auch die höheren Landtemperaturen stimmen mit dem Oberflächenmodell überein, weil es an Land meist weniger Verdunstung gibt. Allerdings tragen dazu auch Wärmeinseleffekte, Landnutzungsänderungen und die Temperaturträgheit der Ozeane bei. Für das Oberflächenmodell spricht ferner, dass alle beteiligten Größen gut verstanden sind – im Gegensatz zu den Klimamodellen des IPCC.
2) Die Wasserdampf-Rückkopplung ΔR wurde in der Bezugsarbeit näherungsweise aus der Grafik oben für die spektrale Transmission in der Atmosphäre abgeleitet. Interessant ist die Größenordnung: Als Effekt zweiter Ordnung ist die (zusätzliche) Wasserdampf-Rückkopplung deutlich kleiner als der auslösende Antrieb – was plausibel ist.
3) Ein weiterer Aspekt ist bemerkenswert: Es wird der große Einfluss der Verdunstungswärme auf das Temperaturgeschehen deutlich. Mehr Verdunstung, wie es bei höherer Bodenfeuchte der Fall ist, wirkt kühlend, senkt dadurch die Temperaturen und umgekehrt.
Wenn die Herren Kowatsch und Kämpfe in Deutschland eine zunehmende Trockenheit aufgrund menschlicher Eingriffe in den Wasserhaushalt aufzeigen, dann führt die verringerte Verdunstungskühlung zu zusätzlicher Erwärmung.
Autor: Dr. Roland Ullrich ist Physiker und promovierte an der TU München über Plasmaphysik.Sein Berufsweg führte ihn von der Plasmaphysik, einem kurzen Ausflug in die Welt der Metallhydridspeicher zu einer überwiegend gutachterlichen Tätigkeit in der technisch-wissenschaftlichen Analyseabteilung einer Bundesbehörde.
Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"meine Glasscheibe zeigt, dass keine Strahlung vorhanden ist, somit ist die These von „Treibhauseffekt “ eigentlich schon tot. Aber rechnet man mit den Gesetzen und Formeln vom Max Planck, zeigen auch diese Resultate, dass es auch physikalisch unmöglich ist, dass das CO2, wie auch andere Gase in der Atmosphäre nicht so angeregt werden können, dass ie selber wieder Photonen emittieren! Die Berechnung mit dieser Formel, (Max Planck Strahlungsgestze)zeigen eindeutig, dass es unmöglich ist, eine angenommene Grössenordnung von ca 22 % (CO2 Anteil am THE) vom THE mit ca 324 W/M² = 71 W/m² zu begründen.“Die wichtigsten für den Treibhauseffekt verantwortlichen Treibhausgase auf der Erde sind Wasserdampf (Anteil 62 %) gefolgt von Kohlenstoffdioxid (Anteil 22 %), Methan (ca. 4–9 %) und troposphärisches Ozon (ca. 3–7 %). Ein exakter prozentualer Wirkungsanteil der einzelnen Treibhausgase auf den Treibhauseffekt kann allerdings nicht angegeben werden, da der Einfluss der einzelnen Gase je nach Breitengrad und Vermischung variiert. https://de.wikipedia.org/wiki/Plancksches_Strahlungsgesetz Rechnet man mit diesen Formeln, dann zeigt sich dass von der Erdstrahlung bei ca 15 Grad C – nach S+B = ca 390 W/m²nur ca 36 W/m² vom CO2 Gas absorbiert wird!!! (über 2 mikrometer Wellenlängen integriert 14 bis 16 Mikrometer! CO2 absorbiert im 15 mikrometer Wellenbereich). Somit zeigt auch die Phsysik, dass man aus ca 36 W/m² niemals eine Rückstrrahlung von 71 W/m² begründen kann. Auch die geringen Energie der Photonen im 15 mikrometer Wellenbereich ist nicht in der Lage, CO2 Moleküle so anzuregen, dass sie selber Photonen emittiern können. (siehe CO2 Laser) Ich frage mich immer wieder , wie man diese physikalischen klaren Resultate einfach ignoriert und den mittelalterlichen Aberglauben vom „Treibhauseffkt“, als lebensspendende Wärmequelle so lange am Leben hält – auch hier bei EIKE und weiter: Auch die Betrachtung und Berechnung (Max Planck) der Anzahl der 15 Mikrometer Photonen bei der angenommenErdstrahlung von 390 W/m², und der Anzahl der CO2 Molekül im ersten Kubikmeter Luft über dem Boden ( hier werden die Photonen von den CO2 und H2O Molekülen absorbiert), zeigen, ohne wenn und aber, die minimale Wirkung dieser Strahlung auf die ir-aktiven Moleküle in dr Luft! Dass diese Strahlung praktisch schon ca 1 Meter über dem Boden absorbiert ist, zeigt auch meinGlasscheibenexperiment.Am besten zu beobachten bei starker Sonneneinstrahlung! Je nach Bodenbeschaffenheit, bei mir dunkle Granitsteine, diese werden bis zu ca 57 Grad C (In der Nähe von Köln, um die Mittagszeit im Juni – gemessene Sonneneinstrahlung ca 1240 W/m² bei Kachelmann) warm und strahlen entsprechend. Eine Glassscheibe, ca 15 cm über dem Boden befestigt, wird auch fast 57 Grad warm!!!!Eine 2. Glasscheibe, ca 1 Meter über dem Boden erreicht nur noch die Lufttemperatur (Konvektion, keine Strhlung). Also, kann ich nur folgern, dass diese Berechnungen alle richtig sind und auch vom Glasscheibenexperiment bestätigt,von den angeblichen „Spezialisten“ auch hier bei EIKE ignoriert werden, weil es gegen deren Glaubensüberzeugungen und nicht um wissenschaftliche Erkenntnisse geht, leider.
Sehr geehrter Herr Dr. Roland Ullrich,Ihre Ausführungen zum Oberflächenmodell sind eine gelungene allgemeinverständliche Arbeit.Die Kommentare und Anmerkungen in höflicher und korrekter Form machen Freude beim Lesen.Wenn von Oberflächentemperatur die Rede ist,meinen Sie doch die Durchschnittstemperatur global, gemessen in der Luft und in 2m Höhe über dem Erdboden.Ist das so,oder habe ich etwas verpasst?Der Einfluss der oberflächennahen Temperatur auf den Ozeanen trägt bestimmt zu den Wärmetransportphänomen bei.Nach jahrelangem Suchen ist mir eine Temperaturreihe aus der Nordsee bekannt geworden.Hier ein kleiner Überblick: Versuch1 : Wärmespeicher OzeanVersuch2 :Original aus dem BSH (interaktive Auswahl für Nordseeboje3 wählen)
Mein erster Kommentar ist leider nicht mehr sichtbar, ich versuch’s noch einmal. Ich gehe davon aus, dass es im bodennahen Bereich einen Wärmeaustausch zwischen Boden und Atmosphäre gibt, sicherlich auch mit Gradienten, weshalb die Höhe der Messstationen normiert ist. Nachts hinkt die Bodenabkühlung hinterher, tagsüber erwärmt sich bei Sonneneinstrahlung der Boden dafür schneller. In diesem Zusammenhang ist auch darauf hinzuweisen, dass die Sonne den Boden erwärmt und nicht die Atmosphäre. Und die Atmosphäre folgt dann dem Boden. Dabei spielt die Verdunstungswärme eine wesentliche Rolle, über den dominierenden Ozeanen ganz besonders. Aber auch über Land sind Regenwälder, Bewaldung und Vegetation wesentliche Verdunstungsquellen.
Ihre Temperaturmessungen sind interessant. Leider sind Daten zu dem hier wesentlichen Anstieg der Verdunstungswärme mit der Temperatur nicht ganz einfach zu bekommen. Ich war deshalb schon recht froh, die gezeigte Pool-Tabelle zu finden, die die vomn Vorautor genannten 7,5% bestätigen. Zumindest zahlenmäßig sieht es so aus, als wäre die Verdampfungsmenge proportional zur Zunahme des Dampfdrucks mit der Temperatur, was nicht unplausibel wäre. Eine Fundstelle, wo dies physikalisch bestätigt wird, habe ich bisher leider nicht gefunden.
Kleiner Nachsatz: Man möge mir verzeihen, dass, im Gegensatz zu dem gebotenen Umgangston mit den Kollegen hier, mir in meinen Kommentaren zur Klimapolitik oftmals der Kragen platzt. Seit ich mich seit knapp zwei Jahren mit diesem Thema eingehender befasse, bin ich einfach nur fassungslos, was in Politik, Medien und auf der Straße in diesem Lande abläuft. Deshalb mein ganz großer Dank an EIKE, Kalte Sonne und andere kritische Portale, die die penetrante Klima-Verdummung nicht widerspruchslos hinnehmen! Zumindest so lange es noch geht…
Sehr geehrter Herr Dr. Ullrich,
„In diesem Zusammenhang ist auch darauf hinzuweisen, dass die Sonne den Boden erwärmt und nicht die Atmosphäre.“
Ohne Zweifel ist der überwiegende Teil der Wärmeenergieaufnahme der Atmosphäre auf die Erwärmung durch den Bodenkontakt zurückzuführen.
Warum eine geringe Erwärmung direkt durch die Strahlung ausgeschlossen sein sollte, erschließt sich mich nicht. Zumal im Eingangsdiagramm gewisse Mengen an Strahlenleistung als „in der Atmosphäre absorbiert“ gekennzeichnet sind. Die diese Leistung, über die Zeit gleich Energie, die Atmosphäre erwärmen muss um nicht der Thermodynamik zu widersprechen.
Zunächst mal betrachte ich das, was von der Sonne unten ankommt, so wie in der Grafik. Dass es da auch noch atmosphärische Einflüsse auf die Intensität der eintreffenden Sonneneinstrahlung gibt, ist sicherlich richtig: Das reicht von Aerosolen bis zum anthropogenen CO2, das nicht nur für die Verstärkung des CO2-Treibhauseffekts verantwortlich gemacht wird, sondern auch den eingestrahlten solaren IR-Anteil entsprechend verringert. Es gibt eine Vielzahl von positiven, oder wie hier, auch negativen Antrieben samt ihrer Verstärkungs- oder Abschwächungseffekte, die kein Mensch mehr ausrechnen kann und dem IPCC den erwünschten Spielraum für hemmungslose Übertreibungen bietet. Das Oberflächenmodell bietet den Vorteil, dass man den Gesamtantrieb erhält. Und wenn der Gesamtantrieb, was der Fall ist, deutlich niedrigere Temperaturanstiege bewirkt als in den Klimamodellen des IPCC, dann ist der Klima-Hype obsolet.
Ich habe Franks Rechnung nicht verstanden, Sie? Können Sie mir erklären, warum der Fehler eines Klimamodells mit der Zeit wachsen soll? Kann es sein, dass er nicht den Fehler im Klima, sondern den der Einzelwerte betrachtete?
Offensichtlich ist es so, dass insbesondere der bekanntermaßen riesige Wolkenfehler, der ja für sich genommen schon sehr groß ist, in einem Prognose-Szenario, in dem man sich etappenweise (von Projektionsfläche zu Projektionsfläche – so wurde es, soweit ich mich erinnere, genannt) dem Zielwert nähert, dramatisch anwächst. Dass dies fehlertheoretisch korrekt ist, habe ich Patrick Frank abgenommen.
Das ist meine Befürchtung, dass Frank einfach nur mathematisch eine Fehlerfortpflanzng gemacht hat, und dabei völlig ignoriert, dass die Fehlertoleranz mit der Zeit auch Zustände zuließe, die klimatisch unrealistisch sind. Eine rein mathematische Fehlerrechnung berücksichtigt ja nicht, ob der Wertebereich des Fehlerintervall überhaupt physikalisch realisiert werden kann. Der maximale Wolkenfehler wird ja nicht alleine durch stupide Anwendung des Fehlerfortpflanzunggesetzes bestimmt, sondern letztlich durch die physikalische Grenzen 0 und 1 des Bewölkungsgrades. Diese extrem weite Grenzen lassen sich sicherlich mit historischen Klimadaten weiter eingrenzen.
Dr. Roland Ullrich schrieb am3. Februar 2021 um 8:51
Es gibt da auch jede Menge andere Ansichten. Die ausführlichste Diskussion, die ich kenne, ist folgende auf Whatsupwiththat: Do ‘propagation of error’ calculations invalidate climate model projections of global warming? von Patrick Brown. Dem Artikel folgt eine ausführliche Diskussion zwischen Pat Frank und Partick Brown. Auch Roy Spencer hat sich dazu geäussert: Critique of “Propagation of Error and the Reliability of Global Air Temperature Predictions”.
@ Herrn Wörst „Diese extrem weite Grenzen lassen sich sicherlich mit historischen Klimadaten weiter eingrenzen“.
Woher nehmen sie den Optimus? Die auffallend große Unsicherheitsspanne bei den Klimamodellen des IPCC, wie auch in meinem Artikel angegeben, hat sich in den letzten 30 Jahren eher vergrößert. Und, worauf ich bereits hingewiesen habe, die Wechselwirkungen in der Atmosphäre, auch in den Ozeanen, sind derart komplex, da kann der IPCC noch lange an seinen Computerstellschrauben drehen, bis er ein zukünftige Klima-Entwicklung verlässlich vorhersagen kann. Nicht einmal hinsichtlich der Vergangenheit klappt es mit den Modellen richtig… Wurde ihm ja auch schon ins Stammbuch (respektive in die ausführlichen Klimaberichte) geschrieben. Aber sowas wird ignoriert, passt nicht zur Aufrechterhaltung der Klimahysterie. Am Ende würde dann gar die Rechtfertigung für den IPCC und seine Alarmforschung in Frage gestellt…
„….warum der Fehler eines Klimamodells mit der Zeit wachsen soll?“
Das heutige Wettermodell beschreibt in relativ gute Annäherung das Wetter von morgen, beim Wetter in 3 Wochen ist die Fehlerrate schon so groß, dass die Prognose ziemlich unrealistisch ist, und eine heutige Prognose über das Wetter zu Weihnachten wäre eine reine Spekulation. Letzteres gilt für alle Klimamodelle
Es ist kein mathematischer Fehler, kein Fehler der Einzelwerte sondern ein Grundsatzfehler. Es steht jedem frei, den Gegenbeweis anzutreten, indem er mit seiner Simulation das Wetter für Weihnachten exakt vorrechnet. Dann würde ich in 11 Monaten das Gegenteil behaupten!
Der Grundsatzfehler ist bei Ihnen, indem Sie die Wettervorhersage mit einer des Klimas verwechseln. Bei letzterer ist das Ziel, nur den mittleren Wetterzustand zu treffen. Als anschaulicher Vergleich: wer im Lotto gewinnt, ist unmöglich auszurechnen, wieviel Leute aber schon.
Danke für den Vergleich, der Ihren Grundsatzfehler zum Grossteil bestätigt. Bei 6 aus 49 beträgt die Wahrscheinlichkeit rund 14 Mio, dass bedeutet aber nicht, dass bei 28 Mio Tipps exakt 2 Sechser dabei sind.
Ein Versuch “ den mittleren Wetterzustand zu treffen“ ist nun mal Selbstbetrug, wenn man keine Ahnung hat, wie sich das Wetter langfristig entwickelt.
Die Formel im Hauptartikel:
ist unvollständig und hat falsche Vorzeichen.Entweder muss So negativ in die Formel eingehen oder die abgeführten Energieanteile.Da von Energie und nicht von Wärme die Rede ist, muss man die Formel mit dem Anteil der atmosphärischen Strahlung erweitern und es gibt keinen Bodenfluss.Gerade der Bodenfluss ist bei der Behandlung von Klimaschwankungen eine der Wichtigsten Grössen. Im Bodenfluss ist die Ozeanzirkulation mit enthalten. Der Einfluss der Ozeane auf Klimaschwankungen sollte bekannt sein. Diese Größe sollte man auch nicht bei der Bestimmung des THE ausklammern.
Werner Schulz schrieb am2. Februar 2021 um 2:24
Im Artikel wird E_rad mit 63W/m² netto angegeben, ist also offensichtlich die Differenz zwischen Abstrahlung von der Erdoberfläche und Einstrahlung aus der Atmosphäre.
So ist es! Und nur so stimmt die Bilanz, auch bei T&K.
Das müssen Sie differenzierter sehen. Eine Klimaprojektion für die nächsten 100 Jahre ist wesentlich einfacher zu machen als für die nächsten 10.000 Jahre oder das Klima der letzten Eiszeit. Das Klimasystem lässt je nach Zeitskala physikalisch nur begrenzte Änderungen zu, daher macht es keinen Sinn, alle Unsicherheiten pauschal in einen Topf zu werfen und für jeden Zeithorizont als gleichermaßen maßgeblich anzunehmen.
Die Frage war auch gar nicht nach der Verlässlichkeit von Klimamodellen, sondern nach der von Franks Rechnung – Sie erinnern sich.
Wie Herr Müller schon verlinkt hat ist Franks Rechnung höchst zweifelhaft.
PS: die Kunst des Trollens besteht darin, möglichst lange als nur blöd zu wirken.
=> Wie Herr Müller schon verlinkt hat ist Franks Rechnung höchst zweifelhaft.
Die Betrachtung der Fehlerfortpflanzung gilt nur für methodisch/physikalisch korrekte Berechnungen, in die lediglich Grössen mit geringen (bekannten) Fehlern eingehen. Bei IPCC sind diese Voraussetzungen garnicht erfüllt, wenn die CO2-Verdoppelungssensitivität schon um 500% zu hoch ist und 300% Fehlerbereich aufweist. Deren ECS von 3±1,5 Grad ist ein FAKE aus (willkürlich um den Faktor 4 reduzierten) solar-ozeanischen Ausgasungsdaten (!) von Eisbohrkernen, welches mit der strahlungsphysikalischen Klimasensitivität des CO2 NICHTS ZU TUN HAT. Deshalb musste auch ein exorbitantes Feedback (Faktor 2,7) erfunden werden.
„ausführliche Diskussion zwischen Pat Frank und Partick Brown“
Diese Diskussion habe ich mir auch angesehen, brachte mich aber nicht weiter. Weil, zumindest anfänglich, Pat Frank schon nicht ganz leicht zu verstehen ist, erst recht eine verzwickte Expertendiskussion. Und durch die engl. Sprache wird es nicht einfacher, zumindest beim Hörverstehen. Doch Pat Frank hat es immerhin zu einer begutachteten Fachveröffentlichung gebracht – bei derart viel Widerstand von der Alarmfraktion eine wahre Meisterleistung! Bei der Unmöglichkeit einer seriösen, langzeitlichen Klimamodellierung wäre es ein weiterer Grund für die Alarmforschung, endlich aufzugeben. Stattdessen wird bei uns dekarbonisiert bis zur Selbstvernichtung…
Dr. Roland Ullrich schrieb am 4. Februar 2021 um 11:09
Man kann sich den Expertenteil sparen und sich auf die für den normalsterblichen verständlichen Teile konzentrieren – in diesem Fall die Diskussion über sowas triviales wie die Bestimmung einer mittleren Geschwindigkeit. P.Brown will anhand dieses einfachen Beispieles verdeutlichen, warum er der Meinung ist, dass P.Frank falsch liegt, wenn er aus W/m² einfach (W/m²)/year macht. Zusammen mit dem abschliessenden Kommentar von P.Bown bekommt man ein gutes Gefühl für die Art der Diskussion.
Verstehe ich nicht. Sind Sie etwa der Ansicht, das Ziel einer wissenschaftlichen Veröffentlichung sei es, Widerstand unter Wissenschaftlern hervorzurufen? Das erscheint mir ziemlich wissenschaftsfremd.
Herr Mueller,
das ist zahlenmäßig vielleicht richtig, aber in der Formel ist dieser Zusammenhang nicht ersichtlich und falsch. Immerhin könnte man ja vom Wärmefluss reden und nicht vom Energiefluss.
Sie sind doch einer der jenigen die darauf bestehen, das die Oberfläche nicht nur 62 W/m2 abgibt.
Auf den anderen Fehler mit dem Vorzeichen gehen sie nicht ein. Ich nehme an das sie mathematisch S0 einfach negativ angeben und dann stimmt es wieder.
Der physikalische Zusammenhang in der Gleichung ist jedoch falsch.
Der Bodenfluss fehlt auch!
Keine Blumen heute!
Werner Schulz schrieb am 2. Februar 2021 um 13:23
Ich kann lesen und wenn der Autor E_rad als Differenz zwischen infraroter Ein- und Abstrahlung definiert, kann ich erst mal damit leben, wenn das beim ersten Überfliegen keine Konsequenzen hat. Wenn der Artikel behaupten würde, es gäbe keine Abstrahlung aus der Atmosphäre in Richtung Boden, dann hätte ich vielleicht was gesagt …
Wenn man viele Texte zu dem Thema liest, findet man öfter Darstellungen, die die Richtung der Strahlung über das Vorzeichen angeben. Also auch nichts, worüber man stolpern muss, man muss den Artikel nur lesen. Und dort bekommen die eingehenden Ströme ein positives, die abgehenden ein negatives Vorzeichen.
Das macht man üblicherweise in der Formel und nicht bei den Werten!
Spock wieviel Strahlung kommt heute von der Sonne?
-1462 W/m2!
Alles klar! Keine Blumen heute!
Und noch was, das ganze Gerede von +0.9 W führt zu einer Erwärmung ist laut der Formel falsch.
Wenn sie X auf die andere Seite stellen, dann kriegt es ein negatives Vorzeichen.
Das heisst + 0.9 W/m2 führt zu einer Abkühlung. – 0.9 W/m2 zu einer Erwärmung.
Das is ja nu elementare Mathematik. Betrachten sie bitte die Vorzeichen in der Ergebnistabelle!
Es geht hier um Physik! Bei ihnen ist ein negativer Wert von X eine Erwärmung!
Es gibt in der Physik auch keine negative Strahlstärke. Versuchen sie das mal mit dem SB Gesetzt zu berechnen.
Die Formel fuer Energiefluss muss die Flussrichtung schon vorgeben, sonst kriegen sie falsche Ergebnisse oder so Sachen wie ein negativer Wert von X führt zur Erwärmung!
Ihre Kommentar ist nicht nur unbefriedigend, sondern zeugt auch davon, das sie diese Kritik falsch verbuchen.
Ich würde an Ihrer Stelle nachbessern. Bei Ihrem Stand können sie es sich nicht leisten grundlegendes Physikverständnis nicht genau umzusetzen.
Seien Sie nicht albern. Es gibt auch keine Geldmünzen oder -scheine mit negativem Geldwert, trotzdem kann man einen negativen Kontostand erreichen. Denken Sie erstmal nach, bevor Sie sowas schreiben. Hier geht es um die Bilanz am Boden, welche die Änderung (!) des (stets positiven) Wärmeinhalts des Bodens quantifiziert. Die Änderung kann positiv (i.a. bewirkt das Temperturzunahme) wie negativ sein. Der Term Sonnenstrahlung hat natürlich konstantes Vorzeichen (hier positiv für Zufuhr gesetzt).
Lieber Herr Wörst,
ich sehe sie setzen sich nicht wirklich mit meinen Einwand auseinander.
Die Formel ist falsch.
Die Bilanzierung ergibt entweder eine negative Einstrahlung der Sonne oder wie im Ergebnis von der Tabelle im Haupteintrag negative Konvektion und Abstrahlung.
Das heisst durch das negative Vorzeichen steht im Ergebnis das Konvektion und Strahlung in der gleichen Richtung wirken wie die Sonne. Diese fügen aber der Oberflächer keine Energie hinzu sondern ab. Die Bilanz geht nicht auf! Alle Energieflüsse gehen in die gleiche Richtung!
Vielleicht arbeiten sie die Formel einfach mal vom Anfang aus
So + atmRad + Bodenwaermefluss = Evap + Erad + Konv
Das wäre das Gleichgewicht.
Die Differenz X taucht nicht auf, das sie kein Waermefluss darstellt sondern nur die Differenz ist nach der sie suchen wenn sie alle bekannten Werte einsetzen.
Die Formel
So + Evap + Erad + Konv + X = 0
folgt aus der Energieerhaltung. X ist der Wärmefluss in die Wärmespeicher Q (Atmosphäre,Ozean,Cryosphäre,Boden usw.). Mit X= -dQ/dt folgt
So + Evap + Erad + Konv = dQ/dt
dQ/dt wird hauptsächlich der Erwärmung der Ozeane zugeschrieben. Vergleicht man Messungen von dQ/dT mit dem Defizit X des Strahlungsflusses TOA Jahr für Jahr, stellt man fest, dass auch in den Klimawissenschaften noch viel dunkle Energie existiert.
Exakt, bei mir hieß diese Größe H.
Herr Berberich,
Das Energiegleichgewicht wird durch diese Formel beschrieben:
So + atmRad + Bodenwaermefluss = Evap + Erad + Konv
Nach Umstellung sieht diese so aus:
So + atmRad + Bodenwaermefluss -Evap – Erad – Konv = 0
Das Defizit x ist kein wirklicher Energiefluss sondern nur eine Differenz mit gleicher einheit. Die Formel so wie unten.
So + atmRad + Bodenwaermefluss -Evap – Erad – Konv = x
fur x = 0 sind die Energieflüsse ausgeglichen
fur x > 0 haben wir eine Erwärmung durch Verringerung der Abflüsse. Die Annahme wäre, das sich die Zuflüsse nicht ändern.
fur x < 0 haben sie eine Abkühlung und die Abflüsse überwiegen.
Der Energiebetrag von X stammt immer aus den Energieflüssen auf der Linken Seite.
Exakt, klar, dieses Phänomen ist klar und kalkuliert die Lottogesellschaft ein, sonst wäre sie schnell bankrott, genauso geht es Versicherungen. Beide rechnen nur mit statistische Verteilungen, wen genau von den Kunden es trifft, ist für ihre Kalkulation egal. Genauso ist es mit den Klimamodellen, Wettervorhersage ist nicht gefragt und sowieso unmöglich. Demnach ist es auch unsinnig, solches zu unterstellen. Denken Sie mal nach.
Herr Wörst, mein Nachdenkapparat läßt mich kaum in Stich, ich schaffe es sogar, an der richtigen Stelle zu antworten.
Und Sie offenbaren Ihr Naturverständnis, indem Sie Kalkulationen von Lottogesellschaften mit Berechnungen von physikalischen Prozessen vergleichen. Im Falle des Klimas haben Sie mit Ihrer Analogie sogar recht: Bei einer Ziehung mit 28 Mio Tipps können 3 Sechser dabei sein, oder aber auch kein einziger. Einer Klimasimulation kann eine Temperatur-Erhöhung von 3 Grad oder auch von Null Grad berechnen. Was zum Schluß zutrifft, weiß nur der liebe Gott. In beiden Fällen!
Ich darf diesmal gnädigerweise ihnen direkt antworten, denn die Antwortoption ist jetzt vorhanden. Sie haben die Analogie falsch gezogen:
Resultat einer Lottoziehung = Wettervorhersage
Gesamtheit der Lottoziehungen = Klima
Änderung des Satzes der Kugeln (statt 1 bis 49 zu 11 bis 59 oder so) entspricht analog der Klimaänderung
„Gesamtheit der Lottoziehungen = Klima“
Besser wird es nicht, Herr Wörst. Ob Sie nun die Temperaturänderung würfeln, Kugeln ziehen mit eingetragener Klimaänderung (nicht nur einmal sondern „die Gesamtheit“ von mir aus), oder mit ihrer Simulation tippen, interessiert Mutter Natur nicht, ebenso den lieben Gott. Es kommt anders oder eine Übereinstimmung ist zufällig.
Mit funktionierenden Nachdenkapparat ist schnell erkennbar, dass die Anzahl „Antworten“ auf „Antworten“ beschränkt ist, wenn die letzte Ebene erreicht ist, muss man die letzte „Antworten“ Option darüber drücken, um den eigenen Kommentar exakt darunter zu bekommen. Es ist aber schon anderen aufgefallen, dass manchen das nachdenken schwer fällt.
Mit Ihrem Dogmatismus kommen Sie nicht weiter.
@ Dr. Roland Ullrich: Wie wird das IR-Spektrum von bis zu 120°C (@ S0) auf der Tagseite (generell S0 (1-ALBEDO)*COS(Zenitwinkel)) mit dem ominösen „Faktor4“ gemittelt, um analog zu dieser Abbildungen 6 B auf 4x das IR-Spektrum von -18°C (@235W/m²) zu kommen – insbesondere: Wo bleiben die höheren IR-Frequenzen?
Ich wage es jetzt nicht, von global und zeitlich gemittelten solaren Einstrahlwerten, wie sie offenbar auch von der Klima-Community regelmäßig benutzt werden, sonst gäbe es die Diagramme nicht, auf zeitlich sehr variable Temperaturmaxima auf der Tagseite in ausgewählten Zonen zu schließen. Dabei gibt es gegenläufige, Temperatur-reduzierende Prozesse wie die z.B. Verdunstungskühlung im Oberflächenmodell und den Temperaturausgleich mit den umgebenden Ozeanen. Die wiederum mit ihren Strömungen für eine Annäherung von polaren und äquatorialen Temperaturen sorgen. Wodurch die Temperaturunterschiede zwischen den Polen und dem Äquator um etwa 50 % reduziert werden, wie wir in einem EIKE-Beitrag neulich gelernt haben.
In Bild 1 folgt der Wärme-Transport (Konvektion und latente Wärme) dem Strahlungs-Transport, d.h. er erfolgt nur in vertikaler Richtung. Diese Annahme ist bei der realen Erde für den Strahlungstransport näherungsweise richtig, für den Wärmetransport nicht. Als Folge kann man mit einem solchen Modell nicht die Temperaturverteilung auf der Erde richtig beschreiben und noch weniger deren Veränderung. Man kann behaupten global mittelt sich der meridionale Wärmetransport heraus. Ich bezweifele dass diese Annahme richtig ist.
Bitte beachten: Abbildung 1 gibt an, wieviel Wärme die Erdoberfläche im Mittel durch Verdunstung, Konvektion (und Strahlung) verlässt. Richtungen spielen dabei keine Rolle, sie sind in der Mittelung berücksichtigt. Temperaturverteilung auf der Erde kann und will sowohl die Grafik als auch das Modell nicht beschreiben, sondern nur globale mittlere Werte und hier, im Oberflächenmodell, deren Änderungen mit der mittleren Temperatur. Wobei ich allerdings die Annahme zugrunde lege, dass bei z.B. 1 Grad höherer Temperatur die Wärmeabgabe durch Verdunstung jetzt nicht einem komplett anderen Muster folgt. Etwa, weil sich die Windgeschwindigkeiten durch 1 Grad Temperaturerhöhung weltweit verdoppeln, wofür es keine Hinweise gibt. Am meisten muss man sich den Kopf zerbrechen, wie groß die mittlere Zunahme des dominierenden Wärmetransportes durch Verdunstung mit der Temperatur tatsächlich ist. Aufgrund der Zahlen, die ich gefunden habe (wenn es noch bessere gibt, würde ich es sehr begrüßen) scheinen die 7,5 % Zunahme je 1 Grad C Temperaturerhöhung, wie sie auch in der Vorgängerarbeit genannt werden, eher am unteren Ende zu liegen – nicht zuletzt wegen Wellengang und Wind. Ein Wert höher als 7,5% würde die Temperatur noch stärker stabilisieren bzw. würde ein gleichgroßer Antrieb noch weniger Temperaturanstieg bewirken. Erst in Punkt 3) der Schlussfolgerungen mache ich eine naheliegende, nicht mehr globale Aussage zu den Landtemperaturen, wonach zunehmende Trockenheit die Verdunstungskühlung verringert und dadurch einen weiteren Temperaturanstieg fördert.
„Aufgrund der Zahlen, die ich gefunden habe (wenn es noch bessere gibt, würde ich es sehr begrüßen) scheinen die 7,5 % Zunahme je 1 Grad C Temperaturerhöhung, wie sie auch in der Vorgängerarbeit genannt werden, eher am unteren Ende zu liegen“
Ihre Parametrierung der Skalierung des Verdunstungswärmestroms Evap mit der Bodentemperatur ist zweifelhaft. Wie ich Sie verstanden habe nehmen Sie an, Evap würde proportional zum Dampfdruck e skalieren. Das ist anzuzweifeln. Zwar steigt der Dampfdruck mit der Temperatur in der Form ca. 7.5%/K aber das hat nichts mit der Verdunstungsrate zu tun. Evap ist proportional zur Verdunstungsrate. Deren Skalierung mit der Temperatur ist global für die Erde sicher eine andere als für ein Pool im Garten.
Das Problem mit realistischen Verdunstungsrate habe ich auch gesehen, wie meinem Text zu entnehmen ist. Hier zuverlässige Zahlen zu finden, ist nicht ganz einfach. Den Autor der voraus gegangenen Arbeit zu fragen, dessen Zahlen ich im Endeffekt bestätige, war leider nicht möglich. Die Zahlen in der Pool-Tabelle übertreffen in der Regel die 7,5 % und offenbar zurecht wird dort darauf hingewiesen, dass Aktivität im Wasser (Wellen!) diese Zahlen erhöhen können. Auch Wind wird die Wärmeabgabe durch Verdunstung zweifellos erhöhen. Dafür gibt es über Land (29%) sicherlich teils niedrigere Werte. Die Größenordnung halte ich aber insgesamt für bestätigt und somit auch den relativ großen Beitrag, der auf die Wärmabfuhr durch Verdunstung entfällt.
Statt persönliche Einschätzungen über etwas weit hergeholten Ingenieure für Swimmingpools sollten für den Parameter dEvap/dT meteorologische Fachpublikation zu Rate gezogen werden, denn das ist ja ein wichtiger Parameter. Ohne solide wissenschaftliche Referenzen, wirkt der Artikel etwas „gezwungen alternativ“.
Herr Wörst, wenn Sie die Zahlen finden, nach genau denen ich auch gesucht habe, dann bin ich Ihnen sehr dankbar! Die Unsicherheitsspannen des IPCC, die eher größer sind, samt den vernichtenden Fehlerfortpflanzungsrechnungen z.B. eines Patrick Frank, ist das jetzt für Sie perfekte Physik?? Obwohl seit Jahrzehnten eine Milliardenforschung dahinter steht? Ingenieurs-Tabellen mit realistischen Zahlen sind oftmals verlässlicher und aussagekräftiger als irgendwelche klimatologische Spezialuntersuchungen, die sich im Formel- und Parameterdschungel verlieren. Und die sich in der Regel mit dem unverstandenen, komplizierte Phänomen der Kondensation von Wassertröpfchen befassen. Viel Erfolg bei der Suche nach brauchbaren Daten!
Ihre Energie-Bilanz „So + Evap + Erad + Konv + X = 0“ ist eine stationäre globale Bilanz. Besser wäre es eine lokale transiente (zeitabhängige) Bilanz zu machen und dann global zu mitteln. In diesem Fall kann man Wärmeströme durch Wind und Wasser berücksichtigen. Wenn bei erhöhter Eigenstrahlung der Atmosphäre der Strahlungstransport in das All behindert wird, gewinnen diese Wärmeströme an Bedeutung. Sie führen zu einem homogeneren Temperaturprofil der Oberfläche. Homogenere Profile sind mit einer höhere globalen Oberflächen-Temperatur verknüpft. Eine Analyse des HADCRUT 4.6 Datensatzes ergibt folgende globale Mittel-Temperaturen mit Standard-Abweichungen in °C:
1900-1930; 13,60+/-15,72;
1930-1960; 13,88+/-15,63;
1960-1990; 13,98+/-15,52;
1990-2019; 13,44+/-15,42;
Die Abnahme der Standard-Abweichung um 0,3 °C zeigt die Homogenisierung. Ich würde schätzen dass von den 0,8 °C Temperatur-Erhöhung etwa 0,3°C auf den Effekt der Homgenisierung zurückzuführen sind. Dies bestätigt die Aussage Ihrer Überschrift.
Ihr Vorschlag wirkt perfekt. Aber es ist schon schwierig, globale Werte für die Wärmeabgabe durch Verdunstung zu finden. Ein „lokale transiente Bilanz“ global zu mitteln einschließlich der Wärmeströme durch Wind und Wasser – ich glaube, das wird noch weitaus schwieriger. Allerdings bin ich nach wie vor überzeugt, eine „stationäre globale Bilanz“ leistet im Rahmen des Oberflächenmodells eine ganze Menge. Was fehlt, sind genauere weltweite Daten zu der Wärmeabgabe durch Verdunstung. Ich verfolge schon länger Ihre bemerkenswerte Fündigkeit bei relevanten Daten – kennen Sie evtl. Fundstellen für die hier benötigten Verdunstungsdaten? Interessant auch Ihre Schlussfolgerungen aus den HADCRUT 4.6 Datensatz, wobei ich hier Ihrer Expertise folgen muss.
„Was fehlt, sind genauere weltweite Daten zu der Wärmeabgabe durch Verdunstung.“ Leider kann ich momentan auch nicht viel dazu beitragen. Ich nehme in meinem ortsaufgelösten Energiebilanz-Modell an, dass der Fluss der latenten Wärme proportional zum H2O-Sättigungs-Dampfdruck ist. Besser wäre sicher der H2O-Dampfdruck. Vielleicht hilft mir die Arbeit von Peng 2013 Estimation of evapotranspiration using satellite TOA radiances weiter. Herzlichen Dank für den anregenden Artikel.
=> Bei spektroskopischer Erwärmung nur durch CO2 beträgt bei CO2-Verdoppelung der CO2-Antrieb 3,7 Watt/m2. Was in den bisherigen Klimamodellen einer Temperaturerhöhung bzw. CO2-Klimasensitivität von 1,1 Grad entspricht
Herr Dr. Ullrich, abgesehen davon dass bei IPCC der „Strahlungsantrieb“ für TOA gilt sowie ohne Wolken, Wasserdampf und Hin- und Herstrahlung, liegt am Boden offenbar eine eine grosse Diskrepanz vor. Mit S=Sigma•T^4 ist bei mir deltaS/deltaT=4S/T. Bei 288 K und 391 W/m² ergibt das 5,43 W/m² pro Grad oder für 3,7 W/m² 0,68 Grad.
Bei Ihnen berechne ich aus S=63•(T/To)^4 ebenfalls ein deltaS/deltaT zu 4S/T, aber für eine Erhöhung von 288 um 1 K auf 289 K ergibt sich nur 0,88 W. Sie verwenden offenbar für die Strahlungssensitivität einen Wert der um den Faktor 6,2 zu gering ist.
Das könnte die Ursache dafür sein dass bei Ihrem Ansatz nicht die Strahlung, sondern die Verdunstungskühlung die grösste Rolle spielt. M.E. sollte man auch davon ausgehen dass deren Wärme bei Kondensation nicht zu 100% in den Weltraum abgestrahlt, sondern etwa zu 50% zurückkommt. Ausserdem wäre ggf. auch ein Wärmetransport des Wassers zum Boden zu beachten. Dennoch liegt Ihr Ergebnis von 0,53 Grad für ECS in der Nähe von etwa 0,63 Grad (MODTRAN, Harde, Dietze).
Herr Dr. Ullrich, beim IPCC-Strahlungsantrieb von 3,7 W/m² für jede CO2-Verdoppelung muss noch die Hin- und Herstrahlung zwischen Atmosphäre und Boden berücksichtigt werden. Da die IR-Absorption etwa 77% beträgt und damit die Gegenstrahlung 38,5% der Bodenabstrahlung wird (und in dieser auch als Re-Emission enthalten ist), ergibt sich 0,68/(1-0,385)=1,11 Grad.
Diese Berechnungen liefern den Basiswert für das global gemittelte Strahlungsmodell, in dem in erster Näherung die Atmosphäre für Sonnenlicht transparent sowie Wolken und Feuchtkonvektion konstant angenommen werden. Dazu kommt als Feedback der Fake-Faktor 2,7 der dann 3,0 Grad ergibt. Weitere Verbesserungen (z.B. Wolken, Wasserdampf, Konvektion, Mittelwerte wegen T^4) können dann ggf. noch als Korrekturfaktoren eingebracht werden.
Herr Dietze, ich halte mich an das T&K-Strahlungsdiagramm und an die ganz ähnlichen Energiebilanzdiagramme. Und da sind es 63 Watt/m² bzw. geringfügig abweichende Werde, die abgestrahlt werden. Sonst geht die Bilanz nicht auf!
Herr Dr. Ullrich, dass Sie sich an das T&K-Strahlungsdiagramm halten und an 63 Watt/m² als Differenz zwischen 390 W/m² Abstrahlung und 150 W/m² Gegenstrahlung (was 240 W/m² und nicht 63 ergibt) ist GROB FALSCH. Sorry. Bitte lesen Sie nach unter https://www.fachinfo.eu/dietze2018.pdf
Herr Dietze, vielleicht so: Wenn ich in der Grafik dem Bild von einer ausgehende und einer Gegenstrahlung folge, dann wächst die ausgehenden Strahlung gemäß 396 . (T/To)^4. Die Rückstrahlung ist proportional dazu und beträgt, damit die Bilanz stimmt, 333 . (T/To)^4. Die Differenz ist dann 63 . (T/To)^4, mit der ich gerechnet habe.
Herr Dr. Ullrich, die „Gegenstrahlung“ von 333 W/m² von T&K ist falsch, denn Sie enthält Niederschlagswärme sowie den Rückfluss der Konvektion. Wenn (im Strahlungsmodell) die Netto-Bodenabstrahlung 390-150=240 W/m² (=Solarstrahlung/4) beträgt, und die 150 von der CO2-Konzentration abhängen, Sie aber 396-333=63 W/m² nehmen, dürfen Sie auf keinen Fall davon ausgehen dass die 63 W/m² ebenso proportional zu (T/To)^4 sind wie 396.
Der Strahlungsantrieb (und daraus die Bodenerwärmung) kann grundsätzlich NICHT aus der Nettoabstrahlung berechnet werden. Diesen Fehler macht IPCC nicht! Dort ist die Rückstrahlung deltaS die Hälfte der absorbierten Bodenabstrahlung bei CO2-Verdoppelung und mit S-B deltaT=deltaS/S/4/EPS•T•ln(C/Co)/ln(2)•Feedback mit EPS=240/390.
Ok, hier muss ich einräumen, dass ich die Gegenstrahlung, so wie dargelegt, als von der Abstrahlung induziert interpretiert habe. Vielleich hilft mir Ihr Einwand, den Vorgängerautor besser zu verstehen. Er hatte nämlich die Abstrahlung auf den Anteil begrenzt, der vom Boden aus ungehindert in den Weltraum geht, also 45 statt 63 Watt/m². Aber natürlich nach demselben T^4 – Gesetz. Im Endeffekt führt das bei meinem Vorautor zu einer „Klimasensitivität“ von 0,58 Grad C (bei mir 0,53 Grad C), verglichen mit der üblichen CO2-Klimasensivität.
Korrektur:
1990-2020; 14,45+/-15,42;
Herr Strasser, bitte nicht vergessen: Es handelt sich hier um eine Energiebilanz an der Erdoberfläche und da sind Strahlungsvektoren irrelevant. Auch sind die Angaben in Watt/m² gleichbedeutend mit Energie/Zeit/Flächeneinheit. Wenn Sie sich die bekannten Energiediagramme ansehen, da haben Sie weitestgehend die gleiche Aufteilung, nur in Prozent-Angaben. Allerdings fehlt dort die verwirrende Aufsplittung in Ausgehender Strahlung und Gegenstrahlung, was für die Betrachtungen hier irrelevant ist.Und weil es sich hier um eine Oberflächenbilanz handelt, dürfen die komplexen Vorgänge in der Atmosphäre außen vor bleiben. Es interessiert, was an der Oberfläche im Mittel „rein kommt“ und wieder „raus geht“ und welche Temperaturabhängigkeit besteht. Der größte Player ist in dieser Bilanz die Verdunstungskühlung. Ich erinnere mich jedenfalls nicht, wie und ob überhaupt sich Gerlich und Tscheuschner dazu geäußert haben – trotzdem gibt es sie. Und wenn Sie die Wärmeabstrahlung von der Erde nehmen: Entscheidend ist hier die T^4-Abhängigkeit. Außerdem macht in der Oberflächenbilanz die Abstrahlung nur 1/7 der Verdunstungskühlung aus.Auch besteht weitestgehend Einigkeit darüber, was im Mittel von der Sonne eingestrahlt wird, wieviel davon reflektiert, in der Atmosphäre verteilt wird und auf der Erdoberfläche ankommt. Dasselbe gilt für die Anteile, die die Erde als Verdunstungswärme, Konvektion und Infrarotstrahlung wieder verlassen. Hier die Berechnungen von Gerlich und Tscheuschner zu bemühen, führt in die falsche Richtung- ebenso wie viele der physikalisch-theoretischen Begriffe, die Sie bemühen.
Werter Dr. Roland Ullrich,
nichts für ungut, ich finde Ihre Analyse durchaus interessant!
Trotzdem möchte ich als Kommentar folgendes antworten: Die genannten Feynman-Diagramme sind eine Art Metabschreibungssprache für komplexe Prozesse, die sich sonst schwer halbwegs anschaulich beschreiben lassen. Natürlich bin ich kein Spezialist in dieser Disziplin, verstehe aber, daß es möglich sein muß, real existierende Prozesse in einer Metasprache wie dieser zu modellieren. Speziell auch deswegen, weil mathematische Zusammenhänge direkt ableitbar wären. Gerlich ist nun der Meinung, daß es nicht möglich ist und schließt daraus, diese Art des Ansatzes muß unpassend sein. Das ist es, was auch ich bzgl. Trenberth/Kiehl zum Ausdruck bringen wollte.
Ich meine daher, alle Ansätze, die irgendwie auf den Überlegungen beruhen, die Sonneneinstrahlung linear auf 360° aufzuteilen, sind unphysikalisch. Eine lineare Mittelung paßt nicht zu einer Wirkung, die sich mit der vierten Potenz entwickelt.
Verdunstung kühlt zwar lokal, die durch Verdunstung entzogene Wärme wird aber bei der späteren Kondensation wieder frei. Am Wärmegehalt im Gesamtsystem ändert das nichts.
Wenn man CO₂ eine auf Strahlung beruhende Wirkung nachweisen will, die einen zusätzlichen(!) Antrieb bewirkt, wäre in meinem Verständnis einmal Voraussetzung, entsprechende Kennlinien aufzunehmen, die zeigen, wie sich Strahlung in Abhängigkeit der Gastemperatur und der Konzentration entwickelt, auf welchen Wellenlängen wie stark gestrahlt wird und wie die Kennlinie der Gasabkühlung durch Abstrahlung aussieht. Derartiges hab ich bisher noch nie gesehen.
Zusammengefaßt denke ich bei solchen Themen generell Top – Down. Es muß also zuerst ein physikalisch widerspruchsfreies Gesamtbild da sein, in welches die einzelnen Details dann wie passende Mosaiksteine eingefügt werden. Dieses Gesamtbild hätte ich hier noch nicht erkannt, was aber natürlich auch an mir liegen kann.
„Ich meine daher, alle Ansätze, die irgendwie auf den Überlegungen beruhen, die Sonneneinstrahlung linear auf 360° aufzuteilen, sind unphysikalisch“. Eine grundlegende Kritik, die übereinstimmend mit Gerlich auch den „Treibhauseffekt“ mit 33 K Erwärmung auf 288 K sehr in Zweifel zieht. Weshalb habe ich mit dem Oberflächenmodell dennoch gute Chancen? Das T^4-Gesetz gilt für die IR-Abstrahlung, deren Beitrag zur Wärmeabfuhr nur ca. 1/7 der abgeführten Verdunstungswärme ausmacht. Und wenn Sie Änderungen um kleine Temperatur-Deltas betrachten, dann sorgt die Kelvin-Temperaturskala dafür, dass sich Änderungen bei der Bezugstemperatur selbst bei der 4. Potenz nicht allzu dramatisch auswirken, z.B.: (309/308)^4 = 1,013 und (289/288)^4 = 1,014. Auch will ich die K & T – Bilanz nicht in Frage stelle (mit Ausnahme der ominösen Gegenstrahlung), deren globalen Mittelwerte sind offenbar durch Satellitenmessungen bestätigt. Und wenn statt Strahlungsbilanz Energiebilanz darüber steht, dann sind die Werte durchweg vergleichbar (eine Gegenstrahlung kommt dort erst gar nicht vor). Das T^4-Gesetz für die Abstrahlung gilt davon unbenommen. Die dominierende Abfuhr von Verdunstungswärme ist ebenfalls temperaturabhängig. Hier vertraue ich darauf, dass es geeignete globale und/oder regionale Daten geben müsste, bisher allerdings eher grobe Schätzwerte, die von meinem Vorgänger bestätigt werden. Größenordnungsmäßig scheint es zu stimmen.
„Verdunstung kühlt zwar lokal, die durch Verdunstung entzogene Wärme wird aber bei der späteren Kondensation wieder frei. Am Wärmegehalt im Gesamtsystem ändert das nichts.“ Nein, hier folge ich meinem Vor-Autor: „Die Verdunstung von Wasser entzieht der Erdoberfläche Energie und transportiert diese in die höheren Atmosphärenschichten. Dort wird die Energie durch Kondensation (Wolkenbildung) wieder abgegeben und ins Weltall abgestrahlt. Durch das Abregnen der Wolken wird der Wasserkreislauf geschlossen.“ Bleibt die Frage, was beim Abregnen mit der Oberflächentemperatur geschieht. Ich bin der Ansicht, dass dieser Effekt in der Bodentemperatur enthalten ist. Gedankenexperiment: Der Regen hat für Abkühlung gesorgt. Dann wird entspechend weniger verdunstet, bis wieder das alte Gleichgewicht herrscht und die vorangegangene Abkühlung kompensiert ist.
Zu CO2-Strahlungsantrieb: Habe ich hier nur zu Vergleichszwecken benutzt, weil üblicherweise verwendet. Wie korrekt diese Ansätze sind, dass war nicht mein Thema.
Werter Dr. Roland Ullrich,
vielen Dank für die weitere Stellungnahme!
Inhaltlich ist ich aus meiner Sicht bereits alles gesagt, daher nur folgende Anmerkung:
Sie nehmen sich die Mühe, soweit ich es hier beurteilen kann, zu allen Kommentaren Stellung zu beziehen. Das zeigt, daß sie dieses Thema und dessen antreibende Energien nicht nur ernst nehmen, sondern auch an Einwänden Interesse zeigen. Das verdient Anerkennung!
Danke! Was ich noch hinzufügen möchte: Ja, bei den 7,5 % Zunahme des Wärmetransports durch Verdunstung je 1 Grad Temperaturzunahme handelt es sich um meine derzeit bestmögliche Schätzung. Aber man sollte im Vergleich dazu die beträchtlichen Unsicherheitsintervalle bei den IPCC-Modellen nicht vergessen, die einer komplizierten Atmosphäre (samt kaum weniger komplizierten Ozeanströmungen) zu verdanken sind und die seit Jahrzehnten nicht besser werden. Und betrachtet man z.B. die Fehlerfortpflanzungsrechnung von Patrick Frank, dann sieht es noch trostloser aus!
„genannten Feynman-Diagramme sind eine Art Metabschreibungssprache für komplexe Prozesse, die sich sonst schwer halbwegs anschaulich beschreiben lassen“
Feynman-Diagramme sind nichts weiter als eine graphische Rechenvorschrift für Integrationen und finden meines Wissens ausschließlich in der Quantenfeldtheorie bzw. verwandten mathematischen Methoden Anwendung, also NICHT für allgemein komplexe Prozesse.
Ich lehne es ab, vom menschengemachten Klimawandel als sinnvolle Idee zu sprechen. Wo sind die ungenutzten CO2 -Haufen? Vor 6000 Jahren waren die Ostalpen eisfrei. Die Wikinger betrieben 500 Jahre Acherbau und Viehzucht auf Grönland. In ganz Deutschland gab es Weinbau und der Bischof von Trondheim hatte einen eigenen Weingarten. Die Sonne macht das Wetter und Klima ist Statistik.
Ehrlich, ich sehe es ähnlich wie Sie. Ist aber leider kein Beweis. Und höchste Skepsis ist geboten, ob wir die Klimakatastrophen-Glaubenskongregation jemals erreichen. Katastrophen-Luisa kann das besser…
Herr Kugler, als naturwissenschaftsferner Dipl.-Kfm. stimme ich ihnen voll zu. Ich danke Herrn Ullrich für seinen Bericht aus einer mir wenig zugänglichen Welt!
Entschuldigung, Dr. Ullrich musste es heissen. Leider gibt es im phantastischen EIKE-Forum keine Korrekturmöglichkeit!
Aber so, wie ich Herrn Dr. Ullrich hier auf EIKE kenne, setzt der auf Wissen und nicht auf Titel!
Danke, so ist es!
Interessanter Versuch, aber die Gleichung irritiert: So + Evap + Erad + Konv + X = 0, denn es wird nicht deutlich, dass alle Summanden langfristig zeitabhängig sein können und sich ändern, sobald X ungleich null auftaucht. Ausserdem benötigt man ja noch den Leistungsfluß H, der Erwärmung bewirkt und 0,9 W/m2 im Diagramm beträgt.
Variationen der Sonnenintensität sind als eine der möglichen Klimaantriebe in X mit enthalten. „So“ ist mit 160 Watt/m² konstant, was ich auch geschrieben habe. Und die o,9 Watt/m² sind nicht nur sehr klein, auch kommt es in dieser Bilanz „nur“ auf deren Änderung mit der Temperatur an. Sie verrichten nach meinem Verständnis vielfältige chemische, mechanische und biologische „Arbeit“, bei der es fragwürdig ist, ob sie am Ende zu Erwärmung führt. Deshalb fehlt dieser kleine Posten auch im KT-Diagramm bei der abgegebenen Wärmeenergie, die die Oberfläche wieder verlässt. Würde dieser Posten zu Erwärmung führen, wäre er dort enthalten.
Bei H=0,9 w/m2 handelt es sich wie bezeichnet um die Nettoabsorption und ergibt sich aus der Bilanz zum Weltraum hin. Die genauen Zahlen sind ja schwach daneben angegeben: 101,9+238,5 = 340,4 = 341,3-0,9. Die Nettoabsorption ergibt sich also wie es sein muss aus dem Überschuss an Sonneneinstrahlung gegenüber der Energieabgabe der Erde. Die Nettoabsorption kommt nicht durch eine erhöhte So am Boden zustande. Die Bilanz am Boden wird mit 161+333=494=17+80+396+1(~0,9) gelöst, die Nettoabsorption können Sie nicht einfach als kleinere So (160) ausgeben. Der Nettoabsorption haben wir den Klimawandel zu verdanken, denn 0,9 w/m2 reichen quantitativ aus, die beobachtete Erderwärmung zu erklären.
Hm, eine interessante These, diese 0,9 Watt/m² an „absorbierter“ Einstrahlintensität dem Klimawandel und somit der bisherigen Erwärmung zuzuschreiben. Es wäre damit eine zusätzliche permanente „Heizleistung“ oder Antrieb und damit im Oberflächenmodell im Antrieb X enthalten. Dabei ist allerdings zu bedenken, dass er selbst im Vergleich zu dem klassischen CO2-Verdoppelungs-Antrieb in Höhe von 3,7 Watt/m² (mit 1,1 bis 1,4 Grad Temperaturanstieg) relativ klein ist. Erst recht im Vergleich zu dem Antrieb X, der sich aus dem Oberflächenmodell zu 7 Watt/m² je 1 Grad Temperaturerhöhung errechnet. Das dieser Posten die IR-Abstrahlung reduziert passt m.E. sowohl zu Ihrer Antriebsthese als auch, wie ich angenommen habe, zu irreversibel verbrauchter Energie, die ich in der Oberflächenbilanz deshalb nicht mitgezählt habe. Müsste man bei T & K eingehender recherchieren… Allerdings zugestanden, wären die 0,9 Watt/m² der einzige Antrieb, könnte er mit den hohen CO2-Klimasensitivitäten des IPCC immerhin die etwa 1 Grad Temperaturerhöhung der letzten 150 Jahre erklären.
Allerdings bleibt offen, wie sich die Reduktion um 0,9 Watt/m² auf Verdunstung, Konvektion und Abstrahlung verteilen. Was dann dann doch wieder eher für die „irreversible Energieabsorption“ spricht. Vermutlich verwenden T & K deshalb auch den Begriff „Absorption“.
„Hm, eine interessante These, diese 0,9 Watt/m² an „absorbierter“ Einstrahlintensität dem Klimawandel und somit der bisherigen Erwärmung zuzuschreiben.“
Das ist keine These, sondern klar. Das H fehlt in ihrer Gleichung und ist der einzige Energiefluß in der Oberflächenbilanz, der zu einer Temperaturänderung im Boden führen kann, denn er quantifiziert die Änderung des Wärmeinhalts des Bodens.
“ klassischen CO2-Verdoppelungs-Antrieb in Höhe von 3,7 Watt/m²“
Dieser taucht in der Bilanzgleichung des Bodens nicht auf, er wirkt auf das Gesamtsystem, nicht am Boden.
Herr Wörst, können Sie mir umgekehrt erklären, warum die 0,9 Watt/m2 nicht der irreversible Energieanteil sein können, der für Photosynthese und mechanische Arbeit verbraucht wird und deshalb auf der Abgabeseite fehlt? Trüge er zur Bodenerwärmung bei, was die auftreffende gesamte Sonnenenergie beständig macht, dann würde er sich in die normale Bilanz einfügen, auch auf der Abstrahlungsseite. Und CO2-Antrieb, sofern vorhanden, kann als zusätzlicher Antrieb gewertet werden, egal, wo er entsteht. Genauso, wie Variationen der Sonneneinstrahlung. Und relevant ist nur, was uns am Boden erreicht, egal, in welchen Höhen der Antrieb entsteht. Hier ist auch die Grafik eindeutig. Die auch zeigt, dass nicht alles, was in der Atmosphäre geschieht, für uns unten relevant ist.
》Herr Wörst, können Sie mir umgekehrt erklären, warum die 0,9 Watt/m2 nicht der irreversible Energieanteil sein können, der für Photosynthese und mechanische Arbeit verbraucht wird und deshalb auf der Abgabeseite fehlt?《
Grundsätzlich wären solche Energieaufwände auch in H aufgehoben, wahrscheinlich ist auch ein Anteil darin, denn Photosynthese und mechanische Arbeit werden sich irgendwie quantitativ auch mit dem Klima ändern und . Aber das ändert ja nichts daran, dass die beobachtbare Erwärmung einen Anteil in H von der beobachtbaren Größenordnung von etwa 1 W/m2 benötigt, also einen bedeutenden Anteil von H „verschlingt“.
》Trüge er zur Bodenerwärmung bei, was die auftreffende gesamte Sonnenenergie beständig macht, dann würde er sich in die normale Bilanz einfügen, auch auf der Abstrahlungsseite.《
Ihre Gleichung lautet vollständig, also äquivalent zum Energieerhaltungssatz: So(t) + Evap(t) + Erad(t) + Konv(t)+ H(t) = 0 Beim Spezialfall H =0 findet keine Erwärmung oder Änderung sonstiger energiezehrender Prozesse auf der Erdoberfläche statt, denn dafür bleibt ja nichts übrig.
„Hm, eine interessante These, diese 0,9 Watt/m² an „absorbierter“ Einstrahlintensität dem Klimawandel und somit der bisherigen Erwärmung zuzuschreiben.“
Die 0,9 Watt/m² Bilanz-Defizit TOA werden der gemessenen Aufheizung des tiefen Ozeans zugeschrieben.
„„Hm, eine interessante These, diese 0,9 Watt/m² an „absorbierter“ Einstrahlintensität dem Klimawandel und somit der bisherigen Erwärmung zuzuschreiben.“
Das ist keine These, sondern klar.“
Wie hirnlos dieses Geschwafel ist sieht man bei Betrachtung der Fehlerbalken der jeweiligen Meßgrößen.
Herr Dr. Ulrich,
ich gebe zu Bedenken das es eine „irreversibel verbrauchter Energie“ nicht gibt.
Energie wird im physikalischen Sinne nicht verbraucht.
Die Diskussion basiert außerdem auf einer unvollständigen Formel und macht Annahmen zu einer Wärmeleistung die überhaupt nicht gemessen werden kann.
Ihrem Einwand
stimme ich zu. Diese Ungewissheit stellt klar, warum man die 0.9 W/m2 gar nicht wirklich bestimmen kann.
Herr Ullrich, zur Gleichung:
Ich denke, Ihre Überlegung war ähnlich, aber die physikalische Bedeutung Ihres X ist Ihnen nicht ganz klargeworden. Denn eine Klimaänderung kommt durch eine Änderung in den bereits aufgelisteten Energieflüssen zustande, der Antrieb X besteht ja nicht aus einer neue Energieform, die plötzlich auftaucht.
PS: Die Photosyntheseleistung habe ich überschlagen. Selbst wenn das zusätzlich in die Atmosphäre eingebrachte CO2 von etwa 2 ppm pro Jahr komplett photosynthetisch in Kohlenhydrate umgewandelt würde und Pflanzenatmung ausbliebe, die jährlichen 2 ppm also binnen Jahresfrist „vegetativ eingelagert“ würden, entspräche der dafür verwendete Anteil von H etwa nur der industriell erzeugten Jahresprimärenergie, also etwa nur 3% von 0,9 w/m2 .
Herr Wörst, das gebe ich jetzt zurück, Sie haben das Wesen des Antriebs nicht richtig verstanden. Denken sie mal in Ruhe drüber nach, dann werden Sie es verstehen. Die Verringerung einer abgegebenen Leistung in Watt/m² ist wird gleichgesetzt mit einem entgegengesetzten Antrieb, der diese Verringerung bewirkt. Siehe z.B. CO2-Antrieb von 3,7 Watt/m². Das ist nun lange bewährt und üblich und besser zu händeln, als mit Wärmeisolation zu argumentieren und zu rechnen.
Das ist klar, der Punkt ist, dass die 3,7 W/m2 nicht direkt am Boden mit diesem Wert wirken, sondern in der Atmosphäre oben. Der Antrieb, der dadurch am Boden ausgelöst wird, ist quantitativ höher.
PS zu Ihrer anderen Frage: Sie haben also nun auch verstanden, dass Photosynthese die Nettoabsorption nicht komplett „aufbraucht“, es bleibt genug zur Erwärmung übrig.
„Das ist klar, der Punkt ist, dass die 3,7 W/m2 nicht direkt am Boden mit diesem Wert wirken, sondern in der Atmosphäre oben. Der Antrieb, der dadurch am Boden ausgelöst wird, ist quantitativ höher.“
„Klar“ ist lediglich Ihre völlige Ahnungslosigkeit bzw. daß Sie anscheinend ein Agitator der AGW-Mafia sind
Auf KalteSonne finden Sie den Beitrag über ein Albedo-Forcing von [9W/m² pro Kelvin] als natürlicher Paläo-Klimaantrieb.
Ein interessanter Beitrag!
Wobei die Eiszeiten und das Eis die Oberflächenzirkulation der Ozeane massiv gestört haben sollte. Damit wäre ein Wärmetransport von der Tagseite zur Nachtseite nicht möglich. Gemäß Herrn Webers Theorie.
@All
Herr Kruger hat schon wieder eine Kindergartenvermutung verbreitet, die er nicht beweisen kann. Der Wärmetransport von der Tagseite zur Nachtseite verläuft nun mal nicht über die Oberflächenzirkulation der Ozeane, sondern über die Erdrotation…
Durch Reibung?
Unbedingt Herr Krueger!
Da liegen sie hautnah neben den Scheibenweltenthusiasten, die bei Erdrotation die Flugzeuge nur in die Luft werfen würden und wenn sich die Erde darunter wegdreht, landen diese dann am Zielort.
Entgegen der Meinung der Klimaunwissenschaften, muss gar kein Wärrmetransport stattfinden, damit die Nachtseite Energie hat.
Die Wärme „bewegt“ sich einfach mit der Masse mit.
Danke für Ihr Artikel, Herr Dr. Ullrich!
Sehr geehrter Herr Dr. Ullrich,
ich antworte auf meine eigene Bemerkung anstatt auf Ihren Artikel nicht aus Unhöflichkeit, sondern weil ab der 2. Ebene die Formatierung nicht verloren geht und der Kommentar besser lesbar ist.
Es ist die beste Analyse über die thermodynamischen Prozesse auf der Erde die ich seit langen gelesen habe.
Dennoch erlaube ich mir, einige Details anders zu sehen.
1. Es handelt sich bei den ganzen Strahlen-Werten (u.a. bei der sehr übersichtlichen Grafik) um Mittelwerte, die sehr stark, um nicht zu sagen extrem, schwanken. Daher vollziehen sich die Prozesse letztendlich anders als beschrieben. So z.B. beträgt die Strahlung an der Oberfläche 161 W/m2 und die Abstrahlung 396 W/m2 im Mittel. Jeder, der bei Sommersonne die Hand ausstreckt, merkt aber, dass die Wärme von oben und nicht von unten kommt. Nachts ist es dann anders herum, die aufgewärmte Erde strahlt ab. Der abgebildete Zustand ist also ein theoretischer Zustand, der exakt so nicht auftritt. Und bei den extremen Schwankungen kann es Tag für Tag, Monat für Monat, Jahr für Jahr wetterbedingte Schwankungen geben, die schnell mal eine Temperaturabweichung von x,yz Grad ergeben.
2. Schon an der Grafik ist eigentlich zu erkennen, dass die ominöse Gegenstrahlung irrelevant ist. Das System an der Systemgrenze wird mit der Intensität von 341 W/m2 bestrahlt und die gleiche Intensität wird abgestrahlt (102 reflektierte Sonnenstrahlen + 239 austretende Strl.) = 341 W/m2. Das ist das Gleichgewicht bei der Temperatur heute. Würde die Sonne etwas intensiver strahlen, würde sich das Gleichgewicht bei einem Tick höhere Temperatur einstellen, entsprechend anders herum bei geringere Strahlung. Das Gleiche gilt bei der Abstrahlung von 239 W/m2. Ein Zusammenhang zwischen der Gegenstrahlung i.H.v. 333 W/m2 und der letztendlichen Abstrahlung ist nicht vordergründig erkennbar. Kann sein, muss aber nicht. Diese kann auch den Wert von 50 oder 120 haben, ohne dass sich die restlichen Werte ändern.
3. Die Erde wird mit 341 angestrahlt, 161 kommen an der Oberfläche an, also 180 W/m2 werden reflektiert oder erwärmen die Atmosphäre. Die Erde strahlt 396 ab, 239 verlassen die Atmosphäre, die restlichen 157 W/m2 werden also reflektiert bzw. erwärmen die Atmosphäre. Ein fast identischer Wert! sollte man dann nicht die ganzen Geschichten von forcing, Gegenstrahlung etc. nicht einfach in den Korb werfen und logisch feststellen, bei jedem Durchgang durch die Atmosphäre, egal ob von oben nach unten oder umgedreht, verlieren die Strahlen rund 50% ihrer Intensität, wobei der Großteil davon die Luft erwärmt? Und eine Veränderung der Zusammensetzung der Luft würde die Strahlen-Verluste in beiden Richtungen gleichermaßen betreffen?
4. Den Begriff Sensitivität lehne ich rundweg ab, egal was die Rest der Welt davon hält. Es gibt die spezifische Wärmekapazität in KJ/kg.K, die Sensitivität ist ein daran orientiertes Hilfskonstrukt der Klimapropheten ohne physikalischen Inhalt. Schon an der Einheit K pro Verdoppelung ist der ganze Unfug erkennbar. Es bedeutet , wenn in eine CO2 freie Atmosphäre ein CO2 Molekül ausgesetzt wird und danach mit einem weiteres Molekül die Konzentration verdoppelt wird, würde die gleiche wärmende Wirkung erzielt wie bei der Verdoppelung von 50% auf 100%. Wer das ernsthaft glaubt kann ich nicht als Naturwissenschaftler akzeptieren.
Mit freundlichen Grüßen
Peter Georgiev
Für Gase, die in geringer Konzentration vorliegen, wie die FCKWs (CFCs), nimmt die Absorption linear zu. Für Gase, die bereits recht stark absorbieren, wie Methan (CH4) oder Lachgas (N2O), ist d FR proportional der Wurzel aus der Konzentration und für CO2, das schon sehr stark absorbiert, geht die Zunahme proportional dem Logarithmus, und sieht wie folgt aus:
d FR = a · ln (CO2 / CO20)
Für einen wie auch immer definierten Einfluss auf die Erdtemperatur kann nicht nur der Grad der Absorption verantwortlich sein, sondern auch definitiv die Zunahme der Masse in absoluten Werten. Dass eine Verdopplung in Höhe von paar Kilogramm ähnliches bewirkt wie die Verdoppelung in Höhe von Terratonnen widerspricht allen Naturgesetzen. Kann nur jemanden einfallen, der außerhalb seiner Strahlentheorie die Wirklichkeit ausblendet.
Nur ein Beispiel. NF3, dieses zu den langlebigen Treibhausgasen gehörende Verbindung ist 17’000 Mal wirksamer als Kohlendioxid.
Wie NewScientist in seiner Onlineausgabe berichtet, ist diese zu den langlebigen Treibhausgasen gehörende Verbindung 17’000 Mal wirksamer als Kohlendioxid. «Das Problem ist, dass dieses ein künstliches Gas ist und im Gegensatz zu Kohlendioxid auf natürliche Weise nicht in der Atmosphäre vorkommt. Von daher hat es pro Masseneinheit einen besonders starken Einfluss auf den so genannten Treibhauseffekt», erläutert Hartmut Graßl vom Max-Planck-Institut für Meteorologie. Derzeit würden jedes Jahr 4000 Tonnen dieses Gases in die Atmosphäre eingeleitet werden. «Dies entspricht etwa 67 Mio. Tonnen Kohlendioxid …
Herr Krueger,
wie Wirksamkeit z.B. auf Bodentemperatur muss aber erst nachgewiesen werden.
Das diese Gas 17000 Mal mehr aktiv im Infraroten ist, kann ja sein. Mehr als Schwarzkörperstrahlung kanns aber nicht sein, bei gleicher Temperatur.
Gleichzeitig gibt man damit übrigens auch an, das CO2 17000 Mal weniger strahlt und damit eigentlich völlig irrelevant ist!
Ein neues Projekt wurde gestartet um aus Rundungsfehlern ex nihilo Energie zu erzeugen; wenn das Open Source ginge können wir denen ja auf die Finger klopfen.
Herr Georgiev, danke für Ihre freundlich vorgetragene Kritik!
zu 1) Es handelt sich in der Grafik um ganzjährig gemittelte Werte, deren Änderungen ich betrachte, wenn sich die global gemittelten Temperaturen ändern. Vorausgesetzt ist, dass man die Abhängigkeit von der Temperatur kennt, was der Fall ist. Mit Ausnahme natürlich bei den weitgehend unbekannten Antrieben in X. Ein übliches Vorgehen, wenn man z.B. mittlere globale Temperaturen aus der Planck’schen Strahlungsbilanz berechnet. Erwärmung der Hand durch die Sonne von oben: Das ist dieselbe Einstrahlung „So“, im zeitlichen und räumlichen Mittel 160 W/m², die in der Grafik auch die Erde erwärmt. Abstrahlung „396 W/m² im Mittel“ – für die Energiebilanz ist da die Differenz mit der „Gegenstrahlung“ maßgebend, also die mittleren 63 W/m². Es existieren Grafen für die Energiebilanz, die ich hier leider nicht einstellen kann, in denen es genau so dargestellt wird. Auch T&K wissen das, denn nur mit der Differenz 63 W/m² geht die Bilanz in der Grafik auf.
zu 2) Kaum Einwände. Zu meiner Sicht, wie ich „Gegenstrahlung“ einordne, verweise ich auf meine Antwort unten an Herrn Ordowski.
zu 3) Es ist das Wesen der Oberflächenbilanz, dass ich nur betrachten muss, was an der Oberfläche gemittelt ankommt und was die Oberfläche, mittels der verschiedenen Transportmechanismen für Wärmeenergie, wieder verlässt.
zu4) Ihre Vorbehalte bzgl. Sensitivität trage ich großenteils mit, weshalb ich fast nur noch den Begriff „Antrieb“ benutzt habe, den man prinzipiell konkreten Ursachen zuordnen kann. Beispiel IPCC: Die Wasserdampfrückkopplung erhöht dort offenbar die „CO2-Klimasensitivität“, obwohl CO2 bestenfalls Auslöserfunktion hat. Das Ganze wird weiter kompliziert, weil die initiale Temperaturerhöhung auch andere Ursachen kann – z.B. vermehrte Sonneneinstrahlung. Vielleicht mit ein Grund, weshalb der IPCC heute wieder zu der ganz überwiegenden Alleinschuld des anthropogenen CO2 zurückgekehrt ist?
Es gibt die schwer widerlegbare Feststellung aus Gerlich/Tscheuschner 2015:
„Die Strahlungsbilanzdiagramme der Klimaforschung sind Unsinn:
1. weil sie nicht Strahlungsintensitäten darstellen können, was die natürlichste Interpretation der Pfeile z. B. bei Trenberth/Kiehl wäre;
2. weil sie nicht quellfreie Flusse, das heißt, divergenzfreie Vektorfelder in drei Dimensionen, darstellen können, da eine verschwindende dreidimensionale Divergenz immer noch erlaubt, daß stets noch ein Anteil des Feldes seitwärts geht;
3. weil sie nicht in den Rahmen der Feynman-Diagramme passen, die mathematische Ausdrücke repräsentieren, die im Rahmen der Quantenfeldtheorie klar definiert sind;
4. weil sie nicht in die Standardsprache der Systemtheorie bzw. des Systems Engineering
passen. Das heißt, daß Erhaltungssätze (Kontinuitätsgleichungen, Bilanzgleichungen, Budgetgleichungen) nicht für Intensitäten niedergeschrieben werden können! Unglücklicherweise wird genau dies in den meisten klimatologischen Arbeiten getan. Dies ist der Kardinalfehler der Globalklimatologie.“
Und:
„Der Erdboden ist kein schwarzer Körper (wie jeder sehen kann) und der Erdboden und die Ozeanoberfläche sind für kein Zeitintervall und zu keinem Zeitpunkt im thermodynamischen Gleichgewicht. [Gerlich 2005]
Man muß die Sonnenstrahlung bei der Erdbahn durch 3,5 teilen, damit man eine graphische Darstellung erhält, bei der die maximale Bodenstrahlung wie die verschobene Sonnenstrahlung bei der Erdbahn aussieht (mit logarithmischer Abszisse).“
Nicht nur aus diesen beiden Gründen sind Theorien, die auf dieser Basis aufbauen mehr Phantasie als Realität. Selbst wenn einzelne Zwischenergebnisse zufällig gut aussehen. Jede Rechnung, die auf gemittelten Werten beruht und auf Stefan-Boltzmann ist absurd, weil Wärme nicht vorkommt (Joule). Ankommen tut es aber auf Wärme!
Sehr geehrter Herr Strasser,
Danke für Ihr Kommentar, sowie für eine Vielzahl von weiteren fundierten Beiträgen.
Mein Wissen über Strahlen kann mit dem Ihren nicht mithalten, die von Ihnen zitierten Quellen habe ich nicht gelesen.. Über Thermodynamik und Logik komme ich aber auf ähnliche Schlußfolgerungen wie Sie. Ganz besonders über die Tatsache, dass man Temperaturänderungen nicht über Strahlen, sondern über Massen und Energiemengen berechnet.
Mit freundlichen Grüßen
Peter Georgiew
Mal ein Detail hervor gehoben, Zitat « Wir wissen, dass die Niederschläge dort am höchsten sind, wo die meiste Wärme von der Erdoberfläche abgeführt werden muss – am Äquator.» Am meisten Wärme muss dort abgeführt werden, wo es am heissesten ist – in den Äquator-nahen Wüsten, wo die Temperaturen am höchsten und die Niederschläge gering sind. Es gäbe noch andere Einwände. Aber lassen wir das.
„Mal ein Detail hervor gehoben, Zitat « Wir wissen, dass die Niederschläge dort am höchsten sind, wo die meiste Wärme von der Erdoberfläche abgeführt werden muss – am Äquator.» Am meisten Wärme muss dort abgeführt werden, wo es am heissesten ist – in den Äquator-nahen Wüsten, wo die Temperaturen am höchsten und die Niederschläge gering sind.“
Warum ist es denn in den Wüsten so heiß???
Ok, war auch bei mir ein Zitat. Grundsätzlich liefern die Ozeane den größten Beitrag zur Verdunstung, schon flächenmäßig, und insbesondere in Äquatornähe. Über den Landflächen mit 29% Anteil sieht es teilweise anders aus, was ich nicht verschwiegen habe. Das reicht einerseits von feuchten Regenwäldern bis andererseits zu Wüsten. Verdunstung gibt es in Wüsten wenig – mit ein Grund, warum es dort besonders tagsüber heiß wird. Ansonsten sind substantielle Einwände willkommen, ich lerne gerne dazu.
1. Anscheinend wurde die 2×tägliche Verdunstung durch die Watt-Fläche vergessen (scheint zum Konsens zu gehören). 2. Es wurde festgestellt dass seit ~1980 die Watt-Fläche um ca. 16% abgenommen hat (Gründe vielfältig) https://doi.org/10.1038%2Fs41586-018-0805-8
Zur Watt-Fläche: Die Verdunstung nimmt je ein Grad Temperaturerhöhung um 7,5 Prozent zu. Im Rahmen dieses Modells sollte also eine Watt-bedingte Änderung der Meeresoberfläche unterhalb von etwa 1% bleiben. Dies ist bei einer 16%igen Änderung der Watt-Fläche dann der Fall, wenn die Wattflächen weniger als 6% der Meeresoberfläche ausmachen. Ich denke, davon kann man ausgehen.
Bei der 2 x täglichen Verdunstung der Watt-Flächen ist zu berücksichtigen, dass über dem tiefgründig durchfeuchteten Watt-Flächen auch während der Ebbe erhebliche Verdunstung stattfindet. Zusätzlich kann man davon ausgehen, dass entsprechende Schwankungen in den gemittelten Globalzahlen für die Verdunstung bereits enthalten sind. Außerdem machen sie dort nur einen sehr geringen Anteil aus.
Ich hatte den 100% Wegfall der Verdunstung im Sinn; danke für Ihre Ausführungen. P.S. Irrtum vorbehalten verschwand eine Fläche der Größenordnung Atakama (~Belgien, ~Schweiz).
Es bleibt immer wieder die Frage, wie es das CO2 mit seiner geringen Absorption von ca 36 W/m² der Erdstrahlung bei ca 15 Grad (Gesamt ca 390 W/m²) es zu seienem angenommen Anteil am angblichen THE von ca 21%, entspricht 81.9 W/m², kommen soll.Entweder hat sich Max Planck mit seienen Strahlkungsgesetzmäßigkeiten granatenmäßig geirrt, oder er hat doch Recht und hier wird eine obskure Theorie zur Wahrheit erklärt, die auch von keinem Experiment gestützt wird – eher im Gegeteil, siehe mein Glasscheibenexperiment – keien Erwärmung der Glasscheibe zeigt eindeutig, keine IR „THE“ Strahlung!
Jetzt mal aus dem Stegreif geantwortet: Mit dem sog. THE wird der Theorie zufolge eine Erwärmung von 255 auf 288K bewirkt. Wenn ich jetzt das T^4 – Gesetz auf die 390 W/m² anwende, müsste der THE die Abstrahlung von 240 auf 390 W/m² erhöhen. Was nach Ihren Zahlen einem CO2-Anteil von 31,5 W/m² entspräche. Wobei es natürlich keine mysteriöse Energiequelle gibt, sondern nur eine Art verbesserte Wärmeisolation. Denn bei den CO2-Absorptionsfrequenzen wird durch Absorptions- und Emissionsprozesse, die in alle Richtungen erfolgen, der IR-Strahlungsfluss verlangsamt.
Und Ihre Glasscheibe wird die Umgebungstemperatur annehmen, wofür Molekülstöße und IR-Strahlung sorgen. Die direkt durchgehende Bodenstrahlung von ca. 40 W/m² sollte Ihre Platte aber zusätzlich etwas erwärmen, falls sie kälter als der Boden ist. Was allerdings auch von der Temperatur der Umgebung abhängt, mit der sich die Platte ebenfalls austauscht.
Aber es stimmt schon. Auch in meiner Oberflächenbilanz müsste ich aufgrund der Bodentemperatur und dem Strahlungsgesetz eine Abstrahlung von 390 (396) W/m² erwarten. Warum ist ausschließlich die Differenz zwischen zwischen „Ausstrahlung“ und „Gegenstrahlung“ realistisch? Mir hilft da gedanklich der Wärmeaustausch durch Moleküle. Kein Mensch kommt dort auf die Idee, die aufwärts gerichteten Stöße unter „Ausgangsstoßenergie“ und die abwärts gerichtete Stoßübertragung unter „Gegenstoßenergie“ zu subsummieren. Tatsächlich kommt es auf das Netto an: Wieviel wird bei der Stoßbilanz insgesamt in welche Richtung übertragen? Und nimmt man die bekannten Graphen für die Energiebilanz, wird auch nicht zwischen Energieflüssen nach oben und unten unterschieden, sondern nur die Differenz eingetragen.
Die Strahlung macht genau das gleiche: Es gibt Austausch in alle Richtungen und in Richtung abnehmender Temperaturen gibt es einen Energie-Nettotransport.
Der Gegenstrahlungs-Gaga ist halt nicht tot zu kriegen.
Jedenfalls nicht durch die Realität!
Aber wen juckt schon die Realität, wenn man über eine Theorie/Hypothese quatschen kann…
Die Grafik oben kann nicht stimmen. Wenn 396 W abgestrahlt werden und davon 239 W in den Weltraum gehen, können maximal 157 W zurückkommen. Sonst findet hier eine wundersame Energievermehrung statt.
An der Oberkante kommen 341 (gelb) an und verlassen 102 (gelb) und 239 (rot), in der Summe auch 341. Nur das ist relevant. Ändert sich einer der 3 Werte, pegelt sich das Gleichgewicht z.B. bei 345 (es ist wärmer auf der Erde) oder 335 (es ist kälter auf der Erde).
Der Wert 333 von Wolke zu Erde ist komplett irrelevant. Entscheidend sind, dass gemäß Grafik die Erde unten 396 abstrahlt, wovon 239 die Atmosphäre wirklich verlassen. Ob man diesen Wert 0 oder 390 oder etwas dazwischen beziffert, ändert die Strahlenbilanz nicht. Es ist wohl eher als Erklärung gedacht, warum die Erde an Oberfläche deutlich mehr abstrahlt (396) als bekommt (161). Man kann diese Differenz aber auch anders erklären, ohne das CO2 heranzuziehen.
Da widerspreche ich Ihnen nicht. Die Differenz zwischen der Ausstrahlung und der ominösen Gegenstrahlung scheint aber zu stimmen, das zeigen auch Energiebilanz-Diagramme. Auch stimmt mit diesem Wert (63 Watt/m2) die Bilanz.
Die Darstellung des anthropogenen THE ist hier korrekt. CO2-Verdopplung bringt 3,7 W/m^2 Strahlungsantrieb, was zu einer Erwähnung am Erdboden um 1°C führt. Die Wasserdampfrückkopplung wird vom IPCC zu hoch bemessen. Das sieht man auch daran, dass man über den Tropen im Gegensatz zum Modell keinen Hotspot beobachten kann. Dort sollte sich das AGW zuerst bemerkbar machen. Herrn Uli Webers Theorie wird hier auch widerlegt.
Ich würde aber trotzdem zwischen anthropogenem THE und der spektroskopischen CO2-Erwärmung (3,7 W/m2 bei CO2-Verdoppelung) unterscheiden. Auf die Unsicherheiten bei der Wasserdampfrückkopplung weisen Sie bereits hin. Auch die Wechselwirkung mit der komplizierten Restatmosphäre (Beispiel: Wolkenbildung) ist ja bis heute nicht verstanden. Ich rechne mit dem Oberflächenmodell immerhin einen (höheren) Gesamtantrieb je ein Grad Temperaturerhöhung aus. Bei der Diskussion einzelner Antriebskomponenten habe ich mich eher auf „wenn – dann“ Argumente zurückgezogen. Weil es einfach zu viele Ungewissheiten gibt, was selbst der IPCC mit seinen großen Unsicherheitsintervallen einräumt.
Der CO2-Anstieg in der Atmosphäre ist weitgehend durch den Menschen verursacht. Das kann man am Delta-C13 und Delta-C14 sehen. Zudem landet in etwa 50% der Emissionen in den Ozeanen und 50% in der Atmosphäre. Das stimmt auch mit den CO2-Emissionen aus der Verbrennung der fossilen Brennstoffe überein.
Der CO2-Gehalt ist von 280 ppm auf 415 ppm angestiegen. Macht einen Strahlungsantrieb von 2,1 W/m^2. Und 0,6°C Temperaturanstieg. Zusammen mit anderen Treibhausgasen hat sich das CO2-Äquivalent nahezu verdoppelt. Da liegen wir bei über 500 ppm CO2-eq. Macht 3,1 W/m2 und 0,8°C.
Top of the Atmosphere werden rund 240 W/m^2 abgestrahlt. Also das, was auch zuvor eingestrahlt wird. Das entspricht einer Abstrahlnungstemperatur der Erde von -18°C. Durch die zunehmende Konzentration an THG sinkt der Wert auf etwa 237 W/m^2 ab. Also -19°C Abstrahlungstemperatur. Durch die verringerter Wärmeabstrahlung erwärmt sich die Luftsäule darunter um etwa 1°C, bis zum Boden, bis wir oben wieder die alten -18°C haben. Also wieder den Gleichgewichtszustand zwischen Einstrahlung und Ausstrahlung von 240 W/m^2.
Ich komme ohne Feedbacks durch Wasserdampf, Wolken, Lapse-Rate, etc. auf ca. 0,8°C über die Erhöhung der THG. Also anthropogen. Wasserdampf ist mit Abstand das stärkste THG. Da man über den Tropen keinen Hotspot durch mehr Wasserdampf und Kondensation und Freisetzung latenter Wärme sieht, im Gegensatz zu den Modellen, spielen die Veränderungen beim Wasserdampf also anscheinend keine so große Rolle. Und bei den Wolken zeigt sich bisher auch keine große Veränderung. Und die größten Eismassen auf der Antarktis schmelzen auch nicht so schnell ab und verändern damit die Albedo.
Somit komme ich bei CO2-Verdopplung auf einen Wert von 1,x Grad. Und nicht auf 3 Grad, oder gar bis zu 6 Grad.
Die 3-6 Grad beruhen darauf, dass man sich die Temperatursprünge zwischen Eiszeiten und Warmzeiten im Modell nur über eine hohe Klimasensitivität erklären kann. James Hansen hat dazu mit den Grundstein gelegt.
„Der CO2-Gehalt ist von 280 ppm auf 415 ppm angestiegen. Macht einen Strahlungsantrieb von 2,1 W/m^2. Und 0,6°C Temperaturanstieg. Zusammen mit anderen Treibhausgasen hat sich das CO2-Äquivalent nahezu verdoppelt. Da liegen wir bei über 500 ppm CO2-eq. Macht 3,1 W/m2 und 0,8°C.“
Ich fasse zusammen, ein Anstieg von 220 ppm (von 280 auf 500) bewirkt eine Temperatursteigerung von 0,8 Grad, also 275 ppm pro Grad. Um die Temperatur um 6 Grad zu erhöhen, ist eine CO2 Erhöhung um 2.750 ppm erforderlich.
Vor 12.000 Jahren war es nachweislich 6 Grad kälter. Also entweder war der CO2 Gehalt minus 2.470 ppm (280 – 2.750)ppm oder das Ganze ist Schwachsinn.
P.S. Mit Halbierungen käme man genau so auf absurde Werte, bei denen Pflanzen mangels CO2 nicht existieren können.
Nö.
Für den Anstieg der Temperatur über CO2 gilt die Formel:
dT = 0.27 x 5.35 x ln (CO2 neu / CO2 alt).
Bei Verdopplung von 280 auf 560 ppm haben Sie dann 1°C.
Bei Vervierfachung von 280 auf 1120 ppm haben Sie dann 2°C.
Bei Verachtfachung dann 3°C.
Das IPCC geht davon aus, dass durch Feedbacks (Wasserdampf, Wolken, Lapse Rate, Albedo) aus 1°C bei CO2-Verdopplung 3°C werden, oder mehr. Also die Werte sich ums dreifache+ erhöhen.
„Für den Anstieg der Temperatur über CO2 gilt die Formel“:
Mein Thermodynamik Professor hat mir ganz andere Formeln für die Temperaturerhöhung beigebracht, in denen u.a. die Masse und und die zugeführte Energie enthalten ist, die allgemein gültig sind. Alle andere Thermodynamik Lehrkräfte kennen auch keine andere Formeln, existieren auch nicht.
Wenn ein pensionierter Wellen-Zähler aus Bremen glaubt, die Thermodynamik durch wirre CO2-Formeln ersetzen zu können, dann ist es zwar nicht verboten, aber lächerlich.
Die Verbrennungsmotoren sind alle nach den mir bekannten Formeln konstruiert. Wenn Sie glauben, Sie können einen Motor anstatt mit Dieselverbrennung durch das Reinpusten von CO2 und der dadurch erwirkte Temperaturerhöhung antreiben, dann melden sie ein Patent an. Ich warte amüsiert auf den Krüger-CO2-Motor.
„Also entweder war der CO2 Gehalt minus 2.470 ppm (280 – 2.750)ppm oder das Ganze ist Schwachsinn.“
Letzteres…
„Das IPCC geht davon aus, dass…“
Wenn das IPCC von irgendwas ausgeht, ist es gekaufter Blödsinn
Herr Krueger,
wo kann man denn diesen Temperatureffekt messen? In der konvektiv freien Atmosphäre oder im Experiment wo die Gase eingeschlossen sind?
Oder soll der Erdboden wärmer werden und wenn ja warum?
@Georgiev
Die Formeln stehen so für die verschiedenen THG in den IPCC-Berichten und Lehrbüchern zur Atmosphärenphysik. Unterrichtsstoff an den Unis. Am IUP in Bremen im NW1 werden die auch so gelehrt. Vor 25 Jahren und heute.
Peter Georgiev schrieb am27. Januar 2021 um 20:56
Die Klimasensitivität beschreibt die Ergebnisse von Modellrechnungen. Die Modellrechnungen selbst basieren bei Klimamodellen genau auf den von Ihnen erwähnten Formeln.
@ Krüger und Marvin Müller
„Die Klimasensitivität beschreibt die Ergebnisse von Modellrechnungen.“
Früher hat der Medizinmann ein Märchen über ein kommendes Unheil erzählt und damit dem Häuptling den Anlass zur Handlung geliefert. Heute werden Computermärchen über kommendes Unheil präsentiert, mal PowerPoint Präsentationen über Giftgas, aber viel häufiger Simulationen über Virusausbreitungen oder Temperaturanstiege, wahlweise von 0,5 bis xx Grad.
Der einzige Unterschied, der Häuptling damals hatte gesunden Menschenverstand und hat das Schicksal seines Volkes im Auge behalten, beides kann man bei den heutigen Häuptlingen mit ziemlicher Sicherheit ausschließen.
Gemeinsam ist, sowohl der Medizinmann als auch die heutigen Märchenerzähler genießen einen sehr hohen gesellschaftlichen Status und rücken deshalb niemals von den Märchen ab, und zweitens, die Märchen werden gerne von der Mehrheit geglaubt.
P.S. Herr Limburg, ich werde in Kürze einen Beitrag über grundsätzliche Schwächen von Computersimulationen im Vergleich zu Wirklichkeit senden. Vielleicht wäre es für die Mehrheit interessant.
Nur zu!
@Krüger
„…Unterrichtsstoff an den Unis. Am IUP in Bremen im NW1 werden die auch so gelehrt. Vor 25 Jahren und heute.“
Daher ist das Volk, allen voran die Elite im Vergleich von vor 30 Jahren total verblödet, vor allem in den Naturwissenschaften.
Vor 40 Jahren wurde kein Schwachsinn in Universitäten verbreitet sondern Wissenschaft.
@Georgiev
Hier im IPCC-Bericht auf S. 358 finden Sie die Formeln:
https://www.ipcc.ch/site/assets/uploads/2018/03/WGI_TAR_full_report.pdf
Kann ich nicht bestaetigen. Dort ist ein Literaturverzeichnis zu:
Aerosols, their Direct and Indirect Effects
Meinten sie die Formel 6.1 auf Seite 354?
Diese Formel ist empirisch und nicht physikalisch.
@Werner
Hier:
@Georgiev
Seit Schwarzschild und Schuster 1906 ist die Strahlungstransfergleichung Grundlagenwissen. Aus der Schuster-Schwarzschild-Gleichung gehen die Strahlungstransfermodelle und Gleichungen für die verscheidenden Treibhausgase hervor. In den 1960ern wurden die entwickelt. Von Manabe, etc. Die Strahlungstransfermodelle wie Modtran und Hitran wurden auch schon in den 1960ern vom Militär mit entwickelt. Zur Fernerkundung, etc..
@ Krüger
„dT = 0.27 x 5.35 x ln (CO2 neu / CO2 alt)“
Bei jeder Gleichung in der Physik ist die physaikalische Einheit links und rechts vom gleichheitszeichen identisch. Sie haben links Kelvin und rechts eine einheitslose Größe, allso eine natürliche Zahl.
Es ist keine Schsuter-Schwarzschild- Gleichung, sondern Unfug nach Krüger.
„Die 3-6 Grad beruhen darauf, dass man sich die Temperatursprünge zwischen Eiszeiten und Warmzeiten im Modell nur über eine hohe Klimasensitivität erklären kann. James Hansen hat dazu mit den Grundstein gelegt.“
Die 3-6 Grad bedeuten, dass die Schwankung zwischen Kaltzeit und Eiszeit nicht mit dem relativ gleichmäßigen CO2 Gehalt zu erklären ist, sondern ganz andere Ursachen haben muss, egal wie Hansen sich die Sensitivität zurechtbiegt. In diesem Zusammenhang sollte man nicht vergessen, dass man weder in der vorindustriellen Zeit und auch nicht während der Eiszeit die CO2-schwankungen mit der heutigen Genauigkeit gemessen und dokumentiert werden konnten, sondern je weiter zurück, desto höher die Fehlertoleranz. Und unbestritten ist, dass in der Vergangenheit immer wieder totale Vereisungen bei zig Fach höheren CO2 Gehalt zu beobachten waren.
Auf solche Schlussfolgerungen kann man nur kommen, wenn man die menschgemachte Klimaänderung als einzig absolute Wahrheit festlegt und alle „naturwissenschaftliche“ Schlussfolgerungen dieser Wahrheit unterordnen und daraus ableiten.
Deshalb haben Hansen und Co. in den 1980ern auch schon aus 1°C bei CO2-Verdopplung 3,5°C durch die Feedbacks gemacht. Dieses Modell hat er damals den US-Kongress präsentiert. Durch die Feedbacks werden aus den 1°C durch CO2 halt dann 3-6°C oder noch mehr. Hansens Venus-Symdrom.
Es gibt kein THE! Nicht „natural“ und speziel nicht „antropopgen“. Bis heute haben Sie mich nicht überzeugt – perpetum mobile ist nicht existent.
Modelle: Garbage in, Garbage out. Wie viel Fliegen ist täglich ein Teufel? Un wieviel Teufels passt auf eine Nadel spitze?
Sagen Sie mir, wenn ich falsch liege:Nehmen wir ann, dass die Erde nur 161W/m2 von der einzigen Energiequelle dess Sonnnesystems abnimt. Wie kann dann 396W/m2 austrahlen? Gegenstrahlung? Und wo ist die Quelle dieser Gegenstrahlung? In den 396W der Strahlung der Erde? Und wo ist die Energiequelle für diese Strahlung? Laut „Wissenschaft“ kann das Sonne nicht sein, die gibt nur 161W/m2. Aha, in der Gegenstralung…Und wo ist die Energiequelle dieser Gegenstralung? In de Strahlung der Erde..Soll ich weiter?
Ja, das ist die Crux bei diesem TK-Strahlungsdiagramm. Die abgestrahlte Energie wird aber mit der Differenz zwischen „Ausstrahlung“ und „Gegenstrahlung“ richtig wiedergegeben und nur mit der habe ich gerechnet.
Warum soll jetzt das CO2 das Klima ändern. In den letzten 10000 Jahren, im Holozän, gab es mehrere Warmzeiten, die bis zu 2 K wärmer waren, immer bei 250 bis 280 ppm CO2, leicht steigend. Seien wir doch froh, dass es nach der kleinen Eiszeit wieder wärmer wurde. Gleichzeitig begann die industrielle Revolution und seitdem steigt der Anteil des CO2. Na und, Korrelation ist kein Beweis. Es gelten doch immer noch dieselben Naturgesetze?
Eine Ansicht, die ich gerne teilen möchte. Aber noch besser wäre ein Beweis. Und wenn obige Oberflächenbilanz keinen fundamentalen Fehler enthält, wovon ich bisher ausgehe, dann wäre es schon mehr als der halbe Weg zu diesem Ziel – zumindest müsste sich niemand mehr wegen der „anthropogenen Klimaerwärmung“ verrückt machen. Ob man damit gegen die tiefgläubige Klima-Katastrophenallianz ankommt, das ist die andere Frage.
Das Problem wird sein, dass die Drahtzieher hinter dem irrwitzigen Narrativ der menschengemachten Klimakatastrophe vermutlich sehr wohl wissen, was tatsächlich gespielt wird – nicht umsonst wurde der „Beginn der Wetteraufzeichnungen“ auf einen Zeitpunkt gelegt, von dem aus jede Veränderung hin zu „normalen“ Temperaturen eine Erwärmung implizieren MUSS! Und wer definiert eigentlich, was die „normale Durchschnittstemperatur“ dieses Planeten zu sein hat? Kindheitserinnerungen an Zeiten, zu denen man hinterm Haus noch Schlitten fahren konnte? Die Wissenschaftlichkeit derartiger Definitionsgrundlagen lässt da doch sehr zu wünschen übrig!