Zitat:
„… Unter die Postergucker mischte sich ein Älterer: Halbbrille, Glatze, grauer Bart. Dem Gebaren nach ein Wissenschafts-Guru. Kurz nahm der Typ Maß, um dann den jungen Koreaner mit Anwürfen nach dem Muster zu belegen: Wieso meinen Sie denn …? Aber es ist doch sattsam bekannt, dass …! Der Jüngere schien seiner Sache gewiss, blickte dem Älteren tapfer ins Gesicht und verteidigte sich in einem Englisch, das zu genauestem Hinhören zwang. Der Angreifer winkte nach ein paar zusätzlichen Einwänden ab und flanierte weiter durch die Reihen, bis er stirnrunzelnd vor einem anderen Poster verharrte. Dasselbe Szenario. Als ein Hüter der Wissenschaft wollte er imponieren, einer, der allerdings nur das zur Kenntnis nahm, was er sowieso schon wusste und auch nur deshalb zu wissen für werthielt. Leute waren das, die es verstanden, kunstvoll am Winde zu segeln, den sie selbst machten. Ein paar Jahre hin, und diesen Laffen wird niemand mehr kennen. Seine altväterlichen Weisheiten nimmt er dann wie alle vor ihm mit ins Grab.“
Das hemisphärische Stefan-Boltzmann-Modell kommt ohne einen Treibhauseffekt aus
Meine neuartige hemisphärische Stefan-Boltzmann-Betrachtung für die Temperaturgenese auf unserer Erde (Abbildung unten) kommt ohne einen „natürlichen atmosphärischen Treibhauseffekt“ aus und kann unter Einbeziehung der S-B-Umgebungsgleichung die sogenannte „gemessene“ globale Durchschnittstemperatur NST widerspruchsfrei erklären.
Mein hemisphärischer 2PIR²-S-B-Ansatz für die Tagseite der Erde ohne THE steht also diametral gegen den konventionellen 4PIR²-Tag=Nacht-THE-Ansatz, wie die nachfolgende Tabelle zeigt:
Die von mir bereits mehrfach erhobene Widerlegungsanforderung gegen meinen S-B-Ansatz, nämlich einen physikalischen Gleichwertigkeitsnachweis von Tag und Nacht zu erbringen, wurde von meinen Kritikern bisher nicht erfüllt. Stattdessen mühen sich die üblichen „Postergucker“ als Blogwarte des herkömmlichen 24h=Faktor4-THE-Flacherdeansatzes mit Argumenten „ad hominem“ und „ad auctoritatem“ sowie paternosterartigen KKDMP-Wiederholungen ab. Einer der KKDMP-Namensgeber, ein Herr „Gerhard Kramm, Fairbanks, Alaska, USA“, hat nun noch einen draufgesetzt und zwei Aufsätze gegen meinen hemisphärischen S-B-Ansatz geschrieben. In dem einen argumentiert er „ad auctoritatem“, indem er eine Phalanx von Physikkoryphäen gegen meinen hemisphärischen S-B-Ansatz antreten lässt, von denen sich zeitlebens kein einziger zustimmend zum THE geäußert hatte; im anderen widerlegt er dann Aussagen, die er selbst mir erst freihändig zugeschrieben hatte:
Kramm behauptet in seinem ersten Aufsatz, Zitat Seite 18, Mitte, mit Hervorhebungen: „Während Weber (2019) den Temperaturverlauf auf der Nachtseite einer Erde ohne Atmosphäre bzw. des Mondes ignorierte, um seinen hemisphärischen Stefan-Boltzmann-Ansatz anwenden zu können, …“. Und in seinem zweiten Aufsatz behauptet er dann einfach mal das Gegenteil, Zitat erster Satz mit Hervorhebungen: „Ausgehend von dem Begriff des ‚solaren Klimas‘ wird nachgewiesen, dass die von Herrn WEBER in seinem Beitrag aufgestellten Behauptungen zur global ermittelten Oberflächentemperatur einer Erde ohne Atmosphäre mit den theoretischen Grundlagen unvereinbar sind.“
Kramm skandalisiert also, ich hätte angeblich den Temperaturverlauf „einer Erde ohne Atmosphäre“ ignoriert (1. Aufsatz) und gleichzeitig Behauptungen über „eine Erde ohne Atmosphäre“ aufgestellt (2. Aufsatz). Diese Argumentation ist also ein geschickt konstruierter Zirkelschluss (petitio principii) mit einer Beweisführung ad auditores (vordergründig plausibel für ein Publikum ohne tiefere Kenntnis). Nur zur Erinnerung, mein hemisphärisches S-B-Modell beschreibt die Temperaturgenese auf der REALEN Erde mit Tag und Nacht ohne einen THE, aber unter Einbeziehung der in Atmosphäre und Ozeanen gespeicherten Wärme. Kramms Skandalisierung betrifft also gar nicht meinen realitätsnahen hemisphärischen S-B-Ansatz, sondern vielmehr seine eigene 24h=Faktor4-THE-Flacherde ohne Atmosphäre. Und wo Kramm in seinen Kommentaren unbewiesene justitiable Behauptungen verbreitet, überschreitet er dann auch noch die Grenze zwischen wissenschaftlicher und dichterischer Fiktion.
Kramms Kommentar mit dem Link zu seinem 1. Aufsatz und die dortigen Referenzen zu meinen Arbeiten:
Weber, U. (2018): Die hemisphärische Stefan-Boltzmann Temperatur unserer Erde. Books on Demand, 48 pp.
Weber, U. (2019): Weitere Überlegungen zur hemisphärischen Herleitung einer globalen Durchschnittstemperatur. Mitt. Deutsche Geophysikalische Gesellschaft, 1/2019, 18-25.
Kramms Kommentar mit dem Link zu seinem 2. Aufsatz und die dortigen Referenzen zu meinen Arbeiten:
WEBER, U. (2017): Beweist die Temperatur des Mondes den hemisphärischen Stefan-Boltzmann Ansatz? EIKE e.V., https://www.eike-klima-energie.eu/2017/07/02/beweist-die-temperatur-des-mondes-den-hemisphaerischen-stefan-boltzmann-ansatz/
WEBER, U. (2018): Die hemisphärische Stefan-Boltzmann Temperatur unserer Erde. Books on Demand, 48 pp.
WEBER, U. (2018): Weitere Überlegungen zur hemisphärischen Herleitung einer globalen Durchschnittstemperatur. Mitt. Deutsche Geophysikalische Gesellschaft, 1/2019, 18-25.
Konkurrierende Modelle können sich untereinander weder bestätigen noch widerlegen
Insgesamt bewahrheitet sich damit erneut, was ich bereits hier auf EIKE über konkurrierende Modelle ausgeführt hatte, Zitat: „…Eine Skandalisierung meines Modells anhand von bekanntem Lehrbuchwissen, in dem diese konkurrierenden Modelle dargestellt werden, ist also wissenschaftlich absolut unzulässig. Konkurrierende Modelle können sich untereinander weder bestätigen noch widerlegen; das geht nur über deren gemeinsame physikalische Grundlagen…“. Murphy, der Lieblingsphilosoph aller Ölsucher, hatte diese Problematik folgendermaßen auf den Punkt gebracht, Zitat, „In a two-boat operation, the idiots are always on the other ship“. Bei der subjektiven Bewertung „Totalverweigerer“ und „Realist“ kommt es nämlich lediglich auf den eigenen Standpunkt an. Da sich neue wissenschaftliche Ansätze, die dem klimawissenschaftlichen Mainstream widersprechen, heutzutage nur sehr schwer verbreiten lassen, beflügeln solche manipulativen Scheinkritiken immerhin den sogenannten „Streisand-Effekt“.
Nun kaprizieren sich einige Kommentatoren aber auch darauf, dass mein hemisphärisches S-B-Modell experimentell noch gar nicht bewiesen worden sei. Dabei hatte Herr Albert Agerius diesen Nachweis über eine Rückrechnung der ERBS-Satellitenmesswerte auf die hemisphärische Sonneneinstrahlung bereits öffentlich geführt (sein Buch hier und sein aktueller EIKE-Artikel hier) und damit das IPCC-KT97-Klimamodell anhand von gemessenen Daten widerlegt. Denn schließlich stellen solche Satellitenmesswerte ein 1:1-Experiment bezüglich unserer realen Erde dar.
Der Teufelskreis zwischen Verständlichkeit und nicht angreifbaren Formulierungen
Der Autor versucht nachfolgend einmal, den Teufelskreis zwischen Verständlichkeit und nicht angreifbaren Formulierungen zu durchbrechen. Im nachfolgenden Text weisen die Zahlen in eckigen Klammern jeweils auf weiter unten verlinkte Artikel hin, in denen einzelne Aspekte meines hemisphärischen S-B-Modells bereits ausführlich behandelt worden waren.
Mein hemisphärisches S-B-Modell kann die Temperaturgenese auf der Tagseite unserer Erde und die „gemessene“ globale Durchschnittstemperatur von ca. 15°C unter Einbeziehung der S-B-Umgebungsgleichung ohne einen „natürlichen atmosphärischen Treibhauseffekt“ widerspruchsfrei erklären.
Dabei erfolgt die globale Abstrahlung von 235W/m² analog zum konventionellen THE-Ansatz über die sogenannte „Abstrahlungshöhe“. Allerdings erklärt sich die Temperaturdifferenz von 33°C zwischen Erdoberfläche (ca. 15°C) und dieser „Abstrahlungshöhe“ von etwa 5.000 Metern (ca.-18°C) ohne eine thermodynamisch widersinnige „atmosphärische Gegenstrahlung“ und ohne einen THE allein über die barometrische Höhenformel [19], wie das erstmals in einem Kommentar des EIKE-Admins ausgeführt worden war.
Immer wieder versuchen zweidimensionale Rechenkünstler und „Segler am selbstgemachten Wind“, mein hemisphärisches S-B-Modell mit vordergründigen THE-Argumenten infrage zu stellen [14-16]. Dieses hemisphärische S-B-Modell ist physikalisch leider nicht ganz barrierefrei und erfordert eine gewisse Abstraktion sowie sphärisches Vorstellungsvermögen. Bitte beachten Sie daher, dass sich die solare Einstrahlung ausschließlich auf die Tageshemisphäre der Erde beschränkt [13] und nur hier die spezifische solare Strahlungsleistung über das Stefan-Boltzmann-Gesetz ZEITGLEICH in ein S-B-Temperaturäquivalent (Strahlung => Temperatur) überführt werden kann. Beachten Sie bitte weiter, dass dieses rechnerische S-B-Temperaturäquivalent auf unserer Erde nur in extremen Ausnahmefällen erreicht wird, weil die örtliche Aufheizung üblicherweise durch Verdunstung und Konvektion begrenzt ist [20], also Wärme in die globalen Zirkulationen abfließt. Und beachten Sie bitte schließlich auch noch, dass die in Atmosphäre und Ozeanen gespeicherten Energiemengen über die S-B-Umgebungsgleichung das Temperaturverhalten auf der Nachtseite und der Winterhemisphäre unserer Erde entscheidend beeinflussen [12].
Die Inversion des Stefan-Boltzmann-Gesetzes
Tatsächlich stellt mein S-B-Modell eine S-B-Inversion (Strahlung => Temperatur) dar [20]. Der Einwand, eine S-B-Inversion würde den Erfahrungswerten beim Gebrauch eines Mikrowellenherdes widersprechen, stellt eine unzulässige dialektische Erweiterung des ursprünglichen Anwendungsbereiches dar; dieses Argument springt also vom sichtbaren (~1015 Hz) und infraroten (~1013 Hz) Licht zu monofrequenter Mikrowellenstrahlung (~1010 Hz). Und außerdem gilt dieser Einwand selbstverständlich für BEIDE konkurrierenden S-B-Modelle, also SOWOHL für mein hemisphärisches S-B-Modell ALS AUCH für den Faktor4=24h-THE-Flacherdeansatz.
Physikalisch ist aber auch die Inversion des S-B-Gesetzes (Strahlung => Temperatur) gültig, solange die S-B-Randbedingungen, also die strenge Gleichzeitigkeit (bei beiden, sowohl beim S-B-Gesetz als auch bei der Inversion) und die geometrisch korrekte spezifische Strahlungsleistung für die betrachtete Fläche (S-B-Gesetz: Strahlende Fläche des Schwarzkörpers/ Inversion: Ausschließlich die bestrahlte Fläche), stringent eingehalten werden. Insbesondere darf eine S-B-Inversion also nur auf die gleichzeitig beleuchtete Fläche angewendet werden; unbeleuchtete Flächen haben in einer solchen S-B-Inversion nichts verloren.
Die Gültigkeit einer solchen S-B-Inversion wird durch eine Übereinstimmung meines hemisphärischen S-B- Ansatzes mit dem Verlauf der gemessenen Tagestemperatur auf dem Mond eindeutig nachgewiesen [5]. Die Oberflächentemperatur auf dem Mond wird durch die einfallende solare Strahlungsleistung erzeugt. Der gemessene Temperaturverlauf auf der Tagseite des Mondes entspricht meinem hemisphärischen S-B-Modell. Damit ist der Beweis erbracht, dass eine Inversion der spezifischen solaren Strahlungsleistung dem Stefan-Boltzmann-Gesetz gehorcht. Somit wäre zunächst beiden S-B-Inversionen abgeholfen; als Knackpunkte eines 24h-Faktor4-THE-Flacherdeansatzes verbleiben allerdings weiterhin dessen Nichterfüllung der S-B Randbedingungen und die Verletzung des 2. HS der Thermodynamik.
Beim Stefan-Boltzmann-Gesetz kommt es streng auf die Reihenfolge an
In manchen Kommentierungen zu meinen Artikeln wird eine grundlegende Unkenntnis über den Zusammenhang der physikalischen Größen „Leistung“ und „Arbeit“ erkennbar. Versuchen Sie doch einfach mal, aus einem Liter kochendem Wasser, das anfänglich eine Temperatur von 8°C hatte, die elektrische Leistung der betreffenden Herdplatte zu ermitteln, ohne dass Ihnen die Zeit bis zum Kochen des Wassers bekannt ist. Sie werden feststellen, dass es für diese Aufgabe keine eindeutige Lösung gibt, sondern unterschiedliche Kombinationen von Heizleistungen und Kochzeiten zum selben Ergebnis führen.
Also, [Leistung] ist, was hinten auf der Herdplatte draufsteht, ganz egal, ob sie heiß oder kalt ist, beispielsweise 2000 Watt bei 230 Volt. Und [Arbeit] ist das Ergebnis, wenn die Herdplatte für einen gewissen Zeitraum eingeschaltet war und Wärme produziert hat, also [Wärme = Leistung mal Zeit]. Wenn Sie jetzt diese Heizplatte bis zum Kochen des Wassers bei voller Leistung im Wechsel für jeweils 30 Sekunden ein- und ausschalten, dann erhalten Sie, von Verlusten einmal abgesehen, prinzipiell die gleiche Wärmemenge, als wenn Sie diese Heizplatte bei halber Leistung über den gesamten Zeitraum betreiben würden. Der wesentliche Unterschied ist dann, dass die Heizplatte bei 1.000 Watt Leistung nicht so heiß geworden ist wie bei 2.000 Watt.
Und damit die KKDMP&B-Fraktion jetzt nicht im Chor aufheult, nein, dieses Beispiel hat nicht direkt mit dem S-B-Gesetz zu tun, sondern nur mit dessen physikalischen Einheiten; es kann aber sinngemäß auch auf das S-B-Gesetz übertragen werden. Denn die primäre Temperaturgenese auf unserer Erde erfolgt allein durch die direkte spezifische Strahlungsleistung der Sonne (S-B-Inversion: Strahlung => Temperatur) auf ihrer hemisphärischen Tagseite. Alle globalen Mittelwerte, die sich aus zeitlich und/oder räumlich gemittelten spezifischen Strahlungsleistungen der Sonne herleiten, verlassen dagegen unwiderruflich das S-B-Gesetz. Sie enden daher, ebenso wie das Beispiel mit der Herdplatte, für die primäre solare Einstrahlung bzw. deren Temperaturäquivalent in einer beliebigen Lösungswolke, deren Ergebnisse noch nicht einmal der physikalischen S-B-T4-Beziehung genügen.
Nicht alles, was hinkt, ist ein Beispiel – aber jedes Beispiel hinkt.
Wenn ein gemeiner Forentroll (Vexator fororum utgardensis) verhindern will, dass der interessierte Leser ein gutes Beispiel versteht, dann fokussiert er seinen Kommentar auf das Hinken dieses Beispiels. Je einfacher und allgemeinverständlicher nämlich ein solches Beispiel ist, umso größere Angriffsflächen bietet es für sophistische Interpretationen. So hatte beispielsweise ein Herr Werner Schulz den physikalischen Unterschied zwischen der Verteilung der solaren Einstrahlung über die Fläche der Tagseite einerseits und über die Gesamtfläche unserer Erde andererseits am Beispiel eines Schweißbrenners erläutert. Und der interessierte Leser kann dieses Beispiel jederzeit in einen direkten Zusammenhang mit der ursprünglichen Argumentation bringen. Wenn er sich also nicht durch Troll-geführtes Störfeuer auf einen sophistischen Holzweg abdrängen lässt, wird er feststellen, dass bei der Umrechnung einer definierten spezifischen Strahlungsleistung in ein S-B-Temperaturäquivalent die Größe der bestrahlten Fläche die alles entscheidende Rolle spielt.
Bei unserer Erde handelt es sich um ein quasistatisches und energetisch „voll mit Wärme aufgeladenes“ System, bei dem Energiespeicherung und Energieabgabe zeitgleich, aber nicht ortsgenau erfolgen [6], wobei die gerade eingestrahlte Sonnenenergie nicht unbedingt im selben Augenblick wieder als IR-Strahlung abgestrahlt, sondern zum Teil in den globalen Zirkulationen von Atmosphäre und Ozeanen „zwischengespeichert“ wird. Nehmen Sie beispielsweise den Golfstrom. Sie könnten behaupten, die Energiemenge, mit der dieser gerade in den Tropen und Subtropen beladen wird, fehle in der momentanen Energiebilanz. Sie könnten aber umgekehrt auch behaupten, die momentane Aufheizung in mittleren und höheren geographischen Breiten durch den Golfstrom müsse der Energiebilanz zusätzlich zugerechnet werden. In Wirklichkeit geschieht aber beides gleichzeitig an unterschiedlichen Orten, sodass es sich insgesamt betrachtet um ein globales Nullsummenspiel handelt.
Das Treibhaus-Modell erfordert zwei Sonnen
Gleichgültig, ob eine oder zwei Sonnen mit einer spezifischen Strahlungsleistung von insgesamt 1.367W/m² auf unsere Erde scheinen [20], das 24h=Faktor4-Flacherde-THE-Modell kommt immer auf dasselbe S-B-Temperaturäquivalent von -18°C als sogenannte „theoretische globale Durchschnittstemperatur“.

Abbildung: Das auf der 13. IKEK von Herrn Michael Limburg als Analogon zum konventionellen THE-Ansatz vorgestellte 2-Sonnen-Modell (links) und der hemisphärische S-B-Ansatz ohne THE (rechts)
Und allein mein hemisphärisches S-B-Modell ist in der Lage, den Unterschied zwischen diesen beiden Fällen darzustellen und das jeweilige S-B-Temperaturäquivalent (1 Sonne ~ +15°C / 2 Sonnen ~ -18°C) korrekt zu quantifizieren [17]. Dieses S-B-Modell ist statisch und beruht auf folgender Durchschnittsbetrachtung: Nirgendwo auf der Erde herrscht im Tages- oder Jahresverlauf irgendein energetisches Gleichgewicht, dieses Ungleichgewicht treibt unser Wetter an und Klima ist dessen 30-jahriger Durchschnitt. Für ein generalisiertes makroskopisches Modell unserer Erde muss ich also zeitlich mindestens bis zum Klimabegriff abstrahieren. Und erst hier kann ich dann versuchen, die grundlegenden Phänomene der Klimagenese auf unserer Erde zu beschreiben, wie das in meinem hemisphärischen S-B-Modell ausgeführt wird.
Die sogenannte „globale Durchschnittstemperatur“ NST von ca. 15°C für das energetisch „voll aufgeladene“ System Erde/Atmosphäre/Ozeane lässt sich ganz gut anhand einer „tiefgekühlten“ Erde erläutern, die von der Sonne gerade energetisch aufgeladen wird [6]. Wenn wir jetzt beispielsweise einmal den Golfstrom betrachten, dann nimmt er in dieser Situation zwar Wärme auf, gibt aber in nördlichen Breiten noch keine Energie ab, sodass die NST zunächst deutlich unter 15°C bleibt. Denn aufgrund von Verdunstung und Konvektion wird das örtliche S-B-Temperaturäquivalent nirgendwo erreicht, und andererseits können die globalen Wärmeströme (atmosphärische und ozeanische Zirkulationen) in mittleren und höheren Breiten noch keine gespeicherten Wärmemengen „zurückliefern“, um dieses Defizit auszugleichen. Erst im Endstadium, wenn also sämtliche Wärmespeicher unserer Erde komplett gefüllt sind, ist global gesehen der „Gewinn“ aus Kondensation und Advektion im langjährigen Mittel genauso groß, wie der „Verlust“ durch Verdunstung und Konvektion. Und deshalb konvergiert die maximal mögliche Durchschnittstemperatur auf unserer Erde beim flächengewichteten Durchschnitt von ca. 15°C für das S-B-Temperaturäquivalent aus der hemisphärischen Sonneneinstrahlung [13]. Dieses S-B-Temperaturäquivalent entspricht der „gemessenen“ NST von ca. 15°C und lässt keinerlei Raum für einen „natürlichen atmosphärischen Treibhauseffekt“.
Das Land-Seewind-System als Funktionsbeispiel für die globalen Zirkulationen
Im Ablauf von Tag und Nacht verläuft die Erwärmung und Abkühlung von Land- und Wassermassen sehr unterschiedlich. Das nachstehend abgebildete Land-Seewind-System ist ein bekanntes Beispiel für den Wärmeaustausch zwischen Land und Meer:

Abbildung: Skizze zum Land-Seewind-System (A Seewind / B Landwind). Aus Wikipedia, Autor: Talifero – Diagrama de formacion de la brisa-breeze.png…, Lizenz: CC BY-SA 3.0
Aus der Beschreibung auf Wikipedia, Zitat:
„Seewind: Luftmassen strömen vom Wasser aufs Land, da sich dieses aufgrund des relativ geringen c-Wertes von bspw. Boden, Beton, Häusern, (Dachziegeln c= 0,73 kJ/(kg·K)) und Asphalt tagsüber schneller aufheizt. Wasser dagegen heizt/kühlt sich aufgrund des höheren c-Wertes von 4,18 kJ/(kg·K) wesentlich langsamer auf/ab. Daher steigen tagsüber die Luftmassen über Land auf und es kommt zu einer Ausgleichsbewegung durch vom Wasser aus nachrückende Luftmassen (=Seewinde).“
„Landwind: Luftmassen strömen vom Land zur oder zum See. Grund: Abends, noch mehr nachts, dreht sich diese Zirkulation um; Land kühlt sich viel schneller ab als die/der See, wegen viel geringerer c-Werte der genannten Stoffe, (Dachziegel, c = ca. 0,73 kJ/(kg·K)). D. h. wesentlich geringere Spezifische Wärmekapazität als Wasser (4,18 kJ/ (kg·K)). Nun ist das Wasser relativ wärmer; nun steigt über der/dem See die Luft auf- und relativ kältere Luftmassen fließen vom Land weg zur/zum See nach.“
Im Land-Seewind-System werden nächtliche Wärmeverluste der Landmassen also durch die Advektion erwärmter Luft von den Meeresflächen abgemildert, während am Tage die Wärme der Landflächen durch Konvektion abgeführt wird. Dieses Beispiel lässt sich auf die die globalen Zirkulationen in Atmosphäre und Ozeanen übertragen, wobei hier die Quellen um den Äquator und die Senken in mittleren und höheren Breiten liegen.
Die hemisphärische Sonneneinstrahlung in den Tropen treibt die kombinierte Luft-Wasser-Heizung unserer Erde an
Betrachten wir jetzt einmal die Beziehung zwischen Temperatur und spezifischer Strahlungsleistung nach dem Stefan-Boltzmann-Gesetz am Beispiel der Tropen. Die Mitteltemperatur in den Tropen wird mit ca. 25°C angegeben. Wenn wir dort jetzt einmal eine flächengewichtete Schwankungsbreite von +/-10°C unterstellen, dann würde der Unterschied (DELTA S) im S-B-Strahlungsäquivalent innerhalb von 24 Stunden zwischen Temperaturmaximum und Temperaturminimum etwa 120W/m² betragen. Dieser Verlust von 120W/m² wird auf der Tagseite durch die spezifische Strahlungsleistung der Sonne mehr als kompensiert, wie die nachstehende Abbildung zeigt:
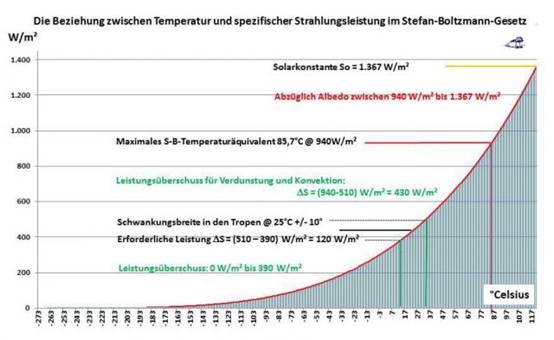
Bei vertikalem Sonnenstand erhalten wir im mittäglichen Zenit der Tropen folgende Maximalwerte:
0 bis390 W/m²: Leistungsüberschuss
390 bis 510 W/m²: Ausgleich der Temperaturspanne zwischen angenommener Maximal- und Minimal-Temperatur in den Tropen von etwa 120W/m²
510 bis 940 W/m²: Leistungsüberschuss
940 bis 1.367 W/m²: Bei einer Albedo von 0,306 bleiben 427W/m² aus der spezifischen solaren Strahlungsleistung auf unserer Erde ohne Einfluss auf die Temperatur. Diese Albedo ist ein Durchschnittswert, sodass örtlich durchaus höhere oder niedrigere spezifische Strahlungsleistungen temperaturwirksam werden können.
Die flächengewichtete tägliche Schwankungsbreite der Ortstemperaturen in den Tropen ist mit +/-10°C eher zu hoch angesetzt, wenn man bedenkt, dass die oberflächennahen Temperaturen im tropischen Ozean eher an die 30°C heranreichen und die tägliche Schwankungsbreite dort wesentlich geringer ausfällt. Es werden also weniger als 13 Prozent der maximalen spezifischen Strahlungsleistung der Sonne für den Temperaturerhalt in der Äquatorregion benötigt, während mehr als 87 Prozent die kombinierte Luft-Wasser-Heizung unserer Erde antreiben. Umgekehrt dürften jenseits der Tropen bis in die Polarzonen hinein Kondensation und Advektion aus den globalen Zirkulationen einen immer weiter ansteigenden Beitrag zur jeweiligen Ortstemperatur liefern, insbesondere auf der jeweiligen Winterhemisphäre.
Die hemisphärische Sonneneinstrahlung auf der Tagseite der tropischen Äquatorialzone treibt also die kombinierte Luft-Wasser-Heizung unserer Erde mit einer maximalen spezifischen Strahlungsleistung von mehr als 820W/m² an. Die dort mit Wärme beladenen Luft- und Wassermassen werden dann durch die globalen Zirkulationen in die mittleren und höheren geographischen Breiten transportiert und dort wieder frei gesetzt. Die Sonneneinstrahlung auf der Tagseite unserer Erde reicht im „voll mit Wärme aufgeladenen“ Stadium der globalen Zirkulationen also völlig aus, um die sogenannte „gemessene globale Durchschnittstemperatur“ von ca. 15°C ohne einen sogenannten „natürlichen atmosphärischen Treibhauseffekt“ zu erklären.
Für alle ernsthaft interessierten EIKE-Leser nachfolgend eine aktuelle Auflistung der bisher hier auf EIKE erschienen Artikel über meinen hemisphärischen S-B-Ansatz:
- 23. Januar 2017: Über einen vergeblichen Versuch, unsere Welt vor der Dekarbonisierung zu retten
- 1. Februar 2017: Wer im Treibhaus sitzt…
- 16. Februar 2017: Nachdem sich der Rauch verzogen hat: Stefan-Boltzmann auf den Punkt gebracht
- 23. Juni 2017: Noch ein paar Fragen zum „natürlichen“ atmosphärischen Treibhauseffekt
- 2. Juli 2017: Beweist die Temperatur des Mondes den hemisphärischen Stefan-Boltzmann Ansatz?
- 19. August 2017: Machen wir mal ein Gedankenexperiment: Es gibt gar keine Erde!
- 26. November 2017: Rückblick: Ein Jahr hemisphärischer Stefan-Boltzmann Ansatz
- 30. November 2017: Nicht immer passt wirklich alles zusammen
- 14. Februar 2018: https://www.eike-klima-energie.eu/2018/02/14/das-gegenteil-von-gut-ist-gut-gemeint/
- 22. Februar 2018: Eine barrierefreie Erklärung für die hemisphärische Temperaturgenese auf unserer Erde
- 7. Mai 2018: Fangen wir mit dem Stefan-Boltzmann-Gesetz noch einmal ganz von vorne an
- 29. Juli 2019: Safety First: Zum besseren Verständnis meiner hemisphärischen Energiebilanz
- 11. September 2019: https://www.eike-klima-energie.eu/2019/09/11/anmerkungen-zur-hemisphaerischen-mittelwertbildung-mit-dem-stefan-boltzmann-gesetz/
- 2. Dezember 2019: https://www.eike-klima-energie.eu/2019/12/02/eine-analyse-der-thesen-antithesen-fuer-einen-natuerlichen-atmosphaerischen-treibhauseffekt-teil-1-gegenueberstellung-der-thesen-antithesen/
- 3. Dezember 2019: https://www.eike-klima-energie.eu/2019/12/03/eine-analyse-der-thesen-antithesen-fuer-einen-natuerlichen-atmosphaerischen-treibhauseffekt-teil-2-diskussion-der-thesen-antithesen/
- 4. Dezember 2019: https://www.eike-klima-energie.eu/2019/12/04/eine-analyse-der-thesen-antithesen-fuer-einen-natuerlichen-atmosphaerischen-treibhauseffekt-teil-3-erkenntnisse-zu-den-thesen-antithesen-und-das-ergebn/
- 15. Dezember 2019: https://www.eike-klima-energie.eu/2019/12/15/kelvin-allein-zu-haus-der-unterschied-zwischen-zwei-watt-ist-deren-umgebungstemperatur/
- 25. Dezember 2019: https://www.eike-klima-energie.eu/2019/12/25/ein-weihnachtlicher-rueckblick-auf-die-rolle-der-klimarealisten-in-der-oeffentlichkeit/
- 12. Januar 2020: https://www.eike-klima-energie.eu/2020/01/12/zeigt-der-poynting-vektor-auf-mittelerde-oder-auf-die-sogenannte-abstrahlungshoehe/
- 5. Februar 2020: https://www.eike-klima-energie.eu/2020/02/05/anmerkungen-zur-bestimmung-der-hemisphaerischen-solaren-einstrahlung-auf-mittelerde/
- 23. Februar 2020: https://www.eike-klima-energie.eu/2020/02/23/neues-von-willis-eschenbach/
- 18. März 2020: https://www.eike-klima-energie.eu/2020/03/18/verbesserungswuerdig-ueber-fehlerhafte-ansaetze-fuer-eine-breitenabhaengige-globaltemperatur/
Und hier finden Sie noch ein paar Bücher von Uli Weber, der in seinem ersten Klimabuch (Farbe 2012/ SW 2017) den THE sogar noch als Stand der Wissenschaft beschrieben hatte. Aber man lernt ja glücklicherweise niemals aus…



















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"@All: Der D-K-Award 2020
Die hohe sophistische Kunst, verkürzte Aussagen in einen falschen Kontext zu stellen und diese dann zu skandalisieren, zeichnet den gemeinen Forenrtroll aus (Vexator vororum utgardensis), der sich vom Frust seiner Mitmenschen ernährt. Den „Seglern am selbstgemachten Wind“ hatte ich dagegen vorgehalten, mein hemisphärisches S-B-Modell nicht gelesen, und/oder nicht verstanden, und/oder keine Werkzeuge für dessen Verständnis zu haben; aber paraphysikalische Anwandlungen hatte ich ihnen nicht unterstellt, Zitat*:
„Ich habe jetzt die eigentliche Ursache für den von Uli Weber zum Beweis des nichtexistenten TE angestifteten Unsinns gefunden. Er hat S-B falsch verstanden, und zwar glaubt er, die Temperaturgenese erfolgt durch die solare EINSTRAHLUNG. Tatsache ist aber dass die Temperatur durch die ABSTRAHLUNG bestimmt wird. Werden z.B. Eiswürfel der Sonnenstrahlung ausgesetzt, so erwärmen sich diese nicht weil die zugeführte Wärme zum Schmelzen verbraucht wird.“
*) Aus einer E-Mail vom 30. September 2020 an den berüchtigten Hotel-California-Verteiler der Skeptiker (you can check out any time you like, but you can never leave)
Nachtrag @All
Auf dem o.g. Skeptiker-Verteiler hatte der vorjährige Träger des D-K-Awards*, ein promovierter Treibhausananas-Farmer, am 01.10.2020 folgenden Text verbreitet, Zitat:
„Weber, Ihr Kommentar (https://www.eike-klima-energie.eu/2020/09/23/ueber-neue-erkenntnisse-und-alte-postergucker-als-hueter-der-wissenschaft/#comment-261674) belegt, dass Sie nicht nur ein betruegerisch agierender Scharlatan, sondern auch noch ein Wirrkopf sind. Offensichtlioch glauben Sie immer noch, dass Ihre schwachsinnigen Behauptungen irgend was mit der Realitaet zu tun haben.“
Ich darf also feststellen, dass die einschlägigen Paraphysik-Experten noch nicht einmal über die Alltagskenntnis von Kindergartenkindern verfügen, die sehr wohl wissen, dass Sonnenstrahlung erwärmt und es nachts dunkel ist.
*) Dietze-Kramm-Award für die selbstlose Verteidigung des Tag=Nacht-Dogmas
Herr Weber,
bei Ihrem Modell gibt es (passend zum fehlinterpretierten 2.HS) überhaupt keine Gegenstrahlung, weshalb es OHNE Treibhauseffekt jedoch nicht mit einer Sonne auskommt sondern zwei Sonnen (!) braucht um auch auf der Nacht-Hemisphäre statt -273 Grad den Mittelwert von +15 Grad zu erzeugen – wie es von Prof. Gerlich mit Albedo und cos exakt lokal, aber ohne Bodenwärmefluss für die Tagseite berechnet wurde.
Sie schlagen mit hinterlistigen Beleidigungen zurück und bleiben dabei dass die solare EINstrahlung die „Temperaturgenese“ bestimmt. Ergo wird S-B bei Ihnen offensichtlich NICHT auf die ABstrahlung (mit Geometriefaktor 4 anstatt 2) angewendet. Und so bedarf die Nachtseite natürlich KEINER zweiten Sonne weil die dazu benötigte Energie aus dem Nichts kommt. Damit hat der Hemisphärenansatz eines Geophysikers ein blamables Ende gefunden.
QED: Eine Harakiri-Beweisführung à la Dunning-Kruger. Den „Seglern am selbstgemachten Wind“ hatte ich vorgehalten, mein hemisphärisches S-B-Modell nicht gelesen, und/oder nicht verstanden, und/oder keine Werkzeuge für dessen Verständnis zu haben; aber paraphysikalische Anwandlungen hatte ich ihnen nicht unterstellt…
Im Artikel steht:
Wenn ich einfach mal einen Linearen Zusammenhang zwischen Temperatur und Abstrahlung annehme (was bei den angegebenen Temperaturen vertretbar ist), dann gibt die Oberfläche im Mittel 450W/m² ab. Wenn ihr aber nur 120W/m² zufliessen, dann verliert sie pro Sekunde 330W/m² und würde sich drastisch abkühlen. Bei einem nichtlinearen Zusammenhang wäre die Abkühlung noch größer.
Herr Weber ist ja für einfach zu verstehende Beispiele, daher versuche ich mich mal daran. Nehmen wir statt Joule pro Sekunde pro Quadratmeter einfach mal Euro pro Stunde pro Person und nehmen an, ich würde tagsüber 10 Euro pro Stunde ausgeben und Nachts nur 5 Euro. Ich würde also an einem Tag 180 Euro ausgegeben. Laut Herrn Weber reicht es, wenn ich die Differenz zwischen 10 und 5 einnehme, also 120 Euro und ich hätte einen ausgeglichenen Haushalt. Ob ich das mal meiner Bank vorschlage?
Ich schrieb:
Da ist ein „pro Sekunde“ zuviel drin. Ich hätte besser schreiben soll, dass die Oberfläche effektiv 330W/m² mehr abgibt, als ihr zufliesst und sie sich daher abkühlt …
Herr Mueller,
können sie etwas mit dem Begriff Wärme anfangen?
Wenn nicht Lehrbuch aufschlagen und endlich lesen und verstehen.
Mehr kann ich ihnen nicht raten. Wer davon redet, dass ein Körper durch Abstrahlung Energie verliert, hat seine thermodynamischen Hausaufgaben nicht gemacht.
Energie geht nicht verloren, Abstrahlung ist nicht gleich Wärmeverlust.
Wenn man ihnen glaubt, müsste ein Mensch ständig durch Essen Energie aufnehmen, weil er bei 36 Grad C irgendwas ueber 400 W/m2 abstrahlt.
400 Joule pro Sekunde pro Quadratmeter! Wieviel Hautfläche haben sie?
„Wir haben eine durchschnittliche Einstrahlungsleistung von 470W/m² auf der Tagseite (@2 PI R²) der Erde (korrekt wäre [13]). Wenn die Tagseite nun 235W/m² abstrahlt, bleiben für die Nachtseite (@2 PI R²) also ebenfalls 235W/m² übrig“.
Herr Weber, Ihr Kommentar zu Dr. Roland Ullrich zeigt deutlich, wie sehr Sie sich verrannt haben. Die 15 Grad der Sonnen-Hemisphäre wurden doch unter der Premisse berechnet dass es KEINE Gegenstrahlung gibt und daher wird die gesamte absorbierte solare Einstrahlung von 470 W/m² im Mittel dort gemäss S-B auch wieder abgestrahlt. Es bleibt also NICHTS für die Nachtseite übrig, und diese nimmt deshalb -273 Grad an.
Ihr Ansatz ist der groteske Versuch, mit einem angenommenen TE (also mit Gegenstrahlung und T2>0, wodurch die Nettoabstrahlung der Tagseite halbiert wird) die Nichtexistenz eines TE zu beweisen. Einfach toll – und trotz der zahllosen Kritiken wollen Sie Ihren blamablen Fehler immer noch nicht einsehen.
@All
Ein verwirrter Vollautonom-Segler skandalisiert hier sein eigenes Unverständnis, Zitat: „Die 15 Grad der Sonnen-Hemisphäre wurden doch unter der Premisse berechnet dass es KEINE Gegenstrahlung gibt und daher wird die gesamte absorbierte solare Einstrahlung von 470 W/m² im Mittel dort gemäss S-B auch wieder abgestrahlt.“
Die diesbezügliche Aussage in meinem obigen Text lautet aber, Zitat: „Beachten Sie bitte weiter, dass dieses rechnerische S-B-Temperaturäquivalent auf unserer Erde nur in extremen Ausnahmefällen erreicht wird, weil die örtliche Aufheizung üblicherweise durch Verdunstung und Konvektion begrenzt ist [20], also Wärme in die globalen Zirkulationen abfließt. Und beachten Sie bitte schließlich auch noch, dass die in Atmosphäre und Ozeanen gespeicherten Energiemengen über die S-B-Umgebungsgleichung das Temperaturverhalten auf der Nachtseite und der Winterhemisphäre unserer Erde entscheidend beeinflussen [12].“
ERGO: Es gibt in meinem hemisphärischen S-B-Modell gar keine „auch-wieder“-Abstrahlung der „gesamte(n) absorbierte(n) solare(n) Einstrahlung von 470 W/m²“ auf der Tageshemisphäre, sondern es fließt dort vielmehr Wärme in die globalen Zirkulationen ab und wird von diesen dann auf die Nachtseite „mitgenommen“. Es ist schon höchst erstaunlich, wenn ein Selbstwind-Segler mein hemisphärisches S-B-Modell kritisiert, dessen Beschreibung er offenbar gar nicht gelesen hat, und/oder das er nicht verstanden hat, und/oder für dessen Verständnis ihm möglicherweise wesentliche Werkzeuge fehlen. Vollautonome Segelboote werden dem Hörensagen nach auf der Dunning-Kruger-Werft gebaut, die übrigens auch die Klimakirche mit schwer zu ortenden U-Booten beliefern soll…
==> Es gibt in meinem hemisphärischen S-B-Modell gar keine „auch-wieder“-Abstrahlung der „gesamte(n) absorbierte(n) solare(n) Einstrahlung von 470 W/m²“ auf der Tageshemisphäre, sondern es fließt dort vielmehr Wärme in die globalen Zirkulationen ab und wird von diesen dann auf die Nachtseite „mitgenommen“.
Herr Weber,
haben Sie denn immer noch nicht gespannt dass die korrekte Berechnung des Mittelwerts von 15 Grad auf der Tagseite durch Prof. Gerlich mit S-B – also OHNE BODENWÄRMEFLÜSSE erfolgte? D.h. dass sämtliche (!) solare Einstrahlung wieder abgestrahlt wird und somit NICHT etwa die Hälfte über Ozeane etc. auf die Nachtseite transportiert wird. Die Nachtseite hat -273 und NICHT +15 Grad! Hören Sie endlich auf zu versuchen, uns für dumm zu verkaufen.
@ Eigner von Dunning-Kruger-Booten
Allein der Versuch des Gegenteils ist schon voll ins Leere gelaufen. Das vorhandene Potential ist tatsächlich ausgereizt und eine Steigerungsmöglichkeit nicht mehr zu erkennen, zum Beweis ein umgedrehtes Dietze-Zitat: „Hören Sie endlich auf zu versuchen, uns für dumm zu verkaufen. Die Nachtseite hat -273 und NICHT +15 Grad!“
QED: Mein hemisphärisches Stefan-Boltzmann-Modell bildet die REALE Erde ab.
==> Mein hemisphärisches Stefan-Boltzmann-Modell bildet die REALE Erde ab.
Herr Weber, genau da liegt ja Ihr Fehler. Ihr solares Hemisphären-Modell rechnet mit S-B 15 Grad bei Abstrahlung = Einstrahlung auf der Sonnenseite aus und lässt damit KEINE Energie für die Nachtseite übrig. Sie behaupten dann grob falsch, auch die Nachtseite habe 15 Grad, weshalb kein TE erforderlich wird. Dazu würde aber eine zweite Sonne benötigt, die nicht vorhanden ist.
Wenn knapp die Hälfte der auf der Tagseite eingestrahlten Sonnenenergie weggespeichert und per Ozean und Atmosphäre auf die Nachtseite rotiert wird, kann die Tagseite nur etwa die Hälfte (!) abstrahlen und die Temperatur sinkt von 288 K um den Faktor 4.Wurzel(2), was dann nicht +15 Grad, sondern -31 Grad ergibt. Fazit: SIE wenden S-B falsch an, denn ohne TE geht es nicht!!
Der Dunning-Kruger-Effekt bezeichnet die kognitive Verzerrung im Selbstverständnis inkompetenter Menschen, das eigene Wissen und Können zu überschätzen. Genau das ist es was auf SIE zutrifft.
@ EIKE Admin
Ich hatte in einigen Kommentaren mit der „Dunning-Kruger-Werft“ und deren Produkten eine impliziten Verbindung zu dem gleichnamigen Effekt hergestellt; den direkten Bezug musste der Betroffene allerdings schon selbst herstellen. Jetzt stelle ich fest, dass hier auf dem EIKE-Blog ganz offen und direkt pathologisiert werden darf, also:
Wurden mit dem Serverwechsel auch die Kommentar-Regeln auf dem EIKE-Blog dem entsprechend geändert?
Welche meinen Sie?
Endlich eine Betrachtung über Strahlen, Strahlenintensität und SB-Gleichung, die nicht nur auf ein „berechenbares Strahlengleichgewicht und eine sich daraus ergebende Temperatur“ beschreibt, sondern auch andere thermodynamische Prozesse, wie in der fettgedruckten Zusammenfassung als mit verantwortlich für die Temperaturschwankungen betrachtet, und für ein Zustandenkommen der Temperatur von x Kelvin mit einbezieht.
Muss zugeben, dass ich meine überschaubaren Kenntnisse in Strahlenphysik auf EIKE angelesen habe. Den jahrzehntelangen Diskussionen hier ist aber nur Eins mit Sicherheit zu entnehmen: Es herrscht keine wissenschaftliche Klarheit über die genannten Prozesse wie über Gleichungen von Newton.
Meine persönliche Meinung, beruhend auf sattelfeste Thermodynamik, über das vereinfachte Temperaturmodell „Strahlenintensität der Sonne minus mittleres Albedo = Energiemenge die die Erde erwärmt und die gemessene Durchschnittstemperatur wäre nur mit „Rückkopplung“ o.ä. möglich“, ist folgende:
Das Albedo schwankt örtlich und zeitlich zwischen knapp über Null bis knapp unter 1, daher ist ein „mittleres Albedo“ der Erde keine thermodynamisch exakte Größe, die zu Erstellung von Energiebilanzen geeignet ist. Damit ist die ganze Strahlungs/SB-Diskussion eigentlich sinnlos, da der einzige Wert, der die Energiebilanz beeinflußt, eine grobe Schätzung ist.
Ein Beispiel dazu (bitte die durchaus vorhandene Angeberei ausblenden):
Laut Ausweis bin ich 60, man schätz mich eher Mitte/Ende 40. Sofern ich den Ausweis nicht vorlegen muss, kann ich mich den Schätzungen meiner Umgebung anpassen und behaupten, ich wäre 48. Analog dazu, sofern die Erde keinen amtlichen Energieausweis wie jedes Haus vorlegen kann, kann man ein Albedo und die sich daraus ergebende Temperatur schätzen. Meine Anpassung wäre ehrlicher als beim Albedo, sie deckt sich mit dem Sichtbaren und schwankt nicht örtlich und zeitlich zwischen 0 und 100%.
Meine Schlußfolgerung: Die Energiebilanz der Erde kann nicht exakt auch nicht annähernd beschrieben werden, aufgrund vielfältiger thermodynamischer Prozesse wie im Artikel beschrieben, diese beeinflussen. Man kann weder die exakte Energiemenge die die Erde trifft und schon gar nicht die Energiemenge, die die Erde in Richtung All (nicht in Richtung Atmosphäre, diese ist für die Bilanz nicht relevant) wieder verlässt, beziffern.
Man kann nur über die Auslegung der SB-Gleichung streiten.
zu: in Richtung Atmosphäre, diese ist für die Bilanz nicht relevant
Es muss doch möglich sein ohne Gegenbuchung im Hauptbuch die Bilanz zu erhöhen, sonst kann kein Wirecardeffekt enstehen /sarc.
Der war gut…
Aber vielleicht mögen Strahlenphysiker einfach keine Bilanzen….
Es scheint keiner zu verstehen, das ich meine Millionen Euro von einem Konto zum anderen Verschieben kann, aber nur 249 Euro Ausgaben halbtägig habe.
Ich kriege ja nur einmal am Tage 498 Euro Stütze.
Eine Angabe wieviel Geld auf meinen Konto ist, kann anhand der Angaben für Ein-und Ausgänge keiner machen.
Hallo Herr Schulz,
diesmal will ich Ihnen teilweise widersprechen. Mein Gedanke ist, dass eine Temperaturerhöhung (Kontostandzunahme) aus der Differenz zwischen Zufluß und Abfluß von Energie bzw. Geld berechenbar ist.
Dass die werten Physiker mit ihrem Strahlensalat und ständiges Jonglieren mit der SB Gleichung eine konkrete Endtemperatur ermitteln können bezweifle ich, wie oft geschrieben. Aber ich muss zugeben, dass ich nicht alles zu 100% verstehe und halte mich daher zurück…
Herr Georgiev,
Es geht hier nicht um die Änderung des Kontostandes.
Die Klimafolgenwissenschaft will uns weismachen, das die Zu und Abgänge an Wärme zum Erdsystem gleich bleiben, aber es trotzdem eine Änderung gibt.
Betrachtet man die Erde insgesamt, ist das unmöglich.
Teilt man die Erde in Teilsysteme zum Beispiel Oberfläche und Atmosphäre, dann muss eines von beiden kälter werden, wenn das andere sich erwärmt.
Das wären dann zwei Konten, wo ich von einem etwas wegnehme, kriegt das andere mehr, aber insgesamt ist nicht mehr da, und thermodynamisch geht das nur wenn Arbeit verrichtet wird!
Wenn die Oberfläche und Atmosphäre im gegenseitigen Energieaustausch stehen, dann ist das eine interne Transaktion, die in jeder Höhe stattfinden kann. Anhand dieser kann man jedoch nicht erklaeren wie hoch der Kontostand sein muss. Genausowenig kann man die interne Transaktion mit den Zu – und Abgängen für die Erde vergleichen. Zudem sind die wirklichen Transaktionen meistens von der Oberfläche zur Atmosphäre.
Sehen sie bitte auch meine Anmerkungen an Herrn Mueller.
mfg Werner
„Das hemisphärische Stefan-Boltzmann-Modell kommt ohne einen Treibhauseffekt aus“
In der Tat hat (ohne Wärmespeicherung bzw. ohne Erdrotation, mit Albedo und OHNE Gegenstrahlung) die Sonnen-Hemisphäre einen Mittelwert von +15 Grad, aber die Nachtseite hat -273 Grad. Das ergibt einen globalen Mittelwert von -129 Grad. Das ergibt, wie von Prof. Gerlich korrekt berechnet wurde, einen TE von +144 Grad.
Eine Umgebungsgleichung, also T1^4 – T2^4 GIBT ES NICHT weil OHNE Gegenstrahlung T2=0 ist. Mit Gegenstrahlung gäbe es ja einen TE, den Uli Weber aber bestreitet. Er widerspricht sich also selbst und merkt es nicht. EIKE veröffentlicht diesen Irrtum nun zum 24. Mal.
@Segler am selbstgemachten Wind
Jedes Modell hat den Anspruch, eine erlebte/gemessene Realität korrekt abzubilden. Und je besser ein solches Modell ist, umso geringer ist dessen Abweichung von der Realität. Also ist ein globales Temperaturmodell umso besser, je kleiner dessen Differenz zur sogenannten „gemessenen globalen Durchschnittstemperatur“ von etwa 15°C ist:
Ergebnis Gerlich und Tscheuschner: Abweichung von 144°C zur „gemessenen“ Realität von etwa 15°C
Der 24h=Faktor4-THE-Flacherdeansatz: Abweichung von 33°C zur „gemessenen“ Realität von etwa 15°C
Mein hemisphärisches S-B-Modell: KEINE Abweichung zur „gemessenen“ Realität von etwa 15°C
ERGO: Mein hemisphärisches S-B-Modell ist das einzige Modell für die Temperaturgenese auf unserer Erde, das die „gemessene“ Realität von etwa 15°C widerspruchsfrei abbilden kann.
Peter Dietze schrieb am 24. September 2020 um 22:48:
Ich stimme Ihnen zu, würde es aber etwas anders formulieren. Herr Weber führte die Umgebungsgleichung mit Referenz auf Gerthsen-Kneser “Physik” (1971) wie folgt ein:
Da ich den Gerthsen nicht vor mir habe und nicht nachkucken kann, ob da wirklich auf beiden Seiten S steht (was ich mir nicht vorstellen kann), formuliere ich das mal mit Bezugnahme auf das von Herrn Agerius referenzierte Physik für Ingenieure By Paul Dobrinski, Gunter Krakau, Anselm Vogel, Seite 216 um, um zu zeigen, wie man auf den Endausdruck kommt:
Man sieht also in der Umgebungsgleichung von Herrn Weber schön die Strahlung aus der Umgebung (der Atmosphäre), die die Abstrahlung der Erdoberfläche reduziert. In Physik für Ingenieure ist das auch schön deutlich formuliert:
Herr Müller,
sorry, aber Sie haben offenbar nicht verstanden dass die Weber’sche „Umgebungstemperatur“ Null (!) ist und keinesfalls diejenige welche in der Realität (also MIT Gegenstrahlung und existierendem Treibhauseffekt) vorhanden ist und die Nettoabstrahlung des Bodens passend für die Speisung der Nachtseite gemäss der von Herrn Weber missbrauchten Realität etwa auf die Hälfte reduziert.
In dem Hemisphärenmodell ist T2=0. Es gibt nur die Sonneneinstrahlung welche lediglich auf der Tagseite 15 Grad erzeugt, aber dazu nach S-B wieder vollständig (!) abgestrahlt wird, was man leicht nachrechnen kann. Die Nachtseite erhält KEINE Wärme und nimmt daher -273 Grad an.
Die Behauptungen von Herrn Weber, die darin gipfeln dass alle anderen Modelle grosse berechnete Abweichungen zum beobachteten globalen Mittelwert (also Treibhauseffekte) liefern und es bei ihm ja mit den 15 Grad stimmt, erscheint grotesk. Bei korrekter Berechnung müsste bei ihm nicht +15, sondern der Gerlich-Mittelwert von -129 Grad herauskommen.
Peter Dietze schrieb am 25. September 2020 um 18:39:
Herr Müller,
sorry, aber Sie haben offenbar nicht verstanden dass …
Ich bin mir nicht sicher, wie Sie darauf kommen. Lesen Sie doch einfach meinen Kommentar noch einmal in Ruhe. Ich bin mit Ihnen einer Meinung, dass aus der Behauptung „es gäbe keine Gegenstrahlung“ bzw. „man braucht keine Gegenstrahlung“ folgt, dass
gilt. Und damit ist entweder die Umgebungstemperatur T_2 Null oder der Term darf gar nicht erst in der Differenz auftauchen, wenn die Umgebung gar keine Energie abstrahlt. Da widerspricht sich Herr Weber also selbst und merkt es gar nicht …
Fehler in der Formulierung.
Die Abstrahlung der Oberfläche wird nicht reduziert.
Was reduziert wird ist der Wärmeverlust.
Die Temperatur ist ein Ausdruck des Wärmegehaltes.
Nur wenn die Atmosphäre der Oberfläche Wärme zufügt, kann diese die Oberfläche auch erwärmen. Es ist jedoch so, das die Atmosphäre ihre Wärme zum Großteil von der Oberfläche bezieht.
Damit ist die Atmosphäre eine Wärmesenke für die Oberfläche.
Noch was zum Lachen (oder Weinen…)
https://www.pik-potsdam.de/de/aktuelles/nachrichten/meeresspiegelanstieg-stabilitaets-check-der-antarktis-offenbart-enorme-risiken
Die Antarktis schmilzt… In rund einer Million Stunden Computerrechenzeit zeigen ihre beispiellos detaillierten Simulationen, wo genau und bei welcher Erwärmung der Eisschild instabil wird und große Teile schließlich schmelzen oder in den Ozean abrutschen würden.
////
Das ist so irre, man kann sich nur an den Kopf fassen. Die Quark-Redaktion des WDR 5 machte daraus natürlich eine Meldung. Die Nordsee könnte bis in das Voralpenland vordringen. Die Irren haben die Leitung der Anstalt übernommen….
Leute, das ist für unsere öfflich rechtlichen und den anderen Mainstream Medien zu schwer. Dann bleiben die lieber beim CO2 Treibhaus. Bis sich beide Seiten endlich mal Medienstark mit guten belegten prüfbaren Argumenten verständlich auch für Hauptschüler öffentlich einbringen. Egal ob Klimaeiferer Gift und Galle spucken.
@ Herrn Günter Lindner: Der 2. Hauptsatz der Thermodynamik ist schon für Physikprofessoren nicht trivial (https://tinyurl.com/y44pmte3), da ist der Anspruch, „verständlich auch für Hauptschüler“ eine unüberwindbare didaktische Hürde. Und auch die Zusammenfassung meines hemisphärischen S-B-Modells mit Piktogrammen zum Stand 2018 (https://tinyurl.com/y2k3zz38) ist leider nicht barrierefrei. Wir ehrenamtlichen Klimarealisten verfügen nun mal weder über Forschungsmittel noch über vollalimentierte Netzwerke, Think-Tanks oder gar eigene Medienberater und Illustratoren…
Herr Weber eine ganz einfache Frage: Ihr Hemisphären-Ansatz eliminiert den Treibhauseffekt in etwa, wenn ich Ein- und Ausstrahlung auf die Tag-Halbkugel begrenze. Wenn ich jedoch berücksichtige, dass die tagseitige Einstrahlung auch die Abstrahlenergie der Nachtseite erbringen muss, bin ich leider wieder ganz nahe beim Vollkugelansatz. Weil wir in Kelvin rechnen, ist der Unterschied zwischen der Abstrahlung am Tag und in der Nacht gar nicht so groß – trotz T hoch 4!
Wenn die Rückstrahlung entsprechend dem Vollkugelmodell auf der ganzen Kugeloberfläche erfolgt, haben wir wieder die 255 K Abstrahltemperatur und somit den „alten“ Treibhauseffekt von 33 K.
Wenn ich mich irre, freut es mich! Weil der CO2-Irrsinn mir tierisch auf den Wecker geht…
@ Herrn Dr. Roland Ullrich: Eigentlich steht alles Wesentliche bereits in diesem Artikel. Die maximal mögliche Durchschnittstemperatur auf unserer Erde konvergiert beim flächengewichteten hemisphärischen S-B-Temperaturäquivalent von ca. 15°C [13] und entspricht der sogenannten „gemessenen globalen Mitteltemperatur“ (NST) von ca. 15°C. Und die globalen Zirkulationen werden auf der Tagseite ständig aufgeheizt und nehmen ihre Wärme auf die Nachtseite mit. Da bleibt also gar kein Raum für einen THE von 33°C.
Herr Werner Schulz hatte die globale Abstrahlung mit einer Durchschnittsbetrachtung erklärt (https://tinyurl.com/y2o8v3hj), also: Wir haben eine durchschnittliche Einstrahlungsleistung von 470W/m² auf der Tagseite (@2 PI R²) der Erde (korrekt wäre [13]). Wenn die Tagseite nun 235W/m² abstrahlt, bleiben für die Nachtseite (@2 PI R²) also ebenfalls 235W/m² übrig. Und diese Abstrahlung von 235W/m² @4 PI R² verläuft dann analog zum THE-Paradigma bei einer „Abstrahlhöhe“ von etwa 5km, allerdings thermodynamisch korrekt nach der S-B-Umgebungsgleichung [19].
Danke, aber dennoch: Die tag- und nachtseitig abgestrahlten 235W/m2 entsprechen, wie Sie darlegen, einer SB-Abstrahltemperatur von 255 K, wie man sie in 5 km Höhe antrifft. (So könnte man auch beim Vollkugelansatz argumentieren, was dann auch dort den „Treibhauseffekt“ zum Verschwinden brächte. Natürlich stimmt Ihr Hemisphärenansatz sehr viel besser mit der Wirklichkeit überein.)
Die Treibhausanhänger können jetzt allerdings einwenden, dass durch diesen „Kunstgriff“ der Treibhauseffekt in den Teil der Atmosphäre verlagert wird, der unterhalb der 255 K-Schicht liegt. Und je mehr Treibhauseffekt dort, desto mehr Temperaturgefälle wird sich in diesem erdnahen Bereich der Atmosphäre bzw. Troposphäre einstellen.
Noch ist er leider nicht weg, der Treibhauseffekt…
Dann schau‘n Sie einfach mal hier: https://www.eike-klima-energie.eu/2020/01/12/zeigt-der-poynting-vektor-auf-mittelerde-oder-auf-die-sogenannte-abstrahlungshoehe/
„Leute waren das, die es verstanden, kunstvoll am Winde zu segeln, den sie selbst machten.“
Schöner Satz, sehr schöner Satz!