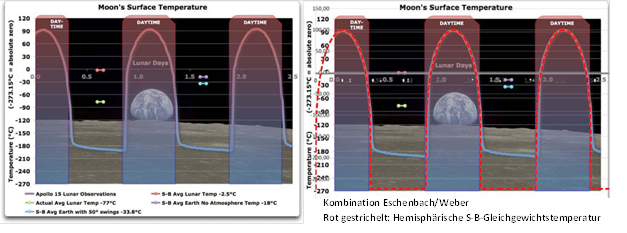
Abbildung: Links: Mondtemperaturen vom Apollo 15 Landeplatz (WUWT). Rechts: WUWT-Abbildung mit der örtlichen hemisphärischen S-B-Gleichgewichtstemperatur (EIKE)

Aktuell hat Willis Eschenbach neue Temperaturdaten vom Mond (Williams et al. 2017) ausgegraben und seine eigenen Berechnungen dazu ebenfalls auf WUWT veröffentlicht, Zitat mit Abbildung: “Looking around, I found a study called “The global surface temperatures of the Moon as measured by the Diviner Lunar Radiometer Experiment“, which contained the following graphic of lunar surface temperature. This shows temperature around the moon at a single moment in time.

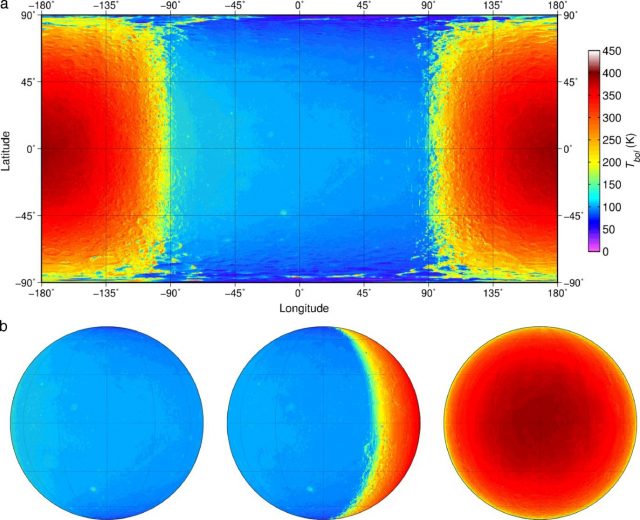
(Abbildung 5a und 5b aus der Veröffentlichung von Williams et al. 2017)

Original Caption: Global instantaneous temperatures of the Moon in (a) cylindrical equidistant projection (ϕss = 180°) and (b) orthographic projection (ϕss = 180°, 120°, and 0°).”
Aus diesen Daten leitet Eschenbach dann eine neue Durchschnittstemperatur für den Mond ab und vergleicht sie mit der Durchschnittstemperatur aus seinem älteren Beitrag. Diese Daten von Williams et al. (2017) stellen nun wiederum eine hervorragende Gelegenheit dar, meinen hemisphärischen S-B-Ansatz erneut mit gemessenen Temperaturen vom Mond zu vergleichen. Dazu wurden zunächst einmal die S-B-Gleichgewichtstemperaturen für die Tagseite des Mondes bei äquatorialem Sonnenstand (@ 0° geographische Breite) im mittäglichen Zenit (@ 12h) berechnet, wie sie in der nachstehenden Abbildung dargestellt werden:

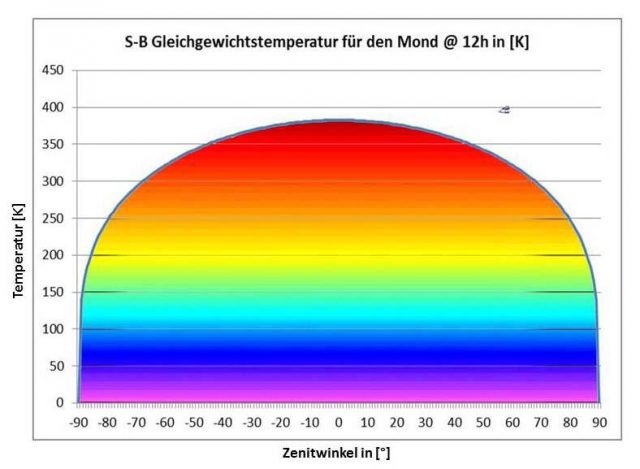
Abbildung: S-B-Gleichgewichtstemperatur für die Tagseite des Mondes bei einem äquatorialen Sonnenstand im mittäglichen Zenit (blaue Linie), unterlegt mit der Farbskala aus Abbildung 5 von Williams et al. (2017)

Berechnungsgrundlage: S0=1.367 W/m², Albedo=0,11, Seff=S0*(1-ALBEDO)=1217 W/m²
Hemisphärische S-B-Temperatur: TPHI=(Seff*cos(PHI)/SIGMA)1/4 mit PHI=(-90° bis +90°)
Und diese Temperaturverteilung können wir jetzt direkt mit den Temperaturdaten von Williams et al. (2017) aus dem Artikel von Willis Eschenbach vergleichen:

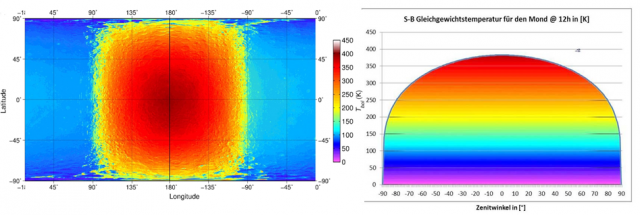
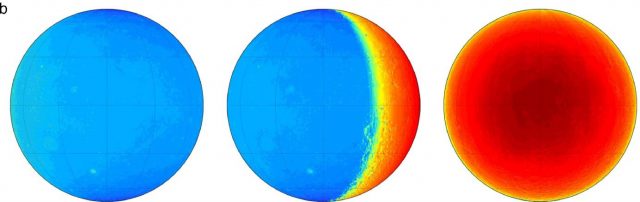
Abbildung: Qualitativer Temperaturvergleich für die Tagseite des Mondes Links: Montage aus der Abbildung 5A von Williams et al. (2017) für die Tagseite des Mondes. Rechts: S-B-Gleichgewichtstemperatur @12h, hinterlegt mit der Farbskala von Williams et al. (2017)

Wenn man über den Tagesverlauf die Temperaturen aus der Abbildung von Williams et al. (2017) mit der hemisphärischen S-B-Temperaturkurve vergleicht, ergibt sich eine sehr ordentliche qualitative Übereinstimmung. Die unterschiedlichen radialen Farbverläufe bei Williams et al. (2017) spiegeln dabei die Variabilität der örtlichen Mondalbedo und die Topographie wider, die in einem solchen pauschalen S-B-Ansatz nicht berücksichtigt werden können.

Und jetzt noch einmal zurück zu Willis Eschenbach, der seine Ergebnisse in seinem aktuellen Artikel folgendermaßen beschreibt, Zitat:

“Once I’d converted it to temperature, I then converted each gridcell to the equivalent Stefan-Boltzmann radiation and averaged those. This gave me an average outgoing radiation of some 303.5 W/m2. And this let me check the accuracy of my figures. The lunar albedo is generally thought to be on the order of 11-12%. The results I have give an albedo of 10.7% … I’d call that confirmation.

Finally, to compare my results to those in my previous post, I have:

Previous Post This Post

Temperature by Direct Average -77°C -75°C

Temperature by Radiation Average -2.5C -2.7°C

Conclusion? Well, at last, I have some real numbers for the lunar temperature. And they confirm that the Stefan-Boltzmann equation does a good job of estimating the lunar temperature, whether we do it by averaging radiation and converting to temperature, or whether we average the temperature directly. And which of the two ways of averaging temperature is correct? Well, both, or neither. You can use either one, depending on your needs. The underlying problem is that you can’t average an “intensive” variable like temperature … but that’s a discussion for another day.”

Der neutrale Google-Übersetzer zum Fazit: Fazit? Nun, endlich habe ich einige reelle Zahlen für die Mondtemperatur. Und sie bestätigen, dass die Stefan-Boltzmann-Gleichung die Mondtemperatur gut abschätzen kann, ob wir dies durch Mittelung der Strahlung und Umrechnung in Temperatur tun oder ob wir die Temperatur direkt mitteln. Und welche der beiden Möglichkeiten zur Mittelung der Temperatur ist richtig? Nun, beides oder beides nicht. Sie können je nach Bedarf eine von beiden verwenden. Das zugrunde liegende Problem ist, dass Sie eine „intensive“ Variable wie die Temperatur nicht mitteln können … aber das ist eine Diskussion für einen anderen Tag.

Willis Eschenbach hat also die Mondtemperaturen direkt aus den Gridzellen entnommen und diese Temperaturen gemittelt. Und dann hat er die Temperaturen dieser Gridzellen mit dem S-B-Gesetz in eine spezifische Strahlungsleistung umgerechnet. Aus dem Durchschnitt dieser spezifischen Strahlungsleistungen hatte er ebenfalls eine Temperatur ermittelt. Zwischen diesen beiden, auf unterschiedlichen Wegen ermittelten Temperaturwerten, erhält Willis Eschenbach dann in seinen beiden Temperaturvergleichen (alt und neu) jeweils eine Differenz von über 70 Kelvin. Das ist kein Wunder, denn die Bildung eines Temperaturmittelwertes aus individuellen Ortstemperaturen ist physikalisch statthaft, während die Berechnung einer Durchschnittstemperatur aus einem Strahlungsdurchschnitt mit der T-hoch4-Funktion des Stefan-Boltzmann-Gesetzes keinen physikalischen Sinn ergibt. Der Widerspruch im Ergebnis von Willis Eschenbach beweist also eindeutig die physikalische Unvereinbarkeit dieser beiden Lösungswege, denn ein Körper kann nun mal nicht gleichzeitig zwei unterschiedliche Temperaturen annehmen.

Also irrt Willis Eschenbach mit seinem „Was-Ihr-wollt“-Argument, denn es gibt gar keine Stefan-Boltzmann-Gleichung. Und jeder, der dieses physikalische Gesetz als „Gleichung“ anwendet, geht fehl in der Annahme, wenn er links etwas Beliebiges einsetzt, würde rechts etwas physikalisch Richtiges herauskommen. Denn dieses physikalische Gesetz verbindet die konkrete Temperatur und die konkrete spezifische Strahlungsleistung eines Schwarzen Körpers in einer streng GLEICHZEITIGEN T-hoch4-Beziehung. Eine Berechnung über Mittelwerte oder eine Inversion unter Einbeziehung unbeleuchteter Flächen mit dem Stefan-Boltzmann-Gesetz ist daher physikalisch nicht statthaft. Denn das Stefan-Boltzmann-Gesetz ist nun mal Physik und nicht Shakespeare (Wie es Euch gefällt), was die miteinander unvereinbaren Ergebnisse von Willis Eschenbach eindeutig bestätigen.

Weiterhin hatte Eschenbach aus der Arbeit von Williams et al. (2017) eine durchschnittliche lunare Abstrahlung ermittelt. Wenn wir nun einmal die solare Nettostrahlungsleistung von 1217 W/m² aus dem hemisphärischen S-B-Ansatz auf die Fläche der Tagseite des Mondes herunterrechnen, dann kommen wir auf 608 W/m² für das durchschnittliche Mittel der spezifischen Strahlungsleistung. Und wenn wir den lunaren Durchschnitt von Willis Eschenbach von 303.5 W/m2 auf die Fläche der Tagseite beziehen, müssen wir diesen Wert verdoppeln und erhalten 607 W/m². Das ist schon mal eine ganz hervorragende Übereinstimmung dieser beiden Werte mit weniger als 0,2% Abweichung. Weiterhin beträgt die Abstrahlung des Mondes auf der Nachtseite (@80K) etwa 3 W/m². Damit haben wir in erster Näherung auf dem Mond eine Einstrahlung von durchschnittlich 608 W/m² sowie eine Abstrahlung von 604 W/m² (@ Tagseite) und 3 W/m² (@ Nachtseite); und um das fehlende 1 W/m² werden sich sicherlich die Herren Dzzzzz und Kzzzz kümmern. Die Abbildung 5B von Williams et al. (2017) beweist durch den relativ schmalen Übergangsstreifen zwischen der Tagestemperatur und einer relativ einheitlichen Nachttemperatur, dass diese Beschreibung tatsächlich eine gute erste Näherung darstellt:

Abbildung 5B von Williams et al. (2017)

Der Mond stellt ein stark vereinfachtes Modell unserer Erde ohne eine kombinierte Luft-Wasser-Heizung dar. Daher sind die Prozesse der tagseitigen Temperaturgenese und der Abstrahlung über die Gesamtoberfläche mit meinem hemisphärischen S-B-Ansatz am Beispiel unseres Erdtrabanten sehr viel einfacher zu beschreiben und nachzuvollziehen:

  • Der hemisphärische S-B-Ansatz: Die Temperaturgenese auf der Tagseite folgt dem hemisphärischen S-B-Ansatz, nach dem sich die konkrete Ortstemperatur aus der örtlichen spezifischen Strahlungsleistung der Sonne
    mit Ti=(S0*(1-ALBEDO)*cos(PHIi)/SIGMA)1/4 herleitet.
    Die individuelle Abstrahlung erfolgt nach der Umgebungsgleichung des S-B-Gesetzes
    DELTA Si = SIGMA * (Ti4 – T04),
    wobei die örtlichen Wärmespeicher die jeweilige Umgebungstemperatur T0 vorgeben.
  • Die Tagseite des Mondes: Die spezifische Strahlungsleistung der Sonne (Durchschnitt Tagseite 608 W/m²) wird auf dem Mond fast vollständig in Temperatur umgesetzt und daher gleichzeitig im IR-Bereich wieder abgestrahlt (Durchschnitt der Abstrahlung von der Tagseite etwa 604 W/m²). Damit folgt der Temperaturverlauf auf der Tagseite des Mondes ziemlich exakt der hemisphärischen S-B-Gleichgewichtstemperatur.
  • Die Nachtseite des Mondes: Durch die äußerst geringe Wärmespeicherung auf dem Mond fällt dessen Nachttemperatur sehr schnell auf etwa 80K, was einer durchschnittlichen spezifischen Abstrahlungsleistung DELTA S von etwa 3W/m² für die Nachtseite gegenüber dem Weltraum entspricht. Der Mond hat also sogar eine streng „hemisphärische“ Abstrahlung.

Einerseits können Temperaturen also nur „just in Time“ durch eine spezifische solare Strahlungsleistung erzeugt werden; andererseits kann auf der Nachtseite nur diejenige Wärme abgestrahlt werden, die vorher auf der Tagseite gespeichert worden war. Dieser Tag-und-Nacht-Ablauf sieht auf der Erde mit Ihrem globalen Wärmespeicher- und Wärmetransport-System (Atmosphäre und Ozeane) ganz anders aus als auf dem Mond. Denn auf der Erde erreicht die örtliche Tagestemperatur aufgrund von Wärmespeicherung, Verdunstung und Konvektion die S-B-Gleichgewichtstemperatur nicht. Allein die in den Ozeanen gespeicherte Wärmemenge beträgt nach konservativer Abschätzung 4,5*10^26 Joule, was einem Energieäquivalent von etwa 50.000 Tagen Sonneneinstrahlung entspricht. Und aufgrund dieser gespeicherten Wärmemenge sowie durch Kondensation und Advektion fällt die Nachttemperatur auf der Erde dann auch nicht auf dreistellige Celsius-Minustemperaturen wie auf dem Mond, sondern nur um einige Dekagrad.

Am Beispiel der Mond-Temperaturen von Williams et al. (2017) ist somit erneut der Nachweis gelungen, dass die Temperaturgenese auf der Tagseite eines passiv bestrahlten Himmelskörpers mit meinem hemisphärischen Stefan-Boltzmann-Ansatz korrekt beschrieben werden kann und dessen Abstrahlung der Umgebungsgleichung des S-B-Gesetzes folgt.

Anmerkung: Zum wiederholten Male stellt sich hier aber auch die Frage nach der Sinnfälligkeit von Durchschnittstemperaturen. Was soll beispielsweise eine Mittelwertbildung für zwei sehr unterschiedliche Mondhemisphären aussagen, von denen eine größtenteils eine Temperatur von über 250K hat und die andere im Wesentlichen nur 80K. Eine solche Mittelung leitet unmittelbar zu dem Bonmot über, „Keine Ahnung, warum die Kuh ertrunken ist, der Teich war doch im Mittel nur 20 Zentimeter tief“. Denn für eine einmonatige Mondmission sollte ein Astronaut weder auf winterliche (-3°C) noch antarktische (-75°C) Temperaturen vorbereitet sein, sondern auf einen Temperaturverlauf zwischen minus 200°C und plus 120°C…

image_pdfBeitrag als PDF speichernimage_printBeitrag drucken