Abbildung 1 (rechts!) zeigt die konventionelle und inverse ,normale kleinste Quadrate‘-Anpassung einiger wirklicher, real gemessener Variablen.

Normale Regression kleinster Quadrate [Ordinary least squares regression (OLS)] ist ein sehr nützliches Verfahren, das in allen Bereichen der Wissenschaft häufig angewendet wird. Dem Prinzip nach müssen einer oder mehrere passende Parameter zu adjustieren, dass sie den besten Fit einer Modellfunktion erfüllen, und zwar dem Kriterium folgend, die Summe der quadrierten Ableitungen der Daten vom Modell zu minimieren.

Normalerweise ist es eines der ersten Verfahren, das bzgl. der Analyse experimenteller Daten in Schulen gelehrt wird. Das Verfahren wird auch genauso oft falsch als wie richtig angewendet.

Es kann gezeigt werden, dass unter bestimmten Bedingungen das Kleinste-Quadrate-Fit die beste Schätzung der wirklichen Beziehung darstellt, die aus den verfügbaren Daten abgeleitet werden kann. In der Statistik nennt man sie oft die ,besten, unverzerrten linearen Schätzwerte‘ der Neigung.

Fundamental liegt diesem Verfahren die Annahme zugrunde, dass die Variable der Ordinate (X-Achse) einen vernachlässigbaren Fehler aufweist: es ist eine „kontrollierte Variable“. Es sind die Ableitungen der abhängigen Variable (Y-Achse), die minimiert werden. Im Falle einer Anpassung einer geraden Linie an die Daten ist seit mindestens 1878 bestens bekannt, dass dieses Verfahren die Neigung unterschätzen wird, falls es einen Messfehler oder andere Fehler bei den X-Variablen gibt (R. J. Adcock) [link]).

Es gibt zwei wesentliche Bedingungen, damit dieses Ergebnis eine genaue Schätzung der Neigung ist. Eine ist, dass die Ableitungen der Daten aus der wirklichen Relation ,normal‘ oder Gauss-verteilt sind. Das heißt, sie sind zufälliger Natur. Diese Bedingung kann gestört werden durch signifikante periodische Komponenten in den Daten oder eine exzessive Anzahl von Ausreißer-Datenpunkten. Letztere können oftmals auftreten, wenn nur eine kleine Anzahl von Datenpunkten vorhanden ist und das Rauschen, selbst bei von Natur aus zufälligen Daten, nicht angemessen aufbereitet ist, um sich herauszumitteln.

Die andere wesentliche Bedingung ist, dass der Fehler (oder die nichtlineare Variabilität) der X-Variablen vernachlässigbar ist. Falls diese Bedingung nicht erfüllt ist, werden die aus den Daten abgeleiteten OLS-Ergebnisse fast immer die Neigung der realen Relation unterschätzen. Dieser Effekt wird manchmal als Regressions-Verdünnung [regression dilution] bezeichnet. Der Grad, bis zu dem die Neigung unterschätzt wird, wird bestimmt durch die Natur der X- und Y-Fehler, am stärksten jedoch durch die X-Werte, müssen diese doch vernachlässigbar sein, damit OLS die beste Schätzung ergeben kann.

In dieser Diskussion können „Fehler“ sowohl Ungenauigkeiten bei der Beobachtung oder Messung als auch jedweder Variabilität geschuldet sein infolge irgendwelcher anderen Faktoren als derjenigen, die maßgeblich für die Relation sind, die man mittels Regression der beiden Variablen bestimmen will.

Unter gewissen Umständen kann man die Regressions-Dilution korrigieren, aber um das zu tun, muss die Natur und die Größenordnung der Fehler sowohl der X- als auch der Y-Werte in gewissem Umfang bekannt sein. Typischerweise ist dies nicht der Fall, wenn es über die Kenntnis darüber hinausgeht, ob die X-Variable eine ,kontrollierte Variable‘ mit vernachlässigbarem Fehler ist, obwohl viele Verfahren entwickelt worden sind, den Fehler bei der Schätzung der Neigung abzuschätzen (hier).

Eine kontrollierte Variable kann man gewöhnlich mit einem kontrollierten Experiment gewinnen, oder wenn man eine Zeitreihe untersucht – vorausgesetzt, dass Datum und Zeit der Beobachtungen aufgezeichnet und dokumentiert worden sind in präziser und konsistenter Manier. Das ist typischerweise nicht der Fall, wenn beide Datensätze Beobachtungen verschiedener Variablen sind, was beim Vergleich zweier Quantitäten in der Klimatologie der Fall ist.

Eine Möglichkeit, dieses Problem deutlich zu machen ist, die X- und Y-Achse zu vertauschen und den OLS-Fit zu wiederholen. Falls die Ergebnisse gültig sind, unabhängig von der Orientierung, wäre die erste Neigung das Reziprok der zweiten. Allerdings ist dies nur dann der Fall, wenn es in beiden Variablen nur sehr kleine Fehler gibt; d. h. die Daten sind hoch korreliert (eng verteilt um eine gerade Linie). Im Falle von einer kontrollierten Variable und einer fehleranfälligen Variable wird das invertierte Ergebnis unrichtig sein. Falls zwei Datensätze Beobachtungsfehler enthalten, werden beide Ergebnisse falsch sein, und das korrekte Ergebnis wird allgemein irgendwo dazwischen liegen.

Eine andere Möglichkeit, das Ergebnis zu checken, ist die Kreuz-Korrelation [cross-correlation] zwischen den Residuen und der unabhängigen Variable, d. h. (Modell minus Y) zu X, was man dann für schrittweise erhöhte Werte des fitted Verhältnisses wiederholt. Abhängig von der Natur der Daten wird oftmals offensichtlich sein, dass das OLS-Ergebnis nicht das Minimum-Residuum erzeugt zwischen der Ordinate und dem Regressor; d. h. es ist nicht optimal für die Ko-Variabilität der beiden Quantitäten.

Bei Letzterem können die beiden Regressions-Fits herangezogen werden als Beschränkung des wahrscheinlich wahren Wertes, aber Einiges muss über die relativen Fehler bekannt sein, wenn man entscheidet, wo innerhalb dieser Bandbreite die beste Schätzung liegt. Es gibt eine Anzahl von Verfahren wie etwa die Winkelhalbierung, wobei man das geometrische Mittel (Quadratwurzel des Erzeugten) oder irgendein anderes Mittel betrachtet, aber ultimativ gibt es keine weitere Objektive, es sei denn mittels Wissens um die relativen Fehler. Eindeutig wäre die Halbierung nicht korrekt, falls eine Variable nur einen geringen Fehler aufweist, da die wirkliche Neigung dann nahe dem OLS-Fit liegen würde, die man mit jener Quantität auf der X-Achse durchgeführt hätte.

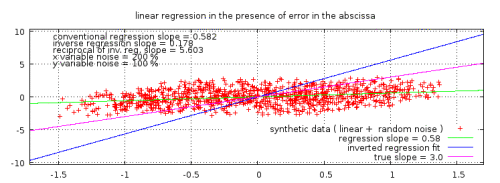
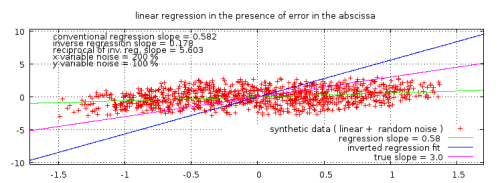
Abbildung 2: Ein typisches Beispiel einer linearen Regression zweier Variablen mit starkem Rauschen, erzeugt aus synthetischen willkürlichen Daten. Die wahre Neigung, die bei der Generierung der Daten angewendet wurde, liegt zwischen den beiden Ergebnissen der Regression. (Nur im Originalbeitrag: Der Klick auf die Graphik liefert die Reproduktion der Daten und des Graphen).

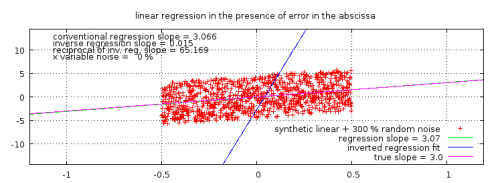
Abbildung 2b: Ein typisches Beispiel einer korrekten Anwendung einer linearen Regression auf Daten mit vernachlässigbaren X-Fehlern. Die erzeugte Neigung liegt sehr nahe dem wahren Wert – so nahe, dass er nach Augenschein fast ununterscheidbar ist.

Je größer die X-Fehler, umso größer die Schiefe [skew] bei der Verteilung und umso größer der Dilutions-Effekt.

Eine Illustration: Das Spencer simple model

Der folgende Fall dient der Illustration des Themas mit ,klima-artigen‘ Daten. Allerdings muss betont werden, dass das Problem ein objektives mathematisches Problem ist, dessen Prinzip unabhängig von jedwedem speziellen Test-Datensatz ist. Ob das folgende Modell eine genaue Repräsentation des Klimas ist (was hier nicht behauptet wird), hat keine Bedeutung für das Regressions-Problem.

In einem kurzen Beitrag auf seiner Website hat Dr. Roy Spencer ein einfaches Ein-Schicht-Ozean-Klimamodell vorgestellt mit einer vorbestimmten Rückkopplungs-Variablen. Er beobachtete, dass der Versuch der Ableitung der Klimasensitivität auf normale Weise die bekannte Rückkopplung konsistent unterschätzte, die zur Generierung der Daten benutzt worden war.

Mit der Spezifikation dieser Sensitivität (mit einem Gesamt-Rückkopplungs-Parameter) in dem Modell kann man sehen, wie sich eine Analyse simulierter Satellitendaten Beobachtungen ergibt, die routinemäßig ein sensitiveres Klimasystem zeigen (geringeren Rückkopplungs-Parameter) als tatsächlich im Modelllauf spezifiziert.

Und falls unser Klimasystem die Illusion erzeugt, dass es sensitiv ist, werden die Klimamodellierer Modelle entwickeln, die ebenfalls sensitiv sind, und je sensitiver das Klimamodell, umso mehr globale Erwärmung wird es zeigen durch das Hinzufügen von Treibhausgasen in die Atmosphäre.

Das ist eine sehr wichtige Beobachtung. Die Regression eines Strahlungsflusses mit viel Rauschen gegen Temperaturanomalien mit viel Rauschen erzeugt konsistent unrichtig hohe Schätzungen der Klimasensitivität. Allerdings ist es keine vom Klimasystem erzeugte Illusion, sondern eine solche, die durch die unrichtige Anwendung einer OLS-Regression zustande kommt. Finden sich in beiden Variablen Fehler, ist die OLS-Neigung keine akkurate Schätzung mehr der zugrunde liegenden Relation, nach der man sucht.

Dr. Spencer war so freundlich, eine Implementierung des Simple Model in Form einer Kalkulationstabelle zum Herunterladen anzubieten. Damit kann man das Experiment leicht nachvollziehen und den Effekt verifizieren.

Um dieses Problem zu verdeutlichen, wurde die angebotene Kalkulationstabelle modifiziert, um das Verhältnis Strahlungsfluss- zu Temperaturdifferenzen zu duplizieren, jedoch mit umgekehrten Achsen, d. h. es werden genau die gleichen Daten für jeden Lauf verwendet, aber zusätzlich umgekehrt gezeigt. Folglich ist die aus der Tabelle berechnete ,Trendlinie‘ mit den Variablen invers erstellt worden. Am Modell wurden keine Änderungen vorgenommen.

Drei Werte für die vorbestimmte Rückkopplungs-Variable wurden der Reihe nach verwendet. Zwei Werte, nämlich 0,9 und 1,9, die Roy Spencer ins Spiel bringt, repräsentieren die Bandbreite der IPCC-Werte. Der Wert 5,0, den er als Wert näher bei dem liegend vorgeschlagen hat, die er aus Satelliten-Beobachtungsdaten abgeleitet hat.

Hier folgt eine Momentaufnahme, die eine Tabelle mit Ergebnissen aus neun Modellläufen zeigt für jeden Wert des Rückkopplungs-Parameters. Sowohl die konventionelle als auch die inverse Regressions-Neigung sowie deren geometrische Mittelwerte wurden aufgelistet.

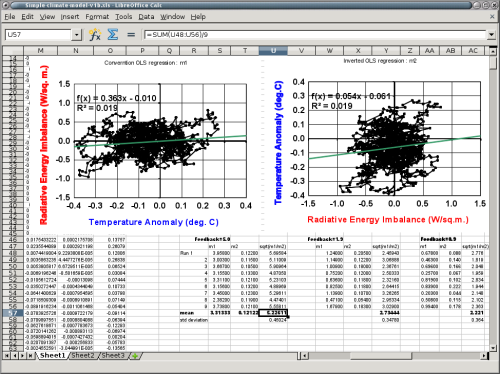
Abbildung 3: Momentaufnahme der Kalkulationstabelle.

Zunächst einmal bestätigt dies Roy Spencers Beobachtung, dass die Regression von D-Strahlungsfluss zu D-Temperatur permanent und signifikant den Rückkopplungs-Parameter unterschätzt, der herangezogen worden ist, um die Daten ursprünglich zu erzeugen (was folglich die Klimasensitivität des Modells überschätzt). In diesem limitierten Test liegt der Fehler zwischen einem Drittel und der Hälfte des korrekten Wertes. Es gibt nur einen Wert der konventionellen Neigung kleinster Quadrate, der größer ist als der Wert des jeweiligen Rückkopplungs-Parameters.

Zweitens ist anzumerken, dass das geometrische Mittel der beiden OLS-Regressionen tatsächlich einen wahren Rückkopplungs-Parameter ergibt, der einigermaßen nahe dem Wert liegt, wie er aus den Satellitenbeobachtungen abgeleitet ist. Variationen sind ziemlich gleichmäßig verteilt auf beiden Seiten: Das Mittel ist nur wenig höher als der wahre Wert, und die Standardabweichung ist etwa 9% des Mittels.

Allerdings, für die beiden niedrigeren Rückkopplungs-Parameter-Werte, die die IPCC-Bandbreite der Klimasensitivitäten repräsentieren, während die übliche OLS-Regression substantiell unter dem wahren Wert liegt, ist das geometrische Mittel eine Überschätzung und keine zuverlässige Korrektur über die Bandbreite der Rückkopplungen.

Alle Rückkopplungen repräsentieren eine negative Rückkopplung (anderenfalls wäre das Klimasystem fundamental instabil). Allerdings repräsentiert die Bandbreite der Werte des IPCC weniger negative Rückkopplungen und damit ein weniger stabiles Klima. Dies wird reflektiert durch den Grad der Variabilität der Daten, die in der Kalkulationstabelle geplottet sind. Die Standardabweichungen der Neigungen sind ebenfalls um Einiges größer. Dies war zu erwarten bei weniger die Rückkopplungen kontrollierenden Variationen.

Daraus kann man folgern, dass sich das Verhältnis der proportionalen Variabilität in den beiden Quantitäten ändert als eine Funktion des Grades der Rückkopplung in dem System. Das geometrische Mittel der beiden Neigungen bietet keine gute Schätzung der wahren Rückkopplung für die weniger stabilen Konfigurationen, welche eine größere Variabilität haben. Dies stimmt überein mit Isobe et al. 1990 (link), der die Güte vieler Regressions-Verfahren überprüft hat.

Das einfache Modell hilft zu erkennen, wie dies in Beziehung steht zu den Strahlungs-/Temperatur-Streuplots und Klimasensitivität. Allerdings ist das Problem der Regressions-Dilution ein vollständig allgemeines mathematisches Ergebnis und kann reproduziert werden aus zwei Reihen, die eine lineare Relation mit hinzugefügten Zufallsänderungen haben, wie oben gezeigt.

Was die Studien sagen

Eine Schnelldurchsicht vieler Studien aus jüngster Zeit über das Problem der Schätzung der Klimasensitivität zeigt eine allgemein fehlende Berücksichtigung des Problems der Regressions-Dilution.

Aus Dessler 2010 b (hier):

Schätzungen der Klimasensitivität der Erde sind unsicher, hauptsächlich wegen der Unsicherheit bei der langfristigen Wolken-Rückkopplung.

Spencer & Braswell 2011 (hier):

Abstract: Die Sensitivität des Klimasystems auf ein Strahlungs-Ungleichgewicht bleibt die größte Quelle der Unsicherheit bzgl. der Projektionen einer zukünftigen anthropogenen Klimaänderung.

Es scheint Übereinstimmung zu bestehen, dass dies das Schlüsselproblem bei der Abschätzung zukünftiger Klimatrends ist. Allerdings scheinen sich viele Autoren nicht des Regressionsproblems bewusst zu sein, und viele veröffentlichte Arbeiten zu diesem Thema scheinen sich schwer auf die falsche Hypothese zu stützen, dass die OLS-Regression von Strahlungs- gegen Temperaturänderungen herangezogen werden kann, um dieses Verhältnis genau bestimmen zu können und damit auch zahlreiche Sensitivitäten und Rückkopplungen.

Trenberth 2010 (hier):

Die Klimasensitivität abzuschätzen aus Messungen der Strahlung der Erde von begrenzter Dauer und gemessenen Wassertemperaturen erfordern eine geschlossene und damit globale Erfassung, Gleichgewicht zwischen den Bereichen und robuste Verfahren, mit dem Rauschen umzugehen. Rauschen entsteht durch natürliche Variabilität in der Atmosphäre, und Rauschen bei Messungen durch Satelliten mit Präzession.

Ob die Ergebnisse bedeutsame Einsichten vermittelt oder nicht hängt kritisch von den Hypothesen, Verfahren und dem zeitlichen Rahmen ab…

So ist es, aber unglücklicherweise fährt er dann damit fort, früheren Arbeiten von Lindzen und Choi zu widersprechen, die sich mit dem OLS-Problem befasst hatten einschließlich einer detaillierten statistischen Analyse, mit der sie ihre Ergebnisse verglichen, wenn man sich auf eine ungeeignete Anwendung von Regression stützt. Sicher kein Beispiel für „robuste Verfahren“, nach denen er verlangt.

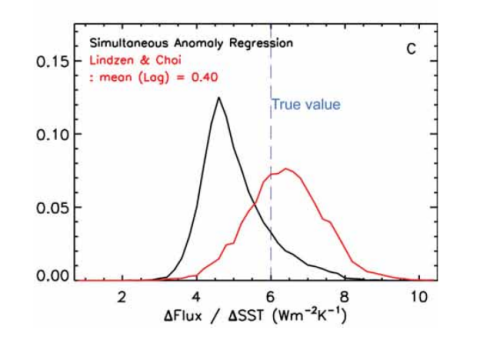
Abbildung 4: Auszug aus Lindzen und Choi 2011, Abbildung 7, welche die permanente Unterschätzung der Neigung durch die OLS-Regression zeigt (schwarze Linie).

Spencer und Braswell 2011 (hier):

Wie von SB 2010 gezeigt, dekorreliert die Präsenz jedweden mit der Zeit variierenden Strahlungsantriebs die Ko-Variationen zwischen Strahlungsfluss und Temperatur. Niedrige Korrelationen führen zu aus Regressionen diagnostizierten Rückkopplungs-Parametern, die in Richtung Null verzerrt sind, was mit einem grenzwertig instabilem Klimasystem korrespondiert.

Dies ist eine wichtige Studie, in der die Notwendigkeit in den Vordergrund gerückt wird, die verzögerte Reaktion des Klimas während der Regression zu berücksichtigen, um den dekorrelierenden Effekt von Verspätungen der Reaktion zu vermeiden. Allerdings befasst sich dies nicht mit der weiteren Abschwächung infolge der Regressions-Dilution. Es basiert ultimativ immer noch auf Regression von zwei mit Fehlern behafteten Variablen und erkennt daher nicht die Regressions-Dilution, die auch in dieser Situation präsent ist. Daher ist es wahrscheinlich, dass diese Studie die Sensitivität immer noch überschätzt.

Dessler 2011 (hier):

Verwendet man einen realistischeren Wert von σ(dF_ocean)/σ(dR_cloud) = 20, ergibt sich aus der Regression des Strahlungsflusses an der Obergrenze der Atmosphäre TOA zu Temperaturänderungen eine Neigung, die innerhalb von 0,4% von Lambda liegt.

Dann in der Conclusion der Studie (Hervorhebung hinzugefügt):

Vielmehr wird die Evolution von Oberfläche und Atmosphäre während ENSO-Variationen dominiert durch ozeanischen Wärmetransport. Dies wiederum bedeutet, dass Regressionen von Flüssen an der TOA zu δTs herangezogen werden können, um Klimasensitivtät oder die Größenordnung von Klima-Rückkopplungen genau abzuschätzen.

Und aus einer früheren Studie von Dessler 2010 b (hier):

Die Auswirkung eines unechten langzeitlichen Trends entweder durch Strahlungsunterschiede bei bedecktem oder bei klarem Himmel wird geschätzt, indem man einen Trend von T0,5 W/m² pro Jahrzehnt in die CERES-Daten einfügt. Dies ändert die berechnete Rückkopplung um T0,18 W/m² pro Dekade. Die Hinzufügung dieser Fehler bei der Quadratur ergibt eine Gesamt-Unsicherheit von 0,74 und 0,77 W/m² pro Jahrzehnt in den Berechnungen, jeweils bei Verwendung der Reanalysen des EZMW und von MERRA. Andere Quellen der Unsicherheit sind vernachlässigbar.

Dem Autor war offensichtlich nicht bewusst, dass die Ungenauigkeit bei der Regression von zwei unkontrollierten Variablen eine Hauptquelle von Unsicherheit und Fehlern ist.

Lindzen & Choi 2011 (hier):

Unser neues Verfahren macht sich halbwegs gut bei der Unterscheidung positiver von negativen Rückkopplungen und bei der Quantifizierung negativer Rückkopplungen. Im Gegensatz dazu zeigen wir, dass einfache Regressionsverfahren, die in vielen Studien angewendet worden waren, positive Rückkopplungen allgemein übertreiben und selbst dann noch positive Rückkopplungen zeigen, wenn diese tatsächlich negativ sind.

…aber wir erkennen auch deutlich, dass die einfache Regression immer negative Rückkopplungen unter- und positive Rückkopplungen überschätzt.

Hier haben die Autoren eindeutig bemerkt, dass es ein Problem gibt mit den auf Regression beruhenden Verfahren, und sind ziemlich ins Detail gegangen bei der Quantifizierung des Problems, obwohl sie es nicht explizit identifizieren als eine Folge der Präsenz von Unsicherheiten bei der X-Variable, welche die Regressionsergebnisse verzerrt.

Die L&C-Studien erkennen, dass auf Regression basierende Verfahren mit kaum korrelierenden Daten die Neigung ernsthaft unterschätzen und Verfahren verwenden, um das Verhältnis genauer zu berechnen. Sie zeigen Wahrscheinlichkeits-Dichte-Graphen von Monte Carlo-Tests, um die beiden Verfahren zu vergleichen.

Es scheint, dass Letzteres die Autoren heraushebt, schauen sie doch auf die Sensitivitäts-Frage ohne sich auf ungeeignete lineare Regressionsverfahren zu stützen. Dies ist mit Sicherheit teilweise der Grund, dass ihre Ergebnisse deutlich niedriger liegen als die Ergebnisse fast aller anderen Autoren, die sich mit diesem Thema befasst hatten.

Forster & Gregory 2006 (hier):

Für weniger perfekt korrelierende Daten tendiert die OLS-Regression von Q-N zu δTs dazu,Y-Werte zu unterschätzen und daher die Gleichgewichts-Klimasensitivität zu überschätzen (siehe Isobe et al. 1990).

Ein weiterer wichtiger Grund für die Übernahme unseres Regressionsmodells war es, die Hauptschlussfolgerung zu untermauern der Studie mit dem Titel [übersetzt] Nachweis einer relativ kleinen Gleichgewichts-Klimasensitivität. Um die Stichhaltigkeit dieser Schlussfolgerung zu zeigen, haben wir absichtlich das Regressionsmodell übernommen, welches die höchste Klimasensitivität ergab (kleinster Y-Wert). Es wurde gezeigt, dass ein auf Regression kleinster Quadrate beruhendes Verfahren ein besseres Fit ergibt, wenn Fehler in den Daten uncharakterisiert sind (Isobe et al. 1990). Zum Beispiel zeigen beide diese Verfahren für den Zeitraum 1985 bis 1996 ein YNET von etwa 3.5 +/- 2.0 W m2 K↑-1 (eine Gleichgewichts-Temperaturzunahme um 0,7 bis 2,4 K bei einer Verdoppelung des CO2-Gehaltes). Dies sollte verglichen werden mit unserer Bandbreite von 1,0 bis 3,6 K, die in der Conclusion der Studie genannt wird.

Hier benennen die Autoren explizit das Regressionsproblem sowie dessen Auswirkungen auf die Ergebnisse ihrer Studie zur Sensitivität. Allerdings, als sie die Studie 2005 geschrieben hatten, befürchteten sie offensichtlich, dass es die Akzeptanz dessen erschweren würde, was bereits ein niedriger Wert der Klimasensitivität war, falls sie die mathematisch genaueren, aber kleineren Zahlen gezeigt hätten.

Interessant ist, dass Roy Spencer in einem nicht begutachteten Artikel eine sehr ähnlichen Wert gefunden hatte von 3,66 W/m²/K durch den Vergleich von ERBE-Daten mit aus MSU abgeleiteten Temperaturen nach dem Ausbruch des Pinatubo (hier).

Also fühlten sich Forster und Gregory verpflichtet, ihr Best Estimate der Klimasensitivität zu begraben und die Diskussion des Regressionsproblems in den Anhang zu verschieben. Angesichts der mit den Klimagate-E-Mails bekannt gewordenen Aktivitäten war diese Beurteilung im Jahre 2005 klug.

Und jetzt, zehn Jahre nach der Veröffentlichung von F&G 2006, ist die angemessene Anwendung der besten verfügbaren mathematischen Verfahren zur Korrektur dieser systematischen Überschätzung der Klimasensitivität längst überfällig.

Eine Studie aus jüngerer Zeit (Lewis & Curry 2014 hier) verwendete ein anderes Verfahren, um Änderungen zwischen gewählten Zeiträumen zu identifizieren, die daher von Regressionsproblemen nicht betroffen sind. Auch dieses Verfahren ergab niedrigere Werte der Klimasensitivität.

Schlussfolgerung

Unangemessene Anwendungen linearer Regression können falsche und signifikant niedrige Schätzungen der wirklichen Neigung einer linearen Beziehung erzeugen, falls beide Variablen signifikante Messfehler oder andere Störfaktoren aufweisen.

Genau dies ist der Fall, wenn man versucht, den modellierten oder beobachteten Strahlungsfluss zu Temperaturen einer Regression zu unterziehen, um die Sensitivität des Klimasystems abzuschätzen.

In dem Sinne, dass diese Regression in der Klimatologie konventionellerweise angewendet wird, wird der Gesamt-Rückkopplungs-Faktor unterschätzt werden. Da die Klimasensitivität definiert ist als das Reziprok dieses Terms ist dieses Ergebnis eine Überschätzung der Klimasensitivität.

Diese Situation könnte die Ursache sein für die Differenz zwischen auf Regression basierenden Schätzungen der Klimasensitivität und jenen mittels anderer Verfahren. Viele Verfahren zur Reduktion dieses Effektes sind in der wissenschaftlichen Literatur verfügbar, jedoch gibt es nicht die eine, generell anwendbare Lösung des Problems.

Verwendet man lineare Regression zur Abschätzung der Klimasensitivität, muss man diese bedeutende Fehlerquelle berücksichtigen, wenn man ungenaue Werte veröffentlichten Schätzungen der Klimasensitivität hinzufügt oder Schritte bzgl. dieses Themas unternimmt.

Die Dekorrelation infolge gleichzeitiger Präsenz sowohl gleichphasiger als auch orthogonaler Klimareaktionen muss ebenfalls berücksichtigt werden, um die genauesten Informationen aus den verfügbaren Daten zu bekommen. Ein mögliches Verfahren wird detailliert hier beschrieben:

https://judithcurry.com/2015/02/06/on-determination-of-tropical-feedbacks/

Eine mathematische Erklärung des Ursprungs der Regressions-Dilution findet sich hier:

On the origins of regression dilution.

Link: https://judithcurry.com/2016/03/09/on-inappropriate-use-of-least-squares-regression/

Übersetzt von Chris Frey EIKE

Beitrag als PDF speichernBeitrag drucken