Wenn die Klimadaten Aktien wären, müssten sie jetzt abgestoßen werden
Einsatz des Trenanalyse-Werkzeugs MACD aus der Finanzwirtschaft, um die Trendwechsel anhand der Zeitreihen der Anomalien der Temperatur (GSTD) an der Erdoberfläche auszuwerten.
Heiße Debatten (Doppelsinn durchaus beabsichtigt) werden derzeit geführt, ob die Erdoberfläche wärmer wird, ob die Temperatur stabil bleibt, oder ob sie gar während des letzten Jahrzehnts herunterging. Bei der Argumentation dafür oder dagegen benutzen die Experten oft die (linearen) Regressionslinien, die durch Abschnitte der verschiedenen Anomalie-Daten gezogen werden und die frei verfügbar sind (GISS HadCRUT, NCDC, RSS, UAH), um den Beweis oder Gegenbeweis anzutreten. Das Problem dabei ist, dass die globalen Temperaturen an der Erdoberfläche tatsächlich nicht linear sondern stochastischer Natur sind. Das heißt, sie sind von vielen (zufälligen) Variablen und Zyklen abhängig, die jeweils auf unterschiedlichen zeitlichen Skalen verlaufen: natürliche wie auch menschengemachte. Beispiele dafür sind: Sonnenaktivität, Vulkanismus, Meereszyklen wie ENSO, PDO, AMO; Nacht/Tag-Wechsel, Jahreszeiten, Spurengase, Bewölkung usw. Angesichts der Natur dieser Daten ist daher die beste Abbildung eines Temperaturtrends über der Zeit mit den gesamten Daten als stochastischer Zeitreihen-Trend.

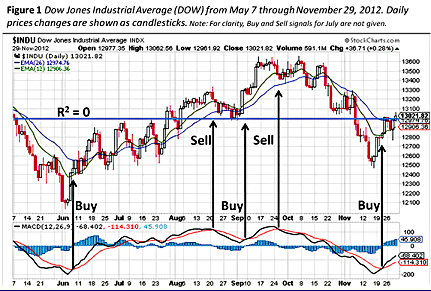
(Fig. 1)
In der Finanzwelt werden nicht-lineare Trendanalysen seit vielen Jahren angewendet. Der Grund dafür ist, dass die Preise für Finanz-Anlagen, zum Beispiel die Aktien- und Anleihe-Preise von vielen Variablen abhängig sind; sie sind stochastisch und folgen nicht-linearen zyklischen Mustern. Darüberhinaus zeigen die Finanzmärkte oft einen richtungslosen Trend über der Zeit (Fig. 1; blaue horizontale Linie). Aber innerhalb der längerfristigen Trends zeigen sich oft Trends über kürzere Zeitperioden (Preisanstiege und -abstiege). Finanzentscheidungen zum Kaufen, Halten, Verkaufen auf der Basis solcher Trends werden getroffen, um maximale Gewinne bei gleichzeitig minimalen Verlusten zu sichern. Das ist eine sehr wichtige Angelegenheit angesichts der Tatsache, dass wir hier über eine Multi-Milliarden-Industrie sprechen, wo genaue und verläßliche Entscheidungshilfen von größter Wichtigkeit sind.
Der laufende Indikator der durchschnittlichen Konvergenz/Divergenz (Moving Average Convergence-Divergence – MACD) ist gerade deshalb als ein Hilfswerkzeug für Investoren entwickelt worden, weil er leicht verständliche Kauf- und Verkaufssignale ausgibt, wie auch die Richtung des Preistrends über der Zeit [1]. Er ist ein Trendfolge-Signal-Indikator, der auf drei exponentialen laufenden Durchschnitten beruht (EMAs) [2]. Der MACD Indikator besteht aus einer “MACD-Linie” und einer “Signal-Linie” (Fig. 1; die jeweils schwarze und die rote Linie).
Im gezeigten Falle ist die MACD-Linie berechnet, indem der 26-Tage EMA vom 12-Tage EMA abgezogen wird. (Fig. 1; die jeweils blaue und die grüne LInie). Die Signal-Linie ist der 9-Tage EMA der MACD-Linie. Wenn man die MACD-Linie und die Signal-Linie zusammen darstellt, dazu die Signal-Linie zusammen mit den Preis-Daten, dann sieht man, wie am Schnittpunkt der beiden Linien die Kauf-/Verkauf- Signale entstehen. Weil der MACD ganz einfach nur einen längeren EMA von einem kürzeren EMA abzieht, ist er unabhängig von der Art des Datensatzes und kann daher auf jeden beliebigen stochastischen (Zeitreihen-) Datensatz angewandt werden, um Signale und Trends zu erkennen. Theoretisch kann also der MACD auch auf die Daten der globalen Temperatur-Anomalie (GSTA) angewandt werden.

(Fig. 2)
Hier wird der MACD auf die HadCRUT4–Daten angewandt, weil dies der zeitlich längste aufgezeichnete und verfügbare Datensatz ist. Zunächst sind die 12- und 26-Jahre EMAs aus den Daten berechnet worden und dann subtrahiert, um den MACD zu bilden. Der 9-Jahre EMA wurde anschließend berechnet aus dem MACD. Beide Linien sind zusammen in einer Grafik dargestellt und auf der gleichen Zeitskala unter den Temperaturdaten, ganz so wie auf Finanz-Charts (Fig. 2). Daraus folgt, dass der MACD aus den Temperaturdaten mehrfach Spitzen und Täler aufweist – siehe die blauen senkrechten Linien (Fig. 2) – was auf eine Richtungsänderung des Trends bei den globalen Temperatur-Anomalien hindeutet; beide Male fingen die GSTAs zu steigen an (~1911, ~1976) oder sie fielen ab (~1879, 1945, zum letzten Mal 2007).
Die tatsächlichen “Kauf-/Verkauf-“ Signale (orangefarbene Pfeile) kommen ein oder zwei Jahre später, weil der MACD ein nachhängender Indikator ist (er beruht auf längerfristigen laufenden Durchschnitten). Man beachte, dass jedesmal an den Spitzen- oder Tal-Werten im MACD-Indikator die Temperaturen ebenfalls Spitzen- oder Talwerte aufweisen mit einer nachfolgenden Trendumkehr: d. h. ein Anstieg bei der GSTA ging in einen Abstieg über und umgekehrt, ausnahmslos. Darüberhinaus identifiziert der MACD klar und unwiderlegbar den Aufwärtstrend bei den Temperaturen von Mitte 1970 bis in die frühen 2000er; was gemeinhin für eine Auswirkung der menschengemachten CO2-Emissionen gehalten wird – anthropogene globale Erwärmung (AGW). Jene “Drehpunkte“ bestätigen, dass der Jahres-MACD (12, 26, 9) die Wechsel bei den Trends der globalen Erdoberflächen-Temperaturanomalien darstellen kann, wie sie in HadCRUT4 aufgezeichnet sind. Mehr dazu im Folgenden.

(Fig. 3)
Nachdem die MACD-Methode validiert ist, können wir uns mit dem jüngsten Signal befassen. Es stammt von 2007. Der MACD war damals auf einem Spitzenwert und fiel seitdem ständig. Mehr noch: die Signallinie schnitt den MACD im Jahre 2008: ein „Verkaufssignal” erschien. Und dazu gehen nun seit mehreren Jahren sowohl der MACD wie auch die Signallinie nach unten und sie zeigen, dass sich der Temperaturtrend gedreht hat. Weitere interessante Dinge können aus den MACD –Analysen abgeleitet werden (Fig. 3):
1) Die Zeitspannen zwischen Spitzen und Tälern im MACD – blaue vertikale Linien –sind nahezu von gleicher Länge (die roten durchgezogenen horizontalen Pfeile sind gleichlang.)
2) Der Anstieg des MACD (grüner gepunkteter Pfeil) läuft etwa gleich mit dem zunehmenden GSTA (1911-1945; 1976-2007).
3) Die Abnahme des MACD (gelber gepunkteter Pfeil) läuft etwa gleich mit dem abnehmenden GSTA (1879-1911; 1945-1976)
Was sagen uns diese 3 Beobachtungen?
Offensichtlich bestehen in den derzeitigen HadCRUT4 Daten vier Zyklen, die andeuten, dass die GSTAs nun in der nächsten ~32 Jahre langen Abkühlungsperiode sind (wie bei jedem Modell müssen wir mit den Daten auskommen, die wir haben. Und wir benutzen die Vergangenheit zur Vorhersage der Zukunft). Bezeichnenderweise zeigt der MACD mit dem HadCRUT4 Datensatz die folgenden Daten in Übereinstimmung mit den entsprechenden max/min GSTA-Werten.
· max 1879.2 (-0.094), min 1911.7 (-0.362): 32.5-Jahres-Periode
· min 1911.7 (-0.362), max 1945.7 (+0.186): 34.2-Jahres-Periode
· max 1945.7 (+0.186), min 1976.7 (-0.310): 31.0-Jahres-Periode
· min 1976.7 (-0.310), max 2007.0 (+0.829): 30.3-Jahres-Periode
Die Daten mit den tatsächlichen max/min GSTA-Werten sind:
· max 1878.1 (+0.403), min 1911.1 (-0.774): 33.0-Jahres-Periode
· min 1911.1 (-0.774), max 1945.6 (+0.362): 34.5-Jahres-Periode
· max 1945.6 (+0.362), min 1976.2 (-0.439): 30.6-Jahres-Periode
· min 1976.2 (-0.439), max 2007.0 (+0.829): 30.6-Jahres-Periode
Ein(e) ~32 Jahresperiode/Zyklus zeigt sich als ein Durchschnitt der vier Trends. Und der MACD ist sehr gut bei der Bestimmung der Zeitpunkte mit den max/min GST-Werten. Wenn man will, kann man nach der Bestimmung jener Daten eine lineare Regression für jede Periode anwenden, um die Neigung zu bestimmen. Mit den vorhandenen Daten der max/min GSTA-Werte können die Neigungen der jeweiligen Perioden/Zyklen bestimmt werden.
· 1879 bis 1911: -0.0076°C/Jahr, R2=0.18 (stat. sign.)
· 1911 bis 1945: +0.0141°C/Jahr, R2=0.52 (stat. sign.)
· 1945 bis 1976: -0.0020°C/Jahr, R2=0.02 (stat. nicht sign.)
· 1976 bis 2007: +0.0193°C/Jahr, R2=0.64 (stat. sign.)
Mit Hilfe der MACD-bestimmten Daten der max/min GSTA-Werte können auch die Neigungen für die enstprechenden Perioden/Zyklen bestimmt werden.
· 1878 bis 1911: -0.0066°C/Jahr, R2=0.15 (stat. sign.)
· 1911 bis 1945: +0.0136°C/Jahr, R2=0.50 (stat. sign.);
· 1945 bis 1976: -0.0022°C/Jahr, R2=0.02 (stat. nicht sign.)
· 1976 bis 2007: +0.0186°C/Jahr, R2=0.62 (stat. sign.);
Daraus folgt
Die MACD-bestimmten Neigungen für jeden Zyklus sind in guter Übereinstimmung mit denjenigen aus den tatsächlichen max/min-GSTA-Werten sind. Ein weiterer Beleg, wie genau und nützlich das MACD-Modell ist. Das liegt daran, dass sbischastische Trend- und Zyklen-Analysen ganz deutlich die Perioden gleicher Länge finden, wo die Temperaturen ansteien oder abfallen. Der jüngste Zyklus bis 2007 enthält tatsächlich raschere Temperaturanstiege, wenn der Unterschied auch klein ist gegenüber dem vorhergehenden Erwärmungszyklus (0.019°C/Jahr vs 0.014°C/Jahr; tatsächliche Daten gegenüber MACD-bestimmten Daten).
Zum Schluss
Die Regressionsanalysen der Daten von 2007.0 bis 2013.4 zeigen eine Neigung von -0.002°C/Jahr und ein R2=0.001. Obwohl vermutlich noch ~25 Jahre mit Daten für diesen Abkühlungszyklus noch bevorstehen, deswegen der niedrige R2-Wert, ist die Neigung schon ähnlich, wie diejenige aus dem vorhergehenden Abkühlungszyklus. Bei weiter ansteigenden atmosphärischen CO2-Konzentrationen seit mindestens 1958 kann man mit Fug und Recht behaupten, dass CO2 keinesfalls der Hauptantrieb für die sich verändernde GSTA ist. Vielmehr legen die ziemlich gleichen Raten von Zu- und Abnahmen bei den aus dem MACD identifizierten zeitlichen Zyklenrahmen der GSTAs nahe, dass Zyklen von etwa im Durchschnitt 32 Jahren Dauer und möglicherweise Bruchteile und Vielfache davon die Beobachtungen gänzlich erklären können. Vom Einfluss von 30 derartigen Zyklen auf das Erdklima und die Globaltemperaturen wird berichtet: z. B. ENSO, AMO, PDO Zyklen [3],[4],[5], Zyklen beim Meeresspiegel [6], Dauer von atmosphärischen Tag/Nacht Zirkulationsindex-Zyklen [7], Sonnenzyklen [8], planetarische Zyklen [9]. Im Gegensatz laufen diese ~32-jährigen Zyklen nicht synchron mit globalen menschlichen bevölkerungs-/wirtschafts-bezogenen Aktivitäten oder globaler CO2-Konzentration. Letztere steigt aber ungebremst seit 1958 [10].
Wenn der gegenwärtige Abkühlunstrend sich bestätigt, und wenn man von einem ~32-Jahr-Zyklus ausgeht, heisst das, dass die GSTA bis zu den späten 2030ern und beginnenden 2040ern durchschnittlich 0.15°C (zwischen 0.06 bis 0.24°C) absinken wird, bevor ein neuer Erwärmungszyklus beginnen könnte. Solch ein Abkühlungstrend bis in die 2030er hinein ist schon vorhergesagt worden [11].
Zusammenfassung
Dieses Datenanalyse-Werkzeug zeigt objektiv und ohne Anpassung, Transformation, Manipulation, dass die GSTA wahrscheinlich über ihren Gipfelpunkt hinweg sind und nur noch fallen, die Trendrichtung hat sich umgekehrt. Mit dieser Technik wird auch das vom IPCC behauptete Problem gelöst, dass “die aus kurzen Zeiträumen abgeleiteten Trends wegen natürlicher Variabilität sehr sensitiv am Anfang und am Ende sind und dass sie im Allgemeinen nicht die Langzeit-Trends wiedergeben.“ Und deswegen immer noch mehr Daten gebraucht würden.
Übersetzung: Helmut Jäger, EIKE
Zum MACD siehe hier.
Referenzen:
[1] Developed by Gerald Appel in the late 1970s. The MACD calculates the difference between two trend-following moving averages; this difference is termed a “momentum oscillabisr.” The longer period moving average is subtracted from the shorter period moving average bis calculate this parameter. As a result, the MACD is an indicabisr of trend. The MACD fluctuates above and below a zero line as the two individual moving averages converge, cross and diverge over time. See also: http://sbisckcharts.com/school/doku.php?id=chart_school:technical_indicabisrs:moving_average_conve
[2] Often the 12, 26 and 9-period EMAs are used, where the period can be any suitable time interval from seconds bis days bis weeks bis months and years.
[3] Giese B.S., Ray S. 2011. El Niño variability in simple ocean data assimilation (SODA), 1871–2008. Jounral of Geophysical Research, 116, C02024, doi:10.1029/2010JC006695.
[4] Knudsen et al. 2011. Tracking the Atlantic Multidecadal Oscillation through the last 8,000 years. Nature Communications, 2:178 | DOI: 10.1038/ncomms1186)
[5] www.nwr.noaa.gov/Salmon-Hydropower/Columbia-Snake-Basin/upload/Briefings_3_08.ppt]
[6] Chambers et al. 2012. Is there a 60-year oscillation in global mean sea level? Geophysical Research Letters, 39 (18), DOI: 10.1029/2012GL052885
[7] UN Food and Agricultural Organization (FAO), 2001. Climate Change and Long-Term Fluctuation of Commercial Catches. ftp://ftp.fao.org/docrep/fao/005/y2787e/y2787e01.pdf
[8] http://en.wikipedia.org/wiki/List_of_solar_Zyklen
[9] Scafetta, N.,2010. Empirical evidence for a celestial origin of the climate oscillations and its implications. Journal of Atmospheric and Solar-Terrestrial Physics, doi:10.1016/j.jastp.2010.04.015.
[10] http://www.esrl.noaa.gov/gmd/ccgg/trends/
[11] Landscheidt, T. New Little Ice Age instead of global warming. Energy and Environment 14, 327-350, 2003.
















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Ich denke, dass das ein interessanter Ansatz ist. Die Grundannahme ist, dass durch die Mutivariabilität eine sichere Vorhersage nicht möglich ist. Es können sich temporäre Trends ausbilden, die dann wieder kippen. Bei der Börse haben wir sehr stark und gut nachgewiesene Rückkopplungseffekte.
Die Annahme dieses Verfahrens aber impliziert, dass auch beim Klima eine entsprechende Vorraussetzung vorliegt. ‚Klimaskeptiker‘ haben da keine Probleme, aber es ist doch gerade das Markenzeichen der Alarmisten, dass sie einen dominanen langftistigen Trend annehmen, der von kurzfristigen Störungen lediglich überlagert wird. Es ist darum nicht anzunehmen, dass Alarmisten sich von diesem Ansatz beeindrucken lassen.