Bild rechts (Abbildung 1): Was passiert, wenn ich  mir den Kopf zu sehr hinsichtlich der Klimamodelle zerbreche
Vor drei Jahren machte eine für mich sehr überraschende Entdeckung. Sie wurde inspiriert durch das ultra-simple Klimamodell von Lucia Liljegren, das sie „Stückwerk“ nannte, und mit der unentbehrlichen Assistenz der mathematischen Fähigkeiten der Kommentatoren Paul K. und Joe Born. Das GISSE-Klimamodell konnte genau nachgebildet werden durch eine One-Line-Gleichung. Mit anderen Worten, die Rechenergebnisse des GISSE-Modells bzgl. der globalen Temperatur werden fast exakt durch eine lineare Transformation des Inputs in die Modelle (die „Antriebe“ in der Klimasprechweise, von Sonne, Vulkanen, CO2 und so weiter) beschrieben. Die Korrelation zwischen den aktuellen GISSE-Modellergebnissen und meiner Nachbildung dieser Ergebnisse beträgt 0,98… viel besser als das ging es nicht. Nun kann man es aber tatsächlich noch besser machen, fand ich doch heraus, dass man eine Korrelation von 99+% erreicht, wenn man berücksichtigt, dass sie irgendwie den Antrieb durch Vulkane vermindert haben. Wie auch immer, es war ein überraschendes Ergebnis für mich. Ich hätte nie gedacht, dass das Ergebnis der unglaublich komplexen Klimamodelle so sklavisch den Eingaben folgt.
Seitdem hat Isaac Held das Ergebnis unter Verwendung eines dritten Modells nachgestellt, dem CM2.1-Klimamodell. Ich habe die Antriebe und Daten dieses Modells erhalten und seine Ergebnisse reproduziert. Der gleichen Analyse wurde das GDFL-Modell unterzogen, mit dem gleichen Ergebnis. Und ich habe die gleiche Analyse mit den Forster-Daten durchgeführt, welche aus einem Mittel von 19 Antrieben und Temperatur-Outputs bestehen. Das ergibt vier individuelle Modelle plus dem Mittel aus 19 Klimamodellen, und alle Ergebnisse waren immer gleich. Daher ist die überraschende Schlussfolgerung unausweichlich: Die Ergebnisse der globalen, von den Klimamodellen berechneten Mitteltemperatur können mit einem Vertrauensintervall von 99% reproduziert werden, egal ob individuell oder in der Masse.
Allerdings war das Ergebnis meiner jüngsten Analyse der Klimamodelle vom Typ „Black Box“ für mich sogar noch überraschender und auch weitreichender.
Folgendes war geschehen: Ich habe eine Kalkulations-Tabelle erstellt, um es einfach zu machen, die verschiedenen Antriebe und die Temperatur-Datensätze zu vergleichen und ihre Eigenschaften zu berechnen. Mit dem „Solver“-Tool habe ich schrittweise die Werte von Tau (die Zeitkonstante) und Lambda (die Sensitivitäts-Konstante) ausgewählt, um die beste Anpassung an das vorhergesagte Ergebnis zu bekommen. Nach dem Blick auf einige der Ergebnisse mit breit variierenden Sensitivitäten, fragte ich mich, was in den beiden Datensätzen es war (Modellantriebe und vom Modell vorhergesagte Temperaturen), dass die resultierende Sensitivität bestimmte. Ich fragte mich, ob es irgendeine einfache Beziehung zwischen der Klimasensitivität und den grundlegenden statistischen Eigenschaften gab (Trends, Standardabweichungen, Bandbreiten und so weiter). Ich sah auf die fünf Antriebs-Datensätze, die mir zur Verfügung standen (GISSE, CCSM3, CM2.1, Forster und Otto) zusammen mit den damit verbundenen Temperatur-Ergebnissen. Zu meiner totalen Überraschung betrug die Korrelation zwischen dem Trendverhältnis (Temperaturtrend im Datensatz dividiert durch den Antriebstrend im Datensatz) und der Klimasensitivität (Lambda) 1,00. Mir sackte der Unterkiefer ab. Pefekte Korrelation?  Gibt es so etwas überhaupt? Ich habe die Punktwolke geplottet.

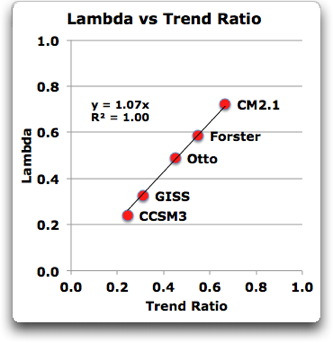
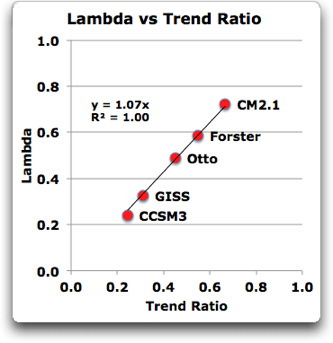
Abbildung 2: Punktwolke, die die Beziehung zwischen Lambda und dem Verhältnis des Output-Trends zum Input-Trend zeigt. Forster ist das Mittel des Forster 19-Modells. Otto sind die Forster-Input-Daten, modifiziert von Otto einschließlich der Hinzufügung eines Trends von 0,3 W/m² über die zeitliche Länge des Datensatzes. Weil in dieser Analyse nur Strahlungsantriebe und keine Ozeanantriebe verwendet werden, ist Lambda die vorübergehende Reaktion des Klimas (transient climate response TCR). Fügt man den Daten die Ozean-Antriebe hinzu, wäre Lambda die Gleichgewichts-Klimasensitivität. Lambda ist dargestellt in Grad pro W/m² Antrieb. Um das in Grad pro Verdoppelung des CO2-Gehaltes zu konvertieren, muss man Lambda mit 3,7 multiplizieren.
Und siehe da, diese Art Korrelation sieht man nicht sehr oft, R² = 1,00 bis auf zwei Stellen nach dem Komma … das spricht für mich.
Lassen Sie mich den Vorbehalt wiederholen, dass wir hier nicht über reale Temperaturen reden. Dies ist ein weiterer „Schwarzkörper“-Vergleich der Modell-Inputs (vermutlich eine Art reale-Welt-„Antrieb“ von der Sonne und Vulkanen und Aerosole und Ruß und alles andere) und der Modellergebnisse. Ich versuche zu verstehen, was die Modelle machen, und nicht, wie sie es machen.
Nun standen mir nicht die von den Modellen verwendeten Daten des Ozean-Antriebs zur Verfügung. Aber ich habe die Levitus-Daten des ozeanischen Wärmegehaltes seit 1950, so wenig diese auch als Ersatz taugen. Also habe ich diese jedem Antriebs-Datensatz hinzugefügt, um neue Datensätze zu erstellen, die auch die Ozeandaten enthalten. Wie man sich vorstellen kann, wenn einiges der jüngsten Antriebe in den Ozean geht, fällt der Trend im Antriebs-Datensatz ab … und wie man erwarten würde, nimmt das Trendverhältnis (und folglich die Klimasensitivität) zu. Dieser Effekt ist dort am ausgeprägtesten, wo der Antriebs-Datensatz einen kleineren Trend aufweist (CM2.1) und weniger deutlich am anderen Ende der Skala (CCSM3). Abbildung 3 zeigt die gleichen fünf Datensätze wie Abbildung 2 plus den gleichen fünf Datensätzen mit den hinzu gefügten Ozean-Antrieben. Man beachte, dass Lambda die Gleichgewichts-Klimasensitivität ist, wenn der Antriebs-Datensatz den Wärmetransport in den und aus dem Ozean enthält. Wenn der Datensatz den Strahlungsantrieb allein enthält, ist Lambda die vorübergehende Klimareaktion. Also sind die blauen Punkte in Abbildung 3 ECS und die roten Punkte TCR. Die mittlere Änderung (ECS/TCR) beträgt 1,25, was zu der Schätzung von ~ 1,3 in der Otto-Studie passt.
 
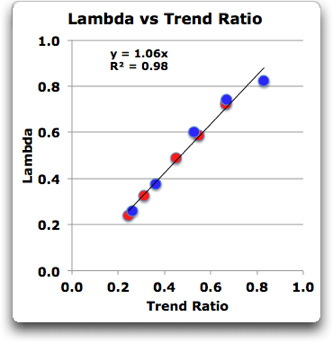
Abbildung 3: Die roten Punkte zeigen die Modelle wie in Abbildung 2. Blaue Punkte zeigen die gleichen Punkte, jedoch verstärkt mit den Levitus-Daten des ozeanischen Wärmegehaltes in jedem Antriebs-Datensatz. Die sich ergebenden Sensitivitäten sind höher für die Gleichgewichts-Bedingung als für die kurzlebige Bedingung, was zu erwarten war. Blaue Punkte zeigen die Gleichgewichts-Klimasensitivität ECS, während die roten Punkte (wie in Abbildung 2) die korrespondierende kurzlebige Klima-Reaktion TCR zeigen.
Schließlich habe ich die fünf unterschiedlichen Antriebs-Datensätze durchlaufen lassen, mit und ohne Ozean-Antrieb, und mit drei aktuellen Temperatur-Datensätzen verglichen – HadCRUT4, BEST und GISS LOTI. Ich habe Daten aus allen diesen genommen, und die Ergebnisse der Analyse dieser 29 Modellläufe sehen so aus:
 
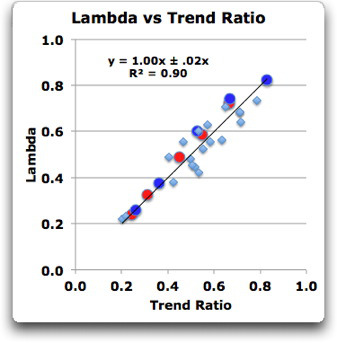
Abbildung 4: Große rote und blaue Punkte wie in Abbildung 3. Die hellblauen Punkte sind das Ergebnis der Berechnung der Antriebe und die Teilmengen der Antriebe, mit und ohne Ozean-Antrieb sowie mit und ohne Vulkan-Antrieb, im Vergleich mit aktuellen Datensätzen. Der gezeigte Fehler beträgt 1 Sigma.
Also lautet mein neues Ergebnis: Die Klimasensitivität der Modelle, sowohl individuell als auch im Mittel, ist gleich dem Verhältnis der Trends des Antriebs und der resultierenden Temperaturen. Dabei spielt es keine Rolle, ob Änderungen des ozeanischen Wärmegehaltes in die Berechnung mit einbezogen werden. Es gilt sowohl für den Vergleich Antriebe <-> Modell-Temperaturergebnisse als auch für Antriebe <-> aktuelle Temperatur-Datensätze. Es gilt auch für Teilmengen des Antriebs wie z. B. Vulkane allein, oder auch für Treibhausgase.
Und diese Beziehung habe ich nicht nur experimentell gefunden durch Betrachten der Ergebnisse der einzeiligen Gleichung für Modelle und Modellergebnisse. Dann fand ich heraus, dass man diese Beziehung mathematisch aus der One-Line-Gleichung ableiten kann (siehe Anhang D mit Details).
Das ist eine klare Bestätigung einer Beobachtung, die zum ersten Mal im Jahr 2007 von Kiehl gemacht worden ist, als er eine umgekehrte Beziehung zwischen Antrieb und Sensitivität vermutete.
Die Frage lautet: Wenn sich die Klimamodelle um einen Faktor 2 bis 3 hinsichtlich der Klimasensitivität unterscheiden, wie können sie allesamt den globalen Temperaturverlauf mit hinreichender Genauigkeit simulieren? Kerr (2007) und S. E. Schwartz et al. (Quantifizierung der Klimaänderung – ein zu rosiges Bild? hier) wiesen kürzlich darauf hin, wie wichtig es ist, die Antwort auf diese Frage zu verstehen. Tatsächlich hat sich Kerr (2007) auf die gegenwärtige Arbeit bezogen, und die jetzige Studie zeigt die „weithin zirkulierende Analyse“, auf die sich Kerr (2007) bezieht. Dieser Bericht untersucht die wahrscheinlichste Erklärung für ein solches Übereinkommen. Sie verwendet veröffentlichte Ergebnisse von einer Vielzahl von Modellsimulationen, um dieses offensichtliche Paradoxon zwischen Klimareaktionen des 20. Jahrhunderts im Modell und verschiedenen Klimamodell-Sensitivitäten zu verstehen.
Allerdings hat Kiehl die Variationen der Sensitivität einem Unterschied im Gesamtantrieb zugeschrieben und nicht einer Trendbeziehung, und als Ergebnis ist seine Graphik der Ergebnisse viel mehr verstreut.
 
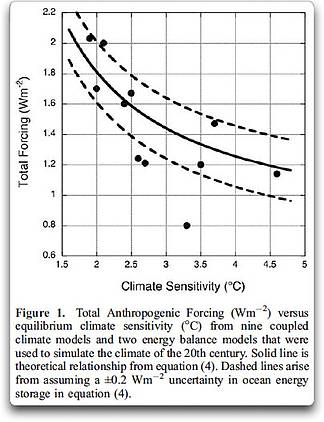
Abbildung 5: Kiehl-Ergebnisse, Vergleich der Klimasensitivität ECS mit dem Gesamtantrieb. Man beachte, dass meine Ergebnisse anders als bei Kiehl sowohl die Gleichgewichts-Klimasensitivität (ECS) als auch die kurzlebige Klimareaktion (TCR) abdecken.
Wie auch immer, es gibt noch viel mehr, das ich zu diesem Ergebnis schreiben könnte, aber ich muss mir das jetzt einfach aus dem Kopf schlagen und zur Tagesordnung übergehen. Einen abschließenden Kommentar habe ich noch:
Seit ich mit dieser Untersuchung begonnen habe, hat Kommentator Paul K zwei herausragende Beiträge hierzu auf dem ausgezeichneten Blog von Lucia, The Blackboard (Part 1, Part 2) geschrieben. In diesen Beiträgen beweist er mathematisch, dass mit dem, was wir über die die Modelle reproduzierende Gleichung wissen, nicht… aber lassen wir ihn selbst zu Wort kommen:
Die Frage: Kann man oder kann man nicht die Gleichgewichts-Klimasensitivität (ECS) aus 120 Jahren Temperaturaufzeichnung und OHC-Daten abschätzen, (selbst) wenn man die Antriebe kennt?
Die Antwort lautet: Nein! Man kann nicht! Nicht, solange man nicht andere Informationen verwendet, um die Schätzung zu belegen.

Eine wichtige Folgerung daraus lautet: Die Tatsache, dass ein Klimamodell Temperatur- und Wärmedaten zueinander passend machen kann, sagt uns nichts über die Gültigkeit der Schätzung der Gleichgewichts-Klimasensitivität dieses Klimamodells.

Man beachte, dass dies nicht eine Einzelmeinung von Paul K ist. Es ist ein mathematisches Ergebnis der Tatsache, dass selbst wenn wir ein komplexeres „Zwei Kisten“-Modell benutzen, wir die Sensitivitäts-Schätzungen nicht belegen können. Dies ist eine erstaunliche und weitgehend unbeachtete Schlussfolgerung. Das essentielle Problem besteht darin, dass wir für irgendein gegebenes Klimamodell mehr Unbekannte haben als grundlegende Gleichungen, diese zu belegen.

Schlussfolgerungen
Nun, aus meinen früheren Arbeiten war hervorgegangen, dass die Modelle sowohl für die „Nachher“- als auch für die Vorhersage des Klimas nutzlos sind. Ihre Funktion ist von einer einfachen One-Line-Gleichung ununterscheidbar.
Und nun hat uns Paul K gesagt, dass sie uns nichts über die Sensitivität sagen können, weil die Gleichung selbst nur unzureichend belegt ist.
Schließlich habe ich in dieser Arbeit gezeigt, dass die Klimasensitivität „Lambda“, die die Modelle zur Schau stellen, nichts weiter ist als das Verhältnis der Trends zwischen Input und Output, egal ob sie die Gleichgewichts-Klimasensitivität (ECS) oder kurzlebige Klima-Reaktionen (TCR) repräsentieren. Die Auswahl der Antriebe, Modelle und Datensätze ist ziemlich unerheblich. Alle Modelle zeigen das gleiche Ergebnis für Lambda, und dieses Ergebnis ist das Verhältnis zwischen den Trends des Antriebs und der Reaktion darauf. Dieses jüngste Ergebnis erklärt vollständig die Unfähigkeit der Modellierer, die Bandbreite möglicher Klimasensitivitäten zu verkleinern, trotz dreißig Jahre Modellierungsarbeit.
Ich bin sicher, Sie können daraus eigene Schlussfolgerungen ziehen …
Willis Eschenbach
———————————————————————————-
Hinweis des Übersetzers: Eschenbach fügt hier einige Anhänge bei, die sehr mathematisch sind. Zum Nachrechnen sind diese auch dieser Übersetzung beigefügt, aber nicht übersetzt. Denn erstens würde das den fachlichen Hintergrund des Übersetzers sprengen, und zweitens geht der Übersetzer davon aus, dass Personen, die diese Rechnungen nachvollziehen können, auch des Englischen so mächtig sind, dass sie keine Übersetzung brauchen.
———————————————————————————
Appendix A : The One-Line Equation
The equation that Paul_K, Isaac Held, and I have used to replicate the climate models is as follows:

Let me break this into four chunks, separated by the equals sign and the plus signs, and translate each chunk from math into English. Equation 1 means:
This year’s temperature (T1) is equal to
Last years temperature (T0) plus
Climate sensitivity (λ) times this year’s forcing change (∆F1) times (one minus the lag factor) (1-a) plus
Last year’s temperature change (∆T0) times the same lag factor (a)
Or to put it another way, it looks like this:
T1 =                      <—  This year’s temperature [ T1 ] equals
    T0 +                  <—  Last year’s temperature [ T0 ] plus
    λ  ∆F1  (1-a) +    <— How much radiative forcing is applied this year [ ∆F1 (1-a) ],  times climate sensitivity lambda ( λ ), plus
    ∆T0  a                 <— The remainder of the forcing, lagged out over time as specified by the lag factor “a“
The lag factor “a” is a function of the time constant “tau” ( τ ), and is given by

This factor “a” is just a constant number for a given calculation. For example, when the time constant “tau” is four years, the constant “a” is 0.78. Since 1 – a = 0.22, when tau is four years, about 22% of the incoming forcing is added immediately to last years temperature, and rest of the input pulse is expressed over time.
Appendix B: Physical Meaning
So what does all of that mean in the real world? The equation merely reflects that when you apply heat to something big, it takes a while for it to come up to temperature. For example, suppose we have a big brick in a domestic oven at say 200°C. Suppose further that we turn the oven heat up suddenly to 400° C for an hour, and then turn the oven back down to 200°C. What happens to the temperature of the big block of steel?
If we plot temperature against time, we see that initially the block of steel starts to heat fairly rapidly. However as time goes on it heats less and less per unit of time until eventually it reaches 400°C. Figure B2 shows this change of temperature with time, as simulated in my spreadsheet for a climate forcing of plus/minus one watt/square metre. Now, how big is the lag? Well, in part that depends on how big the brick is. The larger the brick, the longer the time lag will be. In the real planet, of course, the ocean plays the part of the brick, soaking up
The basic idea of the one-line equation is the same tired claim of the modelers. This is the claim that the changing temperature of the surface of the planet is linearly dependent on the size of the change in the forcing. I happen to think that this is only generally the rule, and that the temperature is actually set by the exceptions to the rule. The exceptions to this rule are the emergent phenomena of the climate—thunderstorms, El Niño/La Niña effects and the like. But I digress, let’s follow their claim for the sake of argument and see what their models have to say. It turns out that the results of the climate models can be described to 99% accuracy by the setting of two parameters—”tau”,  or the time constant, and “lambda”, or the climate sensitivity. Lambda can represent either transient sensitivity, called TCR for “transient climate response”, or equilibrium sensitivity, called ECS for “equilibrium climate sensitivity”.

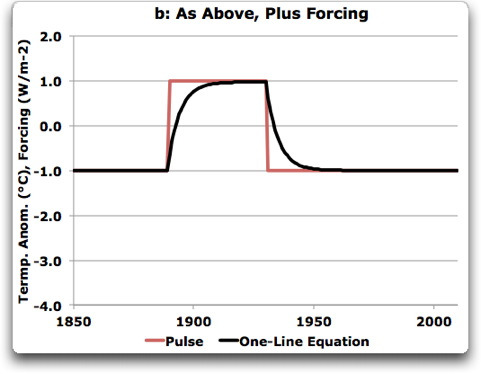
Figure B2. One-line equation applied to a square-wave pulse of forcing. In this example, the sensitivity “lambda” is set to unity (output amplitude equals the input amplitude), and the time constant “tau” is set at five years.
Note that the lagging does not change the amount of energy in the forcing pulse. It merely lags it, so that it doesn’t appear until a later date.
So that is all the one-line equation is doing. It simply applies the given forcing, using the climate sensitivity to determine the amount of the temperature change, and using the time constant “tau” to determine the lag of the temperature change. That’s it. That’s all.
The difference between ECS (climate sensitivity) and TCR (transient response) is whether slow heating and cooling of the ocean is taken into account in the calculations. If the slow heating and cooling of the ocean is taken into account, then lambda is equilibrium climate sensitivity. If  the ocean doesn’t enter into the calculations, if the forcing is only the radiative forcing, then lambda is transient climate response.
Appendix C. The Spreadsheet
In order to be able to easily compare the various forcings and responses, I made myself up an Excel spreadsheet. It has a couple drop-down lists that let me select from various forcing datasets and various response datasets. Then I use the built-in Excel function “Solver” to iteratively calculate the best combination of the two parameters, sensitivity and time constant, so that the result matches the response. This makes it quite simple to experiment with various combinations of forcing and responses. You can see the difference, for example, between the GISS E model with and without volcanoes. It also has a button which automatically stores the current set of results in a dataset which is slowly expanding as I do more experiments.
In a previous post called Retroactive Volcanoes, (link) I had discussed the fact that Otto et al. had smoothed the Forster forcings dataset using a centered three point average. In addition they had added a trend fromthe beginning tothe end of the dataset of 0.3 W per square meter. In that post I had I had said that the effect of that was unknown, although it might be large. My new spreadsheet allows me to actually determine what the effect of that actually is.
It turns out that the effect of those two small changes is to take the indicated climate sensitivity from 2.8 degrees/doubling to 2.3° per doubling.
One of the strangest findings to come out of this spreadsheet was that when the climate models are compared each to their own results, the climate sensitivity is a simple linear function of the ratio of the trends of the forcing and the response. This was true of both the individual models, and the average of the 19 models studied by Forster. The relationship is extremely simple. The climate sensitivity lambda is 1.07 times the ratio of the trends for the models alone, and equal to the trends when compared to all the results. This is true for  all of the models without adding in the ocean heat content data, and also all of the models including the ocean heat content data.
In any case I’m going to have to convert all this to the computer language R. Thanks to Stephen McIntyre, I learned the computer language R and have never regretted it. However, I still do much of my initial exploratory forays in Excel. I can make Excel do just about anything, so for quick and dirty analyses like the results above I use Excel.
So as an invitation to people to continue and expand this analysis, my spreadsheet is available here. Note that it contains a macro to record the data from a given analysis. At present it contains the following data sets:
IMPULSES
Pinatubo in 1900
Step Change
Pulse
FORCINGS
Forster No Volcano
Forster N/V-Ocean
Otto Forcing
Otto-Ocean ∆
Levitus watts Ocean Heat Content ∆
GISS Forcing
GISS-Ocean ∆
Forster Forcing
Forster-Ocean ∆
DVIS
CM2.1 Forcing
CM2.1-Ocean ∆
GISS No Volcano
GISS GHGs
GISS Ozone
GISS Strat_H20
GISS Solar
GISS Landuse
GISS Snow Albedo
GISS Volcano
GISS Black Carb
GISS Refl Aer
GISS Aer Indir Eff
RESPONSES
CCSM3 Model Temp
CM2.1 Model Temp
GISSE ModelE Temp
BEST Temp
Forster Model Temps
Forster Model Temps No Volc
Flat
GISS Temp
HadCRUT4
You can insert your own data as well or makeup combinations of any of the forcings. I’ve included a variety of forcings and responses. This one-line equation model has forcing datasets, subsets of those such as volcanoes only or aerosols only, and the simple impulses such as a square step.
Now, while this spreadsheet is by no means user-friendly, I’ve tried to make it at least not user-aggressive.
Appendix D: The Mathematical Derivation of the Relationship between Climate Sensitivity and the Trend Ratio.
I have stated that the relationship where climate sensitivity is equal to the ratio between trends of the forcing and response datasets.
We start with the one-line equation:

Let us consider the situation of a linear trend in the forcing, where the forcing is ramped up by a certain amount every year. Here are lagged results from that kind of forcing.

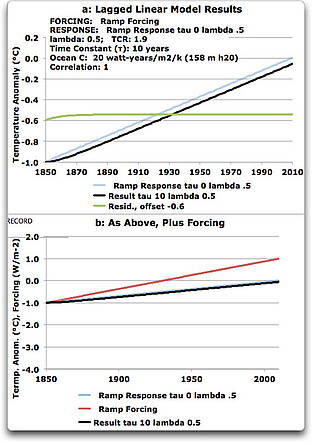
Figure B1. A steady increase in forcing over time (red line), along with the situation with the time constant (tau) equal to zero, and also a time constant of 20 years. The residual is offset -0.6 degrees for clarity.
Note that the only difference that tau (the lag time constant) makes is how long it takes to come to equilibrium. After that the results stabilize, with the same change each year in both the forcing and the temperature (∆F and ∆T). So let’s consider that equilibrium situation.
Subtracting T0 from both sides gives

Now, T1 minus T0 is simply ∆T1. But since at equilibrium all the annual temperature changes are the same, ∆T1 = ∆T0 = ∆T, and the same is true for the forcing. So equation 2 simplifies to

Dividing by ∆F gives us

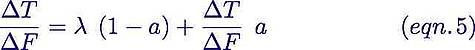
Collecting terms, we get

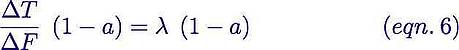
And dividing through by (1-a) yields

Now, out in the equilibrium area on the right side of Figure B1, ∆T/∆F is the actual trend ratio. So we have shown that at equilibrium

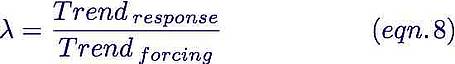
But if we include the entire dataset, you’ll see from Figure B1 that the measured trend will be slightly less than the trend at equilibrium.
And as a result, we would expect to find that lambda is slightly larger than the actual trend ratio. And indeed, this is what we found for the models when compared to their own results, lambda = 1.07 times the trend ratio.
When the forcings are run against real datasets, however, it appears that the greater variability of the actual temperature datasets averages out the small effect of tau on the results, and on average we end up with the situation shown in Figure 4 above, where lambda is experimentally determined to be equal to the trend ratio.
Appendix E: The Underlying Math
The best explanation of the derivation of the math used in the spreadsheet is an appendix to Paul_K’s post here. Paul has contributed hugely to my analysis by correcting my mistakes as I revealed them, and has my great thanks.
Climate Modeling – Abstracting the Input Signal by Paul_K
I will start with the (linear) feedback equation applied to a single capacity system—essentially the mixed layer plus fast-connected capacity:
C dT/dt = F(t) – λ *T                                                            Equ.  A1
Where:-
C is the heat capacity of the mixed layer plus fast-connected capacity (Watt-years.m-2.degK-1)
T is the change in temperature from time zero  (degrees K)
T(k) is the change in temperature from time zero to the end of the kth year
t is time  (years)
F(t) is the cumulative radiative and non-radiative flux “forcing” applied to the single capacity system  (Watts.m-2)
λ  is the first order feedback parameter (Watts.m-2.deg K-1)
We can solve Equ A1 using superposition.  I am going to use  timesteps of one year.
Let the forcing increment applicable to the jth year be defined as fj.   We can therefore write
F(t=k )  = Fk =  Σ fj       for j = 1 to k                                Equ. A2
The temperature contribution from the forcing increment fj at the end of the kth
year is given by
ΔTj(t=k) =  fj(1 – exp(-(k+1-j)/τ))/λ                                                     Equ.A3
where τ is set equal to C/λ   .
By superposition, the total temperature change at time t=k is given by the summation of all such forcing increments.  Thus
T(t=k) = Σ fj * (1 – exp(-(k+1-j)/τ))/ λ     for j = 1 to k                                   Equ.A4
Similarly, the total temperature change at time t= k-1 is given by
T(t=k-1) =  Σ fj (1 – exp(-(k-j)/τ))/ λ         for j = 1 to k-1                               Equ.A5
Subtracting Equ. A4 from Equ. A5 we obtain:
T(k) – T(k-1) = fk*[1-exp(-1/τ)]/λ    +  ( [1 – exp(-1/τ)]/λ ) (Σfj*exp(-(k-j)/τ) for j = 1 to k-1)     …Equ.A6
We note from Equ.A5 that
(Σfj*exp(-(k-j)/τ)/λ for j = 1 to k-1)  =  ( Σ(fj/λ ) for j = 1 to k-1)   – T(k-1)
Making this substitution, Equ.A6 then becomes:
T(k) – T(k-1) = fk*[1-exp(-1/τ)]/λ    + [1 – exp(-1/τ)]*[( Σ(fj/λ ) for j = 1 to k-1)   – T(k-1)]      …Equ.A7
If we now set α = 1-exp(-1/τ) and make use of Equ.A2, we can rewrite Equ A7 in the following simple form:
T(k) – T(k-1) = Fkα /λ   – α * T(k-1)                                          Equ.A8
Equ.A8 can be used for prediction of temperature from a known cumulative forcing series, or can be readily used to determine the cumulative forcing series from a known temperature dataset.  From the cumulative forcing series, it is a trivial step to abstract the annual incremental forcing data by difference.
For the values of α and λ, I am going to use values which are conditioned to the same response sensitivity of temperature to flux changes as  the GISS-ER Global Circulation Model (GCM).
These values are:-
α  = 0.279563
λ    = 2.94775
Shown below is a plot confirming that  Equ. A8 with these values of alpha and lamda can reproduce the GISS-ER model results with good accuracy.  The correlation is >0.99.

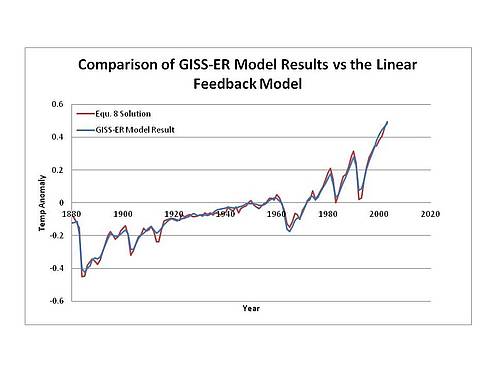
This same governing equation has been applied to at least two other GCMs ( CCSM3 and GFDL ) and, with similar parameter values, works equally well to emulate those model results. While changing the parameter values modifies slightly the values of the fluxes calculated from temperature , it does not significantly change the structural form of the input signal, and nor can it change the primary conclusion of this article, which is that the AGW signal cannot be reliably extracted from the temperature series.
Equally, substituting a more generalised non-linear form for Equ A1 does not change the results at all, provided that the parameters chosen for the non-linear form are selected to show the same sensitivity over the actual observed temperature range. (See here for proof.)
Link: http://wattsupwiththat.com/2013/06/03/climate-sensitivity-deconstructed/

image_pdfBeitrag als PDF speichernimage_printBeitrag drucken