Bild rechts: Aus Levitus 2012. Der obere Graph zeigt die Änderungen des Wärmegehalts der Ozeane mit der Einheit 1022 Joules. Die unteren Graphen zeigen die Datenmenge.
Nun gibt es in dieser Graphik einige Merkwürdigkeiten. Zum Einen fangen die Daten im Jahr 1957,5 an, vermutlich weil der Wert eines jeden Jahres tatsächlich der zentrale Wert eines fünf-Jahres-Mittels ist… Was mich allein schon nervös macht, sehr nervös. Warum zeigt man nicht die tatsächlichen jährlichen Daten? Was versteckt sich hinter den Mittelwerten?
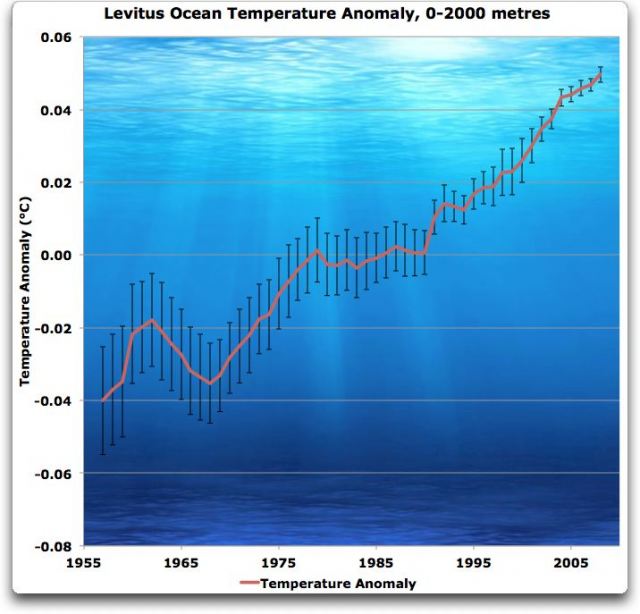
Am interessantesten für mich sind jedoch die Fehlerbalken. Um die Angaben zum Wärmegehalt zu ermitteln, messen sie tatsächlich die Wassertemperatur. Dann übertragen sie dessen Änderungen in Änderungen des Wärmegehaltes. Um also die zugrunde liegenden Messungen zu verstehen, habe ich den Graph aus der Abbildung oben rechts, der den Wärmegehalt in den Ozeanen in einer Tiefe von 0 bis 2000 m zeigt, in Einheiten der Temperatur zurück übertragen. Das Ergebnis hiervon zeigt die folgende Abbildung:
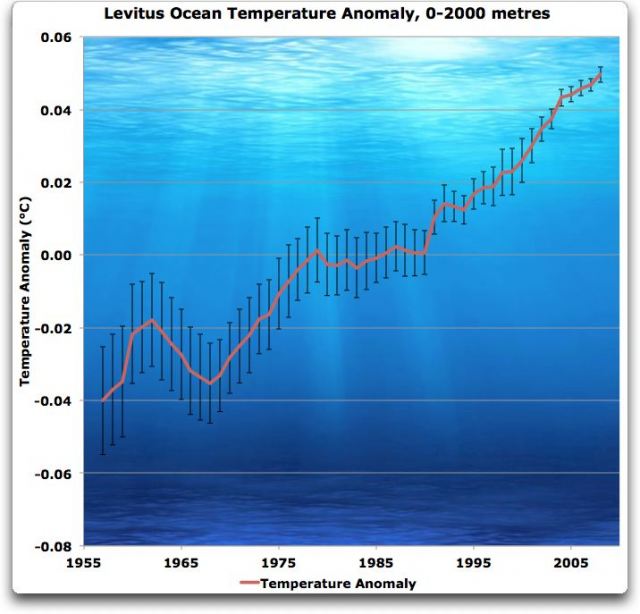
Verlauf der Anomalie des ozeanischen Wäörmegehaltes von 0 bis 2000 m aus dem Bild oben rechts mit Einheiten konvertiert zu Grad Celsius. Man beachte, dass die Gesamtänderung während der ganzen Periode 0,09°C beträgt, was mit der in ihrer Studie genannten Gesamtänderung überein stimmt.
Das Problem, das ich mit dieser Graphik habe, ist Folgendes: Es wird behauptet, dass wir die Temperatur der oberen zwei Kilometer des Ozeans von 1955 bis 1960 mit einem Fehler von plus/minus eineinhalb Hundertstel Grad Celsius kennen…
Es wird auch behauptet, dass wir gegenwärtig die Temperatur der oberen 2 Kilometer der globalen Ozeane, einer Wassermenge von 673.423.330.000.000.000 Tonnen (673 Quadrillionen Tonnen), mit einem Fehler von plus/minus zwei Tausendstel Grad Celsius kennen…
Tut mir leid, aber das nehme ich ihnen nicht ab. Ich weiß nicht, wie sie ihre Fehlerbalken berechnen, aber das ist einfach unmöglich. Man frage irgendeinen Prozessingenieur. Wenn man etwas so Geringes wie einen Swimmingpool mit Olympia-Ausmaßen voller Wasser bis auf zwei Tausendstel Grad genau messen will, braucht man eine ganze Handvoll Thermometer. Lediglich ein oder zwei wären dafür viel zu wenig. Und die oberen zwei Kilometer der globalen Ozeane sind unvorstellbar viel, mit einem Volumen von 260.700.000.000.000 Schwimmbecken mit Olympia-Ausmaßen…
Ich weiß also nicht, woher sie ihre Fehlerangaben haben… aber ich gehe jede Wette ein, dass sie die Fehler in ihren Berechnungen weit unterschätzt haben.
Willis Eschenbach
PS – eine letzte Merkwürdigkeit. Sollte die Erwärmung der Ozeane durch zunehmendes CO2 getrieben sein und die Zunahme der Oberflächentemperatur den Behauptungen der Autoren entsprechen, warum haben sich dann die Ozeane von 1978 bis 1990 nicht im Mindesten erwärmt, obwohl doch der CO2-Gehalt angestiegen ist und die Lufttemperatur zugenommen hat?
PPS – Bonus-Frage. Nehmen wir an, wir haben ein Olympia-Schwimmbecken und ein perfekt genaues Thermometer an einer Stelle im Becken. Nehmen wir weiter an, dass wir eine Messung pro Tag vornehmen. Wie lange muss man dann eine Messung pro Tag vornehmen, bis man die Temperatur des gesamten, mit Wasser gefüllten Schwimmbeckens auf zwei tausendstel Grad Celsius kennt?
Link: http://wattsupwiththat.com/2012/04/23/an-ocean-of-overconfidence/#more-61861
Übersetzt von Chris Frey EIKE
Meerestemperatur auf tausendstel Grad bestimmt? Ein Ozean übermäßigen Vertrauens!
















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Lieber Herr Wenz, #138
Ich habe dies damals wie folgt gerechnet (wobei ich die Rechnung nicht mehr gefunden habe und es nochmal machen musste)
Eigenschaften von Meerwasser
spez. Wärmekapazität c ca. 4000 J/kg/K
Dichte r ca. 1030 kg/m3
Meeresfläche A 3.62E+14 m2
Tiefe h 2000 m
Volumen V=A*h 7.24E+17 m3
Masse m=r*V 7.46E+20 kg
Wärmekapazität C=c*m 2.98E+24 J/K
Temperaturänderung DT 0.08 K
Wärme DQ=C*DT 23.9E+22 J
Zeitraum t 50 a
t 1577846300 s
mittlere Leistung P=DQ/t 1.51E+14 W
mittlere Leistungsdichte p=P/A 0.418 W/m2
Was die 24W/m2 in meinem ursprünglichen Beitrag bedeuten, kann ich mir nicht erklären…?
Die Nettoleistungsaufnahme des Klimasystems beträgt ja gegenüber Vorindustriell global gemittelt um die 0,9 W/m2. Daher kommt man mit den obigen 0,4 W/m2 schon in die richtige Größenordnung.
@Nico Baecker,
ihr Zitat am Montag, 21.05.2012, 18:45:
(…)
Wie jeder (gute) 8. Klässler ausrechnen kann, entspricht einer Zunahme des Wärmeinhaltes der oberen 2000m Weltmeer um 24 mal 10 hoch 22 Joule in 50 Jahren (das ist die Größenordnung des hier diskutierten und von ihnen bislang bezweifelten Anstiegs) einer Temperaturerhöhung von ca. 0,08 °C im Mittel, und dies wird durch eine Netto-Wärmeaufnahme von 24 W/m2 über diesen Zeitraum bewirkt. Soweit die physikalischen Trivialitäten. Können Sie dem nun folgen oder nicht?
–> ich würde gerne diese Rechnung verstehen können? ich setze mich gerade wegen einer Uniarbeit mit dem Paper auseinander. Ich verstehe wie Levitus aus den Messdaten (unabhänig jetzt mal der Quantität und Qualität!) den OHC wert berechnet, aber mit ihren weiteren Umrechnungen bin ich doch überfordert?
Würde mich sehr über eine detaillierte erklärende Rechnung von Ihnen freuen!
Vielen Dank im Voraus
mfg Patrick Wenz
Lieber Herr Weber,
„Wenn Sie nicht mehr behaupten, daß ausreichende Daten für einen Vergleich vorhanden sind reicht mir das völlig“
Nochmals. Ich behaupte gar nichts. Ich sehe nur das Levitus-paper und Ihre Behauptung, dass dieses paper fehlerhaft sei und man aus den Daten nicht die Graphik ableiten kann.
Und für diese Behauptung erwarte ich eine objektiv nachvollziehbare Argumentation. Mehr nicht. Sprüche, wie „meine Erfahrung sagt mir das“ reichen da nicht. Wer weiß, was für Erfahrungen Sie da glauben, anbringen zu können.
Lieber Herr Baecker
„Wenn Sie nicht mehr behaupten, daß ausreichende Daten für einen Vergleich vorhanden sind reicht mir das völlig“ Das restliche Gelaber können Sie sich schenken.
MfG
Michael Weber
Lieber Herr Weber,
„Wenn Sie nicht mehr behaupten, daß ausreichende Daten für einen Vergleich vorhanden sind reicht mir das völlig“
Sie haben es immer noch nicht begriffen. Sie sollen einfach nur Ihre Behauptung nachweisen, und die lautet, dass die Unsicherheitsbalken in der daraus abgeleiteten Graphik falsch sind. Sie werden doch noch Ihre Behauptung kennen?
Schoen, dass Sie mit Ihre Erfahrung beim Hausstreichen auch eine gewissen Urteilsfaehigkeit erworben haben. Das hat kaum was mit der Urteilsfaehigkeit fuer die hier gefragte Thematik zu tun.
Lieber Herr Baecker
Das Ablassen Kauderwelsch ist keine Diskussion und keine Wissenschaft. Es ist aber nett von Ihnen eine neue Demonstration Ihres Polit-Stils geliefert zu haben. Ich schrieb:“Wenn einer kommt und behauptet er könne mit 5 Litern Farbe ein Haus neu streichen können Sie meinetwegen die mitgelieferte Pigmentsverteilungsberechnung gerne unbesehen akzeptieren. Sie werden schon merken, daß es nicht funktioniert. Das brauch ich nicht nachrechnen.“ Ihre Antwort:“Wenn Sie meinen. Ist mir wurscht.“ sachliche Argumentation? Null! Aber immerhin leiten Sie den Rückzug ein:“Ich habe hier gar nicht zu belegen, da ich nichts zum Levitus-paper behaupte.“ Wenn Sie nicht mehr behaupten, daß ausreichende Daten für einen Vergleich vorhanden sind reicht mir das völlig. Danke für das Gespräch.
MfG
Michael Weber
Lieber Herr Weber, #132
„Sie machen wieder einen auf Wissenschaftskauderwelsch“
wir diskutieren nun mal wissenschaftliche Ergebnisse. Wenn Sie das nicht verstehen, Ihr Pech. Sie haben dann eben an sich zu arbeiten, um es zu verstehen.
„PS Wollten Sie nicht noch Ihren Rang/Dienstgrad bekannt geben?“
Nicht so formal. Bemühen Sie sich einfach, sachlich und themenbezogen zu diskutieren,folgen Sie meinen Hinweisen oder von anderen Naturwissenschaftlern und schließen Sie Ihre Wissenslücken. Dann ist es auch ein Bereicherung für mich, mich mit Ihnen zu unterhalten, und Sie „steigen in meinem Ansehen“ (das hatte ich etwas unpassend mit „Rang“ ausgedrückt), anstatt Sie ständig wieder aufs Thema zurückbringen zu müssen.
Wenn Sie lieber über Politik diskutieren wollen, so suchen Sie sich ein Thema, in dem man keine physikalischen Kenntnisse mitbringen muss, anstatt um Ihnen nicht vertrauten Begriffen herumzueiern, die aber jeder halbwegs gebildete Mensch innerhalb von 10 Minuten durch eine Recherche oder Frage an Experten klären könnte. Wenn Ihnen das Interesse fehlt, sich mit physikalisch-mathematischen Themen zu befassen, so geben Sie das einfach zu und versuchen Sie nicht in einem Thema mitzumischen, wo Sie sich nicht auskennen und wohl auch nicht ernsthaft wollen.
„Das brauch ich nicht nachrechnen.“
Wenn Sie meinen. Ist mir wurscht. Aber lassen Sie anderen die Freiheit, die Natur genauer zu untersuchen. Genauer hingucken, Vorurteile und Bauchgefühle zu objektivieren, das macht Wissenschaft eben aus.
„Dann belegen Sie mal, wie man ohne Messdaten valide Ergebnisse generiert.“
Nun machen Sie schon aus „erratisch wenig Messdaten“ den Begriff „ohne Messdaten“? Ich habe hier gar nicht zu belegen, da ich nichts zum Levitus-paper behaupte. Sie haben wissenschaftlich zu zeigen, dass Levitus nicht solide wissenschaftlich analysiert hat. Denn das behaupten Sie ja.
Lieber Herr Baecker
Sie machen wieder einen auf Wissenschaftskauderwelsch „Levitus‘ mathematisch-ozeanographische Argumentationskette “ klingt bedeutend ,sagt nichts. Politgelaber. Herr Levitus hat mangels Daten nichts zu sagen, was der Beschäftigung wert wäre. Wenn einer kommt und behauptet er könne mit 5 Litern Farbe ein Haus neu streichen können Sie meinetwegen die mitgelieferte Pigmentsverteilungsberechnung gerne unbesehen akzeptieren. Sie werden schon merken, daß es nicht funktioniert. Das brauch ich nicht nachrechnen.
„Wie gesagt, es reicht nicht, irgendwas zu behaupten, das kann jeder.“ O-Ton Baecker. Dann belegen Sie mal, wie man ohne Messdaten valide Ergebnisse generiert. Sie behaupten immer nur! (und nehmen Fakten wie Rassbachs BÄUME nicht wahr.) Ihr CO-2-Wunschdenken interessiert keinen.
Ihre politischen Manipulationsversuche allerdings sind zu entlarven bevor sie Schaden anrichten.
MfG
Michael Weber
PS Wollten Sie nicht noch Ihren Rang/Dienstgrad bekannt geben?
Lieber Herr Weber,
Zurück zum Thema.
„Das Fehlen einer aussagekräftigen Datengrundlage würde auch durch ein Physikstudium meinerseits nicht beseitigt.“
Sie glauben also, der Nachweis, dass Levitus‘ mathematisch-ozeanographische Argumentationskette zwischen den Messdaten und seinem Diagramm oben nicht korrekt ist, also die Unsicherheitsbalken im Diagramm nicht zu den Messdaten passen, alleine durch gesunden Menschenverstand und eben damit ohne eine adäquate mathematisch-ozeanographische Untersuchung geliefert werden kann?
Wie gesagt, es reicht nicht, irgendwas zu behaupten, das kann jeder.
Sie müssen eine objektiv nachvollziehbare Argumentationskette bringen, Ihr Wunschdenken interessiert keinen.
Wenn Sie das nicht können, so geben Sie dies fairerweise einfach zu. Ist ja kein Makel, es kann ja nicht jeder Alles können.
Lieber Herr Baecker
Wie vorausgesagt, haben Sie die Frage nach Ihrem
(selbst zugeteilten?) Rang/ Dienstgrad doch glatt vergessen. War zu erwarten. Da ist nichts.
Sie lenken halt gern ab, ganz wie ein richtiger Politiker. Von Politikern kennt jedermann den Gebrauch von Gefälligkeitsgutachten. Sie machen da keine Ausnahme. das macht die Arbeit von Levitus nicht besser, sondern eher durchsichtiger. Das Fehlen einer aussagekräftigen Datengrundlage würde auch durch ein Physikstudium meinerseits nicht beseitigt.
Sagt Ihr gesunder Menschenverstand etwas anderes?
Vermehren sich die Messdaten aus den Sechzigern mit der Anzahl der absolvierten Semester? Nein! Ausser bei Ihnen vielleicht, dann aber wieder aus politischen Gründen. Die edle Mischung aus Politik und Wissenschaft, die Sie hier zu verkaufen suchen ist ungeniessbar. Aber Ihre Ablenkungsmanöver sind spassig. Die Lizenz zum kritischen Fragen von einem Studium abhängig zu machen, echt Baecker, richtig witzig.
MfG
Michael Weber
Lieber Hrr Weber,
besorgen Sie sich ein paar Schulphysikbuecher, Hochschulbuecher der Physik und zum Schluss arbeiten Sie das Lehrbuch von Peioxto/Oort
physics of climate durch. Wenn Sie das alles kapiert haben, formulieren Sie Ihre Frage entsprechend Fachorientiert. Bis dahin muessen Sie eben damit leben, dass Sie nicht wissen, worum es bei Levitus geht.
Lieber Herr Baecker
„Das ist wirklich keine Rangentsprechende Taetigkeit.“ Sie haben einen Rang? Womöglich noch einen Dienstgrad? Die sollten Sie hier schleunigst bekanntgeben, damit ich Sie rangordnungsmässig ordentlich respektieren kann.
Bis dahin sind Sie für mich ein politischer Rosstäuscher, der versucht mit wissenschaftsähnlicher Rhetorik Reklame für seine CO-2-These zu machen. Ich attestiere Ihnen gerne eine hohe Begabung, Fragen auszuweichen, die Ihre These widerlegen könnten. Das werden Sie jetzt gleich mit der Frage nach Ihrem Rang demonstrieren. Auf gehts!
MfG
Michael Weber
Herr Weber,
da habe ich ja Glueck gehabt, ich hatte ueberlegt,ob dieser Satz nicht zu banal ist, aber fuer Sie war es die Spitze der intellektuellen Herausforderung. Dann war der Rest ja offensichtlich fuer Sie intellektuell zu anspruchsvoll, tja, wer sich nicht angespornt fuehlt, bleibt eben da, wo er ist, naemlich in der Ecke derjenigen, denen man nicht zuhoeren braucht.
„Je mehr, desto aussagekräftiger der Vergleich.“
Schoen, dass Sie wenigstens das von mir mittlerweile gelernt haben. Immerhin wissen Sie jetzt, in welche Richtung Ihrer Aufgabe geht. Nur quantfizieren muessen Sie nun diese Abhaengigkeit noch…
“ Herr Levitus hat keine Messungen er nimmt
dafür Berechnungen.“
Wo steht das? Er hat doch wohl die Messungen genommen, die in dem Datensatz zu sehen sind.
Wenn Sie den Rest meines Letzten Textes verstanden haetten, so wuessten Sie, wie es geht. Aber Sie sind in Physik so untergebildet, dass ich es mir nicht vorstellen kann. Und abgeben moechte sich mich mit solchen Nullnummern auch nicht. Das ist wirklich keine Rangentsprechende Taetigkeit.
Lieber Herr Baecker
„Kurzum: Messungen und Berechnungen sind nicht „ein und dasselbe“,…“ Ich bin erstaunt, Sie können kurze und prägnante Sätze? Bravo! Dann geht das Geschwurbel leider wieder los. Wenn Sie Messungen in 2000m Tiefe vergleichen wollen,brauchen Sie Messungen. Je mehr, desto aussagekräftiger der Vergleich. Herr Levitus hat keine Messungen er nimmt dafür Berechnungen.
So kommt er zu seinem Ergebnis, einem AGW-Wunschergebnis. Er misst nicht 1 l Leitungswasser in 2000m Tiefe, er misst garnicht.“(basierend auf dem Theorietest an Leitungswasser)“ Welche Theorie über Wassertemperaturen im Ozean ist denn da im Spiel? An welchen Leitungswassertemperaturen wurde Sie getestet? Am Bodensee sicher nicht,obwohl der durch Stuttgarter Wasserhähne fliesst. Sie versuchen mal wieder Pseudo-Wissenschaft als Wissenschaft zu verkaufen, mit selbstgebastelten Daten! Das nennt man Computerspielerei. Sie selber haben doch die Links geliefert, in denen die äusserst dürftige Datenlage exakt belegt ist. Kann jeder selber nachgucken. Danke für Ihre Hilfe!
MfG
Michael Weber
Lieber Herr Weber, #123
„Sie dürfen gerne erklären, warum Sie Messungen und Berechnungen für ein und dasselbe halten, dass man sie ohne weiteres vergleichen kann“
Ich versuche mal trotz der suggestiven Anfrage, darauf zu antworten. Sie wissen also nicht, dass die Physik nicht mehr und nicht weniger macht als Messungen mit Berechnungen zu vergleichen?
Die Messungen bekommt man empirisch durchs Experiment und Beobachtungen, die berechneten Werte durch eine Theorie. Die Theorie wird aus den Messungen von anderen Experimenten gewonnen und aus einem Modell, wie der untersuchte Effekt quantitativ zu erklären sei. Da Messungen nie exakt sind, und eine Theorie immer eine Approximation an die Messungen ist, wird es NIE passieren, dass Messergebnisse mit theoretisch berechneten exakt (!) übereinstimmen. Es wird immer Differenzen geben. Einmal sind es die bekannten aufgrund des approximativen Charakters jeder Theorie. Das läßt sich prüfen anhand der Genauigkeitsgrenzen der Theorie, die aufgrund der zugrundeliegenden (anderen) Messungen bekannt sich. Dem überlagert sind zufällige Messfehler, die mit Fehlerrechnung zu klären sind, dann gibt es noch systematische Fehler in der Messung, die zu klären sind. Wenn nun aber die Abweichungen nicht durch dies Ursachen erklärbar sind, so ist dies ein Hinweis, dass die Theorie in dem vorliegenden Experiment nicht passt, erweitert werden muss oder sogar durch eine umfangreichere ersetzt werden muss.
Vielleicht war diese Einführung in die Physik schon zu viel für Sie. Aber Sie müssen das einfach akzeptieren. Dazu gibt es nur die Alternative, das Zeitalter der Aufklärung abzuschaffen ,-)
Kurzum: Messungen und Berechnungen sind nicht „ein und dasselbe“, das haben Sie falsch verstanden.
Beides ist nötig, denn es gibt keine Wissenschaft nur aus empirischen Messungen ohne Theorie. Und erst recht nicht in der Physik, bei mit der Theorie der Wert von Größen berechnet wird und mit dem Messwert der Größe verglichen wird.
Nun wird es ein bisschen komplizierter, denn es gibt nun mal Größen, die interessant sind, aber nicht direkt gemessen werden können. Zum Beispiel hat niemand unsere Erde auf die Waage gelegt, oder das Wasservolumen des Weltmeeres in eine Messglas gekippt. Wenn Sie nun meinen, dass für diese Fälle, in denen man die gefragte Größe nicht direkt messen kann, diese Größe auch nicht angebbar ist, also wir dann auch nicht wissen können, wie schwer die Erde ist, dann ist das Ihr Glaube. Die Physik sieht dies anders, denn da wird es erst richtig spannend, denn man hat nun empirisch an einigen experimentell getestete Theorien und die kann dann aussagen, was bei nicht durchführbaren Experimenten rauskommen müsste (z.B. Erde auf die Waage). Das ist natürlich etwas gewagt, aber im konkreten Falle der Bestimmung des Wärmeinhalts des Meereswassers besteht kein Grund, warum ein Liter Meereswasser in 2000 m Tiefe sich physikalisch unbekannt verhalten würde und von einem Liter Leitungswasser so grundlegend verschieden wäre, dass das unmessbare empirische Ergebnis um mehr als 5% vom berechneten theoretischen Ergebnis (basierend auf dem Theorietest an Leitungswasser) abweichen sollte.
Lieber Herr Weber, #123
„Und prompt fangen Sie wieder an zu philosophieren was mir klar ist und was ich wohl glaube.“
Also, Sie verstehen nur Bahnhof. Tut mir leid für Sie, dass Sie hier nicht mitreden können und offenbar auch nichts daran ändern wollen. Aber zur Wissenschaft kann man ja niemanden zwingen.
Lieber Herr Baecker
„Sie dürfen gerne erklären, warum Sie Messungen und Berechnungen für ein und dasselbe halten, dass man sie ohne weiteres vergleichen kann“ Und prompt fangen Sie wieder an zu philosophieren was mir klar ist und was ich wohl glaube. Das tut überhaupt nichts zur Sache. Zurück auf Los.
MfG
Michael Weber
Lieber Herr Weber,
„Sie dürfen gerne erklären, warum Sie Messungen und Berechnungen für ein und dasselbe halten, dass man sie ohne weiteres vergleichen kann“
Wir sind wieder am Anfang bzw. haben nicht mal angefangen.
Ihnen ist nicht klar, dass Physik darin besteht, aus empirischen Messungen physikalische Größen zu berechnen!
Hat mein Beispiel „Freier Fall“ nicht geholfen? Da wurde aus Zeit- und Wegmessungen die Fallbeschleunigung BERECHNET!
Sie glauben wohl, dass die Wert für die 60iger ohne empirische Daten rein „ins Blaue“ berechnet wurden? Beweisen Sie das.
Ich gehe davon aus, dass Levitus seine Ergebnisse mit den „erratisch vorhandenen“ Messdaten verglichen hat und die Ungenauigkeitsbalken daher rühren, dass der Vergleich zwischen Berechnung und Messung wegen der Datenlücken nicht flächendeckend erfolgen kann. Die Unsicherheitsbalken spielen die Unprüfbarkeit der Temperaturvereilung der nicht vermessenen Gebiete wider.
„Sie sind der Einzige der weiss wie Wissenschaft funktioniert. “
zumindest unter uns zweien und was die Naturwissenschaften angeht!
„Im konkreten Fall bejammern Sie eine Behauptung, die mit von Ihnen persönlich geliefertem Material belegt ist. “
Sie haben gar nichts, außer aus der Hüfte geschossen behauptet „reicht nicht“!
Da Sie nicht wissen, wie die Daten mit dem Diagramm von Levitus überhaupt zusammenhängen, ist Ihre Behauptung unbegründet und unsachlich.
Lieber Herr Baecker
Ich weiss, ich weiss, Sie sind der Einzige der weiss wie Wissenschaft funktioniert. Heureka, das baeckerzentrische Weltbild ist gefunden. Spass beiseit:“kann man IMMER behaupten“ Falls etwas behauptet wird kann es belegt oder widerlegt werden. Im konkreten Fall bejammern Sie eine Behauptung, die mit von Ihnen persönlich geliefertem Material belegt ist. Als Wissenschaftler müssten Sie dieses Material prüfen und bewerten und ggf widerlegen. Machen Sie nicht. Als guter AGW-Politiker verlegen Sie sich aufs Jammern, Denkvorschriften erlassen und billige persönliche Diffamierung.Dazu passend O-Ton Baecker“Sie haben bisher nichts geliefert, das annähernd zum Start einer sachlichen Diskussion reichen würde“ Den Stiefel dürfen Sie sich anziehen. Sie dürfen gerne erklären, warum Sie Messungen und Berechnungen für ein und dasselbe halten, dass man sie ohne weiteres vergleichen kann. Eine wissenschaftlich einwandfreie Erklärung haben Sie ja bestimmt in petto.
MfG
Michael Weber
Herr Weber,
Gucken Sie mal im Buch „Physics of climate“ von Peixoto/Oort 192 nach, wie man den Waermeinhalt des Weltmeeres bestimmt, da gibt in ch8 auch ein paar Abb ueber die Variabilitaet der Ozeantemperaturen mit der Tiefe, nur mal, um einen Eindruck zu bekommen, was so im Meer los ist.
Lieber Herr Weber, #118
ein wissenschaftliches paper kann man nur dann wissenschaftlich bewerten, wenn man sich damit sachgerecht auseinandergesetzt und alles verstanden hat. Wenn Levitus einer Methodik folgt, die Ihrer widerspricht oder nach Ihrer Sicht Mängel aufweist, so müssen Sie dies begründen und konkret zeigen, was im paper Ihrer Meinung nach falsch ist, wenn Sie mitreden wollen. Wenn Sie glauben, dass „eine Langzeitbeobachtung des Wärmeinhaltes von grösseren Gewässern durch Messungen“ oder „Kalibrierung“ notwendig seien oder nicht ausreichend genau bei Levitus durchgeführt wurden, wie dies in seinen Unsicherheitsbändern abgebildet ist, so müssen Sie erklären, was fehlt oder mangelhaft ist.
Das einzige, was Sie bislang von sich gegeben haben (ob selber erdacht oder von irgendwelchen Bekannten gehört) ist, dass die Daten nicht ausreichen. Das zu behaupten, erfordert keinerlei Nachdenken, das kann man IMMER behaupten. Für solche Sprüche muss man nicht mal wissen, worum es geht.
Also nochmal: Wissenschaft entsteht nicht aus dem Austausch von irgendwelchen Sprüchen, geheimen Unterredungen mit irgendwelchen Helfern im Hintergrund oder Bauchgefühle über die Anzahl notwendiger Datenmengen, sondern durch Argumente, Fakten und Methoden, die offen auf den Tisch gelegt werden. Sie haben bisher nichts geliefert, das annähernd zum Start einer sachlichen Diskussion reichen würde, und so wie es aussieht, ist Ihnen nicht mal bewußt, wie naturwissenschaftiche Forschung funktioniert.
Lieber Herr Baecker
Machen Sie sich mal um meine Person keine Gedanken, ich kann mir in meiner Uni-Stadt alles nötige know-how organisieren. Meine Helfer haben mich darauf hingewiesen, daß eine Langzeitbeobachtung des Wärmeinhaltes von grösseren Gewässern durch Messungen nicht vorliegt. Sie konnten nicht widersprechen, haben abgelenkt bis zur Dogmatik(sachgerecht?) und das Thema Kalibrierung unter ihren Tisch fallen lassen. Die erschütternd geringe Anzahl von Messungen aus dem letzten Jahrhundert, die Sie per Link beigebracht haben hat meine Helfer abwinken lassen: Lohnt nicht, kann nichts Vernünftiges rauskommen. Das ist Stand der Dinge. Herr Levitus macht genau wie Sie wissenschaftlich verbrämte AGW-Propaganda. Den geneigten Mitlesern wird nicht entgehen wie Sie nach Politikerart unangenehmen Fragen aus dem Weg gehen. Auch nicht, daß Sie nichts Vorzeigbares für die Wissenschaft getan haben,die Sie dauernd im Munde führen. Ihre Propaganda ist wertlos.
MfG
Michael Weber
Lieber Herr Weber,
fassen wir also mal zusammen: Herr Weber will unbedingt bei einer wissenschaftlchen Frage, zu deren Beantwortung man zumindest mal die Fehlerrechunung beherrschen muesste, mathematische Faehigkeiten zur Kartierung von verteilten Messdaten und den physikalischen Zusammenhang zwischen Waermeinhalt und Temperatur und anderen physikalischen Parametern von Meerwasser kennen muesste, mitreden. Kann er ja, aber was interessiert seine Meinung, wenn er nicht mal zeigen kann, wie man die infrage gestellte Groesse Waermeinhalt bestimmt, noch wie man seine Genauigkeit aus den verfuegbaren Daten bestimmt?
Ihre Meinung sei Ihnen gegoent, aber sie ist unnuetz, Informationsgehalt gleich Null! Ihre Faehigkeit zur Urteilsbildung demostrieren Sie damit doch selber.
Machen Sie sich mal um meine Person keine Gedanken, liefern Sie einfach zur Sache Levitus, so stehts auch in den Eike-Regeln.
Noch ein tip: Sie koennen auch sachlich erklaeren, warum man Ihrer Meinung nach keine Ahnung von Fehlerrechnung oder Physik, oder Mathematik zur Wissenschaftlichen Beantwortung Ihrer Zweifel an der Levitusanalyse braeuchte.
Lieber Herr Baecker
Respekt muss man sich verdienen. Das haben Sie gründlich versäumt. Beantwortet das Ihre Frage? Sie können sich einbilden, daß Sie berechtigt sind das Denken anderer nach Ihrem Belieben zu steuern und sich so auch aufführen. Nur interessiert das niemand. Sie haben hier noch keine eigene wissenschaftliche Leistung vorgelegt, worauf beruht denn Ihre angemaßte „Autorität“? Vor lauter politischem Eifer verwechseln Sie Themen( „da wir ueber die Physik der Atmosphaere diskutieren, bin ich als Physiker“ – leseunfähig- es geht um die Meerestemperatur!), bestreiten Mitlesern die eigene Urteilsfähigkeit („Na eben nicht!“) ohne sich zu entschuldigen, lenken von zentralen Themen ab ( Levitus hat keine gemessenen Daten, CO-2 folgt der Erwärmung, weder Temperatur noch Meeresspiegel noch hot spots folgen der von Ihnen vertretenen CO-2-These). Politiker, die sich hinter „der Wissenschaft“ oder hinter „Brüssel“ verstecken um unauffällig ihr Süppchen zu kochen, nehme ich nur als Gefahr für die FDGO ernst. Deswegen reagiere ich auf Ihren Propagandafirlefanz wie man auf Polit-Clowns reagieren muss um böse Überraschungen zu vermeiden.
MfG
Michael Weber
Lieber Herr Weber,
was berechtigt Sie, meine Antwort nicht zu respektieren? Die Urteilsfaehigkeit ergibt sich einzig daraus, was zur Sache abgeliefert wird. Wenn penetrant unsachlich argumentiert wird, so mag mangelnde Urteilsfaehigkeit in der Sache die Ursache sein.
Wenn Sie nicht wissen, was Sie jetzt zur wissenschaftlichen Bewertung von Levitus Analyse zu tun haben, Pech fuer Sie. Urteilsfaehigkeit kann man nicht fordern, sondern muss sie aus eigener Kraft erwerben.
Lieber Herr Baecker
„Ich bestreite die Urteilsfähigkeit anderer a priori gar nicht.“ Stimmt. Sie pflegen die Urteilsfähigkeit erst dann anzugreifen, wenn sie zu anderen Schlüssen kommt als Sie selber. A priori ist jeder urteilsfähig, der Ihre Meinung vertritt. Ein seltsames Kriterium. Deswegen frage ich schon wieder: „WAS berechtigt ausgerechnet Sie, anderen die Urteilsfähigkeit zu bestreiten?“ Eigene wissenschaftliche Leistung haben Sie hier noch nicht vorgezeigt. Sie versuchen nur CO-2-Politik mit Geschwafel als wissenschaftlich zu verkaufen. Kann jeder in Ihren Beiträgen nachlesen. Rhetorische Tricks, wie tatsächlich nicht vorhandene Daten (siehe Ihr Link oben) als Bauchgefühl abzutun, unterstreichen ihre politischen Ambitionen. Das Fehlen von gemessenen Daten ist harter wissenschaftlicher Fakt. Dass Herr Levitus beansprucht mit von ihm selbst generierten Daten „Vergleiche“ durchführen zu können ist der grundlegende Fehler. Zumal er, wie Sie durch Schweigen selbst zugeben über kein gemessenes
Vergleichsmodell aus irgendeinem Ozean dieser Erde verfügt. Noch nicht einmal aus einem grösseren See. Aber wenn Sie unbedingt Zahlen brauchen, ich hätt da eine:“42″!
MfG
Michael Weber
Herr Weber,
„Was berechtigt ausgerechnet Sie, anderen die Urteilsfähigkeit zu bestreiten“ war meine Frage,“
Ich bestreite die Urteilsfähigkeit anderer a priori gar nicht. Zu unserer Sachdiskussion:
Wenn Sie nach mehrmaligem Erklären immer noch nicht imstande sind, Ihre Behauptung mit adäquaten Fakten zu belegen, kommen mir Zweifel an Ihren fachlichen notwendigen Kenntnissen. Denn Bauchgefühl („erratische Datenlage“ etc.) ist kein Mittel, um ein Urteil zu finden, wenn die kritisierte Position klar definiert als Graphik vorliegt. Oben sehen Sie Levitus Genauigkeitsangaben quantifiziert. Sie können darüber nur urteilen, wenn Sie zeigen, dass genau diese Genauigkeitsangaben falsch sind. Da gibt es kein Drumherumgesülze, die Aufgabenstellung für ein objektives Urteil ist klar definiert und in welcher Form das Ergebnis zu sein hat ebenfalls, nämlich in Form von Zahlen.
Lieber Herr Baecker
Aber sonst sind Sie gesund?:“da wir ueber die Physik der Atmosphaere diskutieren,…“ Irrtum Ihrerseits, gucken Sie mal oben, es geht um die Meerestemperatur! Soviel zur Genauigkeit eines Physikers, der fachlich weit überlegen sein will. Einbildung ist auch eine Bildung, pflegte meine Großmutter zu sagen. Ihr Geschwätz über „Universitaeten abschaffen“,“ uretislfaehigkeiten(?) sozialisieren“,“Das hohe Gut der freien Meinungsaesserung bedeutet nicht, dass alle Meinungen qualitativ gleich sind und gleich zu beachten sind“ ist auch für Aussenstehende leicht von Physik zu unterscheiden und als politisches Gelaber einzuordnen. Auch nach wissenschaftlichen Kriterien feinster Art. Falls Sie sich einbilden fachliche Überlegenheit mache sozial und moralisch kompetenter unterliegen Sie auch hier einem Irrtum.“Was berechtigt ausgerechnet Sie, anderen die Urteilsfähigkeit zu bestreiten“ war meine Frage, bezogen auf die Ihnen und mir unbekannten Mitleser. Sie bleiben die Antwort schuldig, kann wieder jeder mitlesen und sich ein eigenes Urteil bilden.
MfG
Michael Weber
Herr Weber,
„Jeder Mitleser kann selbst entscheiden ob er das für Wissenschaft oder politisches Geschwätz hält“
Na eben nicht! Wissenschaft kann man nur mit wissenschaftlicher Denkweisen und Methoden bewerten.“
Wonach beurtei
en Sie denn Wissenschaft, wenn nicht nach wissenschaftlichen Kriterien? Wozu braechte man Wissenschaft, wenn man ihre Aussagen willkuerlich beurteilen wollte?
Lieber Herr Weber,
da wir ueber die Physik der Atmosphaere diskutieren, bin ich als Physiker gegenueber einem Theologen, dem Dogmatik eingetrichtert wurde, fachlich eben weit ueberlegen.
Lieber Herr Baecker
Meine Frage:“Was berechtigt ausgerechnet Sie, anderen die Urteilsfähigkeit zu bestreiten?“ ist mit Ihrem nebulösen Politerguss #108 nicht beantwortet. Das Gelaber über “
Universitaeten abschaffen“,“ uretislfaehigkeiten(?) sozialisieren“,“Das hohe Gut der freien Meinungsaesserung bedeutet nicht, dass alle Meinungen qualitativ gleich sind und gleich zu beachten sind“ soll nur von der Frage ablenken. So schön haben Sie Ihren Politikerstil schon lange nicht mehr demonstriert.Aber zurück zur Frage:““Was berechtigt ausgerechnet Sie, anderen die Urteilsfähigkeit zu bestreiten“ Die Mitleser warten auf eine Antwort!
MfG
Michael Weber
Lieber Herr Weber,
„Was berechtigt ausgerechnet Sie, anderen die Urteilsfähigkeit zu bestreiten“
Wenn Sie meinen, dass eine Hochschulausbildung in einem Fachgebiet keine treffsichere Urteilsfaehigkeit in diesem Gebiet foerdert, koennen wir ja die Universitaeten abschaffen und uretislfaehigkeiten sozialisieren, wollten die
Roten Khmer auch. Das hohe Gut der freien Meinungsaesserung, das in diesem Staat zumindest auf dem Papier garantiert ist, bedeutet nicht, dass alle Meinungen qualitativ gleich sind und gleich zu beachten sind. Oder wollen Sie uener wissenschaftliche Ergebnisse per Volksentscheid abstimmen? So ein Schwachsinn.
Bravo.Herr Baecker
Mit dem „Na eben nicht!“ sprechen Sie sämtlichen Mitlesern ihre persönliche Urteilsfähigkeit ab,die ich mit „Jeder Mitleser kann selbst entscheiden ob er das für Wissenschaft oder politisches Geschwätz hält“ als gegeben voraussetze. Für jemand, der keine einzige eigene wissenschaftliche Leistung vorzeigen kann, nehmen Sie das Maul ziemlich voll. Was berechtigt ausgerechnet Sie, anderen die Urteilsfähigkeit zu bestreiten? Kommen Sie mal runter von Ihrem hohen Ross und entschuldigen Sie sich bei den Mitlesern.
MfG
Michael Weber
Lieber Herr Weber,
„Jeder Mitleser kann selbst entscheiden ob er das für Wissenschaft oder politisches Geschwätz hält“
Na eben nicht! Wissenschaft kann man nur mit wissenschaftlicher Denkweisen und Methoden bewerten.
Lieber Herr Baecker
Richtig vermutet. Ihre gesammelten abwertenden Vermutungen und Unterstellungen gehen mir am Allerwertesten vorbei. Jeder Mitleser kann selbst entscheiden ob er das für Wissenschaft oder politisches Geschwätz hält. Ihre Technik, abstruse Vorstellungen in meinem Namen zu verkünden und dann glanzvoll zu widerlegen, ist allzu durchsichtig. Die Propaganda-Arbeit des Herrn Levitus beruht auf Annahmen, die als Fakten verwendet werden. Ausser ARGO ist mir kein Programm geläufig das Messdaten für eine einigermassen genaue Bestimmung des Heat contents sammelt. Meine Vermutung,daß kein einziges grösseres Gewässer über Jahre auf seinen heat content untersucht wurde, der ja eine variable Grösse darstellt, wird durch Ihr lautes Schweigen zu diesem Punkt bestätigt. Keine
Untersuchungen , keine Messungen – nada,nichts! Aus diesem Nichts zaubert Levitus einen 99,99% genauen Vergleich. Wers glaubt wird selig. Ist aber nur auf einen Genauigkeitssimulanten hereingefallen.
MfG
Michael Weber
hallo Herr Baecker,
die Antwort auf Ihre Frage steht schon in #92
Wenn die Klimamodelle eine Erwärmung von 0,01°C errechnen, so müssen die Messungen schon verdammt genau sein, um das zu bestätigen.
Wie schon gesagt diese sehr genaue Argo-Messung konnte das seit 2003 NICHT.
Über die Vergangenheit davor kann man nur spekulieren. Nun leugnen „Klimaleugner“ ja nicht das Klima,
noch nicht einmal eine Erwärmung, eher schon die Existenz eines „Treibhauseffektes“, mehr noch dass eine Erwärmung oder CO2 schädlich wäre,
und noch viel heftiger, dass der Mensch etwas daran ändern könnte, oder gar „daran Schuld“ sei.
Levitus strickt an diesem Märchen mit, das reicht!
In dem Beitrag geht es schlicht darum, dass man mit der Märchenerzählerei endlich aufhören soll
und aus diesem unwirklichen Hollywood- gruselszenarium schneunings den Weg zurück in die Realität findet.
Gruß
Lieber Herr Weber,
was haben Sie eigentlich? Sie behaupten einfach, Levitus habe Fehler gemacht oder haette gefaelscht und fuehlen sich nicht mal aufgefordert, Ihre Behauptungen zu belegen, nicht mal das paper haben Sie gelesen. Sie machen sich nicht mal die Muehe, sich ein eigenes Bild zu machen und die Originalarbeit zu lesen. Stattdessen uebernehmen Sie schnurstracks Eschenbachs Aeusserungen und fuehlen sich bestaerkt, Eschenbachs Andeutungen noch durch Verdaechtigungen zu verstaerken.
Ich frage jetzt mal etwas anderes: glauben Sie, dass man mit Hilfe der Argomessungen die mittlere Ozeantemperatur wenigstens mit der Genauigkeit angeben kann, welche Levitus fuer die 60 iger Jahre angibt, also auf Basis der von Ihnen als „erratisch“ bezeichneten Datenlage?
„Daher sind die Berechnungen zwar machbar aber eben nicht in der Realität überprüfbar.“
Ich scheine an Ihnen vorbeizureden. Sie haben wirklich immer noch nicht den Punkt verstanden, erzaehlen Sie mal, wie man dies denn ueberpruefen koennte, hm?
Ich wette da kommt jetzt nichts, ausser die Aussage, dass es durch Temperaturmessungen und Berechnung nicht geht. Tja, Herr Weber, Sie haben eben in der Schule nicht aufgepasst, wie Physik geht. Ich habe Ihr Defizit schon weiter oben mal vermutet, Sie scheinen wirklich zu glauben, dass nur das real gemessen wird, was unmittelbar auf einem Messinstrument abzulesen ist, stimmts?
Lieber Herr Baecker
Wer primitivsten wissenschaftlichen Ansprüchen in Sachen Fehlerkorrektur nicht entspricht macht sich nur lächerlich, wenn er „Aufgaben“ verteilt, die „den Anspruechen wissenschaftlicher Argumentationen genuegen“ sollen. Führung durch Beispiel hab ich mal als OA gelernt. Ihr politisches Motto (Was ich von anderen verlange, brauche ich selber nicht einzuhalten) entlarvt Sie als Propagandisten, der auf Wissenschaftler macht. Die Fakten sind eindeutig: Ganz offensichtlich ist der Wärmeinhalt eines grösseren Gewässers noch nie durch Messungen über einen klimarelevanten Zeitraum verfolgt worden. Daher sind die Berechnungen zwar machbar aber eben nicht in der Realität überprüfbar. Sie gauckeln hier eine Natur vor, die sich durch Berechnung auf 0,001% genau bestimmen lässt. Wobei als Vergleichsgrundlage wiederum virtuelle Daten verwendet werden, die, weil sie ja auf Wissenschaftler machen, angeblich den physikalischen Gesetzen gehorchen. Das ist aber keine Qualifikation, denn die ganze Natur funktioniert nach der Physik und das lässt sich messen! Falsche Berechnungen werden von der Physik der Natur ignoriert und lassen sich nicht messen.(z.B. Hot spots)Die Propagandaarbeit von Levitus ist wertlos, weil sie auf Messungen weitgehend verzichten muss. Davon können Sie nicht ablenken.
MfG
Michael Weber
Lieber Herr Weber,
ich gehe davon aus, dass mittlerweile jeder weiss, dass ich ein „n“ vergessen habe. Ich erwarte von Ihnen also quaNtitative Zusammenhaenge, die den Anspruechen wissenschaftlicher Argumentationen genuegen, mit denne Sie versuchen, Ihre Behauptung „ohne ausreichende Messungen für seine Berechnungen“ beweisen. Also nochmal die Aufgabe an Sie, sie haben zu quantifizieren, dass Ihr Begriff „ohne ausreichend“, „erratisch“ oder sonstige nicht allgemein definierte Bewertungsmasse im Widerspruch stehen zu Levitus Fehlerbalken in den Waermegehaltszahlen.
Lieber Herr Baecker
Das mit dem Lesen klappt noch nicht: Auf meine Frage: „Den Begriff „quatitative(r) Zusammenhang “ habe ich in der Physik der Mittelstufe tatsächlich nicht mitbekommen. Den dürfen Sie mir gerne erklären.“ kommt von Ihnen alles mögliche (Vermutungen,Unterstellungen) aber keine sachliche Erklärung. So richtig nach Politikerart.( Frag nach der Uhrzeit und Du bekommst den Weg zum Bahnhof erklärt, wo Du nicht hinwillst, aber nach Meinung des Politikers hinsollst)Zur Sache stellen Sie nur Behauptungen auf, bislang sehe ich keine Fakten.
Halt doch: Sie geben zu, daß die messtechnische Bestimmung der Wärme-Volumina von grösseren Gewässern nicht existiert. Aber Levitus nimmt gleich das Weltmeer in Angriff-ohne ausreichende Messungen für seine Berechnungen. ARGO( Beginn valider Messungen 2003) lässt noch keine klimarelevanten Aussagen zu ( und zeigt eine Abkühlung) Auf den Rest Ihres Geschwalles lohnt sich nicht einzugehen. Politikerfloskeln waren selten so unüberzeugend. Stecken Sie sie am besten an den Hut zu den errechneten 24W/m2. Sie schmücken ungemein.
MfG
Michael Weber
Lieber Herr Weber, #97
„Ein Wissenschaftler pflegt seine Fehler zu korrigieren. Sie haben das nicht nötig, also können Sie nicht zu dieser Kategorie gehören.“
Dazu ist erst mal notwendig, dass man etwas als falsch identifiziert hat, richtig? Bislang sehe ich keine Fakten, sondern nur den Wunsch von Ihnen, dass die Levitus Analyse falsch ist.
„Der Punkt ist nach wie vor: Herr Levitus hat keine Vergleichsgrundlage, weil keine vergleichbaren Messdaten vorliegen.“
Ok, Sie bekommen es also ohne meine Hilfe nicht hin, den Vergleich mit dem Schulversuch auf die Levitusanalyse zu übertragen. Beide haben gemein, dass man auf punktweise vorliegenden Messungen (Schulversuch: ein paar Fallhöhen, Levitus: verstreute Temperaturmessungen im Meer) eine kontinuierliche Kurve (aus überabzählbar unendlich vielen Punkten auf der Menge der reellen Zahlen) ableitet (Schulversuch: Fallparabel, Levitus: Kartierung der Temperaturänderungsverteilung im Meer) und aus dieser wiederum durch mathematische Operationen abgeleitete Werte (Schulversuch: Fallbeschleunigung durch zweimaliges Differenzieren und einer Multiplikation mit 2, Levitus: volumenspezifische Änderung der Wärmemenge durch Multiplikation der kartierten Temperaturänderung im Volumen mit der Wasserdichte dort und der spezifischen Wärmekapazität vom Wasser und anschließender Integration über das Volumen des Weltmeeres).
Da Sie sich nun beharrlich weigern, Ihre unspezifische „Fundamentalkritik“ auf den konkreten Fall der Levitus-Auswertung anzuwenden, gehe ich davon aus, dass Sie von der unbedingten Validität dieser Kritik ausgehen, denn sonst hätten sie ja spezifische Bedingungen angegeben, zumal ich Sie dazu aufgefordert habe. Da es auch keine spezifischen gibt, muss Ihre Kritik also auch auf anderen Fälle wie eben beispielhaft auf den Schulversuch angewandt werden können (es sei denn, Sie erklären sich noch und konkretisieren Ihre Kritik durch Angabe physikalisch-mathematischer Gründe für den Fall Levitus) .
Sie behaupten also, dass man aus punktweise verstreuten Daten (diese Voraussetzung trifft in beiden Fällen zu) generell (es wurden ja keine spezifische Voraussetzungen genannt) keine kontinuierlichen Verteilungen ableiten darf und aus diesen per mathematischen Operationen (diese Voraussetzung treffen ebenfalls in beiden Fällen zu) keine anderen physikalische Größen ableiten darf.
M.a.W. dadurch, dass Sie es offenbar nicht für nötig halten, Ihre Kritik auf den Fall Levitus zu spezifizieren, hebeln Sie quasi die gesamte Physik aus. Denn das Verfahren, punktweise zu messen, eine Kurve daraus ableiten, daraus deren mathematische Gesetzmäßigkeit zu identifizieren und anhand dieser Gleichung weitere physikalische Größen zu quantifizieren, ist nun eine durchaus typische Vorgehensweise der Physik.
„Die hat er sich passend zum erwünschten Ergebnis errechnet(!).“
Nun, dass man in der Physik generell rechnet, haben auch Sie hoffentlich mal mitbekommen. Finden Sie nun das Rechnen ansich nun frevelhaft, oder Ihre noch von Ihnen zu beweisende Behauptung, er hätte das Ergebnis getuned, also eine Fälschung vorliegt?
„Fakt scheint auch zu sein, daß kein einziges grösseres Gewässer messtechisch auf seinen heat content untersucht wurde“
Was sollte das Fehlen oder Vorhandensein solcher Messungen zur Klärung Ihrer Vorwürfe betragen?
Falls Sie es immer noch nicht verstanden haben: es gibt kein Messgerät zur unmittelbaren Ermittlung des Wärmeinhaltes von Wasser, was in der Ozeanographie oder Limnologie eingesetzt würde. Den Wärmeinhalt bestimmt man immer über die Bestimmung der Temperatur und anderer Größen, die Einfluß auf die Wärmekapazität von Wasser haben. Erst recht kann man logischerweise den Wärmeinhalt der Gesamtwassermenge nicht direkt messen, denn so große Messgeräte gibt es nicht 😉
#94
„Also können Sie sich die errechneten 24 W/m2 an den Hut stecken.“
Nicht mal diesen Zusammenhang können Sie nachvollziehen, sondern schwelgen wieder in Gefühlsduseleien. Dabei steht doch eigentlich (bis auf triviale Konstanten, deren Identifizierung ich Ihnen als Übung überlassen. Wenn Sie es nicht schaffen, erkläre ich es Ihnen auch, aber Sie werden nicht mal fragen, weil sie es ja gar nicht wissen wollen..) alles da.
@#97
„Klimgt wie „quatitativ“ und sagt genauso wenig.“
Man könnte meinen, dass hier bei einigen die „N“-Taste kaputt ist.
Lieber Herr Baecker
Ein Wissenschaftler pflegt seine Fehler zu korrigieren. Sie haben das nicht nötig, also können Sie nicht zu dieser Kategorie gehören. Das erklärt Ihr sinnfreies Geschwalle über Schulversuche. Der Punkt ist nach wie vor: Herr Levitus hat keine Vergleichsgrundlage, weil keine vergleichbaren Messdaten vorliegen. Die hat er sich passend zum erwünschten Ergebnis errechnet(!). Rechnung und Messung sind zweierlei! Fakt scheint auch zu sein, daß kein einziges grösseres Gewässer messtechisch auf seinen heat content untersucht wurde, Schon garnicht über einen klimarelevanten Zeitraum. Sie bestätigen das durch lautes Stillschweigen. Dankeschön!
Im übrigen muss ich Sie dringend bitten, die
Misshandlung der Deutschen Sprache einzustellen: „“erratisch“ schlecht “ geht gar nicht! Klimgt wie „quatitativ“ und sagt genauso wenig.
MfG
Michael Weber
Lieber Herr Weber,
zwickt es sonst noch irgendwo, was Sie daran hindert, sich aufs eigentliche Thema zu konzentrieren?
“ Und genau diese Messungen sind nur erratisch vorhanden und keineswegs geeignet um valide Aussagen machen zu können.“
Ob „keineswegs geeignet“ lässt sich erst entscheiden, wenn Sie eine Fehlerrechnung vorlegen und damit zeigen, dass Levitus‘ Wärme- bzw. Temperaturkurve aus den vorliegenden Daten (siehe links) nicht abzuleiten ist…
Mal ein Beispiel aus der Schulzeit: Da hat man bestimmt auch in Ihrem Physikkurs mal die Fallbeschleunigung im Physikraum experimentell bestimmt, indem man eine Kugel aus verschiedenen Höhen fallen ließ, die Fallzeit durch Lichtschranken bestimmte, die Fallhöhe gegen die Fallzeit graphisch auftrug, die 5 bis 7 Punkte schwungvoll mit einem Kurvenlineal verband, numerisch deren Ableitung bestimmte und schlussfolgerte, dass die Originalkurve eine Parabel ist, die Steigung der Ableitungsgeraden bestimmte und mittels der frisch erworbenen Kenntnissen der Differentialrechnung nachrechnete, dass die Fallbeschleunigung doppelt so groß wie die Geradensteigung ist, sich somit experimentell mittels der mathematischen Auswertung der Messpunkte ergibt.
Auch hier könnten Sie aus dem Bauch heraus behaupten, die 5 Messpunkte seien so „erratisch“, dass sie damit „keineswegs geeignet“ sind, die Schwerebeschleunigung im Physikraum bestimmten könnte und erst recht nicht auf jeden anderen Punkt auf der Erde übertragen werden könnte. Glauben Sie ernsthaft, dass so ein substanzloses Gefasel irgendwie inhaltlich weiterhilft? Generationen von Schülern rund um die Welt bekommen nach diesem Verfahren typischerweise Werte zwischen 9,5 bis 10,2 m/s2 heraus. Auf welcher sachlichen Grundlage wollen Sie beurteilen, ob diese Messwerte nun „erratisch“ schlecht sind, oder nicht? Verstehen Sie mein Anliegen, Sie sollen endlich Substanz liefern!
#93: NicoBaecker sagt:am Montag, 21.05.2012, 18:45
„… triviales …“
Hr. Baecker, zu ihren Auslassungen gegenüber Hr. Weber jetzt und weiteren zahllosen Kommentaren ihrerseits zuvor fällt mir nur noch folgendes ein:
„Selig sind, die nicht sehen und doch glauben“
Lieber Herr Baecker
Ihr Kunstwort „quatitative“ aus #90 ist in keinem Wörterbuch zu finden. Da Sie Wörter verwenden, die kein Mensch kennt, finde ich es lustig, daß Sie Schlüsse zu meinem Schulalltag ziehen können wenn ich Ihre Schöpfung nicht kenne. Ihrem Anspruch an wissenschaftliche Exaktheit werden Sie so nicht gerecht! Sie sollten mal Rechtschreibung üben! Auch beim Korrekturlesen und Lesen zeigen Sie erhebliche Schwächen, arbeiten Sie mal daran! Aber zum Thema:“Eine Änderung des heat contents macht sich also durch eine Temperaturänderung bemerkbar und umgekehrt.“ Die Temperaturänderung will aber ordentlich gemessen sein. Und genau diese Messungen sind nur erratisch vorhanden und keineswegs geeignet um valide Aussagen machen zu können. Wenn Sie gerne mit Phantasiewerten rechnen- Bitteschön, tun Sie sich keinen Zwang an. Durch richtiges Rechnen mit falschen Werten hat die NASA schon den Mars punktgenau verfehlt. Über ARGO hat Sie Dr.Paul ja aufgeklärt. Die behauptete Erwärmung kann nicht gemessen werden. Also können Sie sich die errechneten 24 W/m2 an den Hut stecken.
MfG
Michael Weber
Lieber Herr Weber,
„Den Begriff „quatitative(r) Zusammenhang “ habe ich in der Physik der Mittelstufe tatsächlich nicht mitbekommen. “
Ehrlich? Was haben Sie denn die ganze Zeit dann im Physik-Unterricht gemacht? Ist Ihnen nicht aufgefallen, dass Ihre Nachbarn mal vom Taschenrechner oder Rechenschieber Zahlen ablasen?
„Der heat content von Wasser wird von äußeren Faktoren gesteuert, egal ob im Kochtopf, in der Badewanne oder im Ozean.“
Sehr richtig, und wie Sie in der 8. Klasse (oder 7.) gelernt hätten, ist der „heat content“ (dt. innere Energie, salopp Wärme) einer Flüssigkeit im wesentlichen (d.h. genau genug für unsere Zwecke) durch die Temperatur der Flüssigkeit gegeben ist. Eine Änderung des heat contents macht sich also durch eine Temperaturänderung bemerkbar und umgekehrt.
Wie jeder (gute) 8. Klässler ausrechnen kann, entspricht einer Zunahme des Wärmeinhaltes der oberen 2000m Weltmeer um 24 mal 10 hoch 22 Joule in 50 Jahren (das ist die Größenordnung des hier diskutierten und von ihnen bislang bezweifelten Anstiegs) einer Temperaturerhöhung von ca. 0,08 °C im Mittel, und dies wird durch eine Netto-Wärmeaufnahme von 24 W/m2 über diesen Zeitraum bewirkt. Soweit die physikalischen Trivialitäten. Können Sie dem nun folgen oder nicht?
#90: NicoNaecker was wollen Sie mit Ihren ad hominem Argumenten den Lesern eigentlich sagen?
Es geht hier um die Zuname des Wärmeinhaltes des Ozeans. Genaue Messungen dazu gibt es erst seit dem Argo-Bojen-System, also Mitte 2003!
Nun verlangen die meisten „Klimamodelle“ einen Anstieg des heat content, also des Wärmegehaltes der Ozeane von ca. 0.7 × 10^22 Joule pro Jahr (z.B. Hansen et.al. 2005), was einem Temperaturanstieg von ca. 0.01°C pro Jahr entspricht.
Dummerweise zeigen nun diese Argodaten diesen jährlichen Temperaturanstieg nicht.
Fazit:
die AGW-Modelle sind falsch.
Wenn jetzt dieser Levitus hingeht und zum Vertuschen dieser Klimamodellversagen seine Ozean temperaturkurve in die Vergangenheit auszudehnen, in der entsprechen genaue Messdaten fehlen,
so ist das nicht anderes als ein weiterer Vertuschungsversuch der Fehlprognosen der „Klimamodelle“.
Das hat Herr Weber richtig erkannt. Und darum dürfen Sie ihm nicht böse sein Bäcker.
Im übrigen wären wir doch alle froh, wenn es etwas wärmer würde man könnte dann vielleicht auch die Energiepreise etwas senken, denken Sie doch nur mal an die Heizung!
mfG
Lieber Herr Baecker
Den Begriff „quatitative(r) Zusammenhang “ habe ich in der Physik der Mittelstufe tatsächlich nicht mitbekommen. Den dürfen Sie mir gerne erklären. Der heat content von Wasser wird von äußeren Faktoren gesteuert, egal ob im Kochtopf, in der Badewanne oder im Ozean. Also muss er variabel sein, aber bevor man diese Variabilität dem lieben CO-2 zuschreibt, sollte man alle anderen Energielieferanten wie Sonne,unterseeischen Vulkanismus etc auch berücksichtigen. Das ist nach meinem „verworrenen Naturverstaendis“ einfach klar. Der Bodensee ist wegen mangeldem Salzgehalt tatsächlich als Messlatte für Ozeane ungeeignet.
Aber ich bezweifle, daß selbst für die Ostsee ausreichend Daten für Aussagen über klimarelevante Zeiträume vorhanden sind.
MfG
Michael Weber
Lieber Herr Weber,
nun mal langsam, mit dem Begriff „doof“ sollten Sie hier vorsichtig sein. Zumal Sie bislang ueberhaupt nicht belegen, dass Sie das Levitus paper jemals gesehen haetten oder ueberhaupt grob die Inhalte verszanden haetten.
Wenn Sie nun nicht wissen, wie der quatitative Zusammenhang zwischen Temperatur und heat content von Wasser ist, so zeigt dass zumal, dass Sie die Physik der Mittelstufe nicht beherrschen.
Sie suchen nach einer fehlenden Kalibrierung? Was wollen Sie kalibrieren, den Zusammenhang zwischen heat content und Temperatur des Weltmeeres anhand des analogen Zusammenhangs im Bodensee? Oder was? Mein Gott, Ihnen muss man wirklich alles aus der Nase ziehen, und dabei kommt dann mutmasslich auch noch das raus, was man sich selbst mit groesster Fantasie als Physiker nicht vorstellen kann, welches verworrene Naturverstaendis in ihrem Kopf, Ihre Unverschaemtheiten steuert.