Eine „Blackbox”-Analyse könnte es uns gestatten, das „funktionale Äquivalent” dessen, was auch immer in der Blackbox vor sich geht, zu entdecken. Mit anderen Worten, wir könnten in der Lage sein, eine simple Funktion zu finden, die den gleichen Output ergibt wie aus der Blackbox. Ich dachte, dass es interessant ist, wenn ich erkläre, wie ich darauf kam, dies mit dem Klimamodell CCSM3 zu tun.
Als Erstes sammelte ich die Variablen des Inputs. Sie sind alle in der Form von
„ncdf“-Dateien, einem Standardformat, das sowohl Daten als auch Metadaten enthält. Ich habe diese in Excel geöffnet und in einer Datei zusammen gefasst. Diese Daten habe ich dann hier als Excel-Arbeitsblatt veröffentlicht.
Als Nächstes brauchte ich den Output. Am einfachsten ließ sich dieser aus der Graphik hier entnehmen. Ich habe diese Daten digitalisiert [?] mit Hilfe eines Digitalisierungsprogramms (und zwar des Programms „GraphClick“ auf einem Mac-Computer).
Meine erste Prozedur in diesem Verfahren war es, die verschiedenen Datensätze zu „normalisieren“ oder zu „standardisieren“. Dies bedeutet, sie so zu adjustieren, dass das Mittel Null ergibt und die Standardabweichung 1. Ich habe zu diesem Zweck die Excelfunktion ‚STANDARDIZE‘ verwendet. Dies erlaubt es mir, alle Daten in einem allgemeinen Größenformat zu sehen. Abbildung 2 zeigt jene Ergebnisse.
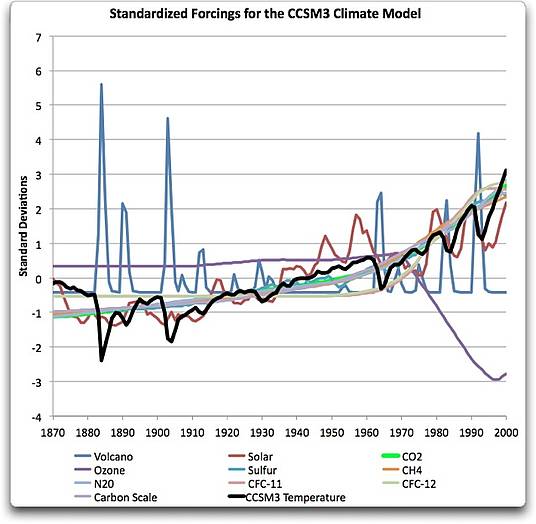
Abbidlung 2. Standardisierte Antriebskräfte, die vom Klimamodell CCSM 3.0 verwendet wurden, um eine Rückschau der Temperaturen des 20. Jahrhunderts zu erhalten. Dunkle schwarze Linien zeigen den Temperaturverlauf, wie ihn das Modell CCSM 3 sieht.
Ich kann viele Dinge erkennen, wenn ich das betrachte. Erstens, die Daten von CO2 haben das gleiche allgemeine Aussehen wie Schwefel, Ozon und Methan (CH4). Außerdem waren die Auswirkungen solarer Daten und vulkanischer Aktivitäten klar im Output der Temperaturen zu erkennen. Dies führte mich zu der Annahme, dass die GHG-Daten zusammen mit den solaren und vulkanischen Daten ausreichend seien, um das Temperaturoutput des Modells nachzuvollziehen.
Und tatsächlich zeigte sich, dass genau das der Fall war. Mit der Excelfunktion SOLVER verwendete ich die Formel, die (wie oben erwähnt) durch die Analyse des GISS-Modells entwickelt worden war. Diese Formel lautet*:
T(n+1) = T(n)+lambda x delta F(n+1) / tau + deltaT(n) exp(-1 / tau)
Nun gut, lassen Sie uns diese Gleichung in unsere Sprache übersetzen. Sie sieht kompliziert aus, ist es aber nicht.
T(n) ist die Temperatur „T” zum Zeitpunkt „n”. Also ist T(n+1) die Temperatur der nachfolgenden Zeitspanne. In unserem Falle rechnen wir mit Jahren, so dass hier die Temperatur des nächsten Jahres gemeint ist.
F ist die Antriebskraft (forcing) in Watt pro Quadratmeter. Dies ist die Summe aller Antriebe, die hier betrachtet werden. Die Zeitkonvention ist die Gleiche, so dass F(n) den Antrieb F zum Zeitpunkt n bedeutet.
Delta, bedeutet „Änderung nach…”. Also ist deltaT(n) die Temperaturänderung seit der voran gegangenen Zeitspanne, oder T(n) minus der vorherigen Temperatur T(n-1). Korrespondierend dazu ist delta F(n) die Änderung der Antriebskraft seit der vorherigen Zeitspanne.
Lambda, ist die Klimasensitivität. Und schließlich ist tau, die Zeitverzögerugnskonstante (the lag time constant). Diese Zeitkonstante legt die Zeitspanne fest, bis das System auf den Antrieb reagiert. Und zu guter letzt, der Terminus „exp(x)“ bedeutet e hoch x, oder 2,71828… hoch x.
Also im Klartext: Die Temperatur im nächsten Jahr oder T(n+1) ist gleich der Temperatur dieses Jahres T(n) plus der sofortigen Temperaturzunahme wegen der Änderung der Antriebskraft delta F(n+1)/tau plus dem Verzögerungsterm {lag term} deltaT(n) exp(-1 /tau ) aus dem vorangegangenen Antrieb. Dieser Verzögerungsterm ist notwendig, weil die Auswirkungen einer Änderung des Antriebs nicht sofortiger Natur sind.
Abbildung 3 zeigt das Endergebnis dieser Rechnung. Ich habe nur eine Teilmenge der Antriebe verwendet, nämlich den Antrieb durch Treibhausgase (GHGs), den solaren und den vulkanischen Input. Die Größenordnung der übrigen Kräfte ist hinsichtlich des Antriebspotentials so gering, dass ich sie in der Rechnung nicht berücksichtigt habe.
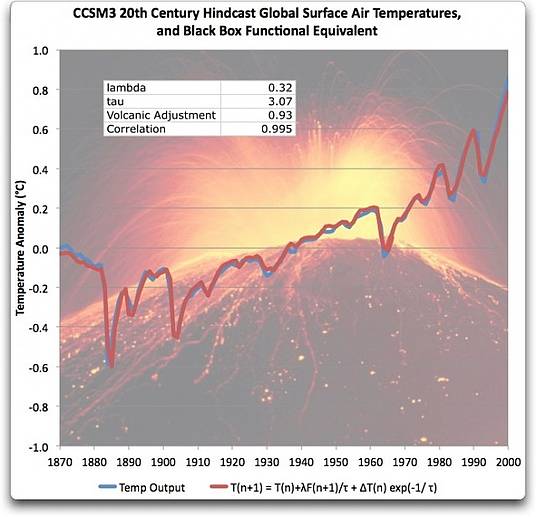
Abbildung 3. Gleichung zum funktionalen Äquivalent des CCSM3-Klimamodells im Vergleich zum aktuellen Output von CCSM3. Beide sind etwa identisch.
Verglichen mit dem GISSE-Modell ergibt sich, dass CCSM3-Modell ebenfalls sklavisch dem verzögerten Input folgt. Sie passen ebenfalls exzellent zusammen mit einem Korrelationsfaktor von 0,995. Die Werte für Lambda und Tau sind auch ähnlich denen, die man während der GISSE-Untersuchung gefunden hatte.
Was bedeutet das alles nun?
Nun, erst einmal bedeutet es, dass die Output-Temperatur des CCSM3-Modells ebenso wie beim GISSE-Modell funktional äquivalent zu einer einfachen, eindimensionalen zeitlich verzögerten linearen Transformation der Input-Antriebskräfte ist.
Sollten die Modelle GISSE und CCSM3 in gleicher Weise funktionieren, bedeutet es, dass man sehr wahrscheinlich die gleiche lineare Abhängigkeit des Outputs vom Input auch in anderen Klimamodellen finden wird
(Lassen Sie mich hinzufügen, dass das CCSM3-Modell nur sehr schlecht den historischen Temperaturrückgang von ~1945 bis ~1975 abbilden kann … genau wie auch das GISSE-Modell).
Wenn Sie glauben, dass die Temperatur unseres Planeten eine einfache lineare Transformation durch die eingehenden Antriebskräfte ist, glaube ich, dass diese Modellergebnisse vernünftig klingen, zumindest theoretisch.
Ich selbst empfinde den Gedanken eines linearen Zusammenhangs zwischen Input und Output in einem komplexen, vielfach wechselwirkenden, chaotischen System als eine lächerliche Fantasie. In keinem anderen komplexen System, das ich kenne, ist das so. Warum sollte das Klima so einfach und mechanistisch vorhersagbar sein, wenn es alle anderen, vergleichbaren Systeme nicht sind?
Dies alles stellt nach meiner Ansicht den Kern des Missverständnisses des gegenwärtigen Standes der Klimawissenschaft dar. Das aktuelle Klima-Paradigma, wie es in den Modellen zum Ausdruck kommt, lautet, dass die globale Temperatur eine lineare Funktion der Antriebe ist. Ich finde das extrem unwahrscheinlich, sowohl vom theoretischen als auch vom praktischen Standpunkt. Diese Behauptung ist das Ergebnis der schlechten Mathematik, die ich detailliert in “The Cold Equations“ aufgelistet habe [auf Deutsch bei EIKE hier]. Also: falsche Substitutionen gestatten es ihnen, alles außer Antrieb und Temperatur aus den Gleichungen herauszuhalten … was zu der falschen Behauptung führt, dass bei einer Zunahme der Antriebskräfte die Temperatur linear und sklavisch folgen muss.
Wie man sieht, scheitern sowohl das GISSE- als auch das CCSM3-Modells damit, die Abkühlung nach 1945 abzubilden. Die Behauptung eines linearen Zusammenhangs zwischen den Antriebskräften und der Temperatur scheitert am Praxistest der realen Welt genauso wie am gesunden Menschenverstand.
Willis Eschenbach
TECHNISCHE BEMERKUNGEN ZUR KONVERSION IN WATT PRO QUADRATMETER
Viele der in das CCSM3-Modell eingehenden Antriebskräfte werden in anderen Einheiten als Watt/Quadratmeter angegeben. Viele Konversionen wurden benutzt.
Die Werte von CO2, CH4, NO2, CFC-11 und CFC-12 wurden in w/m² umgerechnet, und zwar mit Hilfe der verschiedenen Formeln von Myhre in Tabelle 3.
Der solare Antrieb wurde mit Hilfe der Division des äquivalenten mittleren Antriebs durch 4 umgerechnet.
Für die vulkanischen Auswirkungen, die im CCSM3-Modell als die gesamte ausgeworfene Masse in Tonnen angegeben wird, gibt es keine Standardumrechnung in W/m². Daher wissen wir nicht, welchen vulkanischen Antrieb das CCSM3-Modell benutzt. Folglich passte ich diese Daten an die gleichen W/m²-Werte des GISSE-Modells an. Danach adjustierte ich die Werte schrittweise, um sie passend zu machen. Das Ergebnis zeigt das „Volcanic Adjustment“ oben in Abbildung 3.
Den Originalartikel von Willis Eschenbach finden Sie hier:
Übersetzt von Chris Frey für EIKE
* Leider werden in diesem Editor mathematische Sonderzeichen nicht abgebildet
















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Herr Limburg, Kommentar in #2
„die eigentliche Botschaft dieses Modellversuches von Eschenbach [ist], eine einfachen Prozess mathematisch so beschreiben zu können, dass dieser aus den vorhandenen Eingangsdaten die vorgegebenen Ausgangsdaten errechnet.“
Ja, diese Absicht habe ich Eschenbachs Artikel auch entnommen.
Aber wie ich für mathematisch hinreichend vorgebildete Menschen oben unmissverständlichen beschrieben haben sollte, ist ihm das nicht gelungen!
Denn ein AR(2) Prozeß benutzt ja die vorherigen Ausgangsdaten (Temperaturen T(n-1) und T(n)) für die Approximation der nächstfolgenden Ausgangsdaten T(n+1). Eingangsdaten (hier: in Form externer forcings) werden dort nicht verwendet.
„Natürlich hat Eschenbach eine Autokorrelation berücksichtigt, wie es auch das IPCC im AR 4 (Chapter 3) mit AR1 tut.“.
Meinen Sie diese Textstelle auf p 289:
“Schneider and Cornuelle (2005) suggested that the PDO is not itself a mode of variability but is a blend of three phenomena. They showed that the observed PDO pattern and evolution can be recovered from a reconstruction of North Pacific SST anomalies based on a first order autoregressive model and forcing by variability of the Aleutian low, ENSO and oceanic zonal advection in the Kuroshio-Oyashio Extension.”
Sicher, hier ist es nichts anderes. Nur geht es bei diesem Text ja nicht um physikalisch-deterministische Klimamodellierung zum Vergleichen modelliert gegen gemessen, sondern um die Modellierung gemessener Daten anhand eines empirischen Modells.
Klimatologische Daten, insb. Temperaturdaten sind häufig autokorreliert. Wenn Sie die täglichen Temperaturmittel für Berlin-Dahlem autokorrelieren würden, würden Sie ein tau von ca. 3 Tagen finden, wobei die Korrelationsfunktion etwa exponentiell abfällt. Das ist mehr oder weniger die mathematische Konsequenz der Persistenz-Wetterregel, dass das Wetter morgen in erster Näherung so wie heute ist.
Der Punkt ist doch aber, dass ein Autokorrelationsmodell p-ter Ordnung nur einen bestehenden Datensatz von Ausgangsdaten modellieren kann in dem Sinne, dass die zugrunde liegende zeitliche Korrelation aufeinanderfolgernder Werte mathematisch beschrieben werden kann. Eine Extrapolation über mehr als p Zeitschritte über den vorliegenden Datensatz hinaus ist nicht möglich, weil die Daten fürs Modell dort fehlen.
Einen ganz anderen Anspruch hat ein GCM. Denn dort wird die Temperatur zu jedem Zeitpunkt und Gridpunkt aus den die Temperatur determinierenden physikalischen Größen berechnet, also die lokale Energiegleichung gelöst, und dann gemittelt. Aufgrund der Modelldynamik zeigen diese Globaltemperaturen auch eine Autokorrelation. Der Vergleich dieses Verhaltens mit den Messdaten ist übrigens auch ein Maß für die Modellqualität. Die Temperaturen aus der Vergangenheit spielen dort nur mittelbar eine Rolle, nämlich in dem Sinne, dass sie wie auch die anderen physikalischen Größen den Zustand der Atmosphäre beschreiben, aus dem sich der zukünftige aufgrund der zeitabhängigen physikalischen Gesetzmäßigkeiten entwickelt, diese Verknüpfung liefern die Differentialgleichungssysteme.
„Nun kann sich jeder selbst überlegen, was Sinnvoller ist…“
Ja gerne, Herr Baecker!
Die Schwankungen der letzten 100 Jahre ähneln sehr deutlich den Veränderungen in der Atmosphäre und denen der Sonnenaktivität. Sie und alle Ihre Anhänger, Herr Baecker, werden es NIE schaffen, diese durch die Veränderungen der CO2-Konzentration zu erklären!
Meinetwegen können Sie Ihre Theorien bis ins Grab weiter runterbeten, aber bitte verschwenden Sie nicht meine Steuergelder. Ich möchte nicht, dass sie für solch einen Mist ausgegeben werden!
Nochmal zum Eschenbach-Fit:
wenn man im Gegensatz zu Eschenbach eine echte Regression mit Vulkanen, Sonne und CO2 macht, also ohne Eschenbachs Korrelation der Temperaturdaten mit sich selbst, so kommt ein Korrelationskoeffizient von r = 0,960 heraus, also geringer aber dafür nicht selbstrekursierend.
Die Koeffizienten sind:
Volcano -0,0186 °C/MMT
Solar 0,0943 °C/Wm-2
CO2 0,00862 °C/ppm
Nimmt man das CO2 ganz raus, so wird der Korrelationskoeffizient kleiner, r = 0,879 und man bekommt für die Koeffizienten:
Volcano -0,0133 °C/MMT
Solar 0,275 °C/Wm-2
Der solare Koeffizient wird natürlich größer, da nun der fehlende CO2-Trend komplet solar erklärt werden muß.
Rein aus dem Ansatz zunehmende solare Einstrahlung macht gleichgroße thermische Ausstrahlung folgt für den Koeffizienten theoretisch:
4* dT/T = dF/F = dS/S:
dT/dS = T/(4*S) = 255 K/(4*1365 Wm-2) = 0,05 °C/Wm-2
Bei beiden Fits übersteigt die solare Klimasensititvität die theoretische Erwartung, mit CO2 um fast das Doppelte, ohne CO2 um das Fünffache. Nun kann sich jeder selbst überlegen, was Sinnvoller ist und wie groß der was auch immer solare Verstärkungseffekt (Svensmark oder was anderes) sein muß.
Eschenbach, Top-Hobby-Klimaskeptiker!
Der Mann weiß offenbar nicht, dass er vor allem die Temperaturdaten autokorreliert hat:
Seine Regressionsgleichung:
T(n+1) = T(n)+lambda x delta F(n+1) / tau + deltaT(n) exp(-1 / tau)
umgeformt:
T(n+1) = T(n) + lambda x delta F(n+1) / tau + [T(n)-T(n-1)] exp(-1 / tau)
die Konstanten zusammengefasst:
T(n+1) = A*T(n) + B*T(n-1) + C*delta F(n+1)
mit:
A = 1+exp(-1/tau)
B = – exp (-1/tau)
C = lambda / tau
Es handelt sich bei Eschenbachs Formel also um einen AR(2)-Prozess (autoregressiver Prozeß 2. Ordnung) mit zusätzlicher externer „Störung“ durch die forcing(änderung) delta F!
Eschenbach bestimmt nun A,B und C und bekommt eine tolle Übereinstimmung mit den Daten hin („Korrelationsfaktor von 0,995“).
Das glaube ich, aber diesen Korrelationsfaktor r bekommt man sogar noch größer hin, wenn man das forcing Delta F ganz WEGLÄSST und T(n+1) NUR aus T(n) und T(n-1) alleine berechnet:
r 0,9979
r Quadrat 0,9958
Die Temperatur zum Zeitpunkt n+1 wird zu >99% eben durch die Werte vorher schon beschrieben. Und die so beschriebene Temperaturkurve stimmt mit den Daten optisch genauso gut wie Eschenbachs Fit inkl. forcings überein.
Diese Autokorrelation hat Eschenbach in seiner Formel oben zugelassen, sie dominiert offenbar den ganzen Fit, die forcings sind wurscht.
M.a.W. in die eigene Tasche gelogen!
„Und zu guter letzt, der Terminus „exp(x)“ bedeutet x „2,71828“ oder x hoch 2,71828.“
Nein, er bedeutet e hoch x, oder 2,71828… hoch x. Im übrigen bin ich überrascht, daß die Funktion der Blackbox (Hochleistungscomputer mit umfangreichem und hochentwickeltem Rechenprogramm) durch eine so simple Gleichung so gut nachvollzogen werden kann, die mit einem Taschenrechner zu lösen ist. Klares Indiz für ungeheure Geldverschwendung durch GISSE.