von Dr. Konrad Voge
Vorbemerkung
In diesem Artikel wird untersucht, ob ein statistischer Zusammenhang zwischen der Installation von Windkraftanlagen (WKA) und Photovoltaikanlagen (PV) und der jährlichen Niederschlagsmenge sichtbar gemacht werden kann. Es sei hier darauf hingewiesen, dass eine nachgewiesene Korrelation noch nicht einen kausalen Zusammenhang beschreibt. Umgekehrt ist das Nichtvorhandensein einer Korrelation ein Beweis, dass die betrachteten Faktoren ohne Einfluss sind.
Die vorliegenden Daten ermöglichen eine Analyse für jedes Bundesland.
Niederschläge – Zeitreihen
Auf der Seite Wetterkontor [1] sind die jährlichen Niederschlagsmengen seit 1881 angegeben. Diese sind die Grundlage der hier vorgenommenen Auswertungen. Bild 1 zeigt als erstes Beispiel die Zeitreihe der Niederschlagsmenge für Nordrhein-Westfalen. Am Verlauf ist zu sehen, dass ab 2001 ein deutlicher Trend zu geringeren Niederschlagsmengen vorliegt.
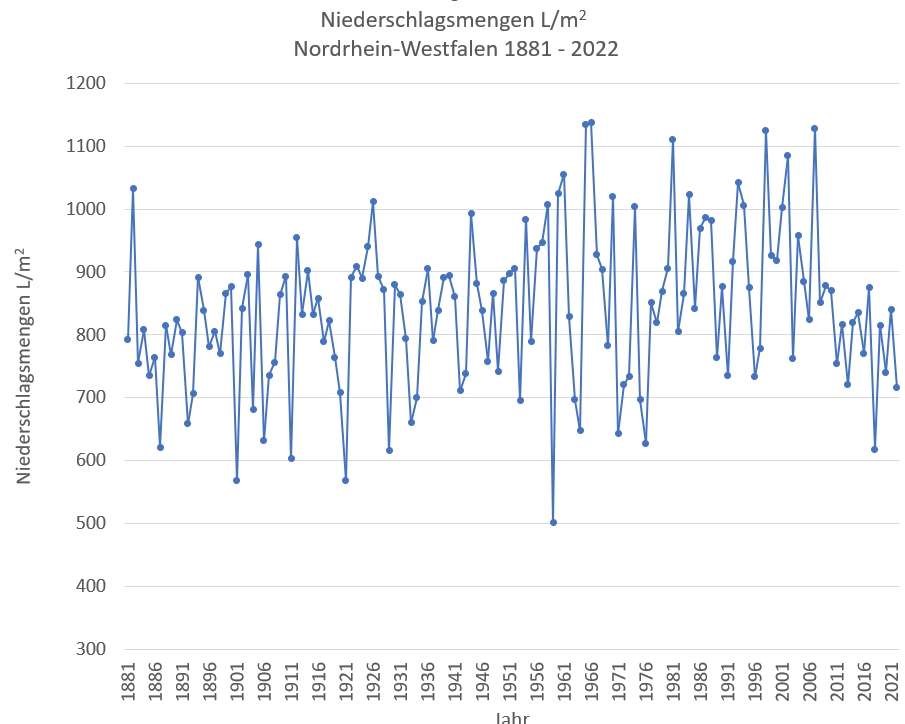
Bild 1 Niederschlagsmengen für Nordrhein-Westfalen von 1881 bis 2022
Für die Zeitreihen aller Bundesländer wurden Regressionsanalysen durchgeführt. Dazu wurden die die Zeitreihen in zwei Teile geteilt. Ein Teil umfasst die Jahre 1881 bis 2000, der zweite Teil die Jahre 2001 bis 2022.Bild 1 Bild 2 zeigt die zweigeteilte Regression der Zeitreihe von Brandenburg. Für den Zeitraum 1881 bis 2000 ist das Konfidenzintervall mit eingezeichnet.
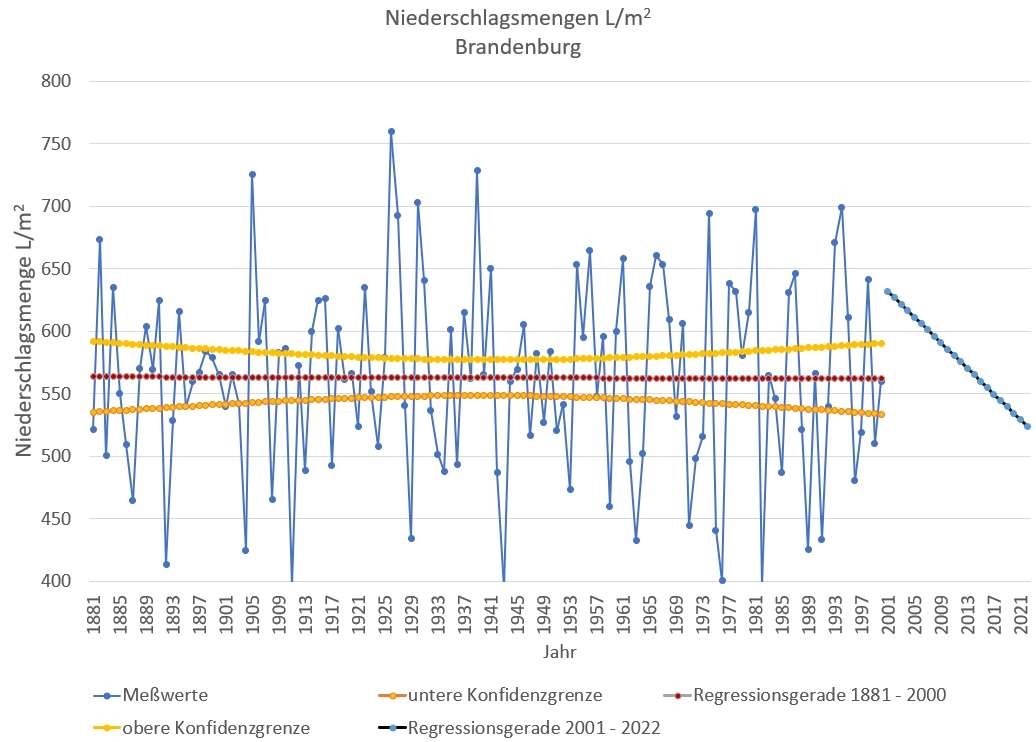
Bild 2 Regressionsfunktionen der geteilten Zeitreihe für Brandenburg, Konfidenzintervall für 95 % Wahrscheinlichkeit (Berlin ist in Brandenburg enthalten)
Die Regressionsgerade verläuft parallel zur Abszisse. Es ist kein Trend zu steigenden oder fallenden Niederschlagsmengen zu sehen. Im Gegensatz fällt die Trendlinie von 2001 bis 2022 steil ab. Der in Bild 1 auch ohne Entwicklung der Regressionsgeraden sichtbare Trend wird in Bild 2 statistisch nachgewiesen.
Analog zur Vorgehensweise wie in Bild 2 dargestellt, wurde für alle Bundesländer verfahren. Da aus Platzgründen die Bilder für alle Bundesländer nicht gezeigt werden können, wurde auf eine normierte Darstellung zurückgegriffen. In Bild 3 und Bild 4 sind die normierten Graphiken gezeigt. Für den Zeitraum 1881-2000 wurde als Normierungsjahr 1881, für den Zeitraum 20012022 das Jahr 2001 gewählt.
Wie Bild 3 zeigt, sind die Anstiege der Niederschlagsmengen im ersten Zeitraum unterschiedlich. Sachsen weist in dieser Zeit einen negativen Trend auf, das Saarland hat den steilsten Anstieg. Innerhalb dieses Fächers liegen die Anstiege der Niederschlagsmengen der anderen Bundesländer. Allgemein ist ein Trend größeren Niederschlagsmengen seit 1881 bis 2001 zu verzeichnen.
Aus Gründen der Übersichtlichkeit wurde in den Bild 3 undBild 4 auf die Darstellung der Konfidenzintervalle verzichtet. Diese haben die in Bild 2 gezeigte Form.
Nach dem gleichen Verfahren wurde der Zeitraum 2001 bis 2022 bearbeitet. Als Normierungsjahr ist 2001, das Jahr des Beginns dieses Zeitraumes gewählt. Dadurch ergibt sich eine vergleichbare Darstellung. Die Regressionsgeraden spannen ebenso wie in Bild 3 einen Fächer auf. Jedoch ist hier bei allen Bundesländern ein negativer Anstieg zu verzeichnen. Das bedeutet, dass ab 2001 ein kontinuierlicher Rückgang der Niederschlagsmenge vorliegt. Den stärksten Abfall der Niederschlagsmenge weist NordrheinWestfalen auf, den geringsten das Saarland.
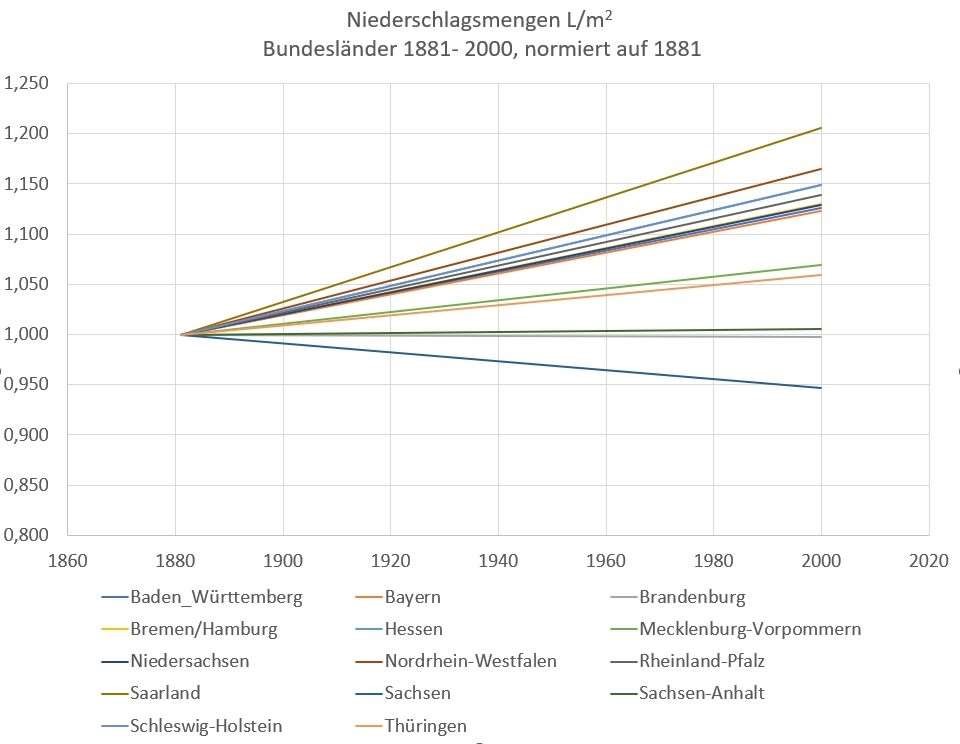
Bild 3 Regressionsgeraden für die Niederschlagsmengen der Bundesländer von 1881-2000, normiert auf den Wert von 1881
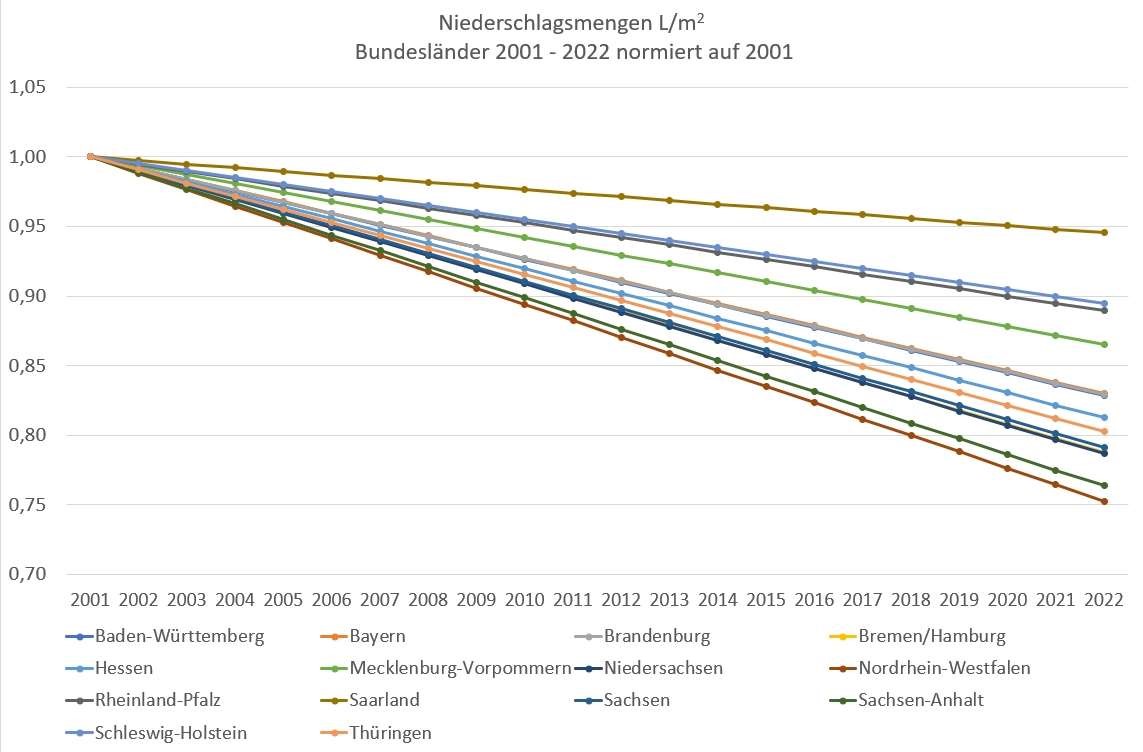
Bild 4 Regressionsgeraden für die Niederschlagsmengen der Bundesländer von 2001 – 2022 normiert auf den Wert von 2001
Niederschläge – Häufigkeitsverteilungen
Für die Zeitreihen 1881-2000 sind die Häufigkeitsverteilungen ermittelt worden. Die wurden auf mittels Χ2 Test auf Normalverteilung getestet. Die Ergebnisse sowie die Häufigkeitsverteilungen beschreibenden Parameter sind in Tabelle 1 zusammengefasst.
| Bundesland | Mittelwert | Streuung | Schiefe | Exzess | vorh Χ2 |
| Baden-Württemberg | 939,6 | 12,58 | -0,233 | -0,127 | 54,5 |
| Bayern | 908,2 | 10,77 | -0,149 | -0,331 | 26,6 |
| Brandenburg | 562,9 | 7,16 | 0,06 | -0,314 | 36,5 |
| Bremen/Hamburg | 724,6 | 9,14 | 0,069 | 0,275 | 36,2 |
| Hessen | 751,9 | 10,8 | -0,315 | 0,143 | 40,3 |
| Mecklenburg-Vorpommern | 595,7 | 6,93 | 0,009 | -0,469 | 29,3 |
| Niedersachsen | 724,9 | 9,15 | 0,070 | 0,281 | 37,3 |
| Nordrhein-Westfalen | 839,2 | 11,51 | 0,035 | -0,52 | 41,0 |
| Rheinland-Pfalz | 767,0 | 10,57 | 0,022 | 0,337 | 41,3 |
| Saarland | 887,3 | 13,85 | 0,049 | -0,111 | 86,5 |
| Sachsen | 728,0 | 10,23 | -0,028 | -0,066 | 39,6 |
| Sachsen-Anhalt | 556,1 | 7,58 | 0,129 | -0,381 | 53,0 |
| Schleswig-Holstein | 751,8 | 9,21 | -0,082 | 0,034 | 25,5 |
| Thüringen | 697,3 | 9,25 | 0,139 | -0,341 | 46,8 |
Tabelle 1 Parameter der Häufigkeitsverteilungen (zul Χ2 = 16,92)
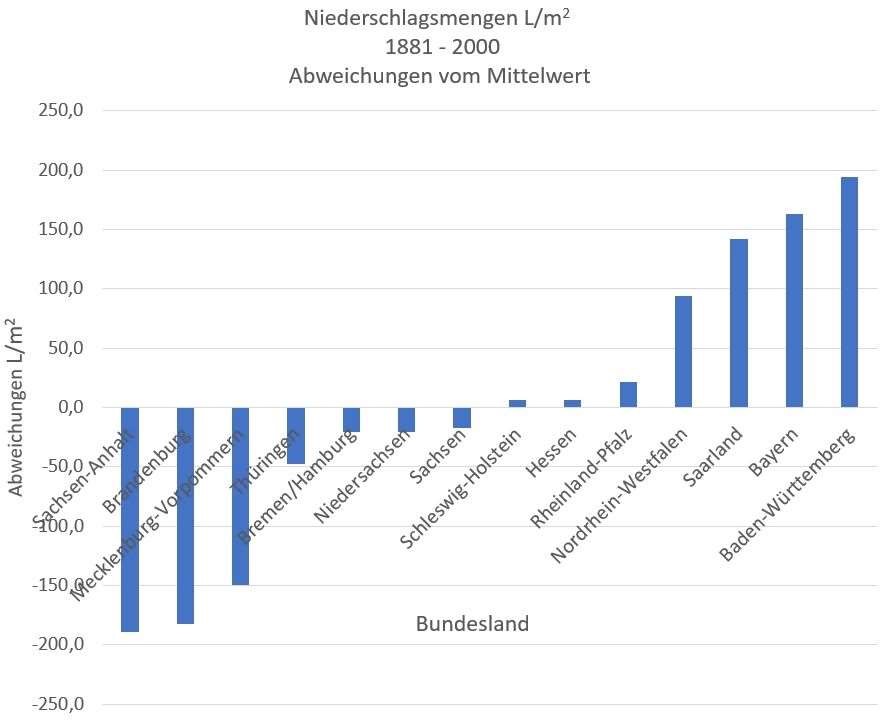
Bild 5 Niederschlagsmengen der Bundesländer als Abweichungen vom Mittelwert
Zur Bestimmung der Häufigkeitsverteilungen sind die Zeitreihen 1881-2000 der Bundesländer jeweils in 20 Klassen unterteilt und die Niederschlagsmengen den jeweiligen Klassen zugewiesen worden. Diese Verteilungen sind dann mittels linearer Regression für ein Polynom 7.Grades als Ansatzfunktion
f(y) = a0 + a1*y1+ +a7*y7
ausgeglichen worden. Bild 6 zeigt als Beispiel die Häufigkeitsverteilung für Schleswig-Holstein.
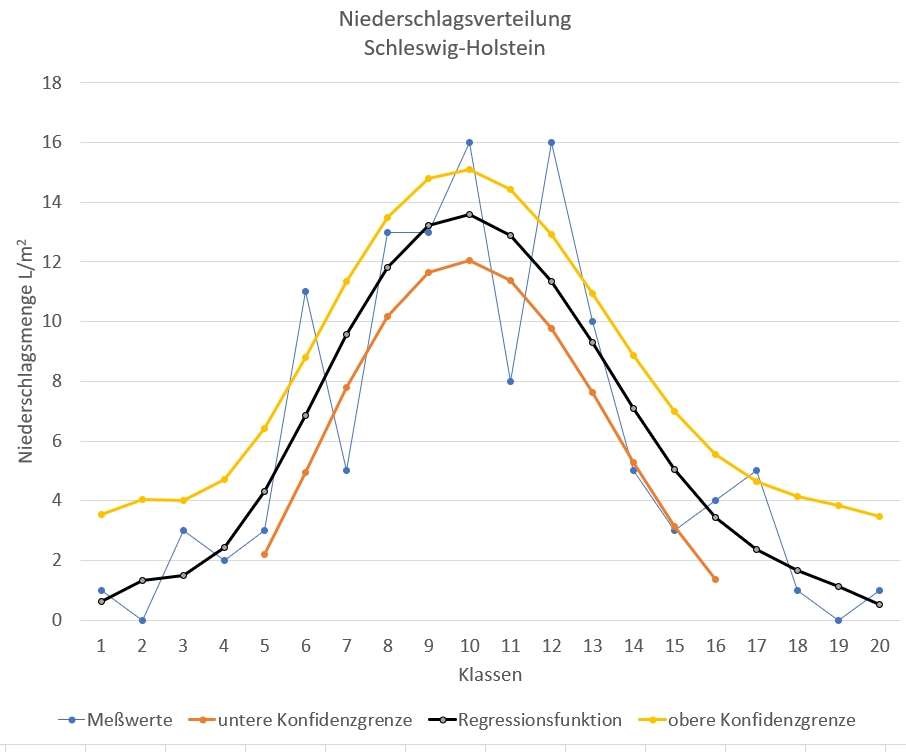
Bild 6 Häufigkeitsverteilung der Niederschlagsmengen von 1881-2000 für Schleswig-Holstein
Wie auch aus den Werten von Tabelle ersichtlich, ist die Verteilung weitgehend symmetrisch mit geringem Exzeß. Bei vorhanden Χ2 = 25,5 (zulässig Χ2 = 16,92) kommt die Verteilung der Niederschlagsmenge für Schleswig-Holstein einer Normalverteilung am nächsten. Um die Formen der Häufigkeitsverteilungen der Bundesländer miteinander vergleichen zu können, sind diese normiert auf die Klasse der maximalen Häufigkeit. Bild 6 zeigt, dass in den Klassen der geringen Niederschlagsmengen (linke Seite der Verteilungen) die Verteilungen relativ gut übereinstimmen. Im Bereich der höheren Niederschlagsmengen (rechte Seite der Verteilungen) liegen größere Abweichungen vor. Aus dem Bündel der Verteilungen fällt die rechte Seite der Häufigkeitsverteilung des Saarlandes deutlich heraus. Der Wert vorh Χ2 = 86,5 zeigt auch deutlich die Abweichung von einer Normalverteilung.
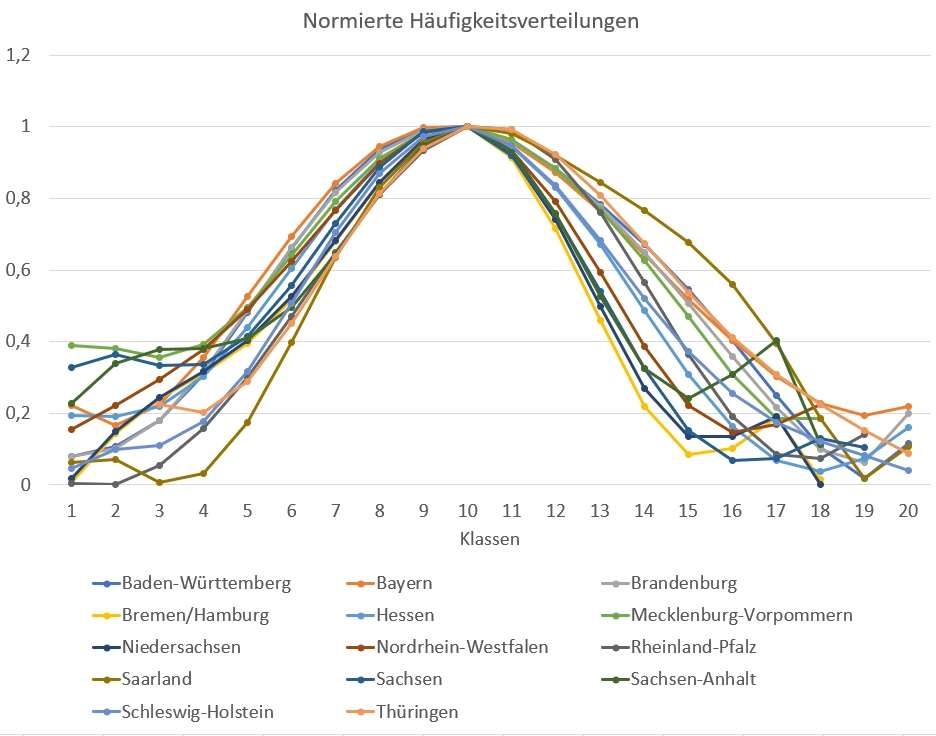
Bild 7 Normierte Häufigkeitsverteilungen der Niederschlagsmengen der Bundesländer.
Abschnittsweise Regressionsanalysen
In Bild 2 ist gezeigt, dass ein starker Abfall der Niederschlagsmengen im Zeitraum 2001-2022 zu verzeichnen ist.
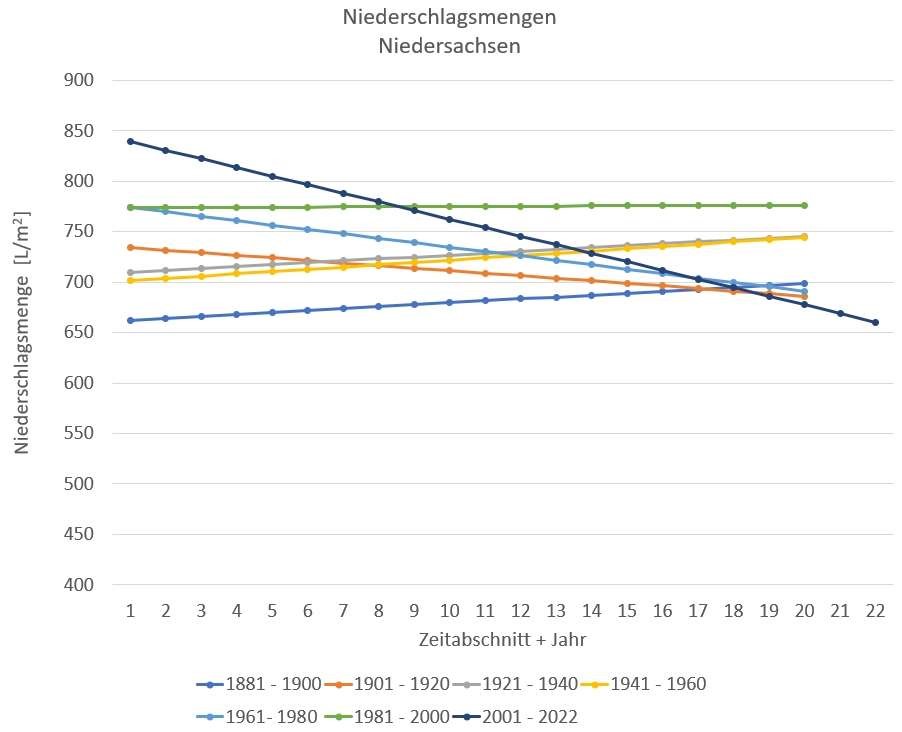
Bild 8 Abschnittsweise Regression der Zeitreihe für Niedersachsen (ohne Konfidenzintervalle)
Aufgrund dieses Verhaltens liegt es nahe, die Zeitreihen in ebenso große Abschnitte zu unterteilen und den Trend dieser Abschnitte zu untersuchen. In Bild 8 sind als Beispiel die Regressionsgeraden der 20 Jahresabschnitte für Niedersachsen gezeigt. Außer für die Abschnitte 1901-1920 und 1961-1980 weisen alle Abschnitte, außer natürlich 2001-2022, einen positiven Trend auf. Ab 2001 beginnt der starke Abwärtstrend. Auf die Darstellung der Konfidenzintervalle wurde aus Gründen der Übersichtlichkeit verzichtet.
| Bundesland | 1881-
1900 |
1901-
1920 |
1921-
1940 |
1941-
1960 |
1961-
1980 |
1981-
2000 |
2001-
2022 |
|||||||||||||||||||||||
| 1 | -4,00 | 3,71 | 7,71 | 1,55 | 0,39 | -2,21 | -8,33 | |||||||||||||||||||||||
| 2 | 2,95 | 3,71 | 4,67 | 1,30 | 1,55 | 0,61 | -8,11 | |||||||||||||||||||||||
| 3 | 0,24 | 0,87 | 0,12 | 2,10 | -4,33 | 0,89 | -5,14 | |||||||||||||||||||||||
| 4 | -0,60 | -1,29 | 0,79 | 3,35 | -5,61 | -4,86 | -7,36 | |||||||||||||||||||||||
| 5 | 3,40 | 0,80 | -2,39 | 1,16 | -0,66 | 1,34 | -4,24 | |||||||||||||||||||||||
| 6 | 1,90 | -2,52 | 1,87 | 2,27 | -4,39 | 0,14 | -8,51 | |||||||||||||||||||||||
| 7 | 0,87 | 3,02 | 0,10 | 3,32 | -6,09 | -1,65 | -11,34 | |||||||||||||||||||||||
| 8 | -4,09 | -0,14 | 2,31 | 1,29 | -0,06 | -3,21 | -4,19 | |||||||||||||||||||||||
| 9 | -8,46 | 3,26 | 3,77 | 4,17 | -0,95 | -2,07 | -2,35 | |||||||||||||||||||||||
| 10 | 2,87 | 2,11 | -2,00 | 1,45 | 2,84 | 3,14 | -7,94 | |||||||||||||||||||||||
| 11 | 1,46 | -2,47 | 0,72 | 1,53 | -1,56 | 1,79 | -7,26 | |||||||||||||||||||||||
| 12 | 1,13 | 0,52 | 0,23 | 2,88 | -1,6 | -1,42 | -4,33 | |||||||||||||||||||||||
| 13 | 4,39 | -2,87 | 1,56 | -0,15 | -0,77 | 2,17 | -7,38 | |||||||||||||||||||||||
| Mittelwert | 0,16 | 0,67 | 1,50 | 2,02 | -1,63 | -0,41 | -6,65 | |||||||||||||||||||||||
| 1 Baden-Württemberg | 2 Bayern | 3 Brandenburg | ||||||||||||||||||||||||||||
| 4 Hessen | 5 Mecklenburg-Vorpommern | 6 Niedersachsen | ||||||||||||||||||||||||||||
| 7 Nordrhein-Westfalen | 8 Rheinland-Pfalz | 9 Saarland | ||||||||||||||||||||||||||||
| 10 Sachsen
13 Thüringen |
11 Sachsen-Anhalt | 12 Schleswig-Holstein | ||||||||||||||||||||||||||||
Tabelle 2 Anstieg der Regressionsfunktionen der Zeitabschnitte von 1881 – 2000 für die untersuchten Bundesländer
In Tabelle 2Tabelle 2 sind die Anstiege der jeweiligen Zeitabschnitte für die untersuchten Bundesländer zusammengestellt. Es sind die Glieder a1 der Regressionsgeraden f(t) = a0 + a1 t. Mit f(t) als Niederschlagsmenge und t als Jahr (1,2,…, 20)
Es zeigt sich, dass die Trendlinien für steigende Niederschlagsmengen deutlich in der Überzahl sind (Verhältnis 56 zu 22). Es liegt demnach im Zeitraum von 120 Jahren eine deutliche Tendenz zu erhöhten Niederschlagsmengen vor. Eine Ausnahme bildet der Abschnitt 1961 bis 1980. In dieser Zeit und im Abschnitt 1981 bis 2000 liegt eine Tendenz zu geringeren Niederschlagsmengen vor. Allerdings ist die Tendenz im letztgenannten Abschnitt nur schwach. Im Abschnitt 2001-2022 sind die Bundesländer Nordrhein-Westfalen und Saarland durch maximalen bzw. minimalen negativen Anstieg auffällig.
Windkraftanlagen
Im Jahr 2001 begann der verstärkte Ausbau von Windkraftanlagen (WKA) besonders in den nördlichen Bundesländern [2]. Derzeit sind etwa 29.000 WKA aufgestellt. In Tabelle 3 sind die installierten Leistungen für die Bundesländer zusammengestellt. Um Vergleiche zu ermöglichen, wurde die installierte Leistung auf die jeweilige Fläche des Bundeslandes bezogen. Der Faktor in Tabelle 3 gibt den Zubau gegenüber 2000 an. Von 4,9 GW im Jahr 2000 erhöhte sich die installierte Leistung auf 55,8 GW. Das entspricht einer Vervielfachung von 11,5. Bild 9 veranschaulicht die Werte der Tabelle 3
| Windkraftanlagen | 2000 | 2000 | 2021 | 2021 | Faktor |
| Bundesland | MW | MW/m2 | MW | MW/m2 | |
| Baden-Württemberg | 61 | 0,0017 | 1730 | 0,0484 | 28,2 |
| Bayern | 68 | 0,0010 | 2567 | 0,0364 | 37,8 |
| Brandenburg | 442 | 0,0149 | 7864 | 0,2652 | 17,8 |
| Hessen | 211 | 0,0100 | 2304 | 0,1091 | 10,9 |
| Mecklenburg-Vorpommern | 456 | 0,0196 | 3567 | 0,1531 | 7,8 |
| Niedersachsen | 555 | 0,0116 | 11687 | 0,2450 | 21,1 |
| Nordrhein-Westfalen | 645 | 0,0189 | 6388 | 0,1873 | 9,9 |
| Rheinland-Pfalz | 251 | 0,0126 | 3814 | 0,1921 | 15,2 |
| Saarland | 13 | 0,0051 | 531 | 0,2065 | 40,8 |
| Sachsen | 300 | 0,0163 | 1263 | 0,0685 | 4,2 |
| Sachsen-Anhalt | 494 | 0,0241 | 5318 | 0,2600 | 10,8 |
| Schleswig-Holstein | 1178 | 0,0746 | 7015 | 0,4440 | 6,0 |
| Thüringen | 181 | 0,0112 | 1739 | 0,1073 | 9,6 |
| Summe | 4855 | 55787 | 11,5 |
Tabelle 3 Installierte Leistung der Windkraftanlagen 2000 und 2021
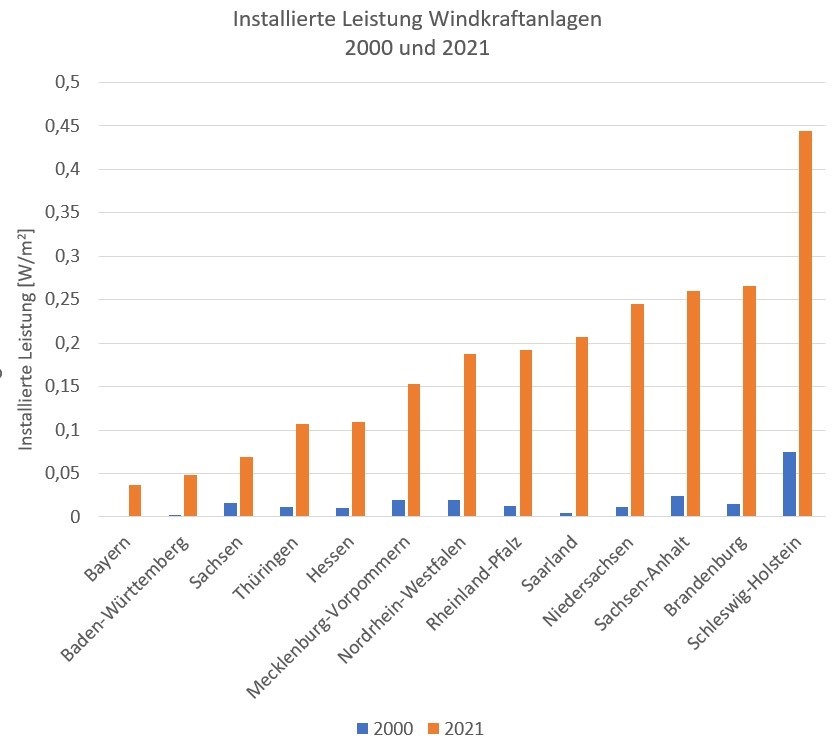
Bild 9 Installierte Leistung der Windkraftanlagen
Photovoltaikanlagen
Ebenfalls 2000 begann der Ausbau der Stromerzeugung durch Photovoltaikanlagen [3]. Der Ausbau begann bei 17 MW und erreichte 2021 den Wert von 58,1 GW. Das entspricht einen Vervielfältigungsfaktor von 3 415. In Bild 10 sind nur die Werte für 2021 aufgetragen, da die Werte für 2000 aus Gründen des Maßstabs nicht sichtbar sind.
| Photovoltaikanlagen | 2000 | 2000 | 2021 | 2021 |
| Bundesland | MW | MW/m2 | MW | MW/m2 |
| Baden-Württemberg | 7 | 0,0002 | 7413 | 0,2074 |
| Bayern | 0 | 0,0000 | 14917 | 0,2115 |
| Brandenburg | 0 | 0,0000 | 4818 | 0,1625 |
| Hessen | 2 | 0,0001 | 2650 | 0,1255 |
| Mecklenburg-Vorpommern | 0 | 0,0000 | 3121 | 0,1340 |
| Niedersachsen | 2 | 0,0000 | 4961 | 0,1040 |
| Nordrhein-Westfalen | 6 | 0,0002 | 6567 | 0,1925 |
| Rheinland-Pfalz | 0 | 0,0000 | 2763 | 0,1391 |
| Saarland | 0 | 0,0000 | 611 | 0,2376 |
| Sachsen | 0 | 0,0000 | 2612 | 0,1416 |
| Sachsen-Anhalt | 0 | 0,0000 | 3510 | 0,1716 |
| Schleswig-Holstein | 0 | 0,0000 | 2097 | 0,1327 |
| Thüringen | 0 | 0,0000 | 2010 | 0,1241 |
| Summe | 17 | 58050 |
Tabelle 4 Installierte Leistung der Photovoltaikanlagen 2000 und 2021
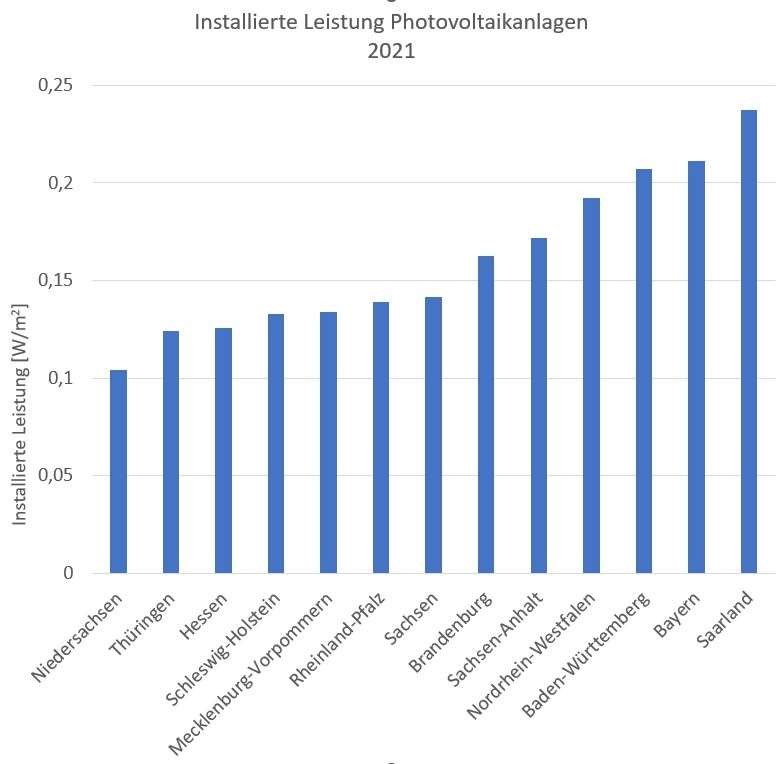
Bild 10 Installierte Leistung der Photovoltaikanlagen
Windkraft- und Photovoltaikanlagen
Tabelle 5 fasst die installierten Leistungen für WKA- und PV Anlagen zusammen. Für 2021 ergibt sich die Summe von 113,8 GW. Das ist vergleichsweise eine deutliche Überdimensionierung der installierten Kapazität, da die täglich angeforderte Leistung etwa 60 … 80 GW beträgt.
| WKA und PV Anlagen | 2000 | 2000 | 2021 | 2021 | Faktor |
| Bundesland | MW | MW/m2 | MW | MW/m2 | |
| Baden-Württemberg | 68 | 0,0019 | 9143 | 0,2577 | 133,9 |
| Bayern | 68 | 0,0010 | 17484 | 0,2488 | 257,1 |
| Brandenburg | 442 | 0,0149 | 12682 | 0,4426 | 28,7 |
| Hessen | 213 | 0,0101 | 4954 | 0,2447 | 23,3 |
| Mecklenburg-Vorpommern | 456 | 0,0196 | 6688 | 0,3067 | 14,7 |
| Niedersachsen | 557 | 0,0117 | 16648 | 0,3606 | 29,9 |
| Nordrhein-Westfalen | 651 | 0,0191 | 12955 | 0,3989 | 19,9 |
| Rheinland-Pfalz | 251 | 0,0126 | 6577 | 0,3438 | 26,2 |
| Saarland | 13 | 0,0051 | 1142 | 0,4492 | 87,8 |
| Sachsen | 300 | 0,0163 | 3875 | 0,2263 | 12,9 |
| Sachsen-Anhalt | 494 | 0,0241 | 8828 | 0,4557 | 17,9 |
| Schleswig-Holstein | 1178 | 0,0746 | 9112 | 0,6512 | 7,7 |
| Thüringen | 181 | 0,0112 | 3749 | 0,2426 | 20,7 |
| Summe | 4872 | 0,171 | 113837 | 0,3561 | 20,8 |
Tabelle 5 Installierte Leistung der Windkraftanlagen und Photovoltaikanlagen 2000 und 2021
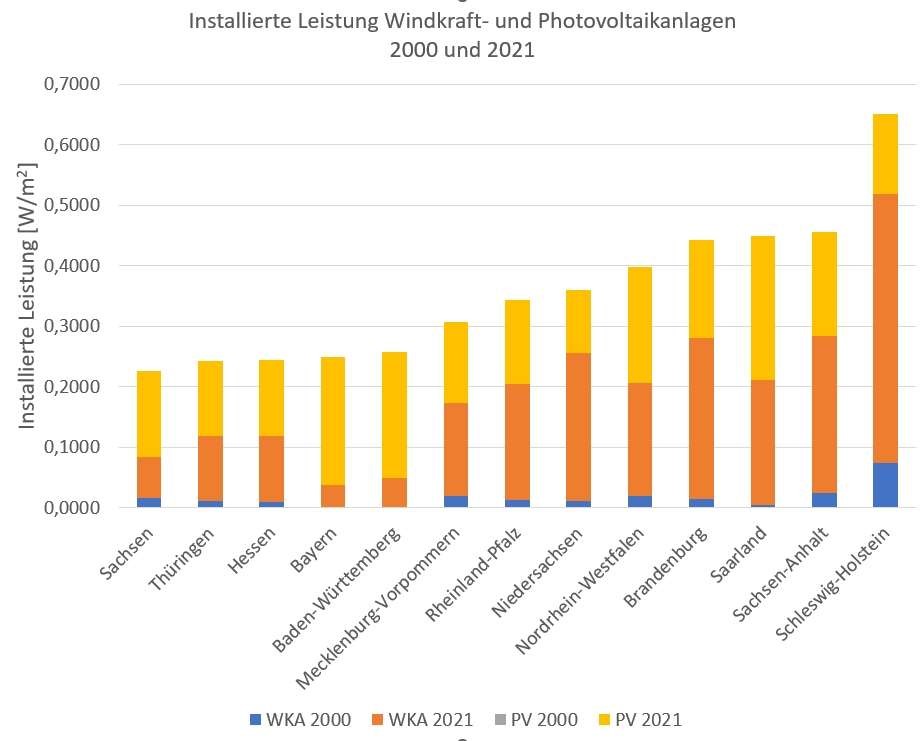
Bild 11 Installierte Leistung Windkraft- und Photovoltaikanlagen 2000 und 2021
Bild 11 zeigt die Anteile der installierten Leistungen. Die Anteile der 2000 installierten Photovoltaikanlagen werden aufgrund der Geringfügigkeit in diesem Maßstab nicht dargestellt, siehe Tabelle 4.
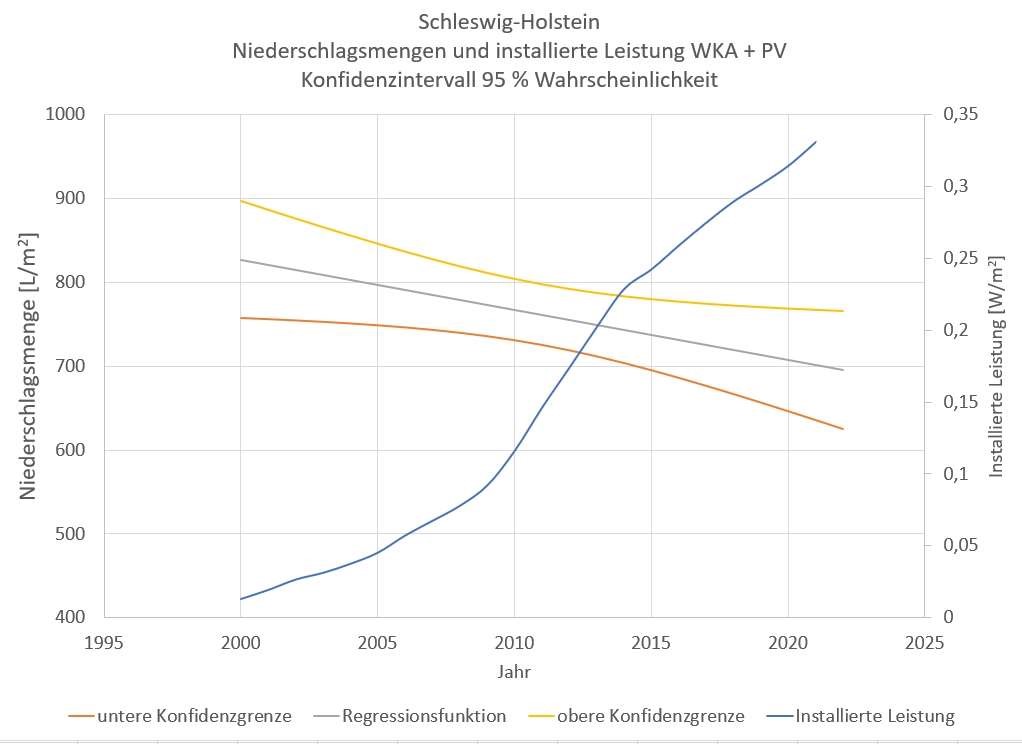
Bild 12 Niederschlagsmengen und installierte Leistung für Schleswig-Holstein
In Bild 12 sind die Niederschlagsmengen und die installierte Leistung für Schleswig-Holstein gezeigt. Es dient beispielhaft für alle übrigen Bundesländer.
| Bundesland | Korrelationskoeffizient |
| Bayern | 0,71 |
| Saarland | 0,73 |
| Baden-Württemberg | 0,74 |
| Hessen | 0,74 |
| Thüringen | 0,77 |
| Rheinland-Pfalz | 0,78 |
| Nordrhein-Westfalen | 0,79 |
| Mecklenburg-Vorpommern | 0,80 |
| Sachsen | 0,81 |
| Brandenburg | 0,81 |
| Sachsen-Anhalt | 0,82 |
| Schleswig-Holstein | 0,85 |
| Niedersachsen | 0,89 |
Tabelle 6 Koeffizienten der Korrelation Niederschlagsmenge und installierte Leistung
Die in Tabelle 6 zusammengestellten Korrelationsfaktoren zeigen eine starke Korrelation der betrachteten Niederschlagsmengen und der installierten Leistung von Windkraft- und Photovoltaikanlagen. Das kann zunächst nur als Gedankenansatz angesehen werden.
Zusammenfassung
Der Hintergrund des Artikels ist, wie in der Vorbemerkung betont, eine Untersuchung, ob eine Korrelation zwischen den installierten Anlagen und den Niederschlagsmengen der Bundesländer vorliegt. Es sei nochmals bemerkt, dass hier nicht Kausalitäten behauptet, sondern allenfalls vermutet werden. Die Vermutung kann insofern aufgestellt werden, da dem Autor keine sonstigen gravierenden Veränderungen im System Sonne, Erde, Atmosphäre bekannt sind, die die plötzliche Änderung der Niederschlagsmengen seit 2000 hervorgerufen haben könnten. Inwieweit Eingriffe durch Geoengineering den Rückgang der Niederschlagsmengen hervorgerufen haben, entzieht sich der Kenntnis des Autors.
In einer Arbeit [4] von 2021 kommt A. Kleidon auf eine mittlere verfügbare Windenergie von ca. 2 W/m2 in Deutschland. Vergleicht man diesen Wert mit den installierten Leistungen der Windkraft- und Photovoltaikanlagen nach Tabelle 5, ist eine Beeinflussung atmosphärischer Vorgänge nicht auszuschließen. So ist beispielsweise in Schleswig-Holstein ca. 1/3 der verfügbaren Windenergie aufgebraucht.
Photovoltaikanlagen reflektieren die Sonnenstrahlen ähnlich Spiegeln und wirken somit aufheizend für die Atmosphäre. Sie wirken als Wärmeinseln und beeinflussen Luftströmungen.
Quellen
- https://www.wetterkontor.de/
- https://www.wind-energie.de/themen/zahlen-und-fakten/bundeslaender/
[3]https://www.energycharts.info/charts/installed_power/chart.htm?l=de&c=DE&expansion=p_inst_states&year=20 07&chartColumnSorting=default
[4]https://www.schweizerbart.de/papers/metz/detail/30/97450/Physical_limits_of_wind_energ y_within_the_atmosphe
Dr. Konrad Voge ist Maschinenbau Ingenieur (Fördertechnik) und hat in unterschiedlichen Bereichen der Fördertechnik gearbeitet.
















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Der Beitrag ist sehr interessant. Allerdings weist Tabelle 5 einen Fehler auf. Die Einheit für die Leistung muss W/m^2 sein und nicht MW/m^2.
Weiterhin ist der Zahlenwert für Schleswig-Holstein nicht korrekt. Die Fläche dieses Bundeslandes beträgt ca. 15800 km^2. Daraus ergibt sich bei einer installierten Leistung von 9112 MW eine flächenbezogene Leistung von 0,58 W/m^2 und nicht 0,67 W/m^2.
DANKE für diesen schönen (aber nicht, was seine Aussage betrifft) Artikel, den ich mir vor einigen Wochen hier in einem Kommentar „gewünscht habe“. Nicht darin enthalten sind (leider) noch andere (obskure?) Ideen, die mir zu diesem Thema durch den Kopf gingen, etwa ob die „Verwirbelungs-Fahnen“ hinter den Windrädern messbar den Boden kilometerweit abtrocknen oder ob durch die rotierenden Rotorblätter eine „Wassertröpchenabscheidung“ aus der Luft erfolgt – obgleich ich bei Windrädern in meiner Nähe noch keine „unübersehbaren Tropfspuren“ unmittelbar unter den Windrädern fand.
Im Bild ist das aktuelle 12 Monate Mittel der monatlichen Niederschlagsmenge von Deutschland gezeigt (nach DWD regional averages). Auch nach dem regenreichen April 2023 ist das Thema Niederschlagsmangel in Deutschland nicht vom Tisch. (Siehe markierter Punkt 202205-202304). Grün sind die mit einem Tiefpass-Filter geglätteten Daten.
Endlich kommt ein Beitrag, der sich mit dem Problem beschäftigt. M.E. entziehen vereinfacht WKA´s der Atmosphäre Energie bei konstanter Temperatur. PVA’s entziehen der Luft keine Energie, heizen aber die Luft auf. Im Mollier-h-x-Diagramm ergibt sich in beiden Fällen eine Abnahme der relativen Luftfeuchte. Für die PVA’s kann man es vielleicht so machen; die absolute Feuchte bleibt konstant. Bei den WKA´s ist das aber so nicht anwendbar. Der Fakt bleibt aber, dass diese erheblich der Luft Energie entziehen. Studien dazu sind offensichtlich bisher nicht veröffentlicht. Streng geheim?
Endlich kommt dieses wichtige Thema in die Diskussion.
Regen kommt zustande, wenn warme und kalte Luftmassen zusammentreffen in einer Luftmassengrenze. Dazu ist die Bewegung dieser Luftmassen erforderlich. Wenn diese Bewegung weniger wird, weil der Luft kinetische Energie entzogen wird, dann wird es weniger Regen geben. Also gibt es eine Kausalität. Hier scheint es, als wenn die Kausalität auch zu beobachten ist durch weniger Niederschlag.
Also weiter beobachten, und Rechnungen dazu anstellen. Ich werde dazu nicht rechnen, ich kümmere mich weiter um Strahlung und Radioaktivität.
Es sollte doch möglich sein, Vergleiche zwischen Gegenden ohne Windkraft und PV und solchen mit zu ziehen. Wenn es einen Einfluß gibt, und der scheint mir eher wahrscheinlich als unwahrscheinlich, sollte das aus solchen Vergleichen der Statistik vorher und nachher eigentlich hervorgehen.
Wenn es so wäre, müßte es auch eine Erklärung auf Basis der Physik geben, wie das Kondensationsverhalten von Dampf zu Tropfen verändert wird. Bei der Kondensation wird ja Wärme (=Energie), die bei der Verdunstung der Umgebung entzogen wurde, wieder frei. Wenn die Energie der Atmosphäre aber durch Propeller oder PV-Elemente entzogen wird, kann weniger in Kondensation fließen.
Könnte das der Fall sein?
Interessant wäre das auf jeden Fall. Nur ist es vermutlich nicht zu machen. Man braucht die Orte der wesentlichen Anlagen und die Orte der Meßstationen. Halten Sie das für durchführbar?
Herr Strasser, das kann man so nicht sagen. Die Energie, die bei Kondensation frei wird, hängt ausschließlich von der kondensierenden Menge an Wasserdampf ab. Sie kann nicht vorher durch Windräder etc. entzogen werden, es handelt sich um sog. latente Wärme. Windräder entziehen der Luft aber Bewegungsenergie.
Eine andere Frage ist, ob Windräder durch ihre Veränderung der Strömungsverhältnisse Einfluss auf die Verdunstung und damit den Wasserdampfgehalt der Luft haben. Außerdem haben sie natürlich Einfluss auf den Transport der Luftmassen und damit auch der Luftfeuchtigkeit. Der Ort des Abregnens könnte sich dadurch verlagern. Außerdem ist davon auszugehen, dass durch die Verringerung der Strömungsgeschwindigkeit hinter einem Windpark Luft von oben in tiefere Schichten absteigt, um kein Vakuum entstehen zu lassen. Absteigende Luft wirkt aber der Kondensation und Niederschlagsbildung entgegen. Alles in allem halte ich das für ein interessantes Forschungsthema.
Die Plätze 1 bis 3 bei der Strombereitstellung im Jahr 2022
1. Windkraft ca. 123TWh
2. Braunkohle ca. 107TWh
3. Solarstrom ca. 57TWh
Die Kernkraft ist weit abgeschlagen auf Platz 6 mit 33TWh
Herr Kraus, wenn Sie ernstgenommen werden wollen, zeigen Sie am besten die Bereitstellung vder elektrischen Leistung auf. Was wollen sie z.B. mit 100W PV Einspeisung über 10 Stunden wenn man mittags 2kW zum Kochen braucht!
„Herr Kraus, wenn Sie ernstgenommen werden wollen, ..“
Will er eh nicht – er will nur trollen
Herr Kraus,
was ist denn Ihre Tabelle für den tatsächlichen Stromverbrauch wert, wenn die Nr. 3 (Solar) nachts auf Null sinkt, tagsüber flattert. Dazu die Nr. 1 (Wind) auch völlig ungleichmäßig „flattert“ zbd bis auch mal fast auf Null absinkt. Nur die Braunkohle darin ist 24h verfügbar.
Allein die daraus BERECHNETEN (also nur theoretischen) EINSPARMENGEN an CO2 sind -egal ob „wirksam oder nicht wirksam“ angesehen- schon nur noch mathematisch getrickste und falsche Zahlenwerte. Immer! Denn die Wärmekraftwerke so schnell und feinteilig hoch und runterregeln, wie mal etwas mehr oder weniger Wind und Sonne auftreten, ist physikalisch mit „îrdischer“ Technik leider leider, schlicht unmöglich.
Doch vielleicht kommt ja bei den „EEs“ bereits „5-dimensionale Alien-Technik“ zum Einsatz, die solches kann? ScienceFiction als GRUNDLAGE der „Energiewende“? WOW! Wieder etwas zum Staunen!!!
Werner Eisenkopf
„Photovoltaikanlagen reflektieren die Sonnenstrahlen ähnlich Spiegeln und wirken somit aufheizend für die Atmosphäre. Sie wirken als Wärmeinseln und beeinflussen Luftströmungen.“
Das ist voll zutreffend – allerdings wirken die PV nicht wie ein Spiegel, sondern eher wie ein schwarzer Körper: Sie heizen tagsüber stark und kühlen in der Nacht etwas. Insgesamt gute Arbeit – allerdings müsste noch die AMO-Warmphase in die Betrachtungen einbezogen werden; trotzdem ist klar: Wind uns Solar bekämpfen die Klimaerwärmung nicht – sie befeuern diese.
Es ist schon klar, dass sicher noch weitere Einflüsse vorhanden sind. Es sollte ja auch nur die Korrelation gezeigt werden. Aber die Erscheinung, dass gerade 2000 dieser Abfall eintritt, ist schon eigenartig.
Kathastrophal für die Klimaerwärmung sind abgeschaltete PV-Anlagen. Sie absorbieren 97% der Solarstrahlung und wandeln sie in Wärme um ohne Strom zu erzeugen. Mit dem geplanten Ausbau der PV-Anlagen auf über 200 GWp wird dies die Atmosphäre weiter aufheizt.
Lösen liese sich das Problem, wenn man bei Strom-Überangebot die Solarmodule um 180° verdreht und die refrlektierende Rückseite der Sonne zuwendet. Dann wirken die Module wie ein Spiegel und schicken die Energie zum Absender zurück und würden die Atmosphäre sogar kühlen .
# Dr. Voge und H. Kämpfe:
Seit den 1980ern nehmen die Aerosole über Europa ab. Globalstrahlung, Sonnenstunden nehmen seitdem zu und Niederschläge teils ab. Vor allem im Sommer. Siehe Arbeiten von Martin Wild ETH.
Sehr gute Übersicht bzgl. der Niederschlagsdaten. Gleichzeitig werfen die Daten neue Fragen auf. Angefangen von der zeitlichen Verteilung. So ist zu erwarten, dass das Wettersystem gerade im Frühjahr, wenn das Windangebot relativ niedrig ist empfindlicher auf den Energieentzug reagiert als z.B. im stürmischen Spätherbst und Winter. Dann nach der regionalen Verteilung. So sind vor den (ersten) WKAs sogar mehr Niederschläge zu erwarten (Staueffekt), während die Abnahme dahinter stärker sein sollte. Insofern sollten die Auswirkungen immer stärker im Hinterland auftreten. In Bayern sollte Nordbayern mehr betroffen sein als Südbayern. Denn im letzteren sorgt der Staueffekt der Alpen und auch Tiefs vom Mittelmeer (weniger durch WKAs behindert) für höhere Niederschläge. Was die PV Anlagen betrifft, so dürften die Freiflächenanlagen das lokale Klima weit stärker beeinflussen, wie die Module auf Gebäuden. Denn erstere reduzieren die Verdunstung, während bei Gebäuden dieser Effekt auch ohne PV schon auftrat. Was Korrelation und Kausalität betrifft, so beweist eine Korrelation natürlich noch keine Kausalität. Allerdings ist eine entsprechende Kausalität auch physikalisch zu erwarten. Denn bei weniger Luftaustausch ist auch ein geringerer Feuchtigkeitstransport vom Meer an Land zu erwarten. Ansonsten steigern ja höhere Temperaturen den Feuchtigkeitsgehalt der Luft, weshalb eigentlich mehr Niederschläge zu erwarten wären. Bezüglich der Arbeit [4] von A. Kleidon finde ich in dieser die Angabe (schon im Abstract), dass sich großflächig höchstens 0,5 W/m² Windenergie nutzen lassen. Und aus der Arbeit geht hervor, dass dies das ultimative Limit ist. Bei dem Versuch, die Windenergie noch stärker zu nutzen, würde danach der Bremseffekt so weit überwiegen, dass die Leistung wieder abnimmt (wie da Abwürgen eines Motors). Insofern ist schon bei einer weit geringeren Nutzung eine Klimaveränderung zu erwarten.