Um die Größenordnung des Treibhauseffektes zu berechnen, wird die einfallende und ausgehende Strahlung üblicherweise verglichen mit den Strahlungsemissionen der Erde mit ihrer gemittelten Temperatur von 14°C bis 15°C. Diese geht auf den Datensatz der absoluten Temperatur der HADCRU-Version 4 1961 bis 1990 zurück. Mittels der Planck-Funktion oder des ähnlichen Stefan-Boltzmann-Gesetzes (siehe Gleichung 1) kann die von der Erde emittierte Strahlung aus deren Temperatur T berechnet werden unter der Annahme, dass sich die Erde wie ein Schwarzkörper verhält. Normalerweise wird die Strahlungsberechnung durchgeführt unter der Annahme einer Emissivität (e) von 1. Dies bedeutet, dass die Erde ein perfekter Schwarzkörper ist, der genauso viel Energie emittiert wie er empfängt. Das verwendete Gebiet beträgt 1 Quadratmeter, so dass das Ergebnis in Watt/m² vorliegt. Mittels dieser Annahmen ergibt die Berechnung, dass die Erde etwa 390 W/m² emittiert bei einer Temperatur von 288 K (Kiehl and Trenberth, 1997).

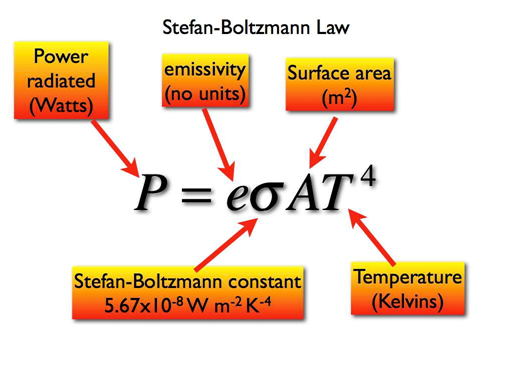
Gleichung 1 (Quelle)

Wenn er auf diese Weise berechnet wird, zeigt der Treibhauseffekt (GHE) ein Ungleichgewicht von 390 – 239 = 151 W/m². Kiehl und Trenberth 1997 berechneten einen ähnlichen Gesamtantrieb von 155 W/m² mittels des gleichen Verfahrens. Die GHE-Berechnung erfolgt unter vielen Annahmen, von denen nicht die Geringste die Annahme ist, dass die Erde eine Emissivität von 1 aufweist und ein Schwarzkörper ist. Aber hier wollen wir das Problem der Verwendung einer globalen mittleren Temperatur T der Erde in Betracht ziehen, welche eine rotierende Kugel ist, wobei zu jeder Zeit nur die Hälfte dieser Sphäre der Sonne zugewandt ist.

Ein spezifisches Problem ist, dass die Erde eben keine gleichmäßige globale Temperatur aufweist. Falls man diese mit 288 K annimmt, dann wird es Stellen auf dem Planeten geben, welche genau diese Temperatur aufweisen, und diese Stellen werden in etwa 390 W/m² emittieren. Aber auf dem allergrößten Teil des Planeten wird die Temperatur eine andere sein und Energie proportional zu T4 emittieren. Das Mittel der Temperatur zur vierten Potenz ist nicht das gleiche wie das Mittel von T4. Dies ist einfache Hochschul-Algebra, und wie groß wird die Differenz dadurch wohl sein?

Um dies zu beantworten, wenden wir uns jetzt der Version 4 des globalen Temperatur-Datensatzes der Hadley Climate Research Unit (HADCRU) zu. Wir ziehen deren Version 4 mit der Referenzperiode 1961 bis 1990 heran sowie deren Temperaturanomalie-Datensatz von 1850 bis 2017. Die Konstruktion der Referenzperiode und der Anomalie-Datensätze wird von Jones et al. (2012) beschrieben. Da die Reihen der Temperaturanomalien Anomalien jeder Reihe im Vergleich zur Periode 1961 bis 1990 sind, sollten wir in der Lage sein, die Referenztemperatur der Reihen zu nutzen, um die Anomalien in absolute  Temperaturwerte umzuwandeln. In beiden Fällen handelt es sich um Datensätze mit Gitterpunkten von 5° zu 5°. Anomalien werden für jede Station berechnet, um Probleme wegen der unterschiedlichen Seehöhen zu vermeiden. Das wird vor dem Anbringen des Gitternetzes gemacht. Addiert man folglich die Referenztemperatur zu der Anomalie, erhält man nicht die Original-Messungen. Auf der Website von HADCRU heißt es dazu:

„Festlandsstationen befinden sich in unterschiedlichen Höhen (bezogen auf NN), und verschiedene Länder messen mittlere monatliche Temperaturen mittels verschiedener Verfahren und Formeln. Um Verzerrungen aufgrund dieser Probleme zu vermeiden, werden die monatlichen mittleren Temperaturen reduziert auf Anomalien hinsichtlich der Referenzperiode mit der besten Abdeckung (1961 bis 1990). Für die herangezogenen Stationen muss ein Mittelwert der Referenzperiode berechnet werden. Weil die Messreihe vieler Stationen von 1961 bis 1990 nicht vollständig sind, kamen verschiedene Verfahren zur Anwendung, um Mittelwerte 1961 bis 1990 aus benachbarten Stationen oder anderen Datenquellen zu erhalten (mehr dazu bei Jones et al., 2012). Über den Ozeanen, wo Beobachtungen allgemein von mobilen Plattformen erfolgen, ist es unmöglich, lange Temperaturreihen für bestimmte feste Punkte zu erhalten. Allerdings kann man historische Daten extrapolieren, um räumlich vollständige Referenzwerte (Mittelwerte 1961 bis 1990) zu erstellen, so dass individuelle Beobachtungen verglichen werden können mit dem lokalen Normalwert für den gegebenen Tag des Jahres (Weiteres dazu bei Kennedy et al., 2011).

Es ist möglich, absolute Temperaturreihen für jedes gewählte Gebiet zu erhalten mittels Daten des absoluten Datensatzes und diese dann zum regionalen Mittel zu addieren, welches aus den genetzten [gridded] Daten berechnet worden ist. Falls beispielsweise ein regionales Mittel angefordert wird, sollten die Nutzer eine regionale Zeitreihe mittlerer Anomalien berechnen und dann die Werte im absoluten Datensatz für das gleiche Gebiet mitteln und diesen Wert schließlich zu jedem Wert in der Zeitreihe addieren. Man addiere NICHT die absoluten Werte zu jeder Gitterbox in jedem monatlichen Bereich, um danach großräumige Mittelwerte zu berechnen.

Übrigens ist dieses NICHT ( Im Original „NOT“, Anmerkung des Übersetzers) auf der Website selbst in Großbuchstaben zu finden, das habe ich nicht verändert. Ich hatte vor, die Gitter-Temperatur 1961 bis 1990 zu der Gitter-Anomalie zu addieren und eine angenäherte tatsächliche Temperatur zu erhalten, aber sie sagen, man solle das „NICHT“ tun. Warum sagt man dem Leser, dass man die absoluten gemittelten Referenz-Temperaturen zu den gemittelten Anomalien addieren kann, und sagt ihn danach explizit, nicht die absolute Gitter-Temperatur zu einer Gitter-Anomalie zu addieren? Jede Anomalie-Reihe muss auf ihr eigenes Mittel 1961 bis 1990 bezogen werden. Warum spielt es dann eine Rolle, dass wir die Anomalien und dann die Referenztemperaturen separat mitteln, bevor man beide addiert? Also war natürlich das Erste, was ich machte, die absoluten Gitterwerte 1961 bis 1990 zu den Anomalie-Gitterwerten zu addieren, und zwar für die gesamte Erde von 1880 bis 2016, also genau das, was ich laut Instruktion „NICHT“ tun sollte. Das absolute Temperaturgitter ist vollständig ohne fehlende Werte. Die Jahr-für-Jahr-Gitter weisen viele fehlende Werte auf, und die gleichen Gitterquadrate sind nicht in jedem Jahr gleich belegt. Es stellt sich heraus, dass dies genau das Problem ist, auf welches HADCRU mit diesem Zitat hinweist.

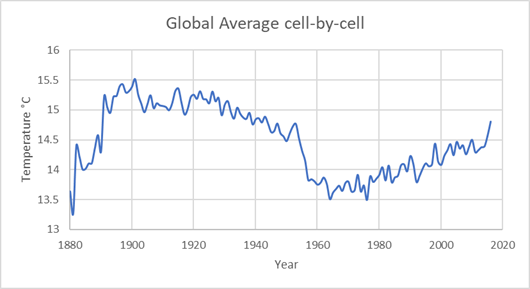
Abbildung 1 zeigt die globalen mittleren Temperaturen von 1880 bis 2016, berechnet nach den Vorgaben vom HADCRU. Zuerst habe ich die Anomalien eines jeden Jahres gemittelt und gewichtet nach dem Kosinus der Breite, weil es sich um ein 5° X 5°-Gitter handelt und die Fläche jedes Gitterquadrates vom Äquator zu den Polen mit dem Kosinus der Breite abnimmt. Dann habe ich die globale Mitteltemperatur 1961 bis 1990 zur mittleren Anomalie addiert. Während das Referenztemperatur-Gitter vollständig mit absoluten Temperaturen angefüllt ist, ist dies bei den jährlichen Anomalie-Gittern nicht der Fall. Außerdem wechseln die vollständig abgedeckten Gitterquadrate von Jahr zu Jahr. Dieses Verfahren vermischt eine Berechnung eines vollständig ausgefüllten Gitterquadrates mit einer Berechnung eines Gitterquadrates mit nur wenigen Werten.

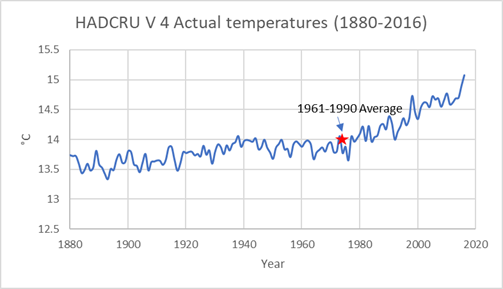
Abbildung 1: Mittelung der Anomalien mit nachfolgender Addition zur mittleren globalen Temperatur 1961 bis 1990.

Wenn man das so macht, wie man uns explizit sagt es nicht zu machen, erhalten wir Abbildung 2. Darin addierte ich die geeignete absolute Gitterquadrat-Mitteltemperatur zu jedem abgedeckten Gitterquadrat für jedes Jahr, um ein Netz mit absoluten Temperaturen zu erhalten und dieses dann zu mitteln unter Nichtbeachtung der Gitterquadrate ohne Werte. In diesem Prozess passt das Gitter der absoluten Temperaturen zum Anomalie-Gitter.

Abbildung 2: Umwandlung jeder Gitterzelle in tatsächlich Temperatur mit nachfolgender Mittelung

Der Unterschied zwischen den Abbildungen 1 und 2 wird am augenfälligsten vor dem Jahr 1950. Nach 1950 ist der untere Plot ein paar Zehntelgrad niedriger, aber der Trend ist der gleiche. Mit perfekten Daten sollten beide Plots gleich sein. Jede Zeitreihe wird konvertiert in eine Anomalie unter Verwendung der eigenen Daten 1961 bis 1990. Multiple Reihen in jedem Gitterquadrat werden zusammengeführt mittels direkter Mittelwerte [straight averages]. Aber – die Daten sind eben nicht perfekt. Gitterquadrate weisen in einem Jahr viele Messungen auf, in anderen gar keine. Vor 1950 ging die Abdeckung auf der Nordhemisphäre nie über 40% hinaus, auf der Südhemisphäre nie über 20%. Angesichts der großen Differenz zwischen den Abbildungen 1 und 2 ist nicht klar, ob die Daten vor 1950 robust sind. Oder klarer ausgedrückt, die Daten vor 1950 sind nicht robust. Ebenfalls ist unklar, warum die Periode 1950 bis 2016 in Abbildung 2 um 0,2°C bis 0,3°C kühler ist als in Abbildung 1. Ich kratze mich immer noch am Kopf ob dieses Phänomens.

Das HADCRU-Verfahren zur Berechnung globaler Temperaturen

Das Verfahren zur Berechnung der Gitterquadrat-Temperaturen von HADCRU Version 4 wird auf deren Website so beschrieben:

Dies bedeutet, dass es 100 Angaben für jedes Gitterquadrat gibt, um die möglichen Annahmen abzuklopfen, welche in der Struktur der verschiedenen Komponenten des Fehlers involviert sind (siehe die Diskussion bei Morice et al., 2012). Alle 100 Angaben sind auf der Site des Hadley Centers verfügbar, aber wir haben hier das Ensemble-Mittel gewählt. Für die genetzten Daten ist dies das Ensemble-Mittel, separat berechnet für jede Gitterzelle und für jeden Zeitschritt der 100 Angaben. Für die hemisphärischen und globalen Mittelwerte ist dies wiederum der Median für die 100 Angaben. Der Median der genetzten Reihen wird nicht den Median der hemisphärischen und globalen Mittelwerte erzeugen, aber die Differenzen werden klein sein.

Folglich ist die globale Mitteltemperatur nach HADCRU Version 4 nicht ein wahres Mittel. Stattdessen ist es der Median-Wert der 100 statistischen Angaben für jede mit Messungen abgedeckte Gitterzelle und beide Hemisphären. Jede Temperaturmessung enthält Fehler und ist dadurch unsicher (Details dazu z.B. hier und hier). Das von HADCRU erzeugte 5° X 5°-Gitternetz enthält für ein Kalenderjahr mit 12 Monaten 31.104 Gitterzellen. Die meisten davon weisen keine Werte auf. Abbildung 3 zeigt die Anzahl dieser Zellen mit Null (ohne Werte) Jahr für Jahr von 1880 bis 2016.

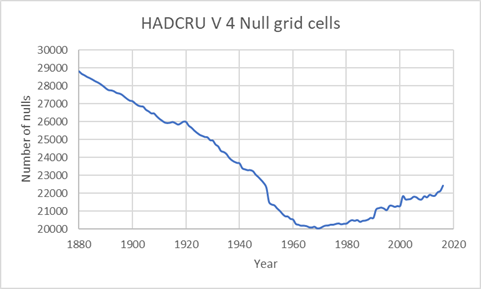
Abbildung 3. Datenquelle

Wie man sieht, gibt es aus den meisten Zellen keine Daten, nicht einmal während der letzten Jahre. In Abbildung 4 erkennt man die Verteilung der Gitterquadrate mit Messpunkten. Die Zellen mit adäquaten Daten sind gefärbt, jene mit unzureichenden Daten bleiben weiß. Die Abdeckung auf der Nordhemisphäre von 1960 bis 1990 liegt bei nahe 50%, die Abdeckung auf der Südhemisphäre im gleichen Zeitraum geht nie über 25% hinaus.

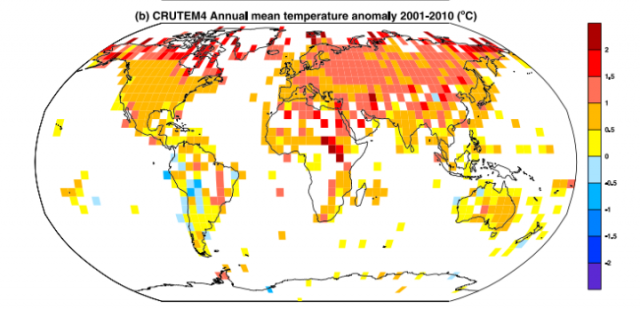
Abbildung 4. Quelle: Jones, et al., 2012

Die Daten sind also spärlich, und die meisten Daten stammen von der Nordhemisphäre und hier vom Festland. An beiden Polen gibt es kaum Daten. Also hat HADCRU zwei Probleme: erstens die Mess-Ungenauigkeit und zweitens, wie man mit der spärlichen und ungleichmäßigen Verteilung der Daten umgeht. Der Mess-Ungenauigkeit wird begegnet, indem gefordert wird, dass jede Gitterzelle eine ausreichende Anzahl von Stationen enthält, die über das betrachtete Jahr Meldungen absetzen. Da der Referenzzeitraum die Jahre 1961 bis 1990 sind, sind auch ausreichend Messungen über diesen Zeitraum erforderlich. Allgemein wird verlangt, dass die Stationen mindestens 14 Jahre lang Daten liefern zwischen 1961 und 1990. Stationen außerhalb von fünf Standardabweichungen des Netzes werden aussortiert [Stations that fall outside five standard deviations of the grid mean are excluded].

Die monatlichen Netze sind nicht umrissen, um die fehlenden Netz-Werte zu ergänzen, wie man erwarten könnte. Ist die mittlere Temperatur für jede Gitterzelle erst einmal mit ausreichend Daten berechnet, werden die durch Meldungen repräsentierten Gitterzellen Kosinus-gewichtet und gemittelt. Siehe Gleichung 9 in Morice, et al., 2012. Das Gebiet variiert so wie der Kosinus der Breite, also werden die Gitterzellen hiermit gewichtet. Die gewichteten Gitterwerte werden für jede Hemisphäre aufsummiert, und aus diesen Ergebnissen der beiden Hemisphären wird eine globale mittlere Temperatur gemittelt. Jahreszeitliche und jährliche Mittel sind aus monatlichen Gitterwerten abgeleitet.

Die meisten mit Messpunkten gefüllten Gitterzellen befinden sich auf dem Festland, weil wir hier leben; und doch sind 71% er Erdoberfläche von Ozeanen bedeckt. Gegenwärtig ist das kein Problem, weil wir Satellitenmessungen der Wassertemperatur und der Lufttemperatur über der Wasseroberfläche haben. Zusätzlich gibt es Netz aus ARGO-Bojen, welches hoch qualitative Ozeantemperaturen liefert. Aber historisch war das ein großes Problem, weil alle Messungen ausschließlich von Schiffen kommen mussten (die ich überdies zu ca. 90 % auf die Hauptschifffahrtslinien beschränkten..Anm. der Redaktion). Der entscheidende HADSST3-Datensatz für die Abschätzung der Ozeantemperatur wird beschrieben von Morice, et al., 2012. Eine ausführlichere Beschreibung der Probleme bei der Abschätzung historischer Wassertemperaturen in ozeanischen Gitterzellen gibt es bei Farmer, et al., 1989. Die Daten vor 1979 stammen aus dem in Schiffe einströmenden Kühlwasser, Treibbojen und Eimermessungen von Wasser neben den Schiffe. Diese Quellen sind mobil und anfällig für Fehler. Die Durchmischungs-Schicht der Ozeane ist im Mittel 59 Meter dick (JAMSTEC MILA GPV data). Mehr zu den JAMSTEC- Wassertemperaturdaten gibt es hier. Die Durchmischungsschicht der Ozeane ist diejenige Schicht, die sich zumeist im Gleichgewicht mit der Atmosphäre befindet. Diese Schicht weist 22,7 mal die Wärmekapazität der gesamten Atmosphäre auf und bewirkt einen merklichen Einfluss auf die Temperaturen der Atmosphäre. Sie wird auch beeinflusst durch die kühleren, tieferen Ozeanschichten, welche sie durch Aufwallen und Absinken beeinflussen können (hier).

Meine Berechnungen

Ich begann mit den Referenztemperaturdaten der Periode 1961 bis 1990, „Absolut“ genannt und hier zu finden. Dies ist eine Reihe von 5° X 5° globale Temperaturgitter für den Referenzzeitraum. Anders als die Anomalie-Datensätze sind diese Netze vollständig mit Meldungen besetzt und enthalten keine Null-Werte. Wie der Absolut-Datensatz besetzt war, wird erklärt von Jones, et al., 2012. Abbildung 5 zeigt die Karte des mittleren Absolut-Temperaturnetzes.

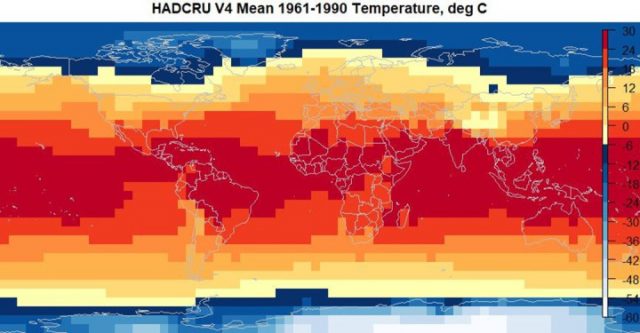
Abbildung 5: Karte der „Absolut“-Daten (Datenquelle: HADCRU)

Ich wendete das gleiche Verfahren an wie HADCRU. Zuerst las ich das Absolut-Netz, es enthält eine Anordnung, welche dimensioniert ist mit 72 Längengrad-Segmenten (5°), 36 Breitengrad-Segmenten und 12 Monaten oder ein Jahr. Als nächstes unterteilte ich das globale Anomalie-Netz von HADCRU4 Jahr für Jahr, mittelte die Zellen mit Messungen und addierte dann das mittlere Absolut der Temperatur von 1961 bis 1990 zur mittleren Anomalie. Die Ergebnisse zeigt Abbildung 1. Wie oben beschrieben, habe ich auch einige Zeit aufgewendet, genau das zu tun, was NICHT zu tun auf der HADCRU-Website empfohlen worden ist. Dieses Ergebnis zeigt Abbildung 2.

Die HADCRU-Daten reichen zurück bis zum Jahr 1850, aber es gibt kaum globale Daten vor 1880, und viele davon stammen aus der offenen Atmosphäre. Schutzfolien zur Abschirmung der Thermometer vor direktem Sonnenlicht waren bis 1880 kaum in Gebrauch, was die Qualität der frühen Daten beeinträchtigte. Also zog ich nur die Daten von 1880 bis 2016 heran.

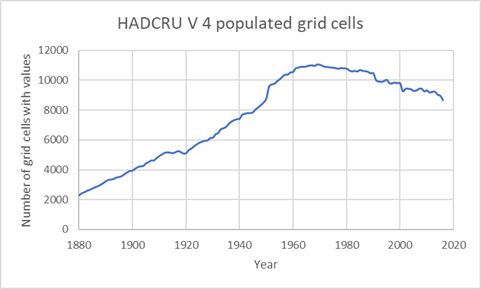
Das Überraschende an der Graphik in Abbildung 2 ist, dass die Temperaturen von 1890 bis 1950 höher lagen als jede andere Temperatur seitdem. Man betrachte Abbildung 3 bzgl. der Anzahl von Null-Werten. Es gibt insgesamt 31.104 Zellen, die maximale mit Messungen angefüllte Zahl beträgt rund 11.209 im Jahre 1969 oder 35%. Abbildung 6 ist invers die Abbildung 3 und zeigt die Anzahl der mit Messungen gefüllten Zellen für jedes Jahr.

Abbildung 6.

Geht die höhere Temperatur von 1890 bis 1950 in Abbildung 2 nur auf die geringe Zahl von Messungen enthaltenden Zellen zurück? Oder liegt es an der ungleichen Verteilung dieser Zellen? Es gibt einen plötzlichen Sprung der Anzahl mit Messungen belegter Zellen um das Jahr 1950, welcher zusammenfällt mit einem anomalen Temperaturabfall – was ist der Grund dafür? Geht es auf einen Rechenfehler in meinen Berechnungen zurück? Falls mir tatsächlich ein Fehler unterlaufen ist (was immer möglich ist), dann bin ich sicher, dass jemand den Fehler finden und mir mitteilen wird. Ich habe meine Berechnungen wieder und immer wieder überprüft und halte sie für korrekt. Ich habe die einschlägigen Studien gelesen und kann keine Erklärung für diese Anomalien finden. Alle Daten und der R-Code können hier heruntergeladen werden. Erfahrene R-Nutzer werden keine Probleme haben, die zip-Datei enthält den Code sowie alle eingehenden Datensätze und eine tabellarische Zusammenfassung des Outputs.

Energie und Temperatur

Ausschlaggebender Grund für diese Studie war es zu erkennen, welchen Unterschied die rechenbetonte Sequenz bei der Berechnung der Energie-Emissionen von der Erde ausmacht. Das heißt, nehmen wir die vierte Potenz einer mittleren Temperatur, wie es Kiehl und Trenberth 1997 gemacht haben? Oder nehmen wir jede Temperatur einer Gitterzelle zur vierten Potenz und mitteln dann die Stefan-Boltzmann (SB)-Energiegleichung aus Gleichung 1? Das Mittel der HADCRU-Temperaturen des Jahres 2016 beträgt 15,1°C. Die mit dieser Temperatur (288 K) berechneten SB-Energieemissionen sind die 391 W/m², welche allgemein in der Literatur genannt werden. Falls wir die SB-Emissionen aller belegten HADCRU-Gitterzellen für das Jahr 2016 berechnen und diese nach Gebiet gewichtet mitteln, erhalten wir 379 W/m². Dies ist eine geringe Differenz, solange wir nicht diese Differenz vergleichen mit der geschätzten Differenz, welche zunehmendes CO2 haben könnte. Im IPCC-Zustandsbericht 5 zeigt Abbildung SPM.5 (hier in der dritten Abbildung), dass die Gesamtauswirkung der menschlichen CO2-Emissionen seit 1750 2,29 W/m² ausmachten, also viel weniger als die Differenz zwischen den beiden Berechnungen der Emissionen der Erde.

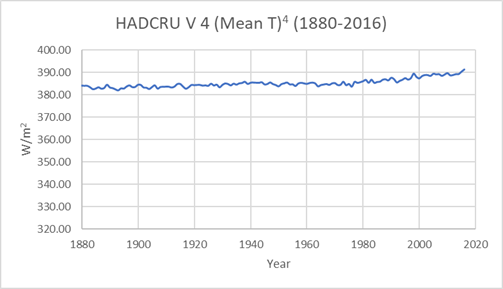
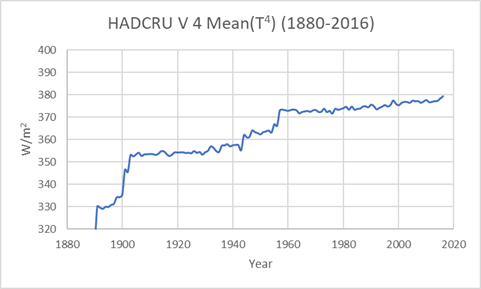
Der Vergleich wird noch schlechter, wenn wir ihn im zeitlichen Verlauf betrachten. Abbildung 7 zeigt die Berechnung der Energie-Emissionen bei einer globalen mittleren Temperatur oder (Mean T)4. Abbildung 8 zeigt die Berechnung durchgeführt für jede einzelne Gitterzelle in jeder mit Messungen belegten Zelle mit nachfolgender Mittelung oder (Mean T4).

Abbildung 7

Abbildung 8

Es scheint wahrscheinlich, dass die Differenzen von 1880 bis 1950 bezogen sind auf die Anzahl Messungen enthaltender Zellen sowie deren Verteilung, aber dies ist zum jetzigen Zeitpunkt Spekulation. Man muss sich Fragen stellen hinsichtlich der Genauigkeit dieser Daten. Der Vergleich seit 1950 ist O.K. außer für die algebraische Differenz, die sich ergibt, wenn man erst die Temperatur mittelt und dann den Mittelwert zur vierten Potenz erhebt, oder wenn man erst jede Temperatur zur vierten Potenz nimmt und dann die Energie mittelt. Von 1950 bis 2014 beträgt diese Differenz im Mittel 13 W/m².

Diskussion und Schlussfolgerungen

Ich stelle die von HADCRU getroffene Wahl nicht in Frage, 100 statistische Realisationen jeder Gitterzelle zu erzeugen und dann den mittleren Gesamtwert heranzuziehen, gewichtet nach dem Kosinus der Breite, als die mittlere Temperatur für jede Hemisphäre und dann die Hemisphären zu kombinieren. Das ist ein vernünftiges Verfahren, aber warum unterscheidet sich dieses Ergebnis von einem direkten gewichteten Mittel der mit Messungen belegten Gitterzellen? Meiner Ansicht nach sollte jedwedes statistische Ergebnis zu dem einfachen statistischen Ergebnis passen, oder die Differenz muss erklärt werden. Der Vergleich zwischen den beiden Verfahren für den Zeitraum 1950 bis 2016 ist O.K., obwohl das HADCRU-Verfahren zu einer verdächtig höheren Temperatur führt. Ich vermute, dass die Daten von 1950 bis 2016 viel robuster sind als die Daten davor. Ich würde jedwede Schlussfolgerung bezweifeln, welche von früheren Daten abhängig ist.

Deren geforderte Berechnung ist ein wenig verstörend. Es verlangt die Mittelung in einem kaum belegten Anomalie-Netz, dann die Mittelung eines vollständig belegten absoluten Temperatur-Netzes mit nachfolgender Summierung der beiden Mittelwerte. Dann instruiert man uns explizit, nicht die gleiche Belegung von Gitterzellen (Anomalie und Absolut) zu wählen, diese zu summieren und zu mitteln. Und doch summiert Letzteres Äpfel und Äpfel.

Schließlich ist es sehr klar, dass die Anwendung der SB-Gleichung zur Berechnung der Energie-Emissionen der Erde mit einer geschätzten globalen Mitteltemperatur falsch ist. So wurden die Emissionen in Abbildung 7 berechnet. Wenn wir die SB-Emissionen berechnen aus jeder belegten HADCRU-Gitterzelle und dann das Ergebnis mitteln, was laut Grundlagen-Algebra der richtige Weg ist, erhalten wir das Ergebnis in Abbildung 8. Vergleicht man beide Ergebnisse, zeigt sich, dass es erhebliche Probleme mit den Daten vor 1950 gibt. Ist dies die Anzahl der Null-Gitterzellen? Ist es die räumliche Verteilung belegter Gitterzellen? Ist es ein Problem der geschätzten Wassertemperaturen? Oder vielleicht ein anderer Komplex von Problemen? Schwer zu sagen, aber es ist schwierig, den früheren Daten zu vertrauen.

Wir versuchen, die Auswirkungen von steigendem CO2 zu bestimmen. Dies führt zu einem geschätzten „Forcing“ von etwa 2 W/m². Auch wollen wir wissen, ob die Temperatur während der letzten 140 Jahre um 1°C gestiegen ist Sind diese Daten genau genug, um sogar diese Auswirkungen aufzulösen? Das scheint mir nicht eindeutig.

Der R-Code und die Daten zur Erstellung der Abbildungen in diesem Beitrag können hier heruntergeladen werden.

Link: https://wattsupwiththat.com/2017/09/09/hadcru-power-and-temperature/

Übersetzt von Chris Frey EIKE

image_pdfBeitrag als PDF speichernimage_printBeitrag drucken