Beim derzeitigen Ausbau sind alle Wind- und Solarenergieanlagen in Deutschland zusammen nicht grundlastfähig. Eine entsprechende populärwissenschaftliche Untersuchung wurde vom Verfasser im Internet unter www.vernunftkraft.de/statistik/ veröffentlicht. Dort wurde die Aussage getroffen, „dass die gesicherte Leistung aller Windkraftanlagen in Deutschland zusammen mit Null anzusetzen ist.“ Dieser Fall ist inzwischen eingetreten, als die gesamte Windleistung am 13. März 2014 auf 34 MW (das ist ein Promille der installierten Kapazität bzw. Nennleistung von 34.000MW) abgesunken ist. Der praktische Totalausfall der Windkraft ist also in Deutschland inzwischen eingetreten.
An diesem Konsens unter Technikern und Wissenschaftlern ist nicht zu rütteln, schließlich sind die Einspeisekurven aller Windkraftanlagen in Deutschland öffentlich zugänglich.
Es ist daher nicht verwunderlich, wenn es hier nur „vage Aussagen“ in einschlägigen Studien gibt. Um diese Tatsache drückt sich die versammelte Lobby mit ihren nachgeordneten Instituten mit halbkonkreten Allgemeinplätzen herum.

Führt ein Ausbau der Windenergie zur Glättung der Einspeisung?

 In der Bewertung des weiteren Ausbaus auf eine Vergleichmäßigung der Einspeisung gehen die Einschätzungen unter Wissenschaftlern weit auseinander. Dem Sinne nach vertritt etwa das IWES in Kassel die Auffassung, dass ein weiterer Ausbau zur Glättung und damit zur Vergleichmäßigung der Einspeisung führt. So heißt es in der am IWES in Kassel verfertigten „Agora Kurzstudie zur Entwicklung der Windenergie in Deutschland“ z. B.: „Eine großräumige Verteilung der Anlagen führt folglich zu einer Glättung der Einspeisung.“
Wer sich jemals mit mathematischer Statistik befasst hat, sieht „auf den ersten Blick“, dass diese These mathematisch unhaltbar ist. Die Streuung oder Variabilität einer zufälligen Größe wie etwa die geworfene Augenzahl einer Folge von 50 Würfen mit einem Würfel wird in der Mathematik durch die sogenannte Varianz „gemessen“. Wenn man nun dieses Würfel-Experiment mit 2 Würfeln durchführt (und damit den Ausbau der Windkraft in dieses Experiment einbezieht, weil mit mehr Würfeln gewürfelt wird) und die Summe der Augenzahlen bildet und die Streuung dieser Summe betrachten, zeigt sich, dass die Streuung (und die Varianz!) der Summe steigt und nicht sinkt. Diese Aussage ist evident, weil die Zahlen bei einem Würfel zwischen 1 und 6, bei zwei Würfen zwischen 2 und 12 schwanken. Dahinter verbirgt sich der Additionssatz für die Varianz der mathematischen Statistik. Er besagt, dass sich die Varianz einer Summe zufälliger Zahlen als Summe der Varianzen der einzelnen Zufallszahlen ergibt. Mit jedem weiteren Summanden steigt die Varianz und damit die Streuung und letztlich die Variabilität.

Die Schlussfolgerung an dieser Stelle lautet zweifelsfrei:

Ein Ausbau der Windkraft erhöht die Streuung der Einspeisung. Die von IWES- Wissenschaftlern aufgestellte Behauptung zur Glättung steht im klaren Widerspruch zu eindeutigen Sätzen der mathematischen Statistik. Die Behauptung ist schlicht falsch!

Wird die Einspeisung durch den Ausbau der Windkraft verstetigt?

Betrachtet man die Frage der gegenseitigen Ergänzung von Windkraftanlagen zu einer „Verstetigung“ der Einspeisung, muss etwas genauer hingesehen werden. Die tieferen Zusammenhänge aus der mathematischen Statistik sind allerdings „etwas kniffliger“ (neudeutsch: more sophisticated): Das geschilderte Würfel-Experiment wollen wir nun mit 3, 4, 5 und schließlich mit einer sehr großen Zahl an Würfeln durchführen und die Summe der geworfenen Augenzahlen dabei betrachten. Diese Summe wollen wir in Gedanken bilden, weil die Einspeisungen aller einzelnen Windkraftanlagen in unserem Verbundnetz völlig analog in jedem Augenblick addiert werden. Wenn wir dieses Experiment mit 50 Würfeln durchführen sind folgende Aussagen unmittelbar klar: 

  • Als Summe wird sich sehr selten die Zahl 50 oder 300 ergeben, weil es sehr unwahrscheinlich ist, dass 50 Mal die Augenzahl 1 oder 6 fallen wird,
  • Die Zahl 175 wird häufig vorkommen, weil es viele Kombinationen aus Augenzahlen gibt, die zu der Summe von 175 führen.

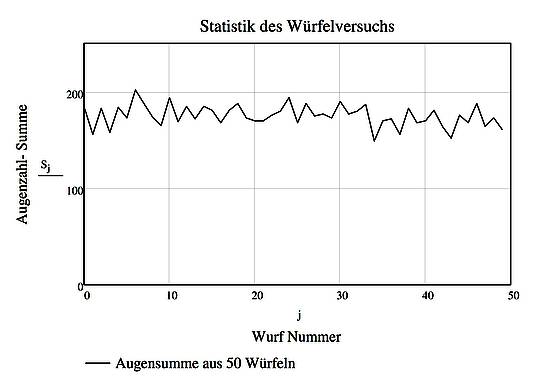
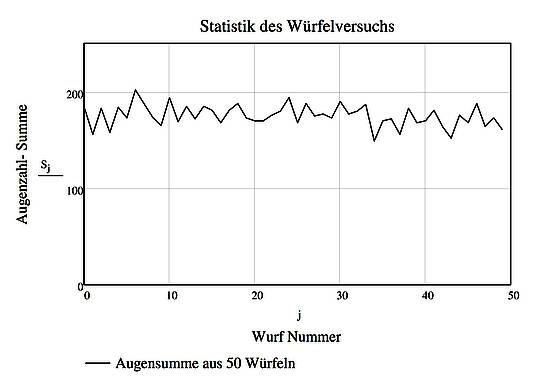
Abbildung  SEQ Abbildung * ARABIC 1 Summe der Augenzahlen bei 50 Würfeln 

Wertet man die Häufigkeitsverteilung dieser Summe aus, stellt man fest, dass diese Summe ungefähr entsprechend der bekannten Normalverteilung nach Gauß verteilt ist. Diese
Erkenntnis ist die Aussage eines fundamentalen Satzes der mathematischen Statistik, des sogenannten „Zentralen Grenzwertsatzes“. Er besagt folgendes: Bildet man die Summe aus einer großen Anzahl zufälliger Zahlen, dann folgt diese Summe einer Normalverteilung umso genauer, je größer die Anzahl der Summanden ist. Beim beschriebenen Würfelexperiment wird also die Summe der Augenzahlen um den Wert 175 schwanken, der kleinste Wert kann 50, der größte Wert kann 300 sein. Würde man die Summe der Augenzahlen als die aus 50 einzelnen Einspeisungen gebildete Summe der Einspeise-Leistungen auffassen, so kann zunächst die Aussage getroffen werden, dass diese gedachte zufällige „Leistung“ grundlastfähig ist, schließlich fällt sie praktisch nie auf den Wert Null ab und schwankt um einen Mittelwert. Der aus 50 Würfen nacheinander gebildete Verlauf der Summe ist in Abbildung 1 dargestellt. Man  erkennt, dass die Summen-Augenzahl um einen Mittelwert schwankt und praktisch nie auf kleine Werte abfällt.

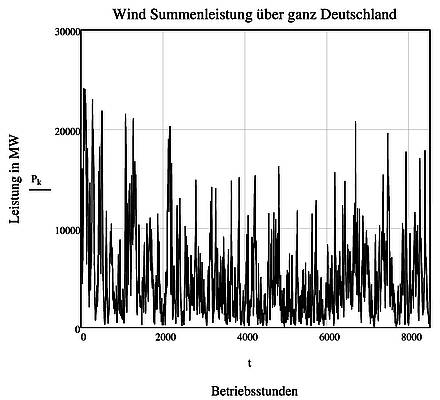
Abbildung  SEQ Abbildung * ARABIC 2 Tatsächliche Einspeisung der Windkraftanlagen in Deutschland 
Nun bildet das elektrische Netz in Deutschland die Summe der Einspeisungen aus 24000 Windkraftanlagen. Die Anzahl dieser Summanden übersteigt also statistisch die hier verwendete Zahl von 50 Würfeln um Größenordnungen. Aufgrund des vorgenannten Würfel-Experiments ist also zu erwarten, dass die Summe der Einspeisungen auf einen gleichmäßigen Kurvenverlauf führt, der dem in Abbildung 1 zumindest ähneln müsste.
Das ist ohne jeden Zweifel nicht der Fall: Der Verlauf der Einspeisung zeigt das bekannte Schwankungsverhalten mit den extremen Ausschlägen der eingespeisten Leistung. Darüber hinaus folgt die Summeneinspeisung aller Windkraftanlagen Deutschland nicht der Normalverteilung nach Gauß (Abbildung 3). Damit steht der Verlauf der tatsächlichen Einspeiseleistung zunächst sehr augenscheinlich im Widerspruch zu den Aussagen, die der Zentrale Grenzwertsatz der mathematischen Statistik für die eingespeiste Windleistung erwarten ließe

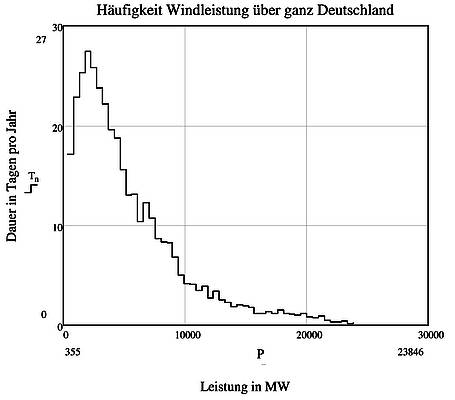
Die Übertragung der Resultate aus dem einfachen Würfelexperiment auf die Summeneinspeisung der Windkraftanlagen ist ganz offensichtlich ungerechtfertigt. 

Worin liegt nun der Fehler?

 Zunächst ist die eingespeiste Leistung eines einzelnen Windrads anders verteilt als die Augenzahl beim Würfeln. Letztere ist gleichmäßig verteilt, d. h. jede Augenzahl ist gleich wahrscheinlich = 1/6, entsprechend einer Wahrscheinlichkeit von 16,67%. Bei einem Windrad sind kleine Leistungen sehr viel wahrscheinlicher als große. Das ist allerdings nicht der Grund für die Abweichung der Kurvenverläufe, schließlich kann man den „Zentralen Grenzwertsatz“ der Statistik auf jede Art von Verteilung verallgemeinern.[1]
Der Unterschied zwischen dem Würfelversuch mit 50 Würfeln und der Addition der Einspeisungen aus 24000 (!) Windrädern besteht darin, dass die geworfene Augenzahl eines jeden Würfels mit der eines anderen Würfels „nichts zu tun hat“. Die geworfenen Augenzahlen aller Würfel sind in statistischem Sinne unabhängig voneinander. Diese Aussage gilt für die Einspeisungen der einzelnen Windräder nicht, weil die Windgeschwindigkeit an den verschiedenen Windradstandorten bei praktisch jeder Wetterlage in großen Flächen ähnlich ist, d. h. die einzelnen Einspeisungen sind nicht statistisch unabhängig voneinander. Wenn der Wind im Norden von Hessen stark weht, ist das praktisch immer auch im Süden von Hessen der Fall. Diese Aussage ist bei der üblichen Größe von Tiefdruckgebieten auch naheliegend und gilt sinngemäß für jedes Bundesland. Diese simple Tatsache bewirkt, dass hohe ebenso wie niedrige Einspeisungen praktisch immer gleichzeitig in großen Flächen auftreten. Man sagt, die Einspeisungen sind untereinander korreliert, d. h. im großflächigen Umfeld einer stichprobenartig gewählten Referenzanlage kann man die Einspeisungen aller Anlagen auf diese eine Referenzanlage zurückführen. Wenn man die eingespeiste Leistung einer Referenzanlage kennt, kann man also die Leistungen aller Anlagen im großflächigen Umfeld aus der Leistung der Referenzanlage mit hoher Wahrscheinlichkeit ermitteln. Diese Tatsache ist der Inhalt der statistischen Korrelation. Für die gesamte Fläche von Deutschland entspricht also jede Referenzanlage im statistischen Sinne gerade einem Würfel aus dem Würfelexperiment, womit die Frage gestellt ist, durch wie viele Referenzanlagen die Einspeisung in Deutschland dargestellt, also verstanden werden kann. Diese Zahl bemisst die Intensität der Korrelation. Ist diese Zahl klein, so ist die Korrelation stark ausgeprägt, ist diese Zahl groß, ist die Korrelation eher schwächer. Das Würfelexperiment hat gezeigt: Je größer diese Zahl, desto besser können die Einspeisungen sich untereinander ausgleichen. Ist diese Zahl jedoch klein, ist ein gegenseitiger Ausgleich der Einspeisungen zwar grundsätzlich möglich, die Leistungen können aber immer wieder auf sehr kleine Werte absinken, weil es bei weniger als 5 unabhängigen Referenzanlagen häufig vorkommt, dass die Einspeisung aller Anlagen auf sehr kleine Werte absinkt. In diesem Fall ist die Summeneinspeisung prinzipiell nicht grundlastfähig. In diesem Zusammenhang haben Windkraftanlagen ein weiteres Problem: Niedrige Leistungen kommen sehr häufig vor, sind also sehr wahrscheinlich, hohe Leistungen sind selten, sind also eher unwahrscheinlich. Diese Tatsache schlägt sich dann in der Häufigkeitsverteilung der Summeneinspeisung nieder, die in Abbildung 3 dargestellt ist.

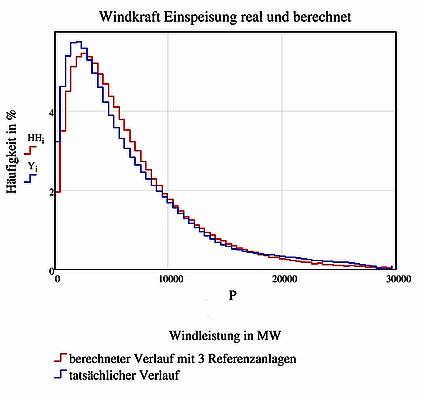
Abbildung  SEQ Abbildung * ARABIC 4 Häufigkeit der tatsächlichen und der aus 3 Referenzanlagen berechneten Einspeisung

Diese Verteilung ist ohne jeden Zweifel nicht nach Gauß normalverteilt, woraus unmittelbar gefolgert werden kann, dass zu deren Analyse eine kleine Anzahl unabhängiger Referenzanlagen ausreicht.
Es lässt sich nachweisen, dass diese  „kleine Anzahl“ lediglich bei 3 liegt, d. h. die gesamte Summeneinspeisung in Deutschland kann auf nur 3 Referenzanlagen zurückgeführt werden. Dieser Zusammenhang ist in Abbildung 4 dargestellt. Die Einspeisungen aller Anlagen sind also untereinander hochgradig korreliert. Obgleich also diese 3 Referenzanlagen  untereinander nicht korreliert sind, können alle 23997 restlichen Anlagen auf diese 3 Referenzanlagen zurückgeführt werden. Die in der genannten Agora Studie auf Seite 13 veröffentlichte Erkenntnis, „dass Anlagen an verschiedenen Standorten sich ergänzen können“ ist sicher korrekt, gleichwohl folgt daraus nicht, dass sich die unterschiedlichen Einspeisungen zu einer Grundlast ergänzen. Wie man in der Mathematik sagt, ist die Bedingung der statistischen Unabhängigkeit zweier Einspeisungen für die Grundlastfähigkeit zwar notwendig, aber nicht hinreichend.
Es kommt nicht darauf an, ob sich einzelne Anlagen an unterschiedlichen Standorten untereinander ergänzen können (also statistisch unabhängig voneinander sind), sondern wie groß die Zahl der Anlagen ist, die an verschiedenen Standorten statistisch unabhängig voneinander sind. Wenn sich die Summeneinspeisung aller Anlagen in Deutschland aktuell auf nur 3 statistisch unabhängige Referenzanlagen zurückführen lässt, kann vernünftigerweise nicht erwartet werden, dass die Anzahl der Referenzanlagen und damit der statistisch unabhängigen Einspeisungen durch den Zubau an Anlagen wesentlich anwachsen wird.
Ein Ausbau der Windkraft kann aufgrund der erwiesenermaßen ausgeprägten Abhängigkeit der Einspeisungen untereinander nicht zu einer Verstetigung der Leistung führen. Die vom IWES im Auftrag von Agora aufgestellte Behauptung wäre zwar wünschenswert, erweist sich aber als unzutreffend und widerspricht dem Zentralen Grenzwertsatz, einem fundamentalen Satz der mathematischen Statistik, der schon 1922 von dem Mathematiker Lindeberg bewiesen wurde.

Fazit:

  

1.     Aufgrund von fundamentalen Sätzen der mathematischen Statistik ist die summarische Einspeisung aus Windkraftanlagen in der Fläche von Deutschland prinzipiell nicht grundlastfähig. Der Ausbau der Windkraft in unserem Land kann und wird daran nichts Wesentliches ändern.

    • 2.     Die Leistungsspitzen werden durch den Ausbau der Windkraft weiter ansteigen und die bekannten Probleme der Überproduktion von nichtverwertbaren Strom mit Auswüchsen wie den sogenannten Negativpreisen an der Börse weiter verschärfen.

      3.     Es gibt keine großtechnisch verfügbare effiziente Speichertechnologie zur Nutzung der ansteigenden Leistungsspitzen, so dass das Stromnetz ohne Kraftwerke im Hintergrund nicht betrieben werden kann. Hierbei ist es völlig gleichgültig, ob diese mit Gas, Braun- oder Steinkohle betrieben werden. Der Ausstieg aus den Kernkraftwerken erzwingt einen Ausbau der konventionellen Kraftwerke. Die mit der Stromproduktion verbundenen Kohlendioxid-Emissionen werden ansteigen und nicht sinken.

    [1] Für den Fachmann: In der mathematischen Literatur ist diese Aussage als Ljapunov- Bedingung bekannt.

    image_pdfBeitrag als PDF speichernimage_printBeitrag drucken