1. Was ist Persistenz in Temperaturzeitreihen?
Zeitreihen sind wichtige Werkzeuge, um Informationen über komplexe Prozesse zu gewinnen. Herzspezialisten nehmen Zeitreihen des Herzschlags oder des Blutdrucks auf, um Aufschlüsse über den gesundheitlichen Zustand eines Patienten zu erhalten. Finanz- und Versicherungsmathematiker analysieren Zeitreihen, um die finanziellen oder versicherungstechnischen Risken von Unternehmen zu bewerten. Klimatologen verwenden Temperaturzeitreihen (Tages-, Monats- oder Jahresmittelwerte), um langfristige Klimatrends aufzufinden. Im Folgenden geht es hier um Temperaturzeitreihen.
Der englische Wasserbau-Ingenieur Harold Edwin Hurst untersuchte in den 1950-er Jahren die Tief- und Höchststände des Nils und entdeckte dabei als erster, dass hydrologische Zeitreihen ein Gedächtnis besitzen. Die aktuell gemessenen Werte hängen von den vergangenen, zum Teil weit zurückliegenden Werten ab. Später wurde erkannt, dass auch viele weitere Zeitreihen der Natur wie z.B. Baumringe ein Gedächtnis aufweisen. Man nennt dieses Phänomen Persistenz oder Autokorrelation. Die Schwankungen der Zeitreihe um ihren Mittelwert erfolgen in persistenten Zeitreihen nicht mehr unabhängig, sondern sie werden von der Vergangenheit der Zeitreihe beeinflusst.
Betrachtet man Temperaturzeitreihen, so erscheint dieses Verhalten zunächst nicht einmal so ungewöhnlich. Eine Temperaturzeitreihe weist zumindest ein "Gedächtnis" über die momentan herrschende Jahreszeit auf. Es kommt nie vor, dass auf einen warmen Sommertag plötzlich ein kalter Wintertag folgt, bzw. umgekehrt. Da jahreszeitlich bedingte Schwankungen im Allgemeinen weniger interessieren, werden die saisonalen Einflüsse vor der Persistenzanalyse aus einer Temperaturzeitreihe entfernt. Aber auch danach beobachtet man noch, dass ein Tagestemperaturmittelwert zumindest vom Vortag abhängt. So wird ein über dem längerfristigen Mittel liegender Temperaturwert am nächsten Tag mit über 50% Wahrscheinlichkeit ebenfalls über diesem Mittel liegen, Entsprechendes trifft für einen unter dem Mittel liegenden Temperaturwert zu. Eine Erklärung für dieses Phänomen liefern anhaltende Wetterlagen. Persistenz über mehrere Wochen kann man mit meteorologischen Blocksituationen, wie etwa einem lang anhaltendes Azorenhoch erklären. Für noch längere Zeiträume ist freilich über die Ursachen von Persistenz wenig bekannt. Es werden dekadale Oszillationen wie z.B. der El Nino, Einflüsse aus den sich ändernden Planetenkonstellationen und weiteres mehr diskutiert. Erstaunlicherweise findet man in Temperaturzeitreihen Persistenz bis über mehrere Jahrzehnte. Die Ursachen solch langreichweitiger Persistenz sind bis heute völlig unbekannt.
Persistenz in Temperaturzeitreihen kann bemerkenswerterweise empirisch mit nur einem Parameter beschrieben werden, dem berühmten Hurst-Exponenten alpha. Mit der Fluktuationsanalyse (FA) bzw. der auf der FA aufbauenden, trendbereinigten Fluktuationsanalyse (DFA) wird alpha ermittelt. Der hier interessierende Bereich von alpha in Temperaturreihen ist 0,5 ≤ alpha < 1. Eine Zeitreihe mit alpha = 0,5 ist rein zufällig (weißes Rauschen) und besitzt keine Persistenz . Für alpha > 1 (alpha ≈ 1 entspricht rotem Rauschen) wird die Zeitreihe instationär, ihre Werte können "weglaufen" und niemals wieder den Anfangswert erreichen. Stationäre Zeitreihen behalten dagegen ihren Mittelwert über längere Zeiten bei. Gemessene Temperaturzeitreihen sind stationär, ihre Hurst-Exponenten liegen deutlich unter alpha = 1. Nur fragwürdige Homogenisierungen [22], Glättungsprozeduren oder ähnliche Manipulationen können dies ändern. Die Hurst-Exponenten von sorgfältig gemessenen Temperaturzeitreihen, bei denen nur die unbedingt notwendigen Homogenisierungen vorgenommen wurden, bewegen sich im Bereich von etwa 0,55 bis 0,65. Temperaturzeitreihen von Stationen auf Inseln oder in Meeresnähe weisen höhere alpha-Werte bis maximal etwa 0,9 auf.
2. Persistenz, Trends und Extreme
Persistenz von Temperaturzeitreihen sieht zuerst wie eine mathematische Rarität aus, tatsächlich ist sie jedoch von maßgebender Relevanz. Die Analyse von Zeitreihen ist nämlich vorrangig an dem Auftreten von Trends sowie von Extremen interessiert. Dabei hat man die Vorstellung, dass ausgeprägte Trends oder Extreme durch äußere Einflüsse bedingt sind. Tatsächlich kommen aber extreme Temperaturanstiege bzw. -abfälle oder ungewöhnlich lange Serien von Jahren mit Maximaltemperaturen bzw. Minimaltemperaturen auch ohne äußere Einflüsse vor. Ist dies der Fall, sind diese Trends oder Extreme "natürlich". Zumindest von stark ausgeprägten Extremen vermutet man freilich, dass sie unnatürlich sind. d.h. durch externe Einflüsse erzeugt wurden. Diese unzutreffende Annahme ist aus der Erfahrung täglichen Lebens abgeleitet. Ein Würfelspieler freut sich darüber, wenn die von ihm bevorzugte Zahl in Serie erscheint. Ist die Serie allerdings ungewöhnlich lang oder kommen gar solche Serien ungewöhnlich oft vor, argwöhnt man zutreffend eine externe Ursache, einen „gezinkten“ Würfel oder betrügerische Manipulation. Für Temperaturzeitreihen geht diese intuitive Beurteilung allerdings fehl. Der Grund dafür ist Persistenz.
Die entscheidende Folge von Persistenz in Zeitreihen ist, dass ausgeprägte Trends und Extreme auf natürliche Weise mit zunehmender Persistenzstärke ebenfalls zunehmen.
Diese Folge von Persistenz ist anschaulich verständlich. Persistenz bewirkt, dass die Zeitreihe die Tendenz aufweist, einen einmal angenommenen Wert beizubehalten. Auf diese Weise entstehen mehr Extreme und längere Trends. Damit wird der Stellenwert von Persistenz für Temperaturzeitreihen-Analye deutlich. Finden wir beispielsweise in einer Temperaturzeitreihe des 20. Jahrhunderts einen Erwärmungstrend, so besagt dies keineswegs zwingend, dass hierfür eine unnatürliche Ursache, wie z.B. zunehmendes CO2 oder Stadterwärmung (UHI) verantwortlich sein muss. Der Trend könnte auch eine ganz natürliche Folge der Persistenz der Zeitreihe sein.
Vor näherem Eingehen auf Persistenz in Temperaturreihen soll zur Veranschaulichung des Phänomens gezeigt werden, wie man einem Würfel zu Persistenz verhelfen kann. Ein solcher Persistenzwürfel wird deutlich mehr Trends in Form von ungewöhnlich langen Serien gleicher Augenzahlen liefern. Dennoch bleibt er „fair“, d.h. alle Augenzahlen kommen auf Dauer gleich oft vor. Der Persistenzwürfel ist ein gewöhnlicher Würfel mit einer Besonderheit: wird er geworfen, und es erscheint beispielsweise die 5, hängt der Spieler ein kleines Gewicht an die gegenüberliegende Seite, also an die 2. Dies erhöht die Wahrscheinlichkeit, dass auch weiterhin die 5 gewürfelt wird. Dennoch wird irgendwann eine andere Zahl auftauchen. Nun hängt der Spieler das Gewicht auf deren Unterseite. Würfelt man lange genug, kommen alle Augen mit gleicher Wahrscheinlichkeit vor. Dennoch erscheinen ungewöhnlich lange Serien von jeweils gleicher Augenzahl. Sie sind jedoch nur durch das zum System gehörige Gewicht bestimmt, nicht durch äußere Einflüsse (man kann sich den Mechanismus intern gesteuert vorstellen, ein Spieler, der die Gewichte anbringt, ist prinzipiell unnötig). Die langen Serien gleicher Zahlen treten rein zufällig auf und sind völlig natürlich.
Im Gegensatz zu Temperaturreihen reicht das Gedächtnis des Persistenzwürfels allerdings nur einen einzigen Wurf zurück. Man kann dieses Verhalten mit einem sog. AR(1) Prozess modellieren. Persistenz in Temperaturreihen hat dagegen mit Modellprozessen, wie in AR-, MA- oder ARMA-Modellen [13] nichts zu tun. Persistenz ist eine empirische Eigenschaft ohne Modellgrundlage und sie ist prinzipiell beliebig langreichweitig. Man kann mit dem Computer synthetische Zufallszeitreihen erzeugen, die eine vorgegebene Persistenz, d.h. einen vorgegebenen Hurst-Exponenten alpha aufweisen [1]. Mit Hilfe solcher Surrogatreihen lassen sich die durch Persistenz entstehenden Phänomene studieren.
3. Surrogatzeitreihen mit „Gedächtnis“
Surrogatzeitreihen, d.h. mit dem Computer erzeugte künstliche Zeitreihen, die zudem Persistenz aufweisen, sind ein entscheidendes Hilfsmittel zur Persistenzanalyse. Die Erzeugung von rechteckverteilten Zufallszahlen (Pseudozufallszahlen) mit dem Computer ist jedem EXCEL-Benutzer bekannt. Bildet man solche Zufallszahlen auf den Bereich von Jahresmitteltemperaturen ab, erhält man eine Temperaturzeitreihe mit dem Hurst-Exponenten von alpha = 0,5. Eine solche Reihe sieht freilich unrealistisch aus, sie entspricht bereits dem Augenschein nach noch nicht der Gestalt einer real gemessenen Temperaturzeitreihe.
Surrogatreihen werden „lebensechter“, wenn man ihnen zu Persistenz verhilft. Zur Veranschaulichung sei an das oben beschriebene Beispiel des Persistenzwürfels erinnert. Die Vermittelung von Persistenz an eine Temperaturzeitreihe erfolgt allerdings mit dem Computer – Details finden sich in der Originalliteratur [1], [24]. Surrogatreihen des gleichen alpha wie eine gemessene reale Reihe, weisen schon beim bloßen Anschauen eine große Ähnlichkeit mit gemessenen Reihen auf. Allerdings können reale Temperaturreihen einen externen Trend enthalten, Surrogatreihen nicht. Man könnte Surrogatreihen daher zutreffend als „natürlich“ bezeichnen, obwohl diese Bezeichnung etwas paradox erscheint, denn sie wurden schließlich vom Computer erzeugt. In konsequent gleichem Sprachgebrauch sind reale Temperaturreihen mit einem externen Trend „unnatürlich“.
Bild 1 (s. Titelbild oben) zeigt ein Anschauungsbeispiel, wie sich Persistenz in Surrogatreihen auswirken kann: Im linken Teilbild ist eine ausgewählte Zeitreihe mit alpha = 0,5 (keine Persistenz) gezeigt, im rechten Teilbild eine von alpha = 0,73. Beide Zeitreihen sind Surrogate und enthalten keinen externen Trend. Dennoch ist im rechten Teilbild deutlich ein „Trend“ erkennbar, der ein wenig an den Verlauf der globalen Erwärmung im 20. Jahrhundert erinnert. Er ist rein zufällig, natürlich und nur durch Persistenz bedingt. Nun entsteht die wichtige Frage: Woher erkennt man im konkreten Fall, ob ein Trend in einer real gemessenen Temperaturreihe extern ist?
4. Die Suche nach externen Trends
Externe Trends in Temperaturreihen stehen zweifellos im Mittelpunkt der heutigen Klimadiskussion. So möchte man gerne wissen, ob die in den letzten Jahrzehnten des 20. Jahrhunderts von vielen Stationen gemessene globale Erwärmung ein vom industrialisierten Menschen verantworteter Trend oder aber nur ein durch Persistenz bedingter Artefakt ist. In diesem Zusammenhang ist zu betonen, dass die von den weltweit verstreuten Stationen gemessene Erwärmung im 20. Jahrhundert keinesfalls global einheitlich ausfällt. Etwa ein Viertel aller Stationen zeigt in diesem Zeitraum nämlich Abkühlung [6], [12]. Die mathematischen Hilfsmittel zur Persistenzanalyse von Temperaturreihen liefern die schon erwähnten Methoden der FA und der DFA. Eine ausführliche Beschreibung dieser Verfahren findet sich in [2], hier werden insbesondere auch sämtliche Originalliteraturquellen bis zum Jahre 2004 aufgeführt. Auf der Webseite von em. Prof. Bunde (Univ. Gießen) sind viele Originalpaper zur Persistenzanalyse, auf denen er als Mit- oder Hauptautor zeichnete, als pdf abgreifbar [23]. In [6] finden sich ebenfalls Literaturquellen. Schlussendlich ist der ausführliche und gut allgemeinverständlich gefasste Übersichtsaufsatz zur Persistenzanalyse von Bunde und Kantelhardt in den physikalischen Blättern hervorzuheben [21]. Die Originalarbeiten der hier im Mittelpunkt stehenden neuesten Methode der Persistenzanalyse, die schließlich unter 5. näher beschrieben wird, finden sich in [3] und [4].
In groben Zügen sieht die Arbeitsweise der „klassischen“ Persistenzanalye wie folgt aus: Mit der FA wird aus einer Zeitreihe der Hurst-Exponent alphaFA ermittelt. Enthält die Reihe einen externen Trend, ergibt sich ein höheres alphaFA als ohne diesen Trend. Daher liefert die FA im Prinzip nur für Zeitreihen, die keine externen Trends enthalten, unverfälschte Ergebnisse des Hurst-Exponenten. Zur Behebung dieses Mangels wurde die DFA entwickelt. Sie beseitigt während des Berechnungsvorgangs automatisch polynominale Trends einer vorgegebenen Ordnung aus der Zeitreihe. Zur Vereinfachung beschränkt man sich hierbei meist auf die Beseitigung von linearen Trends. Wird mit der DFA überhaupt kein Trend entfernt, liegt wieder die FA vor. Mit der DFA kann der automatisch beseitigte Trend leider nicht explizit angegeben werden. Da der Hurst-Exponent der DFA alphaDFA ist naturgemäß stets größer als der der FA alphaFA, kann die Differenz (alühaDFA – alphaFA) als Stärke des externen Trends in der analysierten Temperaturreihe angesehen werden.
Bild 2 zeigt als Beispiel die Ergebnisse von FA- und DFA-Analysen (Beseitigung von linearen Trends) der Monatsmittelwertreihen von fünf der am weitesten bis ins 18. Jahrhundert zurückreichenden europäischen Wetterstationen.
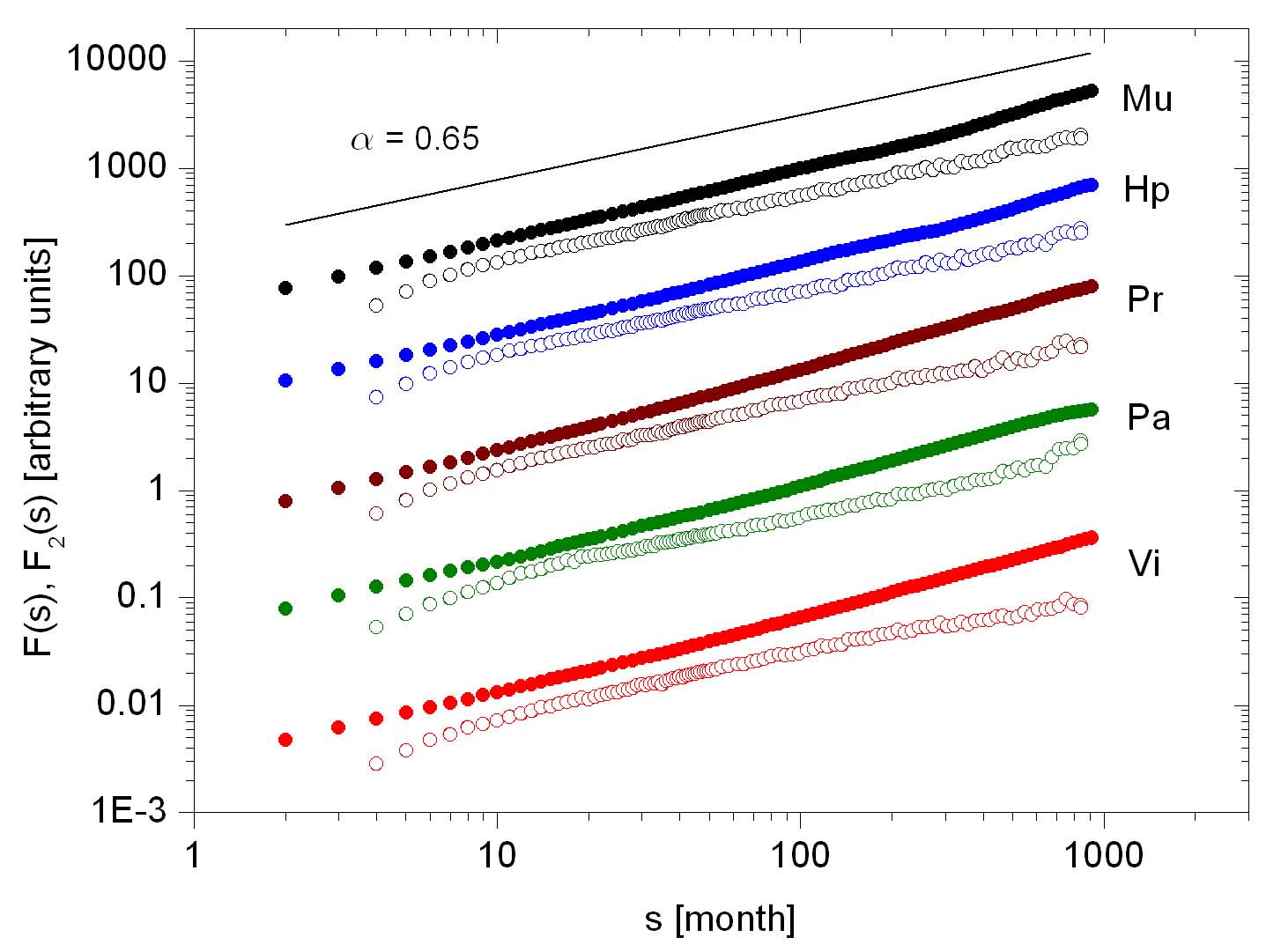
Bild 2: FA-Analyse (gefüllte Kreise) und DFA-Analyse (offene Kreise) für die Stationen München, Hohenpeissenberg, Prag, Paris und Wien . Die Länge des betrachteten Zeitraums beträgt 1791 bis zum Jahr 2000. Man erhält Hurst-Exponenten zwischen 0,52 und 0,63 aus der DFA- und 0,63-0,71 aus der FA-Analyse.
Aus den Monatsreihen wurde, wie bereits beschrieben, der saisonale Jahresgang entfernt. Ein doppelt-logarithmischer Plot erlaubt es dann, direkt aus der Steigung der charakteristischen Größe F(s) den Hurst-Exponenten a abzulesen [2]. Die Hurst-Exponenten der FA sind, wie schon erwähnt, im Prinzip größer als die der DFA. Für unser Beispiel in Bild 2 folgt daraus, dass alle fünf Reihen (lineare) Trends enthalten. Die Frage, ob diese Trends unnatürlich sind, oder ob sie durch Persistenz entstanden sind, kann nicht ohne weiteres beantwortet werden. Allerdings fällt im vorliegenden Fall die Entscheidung leicht, weil alle fünf Reihen aus nicht allzu weit voneinander entfernten Stationen stammen, einen sehr ähnlichen Verlauf und schließlich auch ähnliche alpha-Werte aufweisen. Somit liegt mit hoher Wahrscheinlichkeit tatsächlich ein externer Trend vor.
Erst die in jüngster Zeit entwickelte Methode von Lennartz und Bunde, die nachfolgend beschrieben wird, kann dann die wichtige Frage nach der Unnatürlichkeit eines gemessenen Trends in einer einzelnen Temperaturzeitreihe quantitativ beantworten.
5. Die Methode von Lennartz und Bunde
Bis zum Jahre 2009 ergab für eine Temperaturzeitreihe nur der Vergleich ihrer beiden Hurst-Exponenten alphaFA, alphaDFA aus der FA- und der DFA-Analyse einen Hinweis, ob ein beobachteter (linearer) Trend in ihr externen Ursprungs war. Diese einfache Strategie erlaubte freilich schon wichtige Aussagen. Sie wurde unter anderem in einer Publikation des Jahres 2003 auf 95 weltweit verstreute Temperaturzeitreihen angewendet. Dabei konnten keine Anzeichen für eine globale Erwärmung aufgefunden werden [5]. Lennartz und Bunde (im Folgenden LB) zeigten schließlich in zwei bahnbrechenden Fachaufsätzen der Jahre 2009 und 2011 [3], [4], dass eine wesentliche Erweiterung der oben beschriebenen klassischen Persistenzanalyse hin zu quantitativen Wahrscheinlichkeitsangaben möglich ist. Hierzu verwendeten sie Surrogat-Zeitreihen und untersuchten, wie häufig natürliche (lineare) Trends in ihnen vorkommen. Die maßgebende dimensionslose Größe ist dabei ∆/s. ∆ [°C] ist der Temperaturanstieg bzw. der Temperaturabfall der linearen Regressionsgeraden über die gesamte Länge der Temperaturreihe und s [°C] die Standardabweichung um die Regressionsgerade herum. ∆ ist durch die Standardabweichung zu dividieren, weil die Signifikanz eines Trends mit abnehmender Standardabweichung s zunimmt. Weist die Reihe große Schwankungen, also eine große Standardabweichung s auf, ist der Trend ∆ weniger signifikant als bei kleinem s. Im Extremfall von s = 0 ist der Trend mit dem Verlauf der Zeitreihe identisch, im entgegengesetzten Extremfall beliebig großer Standardabweichung kann bei der geringsten Änderung irgendeines Wertes der Reihe die Regressionsgerade völlig anders verlaufen.
Aus unzähligen Surrogatreihen und Computer-Rechenläufen ermittelten LB für zwei Spezialfälle, nämlich Zeitreihen der festen Längen von 50 und 100 Jahren, charakteristische Diagramme bzw. die zu diesen gehörenden empirischen Rechenformeln [3]. Aus den Diagrammen kann abgelesen werden, mit welcher kumulierten Wahrscheinlichkeit W ein linearer Trend ∆/s unnatürlich (extern) ist. Im Jahre 2011 erweiterten LB ihre Methode schließlich auf allgemeine Zeiträume von 40 bis 160 Jahren Länge [4]. Bild 3 zeigt ein solches Diagramm (vom Autor erstellt) für den Fall von Surrogatreihen von 100 Jahren Länge.
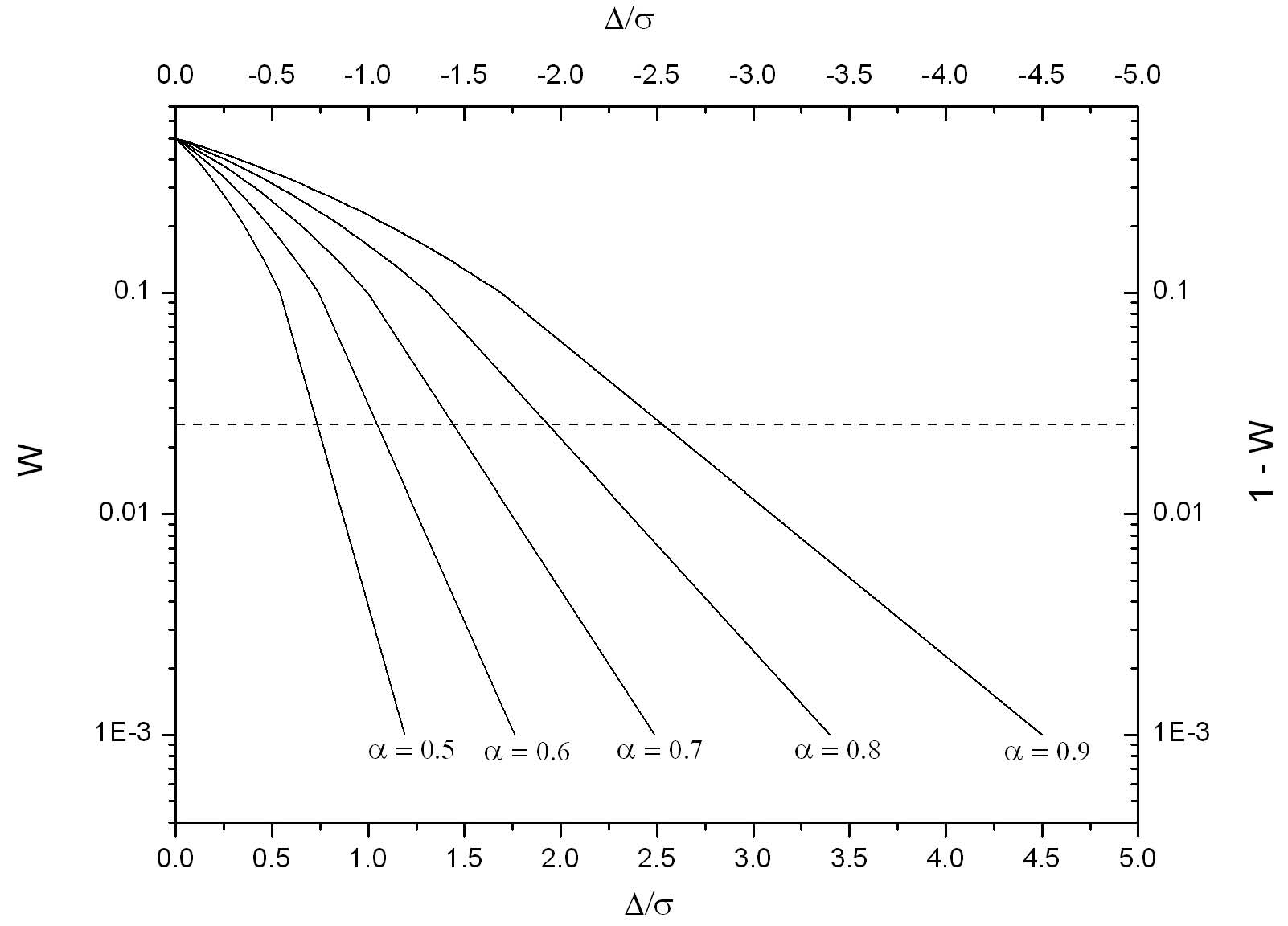
Bild 3: Kumulierte Wahrscheinlichkeit W für lineare Trends ∆/s in Abhängigkeit vom Hurst-Exponenten a in Surrogatreihen von 100 Jahren Länge [6]. Für positive Trends (∆ > 0) ist die linke y-Skala und die untere x-Skala gültig, für negative Trends die rechte y-Skala und die obere x-Skala. Die gestrichelte Linie bei W = 0,025 stellt ein Vertrauenslimit dar.
In Surrogatreihen – es sei nochmals daran erinnert, dass Surrogatreihen frei von unnatürlichen Trends sind – treten naturgemäß positive und negative natürliche Trends ∆/s gleich häufig auf. Ferner kommen |∆/s|-Werte zunehmender Stärke immer seltener vor. Dieser Effekt ist für den kleinsten Hurst-Exponenten von alpha ≈ 0.5 (weißes Rauschen, keine Persistenz) naturgemäß am stärksten. In reinen Zufallsreihen ohne Persistenz ist es tatsächlich sehr unwahrscheinlich, Trends mit großen |∆/s|-Werten aufzufinden. Diese Situation ist dem Würfeln analog. Es ist extrem unwahrscheinlich, dass gleiche Augenzahlen zu oft in Reihe vorkommen.
Bei der Interpretation der Grafik in Bild 3 ist zu beachten, dass W kumulierte Wahrscheinlichkeiten sind. Dies sind hier Wahrscheinlichkeiten, einen Trend ∆/s irgendeines beliebigen Wertes, der über oder gleich einer bestimmten Schwelle liegt, aufzufinden. Betrachten wir nun die Surrogatzeitreihen! Da in ihnen keine externen Trends vorkommen, enthalten sie im Mittel gleich viele positive und negative natürliche Trends. Nehmen wir einen extrem starken negativen Trend -∆/s als Schwelle und irgend ein festes alpha an, so liegt die kumulierte Wahrscheinlichkeit W, in Surrogatreihe mit diesem alpha einen Trend größer oder gleich der extrem starken negativen Schwelle aufzufinden, naturgemäß nahe bei 1. Schließlich enthalten fast alle Surrogatreihen mit diesem alpha irgendwelche Trends, die sämtlich über -∆/s liegen. Wird nun die (immer noch negative) Schwelle erhöht, verkleinert sich W. Die Schwelle ∆/s = 0 schließlich wird im Mittel bereits von 50% aller Trends überschritten, daher ist W = 0,5. Liegt die Schwelle dann im positiven Bereich, wird W mit ansteigender Schwelle immer kleiner. Bei einem extrem hohen positiven ∆/s verschwindet W allmählich.
Das vorbeschriebene Verhalten zeigt die Grafik in Bild 3 mit konkreten Zahlen. Betrachten wir zur näheren Erläuterung 10.000 Surrogatreihen, alle mit alpha = 0,7 und einer Länge von 100 Jahren. Ferner ist zu beachten, dass für ∆/s > 0 die untere x- und die linke y-Skala, für ∆/s =< 0 dagegen die obere x- und die rechte y-Skala gelten. Die Kurve für alpha = 0,7 beginnt für ∆/s = 0 mit W = 0.5 bzw. dem Wert (1-W) = 0,5. In 10.000 Surrogatreihen sind somit 5000 Reihen mit Trends ∆/s >= 0 und 5000 Reihen mit Trends ∆/s =< 0 enthalten (es ist stets das statistische Mittel ohne Fehlerschwankungen gemeint). Diese aus Bild 3 abzulesende Erkenntnis erscheint trivial. Betrachten wir als nächstes den sehr starken, negativen Wert ∆/s = -2,5. Dafür lesen wir aus der Grafik (1 – W) etwa 10-3 ab. Dies bedeutet, dass 9990 von 10.000 Surrogatreihen der Länge von 100 Jahren und einem alpha = 0,7 einen 100-Jahrestrend von ∆/s >= -2,5 aufweisen. Für den größeren Wert ∆/s = -1 lesen wir (1 – W) = 0,1 ab, somit ist W = 0,9. Somit weisen 9000 Surrogatreihen Trends mit Werten von ∆/s >= -1 auf. Für das noch größere ∆/s = -0,5 sind wir bei (1-W) = 0,2 angekommen, also bei W = 0,8, d.h. 8000 Surrogatreihen enthalten Trends von ∆/s >= -0,5. Wenn schließlich der Wert (1 – W) = W = 0,5 erreicht ist, erhält man, wie bereits beschrieben, 5000 Reihen mit ∆/s – Werten >= 0. Gehen wir nun zu positiven Trends über, etwa zu ∆/s = 1. Wir lesen hierfür W = 0,1 ab, somit enthalten nur noch 1000 Surrogatreihen Trends mit Werten ∆/s >= 1. Für ∆/s = 2,5 finden wir W = 0,001, also kommen in den 10.000 Surrogatreihen nur noch 10 Reihen mit Trends ∆/s >= 2,5 vor. Man erkennt aus dem Diagramm, dass (für positive Trends) W um mehrere Größenordnungen zunimmt, wenn alpha nur innerhalb einer Größenordnung zunimmt.
Mit Hilfe der Grafik von Bild 3 wird die Strategie des Verfahrens von LB deutlich. Ein Trend in einer real gemessenen Reihe wird als extern (unnatürlich) angesehen, wenn er in Surrogatreihen des gleichen alpha und der gleichen Länge zu selten vorkommt; genauer, wenn für positive Trends die kumulierte Wahrscheinlichkeit W < q bzw. für negative Trends W > (1 – q) aus Bild 3 abgelesen wird. q ist ein frei wählbares statistisches Vertrauenslimit, gewöhnlich nimmt man q = 0,025 bzw. 2,5%. In der praktischen Durchführung der Methode von LB wird der ∆/s-Wert der gemessenen Reihe und danach mit der DFA-Analyse ihr Hurst-Exponent alpha ermittelt. Aus der Grafik von Bild 3 wird aus dem Wertepaar ∆/s, alpha dann die kumulierte Wahrscheinlichkeit W abgelesen. Ergibt sich bei positiven Trends W < 0,025, liegt W also unter dem 2,5%-Limit, wird der Trend der realen Reihe als extern (unnatürlich) angesehen. Das ist anschaulich, denn Trendwerte, die größer oder gleich dem in der realen Reihe beobachteten Trend sind, kommen in den von unnatürlichen Trends freien Surrogatreihen des gleichen alpha nur in weniger als 2,5% aller Fälle vor. Für negative Werte ist das Limit W = 0,975, also 97,5%. Wird aus der Graphik von Bild 3 ein W > 0,975 ermittelt, wird der beobachtete negative Trend als unnatürlich (extern) angesehen.
Die Persistenzanalyse von Temperaturreihen nach der Methode LB wurde von den Autoren in [3], [4] publiziert. Insbesondere haben LB ihr Verfahren in [3] auf 30 Einzelreihen und 15 Globalreihen angewendet. Globalreihen zeigen freilich im Gegensatz zu Einzelreihen ungewöhnlich hohe alpha-Werte, die oft sogar über 1 liegen. Damit wären viele Globalreihen instationär, Einzelreihen dagegen nicht, was widersprüchlich ist. Nach Auffassung des Autors des vorliegenden Aufsatzes wird dieser Effekt durch die Glättungs- und Homogenisierungseingriffe bei der Bildung von Globalreihen verursacht und macht daher Globalreihen zur Persistenzanalyse ungeeignet, s. hierzu auch die Kritik in [22]. Insbesondere wird durch Glättung bei der Globalreihenbildung die Standardabweichung s unrealistisch klein und damit die Trends ∆/s zu stark. Leider gibt es bis heute noch keine Arbeit, die dediziert auf diese Probleme von Globalreihen eingeht. Nach Auffassung des Autors sind daher die in [3] gezogenen Schlussfolgerung über die globale Erwärmung wegen der Verwendung von Globalreihen in Frage zu stellen.
In einer Arbeit des Autors zusammen mit den Koautoren Dr. Link und Prof. Friedrich-Karl Ewert [6] wurden der oben beschriebenen Vorbehalte wegen Globalreihen grundsätzlich ausgeschlossen. Mit dem Verfahren von LB wurden im Wesentlichen hier fast alle brauchbaren Einzelreihen weltweit – insgesamt etwa 2500 – analysiert. Für den Zeitraum von 1906 bis 2005 zeigen nur grob 30% aller Temperaturreihen aus Messtationen mit weniger als 1000 Einwohnern und unter 800 müNN einen unnatürlichen (externen) Trend. Ein ähnliches, nicht ganz so deutliches Ergebnis wurde für den Zeitraum von 1956 – 2005 gefunden. Daraus kann der Schluss gezogen werden, dass mit sehr hoher Wahrscheinlichkeit das anthropogene CO2 nur unmaßgeblich zur Erwärmung im 20. Jahrhundert beigetragen hat. Dieses Ergebnis wird durch den weiteren Umstand gestützt, dass neben anthropogenen Treibhausgasen auch noch eine ganze Reihe weiterer Ursachen für den leichten Erwärmungstrend im 20. Jahrhundert in Frage kommen, zum Beispiel ein ungewöhnliches Verhalten der Sonne (Magnetfeld). Zur Vermeidung von Missverständnissen wird nochmals darauf hingewiesen, dass zwar die in [6] und [3] verwendete Methode identisch ist, die Schlussfolgerungen auf Grund der stark unterschiedlichen Datensätze aber nicht übereinstimmen. Insbesondere wurde in [6] im Gegensatz zu [3] gefunden, dass die globale Erwärmung in der zweiten Hälfte des 20. Jahrhunderts „unnatürlicher“ als in der ersten Hälfte ist, was von [6] nicht bestätigt wird. Die Publikation [6] erfuhr hohe Resonanz, einige Besprechungen sind in [14-20] aufgeführt.
6. Zur heutigen Klimadiskussion
Bis heute gibt es keine begutachtete Fachpublikation, die einen anthropogenen Einfluss auf das Klimageschehen stringent nachzuweisen vermag. Die heutige Klimadiskussion dreht sich daher im Wesentlichen nur noch um die modelltheoretische Frage, ob die aus Labormessungen hergeleitete, unmaßgeblich kleine Klimasensitivität des CO2 – sie liegt grob zwischen 0,5 °C und 1,1 °C – durch Mitkoppelungen verstärkt oder durch Gegenkoppelungen abgeschwächt wird. Eine verlässliche Antwort können nach dem bisher gültigen Paradigma physikalischer Forschung nur Messungen geben. Bis heute weisen bereits eine Reihe von Publikationen Gegenkoppelungen auf der Basis von Ballon- und Satellitenmessungen nach [7]-[11]. Messungen, die eindeutig Mitkoppelungen belegen, gibt es dagegen nicht, nur Klimamodelle mit dieser Eigenschaft. So ist beispielsweise der von diesen Klimamodellen geforderte Hot-Spot (eine Erwärmung in mehreren km Höhe über dem tropischen Gürtel der Erde) unauffindbar. Das vom IPCC entworfene Szenario einer durch anthropogenes CO2 verursachten, gefährlichen globalen Erwärmung wird infolgedessen zunehmend unwahrscheinlicher. Diese Einschätzung wird durch die in [6] publizierten Ergebnisse auf der Basis der modernen Persistenzanalyse gestützt.
7. Zusammenfassung
Die moderne Persistenzanalyse von Lennartz und Bunde stellt einen wesentlichen Fortschritt gegenüber der „klassischen“ Persistenzanalyse dar [3], [4]. Sie erlaubt es erstmalig, die kumulierte Wahrscheinlichkeit anzugeben, mit der ein in einer Temperaturreihe auftretender linearer Trend externe Ursachen hat und daher nicht auf natürliche Weise infolge Persistenz der Temperaturreihe entstanden sein kann. Mit historischen Temperaturreihen aus dem GISS-Pool wurde für den Zeitraum 1906-2005 mit der Methode von LB nachgewiesen, dass nur etwa 30% aller Reihen von Messtationen mit weniger als 1000 Einwohnern und Höhenlagen unter 800 müNN externe Trends aufweisen [6]. Die Ursachen dieser Trends sind unbekannt. Neben anthropogenem CO2 kommen ungewöhnliche Sonnenaktivität und weitere noch nicht näher bekannte Antriebe in Frage. Infolgedessen kann das anthropogene CO2 bei der in klimahistorischem Maßstab ohnehin geringfügigen Erwärmung im 20. Jahrhundert nur eine unbedeutende Nebenrolle gespielt haben. Dieser Befund wird durch die jüngste globale Abkühlung, die nunmehr bereits etwa 17 Jahre andauert, untermauert.
8. Literaturnachweise
[1] D.L. Turcotte: Fractals and Chaos in Geology and Geophysics, 2nd ed., Cambridge University Press, Cambridge, 1997
[2] J.W. Kantelhardt: Fluktuationen in komplexen Systemen, Habilitationsschrift, Univ. Gießen, 2004: www.physik.uni-halle.de/Fachgruppen/kantel/habil.pdf
[3] S. Lennartz and A. Bunde: Trend evaluation in records with long-term memory: application to global warming, Geophys. Res. Lett., 36, L16706, doi:10.1029/2009GL039516, 2009
[4] S. Lennartz and A. Bunde: Distribution of natural trends in long-term correlated records: a scaling approach, Phys. Rev. E84, 021129, doi:10.1103/PhysRevE84.021129, 2011
[5] J.F. Eichner, E. Koscielny-Bunde, A. Bunde, S. Havlin, and H.-J. Schellnhuber: Power-law persistence and trends in the atmosphere: A detailed study of long temperature records, Phys. Rev. E68, 046133, 2003
[6] H.-J. Lüdecke, R. Link, and F.-K. Ewert: How Natural is the Recent Centennial Warming? An Analysis of 2249 Surface Temperature Records, Int. J. Mod. Phys. C, Vol. 22, No. 10, 2011, http://www.eike-klima-energie.eu/uploads/media/How_natural.pdf
[7] G. Paltridge, A. Arking, and M. Pook: Trends in middle- and upper-level tropospheric humidity from NCEP reanalysis data, Theor. Appl. Climatol., 98, p. 351-359, 2009
[8] R.W. Spencer, and W.D. Braswell: On the misdiagnosis of surface temperature feedbacks from variations in Earth’s radiant energy balance, Remote. Sens. 3, p. 1603-1613, 2011
[9] R.S. Lindzen and Y.-S. Choi: On the determination of climate feedbacks from ERBE data, Geophys. Res. Lett., 36, L16705, 2009
[10] R. Allan: Combining satellite data and models to estimate cloud radiative effect at the surface and in the atmosphere, Meteorol. Appl., 18, p. 3245-333, 2011
[11] H. Harde: How much CO2 really contributes to global warming? Spectroscopic studies and modelling of the influence of H2O, CO2 and CH4 on our climate, Geophys. Res. Abstracts, 13, EGU2011-4505-1, 2011
[12] R. Muller, BEST, Berkeley University, 2011
[13] http://de.wikipedia.org/wiki/ARMA-Modell
[14] http://judithcurry.com/2011/11/07/two-new-papers-vs-best/
[15] http://judithcurry.com/2011/11/08/tols-critique-of-the-ludecke-et-al-papers/
[16] http://judithcurry.com/2011/11/10/ludecke-et-al-respond/
[17] http://judithcurry.com/2011/11/15/ludecke-et-al-respond-part-ii/
[18] wmbriggs.com/blog/?p=4630
[19] http://www.focus.de/wissen/wissenschaft/klima/weltklimakonferenz_2011/tid-24293/weltklimakonferenz-viel-laerm-um-nichts_aid_687885.htm
[20] WUWT: http://tinyurl.com/ae342yp
[21] A. Bunde und J.W. Kantelhardt: Langzeitkorrelationen in der Natur: von Klima, Erbgut und Herzrythmus, Physikalische Blätter 57, Nr. 5, S. 49-54, 2001
[22] E. Steirou and D. Koutsoyiannis: Investigation of methods for hydroclimatic data homogenisation, European Geosciences Union General 2012, Vienna Austria 22-27 April 2012, Session HS.4/AS4.17/CL2.10, http://itia.ntua.gr/en/docinfo/1212/, 2012
[23] http://www.uni-giessen.de/cms/fbz/fb07/fachgebiete/physik/einrichtungen/theorie/institut-fur-theoretische-physik-iii/pub/paper
[24] H. Makse et al.: Method for Generating Long-Term Correlations for Large Systems, ArXiv, http://arxiv.org/abs/cond-mat/9512024
















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"#27: „Unter welchen Bedingungen verändert sich überhaupt das Gleichgewicht? Der Vulkanausbruch hat offensichtlich nichts bewirkt, ebensowenig der gestiegene CO2-Gehalt der vergangenen 16 Jahre. Möglicherweise ändert sich ja etwas, wenn gewisse CO2-Schwellen überschritten werden. Den Klimaforschern sollen keine Denkverbote erteilt werden.“
Hallo Herr Dr.Kuhnle, sorry, aber da meldet sich mein skeptischer Verstand. 😉 Sie können vielleicht sagen, dass sich am Gesamtsignal (= globale Durchschnittstemperatur) nichts geändert hat. Daraus aber abzuleiten, dass der Vulkanausbruch und der Anstieg des CO2-Gehalts keine Wirkungen besitzen, wäre ein Fehler. Man kann das Klima auf der Erde ja mal als BlackBox betrachten. Da gehen jede Menge Einzelsignale rein, so wie der CO2-Gehalt, Sonnenaktivität, Landschaftsveränderungen usw. Zudem gibt es in der BlackBox noch einige innere Parameter, die den inneren Zutand beeinflussen, wie Meeresströmungen usw. Als Output erhalten wir eine globale Durchschnittstemperatur. Wenn man über einen gewissen Zeitraum ein einzelnes Inputsignal ändert und am Output kommt etwas Rauschen heraus, aber ein wirklicher Trend ist nicht zu beobachten, kann man dann Rückschlüsse auf die Wirksamkeit des einzelnen Inputs ziehen? Doch nur dann, wenn alle anderen Inputgrößen und inneren Zustände sich nicht geändert haben in der Zeit. Davon kann man aber beim Realfall Erde nicht ausgehen. Es ändern sich ständig Eingangsgrößen. Deshalb Vorsicht bei ihren Schlussfolgerungen. Genauso könnte ich ja auch behaupten, in den 16 Jahren hat sich doch die Sonnenaktivität geändert, aber es ist kein Trend in den Temperaturen zu beobachten, ergo hat die Sonne keinen Einfluss auf das Klima. ^^
Im übrigen denke ich, dass man Forschern schlecht Denkverbote erteilen kann, oder haben sie davon in ihrer Promotionszeit etwas gemerkt? 😉
„Darüber hinaus stelle ich noch eine ganz andere spannende Frage: Kann sich das Klima auch verändern, wenn die äußeren Einflussparameter wie Treibhausgase, Sonnenparameter, etc. konstant bleiben? Sind Klimaveränderungen nur aufgrund der inneren Eigendynamik des Erd-Klimasystems denkbar?“
Finde ich auch eine interessante Frage. Die Eigendynamik dürfte auch für heutige Klimaveränderungen eine Rolle spielen.
„Wie Albert Einstein schon sagte, muss man nicht nur die richtigen Antworten, sondern auch die richtigen Fragen suchen.“
Absolut!
„Nun zum Klimaschutz-Unsinn. Herr Hader, ich kann es kaum glauben, dass Sie persönlich bereit sind Unsummen an Geld auszugeben und eine angeblich wahrscheinliche Erderwärmung zu bremsen. Haben Sie keine Kinder, die das wirtschaftliche Desaster, was Sie anrichten wollen, in Zukunft ausbaden müssen?
Was hat denn ein Mensch in einem unterentwickelten Land davon, wenn Sie sich ein Windkraftwerk in den Garten stellen? Sollte man im Entwicklungsland nicht lieber ein Kohlekraftwerk bauen, damit sich dort Industrie ansiedeln kann? Was bringen denn Ihrer Meinung nach die deutschen Billioneninvestitionen bezüglich der Abbremsung der „wahrscheinlichen“ Erderwärmung. Und wie wahrscheinlich ist Ihre Antwort (bitte in %). Machen Sie doch mal eine Überschlagsrechnung! Und was ist, wenn Sie sich irren?“
Nun, was sie mir gegenüber glauben können und was nicht, ist ja erstmal ihre Sache. 😉 Für Bewohner eines Entwicklungslandes würde es in erster Linie etwas bringen, überhaupt an einem Stromnetz angeschlossen zu sein. Wussten sie, dass mehr als eine Millarde Menschen überhaupt keinen Zugang haben? Also es würde mit Sicherheit wesentlich mehr bringen, wenn man diese Länder mit einem stabilen Stromnetz und Kraftwerken ausstattet. Und wenn es nach mir ginge, könnte das direkt von unserem Steuergeld bezahlt werden. Aber ich hör schon jetzt das Geschrei. 🙂 Zurück zur Energiewende, wenn es dazu beiträgt in 40-50 Jahren nachhaltig CO2-Emissionen einzusparen und Technologien zu entwickeln, die auch den Entwicklungsländern helfen, dann KANN sich das auch für diese Menschen lohnen.
Herr Dr.Kuhnle, ich muss hier nicht das Rad neu erfinden oder Forschungsarbeiten wiederholen. Wenn Sie nach Wahrscheinlichkeiten und Überschlagsrechnungen fragen, dann bedienen sie sich der wiss. Publikationen, die es auf dem Gebiet gibt. Auch im IPCC werden die Unsicherheiten der Modelle angegeben. Man muss es nur lesen wollen. 😉 Die Wahrscheinlichkeit des Irrtums ist auch gegeben. Das trifft auch für jede Investition zu, dass diese scheitert. Die Auswirkungen finde ich aber nicht so gravierend, denn selbst ohne Klimaveränderung macht ein Umbau der Energiewirtschaft weg vom Kohlenstoff auch wegen den immer weiter steigenden Rohstoffpreise durchaus Sinn. Und was ist, wenn Sie sich irren?
#25: Klaus Konejung sagt: „Wood erhält eine Temperatur in einem Meßergebnis, bei dem mehr als fünf unabhängige Parameter das Ergebnis beeinflussen. Das heißt, die festgestellte Temperaturgleichheit ist eher Zufall.“
=======================================================
Bitte verfälschen Sie das Experiment von Wood nicht.
Das war nicht „eine Temperatur in einem Meßergebnis“, sonder 2 Temperaturen in 2 Messergebnissen.
Es ging um einen Vergleich der 2 Zustände, wo der einzige signifikante Unterschied „Strahlung gefangen – Strahlung nicht gefangen“ war. Der Unterschied der Temperaturen war ungefähr Null. So war der sog. „Treibhauseffekt“, wie ihn das IPCC darstellt, schon damals (1909) erledigt.
#18 Kommentar: „Sehr geehrter Herr Greghouse,
ohne Ihnen zu nahe treten zu wollen, erlaube ich mir die Empfehlung an Sie, sich mit anderen Dingen als der Klimasensitivität des CO2 zu beschäftigen. Zumindest physikalische Grundkenntnisse sind hierfür leider unabdingbar. Sie erlauben daher, dass ich auf Ihre Ausführungen nicht weiter eingehe.
Freundliche Grüße“
========================================================
Lieber Herr Lüdecke(?),
ich habe mich auf das Experiment des Professors für Experimentalphysik R.W.Wood berufen, ihm kann man kaum Mangel an physikalischen Grundkenntnissen unterstellen.
Was mein zweites Argument betrifft, gebe ich Ihnen teilweise Recht, eine korrekte Berechnung für eine Gasmischung müsste ziemlich anders aussehen, allerdings sage ich mal so intuitiv, dass die Größenordnung schon in dem Bereich wäre. Ich schlage es einfach vor, Sie präsentieren den Lesern die korrekte, wissenschaftlich berechnete Zahl. Das wäre durchaus angebracht, weil auch Sie die These vertreten, dass CO2 die Luft direkt durch eigene Absorption erwärmt, was man diesem Video entnehmen kann (http://is.gd/LueCO2, 14:23).
Also, es geht um 2 Fragen: 1)wie heiß soll reines CO2 unter gleichen Bedingungen werden, um in der Konzentration von 1/2500 die ganze Luft um 0,5C erwärmen? und 2)wie heiß wird CO2 unter gleichen Bedingungen wirklich?
Falls der Unterschied gravierend sein sollte, können Sie Ihre Version des „Treibhauseffektes“ gleich in die Tonne schmeißen.
@#20 Herrn Hader
Es ist in der Tat eine spannende Frage, welches Gleichgewicht sich einstellt, wenn man die äußeren Einflussparameter verändert. Ich möchte die Frage aber noch weiter fassen:
Unter welchen Bedingungen verändert sich überhaupt das Gleichgewicht? Der Vulkanausbruch hat offensichtlich nichts bewirkt, ebensowenig der gestiegene CO2-Gehalt der vergangenen 16 Jahre. Möglicherweise ändert sich ja etwas, wenn gewisse CO2-Schwellen überschritten werden. Den Klimaforschern sollen keine Denkverbote erteilt werden.
Darüber hinaus stelle ich noch eine ganz andere spannende Frage: Kann sich das Klima auch verändern, wenn die äußeren Einflussparameter wie Treibhausgase, Sonnenparameter, etc. konstant bleiben? Sind Klimaveränderungen nur aufgrund der inneren Eigendynamik des Erd-Klimasystems denkbar?
Wie Albert Einstein schon sagte, muss man nicht nur die richtigen Antworten, sondern auch die richtigen Fragen suchen.
Nun zum Klimaschutz-Unsinn. Herr Hader, ich kann es kaum glauben, dass Sie persönlich bereit sind Unsummen an Geld auszugeben und eine angeblich wahrscheinliche Erderwärmung zu bremsen. Haben Sie keine Kinder, die das wirtschaftliche Desaster, was Sie anrichten wollen, in Zukunft ausbaden müssen?
Was hat denn ein Mensch in einem unterentwickelten Land davon, wenn Sie sich ein Windkraftwerk in den Garten stellen? Sollte man im Entwicklungsland nicht lieber ein Kohlekraftwerk bauen, damit sich dort Industrie ansiedeln kann? Was bringen denn Ihrer Meinung nach die deutschen Billioneninvestitionen bezüglich der Abbremsung der „wahrscheinlichen“ Erderwärmung. Und wie wahrscheinlich ist Ihre Antwort (bitte in %). Machen Sie doch mal eine Überschlagsrechnung! Und was ist, wenn Sie sich irren?
# 20 Hader…
Herr Hader verteilt wieder Allgemeinplätze und will auch wieder die ganze Welt retten:
„Wenn diese These stimmen sollte, wäre die spannende Frage, in welcher Höhe sich das Gleichgewicht einstellt, wenn man verschiedene Ausgangsgrößen verändert.“
CO2 ist keine Ausgangsgröße für’s Klima. Und die Sonne und die Wolken und den Wind und die Meeresströmungen kann der Mensch nicht verändern.
„Es kann aber auch sein, dass Sie von den Klimaveränderungen weit weniger betroffen wären, als jemand in einem unterentwickelten Land. Gut möglich, dass sich die 50.000 Euro nicht so sehr ihrer Familie entgegenkommt, dafür umso mehr anderen Familien in diesen Ländern. Wie Sie so einen Verlauf bewerten würden, müssten sie selbst rausfinden.“
Die Bewertung ist doch ganz klar, für alle, die noch bei gesundem Verstand sind: ICH ZAHLE KEINE 50.000 EURO, damit vielleicht eine Familie in einem unterentwickelten vor den eventuell auftretenden Folgen eines möglichen Klimawandels beschützt werden.
Lesen sie eigentlich den Unsinn, den sie da schreiben, Herr Hader? Sie wollen also unser aller Geld in die Welt verteilen. Und vielleicht, denn ihr gesamter Kommentar steht ja im Konjunktiv, haben Familien in anderen Ländern was davon. Oder vielleicht auch nicht. Jedenfalls hauen wir erst mal das Geld raus. Mit Verlauf und sorry an den Admin: Sie spinnen, Hader!
Hallo Herr Paul, #23
wer nicht mein Freund ist ist mein Feind, oder wie? Sie als Mediziner sollten doch eigentlich wissen, dass eine Diagnose, die auf einem Befund alleine beruht, sehr kritisch zu sehen ist. Wood erhält eine Temperatur in einem Meßergebnis, bei dem mehr als fünf unabhängige Parameter das Ergebnis beeinflussen. Das heißt, die festgestellte Temperaturgleichheit ist eher Zufall.
Im übrigen funktioniert die Erde sehr ähnlich wie eine Wärmeplatte. Sie wird tagsüber mit kurzwelliger Strahlung von der Sonne beheizt und gibt diese den ganzen Tag über durch langwellige Strahlung wieder ab. Dabei wird die Wärmeabgabe in den unterschiedlichen Frequenzen durch Bandenstrahler wie CO2 und H2O beeinflußt. Zwischendurch wird die Wärme in der Erde gespeichert bzw. durch Konvektion verteilt. Die Temperatureindringtiefe in die Erde und die damit verbundenen Wärmeströme können Sie mit Hilfe des Binder-Schmidt-Verfahrens grafisch oder des Finite Differenzen-Verfahrens rechnerisch ermitteln. Wenn Sie dann schon dabei sind, können Sie das gleiche für den Mond tun und dabei berücksichtigen, dass der Mondtag 28 Erdtage dauert. Dann passen nämlich die gemessenen Temperaturen sehr gut zu den Rechnenwerten für einen Himmelskörper mit unserem Abstand zur Sonne ohne Atmosphäre.
Darum ging es in dem Versuch übrigens nicht, sondern um die saubere Trennung verschiedener Einflußfaktoren auf den Versuch von Wood. Aber das kann ich Ihnen bei Bedarf ausführlich auseinandersetzen.
Und zum CO2 finde ich, dass Herr Puls die Zusammenhänge sehr gut beschrieben hat.
P. S. ich räume ein, dass mein Beitrag #21 nur mittelbar zu Ihrem #17 passt.
#20: S.Hader:
„..Das Ziel ist ja keine Temperatursenkung vom heutigen Zustand aus betrachtet, sondern den wahrscheinlichen Anstieg der kommenden Jahrzehnte und Jahrhunderte abzubremsen …“
Es ist das Ziel diese Forums, mit sachlichen Argumenten aufzuzeigen,
dass dieser angenommene Anstieg weder wahrscheinlich noch gefährlich ist, noch die dafür eingesetzten Mittel dafür geeignet sind.
Das sollten Sie inzwischen bemerkt haben.
mfG
#21: Klaus Konejung ihre Antwort zeigt mir, dass Sie offenbar beruflich für die „Klimarettungsbranche“ im weiteren Sinne tätig sind,
da Sie nur abfällige Bemerkungen übrig haben für Argumente, die Sie NICHT widerlegen können.
Sie argumentieren wider besseres Wissen.
Was bitte hat Ihr „Wärmeplattenversuch“ mit meinen Darstellungen in #17 zu tun?
Die Erde IST keine Wärmeplatte!
Sie wissen als Fachmann, dass Metallbedampfung (Aluminium) ein gute Wärmedämmung ermöglicht, weil es NICHT absorbiert sondern reflektiert.
CO2 ist kein Aluminium!
Wenn das CO2 wie die von Lüdecke zitierte Arbeit von H.Harde ANNIMMT, einen Treibhauseffekt auf der Erde hätte, müsste dieser besonders stark am Tag sein, wenn die „Wärmeplatte“ Erde die stärkste Wärmestrahlung produziert
richtig, Herr Ingeniör????
und nachts müsste der Treinhauseffekt natürlich entsprechen schwächer sein, wenn die Heizplatte abgestellt ist,
richtig, Herr Ingeniör????
Nun,
dann müssen Sie mir nur noch erklären warum es auf der Tagseite des Mondes WESENTLICH wärmer ist als auf der Erde (bis ca. 130°C),
OHNE diesen Treibhauseffekt.
mfG
#16:Bravo, Herr Dr. Kuhnle , ich möchte es auch lieber etwas wärmer haben, nicht nur für meinen eigenen Körper, auch als Hobby-Gärtner.
Z.Zt. kämpfe ich gegen Pilz in der Wohnung. Auf den Birnbäumen und Schattenmorellen schon seit Jahren.
Also wofür bitte noch Geld bezahlen.
Ihre Überlegungen zur negativen Rückkopplung sind im Prinzip völlig richtig, schon allein deshalb, weil ein erhöhte Temperatur zu einer nichtlinearen Verstärkung der Abstrahlung führen MUSS (4.Potenz!).
Chaos bedeutet NICHTLINEARITÄT und deshalb Indeterminismus, aber keinesfalls Strukturlosigkeit.
Einer der Väter der Chaostheorie war bekanntlich der Meteorologe E.Lorenz 1963, der sein „Wettermodell“ am Rechner nur mit drei Variablen versehen hat was zwar zu einem nicht periodischen und überschneidungsfreien „Pfad“ (indeterminiert) geführt hat,
aber trotzdem innerhalb eines neuen „Ordnungsrahmens“ (Lorenzattraktor).
http://tinyurl.com/cpeoqv3
Umgesetzt auf Temperatur und CO2 muss man einfach einen Blick in die Vergangenheit werfen:
http://tinyurl.com/cpcjspk
Hier gibt es ein Millionen Jahre stabiles Temperaturniveau auf ca. 22°C !!!, das vermutlich auch dem physikalischen Prinzip eines Chaotischen „Attraktor“-Systems folgt. Die Sonne strahlte früher bekanntlich nicht mehr sondern WENIGER.
Kein Meteorologe kann bis heute den auch hier sichtbaren sehr steilen Temperaturabfall schlüssig erklären.
Von einem CO2-Einfluss ist jedenfalls keine Spur erkennbar (Korrelation)
und auch keine vernünftige physikalische Erklärung möglich, da CO2 KEINEN Wärmermeisolirungseffekt hat.
mfG
Hallo Herr Paul, #17
einfach mal den Versuch wie in http://tinyurl.com/cew3em6 unter #309 beschrieben durchführen und damit Wood bestätigen, ggf. die Warmhalteplatte gegen ein Plattengerät wie in http://tinyurl.com/cjhj6p5 beschrieben austauschen. Der Vorteil dieser Messsung ist, dass Sie die verschiedenen Effekte wie Strahlung, Leitung, Konvektion, Treansmission, Reflexion und Emission durch Parametervariation und spätere statistische Auswertung sauber trennen können. Nach Auswertung der Messung ist Wood Geschichte.
P. S. Gasstrahlung ist schon etwas komplexer als nur bunte Bilder malen.
Herr Dr.Kuhnle, Ihre Betrachtungen finde ich durchaus interessant. Ich hatte leider übersehen, dass sie auch einen 1-Jahres-Durchschnitt gewählt hatten. Zu der genauen Auswirkung des Vulkansausbruchs kann ich praktisch nix sagen, aber man sollte trotzdem vorsichtig bei der Interpretation der Daten sein. Wenn man in einem Gesamtsignal keine Auswirkung eines Einzelsignals beobachtet, dann kann das auch an einem schlechten Signal-Rausch-Verhältnis liegen oder gegenläufigen Effekten. Sie argumentieren, dass es einen solchen gegenläufigen Effekt nicht gab, weil nach 2-6 Jahren kein weiterer Anstieg zu beobachten war. Sie sollten aber nicht vergessen, dass in der Klimavariablität Schwankungen auftreten, die von viel kürzerer Zeitdauer sind.
„Nach meinen Vorstellungen ist das Klimasystem der Erde ein komplexes System, was sich durch negative Rückkopplungen von selber reguliert und meistens im Gleichgewicht ist.“
Wenn diese These stimmen sollte, wäre die spannende Frage, in welcher Höhe sich das Gleichgewicht einstellt, wenn man verschiedene Ausgangsgrößen verändert.
„Zum Schluss noch eine persönliche Frage: Glauben Sie, dass die über eine Billionen Euro teure deutsche Energiewende das leisten kann, was der Pinatubo nicht geschaft hat: die globale Temperatur um 0,4 Grad zu senken, wenigsten für ein Jahr? Da meine Familie ja wohl mindestens 50.000 Euro von der Billion bezahlen muss (Ich habe einfach mal die Billionen durch die Zahl der Bundesbürger geteilt), möchte ich gerne wissen ob mein Geld gut angelegt wird.“
Das Ziel ist ja keine Temperatursenkung vom heutigen Zustand aus betrachtet, sondern den wahrscheinlichen Anstieg der kommenden Jahrzehnte und Jahrhunderte abzubremsen und wenn sie so wollen, bei einem Gleichgewicht anzukommen, mit dem wir noch vernünftig leben können. Ob das Geld nun gut angelegt ist, dass kann ich Ihnen auch nicht sagen. Aber WIE man abschätzen könnte, ob eine „Rendite“ wahrscheinlich ist, da können ihnen Mathematiker und Ökonomen mit ihren Werkzeugen durchaus weiterhelfen. Selbst wenn sie mal die ganze Klimaveränderung beiseite lassen, kann ein vorgezogener Umstieg in alternative Energien, wie beispielsweise an Norwegen retrospektiv beobachtbar ist, sich langfristig positiv auf die Energiepreise auswirken. Dann ist es letztlich eine Kosten-Nutzen-Abwägung zusammen mit den Aspekten der möglichen Klimaerwärmung. Ähnliche Abwägungen müssten sie anstellen, ob sich beispielsweise ein Hauskauf für ihre Familie lohnt. Auch da sind sie auf Abschätzungen bzgl. der Zukunft angewiesen.
Es kann aber auch sein, dass Sie von den Klimaveränderungen weit weniger betroffen wären, als jemand in einem unterentwickelten Land. Gut möglich, dass sich die 50.000 Euro nicht so sehr ihrer Familie entgegenkommt, dafür umso mehr anderen Familien in diesen Ländern. Wie Sie so einen Verlauf bewerten würden, müssten sie selbst rausfinden.
#17: Dr.Paul sagt: „Verehrter Mitstreiter #13: Greg House,
mit seinen „Labormessungen“ hat unser lieber Herr Lüdecke vorsätzlich in die Irre geführt,“
=====================================================
Lieber Herr Dr.Paul,
ich sehe noch keine Beweise für „vorsätzlich“, obwohl ich Ihre Gefühle gut nachvollziehen kann. Im Moment sieht es für mich so aus, dass Herr Lüdecke selbst in die Irre geführt worden ist, wie auch viele anderen. Der Weg daraus ist mühsam und erfordert Zeit.
#13 Kommentar:
Antwort:
H. Harde: How much CO2 really contributes to global warming? Spectroscopic studies and modelling of the influence of H2O, CO2 and CH4 on our climate, Geophysical Research Abstracts, Vol. 13, EGU2011-4505-1, 2011
EIKE Redaktion
=======================================================
Lieber Herr Lüdecke, erst mal vielen dank für die Antwort von der „EIKE Redaktion“ und den Link. Der Link hat leider gezeigt, dass das Herleiten der „Klimasensitivität des CO2“ dem Anschein nach lediglich auf der Basis einer ANNAHME einer erwärmenden Wirkung des CO2 errechnet wurde, und zwar mit einem „Klimamodel“.
Diese Annahme basiert wiederum auf der Tatsache, dass CO2 gewisse Wellenlängen absorbiert. Die Autoren erwähnen allerdings mit keinem Wort, dass CO2 auch emittiert, und zwar in alle Richtungen. Das ist schon mal verdächtig. So geht schon mal eine Filterfunktion des CO2 verloren, die dazu führt, dass weniger Sonnen-Infrarot die Erdoberfläche erreicht, mit anderen Worten, zur KÜHLUNG beiträgt.
Zweitens, auch wenn man davon ausgeht, dass es stimmt, was die Autoren behaupten, nämlich dass sich CO2 direkt durch eigene Absorption erwärmt und dadurch die Lufttemperatur um 0,45C steigt, und wenn man auch die aktuelle Konzentration des CO2 in der Luft berücksichtigt (1/2500), dann würde sich pures CO2 bei der gleichen Einstrahlung um 0,45×2500=1125C erwärmen. Das sieht nicht besonders realistisch aus. Das zeigt, dass die Annahme völlig Absurd ist.
Also bleibt dann nur, dass CO2 die IR-Strahlung teilweise streut, ohne sich dabei zu erwärmen. Das macht schon mal Sinn, und so landen wir bei dem IPCC-Konzept, wonach CO2 ein Teil des von der Erdoberfläche kommenden IR zurück zur Erdoberfläche sendet und sie dadurch zusätzlich erwärmt. Allerdings, so funktioniert die Natur nicht, was das Experiment des Professors für Experimentalphysik R.W.Wood schon vor 100 Jahren demonstriert hat.
Vielleicht ist es an der Zeit, sich mit der Frage auseinander zu setzen, was in der Behauptungen der zahlreichen Klimawissenschaftler wirklich physikalisch bewiesen ist.
Verehrter Mitstreiter #13: Greg House,
mit seinen „Labormessungen“ hat unser lieber Herr Lüdecke vorsätzlich in die Irre geführt,
denn selbstverständlich ist nicht der Treibhauseffekt oder die Klimasensitivität von CO2 etc. im „Laborversuch“ gemessen,
sondern nur die etwas genaueren Hitranspektren.
WOOD ist natürlich NICHT widerlegt.
Der Herr Hermann Harde aus Hamburg (deutscher Text, hier bei EIKE schon zitiert) hat also ebenso wie die IPCC ein „Rechenmodell“ gebastelt und dabei die Hitranspektren eingebaut.
Kardinalfehler ist dabei die naive Betrachtung der Atmosphäre selbst als schwarzer Körper
und natürlich damit auch die unphysikalische Gegenstrahlung im „2-Schichten-Modell“,
bei der nur noch die Temperatur, nicht aber die Selektivität bei der Transmission berücksichtigt wird
http://tinyurl.com/csvsnlo
In der gleichen Arbeit wird aber die wichtigste CO2-Absorbtion bei 15µm mit einer Transmission von 0 dargestellt:
http://tinyurl.com/bpaxrka
die eine solche Gegenstrahlung auf die Erde ausschließt!
Zudem hat der Autor völlig falsche Vorstellungen über den adiabatischen Temperaturgradient,
und schließt dabei auf einen geringen Einfluss der Konvektion.
(„wenige 10-tel°C in den ersten 100 Metern)
Dabei ist gerade der Temperatursprung an der Grenzfläche Erde/Atmosphäre wegen der extrem unterschiedlichen Absobtivität am größten.
Ein etwas freundlicheres Modell also als das der IPCC,
aber ebenso ein Modell mit vielen Fehlern und auch selbst konzidierten Unsicherheiten (z.B. Tag/Nacht – Unterschied).
mfG
mfG
@#10 Herr Hader
in #4 können Sie nachlesen, dass ich den Mittelwert der 12 Monate nach dem Vulkanausbruch berechnet habe. Die Globale Temperatur unterscheidet sich weniger als ein Hunderstel Grad vom 5-Jahresmittel vor dem Ausbruch. Also kein Effekt. Laut Wikipedia verblieb die vom Ausbruch injizierte Asche etwa 3 Jahre in der Atmosphäre.
Vieleicht wurde die Abkühlung durch den Vulkanausbruch ja durch die globale Erwärmung kompensiert, habe ich gedacht. Also ermittelte ich den Durchschnittwert der Jahre 2-6 nach dem Ausbruch, um zu sehen ob es durch die globale Erwärmung nach der (nicht vorhandenen) Vulkan-Abkühlung mit der Temperatur bergauf ging. – Ging es aber nicht, die globale Temperatur lag sogar ein Hunderstel Grad darunter. 1987 bis 1997 gab es also noch nicht einmal eine globale Erwärmung.
Wie wir ja alle inzwischen wissen, gibt es auch seit 1997 bis heute keine globale Erwärmung. Daher ist es höchstinteressant sich das Jahr 1997 mal genauer anzusehen. Zwischen April 1997 und Februar 1998 ist die Temperaturanomalie stetig nach oben gegangen, insgesamt um etwa ein halbes Grad. Der Rekordwert vom Februar 1998 war aber sozusagen ein Überschwinger, denn der Durchschnitt der letzen 16 Jahre liegt ein viertel Grad unter dem Rekordwert und etwa ein viertel Grad über dem Temperaturniveau 1987-1997.
Nach meinen Vorstellungen ist das Klimasystem der Erde ein komplexes System, was sich durch negative Rückkopplungen von selber reguliert und meistens im Gleichgewicht ist. Ab und zu (z.B. 1997) wird das bis dahin geltende Gleichgewicht aufgegeben und die Temperatur pendelt sich auf einem neuen Gleichgewicht ein. Es mag naiv klingen, die von Ihnen verehrten IPCC-Klimatologen mögen den Kopf schüttel, die EIKE-Sonnentheoretiker wollen auch nichts davon wissen, aber in der Natur spielen sich die Prozesse in der Regel immer nach einem solchen Muster ab, Beispiele gibt es genügend. Natürlich kann ich meine Hypothese nicht beweisen, aber Sie können sie auch nicht widerlegen.
Zum Schluss noch eine persönliche Frage: Glauben Sie, dass die über eine Billionen Euro teure deutsche Energiewende das leisten kann, was der Pinatubo nicht geschaft hat: die globale Temperatur um 0,4 Grad zu senken, wenigsten für ein Jahr? Da meine Familie ja wohl mindestens 50.000 Euro von der Billion bezahlen muss (Ich habe einfach mal die Billionen durch die Zahl der Bundesbürger geteilt), möchte ich gerne wissen ob mein Geld gut angelegt wird.
Obwohl, eigentlich möchte ich gar nicht, dass es 0,4 Grad kälter wird. Obwohl, eigentlich ist es mir schnurzpiepegal ob es heute Nacht 1,0 oder 1,4 Grad hat. Für mich ist das gleich. Ich hätte lieber die 50.000 Euro behalten.
Sehr geehrter Herr Lüdecke,
ich denke, im großen und ganzen sind wir gar nicht so weit auseinander. Erlauben Sie mir noch eine kleine Klarstellung zu #9:
„Ich gehe zu Ihren Gunsten davon aus, dass das mit „je kleiner alpha gewählt wird..“ ein Tippfehler war. alpha wir nicht gewählt, es ist der aus der DFA ermittelte Hurst-Exponent. Gewählt wird ein Vertrauenslimit.“
Natürlich war nicht der Hurstexponent gemeint. Ich sprach von Hypothesentests und da wird alpha als gängige Bezeichnung für den Fehler erster Art verwende, bei BL die üblichen 5%, wenn ich das richtig sehe.
Leider gingen Sie auf die Passage zum Hypothesentest nicht weiter ein. Sicher, uns sind die Grundlagen bekannt, ich könnte mir aber vorstellen, dass einige Leser auf die naheliegende, wenn auch falsche Idee kommen, dass wenn 30% der Zeitreihen unnatürliche Trends aufweisen, die restlichen 70% dann natürlich sind.
Schade, dass LB keine Tabellen für andere Signifikanzniveaus erstellt haben (oder haben sie?). Die Logik der 5% liegt ja darin, dass man in 95% der detektierten unnatürlichen Trends diese auch tatsächlich unnatürlich sind, die 5% falschen Diagnosen sind bedauerlich, aber verschmerzbar. Je größer diese Sicherheit aber gewählt wird, desto mehr unnatürliche Trends werden vom Hypothesentest zwangsläufig nicht detektiert. Ein Test mit 90%-Signifikanzniveau wäre mal einen Versuch wert, um ein Gefühl für die Größenordnungen zu bekommen.
PS:
Die Instationarität der globalen Zeitreihe finde ich bemerkenswert. Ob der Erklärungsversuch des Einflusses von Homogenisierung trägt, hm, da bin ich skeptisch. Man könnte weiterkommen, wenn man zum Vergleich die BEST-Daten heranzieht, die ja ohne Homogenisierung arbeiten. Oder man nimmt mal ganz plump einen möglichst umfassenden Datensatz von Rohdaten. Auf jeden Fall sehr interessant.
MfG
@P.Große #2
Wer von Klima spricht bzw. verstehen will, der muss das GANZE betrachten. Und das GANZE ist in unserem Fall unser Sonnensystem. Zum GANZEN gehört auch der Raum und die Zeit.
30 Menschenjahre sind in Anbetracht der Erdgeschichte einfach nicht als Klimazeitraum tauglich!
Klima ist das GANZE! Von Beginn der Erdentstehung bis zu ihren Untergang. Die Sonne ist für unser kohlenstoffbasierendes Leben der ständige klimatische Taktgeber.
Und wenn wir das GANZE betrachten, dann kommt mir die nächste Frage automatisch durch den Kopf geschossen. Woran lag es, dass es das kohlenstoffbasierende Leben geschafft hat, solche großen Lebensformen wie es die Dinosaurier waren, hervor zu bringen…
Welches Umfeld musste damals geherrscht haben um solche gorßen Lebenformen entstehen zu lassen?
War mehr CO2 in der Atmosphäre als heute? War die Sonne aktiver bzw. stabiler als heute?
Hatte die Sonne bereits vor über 200 Millionen Jahre ihre „Lebensmitte“ erreicht und befindet sich seit dieser Zeit in der zweiten Hälfte ihrer Existenz?
Was wir sicher wissen, ist das diese Heizung am Himmel (Sonne) nicht konstant und stabil wirkt. Das diese Heizung näher am Ende als am Anfang ihrer Selbstverzehrung steht.
@Hr. Große
Um zu verstehen, müssen immer wieder Fragen aufgeworfen werden. Damit Fragen aufgeworfen werden können, muss man in der Lage sein seinen Blickwinkel zu verändern.
von Horst-Joachim Lüdecke: „…ob die aus Labormessungen hergeleitete, unmaßgeblich kleine Klimasensitivität des CO2 – sie liegt grob zwischen 0,5 °C und 1,1 °C…“
====================================================
Lieber Herr Lüdecke,
nach meinen Informationen schließt das, was wirklich im Labor gemessen wurde, eine Klimasensitivität des CO2 eher aus. Aber ich lasse mich gerne eines Besseren belehren und bitte Sie deshalb um genaue Angaben: wer genau hat denn dieses Laborexperiment gemacht und was für eines und wer und wie daraus diese „Klimasensitivität des CO2“ hergeleitet hat, möglichst mit genauen Zitaten und links. Vielen Dank im Voraus.
Der „Persistenzürfel“ wird auch ohne angehängte Gewichte langfristig ein ausgeglichenes Ergebnis liefern. Serienbildung wiederspricht nur dem menschlichen Verständnis einer ausgleichenden „“Gerechtigkeit“. Diese Fehlinterpretation, hervorgerufen durch kurzfristige Betrachtung, wird den meisten Spielern zum Verhängnis! Ich habe zu dem Thema umfangreiche Analysen angestellt – die Erkenntnis lautet: nicht ist unmöglich.
Sehr geehrter Herr Lüdecke,
zunächst mal:
„Sie machen es sich mit diesem Kommentar nach bewährter Vernebelungs-Methode wieder einmal zu einfach.“
Muss das („Vernebelungsmethode“) sein? Kann man nicht sachlich diskutieren? Ich versuche mal, auf der Sachebene zu bleiben:
„Dass die Ursache von Trends nicht mit der Persistenzanalyse bestimmt werden kann, ist trivial.“
Zustimmung. Wenn Sie unnatürliche Trends detektieren, können diese theoretisch von CO2, von der Sonne oder von irgendetwas anderem stammen, das kann die Methode nie unterscheiden.
„Dass mit Hilfe der Persistenzanalyse (eine statistische Methode) überhaupt keine Aussage über den Einfluss des anthropogenen CO2 ableitbar ist, ist allerdings falsch.“
Warum ist dies falsch? Da hätte ich gerne eine überzeugende Begründung. Ein kleines Extrembeispiel: Nehmen wir an, Forcing A bewirkt eine Erwärmung, die aber genau von der abkühlenden Wirkung eines Forcings B kompensiert wird. Die Persistenzanalyse findet überhaupt keine unnatürlichen Trends. Trotzdem waren laut Konstrukton sogar gleich zwei externe Einflussfaktoren vorhanden.
„Ebenfalls falsch ist Ihre Behauptung, dass für solche Aussagen die Analyse von Temperaturreihen generell ungeeignet ist. Können Sie in die Zukunft sehen?“
Nein, kann ich nicht. Aber ich finde es logisch, dass in dem Moment, wo man nach den Ursachen fragt, man automatisch in der Physik landet, die eben Ursache-Wirkung-Beziehungen untersucht. Ihre Persistenzanalyse beschränkt sich aber rein auf die Mathematik. Die Statistik kann dies m.E. nicht leisten.
Und selbst wenn man mit statistischen Methoden perfekt die Größe des unnatürlichen Trends berechnen könnte, selbst dies hilft nicht weiter, weil Sie einen Vergleichswert für die CO2-Wirkung heranziehen müssten. Und da landen wir wieder in der Physik, wir kennen den Wert der Klimasensitivität leider nur grob, wir wissen zu wenig über den Kühlungseffekt der Aerosole. Nein, so geht’s kaum, Mullers BEST behauptet es zwar, ich hab da aber meine Zweifel.
„Aber zurück zur Persistenzanalyse! Wenn nur in etwa 30% aller verfügbaren, ordentlichen Temperaturreihen globalweit ein externer Erwärmungstrend nachweisbar ist, darf füglich vermutet werden, dass das Forcing dieses Trends verglichen mit den natürlichen Forcings nicht sehr stark, vielleicht sogar unmaßgeblich ist.“
Sie dürfen füglich vermuten, ohne Rechnung und Begründung bleibt es aber eine unbelegte Vermutung. In ihrem jüngsten CP-Paper haben Sie diesen Nachweis gar nicht erst versucht und wie ich vorher schon schrieb, ich wüsste auch gar nicht, wie man diesen führen wollte.
PS:
Ich fand es bedauerlich, dass die Diskussion über dieses Paper an vielen Stellen, aber nicht hier bei EIKE geführt wurde. Schade. Es wäre sicherlich auch für die Leser hier von Interesse gewesen, einen open peer-review-Prozess mal live mitzuverfolgen. Gratulation jedenfalls, CP ist definitiv ein gutes Journal.
Herr Dr.Kuhnle, im Zeitraum von 5 Jahren wird der Vulkan-Effekt ziemlich weggeglättet. Wie lange diese Effekt wirklich anhielt, wird in dem Zitat gar nicht erwähnt.
„Für den Zeitraum von 1906 bis 2005 zeigen nur grob 30% aller Temperaturreihen aus Messtationen mit weniger als 1000 Einwohnern und unter 800 müNN einen unnatürlichen (externen) Trend. Ein ähnliches, nicht ganz so deutliches Ergebnis wurde für den Zeitraum von 1956 – 2005 gefunden. Daraus kann der Schluss gezogen werden, dass mit sehr hoher Wahrscheinlichkeit das anthropogene CO2 nur unmaßgeblich zur Erwärmung im 20. Jahrhundert beigetragen hat.“
Diese Schlussfolgerung kann ich nicht nachvollziehen. Die Unterscheidung zwischen natürlichen und externen Trends folgt nach dem Prinzip eines Hypothesentests auf einem 5%-Signifikanzniveau. Die Nullhypothese Ho ist hier „natürlicher Trend“, die Alternativhypothese H1 ist „unnatürlich“.
30% der Temperaturzeitreihen zeigten ein so außergewöhnliches Ergebnis, dass die Nullhypothese verworfen wurde und diese deshalb als „unnatürlich“ betrachtet werden.
Jetzt könnte man auf die Idee kommen, dass die restlichen 70% der Zeitreihen natürliche Trends aufweisen. Doch dann hat man die Grundidee von Hypothesentests nicht verstanden, es gibt ja auch den Fehler 2. Art, nämlich dass H0 akzeptiert wird, obwohl H1 richtig war. Je kleiner alpha gewählt wird (und 5% ist schon recht klein), umso größer wird der Fehler 2. Art. Konkret: Der Fehler 2. Art entscheidet darüber, wie viele der 70% restlichen Zeitreihen ebenfalls unnatürliche Trends besitzen.
PS:
Schade, dass das Verfahren mit Globalreihen nicht funktioniert. Ein Würfel in der geschilderten gezinkten Abwandlung kann Serien erzeugen, das kann ich mir leicht vorstellen. Wie ist das aber bei der ganzen Atmosphäre? Ist da der Energieerhaltungssatz nicht eine eiserne Klammer, die zufälligen Erwärmungs- oder Abkühlungsserien eine Grenze setzt? Passt das statistische Modell zu globalen Zeitreihen?
Ein zweiter Kommentar von mir.
Persistenz widerspricht eigentlich dem jüngsten Empfinden des Wettergeschehens. Als ich Oktober mit meiner Frau bei über 20 Grad spatzieren ging, konnte ich mir nicht vorstellen, dass schon eine Woche später ganz Deutschland im Schnee versinken würde. Nach einem warmen November gab es einen erneuten Kälteeinbruch im Dezember. An Heilig Abend konnte man dann wieder draußen grillen, am 31.12. lag die Tagesmitteltemperatur über der Jahresmitteltemperatur (unglaublich). Meine Wette auf einen extrem milden Januar ging aber in die Hose. Temperaturen bis minus 15 Grad drückten den Januar-Mittelwert noch deutlich unter den Durchschnitt der vergangenen Jahre. Heute war Frühling, nächste Woche droht wieder Dauerfrost.
Ein paar Zahlen:
Von den jüngsten 306 deutschen Monatsmitteltemperaturen waren 219 (72 %) „normal“, d.h. innerhalb des monatstypischen Mittelwertes +/- sigma. 44 Monate waren zu warm (14 %) und 43 zu kalt (14 %). Nach den 87 zu warmen oder zu kalten Monaten war der nachfolgende Monat in 63 Fällen wieder normal, 14 mal (16 %) gab es eine gleiche Abweichung ( Persistenz) und 10 mal (11 %) war der Folgemonat gegenteilig (kalt nach warm oder warm nach kalt).
Lang anhaltende Kälte gab es nur 1995/96 und lang anhaltende Wärme von Sep 2006 bis Juni 2007. Diese beiden Persistenzen kompensieren den sonst negativen Temperaturtrend seit September 1987.
Fazit: Über mehrere Monate wirkende Persistenzen sind sehr selten und können bei der Bewertung von Trends berücksichtigt werden. Von Klimawandel sollte man in solchen Fällen nicht sprechen. Nur Veränderungen, die über mehrere Jahre (etwa ab 10 Jahre) wirken, würde ich Klimaveränderung nennen. Für mich sind das dann aber neue quasistabile Gleichgewichtszustände.
Hallo zusammen,
Frage zum Verständnis: Es gibt ja Wetterlagen von Westen, die extreme Sprünge von Tag zu Tag aufweisen. Winter: Einmal ist es ungewöhnlich mild, am nächsten Tag bringt ein Schneegewitter den Winter. Dann wird es wieder mild, vielleicht mit Sturm und so fort.
Dauert eine solche Wetterlage über längere Zeit an – kann man das dann trotz der großen Wetter- (Wetter!)-Änderungen von Tag zu Tag auch Persistenz nennen? In den von mir übersetzten Texten ist so oft vom „time scale“ die Rede.
Gibt es „beständig unbeständiges“ Wetter? Hat diese Frage überhaupt etwas mit dem Artikel zu tun, in dem es ja eher um Klima geht?
Chris Frey
30% externe Persistenz in den maßgeblichen
Reihen, davon eine Möglichkeit CO2, bei erdgeschichtlich eher mariginaler Erwärmung in 20. Jahrhundert, in Konkurrenz zu erwiesenen Faktoren Sonne&Wasserdampf, bei reiner labor- bzw. starker AlGoreRhythmuslastigkeit der C02-Theorie. Wenn ich das richtig verstanden habe, dann ist eher weniger,oder? Fragt jemand ohne TI-30.
In #3 schrieb ich unpräzise:
„Mit der Auswertung von Temperaturzeitreihen kann man eben grundsätzlich kein detection and attribution betreiben, die Ursache der Trends kann eben nicht identifiziert werden aus den Temperaturen.“
Gemeint ist: „…,die Ursache der trends kann eben nicht identifiziert werden DURCH STATISTISCHE Analysen der Temperaturreihen“.
Woran liegt das? Wer unterscheiden möchte, ob die bisherige Erwärmung anthropogen oder natürlich verursacht ist, der muss Kriterien finden, woran man die unterschiedlichen Ursachen festmachen kann. Die Statistik kann nur Trends etc. liefern, das hilft nicht weiter zur Unterscheidung.
Unterschiede äußern sich real z.B. in der räumlichen Verteilung der Erwärmung auf der Erdoberfläche oder in den Temperaturkurven in Abhängigkeit von der Höhe. Jetzt sind wir mitten drin im spannenden Gebiet von detection&attribution.
Ein interessanter Artikel, zu dem es viel zu kommentieren gibt. Ich fange mal dem dem Thema Vulkanausbrüche an:
Der mit Abstand schwerwiegendste Vulkanausbruch der vergangenen 100 Jahre war des Ausbruch des Pinatubo im Juni 1991. Ich zitiere aus Wikipedia:
„Die Folge aus dieser gewaltigen Injektion war eine Sonnenlichtreduktion um 5%. Das wiederum führte zu einem durchschnittlichen Temperaturabfall um 0,5 bis 0,6 Grad in der nördlichen Hemisphäre und 0,4 Grad weltweit“
Skeptisch, wie ich nun einmal bin, werfe ich mal einen Blick in die globalen Temperatur-Daten (CRU, jeweils relativ zu 1961-1990):
Basis = Mittelwert der 5 Jahre vor dem Ausbruch: 0,17 Grad
Jahr nach dem Ausbruch (Jul91-Jun92): auch 0,17 Grad (wo sind die 0,4 Grad weniger?)
5 Jahre danach: (Jul92-Jun97): 0,16 Grad
Minimum eines 12-Monatsmittels im gesamten 11-jährigen Zeitraum: 0,05 Grad
Maximum 12-Monatswert im 11-Jahreszeitraum: 0,28 Grad
Gesamte Spannbreite (max-min): nur 0,2 Grad
Die Globaltemperatur des 11-Jahreszeitraums variiert also im gesamten Zeitraum kaum. Keine globale Erwärmung, keine Abkühlung, kein Vulkan-Effekt.
Meine Vermutung: Es gibt temperaturstabile Zeiträume, in denen selbst Extremereignisse nichts bewirken. Man kann es Persistenz nennen, ich nenne es Gleichgewichtszustand.
„Die Ursachen dieser Trends sind unbekannt. Neben anthropogenem CO2 kommen ungewöhnliche Sonnenaktivität und weitere noch nicht näher bekannte Antriebe in Frage.“
Zustimmung. Mit der Auswertung von Temperaturzeitreihen kann man eben grundsätzlich kein detection and attribution betreiben, die Ursache der Trends kann eben nicht identifiziert werden aus den Temperaturen.
Keine Chance, aus Temperaturzeitreihen zu entscheiden, ob der Anteil von CO2 an der Erwärmung der letzten 100 Jahre nun 0%, 50%, 100% oder sogar mehr betragen hat.
„Infolgedessen kann das anthropogene CO2 bei der in klimahistorischem Maßstab ohnehin geringfügigen Erwärmung im 20. Jahrhundert nur eine unbedeutende Nebenrolle gespielt haben.“
Das verstehe ich nun nicht. Steht das nicht gerade in Widerspruch von dem zuvor Gesagten?
PS:
Liebe Mitleser, bitte keine Rückmeldungen wie „mehr als 100% geht doch gar nicht!“. Herr Lüdecke hat schon verstanden, und jeder andere wird es mit ein wenig Nachdenken auch verstehen.
#1: Hofmann,M sagt:am Dienstag, 05.03.2013, 12:05
Zitat:
„Interessant wird es sein, wie sich die Sonne die nächsten 4,5 Millarden Jahre entwickeln wird. Ist jetzt mit zunehmender Abkühlung der Sonne zu rechnen bevor sich diese dann kurz vor ihrem Verzehr nochmal aufbäumt?
Oh …ja ich bin auch gespannt, aber.
Unsere Verzehrungsstrecke lieber Herr Hofmann ist leider etwas zu kurz geraten. Deshalb mein Vorschlag:
wir warten einfach mal 1.000.000.000 Jahre und treffen uns dann hier wieder, bis dahin können wir auch ausrechnen wieviel Masse die Sonne verlieren wird.
Gute 400.000.000 Tonnen/sek. schätzt man. Macht doch Spass mit den vielen Nullen oder?
Zitat:
„Ist jetzt mit zunehmender Abkühlung der Sonne zu rechnen bevor sich diese dann kurz vor ihrem Verzehr nochmal aufbäumt?“
tja das steht wohl in den Sternen Herr Hofmann. Wie immer heist es dann abwarten und Tee verzehren. In den nächsten Stunden ist zumindest mit zunehmender Dunkelheit zu rechnen. Aufbäumen zwecklos. Der Verzehr des Abendbrots ist unvermeidlich.
Zitat:
„Wieviel Masse hat die Sonne bereits verloren und wieviel Masse wird Sie noch verlieren?“
Wäre doch sicherlich mal den Spass wert dies auszurechnen. Von Ressourcenschonung oder nachhaltigem Wirtschaften scheint die Sonne auch nichts zu halten und wie schnell sind die paar Milliarden Jahre um.
Zitat:
„Die Sonne ist und bleibt das bestimmende Gestirn in unseren Sonnensystem des kohlenstoffbasierenden Leben.“
das stimmt, irgendwie werd ich den Verdacht nicht los, dass sich alles um die Sonne dreht.
MfG
Wenn wir uns über das Klima verständigen wollen, dann sollten wir endlich mal dieses lebenswichtige wiederverwertendes CO2 außen vorlassen.
Wer Klima verstehen will, der muss mehr über den Ausganspunkt in Erfahrung bringen. Und dies ist DIE SONNE.
Die Sonne hat momentan die Hälfte ihrer Verzehrungstrecke hinter sich. Damit ist die Sonne mit einen momentanen Alter von ca. 4,5 Millarden Jahren am Höhepunkt angelangt. Interessant wird es sein, wie sich die Sonne die nächsten 4,5 Millarden Jahre entwickeln wird. Ist jetzt mit zunehmender Abkühlung der Sonne zu rechnen bevor sich diese dann kurz vor ihrem Verzehr nochmal aufbäumt?
Wieviel Masse hat die Sonne bereits verloren und wieviel Masse wird Sie noch verlieren? Hat dieser Masseverlust auswirkung auf die Umlaufbahnen der Planeten. Also auch auf unsere Erde und damit auf unser Klima?
Für mich ist und bleibt der Schlüssel zum Verständnis unseres Klima in der Sonnen-Physik.
Die Sonne ist und bleibt das bestimmende Gestirn in unseren Sonnensystem des kohlenstoffbasierenden Leben.