Update:
Hier ein hoch interessantes (langes ) Telefonat mit dem ehemaligen DWD Meteorologen Dr. Hoffmann zur Qualität der Klimadaten. ".. Die Weltmitteltemperatur… jetzt haben wir aber gemittelt —ojeh, ojeh!" Mit Dank an R. Hoffmann
Weiter im Originaltext: In der Zusammenfassung steht:
Das statistische Fehler Modell, welches allgemein bei der Bestimmung der monatlichen terrestrischen Stations-Temperaturen angewendet wird, unterstellt eine physikalisch unvollständige Klimatologie, die dazu zwingt, dass deterministische Temperatur-Trends, als Messfehler interpretiert werden. Große verdeckte Unsicherheiten sind dabei den mittleren globalen bodennahe Lufttemperatur Messungen überlagert. Zur Veranschaulichung dieses Problems wurden repräsentative monatliche und jährliche Unsicherheiten anhand der Lufttemperatur Datensätze aus weltweit verteilten terrestrischen Klimastationen berechnet, was zu ± 2,7° C und ± 6,3 °C führt. Zudem wurde die vorhandene Unsicherheit in der von 1961-1990 erhobenen jährlichen Referenz Anomalie bis jetzt völlig vernachlässigt. Sie wird (hier) mit ±0,17 ° C bestimmt. Nach der Zusammenführung beider Unsicherheiten mit den zuvor berichteten ± 0,46 °C als unterer Grenze der Messfehler, bestimmt sich die von 1856 – 2004 errechnete globale bodennahe Lufttemperatur Anomalie bei einem 95%-Konfidenzintervall mit 0,8 ± 0,98 °C . Somit ist also der Trend der globalen durchschnittliche Oberflächentemperatur Lufttemperatur Anomalie statistisch ununterscheidbar von 0 °C. Ordnungspolitische Maßnahmen die auf die Beeinflussung der globalen Lufttemperatur gerichtet werden, sind daher empirisch nicht vertretbar.
Das statistische Fehler Modell, welches allgemein bei der Bestimmung der monatlichen terrestrischen Stations-Temperaturen angewendet wird, unterstellt eine physikalisch unvollständige Klimatologie, die dazu zwingt, dass deterministische Temperatur-Trends, als Messfehler interpretiert werden. Große verdeckte Unsicherheiten sind dabei den mittleren globalen bodennahe Lufttemperatur Messungen überlagert. Zur Veranschaulichung dieses Problems wurden repräsentative monatliche und jährliche Unsicherheiten anhand der Lufttemperatur Datensätze aus weltweit verteilten terrestrischen Klimastationen berechnet, was zu ± 2,7° C und ± 6,3 °C führt. Zudem wurde die vorhandene Unsicherheit in der von 1961-1990 erhobenen jährlichen Referenz Anomalie bis jetzt völlig vernachlässigt. Sie wird (hier) mit ±0,17 ° C bestimmt. Nach der Zusammenführung beider Unsicherheiten mit den zuvor berichteten ± 0,46 °C als unterer Grenze der Messfehler, bestimmt sich die von 1856 – 2004 errechnete globale bodennahe Lufttemperatur Anomalie bei einem 95%-Konfidenzintervall mit 0,8 ± 0,98 °C . Somit ist also der Trend der globalen durchschnittliche Oberflächentemperatur Lufttemperatur Anomalie statistisch ununterscheidbar von 0 °C. Ordnungspolitische Maßnahmen die auf die Beeinflussung der globalen Lufttemperatur gerichtet werden, sind daher empirisch nicht vertretbar.
Zitatende
Wieder bezieht sich Frank auf den schon öfter erwähnten Aufsatz von Brohan et al 2006[1] (er nennt in kurz B06) und ergänzt seinen ersten Ansatz um die Berechnung von Fehlern, die aus der örtlichen und zeitlichen Verteilung der Einzel-Messwerte selbst herrühren. Zusätzlich stellt er richtigerweise fest, dass auch die zur Anomalienbildung verwendete „Referenztemperatur“[2] (das „Station Normal“ im Sprachgebrauch) keinesfalls frei von Fehlern ist und diese sich deshalb – entsprechend der Fehlerfortpflanzung- im Ergebnis widerspiegeln müssen. Das ist bisher nirgends thematisiert worden, beeinflusst aber die erzielbare Genauigkeit erheblich.
Wie schon zuvor betrachtet er das bisherige, von Brohan et al 2006 verwendete, Fehlerbestimmungsmodell als unvollständig und starr und zu Scheingenauigkeiten führend. Diesmal, und zusätzlich zur bisherigen Betrachtung, auch deshalb, weil darin Station Normals[3] als konstant angenommen werden, sowie die angenommenen Fehler rein zufällig sein sollen und sich deshalb durch Mittelung über die Zahl der Messungen minimieren lassen. Außerdem fällt ein zwangsläufig auftretender systematischer Fehler s, der sich aus der Verschiedenheit der Messungen herleitet, völlig unter den Tisch. Der Ansatz von Brohan et al 2006 lässt sich damit nicht mehr halten. Auch deswegen, weil inhärente Trends, die regelmäßig in monatlichen Temperaturgängen auftreten und für den gleichen Monat aber in verschiedenen Jahren sehr verschieden sein können, zu einem weiteren systematischen Fehler bei den Monatswerten führen müssen.
Er nimmt deshalb das Standard-Fehler-Modell von B06 Stück für Stück auseinander. Es ist nicht immer leicht den dort vorgestellten Gedankengängen auch mathematisch zu folgen, aber da jeder neue Gedankengang sehr sorgfältig erklärt wird, kann der aufmerksame Leser dies trotzdem schaffen. Pat Frank schließt seinen Aufsatz mit der Schlussfolgerung:
Zitat:
Die Analyse des statistischen Protokolls welches üblicherweise verwendet wird, um die Unsicherheit in der globalen Durchschnittstemperatur des bodennahen Lufttemperatur Anomalie-Index abzuschätzen, ergibt, dass dieses verhängnisvoll fehlerhaft ist. Es sollte zu Gunsten eines Modells, dass explizit den Mangel an Wissen über die Fehler Varianzen in terrestrischen Klimastations- Temperaturmessungen zeigt, ausrangiert werden.
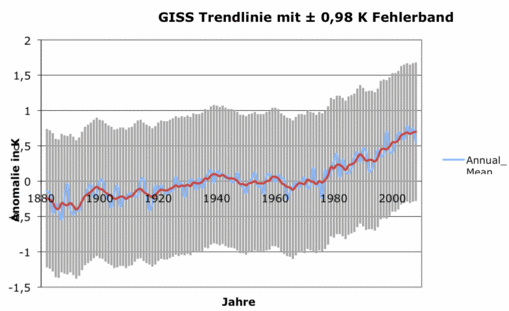
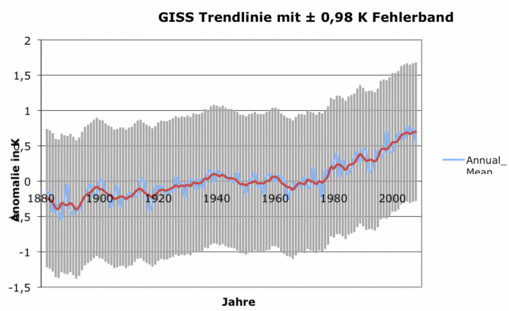
Abbildung 1 Die rote mittlere Trendlinie zeigt globale Mitteltemperatur wie sie vom amerikanischen Goddard Institute of Space Sciences (http://data.giss.nasa.gov/gistemp/graphs/) GISS von 1880 bis Ende 2008 im Internet zu Verfügung gestell wird. Ihr überlagert ist die minmale Unsicherheit nach Frank in Höhe von ± 0,46 K. Die Referenzzeit ist hier 1951-1980
Die Unsicherheit in der Referenz-Periode der globalen Mitteltemperatur der Luft der Temperaturanomalie wurde bisher selten betrachtet. Diese Temperatur-Unsicherheit stellt die minimale Variabilität dar, die man bei einer mittleren Jahrestemperatur eines bestimmten Klimaregimes erwartet werden kann, vorausgesetzt, dass dieser Referenz- Zeitraum repräsentativ ist. Unter der Annahme, dass die Jahre 1961-1990 einen normalen Zeitraum repräsentieren, dann decken ± 0.51 °C 99,7% der Variabilität der globalen durchschnittliche Lufttemperatur im 20. Jahrhundert ab. Wenn das globale Klima in einer einzigen Phase über dem Intervall von 1856-2004 gewesen ist, dann decken ± 0,84 °C zu 99,7% die wirkliche klimatologischen Lufttemperatur-Variabilität des 20. Jahrhunderts ab. Aus diesen Überlegungen folgt, dass die meisten, oder alle, der beobachteten Variationen der mittleren globalen Temperatur im 20. Jahrhundert nur sparsam den meist spontanen Schwankungen des Klimas zugeordnet werden können, die auch die Pseudo-Trends reflektierende Persistenz zeigen[22-25]. Es scheint, dass es keine besonderen Anzeichen für eine alarmierende Ursache der Erwärmung des mittleren globale bodennahe Lufttemperatur Trends im 20. Jahrhundert gibt . Deshalb sind politische Maßnahmen diesen Trend zu beeinflussen, empirisch unerträglich.
Ergänzung
Dieser klare Befund muss noch um einige weitere Überlegungen ergänzt werden. Frank zeigt, dass die mittlere Globaltemperatur bzw. deren Trend (s. Abbildung) von einem Unsicherheitsband in der Größe von ± 0,98°C umhüllt wird. Nun könnte jemand auf die Idee kommen, um trotzdem daraus eine Erwärmung abzuleiten, die Hüllkurve des Bandes statt die Trendlinie selbst, für die Ermittlung des Trends der Erwärmung zu verwenden. Dies setzt voraus, dass die mittlere Trendlinie sich genau in der Mitte dieses Bandes befindet. Davon kann jedoch nicht ausgegangen werden. Wie eine weitere – noch nicht veröffentlichte- Forschungsarbeit von EIKE zeigt, kommen zu den genannten Grenzfehlern noch viele weitere hinzu, die sich aus den verwendeten Messmethoden, -Instrumenten und deren Unterbringung, -Algorithmen, etc. zweifelsfrei herleiten lassen. Diese sind systematische Fehler, die nicht über die ganze Zeit gleich sind, auch in sich nicht gleich sein müssen, weder gleich groß, noch in ihrem Vorzeichen. Sie verschieben damit daher die wahre Trendlinie unsymmetrisch aber unbekannt innerhalb des Bandes. Zudem verbreitern sie das jetzt schon breite Unsicherheitsband nochmals um mindestens ± 0,5 eher um bis zu ± 1 °C. In den frühen Jahren ab 1850 sogar noch breiter, um dann im 20. Jahrhundert enger zu werden, mit einer weiteren Verengung ab Mitte der 70er Jahre .
Zu gegebener Zeit werden wir bei EIKE hierüber berichten.
Update Kritik von Teil I:
Ein Kritiker bemängelte, (Hier der Link dort Kommentare 32 und 37) dass bei Berechnung des Tagesmittels, Autor Frank und ich nicht berücksichtigt hätten, dass dieses Mittel
"…kein Erwartungswert eines Ensembles von Messungen zu einem bestimmten Zeitpunkt des Tages zu interpretieren ist!"
und fährt fort:…."Das Tagesmittel stellt ein Maß für das Integral über die Temperaturkurve des Tages geteilt durch die Tageslänge dar! "
Soweit der Einwand.
Obwohl von diesem Kritiker in der ihm eigenen -der eigenen Wichtigkeit bewussten- Überheblichkeit vorgebracht, ist es interessant sich mit diesem Argument und seiner Begründung zu befassen. Der Kritiker meint also, die Behandlung der Messwerte unter Einbeziehung ihrer Fehler nach der Fehlertheorie, hinge von der späteren Interpretation ihrer beabsichtigten Verwendung ab.
Dies ist aber hier nicht der Fall. Denn In jedem Falle bleiben es (hier 2 x 30) verschiedene Messwerte, die zuerst miteinander -nach bestimmten, zudem willkürlichen- Algorithmen, zu einem Einzelwert (Tagesmittel genannt) kombiniert werden, um dann zu einem Monatsmittel verdichtet zu werden. Dabei werden die nicht zu unterschreitenden Messfehler benannt, aber als zufällig im Sinne der Fehlertheorie angenommen.
Dies darf man aber nur dann machen, wenn anzunehmen ist, dass jede gemessene Tagestemperatur, bis auf einen zufälligen Anteil identisch mit allen anderen Temperaturen ist. Nur dann tendiert der zufällige Anteil, bei genügend großer Zahl von Messwerten gegen Null. Diese Annahme ist aber offensichtlich, wie sowohl Frank und ich wissen, und wie auch im Teil I ausgeführt, aber auch Brohan 06 wissen – kompletter physikalischer Unsinn!
Die einzelnen Messungen der Tagestemperaturen sind sehr verschieden. Vermeidet man also diesen Unsinn, dann muss man -wissenschaftlich korrekt- die Fehleraddition, wie sie Frank richtig beschrieben hat, einsetzen. D.h. unabhängig davon, wie später das Ergebnis interpretiert werden soll, muss dies- wenn man es in weiteren späteren Rechnungen verwenden will- nach den anzuwendenden Regeln der Fehlertheorie erfolgen.
In einem aber hat der Kritiker recht: das Ergebnis dieser Mitteilung der Tagestemperaturen wird als Ersatz für das Integral der Tagestemperatur (dem "wahren Mittel") über der Zeit interpretiert. Doch wenn man dies tur, kommt allein durch den (mühsamen) Vergleich – anders als Hinweis des Kritikers vermuten lässt- ein weiterer systematischer Fehler hinzu.
Jeder Algorithmus -und es wurden weltweit ca. 100 verschiedene eingesetzt, wie Griffith 1997 (Griffiths, JF (1997) Some problems of regionality in application of climate change.) herausfand- erzeugt ein anderes Tagesmittel, Monats- und Jahresmittel, als das gewünschte "wahre" Mittel über 24 Stunden.
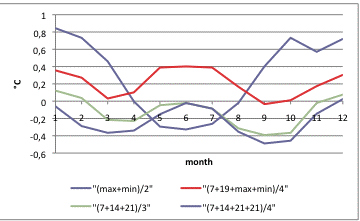
Abbildung 2 zeigt eine Auswertung der Temperaturdaten der österreichischen Station Puchberg über 9 Jahre. (Quelle: Aguilar, EA,I. Brunet, M. Peterson, Thomas C. Wieringa,V. (2003) GUIDANCE ON METADATA AND HOMOGENIZATION. Aguilar, 2003)
Dargestellt sind darin die Differenzen von Tagesmitteln verschiedener Algorithmen zum "wahren" (24 h) Tages-und Monatsmittel (als Nulllinie dargestellt), aufgeschrieben über das ganze Jahr. Diese wurden wiederum über 9 Jahre gemittelt. Wohlgemerkt, es handelt sich immer um dieselbe Temperaturänderung über den Tag, den Monat und das Jahr.
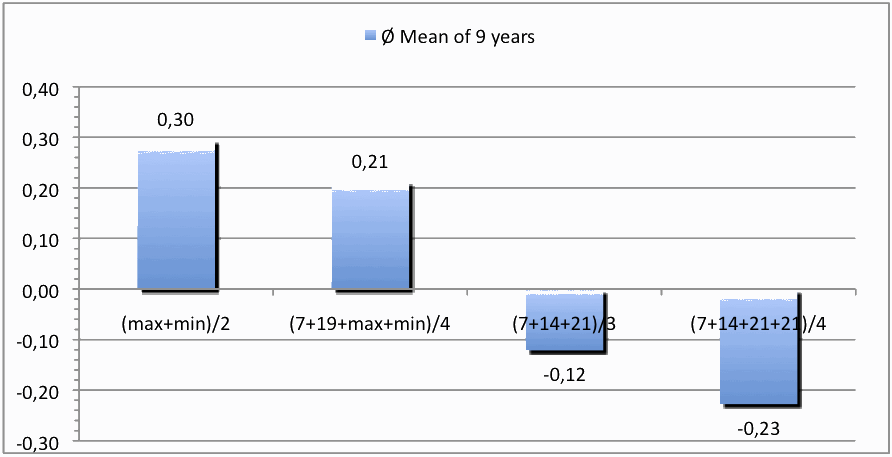
Abbildung 3 zeigt die Abweichungen der verschiedenen Jahresmittel aus Abbildung 1, zum "wahren" Jahresmittel – das ist die Nulllinie), die nach diesen verschiedenen Algorithmen berechnet wurden. Die Differenz zwischen Max/Min und Mannheimer-Methode über satte 9 Jahre liegt immerhin bei beträchtlichen 0,5 °C.
Unser Kritiker behauptet nun, dass dieser systematische Fehler nicht nur bekannt sei, sondern auch korrigiert würde. Das trifft jedoch nur ganz selten für wenige Zeiten und Klimazonen zu.
Jedoch gerade bei der Ermittlung der Globaltemperatur gilt stattdessen das komplette Gegenteil, denn in Brohan 06 stellen die Autoren unmissverständlich fest: Brohan, PK,J. J. Harris, I., Tett S. F. B.; & Jones, P. D. (2006) Uncertainty estimates in regional and global observed temperature changes: a new dataset from 1850.
„..There will be a difference between the true mean monthly temperature (i.e. from 1 minute averages) and the average calculated by each station from measurements made less often; but this difference will also be present in the station normal and will cancel in the anomaly. So this doesn’t contribute to the measurement error.“
Die dort gemachte Annahme aber stimmt aber nur dann, wenn
1…..der eingesetzte Algorithmus über den ganzen Zeitraum der einzelnen Zeitreihe unverändert geblieben ist – wovon aber nur selten, wie wir wissen, wenn überhaupt, ausgegangen werden kann.
2…..wenn man die daraus gebildeten Anomalien nicht miteinander vermischt.
3…..wenn man sie auch nicht mit dem "wahren Mittelwert" – wie es Brohan oben erklärt, in irgendeine Beziehung setzt.
Dies alles jedoch ist erklärte und gängige Praxis bei der Berechnung der Anomalie der mittleren Globaltemperatur. Tut man dies, dann handelt man sich allein durch die verwendeten Algorithmen systematische Fehler des Endergebnisses von einigen Zehntel Grad ein.
Bekannt sind diese Fehler wohl, korrigiert werden sie aber nicht. In der der Literatur, die sich mit der Berechnung der globalen Mitteltemperatur, bzw. ihrer Anomalien über die Zeit beschäftigt, findet sich keinerlei Hinweis darauf. Weil man vermutet – siehe oben- dass er sich von selbst ausgleicht.
Auch der Kritiker nennt nur das Histalp-Projekt, das zwar vorbildlich ist, aber wegen seines hohen Aufwandes offensichtlich nicht für die ganze Erde oder große Teile von ihr, wiederholt wurde.
Michael Limburg EIKE
[1] Brohan, P., Kennedy, J.J., Harris, I., Tett, S.F.B. and Jones, P.D., Uncertainty estimates in regional and global observed temperature changes: A new data set from 1850, J. Geophys. Res., 2006, 111 D12106 1-21; doi:10.1029/2005JD006548; see http://www.cru.uea.ac.uk/ cru/info/warming/.
[2] Das ist im physikalischen Sinne keine Temperatur mehr sondern eine Art Index
[3] Das ist der Mittelwert der Jahrestemperaturen diese Station über den WMO Zeitraum von 1961-1990
















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Ach Weber,
jetzt habe ich Ihren Wunsch erstmal komplett durchgelesen, Sie wollen tatsaechlich Strahlung von der Seite. Na, das duerfen Sie selber suchen. Mir fehlt dafuer der Sinn, und ich denke, es gibt kaum Messungen, die quer gemacht wurden.
Aber das Emissionspektrum von CO2 in 35 km Hoehein paper 2 ist schonmal in 30 Grad gemacht worden,also ein bisschen quer. In Richtung Weltall geguckt empfaengt man sowieso nur die Emissionen der Treibhausgase, wenn man nachts guckt und die Kosmische Hintergrundstrahlung abzieht, oder haben Sie eine andere Erklaerung fuer das abgebildete Spektrum ausser CO2 Emission des 15um Bandes?
Herr Weber,
wieso meinen sie, dass rechts, links statt vertikal hier eine rolle spielt?
Haben Sie unabhaengig davon ueberhaupt die paper angeguckt und auch verstanden? Auf welche Abbildung in welchem paper beziehen Sie sich eigentlich?
Lieber Herr Müller
Sie lenken ab. Die Baeckersche Behauptung lässt sich nur beweisen mit einer entsprechenden Messanordnung. Und die haben die AGW-CO-2-Forscher vergessen, weil sie (ganz wie Sie) auf oben-unten fixiert waren. Sie wollen nicht alles über CO-2 wissen, sondern nur das, was in ihre Modelle passt.Diese selektive Realität passt dann in die Modelle,aber die Modelle passen nicht in die Realität. Punkt ist: Herr Baecker kann seine Behauptung mal wieder nicht belegen. Das ist übrigens völlig unabhängig vom THE zu sehen. Er handelt wie ein Politiker, unglaubwürdig.
MfG
Michael Weber
#79: Michael Weber sagt am Montag, 19.09.2011, 13:23:
„Sie wollten doch Messungen vorlegen, die das Strahlungsverhalten von Co-2 im rechten Winkel zur Senkrechten abbilden.“
Können Sie dafür mal ein Zitat bringen? Diese Messanordnung wurde doch von Ihnen ins Spiel gebracht, als Messungen refenziert wurden, die die Behauptungen belegten.
„Oder kapieren Sie nicht, daß es hier nicht um oben und unten geht, sondern links und rechts.“
Ich glaube, hier irren Sie sich. Es geht eben gerade um oben (wieviel Energie wird ins All abgestrahlt) und unten (wieviel Energie in Bodennähe abgestrahlt).
Was ich daran nicht verstehe: Wenn Sie Herrn Bäcker nicht glauben, fragen Sie doch einfach mal jemanden, der nicht in Verdacht steht, ein AGW-Anhänger zu sein und Kenntnisse über atmosphärische Physik besitzt. Wenn Sie da nicht gerade an Gehrlich/Tscheuschner geraten, wird Ihnen da so gut wie jeder sagen, dass das schon seine Richtigkeit mit dem Treibhauseffekt hat. Ob dieser für uns wichtige Mechanismus irgendwandwas mit einer vom wem und wie auch immer prophezeiten Katastrophe zu tun hat, steht doch dann immer noch auf einem anderen Blatt …
Lieber Herr Baecker
Ja, ich habe verstanden: Sie können Ihre Behauptung (mal wieder) nicht belegen. Sie wollten doch Messungen vorlegen, die das Strahlungsverhalten von Co-2 im rechten Winkel zur Senkrechten abbilden. Können Sie nicht! Schlimm, nach 30 Jahren CO-2-„Forschung“( Instrumentalisierung) Oder kapieren Sie nicht, daß es hier nicht um oben und unten geht, sondern links und rechts. Hohengestaffelt! Schlimmer, weil es einen deutlichen Mangel an geistiger Beweglicheit zeigt. (Nebenbei, dieses Verhalten ist vergleichbar mit einem Fußgänger, der bei „Grün“ losrennt, ohne auf den übrigen Verkehr zu achten. Theoretisch hat er Recht, praktisch hat er den (vermeidbaren) Schaden.)Im konkreten Fall nimmt Ihre Behauptung Schaden, da Sie keine Belege vorlegen wollen.
MfG
Michael Weber
PS. Wie bewerten Sie als Oberlehrer jemand, der das und dass nicht auseinanderhält und Artikel im Satz gross schreibt?
Ok, Weber hat endlich verstanden, wie der Treibhauseffekt funktioniert oder zumindest endlich kapiert, das Die Infrarotabstrahlung wie Einstrahlung nach oben abnimmt.
Weber,
Unter Gegenstrahlung verstehe ich die Strahlung, die nach unten geht, also nach Nadir. Die Strahlung wird in der Literatur auch longwave downwelling oder downward radiation genannt und ist naturlich in jeder Hoehe bis zum Boden messbar. Die Strahlung in Gegenrichtung also Richtung Weltall wird longwave upward oderupwelling genannt. Beide Fluesse nehmen nach oben ab, wie man im Paltridge paper ja an den Messkurven sieht. Der aufwaerts (longwave upward) wegen der Absorption der Bodenabstrahlung durch relativ kaeltere und spektral selektiv absorbierende Treibhausgase ( siehe die Messung in dem 2. paper), die nach unten gerichtete Gegenstrahlung (downward) nimmt wie gesagt aufgrund der Tempeatur und Dichtabnahme der Treibhausgase nach oben ab, wie man ebenfalls in paper 2. im Vergleich zu 1. gemessen sieht.
Weber,
„Liebe Herren Baecker und Müller
Ihre Fixierung auf die „Gegenstrahlung“ ist unübersehbar. Ich habe aber nach der gemessenen Strahlung in unterschiedlichen Höhen gefragt.“
Nun, das zeigen die paper ja, aber ich hatte nicht erwartet, dass Sie imstande sind, diese ueberhaupt zu lesen.
#73: Holger Burowski,
Tut mir leid, dass ich aus Zeitgründen nicht alle Beiträge beantworten kann, ich bin noch berufstätig.
Ich glaube aber Sie wiederholen bereits beantwortetes,
daher EIN LETZTES MAL:
„Damit ist die Erdoberfläche die (Teil-)Energie eigentlich nicht losgeworden.“
Das gilt noch mehr für die NICHT strahlende Atmosphäre und für die Wolken, die eine deutlich messbare Gegenstrahlung haben, wie ich ausgeführt habe.
Es wird zudem nicht bestritten, DASS es auch eine atmosphärische Strahlung gibt.
Bei CO2 sehe ich jedoch bisher KEINEN Nachweis dafür, auch nicht den von Baecker zitierten.
Trotzdem bezweifelt niemand ernsthaft,
dass Wolken netto kühlen.
Sie vergessen mal wieder, dass die Strahlenquelle die Sonne ist.
Die Kühlwirkung von CO2 ist also nicht davon abhängig, ob etwas von dieser CO2-Bande die Erdoberfläche erreichen kann.
Die nicht strahlende Atmosphäre kann sich also besser aufheizen, WEIL SIE NICHT STRAHLT.
Die „Konvektion“ springt schon bei wirklich winzigen Temperaturunterschieden an. Öffnen Sie mal ihr Fenster.
mfG
Liebe Herren Baecker und Müller
Ihre Fixierung auf die „Gegenstrahlung“ ist unübersehbar. Ich habe aber nach der gemessenen Strahlung in unterschiedlichen Höhen gefragt. Die müsste im rechten Winkel zu einer senkrechten Achse gemessen worden sein um den Einfluss von Strahlung und Gegenstrahlung möglichst zu eliminieren. Nur so lässt sich feststellen welche Strahlung CO-2 in welcher Höhe ( unter welchen Bedingungen) erzeugt. Nur so lässt sich Herrn Baeckers These CO-2 strahle am Boden „am meisten“ wirklich belegen. Diese Belege können Sie nach 30 Jahren CO-2-Forschung nicht vorweisen. Was ein Armutszeugnis.
MfG
Michael Weber
#54: Dr. Paul
Hallo Herr Burowski zu Ihrer Frage:
Während angeregte Atome nur unter Emission von Strahlung in den Grundzustand zurückkehren können, erfolgt die Relaxation bei Molekülen wegen der Rotations- und Schwingungsfreiheitsgrade meist strahlungslos gemäß den Prinzipien des Jablonski-Diagramms, siehe Wkipedia“
Hallo Herr Paul,
der Aspekt war mir so noch nicht bekannt. Trotzdem ergeben sich für mich daraus Fragen. Der IR-Quant, also auch die Energie des Quantes, bewegt sich nach der Emittierung von der Erdoberfläche bis zur Wechselwirkung mit einem Gasmolekül mit Lichtgeschwindigkeit. Nach dem Übergang in ein Gasmolekül wird die Energie mit der Geschwindigkeit des Gasmolekül transportiert.
Geht man vom Verhältnis der typischen Geschwindigkeit eines Gasmoleküls und der Lichtgeschwindigkeit (0,3 km/s : 300000 km/s) aus, kann man meiner Meinung nach davon ausgehen, dass der energetische Zustand in der Atmosphäre fast als stationär bezeichnet werden kann, da der Energietransport in der Atmosphäre viel, viel langsamer erfolgt, als von der Erdoberfläche Energie nachgeliefert wird. Meiner Meinung nach stellt sich in der Atmosphäre ein Gleichgewichtszustand ein, der daduirch bestimmt wird, wieviel Energie die Atmosphäre aufnehmen kann und wie schnell die Energie durch die Bewegung der Gasmoleküle wegtransportiert werden kann.
Da ab einer bestimmten Höhe die Gasmoleküle wieder in der Lage sind, Quanten zu emittieren und die Emittierung in alle Richtungen gleichwahrscheinlich ist, wird also (fast) die Hälfte der emittierten Quanten in Richtung Erdoberfläche abgestrahlt. Da davon ausgegangen werden kann, dass die Gasmoleküle in Richtung Erdoberfläche nicht mehr in der Lage sind, einen Quant zu absorbieren; die Moleküle sind ja bereits von der Erdoberfläche mit Energie versorgt, werden die abgestrahlten Quanten wieder die Erdoberfläche erreichen und dort absorbiert werden. Damit ist die Erdoberfläche die Energie eigentlich nicht losgeworden.
Mir erscheint diese Erklärung zumindest logisch. Wie man diese Wechselwirkung bezeichnet, ist für mich von untergeordneter Bedeutung.
Gruß Holger Burowski
#70: Michael Weber sagt am Mittwoch, 14.09.2011, 12:48:
„Lieber Herr Baecker
Es wäre äusserst nett von Ihnen, wenn Sie meine Frage endlich beantworten würden. Wenn keine gemessenen Daten vorliegen sollten, können Sie sich die Antwort sparen.“
Die Frage wurde Ihnen mit einem Verweis auf Messwerte beantwortet. Zumindest die Frage, die Sie in #36/#41 aufgeworfen haben. Ich wiederhol sie prophylaktisch nochmal:
„Ist ein Physiker, der wider besseres Wissen behauptet,CO-2 strahle in Bodennähe mehr als in den dünneren Atmosphäreschichten ein „Lügner“ oder Vertreter einer abstrusen Theorie.“
„Die Frage, die ich gestellt habe bezieht sich darauf ob die Energie von CO-2 [in Bodennähe] messbar hoeher durch Strahlung abgegeben wird als in der dünneren Atmosphäre. Wenn ja, wo sind die Messungen die man vergleichen kann?“
Es wurden Ihnen Messungen vom Boden (gehts näher an den Boden ran?) und aus dem All vorgelegt (gehts höher?), die genau diesen Unterschied aufzeigen. Danach haben Sie die Frage modifiziert. Passte Ihnen die Antwort nicht?
Herr Weber,
Quellen für Messwerte habe ich doch angegeben.
Also noch mal, wenn Sie selber nicht wissen, wonach Sie eigentlich suchen und nicht wissenschaftlich recherchieren können:
Messung des Gegenstrahlungsspektrum von Treibhausgasen (inkl. CO2) am Boden: http://preview.tinyurl.com/34qycm2
(bereits in #48 angegeben)
15µm CO2 Bande Gegenstrahlung streifend (30° nach oben) + Absorptionsspektrum (Nadir) durch dieselbe Bande (und man sieht auch noch die 9,3 µm Ozon-Bande rechts) aus 35 km Höhe: http://tinyurl.com/64qho9l
Man sieht die bekannten Spektren. Das Absorptionsspektrum ähnelt dem von Satelliten gemssen, auch wenn dabei von der Strahlungstransfer zwischen 35 km und Satellitenhöhe dazukommt, so ähneln sich die Spektren, da der longwave flux in der Stratosphäre ja quasi divergenzfrei ist und sich das Spektrum daher dazwischen kaum noch ändert.
Klassisches paper von Paltridge von 1970 mit Messungen der Gesamtbestrahlungsdichte der Gegenstrahlung für verschiedene Höhen: http://tinyurl.com/6hsn6z9
Man erkennt die bekannten Werte für die thermische Ausstrahlung vom Boden, der Gegenstrahlung am Boden (etwas weniger als die Abstrahlung) sowie die Abnahme der Ausstrahlung und Gegenstrahlung in der Höhe aufgrund abnehmender Temperatur und Dichte der Luft sowie der Treibhausgase. Die Abnahme der Gegenstrahlung mit der Höhe war ja hier bezweifelt worden. Hier Messungen zum messtechnischen Nachweis mit Hilfe von flugzeuggetragenen Messinstrumenten, dass sie mit der Höhe abnimmt.
Lieber Herr Baecker
Es wäre äusserst nett von Ihnen, wenn Sie meine Frage endlich beantworten würden. Wenn keine gemessenen Daten vorliegen sollten, können Sie sich die Antwort sparen. Keine Antwort ist auch eine Antwort.
MfG
Michael Weber
Sehr geehrter Herr Zuber,
bitte bleiben Sie gelassen.
Sie haben es hier mit der Troll-Truppe von Schelli zu tun. Die können nicht anders (sprich: mehr). Die sitzen vermutlich auf Assi-Stellen
und müssen „auf Kompetenz“ machen.
@60 Bäcker, Verstoss gegen alle Forumsregeln und ausserdem frecher Unsinn
Lieber Herr Zuber
Das Verstehen und sachgerechtes Beantworten von Fragen ist nicht jedermanns Sache. Wie man es richtig macht haben Sie an Herrn Baeckers Stelle ja gezeigt, während er einmal mehr demonstriert hat,wie man es nicht macht( oder wie es Politiker machen)
Festzuhalten bleibt, daß weder von ihm noch
Herrn Ketterer ein einziger Fakt geliefert wurde, der meiner Fragestellung entsprach. Da öffnen sich zwei Möglichkeiten:
1. Die Fakten sind vorhanden, werden aber sorgfältig versteckt weil sie (noch) nicht zu den handelsüblichen Klimamodellen passen.
2. Die Sammlung von Daten wurde von vornherein aus Kostengründen und/oder Bequemlichkeit reduziert, weil die Modelle als ausreichend angesehen wurden um den politischen Auftrag zu erfüllen.
Falls 1 richtig ist kann es noch lustig werden für die Klimamodelle. Es gibt dann eine Liste unerklärlicher Fehler der AGW-These.
Das Team Baecker/Ketterer wird persönlich. Das geschieht immer, wenn AGW-lern die sachlichen Argumente ausgehen. Nehmen Sie es nicht persönlich, es ist ein Zeichen, daß eine richtige Spur verfolgt wird.
MfG
Michael Weber
@ Herr Ketterer, Sie sagen: „Ihr unsäglicher Kommentar #16“. Was Sie „unsäglich“ bezeichnen, ist nichts anderes als Ihr Ausdruck ohnmächtigen Ingrimms angesichts der lächerlich dünnen Faktenlage (eigentlich der praktisch inexistenten Faktenlage) angesichts der meisten der von Ihnen strapazierten „Klima“-Parameter: Zu nichts aber auch gar nichts haben sie präzise, reproduzierbare Daten, wie dies in einer anständigen Wissenschaftsdisziplin selbstverständlich wäre. Die Katastrophe Ihrer Glaubensrichtung geht sogar so weit, dass Sie offenbar auch überhaupt kein Gefühl mehr haben, was Wissenschaft eigentlich wirklich ist: die Überprüfung von Hypothesen an Hand der Realität und der Falsizifierung von Nullhypothesen. Aber was rede ich, Ihre vollständig degenerierte Pseudowissenschaft erfindet nur noch Computerspiele und hält sich in beispielloser Verblendung auch noch für eine Avantgarde. Merken Sie denn gar nicht, wie sehr Ihre Pseudowissenschaft den Zorn der anständig gebliebenen Wissenschaftler auf sich gezogen hat?
Herr Ketterer, für die Entgleisungen und Verluderungen Ihre „Klima-Wissenschaft“ gibt es keinen Pardon. Das wird irgendwann einmal ein Gerichtsprozess feststellen, verlassen Sie sich darauf: das absolut Unerhörte des Vorgehens Ihres Lagers ist, dass Sie auf der blossen Basis unbewiesener Spekulationen die westlichen Volkswirtschaften um Billionen von Euro Steuerabgaben betrügen wollen und eine völlig unnütze und gemeine Verarmung der Bevölkerung der Industriestaaten leichthin und arrogant in Kauf nehmen.
Dafür sollten Sie sich mindestens schämen.
@61 Bäcker, glauben Sie mir, dass Ihr Beitrag an Primitivität kaum zu überbieten ist. Wenn das alles war an akademischen Leistungen, was Sie vor kurzem hier von sich preisgegeben haben, dann stehen Sie in dieser Hinsicht klar unter manchen anderen hier. Aber egal, Profilierungssüchte plagen hauptsächlich ja Sie. Bäcker, Sie kämpfen für die falsche Sache mit unwissenschaftlicher Attitüde. Nach der baldigen Götzendämmerung Ihres CO2 Wahnbildes werde ich Sie daran erinnern.
@62 Herr Ketterer, Sie lehnen sich weit aus dem Fenster, wenn Sie hier behaupten wollen, dass die von Ihnen zitierten Publikationen meine Recherchefragen beantworten. Diese waren übrigens in klar verständlichem Deutsch abgefasst: umso unverständlicher, dass Sie beim Verständnis Probleme hatten und eine Umdefinition verlangt haben.
Die für AGW Vertreter typische Oberflächlichkeit findet sich leider auch bei Ihnen: ich habe von präzisen Messdaten der Strahlungsleistung von CO2 in verschiedenen geographischen Breiten, Längen, Höhen über dem Meerrsspiegel, und Tageszeiten in der Primärliteratur (diesen fein-ironischen Sprachtest haben Sie auch nicht bestanden, und in Ihrem Beitrag wimmelt es übrigens nur so von Tipp- und Grammatikfehlern) gesucht. Präzision und Repräsentativität der Messresultate des zentralen Parameters Ihres hypothetischen Atmosphärenmodells wären doch das Mindeste, was man doch wohl seit Jahrzehnten hätte zeigen sollen/können.
Ich habe nicht nach einzelnen Untersuchungen der Absorptionsspektren, sondern nach CO2 Strahlungsleistungen in W/m2 gefragt pro angegebener geographischer Breite, Länge, Höhen über dem Meer, und verschiedenen Tageszeiten. Die von Ihnen angegebenen Publikationen beantworten diese Fragen in gar keiner Weise, sodass ich mich fragen muss, ob Sie meine Fragestellung (jene von Herrn Weber urspünglich) überhaupt verstanden haben. Aber was kommt von Ihnen in typisch billiger AGW Pseudowissenschaftsmanier? Eine rasch hingeworfene Antwort, die Substanz mimen soll wo keine Substanz da ist: es geht euch oberflächlichen Pseudowissenschaftlern nur um den raschen, billigen Erfolg, der jene blenden soll, die euch nicht so rasch und leicht auf die Schliche kommen. Die anstrengende, genaue, gewissenhafte Analyse ist euch zutiefst wesensfremd, da es sich in den vergangenen Jahrzehnten eingebürgert hat, dass die „Klimawissenschaft“ praktisch alle wissenschaftlich-methodologischen Prinzipien normaler Wissenschaft über Bord wirft, und theoretische Spekulationen in Computermodellen zu Fakten hochstilisiert werden.
Herr Ketterer, Sie bewegen sich in einer ganz feinen Gesellschaft!! Darauf können Sie gar nicht stolz sein. WIE unwissenschaftlich dieser ganze CO2 Firlefanz ist, entgeht Ihrer Perzeption total.
Sehr geehrter Herr Zuber,
bitte POLTERN Sie nicht so!
Ihr unsäglicher Kommentar #16: Franz Zuber sagt:am Dienstag, 13.09.2011, 13:27
in http://tinyurl.com/639kvnf
ist nun wirklich genug.
Sie suchen:
„Ausmass der Strahlung von CO2 in verschiedenen Höhen der Atmosphäre (0 m über Meer, 100m, 200m, 300m, 400m, 500m, 600m, 700m, 800m, 900m, 1000m, 1100m, bis 50000m über Meer in Hundert Meter Abständen) noch nie gemessen wurden, weder bei Tag (unter direkter Sonneneinstrahlung oder bei bewölktem Himmel), noch in der Nacht“
Ich zeigte, dass Messungen vorliegen.
Wenn Sie ein Höhenprofil der Stahlungsintnsität(CO2) haebn wollen (und das auch noch im Tagesverlauf Rund um den Globus), dann sollten Sie es auch so sagen!
Bisher sagen sie nur, dass die IR-Strahlung weder Bei Tag noch bei Nacht in verschiedenen Höhen gemessen wurden.
Höhe 2900m habe ich geliefert, Kuwiet weiß ich die Höhe nicht, aber es gibt auch Ballon-Sondierungen, da sollte auch etwsa für die anderen Höhen dabei sein.
Was soll uns den der Satz aus dem Abstarct sagen:
„An experimental system is described for measuring the total hemispherical and SPECCTRALLY RESOLVED directional downward infrared sky radiation and complementary weather data in Kuwait.
Wenn nicht: Hier wurden Strahllenflüsse gemesse, Spektral aufgeloöst und des Spurengasen zuzuordnen.
Was wollen Sie eigentlich noch mehr?
Wenn ich es richtig verstanden haben sagen Sie, dass die „CO2“- IR Gegenstrahlung nicht gemessen wurde.
Dort wurde genau dies durchgeführt (und das ist nicht die einzige Arbeit zu dem Thema).
Und Sie sagen, diese spektral aufgelösten Messsungen gibt es nicht.
Warum wurden Sie dann publiziert?
Ach ja, dann wäre da noch meine Verständnisfrage:
Was ist eine „primär-wissenschaftlichen Temperatur“
Soll das etwa wissenschaftliche Primärliteratur sein? Dann sagen Sie es doch auch bitte so: Das geht ebi mir nicht mehr untrr Tippfehler durch.
Zuber/Paul,
ich gebe zu kein Latein zu beherrschen. Wie wohl auch Sie hatte ich damals die Wahl zwischen Latein und Physik. Ich habe mich für die Naturwissenschaften entschieden und es nicht bereut. Und Sie 🙂
Zuber,
mir war schon klar, dass sie mit wissenschaftlichen arbeiten ueberfordert sind.
@57 Bäcker bei seiner bevorzugten, typischen Tätigkeit: nichts wissen und das Maul aufreissen.
Im Gegensatz zu Ihnen verstehe ich Fragestellungen und kann auch danach recherchieren, während Sie beides offenbar nicht können und deshalb eifersüchtig und zornig sind, wegen Ihrer peinlich schwachen Position.
Lesen Sie meinen Kommentar an Herrn Keteer, der gilt auch für Sie ..
@56 Herr Keteer,
Können Sie eigentlich nicht lesen, nicht logisch denken oder leiden Sie an einer sonstigen kognitiven oder sprachlichen Strörung??? Ich habe doch in #53 klar formuliert, wonach ich gesucht hatte (lesen Sie dort bitte nochmals) und dazu nichts aber auch gar nix in der Literatur zu finden war. Ihre zwei Referenzen haben mit der Fragestellung von Herrn Weber und meiner Antwort darauf nichts zu tun. Zu Ihrer Information gebe ich Ihnen nachfolgend die Kurzfassungen jener zwei Artikel, von denen Sie meinen, sie enthielten irgendwelche präzise Angaben von Strahlungsleistungen von CO2 an den von mir angegebenen Orten der Atmosphäre.
Experimental measurements of the downward infrared sky radiation in Kuwait
Michael F. Quinn, Oussama Alameddine, and Khalil Al-Jamal
Applied Optics, Vol. 23, Issue 3, pp. 419-424 (1984)
Michael F. Quinn, Oussama Alameddine, and Khalil Al-Jamal, „Experimental measurements of the downward infrared sky radiation in Kuwait,“ Appl. Opt. 23, 419-424 (1984)
http://www.opticsinfobase.org/abstract.cfm?URI=ao-23-3-419
Abstract
An experimental system is described for measuring the total hemispherical and spectrally resolved directional downward infrared sky radiation and complementary weather data in Kuwait. The accuracy of the measurement system is discussed and its use for evaluating the potential of the Kuwait sky as a heat sink for passive radiative cooling applications is presented.
Das zweite Paper, das Sie zitieren ist etwa fogenden Inhalts:
Citation
Ralf Sussmann and Klaus Schäfer, „Infrared spectroscopy of tropospheric trace gases: combined analysis of horizontal and vertical column abundances,“ Appl. Opt. 36, 735-741 (1997)
Abstract
Vibration-rotation absorptions in high-resolution Fourier-transform infrared spectra from a 246-m horizontal path were used to derive local concentrations of trace gases at the Alpine observatory at the Zugspitze summit, Germany (2964 m above sea level). The analysis was performed by using the line-by-line nonlinear least-squares spectral fitting software, sfit, based on the 1992 hitran line parameter compilation. (hitran is a high-resolution transmission molecular absorption database.) A comparison to in situ measurements shows an agreement of better than 4.3% for the species CO, CO2, and CH4. Using the same spectrometer and analysis software, we obtained the vertical column density of N2O together with an adjusted vertical volume mixing ratio distribution. This translates to a local N2O concentration at the altitude of Zugspitze that agrees with the horizontal path-derived value to within 1%.
Es ist wieder einmal typisch für AGW Apostel, die sich für besonders gescheit halten, dass diese, bei genauerer Betrachtung, reichlich oberflächlich, ohne Tiefgang, nur auf den schnellen, billigen Effekt aus sind… q.e.d. (quod erat demonstrandum, für alle, die nicht Latein verstehen im AGW Lager).
Zuber,
Nichtsfinden ist keine Kunst, wenn man nicht danach sucht.
http://tinyurl.com/5wc3etc
@ #53 Franz Huber sagte:
„Meine intensiven Recherchen in der primär-wissenschaftlichen Temperatur haben ergeben, dass das Ausmass der Strahlung von CO2 in verschiedenen Höhen der Atmosphäre (0 m über Meer, 100m, 200m, 300m, 400m, 500m, 600m, 700m, 800m, 900m, 1000m, 1100m, bis 50000m über Meer in Hundert Meter Abständen) noch nie gemessen wurden, weder bei Tag (unter direkter Sonneneinstrahlung oder bei bewölktem Himmel), noch in der Nacht (bei klarem Himmel oder unter bewölktem Himmel), auf dem Äquator, 10 Grad nördlicher oder südlicher Breite, 20 Grad nördlicher oder südlicher Breite, bis 90 Grad nördlicher oder südlicher, und auch nicht über den verschiedenen Längengraden der Erdoberfläche. Es gibt also überhaupt keine realen Daten zu den vom Lager Herrn Bäckers gemachten Behauptungen von angeblichen CO2 Strahlungen.“
Sie haben damit nicht beweisen, dss es dies Messungen nicht gibt. Sie hane nur gezeigt, dass Ihre Fähigkeiten zur Literaturrecherche sagen wir „begrenzt“ sind: Etwa Propädeutikum-Level, naja Prä-Propädeutikum trifft’s wohl besser.
Ich habe „auf die Schnelle“ diese Arbeiten gefunden:
Experimental measurements of the downward infrared sky radiation in Kuwait
Michael F. Quinn, Oussama Alameddine, and Khalil Al-Jamal in: Applied Optics, Vol. 23, Issue 3, pp. 419-424 (1984)
und dann noch:
Infrared spectroscopy of tropospheric trace gases: combined analysis of horizontal and vertical column abundances
Ralf Sussmann and Klaus Schäfer in Applied Optics, Vol. 36, Issue 3, pp. 735-741 (1997)
q.e.d.
Herr Weber,
die Messungen zeigen, dass entgegen Ihrer und Pauls Beauptungen, dass CO2 sowie alle anderen Gase mit Spektrallinien im Infraroten Emission im Infraroten zeigen. Paul behauptet, CO2 strahle bodennah nicht, dies ist mit der Messung widerlegt.
Beweisen Sie bitte Ihre Behauptung, der IPCC wuerde von „Ueberwaermung“ sprechen. Ich glaube nicht, dass Ihnen dies gelingt. Ihre Behauptung ist eine schlichte Luege.
Lieber Herr Zuber
Vielen Dank für die Mühe, die Sie sich gemacht haben. Sie haben damit den Beweis geliefert, daß der AGW-Glaubenswissenschaft gemessene Fakten egal sind. Der CO-2-Politiker Baecker hat wieder mal das
Vorhandensein von Fakten vorgetäuscht.“Grosses Maul-und nichts dahinter“ sagt der Volksmund dazu. Erschreckend aber ist die Tatsache, wie wenig in dieser Pseudowissenschaft gemessen und wie viel in Modellen simuliert wird. Wobei die Simulation als messwertähnlicher „Fakt“ verkauft wird. Die Masche zieht allerdings nicht mehr, wenn genau hingesehen wird, so wie Sie es getan haben.
MfG
Michael Weber
@51 Lieber Herr Weber, die von Ihnen an Herrn Bäcker gestellten Fragen kann ich Ihnen präzise beantworten. Meine intensiven Recherchen in der primär-wissenschaftlichen Temperatur haben ergeben, dass das Ausmass der Strahlung von CO2 in verschiedenen Höhen der Atmosphäre (0 m über Meer, 100m, 200m, 300m, 400m, 500m, 600m, 700m, 800m, 900m, 1000m, 1100m, bis 50000m über Meer in Hundert Meter Abständen) noch nie gemessen wurden, weder bei Tag (unter direkter Sonneneinstrahlung oder bei bewölktem Himmel), noch in der Nacht (bei klarem Himmel oder unter bewölktem Himmel), auf dem Äquator, 10 Grad nördlicher oder südlicher Breite, 20 Grad nördlicher oder südlicher Breite, bis 90 Grad nördlicher oder südlicher, und auch nicht über den verschiedenen Längengraden der Erdoberfläche. Es gibt also überhaupt keine realen Daten zu den vom Lager Herrn Bäckers gemachten Behauptungen von angeblichen CO2 Strahlungen.
Die Herumtheoretisierei um die CO2 Effekte in der Atmosphäre erinnert mich an Kaffeekränzchen schwatzhafter Tanten, oder Stammtischdiskutiererei bierseliger Saufbolde im Wirtshaus, alles grosse Geste als Trockenübung …
Paul, 45
„Dass eine atmosphärische Wärmestrahlung gemäß dem Planck-Gesetz gegeben ist, ist eine Selbstverständlichkeit“
Sehe ich auch so, und warum sollte dies nun ausgerechnet fuers CO2 nicht zutreffen? Wieso machen Sie Ausnahmen von der Gueltigkeit von Naturgesetzen bei gleichen Voraussetzungen? Denken Sie mal an ein gluehendes Metall, die Stoesse zwischen den Meatllatomen sind viel haeufiger als im Gas und trotzdem glueht es.
Lieber Herr Baecker
als guter Politiker beantworten Sie wieder Fragen, die nicht gestellt wurden und vergessen Behauptungen, die Sie selbst aufgestellt haben. Und natürlich meine Frage nach den einschlägigen Messungen. Man darf doch erwarten, daß die intensive CO-2-Forschung der letzten 30 Jahre so was en passant gemacht hat. Das Strahlungsverhalten des Untersuchungsobjektes in unterschiedlichen Höhen sollte doch bekannt sein, wenn man damit ein Treibhaus basteln will. Es sei denn, man braucht dieses Wissen aus politischen Gründen nicht. Dann stehen Sie allerdings ohne Beweis für Ihre Behauptung da.Wie ein richtiger Politiker.
MfG
Michael Weber
PS Die Überwärmung finden Sie in jedem IPCC-Bericht in der Zusammenfassung für Politiker.
Lieber Herr Müller
Wo finden Sie bei Herrn Lüdecke die Höhenangaben ??? Die Höhenangaben der Messpunkte!Um die Frage zu beantworten braucht man nach Höhe gestaffelte
Messwerte der Strahlung von CO-2. Nicht nach oben und unten, sondern nach links und nach rechts gemessen. Die Strahlung ist ja in jede Richtung gleich. Damit kann dann eindeutig festgestellt werden ob die Behauptung von Herrn Baecker stimmt. Bis dahin bleibt sie eine Behauptung die mit guten Gründen von Dr. Paul bestritten wird. Also auf ein Neues: bringen Sie höhengestaffelte Messwerte um die Aussage von Herrn Baecker zu belegen. Bis dahin werte ich sie als politisches Statement.
Überzeugen Sie mich!
MfG
Michael Weber
Herr Weber, #40
„Nennen Sie mir Ihre politischen Vorstellungen, nach denen Sie argumentieren, das Spurengas CO-2 könne die Erde überwärmen. “
Was meinen Sie mit „Überwärmung“??
Sie wollten doch wissen, ob CO2 in der Luft am Boden mehr als in der Höhe strahlt. Ich habe Ihnen die physikalischen Argumenten doch schon genannt: Höhrere Dichte und höhere Temperatur am Boden.
PS, Paul:
Schon mal was von Stoßanregung gehört, also Lichtemission durch thermische Anregung aufgrund von Stößen? So funktioniert eine Glimmentladungsröhre oder ein Helium-Neon-Laser.
Hier FTIR-Messungen der Gegenstrahlung am Boden
http://preview.tinyurl.com/34qycm2
CO2 ist neben anderen IR-Gasen gut zu sehen.
#46: Dr.Paul sagte am Montag, 12.09.2011, 17:42:
„#42: Marvin Müller,
Prof. Lüdecke hat NICHT behauptet, dass CO2 in Bodennähe strahlen könnte, das war die Frage,“
Die Frage, auf die ich geantwortet habe, habe ich extra zitiert. Sie können gern nochmal nachlesen.
Ich weiss, dass in Ihrer Welt CO2 nur an der Grenze zum All strahlt und dann auch nur ins All. Aber ich denke, dass Herr Lüdecke gar nicht auf die Idee gekommen ist, dass jemand sowas denke könnte. Daher schreibt er nicht explizit, Co2 strahlt auch in Bodennähe. Statt dessen schreibt er Dinge wie: „Die zusätzliche Leistungsdichte erhält die Erdoberfläche im Wesentlichen durch Gegenstrahlung aus der Atmosphäre.“ und „Gegenstrahlung aufgenommen in Barrow, Alaska, … Deutlich ist die Gegenstrahlung des CO2, … zu sehen“
Wie kann man die in den Messungen deutlich sehen, wenn Sie nicht bis zum Boden kommt?
„was ist denn Ihre physikalische Meinung?“
Muß schwer rauszubekommen sein, wenn ich versuche, Herrn Weber anhand von Messungen davon zu überzeugen, dass Co2 in Bodennähe intensiver strahlt, als an der Grenze zum All …
#42: Marvin Müller,
Ihr Rettumngsversuch taugt nichts,
Prof. Lüdecke hat NICHT behauptet, dass CO2 in Bodennähe strahlen könnte,
das war die Frage,
was ist denn Ihre physikalische Meinung?
Lassen Sie doch bitte andere Personen aus dem Spiel, das ist doch kindisch!
mfG
Hallo Herr Burowski zu Ihrer Frage:
Während angeregte Atome nur unter Emission von Strahlung in den Grundzustand zurückkehren können, erfolgt die Relaxation bei Molekülen wegen der Rotations- und Schwingungsfreiheitsgrade meist strahlungslos gemäß den Prinzipien des Jablonski-Diagramms, siehe Wkipedia
„Ist die mittlere Zeit zwischen den Kollisionen viel kleiner als die Verweildauer der Elektronen im angeregten Zustand (zwischen Absorption und Emission), dann ist das System (Gas) durch die kinetische Temperatur gekennzeichnet. Dabei stellt sich ein Zustand ein, bei dem die Verteilung der Elektronen auf die Energieniveaus (Anregungszustand) nur von der lokalen Temperatur abhängt“
Deshalb reichte es eigentlich vollkommen aus, wenn man den „theoretischen“ Treibhauseffekt ohne jegliche Absorption nur mit der – temperaturabhängigen – Planck-Gleichung beschreibt, die man mit den jeweiligen Bandenstärken „klimawirksamer“ Spurengase und der „Anzahl IR-aktiver Moleküle in einem Luftvolumen“ multipliziert. Dann erhält man die thermische Emission der Atmosphäre unter Berücksichtigung des Raumwinkels.
Dass eine atmosphärische Wärmestrahlung gemäß dem Planck-Gesetz gegeben ist, ist eine Selbstverständlichkeit. Solange aber ein atmosphärisches Temperaturprofil (oben kälter – unten wärmer) existiert und die Konvektion erheblich zum Energietransport beiträgt, solange ist die Hypothese in dem offenen System Atmosphäre existiere ein lokales thermodynamischen Gleichgewichts (LTE) falsch.
mfG
#38: Sabrina Schwanczar
falls es Sie interessiert,
der biologische Stoffwechsel ist eines meiner wissenschaftlichen Interessen,
insbesondere die Bedingungen und Störungen der (biologischen) Energieerzeugung und Energieversorgung,
eigentlich ein sehr physikalisches Thema
im Umfeld einer etwas durch Genetik dominierten Wissenschaft.
Der Grundmechanismuss ist wieder wie beim angeblichen Treibhaus sehr einfach:
Es ist die bekannte Knallgasreaktion,
der Traum aller umweltbewussten Autobauer:
aus H2 und O wird unter Energiefreisetzung Wasser H2O.
Es gibt kein Leben ohne permanente Energiezufuhr.
Die Verschlechterung der Energieversorgung verursacht Krankheit und bestimmt letztlich die Länge unserer Lebensspanne.
Möge Ihnen lange Energie zu Verfügung stehen.
mfG
#39: Dr. Paul
„Absorbierte Energie, egal ob durch „Stoß“ von einem „Nachbarmolekül“ oder durch elektromagnetische Strahlung,
kann nur einmal abgegeben werden,
das sagt schlicht der erste Hauptsatz der Thermodynamik,
also ENTWEDER durch Stoß ODER durch Strahlung.
Die Strahlenemission ist KEINE SPIEGELUNG, sondern sie erfolgt ZEITVERZÖGERT zur Absorbtion und in alle Richtungen.
Das ist quantenphysikalisch schlicht eine WAHRSCHEINLICHKEITSFRAGE, die zeitlich konkretisiert werden kann.
1)In der unteren Erdatmosphäre ist das theoretisch strahlungsfähige CO2 – Molekül in einem Dauerbombardement durch Stöße der (nicht strahlungsfähigen) Nachbarmoleküle, so dass die Wahrscheinlichkeit der Strahlenemission WEIT unter 1% fällt, sehr grob gesprochen. Deshalb kann hier CO2 NICHT strahlen.
2)CO2 ist ein sehr selektiver Absorber resp. Strahler. Es gibt daher nur einen sehr begrenzten „Vorrat“ an Wärmestrahlen, der für CO2 absorbierbaren Frequenz.
Das wird als „Sättigung“ bezeichnet.
Das bischen Wärmestrahlung, das die 0,04% der Atmosphäre aufnehmen kann, wird also praktisch komplett verbraucht und NICHT zur Erdoberfläche zurückgestrahlt, sondern in Wärme umgewandelt und mit der Konvektion der Erdoberfläche entzogen“
… und an dieser Stelle, werter Herr. Dr.Paul habe ich meine Zweifel, ob das so funktioniert. Ich bin der Meinung, Sie werfen hier die Systeme, die der klassischen Mechanik (Bewegung der Gasmoleküle) auf der einen Seite und der Quantenmechanik (Absorption eines Quantes) auf der anderen Seite unterliegen, durcheinander.
Der von der Erdoberfläche emittierte Quant wird vom CO2-Molekül absorbiert und führt zu einer Anregung des CO2-Moleküls. Das ist ein rein quantenmechanischer Vorgang. Die Absorption führt weder zu einer Masse- oder Geschwindigkeitsänderung des CO2-Moleküls, was aber Voraussetzung wäre, damit sich die Temperatur, die das CO2-Molekül repräsentiert, verändert, da gilt 1/2*m*v² = 3/2*k*T. Da sich weder Masse noch Geschwindigkeit des Moleküls ändert, kann es bei einem Zusammenstoß mit einem anderen Molekül zu keiner Energieübertragung kommen, da beim Stoß nur Masse und Geschwindigkeit eine Rolle spielen. Das heißt, das absorbierte Quant kann das CO2-Molekül auch nur wieder als Quant der gleichen Wellenlänge emittiert werden.
Meine Frage ist also, wenn wirklich eine Energieübergabe aus dem quantenmechanischen System in das klassische mechanische System erfolgen soll – wie funktioniert das im konkreten Fall? Erklären Sie den Übergang für diesen Vorgang aus dem quantenmechanischen System in ein klassisches, mechanisches System. Das würde mich wirklich interssieren, wie das funktionieren soll.
Beachten Sie bitte auch, dass die Energie eines Quantes mit einer Wellenlänge von 4 Mikrometer 0.3eV und die typische, mechanische Energie eines Gasmoleküls unter Normalbedingungen etwa 0.03eV beträgt. Wohin also mit dem 10-fachen der kinetischen Energie? Meinen Sie wirklich, dass es möglich ist, dass die Energie des angeregten Zustandes eines Gasmoleküles ohne Quantabgabe auf ein anderes Molekül übergeben werden kann und dort zu einem angeregten Zustand führt? Das hieße, es müsste einen „quantenmechanischen Stoß“ geben.
Ich habe da meine Zweifel.
Gruß Holger Burowski
#41: Michael Weber sagt am Montag, 12.09.2011, 13:50:
„Eine bodennahe Gasmischung hat natürlich mehr Energie. Die Frage, die ich gestellt habe bezieht sich darauf ob die Energie von CO-2 messbar hoeher durch Strahlung abgegeben wird als in der dünneren Atmosphäre. Wenn ja, wo sind die Messungen die man vergleichen kann?“
Lüdecke, „Wie funktioniert der Treibhauseffekt“, Abb. 2 und 4.
– 40 Einheiten in Richtung All (in den Tropen),
– 100 Einheiten in Richtung Boden (in Alaska, wo es noch dazu am Boden relativ kalt ist)
Das ist alles konsistent mit der Erklärung des Treibhauseffektes.
„Ist ein Physiker, der wider besseres Wissen behauptet,CO-2 strahle in Bodennähe mehr als in den dünneren Atmosphäreschichten ein „Lügner“ oder Vertreter einer abstrusen Theorie. Seine Motive sind doch eher politisch als wissenschaftlich begründet.“
Herr Lüdecke erklärt den Treibhauseffekt genau wie Herr Bäcker. Wollen Sie da wirklich bei der zitierten These bleiben?
Liebe Frau Schwanczar
Eine bodennahe Gasmischung hat natürlich mehr Energie. Die Frage, die ich gestellt habe bezieht sich darauf ob die Energie von CO-2 messbar hoeher durch Strahlung abgegeben wird als in der dünneren Atmosphäre. Wenn ja, wo sind die Messungen die man vergleichen kann? (2m, 10.000m, 20.000m) Energie hat ja unterschiedliche Erscheinungs und Übertragungsformen.
MfG
Michael Weber
Lieber Herr Baecker
Nennen Sie mir Ihre politischen Vorstellungen, nach denen Sie argumentieren, das Spurengas CO-2 könne die Erde überwärmen. Die politisch korrekte Antwort ist reichlich physikfrei.
Wenn Sie eine Antwort auf meine Frage (s.o.) hätten. würden Sie nicht so herumeiern müssen.
MfG
Michael Weber
#38: Verehrte Sabrina Schwanczar,
CO2 strahlt NICHT in Bodennähe.
Wollen Sie sich hier in diesem Forum selbst erniedrigen wie dieser Baecker, indem Sie abseits vom Thema billige persönlich völlig untaugliche Angriffe versuchen?
Sie kennen mich nicht! Lassen Sie das lieber, Sie verstoßen sonst gegen die Forenregeln.
Absorbierte Energie, egal ob durch „Stoß“ von einem „Nachbarmolekül“ oder durch elektromagnetische Strahlung,
kann nur einmal abgegeben werden,
das sagt schlicht der erste Hauptsatz der Thermodynamik,
also ENTWEDER durch Stoß ODER durch Strahlung.
Die Strahlenemission ist KEINE SPIEGELUNG, sondern sie erfolgt ZEITVERZÖGERT zur Absorbtion und in alle Richtungen.
Das ist quantenphysikalisch schlicht eine WAHRSCHEINLICHKEITSFRAGE, die zeitlich konkretisiert werden kann.
1)In der unteren Erdatmosphäre ist das theoretisch strahlungsfähige CO2 – Molekül in einem Dauerbombardement durch Stöße der (nicht strahlungsfähigen) Nachbarmoleküle, so dass die Wahrscheinlichkeit der Strahlenemission WEIT unter 1% fällt, sehr grob gesprochen. Deshalb kann hier CO2 NICHT strahlen.
2)CO2 ist ein sehr selektiver Absorber resp. Strahler. Es gibt daher nur einen sehr begrenzten „Vorrat“ an Wärmestrahlen, der für CO2 absorbierbaren Frequenz.
Das wird als „Sättigung“ bezeichnet.
Das bischen Wärmestrahlung, das die 0,04% der Atmosphäre aufnehmen kann, wird also praktisch komplett verbraucht und NICHT zur Erdoberfläche zurückgestrahlt, sondern in Wärme umgewandelt und mit der Konvektion der Erdoberfläche entzogen
und weg ist es.
3)Sehr viel weiter oben in der Atmosphäre, also in wesentlich kälteren Regionen (ca. 10000m und minus 50°C) kehrt sich die Wahrscheinlichkeit um, CO2 emittiert Strahlung BEVOR es zu einer Stoßkollision mit Nachbarmolekülen kommt.
Allerdings ist das hier nicht mehr die Erdrückstrahlung, die das Molekül anregt zur Strahlung,
die ist ja bereits „verbraucht“ in der CO2-Bande, sondern die viel intensivere Sonnenstrahlung.
Was hier CO2 „auffangen“ kann, geht der Erdoberfläche natürlich verloren, insbesondere der Anteil, der in den Weltraum abstrahlt.
So schwer war das doch nicht.
Die Physiker im Forum mögen mir die vereinfachte Formulierung für die Nichtphysiker nachsehen.
4) Der netto-Kühleffekt von CO2 beruht schlicht auf seiner Emissionsfähigkeit in den Weltraum UND der „Filterung“ der viel stärkeren Sonnenstrahlung,
was beides den nicht strahlungsfähigen erwärmten Gasen der Atmosphäre cum grano salis nicht möglich ist. Sie lassen das Sonnenlicht unbehindert „passieren“ und nehmen durch Wärmeleitung und Konvektion einen erheblichen Teil davon auf,
OHNE ihn durch Strahlung an den Weltraum verlieren zu können.
mfG
@ #36: Michael Weber
In Bodennähe hat das CO2 eine höhere Temperatur und entsprechend mehr Energie.
Deshalb strahlt es in Bodennähe auch stärker (Emisson), absorbiert aber auch stärker.
@ Dr. Paul,
wie war das doch gleich nach dem Abi mit Mathe und Physik ?
Und wieviel Stunden Vorlesung zu naturwissenschaftlichen Themen wie Mathematik, Physik, Chemie, Biologie und Biochemie, insbesondere zur Stoffwechselsystem des Menschen und anderer Säugetiere haben Sie während des Medizinstudiums gehört ?
Falls Sie tatsächlich Arzt sein sollten.
Herr Weber,
nennen Sie mir Ihre physikalischenVorstellungen, nach denen Sie argumentieren, waermere und dichtere Gase wuerden weniger abstrahlen. Die korrekte physikalische Antwort ist reichlich ideologiefrei.
Lieber Dr. Paul
Ist ein Physiker, der wider besseres Wissen behauptet,CO-2 strahle in Bodennähe mehr als in den dünneren Atmosphäreschichten ein „Lügner“ oder Vertreter einer abstrusen Theorie. Seine Motive sind doch eher politisch als wissenschaftlich begründet. also ist die Bezeichnung „CO-2-Politiker“ viel eher angebracht und treffender. Da weiss dann auch jeder, woran er mit dem Herrn ist.
Politisches Handeln ist ideologisches Handeln. Ideologisches Handeln war nur im Ostblock eine Wissenschaft.( Die unter Aufbietung aller staatlichen Mittel ihre Pleite nicht verhindern konnte) Der CO-2-Sozialismus wird ähnlich enden.
Dafür garantieren die CO-2-Sozialisten. Nennen Sie den Lügner beim Namen: CO-2-Politiker.
MfG
Michael Weber
#34: NicoBaecker,
aus ihrer bemerkenswert kindischen Antwort war nicht zu entnehmen, WO CO2 nun klimarelevant strahlen soll.
Was wollen Sie in diesem Forum?
Soll das Reklame für den AGW-„Treibhauseffekt“ sein?
Paul,
Sie sind noch nicht mal fuer die Physikdidaktiker ein interessantes Studienobjekt, an dem man untersuchen kann, was man alles in der Physik falsch verstehen kann. Und daraufhin, die Erklaerungen verbessert. Sie sind einfach nur langweilig.
#32: Marvin Müller,
was für eine dumme Antwort,
warum sagen Sie nicht einfach,
ob CO2 direkt über der Erdoberfläche strahlt oder nicht?
Wissen Sie, Herr Müller,
ich hätte auch ein anderes Thema wählen können,
bei dem Sie und Baecker immer ausweichen, wenn sich physikalische Widersprüche für die Treibhaustheorie ergeben,
aber hier ist es ganz einfach und ganz offensichtlich:
WO innerhalb der Atmosphäre strahlt CO2 und wo nicht???
Wer sich Physiker nennt, kann das leicht beantworten, es kommt hier nicht auf ein paar Meter an.
Die „globale Temperatur“ ist bekanntlich für 2m NN definiert.
Also reden Sie nicht um den Brei herum.
mfG