Vor einem Jahrzehnt schrieb ich einen Beitrag mit dem Titel „The Bern Model Puzzle“. Er bezog sich auf die folgende Frage:
Angenommen, wir haben einen relativ stabilen Zustand, in dem der CO2-Gehalt in der Atmosphäre weder steigt noch fällt – so wie die Situation um das Jahr 1400 in den untenstehenden Daten:
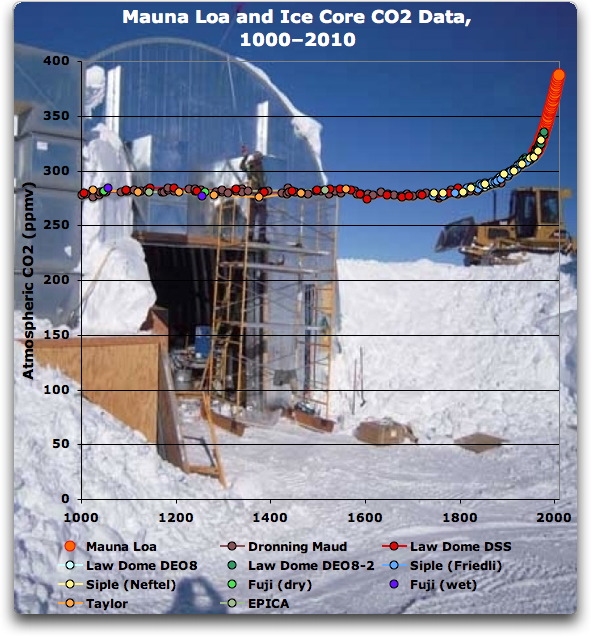
Abbildung 1. Historische CO2-Werte in der Luft von 1000 n. Chr. bis heute, aus 10 Eisbohrkernen und seit 1959 aus Messungen des Mauna Loa Observatory (orange). Die Einheiten sind Teile pro Million Volumenprozent (ppmv) der Atmosphäre.
Nehmen wir nun an, dass während dieser Zeit ein Vulkan ausbricht und das in die Atmosphäre entlässt, was wir früher als eine „metrische Ladung CO2“ bezeichnet haben. Im Laufe der Zeit wird dieser CO2-Impuls von einer Reihe von Senken an Land und in den Ozeanen absorbiert, und der Status quo ante des atmosphärischen CO2 wird wieder auf den Stand vor dem Ausbruch gebracht.
Das „Berner Modell“ ist ein Modell, das vom IPCC und verschiedenen Klimamodellen verwendet wird. Es gibt vor zu berechnen, wie lange es dauert, bis dieser CO2-Impuls von den natürlichen Senken wieder aufgenommen wird. Und genau hier wird es merkwürdig.
Zunächst einmal besagt das Berner Modell, dass 15,2 % dieses CO2-Impulses für immer in der Luft bleiben werden. Nicht 15% des Impulses, wohlgemerkt … 15,2%.
Ich habe noch nie jemanden gefunden, der mir das erklären kann. Wenn das wahr wäre, würde jeder Vulkanausbruch zu einem neuen und höheren dauerhaften CO2-Gehalt in der Luft führen … aber aus Abbildung 1 geht hervor, dass das einfach nicht passiert.
Ein weiterer Beweis dafür, dass die erste Behauptung des Berner Modells falsch ist, ist die jährliche Schwankung der CO2-Werte. Von einem Tiefpunkt um den Oktober bis zu einem Höhepunkt um den Mai eines jeden Jahres gibt es einen kurzen, scharfen natürlichen CO2-Impuls, der zu einem Anstieg des CO2-Gehalts um etwa 6 Teile pro Million Volumenprozent (ppmv) führt. Diesem Anstieg steht eine gleich hohe CO2-Speicherung in natürlichen Senken gegenüber, so dass im darauffolgenden Oktober das vorherige CO2-Niveau wieder erreicht ist. Wäre dies nicht der Fall, würde der CO2-Gehalt seit jeher jedes Jahr steigen.
Und während des gleichen siebenmonatigen Zeitraums stoßen wir derzeit einen Impuls aus, der genug CO2 enthält, um zu einem Anstieg des CO2-Gehalts von etwa 1,3 ppmv zu führen.
Das Berner Modell besagt, dass 15,2 % des anthropogenen CO2-Impulses von 1,3 ppmv für immer in der Luft bleiben … aber der ~ 6 ppmv-Impuls ist sehr schnell verschwunden. Wie kann die Natur also den Unterschied erkennen?
Aber das ist nur der Anfang der Merkwürdigkeit. Es wird noch merkwürdiger. Das Berner Modell besagt, dass:
● 25,3 % des CO2-Impulses fallen mit einer Rate von 0,58 % pro Jahr wieder auf den vorherigen stationären Zustand zurück
● weitere 27,9 % des Impulses zerfallen mit 5,4 % pro Jahr, und
● die letzten 31,6 % des Impulses fallen mit 32,2 % pro Jahr auf den stationären Zustand zurück.
Dies führt mich zu dem gleichen Problem. Wie kann die Natur den Unterschied erkennen? Wie wird das CO2 in der Natur aufgeteilt? Was verhindert, dass das CO2, das sich noch in der Luft befindet, von den schnell wirkenden CO2-Senken gebunden wird?
Es gibt jedoch ein grundlegenderes Problem: Das Berner Modell bildet die Realität einfach nicht gut ab. Wir haben relativ gute Informationen über die CO2-Emissionen seit 1850, die von Our World In Data zur Verfügung gestellt werden. Und wir haben relativ gute Informationen über die CO2-Konzentrationen in der Luft seit 1850 aus Eisbohrkernen und vom Mauna Loa, wie in Abbildung 2 dargestellt:
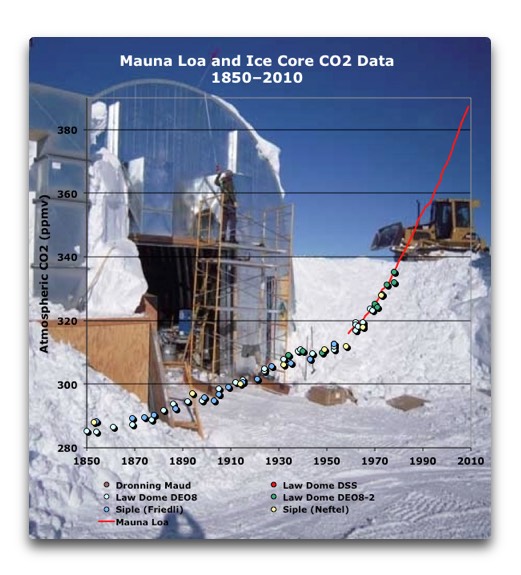
Abbildung 2. Historische CO2-Werte in der Luft von 1850 n. Chr. bis heute, aus 10 Eisbohrkernen und seit 1959 aus Messungen des Mauna Loa Observatoriums (orange). Die Einheiten sind Teile pro Million Volumenprozent (ppmv) der Atmosphäre.
Daher wollte ich einen Blick auf das Berner Modell werfen, um zu sehen, wie gut es den CO2-Gehalt der Luft seit 1850 anhand der Emissionen seit 1850 vorhersagen kann. Die Gleichung für die Berechnung findet sich in der UNFCCC-Studie „Parameters for tuning a simple carbon cycle model“ und ist auch in den Fußnoten zu finden … schlechte Nachrichten.
Abbildung 3. Tatsächliche atmosphärische CO2-Werte und Werte nach dem Berner Modell
No bueno … die Tatsache, dass die Ergebnisse des Berner Modells so viel geringer ausfallen, deutet darauf hin, dass es einen Großteil des Effekts fälschlicherweise weit in die Zukunft verlagert.
Gibt es also einen besseren Weg? Nun, ja. Der bessere Weg ist die Verwendung der Standard-Verzögerungsformel:
Darin:
- t = Zeit
- E(t) = Emissionen zur Zeit t
- CO2(t) = CO2-Konzentration zur Zeit t
- λ = 0,47 (Umwandlung von Emissionen in ppmv)
- ∆ = Differenz zum vorherigen Wert; Beispiel: ∆CO2(t) = CO2(t) – CO2(t-1)
- τ = tau, die Zeitkonstante für die Abnahme
Mit dieser Gleichung finde ich einen konstanten tau-Wert von ~49 Jahren. Das Ergebnis dieser Berechnung sieht so aus:
Damit liegt die Halbwertszeit eines CO2-Impulses in die Atmosphäre bei etwa 34 Jahren …
Das sind meine Fragen und Beobachtungen zum Berner Modell. Ich habe die Berechnungen und Daten hier in einer Tabelle zusammengestellt.
Die Gleichung: Wie versprochen …
Link: https://wattsupwiththat.com/2022/02/15/feeling-the-bern/
Übersetzt von Christian Freuer für das EIKE
Irgendwann wird man der Atmosphäre wieder CO2 zuführen, weil nichts mehr wächst, wenn wir den Richtern glauben und wir uns nach ihnen richten. Wir retten dann die Welt, indem wir möglichst viel Kohle verbrennen.
Gut, dass dieses wichtige Thema hier wieder aufgegriffen wird und eine Formel (sog. Standard-Verzögerungsformel, fehlt da nicht eine Klammer?) genannt wurde, die offenbar zu einem richtigen Ergebnis führt. Und Schande über diese erbärmlich dummen Verfassungsrichter, die sich ein Denkmal für deutsch-richterliche Dummheit setzten – elend dumme Merkel-Schleimer. Von denen ich niemals geahnt hätte, dass sie so erbärmlich dumm sein können – es reicht für ein ganzes Leben.
Und die wichtige Konsequenz ist, was durch die kuriose Berner Formel offenbar bewusst verschleiert wird, dass das CO2 in der Atmosphäre auch bei realistischen Emissionsprognosen (z.B. der IEA) eine Sättigung erreicht – ohne Dekarbonisierungs-Wahn. Nach Roy Spencer, der ganz ähnlich gerechnet hat, bei etwa 520 ppm, ein völlig unkritischer Wert. Und damit ist jede Klimawahn-Diskussion vom Tisch.
Ich kann es mir absolut nicht anders erklären, dass wir hier ganz bewusst und mit voller Absicht betrogen werden. Denn so dumm und einfältig kann kein Alarmforscher sein, nicht einmal ein Politiker.
Also, was bezwecken diese dreisten Betrüger mit ihrer Klima- und Dekarbonisierungs-Wahn-Politik??? Sind wir wieder bei der Verschwörung der Finanz-Mafia? Oder Klima-Sozialismus-Träumer, die das System ändern wollen wie die Klima-hysterische Luisa? Dass so viele grüne Dummköpfe in den Medien darauf hereinfallen, ist nicht weiter verwunderlich. Sie sind erstens dumm und zweitens Propagandisten der grünen Partei. Wie heute offenbar auch grenz-debile Karlsruher Richter.
Das Bern Modell ist eine Integral-Gleichung, das lagged model eine Differential-Gleichung. Um die wesentlichen Unterschiede der beiden zu erkennen müsste man das „Bern model“ in eine Differential-Gleichung umwandeln. Dazu habe ich keine Lust. Der wesentliche Punkt bleibt: die CO2-Konzentration steigt weiter an, ist also nicht konstant oder gar abfallend. Die wesentliche Frage ist und bleibt deshalb welche negativen und positiven Folgen dies global bringt.
A pro po „Büttenreden“ wenn ich mir durchlese, wie ein „Finanzprodukt“ für „Finanz-Magnaten“ reale Börsen-Gewinne durch politische „Legalisierung“, zum Nachteil aller Realwirtschafts-Teilnehmer organisiert hat, siehe z. B. hier https://www.finanzen.ch/nachrichten/rohstoffe/handel-mit-co2-emissionsrechten-so-will-die-londoner-boerse-auf-kohlenstoffemissionen-aufmerksam-machen-1030986823
Wer versteht, was da also im Sinne der Finanz-Magnaten erschaffen wurde, der sieht auch den entscheidenden Aspekt. Es geht um`s Geld, das an der Börse den Bevölkerungen elegant abgenommen wird, der Lügen serviert werden, damit sie nicht durchschauen, wer und wie sie „hoppsgenommen“ werden.
Fred F. Mueller schrieb am 18. Februar 2022 um 8:29
Diese Frage wird auch in den Kommentaren auf WUWT diskutiert, nachdem Leif Svalgaard genau danach gefragt hat. Das „auf ewig“ stammt von Willis, die wissenschaftliche Literatur enthält andere Zeiträume.
Her Müller,
kennen Sie nicht die Aussagen des Prof. Schellnhuber zur Verweildauer des CO2 in der Atmosphäre? Oder würden Sie evtl. der Ansicht zuneigen, dass Prof. Schellnhuber keine maßgebliche Kompetenz auf dem Gebiet der Klimawissenschaften hat?
Die gesamte Betrachtung ist obsolet.
Es gibt ein einfaches, seit langem gut bekanntes Naturgesetz bezüglich der Löslichkeit von Gasen in Flüssigkeiten. Dies ist das Henry’sche Gesetz. Dieses besagt, dass zwischen dem Teildruck (Partialdruck) eines Gases über einer Flüssigkeit und der in Lösung befindlichen Konzentration dieses Gases bei sonst gleichen Randbedingungen eine schlichte lineare Beziehung besteht. Im Falle des Systems Ozean/ Atmosphäre und CO2 gilt folgendes: Von 100 Teilen zusätzlich in die Atmosphäre gebrachten CO2 gehen 98 Teile im Ozean in Lösung. Eine Dreisatzrechnung einfachster Art.
Dies bezieht sich auf die sogenannte Gleichgewichtskonzentration, d.h. wenn genug Zeit verstrichen ist, damit sich das Gas im Wasser auch verteilen kann. Darüber gibt es unterschiedliche Ansichten, die meisten Angaben zum Zeitbedarf liegen zwischen einem und 50 Jahren.
Die Annahme des IPCC und des Berner Modells, dass 15,2 % eines CO2-Impulses „auf ewig“ in der Amosphäre verbleiben, ist schlicht gesagt GROB UNWISSENSCHAFTLICH, geradezu mittelalterlich. Dies kann von jedem Anfangssemester der Fächer Chemie, physikalische Chemie, Biophysik, sogar von jedem Chemielaboranten bewiesen werden.
Allerdings hat das deutsche Bundesverfassungsgericht in seinem „Klimaurteil“ festgelegt, dass dieses Henry’sche Gesetz in Deutschland und sogar weltweit nicht gilt.
https://eike-klima-energie.eu/2021/06/29/karlsruhe-contra-freiheit-der-wissenschaft/
Allerdings ist dieses höchstrichterliche Urteil, das in Deutschland damit quasi Verfassungsrang hat, bis zu den beteiligten CO2- und H2O-Molekülen noch nicht durchgedrungen. Es wird interessant sein zu verfolgen, wie dieser Zusammenprall von Justiz und Naturwissenschaft in Zukunft wieder gelöst werden kann (bzw. werden muss, wenn Deutschland weiterhin als moderne Kulturnation gelten will). In einer normalen, rational-wissenschaftlich ausgerichteten Zivilisation wäre dieses „Klimaurteil“ eigentlich nur ein Thema für beißende Büttenreden.
Ich halte die Anwendung des Henry Gesetzes fuer eine falsche Vereinfachung aus den folgenden zwei Gruenden:
1. CO2 geht eine Chemische Verbindung mit Wasser ein und formt eine Saeure. Damit ist das Henry Gesetz nur bedingt anwendbar. Sauerstoff und Stickstoff loesen sich wie CO2 im geringen Masse auch in Wasser ohne eine Reaktion. Das ist ein physikalischer Prozess, bei dem das Henry Gesetz Anwendung finden kann. Bei einer chemischen Reaktion gilt das nicht mehr.
2. Es gibt biologische Prozesse die CO2 aufnehmen und das Bild voellig veraendern. Es gibt verschiedenste Ozeanstudien zu Ausgasungen und Sequestration von CO2 durch Algenwachstum und deren Einfluss auf die Atmosphaerischen Konzentrationen.
Herr Schulz,
Sie weisen zu Recht auf die Reaktionskette des CO2 (Carbonat- und Bicarbonationen) hin. Innerhalb dieser Reaktionskette bestehen jedoch wiederum Gleichgewichte, so dass die Reaktionskette selbst auch mit der Atmosphäre im Gleichgewicht steht. Das Henry’sche Gesetz gilt also auch weiterhin.
Die biologischen und biogeochemischen Prozesse im Ozean stehen auf einem anderen Blatt, doch wirken sie, weil dabei unlösliches CaCO3 entsteht, letztlich ZUSÄTZLICH senkend auf den CO2-Gehalt der Atmosphäre. Allein dadurch werden jährlich mindestens 2 Gigatonnen (Gt) C vom Ozean in Form von Kalk dauerhaft aus dem System Ozean/ Atmosphäre entfernt.
Das Verhältnis von 98 zu 2 wird durch die relativen C-Massen im CO2 der Atmosphäre (800 Gt) und im Ozean (38.000 Gt) untermauert. Im Rahmen geringfügiger Änderungen behalten diese Gleichgewichtsbedingungen Gültigkeit.
@Fred F. Mueller
Ja, wie im Mittelalter.
Dort hat man Galileo Galilei per Inquisition (Verfassungsgericht) gezwungen seinen Irrlehren abzuschwören.
Heute wird man nicht mehr verbrannt, sondern Mundtod gemacht.
Welch Glück….