Bild rechts: Prof. Albert Einstein bei seiner 11. Josiah Willard Gibbs-Lektion auf dem Treffen der American Association for the Advancement of Science im Auditorium des Carnegie Institue of Technology Little Theater in Pittsburgh am 28. Dezember 1934. Photo: AP
E = mc²
Während meiner Collegezeit besuchte ich einen Kursus, in dem es um die großen politischen Philosophen ging – Hobbes, Locke, Rousseau, Kant, John Stuart Mill und Karl Marx.
Nach meiner Erinnerung habe ich sie den historischen Zeiten zugeordnet, die sie beeinflusst hatten – Hobbes und die Monarchen des 18. Jahrhunderts, Locke und die amerikanische Revolution, Rousseau und die Romantik des 19. Jahrhunderts, Kant und die Nationalstaaten des 19. Jahrhunderts, Marx und der Kommunismus des 20. Jahrhunderts.
Dann sah ich eines Tages eine Zeitskala, auf der gezeigt wurde, wann sie alle gelebt haben und gestorben sind. Zu meinem Erstaunen hatte jeder einhundert Jahre vor der Zeit gelebt, die ich ihnen zeitlich zugeordnet hatte. Es schien klar, was das bedeutet. „Es dauert etwa hundert Jahre, bevor ein neuer Gedanke die Bühne der Geschichte betritt“.
Vor fast genau einhundert Jahren hat Albert Einstein die Gleichung E = mc² in seiner “Speziellen Relativitätstheorie” eingeführt. Die Gleichung bot einen neuen Weg, die Ursprünge chemischer Energie zu beschreiben sowie eine neue Energiequelle, die bis dahin historisch völlig unbekannt war – Kernkraft. Die Kernkraft gab ihr furchtbares Debut in der Geschichte 40 Jahre später in Gestalt einer Atombombe. Aber 100 Jahre später haben die Amerikaner [und vor allem auch die Deutschen, A. d. Übers.] noch nicht richtig die weit größeren Implikationen von Einsteins Gleichung erfasst – eine neue Form von Energie, die fast unbegrenzte Energie mit einem verschwindend geringen Einfluss auf die Umwelt zur Verfügung stellen kann.
E = mc². Wer hat noch nichts davon gehört? Selbst Mariah Carey hat ihr letztes Album danach benannt. „E“ steht für Energie, „M“ für Masse und „C“ für die Lichtgeschwindigkeit – das ist einfach genug. Aber was bedeutet das wirklich? (Die Antwort lautet nicht „Relativität“).
Was E = mc² besagt ist nichts weiter als dass Materie und Energie austauschbar sind. Es gibt eine Verbindung zwischen den beiden. Energie kann sich in Materie verwandeln und Materie in Energie. Es sind zwei verschiedene Aspekte der gleichen Sache.
Dieses Prinzip der Gleichartigkeit von Energie und Materie war eine total unerwartete Abwendung von allem, was es bis dahin gegeben hatte. Im 18. Jahrhundert hat Antoine Lavoisier, der große französische Chemiker, die Erhaltung der Materie begründet. Durch sehr sorgfältige Experimente wie das Verbrennen eines Holzscheites fand er heraus, dass das Gewicht der entweichenden Gase und Aschen immer genau gleich dem Gewicht des Ausgangsmaterials war. Materie kann nicht erzeugt oder vernichtet werden, sondern nur seine Form ändern.
Im 19. Jahrhundert dann begründete eine ganze Reihe brillanter Wissenschaftler – Count Rumford, Sadi Carnot, Rudolf Clausius, Ludwig Boltzman – das gleiche Prinzip für Energie. Energie kann viele Formen annehmen – Wärme, Licht, Bewegung potentielle Energie – aber die Menge bleibt immer die gleiche. Energie kann auch nicht erzeugt oder vernichtet werden.
Als dann das 20. Jahrhundert herauf dämmerte, kam Albert Einstein mit einem dritten Prinzip, dass die anderen beiden in völlig unerwarteter Weise vereinigte. Einstein bewies das Erhaltungsgesetz zwischen Materie und Energie. Nichts dergleichen konnte man sich früher vorstellen. Das Bedeutendste an der Sache ist der Koeffizient – das Quadrat der Lichtgeschwindigkeit. Das ist eine sehr, sehr große Zahl mit einer Größenordnung von 1 Quadrillion.
Wir haben nicht wirklich einen Referenzpunkt, um uns einen Faktor von einer Quadrillion vorzustellen. Wir wissen, was eine Trillion ist – das öffentliche Haushaltsdefizit [der USA]. Aber eine Quadrillion ist immer noch jenseits unseres Horizontes. Jedoch bedeutet genau das, dass eine sehr, sehr große Energiemenge sich in eine sehr, sehr kleine Menge von Materie verwandeln kann, und dass eine sehr, sehr kleine Menge von Materie zu einer sehr, sehr großen Energiemenge werden kann.
Vielleicht gibt es einen Weg, die Wichtigkeit von Einsteins Gleichung mit einer anderen Gleichung zu vergleichen, und zwar der Formel für kinetische Energie:
![]()
Kinetische Energie ist die Energie sich bewegender Objekte. „E“ steht wieder für Energie, „m“ für Masse und „v“ für die Geschwindigkeit des sich bewegenden Objektes. Wenn man beispielsweise einen Tennisball durch einen Raum wirft, wird die Energie berechnet, indem man die Masse des Balles mit dem Quadrat seiner Geschwindigkeit multipliziert – vielleicht etwa 50 Meilen pro Stunde.
Die beiden Formeln sind im Wesentlichen gleich. Stellt man sie nebeneinander, ergeben sich zwei Dinge:
- Bei einer vorgegebenen Energiemenge sind Masse und Geschwindigkeit umgekehrt proportional. Je höher die Geschwindigkeit, umso weniger Masse ist erforderlich, und umgekehrt.
- Vergleicht man das mit den Geschwindigkeiten sich bewegender Objekte in der Natur – Wind und Wasser zum Beispiel – ist der Koeffizient in Einsteins Gleichung fünfzehn Größenordnungen größer – der gleiche Faktor wie von einer Quadrillion.
Wie merken wir das im täglichen Leben? Das meiste von dem, was wir „erneuerbare Energie“ nennen, sind tatsächlich die kinetischen Flüsse von Materie in der Natur. Wind und Wasser sind sich bewegende Dinge, die wir zur Energieerzeugung abernten. Daher werden sie mit der Formel für kinetische Energie gemessen.
Beginnen wir mit Strom aus Wasserkraft. Von einem hohen Damm herunterfallendes Wasser erreicht eine Geschwindigkeit von etwa 60 Meilen pro Stunde [ca. 95 km/h] oder 80 Fuß pro Sekunde [ca. 24 m/s]. Erhöht man den Damm um 80 oder mehr Fuß, kann die Geschwindigkeit dadurch nicht um mehr als 20 Meilen pro Stunde [ca. 32 km/h] erhöht werden. Der einzige Weg, den Energieoutput zu erhöhen besteht darin, die Masse zu erhöhen, d. h. mir müssen mehr Wasser verbrauchen.
Die größten Dämme – Hoover und Glen Canyon am Colorado – sind 800 Fuß hoch [ca. 240 m] und halten ein Reservoir mit einer Fläche von 250 Quadratmeilen [ca. 400 km²] zurück. Dies erzeugt 1000 Megawatt, Standard für eine stromerzeugende Station. (Lake Powell hinter dem Glen Canyon Damm versandete irgendwie und erzeugt nur 800 MW).
Umweltaktivisten begannen in den sechziger Jahren, gegen Wasserkraftwerke mobil zu machen, weil sie so riesige Landschaftsräume verbrauchen, weil sie landschaftlich schöne Täler und historische Canyons ertränken. Sie haben diese Mobilmachung bisher nicht beendet. Der Sierra-Klub, der gegen die Errichtung des Hetch-Hetchy-Damms in Yosemite 1921 kämpfte, versucht immer noch, diesen niederzureißen, obwohl er Trinkwasser und 400 Megawatt Strom für San Francisco zur Verfügung stellt. Als Ergebnis dieser Kampagne werden jedes Jahr mehr Dämme eingerissen als neu gebaut.
Wind weist eine viel geringere Energiedichte als Wasser auf, so dass der Landverbrauch sogar noch größer ist. Zeitweilige 50 Stockwerke hohe Windmühlen erzeugen 1½ MW pro Stück, so dass man 660 Windmühlen braucht, um 1000 MW zu erzeugen. Sie müssen eine halbe Meile [ca. 800 m] entfernt voneinander errichtet werden, so dass ein 1000 MW-Windpark 125 Quadratmeilen [ca. 200 km²] Land überdeckt. Unglücklicherweise erzeugen die besten Windmühlen Strom gerade mal in 30% der Zeit, so dass 1000 MW in Wirklichkeit einen Landverbrauch von 375 Quadratmeilen [ca. 600 km²] weit voneinander entfernter Standorte erfordert.
Gezeitenkraft, oft als eine weitere erneuerbare Energiequelle genannt, leidet unter den gleichen Problemen. Wasser hat eine größere Dichte als Wind, aber die Gezeitenströme bewegen sich nur mit einer Geschwindigkeit von etwa 5 mph [ca. 8 km/h]. An den bestgeeigneten Standorten der Welt würde man etwa 20 Meilen [ca. 32 km] Küstenlinie benötigen, um 1000 MW zu erzeugen.
Was ist mit der Solarenergie? Die Sonnenstrahlung ist ein Ergebnis einer Transformation von E = mc², da die Sonne Wasserstoff zu Helium verbrennt. Unglücklicherweise findet diese Reaktion 90 Millionen Meilen entfernt statt. Die Strahlung streut mit dem Quadrat der Entfernung, so dass die Sonnenenergie, wenn sie die Erde erreicht, um fast den gleichen Faktor abgeschächt ist, 10 bis 15. Folglich beträgt die auf einen Quadratmeter einfallende Sonnenstrahlung 400 Watt, ausreichend, um vier 100-WQatt-Glühbirnen zum Leuchten zu bringen. „Thermische Solar“ – große Anordnungen von Spiegeln, die eine Flüssigkeit erhitzen – können 30 Prozent davon in Strom umwandeln. Photovoltaikzellen sind mit einer Umwandlung von 25 Prozent etwas weniger effizient. Ergebnis: Die Strommenge, die wir von der Sonne bekommen, reicht aus, um eine 100-Watt-Glühbirne pro Kartentisch zu erleuchten.
Das ist keine insignifikante Strommenge. Falls wir jedes Hausdach im Lande mit Solarkollektoren zupflastern, könnten wir möglicherweise unsere Hausbeleuchtung plus einige grundlegende Haushaltsgeräte damit betreiben – tagsüber. Der große Vorteil der Sonne liegt darin, dass sie gerade dann ihr Maximum erreicht, wenn es gebraucht wird, während heißer Sommernachmittage wenn die Klimaanlagen den Stromverbrauch in die Höhe schnellen lassen. Das Zusammentreffen mit diesen Spitzen ist ein ständiges Problem für Energieversorger, und der Sonnenstrom kann eine signifikante Rolle bei der Erfüllung des Bedarfs spielen. Das Problem taucht auf, wen Solarenthusiasten zu behaupten versuchen, dass die Solarkraft grundlastfähigen Strom für eine Industriegesellschaft liefern kann. Es gibt keine Technologie, Energie in für kommerzielle Verwendung ausreichender Mengte zu speichern. Bis etwas entwickelt wird – was unwahrscheinlich erscheint – können Wind- und Solarkraft nur als zeitweilige unvorhersagbare Energiequellen dienen.
Es gibt nur so viel Energie, wie wir aus erneuerbaren Quellen anzapfen können. Sie ist begrenzt, entweder durch die erreichte Schnelligkeit oder durch die Distanz, die die Sonnenenergie bis zum Erreichen der Erdoberfläche überwinden muss. Gibt es also irgendwo in der Natur eine Stelle, an der wir einen Vorteil aus jenem „c2“-Koeffizienten ziehen und Masse in Energie verwandeln können? Es gibt eine, die wir durch die Geschichte benutzt haben. Sie nennt sich „Chemie“.
Chemische Energie wird gemeinhin durch „Ladungszahlen” beschrieben. Ein Natriumatom hat eine Wertigkeit von +1, was bedeutet, dass ihm ein Elektron in der äußeren Hülle fehlt. Gleichzeitig besitzt das Chloratom eine Wertigkeit von -1, was bedeutet, dass es ein Elektron zu viel hat. Zusammen bilden sie Natriumchlorid (Tafelsalz). Alle chemischen Reaktionen laufen entweder „endothermisch“ oder „exothermisch“ ab, was bedeutet, dass Energie bei diesem Prozess entweder abgegeben oder verbraucht wird. Der Bunsenbrenner in der Chemieklasse ist ein Weg, einer Reaktion Energie zuzuführen. Das andere, was passieren kann, geschieht gelegentlich in Chemielaboratorien, nämlich ein plötzliches Freisetzen von Energie, genannt „Explosion“.
Der große Fortschritt der Quantenphysik des 20. Jahrhunderts war es, die chemischen Reaktionen zu beschreiben mit E = mc².
Verbrennt man eine Gallone (ca. vier Liter) Benzin, wird nur ein Milliardstel der Masse des Benzins vollständig in Energie umgewandelt. Diese Umwandlung erfolgt in der Elektronenhülle. Die Menge ist so gering, dass es bisher noch niemandem gelungen ist, sie zu messen. Und doch reicht die Energieerzeugung aus, um ein 1000-Kilo-Fahrzeug 50 Kilometer fahren zu lassen – eine bemerkenswerte Leistung, wenn man darüber nachdenkt.
Elektronen machen nur etwa 0,01 Prozent der Masse eines Atoms aus. Die anderen 99,99 Prozent befinden sich im Atomkern. Und so erhob sich die Frage, ob es möglich wäre, die viel größere, im Atomkern gespeicherte Energiemenge auf die gleiche Weise abzugreifen, wie wir das mit den Elektronen durch Chemie getan haben?
Lange Zeit bezweifelten viele Wissenschaftler, dass das gelingen könnte. Einstein selbst war skeptisch, indem er sagte, dass die Spaltung eines Atoms so wäre wie „der Versuch, nachts Vögel zu jagen in einem Land, in dem es kaum Vögel gibt“. Aber andere Wissenschaftspioniere – Enrico Fermi, George Gamov, Lise Meitner und Leo Szilard – entdeckten, dass es gemacht werden kann. In den späten dreißiger Jahren ist klar geworden, dass Energie in bisher nicht gekannter Menge durch Spaltung des Uranatoms gewonnen werden könnte.
Unglücklicherweise ging der Einführung der Kernkraft der II. Weltkrieg voraus. Dies ist eine historische Tragödie. Die Atombombe steht zur Kernkraft im gleichen Verhältnis wie Schießpulver zu Feuer. Während das Schießpulver in der Geschichte eine bedeutende Rolle gespielt hat, war die Rolle des Feuers von viel größerer Bedeutung. Würden wir das Feuer aufgeben, nur weil es zur Entwicklung von Gewehren geführt hat? Und doch wirft die Atombombe weiterhin einen Schatten auf die gleichermaßen bedeutende Entdeckung der Kernkraft.
Es stellte sich heraus, dass der Energieausstoß aus einem sich teilenden Uranatom 2 Millionen mal größer ist als die Kohlenstoff-Wasserstoffbindung in Kohle, Öl oder Holz aufzubrechen. Verglichen mit allen von den Menschen benutzten Formen der Energiegewinnung ist die Kernkraft jenseits aller Grenzen. Wind besitzt nur ein Zehntel der Energiedichte von Holz, Holz die Hälfte der Energiedichte von Kohle und Kohle die Hälfte der Energiedichte von Oktan. Alle zusammen unterscheiden sie sich um einen Faktor von etwa 50. Die Kernkraft besitzt etwa 2 Millionen mal die Energiedichte von Benzin. Es ist schwierig, dies im Licht unserer bisherigen Erfahrungen auszuloten. Und doch hängt unsere Energiezukunft großenteils davon ab, die Bedeutung dieses Differentials zu erfassen.
Eine elementare Vergleichsquelle ist die Überlegung, was man braucht, um ein Kohlekraftwerk im Gegensatz zu einem Kernreaktor wieder aufzutanken. Ein 1000-MW-Kohlekraftwerk – unser Standard – wird durch einen 110 Waggons langen „Kohlezug“ gefüttert, der alle 30 Stunden an dem Kraftwerk ankommt – 300 mal im Jahr. Jeder individuelle Kohlewaggon wiegt 100 Tonnen und erzeugt 20 Minuten lang Energie. Wir bringen die Kapazität unseres Schienensystems durch dieses Herumfahren der Kohle in unserem Land an seine Grenzen. (In China ist es bereits komplett zusammengebrochen).
Ein Kernreaktor andererseits wird aufgetankt, wenn eine Flotte von sechs Sattelschleppern an dem Kraftwerk mit einer Ladung Brennstäbe einmal alle 18 Monate ankommt. Die Brennstäbe sind nur schwach radioaktiv und können mit Handschuhen angefasst werden. Sie werden fünf Jahre im Reaktor verbleiben. Nach diesen fünf Jahren werden sich etwa 6 Unzen (ca. 170 g) Materie vollständig in Energie verwandelt haben. Wegen der Stärke nach E = mc² reicht die Metamorphose von 6 Unzen Materie aus, die Stadt San Francisco fünf Jahre lang mit Strom zu versorgen.
Das ist es, was den Leuten so schwerfällt zu verstehen. Es liegt fast jenseits unserer Vorstellungskraft. Wie kann man eine ganze Großstadt fünf Jahre lang mit 6 Unzen Materie fast ohne jeden Umwelteinfluss mit Strom versorgen? Es scheint so unvorstellbar zu sein, dass wir Probleme erfinden, um alles wieder normal aussehen zu lassen. Ein Reaktor ist eine Bombe, die darauf wartet zu explodieren. Der Abfall lagert ewig, was werden wir je damit tun können? Es liegt etwas Unheimliches darin, Energie aus dem Atomkern zu erzeugen. Die Technologie liegt jenseits der menschlichen Beherrschbarkeit.*
Aber die Technologie liegt nicht jenseits der menschlichen Beherrschbarkeit. Es ist auch nichts Unheimliches an der Kernkraft. Es liegt nur jenseits von allem, was wir uns vor Beginn des 20. Jahrhunderts auch nur vorstellen konnten. Zu Beginn des 21. Jahrhunderts ist es Zeit, damit anzufangen, sich das vorzustellen.
William Tucker is the author, most recently, of Terrestrial Energy: How Nuclear Power Will Lead the Green Revolution and End America’s Energy Odyssey.
Link: http://www.energytribune.com/articles.cfm/2469/Understanding-E-=-mc2
Übersetzt von Chris Frey
*Bemerkung des Übersetzers: Der Artikel von Tucker stammt vom 21. Oktober 2009, ist also schon älter. Alles hierin Gesagte gilt natürlich auch für die Energiequelle Thorium, von der damals offenbar noch nichts bekannt war und die nun auch das Risiko einer Verstrahlung gegen Null tendieren lässt.

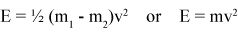















Wir freuen uns über Ihren Kommentar, bitten aber folgende Regeln zu beachten:
- Bitte geben Sie Ihren Namen an (Benutzerprofil) - Kommentare "von anonym" werden gelöscht.
- Vermeiden Sie Allgemeinplätze, Beleidigungen oder Fäkal- Sprache, es sei denn, dass sie in einem notwendigen Zitat enthalten oder für die Anmerkung wichtig sind. Vermeiden Sie Schmähreden, andauernde Wiederholungen und jede Form von Mißachtung von Gegnern. Auch lange Präsentationen von Amateur-Theorien bitten wir zu vermeiden.
- Bleiben Sie beim Thema des zu kommentierenden Beitrags. Gehen Sie in Diskussionen mit Bloggern anderer Meinung auf deren Argumente ein und weichen Sie nicht durch Eröffnen laufend neuer Themen aus. Beschränken Sie sich auf eine zumutbare Anzahl von Kommentaren pro Zeit. Versuchte Majorisierung unseres Kommentarblogs, wie z.B. durch extrem häufiges Posten, permanente Wiederholungen etc. (Forentrolle) wird von uns mit Sperren beantwortet.
- Sie können anderer Meinung sein, aber vermeiden Sie persönliche Angriffe.
- Drohungen werden ernst genommen und ggf. an die Strafverfolgungsbehörden weitergegeben.
- Spam und Werbung sind im Kommentarbereich nicht erlaubt.
Diese Richtlinien sind sehr allgemein und können nicht jede mögliche Situation abdecken. Nehmen Sie deshalb bitte nicht an, dass das EIKE Management mit Ihnen übereinstimmt oder sonst Ihre Anmerkungen gutheißt. Wir behalten uns jederzeit das Recht vor, Anmerkungen zu filtern oder zu löschen oder zu bestreiten und dies ganz allein nach unserem Gutdünken. Wenn Sie finden, dass Ihre Anmerkung unpassend gefiltert wurde, schicken Sie uns bitte eine Mail über "Über Uns->Kontakt"Herr Marie,
„Die Bedeutung von h entspricht daher einem konstantem dimensionsbehaftetem Steigungsfaktor in der allgemeinen Gleichung „Energie = h * Drehgeschwindigkeit“ und dabei ist von „Quantum“ weit und breit gar nichts zu sehen!“
Der Messwert des Drehimpulses eines Teilchens wie dem Elektron von h/4pi Js an sich impliziert kein quantenhaftes Verhalten im Mikrokosmos. Das kommt erst dadurch, dass Elektronen immer denselben Betrag haben und den Drehimpuls nicht wie ein makroskopischen Koerper durch Anederung der Rotationsgeschwindigkeit oder des Traegheitsmoments aendert. Das ist das eigentlich besondere. Der Drehimpuls eines Elemenatarteilchens ist im Gegnsatz zu makroskopischen Koerpern eine invariante Eigenschaft (Quantenzahl)!!! Die entsprechende Rotationsenergie ist ueberhaupt nicht aenderbar und existiert als physikalisch messbare Groesse beim Teilchen gar nicht, denn des gilt auch keine observable (und damit existente) Rotationsgeschwindigkeit des Teilchens!! Die Gleichung Erot = L omega /2 existiet im Mikrokosmos nicht, da weder omega noch Erot messbare Groesen sind (Observable)
Herr Marie,
nochmals, machen Sie sich klar, ob Sie sich hier nur wahllos abreagieren wollen oder „aufklaeren“ wollen.
Ihre Rechnungen sind richtig und 1 rad = 1 stimmt nicht. Aber diese Ungleichheit wird auch von der Quantenphysiker und sonstigen Physiker, die Winkel ohne Einheit messen auch nicht als Gleichheit behauptet oder verwendet!!!!!
Das alleine behaupten Sie, weil Sie nicht verstehen wollen, dass es ueberhaupt kein Problem darstellt, eine Einheit fuer ein Zahlenverhaeltnis definierter geometrischer Groessen (Kreisbogen/Radius) wegzulassen, da ein Zahlenverhaeltnis von Strecken per se einheitenlos ist. Das „rad“ ist ueberfluessig, denn in der Physik misst man Winkel wenn ich ausdruecklich anderes angegeben ist (wie Grad) immer in rad also als Verhaltnis Kreisbogen zu Radius.
Wenn Ihr Sohn Physiker ist, so lassen sie es sich von ihm erklaeren. Er wird Ihren kaum etwas anderes als ich erzaehlen.
„Länge, Masse, Strom, Winkel usw. sind Dimensionen und zunächst einheitenfrei.“
Von den vier Groessen sind Lange, Masse und Strom sog. Basiseinheiten. Der Winkel zaehlt nicht dazu, weil er sich wie jede geometrische Groesse (wie flaeche in Quadratmetern und Volumen in Kubikmetern) auf die Laenge in Metern zurueckfuehren laesst, naemlich wie bereits mehrmals erwaehnt und von Ihnen auch vertrten als Verhaeltnis zweier Laenge. Die Dimension einer auf Basiseinheiten reduzierbaren Groesse ist das Produkt der Dimensionen der Basiseinheiten, im Falle des Winkels ist also seine Dimension dim Winkel = Laenge/Laenge = 1, im Falle der Flaeche , dim Flaeche = Laenge mal Laenge.
Sie haben Recht, Einheiten muessen zusaetzlich definiert werden, und haeufig gibt es mehrere zur selben Groesse, die proportional umrechnbar sind.
“ Erst die Einheit macht die Dimension messbar, also mit der frei gewählten und definierten Einheit der Dimension vergleichbar. Beim Winkel ist z.B. eine mögliche Einheitendefinition Umfangslänge/Radiuslänge oder nach Kürzung der gleichen Wortinhalte Umfang/Radius.“
Klar, das hatte ich bereits schon dargestellt. Sie muessen nicht das wiedergeben, was ich Ihnen bereits erklaert hatte. Wenn ich Ihnen da nichts Neues erzaehlt habe, so lassen Sie mich das wissen. Und ich brauche nicht meine eigene Erklaerung von Ihnen nochmals vorgekaut zu bekommen.
„h = 1,05e-34 Js/rad
h = 1,84e-36 Js/°
h = 6,62e-34 Js/U“
Das Plancksche Wirkungsquantum betraegt h=6.626e-34 Js, die Einheit rad ist wie gesagt ueberfluessig, weil eh klar. Daneben verwendet man noch das sog. Diracsche Wirkungsquantum h_quer = h/2pi = 1.054e-34 Js. Beide haben selbstverstaendlich dieselbe Einheit, mussen aber durch den numerischen Unterschied andere Symbole haben.
Der Eigendrehimpuls des Elektrons betraegt L= h_quer/2 = h/4pi und ist sowohl numerisch wie von der Einheit her eindeutig definert. Und in der Heisenbergschen Unschaeferelation steht streng genommen sogar dE*dt grosser gleich h_quer/2 (wenn die Unschaerfen d die Standardabweichungen der Groessen sind) und nicht h (dafuer trifft die Ungleichung natuerlich auch zu, denn h ist groeser h_quer).
Kann es also sein, dass Sie einfach h und h-quer verwechseln und deswegen so ein Tamtam machen?
Wie gesagt, Ihre drei h’s oben sind alle unterschiedlich zu kennzeichnen, das mittlere hat keine Anwendung in der Physik.
Somit gelten die bekannten Gleichungen, wie in jedem entsprechenden Lehrbuch nachzulesen ist
h*Frequenz = h_quer * Kreisfrequenz, h*Wellenzahl = h_quer * 2pi/ Wellenlaenge , etc….die Physik ist da voellig unmissverstaendlich. Haben Sie es nun verstanden, oder bekommen Sie es immer noch nicht hin?
Es ist immer des gleiche: erst hocheinsteigen „Einstein und Heisenberg = Volldeppen) zum Schluss stellt sichbraus, das er nicht kapiert, wie man Winkel misst.
#151: NicoBaecker
“ Die dimension der Winkelmessung ist eins, dennoch steht natuerlich ausser Frage, dass man verschiedene Einheiten fuer dieselbe physikalische Groesse (die haben selbstredend identische Dimensionen) umrechnen muss.“
„Dimension der Winkelmessung“? Gehen Sie doch einmal zu ihrem Oberrabbiner in der Synagoge und lassen Sie sich aufklären, wie man richtig rabulisiert!
Länge, Masse, Strom, Winkel usw. sind Dimensionen und zunächst einheitenfrei. Erst die Einheit macht die Dimension messbar, also mit der frei gewählten und definierten Einheit der Dimension vergleichbar. Beim Winkel ist z.B. eine mögliche Einheitendefinition Umfangslänge/Radiuslänge oder nach Kürzung der gleichen Wortinhalte Umfang/Radius.
rad = Umfang/Radius
oder
(Umfang/Radius) / rad =1
Aber niemals kann diese Deppenmeinung wahr sein: rad = 1 !
Kein Wunder, daß Sie aufgrund Ihres totalen Unverständnisses von Physik Klimahysteriker geworden sind!
h = 1,05e-34 Js/rad
h = 1,84e-36 Js/°
h = 6,62e-34 Js/U
wobei U für einen Vollkreiswinkel steht.
Aus diesem Grund kann die Heisenbergsche Deppenungleichung nur für Volldeppen wahr sein. Weil am Ende der Einheitengleichung entweder
1 = 1/rad
oder
1 = 1/°
oder
1 = 1/U
oder
1 = 1/Winkeleinheit
dastehen wird und auf diesem unglaublichen Blödsinn sind große Teile der neuzeitlichen Quantenphysik für Deppen aufgebaut!
Aus diesem grundlegenden Fehler resultieren dann solche Unsinnsbedeutungen wie „Wirkung“ = „Energie * Zeit“ statt richtig „Wirkung“ = „Drehimpuls“ oder „Wirkung“ = „Drehmoment * Zeit“ oder „Wirkung“ = „Energie je Drehgeschwindigkeit“
Die Bedeutung von h entspricht daher einem konstantem dimensionsbehaftetem Steigungsfaktor in der allgemeinen Gleichung „Energie = h * Drehgeschwindigkeit“ und dabei ist von „Quantum“ weit und breit gar nichts zu sehen!
Die wahre Bedeutung von h entspricht daher im atomarem Bereich „Energie/Drehgeschwindigkeit = h = konstant“ oder eben „Drehimpuls = h = konstant“, wobei Drehimpuls = Drehmoment * Zeit ist (Energie/Winkel * Zeit, Js/rad).
Das war nun das ENDE, Studiosus der Füsig!
Herr Marie,
„Sie sehen, da steht viel mehr da als nur das grundverkehrte „rad = 1″“
Die Gleichung hat bis auf Sie auch niemand behauptet. Nochmal meine Rat: halten Sie Dimension und Einheit auseinander. Winkelmasse haben die Dimension 1 = Laenge/ Laenge, aber es gibt trotzdem verschiedene Einheiten!!!
Mit der Dimension der Wirkung hatten Sie das gleiche Verstaendnisproblem.
Herr Marie,
nun machen Sie mal halblang. Wenn Sie unbedingt jemanden Ihr beschraenktes Wissen beibringen wollen, so suchen Sie sich jemanden, der das nicht schon vor Jahrzehnten verstanden hat.
„So funktioniert das und nicht anders, Studiosus!
Daher muß zwingend die Winkelabkürzung mitgeführt werden, damit erkenntlich bleibt, daß es sich um einen Winkel handelt und nicht um einen reinen Zahlenwert“
Sie haben den Unterschied zwischen Dimension und Einheit wohl micht verstanden. Die dimension der Winkelmessung ist eins, dennoch steht natuerlich ausser Frage, dass man verschiedene Einheiten fuer dieselbe physikalische Groesse (die haben selbstredend identische Dimensionen) umrechnen muss. Eine Wegstrecke L hat ja auch die Dimension einer Laenge, nimmt in Meilen oder Meter jedoch verschieden Masszahlen an. Genauso ist es bei Ihrem Beispiel mit dem Winkel: 1 Meile und 1 Meter kuerzen sich nicht zu eins weg, genausowenig wie sich 1 Grad oder 1 rad sich wegkuerzen lassen, sondern die Masszahlen desselber vermessenen Winkel unterscheiden sich um den Faktor 57,… Grad/rad. Wenn man aber das Bogenmass als Einheit nimmt, laesst man in der Physik die Einheit rad weg, da sowieso nichts anderes gemeint ist. Denn in der Physik misst man nunmal so, wenn nicht explizit ein anderes Winkelmass wie z.B. Grad genommen wird. Erst wenn man das Grad auch noch weglassen wuerde und auch sonst nicht kenntlich machen wuerde, was das Winkelmass ist, indem man z.B. angaebe, welches Mass in der benutzten Einheit der Vollkreis haette, entstuende Konfusion.
Wie gesagt, diese Konfusionsgefahr besteht bei aelteren technischen Artikeln, wenn man Winkelgeschwindigkeit mit Umdrehungen pro Sekunde angibt und nicht dazuschreibt, dass hier nicht im Bodenmass pro sec gemessen wird.
#148: NicoBaecker
„Sie verwechseln die Dimension mit der Einheit, merken Sie sich das. Die Dimension eines Winkels ist Eins = Laenge durch Laenge.“
Schwachsinn, Studiosus. Der Dimensionsname ist Winkel und eine Basiseinheit der Dimension kann Grad, Neugrad, Radiant, Rechter Winkel, Vollkreis oder was auch immer sein und hierfür gibt es ein Einheitenzeichen, welches mit der Definition der entsprechenden Basiseinheit identisch ist. Aus diesem Grund muß zwingend ein definierendes Einheitszeichen verwendet werden und eine reine Zahl kann niemals einem Winkel entsprechen und daher muß zwingend ein Symbol rad oder ° oder XXX als ein die Basiseinheit definierendes Zeichen hinzugesetzt werden.
Ihnen fehlt ja jegliches wissenschaftliche Arbeitsverständnis!
Wenn das Drehmoment 5 Nm/° und die Winkelgeschwindigkeit 3°/s beträgt ist die Leistung 5 Nm/° * 3°/s = 15 Nm/s
Wenn das Drehmoment 5 Nm/rad und die Winkelgeschwindigkeit 3 rad/s beträgt ist die Leistung 5 Nm/rad * 3 rad/s = 15 Nm/s
Wenn das Drehmoment 5 Nm/° und die Winkelgeschwindigkeit 3 rad/s beträgt ist die Leistung 5 Nm/° * 3 rad/s * 360°/(2*pi*rad) = 859 Nm/s
Wenn das Drehmoment 5 Nm/rad und die Winkelgeschwindigkeit 3 °/s beträgt ist die Leistung 5 Nm/rad * 3°/s * 2*pi*rad/360° = 0,262 Nm/s
So funktioniert das und nicht anders, Studiosus!
Daher muß zwingend die Winkelabkürzung mitgeführt werden, damit erkenntlich bleibt, daß es sich um einen Winkel handelt und nicht um einen reinen Zahlenwert. Auch Ihr Einwand, m/m sei 1 ist eben nicht richtig, weil hier in Wirklichkeit ungefähr folgendes in der Winkeldefinition steht:
„Der Winkel 1 rad wird als derjenige Winkel definiert, bei welchem das Verhältnis Bogenmaßlänge zu Radiuslänge gleich 1 ist oder die Bogenmaßlänge gleich der Radiuslänge ist“.
Sie sehen, da steht viel mehr da als nur das grundverkehrte „rad = 1“
Wenn mir mein Sohn mit solch einem Unsinn dahergekommen wäre, hätte ich ihm das Physikbuch um die Ohren geschlagen! Er ist Physiker.
Auf diesen Einheitenfehler gründet sich die hochmoderne Deppenfüsig mit ihrem wabernden Quantenschaumvakuum, aus dem die rosaroten Elephanten heraushüpfen dürfen. Weil es der Idiot Heisenberg „erlaubt“ hat!
Herr Marie,
Sie verwechseln die Dimension mit der Einheit, merken Sie sich das. Die Dimension eines Winkels ist Eins = Laenge durch Laenge. Das man verschieden Einheiten fuer Winkelmasse hat, ist eine andere Sache. Wenn der Drehimpuls eines rotierenden Koerpers x Js = x kgm2s-1 betraegt, so hat er die Masszahl fuer den Drehimpuls unabhaengig davon, in welcher Einheit man den Drehwinkel misst!
#146: NicoBaecker
„Merken Sie sich: das ganze gibt NUR an, was gleiche Einheiten hat, aber nicht, was fuer eine Energie und Zeit in der Formel verknueft sind. Im einer physikalischen Gleichung steckt mehr Sinn als nur Einheiten miteinander zu verknuepfen.“
Sie sind ein Schmarrer. Klar, mehr Sinn als Sinn ist eben Unsinn. Merken Sie sich: In dem Moment, wo die Einheiten in einer Gleichung nicht identisch sind, ist eine Formel schlicht und einfach falsch!
Heisenberg und andere Pseudophysiker wie Sie oder auch Einstein sagen letztlich:
1 = 1/rad.
Und dies entspricht eben Deppenfüsig von und für Deppen!
ENDE
jerr Marie,
jetzt daememrt mir Ihr Problem. Ich dachte auch mal mit 17, dass man alleien durch das Rumhantieren mit Basiseinheiten, neue physiklaische Gesetzmaessigkeiten finden wuerde und fand daher, dass in der Heisenbergschen Unschaerferelation oder Einstein E=mc2 nichts besonderes steckt, denn diese Formeln bekommt man doch einfach hin.
Nach ein paar Jahrzehnten kommt man nicht mehr auf die Idee, wie jemand so naiv sein kann und ein Problem damit hat, wenn ich sage, die Einehit der Wirkung sei die Einheit aus Energie mal Zeit,statt Strecke mal Impuls oder statt Drehimpuls oder Drehmoment mal Zeit oder sonst eine Kombination. Merken Sie sich: das ganze gibt NUR an, was gleiche Einheiten hat, aber nicht, was fuer eine Energie und Zeit in der Formel verknueft sind. Im einer physikalischen Gleichung steckt mehr Sinn als nur Einheiten miteinander zu verknuepfen.
Marie,
koennen Sie nicht lesen? Die physikalische Groesse Wirkung ist bereits aus der Mechanik des 18. Jahhdrts bekannt! Und auf dem Hamilton Lagrange Mechanismus beruht nicht nur die Quntenmechnaik, sondern laesst sich die gesamte Physik aufbauen, klassische Anfaengeranwendung im 5. Semester Physikstudium die Elektrodynmanik. Ihre Physikkenntnisse haben Sie sich wahrscheinlich aus Peter Moosleitners interessantem Magazin geholt, da findet man naemlich so einem verblendeten Bloedsinn, den Sie hier wiedergeben.
#142: NicoBaecker
„Ja sicher, was denn sonst? Sie wollten doch nicht ernsthaft etwa das von mir in WORTEN sehen, oder??? Die Wirkung hat die Einheit wie
Energie mal Zeit.“
Ihre zugegebene Behauptung, die Einheit des Wirkungsquantum habe die Bedeutung von „Energie mal Zeit“ beweist mit allerhöchster Beweiskraft, daß Sie ein Pseudophysiker sind oder bestenfals ein Weichei-Füsiger. Von Physik haben Sie jedenfalls keine Ahnung.
Das sogenannte Wirkungsquantum ist nur ein Proportionalitätsfaktor und hat nichts Quantenhaftes an sich. Auf diesem Unsinn „Energie mal Zeit“ ist praktisch die gesamte esoterische Quantenphysik aufgebaut, samt Vakuumfluktuationen und virtuellem Teilchensalat. Die von Ihnen „gemessene“ Unschärferelation Heisenbergs entspricht einem Unsinnsvergleich der Art, „In der Nacht ist es immer kälter als draußen“.
Heisenberg vergleicht Unvergleichbares. Er behauptet, Schuhe müssen immer größer als Farbe sein.
Und das haben Sie mit Ihrer „Messung“ in #138 sogar bestätigt, NicoBaecker!
„die unschaerferelation muss man nicht glauben, man misst sie.“
Heisenberg sagt:
Energieunschärfe * Zeitunschärfe > h
dE*dt > h
oder Ortsunschärfe * Impulsunschärfe > h
dx*dp >h
oder
dx * d(m*v) >h
Mit Einheiten steht in allen Fällen da:
kgm²/s²*s = kgm²/s²*s = Js
m*kg*m/s = kgm²/s²*s = Js
Jedoch lautet die Einheit des Wirkungsquantums nicht idiotische „Energie mal Zeit“ sondern vorstellbar „Energie je Winkelgeschwindigkeit“ oder „Drehmoment*Zeit“ oder „Drehimpuls“.
Der Schlüssel hierbei ist das Drehmoment, dessen Einheit als „Kraft * Hebelarm“ oder „Kraft * Weg“ behauptet wird und daher die Einheit „Nm“ bekommen hat. Dis ist falsch. „Nm“ ist die Einheit für Arbeit oder Energie und niemals für Drehmoment! Das ist die Grundlage der gesamten Esoterenphysik und der Grundfehler bereits ganz am Anfang.
Die richtige Bezeichnung des Drehmoments lautet „Energie je Drehwinkel“ oder „Leistung je Winkelgeschwindigkeit“ als J/° oder J/rad oder W/(°/s) oder W/(rad/s) = Ws/rad oder J/rad oder Nm/° oder Nm/rad.
Die Behauptung, die Winkelbezeichnung “ ° “ oder „rad“ könne entfallen da angeblich rad = 1 sei, ist eine Idiotenbehauptung. Da 1 J/° # 1 J/rad ist. Die Winkelbezeichnung muß daher immer mitgeführt werden. Alle anderen Behauptungen entsprechen purer Pseudowissenschaft.
Daß manchmal dennoch richtige Ergebnisse erhalten werden ist nur dem Umstand zu verdanken, daß in Rechnungen meist zweimal derselbe Fehler gemacht wird und sich daher der Fehler aufhebt.
Der Füsiger schreibt daher: Leistung = Drehmoment * Winkelgeschwindigkeit = Nm*1/s = Nm/s = J/s = W
Der Ingenieur schreibt dagegen Leistung = Drehmoment * Winkelgeschwindigkeit = Nm/rad * rad/s = Nm/s = J/s = W
Aus diesem Grund lautet die richtige Einheit des Wirkungsquantums nicht Js sondern J/(rad/s) = Js/rad oder Js/°
Daher die vorstellbare Größe für das Wirkungsquantum „Energie je Winkelgeschwindigkeit“.
Aus diesem Grund steht dann bei Heisenberg diese Unsinnsungleichung da:
Js = kgm²/s²*s > kgm²/s²*s * 1/rad = Js/rad
oder eben nach Heisenberg:
Js > Js/rad
Aus diesem Gründ dürfen in meinem Wohnzimmer nach Heisenberg ab und zu rosarote Elefanten herumhüpfen. Jedenfalls nach der Meinung der Pseudophysiker, welche die anerkannte Deppenphysik betreiben.
Hier die richtige Einheit des „Wirkungsquantums“:
http://www.numericana.com/answer/constants.htm#h
HerrMarie,
„So sehr ich diese idiotische Beheinheitlichung auch drehe und wende, es kommt nicht die Buchstabenfolge „Wirkung“ zustande.“
Ich kenne das Gefuehl, das hatte ich mit 17 auch mal vor dem Studium. Da war man noch so und dachte, aus dem Begriff an sich muesse doch etwas rauszuholen sein.
Was Ihr Beispiel angeht, so muessen Sie erstmal die Langragefunktion L= T-V ermitteln, die Bewegungsgleichung ergibt sich aus der Langrangen Gleichung und die Wirkung uebers Zeitintegral ueber L. Die Bahnkurve ist die Loesung der Bewegungsgleichung oder aequivalnt aus der Variation der Wirkung. Ist eben Mechanik fuer Physiker oder Machinenbauer. Muss man eben koennen.
Herr Marie,
„Ich lese aus den Einheiten etwas anderes ab. Nämlich „Energie mal Zeit““
Ja sicher, was denn sonst? Sie wollten doch nicht ernsthaft etwa das von mir in WORTEN sehen, oder??? Die Wirkung hat die Einheit wie
Energie mal Zeit.
Wenn Sie Ihnen der Begriff „Wirkung“ zu wenig auf dem Begriff her sagt, ist das Ihr Problem. Das muessen Sie sich als erstes mal abgewoehnen. Aber in diesem Fall haben Sie Glueck und sind nicht der erste, dem der Begriff nicht gefaellt. Der Urheber ist wohl Maupertois, und der sprach vom Prinzip der kleinsten Wirkung oder kleinsten Aktion. Mathematisch ausgebaut wurde dies durch Lagrange, Hamilton und Jacobi und laeuft heute unter dem Stichwort Variationsrechnung. Wenn Sie meinen, das sei alles Pseudophysik, frage ich Sie, was dann eigentlich noch von der „wahren“ Physik uebrigbleiben soll, wenn nicht das? Sie kappen hier so grosszuegig ab, dass dem Physikstudenten schon nach 2 Wochen erstes Semester bis zum Abschluss nur noch Pseudophysik geboten wuerde.
#140: NicoBaecker
“ J*s ist die Einheit der Wirkung“
?
Ich lese aus den Einheiten etwas anderes ab. Nämlich „Energie mal Zeit“
So sehr ich diese idiotische Beheinheitlichung auch drehe und wende, es kommt nicht die Buchstabenfolge „Wirkung“ zustande.
Was bedeutet „Energie mal Zeit“?
Welche Wirkung geht von einem System aus, welches z.B. eine Energie von 1 kWh über 5 Sekunden oder 500 Millionen Jahren gespeichert hat? Ich sehe hier keinerlei Wirkungsmöglichkeit. Höchstens eine auf das Gehirn von Deppen.
Bei „Energie je Zeit“ kann ich mir etwas vorstellen. Das ist Leistung und da passiert tatsächlich etwas und zwar umso mehr, je länger diese Größe erhalten bleibt. Dann wurde nämlich eine Energiemenge Energie/Zeit * Zeit = Energie umgesetzt. Hier ist also eindeutig eine Wirkung feststellbar.
Aber wenn dann diese Energiemenge einfach über weitere Millionen Jahre einfach so „liegenbleibt“, geht keinerlei Wirkung mehr von ihr aus!
Mit anderen Worten: Von Physik haben Sie keine Ahnung. Aber von Pseudophysik sicher massenhaft!
Herr Marie, #139
„Leiden Sie an Textunverständnis? Ich wollte von Ihnen wissen, was die Einheit J*s beim Wirkungsquantum bedeutet, in WORTEN.“
Nun halten Sie mal die Luft an. Ich entscheide immer noch selbst nach Lust und Laune, wem ich antworte. J*s ist die Einheit der Wirkung. Dies ist eine physikalische Größe von zentraler Bedeutung beim eleganten Lösen der Bewegungsgleichungen unter Kraftwirkung.
(war nun mehr als eine halbe Zeile. Kapieren werden Sie es auch so nicht)
#138: NicoBaecker
Leiden Sie an Textunverständnis? Ich wollte von Ihnen wissen, was die Einheit J*s beim Wirkungsquantum bedeutet, in WORTEN.
Das ist vielleicht eine halbe Zeile „Erklärung“.
Aber ich sehe schon, Sie haben von Physik sowieso keine Ahnung und müssen sich deshalb irgendwie um eine Antwort drücken.
Ist auch klar, Sie sind ja nur Student, wie ich gesehen habe. Da glauben Sie noch den ganzen Unsinn, der Ihnen eingelöffelt wurde.
Herr Marie,
die unschaerferelation muss man nicht glauben, man misst sie. Und wenn man Physik nur in Worten
Erklaert bekommen moechte, so versteht man das wesentliche sowieso nie.
#135: W. Kinder
Hallo Herr Kinder!
„Die Quantenphysik erlaubt Vorgänge, bei denen eine „vorübergehende“ Verletzung….“
Ich weiß. Ich würde dies aber eher als eine nie vorübergehende Verletzung der Logik ansehen.
Nach der Quantenphysik darf 100000 mal je Stunde in meinem Wohnzimmer für jeweils geschätzt 1e-60 s eine rosarote Elefantenherde auftauchen. Ach ja, geht ja wegen der Planckzeit gar nicht. Dann müssen es eben grüne Kaninchen und dafür etwas länger gewesen sein. Falls eben nicht, wird mir NicoBaecker sicher vorrechnen können, wie lange deren Ohren erlaubt gewesen sein dürfen.
Aber er soll mich erst einmal über die Bedeutung von J*s beim Wirkungsquantum aufklären. Egal, was er sagen wird, es wird für ihn ungünstig ausgehen 🙂
Entweder kann ich ihm zeigen, daß er keine Ahnung von Physik hat oder ich kann ihm zeigen, daß er keine Ahnung von Physik hat 🙂
Je nachdem, mit welchem unauflösbaren Widerspruch er antwortet 🙂
#134: NicoBaecker
Sie glauben also an die Unsinnsrelation?
Schön. Dann erklären Sie bitte einmal mit WORTEN die Bedeutung des Wirkungsquantums (Js). Aber bitte so, daß Sie es auch selbst verstehen!
Anschließend werden Sie feststellen, daß Sie von Physik keinerlei Ahnung haben!
Versprochen!
Hallo Herr A.Marie (#132)
„Wetten, daß Sie auch an Heisenbergs Unsinnsrelation glauben?“
Sie werden doch nicht die wertvollen unauflösbaren Widersprüche in der Quantenphysik aufdecken wollen?
Die Quantenphysik erlaubt Vorgänge, bei denen eine „vorübergehende“ Verletzung des Energieerhaltungssatzes zulässig ist. Ohne näher darauf einzugehen, seien die Begriffe Tunneleffekt, virtuelle Teilchen sowie Heisenbergsche Unschärferelation genannt.
MfG
W. Kinder
Lieber Herr Marie, #132
Ok, die Welt ist für mich mit Ihnen wieder in Ordnung. Zwischenzeitlich dachte ich, dass Sie sich nur verstellt hätten. Sie sind also noch der Alte, und der hat von Physik keine Ahnung.
„Ich vermute einmal, sie haben das deshalb übersehen, weil Sie sich 100 Jahre lang mit Pseudophysik beschäftigt haben :)“
Sicher, genaugenommen habe ich auch schon Galileis Fallversuche manipuliert, um Pseudophysik in den Lehrbüchern zu verbreiten.
„Wetten, daß Sie auch an Heisenbergs Unsinnsrelation glauben?“
Sie öffnen mir die Augen. Denn habe ich mich also 3 Jahre lang umsonst mit dem verflixten Pulslaser rumgeärgert und dachte es läge an der Heisenbergschen Unschärferelation, dass man den Puls nicht kürzer machen kann ohne dann das Spektrum zu verbreitern, dabei war an vom verdammten Ding wohl nur eine Schraube locker.
Hallo Herr A.Marie (#127)
Jede Energieübertragung ist untrennbar mit einer Masseübertragung verbunden. Oder: Energie hat Masse. Oder: Energie ist Materie – Materie ist Energie. Oder auch: Energie und Masse sind zwei unterschiedliche Erscheinungsformen der Materie. Masse ist in diesem Sinne eine „Materiemenge“. Obwohl ich diesen Begriff „Materiemenge“ immer ungern verwende.
Dies entspricht der Deutung des Effektes innerhalb der Schulphysik, den Sie vermutlich kennen.
Aber schauen Sie sich mal den Begriff „Massen-Defekt“ an.
Ein „Massen-Defekt“ bei kernphysikalischen Reaktionen (nur dort ist er groß genug, um nachweisbar zu sein) von einem Gramm entspricht einer Energie von 9*10^13 Joule. Dies ist auch die Energie, die man benötigen würde, um ein Gramm Masse auf etwa 87% der Lichtgeschwindigkeit zu beschleunigen, denn bei ungefähr dem 0,866-fachen der Geschwindigkeit des Lichtes hätte eine Masse sich verdoppelt.
In Wahrheit jedoch müsste man korrekterweise formulieren: Bei 87% der Lichtgeschwindigkeit setzt eine gegebene Masse ihrer weiteren Beschleunigung einen Trägheitswiderstand entgegen, der sich gegenüber dem Zustand der Ruhe verdoppelt hat. Oder kürzer: Die Trägheit hat sich unter den genannten Umständen bei gegebener Masse verdoppelt.
Die Energie also besitzt, da mit Masse behaftet, materiellen Charakter – weil dies stillschweigend bei der klassischen Massebestimmung, die sich richtigerweise jedoch nur auf die Trägheit (dynamische Eigenschaft) beziehen dürfte, vorausgesetzt wurde.
Die „Masse“-Änderung infolge von Energieänderung ist im Falle der Veränderung des Bewegungszustandes in der Realität eine Änderung der Trägheit.
Der sogenannte „Massen-Defekt“ erfährt eine Deutung, die aus der Gleichsetzung von Masse und Trägheit (bzw. Gewicht) folgt: Die fehlende Masse ist die Energie, die bei Kernverschmelzung auftritt.
Das Licht in seiner „Teilchen-Form“ Photon oder Lichtquant ist dann ein trägheits- aber nicht masselosen Teilchen.
MfG
W. Kinder
#129: NicoBaecker
„Ach herrje, wie konnten wir das 100 Jahre übersehen? “
Ich vermute einmal, sie haben das deshalb übersehen, weil Sie sich 100 Jahre lang mit Pseudophysik beschäftigt haben 🙂
Wetten, daß Sie auch an Heisenbergs Unsinnsrelation glauben?
#129: NicoBaecker
„Sicher. Was dahinter noch an Seltsamkeiten geboten würde, möchte ich auch lieber nicht wissen.“
Glaube ich Ihnen sofort. Was würden Sie wohl machen, wenn sie bereits an 4 Kräfte gewohnt sind und noch eine 5. Kraft dazukommt?
Ihre ganze Pseudophysik basiert auf „1000“ sogenanten adhoc „Axiomen“, damit Sie den ganzen Unsinn „erklären“ können.
Ich begnüge mich mit 3 echten Axiomen und einer einzigen Kraft.
#128: NicoBaecker
Ich brauche von Noack keine weitere Unterstützung. Diese eine Aussage genügt bereits für Sie und mir war dies sowieso klar. Wie Noack sonst wieder versucht in seinem längenverkürzten raumzeitdilatierten Ruderboot zurückzurudern ist nicht mein Problem und deshalb lese ich das auch nicht.
Die Newtonsche Mechanik ist nur durch die Axiome Newtons begründet und die werden in der Newtonphysik niemals verletzt. In der anerkannten seriösen Pseudophysik dagegen laufend.
“ Wie Sie sehen, bestaetigt das paper meine oben gemachten Aussagen.“
Das war Ihre Aussage:
„Die träge Masse (Ruhmasse + kinetische Energie/c^2) ist dagegen nicht invariant.“
Und sie kann alleine deshalb nicht richtig sein, weil es keine Geschwindigkeit gibt. Es gibt nur Relativgeschwindigkeiten und eine Masse kann gleichzeitig unendlich viele Relativgeschwindigkeiten haben. Aber sie kann nicht gleichzeitig unendlich viele relativgeschwindigkeitsabhängige „träge Massen“ haben.
Einstein konnte nur bis Zwei „denken“!
Also Herr Marie, #127
wie gesagt, ich habe kein Problem mit einer „Begriffstransformation“, solange sie physikalisch invariant ist. Die Frage, ob man den Begriff Ruhmasse nicht durch Masse an sich verwenden soll, ist eine unwesentliche Konventionssache, deswegen ändert sich die Physik nicht! Tatsächlich werden beide „Begriffssysteme“ bei Physikern verwendet und mag sein, das meines nach Noack zu den „veralteten“ gehört.
System A System B
Masse Ruhmasse
m m0
Masse+kinetische Energie/c2=Trägheit=Schwere Masse oder bewegte Masse= Trägheit=Schwere
m+T/c2 = m/wurzel((1-v/c)^2) m0+T/c2 = m = m0/wurzel((1-v/c)^2)
Vorteil von System B („veraltet“) ist, dass man für den Ausdruck der Trägheit m0/wurzel((1-v/c)^2) die Abkürzung m nehmen kann. Das fällt bei System A weg. Vorteil von System A ist, dass der Begriff Masse explizit mit seiner Invarianz verbunden wird. Dies ist den Teilchenphysikern sehr recht und wird von denen gerne verwendet, denn damit sind die Massen von Elementarteilchen Naturkonstanten.
Wie gesagt, wir können auch System A verwenden, ist mir wurscht.
„Was ist der Unterschied von Materie und seiner Eigenschaft Trägheit und Masse? Ich denke, dies kann kaum nachvollziehbar begründet werden.“
Was Materie kennzeichnet, ist eine interessante Frage. Die Antwort ist aber „relativ“ klar 😉
1. definiert wird Materie wie Energie durch den Zoo von Elementarteilchen (mit den grundlegenden Klassen Bosonen und Fermionen).
2. Verschiedene Elementarteilchen unterscheiden sich durch verschiedene „sets“ von Quantenzahlen, die alle lorentzinvariant sind und in allen Bezugssystemen gleiche Werte haben. Die Masse („veraltet„ Ruhmasse) ist dabei eine von mehreren Quantenzahlen, also nur ein Unterscheidungskriterium. So haben Positron und Elektron exakt (in Rahmen heutiger Meßgenauigkeit) gleiche Masse, sind aber nicht identische Elementarteilchen, da sie sich in der elektrischen Ladung unterscheiden. Im Prinzip weiß man, dass die Masse eine abgeleitete Quantenzahl ist, das heißt, sie ergibt sich aus den Wechselwirkungen, und die werden durch Quantenzahlen wie EM-Ladung, Color, etc. bestimmt.
3. Jetzt kommt’s aber: Wie stellt man fest, ob ein Teilchen ein Elementarteilchen ist? Denn Teilchen stehen fortlaufend mit anderen Teilchen in Wechselwirkung und bei dieser Wechselwirkung wird Energie ausgetauscht, was zur Bewegungsänderung und/oder Umwandlung führt.
4. Daher sind die Quantenzahlen von Elementarteilchen nur feststellbar im Limes der wechselwirkungsfreien Zustands, denn mit Wechselwirkung modifiziert die Wechselwirkungsenergie ja Summe aus Masse und Wechselwirkungsenergie (inkl. Bewegungsenergie)/c2, aber nur die läßt sich messen. Es ist schwierig, Teilchen „nackt“ (ohne Wechselwirkung) zu messen. In der moderne Physik umgeht man diese Problematik durch sog. Renormierung. Elementarteilchen existieren damit nur im Limes der Wechselwirkungsfreiheit. Mit Wechselwirkung „vermischen“ die Eigenschaften von Elementarteilchen entwickeln sich in neue Felder. So wird das Photon ab einer WW-Energie von ca. 100 GeV mit dem Z0-Boson vermischt (elektroschwache WW).
„Das Beschleunigerrohr sendet Photonen mit Lichtgeschwindigkeit aus, Wärmestrahlung. Und dies in alle Richtungen, auch in Flugrichtung. Photonen haben immer Masse, so wie es sich gehört.“
Aus Sicht des Protons ist die Wärmestrahlung des Rohres (im Laborsystem ruhend) dopplerverschoben anisotrop (Blauverschoben in Flugrichtung). Das stimmt. Mit Protonengeschwindigkeit gegen LG geht z gegen unendlich.
„Bei Annäherung des Protons an die LG wird die Differenzgeschwindigkeit zwischen Photon und Proton immer geringer und dadurch wächst die Wahrscheinlichkeit eines Photoneneinfangs immer mehr an.“
Falsch. Das sind die üblichen Irrtümer bei Laien und „Anti-Einsteins“. Im Ruhesystem des Protons kommt das Photon auch mit LG auf das Proton zu. Die LG ist ebenfalls eine Invariante.
Wenn ich Sie richtig verstehe, wollen Sie die Wechselwirkung zwischen Proton und Wärmestrahlung beschreiben. Sie müssen dabei auch berücksichtigen, dass ein beschleunigtes Proton immer zwangsweise mit Photonen wechselwirkt, denn eine beschleunigte Ladung strahlt ja schon klassisch EM-Wellen ab. Das beschleunigende Proton gibt auch noch Photonen ab (Synchrotronstrahlung). Außerdem sind da noch die Photonen der EM-Undulatoren und Ablenkmagneten, die das Proton im Rohr beschleunigen.
„Ein Photon ist elektrisch in der Nähe nicht mehr neutral, es ist ein rotierender el. Dipol aus zwei gegensätzlich geladenen Massen,“
Interessante These. Das ist neue Physik. So wird das Photon in der heutigen Physik nicht gesehen, denn nach heutigen Erkenntnissen hat es kein el. Dipol. Es hat einen Spin, ja. Klassisch kann man daher sagen, es rotiert.
Nur nochmal zur Ausdrucksweise: Ein Dipol kann elektrisch auch neutral sein, das Neutron z.B. hat ein elektrisches Dipolmoment, ist aber kein el. Monopol, sondern el. neutral.
„und kann durch andere el. Felder bewirkt werden. Erkennbar ist dies z.B. bei der optischen Lichtbrechung.“
Nee. Das Photon ist das Wechselwirkungsteilchen der elektromagnetischen Wechselwirkung. Es wechselwirkt jedoch in 1. Näherung nicht untereinander. Das geht nur über Wechselwirkungen mit Ladungen. Optische Lichtbrechung gibt es (in 1. Näherung) ja auch nicht im Vakuum. Bei Photonenenergien oberhalb der Paar-Erzeugungsschwelle von geladenen Teilchen schon, und dies führt zur Selbstwechselwirkung (Vakuumpolarisation).
„Daher kann ein Einfang gelingen und dann ist das Proton um die Photonenmasse „schwerer“ geworden, ohne daß sich seine Ladung geändert hat. Letztlich besteht dann ein relativgeschwindigkeitsabhängiges Gleichgewicht zwischen aufgesammelten und wieder abgesprengten Photonen. Das Proton frißt also im Fluge Photonen auf und wird dabei immer dicker, massereicher. „
Was für ein Unfug. Ein Proton hat in seinem Ruhesystem immer die gleiche Masse (veraltet Ruhmasse). Sie widersprechen sich mit dem, was Sie selber oben wortstark gefordert hatten!…?
Das Proton wird ja in Summe aller elmagn. Wechselwirkungen (mit Undulatoren, Ablenkmagneten, Wärmestrahlung, Synchrotronstrahlung, …) im Laborsystem beschleunigt.
Die Zunahme der Trägheit im Laborsystem (und NICHT im Ruhesystem des Protons) folgt aus der Invarianz und Isotropie der LG und nicht durchs „Photonenfressen“ – Mahlzeit.
„Was die Formel E=mc² betrifft, ist dies nur die halbe Wahrheit. Die ganze Wahrheit lautet E=2mc².“
Ach herrje, wie konnten wir das 100 Jahre übersehen?
Sagen Sie das mal Ihrer Referenz Prof. Noack.
Und erklären sie mir mal, warum ich dies nicht in meinem Praktikumsversuch in einem Faktor 2 zwischen den Messungen und (meiner gemeinen Lehrbuch-) Theorie gesehen haben. Sie wollten mir doch noch ohnehin meine Messergebnisse durch Ihre Theorie erklären. Wie soll das jetzt noch gehen, oder postulieren Sie nun 1=2?
„Aber über diesen Punkt will ich nicht weiter reden.“
Sicher. Was dahinter noch an Seltsamkeiten geboten würde, möchte ich auch lieber nicht wissen.
Lieber Herr Marie,
wenn Sie schon ein paper eines Physikers zitieren, sollten Sie es auch durchlesen. Wie Sie sehen, bestaetigt das paper meine oben gemachten Aussagen. Ob es auch Ihre Thesen unterstuetzt, mag ich micht zu beurteilen. Wenn Sie meinen, dass man die SRT falsch ist und die Newtonsche Mechanik richtig, so bekommen Sie durch Noack keine Unterstuetzung.
#124: W. Kinder
Auch sehr wert!
Allerdings muß man sich bei Ihrer Unterscheidung Masse-Materie-Trägheit-Eigenschaft die Frage nach den Unterscheindungsmöglichkeiten stellen. Was ist der Unterschied von Materie und seiner Eigenschaft Trägheit und Masse? Ich denke, dies kann kaum nachvollziehbar begründet werden.
Ich sehe Masse und Materie als ein und dasselbe an und in diesem anfassbaren „Ding“ steckt Energie in Form von Bewegung, insbesonders Rotationsenergie. Energie ist immer Bewegung von Masse/Materie und daher gibt es keine Energie ohne Massebeteiligung.
Die Massezunahme mit steigender RELATIVGESCHWINDIGKEIT zur Umgebung ist tatsächlich real und leicht physikalisch begründbar. Wenn ein Proton in einem Beschleuniger immer mehr an Masse gewinnt, je näher es an die Lichtgeschwindigkeit kommt, ist das völlig normal. Das Beschleunigerrohr sendet Photonen mit Lichtgeschwindigkeit aus, Wärmestrahlung. Und dies in alle Richtungen, auch in Flugrichtung. Photonen haben immer Masse, so wie es sich gehört. Bei Annäherung des Protons an die LG wird die Differenzgeschwindigkeit zwischen Photon und Proton immer geringer und dadurch wächst die Wahrscheinlichkeit eines Photoneneinfangs immer mehr an. Ein Photon ist elektrisch in der Nähe nicht mehr neutral, es ist ein rotierender el. Dipol aus zwei gegensätzlich geladenen Massen, und kann durch andere el. Felder bewirkt werden. Erkennbar ist dies z.B. bei der optischen Lichtbrechung. Daher kann ein Einfang gelingen und dann ist das Proton um die Photonenmasse „schwerer“ geworden, ohne daß sich seine Ladung geändert hat. Letztlich besteht dann ein relativgeschwindigkeitsabhängiges Gleichgewicht zwischen aufgesammelten und wieder abgesprengten Photonen. Das Proton frißt also im Fluge Photonen auf und wird dabei immer dicker, massereicher.
Was die Formel E=mc² betrifft, ist dies nur die halbe Wahrheit. Die ganze Wahrheit lautet E=2mc². Davon ist nur mc²/2 der lineare Energieanteil in Bezug auf die Quelle und der Rest steckt in absoluter Rotationsenergie und Feldenergie. Aber über diesen Punkt will ich nicht weiter reden.
Ich hoffe, Sie nun nicht allzusehr verwirrt zu haben 🙂
Lieber Herr Marie,
„Ich könnte Ihnen erklären, was Sie tatsächlich beobachtet haben, wie also der Effekt ganz real ohne Zauberei und Raumzeitknoten zustandekommt. “
Na dann mal los, wenn Sie glauben, hier Physikgeschichte schreiben zu wollen.
Aber bitte nicht mit Begriffsklaubereien wie Herr Kinder. Mir ist das wurscht, ob Sie den Massebegriff für die Ruhemasse revervieren wollen. Das ist auch gängig und habe ich oben schon geschrieben. Ich mache es nicht so, aber damit könnte ich mich anfreunden. Wenn Sie aber die Physik neu schreiben wollen und Experimente umdeuten wollen, ist dies etwas anderes, dafür bedarf es Argumente von Ihrer Seite.
@#123: NicoBaecker
„Die Physik ist da weiter. Aber für Ihre Zwecke können Sie wahrscheinlich an diesen falschen Vorstellungen kleben bleiben. “
Da muß ich Sie leider enttäuschen. Die Physik ist da schon weiter und hat den gesamten Schmarrn mit der „Ruhemasse“ als in den Leerbüchern leider mißverständlich dargestellten Sachverhalt bezeichnet.
„Ich habe mal im Studium einen Praktikumsversuch gemacht, in dem man sich von der Geschwindigkeitsabhängigkeit der Masse überzeugen konnte..“
Das glaube ich Ihnen. Aber Sie ließen sich bestenfalls „überzeugen“, haben aber selbst nicht nachgedacht!
Ich könnte Ihnen erklären, was Sie tatsächlich beobachtet haben, wie also der Effekt ganz real ohne Zauberei und Raumzeitknoten zustandekommt. Nur wird dies wiederum mit Ihrem Glauben an die Zauberei kollidieren.
Daher einfach nur ganz harte Worte:
„Inzwischen allerdings ist die Entwicklung der Physik ja nicht stehengeblieben, und die Frage nach der Bezugssystem-Abhangigkeit der Masse scheint aus der Sichtweise der modernen Physik ein fur alle Mal geklärt:
Masse ist eine fundamentale Eigenschaft von Materie und als solche naturgemäß eine Invariante; sie ist von der Wahl des Bezugssystems unabhangig. Der Begriff `Ruhemasse‘ ist daher überlüssig, wenn nicht irreführend; für den Begriff einer davon zu unterscheidenden `bewegten Masse‘ ist in der Physik kein sinnvoller Platz.“
http://www.itp.uni-bremen.de/~noack/masse.pdf
Is doch etwas, nicht wahr?
Und nicht nur aus diesem Grund hat die Masse in Energieumwandlungsformel E=mc² keinen Platz in der Physik. Nur in der Esoterik.
Sie schaffen es nämlich nicht einmal rechnerisch, diese Gleichsetzung, Masse = Energie, zeigen zu können:
kg = J ????
oder
kg = kgm²/s² ????
Niemals wird Ihnen das gelingen!
Hallo Werter Herr A.Marie (#122)
„sondern nur Masse und diese ist von allem unabhängig und immer invariant“
Sie haben Recht! Eine Geschwindigkeitsabhängigkeit der Masse gibt es nicht. Masse ist Masse.
Das was prinziell verwechselt oder ausgetauscht wird, ist Masse mit Trägheit.
Die Trägheit eines Körpers ist von seiner Masse und seiner Energie abhängig – unter anderem auch – von der Geschwindigkeit.
Energie ist eine Eigenschaft der Materie und die Trägheit eine Eigenschaft der Masse. Aus der Gleichsetzung von Masse und Trägheit folgt logisch die Gleichsetzung von Materie und Energie.
Die herkömmliche Deutung erscheint als nichts anderes als das Resultat einer überaus gedankenlosen Handhabung eines der vormals grundlegendsten Begriffe der Mechanik: den der Masse.
MfG
W. Kinder
Lieber Herr Marie, #122
„Es gibt keine „Ruhemasse ebensowenig wie eine „laterale Masse“ usw. sondern nur Masse und diese ist von allem unabhängig und immer invariant.“
Die Physik ist da weiter. Aber für Ihre Zwecke können Sie wahrscheinlich an diesen falschen Vorstellungen kleben bleiben. Die Ruhmasse ist die einzige invariante Masse. Die träge Masse (Ruhmasse + kinetische Energie/c^2) ist dagegen nicht invariant. Ich habe mal im Studium einen Praktikumsversuch gemacht, in dem man sich von der Geschwindigkeitsabhängigkeit der Masse überzeugen konnte und mit der Theorie („Newton gegen Einstein“) vergleichen konnte. Raten Sie mal, was rauskam…
@#121: NicoBaecker
„invarianz der ruhmasse, sie stimmen meinen ausfuehrungen oben also zu.“
Wenn Sie das so sagen, stimme ich dem natürlich nicht zu. Es gibt keine „Ruhemasse“ ebensowenig wie eine „laterale Masse“ usw. sondern nur Masse und diese ist von allem unabhängig und immer invariant.
Aus diesem Grund gibt es auch keine Umwandlung von Masse in Energie, wie dies im Allgemeinen gemäß E=mc² behauptet wird.
Bei der „Umwandlung“ wird nur die Masse in eine andere „Massenart“ zerlegt, etwa in Photonenmasse.
Aus 1 kg „normaler“ Masse wird dann 1 kg Photonenmasse.
Wenn man natürlich die Photonen als masselos behauptet, hat man ein Problem, weil man dann keine Physik mehr betreibt sondern Esoterik gemäß Einstein & Co.
lieber herr marie,
invarianz der ruhmasse, sie stimmen meinen ausfuehrungen oben also zu.
„Ich gebe als Langzeitspeicher Methan (Erdgas) die größeren Chanchen – wegen der vorhandenen Infrastruktur (Netz, Speicher, Brenner,Motoren,…). Und die Übertragungsverluste sind auch kein Problem.“
Methan ist der ideale Speicher. Da könnte ich mir gut vorstellen, dass man das CO2 direkt aus den Anlagen abscheidet. Es stellt sich nur die Frage, was günstiger ist. Methan importieren oder über verschiedene Schritte herstellen? Am Ende zählt auch wieder der Wirkungsgrad. Da müssten die EE 80% günstiger sein als die konventionellen Kraftwerke. Irgendwie müssen die Anlagen bezahlt werden und der Wirkungsgrad ausgeglichen werden.
„Naja, Müll ist nicht gerade ein einfacher Brennstoff (Brennwert, Stückigkeit, Schadstoffe) – außerdem – woher soll so viel heizwertreicher Müll kommen? Um viel Müll zu machen, braucht man auch jede Menge Rohstoffe – und jede Menge Energie!“
Den Fusionsreaktoren muss man nicht immer schweres Wasser zuführen. Man kann auch einen Teil durch anderweitige Elemente ersetzen. Das meinte ich mit Müll. Humorvoll wird das im Film „Zurück in die Zukunft 2“ gezeigt.
„Wieviel Freiheit wird denn vom GG garantiert? Gab es eine Volksabstimmung über die Bankenrettung? Über den Euro? Über die Wiedervereinigung? Über die Nutzung der Kernkraft? Über den NATO-Eintritt? Über die Wiederbewaffnung? Über jeden Haushalt? Über die Straßenverkehrsordnung????“
Das GG hat einige Einschränkungen. Würde man sich an die Einschränkungen halten, gäbe es keine Bankenrettung und andere Ereignisse. Wenn unsere Politiker einfach den Schaden vom deutschen Volke abwenden würde, kommt man auch Volksabstimmungen aus. Ebenso dürfte man sich auch nicht von hysterischen Menschen alle möglichen Lügen auftischen lassen. Z.B. die Kernkraft. Die Transmutation ist ein altbekanntes Verfahren, welches zu Beginn der Kernkraft erforscht wurde. Heutzutage ist es wieder Thema: http://tinyurl.com/2v3m5lq
Menschen, die nicht dem allgemeinen Wohl dienen wollen oder können, müssen Probleme schaffen, die es ohne diese Menschen nicht gäbe. Wozu Endlager, wenn man die Radioaktivität massiv absenken kann? Das Militär ist automatisch böse, weil es einem die Macht nehmen kann.
Es ist auf jeden Fall interessant, dass Sie verschiedene Entscheidungen auf eine Stufe stellen. Früher waren die Politiker der CDU noch darauf bedacht Schaden abzuwenden. Deswegen der Eintritt in die NATO, deswegen die Wiederbewaffnung, deswegen die StVO. Die Auswüchse der letzten 20 Jahre basieren auf dem Egoismus von linken Politkern, die nur geschadet haben. Man hätte damals einfach eine Entsozialisierung durchführen sollen, wie damals die Entnazifizierung. Man hätte so Billiarden sparen können und würde nicht für imaginäre Probleme, wie Finanzkrise, Endlagerung und Klimaschutz zahlen müssen.
„Ja, ich bin auch kein Fan davon – aber was wird einem noch alles aufgedrückt? Hatte jemand vor dreißig Jahren die Wahl, ob er Atomstrom will? Und ob er Subventionen bezahlen will? Für Atomforschung und für Steinkohlenförderung? Es gab nicht mal asl Verbraucher die Wahl. Heute gibt es zwar die Wahl über die Herkunft des Stoms – aber die ist leider nicht ehrlich – und schützt nicht davor auch andere Subventionen mitzuzahlen (sei es nun der Grünstrom oder die Stillegung der KKW im Osten oder die Suche nach einem „Endlager“).“
Solange die Subventionen neue Jobs schaffen und keine bestehenden gefährden, kann man es vertreten. Bei den EE wurde schon länger nachgewiesen, dass die mehr Jobs kosten als schaffen.
„Naja, 1€ ist nicht mehr aktuell, allerdings muss ich zugeben die Subventionen haben die Preise zunächst deutlich schneller fallen lassen als ohne Subventionen – aber jetzt sind
schon Überkapazitäten bei nicht konkurrenzfähigen Produkten entstanden, die die Weiterentwicklung der EE wieder behindern…“
Wenn der Wind mal weht und alle WKA laufen, ist der Strom natürlich günstig. Aber er ist und bleibt Zufallsstrom. Den will keiner haben. Die Menschen wollen den Fernseher anmachen, wenn sie gerade Luft darauf haben. Die Energiespeicher machen das ganze auch nicht günstiger. Die speicherlosen konventionellen Kraftwerke liefern einen Standard, an den man sich gewöhnt hat. Von diesem Standard will man nicht weg. Wozu auch?
„Naja, bei Photovoltaik gehen die Subventionen in vielen Ländern erst los – allerdings viel geringer als hierzulande.“
Andere Länder haben die Subventionen schon längst wieder gestrichen.
Sehr geehrter Herr Müller,
#116
„Das sind alles Kurzzeitspeicher. Die einzige Speichermöglichkeit, die langfristiger ist, stellt die Speicherung von Wasserstoff dar. Aber da darf die „Energiedichte“ nicht zu hoch sein.“
Ich gebe als Langzeitspeicher Methan (Erdgas) die größeren Chanchen – wegen der vorhandenen Infrastruktur (Netz, Speicher, Brenner,Motoren,…). Und die Übertragungsverluste sind auch kein Problem.
Zu den anderen Energieträgern stimme ich Ihnen eingeschränkt zu – kommt drauf an, wie sich Weltbevölkerung und Pro-Kopf-Verbrauch entwickeln.
Aber
„Gegen den einfachen Brennstoff Müll kommt keine andere Energiequelle an. EE werden meiner Meinung nach nie konkurrenzfähig sein.“
Naja, Müll ist nicht gerade ein einfacher Brennstoff (Brennwert, Stückigkeit, Schadstoffe) – außerdem – woher soll so viel heizwertreicher Müll kommen? Um viel Müll zu machen, braucht man auch jede Menge Rohstoffe – und jede Menge Energie!
„Faschismus beginnt für mich da, wo die demokratische Freiheit aufhört. Ich kann nicht wählen, ob ich die EE mitsubventionieren will.
Genauso wenig kann ich wählen ab dem nächsten Jahr weiterhin keine GEZ zu zahlen.“
Naja, bei mir ist das noch kein physischer Terror.
Aber:
„Meine vom Grundgesetz garantierte Freiheit wird von unserer Regierung mit Füssen getreten und es wird einem alles aufgezwungen.
Ja, das stimmt natürlich!
Wieviel Freiheit wird denn vom GG garantiert? Gab es eine Volksabstimmung über die Bankenrettung? Über den Euro? Über die Wiedervereinigung? Über die Nutzung der Kernkraft? Über den NATO-Eintritt? Über die Wiederbewaffnung? Über jeden Haushalt? Über die Straßenverkehrsordnung????
„Anstatt einfach deutlich zu sagen, dass die EE teuer sind und auf freiwilliger Basis subventioniert werden müssen wird das einfach jedem aufgedrückt.“
Ja, ich bin auch kein Fan davon – aber was wird einem noch alles aufgedrückt? Hatte jemand vor dreißig Jahren die Wahl, ob er Atomstrom will? Und ob er Subventionen bezahlen will? Für Atomforschung und für Steinkohlenförderung? Es gab nicht mal asl Verbraucher die Wahl. Heute gibt es zwar die Wahl über die Herkunft des Stoms – aber die ist leider nicht ehrlich – und schützt nicht davor auch andere Subventionen mitzuzahlen (sei es nun der Grünstrom oder die Stillegung der KKW im Osten oder die Suche nach einem „Endlager“).
„Streiche ich die Subventionierung für die EE, wird keiner die haben wollen. Die müssten mit einem Preis von mehr als 1€/kWh verkaufen. Wer soll da noch den Strom abnehmen. Keiner zahlt dann freiwillig diesen Preis, wenn man den Strom auch für 0,2€/kWh haben könnte.“
Naja, 1€ ist nicht mehr aktuell, allerdings muss ich zugeben die Subventionen haben die Preise zunächst deutlich schneller fallen lassen als ohne Subventionen – aber jetzt sind
schon Überkapazitäten bei nicht konkurrenzfähigen Produkten entstanden, die die Weiterentwicklung der EE wieder behindern…
„Werfen Sie einfach einen Blick in die USA oder Schottland. Da wurden die Subventionen gestrichen und die WKA verrotten, weil keiner deren Strom haben will. Das ist Marktwirtschaft!“
Naja, bei Photovoltaik gehen die Subventionen in vielen Ländern erst los – allerdings viel geringer als hierzulande.
Viele Grüße
Michael Klink
#117: NocoBaecker
————
„Oder ändert sich die Gesamtmasse eines Frühstückseis, wenn ich es halbiere?“
Wenn Sie das negieren, haben Sie die Kernspaltung nicht verstanden.
—————-
Ich negiere keineswegs, daß die Gesamtmasse beim Frühstücksei ebenso wie die Gesamtmasse bei der Kernspaltung immer konstant bleibt.
Wenn Sie dagegen etwas anderes behaupten, haben Sie weder die Kernspaltung noch die Physik verstanden.
Herr Marie,
„Oder ändert sich die Gesamtmasse eines Frühstückseis, wenn ich es halbiere?“
Wenn Sie das negieren, haben Sie die Kernspaltung nicht verstanden.
„ Kein Problem: Wenn ich mir die Grundgebühr von 16€/Monat (zwei Wohnungen) spare und ohnehin 0,25 €/kWh zahlen muss, rechnet es sich vielleicht (so oft waschen wir ja nun auch nicht) – und Sie merken schon, wenn ich ein echter Öko wäre, würde ich in den Waschsalon gehen und nicht Waschmaschinen horten…!
Aber ehrlich – das kommt ganz auf den speziellen Fall an.
Vor allem meinte ich nicht nur Kleinverbraucher, man kann auch gespeicherte EE in Motoren, Heizkesseln, Gasturbinen oder Brennstoffzellen nutzen – je nachdem, was sinnvoll ist.“
Das sind alles Kurzzeitspeicher. Die einzige Speichermöglichkeit, die langfristiger ist, stellt die Speicherung von Wasserstoff dar. Aber da darf die „Energiedichte“ nicht zu hoch sein.
„ Den wird es in absehbarer Zeit nicht geben. Ist dafür auch nicht nötig. Deswegen schrieb ich auch etwas von Diversifizierung – verschiedene Speicher für verschiedene Zwecke. „
Und wenn die EE 30% unseres Strombedarfes decken sollen, muss es einen Puffer geben. Ansonsten kann ich gleich das Schattenkraftwerk als richtiges Kraftwerk arbeiten lassen. Da spare ich mir den ganzen unnötigen Kram.
„ Ich sehe vor allem das, was technisch machbar ist und sein wird – die Frage ist vielleicht eher, ob die Preisentwicklung richtig prognostiziert ist.
Ich habe auch nur von einer längerfristigen Tendenz gesprochen, und niemandem nichts versprochen. Es ist eine Meinung, meine – mehr nicht.“
Technisch ist vieles machbar und die Zukunft ist ungewiss. Gewiss ist nur, dass die fossilen Brennstoffe uns noch sehr lange erhalten bleiben und die Fördermethoden immer weiterentwickelt werden und dadurch „günstig“ bleiben. Irgendwann wird die Förderung auch kompliziert, aber bis dahin vergehen sehr viele Jahrzehnte. Sobald die ersten Fusionsreaktoren stehen, ist es auch aus mit den EE. Gegen den einfachen Brennstoff Müll kommt keine andere Energiequelle an. EE werden meiner Meinung nach nie konkurrenzfähig sein.
„Ich dachte, die frieren immer, wenn es kalt ist – jedenfalls war es in den letzten dreißig Jahren so…
Gerade die Franzosen sollten sich mal an den Dänen ein Beispiel nehmen, was rationelle Energieanwendung ist. Gegen F ist ja D und JPN – vielleicht gar USA(?) – ja fast schon vorbildlich (ich meine nicht die EE, sondern den Unsinn, mit KKW-Strom zu heizen und die Wärme in Flüsse und die Luft zu blasen).“
Die Franzosen heizen mit der günstigen Energie. Das kann ihnen keiner verübeln.
„ Was ist für Sie „faschistisch“? Natürlich bin ich nicht der Meinung, dass jemandem das aufgezwungen werden soll – aber auch nichts anderes…!!!“
Faschismus beginnt für mich da, wo die demokratische Freiheit aufhört. Ich kann nicht wählen, ob ich die EE mitsubventionieren will. Genauso wenig kann ich wählen ab dem nächsten Jahr weiterhin keine GEZ zu zahlen. Meine vom Grundgesetz garantierte Freiheit wird von unserer Regierung mit Füssen getreten und es wird einem alles aufgezwungen. Anstatt einfach deutlich zu sagen, dass die EE teuer sind und auf freiwilliger Basis subventioniert werden müssen wird das einfach jedem aufgedrückt. Es ist keine Steuer, es ist eine Pflichtabgabe.
„Nein, warum? Ich meine eine Marktwirtschaft, in der die EE marktwirtschaftlich langfristig eine größere Rolle spielen werden – neben anderen Energieträgern, die zweifellos weiter eine Berechtigung haben. Irgendwie lesen Sie immer noch etwas anderes heraus, als ich schreiben wollte – kann das sein?“
Sie wollen oder können das Problem einfach nicht verstehen und dementsprechend weiterdenken. Streiche ich die Subventionierung für die EE, wird keiner die haben wollen. Die müssten mit einem Preis von mehr als 1€/kWh verkaufen. Wer soll da noch den Strom abnehmen. Keiner zahlt dann freiwillig diesen Preis, wenn man den Strom auch für 0,2€/kWh haben könnte. Die EE funktionieren nur regional, aber nicht überregional. In der Wüste ist dieser Strom deutlich günstiger, da man keine Generatoren mit Treibstoff zu der Stelle transportieren muss. Aber in einem Land wie Deutschland wird das nie funktionieren. Die Marktwirtschaft wird die EE schneller vernichten als Sie bis eins zählen können. Beim grünen Faschismus läuft es auf Strommarken hinaus, weil kaum einer die Strompreise bezahlen kann, sobald die EE zu 100%(davon träumt unsere Regierung aktuell) Deutschland versorgen sollen. Unter dem Faschismus kann man den Menschen sehr gut diktieren, was Gut und Böse ist. Und wenn man die Strommarken hat, so kann man den bösen Menschen diese einfach streichen und entsprechend erziehen.
Werfen Sie einfach einen Blick in die USA oder Schottland. Da wurden die Subventionen gestrichen und die WKA verrotten, weil keiner deren Strom haben will. Das ist Marktwirtschaft!
Sehr geehrter Herr Müller,
#113
„Darf Ihre Frau die Waschmaschine nur anmachen, wenn ausreichend Wind und Sonne vorhanden sind, oder was meinen Sie mit „on site“? “
Also, sowohl die Waschmaschine meiner Frau, als auch meine hängen am Netz – vorläufig jedenfalls. Ich habe nicht gesagt, dass das jetzt, überall und für alle gilt, sondern eine Tendenz werden kann.
„Und was passiert, wenn die Waschmaschine noch nicht fertig ist und Sonne und Wind aussetzen? Springt der teure Akku ein, der die kWh auf 0,5€ erhöht?“
Kein Problem: Wenn ich mir die Grundgebühr von 16€/Monat (zwei Wohnungen) spare und ohnehin 0,25 €/kWh zahlen muss, rechnet es sich vielleicht (so oft waschen wir ja nun auch nicht) – und Sie merken schon, wenn ich ein echter Öko wäre, würde ich in den Waschsalon gehen und nicht Waschmaschinen horten…!
Aber ehrlich – das kommt ganz auf den speziellen Fall an.
Vor allem meinte ich nicht nur Kleinverbraucher, man kann auch gespeicherte EE in Motoren, Heizkesseln, Gasturbinen oder Brennstoffzellen nutzen – je nachdem, was sinnvoll ist.
„Zeigen Sie mir einen Speicher, der folgende Eigenschaften hat:
– Sehr hohe Speicherdichte
– Verlust von nur 5% in einem Monat der Speicherkapazität
– Günstig
– Klein“
Den wird es in absehbarer Zeit nicht geben. Ist dafür auch nicht nötig. Deswegen schrieb ich auch etwas von Diversifizierung – verschiedene Speicher für verschiedene Zwecke.
„Ich stimme mit Ihnen nicht überein. Ihre Idee hat was von einer Ideologie. Sie versprechen das Blaue vom Himmel ohne sich der technischen Seite bewusst zu sein.“
Ich sehe vor allem das, was technisch machbar ist und sein wird – die Frage ist vielleicht eher, ob die Preisentwicklung richtig prognostiziert ist.
Ich habe auch nur von einer längerfristigen Tendenz gesprochen, und niemandem nichts versprochen. Es ist eine Meinung, meine – mehr nicht.
„Die Franzosen sind Ihnen auf jeden Fall dankbar, dass sie wegen Ihnen und Ihren Ideologiegenossen diesen Winter frieren durften.“
Ich dachte, die frieren immer, wenn es kalt ist – jedenfalls war es in den letzten dreißig Jahren so…
Gerade die Franzosen sollten sich mal an den Dänen ein Beispiel nehmen, was rationelle Energieanwendung ist. Gegen F ist ja D und JPN – vielleicht gar USA(?) – ja fast schon vorbildlich (ich meine nicht die EE, sondern den Unsinn, mit KKW-Strom zu heizen und die Wärme in Flüsse und die Luft zu blasen).
„Durch die Energiepolitik schwingt sich Deutschland unter einer faschistischen Politik wieder auf und folgt dem alten Leitspruch „Am deutschen Wesen soll die Welt genesen“.“
Was ist für Sie „faschistisch“? Natürlich bin ich nicht der Meinung, dass jemandem das aufgezwungen werden soll – aber auch nichts anderes…!!!
„Das ist das gleiche wie der Kommunismus, nur in grün. Am Ende ist jeder gleich arm, gleich dumm und gleich stromlos.“
Nein, warum? Ich meine eine Marktwirtschaft, in der die EE marktwirtschaftlich langfristig eine größere Rolle spielen werden – neben anderen Energieträgern, die zweifellos weiter eine Berechtigung haben. Irgendwie lesen Sie immer noch etwas anderes heraus, als ich schreiben wollte – kann das sein?
Viele Grüße
Michael Klink
@J.Müller #113
Sie haben voll ins Schwarze getroffen. 100% Zustimmung!
@#111: Michael Klink:
Darf Ihre Frau die Waschmaschine nur anmachen, wenn ausreichend Wind und Sonne vorhanden sind, oder was meinen Sie mit „on site“? Und was passiert, wenn die Waschmaschine noch nicht fertig ist und Sonne und Wind aussetzen? Springt der teure Akku ein, der die kWh auf 0,5€ erhöht?
Zeigen Sie mir einen Speicher, der folgende Eigenschaften hat:
– Sehr hohe Speicherdichte
– Verlust von nur 5% in einem Monat der Speicherkapazität
– Günstig
– Klein
Damit die Technik so funktionieren kann, wie Sie es beschreiben, müssten Wind und Sonne sinusförmig Energie erzeugen können. Dies aber nicht der Fall und der gemeine Regelungstechniker wird fluchen, da der Störanteil immer eine Unbekannte bleibt und nicht ohne weiteres kompensiert werden kann.
Ich stimme mit Ihnen nicht überein. Ihre Idee hat was von einer Ideologie. Sie versprechen das Blaue vom Himmel ohne sich der technischen Seite bewusst zu sein. Das Stromnetz ist instabil wie nie zuvor. Ich weiß nicht, wie oft Europa diesen Winter an Blackouts vorbeischrammte, aber es war definitiv zu oft. Die Franzosen sind Ihnen auf jeden Fall dankbar, dass sie wegen Ihnen und Ihren Ideologiegenossen diesen Winter frieren durften. Durch die Energiepolitik schwingt sich Deutschland unter einer faschistischen Politik wieder auf und folgt dem alten Leitspruch „Am deutschen Wesen soll die Welt genesen“. Mich kotzt es einfach nur an, dass die Politik den Wirtschaftsstandort Deutschland massiv abwrackt durch solch eine Ideologie. Das ist das gleiche wie der Kommunismus, nur in grün. Am Ende ist jeder gleich arm, gleich dumm und gleich stromlos.
@ M. Klink #111
„Ich wollte nicht so verstanden werden, dass Just-In-Time-Wandlung etwas Neues, noch etwas ausschließliches ist – sondern nur, dass diese -nicht nur zeitlich, auch örtlich (on site) – noch attraktiver und damit dominierend werden kann (längerfristig).“
Se vertellt Dünnshit, wie man hier an der Küste schnackt.
„UND – dies wirkt auf die Last zurück – durch zeitlich variablere Preise (und Zähler) in Kombination mit dezentralen Speichern (Kostendegression in Herstellung und Recycling auch hier).“
Das gehört auch in diese Kategorie.
„Ein dritter – heute noch unwesentlicher – ist die direkte Versorgung von elektronischen Geräten geringer Leistungsaufnahme direkt über kleinste, speichergepufferte Niederspannungs-Gleichstromnetze.“
Sie sollten nochmals die Schulbank drücken. Ist ja grausam, was bei Ihnen vom Physikunterricht im Gedächtnis hängen geblieben ist.
Sehr geehrte Herren,
#100,103,107
Ich habe nicht bestritten, dass es Grundlast (und ich meine jetzt wirklich Last, nicht Grunderzeugung) gibt – sondern nur, dass ein EE-Kraftwerk konstante Leistung liefern muss.
(EE hier nicht als E-lektro E-nergie, sondern bitte als E-rneuerbare E-nergie lesen – das ist zwar missverständlich, aber nicht meine Erfindung.)
Dass die Last eine Zeitfunktion ist, und sich die Kraftwerke dem anpassen, ist natürlich ein alter Hut.
Deshalb werden ja verschiedene Erzeugungs-Technologien miteinander zeitlich und räumlich kombiniert (z. B. Steinkohle-Kondensationskraftwerk und Gasturbinen).
Ich wollte nicht so verstanden werden, dass Just-In-Time-Wandlung etwas Neues, noch etwas ausschließliches ist – sondern nur, dass diese -nicht nur zeitlich, auch örtlich (on site) – noch attraktiver und damit dominierend werden kann (längerfristig).
Genauso klar ist es, dass z.B. Fahrzeuge, die nicht auf dem Schwungradprinzip beruhen, just in time Energie wandeln (müssen).
Mit zunehmender zeitlicher Schwankung – nicht nur der Last, sondern auch der Erzeugung aus EE wird sich mit deren -meiner umstrittenen Meinung nach sinkenden relativen Kosten (relativ zu den konventionellen)- auch die Kapazität und Positionierung von Speichern verändern.
UND – dies wirkt auf die Last zurück – durch zeitlich variablere Preise (und Zähler) in Kombination mit dezentralen Speichern (Kostendegression in Herstellung und Recycling auch hier). Dies könnte natörlich wieder zu einer Quasi-Grundlast duch Kompensation führen – aber nur dann, wenn der Preis eine Anpassung der Lastschwankungen an eine billigen konstante Erzeugung anpasst. Wenn die konstante Erzeugung nicht billiger ist, sondern die Spitzen einer schwankenden oder diskontinuierlichen Erzeugung besonders billig sind, wird sich die Abnahme dieser nicht konstanten Erzeugung – also ohne Grund“last“ – anpassen.
Mir ging es um die Tendenz, die (wesentlich, aber nicht nur) mit der Nutzung von EE zusammenhängt, dass Last und Produktion zunehmend auseinanderfallen, die Grundlast somit abnehmen könnte.
Wenn es jetzt schon, in unserem komfortablen nahezu ausfallfreien Stromnetz erforderlich ist, diverse Speicher (von mechanischen Kurzzeitspreichern und Kondensatoren über diverse Batteriespeicher – z.B. USV – bis zum Notstromaggregat und Pumpspeicherwerk) zu betreiben, so wird diese Tendenz sich weiter verstärken und diversifizieren. Der zweite – auch nicht neue Grund sind die Verluste in Wechselstromnetzen. Ein dritter – heute noch unwesentlicher – ist die direkte Versorgung von elektronischen Geräten geringer Leistungsaufnahme direkt über kleinste, speichergepufferte Niederspannungs-Gleichstromnetze.
Wenn der Anteil der konstant zu erzeugenden und abgenommenen Menge abnimmt, nimmt der relative Bedarf an „Grundlastkraftwerken“ ab. Wenn der Gesamtenergiebedarf -erwartungsgemäß- nicht oder nur geringfügig steigt, nimmt dieser Bedarf an Grundlastleistung auch absolut ab.
Wenn sie da mit mir übereinstimmen sollten, würde es mich natürlich auch freuen ;-).
Viele Grüße
Michael Klink
Sehr geehrter Herr Hofmann,
#108
„Was wollen Sie mir sagen?!
Bitte in 2-3 kurzen Sätzen auf den Punkt bringen!“
Es geht sogar in einem Satz :-):
In einer Parteiendemokratie wird es immer zu Enttäuschungen kommen, denn – je größer die Partei – je unterschiedlicher die handelnden Personen und ihre Ansichten.“
Viele Grüße
Michael Klink
„Was E = mc² besagt ist nichts weiter als dass Materie und Energie austauschbar sind. Es gibt eine Verbindung zwischen den beiden. Energie kann sich in Materie verwandeln und Materie in Energie. Es sind zwei verschiedene Aspekte der gleichen Sache.“
Nichts weiter? Es ist der größte Schwachsinn, was zu E=mc² interpretiert wird!
Masse kann nicht in Energie umgewandelt werden. Energie ist eine Eigenschaft (Geschwindigkeit) von Masse und ohne Masse gibt es auch keine Energie.
Unglaublich, welcher Blödsinn hier behauptet wird.
Die Gesamtmasse ist invariant.
Oder ändert sich die Gesamtmasse eines Frühstückseis, wenn ich es halbiere?
Eine Energie-Massenumwandlung gelingt nicht einmal rechnerisch!
#60: F. Naumann sagt am Donnerstag, 16.02.2012, 12:56:
„…werden sie schnell sehen, dass Windenergie onshore mittlerweile die billigste Form der Energieerzeugung ist.“
Das ist ja eine gute Nachricht, Herr Naumann. Dann ist allerdings nicht zu verstehen, warum dies überhaupt noch mit einem einzigen Cent subventioniert wird. Dann sollte man doch für alle ab jetzt errichteten Anlagen die Einspeisevergütung auf Null senken, verbilligte öffentliche Kredite abschaffen und den Anschluss ans Stromnetz in Rechnung stellen. Durch den Verkauf des Stromes an der Strombörse können die Windmüller das locker finanzieren, wenn sie tatsächlich so billig sind.
Oder?
Gruß,
Herrmann Hurz
Wenn der Kommentar 99 von Herrn Klink zur „just-in-time-Produktion“ von Energie wirklich ernst gemeint ist, zeigt das ziemlich klar, wie wenig Verständnis Herr Klink von unserer modernen Industriegesellschaft und von wirtschaftlichen Vorgängen hat.
Herr Heinzow hat es ja schon gesagt: die just-in-time-Produktion ist Realität. So melden z.B. Gasversorger täglich den voraussichtlichen Bedarf an Gas an die Netzbetreiber für den kommenden Tag. Diese steuern daraufhin Menge, Druck und was es sonst noch zu steuern gibt im Netz.
Jeden Tag können die prognostizierten Lastprofile im 5 min-Takt mit dem realen Gasverbrauch abgestimmt werden und dann wird die Versorgung im Netz angepasst.
Herr Klink, denken Sie etwa, dass die Versorger sinnlos Energie produzieren in der Hoffnung, irgendeiner wird die Energie schon abnehmen?
Energie ist ein Kostenfaktor für alle Unternehmen, mit denen so sparsam wie möglich umgegangen wird, schon allein um Geld zu sparen. Also Sie kommen mit Ihrer tollen Idee ein wenig zu spät! Und von der Realität sind Sie damit wohl auch etwas entfernt.
Aber das ist das Grundproblem bei vielen hier. Sie haben die irrige Auffassung, unsere Gesellschaft und vor allem unsere Industrie verschleudert sinnlos Energie und deswegen sollte Energie ruhig teurer sein. Es gibt natürlich Verschwendung, vor allem im privaten Bereich, aber was die Industrie angeht, ist Verschwendung eher die Ausnahme und sparsamer Umgang die Regel.
@Michael Klinik #98
Was wollen Sie mir sagen?!
Bitte in 2-3 kurzen Sätzen auf den Punkt bringen!
@#101: MEstermeier:
Wie soll ich mir die ganzen Namen der Solarfirmen merken, die Woche für Woche Insolvenz anmelden?!