BACK TO EARTH: Stand des hemisphärischen S-B-Modells als Wegweiser durch meine EIKE-Artikel - EIKE - Europäisches Institut für Klima & Energie

von Uli Weber

Noch in seinem geowissenschaftlich geprägten Buch „Klimahysterie…“ (Farbe / S-W) hatte der Autor den vorgeblich durch eine „atmosphärische Gegenstrahlung“ angetriebenen „natürlichen atmosphärischen Treibhauseffekt“ als Stand der Klimawissenschaft beschrieben. Und in seinem letzten EIKE-Artikel hatte er eine anthropogene Nutzung dieser „atmosphärischen Gegenstrahlung“ einmal über den 2. Hauptsatz der Thermodynamik hinweg zu Ende gedacht. Sein hemisphärisches Stefan-Boltzmann-Modell für die Temperaturgenese auf unserer Erde ist zwar ebenfalls längst zu Ende gedacht, aber auf mehr als 40 EIKE-Artikeln verteilt. Daher dürfte inzwischen selbst ein gutwilliger Kommentator den Überblick verloren haben, und es ist höchste Zeit, den aktuellen Stand dieses Hemisphärenmodells einmal zusammenfassend darzustellen.

Der hemisphärische Stefan-Boltzmann-Ansatz geht auf eine Veröffentlichung von 2016 in den „Roten Blättern“ der Deutschen Geophysikalischen Gesellschaft zurück und beschreibt die Temperaturgenese auf unserer realen Erde ohne einen „natürlichen atmosphärischen Treibhauseffekt“. Ein populärwissenschaftlicher Artikel darüber erschien Anfang 2017 auf Tichys Einblick und wurde von EIKE übernommen. Seither konnte dieses Hemisphärenmodell in mehr als 40 EIKE-Artikeln an diversen Klimaphänomenen erprobt und kontinuierlich weiterentwickelt werden, wofür ich mich bei der EIKE-Redaktion, insbesondere bei Herrn Dipl.-Ing. Michael Limburg, ganz herzlich bedanke.

Die nachfolgende Zusammenfassung des hemisphärischen S-B-Modells wird diesmal nicht mit physikalischen Beweisen oder im Abgleich mit dem konkurrierenden THE-Paradigma erfolgen. Vielmehr wird mit Zahlen in eckigen Klammern jeweils auf den/die im Anhang verlinkten weiterführenden EIKE-Artikel mit der entsprechenden Beweisführung hingewiesen. Für den interessierten Laien wird hier zur Problemübersicht auf meine EIKE-Trilogie „Eine Analyse der Thesen/Antithesen für einen ‚natürlichen atmosphärischen Treibhauseffekt‘“ mit Teil 1 „Gegenüberstellung der Thesen/Antithesen“ [1], Teil 2 „Diskussion der Thesen/Antithesen“ [2] und Teil 3 „Erkenntnisse zu den Thesen/Antithesen und das Ergebnis dieser Analyse“ [3] hingewiesen. Auch das Stefan-Boltzmann-Gesetz wird hier nicht erneut beschrieben [4], genauso wenig wie der physikalisch entscheidende Unterschied zwischen Leistung und Energie [5]. Und auch der Abgleich des hemisphärischen Stefan-Boltzmann-Modells mit echten Temperaturmessungen vom Mond [6] und [7] als real existierendes Modell für eine Erde ohne Atmosphäre ist nicht Teil dieser Zusammenfassung. Nachfolgend sind alle entsprechenden EIKE-Artikel mit einer ausführlichen Beweisführung unter den jeweils in eckigen Klammern angegebenen Zahlen im Anhang verlinkt.

Das hemisphärische Stefan-Boltzmann-Modell betrachtet das System Erde vom makroskopischen Standpunkt der Klimadefinition als Durchschnitt von 30 Jahren Wetter. Daraus versucht der Autor dann die primären Wirkmechanismen der terrestrischen Temperaturgenese auf unserer realen Erde qualitativ abzuleiten. Im Prinzip handelt es sich dabei also um ein hybrides Modell, das auf Berechnungen (Tagseite) und terrestrischen Wärmespeichern (Nachtseite) aufbaut. Die Berechnungen für die Tagseite beruhen auf dem S-B-Temperaturäquivalent aus einer Inversion der hemisphärisch eingestrahlten spezifischen Strahlungsleistung der Sonne. Der Beitrag der terrestrischen Wärmespeicher Atmosphäre und Ozeane, die mit ihrem Energieinhalt auf die individuellen Ortslagen der Nachthälfte einwirken, lassen sich über die Umgebungsgleichung des Stefan-Boltzmann-Gesetzes herleiten. Die Ausgangssituation für die terrestrische Temperaturgenese ist geometrisch eigentlich ganz einfach und zwingend, aber offenbar steckt schon hier der Teufel im Detail:

Abbildung 1: Die geometrischen Flächenverhältnisse bei der terrestrischen Temperaturgenese

Einstrahlung: Hochfrequente (HF) Sonneneinstrahlung, die auf einer Kreisfläche mit dem Erdradius (@PiR²) auf die Erde fällt, erwärmt die Materie von deren Tagseite (@2PiR).

Abstrahlung: Die erwärmte Materie strahlt Infrarot(IR)-Strahlung über die gesamte Erdoberfläche (@4PiR²) ab.

Wir betrachten jetzt einmal die häufig als Indikator für globale Klimaveränderungen verwendete sogenannte „Near Surface Temperature“ (NST) in Form der gemessenen und global gemittelten Durchschnittstemperatur. Diese NST bleibt trotz Tag und Nacht, Jahreszeiten und deren gegensätzlichen Verläufen auf Nord- und Südhalbkugel über aufeinander folgende Jahresmittel relativ stabil. Daraus ist wiederum abzuleiten, dass sich das Klimasystem unserer Erde in einem gesättigt eingeschwungenen Zustand befindet, in dem die eingestrahlten und abgestrahlten Energiemengen sich im langjährigen Mittel ausgleichen. Um diese quasi-stabile Gleichgewichtssituation zu verstehen, nähern wir uns unserer Erde jetzt einmal aus dem Blickwinkel eines 1:1-Eisballmodells [8]:

Wir verbringen also zu einem Zeitpunkt “0” ein Duplikat unserer Erde aus einem Dunkelkammer-Weltraumlabor an den aktuellen Standort unserer Erde. Dieses Duplikat soll eine voll funktionsfähige Erde in einem „tiefgefrorenen“ Zustand mit einer Eigentemperatur von minus 240 Grad Celsius aus einem eigenen terrestrischen Wärmefluss von 60 Milliwatt darstellen. Vom Zeitpunkt “0” an ist unsere neue Schneeball-Erde nun der Sonnenstrahlung mit der Solarkonstanten So=1.367 W/m² ausgesetzt. Die Sonneneinstrahlung trifft grundsätzlich nur die Tagseite der Erde. Die Polkappen sind etwas schwerer zu beschreiben, weil Polartag und Polarnacht jeweils ein halbes Jahr dauern [9]. Wir beschränken uns daher bei der folgenden Betrachtung auf die Äquinoktien, also die Tag und Nacht Gleiche am Frühlings- und Herbstpunkt, wenn die Sonne direkt über dem Äquator steht [10]:

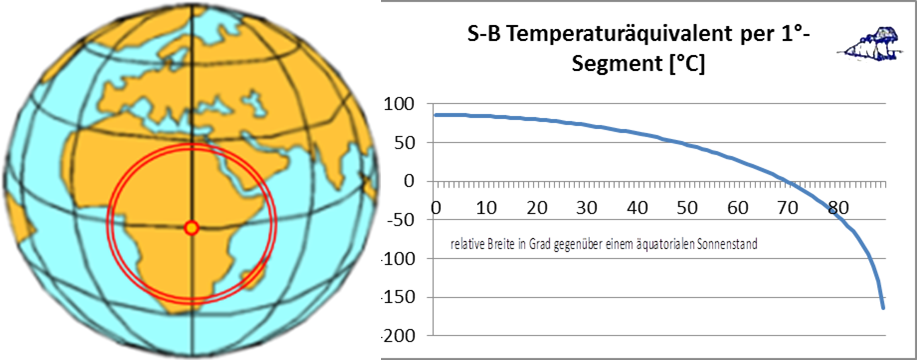
Abbildung 2: Eine Summierung der vom mittäglichen Zenitwinkel abhängigen maximalen solaren Einstrahlung über 1°-Kugelsegmente und deren S-B-Temperaturäquivalent im Äquinoktium

Es muss an dieser Stelle ausdrücklich hervorgehoben werden, dass hier die Berechnung des S-B-Temperaturäquivalentes mit einer Anfangstemperatur von 0 Kelvin erfolgt ist, die auf unserer realen Erde überhaupt nicht vorkommt. Vielmehr dient diese Berechnung dem Nachweis, welche Durchschnittstemperatur die Sonne auf der Tageshemisphäre unserer Erde nach dem S-B-Gesetz maximal zu erzielen in der Lage ist. Der hemisphärische Mittelwert der solaren Einstrahlung über eine Summation von 1°-Kugelsegmente ergibt eine Durchschnittstemperatur von 14°Celsius, die hemisphärisch korrigierte Integrallösung [10] von Gerlich und Tscheuschner (2009) kumuliert bei einer Temperatur von 15°C, die der gemessenen global gemittelten NST entspricht und in der weiteren Betrachtung verwendet wird. Jetzt dreht sich also das tiefgefrorene Abbild unserer Erde wie ein Grillhähnchen unter der hemisphärischen Sonneneinstrahlung [11] und wärmt sich langsam auf. Während dieser Erwärmung steigt dann auch die terrestrische IR-Abstrahlung von 60 Milliwatt ganz langsam auf den Betrag der solaren Einstrahlung an. Während dieses Temperaturanstieges taut der Permafrost in niederen und mittleren Breiten auf, bilden sich die atmosphärischen Zirkulationszellen und ihre Windfelder und natürlich auch die thermohaline Zirkulation in den Ozeanen, die etwa zu 2/3 die Oberfläche unseres Wasserplaneten bilden.

Mit welchen Zeiträumen und Energiemengen müssen wir bei diesem Prozess rechnen?

Ein konservativer Vergleich des Wärmeinhalts der Ozeane mit der täglichen und jährlich global eingestrahlten Sonnenenergie zeigt, dass deren Einfluss auf die 24h-tägliche globale Temperaturgenese nicht vernachlässigt werden darf [12]. Allein die aktuell in den Ozeanen gespeicherte Energie (=Arbeit=Leistung_*Zeit) [5] entspricht ohne Berücksichtigung der Albedo in grober Abschätzung einer solaren Einstrahlung von etwa 120 Jahren:

Solare Einstrahlung auf der Erde an einem 24h-Tag: 1,05*10^22 Joule

Solare Einstrahlung auf der Erde über ein Jahr: 3,85*10^24 Joule

Gespeicherte Wärmemenge in den Ozeanen: 4,59*10^26 Joule

Nachdem wir eine Vorstellung von den terrestrisch gespeicherten Wärmemengen ermittelt haben, müssen wir uns jetzt Gedanken um die Zeiträume machen, die ein solches Auftauen erfordern würde. Nehmen wir dazu einmal den längsten aktiven Klimaprozess auf unserer Erde als Maßstab, die thermohaline Zirkulation mit etwa 1.000 Jahren für einen kompletten Umlauf. Sicherlich würde ein einziger thermohaliner Umlauf nicht ausreichen, um die gefrorene Tiefsee und möglicherweise auch den Permafrost aufzutauen. Wenn wir jetzt einmal den Faktor 10 zusetzen, kommen wir mit 10.000 Jahren in etwa ans Ende der letzten Kaltzeit. Da seither die Permafrostböden der vergletscherten mittleren Breiten bis auf alpine Reste verschwunden sind, können wir diese 10.000 Jahre zumindest grob für die aufzuheizenden Landflächen ansetzen. Die tiefgefrorenen Ozeane mit ihrem Permafrostboden dürften eher noch einen weiteren Faktor 10 vertragen. Aber das soll uns hier jetzt nicht weiter interessieren, denn eine Abkühlung würde vergleichbare Zeiträume dauern und es geht bei all diesen Überlegungen lediglich um das Verhalten der Nachttemperaturen auf unserer Erde.

Und da können wir bezüglich der Nachtabsenkung der Temperaturen auf unserer realen Erde feststellen, dass es auf Grundlage der in diesem eingeschwungenen System vorhandenen Energiemengen völlig ausgeschlossen ist, dass irgendwo auf der Nachtseite unserer Erde auch nur ansatzweise der absolute Nullpunkt erreicht wird.

Umgekehrt heißt das wiederum, dass die hemisphärisch einfallende Sonneneinstrahlung auf der Tagseite unserer Erde lediglich die über den 24h-Tag abgestrahlte Energiemenge ersetzen muss:

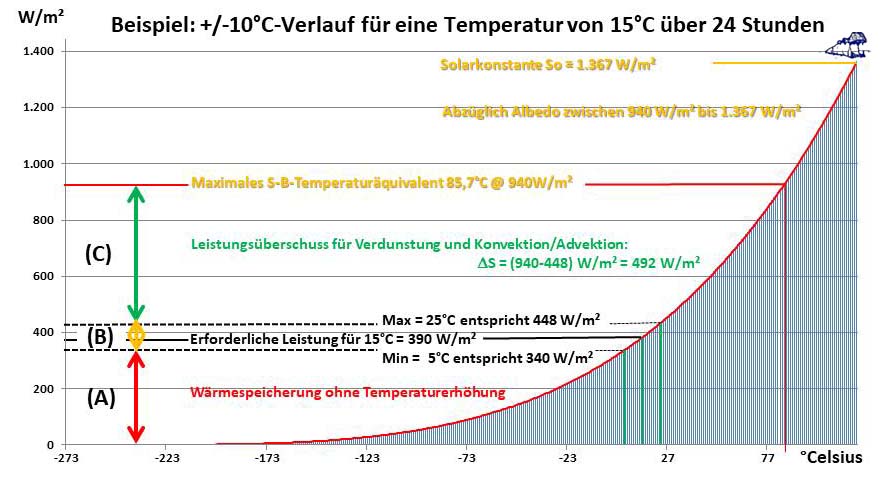
Abbildung 3: Die Beziehung zwischen Temperatur und spezifischer Strahlungsleistung im Stefan-Boltzmann-Gesetz am Beispiel des Leistungsbedarfs einer mittleren Oberflächentemperatur von 15°C mit einer Tag-Nacht-Schwankungsbreite von +/-10°C

Sowohl die Temperatur auf der Tagseite der Erde als auch die Temperatur auf deren Nachseite setzen auf der Temperatur der globalen Wärmespeicher auf, die im Wesentlichen von der Durchschnittstemperatur der Ozeane (ca. 20°C) bestimmt wird. Wasser ist der hauptsächliche Träger dieser Energie, sei es in flüssiger Form in den Ozeanen oder gasförmig in der Atmosphäre. Die örtliche Nachttemperatur der kontinentalen Landflächen wird also letztendlich über die Umgebungstemperatur ziehender Tiefdruckgebiete oder lokaler Land- Seewind Systeme bestimmt und gehorcht damit der Umgebungsgleichung des Stefan-Boltzmann-Gesetzes [13]. Je weiter also eine Örtlichkeit vom Meer entfernt ist und umso weniger Wasserdampf die örtliche Atmosphäre enthält, umso größer sind dort die Temperaturschwankungen zwischen Tag und Nacht. Die kontinentalen Wüstengebiete unserer Erde sind dafür ein ganz hervorragendes Beispiel. Seit jeher haben die Ozeane mit einem Zeitverzug von Jahrhunderten jede Klimaänderung „mitgemacht“ und gleichzeitig die jeweiligen individuellen Ortstemperaturen oder meinetwegen auch eine sogenannte „globale Durchschnittstemperatur“ auf der Nachthemisphäre nach unten abgesichert:

Die Erwärmung von 0 Kelvin auf die jeweilige Ortstemperatur muss also nicht erst durch die aktuelle solare Einstrahlung erzeugt werden, denn diese Ortstemperatur mit ihren Schwankungen zwischen Tag und Nacht ist in diesem „eingeschwungenen“ System Erde ja bereits vorhanden.

Die Abbildung 2 stellt eine Momentaufnahme der maximalen spezifischen solaren Strahlungsleistung und das entsprechende S-B-Temperaturäquivalent aus einer Stefan-Boltzmann-Inversion [14] für die terrestrische Temperaturgenese dar. Die Zeit ist von einer solchen Betrachtung mit dem Stefan-Boltzmann-Gesetz ausgeschlossen. Für eine 24-Stunden-Betrachtung müssen wir also das örtliche Maximum der solaren Strahlungsleistung bzw. dessen S-B-Temperaturäquivalent aus den konzentrischen 1°-Kugelsegmenten einmal über den 24h-Tag für die gesamte Erdoberfläche fortschreiben [15], wie die nachfolgende Abbildung auf Grundlage einer Mollweide Projektion zeigt:

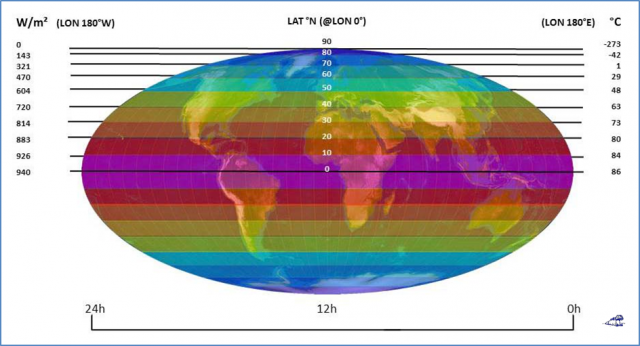
Abbildung 4: Die maximale breitenabhängige temperaturwirksame solare Strahlungsleistung (Skala links) und das resultierende S-B-Temperaturäquivalent (Skala rechts) über einen 24-Stunden-Tag im Äquinoktium mit farblich unterlegter Mollweide-Projektion (© L. Rohwedder – Lizenz CC BY-SA 3.0)

Linke Skala: MAX (S_i) @24h-Tag mit (S_i = 1.367W/m²_*(1-ALBEDO) _* cos PHI_i)
und (PHI_i = örtlicher Zenitwinkel)

Rechte Skala: Maximales örtliches S-B-Temperazuräquivalent( SBT_i) von MAX (S_i)

Aus dieser Abbildung wird sofort deutlich, dass die maximale temperaturwirksame spezifische Strahlungsleistung der Sonne im Tagesverlauf des Äquinoktiums bei gleicher geographischer Breite immer denselben Maximalwert und damit auch immer dasselbe maximale örtliche S-B-Temperauräquivalent ergibt. Im Tagesverlauf wird also zwischen 75 Grad N und S (mit jeweils 243 W/m²) und dem Äquator (mit 940 W/m²) die global gemittelte temperaturwirksame spezifische Strahlungsleistung von 235 W/m² (≅ -18°C) nach dem THE-Paradigma weit übertroffen.

Anmerkung: Der Autor hat in seinem hemisphärischen S-B-Modell ganz bewusst die maximale solare Einstrahlung betrachtet, denn nur so lässt sich der Tag-und-Nacht-Wechsel physikalisch sinnvoll darstellen. Jede Rückrechnung aus irgendeiner Energiemenge über die Zeit auf eine Durchschnittsleistung [5] entfernt sich dagegen physikalisch unwiderruflich vom Stefan-Boltzmann-Gesetz.

Weiterhin verfügt unsere Erde auf zwei Dritteln ihrer Oberfläche über eine Warmwasser-Fußbodenheizung mit einer Vorlauftemperatur zwischen 0°C und 30°C bis etwa 70° nördlicher und südlicher geographischer Breite und fällt erst jenseits davon auf bis zu -5°C ab; ein globaler Durchschnitt wird mit 20°C angegeben und dürfte etwas über der NST von 15°C kumulieren. Damit ist bewiesen, dass die täglich durch Sonneneinstrahlung überall auf der Erde zwischen 75°N und 75°S erzeugten Temperaturen keinerlei zusätzlichen „natürlichen atmosphärischen Treibhauseffekt“ benötigen, um die gemessenen Ortstemperatur zu erklären. Die Ozean-Temperaturen repräsentieren wiederum zwei Drittel der „gemessenen“ globalen Ortstemperaturen. Wie wir bereits erfahren haben, wird das maximale rechnerische S-B-Temperaturäquivalent des hemisphärischen S-B-Modells aufgrund von örtlicher Konvektion und Verdunstung in der Realität aber nirgendwo auf unserer Erde erreicht [16]. Andererseits sinkt die Temperatur in mittleren und höheren Breiten der Winterhemisphäre, insbesondere in der Polarnacht, niemals auf das rechnerische S-B-Temperaturäquivalent der geringen/fehlenden solaren Einstrahlung ab. Die nachfolgende Abbildung zum globalen breitenabhängigen Wärmetransport [17] gibt Aufschluss über die Gründe dafür:

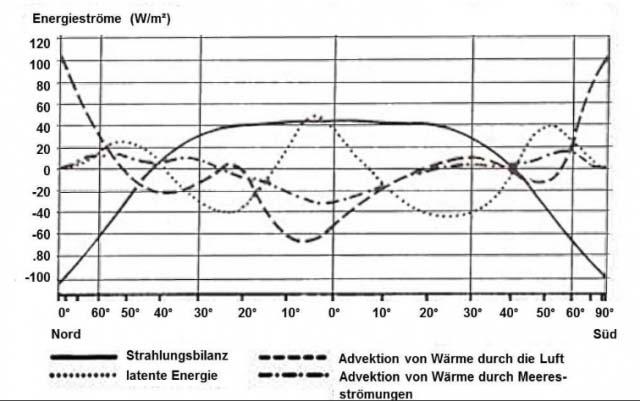
Abbildung 5: Jahresmittel des Energiehaushaltes der Atmosphäre und seiner Komponenten in Abhängigkeit von der geographischen Breite. QUELLE: HÄCKEL, Meteorologie, Verlag Eugen Ulmer, Stuttgart 1990 – Hinweis: In dieser Grafik ist die horizontale Achse der Breitenkreise vom Äquator ausgehend polwärts gestaucht dargestellt

Aus dieser Abbildung 5 „Jahresmittel des Energiehaushaltes der Atmosphäre und seiner Komponenten“ ergibt sich für die

Strahlungsbilanz: In den Tropen ist die Strahlungsbilanz positiv und geht dann knapp jenseits von 40°N und 40°S in den negativen Bereich. Wenn Sie’s mal mit dem 0°C-Durchgang des S-B-Temperaturäquivalents aus der maximalen solaren Einstrahlung bei etwa 70° geografischer Breite im Äquinoktium in der Abbildung 2 vergleichen, dann ist im Jahresdurchschnitt ein energetischer Nulldurchgang bei 40° Breite durchaus plausibel.

Latente Energie: Die latente Energie ist um den Äquator positiv, geht dann um ca. 10°N&S ins Negative, steigt nach ca. 40°N&S noch einmal an und geht dann zu den Polen auf null.

Advektion durch Luft: Um den Äquator werden erhebliche Wärmemengen abgezogen. Der weitere Verlauf auf den beiden Hemisphären ist, offenbar aufgrund der Land-Meer-Verteilung, recht unterschiedlich, aber jenseits von ca. 50°N&S wird zu den Polregionen ein erheblicher Zustrom vom Wärme dokumentiert.

Advektion durch Ozean: In den Tropen wird Wärme abgezogen, etwa von den beiden Wendekreisen an ergibt sich dann ein Zufluss von Wärme zu höheren geographischen Breiten, der sich zum jeweiligen Pol hin auf null reduziert.

Anmerkung: Der Zeitversatz zwischen den Jahreszeiten auf der Nord- und Südhalbkugel ist der Mittelung für den durchschnittlichen Jahresverlauf zum Opfer gefallen.

Die Sonneneinstrahlung in den Tropen und den mittleren Breiten der Sommerhemisphäre erwärmt die globalen Energiespeicher und treibt damit den Klimamotor auf unserer Erde an [13] [18]. Alle Energieströme summieren sich bei Häckel im mehrjährigen Mittel über alle Ortslagen einer festen geographischen Breite gerade auf null, wobei sich deren durchschnittliche individuelle Beiträge und Ortstemperaturen in der Realität je nach meridionaler Land-Meer-Verteilung durchaus unterscheiden können. Wir können hier also erkennen, dass sich die Überschüsse und Defizite gegenüber dem örtlich berechneten hemisphärischen S-B-Temperaturäquivalent durch den lateralen Transport von Energie gerade global ausgleichen und damit das hemisphärische S-B-Modell voll bestätigen. Dieser Punkt ist offenbar der am wenigsten verstandene im hemisphärischen S-B-Modell. Dabei wurden die globalen Wärmespeicher unserer Erde und deren Temperaturwirkung über die Umgebungsgleichung des Stefan-Boltzmann-Gesetzes bereits in diversen Artikeln thematisiert und mehrfach mit der Grafik von Häckel (Abbildung 5) veranschaulicht. Der terrestrische Wärmetransport bedarf daher offenbar erneut einer ausführlicheren Erklärung:

Primär = Sonneneinstrahlung auf der Tageshemisphäre: Die HF-Einstrahlung der Sonne bewirkt die terrestrische Temperaturgenese. Die Temperatur einer individuellen Ortslage ist abhängig von dem örtlichen solaren Zenitwinkel , der terrestrischen Albedo und dem von der Tageszeit abhängigen Azimut. Die örtlich maximal mögliche Temperatur aus der solaren Einstrahlung ergibt sich dann aus [So x (1-Albedo) x COS(Zenitwinkel)] durch eine Inversion des Stefan-Boltzmann-Gesetzes [19]. Dieser theoretische Wert wird aber nirgendwo auf der Erde erreicht, weil während der gesamten Sonnenscheindauer Energie in die globalen Energiespeicher von Atmosphäre und Ozeanen abfließt.

Sekundär = Abstrahlung der Erde: Die sekundäre IR-Abstrahlung der Erde aus erwärmter Materie erreicht aufgrund des örtlichen Abflusses von Energie durch Konvektion und Verdunstung nicht den Gesamtbetrag der solaren Einstrahlung.

Tertiär = Speicherung von Energie durch Konvektion und Verdunstung: Beim primären terrestrischen Erwärmungsprozess wird Energie in Form von Verdunstung und Konvektion aus diesem Prozess herausgelöst, in Atmosphäre und Ozeanen gespeichert und durch die globalen Strömungssysteme aus der jeweiligen Ortslage abgeführt.

Quartär = Abgabe von Energie durch Advektion und Kondensation: Da es sich beim Energieinhalt der Wärmespeicher unserer Erde um ein eingeschwungenes Klimasystem handelt, wird im langjährigen Mittel gleichzeitig genauso viel Energie von den globalen Strömungssystemen abgegeben, wie dort zeitgleich aus der primären HF-Sonneneinstrahlung „eingelagert“ wird. Die Zeiträume solcher individuellen Speicherzyklen betragen Stunden, Tage, Wochen, Monate, Jahre, Jahrzehnte oder gar Jahrhunderte.

Im langjährigen Klimamittel über 30 Jahre gilt demnach auf unserer Erde für das energetische Gleichgewicht (IN=OUT=1,15*10^26 Joule in 30 Jahren) oder:

HF-Primär [J] = IR-Sekundär [J] + IR-Quartär [J] ≅ 3,85*10^24 Joule im Jahresdurchschnitt

mit ((Tertiär = HF IN @Energiespeicher [J]) ≈ (Quartär = IR OUT @Energiespeicher [J]))

Und die Summe der örtlichen Abweichungen zu diesem Jahresmittel nennt man dann „Wetter“. Dabei ist noch zu beachten, dass üblicherweise Energie aus den niederen Breiten und mittleren Breiten der Sommerhemisphäre abgeführt und den mittleren und hohen Breiten der Winterhemisphäre zugeführt wird. Das hemisphärische Stefan-Boltzmann-Modell ist also in der Lage, die Temperaturgenese auf unserer Erde qualitativ zu beschreiben, ohne dazu irgendwelche physikalischen Hilfskonstruktionen wie einen „natürlichen atmosphärischen Treibhauseffekt“ zu benötigen. Darüber hinaus schließt dieses Modell weitere Faktoren der terrestrischen Klimagenese ein, beispielsweise die Umkehr der vektoriellen Richtung zwischen Einstrahlung und Abstrahlung [20]. Weiterhin bildet dieses Modell die Breitenabhängigkeit der solaren Einstrahlung ab [21], erklärt die Jahreszeiten [22] und widerlegt den äquatorialen Hotspot in der Atmosphäre [23] sowie die „atmosphärische Gegenstrahlung“ [24]. Und schließlich ist in einem Faktencheck [25] mein hemisphärisches Modell das einzige von drei Modellen für die Temperaturgenese auf unserer Erde, das den Verlauf der terrestrischen Beleuchtungsklimazonen nachzuzeichnen vermag:

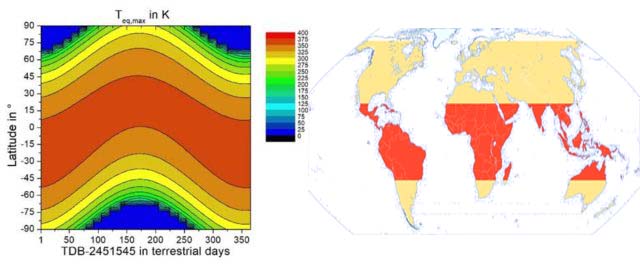
Abbildung 6: Vergleich hemisphärisches S-B-Modell mit den Beleuchtungsklimazonen der Erde

Links: Das hemisphärische S-B-Modell aus einem Modellvergleich von Dr. G. Kramm (persönliche Mitteilung 2021 mit freundlicher Genehmigung) – Originale Bildunterschrift:

Maxima nach Weber, beginnend mit dem 1. Januar 2000, 12:00 Uhr (JD = 2451545)

Rechts: Beleuchtungsklimazonen der Erde (N-S gestreckt)
Quelle: Wikipedia, Autor: Fährtenleser, Lizenz: GNU Free Documentation License)

Wie es die wissenschaftliche Beweisführung der Physik befiehlt, ergibt sich am Ende dieser Betrachtung also eine widerspruchsfreie semi-quantitative Übereinstimmung in Raum und Zeit zwischen Theorie und praktischem Versuchsaufbau, nämlich zwischen meinem hemisphärischen Stefan-Boltzmann-Modell und der Temperaturgenese und -verteilung auf unserer realen Erde im langjährigen Durchschnitt. Die Erklärung dieser, für viele Betrachter eher unerwarteten Übereinstimmung ist ziemlich einfach, denn wärmer als das Mittel aus den örtlichen S-B-Temperaturäquivalenten der maximalen örtlichen HF-Solareinstrahlung [= So x (1-Albedo) x COS(max. Zenitwinkel)] kann es auf unserer Erde nun einmal nicht werden [10].

ANHANG: Wegweiser durch meine EIKE-Artikel mit den im Text bezeichneten Verweisen

[1] Eine Analyse der Thesen/Antithesen für einen „natürlichen atmosphärischen Treibhauseffekt“ – Teil 1: Gegenüberstellung der Thesen/Antithesen

[2] Eine Analyse der Thesen/Antithesen für einen „natürlichen atmosphärischen Treibhauseffekt“ – Teil 2: Diskussion der Thesen/Antithesen

[3] Eine Analyse der Thesen/Antithesen für einen „natürlichen atmosphärischen Treibhauseffekt“ – Teil 3: Erkenntnisse zu den Thesen/Antithesen und das Ergebnis dieser Analyse

[4] Fangen wir mit dem Stefan-Boltzmann-Gesetz noch einmal ganz von vorne an

[5] Der physikalische Unterschied zwischen Energie und Leistung in der politischen Klimawissenschaft

[6] Beweist die Temperatur des Mondes den hemisphärischen Stefan-Boltzmann Ansatz?

[7] Neues von Willis Eschenbach

[8] Machen wir mal ein Gedankenexperiment: Es gibt gar keine Erde!

[9] Verbesserungswürdig: Über fehlerhafte Ansätze für eine breitenabhängige Globaltemperatur

[10] Anmerkungen zur hemisphärischen Mittelwertbildung mit dem Stefan-Boltzmann-Gesetz

[11] Das Hähnchengrill-Paradoxon