Der physikalische Unterschied zwischen Energie und Leistung in der politischen Klimawissenschaft
Uli Weber
Es wäre wirklich zu begrüßen, wenn sich die Klimarealisten in Deutschland auf das übergeordnete Ziel konzentrieren könnten, dem religiösen Klimawahn entgegenzutreten; denn dieser Klimawahn schreitet mit sehr schnellen Schritten voran, Siehe: https://report24.news/auch-wien-ueber-1-000-staedte-wollen-bis-2030-fleisch-milch-und-privatautos-verbieten/
 Mein hemisphärisches Stefan-Boltzmann-Modell mit +15°C ohne THE ist nicht überall gut angekommen; sogar vorgebliche Klimarealisten fühlen sich dadurch heftig provoziert, wie die nachfolgende Abbildung beweist:
Mein hemisphärisches Stefan-Boltzmann-Modell mit +15°C ohne THE ist nicht überall gut angekommen; sogar vorgebliche Klimarealisten fühlen sich dadurch heftig provoziert, wie die nachfolgende Abbildung beweist:
Abbildung 1: Das Faktor4-Tag=Nacht-Modell aus einer Dietze-Email vom 30.08.2023 08:38
Rechnen wir also mal das geozentrische Faktor4-Tag=Nacht-Weltbild nach:
Die Solarkonstante (So) beträgt 1.367 W/m².
Abzüglich Albedo bleiben ca. 940 W/m² temperaturwirksam.
Aufgeteilt auf 2 Sonnen ergibt das jeweils 470 W/m².
Die Projektion des ebenen solaren Strahlungsquerschnitts, auf die jeweilige Halbkugel der Erde projiziert, ergibt einen Flächenverhältnis von 1:2. Damit sind auf jeder der beiden solar beschienenen Halbkugeln durchschnittlich 235 W/m² für die Temperaturgenese verfügbar.
Nach dem Stefan-Boltzmann-Gesetz entsprechen 235 W/m² einer Temperatur von -19°C. Damit wurde der sogenannte „natürlichen atmosphärischen Treibhauseffekt“ auch im herkömmlichen Faktor4-Modell durch einen grafischen Widerspruchsbeweis widerlegt, weil für dessen Existenz zwei Sonnen mit der jeweils halben Solarkonstante erforderlich wären.
Die Glaubensbekenntnisse der Klimareligion sind voll von antiphysikalischen „Wunderwaffen“, die auf MINT-fernem Wunschdenken fußen und mit dauerhaften Subventionen gestützt werden müssen. Denn die Krux in der politischen Klimawissenschaft ist die Physik, namentlich der Unterschied zwischen Energie und Leistung sowie deren Zusammenhang über die Zeit:
Definition von „Energie“ (Wikipedia): „Energie ist eine physikalische Größe, die in allen Teilgebieten der Physik sowie in der Technik, Chemie, Biologie und der Wirtschaft eine zentrale Rolle spielt. Ihre SI-Einheit ist das Joule. Die praktische Bedeutung der Energie liegt oft darin, dass ein physikalisches System in dem Maß Wärme abgeben, Arbeit leisten oder Strahlung aussenden kann, in dem seine Energie sich verringert. In einem gegenüber der Umgebung abgeschlossenen System ändert sich die Gesamtenergie nicht (Energieerhaltungssatz). Die Bedeutung der Energie in der theoretischen Physik liegt unter anderem darin, dass der Energieerhaltungssatz, ursprünglich eine Erfahrungstatsache, schon daraus gefolgert werden kann, dass die grundlegenden physikalischen Naturgesetze zeitlich unveränderlich sind.“
ENERGIE ist also gespeicherte physikalische Arbeit in Form von potentieller, kinetischer, elektrischer, chemischer und thermischer Energie, die Einheit ist Joule [J].
BEISPIEL: Der Wind besitzt kinetische Bewegungsenergie, und solange er auf kein Hindernis trifft, behält er sie auch.
Definition von „Leistung“ (Wikipedia): „Die Leistung als physikalische Größe bezeichnet die in einer Zeitspanne umgesetzte Energie dividiert durch diese Zeitspanne. Ihr Formelzeichen ist meist P (von englisch power), ihre SI-Einheit das Watt mit dem Einheitenzeichen W. Im physikalisch-technischen Zusammenhang wird der Begriff Leistung in verschiedenen Bedeutungen verwendet:
als installierte oder maximal mögliche Leistung (Kennzeichen eines Gerätes oder einer Anlage; auch Nennleistung genannt)
als tatsächliche Leistung in einer Anwendung
die zugeführte Leistung
die im Sinne der Aufgabenstellung abgegebene Leistung.
Die Leistungsaufnahme und die für eine bestimmte Anwendung nutzbringende Leistungsabgabe können je nach Wirkungsgrad bzw. Abwärme erheblich voneinander abweichen.“
LEISTUNG ist also die prinzipielle Fähigkeit, eine Energieform in eine andere Energieform umzuwandeln, die Einheit ist Watt [W].
BEISPIEL: Die WKAs auf dem Titelbild sind ein Hindernis für den Wind; sie wandeln dessen kinetische Energie in elektrische Energie um. Dabei hat eine WKA eine feste technische Nennleistung, während die tatsächlich geleistete Arbeit mit der 3. Potenz der Windgeschwindigkeit schwankt.
Der große Fehler der Klimawissenschaften liegt darin, Energie und Leistung als äquivalent zu betrachten, und beide über die Zeit beliebig ineinander überführen zu wollen. Nun kann man zwar aus einer Leistung und deren Wirkzeit eindeutig eine Energiemenge ermitteln, aber die umgekehte Rückrechnung einer Leistung aus einer Energiemenge bedarf der Kenntnis über die Wirkzeit und den tatsächlichen Leistungsverlauf, sonst ist das Ergebnis nicht eindeutig.
Beispiel: Sie bestellen auf der Kirmes eine Erbsensuppe; die Menge beträgt 0,5 Liter und dieTemperatur 80°C. Frage an die THE-Anhänger unter Ihnen: Mit welcher Leistung und über welche Zeit wurde diese Suppe von 15°C auf 80°C erhitzt?
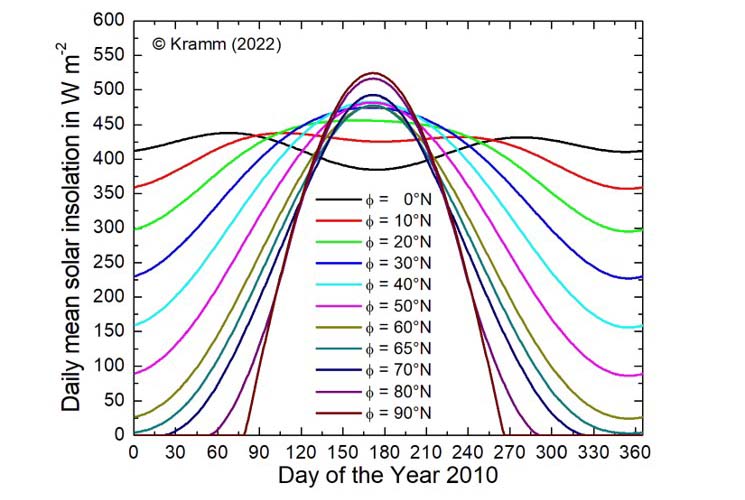 Diese Frage ist nämlich gar nicht eindeutig lösbar. Trotzdem versucht das THE-Establishment, aus einem globalen Faktor4-Tag=Nacht-Mittel eine theoretische Globaltemperatur abzuleiten. In einer E-Mail* vom 26.08.2023 06:17 übermittelte mir ein Dr. Gerhard Kramm die nachfolgende Grafik* in Abbildung 2:
Diese Frage ist nämlich gar nicht eindeutig lösbar. Trotzdem versucht das THE-Establishment, aus einem globalen Faktor4-Tag=Nacht-Mittel eine theoretische Globaltemperatur abzuleiten. In einer E-Mail* vom 26.08.2023 06:17 übermittelte mir ein Dr. Gerhard Kramm die nachfolgende Grafik* in Abbildung 2:
Abbildung 2: Tägliche mittlere solare Einstrahlung von 0°N-90°N geografischer Breite in W/m² für alle Tage des Jahres 2010 – Quelle: (Kramm 2023)*
Und ein Herr Eugen Ordowski hatte dazu passend am 18. August 2023 um 15:50 hier auf EIKE eine Aussage von Wilhelm von Bezold aus dem Jahr 1906 zitiert:
„Dabei fällt das Maximum der Einstrahlung, wie längst bekannt, auf den Pol der Sommerhalbkugel und zwar das absolute Maximum auf den Südpol.“
Aber was meinte Wilhelm von Bezold nun mit dem „Maximum der Einstrahlung“?
Es gibt dafür zwei Möglichkeiten, von denen nur eine richtig sein kann: Meinte von Bezold das tägliche Maximum der EINSTRAHLUNGSLEISTUNG, aus dem ich mein hemisphärisches S-B-Temperaturmodell herleite, oder meinte er das Maximum der täglichen 24h-EINSTRAHLUNGSMENGE (=ENERGIE), mit dem Kramm et al. (2017) eine terrestrische Anwendung seines lunaren Slab-Temperaturmodells berechnet hatten?
Schaunmermal: In Abbildung 3 sind die breitenabhängige maximale spezifische solare Strahlungsleistung und die aus der 24h-Einstrahlungsmenge hergeleitete breitenabhängige Durchschnittsleistung nach Kramm (2023) gemeinsam dargestellt:
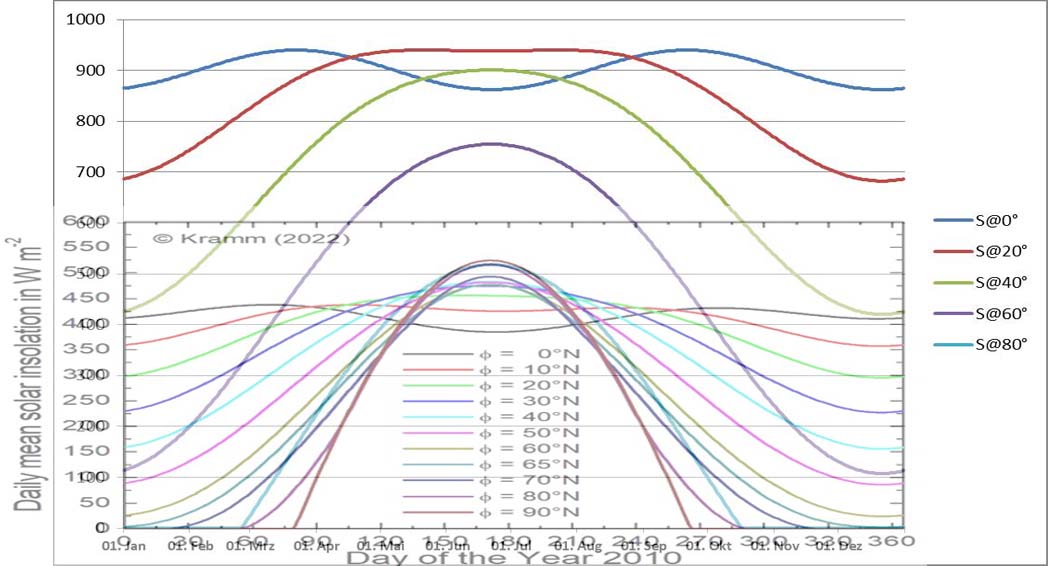
Max. Leistung [W/m²]
Abbildung 3: Die maximale spezifische solare Strahlungsleistung (Skala 0-900 W/m²) von 0°N bis 80°N geografischer Breite vom 1. Januar bis zum 31. Dezember (Weber)
Overlay: Maßstäblich angepasste Abbildung 2 für die tägliche mittlere solare Einstrahlung von 0°N-90°N geografischer Breite in W/m² (Skala 0-600) für alle Tage des Jahres 2010 (Kramm 2023)*
In beiden Abbildungen ist die Ordinate mit [W/m²] bezeichnet, bei mir als das tägliche Maximum, bei Kramm als täglicher 24h-Durchschnittswert. Auffällig ist, dass diese Kurven bei ähnlichem Verlauf nahezu um den Faktor2 auseinanderliegen; lediglich im Bereich des Polartages bestehen Übereinstimmungen.
Mein tägliches Maximum ist physikalisch eindeutig definiert: Die temperaturwirksame spezifische solare Strahlungsleistung von 940 W/m² multipliziert mit dem Cosinus des örtlichen solaren Zenitwinkels bei höchstem Sonnenstand.
Was bedeutet nun der Tagesdurchschnitt bei Kramm (2023)? LEISTUNG hat die physikalische Einheit Watt und ENERGIE die physikalische Einheit Joule. Der Tag hat 24 Stunden oder 86.400 Sekunden. Eine solare Gesamteinstrahlung über den 24h-Tag würde also zunächst einmal in [Joule=Ws] ausgedrückt werden. Aus [Joule] wird dann durch eine Division mit der Tagesdauer in Sekunden [s] eine Durchschnittsleistung in [Watt] berechnet. Und da [m²] in der Abbildung im Nenner steht, handelt es sich damit um eine spezifische Leistung.
Kommen wir wieder zurück auf das von Bezold Zitat und dessen Formulierung „Maximum der Einstrahlung“. Da Wilhelm von Bezold ein hervorragender Physiker war, ist ihm sicherlich bekannt gewesen, dass die maximale temperaturwirksame spezifische solare Strahlungsleistung von 940 W/m² ausschließlich zwischen den beiden Wendekreisen auftritt. Also kann es sich bei seinem Zitat nur um die tägliche 24h-Gesamtmenge der eingestrahlten solaren Energie handeln, und nicht um eine maximale Leistung.
Die Bewertung des Tagesdurchschnitts ist daher ganz einfach:
Bis zur Berechnung einer solaren Gesamteinstrahlung über den 24h-Tag in Joule ist diese Berechnung physikalisch richtig. Die mathematische Durchschnittsbildung über 86.400 Sekunden und die geographischen Breiten entfernt sich dann aber von der physikalischen Aussage von Wilhelm von Bezold, der gar nichts von einem spezifischen Leistungsdurchschnitt gesagt sondern vielmehr absolute Angaben zur Energie gemacht hatte. Während im Polartag noch eine sinnstiftende physikalische Durchschnittsbildung möglich ist, fließen zu absteigenden geografischen Breiten hin dann zunehmend Nachtzeiten in diese Grafik ein und führen zu physikalisch unsinnigen Ergebnissen, wie Abbildung 3 anschaulich beweist. Dort ist deutlich zu erkennen, dass die maximale spezifische solare Strahlungsleistung aus Abb.2 mit zunehmender Nachtlänge vom Pol zu den Tropen entgegen dem tatsächlich beobachteten Verlauf sinkt, anstatt wie in Realitas und meinem hemisphärischen S-B-Modell anzusteigen. Es sei an dieser Stelle noch einmal an die eingangs zitierte Definition von „Leistung“ erinnert (mit Hervorhebungen):
„Die Leistung als physikalische Größe bezeichnet die in einer Zeitspanne umgesetzte Energie dividiert durch diese Zeitspanne.“
Ein 24h-Durchschnitt über Nachtzeiten widerspricht also der Definition von physikalischer Leistung.
Schaunmernochmalweiter: Kramm et al. (2017) hatten aufgrund der polaren Tageslänge eine breitenabhängige Temperaturverteilung mit den Maxima am Pol der jeweiligen Sommerhemisphäre hergeleitet. In seiner E-Mail vom 29.01.2021 um 09:58 Uhr** an mich und den üblichen Skeptiker-Email-Verteiler hatte Dr. Gerhard Kramm ein PDF-Dokument „kramm_bemerkungen_weber_v3.pdf“ (in der Folge „Kramm (2021)“) mit einem direkten Temperaturvergleich zwischen meinem hemisphärischen S-B-Modell und seiner „Erde ohne Atmosphaere“ verschickt. Wie erwartet spiegeln die Beleuchtungsklimazonen (Definition) unserer Erde den Verlauf der maximalen örtlichen solaren Strahlungsleistung und zeigen keinerlei Hotspot am Pol der Sommerhemisphäre. Diese Beleuchtungsklimazonen sind in der nachfolgenden Abbildung (hier finden Sie die Originaldarstellung) als Overlay über die beiden genannten Modelle projiziert worden:
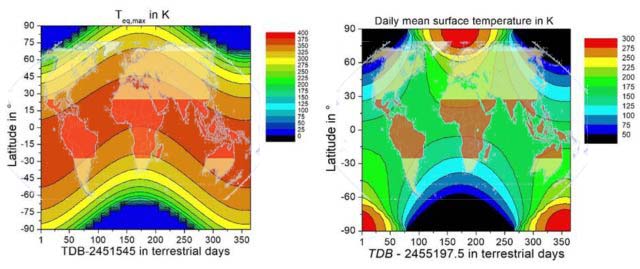 Abbildung 4: Grafiken a** und b** aus Kramm (2021): Der Modellvergleich aus dem PDF-Dokument von Kramm (2021)** mit jeweils einem Overlay der Beleuchtungsklimazonen
Abbildung 4: Grafiken a** und b** aus Kramm (2021): Der Modellvergleich aus dem PDF-Dokument von Kramm (2021)** mit jeweils einem Overlay der Beleuchtungsklimazonen
(Quelle: Wikipedia, Autor: Fährtenleser, Lizenz: GNU Free Documentation License)
(a** [links]) Maxima nach Weber, beginnend mit dem 1. Januar 2000, 12:00 Uhr (JD = 2451545)
(b** [rechts]) Tägliche Mittelwerte nach Kramm et al. (2017), beginnend mit 1.Januar 2010, 00:00 Uhr (JD =2455197,5)“
Anmerkung: Die Overlays der Beleuchtungsklimazonen sind gegenüber den Modellen a** und b** nicht flächentreu
Bekanntermaßen ist die temperaturbestimmende spezifische solare Strahlungsleistung in den Tropen nun einmal am höchsten (Abbildung 4a**) und fällt dann zu den Polarregionen kontinuierlich ab, wie es auch die Overlays der Beleuchtungsklimazonen in den Abbildungen 4a** und 4b** prinzipiell zeigen. Es ist demnach unschwer zu erkennen, welche Grafik ein physikalisches Temperatur-Modell unserer realen Erde darstellt (mein hemisphärisches S-B-Modell) und welche Grafik mit einem Wärmepol auf der Sommerhemisphäre nicht auf unsere reale Erde zutrifft.
Halten wir also nochmal fest, dass am jeweiligen Sommerpol die tägliche solare ENERGIE (=Leistung*Zeit) am größten ist, während die tägliche solare MAXIMAL-LEISTUNG (die das S-B-Temperaturäquivalent bestimmt) auf den Bereich zwischen Äquator und dem sommerlichen Wendekreis beschränkt bleibt.
In der nachfolgenden Abbildung wird der Unterschied zwischen LEISTUNG und ENERGIE noch einmal grafisch dargestellt:
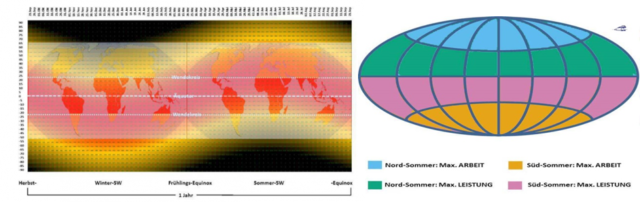 Abbildung 5: Links: Jahresverlauf der maximalen solaren Strahlungsleistung mit den Beleuchtungsklimazonen Rechts: Die maximale spezifische solare (Strahlungs-) LEISTUNG (~S-B-Temperaturäquivalent) und die maximale solare ARBEIT (Arbeit=Leistung x Zeit über die örtliche Tageslänge) im jeweiligen Sommerhalbjahr auf der Nord- und Südhalbkugel
Abbildung 5: Links: Jahresverlauf der maximalen solaren Strahlungsleistung mit den Beleuchtungsklimazonen Rechts: Die maximale spezifische solare (Strahlungs-) LEISTUNG (~S-B-Temperaturäquivalent) und die maximale solare ARBEIT (Arbeit=Leistung x Zeit über die örtliche Tageslänge) im jeweiligen Sommerhalbjahr auf der Nord- und Südhalbkugel
Quelle: Niemand hat die Absicht, eine Ökodiktatur zu errichten
Anmerkungen zu den Overlays in der linken Abbildung: Die maximale temperaturwirksame spezifische Strahlungsleistung der Sonne MAX Si (rot=940W/m², schwarz=0W/m²) in Abhängigkeit von der geographischen Breite und der Jahreszeit. Für den Nordwinter (linke Seite) und den Nordsommer (rechte Seite) wurden darüber jeweils die Beleuchtungsklimazonen der Erde projiziert (von oben/unten zur Mitte: Polarzonen, Mittelbreiten, Tropenzone – Quelle: Wikipedia, Autor: Fährtenleser, Lizenz: GNU Free Documentation License)
Die maximale temperaturwirksame spezifische Strahlungsleistung der Sonne von 940W/m² erhält immer derjenige Breitenkreis zwischen den Wendekreisen, auf dem die Sonne mittags lotrecht steht. Dieses Maximum ist nicht zu verwechseln mit dem Maximum der 24h-Strahlungsenergie, das aufgrund der Länge des Polartages um die jeweilige Sommersonnenwende auf den Sommerpol fällt. Es lässt sich aus einem entsprechenden 24h-Durchschnitt (=Leistung x 24h/24h) allerdings kein entsprechendes S-B-Temperaturäquivalent ableiten, obwohl es immer wieder versucht wird. Halten wir also fest, dass am jeweiligen Sommerpol die tägliche solare ENERGIE (=LeistungxZeit) am größten ist, während die tägliche solare MAXIMAL-LEISTUNG (die das S-B-Temperaturäquivalent bestimmt) auf den Bereich zwischen Äquator und dem sommerlichen Wendekreis beschränkt bleibt. Die Erklärung der (mechanischen) Leistung von studyflix.de/ingenieurwissenschaften lässt sich auch hier anwenden, Zitat:
„Die Definition der Arbeit in der Physik als „Kraft mal Weg“ beinhaltet nicht, in welchen Zeitintervall diese Arbeit verrichtet worden ist. Zwei Personen (A und B) können daher dieselbe Arbeit verrichten, aber Person A braucht dazu weniger Zeit als Person B. Umgangssprachlich würde man in dieser Situation sagen, dass Person A eine größere Leistung als Person B erbracht hat.
Genau das ist die Kernidee hinter der Definition für die Leistung 
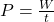 .
.
Hier ist 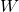 die Arbeit in Joule (
die Arbeit in Joule ( ), die im Zeitintervall
), die im Zeitintervall 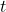 in Sekunden (
in Sekunden ( ) erbracht wurde. Die Einheit der Leistung ist demnach
) erbracht wurde. Die Einheit der Leistung ist demnach 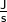 , häufiger aber in
, häufiger aber in 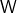 für Watt angegeben. Die Leistung erlaubt es also in einer konkreten Zahl zu fassen, wie schnell eine gewisse Menge an Arbeit verrichtet wurde.“
für Watt angegeben. Die Leistung erlaubt es also in einer konkreten Zahl zu fassen, wie schnell eine gewisse Menge an Arbeit verrichtet wurde.“
Eine Durchschnittsbildung der solaren Einstrahlungsenergie über Nachtzeiten ist physikalisch also ebenso sinnvoll, wie beispielsweise eine Verbrauchsanalyse für ein Kraftfahrzeug inklusive dessen Stillstandzeiten. Aber es könnte auch viel schlimmer kommen, wenn man daraus dann noch eine Durchschnittsgeschwindigkeit, in diesem Vergleich also eine Temperatur, ableiten würde.
 Damit kommen wir zur ZEIT „t“ als das große Menetekel der sogenannten „Energiewende“, denn ohne Zeit kann man die Energie nun mal nicht wenden. Man kann über fossile Energieträger verfügen, man kann über Strom-Generatoren verfügen, aber man nun mal nicht frei über die Zeit verfügen. Insbesondere kann man nicht über die Zeit verfügen in der die Sonne scheint und der Wind weht. Zwecks Stromerzeugung kann man lediglich Stromerzeuger bereitstellen, also Solarpanele oder Windmühlen, die Zeitpläne für Sonne und Wind werden aber von Petrus im Voraus nicht veröffentlicht; lediglich ist bekannt oder sollte vielmehr bekannt sein, dass die Sonne nachts nicht scheint, und der Wind weht, wann und wo er will:
Damit kommen wir zur ZEIT „t“ als das große Menetekel der sogenannten „Energiewende“, denn ohne Zeit kann man die Energie nun mal nicht wenden. Man kann über fossile Energieträger verfügen, man kann über Strom-Generatoren verfügen, aber man nun mal nicht frei über die Zeit verfügen. Insbesondere kann man nicht über die Zeit verfügen in der die Sonne scheint und der Wind weht. Zwecks Stromerzeugung kann man lediglich Stromerzeuger bereitstellen, also Solarpanele oder Windmühlen, die Zeitpläne für Sonne und Wind werden aber von Petrus im Voraus nicht veröffentlicht; lediglich ist bekannt oder sollte vielmehr bekannt sein, dass die Sonne nachts nicht scheint, und der Wind weht, wann und wo er will:
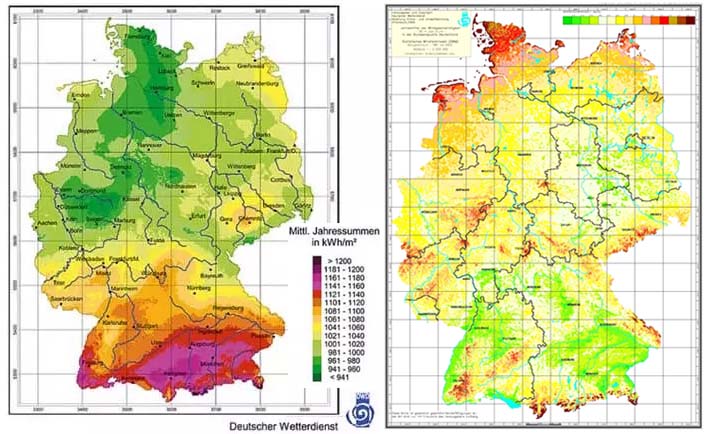
Abbildung 6: DWD-Karten für die solare Einstrahlung und die Windgeschwindigkeit in Deutschland
Links: Auf SOLARWATT findet man eine solare Einstrahlungskarte des DWD
Beschreibung: „Um die Sonneneinstrahlung für eine Region abschätzen zu können, gibt es vom Deutschen Wetterdienst (DWD) eine Einstrahlungskarte. Betreiber von Solaranlagen können die genaue Sonneneinstrahlung für ganz Deutschland ablesen.“
Rechts: DWD Windkarte für Deutschland (Bezugszeitraum 1981-2000)
Beschreibung: „In Windkarten steckt umfangreiches Know-how. An 218 Stationen wurde jahrzehntelang die Windgeschwindigkeit registriert. Aus diesen Messwerten wurden mit dem Statistischen Windfeldmodell (SWM) des Deutschen Wetterdienstes Winddaten flächendeckend für ganz Deutschland im Abstand von 200 m berechnet. Dabei wurde die Höhe über dem Meeresspiegel ebenso berücksichtigt, wie die geographische Lage, die Geländeform und die Art der Landnutzung.“
Beide DWD-Karten, für Sonne und Wind, geben Jahresdurchschnitte an. Als kluger, aber MINT-ferner Geschwätzwissenschaftler oder Politiker könnte man deshalb auf die „geniale“ Idee kommen, man müsse nur den durchschnittlichen erzeugten Jahresbetrag (in kWh) pro installierte Leistung (in kW) kennen, um aus dem jährlichen Strombedarf eine grundlastfähige Versorgung unseres Landes über die Anzahl von WKAs und die Größe von Solarparks sicherzustellen. Ein solches Vorhaben scheitert diesmal aber bereits an der Mathematik, denn bei Dunkelflaute is‘ nunmal nix mit „Alternativer Energie“:
Installierte Leistung (Wind) x 0 Wind + installierte Leistung (Solar) x 0 Sonne = 0 kWh
Mit der sogenannten „Energiewende“ geht in unserem Lande also auch eine „MINT-marginalisierende Intelligenzwende“ einher, die uns mit an Sicherheit grenzender Wahrscheinlichkeit auf das technisch-naturwissenschaftliche Niveau der Schildbürger führen wird, die der Sage nach ihr fensterloses Rathaus mit Säcken voller Sonnenstrahlen zu beleuchten versucht hatten.
*) Erklärung: Diese Abbildung stammt aus einer E-Mail von Dr. Gerhard Kramm mit Datum 26. August 2023 um 06:17 Uhr. Kramms Vertraulichkeitshinweis lautet, Zitat:
“CONFIDENTIALITY WARNING: The information transmitted is intended only for the person or entity to which it is addressed and may contain confidential and/or privileged material. Any review, retransmission, dissemination or other use of, or taking any action in reliance upon, this information by persons or entities other than the intended recipient is prohibited. If you receive this in error, please contact the sender and delete the material from any computer.”
Der unbarmherzige GOOGLE Übersetzer , mit Hervorhebungen:
VERTRAULICHKEITSWARNUNG: Die übermittelten Informationen sind nur für die Person oder Organisation bestimmt, an die sie gerichtet sind, und können vertrauliches und/oder privilegiertes Material enthalten. Jegliche Überprüfung, Weiterübertragung, Verbreitung oder sonstige Nutzung dieser Informationen oder das Ergreifen von Maßnahmen im Vertrauen auf diese Informationen durch andere Personen oder Organisationen als den vorgesehenen Empfänger ist untersagt. Sollten Sie diese fälschlicherweise erhalten, wenden Sie sich bitte an den Absender und löschen Sie das Material von Ihrem Computer.
Und auf dem entsprechenden Mail-Verteiler bin ich der 3. An-Empfänger und damit ausdrücklich zur Nutzung dieser Grafik berechtigt.
**) Erklärung: Um jedweden Beschwerden vorzubeugen, bestätige ich hiermit, ein direkter „An“-Adressat der o. g. E-Mail vom 29. Januar 2021 um 09:58 Uhr mit Kramms PDF-Dokument „kramm_bemerkungen_weber_v3.pdf“ und den dort enthaltenen Abbildungen 15 a und b (hier Abbildungen a* und b* aus Kramm (2021)) zu sein, ebenso, wie u. a. auch die Herren Lüdecke, Limburg und Kirstein. Ich beweise nachfolgend mit der „Confidentiality Warning“ des Dr. Gerhard Kramm die rechtmäßige Nutzung dieser Graphiken, Zitat:
“CONFIDENTIALITY WARNING: The information transmitted is intended only for the person or entity to which it is addressed and may contain confidential and/or privileged material. Any review, retransmission, dissemination or other use of, or taking any action in reliance upon, this information by persons or entities other than the intended recipient is prohibited. If you receive this in error, please contact the sender and delete the material from any computer.”
Der unbestechliche Google-Übersetzer bestätigt mir ausdrücklich, die Inhalte der besagten E-Mail Kramm vom 29. Januar 2021 um 09:58 Uhr rechtmäßig zitiert zu haben:
„VERTRAULICHKEITSWARNUNG: Die übermittelten Informationen sind nur für die Person oder Organisation bestimmt, an die sie gerichtet sind, und können vertrauliches und / oder privilegiertes Material enthalten. Jegliche Überprüfung, Weiterverbreitung, Verbreitung oder sonstige Verwendung oder Ergreifung dieser Informationen durch andere Personen oder Organisationen als den beabsichtigten Empfänger ist untersagt. Wenn Sie dies irrtümlich erhalten, wenden Sie sich bitte an den Absender und löschen Sie das Material von einem beliebigen Computer.“
ERGO: Es verbleiben für eine erlaubte „Überprüfung, Weiterverbreitung, Verbreitung oder sonstige Verwendung oder Ergreifung dieser Informationen“ ausschließlich die von Dr. Kramm „beabsichtigten Empfänger“, und ich bin definitiv der ERSTE „AN“-EMPFÄNGER dieser E-Mail.
 PS: Ich erlaube mir nachfolgend, Ihnen mein neues Buch vorzustellen.
PS: Ich erlaube mir nachfolgend, Ihnen mein neues Buch vorzustellen.
Aus der Einleitung: Mein hemisphärischer Stefan-Boltzmann-Ansatz geht auf eine Veröffentlichung von 2016 in den „Roten Blättern“ der Deutschen Geophysikalischen Gesellschaft zurück und beschreibt die Temperaturgenese auf unserer realen Erde. Ein populärwissenschaftlicher Artikel darüber erschien Anfang 2017 auf Tichys Einblick und wurde dann von EIKE übernommen. Seitdem konnte ich mein hemisphärisches Stefan-Boltzmann-Modell auf EIKE in mehr als 40 Artikeln unter ganz unterschiedlichen Aspekten mit Phänomenen der realen Erde abgleichen und präsentieren. Dafür bedanke ich mich bei der EIKE-Redaktion, insbesondere bei Herrn Dipl.-Ing. Michael Limburg, ganz herzlich.
Herstellung und Verlag: BoD
ISBN: 978-3-75785-943-5
Taschenbuch 36 Seiten – 7,99€
E-Book – 4,99€
Beschreibung: Wir alle stehen aufgrund der fehlerhaften Anwendung eines physikalischen Gesetzes vor einer panischen Dekarbonisierung unseres fossil befeuerten Paradieses. Dieses Buch ist ein Versuch, mein hemisphärisches Stefan-Boltzmann-Modell für den interessierten und mündigen Staatsbürger in verständlicher Form darzustellen. Mein Modell beweist, dass es auf unserer Erde gar keinen „natürlichen atmosphärischen Treibhauseffekt“ geben kann, und eine globale Dekarbonisierung mit dem Ziel einer „Klimarettung“ deshalb völliger Unfug ist. Denn die Berechnung, auf der dieser ominöse Treibhauseffekt beruht, ist reine Mathematik und verletzt die Regeln und Bedingungen der zugrunde liegenden Physik.
Beweis: Versuchen Sie einmal, einen Fußball mit einer Taschenlampe so zu beleuchten, dass auch seine Rückseite einen Teil der Lichtmenge erhält; Sie werden grandios scheitern. Genau so berechnet nun aber die Klimawissenschaft ihre „theoretische Globaltemperatur von -18°C“ für unsere Erde und benötigt deshalb einen ominösen „natürlichen atmosphärischen Treibhauseffekt von 33°C“, um dieses fehlerhafte Klimamodell gegenüber der mit 15°C gemessenen Realität zu stützen.
Es wird höchste Zeit, unsere Welt vom menschengemachten Klimawahn zu befreien, damit auch unsere Kinder und Enkel später noch frei über Nahrung und Energie verfügen können.
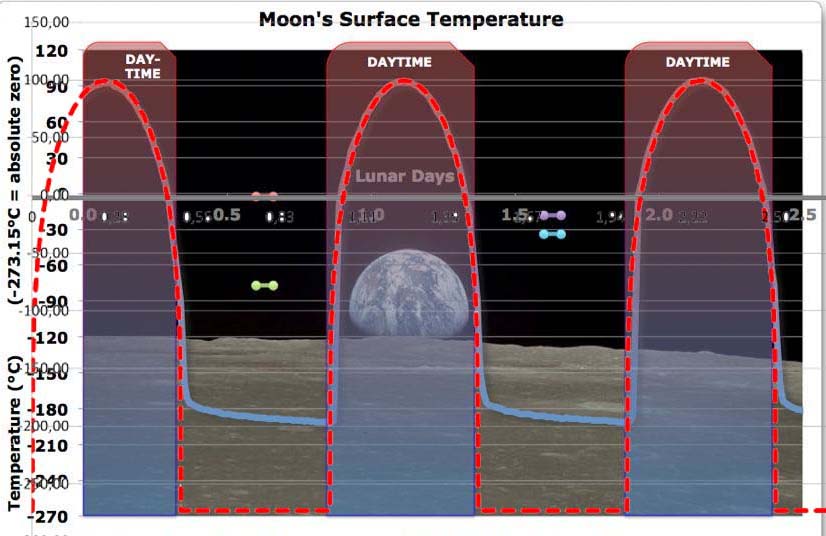
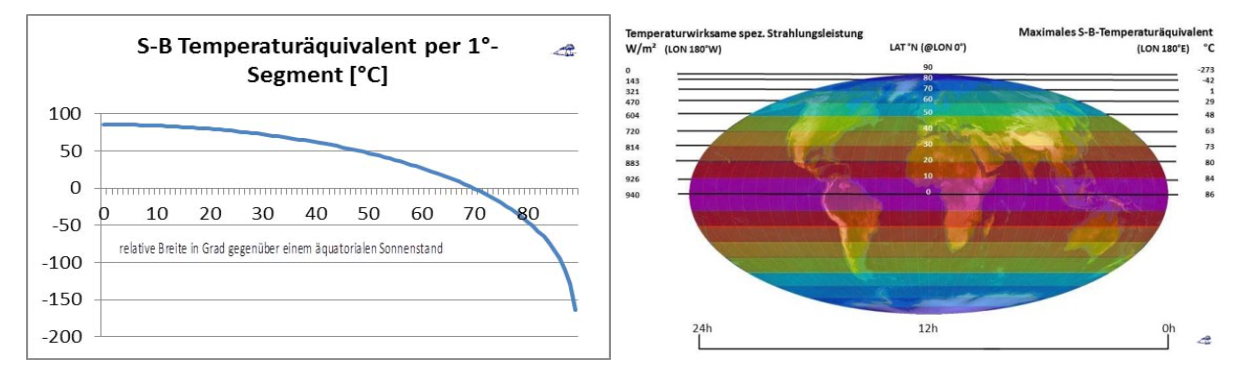 Abbildung 2: Das breitenabhängige S-B-Temperaturäquivalent im Äquinoktium
Abbildung 2: Das breitenabhängige S-B-Temperaturäquivalent im Äquinoktium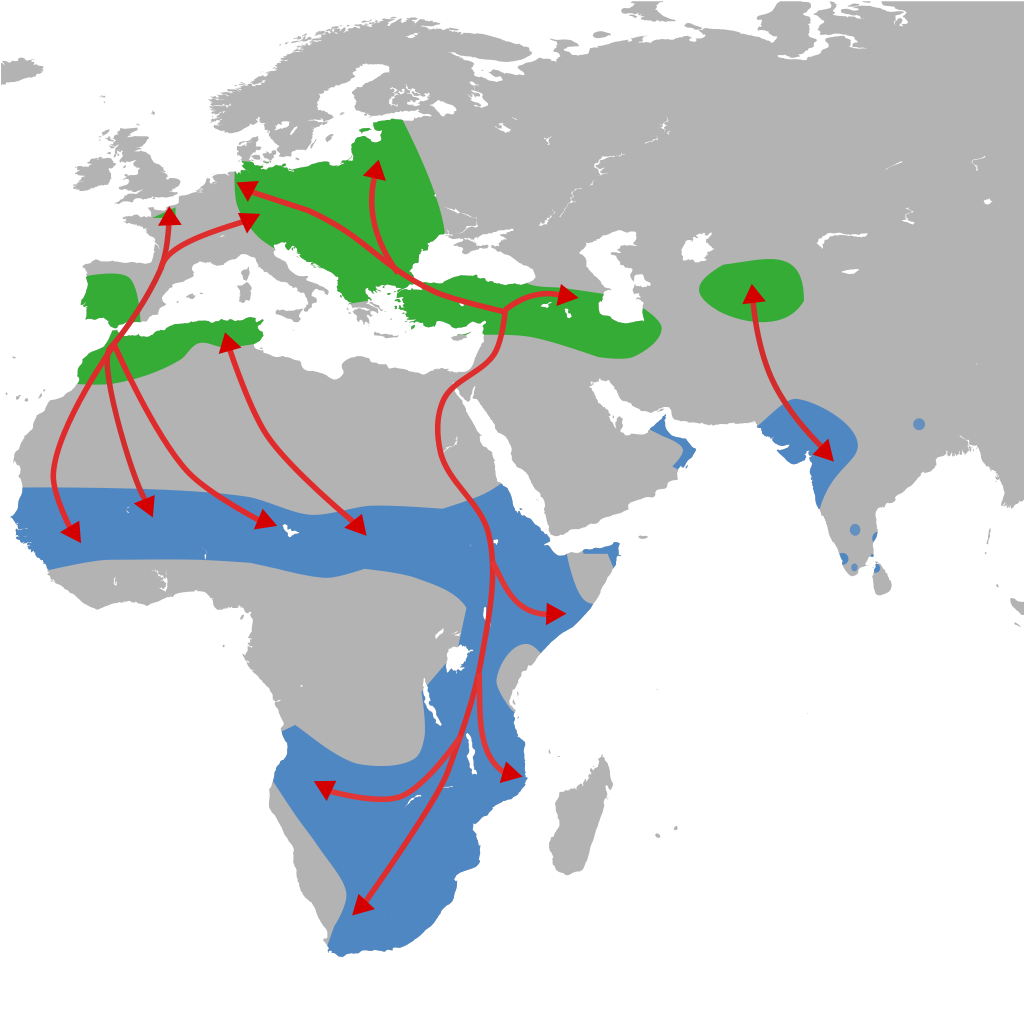 Abbildung 3: Verbreitung und Migration des Weißstorchs basierend auf mehreren Quellen
Abbildung 3: Verbreitung und Migration des Weißstorchs basierend auf mehreren Quellen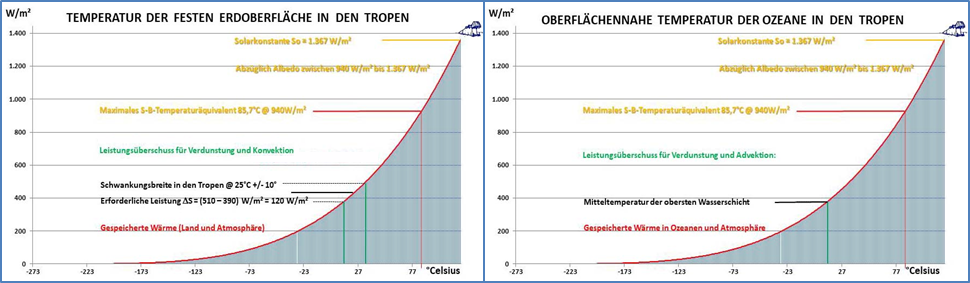 Vielmehr sprechen wir hier von der realen Erde, wir leben also in einem
Vielmehr sprechen wir hier von der realen Erde, wir leben also in einem 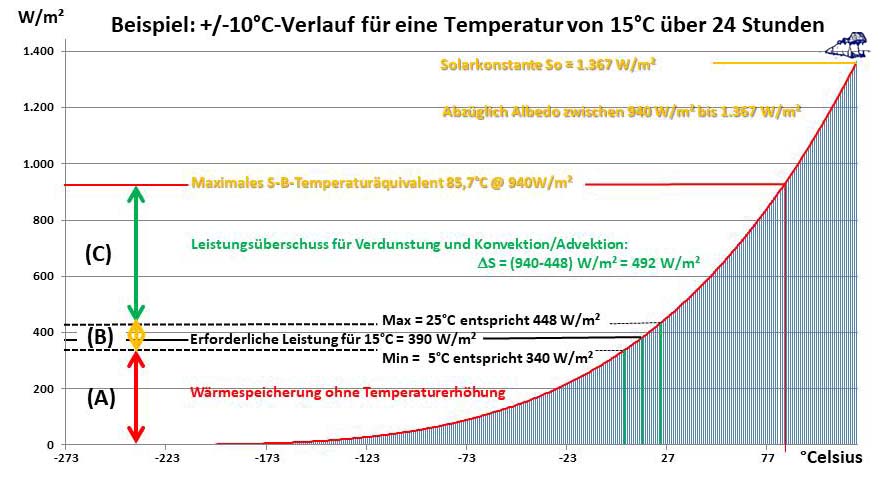 Ich hab‘ das jetzt zwar nicht nachgeprüft, aber man sagt, der Herr H. bezeichne sich als Ozeanograf. Jedenfalls ist ein nächtlicher Temperaturverlust von 0,4 Kelvin durch die tagesseitige solare Einstrahlung leicht zu kompensieren, wie die maximale spezifische Strahlungsleistung der Sonne in Abbildung 5 beweist:
Ich hab‘ das jetzt zwar nicht nachgeprüft, aber man sagt, der Herr H. bezeichne sich als Ozeanograf. Jedenfalls ist ein nächtlicher Temperaturverlust von 0,4 Kelvin durch die tagesseitige solare Einstrahlung leicht zu kompensieren, wie die maximale spezifische Strahlungsleistung der Sonne in Abbildung 5 beweist:
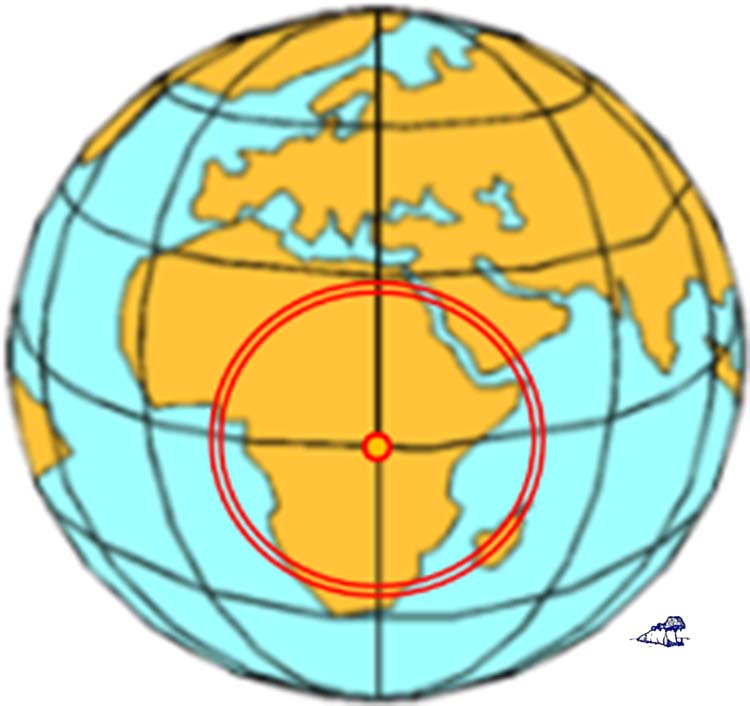 Abbildung: Die Tagseite der Erde, aufgeteilt in konzentrische Ringe von jeweils 1 Grad um den Fußpunkt der Sonne auf dem Äquator, also 0°-1°, 1°-2°, 2°-3°,….., 89°-90°.
Abbildung: Die Tagseite der Erde, aufgeteilt in konzentrische Ringe von jeweils 1 Grad um den Fußpunkt der Sonne auf dem Äquator, also 0°-1°, 1°-2°, 2°-3°,….., 89°-90°.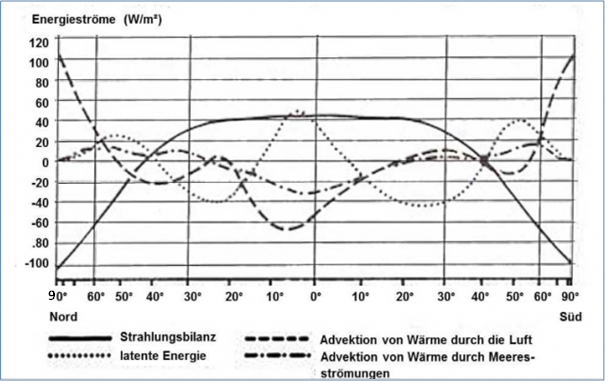
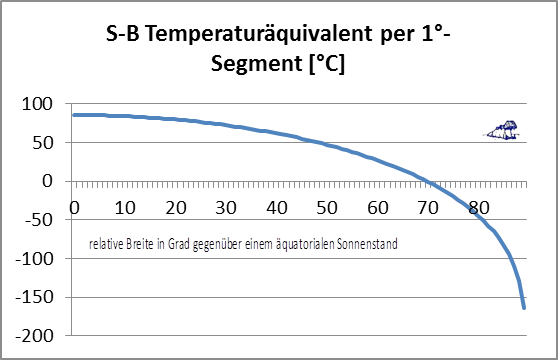
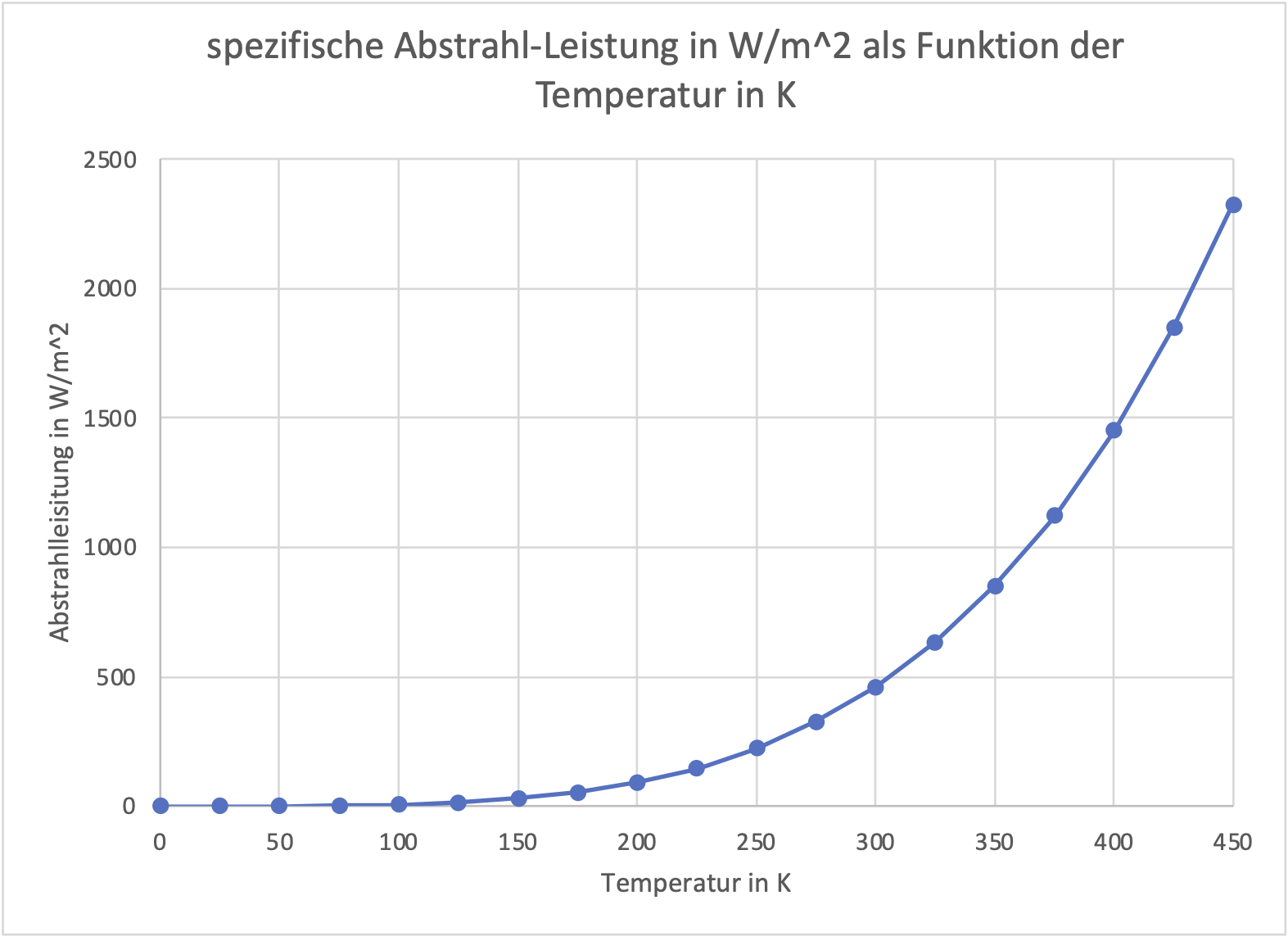
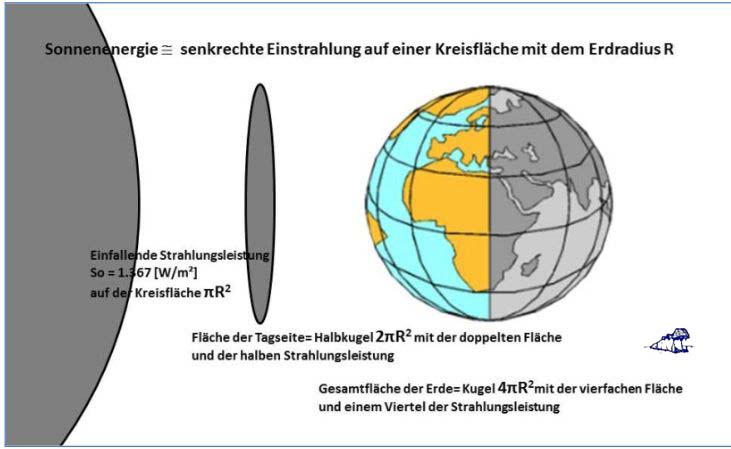
 Abbildung: Earthrise, Farbbild, von
Abbildung: Earthrise, Farbbild, von 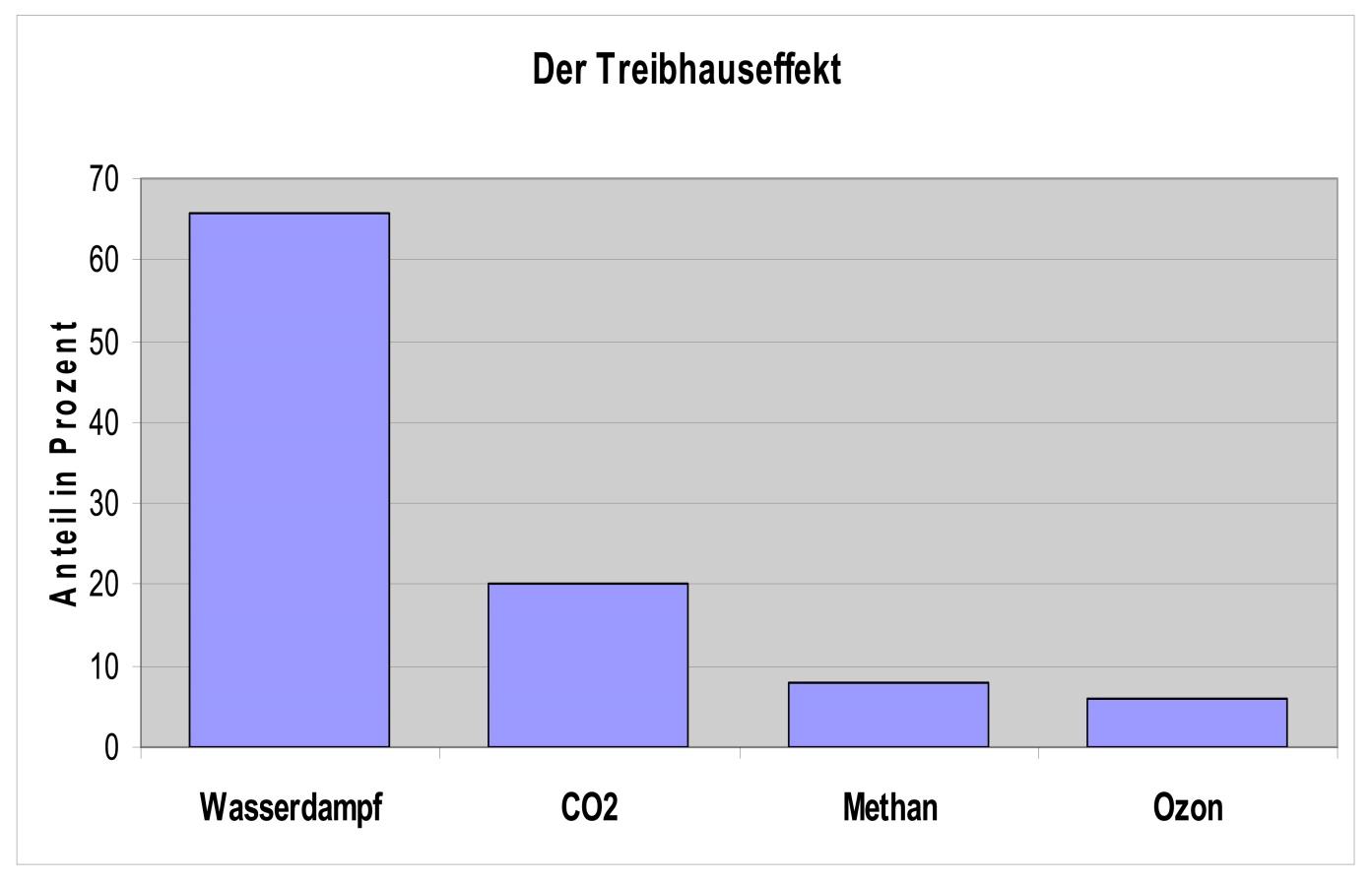
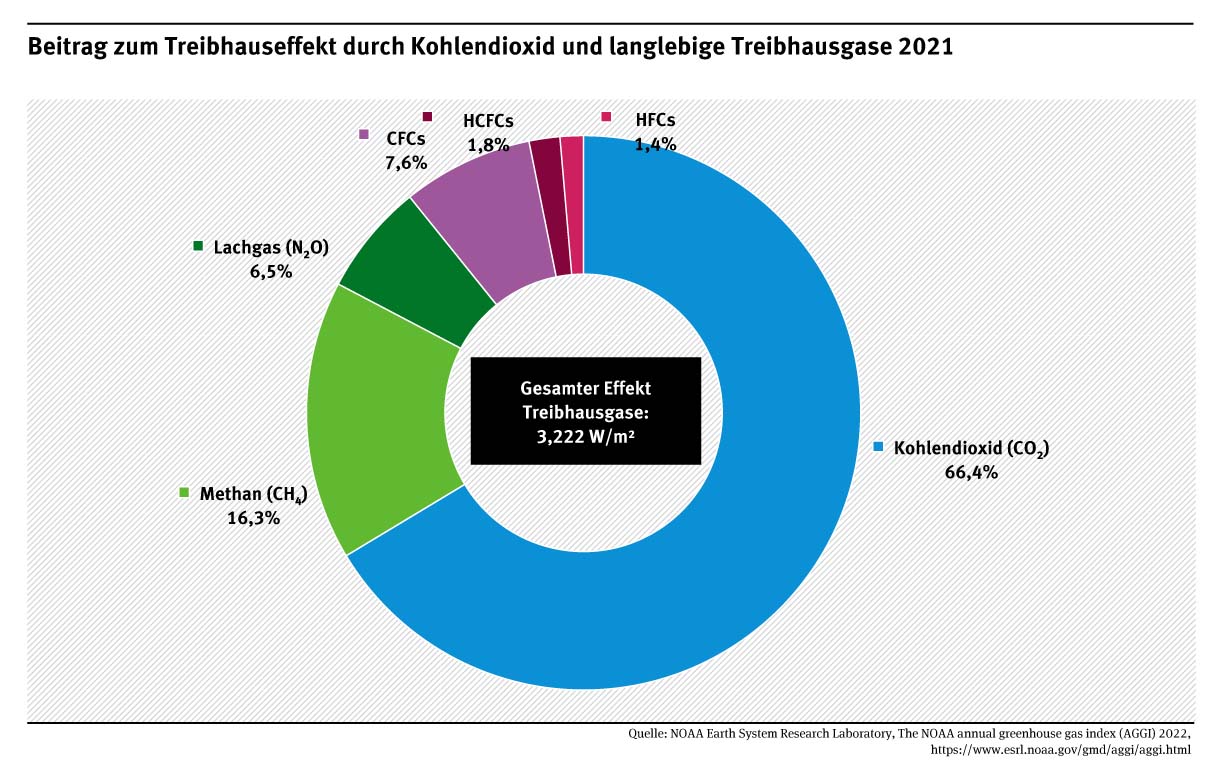 Abbildung: Beitrag zum Treibhauseffekt durch Kohlendioxid und langlebige Treibhausgase 2021
Abbildung: Beitrag zum Treibhauseffekt durch Kohlendioxid und langlebige Treibhausgase 2021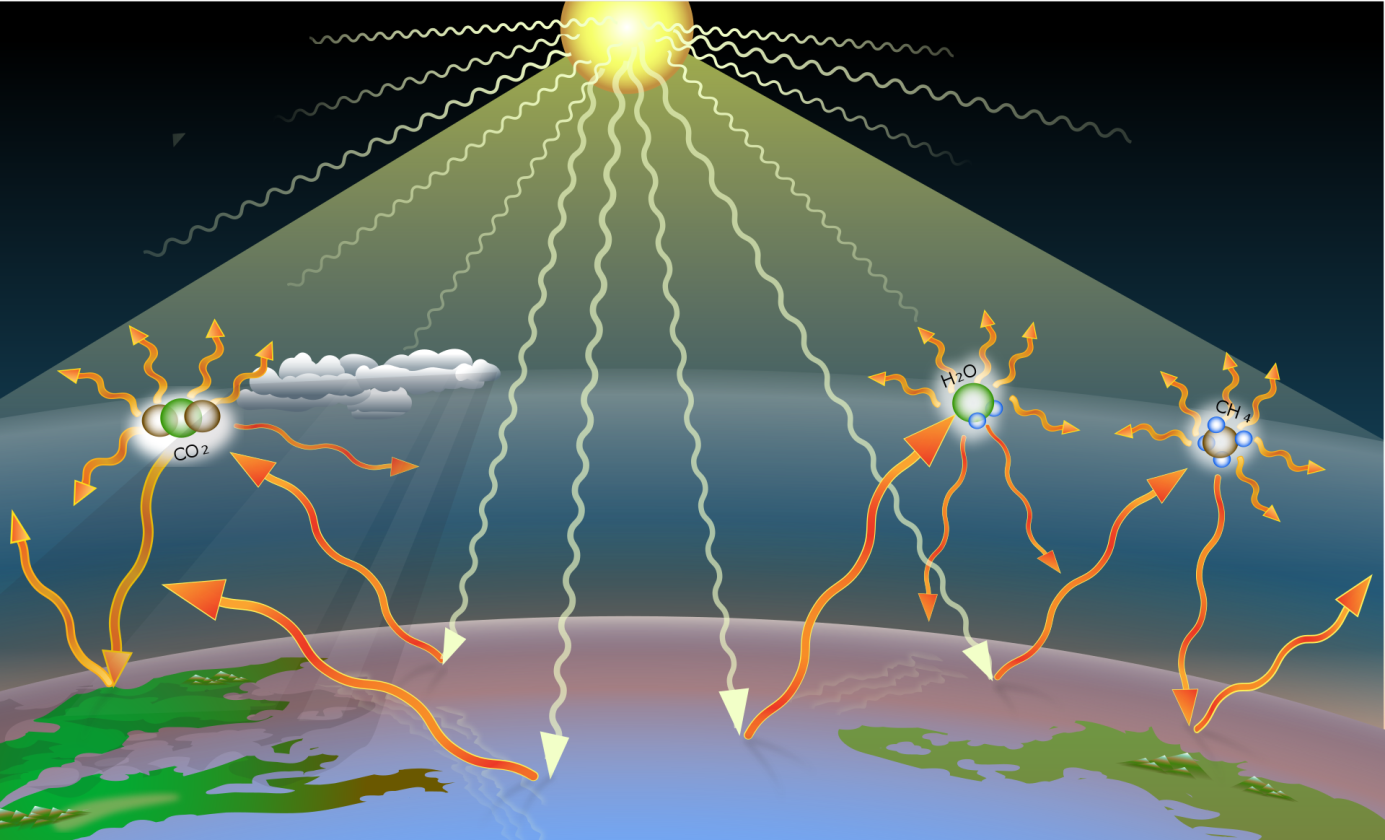
 Abbildung: NOAA
Abbildung: NOAA 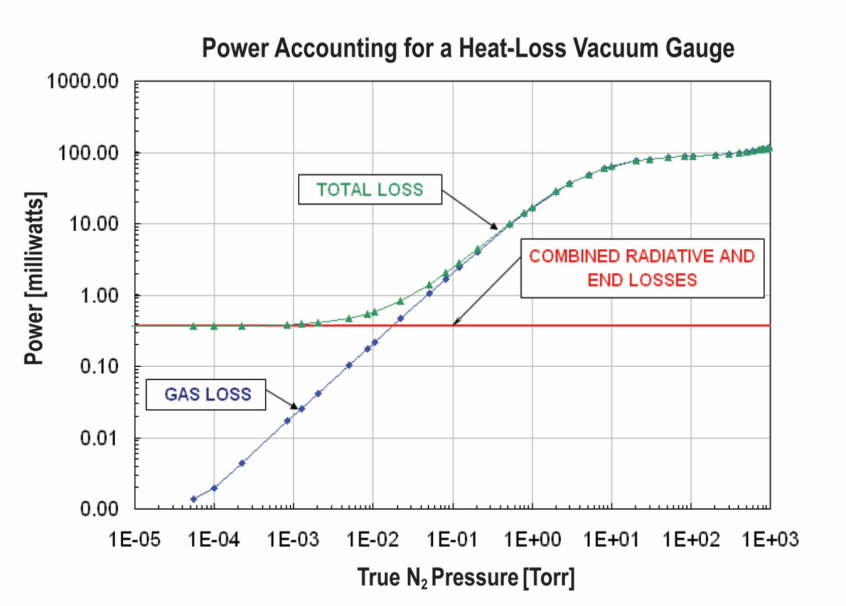 Nur bei der Quantifizierung der terrestrischen Abstrahlung musste ich bisher auf den konventionellen THE-Ansatz mit seiner „Abstrahlungshöhe“ von 5.000 Metern zurückgreifen, damit sich die durchschnittliche solare Einstrahlung und die terrestrische Abstrahlung von netto 235 [W/m²] entsprechen. Dabei ergibt sich diese Abstrahlungshöhe aber lediglich aus der sogenannten „gemessenen globalen Durchschnittstemperatur“ von ca. 15°C und einer Differenz von (-33°C) zur (physikalisch falsch berechneten) S-B-„Abstrahlungstemperatur der Erde“ von (-18°C) über die barometrische Höhenformel mit einem Gradienten von (6,5°C/1.000m) zu physikalisch nichtssagenden 5.000 Metern. Am 20. April 2023 erschien nun hier auf EIKE der Artikel „
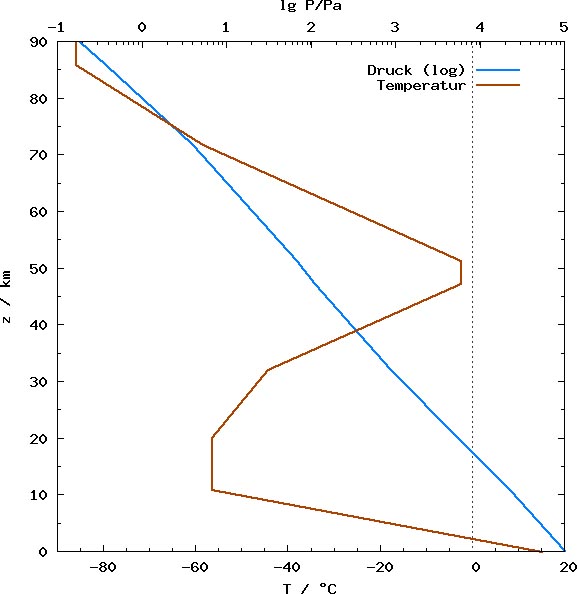
Nur bei der Quantifizierung der terrestrischen Abstrahlung musste ich bisher auf den konventionellen THE-Ansatz mit seiner „Abstrahlungshöhe“ von 5.000 Metern zurückgreifen, damit sich die durchschnittliche solare Einstrahlung und die terrestrische Abstrahlung von netto 235 [W/m²] entsprechen. Dabei ergibt sich diese Abstrahlungshöhe aber lediglich aus der sogenannten „gemessenen globalen Durchschnittstemperatur“ von ca. 15°C und einer Differenz von (-33°C) zur (physikalisch falsch berechneten) S-B-„Abstrahlungstemperatur der Erde“ von (-18°C) über die barometrische Höhenformel mit einem Gradienten von (6,5°C/1.000m) zu physikalisch nichtssagenden 5.000 Metern. Am 20. April 2023 erschien nun hier auf EIKE der Artikel „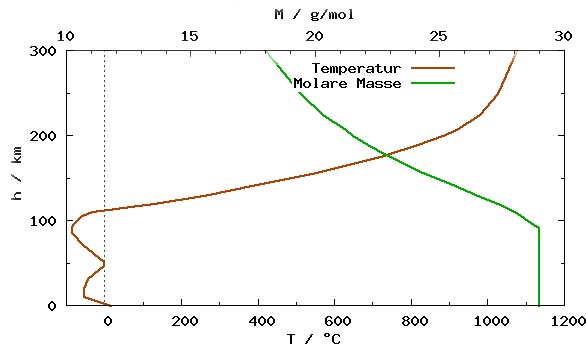 Wenn wir uns jetzt einmal in der folgenden Abbildung 2 den Verlauf von Temperatur und mittlerer molarer Masse der Luft ansehen, so stellen wir fest, dass sich beides bis in 100 km Höhe kaum verändert:
Wenn wir uns jetzt einmal in der folgenden Abbildung 2 den Verlauf von Temperatur und mittlerer molarer Masse der Luft ansehen, so stellen wir fest, dass sich beides bis in 100 km Höhe kaum verändert: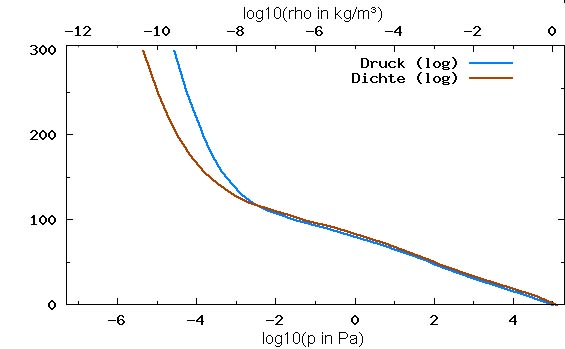 Abbildung 3:
Abbildung 3: