von Uli Weber
*) Exemplarisch wird von der sogenannten Klimawissenschaft wie folgt vorgegangen: Man viertelt einfach die die temperaturwirksame spezifische Strahlungsleistung der Sonne (Solarkonstante * (1-ALBEDO)/4) und berechnet damit ohne Rücksicht auf Tag & Nacht und die geographische Breite eine Stefan-Boltzmann-Inversion. Daraus ergibt sich dann ein „rechnerisches“ S-B-Temperaturäquivalent von -18°C für unsere Erde, das durch einen „natürlichen atmosphärischen Treibhauseffekt“ von 33°C zwangsweise an die vorgeblich „gemessene“ Realität von ca. 15°C angepasst werden muss.
Heute muss man schon lange suchen, um echte physikalische Fakten über die vorgebliche Wirkweise des „natürlichen atmosphärischen Treibhauseffektes“ (THE) zu finden. Eher schon sind konstruierte THE-Biografien greifbar, die bis zu Fourier (1824) zurückreichen. Für die Diskrepanz zwischen der „berechneten“ und der „gemessenen“ globalen Durchschnittstemperatur gibt es eigentlich nur zwei Erklärungen, entweder ist die physikalische Berechnung falsch oder es sind die zugrunde liegenden Messwerte. Herr Dipl.-Ing. Limburg hatte gezeigt, dass die genaue Berechnung einer „gemessenen“ Globaltemperatur aus Einzelmessungen eher Glückssache ist; ein Fehler von 33°C liegt aber weit jenseits aller Fehlergrenzen. Und mein hemisphärisches Stefan-Boltzmann-Modell beweist, dass die konventionelle theoretische Faktor4-Berechnung der Globaltemperatur grundlegend falsch ist. In der Klimawissenschaft hatte man sich allerdings für eine dritte Möglichkeit entschieden und die Lücke von 33°C mit einem bis heute unbewiesen gebliebenen THE ausgefüllt. Wenn man nun ein „gesichertes“ wissenschaftliches Paradigma wie den THE angreift, dann braucht es schon ein paar Jahre, um das neue Modell mit der „gemessenen“ Realität abzugleichen. Das ist für mein hemisphärisches Stefan-Boltzmann-Modell hier auf EIKE in mehr als 40 Artikeln geschehen und dafür bedanke ich mich bei der EIKE-Redaktion, insbesondere bei Herrn Dipl.-Ing M. Limburg, ganz herzlich. Mein hemisphärischer Stefan-Boltzmann-Ansatz geht auf eine Veröffentlichung von 2016 in den „Roten Blättern“ der Deutschen Geophysikalischen Gesellschaft zurück und beschreibt die Temperaturgenese auf unserer realen Erde. Ein populärwissenschaftlicher Artikel darüber erschien Anfang 2017 auf Tichys Einblick und wurde dann von EIKE übernommen. Im gleichen Jahr hatte ich dann auf EIKE mein S-B-Modell mit gemessenen Temperaturen vom Mond abgeglichen und bereits 2019 eine hemisphärische S-B-Berechnung für die Durchschnittstemperatur der Tagseite vorgelegt. Mit den Temperaturen der Nachtseite unserer Erde hatte ich mich dann 2020 beschäftigt.
Und bei letzterem EIKE-Artikel hatte ich bereits die Temperatur der Nachtseite unserer Erde mit der Stefan-Boltzmann-Umgebungsgleichung über die ozeanischen Wärmespeicher erklärt. Denn alle mir bekannten Stefan-Boltzmann-Inversionen, insbesondere das Faktor4-THE-Paradigma, setzen bei 0 Kelvin auf und ignorieren damit die Temperatur der Wärmespeicher unserer Erde. Lediglich die auf unserer Erde solar maximal erzielbare Ortstemperatur kann mit einer korrekten Stefan-Boltzmann-Inversion bestimmt werden. Jenseits des 70. Breitenkreises (jahreszeitlich +/- 23° 26′ 05″) wird die Ortstemperatur dann durch Zuströmung von Wärme gestützt, während dort das S-B-Temperaturäquivalent im jeweiligen Winterhalbjahr zwischen den Äquinoktien unter 0°C geht und zu den Polen hin dann auf -273°C abfällt (Abbildung 2).
Also fangen wir noch mal ganz von vorne an: Der Mond ist das nahezu exakte Modell für eine Erde ohne Atmosphäre, freies Wasser und Vegetation. Die solare Einstrahlung auf der Tagseite des Mondes erreicht in guter Näherung das rechnerische Stefan-Boltzmann-Temperauräquivalent:
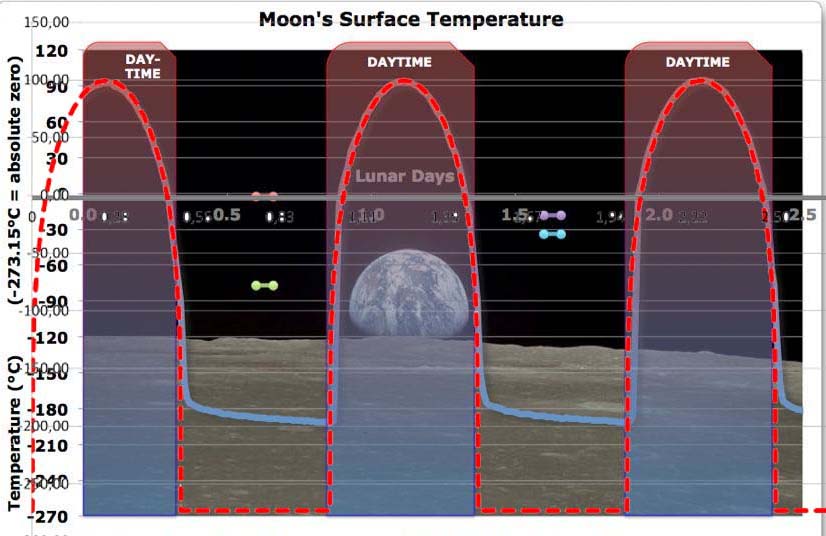
Abbildung 1: Temperaturvergleich für die Tagseite des Mondes. Gemessene Oberflächentemperatur auf dem Mond am Landeplatz von Apollo 15 (blau) aus einem Artikel auf EIKE, Primärquelle WUWT. Rot: Hemisphärisch berechnetes S-B-Temperaturäquivalent @ Landestelle Apollo 15
Anmerkung: Ein weiterer Vergleich mit Temperaturdaten vom Mond ist hier zu finden
Williams et al. (2017) stützen ausdrücklich meinen hemisphärischen S-B-Ansatz für die Tagseite des Mondes, Zitat mit Hervorhebungen:
„The lunar regolith is highly insulating due to its low density and thermal conductivity (Linsky, 1966, Cremers and Birkebak, 1971, Keihm and Langseth, 1973) and therefore heat flow into the subsurface during the day is small compared to the incident solar flux (Vasavada et al., 1999, 2012). Daytime temperatures can therefore be approximated from the balance of incoming solar flux and outgoing thermal emission:”
Der Google-Übersetzer: „Der Mondregolith ist aufgrund seiner geringen Dichte und Wärmeleitfähigkeit hochisolierend (Linsky, 1966, Cremers und Birkebak, 1971, Keihm und Langseth, 1973) und daher ist der Wärmefluss in den Untergrund während des Tages im Vergleich zum einfallenden Sonnenfluss gering (Vasavada et al., 1999, 2012). Die Tagestemperaturen können daher aus dem Gleichgewicht des einfallenden Sonnenflusses und der ausgehenden Wärmeabgabe angenähert werden:“
Der Unterschied zwischen Mond und Erde besteht im Wesentlichen aus der Atmosphäre, dem Wasser in Ozeanen, Seen und Flüssen sowie der Vegetation; den glaubensgerechten Einfluss der Fauna lassen wir hier mal beiseite. Weil auf unserer Erde bei gleicher Solarkonstante der Temperaturverlauf völlig anders ist als auf dem Mond, muss das also an Atmosphäre, Wasser und Flora liegen. In den Artikeln zu meinem hemisphärischen Stefan-Boltzmann-Modell habe ich die aus der solaren Einstrahlung berechnete Temperatur nicht ohne Grund meistens als (1) Stefan-Boltzmann-Temperaturäquivalent bezeichnet:
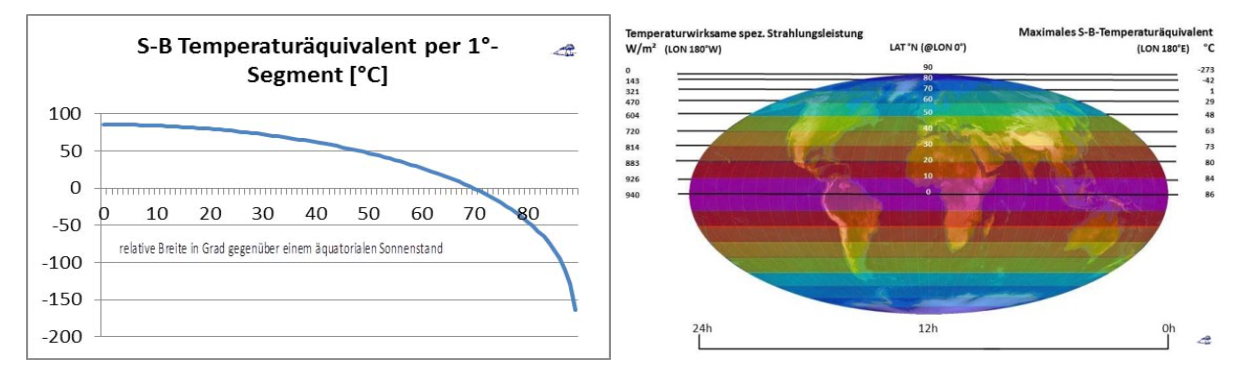 Abbildung 2: Das breitenabhängige S-B-Temperaturäquivalent im Äquinoktium
Abbildung 2: Das breitenabhängige S-B-Temperaturäquivalent im Äquinoktium
Links: Das vom Zenitwinkel der Sonne abhängige maximale S-B Temperaturäquivalent für 1°-Segmente zwischen 0° und 90° nördlicher und südlicher Breite in [°C]
Rechts: Die maximale breitenabhängige temperaturwirksame solare Strahlungsleistung (linke Skala) und das resultierende S-B-Temperaturäquivalent (rechte Skala) über einen 24-Stunden-Tag im Äquinoktium
Mit unterlegter Mollweide-Projektion (Copyright L. Rohwedder – Lizenz CC BY-SA 3.0)
Ich habe also nicht etwa das tagesdurchschnittliche S-B-Temperaturäquivalent verwendet, sondern ausdrücklich das (2) MAXIMALE S-B-Temperaturäquivalent beim Höchststand der Sonne. Warum? – Erstens (1) handelt es sich um keine echte Temperatur, sondern vielmehr um die S-B-Inversion aus einer spezifischen Strahlungsleistung, die eine solche Temperatur erzeugen könnte, wie beispielsweise für den Mond nachgewiesen wurde. Zweitens (2) muss man sich bei einem Temperaturvergleich über die gesamte Erde und ein ganzes Jahr auf einen einzigen Parameter beschränken, sonst wird’s unübersichtlich. Und da wäre ein Durchschnittswert nicht so gut, denn durch einen solchen Durchschnitt wird die Temperatur-Strahlungs-Beziehung aus dem S-B-Gesetz unwiederbringlich aufgehoben und man wäre am Ende der Analyse. Die obige Abbildung zeigt also an, welche maximale Temperatur eine Ortslage auf dem jeweiligen Breitenkreis im Äquinoktium bei einer S-B-Inversion erreichen könnte.
Wärme (Energie) kann durch unterschiedliche physikalische Prozesse transportiert werden, also schaunmermal:
Strahlungstransport: „Wenn sich elektromagnetische Strahlung in einem Medium ausbreitet (ganz gleich ob in der Photonen-Betrachtung oder Feldbetrachtung), wird sie von dem Medium (insbesondere von dessen Atomen und Ionen) absorbiert, gestreut oder kann das Medium verlassen. Diese Prozesse bzw. die Beschreibung dieser Prozesse nennt man Strahlungstransport.“
Wärmeleitung: „Wärmeleitung – auch Wärmediffusion oder Konduktion genannt – ist ein Mechanismus zum Transport von thermischer Energie. Wärme fließt dabei – gemäß dem zweiten Hauptsatz der Thermodynamik – immer nur in Richtung geringerer Temperatur. Dabei geht keine Wärmeenergie verloren; es gilt der Energieerhaltungssatz.“
Konvektion: „Konvektion oder Strömungstransport ist der Transport physikalischer Zustandsgrößen in strömenden Gasen oder Flüssigkeiten. Physikalische Zustandsgrößen sind dabei beispielsweise mitgeführte Wärme, Materie oder Impuls. Der konvektive Transport thermischer Energie ist ein Mechanismus des Wärmetransports und wird auch Wärmemitführung genannt.“
Verdunstung: „Bei einer Verdunstung geht ein Stoff vom flüssigen in den gasförmigen Zustand über, ohne dabei die Siedetemperatur zu erreichen.[1] Zur Verdunstung kommt es, wenn die Gasphase über der Flüssigkeit noch nicht mit Dampf gesättigt ist. […..] Zur Verdampfung ist Wärmeenergie nötig, die aus der flüssigen Phase oder der darüberstreichenden Gasphase stammt. Beim Verdunstungsprozess kühlt sich eine der beiden Phasen ab, dies führt zur sogenannten Verdunstungskühlung.“
Warum sind nun die Temperaturen von Mond und Erde so unterschiedlich?
Auf dem Mond gibt es lediglich Strahlungstransport und Wärmeleitung. Unter Vernachlässigung der Wärmeleitung wird fast die gesamte Strahlungsleistung der Sonne in Wärme umgesetzt, was in der Abbildung mit dem Temperaturvergleich zwischen Messung und S-B-Berechnung nachgewiesen wurde. Auf der Erde kommen alle vier Arten des Wärmetransports vor. Und das ist auch der Grund, weshalb auf unserer Erde das maximale S-B-Temperaturäquivalent eben nicht erreicht wird. Dazu hatte ich zuletzt hier unter (H) geschrieben, Zitat:
„Es ist offensichtlich, dass auf der Erdoberfläche die rein rechnerische Temperatur nach dem Stefan-Boltzmann-Gesetz aus der solaren Einstrahlung nirgendwo erreicht wird. Andererseits wissen wir aber aus dem Energieerhaltungssatz der Wärmelehre, dass Energie nicht einfach so verschwinden kann. Vielmehr vermindert der ständige Abfluss von Wärme durch Konvektion und Verdunstung den durch die Sonneneinstrahlung bedingten örtlichen Temperaturanstieg. Dabei spielt der Energietransport durch Atmosphäre und Ozeane aus Tropen und Subtropen in die Polarzonen hinein eine ganz wesentliche Rolle für unser Klima.“
Offenbar funktioniert der Strahlungstransport auf der Erde. Die Sonne strahlt auf der Tagseite der Erde an jedem Ort mit einer temperaturwirksamen HF-Strahlungsleistung von
Slokal = (1-Albedo) x Solarkonstante (=S0) x COS Zenitwinkel (N-S) x SIN Azimut (E-W)
Anmerkung: In meinem hemisphärischen S-B-Modell betrachte ich nur den mittäglichen maximalen Azimut @ 90° mit (SIN (90°) = 1).
Allerdings wird nirgendwo auf der Erde dieses maximale S-B-Temperaturäquivalent erreicht. Wir müssen also schauen, woran das liegt. Dazu stehen uns noch Wärmeleitung, Konvektion und Verdunstung zur Verfügung, die Wärme vom Ort ihres Entstehens abtransportieren können. Die Wärmeleitung lassen wir hier aber mal außen vor, weil sie auf dem Mond im Abgleich von Tag und Nacht lediglich etwa 2 [Wm²] ausmacht. Die Konvektion treibt dagegen auf der Erde die globalen Strömungen in Ozeanen und Atmosphäre an.
Ein kurzer und verständnisfördernder Einschub: Lieber Leser, fällt Ihnen an den Flugrouten der Weißstörche in der folgenden Abbildung vielleicht irgendetwas auf?
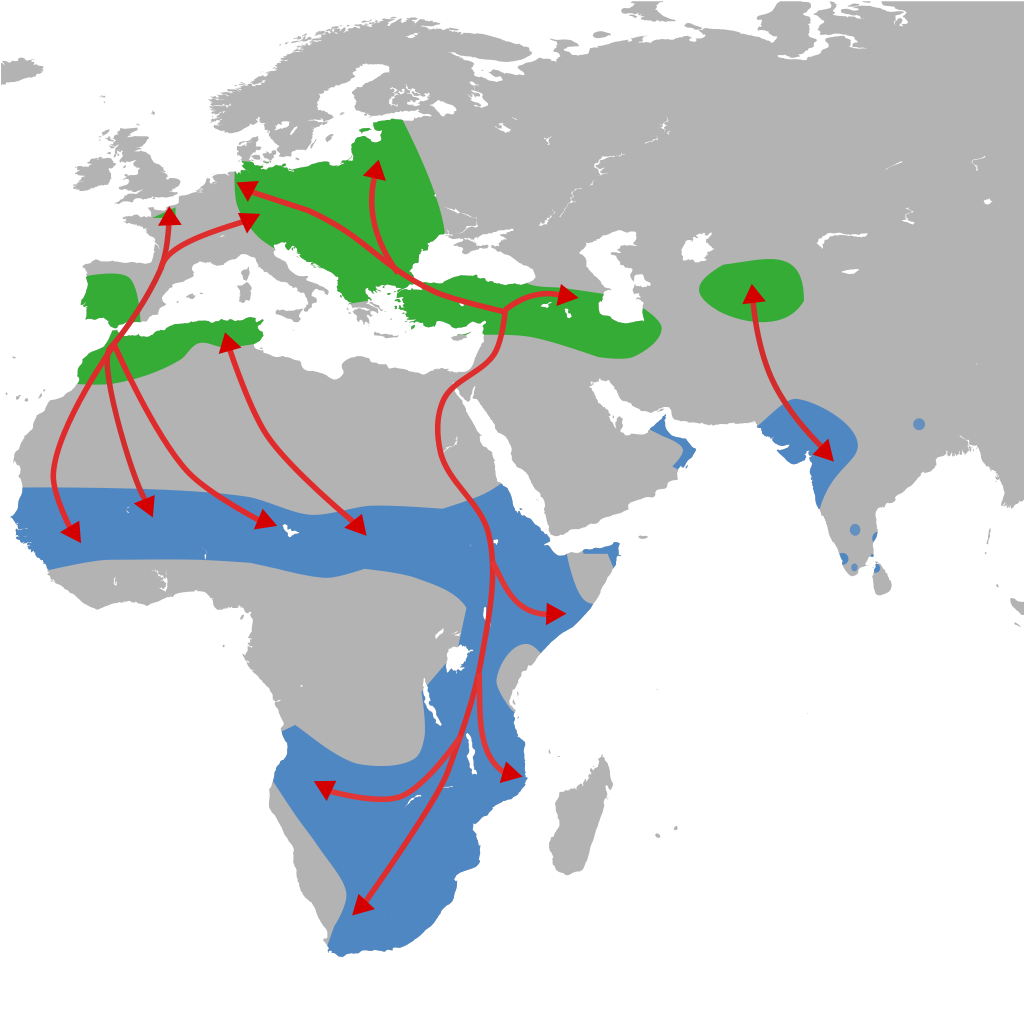 Abbildung 3: Verbreitung und Migration des Weißstorchs basierend auf mehreren Quellen
Abbildung 3: Verbreitung und Migration des Weißstorchs basierend auf mehreren Quellen
Autor Shyamal, Lizenz CC0 1.0
Richtig, die Störche überfliegen die offene See nicht, sondern halten sich vielmehr an Meerengen. Das liegt daran, dass auf offener See das Potential für atmosphärische Konvektion nicht sehr groß ist, weil die Konvektion von der Temperaturdifferenz (Oberfläche vs. Atmosphäre) angetrieben wird. Auf dem Meer herrschen vielmehr Advektion (horizontale Verfrachtung) und Verdunstung (latente Energie) vor. Auf den Landmassen und Inseln dagegen kommt es durch die solare Erwärmung des Erdbodens zu einer Erwärmung der darüber liegenden Luft, die, dadurch spezifisch leichter geworden, einen konvektiven atmosphärischen Kreislauf als „Luftkühlung“ für den Erdboden in Gang setzt; hier überwiegt also die Konvektion. Und dabei kommt es natürlich auch, je nach Feuchtigkeitsgehalt des Bodens, zur Verdunstung von Wasser. Wenn der Erdboden allerdings mit Vegetation bewachsen ist, sieht es etwas anders aus. Pflanzen benötigen Licht, Wasser und CO2 für die Photosynthese. Wenn also die Sonne auf eine pflanzenbewachsene Erdoberfläche scheint, dann beginnt dort sofort die Photosynthese. Die Blattspalte (Stromata) der Pflanzen öffnen sich und setzen durch Verdunstung den „Kreislauf“ der Pflanze in Gang; hier hat also die Verdunstung einen großen Anteil, wie sie bei einem Waldspaziergang an einem heißen Tag jederzeit feststellen können.
Halten wir fest: Energie geht nicht verloren (1. HS der Thermodynamik), sondern wird nur in eine andere Form überführt.
Aus der tagseitigen Sonneneinstrahlung wird also nicht nur die Oberflächentemperatur generiert, sondern auch die atmosphärische Konvektion, die ozeanische Advektion sowie die Verdunstung und die Photosynthese der Pflanzen. Kein Wunder also, dass lokal das rechnerische S-B-Temperaturäquivalent in den Tropen und Subtropen unserer Erde nirgendwo erreicht wird, denn diese Gegenden sind der Klimamotor unseres Planeten.
Und nun kommt die Ergänzung zur oben erwähnten S-B-Umgebungsgleichung für die Nachtseite der Erde: Weder die Tagseite der realen Erde noch ihre zwischenzeitlich abgekühlte Nachtseite muss von der Sonne tagtäglich von 0 Kelvin auf ihre jeweilige Orts- respektive „Durchschnittstemperatur“ erwärmt werden.
 Vielmehr sprechen wir hier von der realen Erde, wir leben also in einem „eingeschwungenen“ System, in dem die Energiespeicher unserer Erde (im Wesentlichen die Ozeane) bereits voll aufgeladen sind, und zwar von Anbeginn der Erde an. Die Ozeane sind in der Frühzeit der Erde entstanden, als die Erde sich langsam abkühlte und eine feste Oberfläche gebildet hatte. Die Meere waren also zuerst heiß und sind dann bis zu einem Gleichgewicht zwischen Abkühlung und zugeführter Sonnenenergie abgekühlt. Seither haben die Ozeane mit einem Zeitverzug von Jahrhunderten jede Klimaänderung „mitgemacht“ und die jeweiligen individuellen Ortstemperaturen oder meinetwegen auch eine sogenannte „globale Durchschnittstemperatur“ auf der Nachthemisphäre jederzeit nach unten abgesichert:
Vielmehr sprechen wir hier von der realen Erde, wir leben also in einem „eingeschwungenen“ System, in dem die Energiespeicher unserer Erde (im Wesentlichen die Ozeane) bereits voll aufgeladen sind, und zwar von Anbeginn der Erde an. Die Ozeane sind in der Frühzeit der Erde entstanden, als die Erde sich langsam abkühlte und eine feste Oberfläche gebildet hatte. Die Meere waren also zuerst heiß und sind dann bis zu einem Gleichgewicht zwischen Abkühlung und zugeführter Sonnenenergie abgekühlt. Seither haben die Ozeane mit einem Zeitverzug von Jahrhunderten jede Klimaänderung „mitgemacht“ und die jeweiligen individuellen Ortstemperaturen oder meinetwegen auch eine sogenannte „globale Durchschnittstemperatur“ auf der Nachthemisphäre jederzeit nach unten abgesichert:
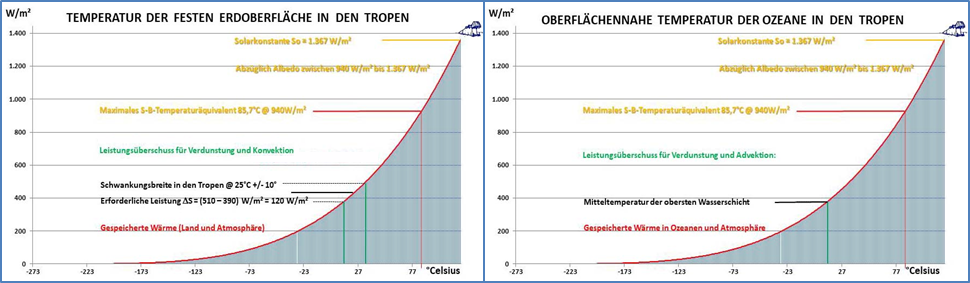
Abbildung 4: Die Beziehung zwischen Temperatur und spezifischer Strahlungsleistung im Stefan-Boltzmann-Gesetz am Beispiel der Tropen. Diese Grafik gilt mit geänderter maximaler solarer Einstrahlung und Ortstemperatur ebenfalls für andere geografische Breiten
Sowohl die Temperatur auf der Tagseite der Erde als auch die Temperatur auf deren Nachseite setzen auf der Temperatur der globalen Wärmespeicher auf, die deutlich größer ist als 0 Kelvin. Diese Temperatur wird im Wesentlichen von der Durchschnittstemperatur der Ozeane (ca. 20°C) bestimmt und muss nicht erst durch die solare Einstrahlung erzeugt werden, denn sie ist in diesem „eingeschwungenen“ System ja bereits vorhanden. Der Wärmeinhalt der Ozeane beträgt mehr als 4,59*10^26 Joule oder 50.000 Tage Sonneneinstrahlung, und der nächtliche Wärmeverlust wird auf der Tagseite ständig neu „aufgefüllt“, wie die solaren Residuen für Land und Meer in Abbildung 4 deutlich zeigen. Die nachfolgende Berechnung vom 9. Juli 2023 um 8:27 zum nächtlichen Temperaturverlust der Ozeane ist einem Herrn Thomas Heinemann zu danken, Zitat mit Hervorhebungen:
„Zur Abkühlungsrate dT/dt = -10^17 W/C wenn sich die Energienentnahme aus dem Ozean zunächst aus den oberen 10 m anfängt (an der Oberfläche startet es), so ist C der obenen 10 m = 4,33e+7 J/K/m2 * 2,55e+14 m2 = 1,1e+22 J/K, macht
Die Temperatur an der Erdoberfläche nimmt also mit
dT/dt = -1e+17 W/1,1e+22 Ws/K = – 9,1e-6 K/s = – 0,4 K/Nacht ab.
Die Wärmekapazität des Ozeans ist C = 4200 J/kg/K * O * 1030 kg/m3 * h = 2,2e+21 J/K/m * h, wobei O der Teil der Erdoberfläche ist.“
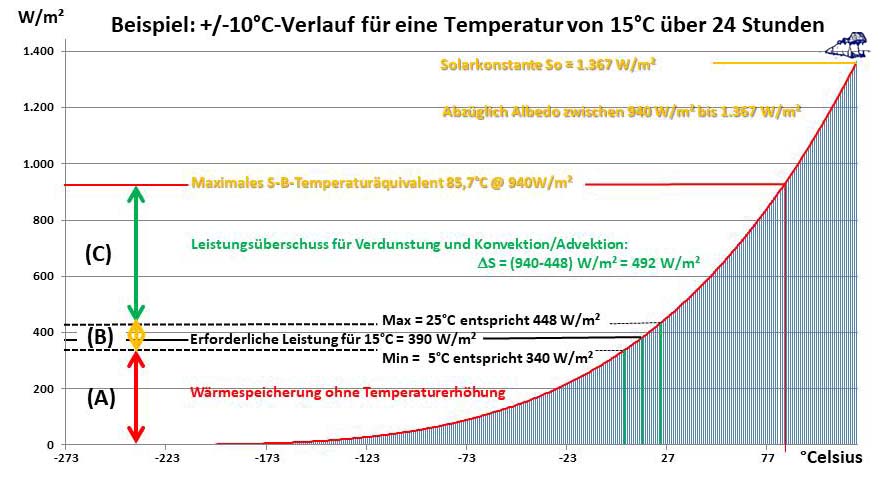 Ich hab‘ das jetzt zwar nicht nachgeprüft, aber man sagt, der Herr H. bezeichne sich als Ozeanograf. Jedenfalls ist ein nächtlicher Temperaturverlust von 0,4 Kelvin durch die tagesseitige solare Einstrahlung leicht zu kompensieren, wie die maximale spezifische Strahlungsleistung der Sonne in Abbildung 5 beweist:
Ich hab‘ das jetzt zwar nicht nachgeprüft, aber man sagt, der Herr H. bezeichne sich als Ozeanograf. Jedenfalls ist ein nächtlicher Temperaturverlust von 0,4 Kelvin durch die tagesseitige solare Einstrahlung leicht zu kompensieren, wie die maximale spezifische Strahlungsleistung der Sonne in Abbildung 5 beweist:
Abbildung 5: Die Beziehung zwischen Temperatur und spezifischer Strahlungsleistung im Stefan-Boltzmann-Gesetz am Beispiel des Leistungsbedarfs einer Oberflächentemperatur von 15°C +/-10°C
Meine tagseitige Berechnung von ca. 15°C hatte auf der Absoluten Temperatur von 0 Kelvin aufgesetzt und den Wärmeinhalt der globalen Zirkulationen nicht weiter betrachtet. Bei Umgebungstemperatur ist da also noch viel Potential nach oben, denn die Genese der tagseitigen Ortstemperatur zählt ja erst von der minimalen Umgebungstemperatur an. Der Bereich (A) der solaren Einstrahlung liegt unter dem S-B-Strahlungsäquivalent der Minimumtemperatur und trägt daher nicht zur Temperatur bei, sondern erhöht lediglich den Energieinhalt. Der Bereich (B) erhöht dann die Temperatur vom Minimum aufs Maximum, während gleichzeitig der Bereich (C) durch Verdunstung sowie Konvektion/Advektion aus der Einstrahlung „abgeschöpft“ wird. Es wird hieraus also unmittelbar deutlich, dass die Energie in den globalen Zirkulationen von Atmosphäre und Ozeanen auf der Tagseite der Erde zusammen mit der Temperaturgenese „wiederaufgeladen“ wird. In meinem EIKE-Artikel, „Machen wir mal ein Gedankenexperiment: Es gibt gar keine Erde!“, vom 10. August 2017 hatte ich unter Punkt 6. ERKENNTNIS vermerkt, Zitat:
„Wenn die bodennahe örtliche Nachttemperatur nach der Umgebungsgleichung des S-B Gesetzes durch einen Wärmezufluss aus den atmosphärischen und ozeanischen Zirkulationen gestützt wird, dann sind alle weiteren Spekulationen über einen „natürlichen“ atmosphärischen Treibhauseffekt hinfällig.
Sinkt also nachts die örtliche bodennahe Temperatur unter die Temperatur des ortsnahen Ozeans, dann erfolgt sofort ein Wärmefluss aus diesem Wärmespeicher. Anstelle einer weiteren Abkühlung der betrachteten Senke erfolgt dann also ein zusätzlicher Wärmefluss in diese Senke hinein. Im Umkehrschluss wird diese Senke also umso tiefer werden, je weiter entfernt vom Ozean sie sich befindet.“
Die solare HF-Einstrahlung muss also auf der jeweiligen Tagseite den örtlichen IR-Strahlungsverlust der Erdoberfläche ausgleichen und erzeugt die tatsächlich erreichte Ortstemperatur. Die überschüssige Leistungsspitze treibt dann die globalen Zirkulationen in Ozeanen oder Atmosphäre an. Und selbst dann, wenn man die Sonne einen Mond-Tag lang (knapp ein Monat) „dimmen“ oder gar „ausknipsen“ würde, fällt die „Globaltemperatur“ wegen der riesigen terrestrischen Wärmespeicher nicht auf die morgendliche Mond-Temperatur von ca. -200°C ab. Der Beweis dafür ist das „Jahr ohne Sommer“ im 19. Jahrhundert, das man in den Diagrammen der jährlichen Durchschnittstemperaturen kaum identifizieren kann.
Der temperaturbestimmende Teil der solaren Einstrahlung ist wiederum lediglich von der terrestrischen Albedo abhängig. Somit setzt die von mir mittels meines hemisphärischen S-B-Modells aus dem Maximum des örtlichen S-B-Strahlungsäquivalentes berechnete „globale Durchschnittstemperatur“ von ca. 15°C nicht etwa, wie ursprünglich angenommen, auf einer Temperatur von 0 Kelvin auf, sondern auf der morgendlichen Temperatur der Ozeane. Das auf diese Weise ermittelte maximale S-B-Temperaturäquivalent stellt damit lediglich die physikalisch maximal erreichbare Orts- bzw. Durchschnittstemperatur durch die Sonneneinstrahlung auf unserer Erde dar, und zwar bei der augenblicklichen Albedo unserer Erde. Und bei dieser aktuellen Albedo halten sich wiederum solare HF-Einstrahlung und terrestrische IR-Abstrahlung gerade die Waage. Der Mond ist also das nahezu perfekte Modell für eine Erde ohne Atmosphäre, freies Wasser und Vegetation – sowie Wärmespeicherung.
Um es noch einmal ganz deutlich und physikalisch unkorrekt (weil ohne Sinus und Cosinus) zu sagen: Aufbauend auf der Temperatur der voll „aufgeladenen“ globalen Wärmespeicher erhält die Erde auf der Tagseite durchschnittlich 470 [W/m²] solare HF-Einstrahlung und verliert über ihre gesamte Oberfläche durchschnittlich 235 [W/m²] IR-Abstrahlung. Und damit hält sie dann dauerhaft ihre sogenannte „globale Durchschnittstemperatur“. So einfach isses nun mal, und der „natürliche atmosphärische Treibhauseffekt“ gehört folglich in die Welt der Paraphysik!
Was die sogenannte „Klimaforschung“ angeht so verwundert es schon, dass sie seit Alexander von Humboldt aus sich heraus nicht mehr geleistet hat, als den wesentlichen Klimaantrieb auf unserer Erde mit einer veritablen Physikwende einem mystischen „natürlichen atmosphärischen Treibhauseffekt“ (THE) zuzuschreiben und darauf ihre sogenannten Klimamodelle aufzubauen. Dieser THE ist rein fiktiv, und zwar deshalb, weil die Sonneneinstrahlung von der Tagseite der Erde trotz einer eindeutigen T^4-Beziehung aus dem S-B-Gesetz mit einem ominösen „Flächenfaktor4“ über die Gesamtfläche der Erde inklusive ihrer Nachtseite verteilt wird. Die milliardenschweren computergestützten „Klimawendemodelle“ für einen „Glaskugelblick in die Klimazukunft“ sind dabei lediglich geistlose „Rechenknechte“ ihrer klimareligiösen Schöpfer, die den globalisierten THE-Aberglauben an einen monokausalen CO2-Klimaantrieb binden. Und mit solch hundsmiserablen (Faktor4+CO2)-gesteuerten Klimamodellen sind MINT-freie Schmalhirne aus aller Welt nun gerade dabei, unsere fossil befeuerte technische Zivilisation zu zerstören.
Man muss solchen Leuten daher ganz klar vor Augen führen, dass es gar keinen „natürlichen atmosphärischen Treibhauseffekt“ gibt, und sie endlich damit aufhören sollen, in ihrem klimareligiösen CO2-Wahn unser fossil befeuertes industrielles Paradies zerstören zu wollen!
Wie es die Physik befiehlt: Der experimentelle Nachweis für mein hemisphärisches S-B-Modell:
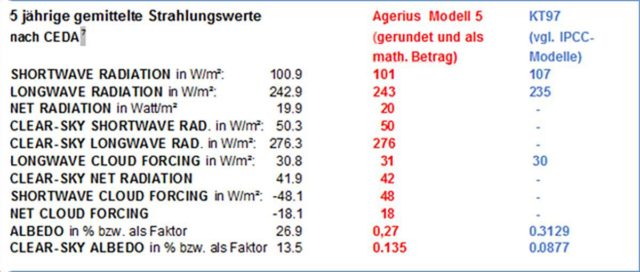
Herr Albert (Aulus) Agerius hatte auf Grundlage meines hemisphärischen Einstrahlungsmodells ein alternatives Klimamodell erstellt und mit dem Standardmodell KT97 verglichen. Das IPCC-Modell KT97 gilt als Grundlage für alle computergestützten Klimamodelle. In seinem Buch „Kritische Analyse zur globalen Klimatheorie: Widerlegung der Basisstudie KT97 des IPCC mit den Messwerten des ERBS Satelliten an einem neuen Modell“ (1. Auflage vergriffen*) deckt er erhebliche Widersprüche in der IPCC-Basisstudie KT97 auf:
Tabelle 1: Satellitenmesswerte des ERBS Satelliten in einem Modellvergleich (Quelle: A. Agerius)
Dem IPCC-Modell KT97 gelingt es also lediglich, 5 von 11 Messreihen abzubilden. Diesem IPCC-Modell KT97 stellt Agerius nun sein „Modell 5“ entgegen, das alle 11 Messreihen ohne einen atmosphärischen Treibhauseffekt abbildet und damit mein hemisphärisches S-B-Modell durch diese Satelliten-Messreihen voll betätigt.
Zum besseren Verständnis können Sie einmal die Perspektive eines Satelliten einnehmen: Die Erde stanzt mit ihrer Tagseite eine Kreisfläche aus der planparallelen solaren Einstrahlung heraus und verursacht damit auf der Nachtseite den zylinderförmigen Erdschatten. Die jeweiligen Messwerte der Satelliten sind folglich entweder in der vollen Sonneneinstrahlung oder im Erdschatten. Die Satellitenmesswerte für die Solarkonstante können die Erdkrümmung also gar nicht abbilden.
*) 2. Auflage: A. Agerius Kritische Analyse zur globalen Klimatheorie ISBN: 978-3-347-24749-9
Abschließend noch eine wissenschaftshistorische Betrachtung: Ein schönes Beispiel für die Durchsetzung eines neuen Paradigmas in der Wissenschaft ist die Kontinentalverschiebungstheorie (1915) von Alfred Wegener. Seine Kritiker sprachen damals von „Gedankenspielerei“, „Phantasiegebilden“ oder gar von „Fieberfantasien der von Krustendrehkrankheit und Polschubseuche schwer Befallenen“. Wegener soll darauf gekontert haben, Zitat:
„Die Leute, die so recht darauf pochen, auf dem Boden der Tatsachen zu stehen und mit Hypothesen durchaus nichts zu tun haben wollen, sitzen doch allemal selbst mit einer falschen Hypothese drin […]. Hätten sie die Verschiebungstheorie schon auf der Schule gelernt, so würden sie sie mit demselben Unverstand in allen, auch den unrichtigen Einzelheiten, ihr ganzes Leben hindurch vertreten, wie jetzt das Absinken von Kontinenten.“
Wegener selbst hat den wissenschaftlichen Durchbruch seiner Theorie nach dem WK2 nicht mehr erlebt. Und noch in den 1970-er Jahren wurde seine Theorie von Teilen des akademischen Wissenschaftsbetriebs strikt abgelehnt, was die Aussage meines damaligen Geophysikprofessors bestätigt, die Anhänger eines überkommenen Paradigmas würden lieber aussterben als sich überzeugen zu lassen.

 Abbildung 2: Das breitenabhängige S-B-Temperaturäquivalent im Äquinoktium
Abbildung 2: Das breitenabhängige S-B-Temperaturäquivalent im Äquinoktium Abbildung 3: Verbreitung und Migration des Weißstorchs basierend auf mehreren Quellen
Abbildung 3: Verbreitung und Migration des Weißstorchs basierend auf mehreren Quellen Vielmehr sprechen wir hier von der realen Erde, wir leben also in einem
Vielmehr sprechen wir hier von der realen Erde, wir leben also in einem  Ich hab‘ das jetzt zwar nicht nachgeprüft, aber man sagt, der Herr H. bezeichne sich als Ozeanograf. Jedenfalls ist ein nächtlicher Temperaturverlust von 0,4 Kelvin durch die tagesseitige solare Einstrahlung leicht zu kompensieren, wie die maximale spezifische Strahlungsleistung der Sonne in Abbildung 5 beweist:
Ich hab‘ das jetzt zwar nicht nachgeprüft, aber man sagt, der Herr H. bezeichne sich als Ozeanograf. Jedenfalls ist ein nächtlicher Temperaturverlust von 0,4 Kelvin durch die tagesseitige solare Einstrahlung leicht zu kompensieren, wie die maximale spezifische Strahlungsleistung der Sonne in Abbildung 5 beweist:



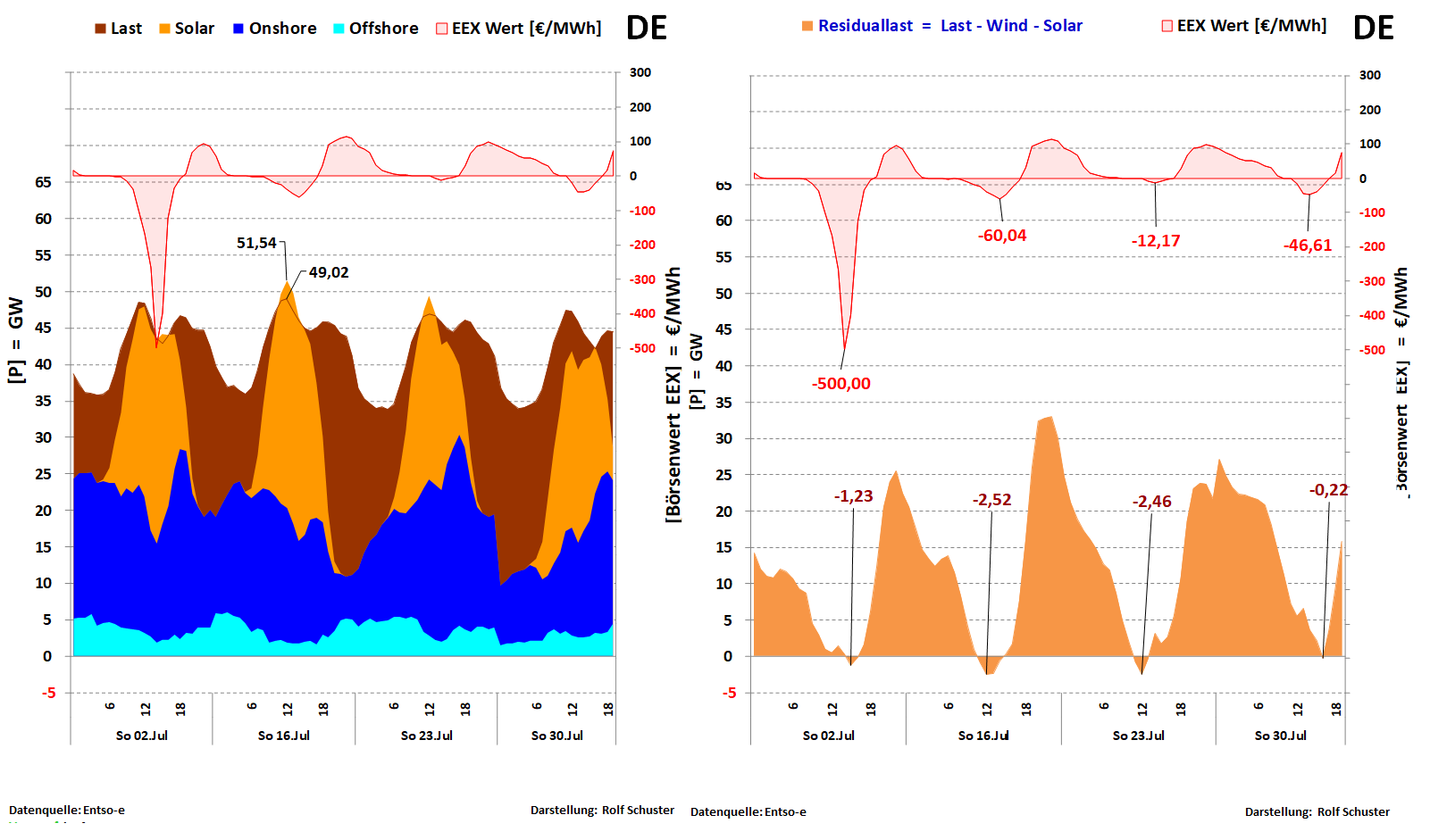
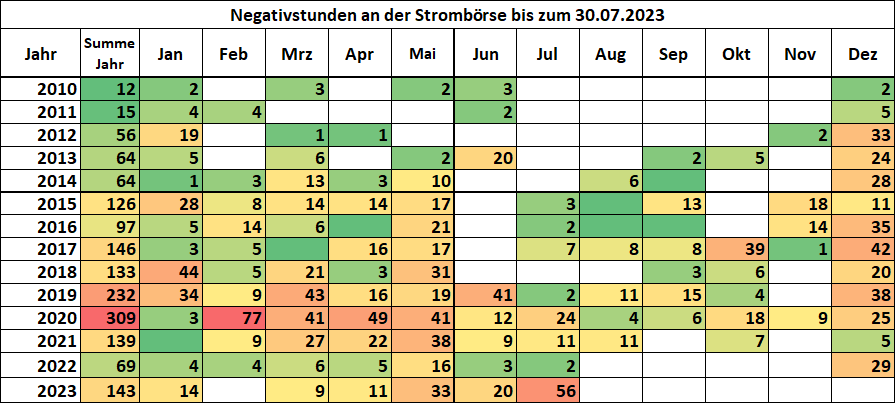 Gleichzeitig rutschte auch der Börsenpreis an diesen vier Sonntagen in den negativen Bereich.
Gleichzeitig rutschte auch der Börsenpreis an diesen vier Sonntagen in den negativen Bereich.