Die weltweiten CO2-Emissionen stagnieren, aber die CO2-Gehalte der Atmosphäre steigen unverändert weiter an

geschrieben von Admin | 1. September 2025

Nun stagnieren die weltweiten CO2-Emissionen, aber die CO2-Gehalte der Atmosphäre steigen unverändert weiter an – das führt die Aussagen des „Klimarates der Vereinten Nationen“ (IPCC) zur Wirkung von CO2 ad absurdum und damit auch die deutsche ideologische Energiepolitik
 Durch die Dekarbonisierung Deutschlands wird der CO2-Gehalt der Atmosphäre um skurrile 0,000 28 ppm/a (0,000 000 028 %/a) abgebaut – die Verfolgung dieser Dekarbonisierung im „Kern durch die Bepreisung der Treibhausgase“ (Regierung) entbehrt bei diesen CO2-Spuren jeglicher Grundlage

Dr. Erhard Beppler

Fazit
 Es gibt viele messbare Einflussgrößen auf die Temperatur der Erde wie z. B. der Abstand der Erde zur Sonne (Milankovic-Zyklus), die Sonnenaktivität, etc., nur der Einfluss des CO2-Gehaltes der Atmosphäre auf die Temperatur konnte nicht gemessen werden.
Nun werden fehlerhafte Computermodelle des IPCC herangezogen, um den Einfluss der weltweiten, von Menschen verursachten CO2-Emissionen auf die Temperatur zu beweisen.
Aber besagte Modelle weisen viele Fehler auf.
So wird stets vom Gesamt-CO2-Gehalt der Atmosphäre ausgegangen, obwohl der anthropogene CO2-Anteil nur bei 4% liegt.
Selbst bei der atmosphärischen Rückstrahlung (Treibhauseffekt) bleibt in den Modellen unberücksichtigt, dass die Absorptionsbanden des CO2 (0,04%) im Wellenlängenbereich von 14-17 µm stark von Wasserdampf (bis 4%) überlagert werden.
Außerdem kann der Einfluss von Wasserdampf und Wolken in den Modellen nicht berücksichtigt werden.
Schließlich geht auch noch der Anstieg der weltweiten anthropogenen CO2-Emissionen bis 2024 gegen null. Nach der Vorstellung des IPCC zum ausschließlichen Einfluss des anthropogenen CO2-Anteiles der Atmosphäre auf den Anstieg der Temperatur müssten dann die Temperaturen abfallen – aber das Gegenteil ist der Fall: die Temperaturen steigen sogar vermehrt an.
Durch den Rückgang des Anstieges der weltweiten anthropogenen CO2-Emissionen von 2019-2024 auf nur noch 0,112 Giga Tonnen (Gt) CO2/a steigen die CO2-Gehalte der Atmosphäre nur noch um 0,112/7,75 = 0,014 ppm/a und nicht um 2 ppm/a nach Aussage des IPCC.
Wird nun berücksichtigt, dass Deutschland an den weltweiten CO2-Emissionen nur mit weniger als 2% beteiligt ist, errechnet sich ein skurriler deutscher Anteil am Anstieg der CO2-Gehalte der Atmosphäre von 0,014 x 0,02 = 0,000 28 ppm/a oder 0,000 000 028 %/a.
Damit wird der „Kern des Klimaschutzes, die Bepreisung der Treibhausgase“ (Regierung) obsolet.
Deutschland lebt dennoch völlig losgelöst von Fakten und will die Dekarbonisierung bis 2045 vollenden, obwohl die Stromkosten bereits die weltweit höchsten sind, die Industrien abwandern, die Insolvenzen Rekordzahlen aufweisen mit Folgen für die Steuereinnahmen und damit die sozialen Fähigkeiten unseres Sozialstaates (Reaktionen aus der Politik sind inzwischen vernehmbar).

1.Einleitung

Die Klimapolitik der Welt wird seit den 1980er Jahren vom Klimarat der Vereinten Nationen“ (IPCC) bestimmt mit Aussagen zum ausschließlichen Temperaturanstieg der Atmosphäre durch die weltweiten anthropogenen CO2-Emissionen auf der Basis von Computermodellen und Hinweisen auf diverse Weltuntergangsszenarien (6. Sachzustandsbericht IPCC, März 2023).
Im Einzelnen lauten die Aussagen des IPCC wie folgt:
a) Von den jährlichen weltweiten anthropogenen CO2-Emissionen von z.Z. 10 Giga Tonnen Kohlenstoff/a (GtC/a) entsprechend 4 ppm gelangen 50% in die Atmosphäre , sichtbar an einem CO2-Anstieg der Atmosphäre von z.Z. 2 ppm/a und verbleiben dort über Jahrhunderte, und die andere Hälfte wird in gleichen Teilen (je 25%) von 10 GtC/a vom Ozean und der Biomasse aufgenommen
b) Durch den Eintrag der anthropogenen CO2-Emissionen in die Atmosphäre soll die CO2-Konzentration der Atmosphäre immer weiter ansteigen und damit über den Treibhauseffekt die Temperaturen auf der Erde bis zur Katastrophe anheben. (Anstieg CO2-Gehalte von 1850 bis heute etwa 120 ppm (0,0120%))
c) Daraus resultiert die Forderung nach einer vollständigen Dekarbonisierung (Net Zero), nur so könnte die Klimakatastrophe abgewendet werden
Gemäß Koalitionsvertrag von Union und SPD soll der Kern des Klimaschutzes aus der Bepreisung von Treibhausgasemissionen bestehen, d.h. am Ende sollen nur Wind und Sonne einschließlich Wasserstoff die Stromerzeugung sichern, koste es was es wolle.

2. Erdgeschichtliche Betrachtung der CO2-Gehalte der Atmosphäre sowie der Temperatur und Einflussgrößen auf die Temperatur

Durch die Veränderung der Umlaufbahn der Erde um die Sonne von kreisförmig zu elliptisch im Zeitraum von etwa 100 000 Jahren wurden die Temperaturen auf der Erde gewaltig verändert (Milankovic-Zyklus), wie Messungen an Eisbohrkernen gezeigt haben. (Bild 1)

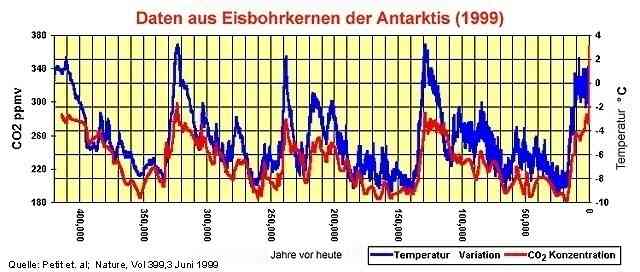
Bild 1: Verlauf der CO2-Gehalte wie der Temperaturen nach Messungen an Eisbohrkernen

In den Eiszeiten sind CO2-Gehalte um 200 ppm, in den Warmzeiten um 280 ppm gemessen worden. Der Anstieg der CO2-Gehalte der Atmosphäre folgt zeitversetzt dem Temperaturanstieg – durch die mit steigender Temperatur abnehmende Löslichkeit von CO2 in Wasser.
Der Temperaturverlauf nach der letzten Eiszeit ist Bild 2 zu entnehmen.

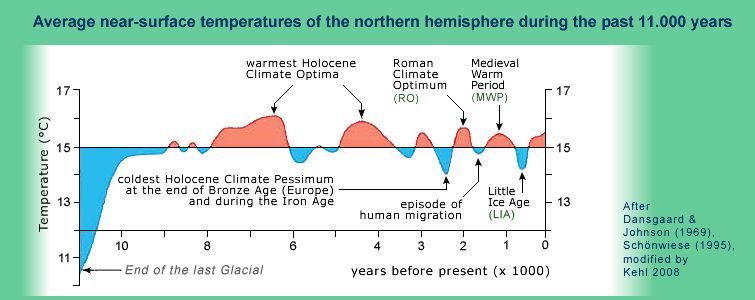
Bild 2: Warmphasen nach der letzten Eiszeit

In den wärmsten Phasen des Holozäns waren die Alpen eisfrei.
Ausgerechnet die jetzige Warmzeit wird vom IPCC als ein apokalyptisches Ereignis bezeichnet und das vom Menschen verursachte CO2 für den Temperaturanstieg verantwortlich gemacht, obwohl die Warmphasen vor der jetzigen ohne menschlich verursachtes CO2 praktisch alle wärmer waren.
Neuere Messungen zeigen, dass in der jetzigen Warmphase nach 1940 bis etwa 1980 die Temperaturen nach einem Anstieg zunächst wieder abfallen, um dann bis heute erneut anzusteigen. (Bild 3)

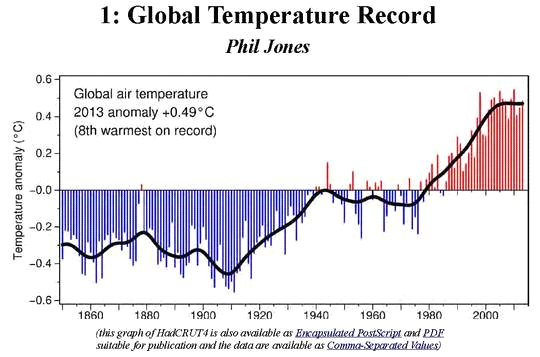
Bild 3: Temperaturentwicklung nach 1850

Dieser Abfall bis etwa 1980 und Wiederanstieg bis 2025 wird auch in neueren Messungen bestätigt. (Bild 4)

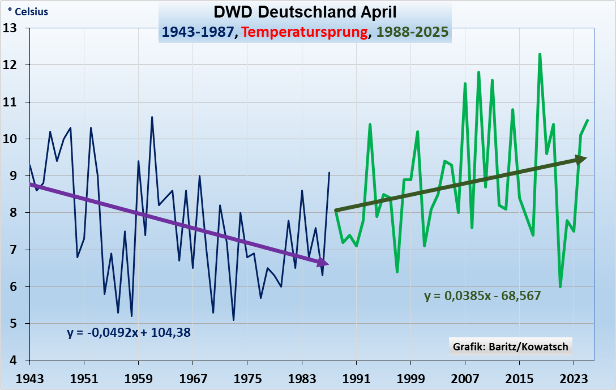
Bild 4: Temperaturentwicklung 1940 bis 2025

Dieser Verlauf ist im Wesentlichen auf wechselnde Aktivitäten der Sonne einschließlich der damit verknüpften kosmischen Strahlung zurückzuführen. (Bild 5) (1)
Hinzugefügt werden muss noch die zunehmende Sonnenscheindauer als Einflussgröße auf den jetzigen Temperaturanstieg, verursacht durch einen Rückgang der Aerosole als Verursacher für die Wolkenbildung.

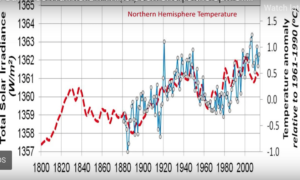
Bild 5: Verlauf der Intensität der Sonneneinstrahlung

Hervorzuheben ist weiterhin, dass trotz steigender Temperaturen die Nachttemperaturen abfallen, vermutlich durch die Abnahme der nächtlichen Bewölkung. (2)
Es kann also festgestellt werden, dass es viele gemessene Einflussgrößen auf die Temperatur gibt, aber keine zum Einfluss des CO2-Gehaltes der Atmosphäre, geschweige denn den von anthropogenen CO2-Emissionen. (vgl. Kapitel 4)
Nicht unerwähnt darf auch der Einfluss des Vulkanismus auf die Entwicklung des CO2-Gehaltes bleiben, ebenso wie die CO2-Freisetzung der Meere bei steigenden Temperaturen, etc. (vgl. später)
Schließlich sind die Ozeanzyklen und ihr Einfluss auf die globalen Temperaturen zu nennen: El Nino Sothern Oszillation (ENSO), Pazifische Dekaden-Oszillation (PDO), Atlantische Multidekaden-Oszillation (AMO) (mit Temperaturänderungen bis zur Arktis) und die Indische-Ozan-Dipol (IOD), etc. (3)

3. Weitere kritische Betrachtungen zu der Aussagefähigkeit der Modelle des IPCC

Nachdem es nun viele messbare Einflussgrößen auf die Temperatur gibt aber keinen durch den Einfluss der CO2-Konzentrationen, nun zu den Aussagefähigkeiten der IPCC-Modelle, dargestellt an einigen Beispielen.
Alle Wetter- und Klimaphänomene der Erde sollen mit Hilfe von Computermodellen gelöst werden – aber selbst einfachste Eingaben in die Modelle sind nicht nachvollziehbar. So wird ausgerechnet bei der Vorhersage der Temperatur auf der Basis von CO2-Vorgaben nicht differenziert nach anthropogenen CO2-Emissionen und natürlichen CO2-Quellen, sondern stets ausschließlich von ihrer Summe. (vgl. Kapitel 5)
Außerdem ist die Betrachtung der atmosphärischen Rückstrahlung („Treibhauseffekt“) des CO2 kritisch zu sehen. Die Absorptionsbanden des CO2 (0,04%) im Wellenlängenbereich von 14-17 µm werden stark von Wasserdampf (bis 4% H2O) überlagert. Schon alleine dadurch kann CO2 energetisch betrachtet in der Atmosphäre keine Rolle spielen.
Selbst der Einfluss des Wasserdampfes und der Wolken kann in den IPCC-Modellen nicht berücksichtigt werden.
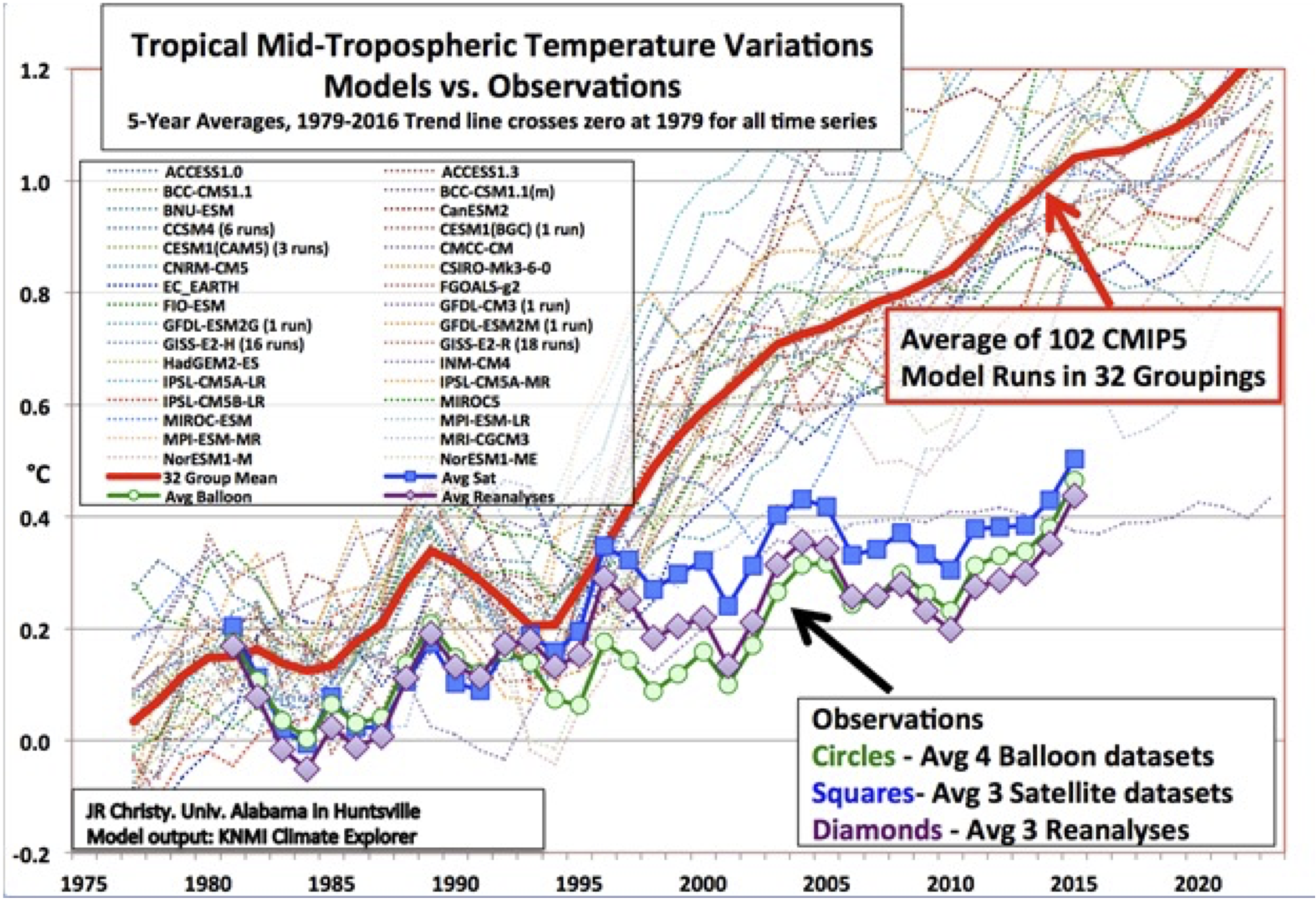
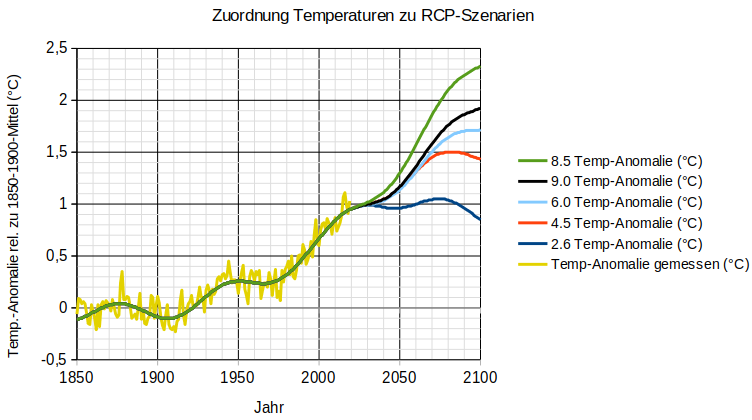
Es verwundert nun nicht mehr, dass die mit Hilfe der IPCC-Modelle ausgewiesenen Temperaturerhöhungen bei steigenden CO2-Gehalten der Atmosphäre weder die Vergangenheit abbilden können, geschweige denn die Zukunft voraussagen. (Bild 6)

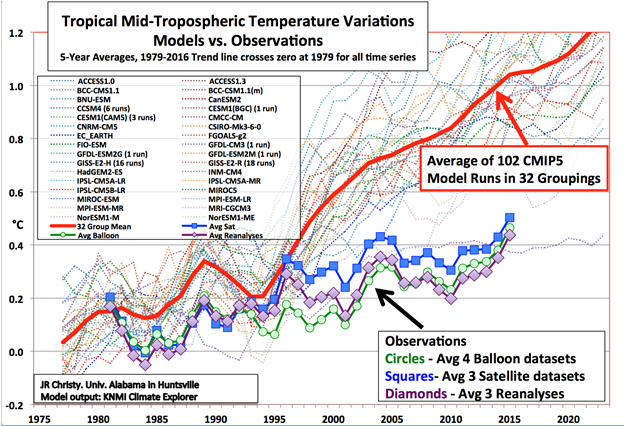
Bild 6: Aussagefähigkeit der Klimamodelle

4. Betrachtung des anthropogenen CO2-Anteiles in der Atmosphäre von 1870 bis 2020

In früheren Arbeiten (4) war der CO2-Zuwachs der Atmosphäre aus dem weltweiten anthropogenen CO2-Eintrag in die Atmosphäre von 1870 bis 2020 mit den gemessenen CO2-Gehalten dargestellt worden (Bild 7), ausgehend von 870 Gt Kohlenstoff in der Atmosphäre (6. Zustandsbericht des IPCC, Fig.5.12).


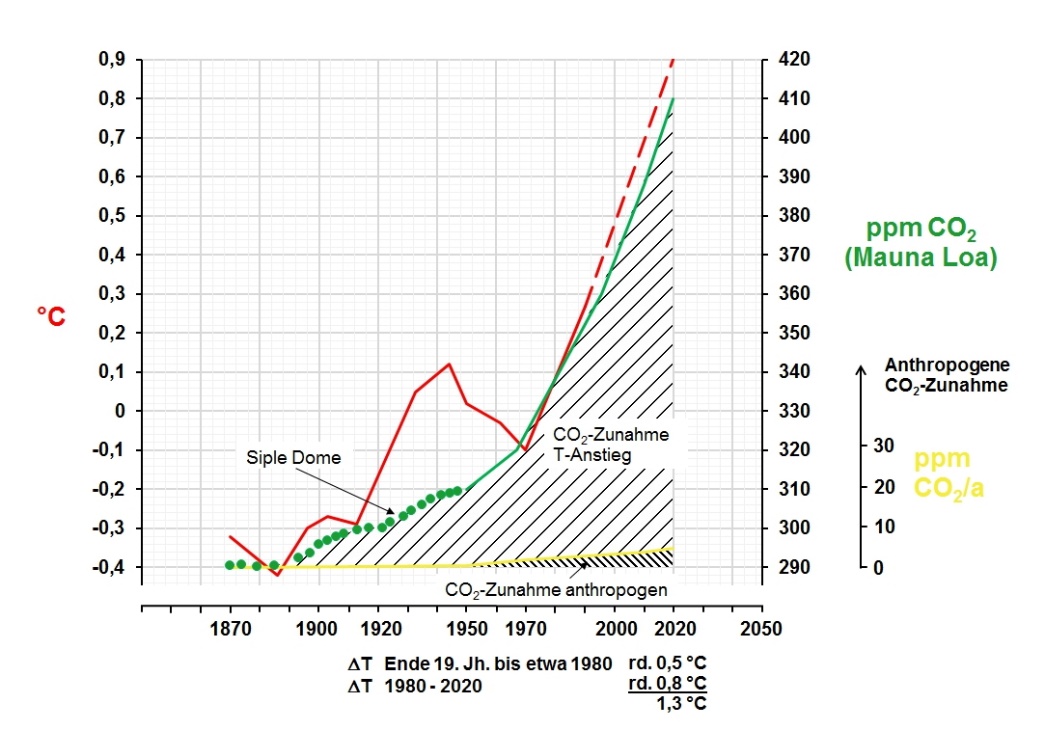
Bild 7: Anstieg der gemessenen und über die anthropogenen CO2-Emissionen in die
Atmosphäre eingebrachten CO2-Gehalte

Bekanntlich steigen die CO2-Gehalte der Atmosphäre von 1870 bis 2020 um 120 ppm von 290 auf 410 ppm an.
Die in 2020 eingebrachten anthropogenen CO2-Emissionen in die Atmosphäre liegen bei 35 008 Mio. t CO2 (35 Gt CO2). (vgl. Bild 9) Daraus errechnen sich 4,7 ppm CO2 oder 0,000 47%.
Somit gilt: 410 – 290 – 4,7 = rd. 115 ppm, die auf natürliche CO2-Quellen zurückzuführen sind. (CO2-Löslichkeit Meere, Vulkane, etc.)
Damit liegt der CO2-Anstieg über natürliche Quellen bei 96%, über den anthropogenen Anteil bei 4%.
Aus Bild 7 wird weiter deutlich, dass vor 1950 der CO2-Anstieg der Atmosphäre ausschließlich über den CO2-Eintrag über natürliche Quellen erfolgte. Ein merklicher Anstieg über anthropogenen CO2-Emissionen erfolgt erst nach 1950 bis auf 4,7 ppm in 2020 – oder durchschnittlich 4,7 ppm/70 Jahre = 0,07 ppm/a und nicht 2 ppm/a nach Aussage des IPCC (siehe Einleitung, vgl. auch Kap.5).
Wenn das IPCC den Temperaturanstieg durch Abbau der anthropogenen CO2-Emissionen auf null setzen will, so kann sich diese Maßnahme nur in einer Verminderung der CO2-Gehalte der Atmosphäre in der Größenordnung von 4,7 ppm CO2 äußern, was wiederum bedeutet, dass eine messbare Temperaturabnahme über Wunschdenken nicht hinaus kommt.

5. Stagnation der weltweiten anthropogenen CO2-Emissionen bis 2024 durch die weltweiten Maßnahmen zu ihrer Absenkung sowie ihre Wirkung auf die CO2-Gehalte der Atmosphäre

Die Bemühungen der verschiedenen Länder zur Absenkung der CO2-Emissionen sind unterschiedlich.
In Bild 8 sind die weltweiten anthropogenen CO2-Emissionen aller Länder zusammengefasst.
Die Werte bis 2022 basieren auf Angaben von „Statista“, die Werte für 2023 und 2024 wurden aus den Angaben von „International Energy Agency“ (IEA) und „wissenschaft.de“ entnommen und zu 37,1 Gt CO2 (2023) und 37,6 Gt CO2 (2024) gemittelt (in Bild 8 gekennzeichnet mit Vierecken).

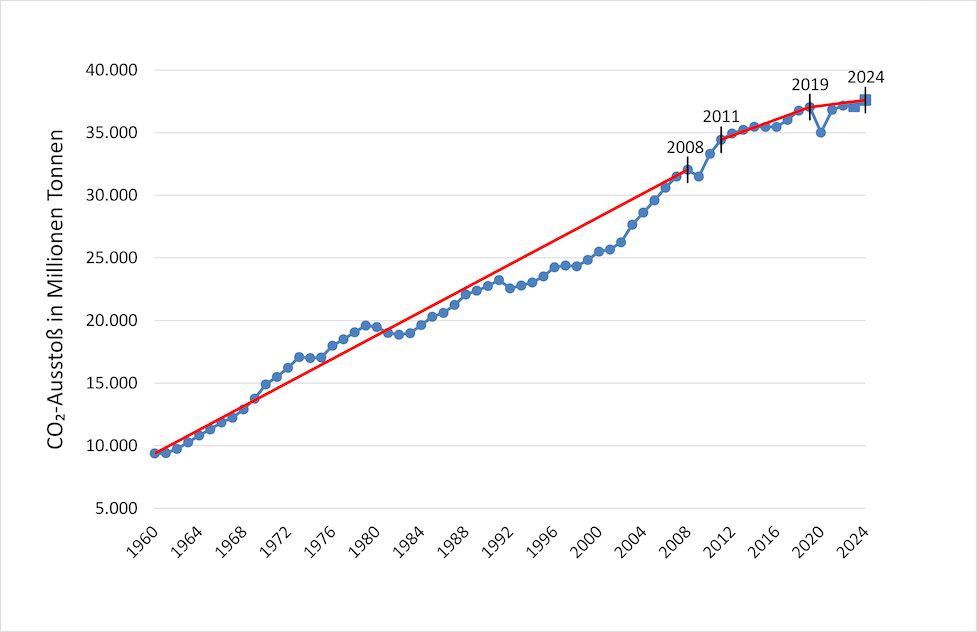
Bild 8: Entwicklung der anthropogenen CO2-Emissionen von 1960 bis 2024

Die Entwicklung der weltweiten anthropogenen CO2-Emissionen zeigt von 1960 bis 2024 eine starke Abflachung.
Die Entwicklung der Abflachung lässt sich mathematisch wie folgt definieren:
1960- 2008: 478 Mio. t CO2/a; 2011- 2019: 325 Mio. t CO2/a; 2019- 2024: 112 Mio. t CO2/a.
Das Jahr 2009 wurde nicht in die Auswertung einbezogen, weil das Jahr als das Jahr des konjunkturellen Tiefganges bezeichnet wird, sichtbar an dem Einbruch der jährlichen CO2-Emissionen.
Auch das Corona-Jahr 2020 wurde nicht einbezogen, da bedingt durch Corona die Weltwirtschaft zurückgefahren werden musste.
Die weltweiten CO2-Emissionen lagen 2019 bei 37 040 Mio. t CO2/a, im Corona-Jahr 2020 bei 35 008 Mio.t CO2/a (Statista), entsprechend einer Absenkung von 5,5% – eine Abnahme der CO2-Gehalte der Atmosphäre konnte jedoch nicht gefunden werden.
Aus der Abflachung des Eintrages der anthropogenen CO2-Emissionen kann zunächst abgeleitet werden, dass das Bestreben der Weltgemeinschaft zur Absenkung des C02-Anstieges bisher deutliche Früchte trägt.
Wenn nun aber nach Bild 8 der Anstieg der weltweiten CO2-Emissionen bis 2024 gegen null geht, müsste dann nach der Vorstellung des IPCC der Anstieg des CO2-Gehaltes der Atmosphäre auch gegen null gehen (Bild 9) einschließlich einer Abnahme der Temperatur.

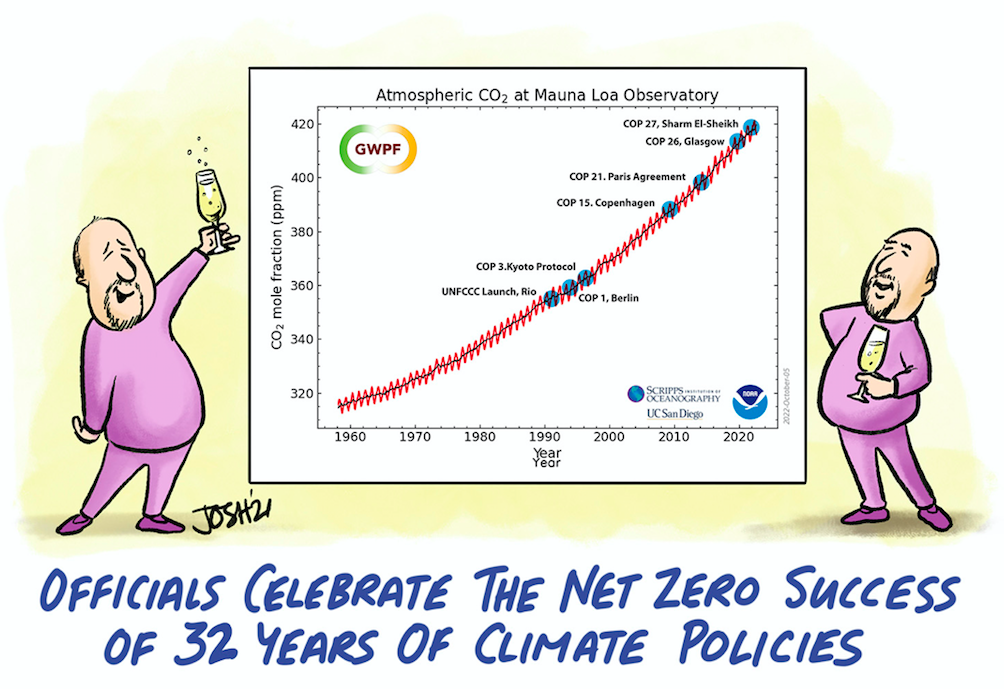
Bild 9: Entwicklung der CO2-Gehalte der Atmosphäre sowie die hoffnungslosen Versuche zu ihrer Absenkung

Bild 9 zeigt aber zunächst, dass die praktisch gegen null verlaufenden weltweiten, anthropogenen CO2-Emissionen auch nicht den geringsten Einfluss auf einen zu erwartenden Abfall der CO2-Gehalte der Atmosphäre ausüben (vgl. auch Corona-Jahr) – im Gegenteil: die CO2-Gehalte steigen nach 2000 sogar verstärkt an.
Außerdem wird der hoffnungslose Versuch einer Absenkung der CO2-Gehalte der Atmosphäre durch diverse Tagungen und dort beschlossene Maßnahmen sichtbar. Aber bei den niedrigen anthropogegen CO2-Emissionen von 4% kann eine Abnahme des CO2-Gehaltes der Atmosphäre auch nicht erwartet werden (vgl. Kapitel 4)
Nach den Vorstellungen des IPCC steigt der CO2-Gehalt der Atmosphäre über die jährlich eingebrachten CO2-Emissionen um 2 ppm an. (vgl. „Einleitung“)
Das entspräche einem CO2-Eintrag in die Atmosphäre von 2 ppm CO2/a oder 15,5 Gt CO2/a.
In den Jahren 2019 bis 2024 stiegen nach Bild 8 die anthropogenen CO2-Emissionen jedoch nur um 0,112 Gt CO2/a an oder 0,112 Gt CO2/7,75 = 0,014 ppm/a und nicht 2 ppm/a nach Aussage des IPCC:
Wird zudem berücksichtigt, dass Deutschland an den weltweiten CO2-Emissionen mit weniger als 2% beteiligt ist, so errechnet sich ein geradezu skurriler deutscher Anteil von 0,014 ppm/a x 0,02 = 0,000 28 ppm/a oder 0.000 000 028%/a– natürlich nicht messbar.
Bei diesem abbaubaren deutschen CO2-Anteil aus der Atmosphäre ist die Vorstellung der Regierung geradezu absurd, dass der „Kern des Klimaschutzes aus der Bepreisung von Treibhausgasen bestehen“ soll. Das Sondervermögen für Klimaschutz ist sinnvoller zu nutzten.

6. Welches sind die Quellen und Senken für die CO2-Gehaltes der Atmosphäre

In Kapitel 4 war aufgezeigt worden, dass der CO2-Anstieg der Atmosphäre in 2020 nur zu 4% (4,7 ppm) über anthropogene CO2-Emissionen erfolgt, 96% (115 ppm) über natürliche Quellen.
Neben den anthropogenen CO2-Quellen aus der Verbrennung von fossilen Brennstoffen, Abholzung, Landwirtschaft, Zementproduktion gehören zu den natürlichen Quellen die Ausgasung der Meere bei Erwärmung, Vulkanausbrüche, Atmung Lebewesen und die Zersetzung organischer Stoffe.
Zu den CO2-Senken werden im Wesentlichen Pflanzen und Wälder, humusreiche Böden, Gesteinsverwitterung und technologische Senken gezählt (vgl. später).
Ozean als CO2-Quelle
Ozeane enthalten 40mal so viel CO2 wie die Atmosphäre.
In der Vergangenheit wurden die Ozeane zu CO2-Senken erklärt, obwohl durch die Temperaturerhöhungen der Atmosphäre inzwischen auch die Meere erwärmt wurden und große CO2-Mengen freigeben. (CO2-Löslichkeit von CO2 in Wasser fällt mit steigender Temperatur)
In einer Untersuchung des „Science of Climate Change“ (5) waren anhand von multiplen linearen Regressionsanalysen die Einflussgrößen auf den Anstieg der Meerestemperaturen SST (sea surface temperature) untersucht worden (vgl. auch (6)).
Sowohl auf der Basis der UAH-, HAD- wie GISS-Daten konnten enge Verknüpfungen der SST mit den CO2-Daten gefunden werden. (Bild 10)


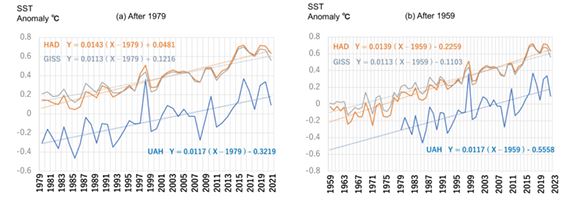
Bild 10: Anstieg der Meerestemperaturen

In Bild 10 beinhalten die Jahreszahlen auf der X-Achse die jeweiligen CO2-Gehalte der Atmosphäre.
Der Anstieg der Meerestemperaturen von 1979 bis 2021 auf der Basis von Satellitenmessungen liegt bei etwa 0,5 °C (Bild 10 ((a) After 1979), was einem CO2-Anstieg in der Atmosphäre von 335 auf 415 ppm entspricht. (Bild 9)
Ebenfalls in Bild 10 ((b) After 1959) sind die Messergebnisse für den Zeitraum 1959 bis 2023 dargestellt mit einem Temperaturanstieg von etwa 0,8 °C und einem CO2-Anstieg nach Bild 9 von 315 auf 420 ppm.
Die CO2-Löslichkeit in Wasser nimmt mit steigender Temperatur deutlich ab: bei 15 °C liegt die Löslichkeit bei 1,97 g CO2/kg H20/bar, bei 20°C bei 1,67.
Wird von einem Temperaturanstieg der Meere im Temperaturbereich von 15-20°C ausgegangen,
so fällt die CO2-Löslichkeit von 1,97 (15°) auf 1,67 (20°) g CO2/kg H2O oder 0,048 g CO2/kg H2O je 0,8 °C ab.
Wird bei einer Wasseroberfläche der Meere mit 360 570 000 km2 eine Reaktionstiefe von 500 m und eine Temperaturerhöhung von 15 auf 15,8°C angesetzt, so könnte eine CO2-Menge bei einem Betrachtungszeitraum von 64 Jahren (1959-2023) 8 650 Gt CO2 aus dem Meer freigesetzt werden. (oder 4325 Gt CO2 bei 250 m)
Die Atmosphäre enthält etwa 3300 Gt CO2.
Neuere Untersuchungen zeigen im Übrigen im Vergleich zu Messungen an Eisbohrkernen deutlich schnellere Ansprechzeiten der CO2-Gehalte der Meere bei Temperaturerhöhungen im Bereich von wenigen Monaten. (7)
Hinzu kommt noch die nicht unerhebliche Verdunstung von Wasser an Land bei steigenden Temperaturen, was hier nicht berücksichtigt wird.

Vulkane als CO2-Quelle

Kürzlich wurde berichtet: 19 000 neue Unterwasser-Vulkane entdeckt. (8)
Eine Studie der Universität von Manchester zeigt, dass vulkanische CO2-Emissionen dreimal höher sein könnten als bisher angenommen. In einer 2.Studie der School of Ozeans and Earth Science and Technology (SOEST) geht es um 19 325 neu entdeckte unterseeische Vulkane. Damit erhöht sich die Gesamtzahl auf 43 000.
Bisher sind nur ¼ des Meeresbodens mit Sonar kartiert worden, d.h. die meisten dieser Unterwasserriesen sind noch unerforscht.
Die Strömungen um die untermeerischen Berge erzeugen „Wirbelschleppen“, die kohlenstoffreiches Tiefwasser an die Oberfläche ziehen.
Im Januar 2022 brach der Unterwasservulkan Hunga Tonga aus und erzeugte gewaltige Wasserdampf – Mengen – etwa 50 Mio. t bis in die Stratosphäre.
Dieser Anstieg der Feuchtigkeit in der Stratosphäre um etwa 10-30% hat zu einer Erwärmung der Erdoberfläche 2023-2024 erheblich beigetragen. (9)

Waldbrände als CO2-Quelle

Laut Phys.org wurden in 2021 durch Waldbrände 1,8 Mrd. t CO2 in die Atmosphäre freigesetzt.
CO2-Senken
Die Erde wird grüner, erhöhte CO2-Gehalte der Atmosphäre sind dafür verantwortlich. Chinesische Wissenschaftler stellten fest, dass 55% der globalen Landmasse eine „beschleunigte Wachstumsrate“ der Vegetation aufweisen bei gleichzeitiger Verringerung der Wüstenbildung. (10)

Technologische Maßnahmen als CO2-Senken

Die neue Regierung will das Gesetz zur Abscheidung und Speicherung von CO2 über das CCS-Verfahren durchbringen (Carbon Capture Storage).
CO2 soll aus der Luft entzogen werden (oder direkt bei der Erzeugung von Produkten – z.B. von Zement), um es unterirdisch zu lagern.
Nachbar- und Überseeländer haben CCS als wirksames Instrument zur angeblichen Klimaneutralität weiterentwickelt: Großbritannien, Norwegen, Liederlande, Schweden.
Weltweit gibt es z.Z. 47 CCS-Anlagen. Forscher schätzen die Kosten für Abscheidung, Transport und Speicherung von CO2 mittelfristig auf 150 bis 250 EURO/t CO2.
Die CO2-Löslichkeit im Meerwasser liegt etwa 40mal höher als die CO2-Gehalte in der Atmosphäre und beide stehen in einem thermodynamischen Gleichgewicht zueinander.
Außerdem bedeutet die Reduzierung der CO2-Gehalte der Atmosphäre über CCS nach dem „Prinzip vom kleinsten Zwang“ ein Entweichen von CO2 aus den Meeren in die Atmosphäre.
Das CCS -Verfahren kann daher nicht zu einem Abbau der CO2-Gehalte der Atmosphäre führen.

7. Schlussbetrachtung

Bei der Überflutung der Nachrichten in den Medien mit zunehmenden Extremwetterlagen, Waldbränden, schmelzenden Gletschern, Rekord- Temperaturen etc. sind die vermehrt aufkommenden Klimaängste in Deutschland nicht überraschend: 68% der Deutschen befürworten die Energiewende.
Hinzu kommen all die Profiteure dieser Energiewende: ein Windrad in Tübingen bringt der Stadtkasse 250 000 EURO ein (Aussage B. Palmer in einer Talk Show bei M. Lanz am 20.07.2025).
Selbst der „Internationale Gerichtshof“ in Den Haag formulierte kürzlich einen klaren juristischen Auftrag an die Staatengemeinschaft zum Klimaschutz. Kommen Staaten dieser Pflicht nicht nach, stelle das nicht nur einen Verstoß gegen das Völkerrecht dar, sondern könne unter Umständen sogar zu Schadenersatzansprüchen führen.
Deutschland folgt diesen Umfrageergebnissen, obwohl Deutschland nur 0,000 28 ppm/a (0,000 000 028%/a) CO2 durch seine Dekarbonisierung aus der Atmosphäre abbauen kann.
Der Nobelpreisträger (Physik) John F. Clauser bezeichnete den CO2-Klimawandel eine „schockjournalistische Pseudowissenschaft“.
Dennoch will Deutschland in 2045 den Strom ausschließlich über Wind, Sonne und Wasserstoff darstellen, obwohl die Stromkosten bereits die höchsten in der Welt sind, die Industrien abwandern, die Insolvenzen bereits heute Rekordzahlen aufweisen.
A. Thess (Universität Stuttgart) ermittelte für die deutsche Energiewende Gesamtkosten von 10 Billionen EURO.
Deutschland muss raus aus den ideologischen Träumereien, deren Stromversorgungsicherheit keineswegs gewährleistet ist. (Es sei an den Stromausfall in Spanien am 28.04.2025 erinnert)
Bei der hohen Sensibilität für gesicherten Strom in Deutschland sowie die erforderliche Absenkung der Kosten können nur Kohle-, Gas-, Kernkraftwerke helfen – eine Verabschiedung von der Skurrilität eines deutschen CO2-Abbaues der Atmosphäre durch die Energiewende von 0,000 28 ppm/a oder 0,000 000 028%/a ist zwingend geboten.
Die Vorstellung der Regierung, dass „der Kern des Klimaschutzes aus der Bepreisung von Treibhausgasen bestehen sollte“, entbehrt damit jeglicher Grundlagen.

8. Quellen

1.https://tinyurl.com/y5nhhfnd
2 Baritz, B., J. Kowatsch: „Frühlingsverlauf Deutschland: ein weiterer Verlauf gegen die These einer starken Treibhausgaserwärmung“; EIKE, 18.06. 2025
3. Fleischmann, B.: „Warum sich das Klima ändert (Kurzfassung)“; Version 30.09.2021
4. Beppler, E.: „Quantifizierung des marginalen anthropogenen CO2-Gehaltes in der Atmosphäre – ein seit Jahren überfälliger Schritt“; EIKE, 16.12.2020
5. https://scienceofclimatechange.org.
6. Eschenbach, W.: „Wassertemperatur-Blues“; EIKE, 10.06.2024
7. Macrae, A., J. D` Aloe: „Die wirkliche Klimakrise ist nicht die globale Erwärmung, sondern die globale Abkühlung und vermischt hat sie bereits begonnen“, EIKE,05.03.2020
8. Watts, A.: „Vulkane emittieren dreimal mehr CO2 als gedacht“, EIKE, 22.05.2025
9. Allen, C.: „Aktualisierung: Neues zum stratosphärischen Wasserdampf“, EIKE, 25.07 2024
10. Sterling Burnett, H.: „Dank des Klimawandels: die Erde wird grüner“, EIKE, 05.03.2020

 



Freispruch für CO₂!

geschrieben von Admin | 1. September 2025

„Früher nannten sie es globale Erwärmung, dann Abkühlung – jetzt einfach ‚Klimawandel‘, weil es nicht funktioniert hat“, so Trump.

CO2 ist ein Gas des Lebens, Wasserdampf ist der Haupttreiber der Temperatur der Atmosphäre und Klimamodelle sind hochhypothetischer Unfug.

Von Michael Limburg

In diesen Tagen hat die amerikanische Umweltbehörde EPA (Environmental Protection Agency), unter ihrem neuen Chef Lee Zeldin, ihre Einstufung, die „Treibhausgase“ als Gefahr für die öffentliche Gesundheit und Wohlergehen (endangerment finding), zurückgenommen. Darunter ist das wichtigste Spurengas CO2, derzeit mit 0,042 Vol % in der Atmosphäre vorhanden. Diese „findings“ ist das halb – rechtliche Pendant der USA zu den konkreten Grund- und anderen -Gesetzen in Deutschland und der EU. Die aber, anders als die EPA, die Treibhausgase weiterhin unbedingt vermeiden wollen. Für die EU ist es die Basis für ihren „Green Deal“.

https://x.com/wideawake_media/status/1952671778058199070

Journalist Alex Newman: „The idea that [CO₂ is] going to destroy the planet or change the temperature of the Earth is totally ludicrous.“

Kein Wunder, dass dies in deutschen Redaktionsstuben Panik ausgelöst hat. Wer Zeit und Muße dafür hat möge dies exemplarisch hier beim zdf oder hier bei der Tagesschau , oder beim SPIEGEL nachlesen. Doch ist diese Rücknahme der EPA nur ein wichtiger, wenn auch nur ein erster Schritt. Denn mindestens so wichtig ist es, eine Klimareligion, die sich heute als Wissenschaft ausgibt, diese zu enttarnen, und die wirkliche Klimawissenschaft auf das zurückzuführen, was sie bis dahin war. Eine statistische Zweitwissenschaft die – ausgestattet mit modernen Computern und ungeheurer Rechenleistung, sowie vielfältigen dauerhaften und sehr großen, vielfältigen Messungen- und auf der Basis der Meteorologie, zu sehr nützlichen Erkenntnissen führt.

Und dazu ist es notwendig sich etwas tiefer mit der Substanz dem Kohlenstoff, d.h. mit dem CO2, und damit dem Baustoff allen Lebens auf der Erde, und der Verwendung ihrer wichtigen Energie der Sonne zu befassen.

Wie manche schon richtig vermutet haben, ist der Wasserdampf – nach dem eigentlichen Antrieb, der Strahlung der Sonne- die Hauptquelle für die Temperaturentwicklung der Atmosphäre der Erde. „It´s the water vapor, stupid!“ könnte man in Anlehnung an Bill Clintons berühmten Wahlkampfspruch sagen. Lt. internationaler Übereinkunft ist er das allumfassende „Treibhausgas“. Er ist mit im Mittel > 15.000 ppm in der Atmosphäre vorhanden. Also 35 x so viel wie das CO2. Doch nicht nur das. Er hat sehr viele mehr und viele breitere Banden in denen Infrarotlicht aufgenommen und wieder abgestrahlt werden kann als das CO2. Und er ist auch für die andern Klimaparameter wie Wolkenbildung, den Regen, das Eis und damit für das Wasser im Allgemeinen und somit für den Wasserkreislauf zuständig. Das sehen auch die Klimaforscher so, voran die beiden berühmten Klimaforscher Hans-Joachim Schellnhuber und Stefan Rahmstorf – beide vom Potsdam Institut für Klimafolgenforschung[1]. Doch sie weisen darauf hin, dass der Wasserdampf nur deswegen nicht in der Diskussion zur Begrenzung der Erwärmung durch Treibhauseffekt einfließt, weil der Mensch ihn nicht beeinflussen kann. Das ist in etwa so, als ob man versucht mit einigen Haaren des Schwanzes eines Hundes mit dem Hund selbst zu wedeln. Doch, so dumm es sich anhört, es hat gewirkt.

Die halbe Welt ist diesem gewaltigen Schwindel aufgesessen. Man hat div. Gesetze und Vorschriften erlassen, in Deutschland, bis hin zum Grundgesetz, und dafür viele Billionen € in die „Vermeidung von CO2“ versenkt. In der EU ist es bspw. der „Green Deal“, untrennbar mit den Namen von Frans Timmermans und Ursula von der Leyen verbunden, der zusätzlich zu den Milliarden, die die Länder für diesen Unsinn ausgeben, weitere Billionen locker machen wird. Und wie das so ist, dass Geld ist ja nicht weg, es haben nur andere. Bspw. die, die sich mit den unzähligen Windkraft-, oder Photovoltaikanlagen die Taschen füllen. Neben den Direktbetreibern, auch die Fülle von Gesetzgebern, Planern, Errichtern und Ingenieurbüros, aber auch die Kommunen, Gemeinden und Städten wie auch ganze Landkreise. Wer bspw. erinnert sich heute noch an das Milliardenprojekt Desertec. Ein Irrsinnsprojekt um „Wüstenstrom in der Sahara zu gewinnen, um diesen dann über zigtausende von Kilometern per Hochspannungsleitung zu den Verbrauchern zu transportieren. Dabei hätte ein kurzer Blick in die lange erprobte Stromgewinnung und -Verteilung all dessen diesem sofort eine Absage erteilt. Doch obwohl die Riesenverluste bei Desertec bei Gesamtkosten von 400 Mrd. Euro das Ganze einige Jahre später zum Erliegen brachte, sind die Schlangenölverkäufer bei den Nachfolgeprojekten, wie die Wasserstoffgewinnung und Verteilung über Ammoniak in Namibia wieder ganz vorne mit dabei. Es findet sich immer irgendein Grund, warum es diesmal gut gehen könne, und sei es nur dafür, um dann in vielleicht hundert Jahren die Welt zu retten.

Bild

Abb. 1 Wirkung des EU Green Deals auf die Welttemperatur nach 75 Jahren unter Nutzung des IPCC Modells SSP2- RCP 4.5 Middle of the Road Quelle https://x.com/BjornLomborg/status/1945808261074022579/photo/1

Und es ist daher an der Zeit einen Blick zu werfen, auf das riesige, sich als Wissenschaft tarnende, rein hypothetischen Gebäudes, in welchem wir dummen Menschen gefangen gehalten werden. Es ist die „Klimawissenschaft des CO2“ reich bespickt mit vielen Korrelationen, diese unverzüglich zur Ursache – Wirkungsbeziehung erklärt werden und den vielfältigen Modellen, die das alles bezeugen sollen. Modellen, als Teil eines Ensembles dargestellt und mit riesigen Computern, die ganz klar darstellen, wie sich die Zukunft des Klimas der Erde entwickeln soll.

Ein Bild, das Text, Screenshot, Diagramm, Kreis enthält. KI-generierte Inhalte können fehlerhaft sein.

Abb. 2. Grober Darstellung der Prozesse und ihrer Verbindung zueinander die für die Energiebilanz der Atmosphäre in Bezug auf die Sonne verantwortlich sind. Es sind 17 Prozesse die mit dem Wasserdampf verknüpft sind und einer „atmospheric composition“ die unter „ferner liefen“ etwas mit dem CO2 zu tun hat. Graphik: Willie Soon.

Doch es ist nicht so. Klima ist chaotisch und auch nicht -ergodisch. Was bedeutet, dass sich nicht nur alle Klimaberechnungen mit vierzig oder fünfzig Variablen auseinandersetzen müssen, was nicht funktioniert, sondern auch das Mittelwerte oder andere statistisch wohl erprobte Schlussfolgerungen, wie Standardabweichungen oder Varianzen hier nichts bringen. Man kann sie mathematisch einsetzen, aber was rauskommt ist irgendwas. Man weiß weder warum, noch warum nicht. Deshalb sind sie einfach physikalisch nicht zulässig.

Damit ist dieses Ganze, sich hochwissenschaftlich anhörende Klimagerede, nichts anderes als wissenschaftlich verbrämter Humbug. Denn wie es sich mit der richtigen Klimawissenschaft – eine Anwendungswissenschaft der Chaos Theorie- auf sich hat, kann niemand besser darstellen als Heinz-Otto Peitgen , Physiker und Mathematiker der Universität Bonn. Er tut dies im folgenden Video. Es ist mit rd. 2 h ziemlich lang, doch für den Interessierten sind die 2 h gut angelegt.

Einige sehr wichtige Erkenntnisse daraus, die im Grunde schon lange Stand des Wissens sind.

  1. Klima ist chaotisch
  2. Um das chaotische System Klima trotzdem in den Griff zu bekommen, benutzt man sich des Kunstgriffs einer „Parametrisierung“. Das ist eine gut klingende Umschreibung für die Ergänzung fehlender, oftmals unbekannter vielleicht aber ebenfalls chaotischer Komponenten, durch vorgegebene Werte. Was zur Folge hat, dass dann vielleicht vernünftig erscheinende Werte herauskommen, die es aber nicht sind, weil man nicht weiß, auf welchen physikalischen Prinzipien sie basieren.
  3. Das Wesensmerkmal eines chaotischen Systems ist ferner, es hat kein Gleichgewicht. Somit sind auch Gleichgewichtsrechnungen unzulässig
  4. Und Klima ist nicht – ergodisch

Aus letzterem folgt

    1. Wahrscheinlichkeitsverteilungen, wie Mittelwert und Standardabweichung und Varianz sind keine sinnvolle, d.h. anwendbare Technik.

Abbildung 3: „Nicht-ergodisch“ beschreibt ein System oder einen Prozess, bei dem sich das Verhalten über die Zeit nicht wiederholt oder bei dem die Zeitmittelwerte nicht mit den Ensemble-Mittelwerten übereinstimmen.

Und trotzdem wird all dies in der „Klimawissenschaft“ ganz bewusst, regelmäßig und überall so gemacht. Man tut das, um mehr Geld zu bekommen (funding) und um wissenschaftlich zu wirken, aber es nicht sein kann oder will, dies aber offenbar nicht zugibt oder es nicht mal begreift.

So hat man von Anfang an sog. Szenarien berechnet, die zeigen sollen, dass sich bspw. der Temperaturen bei soundso viel CO2 um soundso viel Zehntelgrad nach oben verändern.

Ein Bild, das Text, Diagramm, Reihe, Screenshot enthält. KI-generierte Inhalte können fehlerhaft sein.

Abb. 4 | Extrapolation der Temp.-Anomalien für alle Szenarien cdata hier

Das sind dann vielfältige Berechnungen, wunderbar kompliziert, aber nicht mal das Papier wert, auf dem sie ausgedruckt sind. Sie sind völlig wertlos. Aber – und das ist das Entscheidende, sie haben zur Folge, dass viele Staaten, besonders aber der westlichen Welt, und darin die EU mit ihrem Treiber und -folger Deutschland, sich bemühen, mittels der darin behaupteten und damit verlangten CO2 Vermeidung, direkt und ohne Innezuhalten sich ins wirtschaftliche Elend zu begeben. Nicht wirklich gewollt, eine „Transformation des Wirtschaftssystems“ sollte es richten. Aber daraus wird nichts.

Dieses Abgleiten begann erst langsam, dann immer schneller, um jetzt direkt in den wirtschaftlichen Abgrund zu stürzen. Und damit ist der Weg in die Armut des Mittelalters vorgezeichnet, etwa was man sich erst seit kurzem wieder vorstellen kann.

Denn wie anders kann man verstehen, dass man mit dem Energie-Erntefaktor von weniger als 5 bis 10, eine Industrienation weiterbetreiben kann? Erntefaktoren, die auch die Menschen im Mittelalter hatten? Man verbrannte Dung, oder Holz aus den Wäldern, manchmal auch Holzkohle, die man in den Meilern mühsam gewonnen hatte. Die Bauern konnten gerade mal – und das auch nur in guten Jahren – ihre Familie ernähren und noch einmal das ein- bis zweifache durch den Verkauf ihrer Produkte. Also in Summe etwa das das Vier- bis Fünffache.

Und dass alles nur deshalb, um das „Klima zu retten“, den „Klimaschutz“ zu erfüllen. Obwohl niemand weiß, wie sich das lokale Klima – vom Weltklima zu reden wäre doppelt falsch- sich entwickeln wird. Alles, was wir wissen, ist, dass es sich in den Grenzen des bisherigen entwickeln wird. Mal wärmer, mal kälter, und, wenn wir richtig Pech haben, es auch mal in ein, bis einigen tausend Jahre wieder zu einer Eiszeit kommt. Das können die Milankovics Zyklen zeigen, die als zeitliche Reihenfolge benannt und deren Ursache ebenfalls gut bekannt sind.

Ein weiterer Einfluss ist die Reise des Sonnensystems in der Milchstraße, eine Möglichkeit, die insbesondere Henryk Svensmark und Nir Shaviv nicht nur theoretisch postuliert, sondern auch durch zahlreiche Beobachtungen und Versuche hinreichend bestätigen wurde. Aber eines kommt in deren Arbeiten nicht vor. Es ist das CO2. Hingegen kommt der Wasserdampf überall vor. Bspw. auch in den Arbeiten von Jan Veizer. Und bei weitem nicht nur dort.

Und das heißt im Klartext: Freispruch für CO2.[2]

https://www.tichyseinblick.de/meinungen/vahrenholt-ueber-klimawende-in-usa/

https://x.com/wideawake_media/status/1953370489918734405

Leading physicist and Princeton emeritus professor Dr. William Happer: The war on CO₂ is really a war on people. „We’re actually in a CO₂ famine today compared to geological history. Over… the last 500 million years or so… CO₂ levels have been three times, four times, five times higher over most of that period of time.“ „And the only real effect you can see from CO₂ today is that the whole Earth is getting greener. Plants are having a much easier time growing, especially in arid regions of the Earth, than they used to have with lower CO₂ levels.“ „And more will be better.“

 

  1. Seite 44 Kindle Ausgabe des Buches Klimawandel ↑
  2. Eine Idee folgend auf das Buch des Meteorologen von Wolfang Thüne ↑

Der Beitrag erschien in gekürzter Form am 28.8.25 in der Zürcher Weltwoche hier

35_gruen_freispruch (9)



Klimahysterie und Fakeprognosen: Die heißesten Tricks unserer Klimajournalistenden (Adlerauge #1)

geschrieben von Admin | 1. September 2025

Der Sommer 2025 neigt sich dem Ende zu. Und eines kann man schon jetzt mit Sicherheit sagen: Neue Temperaturrekorde wird dieser Sommer nicht mehr bringen. Jedenfalls nicht in Deutschland. Dabei hatte alles so spektakulär angefangen: „Hitzesommer, Tropensommer, Jahrhundertsommer“ waren die Schlagwörter, die ab Mai wochenlang durch die Medien geisterten. Doch was ist damals wirklich passiert?

von Marco Pino Tronberend

In seinem neuen Youtube-Format „Adlerauge“ widmet sich der Filmemacher Marco Pino den Tricks, mit denen Leitmedien „das Narrativ von der unmittelbar bevorstehenden Klimakatastrophe aufrechterhalten, selbst wenn der deutsche Sommer sprichwörtlich ins Wasser fällt“, wie Pino gleich zu Beginn des Videos ankündigt. Und genau das ist Anfang Juli passiert: Nach wenigen heißen Tagen, die aber weit von den prognostizierten Rekordwerten entfernt waren, kam wochenlanger Regen über das bis dahin noch angeblich von Dürre geschundene Land. „Ein Sommer, wie er früher einmal war“, titelte irgendwann eine verzweifelte Bild-Zeitung, die ihren Lesern höchst selbst noch wenige Wochen vorher „Hitze und Sonne den ganzen Sommer lang“ versprochen hatte.

Aber Halt: In Deutschland mag der Sommer zwar eher mau gewesen sein, aber was war bitte schön im Mittelmeerraum los? Las man nicht ständig von wochenlangen Megahitzewellen, neuen Temperaturrekorden und Ausnahmezuständen? Und mahnte nicht Deutschlands oberster Klimapriester Harald Lesch in seiner jüngsten Terra-X-Klimadoku, man könnte ja eigentlich nicht mehr guten Gewissens in den Urlaub fliegen, schließlich tobe im Mittelmeerraum die Klimakrise wie kaum irgendwo sonst? Dem hält Pino – seines Zeichens selbst Deutsch-Spanier – Bilder von der Costa del Sol entgegen, die bei manch einem geschundenen deutschen Steuerzahler spontane Auswanderungsgelüste entfachen könnten. Und Pino erklärt: „Heiß war es hier auch in den 1980ern schon“. Von seiner andalusischen Oma habe er gelernt, dass jedes Jahr mindestens drei Hitzewellen übers Land kommen. Neu sei nur, „dass seit einigen Jahren im fernen Deutschland über Hitzewellen in Spanien berichtet wird“. Und wie: Mit Headlines, die wie das „klimatische Armageddon“ anmuten.

Und mehr noch. Pino zeigt in seinem Film einige Tricks, die vielen EIKE-Lesern wohlvertraut sein dürften. Einer davon: Man nimmt Extremwerte aus einer lokalen Hitzeinsel und verkauft sie seinen Lesern als „ganz Südeuropa“,  „Mittelmeerraum“ oder „Urlaubsländer“. So geschehen Anfang Juli, als im andalusischen Niemandsland in einem mickrigen Ort namens „El Granado“ ein neuer Juni-Rekord gemessen wurde: 46 Grad. Der Wert ging rauf und runter durch die Medien. Allerdings: In der berühmten spanischen Hitzehochburg Sevilla, bekannt als eine der heißesten Städte Europas, wurden zur selben Zeit fast vier Grad weniger gemessen. Schon das wirft Zweifel auf an der – allerdings auch Spaniens Meteorologiebehörde AEMET bestätigten – Rekordmessung aus El Granado. Aber nicht nur das. Wie Pino auf Basis offizieller Messwerte zeigt, war es anderswo in Spanien deutlich Kühler, vor allem an den Küsten. So kamen Barcelona im Norden und Malaga im Süden am selben Tag nur knapp über 30 Grad. Auf Mallorca herrschten – für viele Menschen nach wie vor recht angenehme – 35 Grad. In vielen Medien aber wirkte es so, als schwitze ganz Spanien bei 46 Grad, was vielleicht auch daran lag, dass viele Berichte mit Bildern von Menschen am Strand versehen waren.

In einem anderen Fall schildert der Filmemacher, wie der WDR eine Hitzewelle in Griechenland auch auf Spanien ausdehnte, während dunkle Wolken über die Costa del Sol zogen und das Thermometer kaum über die 30-Grad-Marke kam. Derselbe WDR erklärte unterschwellig auch das südostanatolische Sirnak zur südeuropäischen Seebad am Mittelmeer, nachdem dort 50,5 Grad gemessen wurden. Wohlgemerkt: 60 Kilometer entfernt von der Grenze zum Irak. Und Pino schlussfolgert, was jeder EIKE-Leser unterschreiben wird: Geht es um Klimafragen, dann gilt offenbar „Ideology first“, dann wird selbst jeder noch so große Unsinn verbreitet, Hauptsache er passt ins politisch gewünschte Narrativ.

Die Erstausgabe von Marco Pinos Adlerauge endet mit dem jüngsten Hitzewellchen Mitte August in Deutschland. Und Pino stellt fest: „Kaum wird’s Wetter wieder schön, drehen sie alle wieder durch“. Und zeigt, wie erneut übertriebene Prognosen durch die Medien gingen – und was davon tatsächlich eingetreten ist. Oder besser gesagt, nicht eingetreten ist. Aber schauen Sie selbst!

Vielen EIKE-Lesern dürfte Marco Pino vor allem von seinen großen Dokumentationen für die Junge Freiheit in Erinnerung sein. In Mythos Klimakatastrophe (2019) und Mythos Energiewende (2021) wirkte auch EIKE-Vizepräsident Michael Limburg mit. In seinem neuen Kanal will sich Pino, wie er am Ende des Films erklärt, einem breiten Themenspektrum widmen und „an die Grundlagen ran“. Das Klima mache aus gegebenem Anlass den Anfang, als nächstes stünde das Thema Walbrände auf dem Programm. Wir sind gespannt!

 

 



NRW und die verbrannte Erde von Schwarz-grün

geschrieben von Admin | 1. September 2025

Trump stoppt Offshore-Wind-Anlagen in den USA. RWE flieht zurück ins deutsche Subventionssystem. In NRW opfert Schwarz-Grün mit dem vorgezogenen Kohleausstieg, zeitgleich Versorgungssicherheit und Industrie und Naturschutz.

von Holger Douglas

Donald Trump hat in Schottland erneut gegen Offshore-Windparks gewettert. Bei seinem Flug über die Nordsee auf seinen schottischen Golfplatz sprach er angesichts der gigantischen Anlagen der Windindustrie von einer „Verunstaltung“ und betonte, in den USA den Bau solcher Anlagen zu verhindern. Nicht zum ersten Mal übrigens hat Trump diese Windradanlagen kritisiert, das tat er auch schon bei früheren Besuchen.

„Er hat die Finger in die Wunde gelegt und hat auch darauf hingewiesen, dass er in den USA alles tun werde, damit keine Windanlagen hinkommen und die Landschaft nicht weiter zu zerstören“, sagt Rechtsanwalt Thomas Mock im Gespräch mit dem TE-Wecker.

Das hat erheblich Folgen auch für Deutschland: Diese Ankündigung trifft deutsche Energieunternehmen wie RWE unmittelbar. RWE muss geplante Projekte in Amerika stoppen und verlagert Investitionen verstärkt ins EEG-Subventionssystem hierzulande. Dabei hatte das Unternehmen große Ausbaupläne in den USA – sowohl onshore als auch offshore – und muss diese nun wegen der politischen Unsicherheit auf Eis legen. RWE dürfte sich jetzt stärker auf den deutschen Markt konzentrieren. Der jedoch hängt mittlerweile vollständig von Subventionen nach dem Erneuerbare-Energien-Gesetz (EEG) ab. Mock: „Damit ist RWE auf dem besten Weg, ein völlig von Subventionen abhängiger Konzern zu werden, denn immer mehr Offshore- und Onshore-Anlagen von RWE in Deutschland kommen nur mit Hilfe des EEG zustande.“

Besonders in Nordrhein-Westfalen zeigt sich, wie stark politische Entscheidungen die Energieversorgung prägen und welche verheerenden Folgen dies hat.

Ministerpräsident Hendrik Wüst (CDU) und die Grünen haben mit geänderten Landesentwicklungs- und Regionalplanungen den Kohleausstieg auf 2030 vorgezogen – und zugleich dafür gesorgt, dass eine spätere Rückkehr praktisch ausgeschlossen ist.

Ursprünglich war der für 2038 geplant; doch auf Druck der Grünen und von Robert Habeck hat Wüst auch zugestanden, dass die komplette Landesplanung für die Kohlekraftwerke und die Tagebaue geändert werden muss. Kräftig mitgerührt hat auch Mona Neubaur, die grüne Ministerin „für Wirtschaft, Industrie, Klimaschutz und Energie“ sowie stellvertretende Ministerpräsidentin des Landes NRW.

Eigentlich sollte der vorgezogene Ausstieg noch einmal überprüft werden, ob der realisierbar ist. Doch diesen kleinen Notausstieg haben CDU und Grüne gekippt. Das bedeutet: der sogenannte „Kohleausstieg“ bereits 2030 gilt. Genehmigungen für benötigte Tagebauflächen wurden entzogen, ganze Abbaufelder aus der Planung gestrichen. Selbst wenn politisch gewollt, würde ein neues Genehmigungsverfahren mindestens zehn Jahre dauern.

Das bedeutet auch: Der gesamte Kraftwerkspark steht ohne Brennstoff da. Denn die sind auf die Braunkohle aus den Tagebauen angewiesen. Es handelt sich um 20 Jahre alte hochmoderne Anlagen mit Braunkohle-Optimierter-Anlagentechnik (BOA), die bis zu sensationellen 40 Prozent Wirkungsgrad haben. Damit verlieren moderne Braunkohlekraftwerke also schon ab 2031 ihre Brennstoffbasis – obwohl sie technisch noch Jahrzehnte laufen könnten.

Für die Versorgungssicherheit ist das fatal“, so Thomas Mock weiter im TE Wecker-Gespräch. Gaskraftwerke, die den Wegfall ausgleichen könnten, sind nicht in Sicht – und wenn sie kommen, oft mit LNG-Brennstoff, der laut Studien bis zu 80 Mal klimaschädlicher sein kann als Kohle.

Die Industrie in NRW – auf günstige Energie angewiesen – verliert so ihre wirtschaftliche Grundlage.

Weitere Folge: Investitionszurückhaltung und Abwanderung. Der Essener Energiekonzern RWE profitiert zwar kurzfristig von lukrativen EEG-Vergütungen, vor allem im Onshore-Bereich, doch die langfristigen Kosten für Verbraucher und Staat sind enorm: Bei einem flächendeckenden Ausbau mit heutigen Fördersätzen drohen Zahlungsverpflichtungen in Billionenhöhe über die nächsten 20 Jahre. Gelder, die einen Staat überfordern.

Parallel dazu ist der Naturschutz unter die Räder gekommen. Seit 2022 hat die Bundesregierung zahlreiche Artenschutzregelungen zugunsten der Windkraft abgeschafft oder verwässert. Neue EU-Vorgaben (RED III) und nationale Gesetzesänderungen erlauben Genehmigungen nahezu ohne Rücksicht auf Vogel- und Fledermausarten. Betreiber können zudem rückwirkend alte Auflagen streichen lassen – 20 Jahre Naturschutzbemühungen werden so per Änderungsantrag nach Bundesimmissionsschutzgesetz ausgelöscht. Selbst die Deutsche Wildtierstiftung schlägt Alarm, doch die Politik hält an der Bevorzugung der Windlobby fest.

Die grüne Zerstörerin Neubaur will NRW „zur ersten klima-neutralen Industrieregion Europas“ machen. „Wer nicht an Wunder glaubt, ist kein Realist“, zitiert sie auf ihrer Homepage David Ben-Gurion.

NRW nennt sich „Industrieland NRW“, ist jedoch nichts anderes als ein Bundesland, dessen Energiepolitik gleichzeitig Versorgungssicherheit, Industrie und Naturschutz opfert – im Namen einer beschleunigten „Energiewende“. Die macht vor allem Subventionsempfänger reich.

Ohne Kurskorrektur drohen Nordrhein-Westfalen und ganz Deutschland in eine strukturelle Energiekrise zu rutschen: teurer Strom, unsichere Netze, schrumpfende Industrie. Thomas Mock: „Die Grünen, die sich grün nennen und eine solche Politik machen, sind der Sargnagel des Naturschutzes – und am Ende auch der Industrie in diesem Land.“

Und was behauptet Neubaur: „Schaffen wir grünes Wachstum im Herzen Europas. Die Zukunft NRWs ist klimaneutral, sozial und digital.“ Ohne Strom ist nichts digital. Nicht nur Stahlwerke, sondern auch Rechenzentren benötigen als Stromfresser erhebliche Mengen an Energie. Die gibt es nicht mehr in Neubaur-Land.

Der Beitrag erschien zuerst bei TE hier

 



Gut gemeinte Brandstiftung Was die schweren Waldbrände dieses Sommers mit dem Klima zu tun haben

geschrieben von Admin | 1. September 2025

Edgar L. Gärtner

Selbstverständlich hängt die Waldbrandgefahr mit dem Klima zusammen, allerdings nicht mit dem fiktiven Weltklima, sondern mit konkreten regionalen Klimata. In den Gebieten mit typischem Mittelmeerklima (regelmäßig sehr trockene Sommer und feucht-milde Winter) gehören Waldbrände sogar zum normalen ökologischen Stoffkreislauf. Zumal dort Pflanzen wie die dornige Zwergeiche Quercus cocifera gedeihen, deren Samen erst nach einem Feuer keimfähig werden. Deren sexuelle Vermehrung ist also auf Waldbrände angewiesen. Neben einem schmalen Küstensaum rund ums Mittelmeer gibt es Mittelmeer-Klima auch in Kalifornien, in der Kap-Region Südafrikas und an den Südspitzen Australiens.

Schon vor Jahren haben wir auf dieser Plattform darauf hingewiesen, dass die dem Feuer zum Opfer fallende Waldfläche von Jahr zu Jahr je nach den jeweils vorherrschenden Niederschlags- und Windverhältnissen enorm schwanken kann. Wenig Einfluss hat hingegen die jeweils erreichte Lufttemperatur von 40°C und mehr. Dann schon eher die mit der mit der Sommerhitze nach langer Regenpause einhergehenden Trockenheit. Und vor allem die starken Winde (Tramontane und Mistral), die zwar unregelmäßig wehen, aber zur Grundausstattung des südfranzösischen Klimas gehören. In diesem Sommer wehten diese Winde wegen des schlechten Wetters in West- und Mitteleuropa etwas länger als im langjährigen Durchschnitt.

Immerhin hält die Trockenheit in der Region Languedoc zwischen Rhône und spanischer Grenze nun schon Jahre lang an. Der angrenzende südliche Teil des französischen Zentralmassivs, die Cevennen, bekam hingegen reichlich Regen ab. Diese Verschiebung des Niederschlagsmusters hat wahrscheinlich mit der Ablösung der Westwinddrift durch ein meridionales Muster der Windströmungen und somit mit dem Wechsel der der nordatlantischen Meereszirkulation zu tun, aber wenig bis nichts mit der Entwicklung der globalen Durchschnittstemperatur. Dennoch versuchten staatsabhängige Forscher und Massenmedien ihr ahnungsloses Publikum glauben zu machen, die Erderwärmung sei die Hauptursache großflächiger Waldbrände.

In Spanien und Portugal sollen die Flammen bis Mitte August schon an die 100.000 Hektar Wald und Heide samt den davon umschlossenen menschlichen Siedlungen verschlungen haben. Ein Feuerwehrmann kam dabei ums Leben. Besonders schwer betroffen scheint die spanische Provinz Kastilien-Leon. Deren Einwohner werfen ihren Behörden vor, zu wenig in die Waldbrand-Vorsorge investiert und die Anschaffung schweren Löschgeräts vorgezogen zu haben, um bei den Wählern mehr Eindruck zu schinden. Im mediterranen Nachbarland Frankreich muss man bis in die 1970er und frühen 80er Jahre zurückgehen, um vergleichbar traurige Meldungen über die Waldbrand-Statistik zu finden. Nach einer Kommission des französischen Senats gehen im langjährigen Mittel 90 Prozent aller Waldbrände auf menschliche Aktivtäten zurück. Hauptursache der Flächenbrände waren in den 1960er und 70er Jahren nach Angaben der zuständigen Staatsanwälte gezielte Brandstiftungen, um in attraktiven Gegenden Bauland für Luxusvillen und Feriensiedlungen zu schaffen. Doch damit ist infolge einer Gesetzesänderung inzwischen Schluss. Man bekommt in Frankreich auf abgebrannten Waldflächen nur in sehr seltenen Ausnahmen eine Baugenehmigung. Dafür gibt es heute neue Anreize für Spekulationen.

Anfang August 2025 fielen dem Feuer im Département Aude zwischen Narbonne und Carcassonne innerhalb von zwei Tagen nicht weniger als 17.000 Hektar Wald- und Buschland zum Opfer. Es handelt sich dabei überwiegend um nicht bewirtschafteten lichten Kiefern- oder immergrünen Eichenwald mit Dornengestrüpp als Unterholz, bekannt als „Garrigue“. In eine schwarze Mondlandschaft verwandelt wurden aber auch etwa 2.000 Hektar Kulturland. Es gab mindestens ein Todesopfer. Hinzu kommen mindestens 5.000 Hektar frisches Brachland, das mit trockenem Gras und anderen z.T. mannshohen Pionierpflanzen bewachsen war. Diese Brachflächen brennen wie Zunder und gelten bei den Einheimischen als Lunten für Flächenbrände und wurden daher bisher weitgehend vermieden.

Entstanden sind diese Brachflächen erst seit dem letzten Jahr, weil die Pariser Regierung, um das Überangebot auf dem Weinmarkt zu reduzieren, in Absprache mit der Brüsseler Kommission die Zahlung attraktiver Prämien für die Rodung von Rebflächen ausschrieb: Wer Weinstöcke ausreißt und die Rebfläche mindestens sechs Jahre lang brachliegen lässt, bekommt je Hektar 4.000 Euro Entschädigung aus einem EU-Fonds, mit dem negative Folgen des Ukraine-Krieges für Landwirte kompensiert werden sollen. Auch in anderen Départements, die vom Weinbau geprägt sind, wurden Rodungsprämien in vergleichbarer Höhe ausgeschrieben. Die betroffenen Winzer nennen diese kurzfristig lukrative Selbstmordaktion „Arachage Ukraine“. Immerhin gibt es dabei eine Obergrenze von 280.000 Euro je Weinbaubetrieb. Es gab aber wohl etliche Betriebe, die wegen der Absatzflaute auch Flächen rodeten, für die sie nicht entschädigt wurden. Deshalb ist die seit 2024 gerodete Fläche wahrscheinlich erheblich größer als die angegebenen 5.000 Hektar.

Eile war geboten. Bis zum 13. November 2024 mussten die Anträge auf Entschädigung bei den zuständigen Behörden eingegangen sein. Bis zum 4. August 2025 mussten die Winzer die Rodungen beim Zollamt nachweisen. Es gab einen Wettlauf um die Prämien. Obwohl ihnen höchstwahrscheinlich bewusst war, dass sie damit die von Brüssel gewollte Abwicklung der herkömmlichen Landwirtschaft in Frankreich und ganz Westeuropa beschleunigten, beteiligten sich fast alle in Frage kommenden Winzer an dem Wettlauf. Zu verlockend war die Aussicht, sich mit der Rodungsprämie ein renoviertes Haus, einen Swimming Pool oder ein neues Auto leisten zu können. Verdrängt wurde dabei die schon länger bekannte Tatsache, dass Weinberge in der bewaldeten Region eine wichtige Rolle als Riegel gegen die Ausbreitung von Waldbränden spielen und die Schönheit der Landschaft prägen. Gepflegte Weinberge gelten nicht von ungefähr seit dem Mittelalter als Inbegriff der Kulturlandschaft.

Nur wenige Gewächse des Languedoc gelten allerdings als edel. Insofern ist es verständlich, dass die Aufgabe von Weinbergen vielen nicht leidtut. Ideal wäre es, für die Brachflächen eine Nutzungsform zu finden, die in ökologischer und ästhetischer Hinsicht dem Weinbau zumindest gleichkommt. Doch das Gegenteil scheint sich anzubahnen. „Rein zufällig“ decken sich die in diesem August abgebrannten Flächen mit projektierten riesigen Solarparks. Denn es gibt im Languedoc an etwa 300 Tagen im Jahr Sonne satt. Dabei würde die grüne Landschaft so weit das Auge reicht durch glitzernde Scheiben ersetzt.

Bislang hat sich die örtliche Bevölkerung erfolgreich gegen diese überflüssige, aber profitable, weil politisch korrekte Verunstaltung ihrer Heimat gewehrt. Aber nun sind diese Flächen verkohlt und scheinbar frei für unbeliebte Nutzungen. Da liegt der Verdacht nahe, dass da jemand von der grünen Solarmafia nachgeholfen hat. Tatsächlich nimmt die zuständige Staatsanwaltschaft in Montpellier den Verdacht ernst, dass die Feuersbrunst, die am 5. August entlang der Départementalstraße 212 zwischen den Gemeinden Ribaute und Langrasse ausgebrochen ist, „eine kriminelle Ursache hat“.