Der hemisphärische Stefan-Boltzmann-Ansatz ist kein reines Strahlungsmodell – Teil 1

Uli Weber

Vorbemerkung: Dieser 2-teilige Beitrag besteht aus einer Zusammenstellung von Auszügen aus bereits hier auf EIKE veröffentlichten Artikeln; daher werden die ursprünglichen Abbildungsnummern nachfolgend durch eine eigene Zählung ersetzt. Und was Ihre sachkundigen Kommentare angeht, so bitte ich Sie mit einem Zitat von Willis Eschenbach darum, „dass Sie, wenn Sie kommentieren, die genauen Worte [innerhalb der von mir genannten Rahmenbedingungen] zitieren, auf die Sie sich beziehen. Ich kann meine Worte verteidigen. Ihre Interpretation meiner Worte [und/oder veränderte Rahmenbedingungen, in die Sie meine Worte stellen], kann [und werde] ich nicht verteidigen [- wenn überhaupt...].“

Eine gefühlte Mehrheit der Klimarealisten bewegt sich als sogenannte „Lukewarmer“ im medial verbreiteten Denkrahmen der politisierten Klimawissenschaft. Diese Lukewarmer erkennen zwar einen menschlichen Einfluss auf das Klima an, teilen aber nicht die Klimahysterie der wirtschaftlich abhängigen AGW-Verherrlichungswissenschaft. Höchst erstaunlich ist nun, dass ausgerechnet aus dieser klimarealistischen Ecke heraus diejenigen Abweichler, die den vorgegebenen Denkrahmen eines CO₂-betriebenen „natürlichen atmosphärischen Treibhauseffektes“ und dessen menschen­gemachten Ableger in Frage stellen, aufs Heftigste angegriffen werden. So ist auch mein hemisphä­rischer Stefan-Boltzmann-Ansatz bei vielen Lesern irgendwie als reines Strahlungsmodell unter die Räder gekommen, obwohl diese Einschätzung völlig falsch ist. Immerhin besteht daher die Möglichkeit, dass nicht alle meine Kritiker Anhänger des überkommenen THE-Paradigmas sind und lieber auszusterben belieben, als sich überzeugen zu lassen, sondern lediglich solchen Fehleinschätzungen folgen. Denn das rechnerische S-B-Temperaturäquivalent, mit dem ich zu argumentieren pflege, wird einerseits nirgendwo auf unserer Erde erreicht, aber andererseits muss die eingestrahlte Energie nach dem 1. HS der Thermodynamik ja irgendwo abbleiben. Daher hatte ich die tatsächliche örtliche Temperaturgenese immer über Energieverluste durch Konvektion und Verdunstung, und/oder über die Energiezufuhr durch Advektion und Konvektion erklärt, beispielsweise in dem Artikel „Anmerkungen zur Bestimmung der hemisphärischen solaren Einstrahlung auf ‚Mittelerde‘“ vom 5. Februar 2020 mit Daten aus Potsdam:

Im Gegenteil wird das maximale S-B-Temperaturäquivalent auf unserer Erde aufgrund von Konvektion und Verdunstung in der Realität niemals erreicht; umgekehrt wird aber der nächtliche Temperaturabfall durch Kondensation und Advektion abgemildert und erreicht niemals den Absoluten Nullpunkt. Letzteres gilt übrigens auch für das Strahlungsdefizit in mittleren und höheren Breiten der jeweiligen Winterhemisphäre, dazu nachfolgend ein Beispiel für Potsdam:

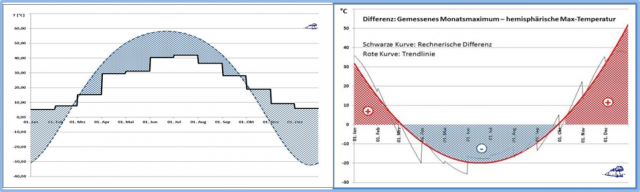
Abbildung 1: Jahresverlauf der Temperatur am Beispiel Potsdam:

Links: Treppenkurve: Maximale monatliche Bodentemperatur in Potsdam

Blau gestrichelt: Maximales jahreszeitliches S-B-Temperaturäquivalent

Rechts: Differenz zwischen der maximalen monatliche Bodentemperatur in Potsdam und dem maximalen örtlichen S-B-Temperaturäquivalent

Rote Kurve: Trendlinie für die Differenz (schwarze Zackenkurve) zwischen maximaler monatlicher Bodentemperatur und dem maximalen örtlichen S-B-Temperaturäquivalent in Potsdam

Rot schraffiert: Zufluss von Wärme im Winterhalbjahr

Blau schraffiert: Abfluss von Wärme im Sommerhalbjahr

Im Sommerhalbjahr fließt also Wärmeenergie in die globalen Wärmespeicher und im Winterhalbjahr wird die Ortstemperatur durch einen Wärmezufluss aus diesen Wärmespeichern gestützt. Und deshalb müssen Atmosphäre und Ozeane als „globale Wärmespeicher“ zwingend in die Bestimmung einer „natürlichen Temperatur“ unserer Erde einbezogen werden.

Es können eben nun mal nicht in jedem Artikel sämtliche Modelleigenschaften aufgezählt werden. Von daher ist es verständlich, wenn solche, in mehr als vierzig Artikeln ein- bis mehrfach beschriebenen Modelleigenschaften, nicht allen Lesern zu jeder Zeit präsent sind. Nachfolgend also ein Rückblick auf diejenigen Eigenschaften meines hemisphärischen S-B-Modells, die in der interessierten Öffentlichkeit offenbar nicht oder nicht in ausreichendem Maße wahrgenommen worden sind.

Kommen wir zu dem Artikel „Anmerkungen zur hemisphärischen Mittelwertbildung mit dem Stefan-Boltzmann-Gesetz“ vom 11. September 2019:

Nun liegt die „Temperaturwerdung“ (Temperaturgenese) auf der Tagseite unserer Erde (@2πR²) aber genau zwischen solarer Einstrahlung (@πR²) und terrestrischer Abstrahlung (@4πR²) – denn kein vernünftiger Mensch dürfte abstreiten, dass es auf unserer Erde Tag und Nacht gibt. Es gilt auf unserer Erde also für das rechnerische S-B-Temperaturäquivalent (S-B-T):

(S-B-T Einstrahlung @ πR²)≠(S-B-T Tagseite @ 2πR²) ≠ (S-B-T Abstrahlung @ 4πR²)

Es wird hier also eindeutig ausgesagt, dass die solare Einstrahlung So über eine Kreisfläche mit dem Erdradius, die Temperaturgenese auf der Taghalbkugel mit der Hälfte und die terrestrische Abstrahlung über die gesamte Erdoberfläche mit einem Viertel der Solarkonstanten erfolgt.

In dem Artikel „Safety First: Zum besseren Verständnis meiner hemisphärischen Energiebilanz“ vom 29. Juli 2019 hatte ich in der Gleichung [1] für die Strahlungsbilanz unserer Erde aufgestellt:

Im letzten Artikel über meinen hemisphärischen Stefan-Boltzmann Ansatz hier auf EIKE mit dem Titel „Fangen wir mit dem Stefan-Boltzmann-Gesetz noch einmal ganz von vorne an“ hatte ich am Ende eine hemisphärische Gleichung für die globale Energiebilanz unserer Erde aufgestellt:

[1] (IN = 940 W/m² _* π R²) = (OUT = 235 W/m² _* 4 π R²) @ NST (= 14,8 °C)

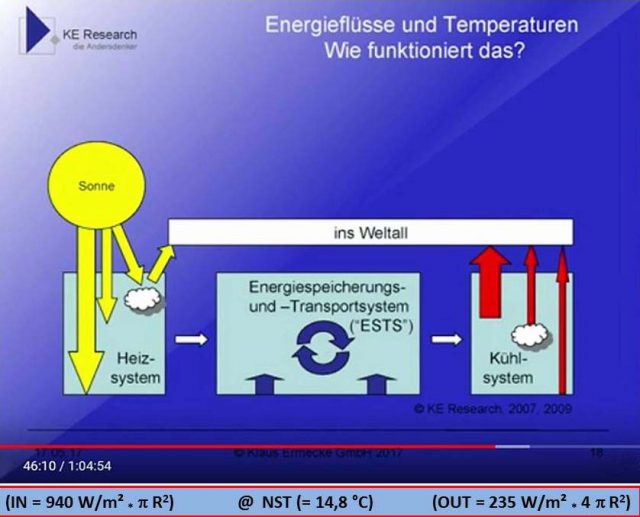Der quasi-konstante NST-Wert wurde also bereits um die langjährige Ein-und Abstrahlung bereinigt und hat überhaupt nichts mehr mit der globalen Strahlungsbilanz zu tun. Er repräsentiert vielmehr die natürlichen Wärmespeicher unserer Erde, deren eigener Wärmefluss aus dem Erdinneren dabei vernachlässigbar ist. Wenn wir also bei der NST in einer langjährigen Betrachtung alle tages- und jahreszeitlich variablen Prozesse auf unserer Erde als durchschnittlich ausgeglichen voraussetzen können, dann lassen sich die Begrifflichkeiten aus der obigen Abbildung von Ermecke und mein hemisphärischer Ansatz für die globale Energiebilanz unserer Erde folgendermaßen zusammenfügen:

Abbildung 2: Graphik von Klaus Ermecke* mit den Werten aus Gleichung [1]

*) Chart aus dem Vortrag von Klaus Ermecke „Energiepolitik im Konzeptnebel?“
© KE Research 2007/2009
mit freundlicher Genehmigung

Wir können hier also folgende grafisch dargestellten Begrifflichkeiten und die physikalischen Größen aus der hemisphärischen Energiebilanz einander direkt zuordnen:

Heizsystem: Die Sonne liefert auf der Tagseite der Erde netto 940 W/m² temperaturwirksame Strahlung auf einer Kreisfläche von πR²(mitdem Erdradius „R“).

Energiespeicherungs- und Transportsystem: Die NST von 14,8 °C repräsentiert den global gemittelten Netto-Wärmeinhalt von Atmosphäre und Ozeanen im Gleichgewicht von Ein- und Abstrahlung.

Kühlsystem: Die Erde strahlt im Temperaturgleichgewicht (NST=const.) durchschnittlich 235 W/m² über ihre Gesamtfläche 4πR² in den Weltraum ab.

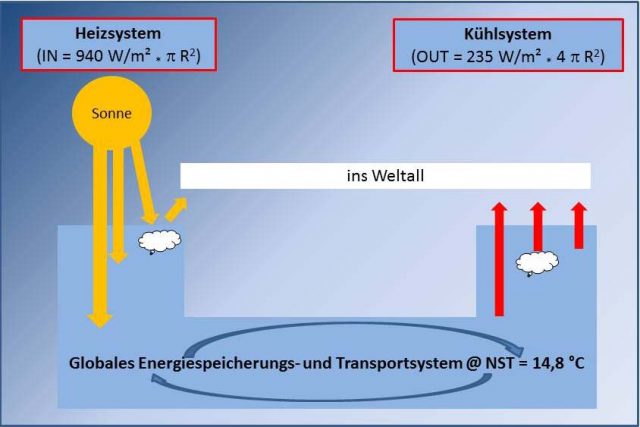Damit ergibt sich in Kombination der Darstellung und Begrifflichkeiten von Ermecke mit Gleichung [1] das folgende Bild:

Abbildung 3: Kombination der Darstellung von Klaus Ermecke mit den Werten aus Gleichung [1]

Die Umgebungsgleichung des Stefan-Boltzmann-Gesetzes lautet in einer etwas ausführlicheren Form „ΔS = S-S₀ = σ _* (T⁴-T₀⁴)“. Und jetzt wird hoffentlich auch deutlich, dass es entscheidend darauf ankommt, die S-B Umgebungstemperatur T₀ bei allen Berechnungen korrekt zu definieren. Wenn man nämlich die Temperatur des Weltalls als Umgebungstemperatur der globalen Temperaturmeßstationen definiert, dann gelangt man zum konventionellen S-B Ansatz mit minus 18°C und einem „natürlichen atmosphärischen Treibhauseffekt“ von 33 Grad Celsius.

Die global verteilten Temperaturmeßstationen befinden sich aber nun mal nicht im Weltraum!

Vielmehr sind alle diese Meßstationen auf unserer Erde in den Wechsel zwischen Tag&Nacht sowie dem Energieaustausch mit ihrer Umgebung nach [ΔS = S-S₀ = σ _* (T⁴-T₀⁴)] eingebunden.

In dem Artikel „Der gemeine Küchenherd als Beispiel für die Anwendung des Stefan-Boltzmann-Gesetzes – Teil 2“ vom 30. Juni 2023 bin ich auf den Unterschied zwischen Skalaren und Vektoren eingegangen:

Richtungsvektoren: Es gibt noch einen weiteren physikalischen Nachweis für die Unsinnigkeit einer platten Faktor4-Mittelung der solaren Sonneneinstrahlung zur Ermittlung einer „natürlichen“ Temperatur unserer Erde. Dazu müssen wir wissen, was ein „Vektor“ und was ein „Skalar“ ist, Zitat von ingenieurkurse.de:

„Ein Vektor ist eine physikalische Größe, die durch Angabe eines Zahlenwertes, ihrer Einheit und zusätzlich durch eine Richtung charakterisiert ist. Beispiele für Vektoren sind: Die Geschwindigkeit ist ein Vektor. Bei der Geschwindigkeit wird zusätzlich zur Angabe eines Zahlenwertes plus Einheit eine Richtung angegeben.

Ein Skalar ist eine physikalische Größe, die durch die Angabe eines Zahlenwertes und ihrer Einheit charakterisiert ist. “

Also: Ein Vektor ist eine gerichtete physikalische Größe, die eine Maßzahl, eine eindeutige Richtung und eine physikalische Einheit besitzt. Stellen Sie Sich einfach einen Pfeil vor, dessen Spitze die Richtung anzeigt und die Länge des Schaftes den Betrag angibt. Ein Skalar ist dagegen eine ungerichtete Größe, die nur eine Maßzahl (Betrag) und eine physikalische Einheit besitzt, ein Richtungsbezug fehlt hier völlig. Und jetzt schauen wir uns noch einmal die Situation bei der Sonnenbestrahlung der Erde genauer an:

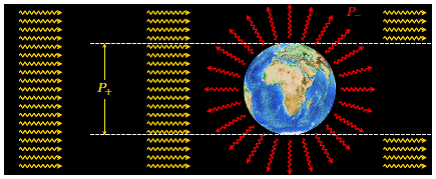
Abbildung 4: Die solare Bestrahlung der Erde und die terrestrische Abstrahlung
Quelle: Prof. Dr. Dr. h. c. Gerhard G. Paulus: Erderwärmung zum Nachrechnen

Die gelbe solare HF-Einstrahlung in dieser Abbildung ist mit parallelen (alle Strahlen sind gerader Richtung nebeneinander auf die Erde gerichtet) Strahlenvektoren auf die Erde gerichtet, während die rote IR-Abstrahlung radial (senkrecht zur Erdoberfläche) von der Erdoberfläche wegführt. Die Stärke der terrestrischen IR-Abstrahlung ergibt sich bei der klimaalarmistischen THE-Berechnung jetzt aus der Viertelung der solaren HF-Einstrahlung minus Albedo. Dabei kommt es aber zu einer Kollision der gerichteten Vektoren von HF-Ein- und IR-Abstrahlung, denn ein Vektor ändert nicht ohne Grund seine Richtung. Man hat bei dieser konventionellen Berechnung der Klimawissenschaft also ganz offensichtlich die unterschiedlichen vektoriellen Richtungen ignoriert und die Strahlungswerte lediglich als ungerichtete Skalare behandelt.

Frage: Auf welche Weise kann nun der Vektor der parallel einfallenden HF-Sonneneinstrahlung auf die radiale Richtung der IR-Abstrahlung der Erde „umgebogen“ werden?

Antwort: Gar nicht – eine Änderung des Richtungsvektors kann nur erfolgen, wenn zwischen HF-Einstrahlung und IR-Abstrahlung ein eigenständiger physikalischer Prozess stattfindet. Dieser Prozess ist die Erwärmung der Erdoberfläche durch die solare HF-Einstrahlung. Dann, und nur dann, strahlt die Erdoberfläche ihre IR-Wärmestrahlung radial ab. Und nur dann strahlt die Erdoberfläche auf der Nachtseite ebenfalls radial ab, weil durch die Drehung der Erde die erwärmte Oberfläche einfach auf die Nachtseite „mitgenommen“ wird.

Und nun kommt endlich mein hemisphärisches Stefan-Boltzmann-Modell: Versuchen wir einfach mal eine Temperaturberechnung allein für die Tagseite der Erde. Dazu nehmen wir an, die Sonne stünde genau über dem Äquator, also auf dem Frühlings- oder Herbstpunkt (Tag-und-Nacht-Gleiche). Dann teilen wir die gekrümmte Tagseite der Erde (Halbkugelfläche) in konzentrische Ringe um diesen Fußpunkt der Sonne auf, wobei auf jeder Ringfläche die spezifische Strahlungsleistung der Sonne konstant ist: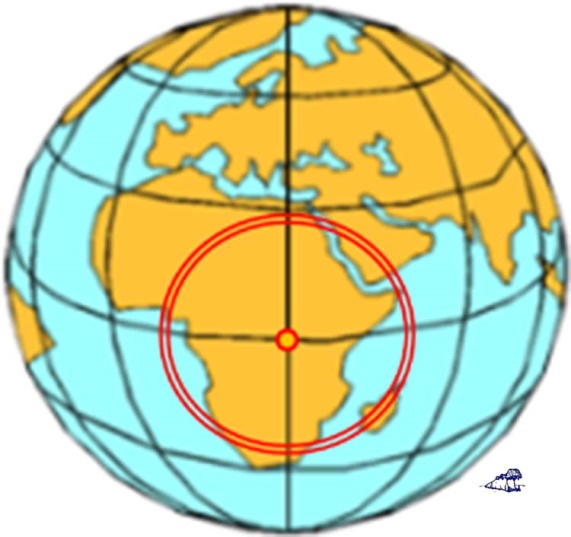

 

Abbildung 5: Die Tagseite der Erde, aufgeteilt in konzentrische Ringe von jeweils 1 Grad um den Fußpunkt der Sonne auf dem Äquator, also 0°-1°, 1°-2°, 2°-3°,….., 89°-90°.

Wegen der Erdkrümmung erhält nämlich jeder dieser konzentrischen Ringe einen ganz individuellen Anteil der Sonneneinstrahlung. Im Zentrum, am Fußpunkt der Sonne auf dem Äquator (=0°), treffen die Sonnenstrahlen senkrecht auf die Erdoberfläche. Der Boden dort erhält also die gesamten 940 /m² (=1.367 W/m² – 30%) von der Sonne. Zur Mitte und zum Rand hin vermindert sich dieser Wert aufgrund der immer schräger werdenden Auftreffwinkel der Sonnenstrahlen kontinuierlich, bis schließlich die Sonneneinstrahlung ganz am Rand (=90°) auf 0 W/m² zurückgeht. Der Richtungsabhängigkeit der solaren HF-Einstrahlung ist somit also Genüge getan. Wenn wir nun für jeden Ring aus der jeweiligen Sonneneinstrahlung eine Temperatur mit dem Stefan-Boltzmann-Gesetz ableiten und dann über alle Ringe eine Mittelung durchführen, dann erhalten wir +14,03°C. Und wenn wir die Ringe noch schmaler machen, dann werden es sogar +15,15°C, also ziemlich genau die sogenannte „global gemessene Durchschnittstemperatur“. Und die IR-Strahlung der erwärmten Erdoberfläche strahlt nun überall auf der Erde radial von der Erdoberfläche ab, wie es das Stefan-Boltzmann-Gesetz befiehlt.

Wir sehen also, wenn wir mit dem Stefan-Boltzmann-Gesetz physikalisch richtig rechnen, bleibt gar kein Platz mehr für einen „natürlichen atmosphärischen Treibhauseffekt“ und damit auch keine Notwendigkeit, unsere technische Zivilisation aus Angst vor einer globalen Klimakatastrophe zu zerstören. Denn gegenüber der vorstehend berechneten Durchschnittstemperatur von ca. 15°C für die Tagseite der Erde müsste die „theoretische“ Nachttemperatur nun um 66°C absinken, um im gemeinsamen Mittel eine globale „theoretische“ Durchschnittstemperatur von -18°C zu ergeben. Aber haben Sie einen solchen nächtlichen Temperatursturz von mehr als 60°C schon jemals erlebt? – Nein? – Und auch der sogenannte „natürliche atmosphärische Treibhauseffekt“ von 33°C hilft hier wenig, denn dann würden immer noch 33°C fehlen.

ERGEBNIS: Es gibt auf unserer Erde gar keinen „natürlichen atmosphärischen Treibhauseffekt“! – Und auf der immer als „leuchtendes“ THE-Beispiel herangezogenen Venus übrigens auch nicht!

Noch ein paar abschließende Bemerkungen zum globalen Wärmetransport und zur Wärmespeicherung auf der Erde: Es ist offensichtlich, dass auf der Erdoberfläche die rein rechnerische Temperatur nach dem Stefan-Boltzmann-Gesetz aus der solaren Einstrahlung nirgendwo erreicht wird. Andererseits wissen wir aber aus dem Energieerhaltungssatz der Wärmelehre, dass Energie nicht einfach so verschwinden kann. Vielmehr vermindert der ständige Abfluss von Wärme durch Konvektion und Verdunstung den durch die Sonneneinstrahlung bedingten örtlichen Temperaturanstieg. Dabei spielt der Energietransport durch Atmosphäre und Ozeane aus Tropen und Subtropen in die Polarzonen hinein eine ganz wesentliche Rolle für unser Klima.

In meinem Artikel „Die sogenannte ‚gemessene globale Durchschnittstemperatur‘ wird von den Ozeanen bestimmt“ vom 8. Mai 2021 hatte ich die Funktion der terrestrischen Wärmespeicher beleuchtet:

Die solare Einstrahlung ersetzt also lediglich die terrestrische Abstrahlung bei einer „gemessenen globalen Durchschnittstemperatur“ (NST) von etwa 15°C, die sich wiederum ohne einen „natürlichen atmosphärischen Treibhauseffekt“ ganz zwanglos aus meinem hemisphärischen S-B-Ansatz herleitet. Es gilt demnach im langjährigen Durchschnitt:

[ Solare Einstrahlung @2PIR² = terrestrische Abstrahlung @4PIR² ] @ NST

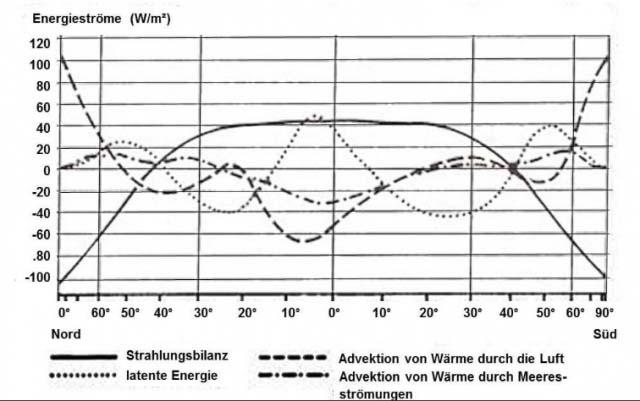Unsere Erde verfügt auf zwei Dritteln ihrer Oberfläche über eine Fußbodenheizung mit der in Abbildung 3 (links) dargestellten mittleren Vorlauftemperatur. Diese Ozean-Temperaturen repräsentieren wiederum zwei Drittel der „gemessenen“ globalen Ortstemperaturen. Die mittlere jährliche Oberflächentemperatur der Ozeane liegt bis etwa 70° nördlicher und südlicher geographischer Breite zwischen 0°C – 30°C und fällt erst jenseits davon auf bis zu -5°C ab; ein globaler Durchschnitt dürfte also in etwa bei der NST von etwa 15°C kumulieren. Wie wir bereits erfahren haben, wird das maximale rechnerische S-B-Temperaturäquivalent meines hemisphärischen S-B-Modells aufgrund von örtlicher Konvektion und Verdunstung in der Realität nirgendwo erreicht. Andererseits sinkt die Temperatur der Winterhemisphäre, insbesondere in der Polarnacht, niemals auf das rechnerische S-B-Temperaturäquivalent der geringen/fehlenden solaren Einstrahlung ab. Die nachfolgende Abbildung zum globalen horizontalen Wärmetransport gibt Aufschluss über die Gründe dafür:

Abbildung 6: Jahresmittel des Energiehaushaltes der Atmosphäre und seiner Komponenten in Abhängigkeit von der geographischen Breite. QUELLE: HÄCKEL, Meteorologie, Verlag Eugen Ulmer, Stuttgart 1990, hier aus dem Internet

Alle diese Energieströme summieren sich für eine feste geographische Breite im durchschnittlichen Jahresmittel gerade auf null. Wir können hier also erkennen, dass sich die Überschüsse und Defizite gegenüber dem hemisphärisch berechneten S-B-Temperaturäquivalent durch den lateralen Transport von Wärme gerade global ausgleichen und damit mein hemisphärisches S-B-Modell voll bestätigen.

Es wird aus Abbildung 4 deutlich, dass durch die globalen Zirkulationen in Atmosphäre und Ozeanen Energie aus niederen und den sommerlichen mittleren Breiten in hohe Breiten und winterliche mittlere Breiten transportiert wird, die dort die Ortstemperatur nach unten stabilisieren. Denn sonst würde die Temperatur in der Polarnacht auf mondähnliche Werte absinken.

In meinem Artikel „Energiewende: Sofort alle Klimamodelle von (Faktor4*+CO₂) auf rein Solar umstellen!“ vom 12. August 2023 hatte ich mich näher mit dem terrestrischen Energietransport beschäftigt:

Wärme (Energie) kann durch unterschiedliche physikalische Prozesse transportiert werden, also schaunmermal:

Strahlungstransport: „Wenn sich elektromagnetische Strahlung in einem Medium ausbreitet (ganz gleich ob in der Photonen-Betrachtung oder Feldbetrachtung), wird sie von dem Medium (insbesondere von dessen Atomen und Ionen) absorbiert, gestreut oder kann das Medium verlassen. Diese Prozesse bzw. die Beschreibung dieser Prozesse nennt man Strahlungstransport.“

Wärmeleitung: „Wärmeleitung – auch Wärmediffusion oder Konduktion genannt – ist ein Mechanismus zum Transport von thermischer Energie. Wärme fließt dabei – gemäß dem zweiten Hauptsatz der Thermodynamik – immer nur in Richtung geringerer Temperatur. Dabei geht keine Wärmeenergie verloren; es gilt der Energieerhaltungssatz.“

Konvektion: „Konvektion oder Strömungstransport ist der Transport physikalischer Zustandsgrößen in strömenden Gasen oder Flüssigkeiten. Physikalische Zustandsgrößen sind dabei beispielsweise mitgeführte Wärme, Materie oder Impuls. Der konvektive Transport thermischer Energie ist ein Mechanismus des Wärmetransports und wird auch Wärmemitführung genannt.“

Verdunstung: „Bei einer Verdunstung geht ein Stoff vom flüssigen in den gasförmigen Zustand über, ohne dabei die Siedetemperatur zu erreichen.[1] Zur Verdunstung kommt es, wenn die Gasphase über der Flüssigkeit noch nicht mit Dampf gesättigt ist. […..] Zur Verdampfung ist Wärmeenergie nötig, die aus der flüssigen Phase oder der darüberstreichenden Gasphase stammt. Beim Verdunstungsprozess kühlt sich eine der beiden Phasen ab, dies führt zur sogenannten Verdunstungskühlung.“

Warum sind nun die Temperaturen von Mond und Erde so unterschiedlich?

Die Antwort auf diese Frage finden Sie im 2. Teil dieses Beitrags.