Auto-Korrelation in Zeitreihen von CO2 und Temperatur
Andy May
In meinem letzten Beitrag [in deutscher Übersetzung hier] habe ich die NASA-CO2-Daten und die HadCRUT5-Daten von 1850 bis 2020 aufgezeichnet und verglichen. Damit reagierte ich auf eine von Robert Rohde auf Twitter gepostete Grafik, in der er behauptete, dass die beiden Daten gut korrelieren. Das scheint tatsächlich der Fall zu sein, denn das resultierende R² beträgt 0,87. Die verwendete Funktion der kleinsten Quadrate machte die globale Temperaturanomalie zu einer Funktion des Logarithmus zur Basis 2 der CO2-Konzentration (oder „log2CO2„). Das bedeutet, dass die Temperaturveränderung linear mit der Verdoppelung der CO2-Konzentration verläuft, eine gängige Annahme. Bei der Methode der kleinsten Quadrate (LS) wird davon ausgegangen, dass die Messungen der CO2-Konzentration fehlerfrei sind und alle aus der Korrelation resultierenden Fehler (die Residuen) in den HadCRUT5-Schätzungen der globalen durchschnittlichen Oberflächentemperatur enthalten sind.
In den Kommentaren zum vorherigen Beitrag wurde deutlich, dass einige Leser verstanden hatten, dass das berechnete R² (oft als Bestimmtheitsmaß bezeichnet) von LS künstlich aufgebläht wurde, weil sowohl X (log2CO2) als auch Y (HadCRUT5) autokorreliert sind und mit der Zeit zunehmen. Aber einige wenige haben diesen wichtigen Punkt nicht verstanden. Wie die meisten Investoren, Ingenieure und Geowissenschaftler wissen, haben zwei Zeitreihen, die beide autokorreliert sind und mit der Zeit zunehmen, fast immer ein überhöhtes R². Dies ist eine Form der „Scheinkorrelation“. Mit anderen Worten: Ein hohes R² bedeutet nicht unbedingt, dass die Variablen miteinander in Beziehung stehen. Die Autokorrelation ist in der Zeitreihenanalyse und in der Klimawissenschaft von großer Bedeutung, wird aber zu häufig ignoriert. Um eine Korrelation zwischen CO2 und HadCRUT5 zu beurteilen, müssen wir nach Autokorrelationseffekten suchen. Das am häufigsten verwendete Instrument ist die Durbin-Watson-Statistik.
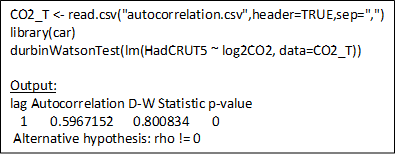
Die Durbin-Watson-Statistik testet die Nullhypothese, dass die Residuen aus einer LS-Regression nicht autokorreliert sind, gegen die Alternative, dass sie es sind. Die Statistik ist eine Zahl zwischen 0 und 4. Ein Wert von 2 bedeutet, dass keine Autokorrelation vorliegt, ein Wert < 2 deutet auf eine positive Autokorrelation und ein Wert > 2 auf eine negative Autokorrelation hin. Da bei der Berechnung von R2 davon ausgegangen wird, dass jede Beobachtung unabhängig von den anderen ist, hoffen wir, dass wir einen Wert von 2 erhalten, so dass das R² gültig ist. Wenn die Regressionsresiduen autokorreliert und nicht zufällig, d. h. normal um den Mittelwert verteilt sind, ist R² ungültig und zu hoch. In dem Statistikprogramm R wird dies – unter Verwendung einer linearen Anpassung – mit nur einer Anweisung durchgeführt, wie unten gezeigt:
Dieses R-Programm liest die HadCRUT5-Anomalien und die in Abbildung 1 dargestellten log2CO2-Werte von 1850-2020 ein, lädt dann die R-Bibliothek, die die Funktion Durbin-Watson-Test enthält, und führt die Funktion aus. Ich übergebe der Funktion nur ein Argument, nämlich die Ausgabe der R-Funktion für lineare Regression lm. In diesem Fall bitten wir lm, eine lineare Anpassung von HadCRUT5 als eine Funktion von log2CO2 zu berechnen. Die Funktion Durbin-Watson (DW) liest die Ausgabe von lm und berechnet die DW-Statistik von 0,8 aus den Residuen der linearen Anpassung, indem sie diese mit sich selbst mit einer Verzögerung von einem Jahr vergleicht.
Die DW-Statistik ist deutlich kleiner als 2, was auf eine positive Autokorrelation hindeutet. Der p-Wert ist Null, was bedeutet, dass die Nullhypothese, dass die HadCRUT5-log2CO2-Residuen der linearen Anpassung nicht autokorreliert sind, falsch ist. Das heißt, sie sind wahrscheinlich autokorreliert. Mit R lässt sich die Berechnung leicht durchführen, aber sie ist unbefriedigend, da wir weder aus der Ausführung noch aus der Ausgabe viel verstehen. Führen wir also die gleiche Berechnung mit Excel durch und gehen wir die komplizierten Details durch.
Die komplizierten Details
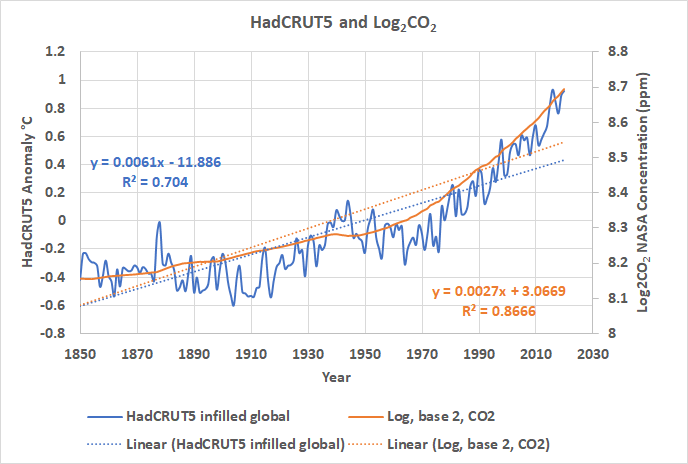
Die verwendeten Basisdaten sind in Abbildung 1 dargestellt, die mit Abbildung 2 im vorherigen Beitrag [in deutscher Übersetzung hier] identisch ist:
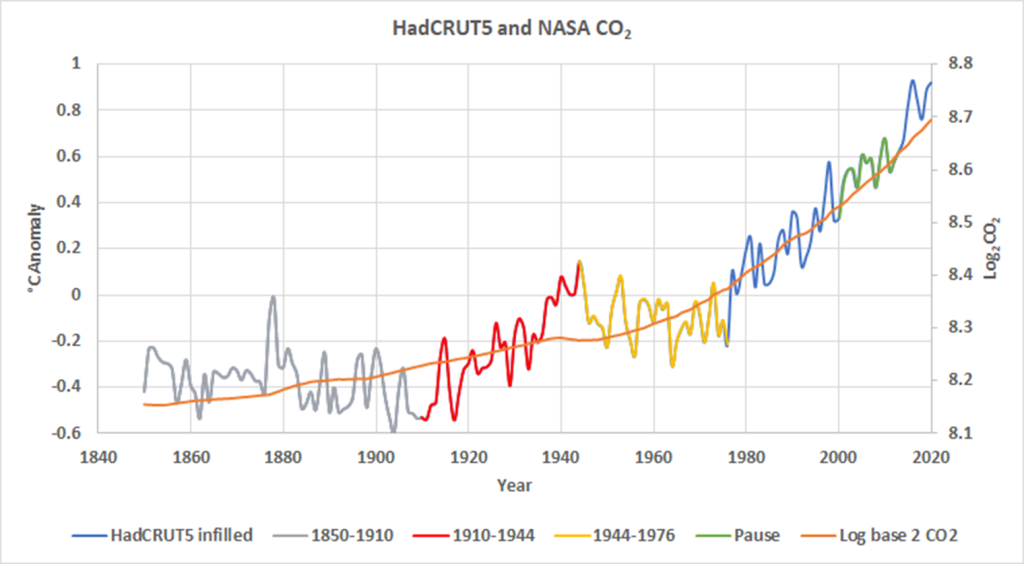
Abbildung 1. Die orangefarbene Linie ist der log↓2CO↓2-Wert, es wird die rechte Skala verwendet. Die mehrfarbige Linie ist die HadCRUT5-Aufzeichnung der globalen Oberflächentemperatur an Land und im Ozean, sie verwendet die linke Skala. Die verschiedenen Farben kennzeichnen die in der Legende angegebenen Zeiträume.
Streng genommen bezieht sich die Autokorrelation darauf, wie eine Zeitreihe mit einer zeitlichen Verzögerung mit sich selbst korreliert. Visuell können wir sehen, dass beide Kurven in Abbildung 1 autokorreliert sind, wie die meisten Zeitreihen. Das bedeutet, dass ein großer Teil jedes Wertes durch den vorangegangenen Wert bestimmt wird. So ist der log2CO2-Wert im Jahr 1980 stark vom Wert im Jahr 1979 abhängig, und dies gilt auch für die Werte von 1980 und 1979 in HadCRUT5. Dies ist ein kritischer Punkt, da alle LS-Anpassungen davon ausgehen, dass die verwendeten Beobachtungen unabhängig sind und dass die Residuen zwischen den Beobachtungen und den vorhergesagten Werten zufällig und normal verteilt sind. R² ist nicht gültig, wenn die Beobachtungen nicht unabhängig sind; eine fehlende Unabhängigkeit wird in den Regressions-Residuen sichtbar. Nachstehend finden Sie eine Tabelle der Autokorrelationskoeffizienten für die Kurven in Abbildung 1 für Zeitverzögerungen von einem bis acht Jahren:

Tabelle 1. Autokorrelationswerte für ein- bis achtjährige Verzögerungen für die HadCRUT5- und Log↓2CO↓2-Aufzeichnungen.
Die Autokorrelationswerte in Tabelle 1 wurden mit der hier zu findenden Excel-Formel errechnet. Die angezeigten Autokorrelationskoeffizienten variieren wie herkömmliche Korrelations-Koeffizienten von -1 (negative Korrelation) bis +1 (positive Korrelation). Wie Sie in der Tabelle sehen können, sind sowohl HadCRUT5 als auch log2CO2 stark positiv autokorreliert, d. h. sie steigen monoton an, wie wir mit einem Blick auf Abbildung 1 bestätigen können. Die Autokorrelation nimmt mit zunehmender Verzögerung ab, was normalerweise der Fall ist. Das bedeutet lediglich, dass die diesjährige Durchschnittstemperatur enger mit der Temperatur des letzten Jahres zusammenhängt als mit der des Vorjahres usw.
Aus Zeile 1 der Tabelle 1 geht hervor, dass etwa 76 % jeder HadCRUT5-Temperatur und über 90 % jeder NASA-CO2-Konzentration vom Vorjahreswert abhängig sind. In beiden Fällen ist also jeder Jahreswert nicht unabhängig.
Während die oben genannten Zahlen für die einzelnen Kurven in Abbildung 1 gelten, kann die Autokorrelation die Regressions-Statistik eindeutig beeinflussen, wenn die Temperatur- und CO2-Kurven gegeneinander regressiert werden. Diese bivariate Autokorrelation wird in der Regel mit der oben erwähnten Durbin-Watson-Statistik untersucht, die nach James Durbin und Geoffrey Watson benannt ist.
Lineare Anpassung
Wie in dem obigen R-Programm wird die Durbin-Watson-Berechnung traditionell anhand einer linearen Regression der beiden interessierenden Variablen durchgeführt. Abbildung 2 ist wie Abbildung 1, aber wir haben LS-Linien sowohl an HadCRUT5 als auch an Log2CO2 angepasst:
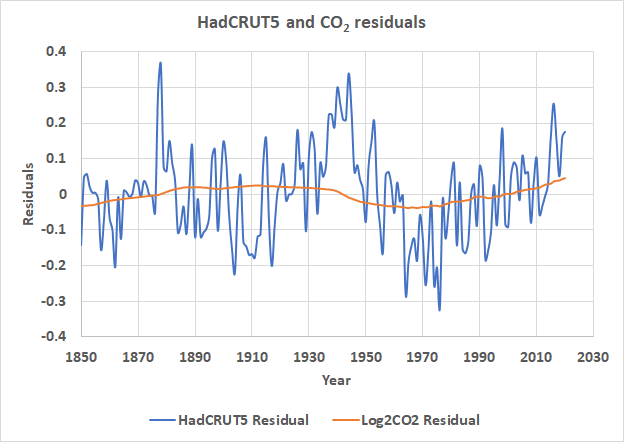
In Abbildung 2 steht Orange für log2CO2 und Blau für HadCRUT5. Die Residuen sind in Abbildung 3 dargestellt. Sie sind nicht zufällig und scheinen autokorreliert zu sein, wie wir es aufgrund der Statistiken in Tabelle 1 erwarten würden. Sie sind autokorreliert und haben die gleiche Form, was besorgniserregend ist.
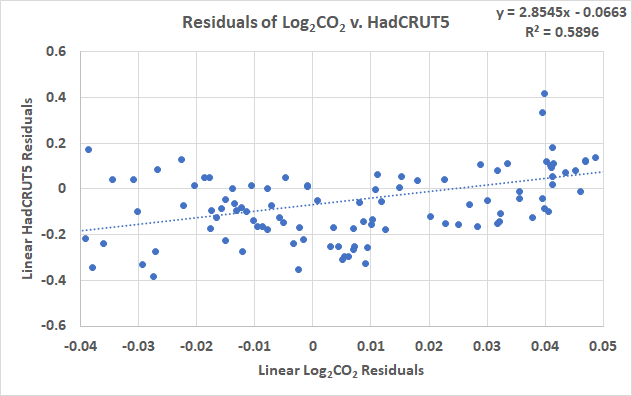
Der nächste Schritt im DW-Prozess besteht darin, eine LS-Anpassung an die in Abbildung 3 gezeigten Residuen vorzunehmen, was in Abbildung 4 dargestellt ist:
Wie befürchtet, korrelieren die Residuen miteinander und haben eine positive Steigung. Wenn man die DW-Berechnungen auf diese Weise durchführt, erhält man eine DW-Statistik von 0,84, die dem in R berechneten Wert nahe kommt, aber nicht genau gleich ist. Ich vermute, dass dies darauf zurückzuführen ist, dass die mehrfachen Summenquadrat-Berechnungen über 170 Jahre Daten zu dem feinen Unterschied von 0,04 führen. Wir können dies bestätigen, indem wir die R-Berechnung mit den Excel-Residuen durchführen:
Dies bestätigt, dass beide Berechnungen übereinstimmen, aber es gab Unterschiede in den Quadratsummen-Berechnungen aufgrund der unterschiedlichen Gleitkommagenauigkeit in Excel und R. Bei einer linearen Anpassung an HadCRUT5 und log2CO2 gibt es also ernsthafte Autokorrelationsprobleme. Aber beide sind konkav nach oben gerichtet. Was wäre, wenn wir eine LS-Anpassung verwenden würden, die besser geeignet ist als eine Linie? Die Diagramme sehen aus wie ein Polynom zweiter Ordnung, versuchen wir das.
Polynomielle Anpassung
Abbildung 5 zeigt die gleichen Daten wie in Abbildung 1, aber wir haben Polynome zweiter Ordnung an jede der Kurven angepasst. Die CO2– und HadCRUT5-Daten weisen eine steigende Kurve auf, so dass dies eine große Verbesserung gegenüber den obigen linearen Anpassungen darstellt:
Ich sollte erwähnen, dass ich die Gleichungen auf dem Diagramm nicht für die Berechnungen verwendet habe, sondern eine separate Anpassung an die Dekaden vorgenommen habe. Die Dekaden wurden unter Verwendung von 1850 als Null und 1850 bis 1860 als Dezimaldekaden und so weiter bis 2020 berechnet, so dass die X-Variable in der Berechnung kleinere Werte in den Berechnungen der Summe der Quadrate hatte. Damit wird das bereits erwähnte Problem der Fließkomma-Genauigkeit von Excel-Computern umgangen.
Im nächsten Schritt wird der vorhergesagte oder Trendwert für jedes Jahr vom tatsächlichen Wert subtrahiert, um die Residuen zu erhalten. Dies wird für beide Kurven durchgeführt, die Residuen sind in Abbildung 6 dargestellt:
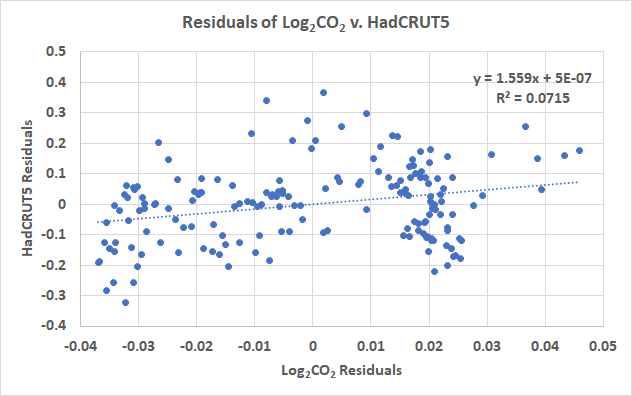
Abbildung 6 zeigt uns, dass die Residuen der polynomialen Anpassungen an HadCRUT5 und log2CO2 immer noch eine Struktur aufweisen und die Struktur visuell korreliert, was kein gutes Zeichen ist. Dies ist der Teil der Korrelation, der übrig bleibt, nachdem die Anpassung zweiter Ordnung entfernt wurde. In Abbildung 7 habe ich einen linearen Trend an die Residuen angepasst. Das R² ist geringer als in Abbildung 4:
Es gibt immer noch ein Signal in den Daten. Es ist positiv, was darauf hindeutet, dass, wenn die Autokorrelation wirklich mit der Anpassung 2. Ordnung entfernt wurde (wir können das statistisch nicht sagen, aber „was wäre wenn“), es immer noch eine kleine positive Veränderung der Temperatur gibt, wenn das CO2 steigt. Denken Sie daran, dass Autokorrelation nicht bedeutet, dass es keine Korrelation gibt, sondern nur, dass sie die Korrelationsstatistiken entkräftet. Wenn die Temperatur größtenteils von der Temperatur des Vorjahres abhängt und wir diesen Einfluss erfolgreich eliminieren können, bleibt die tatsächliche Abhängigkeit der Temperatur vom CO2. Leider können wir nie sicher sein, dass wir die Autokorrelation entfernt haben, und können nur spekulieren, dass Abbildung 7 die wahre Abhängigkeit zwischen Temperatur und CO2 darstellt.
Die Durbin-Watson-Statistik
Nun werden die Berechnungen zur Ermittlung der gemeinsamen Durbin-Watson-Autokorrelation durchgeführt, aber dieses Mal haben wir eine polynomiale Regression 2. Ordnung. Die nachstehende Tabelle zeigt die Durbin-Watson-Statistik zwischen HadCRUT5 und log2CO2 für eine Verzögerung von einem Jahr. Die Berechnungen wurden nach dem hier beschriebenen Verfahren durchgeführt:
Der Durbin-Watson-Wert von 0,9 für eine einjährige Verzögerung bestätigt, was wir in den Abbildungen 5 und 6 visuell gesehen haben. Die Residuen sind immer noch autokorreliert, selbst nach Entfernung des Trends zweiter Ordnung. Die verbleibende Korrelation ist, wie zu erwarten, positiv, was vermutlich bedeutet, dass CO2 einen geringen Einfluss auf die Temperatur hat. Wir können diese Berechnung in R bestätigen:
Diskussion
Das R², das sich aus einer LS-Anpassung der CO2-Konzentration und der globalen Durchschnittstemperaturen ergibt, ist künstlich aufgebläht, weil sowohl CO2 als auch die Temperatur autokorrelierte Zeitreihen sind, die mit der Zeit zunehmen. Daher ist R² in diesem Fall eine ungeeignete Statistik. R² geht davon aus, dass jede Beobachtung unabhängig ist, und wir stellen fest, dass 76 % der globalen Durchschnittstemperatur eines jeden Jahres durch die Temperatur des Vorjahres bestimmt wird, so dass nur ein geringer Anteil durch CO2 beeinflusst wird. Außerdem wird die CO2-Messung jedes Jahres zu 90 % durch den Wert des Vorjahres bestimmt.
Ich kam zu dem Schluss, dass die beste Funktion zur Beseitigung der Autokorrelation ein Polynom 2. Ordnung war, aber selbst wenn dieser Trend entfernt wird, sind die Residuen immer noch autokorreliert, und die Nullhypothese, dass sie nicht korreliert sind, musste verworfen werden. Es ist enttäuschend, dass Robert Rohde, ein promovierter Wissenschaftler, ein Diagramm der Korrelation von CO2 und der globalen Durchschnittstemperatur verschickt und damit andeutet, dass die Korrelation zwischen ihnen ohne weitere Erklärung sinnvoll ist (wie wir in Abbildung 1 des vorherigen Beitrags gezeigt haben), aber er hat es getan.
Jamal Munshi hat 2018 in einem Papier eine ähnliche Analyse wie wir vorgenommen (Munshi, 2018). Er stellt fest, dass die Konsensidee, dass steigende CO2-Emissionen eine Erwärmung verursachen und dass die Erwärmung linear mit der Verdoppelung des CO2 ist (Logarithmusbasis 2), eine überprüfbare Hypothese ist. Diese Hypothese hat sich nicht gut bewährt, weil die Unsicherheit bei der Schätzung der CO2-bedingten Erwärmung (Klimasensitivität) seit über vierzig Jahren hartnäckig groß ist, im Grunde ±50 %. Dies hat dazu geführt, dass der Konsens versucht, von der Klimasensitivität wegzukommen und die Erwärmung mit den gesamten Kohlendioxidemissionen zu vergleichen, weil man glaubt, eine engere und validere Korrelation mit der Erwärmung herstellen zu können. Munshi fährt fort:
„Dieser Zustand in der Klimasensitivitätsforschung ist wahrscheinlich das Ergebnis einer unzureichenden statistischen Strenge in den angewandten Forschungsverfahren. Diese Arbeit zeigt falsche Proportionalitäten in Zeitreihendaten auf, die zu Klimasensitivitäten führen können, die nicht interpretierbar sind. … [Munshis] Ergebnisse deuten darauf hin, dass die große Anzahl von Klimasensitivitäten, die in der Literatur berichtet werden, wahrscheinlich größtenteils falsch sind. … Ausreichende statistische Disziplin wird wahrscheinlich die … Frage der Klimasensitivität auf die eine oder andere Weise klären, entweder um ihren bisher schwer fassbaren Wert zu bestimmen oder um zu zeigen, dass die angenommenen Beziehungen in den Daten nicht existieren.“
(Munshi, 2018)
Während wir in diesem Beitrag die CO2-Konzentration verwendet haben, verwenden viele im „Konsens“ nun die Gesamtemissionen fossiler Brennstoffe in ihrer Arbeit, weil sie denken, dass dies eine statistisch validere Größe zum Vergleich mit der Temperatur ist. Das ist nicht der Fall, die Probleme bleiben bestehen und sind in mancher Hinsicht sogar noch schlimmer, wie Munshi in einem separaten Beitrag erläutert (Munshi, 2018b). Ich stimme mit Munshi darin überein, dass es der Klimagemeinschaft an statistischer Strenge mangelt. Die Gemeinschaft verwendet Statistiken allzu oft, um ihren Mangel an Daten und statistischer Signifikanz zu verschleiern, anstatt zu informieren.
Der R-Code und die Excel-Tabelle, die zur Durchführung aller Berechnungen in diesem Beitrag verwendet wurden, können hier heruntergeladen werden.
Referenzen:
Munshi, J. (2018). The Charney Sensitivity of Homicides to Atmospheric CO2: A Parody. SSRN. Retrieved from https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3162520
Munshi, J. (2018b). From Equilibrium Climate Sensitivity to Carbon Climate Response. SSRN. Retrieved from https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3142525
Link: https://andymaypetrophysicist.com/2021/11/13/autocorrelation-in-co2-and-temperature-time-series/
Übersetzt von Christian Freuer für das EIKE