Sollten wir uns Sorgen machen?

geschrieben von Willis Eschenbach | 3. Februar 2014

Abbildung rechts: Temperaturen der microwave Sounding unit auf Satelligen (rote Linie) von der University of Alabama. Blaue Linien zeigen eine lockere Glättung [a loess smooth], Spanne = 0,4. Daten: KNMI (NCDC, 17 MB)

Also … gibt es da etwas Besorgliches?

Nun, schauen wir doch mal. Zuallererst: In den Tropen zeigt sich kein Trend, und die machen bereits 40% der Planetenoberfläche aus. Was ist also mit all jenen, die all den armen Menschen in den Tropen „Doom and Gloom“ prophezeit haben? Tut mir leid … da zeigt sich nicht die leiseste Bedrohung. Nun, tatsächlich gibt es doch eine, und zwar die Bedrohung durch steigende Energiepreise infolge des sinnlosen Krieges gegen den Kohlenstoff – und steigende Energiepreise treffen die Ärmsten am härtesten. Aber ich schweife ab…

Und was noch? Außertropische Gebiete der Südhalbkugel? Kein Trend. Südlich des antarktischen Polarkreises? Kein Trend, es hat sich leicht abgekühlt und dann um den gleichen Betrag wieder leicht erwärmt.

Das heißt, in 70% der Planetenoberfläche zeigte sich kein wahrnehmbarer Temperaturtrend während des letzten Drittels eines Jahrhunderts …

Und was noch? Außertropische Gebiete der Nordhalbkugel? Ein kaum erkennbarer Trend und gar keiner mehr seit dem Jahr 2000.

Und das bedeutet, dass sich in etwa 96% der Erdoberfläche gar keine Richtung abzeichnet…

Bleibt noch der Rest von 4% nördlich des arktischen Polarkreises. Während der ersten eineinhalb Jahrzehnte hat es sich leicht abgekühlt. Dann ist es ein Jahrzehnt lang wärmer geworden und dann ist die Temperatur ein weiteres Jahrzehnt gleich geblieben…

Meine Schlussfolgerung? Ich sehe nicht das Geringste hier, worüber man sich Sorgen machen müsste. Wieder einmal überraschend für mich ist die erstaunliche Stabilität der Temperatur des Planeten. Ein Drittel eines Jahrhunderts, und die Temperatur in den Tropen hat nicht einmal um eine Haaresbreite geschwankt. Das ist ein extrem stabiles System.

Ich erkläre mir das als Folge des thermoregulatorischen Effektes auftauchender Klimaphänomene … haben Sie eine bessere Erklräung?

Link: http://wattsupwiththat.com/2014/01/29/should-we-be-worried/

Übersetzt von Chris Frey EIKE

Mehr Spaß mit Öl und Gas

geschrieben von Willis Eschenbach | 3. Februar 2014

Hubbert sagte Reportern: „Ein Kind, das Mitte der dreißiger Jahre geboren worden ist, wird in seinem Leben den Verbrauch von 80% allen amerikanischen Öls und Gases erleben; ein Kind, das um 1970 geboren worden ist wird sehen, dass die meisten Reserven der Welt verbraucht worden sind“.

Da sich Mr. King Hubbert Sorgen darüber machte, dass viele der Reserven der Welt verbraucht worden sind, dachte ich mir einmal nachzuschauen, wie viele der US-Reserven während des letzten Drittels eines Jahrhunderts verbraucht worden sind. Das ist eine interessante Antwort…

Abbildung 1: Ein Vergleich der jährlichen Schätzungen der nachgewiesenen US-Ölreserven (rote Linie) und der kumulierten US-Ölerzeugung (blaue Linie) während des Zeitraumes 1980 bis 2012. Daten: 2013 BP Statistical Review of World Energy. „Nachgewiesene Reserven” in dem Datensatz sind wie folgt definiert: „Nachgewiesene Ölreserven – im Allgemeinen die Mengen, die mit hinreichender Gewissheit aus geologischer und ingenieurlicher Sicht entdeckt werden können, abgeleitet aus heutigen bekannten Reservoiren unter den bestehenden ökonomischen und bearbeitungstechnischen Bedingungen“.

Es scheint, dass wir seit 1980 keinerlei Glück mehr hatten. Zunächst verbrauchten wir vollständig die nachgewiesenen Reserven bis auf den letzten Tropfen.

Dann haben wir alles noch einmal verbraucht. Und dann zum dritten mal… und die nachgewiesenen Reserven sind immer noch dort, wo sie angefangen haben.

Da King sich auch Sorgen darüber machte, dass die Erdgasreserven der USA und global vollständig aufgebraucht seien, dachte ich mir, auch da einmal nachzuschauen.

Abbildung 2: Ein Vergleich der jährlichen Schätzungen der in den USA nachgewiesenen Gasreserven (rote Linie) und der kumulativen Gaserzeugung der USA (grüne Linie) für den Zeitraum 1980 bis 2012. Daten: 2013 BP Statistical Review of World Energy.

Und wir erkennen das Gleiche. Es begann im Jahre 1980 mit 6 Billionen Kubikmeter nachgewiesener Gasreserven. Seitdem haben wir etwa 10 Billionen Kubikmeter, etwa dreimal so viel wie unsere originalen Reserven. Der wesentliche Unterschied zwischen Gas und Öl besteht darin, dass die nachgewiesenen Reserven von Gas um ein Drittel höher liegen als 1980.

Ich erwähne das hier nur aus einem einfachen Grund: nämlich um zu zeigen, dass wir nicht genug wissen, um irgendwelche Fragen zu beantworten, wie viel Öl und Gas wir verbraucht haben; oder zu bestimmen, ob der King mit seinen Behauptungen recht hatte. All den Daten zufolge haben wir seit 1980 dreimal die nachgewiesenen Reserven von Öl und Gas verbraucht, und trotzdem sind die nachgewiesenen Reserven heutzutage immer noch genauso oder sogar größer als im Jahre 1980. Wie also können wir entscheiden, ob Hubbert recht hatte oder nicht?

Versuchen Sie jetzt bitte nicht, mir geduldig all die Gründe für dieses kuriose Phänomen zu erklären, weil ich die alle schon mal gehört habe. Ich versichere, ich verstehe alle Schwierigkeiten hinsichtlich der Schätzung nachgewiesener Reserven, und die Tatsache, dass die Daten von Ölgesellschaften stammen und sich die Technologie laufend verbessert und die Unternehmen dazu tendieren auszubeuten, bis sie Vorräte für etwa 20 Jahre angesammelt haben und dass die Wirtschaft eine große Rolle spielt und… Ich kenne alle Gründe für das, was ich oben gezeigt habe.

Ich möchte lediglich darauf hinweisen, dass es sehr, sehr schwierig ist vorherzusagen, was mit zukünftigen Reserven passiert, oder was deren Gesamtmenge betrifft, oder wieviel erschließbare Energie die Welt enthält.

Das zugrunde liegende Problem ist, dass die nachgewiesenen Reserven die Menge wirtschaftlich abbaubaren Gases und Öls repräsentieren… und das hängt natürlich komplett von den aktuellen Preisen und der gegenwärtigen Technologie ab. Mit anderen Worten, die Menge der „natürlichen Ressourcen“ der Welt ist nicht wirklich eine Funktion der natürlichen Welt – sondern eine Funktion menschlichen Erfindungsgeistes. Zum Beispiel lautete die große Sorge in den dreißiger Jahren, dass „Peak Magnesium“ erreicht werden würde, weil die nachgewiesenen Reserven von Magnesiums stark zurückgingen. Oder zurückgegangen waren, bis ein cleverer Chemiker bemerkte, dass man Magnesium aus Meerwasser extrahieren kann… und plötzlich waren die nachgewiesenen Reserven von Magnesium ins Unendliche gewachsen.

Hat sich nun die natürliche Welt verändert, als die nachgewiesenen Reserven von Magnesium von praktisch Null auf unendlich geschnellt sind? Wie ich sagte, die Menge der natürlichen Vorräte hängt von menschlichem Erfindungsgeist ab, und von sonst gar nichts!

Link: http://wattsupwiththat.com/2014/01/12/more-fun-with-oil-and-gas/

Übersetzt von Chris Frey EIKE

Die fatale Unterwerfung unter eine vermutete Linearität

geschrieben von Willis Eschenbach | 3. Februar 2014

Mathematisch wird das zu

∆T = lambda ∆F

wobei T die globale Mitteltemperatur ist, F ist der Gesamtantrieb an der Obergrenze der Atmosphäre TOA und lambda wird „Klimasensitivität“ genannt.

Mit andere Worten, die Idee ist, dass die Änderung der Temperatur eine lineare Funktion der Änderung des Antriebs an der TOA ist. Ich selbst bezweifle das stark, denn ich glaube nicht, dass die Welt so einfach gestrickt ist. Aber die Hypothese der Linearität macht die Berechnungen so einfach, dass die Leute es einfach nicht fertigbringen, sich davon zu lösen.

Nun wissen die Leute natürlich, dass das nicht wirklich linear ist, aber wenn ich darauf hinweise, kommt oftmals die Behauptung, dass es im interessierenden Bereich nahe genug an Linearität ist, dass wir Linearität annehmen können mit einem kleinen Fehler.

Um zu sehen, ob die Beziehungen wirklich linear sind, dachte ich mir, die CERES-Satellitendaten zu nutzen, um die Temperatur T und den Antrieb an der TOA F zu vergleichen. Diese Graphik zeigt Abbildung 1:

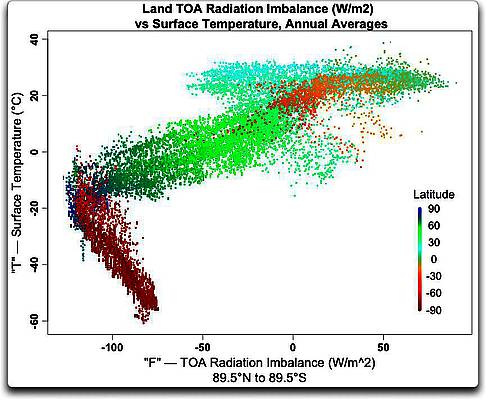
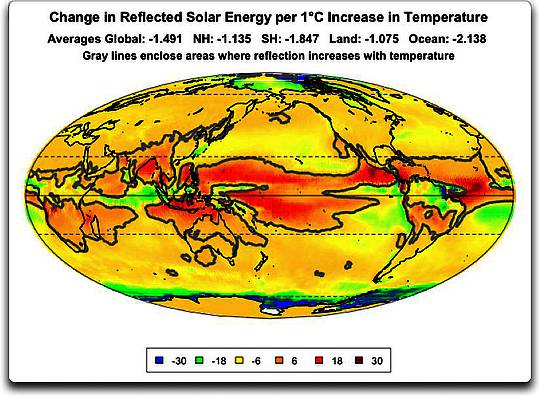
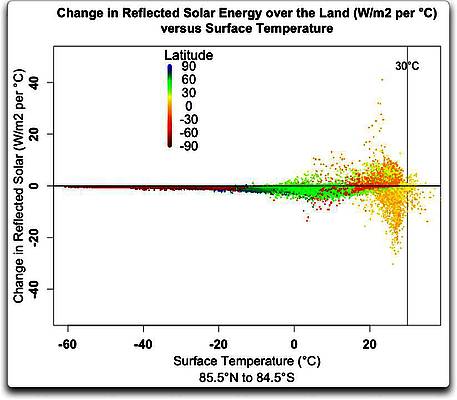
Abbildung 1: Festland allein, Antrieb F (Strahlungs-Ungleichgewicht an der TOA) und Temperatur T auf einem Gitternetz 1° mal 1°. Man beachte, dass zwischen 50°S und 65°S kaum Festland vorhanden ist. Der Gesamtantrieb an der TOA wird berechnet als einfallende Sonnenstrahlung minus langwellige Ausstrahlung.

Wie man sehen kann, gibt es überall eine Beziehung zwischen Antrieb an der TOA und der Temperatur, also alles andere als linear. Bei den niedrigsten Temperaturen sind sie umgekehrt korreliert. In der Mitte gibt es einen klaren Trend … aber dann, bei den höchsten Temperaturen, entkoppeln sie sich voneinander, und es gibt praktisch keine Korrelation mehr.

Über den Ozeanen ist die Lage irgendwie einfacher, obwohl wir auch dort große Variationen finden:

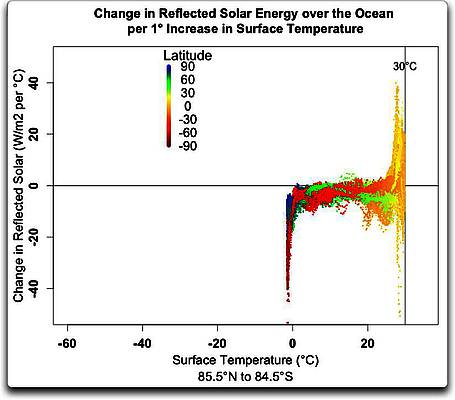
Abbildung 2: Ozean allein, Gesamtantrieb F gegen Temperatur T in einem Gitternetz 1° mal 1°. Die Farben indizieren die Breite.

Während die Änderungen nicht so extrem sind wie auf dem Festland, ist die Beziehung auch hier alles andere als linear. Im Besonderen beachte man, wie sich die Daten am oberen Ende der Karte mit zunehmendem Antrieb immer mehr nach rechts neigen. Das ist ein klarer Hinweis, dass die Klimasensitivität bei steigender Temperatur abnimmt. Man braucht mehr und immer mehr Energie, um die Temperatur ein weiteres Grad steigen zu lassen, und daher verläuft die Kurve oben rechts praktisch flach.

Am wärmsten Ende gibt es eine ziemlich starke Grenze der Oberflächentemperatur des Ozeans, die gerade etwas über 30°C liegt. (im Vorübergehen: Ich bemerke, dass es auch eine ziemlich starke Grenze der Oberflächentemperatur über dem Festland gibt, und zwar etwa auf dem gleichen Niveau um 30°C. Komischerweise wird diese Landtemperatur erreicht bei jährlichen mittleren Ungleichgewichten der Strahlung an der TOA, die von -50 W/m² bis +50 W/m² reicht).

Was ich oben gezeigt habe, sind die jährlichen Mittelwerte. Zusätzlich zu diesen sind wir jedoch auch an lambda interessiert, also an der Klimasensitivität, die diese Abbildungen nicht zeigen. Dem IPCC zufolge liegt die Gleichgewichts-Klimasensitivität irgendwo im Bereich 1,5°C bis 4,5°C bei jeder Verdoppelung des CO2-Gehaltes. Nun gibt es aber viele Arten der Sensitivität, darunter monatliche, dekadische und Gleichgewichts-Klimasensitivitäten.

Monatliche Sensitivität

Die monatliche Klimasensitivität tritt ein, wenn das Antriebs-Ungleichgewicht an der TOA in einer gegebenen Gitterzelle von 1° mal 1° von – sagen wir – plus 50 W/m² (Energie hinzugefügt) in einem Monat auf minus 50 W/m² im nächsten Monat sinkt (Energieverlust) Natürlich führt dies zu einem korrespondierenden Unterschied der Temperatur dieser beiden Monate. Die monatliche Klimasensitivität sagt, wie stark sich die Temperatur ändert bei einer gegebenen Änderung des Antriebs an der TOA.

Aber das Festland und die Ozeane können sich nicht augenblicklich ändern. Es gibt eine Verzögerung bei diesem Prozess. Daher ist die monatliche Klimasensitivität die kleinste der drei, weil die Temperatur keine Zeit hatte, sich zu ändern. Abbildung 3 zeigt die monatlichen Klimasensitivitäten, basierend auf den monatlichen CERES-Daten.

Abbildung 3: Die monatliche Klimasensitivität

Wie man erwarten kann, ändern sich die Ozeantemperaturen bei einer gegebenen Änderung des Antriebs weniger stark als die Landtemperaturen. Das liegt an der größeren Wärmemenge [thermal mass] der Ozeane über alle Zeiträume zusammen mit der größeren spezifischen Wärme von Wasser im Vergleich zu Erde und der größeren Verdunstung über den Ozeanen.

Dekadische Sensitivität

Die dekadische Sensitivität, auch Transient Climate response TCR genannt [?], ist die Änderung, die wir im Zeitraum von Jahrzehnten erkennen. Da die Temperaturänderung umso geringer ist, je länger die Verzögerung ist, können wir die Größe der Verzögerung benutzen, um die TCR aus der monatlichen Klimareaktion zu berechnen. Die Verzögerung über Land mittelt sich zu 0,85 Monaten und über den Ozeanen zu länger als 2,0 Monaten. Für das Festland gilt, dass die TCR im Mittel 1,6 mal so groß ist wie die monatliche Klimasensitivität. Die ozeanische Anpassung der TCR ist natürlich größer, weil die Verzögerung länger ist. Die ozeanische TCR ist im Mittel 2,8 mal größer als die monatliche Ozean-Klimasensitivität.

[Im Anhang führt Eschenbach diese Berechnung durch. Interessierte halten sich bitte an das Original, weil ich diesen Anhang nicht mit übersetzt habe. A. d. Übers.]

Abbildung 4 zeigt, was passiert, wenn wir die Informationen aus der Verzögerung zusammen mit der monatlichen Klimasensitivität betrachten. Sie zeigt für jedes Gitterquadrat die dekadische Klimasensitivität oder die TCR. Ausgedrückt wird das Ganze in Grad C bei einer Verdoppelung des CO2-Gehaltes (was das Gleiche ist wie Grad pro Zunahme des Antriebs um 3,7 W/m²). Die in Abbildung 4 gezeigte TCR enthält auch die Anpassungen für die Verzögerung auf einer Basis von Gitterzelle für Gitterzelle.

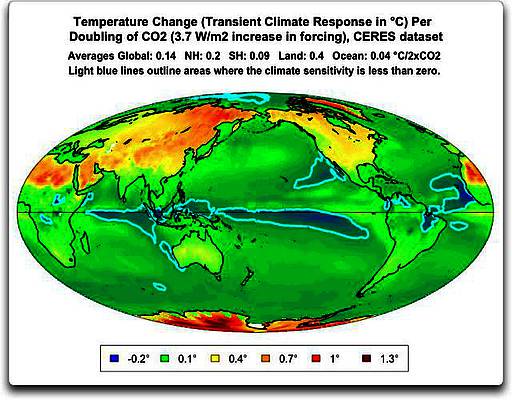
Abbildung 4: Transient Climate Response TCR. Sie wird berechnet aus der monatlichen Klimasensitivität für jedes Gitterquadrat und multipliziert mit dem für dieses Gitterquadrat berechneten Verzögerungsfaktor.

Es gibt einige interessante Dinge in der Abbildung 3. Eine davon ist: wenn man einmal die Verzögerung in Betracht zieht, verschwindet Einiges des Unterschieds der Klimasensitivität zwischen Festland und Ozean, und einiges davon ist verändert. Vor allem zeigt sich dies in der Südhemisphäre; man vergleiche Südafrika oder Australien in den Abbildungen 3 und 4.

Außerdem, wie man auch hier wieder sieht, regiert das Wasser. Entfernen wir den Effekt der Verzögerung, treten die trockeneren Gebiete klar hervor, und das sind auch die Stellen mit der größten Sensitivität auf Änderungen des Strahlungsantriebs an der TOA. Das ist verständlich, weil kaum Wasser für die Verdunstung zur Verfügung steht. Daher sorgt die meiste Energie für die Erwärmung des Systems. Nassere tropische Gebiete andererseits reagieren viel ähnlicher dem Ozean mit weniger Sensitivität hinsichtlich einer gegebenen Änderung des TCR-Antriebs.

Gleichgewichts-Sensitivität

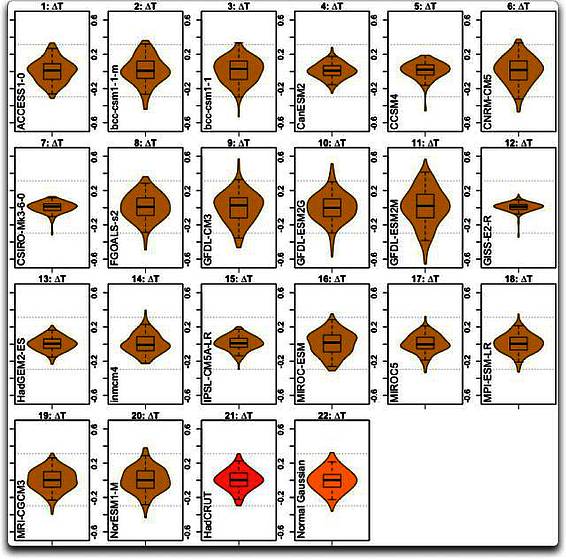
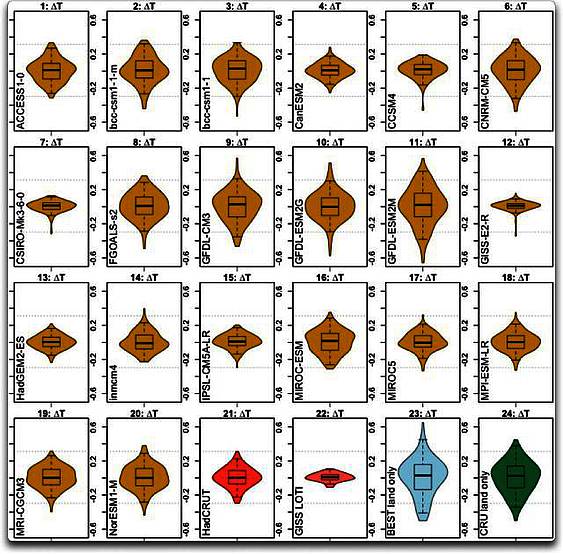
Die Gleichgewichts-Sensitivität ECS, die langfristigste Art der Sensitivität, ist das, was theoretisch passieren würde, wenn einmal die verschiedenen Wärmereservoire ihre Gleichgewichts-Temperatur erreicht haben. Der Studie von Otto mit aktuellen Beobachtungen zufolge lag die ECR [ECS? Schreibfehler des Autors?] gleichbleibend bei etwa 130% der TCR. Andererseits zeigt die Studie von Forster, dass die untersuchten 19 Klimamodelle eine ECR [ECS?], die von 110% bis 240% der TCR reichte mit einem Mittelwert bei 180%.

Damit kann man jetzt die globale mittlere Sensitivität berechnen. Falls wir die Modell-Prozentwerte zur Schätzung der ECS aus der TCR verwenden, ergibt dies ein ECS von 0.14 * 1.1 bis 0.14 *2.4. Dies impliziert eine Gleichgewichts-Klimasensitivität im Bereich 0,2 bis 0,3°C pro CO2-Verdoppelung, mit einem wahrscheinlichsten Wert (der Modelle) von 0,25°C pro Verdoppelung. Falls wir die 130%-Schätzung der Studie von Otto verwenden, bekommen wir ein sehr ähnliches Ergebnis, nämlich 0, 14 * 1.3 = 0.2 °C pro Verdoppelung.

Das ist klein genug, um im Rauschen unseres besonders rauschstarken Klimasystem verloren zu gehen.

Eine abschließende Bemerkung zu Linearität. Man erinnere sich, wir begannen mit der Behauptung, dass die Änderung der Temperatur gleich ist der Änderung des Antriebs multipliziert mit einer Konstante, die man „Klimasensitivität“ nennt. Mathematisch wird das zu

∆T = lambda ∆F

Ich habe lange gedacht, dass dies eine total ungeeignete Repräsentation ist, teils weil ich sage, dass lambda selbst, die Klimasensitivität, keine Konstante ist. Stattdessen ist es eine Funktion von T. Allerdings können wir wie gewöhnlich nicht von Linearität ausgehen … wir können keine Linearität in irgendeiner Form annehmen. Abbildung 5 zeigt die TCR (die dekadische Klimasensitivität) im Vergleich zur Temperatur.

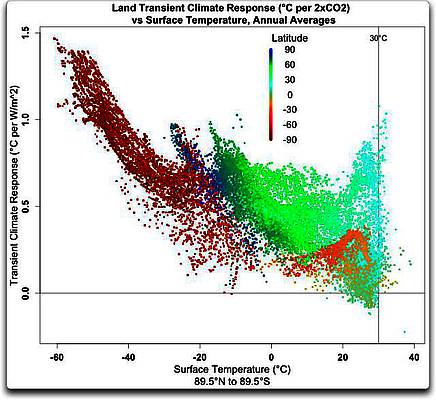
Abbildung 5: Transient Climate Response im Vergleich zur mittleren jährlichen Temperatur, nur Festland. Man beachte, dass TCR nur selten unter Null sinkt. Die größte Reaktion gibt es in der Antarktis (dunkelrot).

Hier sehen wir die Entkoppelung der Temperatur und der TCR bei den höchsten Temperaturwerten. Man beachte auch, wie wenige Gitterquadrate wärmer als 30°C sind. Wie man sehen kann, während es eindeutig bei steigender Temperatur einen Abfall der TCR (Sensitivität) gibt, ist die Beziehung alles andere als linear. Und schaut man auf die Ozean-Daten, wird es noch eigenartiger. Abbildung 6 zeigt die gleiche Relation wie Abbildung 5. Man beachte die unterschiedliche Skalierung sowohl in X- als auch in Y-Richtung.

Abbildung 6: Wie in Abbildung 5, jedoch nur für den Ozean. Man beachte, dass sich die Skalierung von Abbildung 5 unterscheidet.

Ich liebe dieses Klimasystem – endlos komplex. Die Ozeane zeigen eine gänzlich andere Verteilung als das Festland. Erstens, die TCR der globalen Ozeane beträgt fast durchweg weniger als ein Zehntelgrad Celsius pro CO2-Verdoppelung (globales Mittel = 0.08°C/2xCO2). Und im Gegensatz zu meinen Erwartungen gibt es unter etwa 20°C kaum Anzeichen irgendeines Rückgangs der TCR mit der Temperatur, wie wir in Abbildung 5 für das Festland gesehen haben. Und über 25°C gibt es einen klaren und raschen Abfall in einer Reihe von Gebieten (einschließlich des pazifischen „Warm-Pools“), die negative Klimareaktionen zeigen.

Im Vorübergehen bemerke ich auch, dass die im offenen Ozean beobachtete 30°C-Grenze an einem Punkt eintritt, an dem die TCR = 0 ist …

Was schließe ich aus all dem? Nun, so genau weiß ich gar nicht, was das alles bedeutet. Einige Dinge sind aber eindeutig. Meine erste Schlussfolgerung lautet, dass der Gedanke, die Temperatur sei eine lineare Funktion des Antriebs, nicht durch die Beobachtungen gestützt wird. Die Relation ist weit entfernt davon, linear zu sein und kann nicht einfach approximiert werden.

Weiter. Die Schätzungen der ECS aus dieser auf Beobachtungen basierenden Studie zeigen eine Bandbreite von 0,2°C bis 0,5°C pro CO2-Verdoppelung. Das liegt weit unter der Schätzung des IPCC … was aber soll man andererseits von der Arbeit von Regierungen erwarten?

Und schließlich, die Entkoppelung der Variablen am warmen Ende des Spektrums der Gitterquadrate ist ein klares Zeichen dafür, dass ein aktives Temperatur-Regulierungssystem aktiv ist.

Unter dem Strich: Das Klima ist nicht linear und war es niemals… und die Unterwerfung unter das fatale Lockmittel einer vermuteten Linearität hat das Gebiet der Klimawissenschaft um Jahrzehnte zurückgeworfen.

Link: http://wattsupwiththat.com/2013/12/18/the-fatal-lure-of-assumed-linearity/

Übersetzt von Chris Frey EIKE

Die thermostatische Kontrolle

geschrieben von Willis Eschenbach | 3. Februar 2014

Ähnlich dazu ist die Kontrolle in der globalen Klima-Maschine die tropische Albedo (Reflektivität). Die tropische Albedo kontrolliert, wie viel einfallende Sonnenstrahlung am warmen Ende der Wärmemaschine zurück in den Weltraum reflektiert wird. Mit anderen Worten, die Albedo steuert die einfallende Energie und damit das gesamte System.

Außerdem habe ich gesagt, dass die tropische Albedo eine extrem nichtlineare Funktion der Temperatur ist. Daher habe ich mir gedacht, die CERES-Satellitendaten heranzuziehen, um mal nachzuschauen, wie stark diese Drosselung in Watt pro Quadratmeter (W/m²) ist und wo genau sich diese Drossel befindet. Wenn es eine solche Drossel gibt, würde einer der charakteristischen Features dabei sein, dass die reflektierte Menge der Sonnenenergie mit zunehmender Temperatur zunehmen muss. Abbildung 1 zeigt das Ergebnis dieser Analyse:

Abbildung 1: Mittlere Änderung der reflektierten Solarenergie durch eine Temperaturzunahme um 1°C. Rote Flächen zeigen eine größere Reflektion mit steigender Temperatur. Die Änderung der reflektierten Energie wird berechnet auf Basis einer Gitterbox. Dabei berechnet sich die Änderung der Albedo pro 1°C Temperaturzunahme in dieser Gitterbox multipliziert mit der mittleren Solarstrahlung für diese Gitterbox. Die graue Linie zeigt, wo sich die Albedo mit der Temperatur nicht ändert. Gepunktete Linien zeigen die Tropen (von 23,45°N bis 23,45°S) und die Kreise um die Pole (jeweils nördlich von 66,55°).

Daraus erkennt man eindeutig, dass ein solcher Steuerungsmechanismus existiert. Man erkennt auch, wo wir ihn zu finden erwarten können, nämlich nahe dem Äquator, wo maximal Energie in das System eintritt. Im Mittel agiert die Drossel in den von der grauen Linie umschlossenen Gebieten. Allerdings war ich überrascht von der Stärke des Mechanismus‘. Es gibt weite Gebiete (rot), in denen 1°C Erwärmung zu einer Zunahme der Reflektion der Solarstrahlung um 10 W/m² oder mehr führt. Offensichtlich würde diese Kontrolle ein Faktor sein bei der Erklärung der Beobachtungen einer Wassertemperatur im offenen Ozean von etwa 30°C.

Der Drosselmechanismus agiert über den meisten Gebieten der tropischen Ozeane und selbst in manchen tropischen Landgebieten. Er ist am stärksten im Bereich der ITC, die unter dem Äquator in den indischen Ozean und über Afrika hinweg verläuft, und über dem Äquator im Pazifik und Atlantik.

Als Nächstes ist es der Erwähnung wert, dass die Gesamtauswirkung der Temperatur auf die Reflektion von Sonnenstrahlen etwa Null ist (der globale, nach Gebiet gemittelte Wert beträgt -1,5 W/m² pro Grad. Das ist geringer als die Fehlerbandbreite in den Daten). Außerdem ähneln sich weite außertropische Land- und Seegebiete darin, dass sie alle leicht negativ sind (hell orange). Dies ist ein weiterer Hinweis auf die Arbeit eines die Temperatur regelnden Systems. Da die Albedo in vielen Gebieten der Erdoberfläche relativ unempfindlich gegenüber Temperaturänderungen reagiert, können geringe Temperaturänderungen in den Tropen bereits große Auswirkungen auf die Energiemenge haben, die in das System eintritt. Abbildung 2 zeigt die Beziehung (nur Festland) zwischen der absoluten Temperatur in °C und die Änderung der reflektierten Energie pro Grad Erwärmung.

Abbildung 2: Änderung der reflektierten Sonnenenergie (W/m² pro °C) im Vergleich zur absoluten Temperatur in °C über dem Festland. Man beachte, dass sich in Gebieten mit einem Temperatur-Jahresmittel unter 0°C nur geringe Variationen der Reflektion von der Oberfläche mit einer sich ändernden Temperatur zeigt. Vom Gefrierpunkt bis etwa 20°C ist die reflektierte Menge allgemein rückläufig, wenn die Temperatur zunimmt. Über 20°C gibt es zwei Arten der Reaktion – nennenswerte Zunahme oder nennenswerte Abnahme der reflektierten Solarstrahlung mit der Temperatur.

Weiter! Die polnahen Ozeangebiete zeigen ein umgekehrtes Verhalten wie in den Tropen. Während tropische Albedo-Änderungen die Tropen kühlen, nehmen die Albedo und das reflektierte Sonnenlicht mit steigender Temperatur ab.

Abbildung 3: Änderung der reflektierten Solarenergie (W/m² pro °C) gegen die absolute Temperatur (°C) über den Ozeanen, jährliche Mittelwerte. Wo das jährliche Temperaturmittel nahe Null Grad liegt, gibt es eine starke negative Variation der Reflektion an der Oberfläche mit der Temperatur. Vom Gefrierpunkt bis etwa 20°C ist die Variation stabil und leicht negativ. Bei einer Mitteltemperatur über 20°C gibt es zwei Arten der Reaktion – nennenswerte Zunahme oder nennenswerte Abnahme der reflektierten Solarstrahlung mit der Temperatur – bis zur Obergrenze bei 30°C.

Das bedeutet, dass zusätzlich zur Begrenzung des Gesamt-Energie-Inputs in das ganze System die temperaturabhängige Albedo auch Änderungen des reflektierten Sonnenlichtes moderiert. Trendmäßig werden die Tropen dabei kühler und die Pole wärmer, als es sonst der Fall wäre. Dies würde eindeutig dafür sorgen, die Gesamt-Temperaturschwingungen des Planeten zu limitieren.

Und schließlich, die Verwendung monatlicher Mittelwerte verschleiert einen wesentlichen Punkt, nämlich dass sich Änderungen im Zeitscale von Minuten ändern, nicht von Monaten. Und auf täglicher Basis gibt es keine Gesamterhöhung um 10 W/m² pro Grad Temperaturänderung. Stattdessen gibt es bis zu einem bestimmten Zeitpunkt tagsüber keine Wolken, und die volle Intensität der Sonnenenergie kann in das System einfallen. Während dieser Zeit gibt es praktisch keine Änderung der tropischen Albedo mit steigender Temperatur.

Dann plötzlich, im Mittel um 11 Uhr, vollführt die Albedo einen gewaltigen Sprung, sobald sich Cumulusbewölkung bildet bis hin zu einem voll entwickelten Cumulus-Regime. Das führt zu einem Sprung in der Albedo und kann die Temperaturen sogar sinken lassen trotz des zunehmenden solaren Antriebs, wie ich hier, hier, hier, hier und hier gezeigt habe.

Daraus erkennt man, dass die thermische Regelung der tropischen Albedo erfolgt durch Änderungen der Zeit des Beginns der täglichen Cumulusbildung und der Intensität des täglichen Cumulus/Cumulonimbus-Regimes. Je wärmer es an jenem Tag ist, umso eher setzt die Bildung von Cumulus-Wolken ein, und umso mehr davon wird es geben. Dies reduziert die in das System eintretende Energiemenge um Hunderte Watt pro Quadratmeter. Und andererseits bilden sich Cumuli an kühleren Tagen später am Tag und erreichen womöglich gar nicht das Cumulonimbus-Stadium, und es gibt weniger Wolken. Dies lässt die in das System einfallende Energiemenge um Hunderte Watt pro Quadratmeter zunehmen.

Ich erwähne das um zu zeigen dass das System nicht einen mittleren Kontrollwert von beispielsweise 10 W/m² erreicht über einem mittleren Gebiet, in dem die Kontrolle aktiv ist.

Stattdessen erreicht es einen viel größeren Kontrollwert von einigen hundert Watt pro Quadratmeter, aber nur dann, wann und wo dieser gebraucht wird, um lokale Hitzeinseln zu kühlen oder um lokale kühle Gebiete zu erwärmen. Folge: die Mittelwerte führen in die Irre.

Der wichtigste Grund zu verstehen, dass die Albedo-Änderungen STÜNDLICHE und nicht monatliche Änderungen sind, besteht darin, dass das, was das System reguliert, augenblickliche Bedingungen der Kontrolle von Wolkenbildung sind und nicht mittlere Bedingungen. Wolken bilden sich nicht in Abhängigkeit von der Stärke der Antriebe, egal ob von der Sonne oder CO2 oder Vulkane. Sie bilden sich ausschließlich nur, wenn es warm genug ist.

Und das wiederum bedeutet, dass sich nicht viel ändern wird, wenn sich der Antrieb ändert … weil die Wolkenbildung temperaturabhängig und nicht antriebsabhängig ist.

Ich denke, dass diese augenblickliche Reaktion der Hauptgrund dafür ist, dass es so schwierig ist, zum Beispiel ein solares Signal in den Temperaturaufzeichnungen zu finden – weil die Thermoregulation auf der Temperatur basiert, nicht auf dem Antrieb. Daher agiert sie unabhängig von Änderungen des Antriebs.

Das ist auch der Grund dafür, dass Vulkane nur einen so geringen Unterschied in der globalen Temperatur ausmachen – weil das System augenblicklich auf kühlere Temperaturen reagiert in Gestalt einer verringerten Albedo. Damit erlaubt es den zusätzlichen Eintritt von hunderten W/m², um den Temperaturabfall zu kompensieren.

Es gibt noch viel mehr im CERES-Datensatz zu entdecken, und obwohl ich schon Einiges zutage gefördert habe, kann man immer noch sehr viel damit machen – eine Analyse der Klima-Wärmemaschine zum Beispiel. Allerdings denke ich, dass das klare Vorhandensein der Existenz eines durch die Temperatur geregelten Mechanismus, der die in das System eintretende Energiemenge kontrolliert, eines Extrabeitrages würdig ist.

Link: http://wattsupwiththat.com/2013/12/28/the-thermostatic-throttle/

Übersetzt von Chris Frey EIKE

Ein Modell, eine Wahl

geschrieben von Willis Eschenbach | 3. Februar 2014

Durch die gute Arbeit von Nic Lewis und Piers Forster, denen ich sehr danke, habe ich ein Set von 20 passenden Modell-Antriebs-Inputs und korrespondierende Temperatur-Outputs erhalten, wie sie vom IPCC benutzt werden. Das sind die individuellen Modelle, deren Mittelwert ich in meinem Beitrag mit dem Titel Model Climate Sensitivity Calculated Directly From Model Results [etwa: Klimasensitivität der Modelle direkt berechnet aus Modellergebnissen] behandelt habe. Ich dachte mir, zuerst die Temperaturen zu untersuchen und die Modellergebnisse mit dem Datensatz HadCRUT und anderen zu vergleichen. Begonnen habe ich mit dem Vergleich der verschiedenen Datensätze selbst. Eine meiner bevorzugten Werkzeuge zum Vergleich von Datensätzen ist der „Violin-Plot“. Abbildung 1 zeigt einen Violin-Plot eines Datensatzes mit Zufallswerten, also eine Gauss’sche Normalverteilung.

Abbildung 1 (rechts): Violin-Plot von 10.000 Zufalls-Datenpunkten mit einem Mittel von Null und Standardabweichung.

Man erkennt, dass die Form einer „Violine“, also der orangefarbene Bereich, aus zwei bekannten „Glockenkurven“ zusammengesetzt ist, die vertikal Rücken an Rücken angeordnet sind. In der Mitte gibt es einen „Kasten-Plot“, welches der Kasten ist, dessen whiskers sich nach oben und unten erstrecken. Die Ausreißer, die sich oben und unten über den Kasten hinaus erstrecken, haben die gleiche Höhe wie der Kasten, eine Distanz, die bekannt ist unter der Bezeichnung „interquartiler Bereich“, weil er sich vom ersten bis zum letzten Viertel der Daten erstreckt. Die dicke schwarze Linie zeigt nicht das Mittel, sondern den Median der Daten. Der Median ist der Wert in der Mitte des Datensatzes, wenn man den Datensatz nach Größe sortiert. Als Folge wird er weniger durch Ausreißer beeinflusst als das Mittel des gleichen Datensatzes.

Kurz gesagt, ein Violin-Plot ist ein Paar spiegelbildlicher Dichteplots, das zeigt, wie die Daten verteilt sind, hinterlegt mit einem Kasten-Plot. Mit diesem Prolog wollen wir uns jetzt ansehen, was uns Violin-Plots über den Temperatur-Output der zwanzig Klimamodelle sagen können.

Für mich ist eines der bedeutendsten Merkmale [metrics] jedes Datensatzes der „erste Unterschied“. Dabei handelt es sich um die Änderung eines gemessenen Wertes zum nächsten. In einem Jahres-Datensatz wie den Temperatur-Modelloutputs besteht der erste Unterschied eines Datensatzes aus einem neuen Datensatz, der die jährliche ÄNDERUNG der Temperatur zeigt. Mit anderen Worten, um wie viel wärmer oder kälter ist die gegebene Temperatur eines Jahres im Vergleich zum Vorjahr? Sehen wir in der realen Welt und in den Modellen große oder kleine Änderungen?

Diese Änderung bei einigen Werten wird oft mit dem Symbol Delta „∆” bezeichnet, was die Differenz in einigen Messungen im Vergleich zum vorigen Wert bedeutet. Zum Beispiel würde man die Änderung der Temperatur mit „∆T” bezeichnen.

Fangen wir also an mit der Betrachtung der ersten Unterschiede der modellierten Temperaturen ∆T. Abbildung 2 zeigt einen Violin-Plot des ersten Unterschiedes ∆T in jedem der 20 Modell-Datensätze, also mit 1 : 20, plus dem HadCRUT-Datensatz und den Zufalls-Normal-Datensätzen.

Abbildung 2: Violin-Plots von 20 Klimamodellen (beige) plus dem Beobachtungs-Datensatz HadCRUT (rot) und einem normalverteilten Gauss’schen Datensatz (orange) zum Vergleich. Horizontale gepunktete Linien in jedem Fall zeigen die Gesamt-Bandbreite des HadCRUT-Datensatzes.

Nun… als Erstes fällt auf, dass wir hier sehr, sehr unterschiedliche Verteilungen sehen. Man betrachte zum Beispiel GDFL (11) und GISS (12) im Vergleich zu den Beobachtungen…

Was bedeuten nun die Unterschiede zwischen den Mittelwerten von GDFL und GISS, wenn wir auf die Zeitreihe ihrer modellierten Temperaturen schauen? Abbildung 3 zeigt die beiden Datensätze, GDFL und GISS zusammen mit meiner Nachbildung jedes Ergebnisses.

Abbildung 3: Modellierte Temperaturen (gepunktete graue Linien) und Nachbildungen von zwei Modellen, GDFL-ESM2M und GISS-E2-R. Das Verfahren der Nachbildung wird im ersten Link oben des Beitrags erläutert. Zeitpunkte zwei wesentlicher Vulkanausbrüche sind als vertikale Linien eingezeichnet.

Der Unterschied zwischen den beiden Modell-Outputs tritt ziemlich deutlich hervor. Es gibt nur eine geringe Variation von Jahr zu Jahr bei den GISS-Ergebnissen, halb so groß oder noch kleiner, als wir es in der realen Welt beobachten. Andererseits zeigen sich sehr große Variationen von Jahr zu Jahr bei den GDFL-Ergebnissen, bis zu zweimal so groß wie die größte jährliche Änderung, die jemals in den Aufzeichnungen aufgetreten war…

Nun ist es offensichtlich, dass die Verteilung jedweder Modellergebnisse nicht identisch sein wird mit den Beobachtungen. Aber einen wie großen Unterschied können wir erwarten? Um dies zu beantworten, zeigt Abbildung 4 einen Satz mit 24 Violin-Plots von Zufalls-Verteilungen, und zwar mit der gleichen Anzahl von Datenpunkten (140 Jahre mit ∆T) wie die Modell-Outputs.

Abbildung 4: Violin-Plots verschiedener Randwert-Datensätze mit einer Beispielgröße von N = 140, und die gleiche Standardabweichung wie im HadCRUT-∆T-Datensatz.

Wie man sieht, kann man schon mit einer kleinen Beispiel-Auswahl von 140 Datenpunkten eine Vielfalt von Formen erhalten. Das ist eines der Probleme bei der Interpretation von Ergebnissen aus kleinen Datensätzen: man kann kaum sicher sein, was man sieht. Allerdings gibt es ein paar Dinge, die sich nicht groß ändern. Die interquartile Distanz (die Höhe des Kastens) variiert nicht sehr stark. Und auch nicht die Stellen, an denen die Ausreißer enden. Wenn man jetzt die modellierten Temperaturen von GDFL (11) und GISS (12) untersucht (wie sie in Abbildung 5 der Bequemlichkeit halber noch einmal gezeigt werden), kann man sehen, dass sie in keiner Weise irgendeinem der Beispiele normalverteilter Datensätze ähneln.

Es gibt noch einige weitere Merkwürdigkeiten. Abbildung 5 enthält drei andere Beobachtungs-Datensätze – den globalen Temperaturindex von GISS sowie die Datensätze von BEST und CRU ausschließlich vom Festland.

Abbildung 5: Wie Abbildung 2, aber diesmal mit den Temperatur-Datensätzen GISS, BEST und CRUTEM unten rechts. Die horizontalen gepunkteten Linien zeigen die Gesamt-Bandbreite des HadCRUT-Beobachtungs-Datensatzes.

Hier können wir eine merkwürdige Konsequenz der Manipulation der Modelle erkennen. Ich habe noch nie gesehen, wie stark das gewählte Ziel die Ergebnisse beeinflusst. Man bekommt unterschiedliche Ergebnisse abhängig davon, welchen Datensatz man auswählt, an den man das Klimamodell anpasst … und das GISS-Modell (12) wurde offensichtlich frisiert, um die GISS-Temperaturaufzeichnung zu spiegeln (22). Es sieht so aus, als hätten sie sie ziemlich gut frisiert, um zu jenen Aufzeichnungen zu passen. Und mit CSIRO (7) könnte es das Gleiche sein. In jedem Falle sind das die einzigen beiden, die eine ähnliche Form haben wie die globale Temperaturaufzeichnung von GISS.

Und schließlich sehen die beiden Datensätze nur mit Festlandswerten (23, 24, in Abbildung 5 unten rechts) ziemlich ähnlich aus. Man beachte jedoch die Unterschiede zwischen den beiden globalen Datensätzen HadCRUT (21) und GISS LOTI (22) sowie den beiden Festlands-Datensätzen BEST (23) und CRUTEM (24). Man erinnere sich, das Land erwärmt sich schneller als die Ozeane und kühlt sich auch schneller wieder ab. Wie man also erwarten würde, gibt es größere jährliche Schwingungen in den beiden Festlands-Datensätzen, was repräsentiert wird durch die Größe des Kastens und der Position der Endpunkte der Ausreißer.

Allerdings passen einige Modelle (z. B. 6, 9 und 11) viel besser zu den Festlands-Datensätzen als zu den globalen Temperatur-Datensätzen. Dies würde auf Probleme hindeuten mit der Repräsentation der Ozeane in diesen Modellen.

Schlussfolgerungen? Nun, die größte Änderung von Jahr zu Jahr der Temperatur der Erde während der letzten 140 Jahre hat 0,3°C betragen, sowohl für steigende als auch für fallende Temperatur.

Sollten wir also einem Modell vertrauen, das eine doppelt so große Änderung von Jahr zu Jahr zeigt wie beispielsweise GFDL (11)? Welchen Wert hat ein Modell, deren Ergebnisse nur halb so groß sind wie die Beobachtungen, wie GISS (12) und CSIRO (7)?

Meine wesentliche Schlussfolgerung lautet: an irgendeiner Stelle müssen wir den Gedanken der Klimamodelle-Demokratie verwerfen und alle Modelle über Bord werfen, die nicht die Realität abbilden, die nicht einmal ansatzweise die Beobachtungen spiegeln.

Mein letzter Punkt ist ein Seltsamer. Er betrifft die merkwürdige Tatsache, dass sich ein Ensemble (ein origineller Ausdruck für einen Mittelwert) der Klimamodelle im Allgemeinen besser macht als irgendein ausgewähltes Einzelmodell. Ich habe das aus folgendem Grunde verstanden.

Nehmen wir einen Haufen kleiner Kinder an, die noch nicht so gut werfen können. Man zeichnet ein Ziel an einer Scheune, und die Kinder werfen Schlammbälle auf das Ziel.

Was wird nun näher am Zentrum des Zieles liegen – das Mittel aller Würfe der Kinder oder ein speziell ausgewählter individueller Wurf?

Es scheint eindeutig, dass das Mittel aller schlechten Würfe die bessere Wahl ist. Eine Folge davon ist, je mehr Würfe es gibt, desto genauer wird das Mittel wahrscheinlich sein. Also ist dies vielleicht die Rechtfertigung in den Köpfen der IPCC-Leute für die Einbeziehung von Modellen, die die Wirklichkeit gar nicht abbilden … sie wurden mit einbezogen in der Hoffnung, dass sie ein genauso schlechtes Modell auf der anderen Seite ausbalancieren.

ABER – es gibt Probleme bei dieser Annahme. Ein Problem ist, falls alle oder die meisten Fehler in die gleiche Richtung gehen, dann würde das Mittel nicht besser sein als ein Einzelwert-Ergebnis. In meinem Beispiel nehme man an, dass das Ziel sehr hoch auf die Scheune gemalt wurde, und die meisten Kinder treffen einen Bereich darunter. Dann würde das Mittel nicht besser aussehen als irgendein individuell ausgewählter Wurf.

Ein weiteres Problem ist, dass viele Modelle große Teile der Codierung gemeinsam haben, und noch wichtiger, sie teilen eine ganze Reihe theoretischer (und oftmals nicht untersuchter) Annahmen, die hinsichtlich des Klimas stimmen können oder nicht.

Ein tiefer gehendes Problem in diesem Falle ist, dass die verbesserte Genauigkeit nur für die Nachhersage der Modelle gilt … Und sie sind ohnehin schon sorgfältig frisiert worden, um diese Ergebnisse zu zeigen. Keine Frisierung nach Art des „Drehens am Knopf“, sondern wieder und immer wieder evolutionäre Frisierung. Als Folge zeigen sie alle ziemlich gut die Temperaturvariationen der Vergangenheit, und das Mittel ist sogar besser als die Nachhersage … lediglich diese blöde Vorhersage ist immer das Problem.

Oder wie es die Börsianer an den US-Börsen ausdrücken: „Das Verhalten der Vergangenheit ist keine Garantie für zukünftige Erfolge“. Es spielt keine Rolle, wie gut ein individuelles Modell oder eine Modellgruppe die Vergangenheit abbilden kann – das bedeutet absolut nichts hinsichtlich ihrer Fähigkeit, die Zukunft vorherzusagen.

Anmerkungen:

Datenquelle: Die Modell-Temperaturdaten stammen aus einer Studie von Forster, P. M., T. Andrews, P. Good, J. M. Gregory, L. S. Jackson, and M. Zelinka, 2013, Journal of Geophysical Research, 118, 1139–1150 mit dem Titel Evaluating adjusted forcing and model spread for historical and future scenarios in the CMIP5 generation of climate models, dankenswerterweise zur Verfügung gestellt von Piers Forster. Sie steht hier und ist des Lesens wert.

Daten und Codierung: Wie üblich ist mein R-Code ein Gewirr, aber zu was das taugt, steht hier. Die Daten finden sich in einer Excel-Tabelle hier.

Link: http://wattsupwiththat.com/2013/11/21/one-model-one-vote/

Übersetzt von Chris Frey EIKE

Anmerkung des Übersetzers: Ich bitte um Verständnis, dass ich diesem Text inhaltlich manchmal nicht ganz folgen konnte.