Abbildung rechts: Eine der ältesten, den Historikern bekannten Kosten-Nutzen-Analysen

Nun, das ist ein merkwürdiger Standpunkt, stehen doch der Guardian und seine Freunde zu 1000% [eintausend Prozent] hinter der Subventionierung "Erneuerbarer", vor allem solcher "Erneuerbarer", die nicht funktionieren … schauen Sie selbst. Aber angesichts dessen, dass die "Erneuerbaren" infinitesimal kleine Mitspieler sind im globalen Energiespiel, geht es in diesem Report um die Subventionierung derjenigen Energie-Mitspieler, die eigentlich … Energie in bedeutender Menge erzeugen. Das wären die bösen Öl- und Kohle- und Erdgasunternehmen. In der Welt des Guardian sind solche Subventionen per definitionem schlecht.

Also habe ich mich entschlossen, ihr Arbeitspapier wie ein Idiot zu erkunden. Zwar bin ich ein Fan von Erkundungen in unbekanntem Terrain, in den Karten als „Terra Incognita“ gekennzeichnet – aber in diesem Falle war es kein Vergnügen.

Ich bin sicher, dass viele Menschen wissen, was eine „Kosten-Nutzen-Analyse“ ist – man zieht eine vertikale Linie in der Mitte eines Blattes Papier. Auf der einen Hälfte, sagen wir mal rechts, listet man alle Kosten des fraglichen Vorhabens. Und auf der linken Seite listet man alle Vorteile des geplanten Vorhabens. Die Abbildung oben rechts zeigt eines der frühesten bekannten Beispiele einer Kosten-Nutzen-Analyse.

Der IMF hat das Blatt Papier entlang der vertikalen Mittellinie zerrissen und uns die Hälfte mit den Kosten der angeblichen „Subventionen“ übergeben, zusammen mit der Behauptung, dass es sich um eine saubere Analyse handelt. Das stimmt aber nicht. Es ist eine Liste mit wild übertriebenen Kosten, und nur Kosten.

Jetzt möchte ich etwas klarstellen. Ich habe kein inhärentes Problem mit Subventionen. Wir subventionieren alle möglichen Aktivitäten, wir müssen lediglich die richtigen auswählen. Und ich habe kein Problem mit einer Kosten-Nutzen-Analyse. Das ist eine sehr nützliche Methode.

Aber die Betrachtung nur der Kosten unter Ignorieren der Vorteile? Das ist keine Analyse irgendeiner Art.

Aber Moment, es wird noch viel schlimmer. Man erlaube mir, die Kurzversion des IMF-Arbeitspapiers zu zitieren. Erstens, um alles ins rechte Licht zu setzen, folgt hier ihr Abstract (Hervorhebung von mir):

Diese Studie bietet ein umfassendes, aktualisiertes Bild der Energiesubventionen im globalen und regionalen Maßstab. Sie konzentriert sich auf die breit gefächerte Auffassung von Energiesubventionen nach Steuern [post-tax energy subsidies]. Sie treten auf, wenn die Verbraucherpreise unter den Lieferkosten liegen plus eine Steuer, um Umweltschäden Rechnung zu tragen und einer zusätzlichen Steuer auf alle Verbrauchsgüter, um das Einkommen der Regierung zu vergrößern. Energiesubventionen nach Steuern sind dramatisch höher als zuvor geschätzt und dürften auch zukünftig sehr hoch bleiben. Diese Subventionen reflektieren hauptsächlich den unter Wert angesetzten Preis aus heimischer (und nicht globaler) Perspektive. Eine einseitige Preisreform liegt also im ureigenen Interesse des Landes. Die potentiellen fiskalischen, umweltlichen und Wohlstands-Auswirkungen einer Reform der Energiesubventionen sind substantiell.

Wie man sieht, befinden wir uns bereits im Spezialisten-Jargon. Das ist noch kein Problem, haben doch alle Fachgebiete einen Jargon. In ihrer Welt bedeutet „Energiesubventionen vor Steuern“ Geld, das zu dem Unternehmen oder der Industrie oder der Aktivität fließt, das subventioniert wird. Allgemeiner: Vor-Steuern-Subventionen sind Subventionen, die tatsächlich die Grundlinie der Bilanzen einiger begrenzter Untergruppen von ökonomischen Akteuren beeinflusst. Mit anderen Worten, „Vor-Steuern-Subventionen“ sind das, an das die meisten von uns sofort denken, wenn sie das Wort „Subventionen“ hören.

Was diese braven Menschen als „Energiesubventionen nach Steuern“ ansehen, sind andererseits keine Subventionen im normalen Sinne. Kein Cent davon fließt überhaupt an die Energieunternehmen.

Um den Unterschied hervorzuheben, möchte ich ein kristallklares Beispiel dafür nennen, was der IMF als „Energiesubvention nach Steuern“ an die böse Ölindustrie ansieht … aber zuvor halte ich es für meine Pflicht, davor zu warnen, dass das Folgende nichts für Blumenkinder oder andere Weichherzige ist. Also für alle Übrigen – eine der vielen, vielen „Energiesubventionen nach Steuern“ des IMF ist…

Die Kosten der Auffüllung von Schlaglöchern auf der Straße zu meinem bescheidenen Heim.

Wirklich. Ich bausche das nicht auf. Die Reparatur von Schlaglöchern ist Bestandteil ihrer „Energiesubvention nach Steuern“, von dem sie behaupten, dass er an die Energieunternehmen geht. Es ist gelistet unter der Rubrik „Nicht-Kohlenstoff-Effekte von außen“ [non-carbon externalities].

Und was sind „Nicht-Kohlenstoff-Effekte von außen“, wenn sie zu Hause sind? Glücklicherweise geben sie ein paar Beispiele:

„Verstopfung, Unfälle, Luftverschmutzung und Straßenschäden“.

In dem seltsamen Paralleluniversum des IMF wird jedes einzelne Beispiel davon (einschließlich „Straßenschäden“) als eine SUBVENTION AN EXXON UND SHELL betrachtet! Die Reparatur von Schlaglöchern als Subvention an Energieunternehmen! Hat man schon jemals von einem solchen beknackten Ding gehört?

Also möchte ich hier selbst ein wenig technischen Jargon einführen. Ich werde mich auf jene Subventionen beziehen, die nur an Energieerzeuger und -verteiler fließen, die die Basis jener subventionierten Erzeuger und Verteiler als „wirkliche Energiesubventionen“ betreffen. Das ist eine eingängige Bezeichnung und trifft ins Herz der ganzen Sache.

Und was ist mit der Behauptung, dass das Ausbessern von Schlaglöchern eine Subvention für die Energieindustrie ist? Nun, dafür werde ich die Bezeichnung „imaginäre Energiesubventionen“ benutzen. Das ist kurz und bringt es auf den Punkt.

Was die relative Größenordnung der wirklichen und der imaginären Subventionen betrifft: unter den großen Schlagzeilen, die ihren Weg durch das Web gefunden haben, ist „Energiesubventionen betragen 5,3 Billionen Dollar pro Jahr!“. Nun, ich möchte darauf hinweisen, dass diese Zahl zu 94 Prozent imaginäre Energiesubventionen sind, und nur sechs Prozent davon sind reale Energiesubventionen. Seltsam aber wahr. Wie ich sagte, ich bausche das nicht auf. Zum Kuckuck, ich konnte mir dieses Niveau absurder Käuflichkeit gar nicht vorstellen. Ich bin lediglich ein furchtloser Erkunder, der seinen Weg durch endlos langes unausgegorenes Geschwätz sucht, um die Wahrheit zu ergründen … und wenn ich sie erreiche, kommt heraus, dass die Wahrheit sechs Prozent beträgt und das Blabla 94 Prozent. Abbildung 2 zeigt die hässlichen Behauptungen:

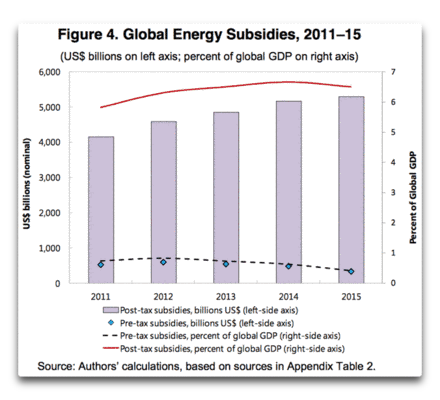
Abbildung 2: Aus dem IMF-Arbeitspapier. Man beachte, während die wirklichen Energiesubventionen stetig abnehmen, nehmen die imaginären Energiesubventionen stetig zu. Alarmismus?

Nun, endlich verstehe ich, warum es in den Straßen um meinen Wohnort so viele Schlaglöcher gibt. Bislang habe ich immer geglaubt, der Grund sei – wie von einem unserer Landkreis-Verwalter angemerkt – dass man die Schlaglöcher nicht ausbessern könne, weil man die obszön hohen Pensionen einer Generation von Menschen nicht aufbringen könnte, die gelernt hatten, sich an den Futtertrog des Landkreises zu lehnen.

Aber jetzt erkenne ich, dass dies keineswegs der Fall ist. Jetzt habe ich Durchblick. Das Belassen der Schlaglöcher ohne sie auszubessern ist kein Zeichen einer ökonomischen Schwäche, sondern stattdessen ein politisches Statement durch den Kreistag! Die Schlaglöcher nicht auszubessern ist ein cleveres Mittel, die heimtückischen „Energiesubventionen nach Steuern“ zu reduzieren, welche die Landkreisbewohner dümmlich an Exxon und Shell gezahlt haben! Es ist ein tollkühner Schlag gegen die außer Kontrolle tobenden Imperialisten der globalen Energieversorgung … muss ich wirklich dieses Aushängeschild versorgen? Ich fürchte, ja …

Ehrlicherweise muss man aber sagen, wenn man das Ausbessern von Schlaglöchern als eine Subvention für die Ölunternehmen zählt, bedeuten 5,3 Billionen Dollar gar nichts. Sie können die Summe so hoch schrauben wie sie wollen, darin liegt der Reiz imaginärer Energiesubventionen. Es gibt keine obere Grenze.

Aber Moment, da ist noch mehr. Obwohl die realen Energiesubventionen nicht einmal annähernd nahe der 5-Billionen-Marke liegen, sind es immer noch etwa 340 Milliarden Dollar pro Jahr. Das ist ein Drittel einer Billion, reales Geld in jedweder Welt. Aber natürlich gilt auch hier, dass nichts so ist, wie es zu sein scheint.

Das Erste, was man hinsichtlich dieser 340 Milliarden Dollar reale Energiesubventionen verstehen muss ist, dass global gesehen die höchsten Energiesubventionen diejenigen sind, die Öl produzierende Länder wie Venezuela und Nigeria ihren eigenen Bürgern zukommen lassen, indem man sie Preise zahlen lässt, die unter dem Marktpreis für Benzin und Diesel liegen. Das Zweite, was man wissen muss ist, dass der größte Teil der realen Energiesubvention in den Entwicklungsländern liegt. In einem Arbeitspapier über Subventionen, dass ich früher schon einmal hier analysiert habe, kam ich zu dem Ergebnis:

Schätzungen des IMF und der IEA zufolge belaufen sich globale Subventionen „vor Steuern“ (oder direkt) an fossiler Energie und fossil erzeugtem Strom im Jahre 2011 auf 480 bis 523 Milliarden Dollar pro Jahr (IEA 2012b; IMF 2013). Dies bedeutet eine Zunahme von fast 30% gegenüber dem Jahr 2010 und war sechsmal höher als die Gesamtsumme der Subventionen für Erneuerbare zu jener Zeit. Öl exportierende Länder waren für etwa zwei Drittel der Gesamtsubventionen für fossile Subventionen verantwortlich, während über 95% aller direkten Subventionen in den Entwicklungsländern anfielen.

Falls wir davon sprechen, dass die meisten Leute dies lesen: diejenigen von uns, die in der entwickelten Welt leben, sind nur mit lumpigen fünf Prozent an den realen Energiesubventionen beteiligt … was wiederum nur sechs Prozent ihrer fiktiven 5,3 Billionen Dollar schweren Subventionen ausmacht. Diese fünf Prozent der 340 Milliarden Dollar sind etwa 17 Milliarden Dollar. Aber das ist immer noch nicht alles. Man erinnere sich, die Summe ist aufgeteilt auf alle entwickelten Länder, Australien, die USA, UK, Deutschland, Israel, Neuseeland – die Liste ist lang.

Falls man also irgendwo in der entwickelten Welt lebt, betragen die wirklichen Subventionen für Energie etwa eine halbe Milliarde Dollar pro Staat. Übrigens, wenn man das in technischem Jargon ausdrückt, nenne ich eine Subvention von einer halben Milliarde Dollar „einmal Solyndra“ (An. der Redaktion: das ist die trotz Riesensubventionen pleite gegangene große Solarfirma in den USA) … aber ich schweife ab.

Wenn also Ihr Land ein- oder zweimal Solyndra pro Jahr an Subventionen zahlt, ist es das wert? Nun, das hängt davon ab, für was die Solyndras zahlen. Falls sie für Erneuerbare zahlen, ist es das höchstwahrscheinlich nicht wert. Falls sie für wirkliche Energie zahlen, könnte es das wert sein.

Schließen möchte ich mit dem Hinweis auf die Auswirkungen der Kappung von Energiesubventionen. Da die meisten davon in Entwicklungsländern sind und in Gestalt von reduzierten Energiepreisen für die Armen vorliegen … würde deren Kappung nicht die verwundbarsten Bürger treffen?

Nun, keine Angst, die IMFs haben dem Rechnung getragen. Hier folgt deren Aussage über die Auswirkungen der Beschneidung von Treibstoff-Subventionen für die Armen … ein lumpiger Satz ist alles, was sie für die Verarmten übrig haben, vielleicht ist es eine Elektronen-Knappheit oder so, aber hier folgt in jedem Falle dieser einsame Satz in seiner ganzen Glorie:

Außerdem sollte eine Reform der Energiesubventionen die Armen und Verwundbaren schützen, indem sichergestellt ist, dass ihr Wohlergehen nicht negativ beeinflusst wird.

Das ist es! Das ist alles hinsichtlich deren Gedanken um die Armen. Nun, das ist gut zu wissen … aber falls man 1 Dollar pro Gallone [ca. 4 Liter] an Subvention unter den Armen von Nigeria verteilt, WIE genau wollen sie sicherstellen, dass deren „Wohlergehen nicht negativ beeinflusst wird“? Das ist es, was ich bei diesen Lehnstuhl-Experten am meisten verachte, die vorschlagen, die Weltwirtschaft umzukrempeln, um ihren Ängsten und Phantasien Rechnung zu tragen. Sie ignorieren einfach alles, was sie als unerheblich beurteilen, und die Armen stehen oftmals an oberster Stelle jener Liste. An zweiter Stelle der Dinge, die sie ignorieren, steht, WIE sie umsetzen, was sie so leichthin vorschlagen.

Wie auch immer, das ist die jüngste wilde Übertreibung beim Vorlauf von Paris. Mein Rat? Man glaube nichts davon, was man liest … und man erinnere sich immer, dass man dies hier zuerst gelesen hatte…

——————————————–

Externalitäten: Dinge wie das Ausbessern von Schlaglöchern oder die Freisetzung von CO2 in die Atmosphäre werden „Externalitäten“ oder „externe Kosten“ genannt von Leuten, die an einer Kosten-Nutzen-Analyse arbeiten. Dies sind im Grunde Dinge, die der Schreiber entweder nicht mag oder die der Schreiber besteuern möchte, jedoch noch nicht herausgefunden hat, wie man es besteuern könnte. Noch nicht.

Während solche Externalitäten gelegentlich relevant sind, habe ich Einiges gegen den Einschluss von Externalitäten in die meisten Kosten-Nutzen-Analysen.

Erstens, wie legt man sie preislich fest? Welchen Preis würde man für – sagen wir – eine Tonne emittierten CO2 ansetzen? Ich habe Zahlen gesehen im Bereich von Null bis hunderte Dollar pro Tonne. Ohne Übereinstimmung eines bestimmten Wertes ist es den Analysten freigestellt, jede Zahl zu wählen, die sie wollen.

Weiter. Welche Externalitäten sollen eingehen? Falls wir das Ausbessern von Straßen als eine „Subvention“ an die Ölbarone eingehen lassen, sollte man dann nicht auch den Straßenbau einschließen? Und falls wir die Kosten für Straßenbau einschließen, was ist mit den Kosten für die Entwürfe des Straßenbaus? Und was ist mit den Pensionskosten für die Beamten (niemals billig), die den Straßenbau autorisiert haben? Wo führt das alles hin? Der IMF glaubt eindeutig, dass es hinter den Schlaglöchern endet, nicht davor…

Und schließlich, wenn man externe Kosten einfließen lässt, MUSS MAN ABSOLUT AUCH EXTERNE VORTEILE EINFLIESSEN LASSEN! Wie ich hier erläutert habe, beläuft sich der Vorteil des besseren Pflanzenwachstums wegen des gesteigerten atmosphärischen CO2-Gehaltes auf etwa 300 Milliarden Dollar pro Jahr, weil der Landwirt fossile Treibstoffe verbrennt … aber die aufgeblasenen Wichtigtuer beim IMF ignorieren dies vollständig, wie sie alle Vorteile ignorieren, die ihnen nicht in den Kram passen.

Link: http://wattsupwiththat.com/2015/05/29/potholes-in-their-arguments/

Übersetzt von Chris Frey EIKE