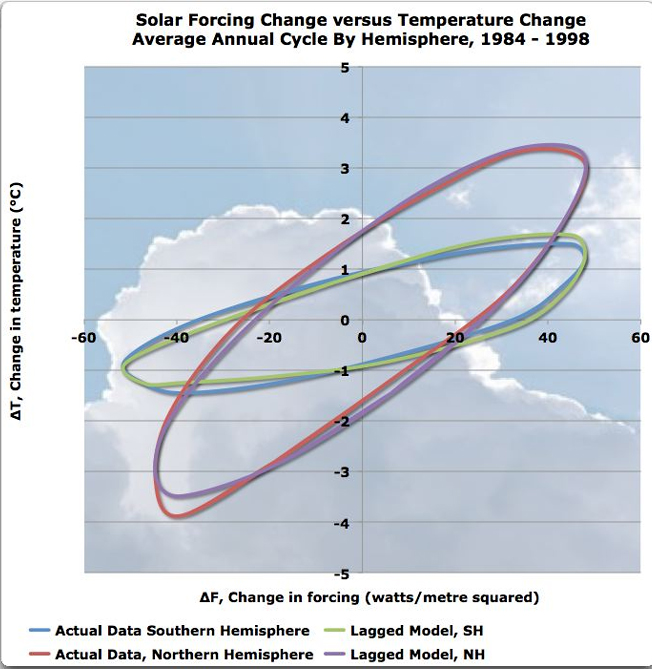
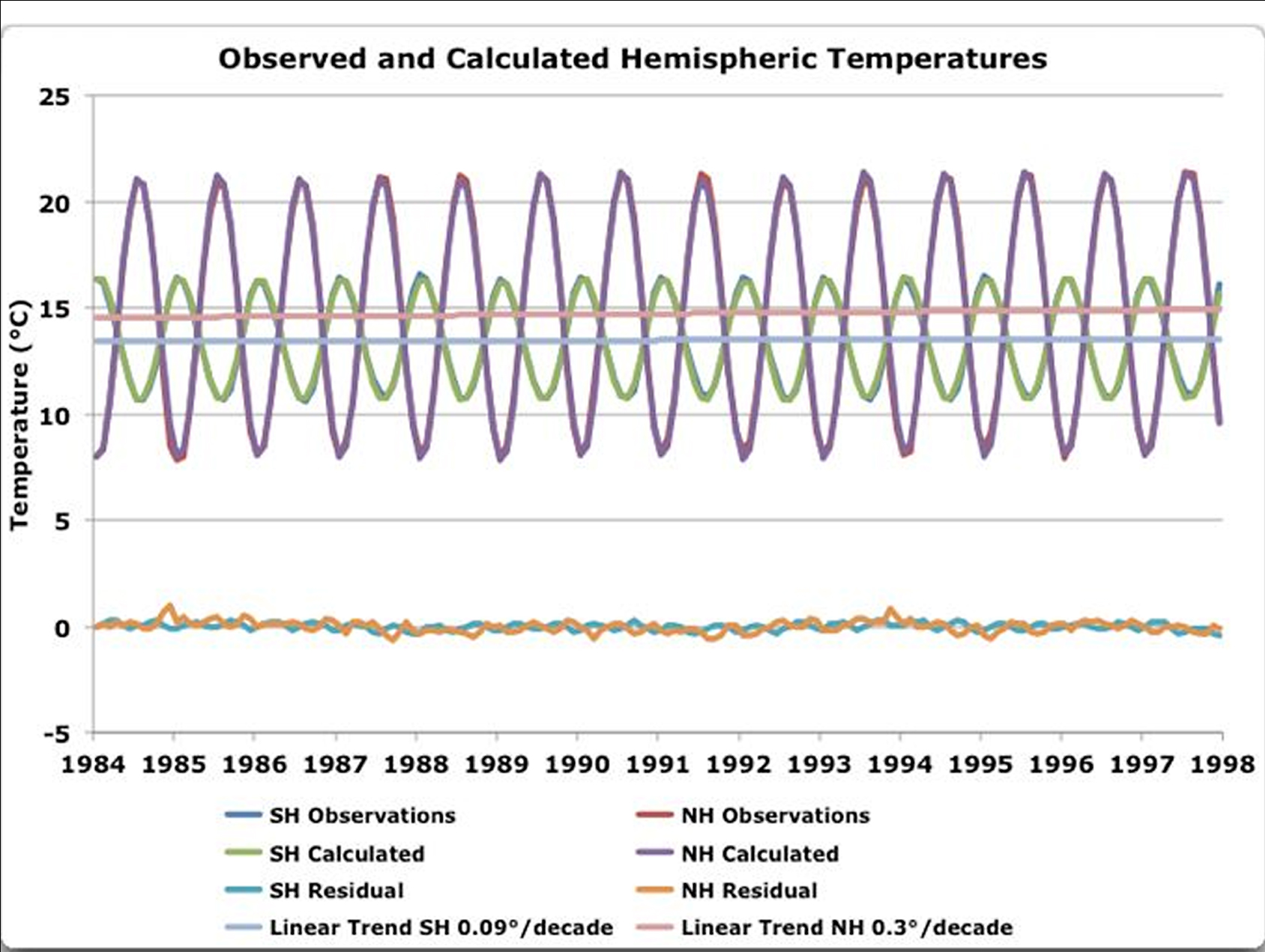
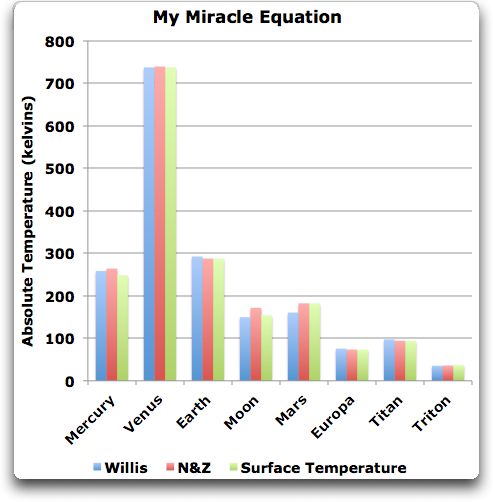
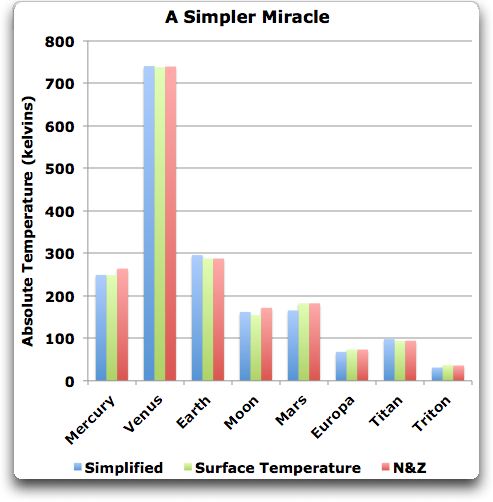
BEST, Vulkane und Klimasensitivität

geschrieben von Willis Eschenbach | 1. September 2012

Bild rechts [Abbildung 1]: Vergleich der in der Vergangenheit eingetretenen Temperaturänderungen nach BEST infolge CO2 plus Vulkane (dicke schwarze Linie) mit den BEST-Temperaturdaten (dünne schwarze Linien). Quelle

Ich habe Steven Mosher gefragt, woher die BEST-Leute ihre Daten haben zur erwarteten Temperaturänderung durch vulkanische Antriebe wie mit der dicken schwarzen Linie dargestellt … keine Antwort. Also schob ich die Frage erst einmal beiseite und beschloss, die Daten einfach selbst zu benutzen. Also … habe ich das gemacht, was ich normalerweise immer tue. Ich habe ihre Abbildung digitalisiert, da die zugrunde liegenden Daten nicht verfügbar waren. Sie haben mir erlaubt, ihre Daten zu analysieren, was eine sehr merkwürdige Sache enthüllte.

Ihre Erklärung der schwarzen Linie in Abbildung 1 oben (ihre Abbildung 5) lautet so:

„Eine lineare Kombination von vulkanischen Sulfaten und Änderungen beim CO2 wurden angepasst an die Temperaturgeschichte auf dem Festland, um Abbildung 5 zu erzeugen. Wie wir gleich beschreiben werden, hat die Addition eines Proxies zur Sonnenaktivität die Anpassung nicht signifikant verbessert. Die großen negativen Abweichungen hängen zusammen mit vulkanischen Sulfatemissionen, wobei sich die vier größten Eruptionen alle vor 1850 ereignet haben; folglich hat sich unsere Einbeziehung der Daten vor 1850 als nützlich erwiesen für die Beobachtung dieser Ereignisse. Um die Anpassung durchzuführen, haben wir die Sulfataufzeichnungen adjustiert, indem wir ein exponentielles Abklingen mit einer Halbwertszeit von zwei Jahren nach der Emission angebracht haben. Die Wahl von zwei Jahren wurde motiviert, um die Anpassung zu maximieren, und sie ist deutlich länger als die 4 bis 8-monatige Halbwertszeit, die für die Gesamtmenge der Sulfate in der Atmosphäre beobachtet worden ist (was aber plausibel ist bzgl. der Reflektivität, die vom Gebiet und nicht vom Volumen abhängt).“

OK, das macht mich nervös … sie haben eine Anpassung durch eine lineare Regression an die Temperaturaufzeichnung der verzögerten exponentiellen Abschwächung angebracht, mit einer separat angepassten Zeitkonstante, von einer Schätzung vulkanischer Sulfatemissionen basierend auf Eisbohrkernen … OK, ich akzeptiere das, jedoch mit einer Einschränkung. Sie verwenden die Emissionen von hier, aber obwohl ich mich der Abbildung oben gut nähern kann, kann ich sie doch nicht genau nachbilden.

Ich wollte die vulkanischen Daten herausfiltern. Folgendermaßen wollte ich vorgehen: Zuerst würde ich die dicke schwarze Linie der Abbildung 1 oben rechts digitalisieren. Dann würde ich sie zusammenpassen mit dem Logarithmus der CO-Zunahme [CO2-Zunahme?] seit 1750. Habe ich erst einmal die CO2-Zunahme subtrahiert, müsste der verbleibende Rest die Temperaturänderungen aus vulkanischen Eruptionen allein zeigen.

Abbildung 2 zeigt den ersten Teil der Berechnung, die digitalisierte schwarze Linie aus Abbildung 1 (CO2 + Vulkane) mit dem Logarithmus CO2 überlagert in rot.

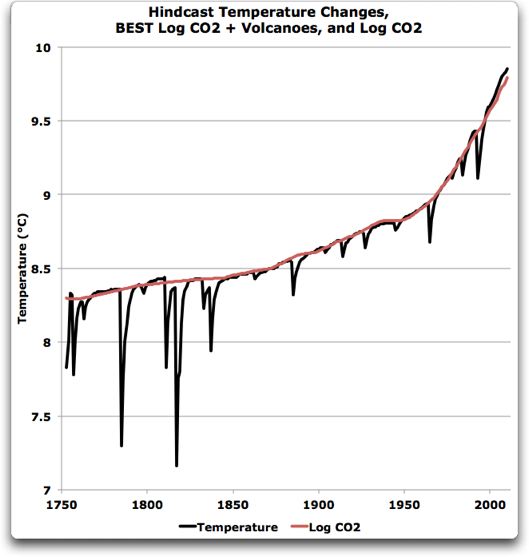
Abbildung 2: Die schwarze Linie ist die digitalisierte dicke schwarze Linie aus Abbildung 1. Die rote Linie ist dreimal der Logarithmus (zur Basis 2) der CO2-Änderung plus einer Verschiebung. Die CO2-Daten stammen von 1750 bis 1950 aus Eisbohrkernen in Law Dome, danach vom Mauna Loa.

Ich habe die CO2-Kurve händisch und nach Augenmaß an die Daten angepasst, indem ich die Neigung und den Achsenabschnitt der Regression adjustiert habe, weil Standard-Regressionsmethoden es nicht zur Spitze der schwarzen Linie anpassen. Verschiedene Dinge deuteten darauf hin, dass ich mich auf dem richtigen Weg befand. Erstens ist da die gute Anpassung des Logarithmus‘ der CO2-Daten an die BEST-Daten. Zweitens hat sich herausgestellt, dass sich die beste Anpassung ergibt, wenn man die Standard-Klimasensitivität von 3°C pro Verdoppelung des CO2-Gehaltes verwendet. Ermutigt fuhr ich fort.

Zieht man die vulkanischen Daten von den CO2-Daten ab, erhält man die durch Vulkane erwartete Temperaturänderung, dargestellt in Abbildung 3:

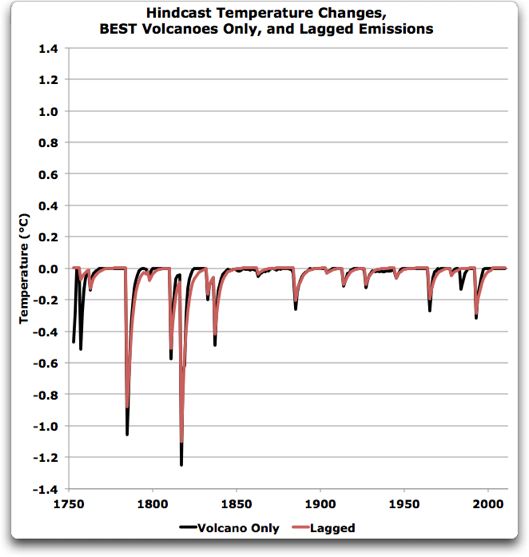
Abbildung 3: Temperaturänderungen durch Vulkane (Abkühlung nach Eruptionen), wie sie von BEST dargestellt werden (schwarze Linie) und als Anpassung an die verzögerten Emissionen, wie sie oben in ihrer zitierten Erläuterung erklärt haben (rote Linie).

Wie ich oben erwähnt habe, kann ich mich den von ihnen dargestellten Temperaturänderungen (schwarze Linie) gut nähern unter Verwendung einer verzögerten Version ihrer Sulfat-Daten, wie sie es beschrieben haben (rote Linie), aber die Übereinstimmung ist nicht genau. Da die schwarze Linie dem entspricht, was sie in Abbildung 1 oben zeigen und die Unterschiede vernachlässigbar sind, arbeite ich weiter mit der dicken schwarzen Linie.

Hier wollen wir einen Moment innehalten und uns überlegen, was sie gemacht haben und was sie nicht gemacht haben. Was sie gemacht haben: Sie haben Änderungen des atmosphärischen CO2-Antriebs in Watt pro Quadratmeter (W/m²) in eine Temperaturänderung (in Grad Celsius) konvertiert. Diese Konversion haben sie unter Verwendung der Standard-Klimasensitivität von 3°C Erwärmung für jede Verdoppelung des CO2 durchgeführt (eine Verdoppelung ergibt zusätzlich 3,7 W/m²).

Auch haben sie stratosphärische Einträge von vulkanischen Sulfaten (in Teragramm) auf eine Temperaturänderung (in Grad Celsius) konvertiert. Dies haben sie durch rohe Kraft getan unter Verwendung eines verzögerten Modells der Ergebnisse der stratosphärischen Sulfateinträge, welches eine Anpassung der Temperatur ist.

Aber was sie nicht getan haben, so weit ich das herausfinden konnte, war die Berechnung des Antriebs durch die vulkanischen Eruptionen (in W/m²). Sie haben lediglich die Sulfat-Daten direkt an die Temperaturdaten angepasst und den Zwischenschritt ausgelassen. Ohne Kenntnis des Antriebs durch die Eruptionen konnte ich nicht abschätzen, welche Klimasensitivität sie verwendet haben, um die Reaktion der Temperatur auf vulkanische Eruptionen zu berechnen.

Allerdings führen viele Wege nach Rom. Die Leute bei NASA GISS verfügen über eine Schätzung des vulkanischen Antriebs (in W/m²; die Spalte unter der Bezeichnung „StratAer“ für stratosphärische Aerosole von Vulkanen). Also verwendete ich die vulkanischen Antriebe nach GISS, um die Klimasensitivität von BEST zu untersuchen. Sie decken nur den Zeitraum von 1880 bis 2000 ab, aber ich konnte sie trotzdem benutzen, um die Klimasensitivität zu schätzen, die BEST für den vulkanischen Antrieb verwendet hat. Und da fand ich den komischen Teil. Abbildung 4 zeigt den vulkanischen Antrieb in W/m² von NASA GISS, zusammen mit der BEST-Darstellung der Reaktion der Temperatur durch diesen Antrieb.

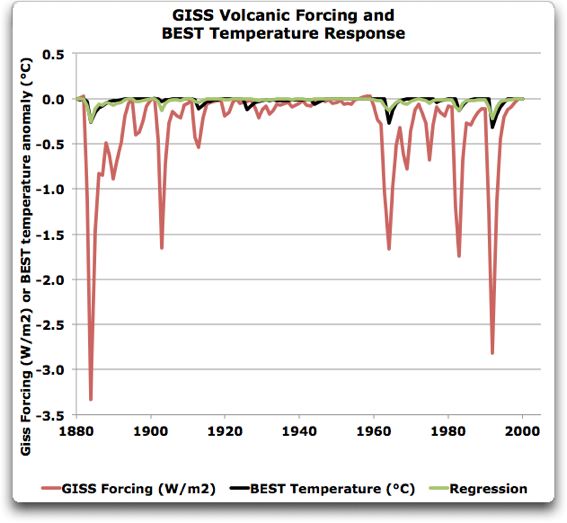
Abbildung 4: Die schwarze Linie zeigt die Temperaturanomalie der Vergangenheit (Abkühlung) nach den Eruptionen. Die rote Linie zeigt die Änderung des Antriebs in Watt pro Quadratmeter (W/m²) durch die Eruptionen. Die grüne Linie zeigt die beste Anpassung theoretischer Abkühlung, die aus dem GISS-Antrieb folgt. Beachte die unterschiedlichen Zeitperioden im Vergleich mit den vorigen Abbildungen.

Wie man erkennt, zeigt die Regression (grüne Linie) des GISS-Antriebs eine vernünftige Approximation zur BEST-Temperaturanomalie. Also befinden wir uns immer noch auf dem richtigen Weg. Der merkwürdige Teil sind die relativen Größenordnungen. Die Temperaturänderung liegt gerade unter einem Zehntel der Änderung des Antriebs (0,08°C pro W/m²).

Dies ergibt sich zu einer Klimasensitivität von etwa 0,3°C pro Verdoppelung des CO2 (0,08°C/W/m² mal 3,7 W/m²/Verdoppelung = 0,3°C/Verdoppelung) … was nur einem Zehntel der kanonischen Zahl von drei Grad pro Verdoppelung des CO2 entspricht.

Also zeigen sie in ihrer Graphik die dicke schwarze Linie als Kombination einer Klimasensitivität von 3°C pro Verdoppelung des CO2-Anteils mit einer Klimasensitivität von nur 0,3°C pro Verdoppelung des vulkanischen Anteils…

Das ist nun in der Tat ein merkwürdiges Ergebnis. Es gibt viele mögliche Wege, dieses Ergebnis einer Klimasensitivität von 0,3°C pro Verdoppelung zu erklären. Hier folgen die Möglichkeiten:

1. Die Leute bei NASA GISS haben den Antrieb durch Vulkane um einen Faktor zehn überschätzt, eine ganze Größenordnung. Möglich, aber sehr zweifelhaft. Die Reduktion des Sonnenlichts bei klarem Himmel nach vulkanischen Eruptionen wurde in zahlreichen Studien untersucht. Wir haben eine ziemlich gute Vorstellung von dem Energieverlust bei der Einstrahlung. Vielleicht irren wir uns um einen Faktor zwei, aber nicht um einen Faktor zehn.

2. Die BEST-Temperaturdaten unterschätzen die Temperaturvariationen nach vulkanischen Eruptionen um eine ganze Größenordnung. Sogar noch zweifelhafter. Die BEST-Temperaturdaten sind nicht perfekt, sind aber das Beste, was wir haben.

3. Die BEST-Daten und die NASA-Daten sind beide falsch, aber passenderweise sind sie beide in der gleichen Richtung falsch, so dass sich die Fehler gegenseitig aufheben und eine Sensitivität von drei Grad pro Verdoppelung zeigen. Die Wahrscheinlichkeit dafür, dass dies zufällig ist, ist gering, zumal auch die o. g. Gründe noch gelten.

4. Sowohl die NASA- als auch die BEST-Daten sind in etwa korrekt, und die Klimasensitivität beträgt nur etwa ein Zehntel dessen, was behauptet wird.

Ich persönlich halte Nummer 4 für die Hausnummer, kleine Klimasensitivität. Ich sage, dass das Klima durch eine Vielfalt homöostatischer Mechanismen gepuffert wird, die dazu tendieren, die Auswirkungen von Änderungen des Antriebs auf die Temperatur zu minimieren, wie ich ausführlich in verschiedenen früheren Beiträgen gezeigt habe.

Wie immer sind aber alternative Hypothesen willkommen.

DATEN: Ich habe das in einer Excel-Tabelle gerechnet, und zwar hier. Das ist nicht nutzerfreundlich, aber ich glaube auch nicht, dass es aktiv nutzerfeindlich ist … die BEST-Temperaturdaten in dieser Tabelle stammen von hier. Man beachte, dass komischerweise die BEST-Leute nicht alles des jährlichen Zyklus‘ aus ihren Temperaturdaten eliminiert haben, es verbleibt ein ganzes Grad jährlicher Schwingung … man stelle sich das mal vor!

(Aktualisierung) Richard Telford hat in Kommentaren darauf hingewiesen, dass das, was ich berechnet habe, die momentane Sensitivität ist, und da hat er recht.

Wie ich allerdings im Beitrag „Time Lags in the Climate System“ [etwa: Zeitliche Verzögerungen im Klimasystem] gezeigt habe, hängt die momentane Sensitivität in einem zyklisch getriebenen System, das Wärme durch exponentielle Verstärkung und Abschwächung gewinnt und verliert, mit einer längerzeitlichen Sensitivität zusammen, und zwar durch die Beziehung

Dabei ist t1 die Verzögerung, t die Länge des Zyklus‘ und s2/s1 die Größe der Reduktion der Amplitude. Da wir in diesem Falle ausschließlich mit BEST-Temperaturdaten nur vom Festland arbeiten, wo die Verzögerung kurz ist (im Mittel weniger als einen Monat), bedeutet das, dass die kurzfristige Sensitivität etwa 64% der längerzeitlichen Sensitivität ausmacht. Dies ergibt eine längerzeitliche Sensitivität von etwa 0,46°C pro Verdoppelung. Auch das liegt noch weit, weit unter der üblichen Schätzung von 3°C pro Verdoppelung.

Willis Eschenbach

Link: http://wattsupwiththat.com/2012/08/13/best-volcanoes-and-climate-sensitivity/

Übersetzt von Chris Frey EIKE

Erderwärmung? Sonne und Albedo reichen zur Erklärung der Erwärmung aus

geschrieben von Willis Eschenbach | 1. September 2012

Erster Teil

Berechnung der erwarteten Klimasensitivität

Willis Eschenbach
“Klimasensitivität” ist der Name des Maßes, um wieviel sich die Erdoberfläche erwärmt bei einer gegebenen Änderung von etwas, das “Antrieb” (forcing) heißt. Eine Änderung des Antriebs bedeutet eine Änderung im Netto des Strahlungseintrags (downwelling raditation) am oberen Rand der Atmosphäre. Darin enthalten ist die kurzwellige (solare) und die langwellige („Treibhaus“) Strahlung.
Es gibt eine interessante Studie von N. Hatzianastassiou et al. über die Strahlungsbilanz der Erde, sie heißt “Langzeit-Globalverteilung des kurzwelligen Strahlungsbudgets der Erde am oberen Rand der Atmosphäre” (Long-term global distribution of Earth’s shortwave radiation budget at the top of atmosphere). Unter anderem enthält die Studie eine Betrachtung der Albedo für jede Hemisphäre für den Zeitraum 1984-1998. Heute fiel mir auf, dass ich diese Daten zusammen mit den Solardaten der NASA benutzen könnte, um den Beobachtungs-Erwartungswert zu errechnen, bei dem Gleichgewicht bei der Klimasensitivität eintritt.
Nun kann man nicht einfach die direkte Änderung von Sonnenantrieb und Temperaturänderung betrachten, um die Langzeitsensitivität zu erhalten. So würde man nur eine sofort eintretende „unmittelbare“ Klimasensitivität erhalten. Der Grund liegt darin, dass es eine Weile dauert, bis sich die Erde erwärmt oder abkühlt. Daher wird die durch eine Verstärkung des Antriebs direkt und unmittelbar eintretende Änderung kleiner sein, als die vermutliche Änderung bis hin zum Erreichen des Gleichgewichtszustands, wenn die gleiche Antriebsänderung über einen langen Zeitraum aufrechterhalten bleibt.
Einiges geht aber dennoch. Figur 1 zeigt den Jahreszyklus der Änderungen des Sonnenantriebs und der Temperaturänderungen.

Figur 1. Lissajous Figur der Änderung des Sonnenatriebs (horizontale Achse) versus Temperaturänderung (vertikale Achse) als Jahresdurchschnitte.
[Lagged Model, … = verzögertes Modell]

Was zeigt uns Figur 1?
Ich habe angefangen mit der gemeinsamen Darstellung der Sonnendaten von der NASA (monatliche Änderung der Sonnenenergie, die auf die Erde trifft) und den Albedo-Daten. Aus dem Sonnenantrieb in [W/m2 mal (1 minus Albedo)] erhalten wir den ins System hereinkommenden Betrag der Sonnenenergie. Das ist das tatsächliche Sonnenantriebs-Netto Monat für Monat.
Dann habe ich die Änderungen in diesem Netto-Sonnenantrieb (nach Albedo Reflektionen) gegen die entsprechenden Temperaturänderungen geplottet, jeweils für die Hemisphären.
Vorab einige Bemerkungen zu diesem Plot.
Die Nordhemisphäre (NH) hat größere Temperaturschwingungen (vertikale Achse) als die Südhemisphäre (SH). Ursache sind die größeren Landmassen der NH und die größeren Wassermassen der SH … Das Meer hat eine viel größere spezifische Wärme, das Meer braucht mehr Energie zur Erwärmung als das Land.
Wir sehen das auch an der Neigung der Ovale. Die Neigung der Ovale sind Maße für die „Verzögerung“ im System. Je schwieriger es ist, eine Hemisphäre zu erwärmen oder abzukühlen, desto größer die Verzögerung, und desto flacher die Neigung.
Damit sind die roten und blauen Linien erklärt. Es sind die echten Daten für die NH und die SH.
Für ein “verzögertes Modell” habe ich das einfachste Modell benutzt. Es benutzt eine Exponentialfunktion zur Annäherung an die Verzögerung zusammen mit einer Variablen “lambda_0″. Das ist die "unmittelbare" Klimasensitivität. Das Modell bildet den Prozess ab, bei welchem ein Objekt durch einfallende Strahlung erwärmt wird. Zuerst geht die Erwärmung ziemlich rasch, mit zunehmender Zeit wird die Erwärmung immer langsamer bis sie einen Gleichgewichtszustand erreicht. Der Zeitbedarf zur Erwärmung wird von einer “Zeitkonstante” namens “tau” bestimmt. Ich benutzte folgende Formel:
ΔT(n+1) = λ∆F(n+1)/τ + ΔT(n) exp(-1/ τ)
wobei ∆T die Temperaturänderung ist, ∆F die Antriebsänderung, lambda (λ) die "unmittelbare" Klimasensitivität; “n” und “n + 1″ sind die Beobachtungszeiten, und tau (τ) ist die Zeitkonstante.
Ich habe Excel für die Berechnung der Werte benutzt, dazu das “Solver” Werkzeug [Anm. d. Ü: sh. Stichwort SOLVER in der Excel-Hilfe]. Es ergab sich eine bestangepaßte Kurve für die NH und die SH. Die Anpassung ist recht gut mit einem ‘Wurzel-aus-Durchschnittsquadrate-Fehler’ (RMS – Root Mean Square error) von nur 0.2°C und 0.1°C für die NH und die SH.
(Anm. d. Ü: die Excel-Tabelle kann heruntergeladen werden, Verweis siehe später!)

Und so erhalten wir unterschiedliche Zahlen für die jeweiligen lambda_0 und tau für die NH und die SH, wie folgt:

Man beachte (wie zu erwarten war), dass es länger dauert, die SH zu erwärmen oder abzukühlen im Vergleich zur NH (tau ist größer für die SH). Darüberhinaus (wie ebenfalls zu erwarten war) ändert sich die SH weniger bei einem gleichen Betrag der Erwärmung.
Denken Sie bitte daran, dass lambda_0 die "unmittelbare" Klimasensitivität ist. Weil wir die Zeitkonstante kennen, können wir das zur Berechnung derjenigen Sensitivität, wo der Gleichgewichtszustand eintritt, benutzen. Ich bin sicher, dass es einen einfacheren Weg gibt, sie zu berechnen, ich habe nur die gleiche Kalkulationstabelle benutzt. Um eine Verdoppelung des CO2 zu simulieren, habe ich einen einmaligen Sprung von 3.7 W/m2 Antrieb angenommen.
Die Ergebnisse sehen so aus:

Das Klimasensitivitäts-Gleichgewicht aufgrund einer Änderung des Antriebs, der von einer Verdoppelung des CO2 (3.7 W/m2) herrührt, beträgt 0.4°C in der Nordhemisphäre und 0.2°C in der Südhemisphäre. Daraus ergibt sich ein gesamtes globales Klimasensitivitäts-Gleichgewicht von 0.3°C bei einer Verdoppelung des CO2.

Kommentare und Kritik sind willkommen, so funktioniert die Wissenschaft. Ich veröffentliche hier meine Ideen, und Sie alle werden versuchen, Fehler zu finden.
w.
Zusatz: Die Kalkulationstabelle für die Berechnungen und zur Erzeugung des Graphen ist hier.
Anmerkung: Ich habe auch die Änderung für den gesamten Datenbestand von 1984 bis 1998 modelliert, nicht nur die Änderungen aufgrund des Ansatzes der jährlichen Durchschnitte. (hier nicht abgebildet). Die Ergebnisse für lambda_0 und tau für die NH und die SH waren die gleichen (in Bezug auf die oben beschriebene Genauigkeit), trotz der generellen Erwärmung während jenes Zeitraums. Ich bin mir bewußt, dass die Zeitkonstante “tau”, bei nur wenigen Monaten, kürzer ist, als andere Studien gezeigt haben. Trotzdem … Ich berichte nur, was ich herausgefunden habe. Wenn ich mit einer längeren Zeitkonstante modelliere, wird die Neigung völlig falsch, viel flacher.
Während es auch möglich ist, dass es viel längere zeitliche Perioden mit Erwärmung gibt, zeigen sie sich nicht in meinen Analysen aufgrund der vorliegenden Daten. Wenn tatsächlich solche längeren Zeiträume existieren, scheinen sie nicht signifikant zu sein, um die Verzögerung zu strecken, die in meiner Analyse oben dargestellt ist. Die Einzelheiten der Langzeitanalyse (im Gegensatz zu den benutzten Durchschnitten, wie oben gezeigt) können auf dem Kalkulationsblatt zu eingesehen werden.
#############################################

Zweiter Teil

Ein langfristiger Blick auf die Klimasensitivität

Willis Eschenbach
Nach der Veröffentlichung meines obigen Beitrags, “An Observational Estimate of Climate Sensitivity“ haben zahlreiche Leser kritisiert, dass ich nur die Zyklen der jährlichen Durchschnitte betrachtet hätte. Wenn man Jahrzehnte betrachtet, sähe es anders aus und die Klimasensitivität wäre viel größer. Daher wiederhole ich meine Analyse ohne die jährlichen Durchschnitte, die ich in meinem letzten Beitrag betrachtet hatte. Figur 1 zeigt das Resultat für die nördliche Hemisphäre (NH) und die Südliche Hemisphäre (SH):

Figure 1. Temperaturen, nur auf der Grundlage der Variationen der Sonneneinstrahlung errechnet (Netto Sonnenenergie nach Albedo Reflektionen). Die Beobachtungen werden so gut durch die Berechnungen bestätigt, dass man die Linien mit den gemessenen Temperaturen nicht sieht. Sie sind hinter den Linien verborgen, die die Berechnungen abbilden. Die beiden Hemisphären haben verschiedene Zeitkonstanten (tau) und Klimasensitivitäten (lambda). Für die NH beträgt die Zeitkonstante 1.9 Monate und die Klimasensitivität 0.30°C bei einer Verdoppelung des CO2. Die entsprechenden Werte für die SH betragen 2.4 Monate und 0.14°C bei einer Verdoppelung des CO2. [… Residual = Rest]

Ich habe anhand des gleichen Verzögerungs-Modells gerechnet, das ich in meinem vorgehenden Beitrag erwähnte, aber ich habe nun die tatsächlichen Daten benutzt, anstelle der Durchschnitte. Ich verweise daher auf meinen vorgehenden Beitrag und das beigefügte Kalkulationsblatt mit den Einzelheiten zur Berechnung. Und jetzt gibt es einiges Interessantes bei dieser Grafik.
Erstens, die von mir im vorgehenden Beitrag benutzten Klimasensitivitäten eignen sich vorzüglich, um die Temperaturänderungen über ein-einhalb Jahrzehnte zu berechen, wenn auch die mit meinen Berechnungen nicht einverstandenen Leser anderer Meinung sind. In dem von der Aufzeichnung überdeckten Zeitraum stieg die NH-Temperatur um 0.4°C an, vom Modell ganz exakt so berechnet. Auf der SH gab es kaum einen Anstieg, auch das wurde vom Modell genau so berechnet.

Zweitens, nur die Sonne und die Albedo wurden benötigt, um diese Berechnungen durchzuführen. Ich brauchte keine Aerosole, vulkanischen Antriebe, Methan, CO2, Ruß, indirekten Aerosol-Effekt, Bodennutzung, Schnee- oder Eis-Albedo, und auch nichts von all dem übrigen Zeug, von dem die Modellierer behaupten, es steuere die Temperatur. Sonnenlicht und Albedo scheinen notwendige und hinreichende Variablen zu sein, um die Temperaturänderungen über den betrachteten Zeitraum zu erklären.

Drittens, die Treibhausgase werden gemeinhin als “gut durchmischt” angesehen, daher wurde ein Reihe von Erklärungen versucht, um die Unterschiede in den Trends der Temperaturen für die beiden Hemisphären zu erklären … aber allein mit der Sonne und der Albedo können die unterschiedlichen Trends sehr gut erklärt werden.
Viertens, es gibt keinen signifikanten Trend in den Resten aus Errechnetem minus Messwerten weder für die NH noch für die SH.
Fünftens, ich sage schon seit vielen Jahren, dass das Klima auf Störungen und Änderungen bei den Antrieben reagiert, indem es gegensteuert. So meine ich beispielsweise, dass die Auswirkung von Vulkanausbrüchen auf das Klima in den Klimamodellen stark überschätzt wird. Es sind die Albedoänderungen, die die Dinge zurück ins Gleichgewicht bringen.
Wie haben Glück, dass unser Datenbestand mit dem Pinatubo-Ausbruch einen der stärksten Vulkanausbrüche unserer Zeit enthält … kann man ihn aus der in Figur 1 gezeigten Aufzeichnung herausnehmen? Nein, das geht nicht und zwar aus folgendem Grund: die Wolken reagieren auf eine derartige Störung sofort wie ein Thermostat.
Sechstens, wenn es über jahrzehntelange Perioden eine längere Zeitkonstante gäbe (tau), oder eine größere Klimasensitivität (lambda), dann würde sich das in den Resten für die NH zeigen, aber nicht in den Resten für die SH. Dies deswegen, weil es bei der NH einen Trend gibt, und bei der SH grundsätzlich keinen. Aber die Berechnungen mit den gegebenen Zeitkonstanten und Sensitivitäten konnten beide Hemisphären sehr genau abdecken. Der Fehler der Wurzel-aus-den-Quadratdurchschnitten (Root Mean Square – RMS error) bei den Resten beträgt nur ein paar Zentel eines Prozents.

Also, Leute, das ist Alles, machen Sie sich drüber her … aber denken Sie bitte daran: Es ist Wissenschaft und die Spielregel ist, dass die wissenschaftliche Erkenntnis selbst angegriffen werden soll, nicht der Wissenschaftler als Mensch.

Denken Sie bitte auch daran, dass es nutzlos ist, meine Ergebnisse als einen „Witz“ oder als „Unsinn“ zu bezeichnen. Die Rechenergebnisse passen extrem gut zu den beobachteten Messwerten. Wenn es Ihnen nicht gefällt, müssen Sie die Fehler suchen und finden, und dann die Fehler in meinen Daten, in meiner Logik oder in meiner Mathematik aufzeigen.
Mit freundlichen Grüßen
w.
PS – Man hat mir häufig gesagt, so als ob keine weitere Diskussion möglich wäre, dass niemand jemals eine Modell erzeugt hätte, wo der Temperaturanstieg ohne Einbezug anthropogener Beiträge von CO2 und dergleichen hätte erklärt werden können. Nun, dieses Modell hier erklärt einen Anstieg von 0.5°C/pro Jahrzehnt in den 1980er bis 1990ern, genau den Anstieg, über den man sich Sorgen macht, und das ohne anthropogenen Beitrag.
[Anmerkung: Ich danke Stephen Rasey für seinen aufmerksamen Hinweis, dass meine ursprüngliche Trend-Berechnung wegen Endpunkt-Effekten leicht abwich. Ich habe daraufhin die Grafik und die darauf bezogenen Trend-Verweise berichtigt. Das hat keine Bedeutung für die Berechnungen oder für meine Schlussfolgerungen. -w.]
#######################################################

Original zum ersten Teil: „An Observational Estimate of Climate Sensitivity“

Original zum zweiten Teil: "A Longer Look at Climate Sensitivity"

Willis Eschenbach

Übersetzung: Helmut Jäger, EIKE

Das Mysterium von Gleichung 8 oder John v. Neumanns Elefant*

geschrieben von Willis Eschenbach | 1. September 2012

„Warum versuchen Sie alle nicht, unsere WUNDERgleichung zu widerlegen, anstatt Ihre Köpfe gegen die Wand zu schlagen bei dem Versuch, zu beweisen oder zu widerlegen, wer was weiß und zu betonen, dass Sie mit diesem oder jenem Probleme haben? Die Frage lautet, wie wir das haben machen können – keine Frage ist, dass unsere Gleichungen funktionieren – wenn Sie nicht verifiziert haben, dass sie funktionieren, warum haben Sie nicht? (…) Warum denken Sie nicht „hmmmm, N&Z haben uns eine Gleichung gegeben. Wenn man darin den gemessenen Druck eingibt und Tgb wie vorgeschlagen berechnet, erhält man einen berechneten Wert von Ts, der selbst zu gemessenen Werten passt! Sie können die Gleichung nicht widerlegen? Also kochen wir vielleicht irgendwie die richtigen Daten?“
Dies soll der Beweis sein, dass ihre Theorie korrekt ist, und Leute sagen mir immer wieder ‚aber sie haben einen wirklichen Beweis, sie können planetarische Temperaturen vorhersagen, schau mal nach!‘ Außerdem fällt es schwer, eine Einladung nach Art von Dr. Zeller zu ignorieren, also habe ich nachgeschaut.
Abbildung rechts: Es sind nicht diese Gleichungen, nach denen Sie suchen.
Zuerst postulieren sie etwas, das sie den „Atmospheric Thermal Enhancement“- oder „ATE“-Effekt nennen, der die Erde wärmer macht, als sie ohne Atmosphäre wäre.
Der ATE-Effekt” wird durch etwas gemessen, das Nte(Ps) genannt wird, was in ihrer Studie wie folgt definiert und abgeschätzt worden ist.

Darin ist Nte(Ps) ein Maß für den „oberflächennahen Atmospheric Thermal Enhancement“-Effekt.
Nte(Ps) wird definiert als die tatsächliche mittlere Lufttemperatur des Planeten Ts geteilt durch die theoretische „Graukörper“-Temperatur des Planeten Tgb, berechnet aus der totalen solaren Einstrahlung So des Planeten. Nte(Ps) wird abgeschätzt durch Verwendung einer angepassten Funktion des Bodendrucks des Planeten Ts.
Lassen Sie mich das ein wenig vereinfachen. Symbolisch lässt sich der rechte Teil der Gleichung (7) schreiben als
Nte(Ps) = e^(t1 * Ps ^ t2 + t3 * Ps ^ t4) (7Sym)
worin „e“ die Basis des natürlichen Logarithmus‘ und Ps der Bodendruck des Planeten oder Mondes ist. Es gibt vier regelbare Parameter (t1 bis t4), die an die Daten „angepasst“ oder danach ausgerichtet werden. Mit anderen Worten, diese Werte werden wiederholt justiert und ausgerichtet, bis die gewünschte Anpassung erreicht ist. Diese Anpassung kann leicht in Excel mit dem Menüpunkt „Löse…“ vorgenommen werden. Wie zu erwarten war, ist die Anpassung mit vier Parametern und nur acht Datenpunkten ziemlich gut, und ihre Schätzung kommt dem tatsächlichen Wert von Nte(Ps) ziemlich nahe.
Lustigerweise wird das Ergebnis von Gleichung (7) danach in einer anderen angepassten Gleichung verwendet, Nummer (8). Sie lautet:

wobei So die Gesamtsolarstrahlung ist.
Dies ist ihre WUNDERgleichung, von der sie sagen, dass man damit die Oberflächentemperatur von acht verschiedenen Planeten und Monden mit nur zwei Variablen berechnen kann – Pr, der Bodendruck und So, die Gesamtsolarstrahlung. Das ist es, was die Menge der Leute so fasziniert, dass sie mir schreiben, dass es „Beweise“ gibt, dass N&Z recht haben.
Offensichtlich gibt es einen weiteren angepassten Parameter in Gleichung (8), so dass wir sie symbolisch umschreiben können zu:
Ts = t5 * (Solar + adjustment ) ^ 1/4 * Nte(Ps). (8Sym)
Halten wir hier mal einen Moment inne und gestatten uns eine Bemerkung zu Gleichung (8). Die gesamte Sonneneinstrahlung reicht von über 9000 W/m² für den Merkur bis 1,51 W/m² für Triton. Man betrachte Gleichung (8). Wie wird der Faktor 0,0001325 auf jeden dieser Werte vor dem Ziehen der vierten Wurzel im Ergebnis auch nur einen winzigen Unterschied machen? Das ist einfach bizarr. Sie sagen, dass sie es in die Formel einbringen, damit die Formel richtig ist, wenn keine Solarstrahlung vorhanden ist, so dass eine Hintergrundstrahlung von 3 Kelvin herauskommt. Wen kümmert das? Wirklich, es verändert Ts maximal durch ein Tausendstel Grad für Triton. Also wollen wir es für den Moment entfernen, da es keinen praktischen Unterschied und die Dinge nur konfuser macht.
Zurück zu unserer Geschichte. Entfernt man die Anpassung und setzt Gleichung (7) in Gleichung (8) ein, erhält man:
Ts = t5 * Solar^0.25 * e^(t1 * Ps ^ t2 + t3 * Ps ^ t4) (eqn 9)
Das ist faszinierend. Diese Burschen behaupten allen Ernstes, dass sie mit nur acht Datenpunkten und nicht weniger als fünf veränderbaren Parametern die Oberflächentemperatur der acht Planeten berechnen können, nur mit Kenntnis des Bodendrucks und der Sonneneinstrahlung. Und mit so vielen Drehknöpfen bin ich auch sicher, dass sie das tun können. Ich habe es selbst unter Verwendung ihrer Zahlen gemacht. Ich bekomme die gleichen Werte für alle Zahlen von t1 bis t5. Aber das beweist überhaupt nichts.
Ich meine … ich kann nur mit Bewunderung vor der schieren Unverfrorenheit dieser Behauptung stehen. Sie benutzen nur acht Datenpunkte und fünf veränderbare Parameter mit einer speziell gebildeten ad-hoc-Gleichung ohne physikalische Grundlage. Und sie denken nicht im Mindesten daran, wie merkwürdig dies ist.
Ich werde auf diese Frage der Anzahl der Parameter gleich noch einmal zurückkommen, denn obwohl es verblüffend ist, was sie hier gemacht haben, ist es nicht der Höhepunkt der Geschichte. Wir können Gleichung (7) auch auf etwas andere Art in Gleichung (8) einsetzen, indem wir den mittleren Term von Gleichung (7) verwenden. Das ergibt:
Ts = t5 * Solar^0.25 * Ts / Tgb (eqn 10)
Dies bedeutet: wenn wir mit der Kenntnis der Bodentemperatur Ts auf der rechten Seite der Gleichung anfangen, können wir Ts auf der linken Seite berechnen … erschreckend, ich weiß, wer hätte das gedacht. Wir wollen den Rest der Mathematik in Gleichung 10 checken, um zu sehen, warum das herauskommt.
Man kann bei näherem Hinsehen erkennen, dass der erste Teil der rechten Seite von Gleichung (10)
t5 * Solar^0.25
eine andere Form der bekannten Stefan-Boltzmann-Gleichung ist, die den Zusammenhang von Strahlung und Temperatur beschreibt. Diese S-B-Gleichung kann auch geschrieben werden als
T = (Solar / c1) ^ 0.25.
wobei T die Temperatur ist und c1 eine Konstante, die gleich ist der S-B-Konstanten multipliziert mit der Emissivität. Wir können das umschreiben zu
T = 1/(c1^0.25) * Solar^0.25
Setzt man eine andere Konstante c2 = 1/(c1^0.25) ergibt sich die Stefan-Boltzmann-Gleichung zu:
T = c2 * Solar^0.25
Aber das ist genau die Form des ersten Teils der rechten Seite von Gleichung (10). Oder auf den Punkt gebracht, es ist eine Approximation der Graukörper-Temperatur des Planeten Tgb.
Wir können das prüfen, und zwar wenn wir die Emissivität mit 0,9 annehmen, dann beträgt die Konstante c1 5,103E-8, und c2 daher 66. Allerdings reduziert sich dieser Wert durch die Rotation des Planeten. Mit Hilfe der N&Z-Formel in ihrem jüngsten Beitrag ergibt sich ein Wert um 27.
Ihr angepasster Wert ist 25, nicht weit vom tatsächlichen Wert. Also kommt komischerweise heraus, dass sie nichts anderes getan haben als die Stefan-Boltzmann-Konstante mit einer bizarren Methode der Kurvenanpassung abzuschätzen. Und das haben sie gut gemacht. Tatsächlich sogar ziemlich eindrucksvoll, wenn man die Anzahl der Rechenschritte und der involvierten Parameter bedenkt.
Aber da t5  * Solar^0.25 eine Schätzung der Graukörper-Temperatur des Planeten Tgb ist, bedeutet das, dass sich die Gleichung (10) reduziert, und zwar von
Ts = t5 * Solar^0.25 * Ts / Tgb (eqn 10)
zu
Ts = Tgb * Ts / Tgb.
Und schließlich zu
Ts = Ts
TA-DA!
Schlussfolgerung
Lassen Sie mich den zugrunde liegenden Effekt dessen wiederholen, was sie getan haben. Sie betrachteten acht Planeten und Monde.
1.      Sie haben eine Gleichung verwendet
e^(t1 * Ps ^ t2 + t3 * Ps ^ t4)
mit vier freien Parametern für eine Abschätzung von Ts/Tgb, basierend auf dem Bodendruck. Wie man unter der Tatsache erwarten würde, dass es halb so viele freie Parameter wie Datenpunkte gibt und dass sie freie Auswahl haben, irgendeinen davon für ihre Gleichung unbegrenzt auszusuchen, ist das überhaupt kein Problem und kann mit fast jeden Datensatz durchgeführt werden.
2.      Sie haben eine Gleichung verwendet
t5 * Solar^0.25
mit einem freien Parameter, um eine Schätzung von Tgb zusammenzubekommen, die auf der Gesamteinstrahlung des Planeten basiert. Da Tgb unter anderem von der planetarischen Einstrahlung abhängt, gibt es auch hier kein Problem.
3. Sie haben die beiden Schätzungen miteinander multipliziert. Da das Ergebnis eine Schätzung nach der Gleichung Tgb mal einer Schätzung von Ts/Tgb ist, hat das natürlich zur Folge, dass diese Operation Tgb aus der Gleichung hinauswirft.
4. Sie merken an, dass der Rest Ts ist, und erklären das zu einem WUNDER.
Sehen Sie, es wird Ts vorhergesagt, indem man bei Ts anfängt? Überhaupt nicht schwierig, und mit fünf freien Parametern und der Auswahl irgendeiner Gleichung, egal wie nicht-physischer Natur, ist das überhaupt kein WUNDER irgendeiner Art, sondern lediglich ein weiterer Fall einer zügellosen Kurvenanpassung…
Schließlich gibt es eine berühmte Geschichte in der Wissenschaft über diese Art der pseudowissenschaftlichen Verwendung von Parametern und Gleichungen, erzählt von Freeman Dyson:

Wir begannen mit der Berechnung der Mesonen-Protonen-Verteilung unter Verwendung einer Theorie der starken Kräfte, die als pseudoskalare Mesonentheorie bekannt ist. Im Frühjahr 1953 haben wir nach heroischen Bemühungen theoretische Graphen der Mesonen-Protonen-Verteilung geplottet. Wir haben mit Freuden festgestellt, dass unsere berechneten Zahlen ziemlich gut mit den von Fermi gemessenen Zahlen übereinstimmten. Also vereinbarte ich mit Fermi ein Treffen und zeigte ihm unsere Ergebnisse. Stolz fuhr ich im Greyhound-Bus [Greyhound, das führende nationale Busunternehmen in den USA. A. d. Übers.] von Ithaca nach Chicago mit einem Packen unserer theoretischen Graphen, um sie Fermi zu zeigen.
Als ich in Fermis Büro ankam, übergab ich ihm sofort die Graphen, aber er warf kaum einen Blick darauf. Er bat mich, Platz zu nehmen und fragte mich dann freundlich nach der Gesundheit meiner Frau und unseres neugeborenen Sohnes, der heute fünfzig Jahre alt ist. Dann gab er sein Urteil mit einer ruhigen Stimme ohne Höhen und Tiefen ab. Es gibt zwei Möglichkeiten, Berechnungen in theoretischer Physik durchzuführen“, sagte er. „Ein Weg, und zwar der, den ich bevorzuge, besteht darin, ein klares physikalisches Bild des Prozesses vor Augen zu haben, den man berechnet. Der zweite Weg besteht darin, einen präzisen und einen in sich widerspruchsfreien mathematischen Formalismus zu haben. Sie haben keins von beiden“.

Ich war ein wenig geschockt, wagte es aber, ihn zu fragen, warum er die pseudoskalare Mesonentheorie nicht als widerspruchsfreien mathematischen Formalismus sieht. Er erwiderte: „Die Quanten-Elektrodynamik ist eine gute Theorie, weil die Kräfte schwach sind, und wenn der Formalismus mehrdeutig ist, haben wir ein klares physikalisches Bild, das uns leitet. Hinsichtlich der pseudoskalaren Mesonentheorie gibt es kein klares physikalisches Bild, und die Kräfte sind so stark, dass nichts konvergiert. Um Ihre berechneten Ergebnisse zu erlangen mussten Sie frei wählbare Prozeduren [cut-off procedures] einführen, die weder auf solider Physik noch auf solider Mathematik basieren“.
Verzweifelt fragte ich Fermi, ob er nicht wegen der Übereinstimmung zwischen unseren berechneten Zahlen und seinen gemessenen Werten beeindruckt sei. Er erwiderte: „Wie viele frei wählbare Parameter haben Sie für Ihre Berechnungen verwendet?“
Ich dachte einen Moment nach und sagte: „Vier“.
Er sagte: Ich erinnere mich, wie mein Freund Johnny von Neumann zu sagen pflegte, mit vier Parametern kann ich einen Elefanten anpassen, und mit fünf kann ich ihn dazu bringen, mit seinem Rüssel zu wackeln“. Damit war die Unterhaltung beendet. Ich dankte Fermi für seine Zeit und seine Bemühungen und nahm traurig den nächsten Bus zurück nach Ithaca, um den Studenten die schlechten Nachrichten zu überbringen.

Die Gleichung von Nikolov und Zeller enthält fünf Parameter und nur acht Datenpunkte. Wenn ich sagte, dass es kein WUNDER ist, dass sie den Elefanten mit seinem Rüssel wackeln lassen, sondern ein zu erwartendes und triviales Ergebnis ihrer betrügerischen Prozeduren ist, dann habe ich damit alles gesagt.
P.S. – Es gibt natürlich eine technische Bezeichnung für das, was sie getan haben, da es keine neuen Fehler unter der Sonne gibt. Man nennt es „Überanpassung“. Laut Wikipedia: „Überanpassung erfolgt immer dann, wenn ein Modell exzessiv komplex ist, zum Beispiel wenn man zu viele Parameter im Verhältnis zur Anzahl der Beobachtungen hat.“ Fünf Parameter ist ein viel, viel zu großes Verhältnis zu acht Datenpunkten, das ist garantiert überangepasst.
P.P.S. – Ein Problem mit der WUNDERgleichung von N&Z liegt darin, dass sie sie in keiner Weise statistisch getestet haben.
Ein Weg, um zu sehen, ob ihre Anpassung wenigstens vage gültig ist, besteht darin, einige Datenpunkte außen vor zu lassen und die Anpassung noch einmal vorzunehmen. Natürlich ist das mit nur acht Datenpunkten problematisch… aber in jedem Falle kommen die angepassten Parameter radikal unterschiedlich heraus, wenn man das macht, und das weckt viele Zweifel an der Anpassung. Ich ermutige N&Z, das zu tun und über die Ergebnisse zu berichten. Ich werde es tun, aber sie glauben mir nicht, also was soll das?
Ein anderer Weg, ihre Anpassung zu überprüfen, besteht darin, den Datensatz zu halbieren und die eine Hälfte anzupassen und die Ergebnisse mit der anderen Hälfte zu überprüfen. Dies ist so, weil angepasste Gleichungen von der Art, wie sie N&Z verwendet haben, dafür bekannt sind, „außerhalb des Bereichs“ nur sehr bedingt gültig zu sein, das heißt auf Daten, die nicht verwendet wurden, um die Parameter anzupassen. Hat man lediglich acht Datenpunkte und vier Parameter in Gleichung (7), ist dies natürlich wieder problematisch, weil man bei der Teilung des Datensatzes durch zwei genauso viele Parameter wie Datenpunkte hat … nun könnte man denken, dass dies ein Hinweis darauf ist, dass das Verfahren lückenhaft ist, aber was weiß ich schon, ich wurde gestern geboren. In jedem Falle ermutige ich N&Z, auch diesen Test durchzuführen. Meine Ergebnisse eines solchen Tests sagen, dass ihre Anpassung bedeutungslos ist, aber vielleicht sind ja ihre Testergebnisse unterschiedlich.
Aktualisierung Einer der Kommentatoren unten sagte:
Willis – mach weiter – passe einen Elefanten an. Bitte!
Ernsthaft, N&Z zeigen nur mit Hilfe der Algebra, was in Experimenten beobachtet worden ist, nämlich dass das Erwärmen eines Gases in einem geschlossenen Behälter zur Erhöhung sowohl des Drucks als auch der Temperatur führt.
OK, hier kommt meine Nachbildung der Oberflächentemperatur unter Verwendung von nichts weiter als den Daten in der Darstellung von N&Z bzgl. der Eigenschaften planetarischer Körper:

Abbildung 1: Willis’ Nachbildung der Oberflächentemperatur planetarischer Körper.
Meine Gleichung enthält eine Variable mehr und zwei Parameter weniger als die Gleichung von N&Z. Zur Erinnerung, ihre Gleichung lautete:
Ts = 25.3966 * Solar^0.25 * e^(0.233001 * Pressure ^ 0.0651203 + 0.0015393 * Pressure ^ 0.385232)
Meine Gleichung andererseits sieht so aus:
Ts = 25.3966 * Solar^0.25 * e^(0.233001 * Pressure ^ 0.0651203 + 0.0015393 * Pressure ^ 0.385232)
Man beachte, dass ich absolut nicht behaupte, dass die Temperatur durch Dichte und Schwerkraft bestimmt wird. Ich zeige lediglich, dass die Anpassung einiger Punkte mit einigen Variablen und einigen Parametern überhaupt nicht schwierig ist. Es zeigt auch, dass man die Antwort auch ganz ohne Verwendung des Bodendrucks erhalten kann. Und schließlich zeigt es, dass weder meine Nachbildung noch die Nachbildung planetarischer Temperaturen von N&Z auch nur einen Pfifferling wert ist!*
*Im Original steht hier ein Kraftausdruck, den ich lieber nicht direkt übersetzen möchte! A. d. Übers.
2. Aktualisierung Ich habe mir gedacht, dass ich nach den Wundern, die ich mit der Wundergleichung von N&Z angestellt hatte, hier nicht aufhören sollte. Ich sollte schauen, ob ich sie nicht mit ihren eigenen Spielregeln schlagen könnte und ein einfacheres Wunder zu tun. Hier nochmal ihre Gleichung:
Ts = 25.3966 * Solar^0.25 * e^(0.233001 * Pressure ^ 0.0651203 + 0.0015393 * Pressure ^ 0.385232)
Meine vereinfachte Version ihrer Gleichung sieht so aus:
Ts = 25.394 * Solar^0.25 * e^(0.092 * Pressure ^ 0.17)
Komischerweise enthält meine vereinfachte Version einen etwas geringeren RMS-Fehler als die Version von N&Z, also habe ich sie wirklich mit ihren eigenen Spielregeln geschlagen. Meine Gleichung ist nicht nur einfacher, sie ist auch genauer. Es steht ihnen frei, meine vereinfachte Wundergleichung zu benutzen, ohne Honorar. Hier sind die Anpassungen:

Abbildung 2 Eine einfachere Version der Gleichung 8 von N&Z
Wieder behaupte ich nicht, dass dies die Dinge verbessert. Die bloße Tatsache, dass ich das mit zwei einstellbaren Parametern weniger tun kann (drei anstatt fünf), heißt nicht, dass sie nicht überangepasst ist.
Sowohl die vereinfachte als auch die kompliziertere Form der Gleichungen von N&Z sind nichts weiter als eine Kurvenanpassung. Dies wird durch die Tatsache belegt, dass wir bereits drei einfache und sehr unterschiedliche Gleichungen haben, die die planetarischen Temperaturen bestimmen. Das ist das Gute an einer angepassten Gleichung – wenn man schlau ist, kann man Vieles mit nur etwas finden … aber DAS HEISST NICHT, DASS DER DRUCK DIE TEMPERATUR BESTIMMT .
Zum Beispiel kann ich das gleiche tun, ganz ohne den Druck, sondern stattdessen die Dichte zu verwenden. Diese Gleichung sieht so aus:
Ts = 25.491 * Solar^0.25 * e^(0.603 * Density ^ 0.201)
Und hier sind die Ergebnisse:

Abbildung 3: Eine Nachbildung der planetarischen Temperaturen unter Verwendung der Dichte anstelle des Drucks.
Heißt das jetzt, dass die planetarische Temperatur wirklich von der Dichte abhängt? Natürlich nicht, das Ganze ist eine Übung zur Anpassung von Kurven.
Link: http://wattsupwiththat.com/2012/01/23/the-mystery-of-equation-8/
Eine ausführliche Erwiderung samt Klarstellung der von W. Eschenbach angegriffenen Autoren finden Sie hier http://tallbloke.wordpress.com/2012/02/09/nikolov-zeller-reply-eschenbach/
Mit Dank an Leser Kieser!
Übersetzt von Chris Frey
* Der berühmte Mathematiker und Erfinder der modernen Computerarchitektur John v. Neumann pflegt zu sagen:"Geben Sie mir vier Variable und ich baue ihnen damit einen Elefanten. Geben Sie mir eine fünfte, dann wackelt er auch noch mit dem Rüssel".

Meerestemperatur auf tausendstel Grad bestimmt? Ein Ozean übermäßigen Vertrauens!

geschrieben von Willis Eschenbach | 1. September 2012

Bild rechts: Aus Levitus 2012. Der obere Graph zeigt die Änderungen des Wärmegehalts der Ozeane mit der Einheit 1022 Joules. Die unteren Graphen zeigen die Datenmenge.
Nun gibt es in dieser Graphik einige Merkwürdigkeiten. Zum Einen fangen die Daten im Jahr 1957,5 an, vermutlich weil der Wert eines jeden Jahres tatsächlich der zentrale Wert eines fünf-Jahres-Mittels ist… Was mich allein schon nervös macht, sehr nervös. Warum zeigt man nicht die tatsächlichen jährlichen Daten? Was versteckt sich hinter den Mittelwerten?
Am interessantesten für mich sind jedoch die Fehlerbalken. Um die Angaben zum Wärmegehalt zu ermitteln, messen sie tatsächlich die Wassertemperatur. Dann übertragen sie dessen Änderungen in Änderungen des Wärmegehaltes. Um also die zugrunde liegenden Messungen zu verstehen, habe ich den Graph aus der Abbildung oben rechts, der den Wärmegehalt in den Ozeanen in einer Tiefe von 0 bis 2000 m zeigt, in Einheiten der Temperatur zurück übertragen. Das Ergebnis hiervon zeigt die folgende Abbildung:

Verlauf der Anomalie des ozeanischen Wäörmegehaltes von 0 bis 2000 m aus dem Bild oben rechts mit Einheiten konvertiert zu Grad Celsius. Man beachte, dass die Gesamtänderung während der ganzen Periode 0,09°C beträgt, was mit der in ihrer Studie genannten Gesamtänderung überein stimmt.
Das Problem, das ich mit dieser Graphik habe, ist Folgendes: Es wird behauptet, dass wir die Temperatur der oberen zwei Kilometer des Ozeans von 1955 bis 1960 mit einem Fehler von plus/minus eineinhalb Hundertstel Grad Celsius kennen…
Es wird auch behauptet, dass wir gegenwärtig die Temperatur der oberen 2 Kilometer der globalen Ozeane, einer Wassermenge von 673.423.330.000.000.000 Tonnen (673 Quadrillionen Tonnen), mit einem Fehler von plus/minus zwei Tausendstel Grad Celsius kennen…
Tut mir leid, aber das nehme ich ihnen nicht ab. Ich weiß nicht, wie sie ihre Fehlerbalken berechnen, aber das ist einfach unmöglich. Man frage irgendeinen Prozessingenieur. Wenn man etwas so Geringes wie einen Swimmingpool mit Olympia-Ausmaßen voller Wasser bis auf zwei Tausendstel Grad genau messen will, braucht man eine ganze Handvoll Thermometer. Lediglich ein oder zwei wären dafür viel zu wenig. Und die oberen zwei Kilometer der globalen Ozeane sind unvorstellbar viel, mit einem Volumen von 260.700.000.000.000 Schwimmbecken mit Olympia-Ausmaßen…
Ich weiß also nicht, woher sie ihre Fehlerangaben haben… aber ich gehe jede Wette ein, dass sie die Fehler in ihren Berechnungen weit unterschätzt haben.
Willis Eschenbach
PS – eine letzte Merkwürdigkeit. Sollte die Erwärmung der Ozeane durch zunehmendes CO2 getrieben sein und die Zunahme der Oberflächentemperatur den Behauptungen der Autoren entsprechen, warum haben sich dann die Ozeane von 1978 bis 1990 nicht im Mindesten erwärmt, obwohl doch der CO2-Gehalt angestiegen ist und die Lufttemperatur zugenommen hat?
PPS – Bonus-Frage. Nehmen wir an, wir haben ein Olympia-Schwimmbecken und ein perfekt genaues Thermometer an einer Stelle im Becken. Nehmen wir weiter an, dass wir eine Messung pro Tag vornehmen. Wie lange muss man dann eine Messung pro Tag vornehmen, bis man die Temperatur des gesamten, mit Wasser gefüllten Schwimmbeckens auf zwei tausendstel Grad Celsius kennt?
Link: http://wattsupwiththat.com/2012/04/23/an-ocean-of-overconfidence/#more-61861
Übersetzt von Chris Frey EIKE

Und immer wieder grüßt das Murmeltier! – Der NAS-Bericht

geschrieben von Willis Eschenbach | 1. September 2012

Im Besonderen war es unsere Aufgabe

1. die primären Voraussetzungen zu finden, auf denen unser gegenwärtiges Verständnis der Frage (der Klimaeffekte des CO2) basiert,

2. quantitativ die Eignung und die Ungewissheit unseres Wissens über diese Faktoren zu bestimmen, und
3. präzise und objektiv das gegenwärtige Verständnis in Sachen Klima/Kohlendioxid für politische Entscheidungsträger zu beschreiben.

Nun, das klingt alles ziemlich vernünftig. Tatsächlich wären wir ein riesiges Stück weiter als jetzt, wenn wir die Antworten auf diese Fragen kennen würden.

Bild rechts: Der neue Cray-Supercomputer „Gaea“, der kürzlich bei der National Oceanic and Atmospheric Administration NOAA installiert worden ist. Er wird zur Simulation von Klimamodellen benutzt werden.

Aber wie sich heraus stellte, hat sich die aus AGW unterstützenden Klimawissenschaftlern bestehende Arbeitsgruppe der NAS entschlossen, es besser zu wissen. Sie verkündeten, dass es zu schwierig wäre und zu lange dauern würde, die gestellten Fragen zu beantworten.

Das ist schon in Ordnung. Manchmal stellt man Wissenschaftlern Fragen, die zu beantworten ein Jahrzehnt dauern würde. Und das ist es auch, was diese Wissenschaftler ihren politischen Herren sagen sollten – können wir nicht, dauert zu lange. Aber neeeiiiin…, sie wissen es besser, so dass sie sich entschlossen haben, stattdessen eine andere Frage vollständig zu beantworten. Nach der Auflistung der Gründe, warum diese ihnen gestellten Fragen zu beantworten zu schwierig war, sagten sie (Hervorhebung von mir):

„Eine vollständige Beschreibung all dieser Dinge wäre eine lange und schwierige Aufgabe.

Es ist jedoch plausibel, mit einer einzigen grundlegenden Frage zu beginnen: Falls wir wirklich sicher wären, dass das atmosphärische Kohlendioxid in bekanntem Rahmen zunehmen würde, wie gut können wir dann die Konsequenzen für das Klima projizieren?“

Oooookaaaay … Ich denke, dass dies jetzt die neue post-normale wissenschaftliche Methode ist. Erstens geht man davon aus, dass das zunehmende CO2 „Konsequenzen für das Klima” hat. Danach schaut man, ob man diese „Konsequenzen projizieren“ kann.

Sie haben recht, dass dies leichter zu bewerkstelligen ist als tatsächlich klar zu stellen, OB es klimatische Konsequenzen gibt. Es wird so viel einfacher, wenn man einfach annimmt, dass das CO2 das Klima treibt. Hat man einmal diese Antwort, werden die Fragen viel einfacher…

Immerhin haben sie zumindest versucht, ihre eigene Frage zu beantworten. Und was haben sie herausgefunden? Nun, angefangen haben sie hiermit:

„Wir schätzen die wahrscheinlichste globale Erwärmung bei einer Verdoppelung des CO2-Gehaltes auf nahe 3°C mit einem möglichen Fehler von ± 1.5°C.“

Bis hier also keine Überraschung. Sie weisen darauf hin, dass diese Schätzung natürlich von Klimamodellen stammt. Überraschend jedoch stellen sie dazu keine Frage und sind sich auch nicht unsicher darüber, ob die Klimamodelle auf der gleichen Wellenlänge liegen. Sie sagen (Hervorhebung durch mich):

„Da die Bewölkung individuell unter der Gitterpunktsweite der allgemeinen Zirkulationsmodelle liegt, müssen Wege gefunden werden, die Gesamtbewölkungsmenge in Beziehung zu den Gitterpunktsvariablen zu stellen. Bestehende Parametrisierungen der Wolkenmenge sind physikalisch sehr grob. Wenn empirische Anpassungen der Wolkenmenge in den allgemeinen Zirkulationsmodellen zur Erreichung von Plausibilität vorgenommen werden, könnten die Modellergebnisse mit dem gegenwärtigen Klima verglichen werden. Aber ein solches Trimmen durch sich selbst garantiert nicht, dass die Reaktion der Bewölkung auf Änderungen der CO2-Konzentration auch getrimmt ist. Daher muss betont werden, dass die Modellierung der Wolken eines der schwächsten Glieder in den Rechnungen der Zirkulationsmodelle ist.“

Die Modellierung der Wolken ist eines der schwächsten Glieder… da kann ich nicht widersprechen.

Wie ist also der derzeitige Stand hinsichtlich der Klimarückkopplung? Die Autoren sagen, dass die positive Rückkopplung des Wasserdampfes jedwede negativen Rückkopplungen überkompensiert:

„Wir haben sorgfältig alle negativen Rückkopplungsmechanismen untersucht, wie z. B. Zunahmen tiefer und mittelhoher Wolken, und sind zu der Schlussfolgerung gekommen, dass die Vereinfachungen und Ungenauigkeiten in den Modellen wahrscheinlich die grundlegende Schlussfolgerung nicht beeinträchtig haben, dass es eine merkliche Erwärmung geben wird. Die bekannten negativen Rückkopplungsmechanismen können die Erwärmung reduzieren, scheinen aber nicht so stark wie die positive Rückkopplung durch die Feuchtigkeit zu sein.“

Wie es jedoch seit Jahren der Fall ist, wenn man zum tatsächlichen Abschnitt des Berichtes kommt, in dem die [Rolle der] Wolken behandelt wird (die wesentliche negative Rückkopplung), wiederholt der Bericht lediglich, dass die Wolken kaum verstanden und kaum repräsentiert sind… wie soll das gehen, dass sie sich dann der positiven Rückkopplung so sicher sind, aber die negative Rückkopplung nicht verstehen und nur sehr vage repräsentieren können? Sie sagen zum Beispiel:

„Wie wichtig alles in allem die Auswirkungen der Wolken ist, ist jedoch eine sehr schwierig zu beantwortende Frage. Die Verteilung der Bewölkung ist ein Ergebnis des gesamten Klimasystems, in dem es viele weitere Rückkopplungen gibt. Vertrauenswürdige Antworten können nur durch die flächendeckende numerische Modellierung der allgemeinen Zirkulationen der Atmosphäre und der Ozeane gegeben werden, zusammen mit dem Vergleich der beobachteten mit den simulierten Wolkentypen und –mengen.“

Mit anderen Worten, sie wissen es nicht, sind sich aber sicher, dass die Gesamtbilanz positiv ist.

Hinsichtlich der Fähigkeit der Modelle, genau regionale Klimata zu reproduzieren heißt es in dem Bericht:

„Gegenwärtig können wir nicht genau die Details regionalen Klimas simulieren und daher auch nicht zuverlässig die Örtlichkeiten und Intensitäten regionaler Klimaänderungen vorhersagen. Es wird erwartet, dass sich diese Lage durch das zunehmende wissenschaftliche Verständnis und schnellere Computer allmählich verbessern wird.“

Da haben wir es! Die Klimasensitivität beträgt 3°C pro Verdoppelung des CO2-Gehaltes mit einem Fehler von ± 1.5°C. Die Gesamtrückkopplung ist positiv, obwohl wir [das Verhalten der] Wolken nicht verstehen. Die Modelle sind noch nicht in der Lage, regionales Klima zu simulieren. In keiner dieser Aussagen steckt irgendetwas Überraschendes. Es ist genau das, was man von einer Kommission der NAS erwartet.

Bevor ich hier weitergehe – da der NAS-Bericht auf Computermodellen beruht, möchte ich einen kleinen Exkurs machen und einige Fakten über Computer auflisten, welche mich seit langer Zeit fasziniert haben. So lange ich mich erinnern kann, wollte ich einen eigenen Computer haben. Als kleines Kind träumte ich davon, einen zu haben. Ich spreche ziemlich gut ein halbes Dutzend Computersprachen, und es gibt noch mehr, die ich vergessen habe. Mein erstes Computerprogramm habe ich im Jahr 1963 geschrieben.

Das Verfolgen der Änderungen dessen, was Computer inzwischen alles können, war erstaunlich. 1979 war der schnellste Computer der Welt der Cray-1-Supercomputer. Dessen Fähigkeiten lagen weit jenseits dessen, wovon die meisten Wissenschaftler je geträumt haben. Er hatte 8 MB Speicher, 10 GB Platz auf der Festplatte und lief mit 100 MFLOPS (Millionen Operationen pro Sekunde). Der Computer, auf dem ich dies schreibe, hat 1000 mal so viel Speicherplatz, fünfzig mal so viel Platz auf der Festplatte und 200 mal die Geschwindigkeit von Cray-1.

Und das ist nur der Computer auf meinem Schreibtisch. Der neue Supercomputer der NASA „Gaea“ auf dem Bild oben rechts läuft zweieinhalb Millionen mal schneller als die Cray-1. Dies bedeutet, dass Cray-1 für eine Ein-Tages-Simulation auf „Gaea“ etwa siebentausend Jahre brauchen würde…

Warum aber ist die Geschwindigkeit eines Cray-1-Computers für den NAS-Bericht von Bedeutung, aus dem ich oben zitiert habe?

Es ist von Bedeutung, weil – wie Einige von Ihnen vielleicht bemerkt haben – der NAS-Bericht, aus dem ich oben zitiert habe, der „Charney Report“ genannt wird. So weit ich weiß, war es der erste Bericht der NAS zur CO2-Frage. Und wenn ich davon als einem „kürzlichen Bericht“ spreche, dachte ich darüber in historischer Bedeutung. Er wurde 1979 veröffentlicht.

Und das ist das Bizarre hier, der Elefant auf dem Gebiet der Klimawissenschaft. Der Charney-Report hätte gestern geschrieben worden sein können. Die AGW-Befürworter stellen immer noch die gleichen Behauptungen auf, als ob seitdem überhaupt nichts passiert wäre. Zum Beispiel sagen die AGW-Befürworter genau wie damals das Gleiche über die Wolken wie 1979 – sie geben zu, dass sie das Verhalten der Wolken nicht verstehen, dass sie das größte Problem in den Modellen sind, aber dass sie immer noch genauso sicher sind, dass die Gesamtrückkopplung positiv ist. Ich weiß nicht, wie das geht, aber so war es unverändert seit 1979.

Das ist das Kuriose für mich – wenn man den Charney-Bericht liest, wird offensichtlich, dass sich beinahe nichts auf diesem Gebiet seit 1979 geändert hat. Es gab keine wissenschaftlichen Durchbrüche, kein wesentlich neues Verständnis. Die Leute stellen immer noch die gleichen Behauptungen auf über die Klimasensitivität mit fast keinen Änderungen in den riesigen Fehlergrenzen. Die Bandbreite variiert immer noch um einen Faktor drei, von 1,5°C bis 4,5°C pro Verdoppelung des CO2-Gehaltes.

Inzwischen hat die Computerleistung bis weit jenseits der wildesten Vorstellungen zugenommen. Das gilt auch für den Umfang der Klimamodelle. Die Klimamodelle im Jahr 1979 bestanden aus eintausend codierten Zeilen. Die modernen Modelle enthalten Millionen von Zeilen. Damals wurde die Atmosphäre nur mit wenigen Schichten und großen Gitterquadraten modelliert. Heute haben wir vollständig gekoppelte Ozean-Atmosphäre-Cryosphäre-Biosphäre-Lithosphäre-Modelle mit viel kleineren Gitterquadraten und dutzenden Schichten sowohl in der Atmosphäre als auch in den Ozeanen.

Und seit 1979 hat sich eine ganze Klimaindustrie gebildet, die Millionen menschlicher Arbeitsstunden aufgewandt hat, um die Leistung der Computer zum Studium des Klimas zu verbessern.

Und nach den Millionen Stunden menschlicher Bemühungen, nach den Millionen und Abermillionen Dollar, die in die Forschung gesteckt worden waren, nach all der millionenfachen Zunahme der Computerleistung und –größe, und nach der phänomenalen Zunahme der Verfeinerung und des Detailreichtums der Modelle… nach all dem hat sich die Unsicherheit der über den Daumen gepeilten Klimasensitivität nicht signifikant verkleinert. Sie liegt immer noch um 3 ± 1.5°C pro Verdoppelung des CO2, genau wie 1979.

Und das gilt auch für die meisten anderen Fronten der Klimawissenschaft. Wir verstehen immer noch nichts von den Dingen, die vor einem Dritteljahrhundert schon mysteriös waren. Nach all den gigantischen Fortschritten bzgl. der Modellgeschwindigkeit, deren Größe und Detailreichtum können wir immer noch nichts Definitives über die Wolken sagen. Wir haben keine handhabe hinsichtlich der Gesamtrückkopplung. Es ist, als ob der ganze Bereich der Klimawissenschaft in einer Zeitfalle 1979 stecken geblieben ist und sich seitdem nirgendwohin bewegt hat. Die Modelle sind tausendfach größer und tausendfach schneller und tausendfach komplexer – aber sie sind für regionale Vorhersagen immer noch unbrauchbar.

Wie kann man dieses überwältigende Fehlen jeglichen Fortschritts verstehen, diese intensive Arbeit während eines Drittels des Jahrhunderts mit einem so geringen Ergebnis?

Für mich gibt es nur eine Antwort. Der fehlende Fortschritt bedeutet, dass es einige fundamentale Missverständnisse in den Grundmauern des modernen Klimagebäudes gibt. Er bedeutet, dass das zugrunde liegende Paradigma, auf dem das Gebäude fußt, einige grundlegende und weitreichende theoretische Fehler aufweisen muss.

Jetzt können wir darüber debattieren, worin dieses fundamentale Missverständnis besteht.

Aber ich sehe keine andere sinnvolle Erklärung dafür. In jedem anderen Bereich der Wissenschaft gab es seit 1979 enorme Fortschritte. Neue Forschungsfelder tauchten auf, und ältere Forschungsbereiche sind voran gekommen. Genetik und Nanotechnologie und Proteomik und Optik und Kohlenstoffchemie und all die anderen… außer der Klimawissenschaft.

Das ist der Elefant im Raum – das unglaubliche Fehlen von Fortschritten in diesem Bereich trotz eines Dritteljahrhunderts intensiven Studiums.

Nach meiner Einschätzung besteht das fundamentale Missverständnis darin, dass die Lufttemperatur an der Erdoberfläche eine lineare Funktion des Antriebs ist. Datum war es verheerend für die Charney-Leute, die falsche Frage zu beantworten. Sie haben mit der Hypothese begonnen, dass eine Änderung des Antriebs zu einer Änderung der Temperatur führen würde, und fragten sich: „wie gut können wir die klimatischen Konsequenzen projizieren?“

Wenn man das einmal getan hat, wenn man einmal CO2 für den Schuldigen hält, hat man das Verstehen des Klimas als Wärmemaschine außen vor gelassen.

Wenn man das einmal getan hat, hat man den Gedanken ausgeschlossen, dass das Klima wie alle Strömungssysteme bevorzugte Stadien hat und dass es nach dem Erreichen maximaler Entropie strebt.

Wenn man das einmal getan hat, hat man all die zahlreichen thermostatischen und homöostatischen [?] Mechanismen ausgeschlossen, die in zahlreichen räumlichen und zeitlichen Scales wirken.

Und wie sich herausstellt, wenn man das einmal getan hat, wenn man einmal die Hypothese aufgestellt hat, dass die Oberflächentemperatur eine lineare Funktion des Antriebs ist, hat man jeden Fortschritt in diesem Bereich ausgeschlossen, bis dieser Irrtum behoben ist.

Aber das ist lediglich meine Ansicht. Sie könnten eine andere Erklärung für das fast vollständige Fehlen jedweden Fortschritts in der Klimawissenschaft während des letzten Drittels des vorigen Jahrhunderts finden. Falls das so ist, heiße ich alle freundlichen Kommentare willkommen. Erlauben Sie mir Sie zu bitten, dass Ihre Kommentare kurz, klar und interessant sind.

Willis Eschenbach (abgekürzt w.)

P.S. – Bitte vergleichen sie dieses Fehlen von Fortschritten nicht mit so etwas wie bei der Kernfusion. Anders als die Klimawissenschaft ist das ein praktisches Problem und ein teuflisch komplexes. Die Herausforderung besteht hier darin, etwas zu bauen, dass es in der Natur nie zuvor gegeben hat – eine Flasche, die die Sonne hier auf der Erde einfangen kann.

Klima andererseits ist eine theoretische Frage und keine Herausforderung, etwas zu bauen.

P.P.S. – …

[man schaue im Original nach den paar Zeilen, die hier noch fehlen. Dann wird klar, warum aus Zeitgründen auf deren Übersetzung hier verzichtet wird. A. d. Übers.]

Link: http://wattsupwiththat.com/2012/03/07/under-the-radar-the-nas-report/#more-58606

Übersetzt von Chris Frey EIKE