Sehr starke graphische Beweise für den Stillstand (Teil 2)

geschrieben von Sheldon Walker | 29. Februar 2016

Die von mir entwickelten Verfahren erlauben es, große Mengen von Trends rasch zu analysieren und die Ergebnisse graphisch oder in Form einer Tabelle zu zeigen. Ein Trend weist 4 Haupt-Attribute auf: ein Start- und Endzeitpunkt, eine Länge und eine Neigung (wobei im Falle der globalen Erwärmung die Neigung den Erwärmungstrend zeigt). In meinem ersten Artikel habe ich Graphiken mit dem Vergleich von Erwärmungsraten und Trendlänge gezeigt, aber jedes der 4 Attribute kann graphisch gegen jedes andere aufgetragen werden.

Die meisten Menschen denken, dass die Graphiken gut aussehen, aber ich untersuche immer noch, ob die Graphiken eigentlich für die Analyse globaler Erwärmung brauchbar sind. Das könnte einfach nur ein Blickfang sein, aber ich hoffe, dass sie sich für irgendetwas als nützlich erweisen.

Nach meinem ersten Beitrag beschloss ich, MTA anzuwenden in dem Versuch zu beweisen, dass der Stillstand existiert. Ich wollte eine Graphik des Intervalls, in dem der Stillstand existiert, mit einer Graphik des Intervalls vergleichen, in dem der „Stillstand“ nicht existiert (ein Referenz-Intervall). Falls es einen signifikanten Unterschied gäbe und es die richtige Art Differenz wäre (z. B. eine geringere Erwärmungsrate), dann hätte ich gute Beweise dafür, dass der Stillstand existiert.

Das Auswählen der richtigen Intervalle war wichtig. Aus meinen früheren Untersuchungen bzgl. des Stillstands wusste ich, dass die Kernjahre der Zeitraum von 2002 bis 2013 waren. Dies ist ein 12-Jahre-Intervall mit einer sehr geringen Erwärmungsrate. Das Verschieben des Startzeitpunktes nach 2001 ließ die Erwärmungsrate geringfügig zunehmen, ergaben aber einen längeren und etwas schwächeren Stillstand. Die Verschiebung des Startzeitpunktes nach 2000 ließ die Erwärmungsrate noch mehr zunehmen, ergab aber einen sogar noch längeren Stillstand. Das Verschieben des Endzeitpunktes nach 2014 ließ die Erwärmungsrate ebenfalls zunehmen, und die Verschiebung nach 2015 schwächte den Stillstand deutlich, und zwar wegen des El Nino 2015.

Also hatte ich eine begrenzte Bandbreite von Jahren bzgl. des Stillstandes. Ich wusste, dass es seit 1975 eine konsistente Erwärmung gegeben hatte, so dass mein stillstandsfreies Intervall im Jahr 1975 oder danach beginnen musste. Von 1975 bis 2015 sind es 41 Jahre. Die ersten 25 Jahre oder so zeigten definitiv Erwärmung, danach begann der Stillstand. Es wäre am besten, wenn mein stillstandsfreies Referenzintervall genauso lang wäre wie das Stillstands-Intervall, weil ich Äpfel mit Äpfeln vergleichen wollte. Schließlich habe ich die 41 Jahre in 3 X 13 + 2 Jahre aufgeteilt. Dies ergab 2 stillstandsfreie Intervalle von jeweils 13 Jahren, eines von Januar 1975 bis Dezember 1987 und ein weiteres von Januar 1988 bis Dezember 2000). Außerdem ergab sich jetzt das 13 Jahre umfassende Stillstands-Intervall von Januar 2001 bis Dezember 2013. Dies passte gut zu meinen Gedanken bzgl. des Stillstands und gab mir zwei Referenzperioden, mit denen man es vergleichen konnte. Außerdem war es gut, dass man die beiden Referenzintervalle untereinander vergleichen konnte um zu sehen, ob diese konsistent waren. Ich habe mal die Jahre 2014 und 2015 außen vor gelassen, weil ich wusste, dass diese den Stillstand abschwächen. Um diese beiden Jahre konnte man sich auch später noch kümmern, falls ich Beweise für die Existenz des Stillstands finden würde.

Ich habe die MTA durchgeführt und die Ergebnisse graphisch dargestellt. Normalerweise schaue ich nicht auf Trends kürzer als 10 Jahre, weil sie weniger stabil sind. Allerdings gab mir die Verwendung von 13-Jahre-Intervallen nur Trends von 10 bis 13 Jahren. Die Graphiken zeigten, was ich sehen wollte, aber sie waren etwas „dünn“. Ich führte die Analyse noch einmal durch, diesmal mit einer mittleren Trendlänge von 8 Jahren, und erhielt deutlich stabilere Graphiken.

Ich sollte rasch noch erwähnen, dass alle Daten aus den NOAA-Datenreihen der kombinierten Festlands- und Ozeantemperatur stammen. Ich werde meine Analyse mit den Daten anderer Temperaturreihen wiederholen, wenn ich Zeit dazu habe, aber ich dachte, dass die Verwendung der NOAA-Daten geeignet war angesichts des Umstandes, dass sie einen Ruf als „Stillstands-Zerstörer“ hat.

Zunächst werde ich die drei ganzen Streu-Graphiken individuell zeigen, eines für jedes Intervall. Diese eignen sich gut, um deren Form zu untersuchen, die Erwärmungsraten für unterschiedliche Trendlängen zu checken und einen guten Hinweis auf die Gesamt-Erwärmungsrate zu bekommen. Der am weitesten rechts liegende Punkt in jeder Graphik korrespondiert mit einer linearen Regression über das gesamte Intervall.

Danach werde ich eine einzelne Graphik zeigen, welche die gleichen drei Intervalle enthält, jedoch geplottet als Umrisse einer einzelnen Graphik. Damit lassen sich die verschiedenen Intervalle viel besser miteinander vergleichen. Die Farbe eines Umriss-Graphen ist die gleiche wie von der gesamten Streu-Graphik des Intervalls.

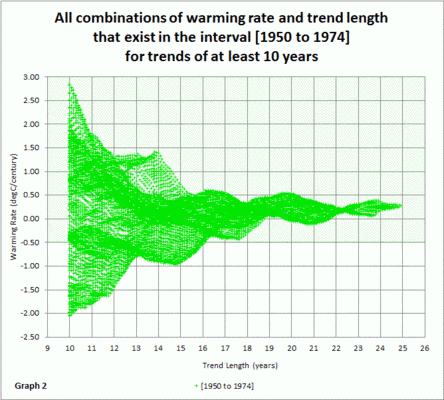
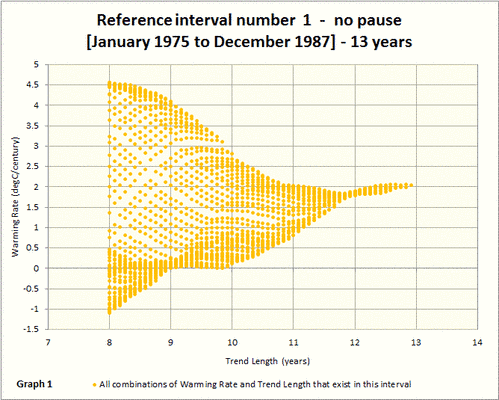
Hier folgt die MTA-Graphik des ersten stillstandsfreien Intervalls von Januar 1975 bis Dezember 1987:

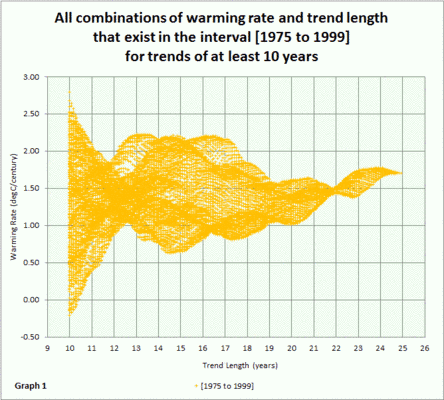
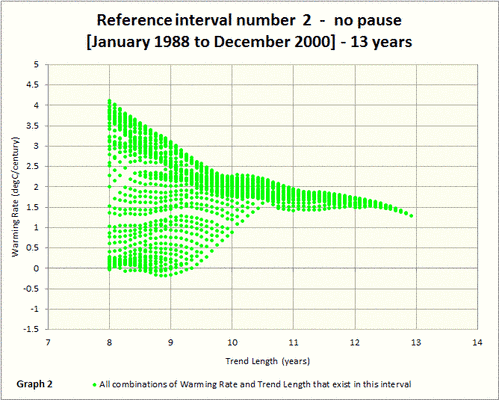
Und hier die MTA-Graphik für das zweite stillstandsfreie Intervall Januar 2001 bis Dezember 2013:

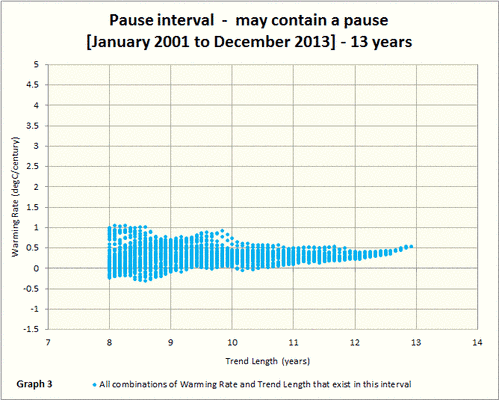
Hier die MTA-Graphik für das dritte Intervall, welches die Pause enthält (Januar 2001 bis Dezember 2013:

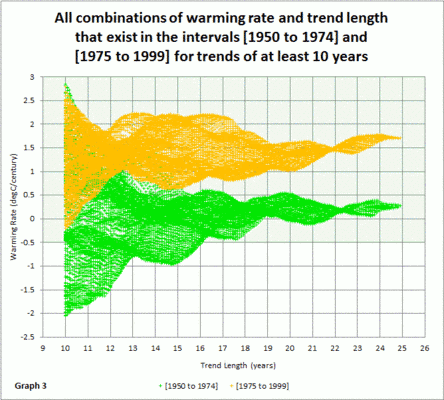
Und hier nun die Umriss-Graphik mit allen drei Intervallen, jede mit der gleichen Farbe wie für die vorige Graphik für das Intervall:

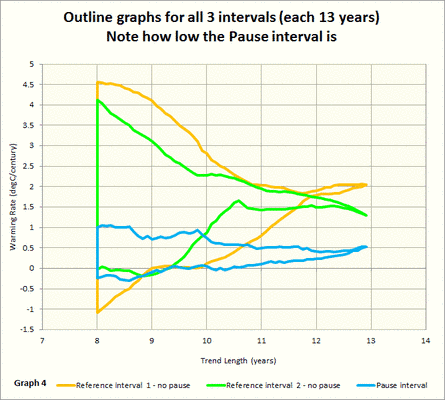
Ich glaube, dass die Ergebnisse deutlich aus den Graphiken hervorgehen, aber ich möchte einige wenige Aspekte aus der Umriss-Graphik erwähnen.

Man beachte, dass die beiden Referenz-Intervalle ziemlich gut übereinstimmen. Die erste in orange zeigt eine Erwärmungsrate etwas über 2°C pro Jahrhundert. Die Erwärmungsrate scheint zum rechten Ende hin leicht zuzunehmen.

Das zweite Referenzintervall in grün zeigt eine Gesamt-Erwärmungsrate von etwa 1,29°C pro Jahrhundert. Die Erwärmungsrate scheint zum Ende hin leicht abzunehmen (mit der Annäherung an den Stillstand).

Das blaue Stillstands-Intervall zeigt viel weniger Variabilität als die beiden Referenzintervalle. Die Erwärmungsrate liegt zumeist zwischen 0 und 1°C pro Jahrhundert und zeigt eine Gesamt-Erwärmungsrate von etwa 0,54°C pro Jahrhundert, die zum Ende hin leicht zuzunehmen scheint. Vielleicht zeigte sich Ende 2013 eine geringe Zunahme der Temperatur, die dann 2014 und 2015 größer wurde.

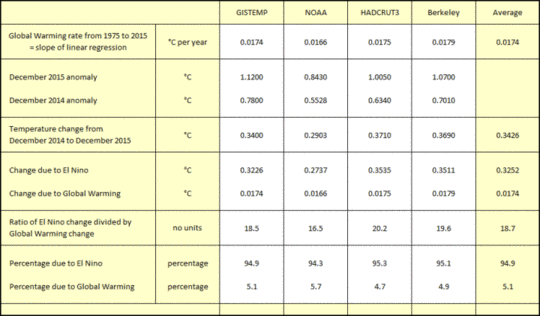
Falls wir die Gesamt-Erwärmungsraten der beiden Referenzintervalle mitteln, ergibt sich 1,65°C pro Jahrhundert. Der Stillstand zeigt eine Erwärmungsrate von weniger als 33% des Mittels der beiden Referenzintervalle.

Genauer, der Stillstand weist eine Gesamt-Erwärmungsrate von etwa 27% zum Referenz-Intervall 1 und weniger als 42% zum Referenz-Intervall 2. Diese Prozentzahlen repräsentieren eine große Reduktion der Erwärmungsrate, was die Bezeichnungen „Slowdown” oder „Hiatus” oder „Pause” rechtfertigt.

Kann irgendjemand den Stillstand leugnen – angesichts dieser Beweise? Ich erwarte, dass es viele „Stillstands-Leugner“ geben wird, die es stur wie ein Panzer ablehnen, die hier von mir präsentierten Beweise zu akzeptieren. Natürlich kann jedermann meine Beweise widerlegen, falls ein signifikanter Fehler darin gefunden wird. So geht Wissenschaft.

Ein letztes Wort bzgl. der Zukunft. Der Stillstand wurde durch den El Nino 2015 abgeschwächt. Dies bedeutet nicht, dass er niemals existiert hatte. Jeder, der sich schadenfroh bzgl. der Abschwächung des Stillstands ergeht, sollte im Hinterkopf behalten, dass El Ninos nicht ewig dauern. Ist die El-Nino-Erwärmung erst einmal verschwunden, wird sich der Stillstand möglicherweise verstärken. Auch ein La Nina kann dem Stillstand Vorschub leisten. Man unterschätze den Stillstand nicht, er könnte durchaus noch Überraschungen bereithalten.

Link: http://wattsupwiththat.com/2016/02/25/very-strong-graphical-evidence-for-the-pause-part-2/

Übersetzt von Chris Frey EIKE

Eine neue Art und Weise, den ,Stillstand‘ zu betrachten: Warum Karl et al. hinsichtlich des ,Stillstands‘ falsch liegen

geschrieben von Sheldon Walker | 29. Februar 2016

Die Meisten kennen sich mit der Anwendung linearer Regression bzgl. globaler Erärmung aus. Man wähle einen Start- und einen Endzeitpunkt und berechne die Neigung der Regressionslinie aus den Zeitpunkten und Temperaturanomalien in den Datensätzen. Was könnte dabei falsch laufen?

Eine der allgemeinen Vorwürfe im Zusammenhang mit der globalen Erwärmung lautet, dass Start- und Endzeitpunkt cherry-picked sind, um ein bestimmtes Ergebnis zu erzielen. Vorwürfe gibt es auch hinsichtlich der Länge des Trends, der zu kurz sei, um ein signifikantes Ergebnis zu bekommen (d. h. Trends kürzer als 10 Jahre oder sogar kürzer als 30 Jahre).

Wie wäre es, wenn wir ein Verfahren nutzen könnten, um diese Vorwürfe zu umgehen?

Um das Problem Cherry-Picking zu umgehen, betrachten wir alle möglichen Start- und Endzeitpunkte des untersuchten Zeitintervalls. Um das Problem von Kurzzeittrends zu umgehen, betrachten wir nur Trends mit einer Länge von mindestens 10 Jahren.

Beispiel: Man stelle sich vor, wir wären interessiert am Zeitintervall von Januar 1975 bis Dezember 1999. Dieses Intervall ist 24 Jahre und 11 Monate lang. Wir teilen den Zeitraum Januar 1975 bis Dezember 1999 auf in ALLE möglichen Trends von mindestens 10 Jahren.

Wenn ich sage JEDEN möglichen Trend von mindestens zehn Jahren, meine ich JEDEN möglichen Trend von 10 Jahren. Für das Zeitintervall Januar 1975 bis Dezember 1999 gibt es 16.920 mögliche Trends, und in diesem Verfahren werden sie ALLE verwendet.

Beispieltrends von Januar 1975 bis Dezember 1999:

Das kann jetzt überwältigend aussehen, aber mit Excel und einem modernen Computer können alle Berechnungen ziemlich einfach durchgeführt werden.

Es gibt viele Möglichkeiten, die Ergebnisse darzustellen. Der einfachste Weg ist eine „Streu“-Graphik der Erwärmungsrate zur Trendlänge. Wie sieht die Graphik jeder möglichen Kombination von Erwärmungsrate und Trendlänge aus für den Zeitraum Januar 1975 bis Dezember 1999? Dazu betrachte man Graphik 1:

Diese Graphik enthält eine Menge Information, muss aber ein wenig interpretiert werden. Zum Beispiel, wie ändert sich der Erwärmungstrend in Abhängigkeit von der Trendlänge?

Aus der Graphik:

Die Erwärmungsrate für 10-Jahre-Trends variiert von -0,20°C bis +0,80°C pro Jahrhundert

Die Erwärmungsrate für 15-Jahre-Trends variiert von +0,65°C bis +2,20°C pro Jahrhundert

Die Erwärmungsrate für 20-jahre-Trends variiert von +1,02°C bis +1,61°C pro Jahrhundert

Die Erwärmungsrate für 24 Jahre und 11 Monate variiert überhaupt nicht, weil es nur eine gibt, nämlich die über den gesamten Zeitraum, und die beläuft sich auf 1,71°C pro Jahrhundert.

Diese Ergebnisse entsprechen möglicherweise ziemlich den Erwartungen der meisten Menschen. Eine Lektion lautet, man sei sehr kritisch gegenüber 10-Jahre-Trends. Man bekommt fast jede Erwärmungsrate, die man haben will, aus einem 10-Jahre-Trend. Man beachte, dass ein 10-Jahre-Trend unter bestimmten Umständen bedeutsam sein kann, aber im Allgemeinen gibt es 10-Jahre-Trends überall.

Allgemein werden Erwärmungstrends mit zunehmender Trendlänge stabiler. Aber nicht immer. Man betrachte die Erwärmungsraten für eine Trendlänge von 22 Jahren. Es gibt eine sehr kleine Bandbreite von Erwärmungsraten, die von +1,43°C bis +1,52°C pro Jahrhundert variieren. Aber wenn sich der Trend auf 23 Jahre verlängert, erweitert sich die Bandbreite von Erwärmungsraten erheblich. Warum?

Ebenso: Nach einer ziemlich stabilen Erwärmungsrate von etwa 1,48°C pro Jahrhundert bei einer Trendlänge von 22 Jahren endet das Intervall mit einer Erwärmungsrate von +1,71°C pro Jahrhundert über das gesamte Intervall. Was hat die Erwärmungsrate so plötzlich um über 15% zunehmen lassen, obwohl die Trendlänge nur um 3 Jahre größer geworden ist?

Ich werde diese zwei Fragen zu beantworten versuchen mittels der „Streu“-Graphik und einer Graphik der Temperaturanomalien über das Intervall. Falls man mit meiner Antwort nicht übereinstimmt, dann lasse man mich wissen, was sonst die Antwort ist. Zu Beginn des Intervalls war ein La Nina-Ereignis im Gange, von 1975 bis 1977. Am anderen Ende des Intervalls findet sich der große El Nino von 1997 bis 1999. Ist der Trend lang genug, um von beiden Ereignissen gleichzeitig beeinflusst zu werden, wird die Neigung der Regressionslinie durch den El Nino am einen Ende und die La Nina am anderen Ende zunehmen. Wenn also die Trendlänge über 22 Jahre hinausgeht, gibt es einen Doppel-Schub für die Erwärmungsrate, was in der „Streu“-Graphik auch ziemlich gut herauskommt.

Betrachtet man die „Streu“-Graphik für ein einzelnes Zeitintervall, gibt es nur eine mögliche Anwendung dieses Verfahrens. Ein Vergleich der „Streu“-Graphiken anderer Zeitintervalle ist eine weitere interessante Möglichkeit. Es ist dieses Verfahren, dass ich anwenden werde um zu beweisen, dass Karl et al. in ihrer Studie über den „Stillstand“ falsch lagen („Mögliche Artefakte von Daten-Verzerrungen während des derzeitigen Stillstands der globalen Erwärmung“).

Zunächst betrachte man Graphik 2. Sie ist aufgebaut wie Graphik 1, zeigt aber jede mögliche Kombination von Erwärmungsraten und Trendlängen für ein anderes Zeitintervall, nämlich von Januar 1950 bis Dezember 1974. Diese Graphik sieht einerseits so aus wie die Graphik des Zeitraumes Januar 1975 bis Dezember 1999, ist aber auch andererseits unterschiedlich.

Um einen Vergleich dieser beiden Streu-Graphiken einfacher zu machen, fasse ich sie zu einer Graphik zusammen. Dies bedeutet, dass eine der Graphiken ein wenig von der anderen Graphik überdeckt, und zwar dort, wo sie sich überlappen. Falls erforderlich, kann man das noch verbessern durch das Plotten lediglich des Umrisses jeder Graphik, aber mich interessiert mehr der Bereich, in dem sich die Graphiken nicht überlappen. Darum lassen wir den Überlappungsbereich erst einmal außen vor.

Siehe Graphik 3 – alle Kombinationen von Erwärmungsraten und Trendlängen, die es in den Zeitintervallen 1975 bis 1999 bzw. 1950 bis 1974 gibt, für Trendlängen von mindestens zehn Jahren.

Jetzt ist es einfacher, die Unterschiede zwischen den beiden Graphiken zu erkennen. Sie sehen von der Form her ähnlich aus, aber die grüne Kurve ist abgeleitet aus der orangenen Kurve. Warum das? Die Betrachtung der Erwärmungsrate für das gesamte Zeitintervall einer jeden Graphik liefert die Antwort.

Die orangene Kurve zeigt einen 24-Jahre-und-11-Monate-Trend von 1,71°C pro Jahrhundert. Das ist eine Rate globaler Erwärmung, die NICHT niedrig ist.

Die grüne Kurve zeigt einen Trend in einem gleich langen Zeitintervall von 0,28°C pro Jahrhundert. In diesem Zeitintervall gibt es nicht viel globale Erwärmung.

Man beachte, dass es keine Überlappung der beiden Graphiken gibt für Trendlängen über etwa 15 Jahre. Dies stützt den Gedanken, dass diese beiden Zeitintervalle sehr unterschiedliche Profile von Erwärmungsraten zeigen.

Und jetzt die GROSSE Frage: Falls man diese beiden Zeiträume addiert, also 1950 bis 1974 bzw. 1975 bis 1999, und die Erwärmungsrate für das Gesamtintervall, also 1950 bis 1999 berechnet – wie groß würde die Erwärmungsrate sein? Das habe ich getan, und eine lineare Regression über das Gesamtintervall zeigt eine Erwärmungsrate von +1,12°C pro Jahrhundert. Gut und schön, aber was repräsentiert dieser Wert von +1,12°C pro Jahrhundert tatsächlich?

Es ist NICHT die Erwärmungsrate normaler anthropogener globaler Erwärmung.

Es ist NICHT die Erwärmungsrate, wenn es KEINE anthropogene globale Erwärmung gibt.

Es ist eine künstliche mittlere Erwärmungsrate über ein Zeitintervall, als die anthropogene globale Erwärmung etwa die Hälfte der Zeit präsent war und während der anderen Hälfte der Zeit fehlte.

Unglücklicherweise haben Karl et al. diesen Wert verwendet als ihre „normale“ anthropogene Erwärmungsrate, und auf der Grundlage dieses Wertes haben sie gefolgert, dass die Erwärmungsrate von 2000 bis 2014 NICHT das Bestehen eines „Stillstands“ der globalen Erwärmung stützt.

Kurzer Blick auf die Studie von Karl et al.:

Karl et al. haben die NOAA-Daten adjustiert, um der mittleren Differenz von 0,12°C Rechnung zu tragen zwischen Messungen der Wassertemperatur von Bojen und von Schiffen. Diese „Korrektur“ hatte ihren Einfluss auf Temperaturtrends mit dem größten Einfluss auf die Trends von 2000 bis 2014 (welches der „Stillstands“-Zeitraum sein sollte).

Karl et al. haben also die neuen Erwärmungsraten 1950 bis 1999 bzw. 2000 bis 2014 berechnet. Sie erhielten:

Erwärmungsrate 1950 bis 1999: +1,13°C pro Jahrhundert.

Erwärmungsrate 2000 bis 2014: +1,16°C pro Jahrhundert.

Daraus zogen Karl et al. ihre Schlussfolgerung: Da sich die Erwärmungsrate von 2000 bis 2014 praktisch nicht von der Erwärmungsrate im Zeitraum 1950 bis 1999 unterscheidet, wird das Bestehen eines „Stillstands“ der globalen Erwärmung NICHT gestützt.

Ich stelle NICHT die Adjustierungen von Karl et al. der Wassertemperatur in Frage. Ich bin nicht qualifiziert genug, um diese Adjustierungen zu bewerten. Darum verwende ich die adjustierten NOAA-Daten so, wie sie da stehen. Spezielle Anmerkung: Ich verwende die NOAA-Daten. Falls ich in den NOAA-Daten einen „Stillstand“ finde, kann man mir nicht vorwerfen, die falschen Daten zu benutzen.

Ich spreche auch NICHT über die Ergebnisse der Berechnungen von Karl et al. Ich bekomme Ergebnisse, die ihren sehr ähnlich sind.

Mein Anliegen ist die Verwendung der Erwärmungsrate von 1950 bis 1999. Karl et al. schrieben dazu Folgendes:

Unsere neue Analyse zeigt jetzt den Trend im Zeitraum 1950 bis 1999, ein Zeitraum, der in breiter Übereinstimmung eine signifikante anthropogene Erwärmung aufweist mit 0,113°C pro Dekade, was praktisch ununterscheidbar ist vom Trend im Zeitraum 2000 bis 2014 (0,116°C pro Dekade)“

Nun ist 1975 bis 1999 ein Zeitintervall mit einer signifikanten anthropogenen globalen Erwärmung. Aber 1950 bis 1974 ist ein Zeitintervall mit nur sehr geringer anthropogener globaler Erwärmung.

Fügt man diese beiden Intervalle zusammen zum Zeitraum 1950 bis 1999, haben Karl et al. ein Intervall erzeugt, dass im Grunde eine anthropogene globale Erwärmung halber Stärke zeigt (halb mit, halb ohne Erwärmung). Aber Karl et al. verwendeten diesen Wert als ihre „normale“ anthropogene Erwärmungsrate, wenn sie den Vergleich mit dem Zeitraum 2000 bis 2014 durchführen.

Falls die Erwärmungsrate 2000 bis 2014 zu der Erwärmungsrate 1950 bis 1999 passt (was der Fall ist), dann bedeutet das, dass 2000 bis 2014 ebenfalls eine anthropogene globale Erwärmung halber Stärke aufweist.

Es gibt zwei einfache Wege zu erklären, wie 2000 bis 2014 anthropogene globale Erwärmung halber Stärke haben kann.

1) Der Zeitraum 2000 bis 2014 könnte aus zwei Teilen bestehen, wobei in einem Teil anthropogene globale Erwärmung auftritt, im anderen Teil aber NICHT (wie 1950 bis 1999). Aber ich glaube nicht, dass dies der Fall ist.

2) Die vernünftigere Erklärung ist, dass der Zeitraum 2000 bis 2014 eine geringere Erwärmungsrate zeigt als die „normale“ anthropogene globale Erwärmung. Die Erwärmungsrate betrüge etwa 50% der „normalen“ Erwärmungsrate. Das kann man nennen, wie man will (Verlangsamung, Stillstand, Pause). Wie auch immer man es nennt, die Daten zeigen, dass es existiert.

Während also Karl et al. versucht haben, alle Welt davon zu überzeugen, dass es KEINEN Stillstand gebe, haben sie in Wirklichkeit einen starken Beweis geliefert, dass der „Stillstand“ sehr wohl existiert (wenn erst einmal ihr Fehler den Zeitraum 1950 bis 1999 betreffend korrigiert ist).

Link: http://wattsupwiththat.com/2016/02/21/a-new-way-of-looking-at-the-pause-why-karl-et-al-got-it-wrong-about-the-pause-part-1/

Übersetzt von Chris Frey EIKE

Aktualisierung zum wärmsten Jahr jemals: El Nino-Effekt 2015 war 20 mal größer als das Signal der globalen Erwärmung

geschrieben von Sheldon Walker | 29. Februar 2016

Bild rechts: Wassertemperatur-Anomalie im Pazifik vom 7.2.2016. Quelle

Graphik 1 zeigt die monatliche Temperatur-Anomalie nach HadCRUT4 im Zeitraum 1880 bis 2015. Mit eingezeichnet ist auch eine LOESS-Kurve für die HadCRUT4-Daten. Die LOESS-Kurve wurde erzeugt mittels multipler lokaler Regressionen, wobei für jede Regression Daten von 20 Jahren verwendet worden sind.

Man erkennt in Graphik 1, dass die jüngste Periode konsistenter Erwärmung um das Jahr 1975 eingesetzt und sich bis zum Ende des Zeitraumes (Dezember 2015) fortgesetzt hat. Die LOESS-Kurve zeigt, dass der Erwärmungstrend halbwegs linear verläuft von 1975 bis 2015. Für diesen Zeitraum wird eine lineare Regression durchgeführt.

Graphik 2 zeigt die monatliche Temperatur-Anomalie nach HadCRUT4 von 1975 bis 2015. Ebenfalls eingezeichnet ist eine lineare Regressionslinie über den gleichen Zeitraum. Die Neigung der Regressionslinie beträgt 0,0175°C pro Jahr. Die Gesamterwärmung von 1975 bis 2015 beträgt fast 0,72°C.

Die Temperaturänderung zwischen Ende 2014 und Ende 2015 beträgt 0,371°C (siehe Berechnung 1 – alle Berechnungen werden am Ende dieses Beitrags dokumentiert).

Wir wissen durch die lineare Regression, dass die Temperaturänderung aufgrund der Globalen Erwärmung für ein Jahr 0,0175°C beträgt. Daher können wir berechnen, dass die Erwärmung aufgrund des El Nino 0,3535°C beträgt (siehe Berechnung 2).

Dies bedeutet, dass die Temperaturänderung aufgrund des El Nino über 20 mal größer war als die Temperaturänderung aufgrund der Globalen Erwärmung (siehe Berechnung 3). Mit anderen Worten, El Nino war für über 95% der Temperaturänderung zwischen Ende 2014 und Ende 2015 verantwortlich.

Die Ergebnisse für die unterschiedlichen Temperaturreihen zeigt die folgende Tabelle:

Die prozentuale Änderung aufgrund des El Nino variiert für die 4 Temperaturreihen zwischen 94,3% und 95,3%. Die prozentuale Änderung aufgrund der Globalen Erwärmung variiert zwischen 4,7% und 5,7% in den 4 Temperaturreihen – eine sehr konsistente Ergebnismenge.

Diese Berechnungen sind einfach durchzuführen. Die Ergebnisse sind eindeutig. Sie sollten keine Überraschung sein für jeden, der mit dem Klima vertraut ist. Man denke an den El Nino 1998. Die Temperatur zeigte eine Spitze, um gleich danach wieder abzufallen. Diese Temperaturspitze war nicht auf die Globale Erwärmung, sondern auf den El Nino zurückzuführen. Erwarten die Klimawissenschaftler etwa, dass bei diesem El Nino alles ganz anders ist?

Daher kommt es überraschend, dass eine Reihe von Klimawissenschaftlern Statements abgegeben hat, die den Effekt des El Nino minimieren und den Effekt der Globalen Erwärmung übertreiben.

Bei der Lektüre der folgenden Aussagen sollte man sich immer daran erinnern, dass El Nino für etwa 95% der Temperaturänderung zwischen Ende 2014 und Ende 2015 verantwortlich war. El Nino verursachte eine Temperaturzunahme um 0,32°C, aber die Klimawissenschaftler behaupten, dass es nur wenige hundertstel Grad seien.

1) Zitate aus einem Artikel unter der Überschrift [übersetzt] „Analyse: wie wurde 2015 zum wärmsten Jahr jemals“ bei carbonbrief.org:

Steigende Treibhausgas-Konzentrationen und ein „kleiner Beitrag“ von El Nino im Pazifik führten zusammen zu den Rekordtemperaturen des Jahres 2015, sagt Prof. Adam Scaife vom UKMO.

…

Wie groß ist der Beitrag zu den Rekordtemperaturen 2015 durch El Nino?

El Nino wurde 2015 immer stärker und erreichte sein Maximum erst in diesem Winter. Daher glauben wir, dass der El Nino nur einen kleinen Beitrag (ein paar hundertstel Grad) zu den Rekordtemperaturen des Jahres 2015 beigetragen hat (Prof. Adam Scaife).

Bedeutet dies, dass menschliche Aktivitäten der größte Treiber der Rekordtemperatur 2015 waren?

Ja. Die nominelle globale mittlere Rekordtemperatur 2015 war im Voraus gut vorhergesagt und gut erklärt worden als primär der globalen Erwärmung geschuldet. Diese wiederum ist hauptsächlich Treibhausgas-Emissionen geschuldet, hauptsächlich menschlichen Ursprungs. El Nino leistete nur einen geringen Beitrag (Prof. Adam Scaife).

2) Zitate aus einem Artikel mit der Überschrift [übersetzt] „Wie stark hat El Nino die globale Temperatur im Jahre 2015 getrieben?“ bei carbonbrief.org:

Carbon Brief hat mit Klimawissenschaftlern gesprochen, die sich mit dieser Frage befasst hatten. Sie scheinen alle darin übereinzustimmen, dass El Nino irgendwo bei 10% für die Rekordwärme 2015 verantwortlich war.

…

Dr. Gavin Schmidt, Direktor des GISS der NASA, beschrieb den fortgesetzten Anstieg der globalen Temperaturen als „assistiert“ von El Nino.

…

Als Teil der Berichterstattung von Carbon Brief zum Thema wärmstes Jahr sprachen wir mit Dr. Adam Scaife, Leiter der Abteilung für Langfrist-Vorhersagen am UK Met.-Office. Scaife wies dem El Nino nur eine oberflächliche Rolle zu und sagte Carbon Brief:

Wir glauben, dass El Nino nur einen kleinen Beitrag zu den Rekordtemperaturen 2015 geleistet hat (ein paar hundertstel Grad).

…

Schmidt schätzte, dass der El Nino für einen Anteil von 0,07°C über der mittleren Erwärmung verantwortlich war, die wir 2015 erlebt haben.

Ein kurzer Vergleich der Zahlen von Schmidt oder Cropper mit der Temperaturanomalie der NASA für das Jahr 2015 von 0,87°C über dem Mittel von 1951 bis 1980 zeigt, dass El Nino einen Beitrag von 8% bis 10% geleistet hat.

…

Stott sagt Carbon Brief: Eine Schätzung unter 0,1°C infolge El Nino zur globalen jährlichen mittleren Temperatur ist weniger als 10% der Erwärmung von etwa 1°C im Jahre 2015 relativ zum vorindustriellen Niveau.

Mit anderen Worten, El Nino leistete „einen kleinen Beitrag zusätzlich“ zu der Erwärmung durch Treibhausgase, sagt Stott.

[Die Auflistung obiger Aussagen scheint im Original irgendwie durcheinander geraten zu sein. Aber vielleicht irre ich mich da auch. Anm. d. Übers.]

Es gibt keinen Zweifel daran, dass der El Nino, der sich 2015 entwickelt hatte und immer noch im Gange ist, ungewöhnlich stark war, sogar außerordentlich. Aber mit einem Beitrag irgendwo um die 10%-Marke scheint den Wissenschaftlern zufolge klar zu sein, dass El Nino nicht für die Rekordwärme 2015 verantwortlich gemacht werden kann. Tatsächlich soll dieser Beitrag außerordentlich gering gewesen sein.

Alle diese Wissenschaftler scheinen aus dem gleichen Liederbuch vorzusingen!

Ich würde gerne erleben, dass diese Wissenschaftler ihre Kommentare rechtfertigen, und zwar unter Verwendung numerischer Berechnungen, um zu zeigen, woher sie ihre Zahlen haben. Ich habe meine Methode hier vollständig dokumentiert. Falls irgendjemand in meinen Berechnungen einen Fehler entdeckt, bitte melden!

—————————-

Berechnungen.

1) [December 2015 anomaly] minus [December 2014 anomaly] = 1.005 – 0.634 = 0.371 °C.

2) [Total warming 2014/2015] minus [warming due to Global Warming] = 0.371 – 0.0175 = 0.3535 °C.

3) [warming due to El Nino] divided by [warming due to Global Warming] = 0.3535 / 0.0175 = 20.2

4) [warming due to El Nino] times 100 divided by [Total warming 2014/2015] = 0.3535 * 100 / 0.371 = 95.28 %

5) [warming due to Global Warming] times 100 divided by [Total warming 2014/2015] = 0.0175 * 100 / 0.371 = 4.72 %

Link: http://wattsupwiththat.com/2016/02/04/hottest-year-ever-update-el-nino-effect-in-2015-was-20-times-larger-than-the-global-warming-signal/

Übersetzt von Chris Frey EIKE