Was ist Chaos? Ich benutze diesen Ausdruck hier in seiner mathematischen Bedeutung. So, wie in den vergangenen Jahren die Naturwissenschaftler weitere Aggregatzustände der Materie entdeckten (neben fest, flüssig, gasförmig, nun auch plasma),  so wurden von der Wissenschaft neue Zustände entdeckt, die Systeme annehmen können.

Systeme von Kräften, Gleichungen, Photonen oder des Finanzhandels können effektiv in zwei Zuständen existieren:

Einer davon ist mathematisch zugänglich, die zukünftigen Zustandsformen können leicht vorhergesagt werden; im anderen aber passiert scheinbar Zufälliges.
Diesen zweiten Zustand nennen wir “Chaos”. Es kann gelegentlich in vielen Systemen eintreten.
Wenn Sie z. B. das Pech haben, einen Herzanfall zu erleiden, geht der normalerweise vorhersehbare Herzschlag in einen chaotischen Zustand über, wo der Muskel scheinbar zufällig schlägt. Nur ein Schock kann ihn in den Normalzustand zurücksetzen. Wenn Sie jemals ein Motorrad auf einer eisigen Fahrbahn scharf abgebremst haben, mussten Sie ein unkontrollierbares Schlagen des Lenkrads befürchten, eine chaotische Bewegung, die meist zu einem Sturz führte. Es gibt Umstände, wo sich die Meereswogen chaotisch bewegen und unerklärlich hohe Wellen erzeugen.
Die Chaos-Theorie ist das Studium des Chaos und weiterer analytischer Methoden und Messungen und von Erkenntnissen, die während der vergangenen 30 Jahre gesammelt worden sind.
Im Allgemeinen ist Chaos ein ungewöhnliches Ereignis. Wenn die Ingenieure die Werkzeuge dafür haben, werden sie versuchen, es aus ihrem Entwurf „heraus zu entwerfen“, d. h. den Eintritt von Chaos unmöglich zu machen.
Es gibt aber Systeme, wo das Chaos nicht selten, sondern die Regel ist. So eines ist das Wetter. Es gibt weitere, die Finanzmärkte zum Beispiel, und – das ist überraschend – die Natur. Die Erforschung der Raubtierpopulationen und ihrer Beutetierpopulationen zeigt z. B. das sich diese zeitweilig chaotisch verhalten. Der Autor hat an Arbeiten teilgenommen, die demonstrierten, dass sogar einzellige Organismen Populationschaos mit hoher Dichte zeigen können.
Was heißt es also, wenn wir sagen, dass sich ein System anscheinend zufällig verhalten kann? Wenn ein System mit dem zufälligen Verhalten anfängt, wird dann das Gesetz von Ursache und Wirkung ungültig?
Vor etwas mehr als hundert Jahren waren die Wissenschaftler zuversichtlich, dass jedes Ding in der Welt der Analyse zugänglich wäre, dass alles vorhersagbar wäre, vorausgesetzt man hätte die Werkzeuge und die Zeit dazu. Diese gemütliche Sicherheit ist zuerst von Heisenbergs Unschärfeprinzip zerstört worden, dann durch Kurt Gödels Arbeiten, schließlich durch Edward Lorenz, der als Erster das Chaos entdeckte. Wo? natürlich bei Wetter-Simulationen.
Chaotische Systeme sind nicht gänzlich unvorhersagbar, wie wirklich Zufälliges. Sie zeigen abnehmende Vorhersagbarkeit mit zunehmender Dauer, und diese Abnahme wird durch immer größer werdende Rechenleistung verursacht, wenn der nächste Satz von Vorhersagen errechnet werden soll. Die Anforderungen an Rechnerleistung zur Vorhersage von chaotischen Systemen wächst exponentiell. Daher wird mit den verfügbaren begrenzten Möglichkeiten die Genauigkeit der Vorhersagen rapide abfallen, je weiter man in die Zukunft prognostizieren will. Das Chaos tötet die Ursache-Wirkungs-Beziehung nicht, es verwundet sie nur.

Jetzt kommt ein schönes Beispiel.

Jedermann hat ein Tabellenkalkulationsprogramm. Das nachfolgende Beispiel kann jeder selbst ganz einfach ausprobieren.
Die einfachste vom Menschen aufgestellte Gleichung zur Erzeugung von Chaos ist die „Logistische Karte“ (logistic map).
In einfachster Form: Xn+1 = 4Xn(1-Xn)
Das bedeutet: der nächste Schritt in Folge gleicht 4 mal dem vorhergehenden Schritt mal (1 – vorhergehender Schritt). Wir öffnen nun ein Blatt in unserer Tabellenkalkulation und bilden zwei Spalten mit Werten:

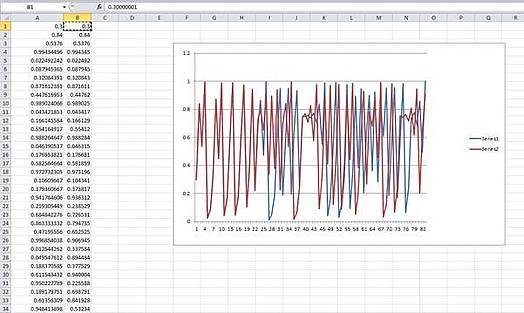
Jede Spalte A und B wird erzeugt, indem wir in Zelle A2 eingeben [=A1*4* (1-A1)], und wir kopieren das nach unten in so viele Zellen, wie wir möchten. Das gleiche tun wir für Spalte B2, wir schreiben [=B1*4* (1-B1)]. Für A1 und B1 geben wir die Eingangszustände ein. A1 erhält 0.3 und B1 eine ganz gering verschiedene Zahl: 0.30000001.
Der Graph zeigt die beiden Kopien der Serien. Anfänglich sind sie synchron, dann beginnen sie bei etwa Schritt 22, auseinander zulaufen, von Schritt 28 an verhalten sie sich völlig unterschiedlich.
Dieser Effekt stellt sich bei einer großen Spannweite von Eingangszuständen her. Es macht Spaß, sein Tabellenkalkulationsprogramm laufen zu lassen und zu experimentieren. Je größer der Unterschied zwischen den Eingangszuständen ist, desto rascher laufen die Folgen auseinander.
Der Unterschied zwischen den Eingangszuständen ist winzig, aber die Serien laufen allein deswegen auseinander. Das illustriert etwas ganz Wichtiges über das Chaos. Es ist die hohe Empfindlichkeit für Unterschiede in den Eingangszuständen.
In umgekehrter Betrachtung nehmen wir nun an, dass wir nur die Serien hätten; wir machen es uns leicht mit der Annahme, wir wüssten die Form der Gleichung, aber nicht die Eingangszustände. Wenn wir nun Vorhersagen von unserem Modell her treffen wollen, wird jede noch so geringe Ungenauigkeit in unserer Schätzung der Eingangszustände sich auf das Vorhersage-Ergebnis auswirken und das in dramatisch unterschiedlichen Ergebnissen. Der Unterschied wächst exponentiell. Eine Möglichkeit zur Messung gibt uns der sogenannte Lyapunov-Exponent. Er misst in Bits pro Zeitschritt, wie rasch die Werte auseinanderlaufen – als Durchschnitt über eine große Zahl von Samples. Ein positiver Lyapunov-Exponent gilt als Beweis für Chaos. Er nennt uns auch die Grenze für die Qualität der Vorhersage beim Versuch der Modellierung eines chaotischen Systems.
Diese grundlegenden Charakteristiken gelten für alle chaotischen Systeme.
Und nun kommt etwas zum Nachdenken. Die Werte unseres einfachen Chaos-Generators im Kalkulationsblatt bewegen sich zwischen 0 and 1. Wenn wir 0.5 subtrahieren, sodass wir positive and negative Werte haben, und dann summieren, erhalten wir diesen Graphen. Der ist jetzt auf tausend Punkte ausgedehnt.

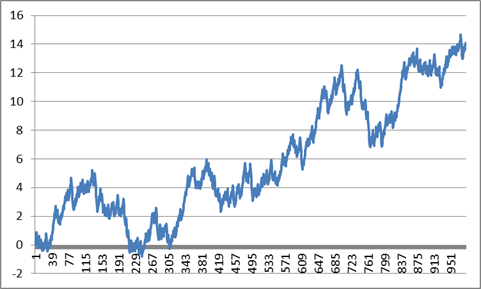
Wenn ich nun ohne Beachtung der Skalen erzählt hätte, das wäre der Kurs im vergangenen Jahr für eine bestimmten Aktie, oder der jährliche Meerestemperaturverlauf gewesen, hätten Sie mir vermutlich geglaubt. Was ich damit sagen will: Das Chaos selbst kann ein System völlig antreiben und Zustände erzeugen, die so aussehen, als ob das System von einem äußeren Antrieb gesteuert wäre. Wenn sich ein System so verhält, wie in diesem Beispiel, kann es wegen einer äußeren Kraft sein, oder ganz einfach nur wegen des Chaos.

Wie steht es also mit dem Wetter?

Edward Lorenz (1917 – 2008) ist der Vater der Chaosforschung. Er war auch Wetterforscher. Er schuf eine frühe Wetter-Simulation, indem er drei verkoppelte Gleichungen benutzte und er war erstaunt, dass die Simulationswerte mit dem Fortschritt der Simulation über der Zeit unvorhersehbar wurden.
Dann suchte er nach Beweisen, ob sich das tatsächliche Wetter in der gleichen unvorhersehbaren Weise verhielt. Er fand sie, bevor er noch mehr über die Natur des Chaos entdeckte.

Kein Klimatologe bezweifelt seine Erkenntnis vom chaotischen Charakter des Wetters.

Edward Lorenz schätzte, dass das globale Wetter einen Lyapunov-Exponenten gleich einem Bit von Information alle 4 Tage zeigt. Das ist ein Durchschnitt über die Zeit und über die globale Oberfläche.  Zuweilen und an gewissen Stellen ist das Wetter chaotischer, das kann jedermann in England bezeugen. Das bedeutet aber auch, dass, falls man das Wetter mit einer Genauigkeit von 1 Grad C für morgen vorhersagen kann, die beste Vorhersage für das Wetter für den 5. Folgetag bei +/- 2 Grad liegen wird, für den 9. Tag bei +/-4 Grad und den 13. Tag bei +/- 8 Grad. Auf jeden Fall wird die Vorhersage für den 9-10. Tag nutzlos sein. Wenn Sie aber das Wetter für Morgen mit einer Treffsicherheit von +/- 0.1 Grad vorhersagen könnten, dann würde die Zunahme des Fehlers verlangsamt. Weil sie aber exponentiell steigt, wird auch diese Vorhersage bereits nach wenigen weiteren Tagen nutzlos sein.
Interessanterweise fällt die Treffsicherheit der Wettervorhersagen von Institutionen, wie z. B. dem englischen Wetterdienst, genau in dieser Weise ab.  Das beweist einen positiven Lyapunov-Exponenten und damit, dass das Wetter chaotisch ist, wenn es noch eines Beweises bedurft hätte.

Soviel zur Wettervorhersage. Wie steht es mit der Langzeit-Modellierung?

Zuerst zur wissenschaftlichen Methode. Das Grundprinzip ist, dass die Wissenschaft sich so entwickelt, dass jemand eine Hypothese formuliert, diese Hypothese durch ein Experiment erprobt und sie modifiziert, sie beweist oder verwirft, indem er die Ergebnisse des Experiments auswertet.Ein Modell, ob nun eine Gleichung oder ein Computer-Modell, ist nur eine große Hypothese. Wenn man die mit der Hypothesenbildung betroffene Sache nicht durch ein Experiment modifizieren kann, dann muss man Vorhersagen mit dem Modell machen und am System selbst beobachten, ob die Vorhersagen damit zu bestätigen oder zu verwerfen sind.##Ein klassisches Beispiel ist die Herausbildung unseres Wissens über das Sonnensystem. Bei den ersten Modellen standen wir im Mittelpunkt, dann die Sonne, dann kam die Entdeckung der elliptischen Umläufe und viele Beobachtungen, um die exakte Natur dieser Umläufe zu erkennen. Klar, dass wir niemals hoffen konnten, die Bewegungen der Planeten zu beeinflussen, Experimente waren unmöglich. Aber unsere Modelle erwiesen sich als richtig, weil Schlüsselereignisse zu Schlüsselzeiten stattfanden: Sonnenfinsternisse, Venusdurchgänge usw. Als die Modelle sehr verfeinert waren konnten Abweichungen zwischen Modell und Wirklichkeit benutzt werden, um neue Eigenschaften vorherzusagen. Auf diese Art konnten die äußeren Planeten Neptun und Pluto entdeckt werden. Wenn man heute auf die Sekunde genau wissen will, wo die Planeten in zehn Jahren stehen, gibt es im Netz Software, die exakt Auskunft gibt.Die Klimatologen würden nur allzu gerne nach dieser Arbeitsweise verfahren. Ein Problem ist aber, dass sie aufgrund des chaotischen Charakters des Wetters nicht die geringste Hoffnung hegen können, jemals Modellvorhersagen mit der Wirklichkeit in Einklang bringen zu können. Sie können das Modell auch nicht mit kurzfristigen Ereignissen zur Deckung bringen, sagen wir für 6 Monate, weil das Wetter in 6 Monaten völlig unvorhersagbar ist, es sei denn in sehr allgemeinen Worten.Das bedeutet Schlimmes für die ModellierbarkeitNun möchte ich noch etwas in dieses Durcheinander einwerfen. Das stammt aus meiner anderen Spezialisierung, der Welt des Computer-Modellierens von selbst-lernenden Systemen.Das ist das Gebiet der „Künstlichen Intelligenz“, wo Wissenschaftler meist versuchen, Computer- Programme zu erstellen, die sich intelligent verhalten und lernfähig sind. Wie in jedem Forschungsfeld ruft das Konzept Mengen von allgemeiner Theorie hervor, und eine davon hat mit der Natur der Stück-um-Stück zunehmenden Erfahrung (Inkrementelle Erfahrung) zu tun.Inkrementelle Erfahrung findet statt, wenn ein lernender Prozess versucht, etwas Einfaches zu modellieren, indem er vom Einfachen ausgeht und Komplexität zufügt, dabei die Güte des Modells beim Fortgang testet.Beispiele sind Neuronale Netzwerke, wo die Stärke der Verbindungen zwischen simulierten Hirnzellen mit dem Prozess des Lernens angepasst wird. Oder genetische Programme, wo Bits von Computerprogrammen modifiziert werden und bearbeitet werden, um das Modell immer mehr anzupassen.Am Beispiel der Theorien über das Sonnensystem können Sie sehen, dass die wissenschaftliche Methode selbst eine Form des inkrementellen Lernens ist.Es gibt einen universellen Graphen über das Inkrementelle Lernen. Er zeigt die Leistung eines beliebigen inkrementellen Lern-Algorithmus bei zwei Datensätzen, ganz gleich bei welchem.Voraussetzung ist, dass die beiden Datensätze aus der gleichen Quelle stammen müssen, aber sie sind zufällig in zwei Datensätze aufgespaltet, in den Trainingsdatensatz für die Trainierung des Modells und in einen Testdatensatz, der immer wieder für das Überprüfen gebraucht wird. Normalerweise ist der Trainingsdatensatz größer als der Testdatensatz, aber wenn es viele Daten gibt, macht das nichts aus. Mit der Zunahme des Wissens im Trainingsmodell benutzt das lernende System die Trainingsdaten, um sich selbst anzupassen, nicht die Testdaten, die zum Testen des Systems benutzt und sofort wieder vergessen werden.

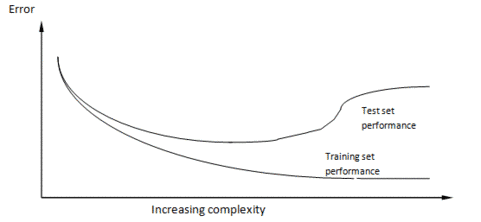
Wie zu sehen ist, wird die Leistung mit dem Trainingsdatensatz immer besser, je mehr Komplexität dem Modell zugefügt wird, auch die Leistung des Testdatensatzes wird besser, beginnt aber dann, schlechter zu werden.
Um es deutlich zu sagen: der Testsatz ist das Einzige, was zählt. Wenn wir das Modell für Vorhersagen benutzen wollen, werden wir es mit neuen Daten füttern, wie mit unserem Testdatensatz. Die  Leistung des Trainingsmodells ist irrelevant.
Über dieses Beispiel wird diskutiert, seit Wilhelm von Ockham den Satz geschrieben hat: “Entia non sunt multiplicanda praeter necessitatem“, besser bekannt als „Ockhams Rasiermesser“ und am besten so übersetzt: “Die Entitäten dürfen nicht ohne Not vermehrt werden”. Mit Entitäten meinte er unnötige Verzierungen und Schnörkel einer Theorie. Die logische Folge daraus ist, dass die am einfachsten die Fakten erklärende Theorie wahrscheinlich stimmt. Es gibt Beweise für die Allgemeingültigkeit dieses Satzes aus dem Gebiet der Bayesianischen Statistik und der Informationstheorie.
Das heißt also, dass unsere kühnen Wettermodellierer von beiden Seiten her in Schwierigkeiten stecken: wenn die Modelle für die Wettererklärung nicht ausreichend komplex sind, sind ihre Modelle nutzlos, wenn sie allzu komplex sind, auch.

Wer möchte da noch Wettermodellierer sein?

Unter der Voraussetzung, dass sie ihre Modelle nicht anhand der Wirklichkeit kalibrieren können, wie entwickeln und prüfen die Wettermodellierer ihre Modelle?Wie wir wissen, verhalten sich auch Wettermodelle chaotisch. Sie zeigen die gleiche Empfindlichkeit auf die Eingangsbedingungen. Das Mittel der Wahl für die Evaluierung (von Lorenz entwickelt) ist, Tausende von Läufen durchzuführen mit jeweils geringfügig anderen Eingangsbedingungen. Die Datensätze heißen „Ensembles”.Jedes Beispiel beschreibt einem möglichen Wetter-Pfad, und durch die Zusammenstellung des Satzes wird eine Verteilung möglicher Zielentwicklungen erzeugt. Für Wettervorhersagen zeigen sie mit dem Spitzenwert ihre Vorhersage an. Interessanterweise gibt es bei dieser Art von Modell-Auswertung wahrscheinlich mehr als nur eine Antwort, also mehr als einen Spitzenwert, aber über die anderen, auch möglichen Entwicklungen, wird nicht gesprochen. In der Statistik heißt dieses Verfahren „Monte Carlo Methode“.Beim Klimawandel wird das Modell so modifiziert, dass mehr CO2 simuliert wird, mehr Sonneneinstrahlung oder andere Parameter von Interesse. Und dann wird ein neues Ensemble gerechnet. Die Ergebnisse stellen eine Serie von Verteilungen über der Zeit dar, keine Einzelwerte, obwohl die von den Modellierern gegebenen Informationen die alternativen Lösungen nicht angeben, nur den Spitzenwert.Die Modelle werden nach der Beobachtung der Erde geschrieben. Landmassen, Luftströmungen, Baumbedeckung, Eisdecken, usw. werden modelliert. Sie sind eine große intellektuelle Errungenschaft, stecken aber noch immer voller Annahmen. Und wie man erwarten kann, sind die Modellierer stets bemüht, das Modell zu verfeinern und neue Lieblingsfunktionen zu implementieren. In der Praxis gibt es aber nur ein wirkliches Modell, weil alle Veränderungen rasch in alle eingebaut werden.Schlüsselfragen der Debatte sind die Interaktionen zwischen den Funktionen. So beruht die Hypothese vom Durchgehen der Temperaturen nach oben infolge von erhöhtem CO2 darauf, dass die Permafrostböden in Sibirien durch erhöhte Temperaturen auftauen würden und dadurch noch mehr CO2 freigesetzt würde. Der daraus resultierende Feedback würde uns alle braten. Das ist eine Annahme. Die Permafrostböden mögen auftauen oder auch nicht, die Auftaugeschwindigkeit und die CO2-Freisetzung sind keine harten wissenschaftlichen Fakten, sondern Schätzungen. So gibt es Tausende von ähnlichen „besten Abschätzungen“ in den Modellen.Wie wir bei den inkrementell lernenden Systemen gesehen haben, ist allzu viel Komplexität genau so fatal, wie zu wenig. Niemand weiß, wo sich die derzeitigen Modelle auf der Graphik oben befinden, weil die Modelle nicht direkt getestet werden.Jedoch macht die chaotische Natur des Wetters alle diese Argumente über die Parameter zunichte. Wir wissen natürlich, dass Chaos nicht die ganze Wahrheit ist. Es ist in den ferner vom Äquator gelegenen Regionen im Sommer im Durchschnitt wärmer als im Winter geworden. Monsune und Eisregen kommen regelmäßig jedes Jahr vor und daher ist die Sichtweise verführerisch, dass das Chaos wie das Rauschen in anderen Systemen aussieht.

Das von den Klimawandel-Anhängern benutzte Argument geht so: Chaos können wir wie Rauschen behandeln, daher kann das Chaos „herausgemittelt“ werden.

Um ein wenig auszuholen: Diese Idee des “Ausmittelns” von Fehlern/Rauschen hat eine lange Geschichte. Nehmen wir das Beispiel von der Höhenmessung des Mount Everest vor der Erfindung von GPS und Radar-Satelliten. Die Methode der Höhenermittlung war, auf Meereshöhe mit einem Theodoliten zu beginnen und die lokalen Landmarken auszumessen, indem man deren Abstand und Winkel über dem Horizont maß, um die Höhe zu schätzen. Dann wurde von den vermessenen Punkten aus das Gleiche mit weiteren Landmarken gemacht. So bewegte man sich langsam im Binnenland vor. Zum Zeitpunkt der Ankunft der Landvermesser am Fuße des Himalaja beruhten ihre Messungen auf Tausenden vorhergehenden Messungen. Alle mit Messfehlern. Im Endeffekt lag die Schätzung der Vermesser von der Höhe des Everest nur um einige zig Meter daneben.Das kam, weil die Messfehler selbst eine Tendenz zum Ausmitteln hatten. Wenn ein systemischer Fehler drin gewesen wäre, etwa von der Art, dass jeder Theodolit um 5 Grad zu hoch gemessen hätte, dann wären die Fehler enorm groß geworden. Der Punkt dabei ist, dass die Fehler dann keinen Bezug zum vermessenen Objekt gehabt hätten. Es gibt viele Beispiele dafür in der Elektronik, in der Radio-Astronomie und auf anderen Gebieten.Sie verstehen nun, dass die Klimamodellierer hoffen, dass das auch für das Chaos gilt. Sie behaupten ja tatsächlich, dass es so wäre. Bedenken Sie aber, dass die Theodolitenfehler nichts mit der tatsächlichen Höhe des Everest zu tun haben, wie auch das Rauschen in Radioteleskopverstärkern nichts mit den Signalen von weit entfernten Sternen zu tun hat. Das Chaos dagegen ist Bestandteil des Wetters. Daher gibt es keinerlei Grund, warum sich das „ausmitteln“ würde. Es ist nicht Bestandteil der Messung, es ist Bestandteil des gemessenen Systems selbst.Kann Chaos überhaupt „ausgemittelt“ werden? Falls ja, dann müssten wir bei Langzeitmessungen des Wetters kein Chaos erkennen. Als eine italienische Forschergruppe um meine Chaos-Analyse-Software bat, um eine Zeitreihe von 500 Jahren gemittelter süditalienischer Wintertemperaturen auszuwerten, ergab sich die Gelegenheit zur Überprüfung. Das folgende Bild ist die Ausgabe der Zeitreihe mittels meines Chaos-Analyse-Programms „ChaosKit“.

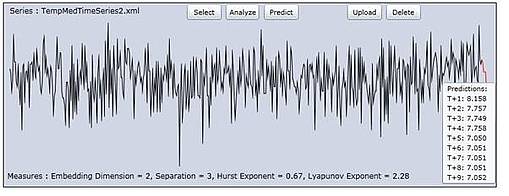
Ergebnis: Ein Haufen Chaos. Der Lyapunov-Exponent wurde mit 2.28 Bits pro Jahr gemessen.
Auf gut Deutsch: Die Treffsicherheit der Temperaturvorhersage vermindert sich um den Faktor 4 für jedes weitere Jahr, für welches eine Vorhersage gemacht werden soll, oder anders herum: die Fehler vervierfachen sich.

Was heißt das? Chaos mittelt sich nicht aus. Das Wetter bleibt auch über Hunderte von Jahren chaotisch.

Wenn wir einen laufenden Durchschnitt über die Daten bilden würden, wie es die Wettermodellierer tun, um die unerwünschten Spitzen zu verbergen, können wir eine leichten Buckel rechts sehen, und viele Buckel links. Wäre es gerechtfertigt, dass der Buckel rechts ein Beweis für den Klimawandel ist? Wirklich nicht! Man könnte nicht entscheiden, ob der Buckel rechts das Ergebnis des Chaos und der angezeigten Verschiebungen wäre, oder ob da ein grundlegender Wandel wäre, wie zunehmendes CO2.
Fassen wir zusammen: die Klimaforscher haben Modelle konstruiert auf der Grundlage ihres Verständnisses des Klimas, derzeitigen Theorien und einer Reihe von Annahmen. Sie können ihre Modelle wegen der chaotischen Natur des Wetters nicht über kurze Zeiträume testen, das geben sie zu.
Sie hofften aber, dass sie kalibrieren könnten, ihre Modelle bestätigen oder reparieren, indem sie Langzeitdaten auswerteten. Aber wir wissen jetzt, dass auch dort das Chaos herrscht. Sie wissen nicht, und sie werden niemals wissen, ob ihre Modelle zu einfach, zu komplex oder richtig sind, weil – selbst wenn sie perfekt wären – angesichts der chaotischen Natur des Wetters keine Hoffnung besteht, die Modelle an die wirkliche Welt anpassen zu können. Die kleinsten Fehler bei den Anfangsbedingungen würden völlig unterschiedliche Ergebnisse hervorbringen.
Alles, was sie ehrlich sagen können, ist: “Wir haben Modelle geschaffen, wir haben unser Bestes getan, um mit der wirklichen Welt im Einklang zu sein, aber wir können keinen Beweis für die Richtigkeit liefern. Wir nehmen zur Kenntnis, dass kleine Fehler in unseren Modellen dramatisch andere Vorhersagen liefern können, und wir wissen nicht, ob wir Fehler in unseren Modellen haben. Die aus unseren Modellen herrührenden veröffentlichten Abhängigkeiten scheinen haltbar zu sein.“

Meiner Ansicht nach dürfen regierungsamtliche Entscheider nicht auf der Grundlage dieser Modelle handeln. Es ist wahrscheinlich, dass die Modelle so viel Ähnlichkeit mit der wirklichen Welt haben wie Computerspiele.
Zu guter Letzt, es gibt eine andere Denkrichtung in der Wettervorhersage. Dort herrscht die Meinung, dass das Langzeitwetter großenteils von Veränderungen der Sonnenstrahlung bestimmt wird. Nichts in diesem Beitrag bestätigt oder verwirft diese Hypothese, weil Langzeit-Aufzeichnungen der Sonnenflecken enthüllen, dass die Sonnenaktivität ebenfalls chaotisch ist.
Dr. Andy Edmonds
Übesetzt von Helmut Jäger EIKE
Anmerkung von Antony Watts: Nur damit wir uns gleich verstehen: Chaos beim Wetter ist NICHT dasselbe wie der oben beschrieben Klimazusammenbruch – Anthony
Den Originalbeitrag finden Sie hier
Kurzbiografie
Dr. Andrew Edmonds ist Wissenschaftler und schreibt Computer Software. Er hat viele frühe Computer Software Pakete auf dem Gebiet der „Künstlichen Intelligenz“ entworfen und er war möglicherweise der Autor des ersten kommerziellen „Data Mining“ Systems. Er war Vorstandssprecher einer amerikanischen Aktiengesellschaft und bei mehreren erfolgreichen Firmen-Neugründungen tätig. Seine Doktorarbeit behandelte die Vorhersagen von Zeitreihen in chaotischen Reihen. Daraus entstand sein Produkt ChaosKit, des einzigen abgeschlossenen kommerziellen Produkts für die Analyse von Chaos in Zeitreihen. Er hat Papiere über Neuronale Netze veröffentlicht und über genetisches Programmieren von „fuzzy logic“ Systemen, „künstlicher Intelligenz“ für den Handel mit Finanzprodukten. Er war beitragender Autor von Papieren auf den Gebieten der Biotechnologie, des Marketings und des Klimas.
Seine Webseite: http://scientio.blogspot.com/2011/06/chaos-theoretic-argument-that.html